Open Access Article
Open Access ArticleCreative Commons Attribution 3.0 Unported Licence
Comparative study of CO2 insertion into pincer supported palladium alkyl and aryl complexes†
Anthony P.
Deziel
a,
Sahil
Gahlawat
 bc,
Nilay
Hazari
bc,
Nilay
Hazari
 *a,
Kathrin H.
Hopmann
*a,
Kathrin H.
Hopmann
 *b and
Brandon Q.
Mercado
a
*b and
Brandon Q.
Mercado
a
aDepartment of Chemistry, Yale University, P. O. Box 208107, New Haven, Connecticut 06520, USA. E-mail: nilay.hazari@yale.edu
bDepartment of Chemistry, UiT The Arctic University of Norway, N-9307 Tromsø, Norway. E-mail: kathrin.hopmann@uit.no
cHylleraas Center for Quantum Molecular Sciences, UiT The Arctic University of Norway, 9037 Tromsø, Norway
First published on 12th July 2023
Abstract
The insertion of CO2 into metal alkyl bonds is a crucial elementary step in transition metal-catalyzed processes for CO2 utilization. Here, we synthesize pincer-supported palladium complexes of the type (tBuPBP)Pd(alkyl) (tBuPBP = B(NCH2PtBu2)2C6H4−; alkyl = CH2CH3, CH2CH2CH3, CH2C6H5, and CH2-4-OMe-C6H4) and (tBuPBP)Pd(C6H5) and compare the rates of CO2 insertion into the palladium alkyl bonds to form metal carboxylate complexes. Although, the rate constant for CO2 insertion into (tBuPBP)Pd(CH2CH3) is more than double the rate constant we previously measured for insertion into the palladium methyl complex (tBuPBP)Pd(CH3), insertion into (tBuPBP)Pd(CH2CH2CH3) occurs approximately one order of magnitude slower than (tBuPBP)Pd(CH3). CO2 insertion into the benzyl complexes (tBuPBP)Pd(CH2C6H5) and (tBuPBP)Pd(CH2-4-OMe-C6H4) is significantly slower than any of the n-alkyl complexes, and CO2 does not insert into the palladium phenyl bond of (tBuPBP)Pd(C6H5). While (tBuPBP)Pd(CH2CH3) and (tBuPBP)Pd(CH2CH2CH3) are resistant to β-hydride elimination, we were unable to synthesize complexes with n-butyl, iso-propyl, and tert-butyl ligands due to β-hydride elimination and an unusual reductive coupling, which involves the formation of new C–B bonds. This reductive process also occurred for (tBuPBP)Pd(CH2C6H5) at elevated temperature and a related process involving the formation of a new H–B bond prevented the isolation of (tBuPBP)PdH. DFT calculations provide insight into the relative rates of CO2 insertion and indicate that steric factors are critical. Overall, this work is one of the first comparative studies of the rates of CO2 insertion into different metal alkyl bonds and provides fundamental information that may be important for the development of new catalysts for CO2 utilization.
Introduction
There is considerable interest in the use of carbon dioxide (CO2) as a carbon containing chemical feedstock due to its low cost, non-toxic nature, and abundance.1 However, only a small number of chemicals are currently industrially produced from CO2.1g This is in part because the kinetic barriers associated with bond forming processes involving CO2 are often prohibitively high. Transition metal catalysts represent a promising method to increase the range of products generated from CO2 because they can create lower energy pathways for activating and functionalizing CO2.1 To date, most transition metal catalysts for CO2 utilization have converted CO2 into other C1 products such as methane, CO, formic acid, and methanol and there are limited examples of catalysts that can form products containing C–C bonds, such as fuels, from CO2.1g As a result, the formation of products containing a C–C bond from CO2 has been identified as a high priority research area by the United States National Academies of Science.2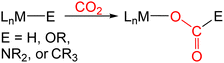 | (1) |
In many transition metal catalyzed processes for CO2 utilization, the insertion of CO2 into a metal–E σ-bond (for example E = H, OR, NR2, or CR3) is a crucial elementary step (eqn (1)).3 This is especially the case for late transition metals, where the relative weakness of the M–O bonds makes subsequent cleavage of the M–O bond more facile.3 The insertion of CO2 into a metal alkyl bond is a particularly important reaction because it can ultimately result in the generation of products containing a C–C bond. For example, Group 10 catalysts have been used for the formation of carboxylic acids through the carboxylation of a variety of alkyl halides and pseudo halides.4 In these reactions, C–C bonds are proposed to form between CO2 and the alkyl electrophile via the insertion of CO2 into a metal alkyl bond. However, at this stage there is limited experimental information on the pathways for CO2 insertion into metal alkyl bonds, as most studies have primarily involved isolated examples with a single metal complex,5–14 and thus, it is unclear how changing the nature of the alkyl group or ancillary ligand impacts the reaction. Further, kinetic studies are relatively rare,6,8a,b,9d,11c,13g,14b which means that computational results cannot be benchmarked against experimental data.
Previous kinetic studies exploring CO2 insertion into well-defined metal alkyl complexes have almost exclusively focused on metal methyl species.6,8a,b,9d,11c,13g,14b This is because of the stability of metal methyl complexes, which in contrast to longer chain alkyl containing complexes, such as metal ethyl complexes, do not undergo β-hydride elimination. A major limitation in studying CO2 insertion into metal methyl bonds, and in particular the types of Group 10 metal alkyl complexes that are relevant to catalysis, is the paucity of systems that are stable and react under mild reaction conditions. Most systems require high temperatures and do not give quantitative yields of products, which prevents kinetic studies. We recently described the insertion of CO2 into palladium and nickel methyl complexes supported by RPBP (RPBP = B(NCH2PR2)2C6H4−; R = Cy or tBu) pincer ligands (Fig. 1a).13g The strong trans-influence of the boryl donor in the pincer ligand destabilizes the methyl group and as a consequence these complexes insert CO2 at room temperature, which enabled us to perform detailed kinetic studies on CO2 insertion into a metal methyl bond.
We hypothesized that the RPBP framework may stabilize palladium complexes with other alkyl ligands, as pincer ligands are known to inhibit β-hydride elimination from square planar palladium(II) complexes.15 Further, given that the RPBP ligand can facilitate CO2 insertion reactions under mild conditions,13g we postulated that the synthesis of a family of RPBP supported palladium alkyl complexes would enable us to perform a rare experimental comparison of the rates of CO2 insertion as the alkyl ligand is varied. In this work, we describe the synthesis of a series of tBuPBP supported palladium complexes with ethyl, n-propyl, benzyl, and phenyl ligands. Although (tBuPBP)Pd(CH2CH3) (1-Et), (tBuPBP)Pd(CH2CH2CH3) (1-nPr), (tBuPBP)PdCH2C6H5 (1-Bn), and (tBuPBP)PdCH2-4-OMe-C6H4 (1-OMeBn), are sufficiently stable in solution to be isolated, attempts to synthesize complexes with n-butyl, iso-propyl, and tert-butyl ligands were unsuccessful due to rapid decomposition via either β-hydride elimination or an unusual reductive pathway that generates a new C–B bond. A similar reductive process to form a new H–B bond occurs in the putative hydride complex (tBuPBP)PdH. The stability of 1-Et, 1-nPr, 1-Bn, and 1-OMeBn allowed us to determine the rates of CO2 insertion into the palladium alkyl bonds. The rate constant for CO2 insertion into 1-Et is over double the rate constant previously measured for CO2 insertion into (tBuPBP)Pd(CH3) (1-Me),13g while insertion into 1-nPr occurs at approximately one-tenth the rate of 1-Me. This is a remarkable difference given the relatively minor changes in the alkyl ligand. The insertion of CO2 into the benzyl complexes, 1-Bn and 1-OMeBn, is significantly slower than any of n-alkyl complexes and CO2 does not insert into the palladium phenyl bond of the related complex (tBuPBP)Pd(C6H5) (1-Ph). DFT calculations enabled the rationalization of the relative rates of CO2 insertion and suggest that steric factors are the predominant reason for the differences in the rates of insertion between 1-Me, 1-Et, and 1-nPr. Overall, the fundamental insight on CO2 insertion provided in this work will likely assist in the development of improved and new catalysts for CO2 utilization.
Results and discussion
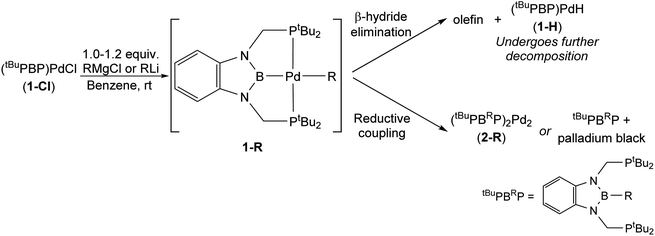
Synthesis of tBuPBP supported palladium alkyl and aryl complexes
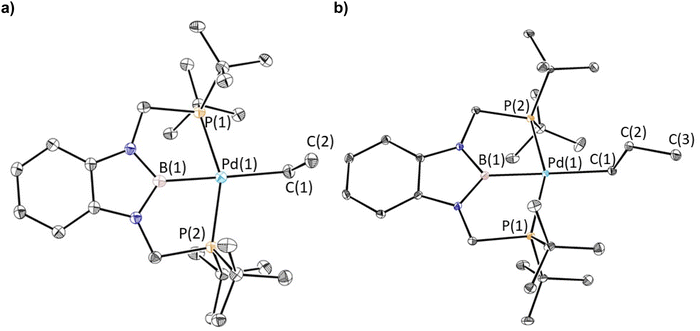
Previous studies have demonstrated that reactions of complexes of the form (RPBP)PdCl (R = iPr or tBu) with MeLi generate stable palladium methyl complexes.13g In an analogous fashion, treatment of (tBuPBP)PdCl (1-Cl) with EtLi or nPrMgCl in benzene results in the formation of (tBuPBP)Pd(CH2CH3) (1-Et) and (tBuPBP)Pd(CH2CH2CH3) (1-nPr), which were isolated in yields of 76 and 59%, respectively, after recrystallization (eqn (2)).161-Et is a rare example of an isolated pincer supported palladium ethyl complex,15,17 while 1-nPr is to the best of our knowledge only the second example of an isolated palladium propyl complex.181-Et and 1-nPr are indefinitely stable at room temperature in benzene and β-hydride elimination to generate ethylene or propene and a putative palladium hydride (vide infra) only occurs at temperatures greater than 60 °C. Recrystallization from pentane generated crystals of 1-Et and 1-nPr suitable for X-ray diffraction (Fig. 2a and b). In both cases, the geometry around Pd is distorted square planar and the P(1)–Pd(1)–P(2) bond angles are 153.99(6) and 154.23(2)° in 1-Et and 1-nPr, respectively, indicating that the phosphorus donors of the pincer ligand deviate significantly from linearity. The Pd–B bond distances are 2.029(7) Å in 1-Et and 2.020(3) Å in 1-nPr, which are significantly longer than the Pd–B bond distance in (tBuPBP)PdCl (Pd–B is 1.972(4) Å in 1-Cl).19 This is consistent with the ethyl or propyl ligand exerting a stronger trans-influence than a chloride ligand. Although, crystallographically characterized examples of palladium ethyl complexes are rare,15,17,20 the Pd–C bond distance in 1-Et is longer than those typically reported (Pd(1)–C(1) is 2.226(6) Å in 1-Et) and is most comparable to a PSiP-supported palladium ethyl complex, which also contains a strong trans-influence donor (silyl) opposite the palladium.15 In 1-nPr the Pd(1)–C(1) is 2.209(2) Å, which is within error of the Pd–C bond distance in 1-Et. The carbon atom bound to palladium (C(1)) is distorted from tetrahedral in both 1-Et and 1-nPr and Pd(1)–C(1)–C(2) angles of 115.8(4)° and 114.49(15)°, respectively, are observed. Analysis of the literature reveals that this is a general trend for Group 10 alkyl complexes.21 Overall, the geometrical parameters around palladium are similar in 1-Me,13g1-Et, and 1-nPr, with the exception that the Pd–C bond distance in 1-Me is slightly shorter than in 1-Et or 1-nPr (Pd(1)–C(1) is 2.185(4) Å in 1-Me), which is qualitatively consistent with DFT calculations (vide infra). This suggests that as expected the change from methyl to ethyl to n-propyl has little impact on the geometry around palladium. | (2) |
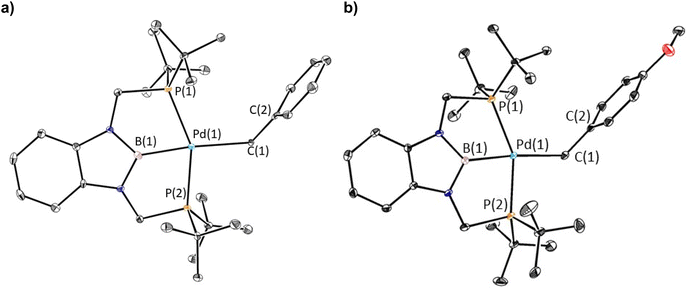
The reaction of 1-Cl with (CH2C6H5)MgCl or (4-OMe-CH2C6H4)MgCl resulted in the isolation of 1-Bn or 1-OMeBn, which are rare examples of pincer supported benzyl complexes,22 in yields of 45% or 55%, respectively (eqn (2)). In both cases, it is important to remove the MgCl2 by-product from the Grignard reagent or the benzyl complexes slowly convert back to 1-Cl in solution. In fact, the relatively low yields of 1-Bn and 1-OMeBn are in part due to the successive recrystallizations that are required to ensure MgCl2 impurities are not present. Both 1-Bn and 1-OMeBn were characterized by X-ray crystallography (Fig. 3a and b). The solid-state structures indicate that the geometry around palladium is distorted square planar and the geometrical parameters associated with the binding of the tBuPBP ligand in 1-Bn and 1-OMeBn are analogous to those in 1-Et and 1-nPr. The long Pd–B bond distances (2.032(4) Å in 1-Bn and 2.025(3) Å in 1-OMeBn) are consistent with the high trans-influence of the benzyl ligand. The benzyl ligand binds in an η1-fashion with Pd–C bond distances of 2.260(3) Å in 1-Bn and 2.249(3) Å in 1-OMeBn, which are longer than almost all other palladium complexes that feature an η1-benzyl ligand.22 Further, the carbon atom bound to palladium (C(1)) is significantly distorted from tetrahedral, with Pd(1)–C(1)–C(2) angles of 127.7(2)° and 123.44(18)° observed for 1-Bn and 1-OMeBn, respectively. Although this deviation from tetrahedral is typical for Group 10 benzyl complexes,21a,c,23 these are some of the largest angles reported perhaps due to the steric congestion around the palladium.
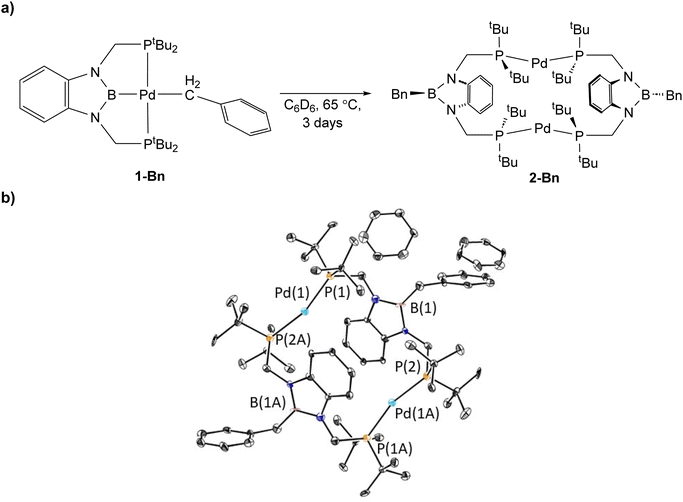
1-Bn is stable when left in C6D6 at room temperature, but complete decomposition is observed when it is heated for 3 days at 65 °C, with the major product being a new dimeric complex, (tBuPBBnP)2Pd2 (2-Bn, Bn = benzyl) (Fig. 4a). Based on NMR spectroscopy we propose that 1-OMeBn decomposes via a similar pathway (see ESI†). 2-Bn was characterized by X-ray crystallography (Fig. 4b). In 2-Bn, two new C–B bonds have formed presumably due to a reductive coupling reaction between the benzyl ligands and the boron atom of the tBuPBP ligands. This causes a reduction in the palladium center from palladium(II) in 1-Bn to palladium(0) in 2-Bn. The boron atom of the pincer ligand no longer coordinates to the palladium center and the two phosphorus donors of the new bidentate tBuPBBnP ligands do not coordinate to the same palladium center but instead coordinate to two different palladium atoms. The pathway for this ligand rearrangement is unclear. Consistent with the reduction in oxidation state, the geometry around the palladium centers in 2-Bn are distorted linear. We have previously observed a similar decomposition pathway for (tBuPBP)Ni(CH3), which results in the formation of a nickel(0) dinitrogen complex,13g but this is the first time the reductive decomposition pathway has been observed for palladium. We hypothesize that reductive coupling occurs more readily in 1-Bn compared to 1-Et or 1-Me (where it is not observed to any significant extent spectroscopically) because there is greater steric congestion in the case of the palladium benzyl complex. This is also in agreement with the observation of reductive coupling in the case of (tBuPBP)Ni(CH3) but not 1-Me, as the smaller nickel center presumably results in a more congested metal center.13g Our results suggest that C–B bond formation is potentially a general decomposition pathway for RPBP supported complexes, rather than a curiosity that is only relevant to a single complex.
Although the reaction between 1-Cl and EtLi results in clean formation of 1-Et, the corresponding reactions between 1-Cl and nBuLi, iPrLi, and tBuMgCl did not result in the generation of isolable palladium alkyl complexes and instead various decomposition products are observed (Table 1).24,25 In the case of tBuMgCl, the initial metathesis reaction is slow and even after three days at room temperature some 1-Cl is still present, along with three new peaks in the 31P NMR spectra. Although we do not observe (tBuPBP)Pd(tBu) (1-tBu) directly, the peaks observed are consistent with the formation and decomposition of (tBuPBP)PdH (1-H) (vide infra and see ESI†). 1-H presumably forms via β-hydride elimination from 1-tBu and in agreement with this proposal iso-butene is observed by 1H NMR spectroscopy. This suggests that 1-tBu is unstable at room temperature and performing the reaction at low temperature is not possible due to the slow rate of the initial metathesis reaction.
| Entry | Reagent | 1-R isolable | Stability of 1-R at rt | Decomposition pathway |
|---|---|---|---|---|
| a See ref. 13g. b 2-OMeBn was characterized by analogy to 2-Bn and was not isolated. | ||||
| 1 | MeLi | Yesa | Stablea | Slow reductive coupling (at 65 °C) to give 2-Me (see ESI) |
| 2 | EtLi | Yes | Stable | β-Hydride elimination (at 65 °C) |
| 3 | nPrMgCl | Yes | Stable | β-Hydride elimination (at 60 °C) |
| 4 | n BuLi | No | Unstable | Reductive coupling to give tBuPBnBuP and palladium black |
| 5 | iPrLi | No | Not observed | Reductive coupling to give tBuPBiPrP and palladium black |
| 6 | t BuMgCl | No | Not observed | β-Hydride elimination |
| 7 | BenzylMgCl | Yes | Stable | Reductive coupling (at 65 °C) to give 2-Bn |
| 8 | 4-OMe-BenzylMgCl | Yes | Stable | Reductive coupling (at 65 °C) to give 2-OMeBnb |
The reaction between 1-Cl and iPrLi is rapid and after 10 minutes at room temperature there is no 1-Cl left in the reaction mixture. At this time, one major peak is observed in the 31P NMR spectrum at 15.6 ppm, which based on its downfield chemical shift is unlikely to be (tBuPBP)Pd(iPr) (1-iPr). Typically, palladium(II) complexes containing a tBuPBP ligand have chemical shifts between 60–120 ppm, whereas the chemical shift of the free tBuPBHP ligand is 17.0 ppm.26 There is also no evidence for the generation of products associated with β-hydride elimination from 1-iPr, as no signals corresponding to (tBuPBP)PdH (1-H) (or related decomposition products, vide infra) are observed in the 1H or 31P NMR spectra, and there are no resonances associated with propene in the 1H NMR spectrum. Instead, we propose that the major species in the 31P NMR spectrum is the organic compound tBuPBiPrP, which was confirmed by mass spectrometry (see ESI†). We propose that tBuPBiPrP forms from the rapid reductive decomposition of 1-iPr, which is generated but not observed in the reaction. The reductive process that 1-iPr is postulated to undergo is akin to what we observed in the decomposition of 1-Bn (vide supra) in that a new C–B bond is formed. However, in the case of 1-iPr, we only see the free organic product tBuPBiPrP and there is no evidence that tBuPBiPrP coordinates to palladium to form a dimer analogous to 2-Bn. Instead, palladium black precipitates out of solution. At this stage, it is unclear why tBuPBiPrP does not coordinate to palladium in a similar fashion to tBuPBBnP, and it is possible although unlikely that tBuPBiPrP is formed through a pathway that does not even involve the formation of 1-iPr.
The reaction between 1-Cl and nBuLi proceeds in an analogous fashion to the reaction between 1-Cl and iPrLi and ultimately gives palladium black and tBuPBnBuP. However, the proposed intermediate alkyl complex, (tBuPBP)Pd(nBu) (1-nBu), is more stable and at −35 °C the reaction mixture contained primarily 1-nBu (∼97%), with only a small amount of the organic decomposition product tBuPBnBuP (∼3%) (see ESI†). Heating the sample to room temperature resulted in an increase in the amount of decomposition product and it was not possible to isolate 1-nBu. In contrast, as described above, it is possible to cleanly isolate 1-nPr from the reaction between 1-Cl and nPrMgCl and decomposition of 1-nPr only occurs at 60 °C (eqn (2)). In this case, propene is observed in the 1H NMR spectra along with products consistent with the formation and decomposition of 1-H (vide infra), suggesting that decomposition primarily occurs via β-hydride elimination. Similar decomposition via β-hydride elimination is observed at 65 °C for 1-Et, with ethylene observed as a by-product. We also examined the stability of previously reported 1-Me13g and demonstrated that at 65 °C it undergoes very slow C–B reductive coupling to form (tBuPBMeP)2Pd2 (2-Me) (see ESI†). Our results indicate that the stability of tBuPBP ligated Pd alkyl complexes is related to the steric bulk of the alkyl group, so the order of stability is 1-tBu ∼ 1-iPr < 1-nBu < 1-nPr ∼ 1-Et < 1-Me. Interestingly, the least and most sterically bulky complexes decompose via β-hydride elimination, while those with intermediate steric properties decompose through reductive coupling. 1-Me is an exception as it lacks any β-hydrogens and therefore despite its small size decomposes via reductive coupling.
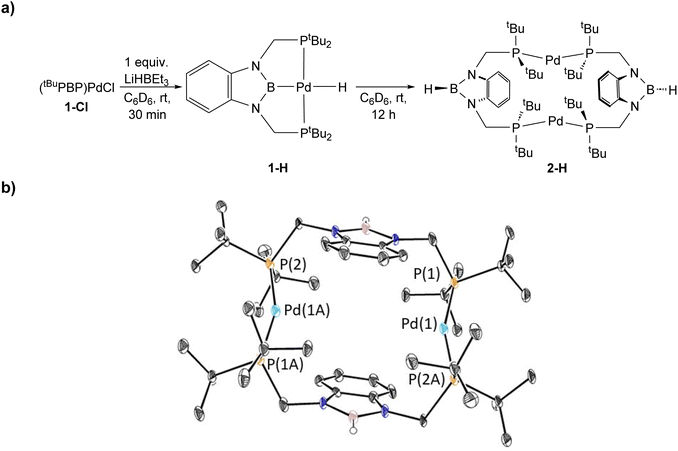
To verify our hypothesis that the rapid decomposition of 1-tBu results in the formation of the palladium hydride complex 1-H, we attempted to independently prepare 1-H. Reaction of 1-Cl with 1 equivalent of LiHBEt3 in C6D6 generated two major products in an approximately 55![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 45 ratio by 1H and 31P NMR spectroscopy (Fig. 5). We propose that one of these is 1-H because the 31P NMR chemical shift (115 ppm, 55%) is very close to the shift for the corresponding (tBuPBP)PtH complex (114.5 ppm).27 The other resonance in the 31P NMR spectra is observed at 96.4 ppm, but even though it is present in both the decomposition of 1-tBu, 1-Et, and 1-nPr, as well as the attempted direct synthesis of 1-H, we are unsure of the identity of the complex giving rise to this signal. Further, although the complex giving rise to the signal at 96.4 ppm is relatively stable over 12 hours, the complex giving rise to the signal at 115 ppm decomposes at room temperature in C6D6 to give a dimeric palladium(0) complex, 2-H, in which the hydride has reductively coupled with the boron atom of the tBuPBP ligand to give a new H–B bond (Fig. 5). This is an analogous process to the decomposition of 1-Bn, except an H–B bond is formed instead of a C–B bond. 2-H was characterized by single crystal X-ray diffraction (Fig. 5b) and contains two distorted linear palladium(0) centers. The phosphorous atoms of the pincer ligands have rearranged so they bind to two different palladium centers rather than a single palladium center. In this case, it is presumably not steric factors that drive the decomposition of the palladium hydride but the formation of a strong H–B bond. Given the large number of stable pincer-supported palladium hydrides,28 we hypothesize that 1-H is unstable because of the trans-influence of the boryl ligand, which significantly destabilizes the hydride relative to other species which have weaker trans-influence ligands opposite the hydride.
45 ratio by 1H and 31P NMR spectroscopy (Fig. 5). We propose that one of these is 1-H because the 31P NMR chemical shift (115 ppm, 55%) is very close to the shift for the corresponding (tBuPBP)PtH complex (114.5 ppm).27 The other resonance in the 31P NMR spectra is observed at 96.4 ppm, but even though it is present in both the decomposition of 1-tBu, 1-Et, and 1-nPr, as well as the attempted direct synthesis of 1-H, we are unsure of the identity of the complex giving rise to this signal. Further, although the complex giving rise to the signal at 96.4 ppm is relatively stable over 12 hours, the complex giving rise to the signal at 115 ppm decomposes at room temperature in C6D6 to give a dimeric palladium(0) complex, 2-H, in which the hydride has reductively coupled with the boron atom of the tBuPBP ligand to give a new H–B bond (Fig. 5). This is an analogous process to the decomposition of 1-Bn, except an H–B bond is formed instead of a C–B bond. 2-H was characterized by single crystal X-ray diffraction (Fig. 5b) and contains two distorted linear palladium(0) centers. The phosphorous atoms of the pincer ligands have rearranged so they bind to two different palladium centers rather than a single palladium center. In this case, it is presumably not steric factors that drive the decomposition of the palladium hydride but the formation of a strong H–B bond. Given the large number of stable pincer-supported palladium hydrides,28 we hypothesize that 1-H is unstable because of the trans-influence of the boryl ligand, which significantly destabilizes the hydride relative to other species which have weaker trans-influence ligands opposite the hydride.
To compare the reactivity of tBuPBP supported palladium alkyl complexes with a tBuPBP supported palladium aryl species, we prepared (tBuPBP)Pd(C6H5) (1-Ph) (eqn (2)). Although, the synthesis of 1-Ph followed the same route as the palladium alkyl species described above,29 the reaction of 1-Cl with PhMgBr was significantly slower than the corresponding reactions with alkyl lithium or Grignard reagents. Specifically, the reaction with PhMgBr took two days to reach completion at room temperature, whereas the reactions with alkyl lithium or Grignard reagents were typically complete in less than one hour at room temperature (except for tBuMgCl). This is likely related to the lower nucleophilicity of aryl Grignard reagents compared with alkyl Grignard reagents. After recrystallization to remove Mg salt impurities, we were able to isolate 1-Ph in 66% yield. 1-Ph was characterized by X-ray crystallography (see ESI†). The Pd–C bond distance in is 2.162(3) Å, which is significantly shorter than the Pd–C bond length in all of our palladium alkyl complexes. This is likely due to the fact that the carbon atom bound to palladium in 1-Ph is sp2-hybridized and is consistent with the trend observed for PCP-supported pincer complexes.14
Reactivity of tBuPBP supported palladium alkyl and aryl complexes with CO2
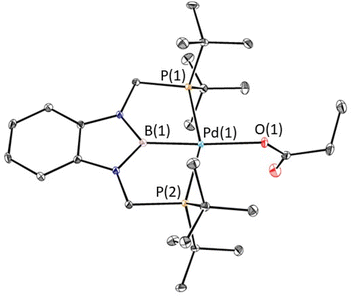
The reaction of 1-Et with 1 atm of CO2 in C6D6 at room temperature quantitively generated the palladium carboxylate complex (tBuPBP)Pd{OC(O)CH2CH3} (3-Et) in approximately 2 hours (Fig. 6). This is the fastest rate of CO2 insertion observed for a pincer supported palladium alkyl species. 3-Et was isolated and characterized using single crystal X-ray diffraction (Fig. 7). The solid-state structure confirms κ1-binding of the carboxylate. The Pd–O bond distance is 2.1803(14) Å, which is relatively long for a palladium(II) carboxylate complex.13g,14a,30 This suggests that it will be easier to cleave the Pd–O bond in 3-Et compared to related palladium carboxylate complexes, which have been generated via CO2 insertion reactions.6,14a The Pd–B bond distance is significantly shorter in 3-Et (1.973(2) Å) compared with 1-Et (2.029(7) Å), which is consistent with the carboxylate ligand exerting a significantly weaker trans-influence than the ethyl ligand.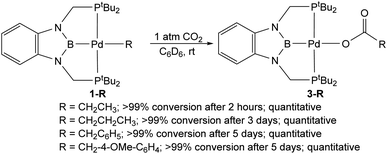 | ||
| Fig. 6 Relative rates of CO2 insertion into tBuPBP supported palladium alkyl complexes to form palladium carboxylate complexes. | ||
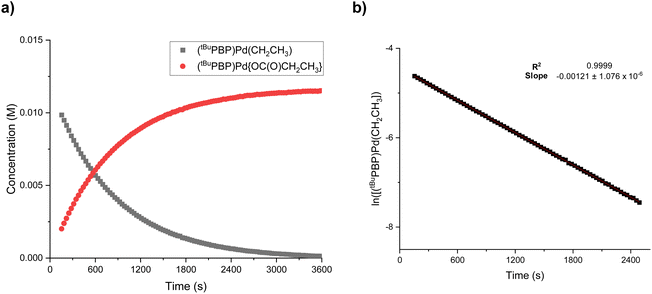
The rapid insertion of CO2 into 1-Et at room temperature enabled us to use NMR spectroscopy to measure the kinetics of the reaction. We performed kinetics experiments under pseudo-first order conditions with an excess of CO2 and measured both the disappearance of 1-Et and the appearance of 3-Et (Fig. 8a). The reaction is first order in both 1-Et and [CO2], so the overall rate law is k1[(tBuPBP)Pd(CH2CH3)][CO2] (Fig. 8b and ESI†). We were able to obtain values of k1 at different temperatures by dividing the kobs values obtained from a plot of ln([(tBuPBP)Pd(CH2CH3)]) versus time by the concentration of CO2 (Table 2 and ESI†). The most striking feature of our k1 values is that at 40 °C, the rate constant for CO2 insertion into 1-Et is more than double the rate constant for insertion into 1-Me that we measured previously.13g In the only other comparative study of the rates of CO2 insertion into metal methyl and ethyl species, Darensbourg and co-workers observed that CO2 insertion into [RW(CO)5]− (R = CH3 or CH2CH3) is 1.5 times faster for methyl than for ethyl, the opposite trend to our system.8b At this stage, given the paucity of other comparative studies on the rates of CO2 insertion into different metal alkyls, it is unclear if either result is an outlier or the nature of the underlying factors that cause the variation in trends.
| Entry | Complex | Temperature (°C) | Solvent | k 1 (M−1 s−1 × 10−2)a |
|---|---|---|---|---|
| a These values are the average of two trials and the errors are ±10%. | ||||
| 1 | 1-Et | 25 | C6D6 | 1.2 |
| 2 | 1-Et | 30 | C6D6 | 2.1 |
| 3 | 1-Et | 35 | C6D6 | 2.9 |
| 4 | 1-Et | 40 | C6D6 | 3.4 |
| 5 | 1-Et | 45 | C6D6 | 4.7 |
| 6 | 1-Me | 40 | C6D6 | 1.3 |
| 7 | 1-Me | 45 | C6D6 | 2.3 |
| 8 | 1-Bn | 30 | Pyridine-d5 | 0.48 |
| 9 | 1-OMeBn | 30 | Pyridine-d5 | 0.43 |
Using the values of k1 at different temperatures we determined the activation parameters for CO2 insertion into 1-Et through Eyring analysis. The enthalpy of activation, ΔH‡, is 11.3 ± 1.1 kcal mol−1, the entropy of activation, ΔS‡, is −29.0 ± 2.9 cal mol−1 K−1, and ΔG‡298 is 20.0 ± 2.0 kcal mol−1 (see ESI†). All of these values are within error to those previously measured for 1-Me,13g suggesting that the reactions proceed via similar pathways. The enthalpy for CO2 insertion into 1-Et is lower than that observed for insertion into palladium methyl complexes with pincer ligands that contain a lower trans-influence donor in the central position. For example, ΔH‡ for CO2 insertion into (tBuPCP)Pd(CH3) (tBuPCP = 2,6-C6H3(CH2PtBu2)2) is 17.4 ± 1.7 kcal mol−1.14b This is consistent with the tBuPBP ligand destabilizing 1-Et by weakening the Pd–C bond of the palladium ethyl ligand. The negative entropy of activation is similar to those observed in other systems for CO2 insertion13g,14b and is in agreement with a rate-limiting transition state in which two molecules are combining to form one compound in the transition state.
The reaction of 1-nPr with 1 atm of CO2 in C6D6 at room temperature also cleanly generated the palladium carboxylate complex (tBuPBP)Pd{OC(O)CH2CH2CH3} (3-nPr) (Fig. 6). Surprisingly, CO2 insertion into 1-nPr is significantly slower than the corresponding insertion reactions with 1-Me and 1-Et. In the case of 1-nPr, the reaction required 3 days to reach completion at room temperature.31 This slow rate of insertion precluded the measurement of a rate constant using our NMR method, but based on the reaction half-life of approximately 11 hours we estimate that insertion into 1-nPr occurs approximately one order of magnitude slower than the rate of insertion into 1-Me. Further, we were unable to heat the reaction of 1-nPr with CO2 to sufficiently speed up the reaction, as this resulted in decomposition of 1-nPr. Overall, our results show that the simple change in alkyl group from 1-Me to 1-Et to 1-iPr results in significant and non-intuitive changes in the rates of CO2 insertion. This is potentially important in catalysis as it implies the rate of CO2 insertion into palladium alkyl complexes (and potentially other metal alkyl complexes) will be heavily substrate dependent.
The reactions of the benzyl complexes 1-Bn and 1-OMeBn with 1 atm of CO2 at room temperature formed the carboxylate complexes (tBuPBP)Pd{OC(O)CH2C6H5} (3-Bn) and (tBuPBP)Pd{OC(O)CH2-4-OMe-C6H4} (3-OMeBn), respectively (Fig. 6). These reactions were significantly slower than the corresponding insertion reactions with 1-Me, 1-Et, or even 1-nPr. For example, in C6D6 at room temperature the reactions took approximately 5 days to reach completion. The slower rate of insertion into palladium benzyl complexes compared with palladium n-alkyl complexes is unsurprising as the benzylic carbon bound to palladium is expected to be a worse nucleophile due to the electron-withdrawing nature of the aromatic group, which makes it less energetically favorable to attack electrophilic CO2. In order to measure the kinetics of insertion into 1-Bn and 1-OMeBn we needed to increase the rate of the reaction. Unfortunately, it is not possible to raise the temperature to promote CO2 insertion into 1-Bn in C6D6 as this leads to decomposition to form the palladium(0) complex, 2-Bn, as well as the CO2 inserted product. However, we have previously demonstrated that the rates of CO2 insertion reactions can be increased by performing the reaction in solvents with a higher Dimroth–Reichardt ET(30) parameter,13g,32 which is an empirical measure of the polarity of a solvent.33,34 When CO2 insertion reactions were performed in pyridine-d5, the reactions with 1-Bn and 1-OMeBn were complete in approximately 5 hours at room temperature, with no evidence for the formation of palladium(0) complexes. This again highlights the dramatic effect of solvent on CO2 insertion reactions.13g,32,35 At 30 °C, the rate constants for CO2 insertion into 1-Bn and 1-OMeBn in pyridine-d5 were 0.0048 ± 0.0005 and 0.0043 ± 0.0004 M−1 s−1, respectively. The fact that these values are the same within error indicates that the substitution on the phenyl ring surprisingly does not significantly affect the nucleophilicity of the carbon bound to palladium and means that in the catalytic carboxylation of benzylic substrates36 the electronic effect of the substituents on the rate of CO2 insertion is likely minimal. Unfortunately, we are unable to measure the rate constants for CO2 insertion into 1-Me or 1-Et in pyridine-d5 because the reaction occurs too fast to obtain an accurate rate constant using NMR spectroscopy. However, we estimate a minimum rate constant of 0.2 M−1 s−1, which is significantly faster than for the benzyl compounds.
In contrast to our results with palladium alkyl complexes, no reaction was observed when 1-Ph was treated with 1 atm of CO2, even after prolonged heating at elevated temperature. Although at this stage it is unclear whether kinetic or thermodynamic factors are responsible for the lack of reactivity, our result is consistent with observations for other pincer supported Group 10 phenyl complexes, which also do not react with CO2.13b,e Hence, although the PBP ligand promotes CO2 insertion into palladium alkyl complexes, it does not facilitate insertion reactions into palladium aryl complexes.
Computational studies of CO2 insertion into palladium alkyl and aryl complexes
We performed DFT calculations (PBE0-D3BJ, IEFPCM) to further understand the mechanism of CO2 insertion into 1-Me, 1-Et, 1-nPr, 1-Bn, and 1-OMeBn. Previously, we have demonstrated that CO2 insertion into 1-Me follows an SE2 (or outersphere) pathway (Fig. 9a),13g in which the first and rate-limiting step is nucleophilic attack of the carbon atom of the palladium methyl on the electrophilic carbon atom of CO2 to form the C–C bond. Notably, there is no interaction between CO2 and the palladium center at the transition state. The second step in CO2 insertion into 1-Mevia an SE2 pathway has a significantly lower barrier and involves the rearrangement of an carboxylate-palladium ion pair, bound through a C–H σ-bond, to the neutral Pd–O containing product.13g An alternative pathway involving 1,2-insertion (innersphere, Fig. 9b) in which both the Pd–O and C–C bonds are formed at the same transition state was calculated to be energetically unfavorable for 1-Me.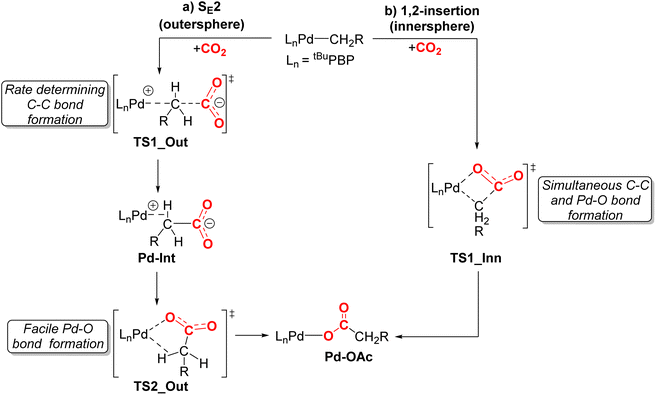 | ||
| Fig. 9 Two plausible mechanisms for CO2 insertion into pincer-supported palladium alkyl complexes: (a) SE2 (outersphere) and (b) 1,2-insertion (innersphere). For 1-Me we previously demonstrated that the SE2 pathway is lower energy and the initial nucleophilic attack of the carbon atom of the methyl group on CO2 is rate-determining.13g | ||
Here, we calculated that for CO2 insertion into 1-Et, the barrier for the first step in the SE2 pathway is 17.7 kcal mol−1 at 298 K (Fig. 10, Table 3).37 This is in good agreement with the experimentally determined barrier of 20.0 ± 2.0 kcal mol−1 (vide supra). The barrier for the innersphere 1,2-insertion pathway is calculated to be 26.0 kcal mol−1, unambiguously indicating that the SE2 pathway is preferred. A surprising feature of 1-Et is that it does not undergo facile β-hydride elimination. We calculated that the barrier for β-hydride elimination is relatively high (32.3 kcal mol−1), consistent with the stability of the complex towards β-hydride elimination. β-Hydride elimination is presumably disfavored because of the rigidity of the pincer ligand, which makes it energetically difficult for the complex to distort to form the syn co-planar arrangement of the palladium, Cα, Cβ, and H required for β-hydride elimination.
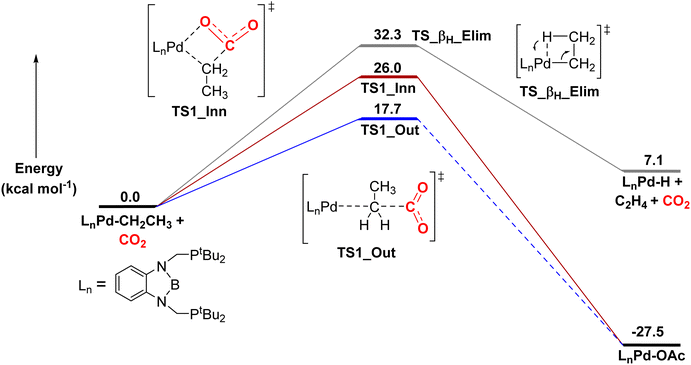 | ||
| Fig. 10 Relative free energies of CO2 insertion into 1-Etvia an SE2 (outersphere) and 1,2-addition (innersphere) pathway, as well as the energy for β-hydride elimination. In the SE2 pathway, we were unable to find the intermediate and barrier for the second rearrangement step to form the palladium carboxylate product, as the rearrangement occurs spontaneously during geometry optimization. However, this process has previously been demonstrated to be low energy in related systems.13g | ||
| Complex | ΔG‡ (kcal mol−1) |
|---|---|
| a The lowest energy pathway for CO2 insertion is the 1,2-insertion (or innersphere) mechanism rather than the SE2 (or outersphere) mechanism. | |
| (tBuPBP)Pd(CH3) (1-Me) | 19.4 |
| (tBuPBP)Pd(CH2CH3) (1-Et) | 17.7 |
| (tBuPBP)Pd(CH2CH2CH3) (1-nPr) | 21.8 |
| (tBuPBP)Pd{CH(CH3)2} (1-iPr) | 28.2 |
| (tBuPBP)Pd(CH2C6H5) (1-Bn) | 20.3 |
| (tBuPBP)Pd(CH2-4-OMeC6H4) (1-OMeBn) | 20.5 |
| (tBuPBP)Pd(CH2-4-CF3C6H4) (1-CF3Bn) | 20.6 |
| (tBuPBP)Pd(C6H5) (1-Ph) | 34.6a |
| (iPrPBP)Pd(CH3) | 16.8a |
| (iPrPBP)Pd(CH2CH3) | 18.7 |
| (iPrPBP)Pd(CH2CH2CH3) | 20.3 |
| (MePBP)Pd(CH3) | 17.5a |
| (MePBP)Pd(CH2CH3) | 17.3a |
| (MePBP)Pd(CH2CH2CH3) | 17.5a |
DFT calculations predict that the barriers for CO2 insertion into 1-Me and 1-nPr are 19.4 kcal mol−1 and 21.8 kcal mol−1(Table 3), respectively, which means that the calculations are in line with the experimental trends in rate (1-Et > 1-Me > 1-nPr).38 The rate-determining transition states for CO2 insertion into 1-Me, 1-Et, and 1-nPr are analogous (the first step in the SE2 mechanism), so the differences in rate are not related to a change in mechanism. Instead, we propose that the difference in rates is due primarily to steric factors, which affect the relative stability of both the reactant complexes and the transition states. 1-Et and 1-nPr are likely slightly destabilized relative to 1-Me because of steric interactions between the ethyl or propyl ligand and the tert-butyl substituents of the tBuPBP ligand. This is reflected by the increased thermodynamic favorability of CO2 insertion into 1-Et and 1-nPr compared to 1-Me (ΔG° = −27.5 and −26.2 kcal mol−1, respectively, versus −22.9 kcal mol−1). Presumably, in the carboxylate complexes, the steric pressure is relieved because of the absence of hydrogens on the oxygen bound to palladium.
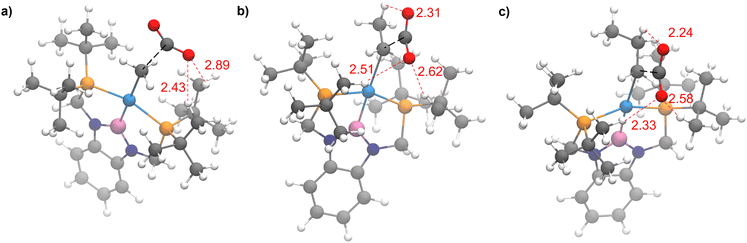
The steric properties of 1-Me, 1-Et, and 1-nPr were quantitatively evaluated by calculating the percent buried volume (%VBur) of these complexes based on their crystal structures using the Salerno molecular buried volume program (SambVca 2.1) (Fig. 11).39 Although there is only a small difference in %VBur between the three complexes (86.9% for 1-Me, 87.7% for 1-Et, and 88.2% for 1-nPr) the absolute magnitude of these numbers indicates the high degree of steric crowding around the palladium centers and suggests that small changes could have a significant impact on the rate of CO2 insertion. Our proposal is that 1-Et is sufficiently sterically crowded to destabilize the ethyl ligand, but still open enough for CO2 to easily approach the ethyl group. This increases the rate of insertion in comparison to 1-Me. In contrast, even though 1-nPr is sufficiently sterically crowded to destabilize the n-propyl ligand, the complex is so congested that it is unfavorable for CO2 to approach, which increases the barrier for insertion. Consistent with this proposal, the computed barrier for CO2 insertion into the even more sterically congested (tBuPBP)Pd{CH(CH3)2} (1-iPr) increases to 28.2 kcal mol−1 (Table 3). Finally, the trajectory of electrophilic attack of CO2 is quite different for 1-Me compared to 1-Et and 1-nPr. In 1-Me the CO2 is nearly orthogonal to the palladium methyl bond, whereas in 1-Et and 1-nPr is it essentially co-planar (Fig. 12). In 1-Et and 1-Pr this geometry leads to close contacts between three C–H bonds and the incipient carboxylate group, which may help stabilize the emerging charge on the carboxylate group. We were unable to locate a similar TS geometry for insertion into 1-Me, and in the calculated TS there are only interactions between two C–H bonds and the incipient carboxylate group. In the case of 1-Pr, destabilization due to steric strain is likely a larger force than stabilization due to an extra non-covalent interaction and therefore the overall barrier is higher.
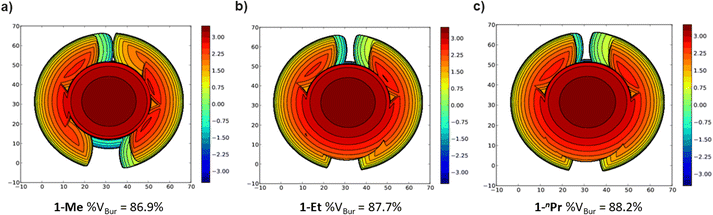 | ||
| Fig. 11 Topographic steric maps of (a) 1-Me, (b) 1-Et, and (c) 1-nPr as viewed down the C–Pd bond towards the plane defined by P–Pd–P.39 | ||
To further probe the role of steric factors on the rates of CO2 insertion, we performed calculations on the smaller model complexes (RPBP)Pd(alkyl) (R = Me or iPr; alkyl = CH3, CH2CH3, or CH2CH2CH3). Interestingly, in the case of MePBP, DFT predicts that the preferred CO2 insertion pathway changes from SE2 to 1,2-insertion for all tested alkyls (see ESI†), suggesting that the size of the ligand is crucial in determining the reaction pathway. We propose that complexes with a smaller steric profile are more likely to react via a 1,2-insertion pathway compared with complexes that are more congested, because in this case it is easier for CO2 to interact with the metal center. Further, in the case of MePBP supported complexes, the calculated rates of insertion are the same for the methyl, ethyl, and n-propyl species, suggesting that the nature of the alkyl group is less important for systems that react through a 1,2-insertion pathway. This is unsurprising, as in the 1,2-insertion pathway the metal center is directly involved, which likely lessens the impact of the alkyl group. For the iPrPBP supported palladium complexes, 1,2-insertion is preferred for (iPrPBP)Pd(CH3), whereas the SE2 pathway is preferred for the ethyl and propyl complexes, with the later showing higher barriers than (iPrPBP)Pd(CH3). The barrier for insertion into (iPrPBP)Pd(CH2CH3) is lower than for (iPrPBP)Pd(CH2CH2CH3), indicating that there is a steric effect with the iPrPBP pincer ligand. The computed results with the smaller ancillary ligands suggest that the observation that CO2 insertion is faster for 1-Et than for 1-Me or 1-nPr is unlikely to be general to all systems. The tBuPBP ligand creates a sufficiently crowded environment where a minor change in the sterics results in non-intuitive changes in rate, whereas for other supporting ligands this will not be the case, as evidenced by our calculated results with iPrPBP and MePBP.
We next investigated the barriers for CO2 insertion into the palladium benzyl complexes 1-Bn, 1-OMeBn, as well as the hypothetical complex (tBuPBP)Pd(CH2-4-CF3-C6H4) (1-CF3Bn) (Table 3). The calculated barrier for CO2 insertion into 1-Bn (20.3 kcal mol−1) is higher than for 1-Me and 1-Et, in agreement with our experimental observations. In contrast, we computationally predict that insertion into 1-nPr is more challenging than insertion into 1-Bn, which contradicts our experimental results, but likely reflects some computational error. When calculations were performed with other functionals (see ESI†), there were cases where the barrier for insertion into 1-Bn was higher than for 1-nPr, indicating that different DFT functionals provide slighty different TS structures. The lowest energy pathway for insertion into 1-Bn involves an SE2 mechanism and the geometric parameters at the transition state for insertion are similar to those observed for 1-Me, 1-Et, and 1-nPr. Previous calculations on CO2 insertion into palladium benzyl species have also invoked an SE2 pathway.40 Calculations on CO2 insertion into 1-OMeBn or 1-CF3Bn indicate that the barriers for insertion into these species are approximately the same as for the unsubstituted palladium benzyl species. This is unexpected as it suggests that the impact of the para-substituent on the nucleophilicity of the benzylic carbon is negligible even though this substituent should impact the energy of the π*-orbital which stabilizes or destabilizes the carbon. Nevertheless, our calculations are in agreement with the experimental rate constants of 1-Bn and 1-OMeBn being within error (vide supra).
In contrast to the facile insertion of CO2 into palladium alkyl complexes supported by tBuPBP ligands, we did not observe CO2 insertion into 1-Ph. To understand this reactivity, we calculated the kinetic and thermodynamic parameters associated with CO2 insertion into 1-Ph. Although the reaction is considerably thermodynamically downhill (by −19.2 kcal mol−1), the kinetic barrier is 34.6 kcal mol−1, which explains why no reaction is observed experimentally. Consistent with our previous results for CO2 insertion into palladium–C(sp2) bonds,40 the transition state is classified as innersphere, with a Pd–CCO2 interaction of 3.03 Å. To understand the influence of the tBuPBP ligand on CO2 insertion into 1-Ph, we calculated the energy of the transition state for CO2 insertion into (tBuPCP)Pd(C6H5) (tBuPCP = 2,6-C6H3(CH2PtBu2)2), which features a pincer ligand with a lower trans-influence donor opposite the phenyl group. In this case, the activation energy associated with an innersphere transition state is 46.3 kcal mol−1, indicating that influence of the tBuPBP ligand is significant. However, in order for CO2 insertion to become kinetically viable experimentally, a different approach needs to be adopted than introducing a stronger trans-influence ligand opposite the phenyl ligand, as the tBuPBP ligand is one of the strongest trans-influence ligands available and it does not lower the activation energy for CO2 insertion enough for the reaction to proceed under mild conditions.
Conclusions
In this work, we prepared and crystallographically characterized an unusual series of tBuPBP supported palladium alkyl and aryl complexes including species with ethyl, n-propyl, benzyl, and phenyl ligands. In contrast, tBuPBP supported palladium complexes with n-butyl, iso-propyl, and tert-butyl ligands were either unstable or could not be observed. The rates of decomposition of the alkyl complexes are related to the steric bulk of the alkyl ligand with a putative tert-butyl complex decomposing faster than the ethyl species. The palladium alkyl complexes decompose via two different routes. The least and most sterically bulky complexes containing ethyl or tert-butyl ligands decompose via β-hydride elimination. In contrast, complexes containing n-butyl and iso-propyl ligands are stable towards β-hydride elimination and along with benzyl complexes decompose via an uncommon reductive coupling reaction, which involves the formation of a new C–B bond and either well-defined palladium(0) dimers or palladium black. Attempts to synthesize a tBuPBP supported palladium hydride were unsuccessful because a similar reductive coupling occurred to generate a dimeric palladium(0) complex with two new H–B bonds. The observation of decomposition via reductive coupling across a series of complexes confirms that this is a general reaction for RPBP supported complexes.tBuPBP ligated palladium complexes with ethyl, n-propyl, and benzyl ligands all cleanly insert CO2 to form the corresponding carboxylate complexes, allowing for a rare study of the rates of CO2 insertion across an analogous series of metal alkyl complexes. Kinetic studies demonstrate that the rate of CO2 insertion into 1-Et is more than double the rate for insertion into 1-Me, which in turn is ten times faster than the rate of insertion into 1-nPr. CO2 insertion into tBuPBP supported palladium benzyl complexes is much slower than insertion into n-alkyl complexes, likely because the carbon atom of the benzyl group is less nucleophilic. DFT calculations indicate that insertion reactions into 1-Me, 1-Et, 1-nPr, and 1-Bn proceed via an outersphere SE2 pathway and steric factors are responsible for the observed differences in rate between the n-alkyl complexes. They also suggest that the counterintuitive trends in the rates of CO2 insertion observed in the present work will not occur for all metal alkyl systems but are related to the specific steric factors present in this group of complexes. Although the strong trans-influence of the boryl ligand in tBuPBP promotes CO2 insertion into palladium alkyl complexes, no reaction is observed between 1-Ph and CO2. Overall, our results highlight how the rates of CO2 vary across an analogous series of palladium alkyl and aryl complexes and DFT calculations provide explanations for the observed trends. This information will be valuable for the development of catalytic reactions that involve CO2 insertion into metal alkyl bonds as an elementary step.
Data availability
Crystallographic data has been deposited at the CCDC with numbers 2243696–2243703 and 2264960. NMR spectra and the coordinates and energies of DFT optimized geometries are provided as part of the ESI.†Author contributions
APD and NH conceptualized the project. APD performed experimental investigations and SG performed computational investigations. NH supervised experimental studies and KHH supervised computational studies. All authors were involved in writing the manuscript.Conflicts of interest
The authors declare no competing financial interests.Acknowledgements
NH acknowledges support from National Science Foundation through Grant CHE-1953708 and the Yale Center for Natural Carbon Capture. KHH and SG thank the Research Council of Norway (No. 300769) and Sigma2 (No. nn9330k and nn4654k), and the European Union's Horizon 2020 research and innovation programme under the Marie Skłodowska-Curie grant agreement No. 859910.References
- (a) E. A. Quadrelli, G. Centi, J.-L. Duplan and S. Perathoner, Carbon Dioxide Recycling: Emerging Large-Scale Technologies with Industrial Potential, ChemSusChem, 2011, 4, 1194–1215 CrossRef CAS; (b) A. M. Appel, J. E. Bercaw, A. B. Bocarsly, H. Dobbek, D. L. DuBois, M. Dupuis, J. G. Ferry, E. Fujita, R. Hille, P. J. A. Kenis, C. A. Kerfeld, R. H. Morris, C. H. F. Peden, A. R. Portis, S. W. Ragsdale, T. B. Rauchfuss, J. N. H. Reek, L. C. Seefeldt, R. K. Thauer and G. L. Waldrop, Frontiers, Opportunities, and Challenges in Biochemical and Chemical Catalysis of CO2 Fixation, Chem. Rev., 2013, 113, 6621–6658 CrossRef CAS PubMed; (c) W.-H. Wang, Y. Himeda, J. T. Muckerman, G. F. Manbeck and E. Fujita, CO2 Hydrogenation to Formate and Methanol as an Alternative to Photo- and Electrochemical CO2 Reduction, Chem. Rev., 2015, 115, 12936–12973 CrossRef CAS PubMed; (d) W. H. Bernskoetter and N. Hazari, Reversible Hydrogenation of Carbon Dioxide to Formic Acid and Methanol: Lewis Acid Enhancement of Base Metal Catalysts, Acc. Chem. Res., 2017, 50, 1049–1058 CrossRef CAS; (e) J. Artz, T. E. Müller, K. Thenert, J. Kleinekorte, R. Meys, A. Sternberg, A. Bardow and W. Leitner, Sustainable Conversion of Carbon Dioxide: An Integrated Review of Catalysis and Life Cycle Assessment, Chem. Rev., 2018, 118, 434–504 CrossRef CAS PubMed; (f) N. Onishi, G. Laurenczy, M. Beller and Y. Himeda, Recent Progress for Reversible Homogeneous Catalytic Hydrogen Storage in Formic Acid and in Methanol, Coord. Chem. Rev., 2018, 373, 317–332 CrossRef CAS; (g) M. D. Burkart, N. Hazari, C. L. Tway and E. L. Zeitler, Opportunities and Challenges for Catalysis in Carbon Dioxide Utilization, ACS Catal., 2019, 9, 7937–7956 CrossRef CAS; (h) C. Hepburn, E. Adlen, J. Beddington, E. A. Carter, S. Fuss, N. Mac Dowell, J. C. Minx, P. Smith and C. K. Williams, The Technological and Economic Prospects for CO2 Utilization and Removal, Nature, 2019, 575, 87–97 CrossRef CAS PubMed; (i) Z. Zhang, S.-Y. Pan, H. Li, J. Cai, A. G. Olabi, E. J. Anthony and V. Manovic, Recent Advances in Carbon Dioxide Utilization, Renewable Sustainable Energy Rev., 2020, 125, 109799 CrossRef CAS; (j) W. Gao, S. Liang, R. Wang, Q. Jiang, Y. Zhang, Q. Zheng, B. Xie, C. Y. Toe, X. Zhu, J. Wang, L. Huang, Y. Gao, Z. Wang, C. Jo, Q. Wang, L. Wang, Y. Liu, B. Louis, J. Scott, A.-C. Roger, R. Amal, H. He and S.-E. Park, Industrial Carbon Dioxide Capture and Utilization: State of the Art and Future Challenges, Chem. Soc. Rev., 2020, 49, 8584–8686 RSC; (k) S. Overa, T. G. Feric, A.-H. A. Park and F. Jiao, Tandem and Hybrid Processes for Carbon Dioxide Utilization, Joule, 2021, 5, 8–13 CrossRef; (l) T. Singh, S. Jalwal and S. Chakraborty, Homogeneous First-row Transition-metal-catalyzed Carbon Dioxide Hydrogenation to Formic Acid/Formate, and Methanol, Asian J. Org. Chem., 2022, 11, e202200330 CAS; (m) C. Das, J. Grover, Tannu, A. Das, D. Maiti, A. Dutta and G. K. Lahiri, Recent Developments in First-Row Transition Metal Complex-Catalyzed CO2 Hydrogenation, Dalton Trans., 2022, 51, 8160–8168 RSC; (n) N. Onishi and Y. Himeda, Homogeneous Catalysts for CO2 Hydrogenation to Methanol and Methanol Dehydrogenation to Hydrogen Generation, Coord. Chem. Rev., 2022, 472, 214767 CrossRef CAS.
- National Academies of Sciences, and Engineering, and Medicine, Gaseous Carbon Waste Streams Utilization: Status and Research Needs, The National Academies Press, Washington DC, 2019 Search PubMed.
- N. Hazari and J. E. Heimann, Carbon Dioxide Insertion into Group 9 and 10 Metal-Element σ-Bonds, Inorg. Chem., 2017, 56, 13655–13678 CrossRef CAS PubMed.
- (a) M. Börjesson, T. Moragas, D. Gallego and R. Martin, Metal-Catalyzed Carboxylation of Organic (Pseudo)halides with CO2, ACS Catal., 2016, 6, 6739–6749 CrossRef; (b) A. Tortajada, F. Juliá-Hernández, M. Börjesson, T. Moragas and R. Martin, Transition-Metal-Catalyzed Carboxylation Reactions with Carbon Dioxide, Angew. Chem., Int. Ed., 2018, 57, 15948–15982 CrossRef CAS.
- For an example of CO2 insertion into a Sc-alkyl bond see: F. A. LeBlanc, A. Berkefeld, W. E. Piers and M. Parvez, Reactivity of Scandium β-Diketiminate Alkyl Complexes with Carbon Dioxide, Organometallics, 2012, 31, 810–818 CrossRef CAS.
- For an example of CO2 insertion into a Zr-alkyl bond see: K.-C. Lau, B. J. Petro, S. Bontemps and R. F. Jordan, Comparative Reactivity of Zr– and Pd–Alkyl Complexes with Carbon Dioxide, Organometallics, 2013, 32, 6895–6898 CrossRef CAS.
- For an example of CO2 insertion into a Cr-alkyl bond see: D. J. Darensbourg and A. Rokicki, Reduction of Carbon Dioxide and Carbonyl Sulfide by Anionic Group VIB Metal Hydrides and Alkyls. Carbon-Hydrogen and Carbon-Carbon Bond Formation Processes and the Structure of [PNP][Cr(CO)5SC(O)H], J. Am. Chem. Soc., 1982, 104, 349–350 CrossRef CAS.
- For examples of CO2 insertion into W-alkyl bonds see: (a) D. J. Darensbourg and R. Kudaroski, Metal-Induced Transformations of Carbon Dioxide. Carbon-Carbon Bond-Forming Processes Involving Anionic Group VIB Metal Derivatives, and the X-ray structure of [PNP][cis-MeW(CO)4PMe3], J. Am. Chem. Soc., 1984, 106, 3672–3673 CrossRef CAS; (b) D. J. Darensbourg, R. K. Hanckel, C. G. Bauch, M. Pala, D. Simmons and J. N. White, A Kinetic Investigation of Carbon Dioxide Insertion Processes Involving Anionic Tungsten-Alkyl and -Aryl Derivatives: Effects of Carbon Dioxide Pressure, Counterions, and Ancillary Ligands. Comparisons with Migratory Carbon Monoxide Insertion Processes, J. Am. Chem. Soc., 1985, 107, 7463–7473 CrossRef CAS; (c) D. J. Darensbourg and M. Pala, Cation-Anion Interaction in the [Na-kryptofix-221][W(CO)5O2CH] Derivative and its Relevance in Carbon Dioxide Reduction Processes, J. Am. Chem. Soc., 1985, 107, 5687–5693 CrossRef CAS; (d) D. J. Darensbourg and G. Grotsch, Stereochemical Studies of the Carbon Dioxide Insertion Reactions into the Tungsten-Alkyl Bond, J. Am. Chem. Soc., 1985, 107, 7473–7476 CrossRef CAS.
- For examples of CO2 insertion into Fe-alkyl bonds see: (a) S. Ittel, C. Tolman, A. English and J. Jesson, The Chemistry of 2-Naphthyl bis[bis(dimethylphosphino)ethane] Hydride Complexes of Iron, Ruthenium, and Osmium. 2. Cleavage of sp and sp3 Carbon-Hydrogen, Carbon-Oxygen, and Carbon-Halogen bonds. Coupling of Carbon Dioxide and Acetonitrile, J. Am. Chem. Soc., 1978, 100, 7577–7585 CrossRef CAS; (b) I. M. Arafa, K. Shin and H. M. Goff, Carbon Monoxide and Carbon Dioxide Carbon-Metal Bond Insertion Chemistry of Alkyliron(III) Porphyrin Complexes, J. Am. Chem. Soc., 1988, 110, 5228–5229 CrossRef CAS; (c) O. R. Allen, S. J. Dalgarno, L. D. Field, P. Jensen, A. J. Turnbull and A. C. Willis, Addition of CO2 to Alkyl Iron complexes, Fe(PP)2Me2, Organometallics, 2008, 27, 2092–2098 CrossRef CAS; (d) K.-C. Lau and R. F. Jordan, Reactivity of (Pyridine-Diimine) Fe Alkyl Complexes with Carbon Dioxide, Organometallics, 2016, 35, 3658–3666 CrossRef CAS.
- For examples of CO2 insertion into Ru-alkyl bonds see: (a) J. F. Hartwig, R. G. Bergman and R. A. Andersen, Insertion Reactions of Carbon Monoxide and Carbon Dioxide with Ruthenium Benzyl, Arylamido, and Aryloxide complexes: A Comparison of the Reactivity of Ruthenium-Carbon, Ruthenium-Nitrogen, and Ruthenium-Oxygen Bonds, J. Am. Chem. Soc., 1991, 113, 6499–6508 CrossRef CAS; (b) O. R. Allen, S. J. Dalgarno, L. D. Field, P. Jensen and A. C. Willis, Insertion of CO2 into the Ru–C Bonds of cis-and trans-Ru(dmpe)2Me2 (dmpe = Me2PCH2CH2PMe2), Organometallics, 2009, 28, 2385–2390 CrossRef CAS.
- For examples of CO2 insertion into Rh-alkyl bonds see: (a) D. J. Darensbourg, G. Groetsch, P. Wiegreffe and A. L. Rheingold, Insertion Reactions of Carbon Dioxide with Square-Planar Rhodium Alkyl and Aryl Complexes, Inorg. Chem., 1987, 26, 3827–3830 CrossRef CAS; (b) T. G. Ostapowicz, M. Hölscher and W. Leitner, CO2 Insertion into Metal–Carbon Bonds: A Computational Study of RhI Pincer Complexes, Chem.–Eur. J., 2011, 17, 10329–10338 CrossRef CAS PubMed; (c) T. Suga, T. Saitou, J. Takaya and N. Iwasawa, Mechanistic Study of the Rhodium-Catalyzed Carboxylation of Simple Aromatic Compounds with Carbon Dioxide, Chem. Sci., 2017, 8, 1454–1462 RSC; (d) L. Pavlovic, J. Vaitla, A. Bayer and K. H. Hopmann, Rhodium-Catalyzed Hydrocarboxylation: Mechanistic Analysis Reveals Unusual Transition State for Carbon–Carbon Bond Formation, Organometallics, 2018, 37, 941–948 CrossRef CAS.
- For examples of CO2 insertion into Cu-alkyl bonds see: (a) T. Ikariya and A. Yamamoto, Preparation and Properties of Ligand-Free Methylcopper and of Copper Alkyls Coordinated with 2,2′-Bipyridyl and Tricyclohexylphosphine, J. Organomet. Chem., 1974, 72, 145–151 CrossRef; (b) S. Sakaki and K. Ohkubo, Ab initio MO Study of Carbon Dioxide Insertion into a Methyl-Copper(I) Bond. Critical Difference from CO2 Insertion into a Hydrogen-Copper(I) Bond, Organometallics, 1989, 8, 2970–2973 CrossRef CAS; (c) N. P. Mankad, T. G. Gray, D. S. Laitar and J. P. Sadighi, Synthesis, Structure, and CO2 Reactivity of a Two-Coordinate (Carbene)copper(I) Methyl Complex, Organometallics, 2004, 23, 1191–1193 CrossRef CAS.
- For examples of CO2 insertion into Ni-alkyl bonds see: (a) T. J. Schmeier, N. Hazari, C. D. Incarvito and J. R. Raskatov, Exploring the Reactions of CO2 with PCP Supported Nickel Complexes, Chem. Commun., 2011, 47, 1824–1826 RSC; (b) K. J. Jonasson and O. F. Wendt, Synthesis and Characterization of a Family of POCOP Pincer Complexes with Nickel: Reactivity Towards CO2 and Phenylacetylene, Chem.–Eur. J., 2014, 20, 11894–11902 CrossRef CAS; (c) A. H. Mousa, J. Bendix and O. F. Wendt, Synthesis, Characterization, and Reactivity of PCN Pincer Nickel Complexes, Organometallics, 2018, 37, 2581–2593 CrossRef CAS; (d) A. H. Mousa, A. V. Polukeev, J. Hansson and O. F. Wendt, Carboxylation of the Ni–Me Bond in an Electron-Rich Unsymmetrical PCN Pincer Nickel Complex, Organometallics, 2020, 39, 1553–1560 CrossRef CAS; (e) J. B. Diccianni, C. T. Hu and T. Diao, Insertion of CO2 Mediated by a (Xantphos)NiI–Alkyl Species, Angew. Chem., Int. Ed., 2019, 58, 13865–13868 CrossRef CAS PubMed; (f) R. J. Somerville, C. Odena, M. F. Obst, N. Hazari, K. H. Hopmann and R. Martin, Ni(I)–Alkyl Complexes Bearing Phenanthroline Ligands: Experimental Evidence for CO2 Insertion at Ni(I) Centers, J. Am. Chem. Soc., 2020, 142, 10936–10941 CrossRef CAS PubMed; (g) A. P. Deziel, M. R. Espinosa, L. Pavlovic, D. J. Charboneau, N. Hazari, K. H. Hopmann and B. Q. Mercado, Ligand and Solvent Effects on CO2 Insertion into Group 10 Metal Alkyl Bonds, Chem. Sci., 2022, 13, 2391–2404 RSC.
- For examples of CO2 insertion into Pd-alkyl bonds see references 6, 13f and: (a) R. Johansson, M. Jarenmark and O. F. Wendt, Insertion of Carbon Dioxide into (PCP)PdII-Me Bonds, Organometallics, 2005, 24, 4500–4502 CrossRef CAS; (b) M. T. Johnson, R. Johansson, M. V. Kondrashov, G. Steyl, M. S. G. Ahlquist, A. Roodt and O. F. Wendt, Mechanisms of the CO2 Insertion into (PCP) Palladium Allyl and Methyl σ-Bonds. A Kinetic and Computational Study, Organometallics, 2010, 29, 3521–3529 CrossRef CAS.
- H.-W. Suh, L. M. Guard and N. Hazari, A Mechanistic Study of Allene Carboxylation with CO2 Resulting in the Development of a Pd(II) Pincer Complex for the Catalytic Hydroboration of CO2, Chem. Sci., 2014, 5, 3859–3872 RSC.
- The change from an organolithium reagent in the synthesis of (tBuPBP)Pd(CH2CH3) to a Grignard reagent for the preparation of (tBuPBP)Pd(CH2CH2CH3) is because EtLi is commercially available but nPrLi is not. In contrast, nPrMgCl is commercially available.
- (a) J. Takaya and N. Iwasawa, Synthesis, Structure, and Reactivity of a Mononuclear η2-(Ge–H)palladium(0) Complex Bearing a PGeP-Pincer-Type Germyl Ligand: Reactivity Differences between Silicon and Germanium, Eur. J. Inorg. Chem., 2018, 2018, 5012–5018 CrossRef CAS; (b) M.-H. Huang, W.-Y. Lee, X.-R. Zou, C.-C. Lee, S.-B. Hong and L.-C. Liang, Amido PNP Pincer Complexes of Palladium(II) and Platinum(II): Synthesis, Structure, and Reactivity, Appl. Organomet. Chem., 2021, 35, e6128 CAS.
- D. L. Reger, D. G. Garza and L. Lebioda, Synthesis of Extremely Stable Alkylpalladium Complexes of the type (Me2NCS2)Pd(PEt3)(alkyl). Crystal and Molecular Structures of the Isomers [cyclic](CH2CH2CH2CH2NCS2)Pd(PEt3)(n-propyl) and [cyclic](CH2CH2CH2CH2NCS2)Pd(PEt3)(isopropyl), Organometallics, 1991, 10, 902–906 CrossRef CAS.
- Y. Ding, Q.-Q. Ma, J. Kang, J. Zhang, S. Li and X. Chen, Palladium(II) Complexes Supported by PBP and POCOP Pincer Ligands: A Comparison of their Structure, Properties and Catalytic Activity, Dalton Trans., 2019, 48, 17633–17643 RSC.
- (a) K. Osakada, Y. Ozawa and A. Yamamoto, Preparation and Properties of Ethylpalladium Thiolate Complexes. Reaction with Organic Halides Leading to C–S Bond Formation; Crystal Structure of Trans-[PdEt(Br)(PMe3)2], J. Chem. Soc., Dalton Trans., 1991, 759–764 RSC; (b) K. Osakada, Y. Ozawa and A. Yamamoto, Molecular Structure and Carbonylation of Ethyl(benzenethiolato)-palladium(II) Complex, trans-PdEt(SPh)(PMe3)2, Bull. Chem. Soc. Jpn., 1991, 6, 2002–2004 CrossRef; (c) A. J. Canty, H. Jin, A. S. Roberts, B. W. Skelton, P. R. Traill and A. H. White, Synthesis and Characterization of Ambient Temperature Stable Organopalladium(IV) Complexes, Including Aryl-, η1-Allyl-, Ethylpalladium(IV), and Pallada(IV)cyclopentane Complexes. Structures of the Poly(pyrazol-1-yl)borate Complexes PdMe3{(pz)3BH} and PdMe3{(pz)4B} and Three Polymorphs of PdMe2Et{(pz)3BH, Organometallics, 1995, 14, 199–206 CrossRef CAS; (d) R. A. Stockland Jr, G. K. Anderson and N. P. Rath, Hydride-Bridged Dipalladium Complexes Containing Diphosphine Ligands, Inorg. Chim. Acta, 1997, 259, 173–178 CrossRef; (e) R. A. Stockland Jr, G. K. Anderson and N. P. Rath, Synthesis and Structures of Hydride-Bridged Palladium A-Frame Complexes, Inorg. Chim. Acta, 2000, 300, 395–405 CrossRef.
- (a) Z. Csok, O. Vechorkin, S. B. Harkins, R. Scopelliti and X. Hu, Nickel Complexes of a Pincer NN2 Ligand: Multiple Carbon–Chloride Activation of CH2Cl2 and CHCl3 Leads to Selective Carbon–Carbon Bond Formation, J. Am. Chem. Soc., 2008, 130, 8156–8157 CrossRef CAS PubMed; (b) L.-C. Liang, W.-Y. Lee, Y.-T. Hung, Y.-C. Hsiao, L.-C. Cheng and W.-C. Chen, Nickel Complexes Incorporating an Amido Phosphine Chelate with a endant Amine Arm: Synthesis, Structure, and Catalytic Kumada Coupling, Dalton Trans., 2012, 41, 1381–1388 RSC; (c) C. Yoo, S. Oh, J. Kim and Y. Lee, Transmethylation of a Four-Coordinate Nickel(I) Monocarbonyl Species with Methyl Iodide, Chem. Sci., 2014, 5, 3853–3858 RSC.
- (a) P. Cui, M. R. Hoffbauer, M. Vyushkova and V. M. Iluc, Heterobimetallic Pd–K Carbene Complexes via One-Electron Reductions of Palladium Radical Carbenes, Chem. Sci., 2016, 7, 4444–4452 RSC; (b) R. Shimokawa, Y. Kawada, M. Hayashi, Y. Kataoka and Y. Ura, Oxygenation of a Benzyl Ligand in SNS-Palladium Complexes with O2: Acceleration by Anions or Brønsted Acids, Dalton Trans., 2016, 45, 16112–16116 RSC; (c) Y. Shigehiro, K. Miya, R. Shibai, Y. Kataoka and Y. Ura, Synthesis of Pd-NNP Phosphoryl Mononuclear and Phosphinous Acid-Phosphoryl-Bridged Dinuclear Complexes and Ambient Light-Promoted Oxygenation of Benzyl Ligands, Organometallics, 2022, 41, 2810–2821 CrossRef CAS.
- S. Min, J. Choi, C. Yoo, P. M. Graham and Y. Lee, Ni(0)-Promoted Activation of Csp2–H and Csp2–O Bonds, Chem. Sci., 2021, 12, 9983–9990 RSC.
- We used tBuMgCl instead of tBuLi for safety reasons.
- In the ESI† we also describe attempts to prepare (tBuPBP)Pd(allyl).
- Y. Segawa, M. Yamashita and K. Nozaki, Syntheses of PBP Pincer Iridium Complexes: A Supporting Boryl Ligand, J. Am. Chem. Soc., 2009, 131, 9201–9203 CrossRef CAS PubMed.
- H. Ogawa and M. Yamashita, Platinum Complexes Bearing a Boron-Based PBP Pincer Ligand: Synthesis, Structure, and Application as a Catalyst for Hydrosilylation of 1-Decene, Dalton Trans., 2013, 42, 625–629 RSC.
- For selected references see: (a) H.-W. Suh, T. J. Schmeier, N. Hazari, R. A. Kemp and M. K. Takase, Experimental and Computational Studies of the Reaction of Carbon Dioxide with Pincer-Supported Nickel and Palladium Hydrides, Organometallics, 2012, 31, 8225–8236 CrossRef CAS; (b) H.-W. Suh, D. Balcells, A. J. Edwards, L. M. Guard, N. Hazari, E. A. Mader, B. Q. Mercado and M. Repisky, Understanding the Solution and Solid-State Structures of Pd and Pt PSiP Pincer-Supported Hydrides, Inorg. Chem., 2015, 54, 11411–11422 CrossRef CAS PubMed.
- An alternative route involving the use of 1,4-dioxane as an additive is described in the ESI†.
- (a) A. J. Canty, N. J. Minchin, B. W. Skelton and A. H. White, Cyclopalladation to Form Planar Tridentate [N–C–N]– Intramolecular Co-ordination Systems Involving Pyridine Donor Groups, Including Ligand Synthesis and X-ray Structural Studies, J. Chem. Soc., Dalton Trans., 1987, 1477–1483 RSC; (b) M. Bröring, C. Kleeberg and E. Cónsul Tejero, Syntheses, Structures and Coordination Modes of Acetatopalladium(II) Complexes with 1,3-Bis(2-arylimino)isoindoline Ligands of Different Steric Influence, Eur. J. Inorg. Chem., 2007, 3208–3216 CrossRef; (c) C. M. Anderson, N. Oh, T. A. Balema, F. Mastrocinque, C. Mastrocinque, D. Santos, M. W. Greenberg and J. M. Tanski, Regioselective C–H/C–X Activation of Naphthyl-Derived Ligands to Form Six-Membered Palladacycles, Tetrahedron Lett., 2016, 57, 4574–4577 CrossRef CAS; (d) M. R. Hoffbauer, C. C. Comanescu, B. J. Dymm and V. M. Iluc, Influence of the Leaving Group on C–H Activation Pathways in Palladium Pincer Complexes, Organometallics, 2018, 37, 2086–2094 CrossRef CAS.
- A reviewer suggested that the presence of different halide salt impurities in variable concentrations may be causing the large changes in the rates of CO2 insertion into 1-Me, 1-Et, and 1-nPr. In the ESI,† we have described experiments that were performed to discount this possibility.
- J. E. Heimann, W. H. Bernskoetter and N. Hazari, Understanding the Individual and Combined Effects of Solvent and Lewis Acid on CO2 Insertion into a Metal Hydride, J. Am. Chem. Soc., 2019, 141, 10520–10529 CrossRef CAS PubMed.
- (a) C. Reichardt, Solvatochromic Dyes as Solvent Polarity Indicators, Chem. Rev., 1994, 94, 2319–2358 CrossRef CAS; (b) C. Reichardt, Empirical Parameters of the Polarity of Solvents, Angew. Chem., Int. Ed., 1965, 4, 29–40 CrossRef.
- The Dimroth-Reichardt ET(30) parameter is determined from the molar electronic transition energy of 2,6-diphenyl-4-(2,4,6-triphenylpyridinium-1-yl)phenolate (conventionally referred to as Betaine 30). It is found by measuring the λmax of Betaine 30 in a particular solvent and a smaller λmax corresponds to a larger wavenumber and therefore a more polar solvent.
- (a) J. E. Heimann, W. H. Bernskoetter, N. Hazari and J. M. Mayer, Acceleration of CO2 Insertion into Metal Hydrides: Ligand, Lewis Acid, and Solvent Effects on Reaction Kinetics, Chem. Sci., 2018, 8, 6629–6638 RSC; (b) J. E. Heimann, W. H. Bernskoetter, J. A. Guthrie, N. Hazari and J. M. Mayer, Effect of Nucleophilicity on the Kinetics of CO2 Insertion into Pincer-Supported Nickel Complexes, Organometallics, 2018, 37, 3649–3653 CrossRef CAS.
- T. Moragas, M. Gaydou and R. Martin, Nickel-Catalyzed Carboxylation of Benzylic C–N Bonds with CO2, Angew. Chem., Int. Ed., 2016, 55, 5053–5057 CrossRef CAS PubMed.
- In the SE2 pathway, we were unable to find the intermediate and barrier for the second rearrangement step to form the palladium carboxylate product, as the rearrangement occurs spontaneously during geometry optimization. However, this process has previously been demonstrated to be low energy in related systems.
- The calculated increase in barrier from 1-Et (17.7 kcal mol−1) to 1-Me (19.4 kcal mol−1) is around 1 kcal mol−1 larger than would be expected for a two-fold difference in rate. Nevertheless, this is good agreement when computational error is considered.
- L. Falivene, R. Credendino, A. Poater, A. Petta, L. Serra, R. Oliva, V. Scarano and L. Cavallo, SambVca 2. A Web Tool for Analyzing Catalytic Pockets with Topographic Steric Maps, Organometallics, 2016, 35, 2286–2293 CrossRef CAS.
- D. García-López, L. Pavlovic and K. H. Hopmann, To Bind or Not to Bind: Mechanistic Insights into C–CO2 Bond Formation with Late Transition Metals, Organometallics, 2020, 39, 1339–1347 CrossRef.
Footnote |
| † Electronic supplementary information (ESI) available. Supporting information about selected experiments, NMR spectra, DFT-optimized geometries and other details are available via the Internet. CCDC 2243696–2243703 and 2264960. For ESI and crystallographic data in CIF or other electronic format see DOI: https://doi.org/10.1039/d3sc01459b |
| This journal is © The Royal Society of Chemistry 2023 |