Magnetic coupling between Fe(NO) spin probe ligands through diamagnetic Ni^II, Pd^II and Pt^II tetrathiolate bridges

Abstract

Reaction of the nitrosylated-iron metallodithiolate ligand, paramagnetic (NO)Fe(N₂S₂), with [M(CH₃CN)_n][BF₄]₂ salts (M = Ni^II, Pd^II, and Pt^II; n = 4 or 6) affords di-radical tri-metallic complexes in a stairstep type arrangement ([FeMFe]²⁺, M = Ni, Pd, and Pt), with the central group 10 metal held in a MS₄ square plane. These isostructural compounds have nearly identical ν(NO) stretching values, isomer shifts, and electrochemical properties, but vary in their magnetic properties. Despite the intramolecular Fe⋯Fe distances of ca. 6 Å, antiferromagnetic coupling is observed between {Fe(NO)}⁷ units as established by magnetic susceptibility, EPR, and DFT studies. The superexchange interaction through the thiolate sulfur and central metal atoms is on the order of Ni^II < Pd^II ≪ Pt^II with exchange coupling constants (J) of −3, −23, and −124 cm⁻¹, consistent with increased covalency of the M–S bonds (3d < 4d < 5d). This trend is reproduced by DFT calculations with molecular orbital analysis providing insight into the origin of the enhancement in the exchange interaction. Specifically, the magnitude of the exchange interaction correlates surprisingly well with the energy difference between the HOMO and HOMO−1 orbitals of the triplet states, which is reflected in the central metal's contribution to these orbitals. These results demonstrate the ability of sulfur-dense metallodithiolate ligands to engender strong magnetic communication by virtue of their enhanced covalency and polarizability.

---

Introduction

The ubiquity of sulfur–metal connections in nature inspires the design of bi- and multi-metallic systems in synthetic inorganic chemistry. Common motifs for biocatalysts developed in evolutionary biology are the placement of metals in close proximity with flexible sulfur bridges as well as the presence of π-acidic/delocalizing ligands.^1,2 In spite of the wealth of synthetic chemistry devoted to these systems in the biological realm, such compounds have rarely been explored in the field of molecular magnetism. Common ligands used to study superexchange and direct exchange interactions in bimetallic or polymetallic systems rely on nitrogen and oxygen donors, many being in π-conjugated flat planes, as well as cyanide ligands. In an effort to expand the database of information on sulfur ligands connected to metal-based linkers, we have explored a redox- and spin-active metallodithiolate complex, nitrosylated iron within a N₂S₂ ligand field. The complex is a nominal analogue of the as-isolated iron-centered nitrile hydratase active site, and it is a versatile metal trapping agent through its cis-dithiolates.^3–5 According to various characterization tools the [Fe(NO)]²⁺ unit is centered above the N₂S₂ plane and displaced by ca. 0.5 Å; the ∠Fe–N–O varies from 151° to 158° depending on the hydrocarbon connectors between the N to N and N to S donors. The accepted oxidation state of Fe within the {Fe(NO)}⁷ manifold (Enemark–Feltham notation)⁶ is interpreted by various spectroscopies as intermediate spin Fe^III (S = 3/2) that is antiferromagnetically coupled to triplet NO⁻, giving an overall S = ½ paramagnetic state.^7,8 In addition to the expected opposite-sign spin polarization on NO and Fe, density functional theory (DFT) computations show Fe spin delocalized onto the cis-dithiolate sulfurs, Fig. 1A, leading to the expectation that bimetallic derivatives should display considerable spin delocalization arising from sulfur interactions.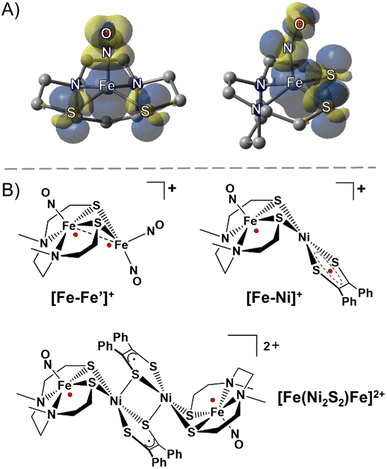

Fig. 1 (A) Side and front views of the spin density plot (isovalue = 0.001) of the paramagnetic (NO)Fe(N₂S₂) metallodithiolate. (B) Selected examples of sulfur-bridged multimetallic complexes with strongly antiferromagnetically coupled radicals (red dots).^9,11

In this vein, an especially stable diiron-trinitrosyl adduct shown in Fig. 1B, was isolated in three redox levels: [Fe–Fe′]⁺, [Fe–Fe′]⁰, and [Fe–Fe′]⁻.^9,10 A short Fe⋯Fe distance of 2.71 Å for [Fe–Fe′]⁺ is consistent with its diamagnetic character, i.e., strong antiferromagnetic (AFM) coupling between each Fe radical ({Fe(NO)}⁷ and {Fe(NO)₂}⁹) essentially results in a bond as indicated in the structure. The more accessible reduction (−0.78 V) deposits the added electron on the dinitrosyl iron unit, whereupon the spin coupled {Fe(NO)₂}⁹ unit becomes diamagnetic{Fe(NO)₂}¹⁰, and releases the paramagnetism to be localized on the {Fe(NO)}⁷. The second reduction (−1.41 V) generates a rare triplet state within the mono-nitrosyl, {Fe(NO)}⁸, or [Fe^II(NO)]⁻.

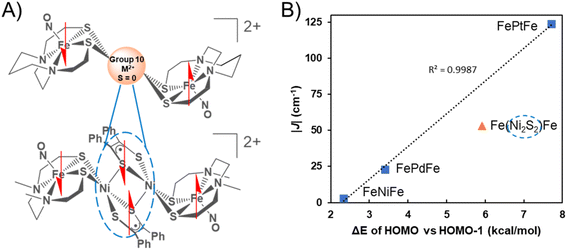
A second magnetically interesting diradical system was observed in solution from an iron-nitrosyl bound to a nickel dithiolene, [Fe–Ni]⁺, Fig. 1B, in which the {Fe(NO)}⁷ unit is AFM coupled with the S = ½ radical dithiolene unit on nickel, showing an estimated exchange coupling constant (J value) of −1200 cm⁻¹.¹¹ The dimeric form of [Fe–Ni]⁺ obtained as the solid state dicationic product, [Fe(Ni₂S₂)Fe]²⁺, Fig. 1B, displayed strong magnetic coupling between the two nickel dithiolene units producing a diamagnetic bridge, in the form of a Ni₂S₂ core, between the {Fe(NO)}⁷ units (at ca. 8 Å apart), coupling these iron spins with a J value of −54 cm⁻¹.¹¹ Thus, heterobimetallic complexes designed with the redox and spin-active (NO)Fe(N₂S₂) metallodithiolate as a donor ligand are predicted to be valuable as exemplars for the possibility of electron spin coupling to exogeneous metals and to define the factors that might affect such coupling. Noting the ability of nickel analogues of the iron nitrosyls, i.e., Ni(N₂S₂), to assemble about Ni^II and Pd^II,¹² we pursued the synthesis of [(NO)Fe(N₂S₂)–M^II–(N₂S₂)Fe(NO)]²⁺ with the prospect of a similar “stair-step” or transoid type arrangement of the iron-dithiolate ligands about the diamagnetic MS₄ plane of the connecting metal ions.^12,13 It is expected that the increased diffuse character of the 4d and 5d orbitals in the heavier group 10 metals will engage in increased covalent bonding with the sulfur ligands as compared to the 3d orbitals, which would lead to stronger long range magnetic interactions with the distal Fe spin centers. Such long-range exchange interactions have been observed for π-delocalized molecular systems typically involving flat bridging ligands however critical analyses of sulfur–metal bridges are incomplete and rare.^14,15

The ubiquitous M–S–M′ units found in nature imply their utility as simpler construction elements for electronic and magnetic linkers. Synthetic chemists nevertheless approach thiolate ligands with caution as their thermodynamic tendencies to form larger metal clusters, as well to mediate radical-based, degradation chemistry, are legend. Of relevance to our report is a linear thiophenolate-bridged tri-iron complex [LFe^III(μ-SR)₃–Fe^II–(μ-SR)₃Fe^IIIL]²⁺ from Wieghardt, et al., in which the magnetic coupling is attributed to a metal-based, double exchange mechanism rather than superexchange via first coordination sphere S-donor atoms.^16,17 Recently, significant superexchange was asserted to occur in a MoS₄³⁻ bridged dilanthanide complex, and its sizeable zero-field splitting parameter was attributed to the appreciable covalency of the sulfide interaction with the heavier 4d metal.¹⁸

Surmising that M–S bridges as building blocks are important to the development of new types of molecular magnetic materials, we aimed to address the absence of, and need for, a definitive study that systematically compares 3d vs. 4d vs. 5d diamagnetic metal bridges for superexchange via sulfur orbitals. The synthetic access, the structural and spectroscopic characterization of all three group 10 derivatives in our study ([FeMFe]²⁺, M = Ni^II, Pd^II, and Pt^II), creates the basis for such explorations. The interpretation of the effect of covalency in the M–S interactions on this set of molecules is described from a combination of experimental and computational data.

Results and discussion

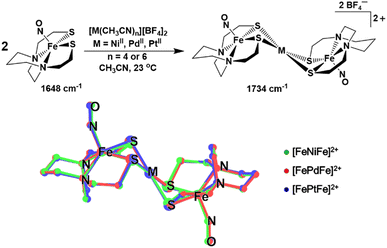
The ν(NO) IR stretch at 1648 cm⁻¹ observed for (NO)Fe(bme-dach) (bme-dach = N,N-bis(2-mercaptoethyl)-1,4-diazacycloheptane) in CH₃CN solution provides a useful spectroscopic handle for monitoring the [FeMFe]²⁺ syntheses, Fig. 2. Upon dropwise addition of [M(CH₃CN)_n][BF₄]₂ (M = Ni^II, Pd^II, Pt^II; n = 4 or 6) this signal shifts to higher wavenumbers, 1734 cm⁻¹. Due to the “stair-step” geometry and C_2h symmetry of these [FePdFe]²⁺ congeners, only the antisymmetric ν(NO) mode is observed. The shift to higher wavenumbers is attributed to the decrease in electron density at the Fe centers as the exogenous metal cations bind to the S atoms. The decrease in the degree of π-back bonding from the Fe centers to the nitrosyl ligands increases the energy of the ν(NO) stretch. It is interesting to note that all three congeners display the same ν(NO) IR value.

Fig. 2 (Top) Synthesis of complexes [FeMFe]²⁺ (M = Ni, Pd, Pt) with ν(NO) values recorded from CH₃CN solutions. (Bottom) Structural overlays of the [FeMFe]²⁺ complexes from SC XRD of their BF₄⁻ salts.

The zero field ⁵⁷Fe Mössbauer spectra of [FeMFe]²⁺ presents as doublets at 4.2 K, Fig. S6.† The “free metallo-ligand”, (NO)Fe(bme-dach) exhibits an isomer shift (δ) of 0.22 mm s⁻¹ and a quadrupole splitting (ΔE_Q) of 1.36 mm s⁻¹.⁷ Bonding to the M^II ions results in little change in the δ value, in the range of 0.25–0.29 mm s⁻¹, however the ΔE_Q significantly decreases into the range 0.65 to 0.97 mm s⁻¹, Table S1.† The difference in ΔE_Q suggests changes in the ligand environment at the Fe center as the bidentate S-donors are shared with the group 10 metal ion, result in a slight difference in coordination geometry, and a change in electron density (as observed by the changes in the ν(NO) IR stretch). Notably, these values are practically identical to those measured for neutral [Fe–Ni]⁰ the reduced form of [Fe–Ni]⁺ in Fig. 1B (δ = 0.28 mm s⁻¹ and ΔE_Q = 0.75 mm s⁻¹),¹⁰ and for [Fe(Ni₂S₂)Fe]²⁺, δ = 0.30 mm s⁻¹ and ΔE_Q = 0.82 mm s⁻¹), for which the iron nitrosyl unit remains {Fe(NO)}⁷.¹¹ However, a substantial shift (δ = 0.73 mm s⁻¹ and ΔE_Q = 2.33 mm s⁻¹ is observed in the case of [Fe–Ni]⁻, the doubly reduced form of [Fe–Ni]⁺. The anion houses the added electron in the iron mono-nitrosyl manifold, generating {Fe(NO)}⁸, concomitant with a substantial displacement of the iron atom out of the N₂S₂ plane, which affects the Mössbauer parameters.¹¹

Single crystals of X-ray quality were grown for all three complexes as [BF₄]⁻ salts by vapor diffusion of Et₂O into a filtered CH₃CN solution at 23 °C. Two independent half molecules of the [FeMFe]²⁺ dications are in the asymmetric unit, but due to their similarity, only one will be described (see Tables S3–S8 in the ESI†). The SC-XRD analysis revealed trimetallic complexes of the well-known stair-step geometry, with square pyramidal Fe centers hinged at the N₂S₂ thiolates to the square planar MS₄ unit, Fig. 2. As the symmetry point group for all [FeMFe]²⁺ complexes is C_2h, both (NO)Fe(N₂S₂) sites have equivalent metrical parameters. The Fe–M and Fe–Fe distances are approximately 3 and 6 Å for all three compounds, respectively. The Fe–N–O angles range from 158.7° to 165.4° and are slightly more linear compared to those found for isolated (NO)Fe(N₂S₂), 152.36°.⁹ The Fe(NO) vector is centered above the N₂S₂ plane in all [FeMFe]²⁺ structures with the Fe atom displaced from the mean N₂S₂ plane (Fe_disp) by 0.615 Å for M = Ni^II; 0.589 Å for M = Pd^II; and 0.589 Å for M = Pt^II. This displacement, Fe_disp, is significantly greater compared to that in the free (NO)Fe(N₂S₂) metallo-ligand, which has an Fe_disp value of 0.49 Å. The hinge angle, defined as the dihedral angle between the FeS₂ and the MS₂ planes, averages to 125.7°, giving [FeMFe]²⁺ its characteristic shape. Note that a second definition of hinge angle is the dihedral angle between the N₂S₂ and the MS₄ mean planes; both are provided in Table 1.

Table 1 Comparison of experimental and computed parameters of [FeMFe]²⁺

Measurable	[FeNiFe]^2+		[FePdFe]^2+		[FePtFe]^2+
	Expt.	Calcd	Expt.	Calcd.	Expt.	Calcd
a The distance between apical Fe and the mean plane of the N2S2 ligand. b Shortest S⋯S intermolecular distance within the MS4 plane. c This hinge is the angle of intersection between the S–Fe–S and S–M–S planes. d This hinge is the angle of intersection between the mean plane of the N2S2 and MS4 planes. e Energy difference between the triplet state HOMO and HOMO−1.
Fe–N–O/°	159.74	159.59	158.69	158.61	159.95	158.93
Fe⋯M/Å	2.956	3.006	3.008	3.092	2.971	3.054
Fe⋯Fe/Å	5.911	6.013	6.017	6.184	5.941	6.10
Fedisp^a/Å	0.615	0.592	0.589	0.567	0.589	0.567
τ value^23	0.012	0	0.0175	0	0.0201	0
S⋯S^b/Å	3.250	3.322	3.475	3.578	3.460	3.568
S–Fe–S/°	83.59	84.07	86.21	86.62	86.20	86.39
Hinge 1^c/°	128.12	129.19	125.88	128.36	123.19	125.43
Hinge 2^d/°	106.41	108.4	104.83	108.21	102.25	105.34
J/cm^−1	−3	15.65	−23	−33	−124.53	−162.12
ΔE^e/kcal mol^−1	2.3		3.4		7.7

---

Electrochemistry

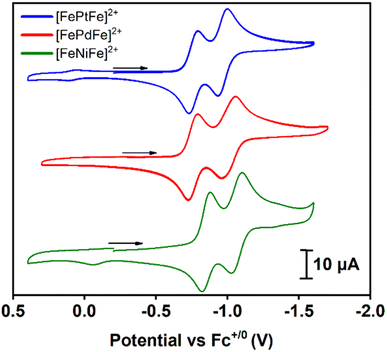
Cyclic voltammograms of [FeMFe]²⁺ were recorded in 0.1 mM CH₃CN solutions under argon at 23 °C with 0.1 M [^tBu₄N][PF₆] as the supporting electrolyte; the data are referenced to Fc^+/0 (E_1/2 = 0.0 V) as an internal standard, Fig. 3. Scans in the cathodic direction from the open circuit potential reveal two reversible reductions; the first reduction ranges from −0.76 to −0.85 and the second from −0.97 to −1.06 V (scan rate dependence studies in the ESI†). As an electrochemical reference, the two reductions of the analogous [Ni(N₂S₂)–Pd^II–Ni(N₂S₂)]²⁺ stairstep complex were shown to be based on the outer Ni(N₂S₂) units and not the PdS₄ core.¹³ Consistently, the two reductions of the [FeMFe]²⁺ series are {Fe(NO)}^7/8 based, with the first process leading to a mixed valence {Fe(NO)}⁷–M^II–{Fe(NO)}⁸ unit, and the second event producing the fully reduced {Fe(NO)}⁸–M^II–{Fe(NO)}⁸ complex. In prior studies, we observed the rare {Fe(NO)}⁸ unit in the case of doubly reduced [Fe–Ni]⁺,^10,11 but attempts to isolate the one- and two-electron reduction products of the [FeMFe]²⁺ complexes have thus far been unsuccessful.

Fig. 3 Cyclic voltammograms of [FeMFe]²⁺ (M = Ni, Pd, Pt) at a scan rate of 100 mV s⁻¹ in CH₃CN.

The separation of the successive redox events (ΔE) recorded in the CV experiment offers information regarding the possible electronic communication between the iron centers and can be converted to the comproportionation equilibrium constant (K_C), eqn (1):¹⁹

K_C = e^ΔEF/RT (1)

The K_C constant of the mixed valent forms were obtained using the ΔE value of 0.21 V for the M = Ni^II and Pt^II complexes and 0.25 V for M = Pd^II giving values of 3500 and 16 800 for the former and latter complexes, respectively. These values are in accord with a Robin–Day class II species, i.e., there is some localization of the added electron but the barrier to site interconversion is low.²⁰ This evaluation assumes that the ΔE value is due to formation of a delocalized mixed-valence species. In contrast, it should be noted that the peak separation could simply be related to the charge difference in the dicationic vs. cation forms as reported by Yang, et al. for a relevant system.²¹

Magnetism

Direct current molar magnetic susceptibility data were collected on powdered crystalline samples of [FeMFe]²⁺ (M = Ni^II, Pd^II, Pt^II), over a temperature range of 2–300 K under an applied field of 10 000 Oe, Fig. 4. The χ_MT value of 0.76 emu K mol⁻¹ for [FeNiFe]²⁺ corresponds to the expected value of 0.75 emu K mol⁻¹ for two uncoupled S = 1/2 centers with g = 2 at 300 K. The value is constant until 25 K after which temperature a steep fall to 0.08 emu K mol⁻¹ is observed. At room temperature, the χ_MT value of [FePdFe]²⁺ is slightly lower, 0.70 emu K mol⁻¹, a signature of weak AFM coupling. The χ_MT value of [FePdFe]²⁺ gradually decreases as the temperature is lowered with a steeper fall at 50 K to virtually zero below 10 K. The χ_MT value at 300 K for [FePtFe]²⁺ is much lower, 0.49 emu K mol⁻¹, indicating stronger AFM coupling. The decrease of the χ_MT value for [FePtFe]²⁺ is more pronounced as the temperature is lowered and is essentially zero at ∼50 K. These results indicate that the {Fe(NO)}⁷ spin centers, separated by 6 Å, are capable of engaging in long range antiferromagnetic interactions through the intervening diamagnetic MS₄ square planar bridging moiety. The interactions are significantly affected by the orbital overlap of the group 10 metals (see Computational section).

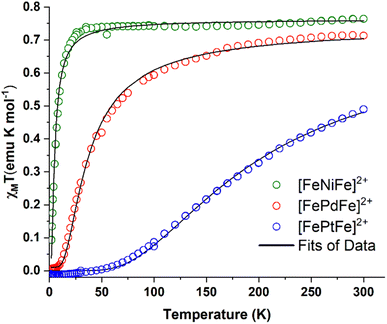Fig. 4 χ _M T vs. T plots for [FeNiFe]²⁺ (green circles), [FePdFe]²⁺ (red circles) and [FePdFe]²⁺ (blue circles). Black curves are the fits of the experimental data.

To obtain an estimate of the magnitude of J, the susceptibility data were fitted using PHI® software²² with the Hamiltonian that is expressed in eqn (2):

H = μBH(gS₁ + gS₂) − 2J(S₁·S₂) (2)

The first term corresponds to Zeeman splitting, whereas the second term is Heisenberg–Dirac–van Vleck magnetic exchange, where S₁ and S₂ are {Fe(NO)}⁷ radical spins (S = 1/2). Best fits were obtained using g values of 2.02 and a coupling constant (J) of −3, −23, and −124 cm⁻¹ for [FeNiFe]²⁺, [FePdFe]²⁺, and [FePtFe]²⁺, respectively. Metrical data from XRD showed no contacts of the magnetic entities closer than 7.9 Å. Additionally, the inclusion of an intermolecular zJ interaction did not improve the fitting.

Computational section

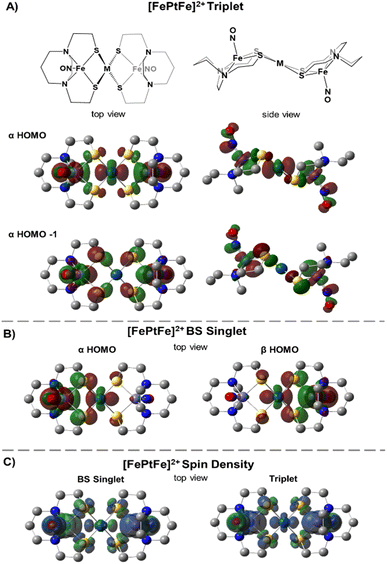
Table 1 compares metrical data from SC-XRD measurements with the optimized, broken symmetry (BS) (AFM-coupled) structures derived from DFT calculations (see details in the ESI†). Good agreement of the metrical sets shows the accuracy of the computational methods utilized to investigate the structures of the three trimetallic molecules; previous success of this methodology in magnetic studies supports its further use here.¹¹Fig. 5C shows the expected parallel and anti-parallel spin alignments of the {Fe(NO)}⁷ radicals as calculated spin density plots for the triplet and BS singlet result, respectively. For the BS singlet significant spin polarization in the M–S₄ orbitals shows how two different spins of the two Fe fragments are coupled through the sulfurs and central metal. As expected, the BS singlet results have large spin contamination (S ∼ 0.6 rather than S = 0), while the triplet excited state had negligible spin contamination (S ∼ 1.01). The J values in Table 1 were calculated from the Yamaguchi formula, eqn (3), which approximately eliminates the spin contamination error; they are in excellent agreement with the experimental trend for the strength of the AFM coupling, i.e., Ni^II < Pd^II ≪ Pt^II.^24,25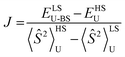

Fig. 5 Molecular orbitals of [FePtFe]²⁺: (A) plots of triplet state α HOMO and α HOMO−1 shown in two views as referenced to the ChemDraw structures and (B) BS singlet α/β HOMOs shown from the top view (isovalue = 0.03). (C) Spin density plots of [FePtFe]²⁺ from the top view (isovalue = 0.001).

We approach the explanation for this trend by examining the frontier orbitals from the electronic structure calculations. Fig. 5 displays the two highest energy α-SOMO's of the triplet state (Fig. 5A) and the α- and β-HOMOs of the BS result (Fig. 5B). The BS solutions are stabilized by the overlap of the α and β orbitals in forming a valence-bond description of the AFM interaction. From Fig. 5 one can see that the two orbitals of the higher energy triplet state are the in-phase and out-of-phase combinations of the BS HOMO's. Thus, J, which exactly reflects the singlet-triplet energy difference, should be related to the energy difference between the two highest α triplet orbitals, i.e., larger triplet orbital splittings result in more stable singlets. These splitting values, shown in Table 1 (last row) as 2.3, 3.4, and 7.7 kcal mol⁻¹ for the [FeMFe]²⁺ series reflect the small, but significant, differences in the J values between [FeNiFe]²⁺ and [FePdFe]²⁺ and the much larger difference between [FePdFe]²⁺ and [FePtFe]²⁺. Comparisons of the orbital plots for all [FeMFe]²⁺ species (Fig. S22 and S23†) show small differences in the central metal's nd (n = 3–5) contribution between Ni and Pd, but a much larger difference for Pt, a reflection of Pt's stronger mixing with the sulfur orbital that engages the {Fe(NO)}⁷ centers in the spin coupling interaction.

Electron spin resonance

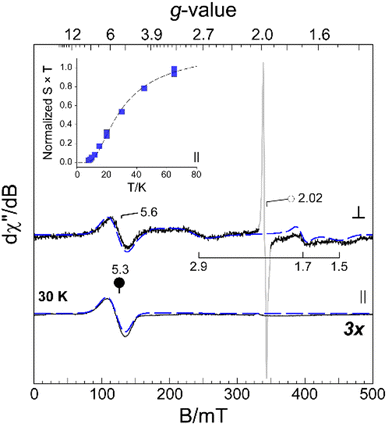
The [FePdFe]²⁺ sample was selected for EPR data collection at X-band for both perpendicular (9.64 GHz, ⊥) and parallel (9.41 GHz, ∥) microwave field (B₁) polarization. Frozen solution samples of [FePdFe]²⁺ exhibit multiple resonances in both perpendicular and parallel mode (Fig. 6, solid lines) which can be attributed to transitions within an integer spin manifold. Integer-spin transitions are frequently observed at g-values ∼4Δm_s. Thus, transitions within an S = 1 spin manifold would be expected near g ∼ 4.²⁶ However, spin–orbit coupling and mixing of m_s-eigenstates can significantly shift the observed g-value. Consequently, the resonance observed near g ∼ 5 in both ⊥ and ∥ B₁-mode can likely be attributed to transitions within a triplet (S = 1) spin manifold. As illustrated in Fig. 6, analytical EPR simulations (dashed lines) of an isolated triplet faithfully reproduce the [FePdFe]²⁺ experimental spectra. An additional, isotropic (S = 1/2) signal observed in the transverse mode at g ∼ 2.02 (Fig. 6, ○) is from an isolated {Fe(NO)}⁷ unit. This signal accounts for less than 3% of the total iron in solution and its characterization is described elsewhere.⁹

Fig. 6 Perpendicular (⊥, 9.64 GHz) and parallel (∥, 9.41 GHz) mode X-band EPR spectra of [FePdFe]²⁺ collected at 30 K. (Inset) Temperature normalized (S × T) signal intensity of the parallel mode (●, g ∼ 5.3) resonance with increasing temperature. Analytical EPR simulations (dashed lines) performed on both microwave field polarizations are overlaid on experimental results (solid line) for comparison.

Among spin-coupled (S = 1) complexes, additional broad features flanking g ∼ 2 can sometimes be observed in the transverse mode providing the magnitude of the axial zero field splitting term (D) is less than the incident microwave frequency (D < hν).^26–30 As shown in Fig. 6, similar signals for samples of [FePdFe]²⁺ are observed at g ∼ 2.9, 1.70, and 1.5. These broad resonances flanking the sharp g = 2.02 peak originate from transitions within the |±1〉 manifold. The position of these features is diagnostic of the magnitude of the zero field splitting terms (D and E).^26,30,31 Here, a reasonable match to all observed resonances in both perpendicular and parallel mode EPR was obtained assuming a small axial zero field splitting (|D| = 0.20 cm⁻¹) and nearly axial rhombicity (E/D = 0.09). The spectral linewidth was reproduced assuming only a minor deviation of coupled system g-values (2.05, 2.06, and 2.00) from the free-electron g-value (g_e, 2.0023) and a minor distribution in E/D (σ_E/D, 0.001). Increased magnetic anisotropy is known to arise from the enhanced spin–orbit coupling of second and third row transition metals.^32,33 This premise coincides with the larger D value of [FePdFe]²⁺vs. the [Fe(Ni₂S₂)Fe]²⁺ dimer complex (|D| = 0.05 cm⁻¹) mentioned above as the former contains the heavier metal.

The intensity of the broad g ∼ 5.3 resonance observed ∥ B₁-mode (Fig. 6, inset) deviates from Curie law behavior in that the temperature-normalized intensity (S × T) of the g ∼ 5.3 signal increases with temperature. This indicates that the observed transition originates within an excited triplet manifold well resolved from the ground state singlet (S = 0). Within the strong coupling limit (J ≫ |D|), the energy separating the ground |0〉 and excited state |±1〉 spin-manifold represents the exchange coupling (J) between two equivalent S = 1/2 sites. This value was determined by fitting the temperature-normalized signal intensity (S × T) data to a Boltzmann population distribution for a 2-level system (see eqn (S2) in the ESI†). As shown in Fig. 6 (inset), the intensity of the g ∼ 4 feature begins to plateau above 40 K suggesting the population of the excited |±1〉 spin-manifold is approaching equilibrium. From this fit a minimum value for the magnitude of J (−20 ± 5 cm⁻¹) was determined. This value is a reasonable match of the value determined by SQUID magnetometry (−23 cm⁻¹).

Conclusions

These studies demonstrate successful new strategies for achieving strong magnetic exchange via 4d/5d metal–thiolate interactions. The ability of the Fe spins on the metalloditholate donor to communicate via spin polarization through the thiolate bridges and the identity of the diamagnetic metal ion, play crucial electronic, rather than steric, roles in tuning the strength of the M–(μ₂-SR)–M′ magnetic interaction. The unexpected homology of the three group 10 transition metals, Ni^II, Pd^II, and Pt^II derivatives to assemble paramagnetic, S = ½, {Fe(NO)}⁷ spin centers with remarkably similar distances and angles of the [FeMFe]²⁺ series in the solid state, including the Fe⋯Fe distances (ca. 6 Å), and the hinge angles (ca. 104°, Table 1) at the bridging thiolate sulfurs atoms that position the three internal planes, extends from SC-XRD to other characterizations. These include ⁵⁷Fe Mössbauer and solution infrared spectroscopies, as well as electrochemistry. The two closely spaced, reversible events in the cyclic voltammograms are assigned to {Fe(NO)}^7/8 reductions indicating that the [FeMFe]⁺ and neutral [FeMFe]⁰ analogues are stable. To date, these compounds have not been isolated from attempts at bulk chemical reduction.

Notwithstanding the structural and spectroscopic similarities within the series, the temperature-dependent magnetic susceptibility data display a dependence on the degree of covalency of the nd orbital (n = 3–5), which to our knowledge is the first to be established for a complete set of group 10 (diamagnetic) transition metal congeners. The J coupling values for the metals ions that link the two metallodithiolate ligands, are −3, −23, and −124 cm⁻¹ for Ni^II, Pd^II and Pt^II, respectively. These results are attributed to superexchange between the {Fe(NO)}⁷ radicals through the central metal d-orbitals mediated by the sulfur bridges. The J values are consistent with the DFT-determined mixing of d-orbitals with well oriented p-orbitals of S, in which Pt^II > Pd^II and is even more pronounced than Pd^II > Ni^II.

The graphical display of experimental |J| values vs. the calculated energy gap between the HOMO and the HOMO−1 of the triplet states of the three complexes reveals a linear correlation into which the results of {Fe(NO)}⁷ radicals bridged by the Ni₂S₂ unit find a remarkably good fit, Fig. 7.

Fig. 7 (A) Comparison of the [FeMFe]²⁺ series to [Fe(Ni₂S₂)Fe]²⁺ complex. Dashed oval encloses strongly coupled radicals resulting in a diamagnetic bridge. (B) Linear relationship between experimental J values vs. the energy gap between the HOMO and HOMO−1 of the triplet states.

The complexity of the orbital interactions in the Ni₂S₂ core bridge was in fact the impetus for developing a simpler description of orbital overlap available in the group 10 metal dication series. Despite the shorter Fe–Fe distance in the [FeNiFe]²⁺ and [FePdFe]²⁺ compounds the superexchange interaction is weaker compared to the tetraradical [Fe(Ni₂S₂)Fe]²⁺ in which stronger coupling (J = −54 cm⁻¹) occurs between the distal iron radicals, separated by about 8 Å.¹¹We conclude that the intricate orbital overlap within the Ni₂S₂core bridge and its interaction with the {Fe(NO)}⁷radicals in the latter facilitate the increased AFM coupling of the Fe(NO) spin centers. In comparison, the highly diffuse and polarizable 5d Pt orbitals result in the strongest AFM coupling interaction amongst all the compounds, a result that is accordant with the difference in the HOMO/HOMO−1 triplet splitting values. For all these species the calculated direct FeS₂–S₂Fe (Fe–Fe) interactions, positioned as they are in the trimetallic complexes, are weak. Thus, DFT calculations suggest that a dimer of the paramagnetic Fe species without any intervening atoms would have a triplet ground state from a near degeneracy of in-phase and out-of-phase MOs of the two Fe fragments. The calculations show that more stable occupied orbitals in the central coupling group of the [FeMFe]²⁺ destabilize one of these nearly degenerate MO's creating a triplet state with splitting values in the order Ni^II < Pd^II < [Ni₂S₂]²⁺ < Pt^II.

We expect that employing other paramagnetic metallodithiolate donors and metal receivers as building blocks or units will result in families of thiolate-bridged heteromultimetallic complexes with strong magnetic communication via sulfur superexchange pathways. For example, although rare, there are precedents for lanthanide ions to bind to the softer thiolate ligands which is promising in terms of extending these studies to paramagnetic metallodithiolates.³⁴ In this vein, there is potential to access unexplored thiolate bridged nd–4f complexes that can be developed as single-molecule magnets with enhanced lanthanide-transition metal magnetic communication.

Data availability

The synthesis and characterization of all compounds, crystallographic analysis of all relevant compounds, and the Cartesian coordinates of all computationally analysed species are available in the ESI.†

Author contributions

MQ synthesized/characterized each compound, performed DFT calculations and magnetic measurements. DJ aided in the synthesis of [FePtFe]²⁺. MML and BSP collected and analyzed the EPR spectroscopic data. SX and YG collected the Mössbauer spectroscopic data. KDR and MB supervised magnetic susceptibility experiments and DFT calculations, respectively. MYD, MQ, KDR, MB, and BSP wrote the manuscript.

Conflicts of interest

There are no conflicts to declare.

Acknowledgements

This work was supported as part of the Reconfigurable Materials Inspired by Nonlinear Neuron Dynamics (REMIND) Energy Frontier Research Center, funded by the U.S. Department of Energy (DOE), Office of Science, Basic Energy Sciences (BES), with synthesis and characterization of the complexes performed at the TAMU Department of Chemistry under award #DE-SC0023353. General laboratory and facility support was provided by the National Science Foundation under Grants MPS CHE 2102159 to MYD and CHE 1808779 to KRD. The R.A. Welch Foundation provided laboratory supplies under Grant A-0924 to MYD and licenses to computational software from the Laboratory for Molecular Simulation at the Texas A&M High Performance Research Computing Facility under Grant A-0648 to MBH. The NIH Institute of General Medical Sciences supported electron paramagnetic resonance system maintenance and measurements under Grant 2R15 GM117511-01 to BSP and Mössbauer instrument maintenance and measurements under Grant R01GM12592 to YG. The Texas A&M High Performance Research Computing Facility is acknowledged for providing computational resources.

References

1. R. M. Bullock, J. G. Chen, L. Gagliardi, P. J. Chirik, O. K. Farha, C. H. Hendon, C. W. Jones, J. A. Keith, J. Klosin, S. D. Minteer, R. H. Morris, A. T. Radosevich, T. B. Rauchfuss, N. A. Strotman, A. Vojvodic, T. R. Ward, J. Y. Yang and Y. Surendranath, Science, 2020, 369, eabc3183.
2. C. Tard and C. J. Pickett, Chem. Rev., 2009, 109, 2245–2274.
3. C.-Y. Chiang, J. Lee, C. Dalrymple, M. C. Sarahan, J. H. Reibenspies and M. Y. Darensbourg, Inorg. Chem., 2005, 44, 9007–9016.
4. J. L. Hess, H. L. Conder, K. N. Green and M. Y. Darensbourg, Inorg. Chem., 2008, 47, 2056–2063.
5. S. Nagashima, M. Nakasako, N. Dohmae, M. Tsujimura, K. Takio, M. Odaka, M. Yohda, N. Kamiya and I. Endo, Nat. Struct. Mol. Biol., 1998, 5, 347–351.
6. J. H. Enemark and R. D. Feltham, Coord. Chem. Rev., 1974, 13, 339–406.
7. N. Sun, L. V. Liu, A. Dey, G. Villar-Acevedo, J. A. Kovacs, M. Y. Darensbourg, K. O. Hodgson, B. Hedman and E. I. Solomon, Inorg. Chem., 2011, 50, 427–436.
8. C. V. Popescu, S. Ding, P. Ghosh, M. B. Hall and M. Cohara, Inorg. Chem., 2019, 58, 7069–7077.
9. P. Ghosh, S. Ding, M. Quiroz, N. Bhuvanesh, C.-H. Hsieh, P. M. Palacios, B. S. Pierce, M. Y. Darensbourg and M. B. Hall, Chem.–Eur. J., 2018, 24, 16003–16008.
10. C.-H. Hsieh, S. Ding, Ö. F. Erdem, D. J. Crouthers, T. Liu, C. C. L. McCrory, W. Lubitz, C. V. Popescu, J. H. Reibenspies, M. B. Hall and M. Y. Darensbourg, Nat. Commun., 2014, 5, 3684.
11. M. Quiroz, M. M. Lockart, M. R. Saber, S. W. Vali, L. C. Elrod, B. S. Pierce, M. B. Hall and M. Y. Darensbourg, Proc. Natl. Acad. Sci. U. S. A., 2022, 119, e2201240119.
12. J. A. Denny and M. Y. Darensbourg, Chem. Rev., 2015, 115, 5248–5273.
13. G. Musie, P. J. Farmer, T. Tuntulani, J. H. Reibenspies and M. Y. Darensbourg, Inorg. Chem., 1996, 35, 2176–2183.
14. Z. Cao, B. Xi, D. S. Jodoin, L. Zhang, S. P. Cummings, Y. Gao, S. F. Tyler, P. E. Fanwick, R. J. Crutchley and T. Ren, J. Am. Chem. Soc., 2014, 136, 12174–12183.
15. E. Pardo, R. Carrasco, R. Ruiz-García, M. Julve, F. Lloret, M. C. Muñoz, Y. Journaux, E. Ruiz and J. Cano, J. Am. Chem. Soc., 2008, 130, 576–585.
16. T. Glaser, T. Beissel, E. Bill, T. Weyhermüller, V. Schünemann, W. Meyer-Klaucke, A. X. Trautwein and K. Wieghardt, J. Am. Chem. Soc., 1999, 121, 2193–2208.
17. L. F. Chibotaru, J.-J. Girerd, G. Blondin, T. Glaser and K. Wieghardt, J. Am. Chem. Soc., 2003, 125, 12615–12630.
18. L. E. Darago, M. D. Boshart, B. D. Nguyen, E. Perlt, J. W. Ziller, W. W. Lukens, F. Furche, W. J. Evans and J. R. Long, J. Am. Chem. Soc., 2021, 143, 8465–8475.
19. R. F. Winter, Organometallics, 2014, 33, 4517–4536.
20. M. B. Robin and P. Day, in Advances in Inorganic Chemistry and Radiochemistry, ed. H. J. Emeléus and A. G. Sharpe, Academic Press, 1968, vol. 10, pp. 247–422.
21. A. H. Reath, J. W. Ziller, C. Tsay, A. J. Ryan and J. Y. Yang, Inorg. Chem., 2017, 56, 3713–3718.
22. N. F. Chilton, R. P. Anderson, L. D. Turner, A. Soncini and K. S. Murray, J. Comput. Chem., 2013, 34, 1164–1175.
23. A. W. Addison, T. N. Rao, J. Reedijk, J. van Rijn and G. C. Verschoor, J. Chem. Soc., Dalton Trans., 1984, 1349–1356.
24. P. Comba, S. Hausberg and B. Martin, J. Phys. Chem. A, 2009, 113, 6751–6755.
25. Y. Kitagawa, T. Saito, Y. Nakanishi, Y. Kataoka, T. Matsui, T. Kawakami, M. Okumura and K. Yamaguchi, J. Phys. Chem. A, 2009, 113, 15041–15046.
26. M. P. Hendrich and P. G. Debrunner, Biophys. J., 1989, 56, 489–506.
27. E. I. Solomon and A. B. P. Lever, Inorganic Electronic Structure and Spectroscopy, Wiley, 2006, vol. I, pp. 1–752.
28. C. J. Curtis, A. V. Astashkin, J. Conradie, A. Ghosh and E. Tomat, Inorg. Chem., 2021, 60, 12457–12466.
29. R. Gautam, A. V. Astashkin, T. M. Chang, J. Shearer and E. Tomat, Inorg. Chem., 2017, 56, 6755–6762.
30. A. Blank and H. Levanon, Concepts Magn. Reson., Part A, 2005, 25, 18–39.
31. J. Telser, in eMagRes, John Wiley & Sons, Ltd, 2017, pp. 207–234.
32. S. C. Coste, T. J. Pearson and D. E. Freedman, Inorg. Chem., 2019, 58, 11893–11902.
33. J. H. Christian, D. W. Brogden, J. K. Bindra, J. S. Kinyon, J. van Tol, J. Wang, J. F. Berry and N. S. Dalal, Inorg. Chem., 2016, 55, 6376–6383.
34. F. Tuna, C. A. Smith, M. Bodensteiner, L. Ungur, L. F. Chibotaru, E. J. L. McInnes, R. E. P. Winpenny, D. Collison and R. A. Layfield, Angew. Chem., Int. Ed., 2012, 51, 6976–6980.

---

Footnote

† Electronic supplementary information (ESI) available. CCDC 2231567–2231569. For ESI and crystallographic data in CIF or other electronic format see DOI: https://doi.org/10.1039/d3sc01546g

---