Open Access Article
Open Access ArticleCreative Commons Attribution 3.0 Unported Licence
How orange carotenoid protein controls the excited state dynamics of canthaxanthin†
Amanda
Arcidiacono
 ,
Davide
Accomasso
,
Davide
Accomasso
 ,
Lorenzo
Cupellini
,
Lorenzo
Cupellini
 and
Benedetta
Mennucci
and
Benedetta
Mennucci
 *
*
Dipartimento di Chimica e Chimica Industriale, Università di Pisa, Via G. Moruzzi 13, 56124 Pisa, Italy. E-mail: benedetta.mennucci@unipi.it
First published on 22nd September 2023
Abstract
Orange Carotenoid Protein (OCP) is a ketocarotenoid-binding protein essential for photoprotection in cyanobacteria. The main steps of the photoactivated conversion which converts OCP from its resting state to the active one have been extensively investigated. However, the initial photochemical event in the ketocarotenoid which triggers the large structural changes finally leading to the active state is still not understood. Here we employ QM/MM surface hopping nonadiabatic dynamics to investigate the excited-state decay of canthaxanthin in OCP, both in the ultrafast S2 to S1 internal conversion and the slower decay leading back to the ground state. For the former step we show the involvement of an additional excited state, which in the literature has been often named the SX state, and we characterize its nature. For the latter step, we reveal an excited state decay characterized by multiple timescales, which are related to the ground-state conformational heterogeneity of the ketocarotenoid. We assigned the slowly decaying population to the so-called S* state. Finally, we identify a minor decay pathway involving double-bond photoisomerization, which could be the initial trigger to photoactivation of OCP.
1. Introduction
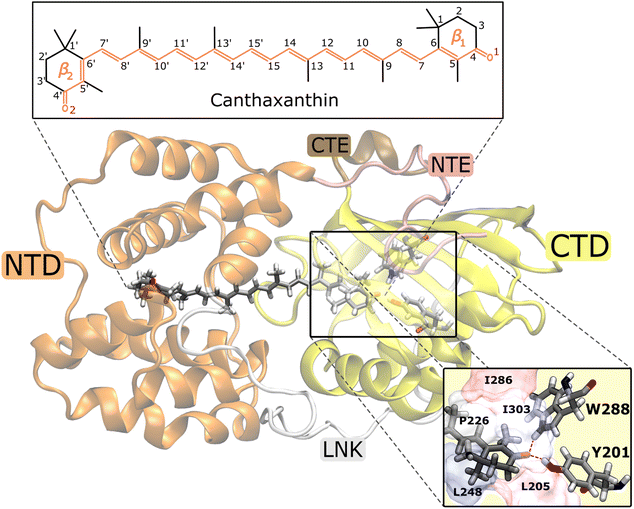
The Orange Carotenoid Protein (OCP)1,2 is a water-soluble protein found in photosynthetic cyanobacteria where it plays a fundamental role in their photoprotection mechanism.3,4 OCP is able to sense the high-light conditions through its chromophore, a keto-carotenoid embedded between the two protein domains, one C-terminal (CTD) and one N-terminal (NTD). The initial excitation of the carotenoid is followed by a translocation of the chromophore in the NTD. This motion initiates a series of conformational changes in the protein's structure, that goes from a “dark adapted” resting form (OCPO) to a “light adapted” active one (OCPR).5–9 It is the latter OCPR form that can quench the excess excitation energy absorbed by the light-harvesting apparatus of cyanobacteria, namely the phycobilisome (PBS), when the system is exposed to intense light.10,11 OCP is able to bind various carotenoids but the crucial feature that determines whether the complex is responsive to light is the possibility of the carotenoid to form hydrogen bonds with two residues of the CTD, Tyrosine 201 (Y201) and Tryptophan 288 (W288). Therefore, the presence of a carbonyl group in the carotenoid is necessary for the protein to be photo-active, even though it is not essential for a stable binding.12 Native OCP can bind either echinenone (ECN), 3′-hydroxy-echinenone (hECN) or canthaxanthin (CAN).13In the last few years, various experimental and theoretical studies have clarified many aspects of the translocation of the carotenoid from the initial binding pocket shared between the CT and NT domains and the final domain separation.7,14–18 The OCPO → OCPR conversion is a multi-step process,19 starting with the rupture of the hydrogen bonds in the CTD.9,20,21 This event results in the first stable product of OCP photocycle in a ps time scale, even though its atomistic mechanism is still under debate.7,15,20 Indeed, what is still largely unknown is the photochemistry that follows the initial π → π* excitation of the carotenoid and how its time evolution can trigger such radical conformational changes in the protein.
What it is expected for a (keto)carotenoid is that the initial photo-absorption induces a transition to the lowest energy bright state (1Bu+, using a simplified C2h symmetry), which rapidly decays to a lower energy dark state (S1 or 2Ag− pseudo-symmetry22). This is known to be an ultrafast process that occurs within few hundred fs. For several carotenoids, including CAN and hECN, spectroscopic signatures from another state were observed in the ultrafast process, and this state was called SX.23–27 The final decay of S1 to S0, which is commonly completed on a time scale of several ps, is even more complex and still openly discussed. It has been suggested that other dark states are involved. One is generally referred to as S*,16,27–32 while the other is an intramolecular charge transfer (ICT) state, strongly coupled with S1.5,14,15,33–36 These states have different decay times. For keto-carotenoids a faster decay to the ground state occurs on the scale of few picoseconds, generally associated with the 2A/ICT decay, while a slower component of tens of picoseconds is attributed to S*. The nature of the couplings between those states is still unknown, along with the nature of S*.
In this context, an explicit simulation of the excited state dynamics of the ketocarotenoid in OCP could represent a powerful approach to disentangle the different decay pathways towards the ground state. However, an accurate ab initio QM description of the electronic structure of (keto)carotenoids is very challenging. The multireference character of their electronic states, in fact, calls for very expensive computational methods, whose applicability is still limited to small molecules. To overcome these limits, an effective strategy is to adopt a semiempirical QM method in combination with a multiconfigurational description of the electronic states, as well as to introduce the effects of the protein and the solvent through a molecular mechanics (MM) model; this integrated approach has been successfully used in previous studies of carotenoids.18,37 In the present work, we employ this strategy to reproduce the multi-step decay pathway of canthaxanthin in OCP. This is obtained by applying QM/MM nonadiabatic excited-state dynamics based on the surface hopping (SH) method.38
Such a computational approach allowed us to simulate both the ultrafast S2 → S1 conversion and the slower S1 decay towards the ground state. In the ultrafast relaxation process, we observed the formation of an intermediate “dark” state of Bu− pseudo-symmetry, which we associated with the spectroscopic SX state, similar to what we found for lutein in a previous study.37 Regarding the S1 → S0 conversion, our simulations indicated that the decay of the S1 population is multi-exponential and the different excited-state lifetimes stem from the ground-state structural heterogeneity of CAN in OCP. In particular, we assigned the slow component of this decay to the S* state. Finally, we found a minor S1 → S0 decay pathway involving the isomerization of a double bond of CAN adjacent to the β1 ring in the CTD. This photoisomerization could be the trigger of OCP light activation.
2. Methods
2.1. Electronic states
The electronic states of CAN were computed using the semiempirical configuration interaction method FOMO-CI.39–41 In particular, we used the AM1 form of the semiempirical Hamiltonian,42 with the parameters optimized for lutein in our previous work.37 In the FOMO-CI calculations we employed an active space of 8 electrons in 10 molecular orbitals of π type, a Gaussian energy width for a floating occupation of 0.075 Hartree, and a determinant space including all single and double excitations within the orbital active space. Additional information regarding the selection of the orbital active space for the FOMO-CI method is provided in Section S1.†In the simulations of CAN in OCP, we used a quantum mechanics/molecular mechanics (QM/MM) scheme,43 in which CAN, treated at the semiempirical QM level, is embedded in the MM protein environment of OCP. For the MM part, we employed the parameters of the ff14SB AMBER force field.44 The interaction between the QM and MM subsystems was treated using the electrostatic embedding scheme. In all the QM/MM simulations, we considered a subsystem of the solvated OCPO as investigated in ref. 45. Specifically, in the MM part we included only the protein residues, water molecules and ions within a distance of 25 Å from CAN. Furthermore, in the molecular dynamics simulations, only the MM residues within 18 Å of CAN were allowed to move, while all the other MM atoms were frozen.
2.2. Nonadiabatic excited-state dynamics
The nonadiabatic excited-state dynamics of CAN was simulated using the “fewest switches” surface hopping (SH) method.38,46 The starting conditions (i.e., nuclear coordinates and velocities, and the initial electronic state) for the SH simulations were sampled from ground-state thermal trajectories at 300 K that we performed with the Bussi–Parrinello stochastic thermostat.47,48 In particular, for the simulations in OCP we sampled the last 5 ps of ten QM/MM equilibrations propagated for 10 ps, while for the gas phase simulations we used the last 20 ps of a single QM thermal MD. More details on the ground state equilibrations are provided in the ESI (see Section S2 in the ESI†). In the sampling procedure, the initial electronic state was selected according to the radiative transition probability from the ground state,41 within an excitation energy range of 2.63 ± 0.15 eV for CAN in OCP, and 2.67 ± 0.15 eV for CAN in the gas phase. In both cases, the selected energy window includes most of the main band of the UV/vis absorption spectrum of CAN, computed along the thermal equilibrations (Fig. S15 in the ESI†).In the SH simulations, the time evolution of the electronic wavefunction was computed by making use of a locally diabatic representation,40,49 and with a time step of 0.2 fs, employed in the integration of both the nuclear degrees of freedom and the electronic ones. Quantum decoherence effects along the SH trajectories were approximately taken into account using the overlap decoherence correction (ODC) scheme, with the following parameters: σ = 1.0 a.u. (Gaussian width) and Smin = 5 × 10−3 (minimum overlap).50,51 For the simulations in OCP, a total of 364 SH trajectories (39 starting from S1, 318 from S2, and 7 from S3) were simulated, while 39 SH trajectories, starting from the S2 state, were computed in the gas phase simulations. All the SH trajectories were propagated for 20 ps, under energy-conserving conditions. The six lowest singlet states were taken into account in the nonadiabatic SH dynamics, which was considered sufficient a posteriori, given that states above S3 are never populated. For each simulation time, the population of each electronic state i was computed as the fraction of SH trajectories running on the i-th PES.
All the simulations were performed using a development version of the MOPAC code,52 interfaced with the TINKER 6.3 (ref. 53) molecular modeling package, in which the SH method and the QM/MM semiempirical FOMO-CI technique were implemented.
3. Results
3.1. Ultrafast S2 → S1 dynamics
We first analyze the ultrafast component of the photoinduced dynamics of CAN, namely the internal conversion between S2 and S1. This process is known to occur in the subpicosecond time scale, therefore we focus on the first 200 fs after photoexcitation (Fig. 2), and follow the time evolution of the adiabatic state populations for CAN in the gas phase and in OCP. In both cases, after vertical excitation, we observe rapid oscillations of the populations of S2 and S3 within the first 100 fs, indicating a back-and-forth population exchange between these two states. This is a symptom of multiple recrossings between two potential energy surfaces, favored by the near degeneracy of S2 and S3 (the energy profile is reported in Fig. 2, panels B and B′, while the energy gap distribution at S2 → S3 and S3 → S2 transitions is shown in ESI Fig. S17†). Analogous behaviour was observed for the ultrafast dynamics of Lutein,37 and was ascribed to the crossing between states of 1Bu+ and 1Bu− character. These states correspond to S2 and S3 respectively at the Franck–Condon point, but they continuously swap along the dynamics. The S2–S3 population recrossing is less pronounced in OCP, compared to the gas phase, likely due to the larger S2–S3 energy gap after the first 10 fs of dynamics. The nuclear dynamics within the first 100 fs is dominated by strong oscillations of the bond-length-alternation (BLA) coordinate (Fig. 2, panels C and C′), which modulates the excitation energy of states S1–S3. This allows S2 and S3 to become very close in energy at regular intervals. Finally, the BLA oscillations are damped after ∼100 fs, although the damping time seems shorter in OCP.To follow the population dynamics in the ultrafast timescale, we analyzed the potential energy curves of the first four excited states of CAN along the BLA coordinate (Fig. S11 in the ESI†). Due to the qualitatively similar picture obtained in vacuo and in OCP, this analysis has been performed for the isolated molecule. Vertical excitation populates 1Bu+ (S2), and then CAN rearranges its geometry towards smaller BLA values, following the excited-state gradient. Since the energy difference between 1Bu+ and 1Bu− is small, the nuclear wavepacket can oscillate back and forth along the BLA coordinate, encountering the crossing region between these two states (see Fig. 2). Although part of the population is transferred to 1Bu−, the majority remains diabatically in the 1Bu+ state, which becomes S3 at small BLA values (Fig. S11 in the ESI†). This explains why the adiabatic state S3 is periodically populated, and the oscillations of adiabatic populations perfectly match the oscillation period of the BLA.
The 1Bu− minimum is close to the S1 one in the BLA picture (Fig. S11 in the ESI†), therefore the transition to 1Bu− might facilitate the decay to S1 in an ultrafast time scale. As CAN settles in the S1 state, the BLA drops to nearly zero (Fig. 2), indicating that single and double bonds have similar strength in this state. This reflects the electron density displacement from double to single bonds in the excited states of CAN, as this displacement is more substantial for the S1 state.18 Along the ultrafast dynamics, other degrees of freedom need to be activated in order to reach the 1Bu− and finally the S1 state. These include both all other C–C and C![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) C modes and out-of-plane torsional motions. The latter are enhanced in OCP, as CAN's geometry is strongly distorted due to the constraints exerted by the protein pocket. This also explains why the initial decay to S1 is slightly faster in OCP than in the gas phase.
C modes and out-of-plane torsional motions. The latter are enhanced in OCP, as CAN's geometry is strongly distorted due to the constraints exerted by the protein pocket. This also explains why the initial decay to S1 is slightly faster in OCP than in the gas phase.
Comparing the population evolution in the adiabatic and diabatic representations (Fig. S12 in the ESI†), we can see that the S2/S3 population oscillations persist for the lifetime of the 1Bu+ state. The 1Bu+ bright state is thus depopulated in <100 fs in the gas phase and in <50 fs in OCP, which is consistent with the ∼20 fs emissive lifetime extracted from fluorescence experiments.54 In contrast to ref. 54 though, we find that the ultrafast decay of 1Bu+ is mediated by the transfer to 1Bu−, before the S1 state is reached.
The results obtained indicate a role of the 1Bu− dark state in the S2 → S1 relaxation process, as observed previously for Lutein.37 This bridge state was also detected experimentally for different carotenoids and it is often referred to as SX.23–27 The relaxation pathway S2 → SX → S1 is shared between the gas-phase and OCP simulations, with a faster conversion between S2 and SX observed in OCP. This result, and the striking analogy to the case of Lutein, suggest that the SX-mediated decay pathway could be a rather common feature in the photoinduced dynamics of carotenoids.
3.2. The S1 → S0 relaxation process
We now consider the slower part of the decay process, up to the first 20 ps. In Fig. 3A and B we again compare the populations of the adiabatic states of CAN in the gas phase and in OCP.In the gas phase simulations, the population of S1 increases within the first picosecond and then decays to S0 with a single-exponential behaviour. We extracted the rise and decay times of S1 assuming the following kinetic model:
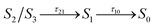 | (1) |
In contrast to gas-phase simulations, in OCP the decay of S1 cannot be described by a single-exponential function (Fig. 3Band C). To fit the S1 population, we used a similar kinetic model (eqn (1)), but with two decay times for S1, namely τA and τB:
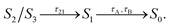 | (2) |
The decay components τA and τB are weighted respectively by wA and wB = 1 − wA (eqn (9) in the ESI†). The fit yielded τ21 = 0.1 ps, and the following S1 lifetimes: τA = 14.3 ps and τB = 0.8 ps, with weights 40% and 60%, respectively. A weighted average gives us a lifetime of 6.2 ps. Although both decay times of S1 in OCP differ significantly from the one obtained in the gas-phase simulations (4.8 ps), the average lifetime is only slightly longer. However, the two substantially different lifetimes obtained in our simulations strongly suggest a heterogeneity within OCP that is not present in gas-phase simulations.
To investigate the origin of such different S1 lifetimes in OCP, we analyzed the structural features of CAN in the ground-state ensemble, namely at the starting geometries for the SH trajectories (t = 0). From this analysis, we noticed that the initial geometries can be divided into two groups according to the puckering of the β1 ring of CAN, located in the CTD (Fig. 1) (see details in Section S6 in the ESI†). Notably, ring puckering was recognized to be a determinant of heterogeneity in OCP.45,55 Here we assign the structures with ϕ ≤ 0° to the p− conformation (52% of the total number of trajectories), and all the other structures (with ϕ > 0° at t = t0) to the p+ conformation (Fig. S14 in the ESI†). We then divided a priori the SH trajectories on the basis of the puckering angle at the initial time.
 | ||
| Fig. 2 Ultrafast portion of CAN excited-state dynamics in vacuo (A, B, C) and in OCP (A′, B′, C′) (see ESI Fig. S12† for the diabatic representation of the vacuo populations and energies). Results are obtained from 39 trajectories and 364 trajectories in vacuo and in OCP, respectively. Panels A/A′ show the adiabatic state populations of CAN during the first 200 fs of the SH simulations. In panels B/B′ and C/C′, respectively, the excitation energies from the ground state and the BLA values are reported. | ||
In Fig. 3C, we report the time evolution of the S1 population for the two groups of SH trajectories, p− and p+. A clear trend appears, as the decay for the p+ group is much faster than the p− trajectories. The S1 population in p+ trajectories can be fitted by a single exponential decay with a time constant of 0.84 ps, close to the fastest time constant of the entire ensemble τA. On the other hand, the population for the p− group shows again a bi-exponential decay, from which we extracted two lifetimes, namely 1.21 ps and 15.30 ps (with relative weights of 0.3 and 0.7, respectively). The longest time constant is again close to the slowest decay time τB obtained for the entire ensemble.
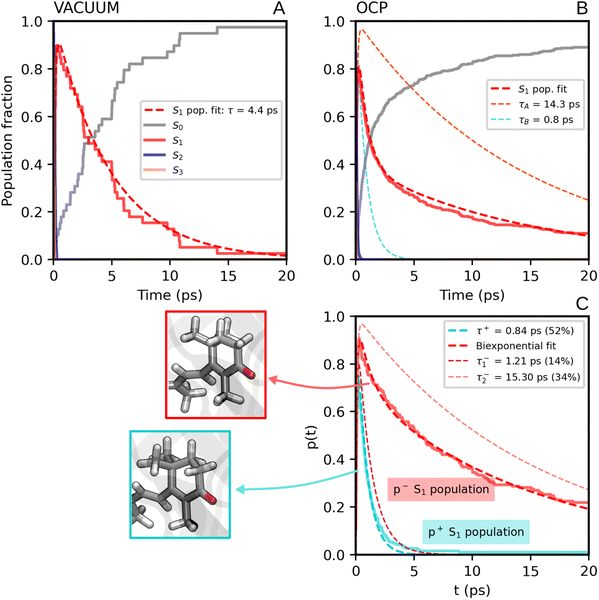 | ||
| Fig. 3 (A) Populations of the adiabatic states of CAN obtained from the SH simulations in the gas phase. The red dashed line is the fitting function for the S1 population (eqn (1) and S8 in the ESI†). (B) Populations of the adiabatic states of CAN for the SH simulations in OCP, with the fitting biexponential function for the S1 population (eqn (2) and S9 in the ESI†) reported as a dashed red line, together with its single-exponential components (light-blue and orange dashed lines). (C) Population of the S1 state for the two groups of SH trajectories obtained from the puckering-based separation (see text). The single-exponential fitting function for the p+ group of trajectories and the bi-exponential fitting function for the p− group, in addition to its single-exponential components, are also reported (dashed lines). | ||
Separating the SH trajectories on the basis of the ground-state conformation allows a clear discrimination between the faster decaying trajectories from the slower ones. In turn, this indicates that the multiexponential behaviour of the S1 population decay is determined by heterogeneity in the ground-state ensemble. Overall, three decay times for S1 can be extracted: a sub-picosecond lifetime of 0.8 ps obtained from the p+ group, and two longer decay times of 1.2 ps and 15.3 ps, both obtained from the p− trajectories.
3.3. Structural changes of CAN during the excited-state decay
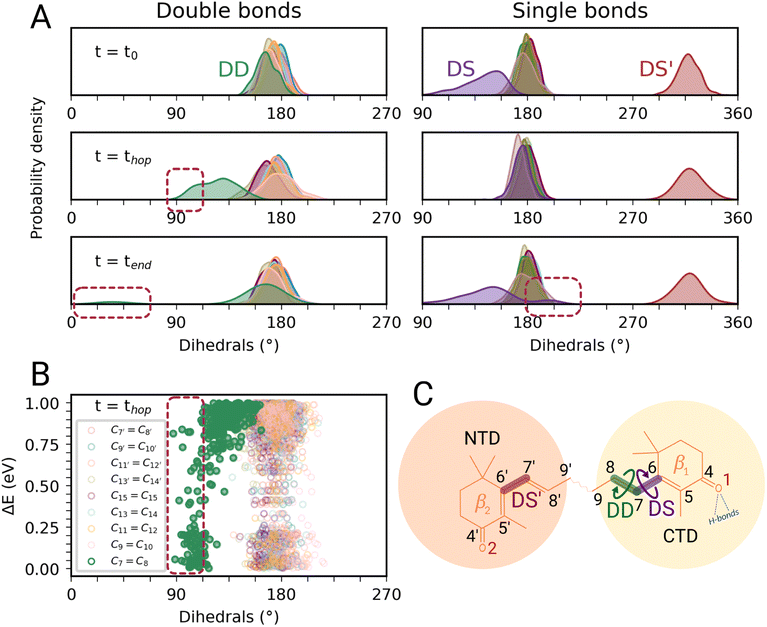
In this section, we characterize the main structural changes of CAN occurring during the S1 → S0 relaxation process. In Fig. 4A, we report the distributions of the dihedral angles around the C![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) C and C–C bonds of the π-conjugated chain of CAN for different times of the SH simulations in OCP. Each dihedral angle of CAN was computed as the clockwise angle between the two half-planes defining the dihedral, i.e., all dihedrals range between 0° and 360°. Under the initial conditions (Fig. 4A, panel t = t0), we find a significant distortion for the single bond connecting the π-conjugated chain with the β1 ring of CAN. This bond is in an s-trans conformation but the corresponding dihedral angle (from now DS) ranges from 180° to almost 90°. The opposite dihedral (DS′, Fig. 4C), involving the β2 ring in the NTD, displays instead an s-cis conformation with values between 300° and 360°. The dihedrals around all the other C–C and C
C and C–C bonds of the π-conjugated chain of CAN for different times of the SH simulations in OCP. Each dihedral angle of CAN was computed as the clockwise angle between the two half-planes defining the dihedral, i.e., all dihedrals range between 0° and 360°. Under the initial conditions (Fig. 4A, panel t = t0), we find a significant distortion for the single bond connecting the π-conjugated chain with the β1 ring of CAN. This bond is in an s-trans conformation but the corresponding dihedral angle (from now DS) ranges from 180° to almost 90°. The opposite dihedral (DS′, Fig. 4C), involving the β2 ring in the NTD, displays instead an s-cis conformation with values between 300° and 360°. The dihedrals around all the other C–C and C![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) C bonds of the π-conjugated chain of CAN assume values between 150° and 210°, typical of a planar all-trans geometry.
C bonds of the π-conjugated chain of CAN assume values between 150° and 210°, typical of a planar all-trans geometry.
During the nonadiabatic dynamics, the most significant structural changes of CAN can be observed at the S1 → S0 transitions. These occur at different times depending on the trajectory, but are analyzed together in Fig. 4A (middle panel t = thop). The distribution of the dihedral around the C7![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) C8 double bond (DD from now on, Fig. 4C) is significantly broader and partially shifted towards 90°. On the other hand, the adjacent single bond dihedral (DS) presents a narrower range of values, closer to the dihedrals around the other conjugated C–C bonds (Fig. 4A). This occurs because, in the S1 geometry, DD and DS exchange their double-bond character and consequently their flexibility. As a consequence, the significant distortion around the β1 ring forces the DD dihedral to twist as soon as the DS dihedral planarizes (Fig. 4C). Conversely, the remaining single and double bonds in the conjugated chain of CAN do not undergo any significant change.
C8 double bond (DD from now on, Fig. 4C) is significantly broader and partially shifted towards 90°. On the other hand, the adjacent single bond dihedral (DS) presents a narrower range of values, closer to the dihedrals around the other conjugated C–C bonds (Fig. 4A). This occurs because, in the S1 geometry, DD and DS exchange their double-bond character and consequently their flexibility. As a consequence, the significant distortion around the β1 ring forces the DD dihedral to twist as soon as the DS dihedral planarizes (Fig. 4C). Conversely, the remaining single and double bonds in the conjugated chain of CAN do not undergo any significant change.
Notably, the distortion of DD is most of the time accompanied by a significant decrease in the adiabatic energy gap between S1 and S0 (ΔE, Fig. 4B). By looking at the distribution of ΔE at the hopping times of the SH trajectories (Fig. S16 in the ESI†), we can notice that for many trajectories the S1 → S0 transition takes place with a very small energy gap (ΔE < 0.25 eV). This indicates the reaching of a S1/S0 crossing region when DD approaches 90° (Fig. 4B), which promotes internal conversion to S0. Such a crossing is not observed in gas phase simulations, where the S1 → S0 hops always occur with ΔE > 0.7 eV and without any particular change in CAN's structure. In OCP, the orientation of the β1 ring likely facilitates distorted structures when CAN is in the S1 state. As a consequence, CAN is able to access structures where the S1 and S0 states are close in energy.
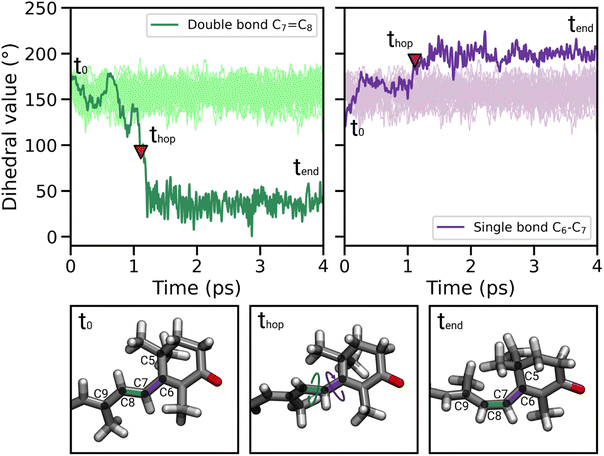
In most of the SH trajectories, after the S1 → S0 transition, DD and DS go back to their original values (Fig. 4A, panel t = tend). However, for a small number (∼12%) of trajectories we observe that DD reaches values close to zero, indicating trans-to-cis isomerization around the double bond, accompanied by a torsion around DS towards the s-cis conformation. This isomerization is illustrated in Fig. 5 for a representative SH trajectory. From the opposite behavior of the two adjacent single and double bonds, we identify the isomerization mechanism as a hula-twist mechanism, a volume-conserving photoisomerization already observed in several protein-bound chromophores, such as retinoids, cryptochromes, and phytochromes.56,57
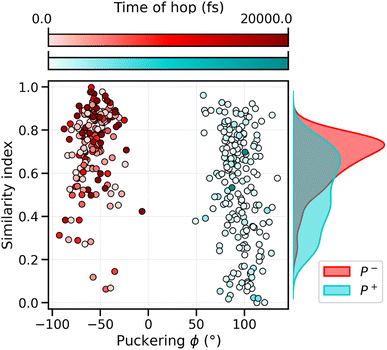
To analyze what determines the likelihood of photoisomerization, we divide the trajectories on the basis of the puckering angle (see Section 3.2). Most of the photoisomerization events occur in the p+ trajectories (Fig. S14 in the ESI†), with a yield of 18%, while the photoisomerization yield for the p− group is only 5%. The higher yield of isomerization and the faster decay of the S1 population obtained for the p+ trajectories can be both related to the initial (t = t0) distortion of DS, which we evaluated using the similarity index, sθ = cos2![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) θ. sθ ranges between 0 and 1, 0 corresponding to the twisted conformation (θ = 90°) and 1 corresponding to the perfectly planar conformation, either s-cis (θ = 0°) or s-trans (θ = 180°). As we can see from Fig. 6, the distribution of sDS for the initial geometries of the p+ trajectories is significantly broader and shifted towards smaller values, compared to the corresponding distribution for the p− group. The mean values at t = 0 are sDS = 0.51 for p+ and sDS = 0.73 for p−, indicating a larger initial deviation of DS from the perfectly planar s-trans conformation. The p+ trajectories are also associated with a smaller S1–S0 energy gap at hops, and a larger twisting of DD at the same S1 → S0 transition geometries (see Table S2†). Therefore, the larger initial distortion of DS, observed in the p+ trajectories, increases the accessibility of highly distorted molecular geometries, where the twisting around DD is large and the S1–S0 energy gap is small, leading to both a faster S1 → S0 decay and a higher photoisomerization yield.
θ. sθ ranges between 0 and 1, 0 corresponding to the twisted conformation (θ = 90°) and 1 corresponding to the perfectly planar conformation, either s-cis (θ = 0°) or s-trans (θ = 180°). As we can see from Fig. 6, the distribution of sDS for the initial geometries of the p+ trajectories is significantly broader and shifted towards smaller values, compared to the corresponding distribution for the p− group. The mean values at t = 0 are sDS = 0.51 for p+ and sDS = 0.73 for p−, indicating a larger initial deviation of DS from the perfectly planar s-trans conformation. The p+ trajectories are also associated with a smaller S1–S0 energy gap at hops, and a larger twisting of DD at the same S1 → S0 transition geometries (see Table S2†). Therefore, the larger initial distortion of DS, observed in the p+ trajectories, increases the accessibility of highly distorted molecular geometries, where the twisting around DD is large and the S1–S0 energy gap is small, leading to both a faster S1 → S0 decay and a higher photoisomerization yield.
To investigate the origin of the larger initial distortion of DS in the p+ trajectories, we analyzed the arrangement of the amino acid residues surrounding the β1 ring of CAN in the ground-state ensemble. Specifically, we computed the minimum distances between the center of the β1 ring of CAN and the following residues of the CTD: L205, L248, I303, P226, and I286 (Fig. 1). The C2 atom was excluded from the definition of the center of the β1 ring to avoid bias coming from the puckering itself. Moreover, the two hydrogen-bonded residues Y201 and W288 (Fig. 1) were not included because their minimum distance from the β1 ring of CAN is not affected significantly by the puckering. From our analysis, it turns out that residues I303, P226, and I286 are generally closer to the β1 ring in the p+ geometries, while for both L248 and L205 the distance from the β1 ring is shorter in the p− geometries (Fig. S18 in the ESI†).
To obtain a more direct visualization of the correlation in the ground-state ensemble between the puckering, the disposition of the aforementioned amino acids, and the value of sDS, we report in Fig. S19 in the ESI† a principal component analysis (PCA) based on the distances from the 5 selected residues. From the left panel of Fig. S19† it is evident that the puckering value follows the separation given by the PC1, with very few exceptions. In addition, at negative values of the PC1, sDS reaches lower values, i.e., geometries that are farther from the planar conformation, showing that the distortion is linked to the disposition of the residues.
Combining all these analyses, we conclude that the larger initial twisting of DS in the p+ trajectories can be attributed to the different, puckering-dependent, placement of the β1 ring inside a rather rigid protein binding pocket.
4. Discussion and comparison with experiments
4.1. Ground-state heterogeneity and multiexponential decay
Our simulations of CAN in the gas phase indicated a single-exponential decay of the S1 population, with a time constant of 4.8 ps. This time is very close to the reported S1 lifetimes determined by transient absorption spectroscopy in solvents of different polarities, namely 4.3–4.9 ps (ref. 30 and 58) (Table S3 in the ESI†). No relevant twisting of the carotenoid chain occurs during the S1 → S0 decay in the gas phase.Within OCP, the S1 → S0 relaxation dynamics is significantly different. First of all, the S1 population decay cannot be described by a single-exponential function, but at least two different decay times are required. This multiexponential decay character of S1 has been reported in several time-resolved spectroscopic studies of OCP.5,14–16,36,59 In particular, up to three different decay components were proposed to explain the S1 → S0 decay of keto-carotenoids bound to OCP, each attributed to a different species: (i) the “proper” dark S1 (pseudo 2Ag−) state, (ii) an intramolecular charge transfer (ICT) state, and (iii) an additional dark state, called S*. The strongly coupled ICT and S1 states are generally associated with lifetimes of 0.5–0.9 ps and 2–5 ps,5,14–16,36,59 respectively, while a longer decay time (>7 ps) has been attributed to S*15,16 (Table S3 in the ESI†). There is still debate on the exact nature of the S* feature, although it is shared between several carotenoids.29 One explanation is that the S* feature arises from a “more twisted” conformation on the S1 potential energy surface. This distinct conformation could be the result of heterogeneity in the ground-state ensemble, or could arise within the excited-state dynamics by branching from S2.29
The experimental evidence of three different lifetimes is consistent with our analysis of the S1 sub-populations obtained from the puckering-based separation of the SH trajectories (Section 3.2). On the basis of our extracted decay times, we can associate the p+ and faster-decaying p− trajectories with the S1/ICT state (0.8 ps and 1.2 ps lifetimes, corresponding to 52% and 14% of the S1 population, respectively), and the slower p− component with S* (15 ps, 34%). This assignment also suggests a connection between the conformational distortion of CAN and the presence of the S* feature. Furthermore, the slower relaxation component can be easily associated with a ground-state conformational feature such as the puckering angle. For this reason, we attribute the appearance of an S* feature to the presence of more conformations of CAN within the ground-state ensemble. Surprisingly, our analysis of the DS dihedral suggests that S* is associated with a more planar structure (in the S1 state) than “proper” S1. Whether this observation could be specific to CAN in OCP, or more general to different carotenoids, has to be further investigated. According to our simulations, most of the relaxation process in OCP occurs through the S1/ICT state, while the slow-decaying S* component represents only a small portion of the S1 population, in agreement with experiments.15,16
Our identification of the S1 sub-populations supports the hypothesis that the multi-exponential character of S1 is due to the ground-state structural heterogeneity of the carotenoid in OCP.14,36,55,60 In fact, we could separate the two S1 sub-populations based only on the CAN conformation in the ground state. Conversely, no significant structural change was identified during the S2 → S1 relaxation. These results thus strongly support the ground-state heterogeneity origin of the S* feature, rather than a branching from a common S2 state. We could clearly associate the ground-state heterogeneity with the puckering conformation of the β1 ring of CAN, which in turn affects the dihedral angle between the π-conjugated chain and the β1 ring (DS, Fig. 4) in the ground state. The importance of the puckering of CAN keto-ring in the photoactivation mechanism of OCP has been previously suggested.45,55 Specifically, in a previous study by some of us,45 it has been shown that the potential of the keto-ring rotation depends on the puckering state. Moreover, Pishchalnikov et al.55 suggested that puckering can affect the position of the CAN keto-group in the CTD, and hence the hydrogen bond lengths between the carotenoid keto-oxygen and residues Y201 and W288.
4.2. Photoisomerization and photoactivation mechanism
For a fraction of SH trajectories (∼12%, most of which with p+ puckering, Table S2†), the twisting of DD at the S1 → S0 transition geometries leads to the trans-to-cis isomerization of C7![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) C8, accompanied by a partial torsion around C6–C7 (Fig. 5). To the best of our knowledge, this kind of photoisomerization, which we identified as a hula-twist mechanism,56,61 has not been reported yet for protein-bound carotenoids. Since this isomerization occurs in the CTD of OCPO, it represents a possible trigger for hydrogen bond rupture between the β1-ring of CAN and residues Y201 and W288 in OCP photoactivation. As a matter of fact, one proposed mechanism for hydrogen bond rupture involves the trans-to-cis s-photoisomerization of the C6–C7 single bond, which would flip the orientation of the β1 ring by 90°.21 The C7
C8, accompanied by a partial torsion around C6–C7 (Fig. 5). To the best of our knowledge, this kind of photoisomerization, which we identified as a hula-twist mechanism,56,61 has not been reported yet for protein-bound carotenoids. Since this isomerization occurs in the CTD of OCPO, it represents a possible trigger for hydrogen bond rupture between the β1-ring of CAN and residues Y201 and W288 in OCP photoactivation. As a matter of fact, one proposed mechanism for hydrogen bond rupture involves the trans-to-cis s-photoisomerization of the C6–C7 single bond, which would flip the orientation of the β1 ring by 90°.21 The C7![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) C8 double bond isomerization observed in our SH simulations involves only a partial twisting of the adjacent C6–C7 single bond, which retains its s-trans conformation, and therefore does not lead to the 90° flip of the β1 ring (Fig. 5). This outcome is consistent with the spectroscopic investigation by Konold et al.,15 who excluded β1 ring rotation on the basis of pump-probe vis-IR absorption anisotropy measurements for OCP binding 3′-hydroxyechinenone (hECN). It should be noted that a complete flip of the β1 ring would be very unlikely in the tight OCP binding pocket, as it would be sterically hindered by the protein residues in close contact with the ring. In contrast, the photoisomerization mechanism observed in our simulations does not involve any large movement (only the movement of the methyl group connected to C9 is needed, see Fig. 5).
C8 double bond isomerization observed in our SH simulations involves only a partial twisting of the adjacent C6–C7 single bond, which retains its s-trans conformation, and therefore does not lead to the 90° flip of the β1 ring (Fig. 5). This outcome is consistent with the spectroscopic investigation by Konold et al.,15 who excluded β1 ring rotation on the basis of pump-probe vis-IR absorption anisotropy measurements for OCP binding 3′-hydroxyechinenone (hECN). It should be noted that a complete flip of the β1 ring would be very unlikely in the tight OCP binding pocket, as it would be sterically hindered by the protein residues in close contact with the ring. In contrast, the photoisomerization mechanism observed in our simulations does not involve any large movement (only the movement of the methyl group connected to C9 is needed, see Fig. 5).
Recent time-resolved X-ray crystallography experiments62 revealed a concerted isomerization of two carotenoid single bonds located in the NTD, namely C6′–C7′ and C8′–C9′ (Fig. 1), through the so-called bicycle-pedal mechanism. This isomerization, occurring near the β2 ring, was proposed as a possible trigger for OCP photoactivation. In our simulations we do not observe this type of photoisomerization, as both the C6′–C7′ and C8′–C9′ single bonds preserve their initial conformations along all the SH trajectories. To resolve this discrepancy, we note that the first structural intermediate collected in time-resolved X-ray experiments corresponds to a 1 minute time delay after illumination. Notably, this time delay is much longer than the entire photoactivation time of OCP, and does not strictly represent the primary photoproduct, which is instead formed in the ps timescale.15 Furthermore, the experimental conditions employed in ref. 62 could have altered the photocycle of OCP due to the crystal packing. Finally, isomerization at the β1 ring seems a more likely cause of photoactivation, as (i) the β1 ring is conserved among different OCP-bound carotenoids, and (ii) it is the location of the H-bond disruption necessary for carotenoid translocation.
In our simulations, most of the photoisomerization events were observed in the early decaying trajectory group, i.e., the one that we associate with the S1/ICT component of the S1 population, rather than S*. This is in agreement with a recently reported spectroscopic investigation,16 which ruled out the idea that S* is responsible for the formation of the primary photoproduct (P1) of OCP photoactivation15 and suggested instead that a small portion of the S1 population evolves into P1. In fact, if photoisomerization is the trigger for photoactivation of OCP, then the primary photoproduct would evolve from the short-lived components rather than from the long-lived one, according to our simulations. If we exclude from the analysis all trajectories that photoisomerize, the remaining p+ trajectories still present a short-lived S1 lifetime (on average 1.2 ps), indicating that photoisomerization is not the cause for the fast decay time, but rather that the two events are associated with the same structural features of CAN.
To conclude, photoisomerization at the C7![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) C8 double bond seems a likely trigger for the H-bond breaking that finally leads to CAN translocation. However, during our simulations we have not observed any breaking of the two hydrogen bonds with Y201 and W288. As the photoisomerization mechanism conserves the orientation of the β1 ring, there is no immediate force steering the CAN carbonyl away from the H-bonding residues. On the other hand, the new isomer state might lower the barrier towards H-bond dissociation and facilitate the translocation of CAN. The confirmation of this hypothesis however would require additional simulations over a longer time scale.
C8 double bond seems a likely trigger for the H-bond breaking that finally leads to CAN translocation. However, during our simulations we have not observed any breaking of the two hydrogen bonds with Y201 and W288. As the photoisomerization mechanism conserves the orientation of the β1 ring, there is no immediate force steering the CAN carbonyl away from the H-bonding residues. On the other hand, the new isomer state might lower the barrier towards H-bond dissociation and facilitate the translocation of CAN. The confirmation of this hypothesis however would require additional simulations over a longer time scale.
5. Conclusions
We have investigated the excited state dynamics of CAN in OCP by using QM/MM surface hopping nonadiabatic dynamics, analyzing both the ultrafast (200 fs) S2 → S1 internal conversion and the slower decay of S1 to the ground state. The ultrafast component of the dynamics presents a clear signature of the intermediate SX state, which corresponds to the dark 1Bu− state, in agreement with our previous results on lutein in methanol solution.37 The similarities between the ultrafast dynamics of CAN in the gas phase and in OCP, and with lutein, suggest that a decay mediated by the SX state may be common among carotenoids in different environments. Moving to the S1 state of CAN in OCP, a clear multiexponential decay has been found, with strikingly different lifetimes (∼1.2 ps and ∼15 ps), in agreement with spectroscopic measurements.5,14–16,36,59 On this basis, we have assigned the slowly decaying population to the so-called S* state. Analysis of the ground-state ensemble has also allowed us to unequivocally associate the S* population with a specific puckering conformation of the β1 ring, which is significantly twisted due to the hydrogen bonds to Y201 and W288. These results strongly support the ground-state heterogeneity model to explain the S* spectroscopic feature.29Surprisingly, a small portion of SH trajectories showed isomerization of the C7![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) C8 double bond, through a space-conserving mechanism. As isomerization occurs exclusively on this double bond, in the CTD side of CAN, we propose this photochemical mechanism as a trigger for OCP photoactivation, possibly causing the rupture of the hydrogen bonds with Y201 and W288. Photoisomerization was strongly associated with the fast decaying portion of S1 population (i.e., what we associate with the S1/ICT state, rather than S*), supporting S1/ICT as the species responsible for OCP photoactivation. Further simulations, covering much longer timescales, are needed to explain how isomerization can lead to the translocation of CAN into the NTD.
C8 double bond, through a space-conserving mechanism. As isomerization occurs exclusively on this double bond, in the CTD side of CAN, we propose this photochemical mechanism as a trigger for OCP photoactivation, possibly causing the rupture of the hydrogen bonds with Y201 and W288. Photoisomerization was strongly associated with the fast decaying portion of S1 population (i.e., what we associate with the S1/ICT state, rather than S*), supporting S1/ICT as the species responsible for OCP photoactivation. Further simulations, covering much longer timescales, are needed to explain how isomerization can lead to the translocation of CAN into the NTD.
Our results reveal a fundamental role of the OCP binding pocket in tuning the photochemistry of CAN. The limited conformational freedom of CAN in OCP, combined with the constraints of hydrogen bonds and steric repulsion, are the keys to explain its specific photochemical response. In particular, the distortion generated by the hydrogen bonds on the β1 ring determines a selective isomerization at the C7![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) C8 double bond, which could be the trigger to OCP photoactivation.
C8 double bond, which could be the trigger to OCP photoactivation.
Data availability
The data underlying Fig. 2, 3, and 4 can be found on Zenodo at DOI: 10.5281/zenodo.8300809.Author contributions
BM and LC conceived this research. DA, LC, and BM developed the methodology. AA performed the simulations. AA, DA, and LC analyzed the results. BM and LC supervised the work. All authors wrote the manuscript.Conflicts of interest
There are no conflicts to declare.Acknowledgements
D. A., L. C. and B. M. acknowledge funding by the European Research Council, under the Grant ERC-AdG 786714 (LIFETimeS). L. C. and B. M. also acknowledge financial support from National Recovery and Resilience Plan (PNRR), Mission 4, Component 2, Investment 1.4, “National Centre for HPC, Big Data and Quantum Computing”, European Union-NextGenerationEU. All authors thank Giovanni Granucci and Maurizio Persico of the University of Pisa for sharing the development version of the MOPAC code interfaced with the TINKER 6.3 package.Notes and references
- T. K. Holt and D. W. Krogmann, Biochim. Biophys. Acta, 1981, 637, 408–414 CrossRef CAS.
- C. A. Kerfeld, M. R. Sawaya, V. Brahmandam, D. Cascio, K. K. Ho, C. C. Trevithick-Sutton, D. W. Krogmann and T. O. Yeates, Structure, 2003, 11, 55–65 CrossRef CAS PubMed.
- D. Kirilovsky and C. A. Kerfeld, Nat. Plants, 2016, 2, 16180 CrossRef CAS PubMed.
- F. Muzzopappa and D. Kirilovsky, Trends Plant Sci., 2020, 25, 92–104 CrossRef CAS PubMed.
- A. Wilson, C. Punginelli, A. Gall, C. Bonetti, M. Alexandre, J.-M. Routaboul, C. A. Kerfeld, R. van Grondelle, B. Robert and J. T. Kennis, et al. , Proc. Natl. Acad. Sci., 2008, 105, 12075–12080 CrossRef CAS PubMed.
- R. L. Leverenz, D. Jallet, M.-D. Li, R. A. Mathies, D. Kirilovsky and C. A. Kerfeld, Plant Cell., 2014, 26, 426–437 CrossRef CAS PubMed.
- R. L. Leverenz, M. Sutter, A. Wilson, S. Gupta, A. Thurotte, C. Bourcier de Carbon, C. J. Petzold, C. Ralston, F. Perreau and D. Kirilovsky, et al. , Science, 2015, 348, 1463–1466 CrossRef CAS PubMed.
- S. Gupta, M. Guttman, R. L. Leverenz, K. Zhumadilova, E. G. Pawlowski, C. J. Petzold, K. K. Lee, C. Y. Ralston and C. A. Kerfeld, Proc. Natl. Acad. Sci., 2015, 112, E5567–E5574 CrossRef CAS PubMed.
- A. Mezzetti, M. Alexandre, A. Thurotte, A. Wilson, M. Gwizdala and D. Kirilovsky, J. Phys. Chem. B, 2019, 123, 3259–3266 CrossRef CAS PubMed.
- J. Ma, X. You, S. Sun, X. Wang, S. Qin and S.-F. Sui, Nature, 2020, 579, 146–151 CrossRef CAS PubMed.
- M. A. Domínguez-Martín, P. V. Sauer, H. Kirst, M. Sutter, D. Bína, B. J. Greber, E. Nogales, T. Polívka and C. A. Kerfeld, Nature, 2022, 609, 835–845 CrossRef PubMed.
- A. Wilson, C. Punginelli, M. Couturier, F. Perreau and D. Kirilovsky, Biochim. Biophys. Acta, 2011, 1807, 293–301 CrossRef CAS PubMed.
- C. A. Kerfeld, Photosynth. Res., 2004, 81, 215–225 CrossRef CAS PubMed.
- V. Šlouf, V. Kuznetsova, M. Fuciman, C. B. de Carbon, A. Wilson, D. Kirilovsky and T. Polívka, Photosynth. Res., 2017, 131, 105–117 CrossRef PubMed.
- P. E. Konold, I. H. Van Stokkum, F. Muzzopappa, A. Wilson, M.-L. Groot, D. Kirilovsky and J. T. Kennis, J. Am. Chem. Soc., 2018, 141, 520–530 CrossRef PubMed.
- S. Niziński, A. Wilson, L. M. Uriarte, C. Ruckebusch, E. A. Andreeva, I. Schlichting, J.-P. Colletier, D. Kirilovsky, G. Burdzinski and M. Sliwa, JACS Au, 2022, 2, 1084–1095 CrossRef PubMed.
- M. Bondanza, L. Cupellini, P. Faccioli and B. Mennucci, J. Am. Chem. Soc., 2020, 142, 21829–21841 CrossRef CAS PubMed.
- M. Bondanza, D. Jacquemin and B. Mennucci, J. Phys. Chem. Lett., 2021, 12, 6604–6612 CrossRef CAS PubMed.
- E. G. Maksimov, N. N. Sluchanko, Y. B. Slonimskiy, E. A. Slutskaya, A. V. Stepanov, A. M. Argentova-Stevens, E. A. Shirshin, G. V. Tsoraev, K. E. Klementiev, O. V. Slatinskaya, E. P. Lukashev, T. Friedrich, V. Z. Paschenko and A. B. Rubin, Sci. Rep., 2017, 7, 15548 CrossRef CAS PubMed.
- S. Bandara, Z. Ren, L. Lu, X. Zeng, H. Shin, K.-H. Zhao and X. Yang, Proc. Natl. Acad. Sci., 2017, 114, 6286–6291 CrossRef CAS PubMed.
- E. Kish, M. M. M. Pinto, D. Kirilovsky, R. Spezia and B. Robert, Biochim. Biophys. Acta, 2015, 1847, 1044–1054 CrossRef CAS PubMed.
- R. Pariser, J. Chem. Phys., 1956, 24, 250–268 CrossRef CAS.
- G. Cerullo, D. Polli, G. Lanzani, S. De Silvestri, H. Hashimoto and R. J. Cogdell, science, 2002, 298, 2395–2398 CrossRef CAS PubMed.
- N. Mohan TM, C. H. Leslie, S. Sil, J. B. Rose, R. W. Tilluck and W. F. Beck, J. Chem. Phys., 2021, 155, 035103 CrossRef CAS PubMed.
- E. E. Ostroumov, R. M. Mulvaney, R. J. Cogdell and G. D. Scholes, Science, 2013, 340, 52–56 CrossRef CAS PubMed.
- M. S. Marek, T. Buckup and M. Motzkus, J. Phys. Chem. B, 2011, 115, 8328–8337 CrossRef CAS PubMed.
- W. F. Beck, M. M. Bishop, J. D. Roscioli, S. Ghosh and H. A. Frank, Arch. Biochem. Biophys., 2015, 572, 175–183 CrossRef CAS PubMed.
- C. C. Gradinaru, J. T. Kennis, E. Papagiannakis, I. H. Van Stokkum, R. J. Cogdell, G. R. Fleming, R. A. Niederman and R. Van Grondelle, Proc. Natl. Acad. Sci., 2001, 98, 2364–2369 CrossRef CAS PubMed.
- T. Polívka and V. Sundström, Chem. Phys. Lett., 2009, 477, 1–11 CrossRef.
- P. Chábera, M. Fuciman, P. Hříbek and T. Polívka, Phys. Chem. Chem. Phys., 2009, 11, 8795–8803 RSC.
- A. E. Jailaubekov, M. Vengris, S.-H. Song, T. Kusumoto, H. Hashimoto and D. S. Larsen, J. Phys. Chem. A, 2011, 115, 3905–3916 CrossRef CAS PubMed.
- V. Balevičius Jr, D. Abramavicius, T. Polívka, A. Galestian Pour and J. Hauer, J. Phys. Chem. Lett., 2016, 7, 3347–3352 CrossRef PubMed.
- J. A. Bautista, R. E. Connors, B. B. Raju, R. G. Hiller, F. P. Sharples, D. Gosztola, M. R. Wasielewski and H. A. Frank, J. Phys. Chem. B, 1999, 103, 8751–8758 CrossRef CAS.
- H. A. Frank, J. A. Bautista, J. Josue, Z. Pendon, R. G. Hiller, F. P. Sharples, D. Gosztola and M. R. Wasielewski, J. Phys. Chem. B, 2000, 104, 4569–4577 CrossRef CAS.
- D. Zigmantas, R. G. Hiller, A. Yartsev, V. Sundström and T. Polívka, J. Phys. Chem. B, 2003, 107, 5339–5348 CrossRef CAS.
- T. Polívka, C. A. Kerfeld, T. Pascher and V. Sundström, Biochemistry, 2005, 44, 3994–4003 CrossRef PubMed.
- D. Accomasso, S. Arslancan, L. Cupellini, G. Granucci and B. Mennucci, J. Phys. Chem. Lett., 2022, 13, 6762–6769 CrossRef CAS PubMed.
- J. C. Tully, J. Chem. Phys., 1990, 93, 1061–1071 CrossRef CAS.
- G. Granucci and A. Toniolo, Chem. Phys. Lett., 2000, 325, 79–85 CrossRef CAS.
- G. Granucci, M. Persico and A. Toniolo, J. Chem. Phys., 2001, 114, 10608–10615 CrossRef CAS.
- M. Persico and G. Granucci, Theor. Chem. Acc., 2014, 133, 1–28 Search PubMed.
- M. J. Dewar, E. G. Zoebisch, E. F. Healy and J. J. Stewart, J. Am. Chem. Soc., 1993, 115, 5348 CrossRef CAS.
- A. Toniolo, G. Granucci and T. J. Martínez, J. Phys. Chem. A, 2003, 107, 3822–3830 CrossRef CAS.
- J. A. Maier, C. Martinez, K. Kasavajhala, L. Wickstrom, K. E. Hauser and C. Simmerling, J. Chem. Theory Comput., 2015, 11, 3696–3713 CrossRef CAS PubMed.
- M. Bondanza, L. Cupellini, F. Lipparini and B. Mennucci, Chem, 2020, 6, 187–203 CAS.
- J. C. Tully and R. K. Preston, J. Chem. Phys., 1971, 55, 562–572 CrossRef CAS.
- G. Bussi, D. Donadio and M. Parrinello, J. Chem. Phys., 2007, 126, 014101 CrossRef PubMed.
- G. Bussi and M. Parrinello, Comput. Phys. Commun., 2008, 179, 26–29 CrossRef CAS.
- D. Accomasso, M. Persico and G. Granucci, ChemPhotoChem, 2019, 3, 933–944 CrossRef CAS.
- G. Granucci and M. Persico, J. Chem. Phys., 2007, 126, 134114 CrossRef PubMed.
- G. Granucci, M. Persico and A. Zoccante, J. Chem. Phys., 2010, 133, 134111 CrossRef PubMed.
- J. J. Stewart, MOPAC2002, Fujitsu Limited, Tokyo, Japan, 2002 Search PubMed.
- J. W. Ponder, TINKER — Software Tools for Molecular Design, version 6.3, Copyright (c), 2014 Search PubMed.
- J. K. Gurchiek, H. Bao, M. A. Domínguez-Martín, S. E. McGovern, C. E. Marquardt, J. D. Roscioli, S. Ghosh, C. A. Kerfeld and W. F. Beck, J. Phys. Chem. B, 2018, 122, 1792–1800 CrossRef CAS PubMed.
- R. Y. Pishchalnikov, I. A. Yaroshevich, D. V. Zlenko, G. V. Tsoraev, E. M. Osipov, V. A. Lazarenko, E. Y. Parshina, D. D. Chesalin, N. N. Sluchanko and E. G. Maksimov, Photosynth. Res., 2022, 1–15 Search PubMed.
- R. S. Liu, Acc. Chem. Res., 2001, 34, 555–562 CrossRef CAS PubMed.
- G. Salvadori, V. Macaluso, G. Pellicci, L. Cupellini, G. Granucci and B. Mennucci, Nat. Commun., 2022, 13, 6838 CrossRef CAS PubMed.
- T. Khan, M. A. Dominguez-Martin, I. Simova, M. Fuciman, C. A. Kerfeld and T. Polívka, J. Phys. Chem. B, 2020, 124, 4896–4905 CrossRef CAS PubMed.
- R. Berera, I. H. M. van Stokkum, M. Gwizdala, A. Wilson, D. Kirilovsky and R. van Grondelle, J. Phys. Chem. B, 2012, 116, 2568–2574 CrossRef CAS PubMed.
- E. G. Maksimov, E. A. Shirshin, N. N. Sluchanko, D. V. Zlenko, E. Y. Parshina, G. V. Tsoraev, K. E. Klementiev, G. S. Budylin, F.-J. Schmitt and T. Friedrich, et al. , Biophys. J., 2015, 109, 595–607 CrossRef CAS PubMed.
- S. Gozem, H. L. Luk, I. Schapiro and M. Olivucci, Chem. Rev., 2017, 117, 13502–13565 CrossRef CAS PubMed.
- V. U. Chukhutsina, J. M. Baxter, A. Fadini, R. M. Morgan, M. A. Pope, K. Maghlaoui, C. M. Orr, A. Wagner and J. J. van Thor, Nat. Commun., 2022, 13, 6420 CrossRef CAS PubMed.
Footnote |
| † Electronic supplementary information (ESI) available: Selection of the active space; thermal equilibrations in the ground state; diabatization; diabatic analysis of the ultrafast process; the S1 → S0 relaxation process; the S1 → S0 relaxation process; puckering; supporting figures. See DOI: https://doi.org/10.1039/d3sc02662k |
| This journal is © The Royal Society of Chemistry 2023 |