Open Access Article
Open Access ArticlepH-Switching of the luminescent, redox, and magnetic properties in a spin crossover cobalt(II) molecular nanomagnet†
Renato
Rabelo
ab,
Luminita
Toma
a,
Nicolás
Moliner
a,
Miguel
Julve
 a,
Francesc
Lloret
a,
Mario
Inclán
a,
Francesc
Lloret
a,
Mario
Inclán
 ac,
Enrique
García-España
ac,
Enrique
García-España
 a,
Jorge
Pasán
a,
Jorge
Pasán
 d,
Rafael
Ruiz-García
d,
Rafael
Ruiz-García
 a and
Joan
Cano
a and
Joan
Cano
 *a
*a
aInstituto de Ciencia Molecular (ICMol), Universitat de València, 46980 Paterna (València), Spain. E-mail: joan.cano@uv.es
bInstituto de Química, Universidade Federal de Goiás, 74690-900 Goiânia, Brazil
cEscuela Superior de Ingeniería, Ciencia y Tecnología, Universidad Internacional de Valencia – VIU, Valencia, Spain
dDepartamento de Química, Facultad de Ciencias, Laboratorio de Materiales para Análisis Químico (MAT4LL), Universidad de La Laguna, 38200 Tenerife, Spain
First published on 27th July 2023
Abstract
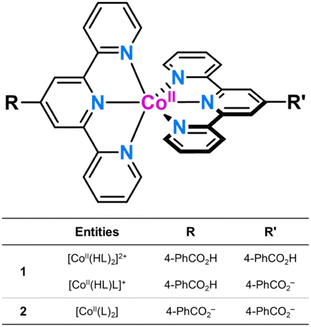
The ability of mononuclear first-row transition metal complexes as dynamic molecular systems to perform selective functions under the control of an external stimulus that appropriately tunes their properties may greatly impact several domains of molecular nanoscience and nanotechnology. This study focuses on two mononuclear octahedral cobalt(II) complexes of formula {[CoII(HL)2][CoII(HL)L]}(ClO4)3·9H2O (1) and [CoIIL2]·5H2O (2) [HL = 4′-(4-carboxyphenyl)-2,2′:6′,2′′-terpyridine], isolated as a mixed protonated/hemiprotonated cationic salt or a deprotonated neutral species. This pair of pH isomers constitutes a remarkable example of a dynamic molecular system exhibiting reversible changes in luminescence, redox, and magnetic (spin crossover and spin dynamics) properties as a result of ligand deprotonation, either in solution or solid state. In this last case, the thermal-assisted spin transition coexists with the field-induced magnetisation blockage of “faster” or “slower” relaxing low-spin CoII ions in 1 or 2, respectively. In addition, pH-reversible control of the acid-base equilibrium among dicationic protonated, cationic hemiprotonated, and neutral deprotonated forms in solution enhances luminescence in the UV region. Besides, the reversibility of the one-electron oxidation of the paramagnetic low-spin CoII into the diamagnetic low-spin CoIII ion is partially lost and completely restored by pH decreasing and increasing. The fine-tuning of the optical, redox, and magnetic properties in this novel class of pH-responsive, spin crossover molecular nanomagnets offers fascinating possibilities for advanced multifunctional and multiresponsive magnetic devices for molecular spintronics and quantum computing such as pH-effect spin quantum transformers.
Introduction and background
Coordination compounds of transition metal ions with non-innocent ligands have attracted much attention in diverse areas of nanoscience due to their unusual combination of chemical (Brønsted or Lewis acidity, redox, and catalytic) and physical properties (optical or luminescent, conducting, and magnetic) resulting from the metal and its ligand counterpart.1–6 The ongoing crucial step towards new nanotechnologies is to successfully modulate their physicochemical properties through a variety of internal factors, either electronic (metal oxidation and spin states) or steric ones (ligand substituents and conformation), and eventually to switch them under the presence of external stimuli, either of chemical (pH and chemical analytes) or physical nature (temperature, hydrostatic pressure, light, electric and magnetic fields).3–6This goal has been successfully achieved using mononuclear first-row transition metal complexes as both synthetic and theoretical models of dynamic molecular systems (DMS).7–26 Hence, this simple class of multifunctional and multiresponsive molecular materials has been found helpful as optical and magnetic sensors for chemical and biological sensing,7–10 photoluminescent emitters for light-emitting electrochemical cells (LECs),11–13 electro- and photocatalysts for bio-inspired molecular recognition and catalysis,14–17 photo- and chemo-responsive contrast agents for magnetic resonance imaging (MRI),18 electrochemical and electrochromic devices for redox flow batteries (RFB), and capacitors for molecular electronics.19–21 In particular, mononuclear spin crossover (SCO) complexes with potentially electro- or photoactive (non-innocent) ligands are promising candidates for spintronic devices or advanced quantum bits (qubits) and quantum gates for molecular spintronics and quantum information processing (QIP).22–26
Along this line, we report herein the synthesis, structural and spectroscopic characterisation, and the magnetic, luminescence and electrochemical properties of two novel mononuclear cobalt(II) complexes with a terpyridine (TERPY)-type ligand containing benzoic/benzoate substituents of formula {[CoII(HL)2][CoII(HL)L]}(ClO4)3·9H2O (1) and [CoIIL2]·5H2O (2) [L = 4′-(4-carboxyphenyl)-2,2′:6′,2′′-terpyridine] (Scheme 1). 1 and 2 are two rare examples of DMS that undergo a thermal-assisted low-spin (LS)/high-spin (HS) transition and a field-induced magnetisation blockage.27–33 Other examples of pH-responsive multiproperty molecular systems of interest in nanoscience and nanotechnology include dinuclear cyanide-bridged iron(III)-cobalt(II) complexes and oxamato-based copper(II) metallacycles.34,35
Results and discussion
The 4-benzoic acid-substituted TERPY ligand was synthesised following a previously reported procedure (see ESI†).36 The first step consists of condensing of 2-acetylpyridine and methyl 4-formylbenzoate (2![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1 molar ratio) in basic media to afford the methyl ester benzoic acid derivative (MeL) with a yield of ca. 42% (Scheme S1, ESI†). The sodium salt of the deprotonated ligand (NaL) and the monoprotic acid (HL) were obtained from basic hydrolysis of MeL with NaOH and subsequent acidification until pH = 3. They were all isolated as white crystalline solids in good to excellent yields [ca. 64 (HL) and 95% (NaL)] and characterised by elemental analysis (C, H, N), proton nuclear magnetic resonance (1H NMR), Fourier-transform infrared (FT-IR), and electronic absorption (UV-Vis) spectroscopies.
1 molar ratio) in basic media to afford the methyl ester benzoic acid derivative (MeL) with a yield of ca. 42% (Scheme S1, ESI†). The sodium salt of the deprotonated ligand (NaL) and the monoprotic acid (HL) were obtained from basic hydrolysis of MeL with NaOH and subsequent acidification until pH = 3. They were all isolated as white crystalline solids in good to excellent yields [ca. 64 (HL) and 95% (NaL)] and characterised by elemental analysis (C, H, N), proton nuclear magnetic resonance (1H NMR), Fourier-transform infrared (FT-IR), and electronic absorption (UV-Vis) spectroscopies.
Compound 1 was prepared by the reaction of cobalt(II) perchlorate hexahydrate and HL in a 1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 2 metal to ligand molar ratio by using acetonitrile/methanol as solvent. The reaction of stoichiometric amounts of cobalt(II) acetate tetrahydrate and NaL in dimethyl sulfoxide/water mixtures afforded compound 2 (Scheme S2, ESI†). Both compounds are soluble in dimethylformamide and dimethyl sulfoxide but are sparingly soluble in water, acetonitrile, and methanol. X-Ray quality crystals were obtained in moderate to good yields (62–83%) by slow evaporation in acetonitrile/methanol at room temperature (1) or under hydrothermal conditions at 100 °C (2). They were characterised by elemental analysis (C, H, N), energy dispersive X-ray (EDX), FT-IR, UV-Vis, and EPR spectroscopies (ESI†).
2 metal to ligand molar ratio by using acetonitrile/methanol as solvent. The reaction of stoichiometric amounts of cobalt(II) acetate tetrahydrate and NaL in dimethyl sulfoxide/water mixtures afforded compound 2 (Scheme S2, ESI†). Both compounds are soluble in dimethylformamide and dimethyl sulfoxide but are sparingly soluble in water, acetonitrile, and methanol. X-Ray quality crystals were obtained in moderate to good yields (62–83%) by slow evaporation in acetonitrile/methanol at room temperature (1) or under hydrothermal conditions at 100 °C (2). They were characterised by elemental analysis (C, H, N), energy dispersive X-ray (EDX), FT-IR, UV-Vis, and EPR spectroscopies (ESI†).
The EDX analysis for 2 shows no chlorine peak, as expected for a neutral deprotonated [CoIIL2] species (Fig. S1b, ESI†). However, 1 reveals a rough 3![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 2 Cl to Co molar ratio (Fig. S1a, ESI†), according to the coexistence of protonated dicationic and hemiprotonated monocationic forms, as a consequence of the weak acid character of the ligand (see discussion below). Unfortunately, attempts to grow single crystals of the fully protonated [CoII(HL)2]2+ form in an acid medium were unsuccessful.
2 Cl to Co molar ratio (Fig. S1a, ESI†), according to the coexistence of protonated dicationic and hemiprotonated monocationic forms, as a consequence of the weak acid character of the ligand (see discussion below). Unfortunately, attempts to grow single crystals of the fully protonated [CoII(HL)2]2+ form in an acid medium were unsuccessful.
Comparing the FT-IR spectra of 1 and 2 allowed establishing the different protonation degree of the ligands in their complexes (Fig. S2, ESI†). Hence, they show strong bands corresponding to the characteristic asymmetric and symmetric stretching vibrations of carboxyl and carboxylate groups [νas(CO2H)/νs(CO2H) = 1698/1263 (1) and νas(CO2)/νs(CO2) = 1554/1371 cm−1 (2)], which are similar to those found for HL and NaL forms [νas(CO2H)/νs(CO2H) = 1706/1261 and νas(CO2)/νs(CO2) = 1562/1402 cm−1] (Fig. S2, ESI†). The large shift between these stretching vibrations for 1 [Δ = νas − νs = 435 (1) and 183 cm−1 (2)] suggests the coexistence of protonated and deprotonated carboxyl groups.37 In addition, 1 shows strong to moderate peaks corresponding to the typical stretching (∼1100 cm−1) and bending (∼635 cm−1) vibrations of the perchlorate group, which are indeed absent in 2 (Fig. S2, ESI†).37
The degree of protonation of the ligand in the compounds was also confirmed by single-crystal X-ray diffraction. The crystal structure of 2 was reported earlier.36 Still, we revisited in order to establish a complete and accurate comparison with 1 at the same temperature, allowing a systematic discussion of the molecular and crystal packing structural features that accompany ligand protonation in the solid state.‡ Indeed, the experimental powder X-ray diffraction (PXRD) patterns of the polycrystalline samples are identical to the calculated ones from the single-crystal XRD analysis (Fig. S3, ESI†), confirming the purity of the bulk materials.
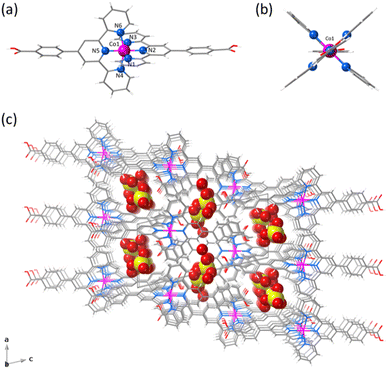
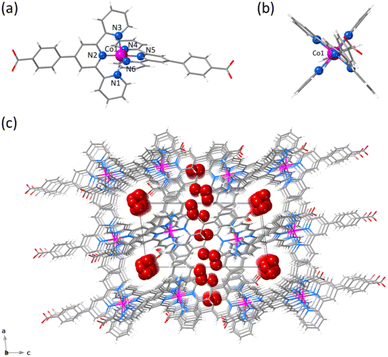
1 and 2 crystallise in the triclinic P![[1 with combining macron]](https://www.rsc.org/images/entities/char_0031_0304.gif) space group (Table S1, ESI†). The structure of 1 consists of statistically disordered protonated and hemiprotonated mononuclear cobalt(II) complex cations, [CoII(HL)2]2+/[CoII(HL)L]+, together with partially disordered, charge-counterbalancing perchlorate anions and crystallisation waters (Fig. 1, S4 and S5, ESI†). Nevertheless, 2 contains only neutral deprotonated mononuclear cobalt(II) complexes, [CoIIL2], and free waters (Fig. 2, S6 and S7, ESI†), in agreement with the earlier reported structure.36
space group (Table S1, ESI†). The structure of 1 consists of statistically disordered protonated and hemiprotonated mononuclear cobalt(II) complex cations, [CoII(HL)2]2+/[CoII(HL)L]+, together with partially disordered, charge-counterbalancing perchlorate anions and crystallisation waters (Fig. 1, S4 and S5, ESI†). Nevertheless, 2 contains only neutral deprotonated mononuclear cobalt(II) complexes, [CoIIL2], and free waters (Fig. 2, S6 and S7, ESI†), in agreement with the earlier reported structure.36
Mononuclear cobalt(II) units of 1 and 2 exhibit similar but not identical molecular dimensions and conformations (Table S2, ESI†). Regardless of the ligand protonation level, they show a cylindrical shape of approximate dimensions 2.0 (length) and 1.0 nm (width) with a pseudo C2v molecular symmetry possessing two almost perpendicularly oriented non-planar ligands (Fig. 1b and 2b). The benzoic/benzoate and terpyridyl fragments are not coplanar but well away from the orthogonality, as shown by the φ dihedral angle [7.08(8)/43.62(11) (1) and 14.30(5)/29.57(6)° (2)]. However, the dihedral angle between the mean planes of the terpyridyl groups (Φ) coordinated to the same CoII ion [83.57(3) (1) and 89.65(2)° (2)] proves that minor but non-negligible deviations from orthogonality give rise to two distinct chiral (helical) isomers, both enantiomers (M and P) being present in the crystal lattice. In addition, there is an overall bending along the long molecular axis of the mononuclear cobalt(II) unit only in 2 (Fig. 1a and 2a), as shown in the superposition view (Fig. S8, ESI†).
Carbon–oxygen bond lengths in carboxyl/carboxylate groups allowed us to estimate the protonation level of the compounds. Hence, the carbon–oxygen bond lengths in 1 [d1(C![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) O) = 1.203(6)/1.216(7) and d2(C–O) = 1.310(5)/1.294(7) Å] are quite different, being related to double and single bonds. Meanwhile, they are almost identical in 2 exhibiting intermediate values [d1(C
O) = 1.203(6)/1.216(7) and d2(C–O) = 1.310(5)/1.294(7) Å] are quite different, being related to double and single bonds. Meanwhile, they are almost identical in 2 exhibiting intermediate values [d1(C![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) O) = 1.263(3)/1.256(4) and d2(C–O) = 1.260(4)/1.252(4) Å], according to the usual π resonance in the carboxylate group.
O) = 1.263(3)/1.256(4) and d2(C–O) = 1.260(4)/1.252(4) Å], according to the usual π resonance in the carboxylate group.
In 1 and 2, the octahedral coordination spheres exhibit an axial compression and a partial rhombic distortion. They are made up of an equatorial plane and an axial axis defined by four (Nd and Nd′) and two (Nc) nitrogen atoms from distal and central pyridyl groups of terpyridyl derivatives (Fig. 1a and 2a), respectively. Overall, the metal-to-nitrogen bond lengths are typical of LS CoII ions regardless of the ligand protonation degree. The average values of the axial Co–Nc lengths are notably shorter than those of the equatorial Co–Nd ones for both compounds [Rax = 1.893(4) (1)/1.898(2) Å (2) and Req = 2.064(4) (1)/2.072(4) Å (2)].
The mononuclear complexes in 1 and 2 are parallelly settled in the crystal packing with their long molecular axis oriented along the crystallographic c axis (Fig. S4 and S6, ESI†). The crystallisation waters are involved in various hydrogen bonding interactions among them and with the carboxyl and carboxylate groups [Ow–H⋯Ow = 2.41(1)–3.04(1) (1) and 2.385(9)–2.927(9) Å (2); Ow–H⋯O = 2.587(5)–2.90(2) (1) and 2.695(6)–2.841(4) Å (2)] (Fig. S9, ESI†). This situation gives rise to hydrogen-bonded single (1) or multiple layers (2) of mononuclear cobalt(II) units within the ac or bc planes (Fig. S4 and S6, ESI†).
A parallel displaced arrangement of hydrogen-bonded single layers of di- and monocationic mononuclear cobalt(II) units in 1 grows in the ac plane (Fig. S5, ESI†). In contrast, a triple interpenetration of parallelly displaced hydrogen-bonded multi-layered nets of neutral mononuclear cobalt(II) units develops along the crystallographic c axis in 2 (Fig. S6 and S7, ESI†). However, the parallel array of supramolecular 2D layers in 1 or the triply interpenetrated 3D network in 2 lead to small channels along the [100] and [010] directions, which are filled by hydrogen-bonded crystallisation waters together with the counterbalancing perchlorate anions in the former case (Fig. 1c and 2c). Once again, the different ligand protonation level in the protonated/hemiprotonated (1) and deprotonated (2) mononuclear cobalt(II) complexes is ultimately responsible for the dissimilarities in crystal packing and potential porosity (relative to the water contents) between both pH isomers.
The magnetic properties of 1 and 2 were measured in both direct (dc) and alternating current (ac) regimes in order to investigate the influence of the protonation level on the spin crossover and spin dynamics in the solid state for this proton transfer pair of mononuclear cobalt(II) complexes (see ESI†).
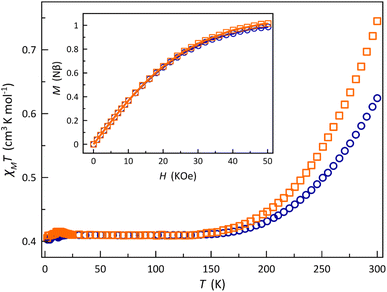
The χMT vs. T plots (χM being the dc molar magnetic susceptibility per mononuclear unit) for 1 and 2 show a similar SCO behaviour (Fig. 3). A gradual but complete, thermally-induced HS–LS transition is observed for both cases, regardless of the protonation degree of each ligand. This scenario contrasts with the observed one in the [2 × 2] iron(II) grid-type complex by Dhers and coworkers, where the protonation of the hydrazone groups from the grid ligand modulates the spin state and spin crossover behaviour.5 Also, no hysteresis occurs in 1 and 2 despite the intermolecular and hydrogen bonding interactions among the mononuclear units in the solid state, as reported earlier for the parent cobalt(II) complexes with 2,2′:6′,2′′-terpyridine and its derivatives.38
At room temperature, χMT is slightly higher for 2 (0.75 cm3 mol−1 K) than for 1 (0.62 cm3 mol−1 K), but both values are much lower than the expected one for a HS CoII ion with an unquenched orbital momentum contribution (2.70 cm3 mol−1 K for S = 3/2 and g = 2.4). Upon cooling, χMT decreases smoothly to reach a plateau around 150 K with a value of 0.41 cm3 mol−1 K, as expected for a LS CoII ion (0.45 cm3 mol−1 K for S = 1/2 and g = 2.2), and which is practically kept until 2.0 K. Surprisingly, in the solid state, 1 exhibits a higher stabilisation of the LS form of the CoII ion at room temperature. This observation appears contradictory at first glance, considering the well-known σ-type electron-withdrawing inductive effect of the benzoic group in para substitution, as reflected by the Hammett constants [σp = 0.00 (p-CO2–) and 0.45 (p-CO2H)].39 However, this can be rationalised by the reduction in the π-type electron-withdrawing resonance effect caused by the loss of ligand aromaticity resulting from the increased deviation from planarity [average φ values of 25.35 (1) and 21.94° (2)]. However, this explanation may be too simple since the SCO phenomenon depends on both molecular and cooperative electronic effects, the latter only linked to the network through molecular organisation and mainly intermolecular interactions. Thus, for example, it has been known since the past century that the same complex can exhibit highly varied SCO behaviours depending on the solvent in the network or its absence.40,41 Therefore, it is difficult to draw a clear and definitive conclusion.
This situation was also supported by the M vs. H plots (M being the magnetisation per mononuclear unit and H the applied dc magnetic field). In both cases, the isothermal magnetisation curves at 2.0 K were perfectly reproduced by the Brillouin function with S = 1/2 and g = 2.110 (1) and 2.137 (2) (inset of Fig. 3). In fact, their solid-state Q-band EPR spectra at 4.0 K (Fig. S10, ESI†) exhibit a rhombic pattern [gx = 2.02 (1)/2.03 (2), gy = 2.08 (1)/2.12 (2), and gz = 2.22 (1)/2.25 (2)] with average g values of 2.11 (1) and 2.14 (2). This situation is in agreement with the aforementioned rhombic distortion observed in the LS CoII ion for the structures of the mononuclear [Co(HL)2]2+/[Co(HL)L]+ (1) and [CoL2] (2) units.
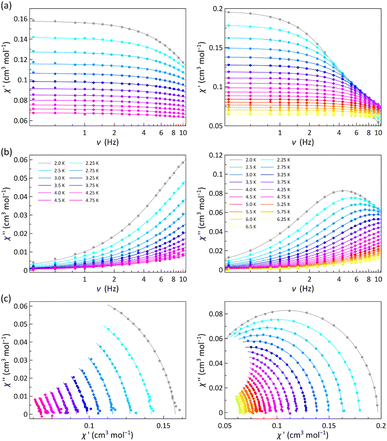
The χM′ and χM′′ vs. ν plots of 1 and 2 (χM′ and χM′′ being the in-phase and out-of-phase ac molar magnetic susceptibilities) under applied dc magnetic fields in the range 1.0–5.0 kOe are characteristic of field-induced single-molecule magnets (SMMs) (Fig. 4 and S11–S13, ESI†).
Neither frequency dependence of χM′ nor a χM′′ signal were observed in the lack of a dc magnetic field (data not shown). However, in the presence of the weakest dc magnetic field (Hdc = 1.0 kOe), 1 develops incipient χM′′ signals and 2 exhibits a maximum that progressively shifts towards lower frequencies as the temperature decreases (Fig. 4b). This maximum also arises in 1 and shifts toward lower frequencies when increasing Hdc (Fig. S11b–S13b, ESI†).
The magnetic relaxation times (τ) were calculated from the joint analysis of the frequency-dependence of χM′ and χM′′ through the generalised Debye equations,42 which consider the adiabatic (χS) and isothermal (χT) magnetic susceptibilities, and the exponential factor (α) that describes the broadness of the spectra, as additional fitting parameters (solid lines in Fig. 4a, b, S11a–S13a and S11b–S13b, ESI†). The Argand or χM′ vs. χM′′ plots for 1 and 2 give both incomplete or nearly complete semicircles, which are well simulated by the best-fit α, τ, χS and χT values (Fig. 4c and S11c–S13c, ESI†). The small α values [0.032–0.24 (1) and 0.016–0.055 (2)] support a narrow distribution of magnetic relaxation processes (α = 0 and 1 for an ideal Debye model with single and infinite magnetic relaxation processes).
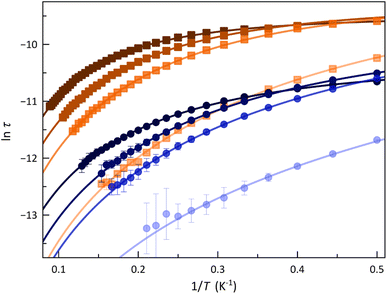
The calculated τ values in the form of the Arrhenius and ln![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) τ vs. ln
τ vs. ln![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) T plots are displayed in Fig. 5 and S14 (ESI†). The most remarkable feature is the systematic more significant τ for 2. This situation conforms with a transformer-like magnetic switch exchanging from field-induced “faster-relaxing” (FR) to “slower-relaxing” (SR) LS CoII ions upon ligand deprotonation. In both cases, the increase in Hdc from 1.0 to 5.0 kOe is followed by a monotonical increase of τ from 8.46 (1) and 35.8 μs (2) up to 23.6 (1) and 47.0 μs (2) at 2.0 K.
T plots are displayed in Fig. 5 and S14 (ESI†). The most remarkable feature is the systematic more significant τ for 2. This situation conforms with a transformer-like magnetic switch exchanging from field-induced “faster-relaxing” (FR) to “slower-relaxing” (SR) LS CoII ions upon ligand deprotonation. In both cases, the increase in Hdc from 1.0 to 5.0 kOe is followed by a monotonical increase of τ from 8.46 (1) and 35.8 μs (2) up to 23.6 (1) and 47.0 μs (2) at 2.0 K.
For a doublet spin ground state, τ is identical to the spin-lattice time (T1 = τ), which in turn acts as a limiting factor for the phase memory time (Tm ≤ T1). Therefore, longer T1 values are available for 2, but all in the microscale time. In this respect, a related square pyramidal LS cobalt(II) complex has been positively tested as a qubit prototype by observing anisotropic Rabi cycles with long enough quantum phase memory times (Tm ≈ 1 μs at T = 5.0 K).30 These results suggest the possibility of switching the spin dynamics and quantum coherence (QC) of the LS CoII ions in 1 and 2 under pH control, opening thus the way for the applications of this novel class of a pH-responsive spin crossover cobalt(II) molecular nanomagnets as molecular magnetic devices in a future spin-based quantum computing machine. Hence, different QC properties can be presumed for the fully or partially protonated FR (1) and deprotonated SR (2) forms.
The Arrhenius plots for 1 and 2 were satisfactorily simulated considering a double relaxation mechanism described by the equation: τ−1 = CTn + τIK−1 (solid lines in Fig. 5 and S14, ESI†). The first term is the well-known two-phonon Raman magnetic relaxation process; the second is a temperature-independent term that accounts for the spin-reversal relaxation between the Zeeman-split mS = ±1/2 ground Kramers doublet. This intra-Kramers (IK) contribution should be seen as a zero-order term of a direct mechanism and not as a quantum tunnelling of the magnetisation (QTM) process, which is physically meaningless for an S = 1/2 ground state since it cannot establish an energy barrier.33
The calculated parameters corresponding to this Raman plus IK relaxation mechanism for 1 and 2 are summarised in Table 1, and their variation with Hdc is illustrated in Fig. S15 (ESI†). For the IK process operating in the lower temperature range, τIK decreases more rapidly for 1 with increasing Hdc. Nevertheless, the Raman process prevails at higher temperatures, C being almost one order of magnitude larger in 1, which would account for their distinct spin dynamics. However, similar exponential Hdc dependence of C is found for both compounds. Otherwise, n values close to 2 suggest that the slow magnetic relaxation is associated with resonant phonon trapping through a phonon-bottleneck process, a rather optical than acoustic phonon.
| H dc (kOe) | C (s−1 K−n) | n | τ IK (s) × 105 | |
|---|---|---|---|---|
| a Pre-exponential and exponential coefficients for the Raman mechanism [τ−1 = CTn]. b Coefficient for the temperature-independent intra-Kramers mechanism [τ−1 = τIK−1]. | ||||
| 1 | 1.0 | 30![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 873 ± 1000 873 ± 1000 |
1.96 ± 0.04 | — |
| 2.5 | 6284 ± 300 | 2.13 ± 0.03 | 7.8 ± 0.5 | |
| 3.5 | 5253 ± 200 | 1.93 ± 0.02 | 6.2 ± 0.3 | |
| 5.0 | 3752 ± 200 | 1.82 ± 0.03 | 3.54 ± 0.09 | |
| 2 | 1.0 | 4700 ± 800 | 2.16 ± 0.09 | 15 ± 6 |
| 2.5 | 1213 ± 60 | 2.02 ± 0.02 | 10.9 ± 0.3 | |
| 3.5 | 841 ± 40 | 1.95 ± 0.02 | 9.5 ± 0.2 | |
| 5.0 | 400 ± 20 | 2.01 ± 0.02 | 7.64 ± 0.09 | |
The relaxation of the magnetisation in these LS cobalt(II) complexes significantly depends on the magnetic field, at least for Hdc ≤2.5 kOe. However, this dependence is dampened and even it stabilises at more intense Hdc. There are only two types of relaxation that depend on the magnetic field, and they are predominant at low temperatures: those governed by the IK [B1/(1 + B2H2)] and direct (A1H4T) mechanisms. Although a Hdc-independent Raman relaxation is usually assumed in the T9 term (R9T9) for ground Kramers doublets, there is an ordinarily negligible influence of Hdc on the T7 contribution (α7R7T7H2). R9 and R7 are material-specific parameters, whereas α7 is a constant. When only an IK relaxation acts at lower temperatures, the spin-reversal gradually slows down with increasing Hdc (Fig. S16a, ESI†); however, a direct relaxation should become faster. Thus, if both mechanisms coincide, a change in the trend of ln![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) τ with Hdc should be reached (Fig. S16b, ESI†), and there should be a Hdc range in which it does not significantly affect ln
τ with Hdc should be reached (Fig. S16b, ESI†), and there should be a Hdc range in which it does not significantly affect ln![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) τ. Indeed, a Raman mechanism involving optical phonons at lower temperatures that competes with the IK mechanism does not speed up magnetic relaxation, but it does reduce its slowing down, at least in the operating temperature range (Fig. S16c, ESI†). One of these two circumstances must occur in these LS cobalt(II) complexes.
τ. Indeed, a Raman mechanism involving optical phonons at lower temperatures that competes with the IK mechanism does not speed up magnetic relaxation, but it does reduce its slowing down, at least in the operating temperature range (Fig. S16c, ESI†). One of these two circumstances must occur in these LS cobalt(II) complexes.
Several factors influence the magnetic relaxation in SMMs, including ZFS and molecular or network vibrations. ZFS, arising from the interaction between the spin and the local crystal field and determining the energy splitting of the spin levels, holds no physical meaning for an octahedral LS cobalt(II) complex (S = ½). In solid-state systems, the interaction between the spin and phonons in the lattice is particularly significant, given the large and varying phonon density of states resulting from crystal packing effects. Experiments conducted in diluted media can offer valuable insights into the single-molecule nature and the spin-lattice relaxation mechanism through spin-phonon coupling, although the conclusions are not always definitive. Unfortunately, the investigation of dynamic magnetic properties of 1 and 2 in frozen solutions is hindered by the low solubility of the involved species in common solvents. Consequently, determining the relative importance of molecular versus network vibrations on the magnetic relaxation upon protonation is precluded in our systems.
However, there are still some considerations to be made. In the solid state, hydrogen bonds between the crystallisation waters and the carboxylate or carboxyl groups build up supramolecular 2D (1) and 3D networks (2). These distinct frameworks are expected to exhibit different spin-phonon couplings and magnetic relaxation behaviours, but the exact nature of these differences remains uncertain. According to Fig. S4a and S6a (ESI†) the water layers lead alternatively to H-bonded 1D and 0D (1) and 2D and 1D frameworks (2), as depicted in Fig. S9 (ESI†). Only in the protonated/hemiprotonated form two neighbouring molecular entities are self-assembled through double hydrogen bonds from carboxyl groups, which also involve some crystallisation waters. However, there is only a single hydrogen bond path in 2 between the carboxylate groups of two adjacent complexes. The more robust dimeric H-bond structure should result in a more pronounced spin-phonon coupling in 1. On the other hand, some water molecules involved in the H-bonded network are disordered in 2, and this structural feature would limit the efficiency of the spin-phonon coupling. This prediction aligns with experimental findings, suggesting a faster magnetic relaxation dynamic in the protonated/hemiprotonated phase (1) compared to the deprotonated one (2).
Nevertheless, it is essential to note that vibrations primarily of a molecular nature cannot be disregarded as contributors to the magnetic relaxation, as well as the protonation or deprotonation of the ligand can influence on them. Further studies on similar novel systems will enhance our understanding of this particular switch in spin dynamics.
The reversible interconversion between the different pH isomers along this proton transfer series of cobalt(II) complexes was monitored through electronic absorption/emission spectra and cyclic voltammetry in order to evaluate the pH-based optical/luminescent and redox chemo-switching in solution.
The electronic absorption/emission spectra of aqueous solutions of [CoII(HL)2]2+ (pH = 3) and [CoIIL2] (pH = 8) at room temperature are compared with those of their HL and NaL ligand counterparts in Fig. S17 (ESI†).
The electronic absorption spectra of [CoII(HL)2]2+ and [CoIIL2] consist of an intense band located in the far UV region at 290 nm with a distinct shoulder at ca. 330 nm (Fig. S17, ESI†). They are attributed to intraligand (IL) π–π* transitions, also present in the spectra of HL and NaL. These absorptions show a slight bathochromic shift from those of the protonated and deprotonated ligand forms [λmax = 280/325(sh) (HL) and 280/320(sh) nm (NaL)], likely explained by the ligand electronic delocalisation on the CoII ion. Additionally, a weak absorption band at 521 nm assigned to a ligand-to-metal charge transfer (LMCT) transition was observed for [CoII(HL)2]2+ and [CoIIL2] complexes, even if a small contribution from d–d transitions cannot be discarded. Hence, the related cobalt(II)-4′-perfluorophenyl-2,2′:6′,2′′-terpyridine derivative, [CoII(F5Ph-TERPY)2]2+, exhibits a similar band around 500 nm alternatively assigned to a metal-to-ligand charge transfer (MLCT) transition.43 This assignment agrees with earlier experimental work and theoretical calculations by Wieghardt et al. on cobalt(I) complexes with terpy-type ligands, which show the corresponding MLCT band at 1300 nm.44
The corresponding electronic emission spectra of [CoII(HL)2]2+ and [CoIIL2] after excitation with UV light (λexc = 295 nm) show the typical Stokes shift of the IL π*–π emission transitions in the near UV region at 370 nm with a distinct shoulder extending into the visible region at ca. 465 nm (Fig. S17, ESI†). The same situation was found in the emission spectra of the protonated and deprotonated ligand forms [λmax = 367/460 (sh) (HL) and 360/460(sh) nm (NaL)]. However, a net five to three-fold decrease of the emission intensity is observed for [CoII(HL)2]2+ and [CoIIL2] complexes compared to their ligand counterparts, as expected due to the quenching effect of the coordinated CoII ion.
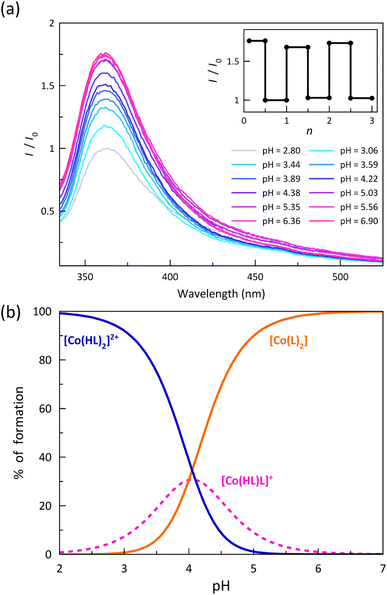
The electronic emission spectra recorded upon acid–base titration of a 0.01 mM DMSO/H2O (80![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 20 v/v) solution of 1 at 25 °C are depicted in Fig. 6a. They show an overall and progressive development of the asymmetric UV band centred at 370 nm upon increasing the pH from 2.8 to 6.9 up to the attainment of the stationary state corresponding to the total formation of the deprotonated [CoIIL2] species. The luminescence enhancement observed upon ligand deprotonation in solution suggests that this phenomenon is likely to be purely molecular in nature. The removal of a proton, which acts as an electron-withdrawing group, could modify the electron-donor characteristics of the benzoate group and, consequently, impact specific electronic transitions. Besides, in some cases, the observed quenching upon protonation may also be associated with deactivation towards a state with a different spin moment, which could be feasible in spin-transition systems. Spin–orbit coupling, a critical parameter in these deactivations of the emitting state, can be further influenced by the slight change in the electronic configuration caused by protonation, thereby promoting deactivation.45,46
20 v/v) solution of 1 at 25 °C are depicted in Fig. 6a. They show an overall and progressive development of the asymmetric UV band centred at 370 nm upon increasing the pH from 2.8 to 6.9 up to the attainment of the stationary state corresponding to the total formation of the deprotonated [CoIIL2] species. The luminescence enhancement observed upon ligand deprotonation in solution suggests that this phenomenon is likely to be purely molecular in nature. The removal of a proton, which acts as an electron-withdrawing group, could modify the electron-donor characteristics of the benzoate group and, consequently, impact specific electronic transitions. Besides, in some cases, the observed quenching upon protonation may also be associated with deactivation towards a state with a different spin moment, which could be feasible in spin-transition systems. Spin–orbit coupling, a critical parameter in these deactivations of the emitting state, can be further influenced by the slight change in the electronic configuration caused by protonation, thereby promoting deactivation.45,46
Even in solution, the environment can play a role on the luminescence quenching.47,48 For instance, solvent molecules participate in emission quenching, even in the solid state. Through hydrogen bonds between carboxylate and carboxyl groups, both in solution and the solid state, self-assembled species such as supramolecular dimers could be formed. These entities, which are absent in the deprotonated form, may inhibit luminescent emission. However, in our experiments conducted at concentrations of 10−5 M, it is expected that the protonated molecules would predominantly exist as monomers. This is especially true because the formation of supramolecular dimers, where two cationic complexes are brought closer without an anion acting as a glue, is not favoured. Therefore, this inhibitory pathway can be ruled out. Nevertheless, carboxylic groups can still form hydrogen bonds with the solvent molecules (DMSO and H2O) in the solution, and such interactions are more prevalent in the protonated form, consistent with observations in the solid-state crystal structure (refer to the crystal structure of 1). Consequently, the solvent, as a quencher, would dampen down more effectively the luminescence of the protonated form.
In any case, it should not be forgotten that in the carboxyl group, the hydrogen atom and also the OH group, due to the C–OH bond weakened after protonation, are sufficiently mobile to trigger an increase in non-radiative deactivations. To gain further insight into these aspects, it will be necessary to synthesise similar systems in future investigations.
The analysis of the pH variation of the normalised emission intensity (I/I0) after acid–base titration was carried out through a simple model that takes into account the presence of two acid-base equilibria between the protonated, hemiprotonated, and deprotonated forms of the mononuclear cobalt(II) species (Scheme 1). However, only one global acidity constant could be determined with a value of −log![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) β = 8.10(2), corresponding to the overall reaction (eqn (1)). The fitting software could not discriminate between the two individual stepwise constants (eqn (2) and (3)) because their pKas are too close since the carboxyl groups at each ligand are sufficiently far from each other to exert any influence on their acidity equilibrium. In this way, we can only conclude that each pKa value is close to 4.05, leading thus to a high degree of overlap between the three coexisting species around pH = 4. As shown in the distribution diagram (Fig. 6b), the dominant species at pH >5 is the deprotonated complex, while almost only the protonated form (above 90%) is found at pH <3. The hemiprotonated [CoII(HL)L]+ species occurs, less than 30%, only at pH around 4.
β = 8.10(2), corresponding to the overall reaction (eqn (1)). The fitting software could not discriminate between the two individual stepwise constants (eqn (2) and (3)) because their pKas are too close since the carboxyl groups at each ligand are sufficiently far from each other to exert any influence on their acidity equilibrium. In this way, we can only conclude that each pKa value is close to 4.05, leading thus to a high degree of overlap between the three coexisting species around pH = 4. As shown in the distribution diagram (Fig. 6b), the dominant species at pH >5 is the deprotonated complex, while almost only the protonated form (above 90%) is found at pH <3. The hemiprotonated [CoII(HL)L]+ species occurs, less than 30%, only at pH around 4.
| [CoII(HL)2]2+ ⇌ [CoIIL2] + 2H+ | (1) |
| [CoII(HL)2]2+ ⇌ [CoII(HL)L]+ + H+ | (2) |
| [CoII(HL)L]+ ⇌ [CoII L2] + H+ | (3) |
The significant enhancement of the luminescence along this proton transfer series of cobalt(II) complexes after the successive deprotonation of the carboxyl groups allows proposing this remarkable example of DMS as a prototype of an optical (luminescent) acid sensor.49,50 As a matter of fact, a comparison of the normalised emission intensities (I/I0) after five acid–base titration cycles in the pH range 3–8 indicates a completely reversible behaviour without any fatigue damage (inset of Fig. 6a). Indeed, this feature is mandatory when practical applications of mononuclear transition metal complexes as pH luminescent probes are envisaged.
The redox behaviour of the bis(benzoic acid-substituted terpyridine)cobalt(II) complexes was investigated through cyclic voltammetry (ESI†).
The cyclic voltammogram (CV) of 2 in dimethylformamide (DMF) shows four distinct redox processes (Fig. S18, ESI†), one reversible oxidation (E0 = −0.11 V vs. Fc/Fc+) and three non-reversible reductions (E1 = −1.08, E2 = −1.50 and E3 = −1.98 V vs. Fc+/Fc). The reversible oxidation wave corresponds to one-electron metal oxidation leading to the corresponding cobalt(III) complex. The formal potential of this CoIII/CoII pair is less negative than that reported for the parent cobalt(II)-2,2′:6′,2′′-terpyridine complex [CoII(TERPY)2]2+ (E = −0.14 V vs. Fc/Fc+ in DMF) as a consequence of the π-type electron-withdrawing nature of the benzoate substituent.51,52 In fact, the cobalt(II)-4′-perfluorophenyl-2,2′:6′,2′′-terpyridine derivative, [CoII(F5Ph-TERPY)2]2+, which features a stronger π-type electron-withdrawing perfluorinated benzene substituent, exhibits an even less negative CoIII/CoII formal potential in CH2Cl2 (E = −0.06 V vs. Fc/Fc+).43
According to the literature, the first and third reduction waves are likely attributed to the stepwise one-electron metal reduction CoII/CoI and CoI/Co0 pairs, while the completely irreversible second wave is most likely a ligand-based reduction process.43,51,52 However, there is still an ongoing debate regarding whether the reduction sites in this class of cobalt(II) complexes with TERPY-type ligands correspond to the metal or the ligand itself.43,53 The benzoate group also affects these metal reductions, occurring at intermediate formal potentials when compared to the parent [CoII(TERPY)2]2+ (E = −1.19 and −2.08 V vs. Fc/Fc+) and [CoII(F5Ph-TERPY)2]2+ complexes (E = −0.99 and −1.99 V vs. Fc/Fc+).43,51
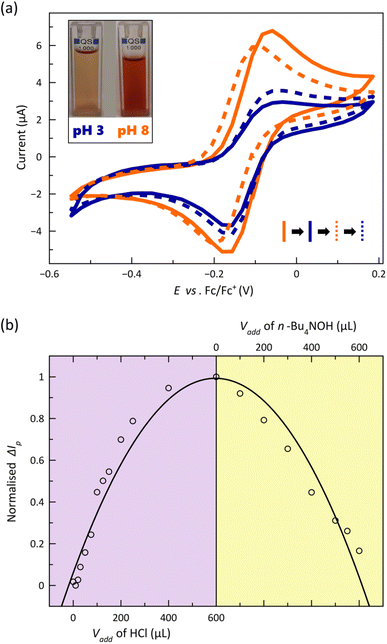
The CVs corresponding to the reversible metal-based oxidation wave recorded upon acid–base titration of a 1.0 mM DMF solution of 2 at 25 °C are depicted in Fig. 7a. As part of this experiment, the acid-base equilibria were simultaneously monitored by electronic absorption spectroscopy (Fig. S19, ESI†).
The gradual and continuous decrease of pH causes a loss in the reversibility of the CoIII/CoII redox process, as evidenced by the symmetric and asymmetric CV shapes at pH = 8 and 3 (Fig. 7a), which is accompanied by a decline of the visible LMCT band centred at 521 nm (Fig. S19a, ESI†) and a colour change from red to orange (inset of Fig. 7a). The partial loss of reversibility in acid media could be associated with the lower kinetic stability towards hydrolysis of the protonated oxidised form, [CoIII(HL)2]3+, even if further protonation of the nitrogen atoms from the coordinated pyridine groups followed by metal–ligand dissociation cannot be ruled out. On the other hand, the cathodic peak current signal and the intensity of the visible band are restored upon increasing the pH, matching almost perfectly the original CV and UV-Vis spectrum of [CoIIL2] (Fig. 7a and S19a, ESI†). The strong dependence on the added volume of acid/base or the pH of the normalised difference between absolute corrected anodic and cathodic current peaks (ΔIp) and that for molar extinction coefficient (ε) summarise these conclusions (Fig. 7b and S19b, ESI†). Thus, in the most acidic solution, ΔIp reaches the highest value, indicating that the CoIII/CoII redox process is less reversible, and ε attains the lowest one, being fully restored with the addition of base, evidencing the reversible interconversion between the [CoL2] and [Co(HL)2]2+ species.
Recently, we reported on the reversible electro-switching (ON/OFF) of the SMM behaviour in an octahedral SCO cobalt(II) complex with a 2,6-pyridinediimine (PDI)-type ligand featuring one-electron oxidation from the slow-relaxing paramagnetic LS CoII (ON) to the diamagnetic LS CoIII (OFF) state in solution.33 In that case, the metal oxidation occurs at +0.39 V vs. Fc/Fc+, a much higher former potential than that for the cobalt(II) complexes with TERPY-type ligand reported herein, which suggests that now a more favoured magnetic electro-switch should be achieved among the two [CoII(HL)2]2+/[CoIII(HL)2]3+ and [CoIIL2]/[CoIIIL2]+ redox pairs under pH control.
Conclusions
A novel pH-responsive dynamic molecular system has been developed through the ligand design based on an octahedral mononuclear cobalt(II) complex with a tailor-made TERPY-type ligand containing benzoic/benzoate substituents in the form of a pair of pH isomers. It constitutes a remarkable example of how the control of a single input (pH) can produce reversible changes in the optical (luminescence), redox, and magnetic (spin crossover and spin dynamics) properties, either in solution or in the solid state.Thermal-assisted spin transition and field-induced magnetisation blockage coexist in the solid state with “faster-relaxing” (FR) or “slower-relaxing” (SR) octahedral CoII ions in the LS state, depending on the ligand protonation degree. A progressive enhancement of luminescence in the UV region occurs upon acid-base equilibrium in solution among the protonated, hemiprotonated and deprotonated forms, which can be reversibly interconverted by varying the pH. These pH isomers also show one-electron oxidation of the paramagnetic LS CoII ion to the diamagnetic LS CoIII ion in solution, whose reversibility is partially lost with decreasing the pH but restored with increasing it.
The reported optical, electronic, and magnetic multistability along this proton transfer series of spin crossover cobalt(II) molecular nanomagnets illustrates the potential of dynamic molecular systems in nanoscience and nanotechnology, offering fascinating possibilities as advanced multifunctional and multiresponsive magnetic devices for molecular spintronics and quantum computing, such as spin chemo-switches for pH sensing. Moreover, the switching of the slow magnetic relaxation (and potential quantum coherence) in this proton transfer series could be exploited to develop a new type of pH-effect spin quantum transformers.
Ongoing research focuses on the synthesis of diamagnetic iron(II) or ruthenium(II) solid dilutions within the proton transfer series of spin crossover cobalt(II) molecular nanomagnets. These efforts aim to delve deeper into understanding the interplay between molecular and network vibrations and their influence on the spin dynamics and quantum coherence properties of these systems.
Data availability
The experimental data is already in the ESI file (see footnote†). Crystallographic data (excluding structure factors) for the structures were already deposited with the Cambridge Crystallographic Data Centre.Author contributions
Conceptualisation, J. C.; investigation, R. R., L. T., J. P., M. I.; methodology, R. R., M. I.; data curation, R. R., N. M., F. L., E. G.-E.; formal analysis, R. R., L. T. R. R.-G., J. C.; writing, R. R., M. J. R. R.-G., J. C.Conflicts of interest
There are no conflicts to declare.Acknowledgements
This work was supported by the Spanish MINECO (PID2019-109735GB-I00 and CEX2019-000919-M), and Generalitat Valenciana (AICO/2021/295). This work has received funding from the European Union's Horizon 2020 research and innovation programme under the Marie Skłodowska-Curie grant agreement No. 748921-SIMOF. R. R. thanks the Generalitat Valenciana and CAPES (88887.798611/2022-00) for doctoral and postdoctoral grants, respectively. J. P. thanks Fundación La Caixa – CajaCanarias for the Senior Excellence Research Contract.Notes and references
- J. Ferrando-Soria, J. Vallejo, M. Castellano, J. Martínez-Lillo, E. Pardo, J. Cano, I. Castro, F. Lloret, R. Ruiz-García and M. Julve, Coord. Chem. Rev., 2017, 339, 17–103 CrossRef CAS
.
- B. Doistau, L. Benda, B. Hasenknopf, V. Marvaud and G. Vives, Magnetochemistry, 2018, 4, 1–15 CrossRef
.
- Y.-S. Meng and T. Liu, Acc. Chem. Res., 2019, 52, 3309–3324 CrossRef PubMed
.
- C. Römelt, T. Weyhermüller and K. Wieghardt, Coord. Chem. Rev., 2019, 380, 287–317 CrossRef
.
- S. Dhers, A. Mondal, D. Aguilà, J. Ramírez, S. Vela, P. Dechambenoit, M. Rouzières, J. R. Nitschke, R. Clérac and J.-M. Lehn, J. Am. Chem. Soc., 2018, 140, 8218–8227 CrossRef CAS PubMed
.
- P. P. Mudoi, A. Choudhury, Y. Li, R. Lescouëzec, R. Marimuthu and N. Gogoi, Inorg. Chem., 2021, 60, 17705–17714 CrossRef CAS PubMed
.
- R. Nowak, E. A. Prasetyanto, L. De Cola, B. Bojer, R. Siegel, J. Senker, E. Rössler and B. Weber, Chem. Commun., 2017, 53, 971–974 RSC
.
- J. Vallejo, E. Pardo, M. Viciano-Chumillas, I. Castro, P. Amorós, M. Déniz, C. Ruiz-Pérez, C. Yuste-Vivas, J. Krzystek, M. Julve, F. Lloret and J. Cano, Chem. Sci., 2017, 8, 3694–3702 RSC
.
- S. Xue, G. F. B. Solre, X. Wang, L. Wang and Y. Guo, Chem. Commun., 2022, 58, 1954–1957 RSC
.
- S. van Vliet, G. Alachouzos, F. de Vries, L. Pfeifer and B. L. Feringa, Chem. Sci., 2022, 13, 9713–9718 RSC
.
- M. Elie, M. D. Weber, F. Di Meo, F. Sguerra, J.-F. Lohier, R. B. Pansu, J.-L. Renaud, M. Hamel, M. Linares, R. D. Costa and S. Gaillard, Chem.–Eur. J., 2017, 23, 16328–16337 CrossRef CAS PubMed
.
- M. D. Weber, E. Fresta, M. Elie, M. E. Miehlich, J.-L. Renaud, K. Meyer, S. Gaillard and R. D. Costa, Adv. Funct. Mater., 2018, 28, 1707423 CrossRef
.
- J. M. Carbonell-Vilar, E. Fresta, D. Armentano, R. D. Costa, M. Viciano-Chumillas and J. Cano, Dalton Trans., 2019, 48, 9765–9775 RSC
.
- S. M. Fatur, S. G. Shepard, R. F. Higgins, M. P. Shores and N. H. Damrauer, J. Am. Chem. Soc., 2017, 139, 4493–4505 CrossRef CAS PubMed
.
- P. Gotico, L. Roupnel, R. Guillot, M. Sircoglou, W. Leibl, Z. Halime and A. Aukauloo, Angew. Chem., Int. Ed., 2020, 59, 22451–22455 CrossRef CAS PubMed
.
- P. Gotico, D. Moonshiram, C. Liu, X. Zhang, R. Guillot, A. Quaranta, Z. Halime, W. Leibl and A. Aukauloo, Chem.–Eur. J., 2020, 26, 2859–2868 CrossRef CAS PubMed
.
- G. Ruan, L. Engelberg, P. Ghosh and G. Maayan, Chem. Commun., 2021, 57, 939–942 RSC
.
- R. Botár, E. Molnár, G. Trencsényi, J. Kiss, F. K. Kálmán and G. Tircsó, J. Am. Chem. Soc., 2020, 142, 1662–1666 CrossRef
.
- H. Wang, S. Y. Sayed, Y. Zhou, B. C. Olsen, E. J. Luber and J. M. Buriak, Chem. Commun., 2020, 56, 3605–3608 RSC
.
- I. F. Mansoor, D. I. Wozniak, Y. Wu and M. C. Lipke, Chem. Commun., 2020, 56, 13864–13867 RSC
.
- S. K. Karuppannan, A. Martín-Rodríguez, E. Ruiz, P. Harding, D. J. Harding, X. Yu, A. Tadich, B. Cowie, D. Qif and C. A. Nijhuis, Chem. Sci., 2021, 12, 2381–2388 RSC
.
- A. C. Aragonès, D. Aravena, F. J. Valverde-Muñoz, J. A. Real, F. Sanz, J. Hihath, I. Díez-Pérez and E. Ruiz, J. Am. Chem. Soc., 2017, 139, 5768–5778 CrossRef PubMed
.
- T. Jasper-Toennies, M. Gruber, S. Karan, H. Jacob, F. Tuczek and R. Berndt, Nano Lett., 2017, 17, 6613–6619 CrossRef CAS
.
- Q.-Q. Su, Q. Yuan, X.-F. Wu, S.-H. Chen, J. Xiang, X.-X. Jin, L.-X. Wang, B.-W. Wang, S. Gao and T.-C. Lau, Chem. Commun., 2021, 57, 781–784 RSC
.
- V. Jornet-Mollá, C. Giménez-Saiz, L. Cañadillas-Delgado, D. S. Yufit, J. A. K. Howard and F. M. Romero, Chem. Sci., 2021, 12, 1038–1053 RSC
.
- M. M. Paquette, D. Plaul, A. Kurimoto, B. O. Patrick and N. L. Frank, J. Am. Chem. Soc., 2018, 140, 14990–15000 CrossRef CAS PubMed
.
- A. Urtizberea and O. Roubeau, Chem. Sci., 2017, 8, 2290–2295 RSC
.
- H.-H. Cui, J. Wang, X.-T. Chen and Z.-L. Xue, Chem. Commun., 2017, 53, 9304–9307 RSC
.
- L. Chen, J. Song, W. Zhao, G. Yi, Z. Zhou, A. Yuan, Y. Song, Z. Wang and Z.-W. Ouyang, Dalton Trans., 2018, 47, 16596–16602 RSC
.
- M.-X. Xu, Z. Liu, B.-W. Dong, H.-H. Cui, Y.-X. Wang, J. Su, Z. Wang, Y. Song, X.-T. Chen, S.-D. Jiang and S. Gao, Inorg. Chem., 2019, 58, 2330–2335 CrossRef CAS PubMed
.
- D. Shao, L. Shi, L. Yin, B.-L. Wang, A.-X. Wang, Y.-Q. Zhang and X.-Y. Wang, Chem. Sci., 2018, 9, 7986–7991 RSC
.
- F. Kobayashi, Y. Komatsumaru, R. Akiyoshi, M. Nakamura, Y. Zhang, L. F. Lindoy and S. Hayami, Inorg. Chem., 2020, 59, 16843–16852 CrossRef CAS PubMed
.
- R. Rabelo, L. Toma, N. Moliner, M. Julve, F. Lloret, J. Pasán, C. Ruiz-Pérez, R. Ruiz-García and J. Cano, Chem.
Commun., 2020, 56, 12242–12245 RSC
.
- I.-R. Jeon, S. Calancea, A. Panja, D. M. Piñero Cruz, E. S. Koumousi, P. Dechambenoit, C. Coulon, A. Wattiaux, P. Rosa, C. Mathonière and R. Clérac, Chem. Sci., 2013, 4, 2463–2470 RSC
.
- W. D. Do Pim, W. X. C. Oliveira, M. A. Ribeiro, E. N. de Faria, I. F. Teixeira, H. O. Stumpf, R. M. Lago, C. L. M. Pereira, C. B. Pinheiro, J. C. D. Figueiredo-Júnior, W. C. Nunes, P. P. de Souza, E. F. Pedroso, M. Castellano, J. Cano and M. Julve, Chem. Commun., 2013, 49, 10778–10780 RSC
.
- J. Yang, R.-X. Hu and M.-B. Zhang, J. Solid State Chem., 2012, 196, 398–403 CrossRef CAS
.
-
K. Nakamoto, Infrared and Raman Spectra of Inorganic and Coordination Compounds, Wiley, 1986 Search PubMed
.
- S. Hayami, Y. Komatsu, T. Shimizu, H. Kamihata and Y. H. Lee, Coord. Chem. Rev., 2011, 255, 1981–1990 CrossRef CAS
.
- C. Hansch, A. Leo and W. A. Taft, Chem. Rev., 1991, 91, 165–195 CrossRef CAS
.
- J. A. Real, M. C. Muñoz, E. Andrés, T. Granier and B. Gallois, Inorg. Chem., 1994, 33, 3587–3594 CrossRef CAS
.
- M. Hostettler, K. W. Törnroos, D. Chernyshov, B. Vangdal and H. B. Bürgi, Angew. Chem., Int. Ed., 2004, 43, 4589–4594 CrossRef CAS PubMed
.
- K. S. Cole and R. H. Cole, J. Chem. Phys., 1941, 9, 341–351 CrossRef CAS
.
- M. Nöβler, R. Jäger, D. Hunger, M. Reimann, T. Bens, N. I. Neuman, A. S. Hazari, M. Kaupp, J. van Slageren and B. Sarkar, Eur. J. Inorg. Chem., 2023, e202300091 Search PubMed
.
- J. England, E. Bill, T. Weyhermüller, F. Neese, M. Atanaov and K. Wieghardt, Inorg. Chem., 2015, 54, 12002–12018 CrossRef CAS PubMed
.
- T. Hofbeck, U. Monkowius and H. Yersin, J. Am. Chem. Soc., 2015, 137, 399–404 CrossRef CAS
.
- M. J. Leitl, V. A. Krylova, P. I. Djurovich, M. E. Thompson and H. Yersin, J. Am. Chem. Soc., 2014, 136, 16032–16038 CrossRef CAS PubMed
.
- C. E. McCusker and F. N. Castellano, Inorg. Chem., 2013, 52, 8114–8120 CrossRef CAS PubMed
.
- D. R. McMillin and K. M. McNett, Chem. Rev., 1998, 98, 1201–1220 CrossRef PubMed
.
- A. Steinegger, O. S. Wolfbeis and S. M. Borisov, Chem. Rev., 2020, 120, 12357–12489 CrossRef CAS PubMed
.
- W. Chen, X. Ma, H. Chen, S. H. Liu and J. Yin, Coord. Chem. Rev., 2021, 427, 213584 CrossRef CAS
.
- C. Arana, S. Yan, M. Keshavarz, K. T. Potts and H. D. Abruna, Inorg. Chem., 1992, 31, 3680–3682 CrossRef CAS
.
- H. Ferreira, M. M. Conradie and J. Conradie, Inorg. Chim. Acta, 2019, 486, 26–35 CrossRef CAS
.
- X. Ma, E. A. Suturina, S. De, P. Négrier, M. Rouzières, R. Clérac and P. Dechambenoit, Angew. Chem., Int. Ed., 2018, 57, 7841–7845 CrossRef CAS PubMed
.
Footnotes |
| † Electronic supplementary information (ESI) available: Experimental details on the synthesis of the ligand and complexes and their physicochemical characterisation, crystallographic details, magnetic measurements and solution studies (Tables S1 and S2, Schemes S1 and S2, and Fig. S1–S19). CCDC 2230369–2230370. For ESI and crystallographic data in CIF or other electronic format see DOI: https://doi.org/10.1039/d3sc02777e. |
| ‡ The structure of 2 is almost identical to that reported earlier,36 but non-negligible differences are found in the molecular dimensions and molecular conformation most likely associated with the temperature of the crystallographic data collection (see Table S2, ESI†). |
| This journal is © The Royal Society of Chemistry 2023 |