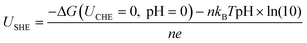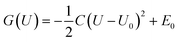–SR removal or –R removal? A mechanistic revisit on the puzzle of ligand etching of Au₂₅(SR)₁₈ nanoclusters during electrocatalysis

Abstract

Accurate identification of active sites is highly desirable for elucidation of the reaction mechanism and development of efficient catalysts. Despite the promising catalytic performance of thiolated metal nanoclusters (NCs), their actual catalytic sites remain elusive. Traditional first-principles calculations and experimental observations suggested dealkylated S and dethiolated metal, respectively, to be the active centers. However, the real kinetic origin of thiolate etching during the electrocatalysis of NCs is still puzzling. Herein, we conducted advanced first-principles calculations and electrochemical/spectroscopic experiments to unravel the electrochemical etching kinetics of thiolate ligands in prototype Au₂₅(SCH₃)₁₈ NC. The electrochemical processes are revealed to be spontaneously facilitated by dethiolation (i.e., desorption of –SCH₃), forming the free HSCH₃ molecule after explicitly including the solvent effect and electrode potential. Thus, exposed under-coordinated Au atoms, rather than the S atoms, serve as the real catalytic sites. The thermodynamically preferred Au–S bond cleavage arises from the selective attack of H from proton/H₂O on the S atom under suitable electrochemical bias due to the spatial accessibility and the presence of S lone pair electrons. Decrease of reduction potential promotes the proton attack on S and significantly accelerates the kinetics of Au–S bond breakage irrespective of the pH of the medium. Our theoretical results are further verified by the experimental electrochemical and spectroscopic data. At more negative electrode potentials, the number of –SR ligands decreased with concomitant increase of the vibrational intensity of S–H bonds. These findings together clarify the atomic-level activation mechanism on the surface of Au₂₅(SR)₁₈ NCs.

---

Introduction

Ligand-protected atomically precise metal nanoclusters (NCs), as a new class of nanomaterials, have motivated researchers from multiple disciplines owing to their unique physiochemical properties and precise structures determined by X-ray crystallography.^1–7 As compared to the nanoparticles, NCs possess large surface-to-volume ratios, atomic precision, molecular purity, and more importantly, unique atomic arrangements and fascinating properties.^8–10 Among various ligand-protected metal clusters, thiolate-protected NCs (denoted as M_n(SR)_m) consisting of tens to a few hundred metal atoms are ultra-small, usually below 2 nm. The special size regime imparted strong quantum confinement effects and low metal coordination numbers that render M_n(SR)_m NCs with properties drastically distinct from their larger bulk counterparts,^11–13 which provide exciting opportunities for diverse applications in biological labeling, sensing, drug delivery, optoelectronics, and catalysis.^14–17 In particular, M_n(SR)_m NCs have recently been identified as promising catalysts to accelerate a broad range of electrocatalytic reactions, such as the oxygen reduction/evolution reaction (ORR/OER), hydrogen evolution reaction (HER), and CO₂ reduction reaction (CO₂RR).^18–22 Given the large number of structurally resolved M_n(SR)_m compositions, a deep understanding of the correlation between the geometrical structure and catalytic behaviors is critical. For these reasons, M_n(SR)_m and its alloy clusters, especially the thiolate-protected Au systems, have been intensively investigated as excellent “nano-models” to fuel the study of the fundamentals of catalysis at the atomic level.

Metal–thiolate bonds, as the outmost protecting layers, play a crucial role in forming an ordered NC structure. In brief, sub-2 nm structures are typically synthesized with a highly symmetric metal core and a self-assembled monolayer of RS–metal–SR motifs as the shell. The presence of these protecting motifs not only prevents aggregation, but also functionalizes the nanostructures to control the morphology and electrochemical properties.^23,24 Despite the enhanced stability, these capping thiols passivate the surface by imposing steric restrictions on the accessibility of molecular reactants, thus blocking the availability of active surface atoms.^11,25 In this regard, the fully ligand-protected NCs are generally considered to be electrochemically inactive with extremely large overpotentials that are in contrast to the experimental proposition.^26–30 Thus, ligand removal at a local site has been proposed to be essential for the high electrocatalytic activity observed in thiolate-protected NCs. Local ligand removal can be realized via two possible modes: either releasing an intact –SR ligand or cleaving the organic –R moiety to generate the exposed metal or S atom, respectively.^28–32 Recent studies on the CO₂RR of thiolate-protected NCs have shown that the ligand removal mode which leads to the formation of dealkylated S is thermodynamically more plausible than the one that leads to the exposure of a metal atom.^29,30 Mpourmpakis' group also claimed from a theoretical point of view that breaking the S–R bond is thermodynamically more favorable than breaking the Au–S bond in thiolate-protected gold NCs.³³ In addition, Jin's group investigated the effect of single atom doping on electrochemical ORR with M₁Ag₂₄(SR)₁₈ NCs (M = Ag/Au/Pd/Pt).³⁴ Based on the computational hydrogen electrode (CHE) model, they again found that the exposure of S atoms on the doped NCs is thermodynamically more feasible for launching the catalytic process at modest overpotentials. However, in contrast to the above findings, the recent report by Lee et al. demonstrated that Au NCs (e.g., Au₂₅(SR)₁₈, Au₃₈(SR)₂₄, Au₁₄₄(SR)₆₀) were activated by removing the thiolate group from the staple motif at the beginning of the CO₂RR, as evidenced by their electrochemical and X-ray photoelectron spectroscopy (XPS) analyses.³⁵ More recently, Lee's group performed the EXAFS (extended X-ray absorption fine structure) spectroscopic analysis of Au₄Ni₂(SR)₈ NC and observed the decrease in the coordination number (CN) of Au–S and Ni–S bonds after electrochemical activation.³⁶ Similarly, Yang et al. also proved that the thiolate ligands can be readily removed under electrochemical biasing at ≤−0.5 V vs. reversible hydrogen electrode (RHE).³⁷ Since the origin of the electrocatalytic activity has been disputed, what is the real active site of thiolate-protected NCs during the electrocatalytic process? So far, the theoretical understanding based on the traditional thermodynamic calculations seems to be in contrast to the experimental results. The apparent contradiction between the thermodynamic claims and the experiments prompts us to implement advanced first-principles model to conduct in-depth mechanistic understanding of the underlying exposure sites at the atomic level.

To resolve this puzzling question, the classic Au₂₅(SR)₁₈ NC was selected as our research model, which can be theoretically represented by a simplified model cluster Au₂₅(SCH₃)₁₈, where each –SR ligand was simplified by the computationally more tractable –SCH₃ group to mimic the ligand fragment. After a series of simulations, we found that the traditional oversimplified calculation without considering the solvent effect and electrode potential yields a strong thermodynamic preference for the S–C breaking. Alternatively, based on more accurate constant-potential simulations including thermodynamics and state-of-the-art ab initio molecular dynamics (AIMD), we detected that the H⁺ species from the water layer tends to attach to the S atom, weakening the Au–S bond and ultimately peeling off SR from the metal surface to form the HSCH₃ molecule, indicating that the dethiolated Au atoms are inclined to shoulder the active sites for electrocatalysis. Our predictions are further supported by the electrochemical experiments: a decrease in the number of SR ligands and an increase in the vibrational intensity of S–H bonds are observed from XPS and FTIR characterizations, respectively, of the electrochemically activated Au₂₅(SR)₁₈ NCs. Our work offers new fundamental insights into the ligand etching mechanism of the prototype Au₂₅(SR)₁₈ NC, uncovering the atomic-level kinetics that are missing in the conventional first-principles calculations of heterogeneous electrochemistry of thiolated metal NCs.

Results and discussion

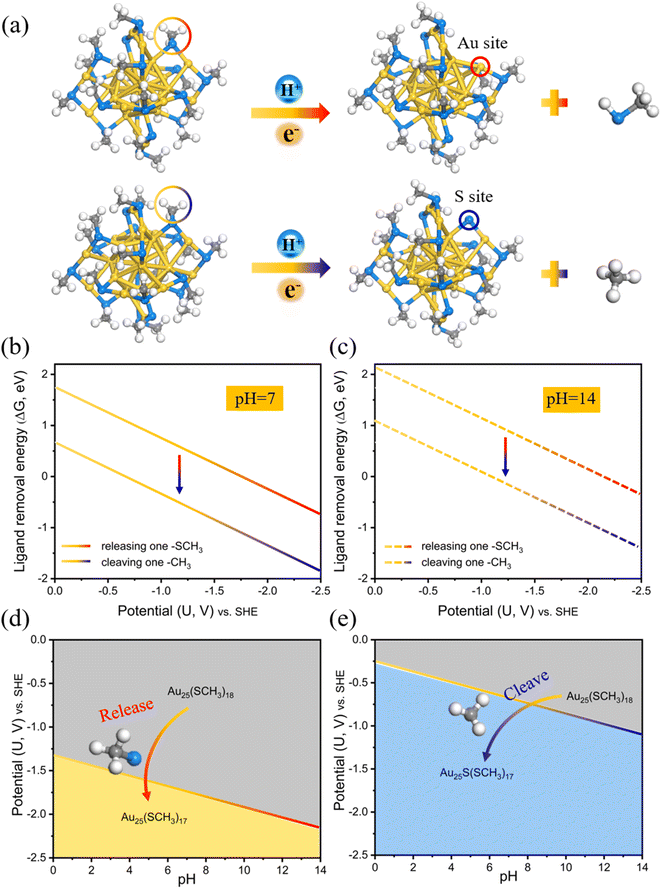
DFT calculations have been used to produce predominance diagrams in a variety of material systems, and one of the most commonly used ones is the Pourbaix diagrams. These plots associated with pH and electric potential can provide insight into the thermodynamic stability in aqueous media. By extending this approach to the ligand etching modes on Au₂₅(SCH₃)₁₈ (Fig. 1a), we first calculated the ligand removal energies, and then explored the stability dependence on pH and electric potential to compare the stability region of the two cleaving modes.

Fig. 1 (a) Two electrochemical ligand removal modes on Au₂₅(SCH₃)₁₈: removal of an entire –SCH₃ ligand (dethiolation) or cleavage of the –CH₃ moiety (dealkylation) to produce an exposed Au or S atom active site, respectively. Calculated ligand removal energy (ΔG) of the two cleaving modes as a function of potential based on the charge-neutral method (CNM) in pH = 7 (b) and pH = 14 (c). (d and e) Two bond breaking reactions' adhesion stability regions in the pH–U_SHE space at T = 298.15 K. Color codes: yellow, Au; blue, S; grey, C; white, H. The same color scheme is used in the figures below.

The corresponding ligand removal energies (ΔG) for the two cleaving modes as a function of potential at the neutral and alkaline electrolyte environments (pH = 7 and pH = 14) are depicted in Fig. 1b and c, calculated using the charge-neutral method (CNM) based on the traditional computational hydrogen electrode (CHE) model. It can be clearly seen that cleavage of the –CH₃ moiety (dealkylation) is thermodynamically more favorable than dethiolation via removing the entire –SCH₃ ligand due to the lower ΔG values of the former. It is then possible to define the stability regions of pH-dependent equilibrium potential space for these two cleaving reactions.^38–40 The relative stability plots are shown in Fig. 1d and e. It can be shown that the dealkylated Au₂₅S(SCH₃)₁₇ structure (blue region) is more stable than the dethiolated Au₂₅(SCH₃)₁₇ (yellow region) in the all-pH range, which means that releasing a –SCH₃ ligand to expose an Au site is always thermodynamically more difficult than cleaving the organic –CH₃ moiety to expose the S site, and a much higher potential is needed for the Au–S cleavage. For example, the –CH₃ ligand can be removed at negative potentials U ≤ −1.09 V_SHE (−0.26 V_RHE) at pH = 14, yet the potential required to strip away the thiolate group can reach up to U ≤ −2.15 V_SHE (−1.33 V_RHE). Note that these oversimplified thermodynamic predictions based on the traditional CHE model without explicitly considering the constant potential and solvation are consistent with the prior theoretical findings by others.^29,30,33

However, the simplified calculations still do not solve our concerns. It is well known that the reaction thermodynamics at the electrochemical interface depends on several factors such as surface coverage, electrode potential, solvent and pH.⁴¹ Although the charge neutral method (CNM) as described above is widely used for the prediction of electrocatalytic activity, it greatly ignores an important aspect: the grand free energy is usually approximated to be a linear function of the electrode potential (e.g., Fig. 1b and c), but in reality, the catalyst is usually charged by accepting/donating electrons from/to the electrode to match the Fermi level with the applied electrode potential.^20,42–44 That is to say, this linear approximation has the drawback of neglecting change in capacitive contributions to the energy. Furthermore, although we have considered the implicit solvation of the Au₂₅ system by a continuous polarizable medium in the above calculation, it cannot describe the hydrogen bonding and ion distributions around the electrochemical interfaces, thus leading to severe underestimation of the solvation effects.⁴⁵ Therefore, the thermodynamic results based on the CHE model could obscure some important facts due to oversimplification. This prompts us to re-evaluate the ligand etching thermodynamics using the constant-potential method (CPM).

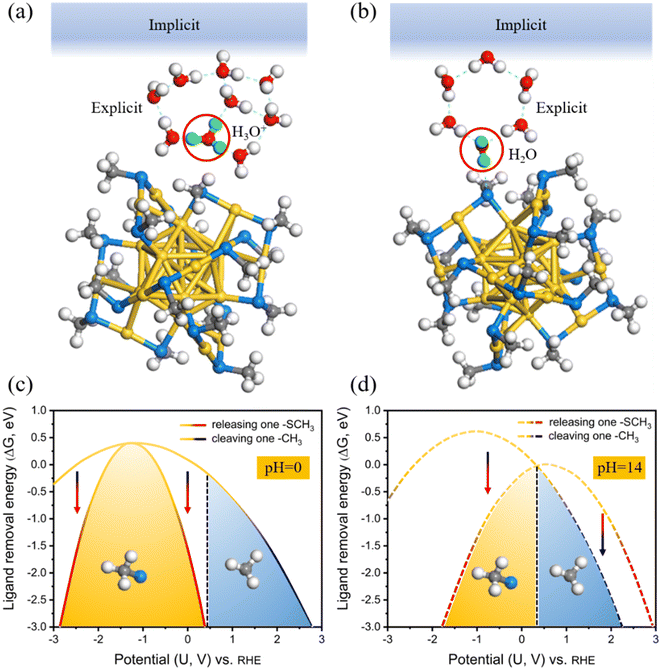
To explicitly consider the electrode potential and solvation, the manual adjustment of extra electrons was introduced to drive the applied potential U, which can be achieved by combining an implicit solvation with the explicit water molecules in our calculations (Fig. 2a and b). Its advantage is that we can continuously control the work function (Φ) by introducing fractional charges at the explicit/implicit interface using Poisson-Boltzmann approximation.⁴⁶ In this way, the Φ of each model can be tuned to match the potential U according to U_RHE = (Φ − 4.44)/e + 0.0592 × pH.⁴⁷ Note that, to highlight the universality of our survey, explicit 8H₂O + 1H₃O⁺ (Fig. 2a) and 6H₂O (Fig. 2b) are introduced at the local surface of Au₂₅ NCs to simulate the acid and alkaline systems (approximately pH = 0 and pH = 14), respectively. The neutral case can be considered as similar to the alkaline model. Two more water molecules are used in the acid model to better imprison one added proton. The relationships between the extra electrons (n − n₀) and the corresponding electrode potential U_RHE could be found in Fig. S1.† For each modeled Au₂₅ structure, calculations were performed at charges of 0e to 4e with decrements of 1e, and five potentials are considered respectively. The potential-dependent free energy can be then fit to a quadratic function (Fig. S2†). From the fitted quadratic functions for the intact Au₂₅ and its two removal systems, the ligand removal energetics as a function of potential can be further predicted at pH = 0 and pH = 14 (Fig. 2c and d), labeled as the CPM. In this case, the dethiolation reaction (yellow potential region) is thermodynamically more superior to the dealkylation in the range of potential U_RHE from −2.85 to 0.39 V at pH = 0 (Fig. 2c) and from −1.77 to 0.32 V at pH = 14 (Fig. 2d). In other words, the exposed Au atom in Au₂₅(SCH₃)₁₇ induced by the preferred Au–S bond breakage should be the active site under the CPM calculations. This thermodynamic result is consistent with the observation of dethiolated Au₂₅ NCs in recent experiments.^35,37 Furthermore, regarding the two theoretical models under current acidic (Fig. 2a) and alkaline (Fig. 2b) conditions, the ligand etching energy for the two cleaving modes as a function of potential was evaluated again by employing the CNM based on the CHE model, i.e. the solvation is explicitly considered but the electrode potential is not included, as shown in Fig. S3.† With the inclusion of explicit molecules, the energy difference of the reaction concerned is significantly reduced compared with the result calculated using the traditional CNM at the beginning, but the result is consistent, that is, it is still inclined to the dealkylation process. Apparently, the contrasting reversal results between the CNM-based simulations and the CPM-based ones also reaffirm that an advanced theoretical model that explicitly considers the potential and solvation effects is essential to study the electrocatalytic process of metal NCs, which can provide more effective and accurate calculation of the reaction thermodynamics at the catalyst–water interface that are not captured by the conventional CHE models.

Fig. 2 Schematic illustration of the explicit + implicit solvation model at the local surface of Au₂₅(SCH₃)₁₈ at pH = 0 (a) and pH = 14 (b). Possible transferred H atoms from H₃O⁺ and H₂O are highlighted in green, and the blue area at the top represents an implicit solvation background. Ligand removal energy (ΔG) of the two cleaving modes as a function of potential U_RHE in pH = 0 (c) and pH = 14 (d), calculated using CPM.

On the other hand, although the constant potential calculations with the hybrid explicit + implicit solvation scheme indeed provide more accurate insight into the active site at the Au₂₅/water interface, these predictions were solely based on the thermodynamics. Since the electrochemical interface under actual reaction conditions is often a dynamic phenomenon, the kinetic information should also be taken into account to further corroborate the thermodynamic conclusions. It is also particularly important to consider the effects of potential and solvation in the investigation of the dynamic processes. Liquid water has numerous configurations with different interactions, and these configurations/interactions with Au₂₅ can evolve along the reaction coordinate.⁴⁸ In our above model, we considered only finite structures with a few water molecules on Au₂₅ NC, which are commonly employed to evaluate thermodynamics but may not accurately describe the electrochemical dynamics of the solid–water interface.

To overcome this shortcoming, we updated the hybrid-solvation model as described above, using a thick explicit water slab in conjunction with implicit solvation on the surface of Au₂₅ along the z-axis direction. Then we set to examine the electrochemical kinetics of the local surface on Au₂₅ by combining constant potential calculations and AIMD simulations. In a similar manner, extra electrons are introduced to drive a defined potential, in which the configuration of water and the net charge are coupled to each other, both fluctuating and evolving along the reaction coordinate.⁴⁸ Due to the difficulty in continuously tuning the pH values, we focus only on the acid (pH = 0) and alkaline media (pH = 14), where the main proton source of acid is hydronium ion (H₃O⁺), while the alkaline environment can be modeled with pure water (without adding or removing H). To give a reasonable initial configuration for the dynamic simulations, each system was pre-optimized before AIMD operation. See Fig. S4a and b† for the specific theoretical models. Besides the Au₂₅(SCH₃)₁₈ substrate, the empty spaces of the simulation box were filled by bulk water with an average density of ∼1 g cm⁻³, which contained 78H₂O molecules plus one H₃O⁺ for the acid system, and 79H₂O molecules for the alkaline system.⁴⁹ The radial distribution functions (RDFs) and the coordination number of O–O and O–H interactions for validation of the liquid water structure (Fig. S6†) are in excellent agreement with experimental characterizations, validating the proper convergence of the water structure to bulk water behaviors.⁵⁰ By inference, our model can correctly describe the behavior of liquid water.

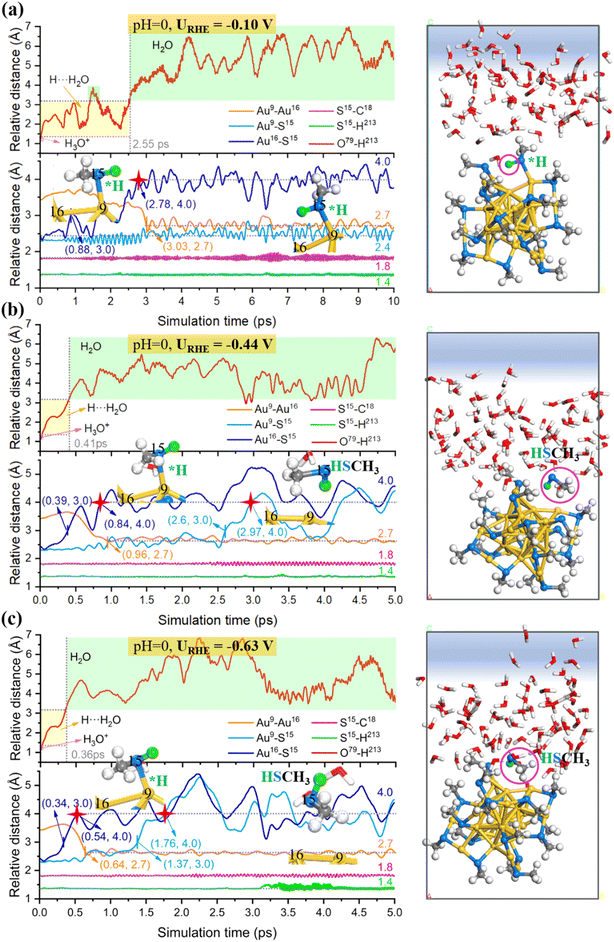
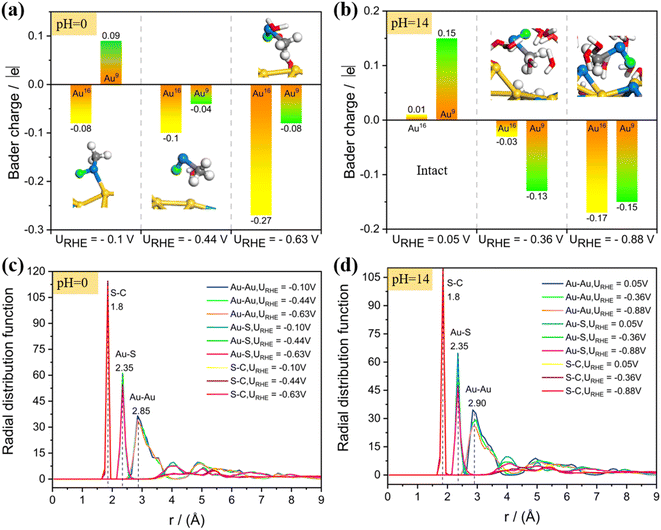
Next, we carried out constant potential AIMD simulations to detect the dynamic behaviors of the gold–ligand interface at a given U_RHE. For the acid model, 0, 1 and 2 extra electrons are introduced, resulting in U_RHE = −0.10 V, −0.44 V and −0.63 V, respectively. As shown in Fig. 3, our AIMD snapshots revealed that one –SCH₃ ligand on Au₂₅ NC is indeed unstable under exposure to potential and liquid water at room temperature (300 K). The proton from H₃O⁺ prefers to be attracted and adsorbed onto the S atom and weaken the Au–S bond. When the potential is sufficiently negative, the Au–S bond can be completely broken to form the HSCH₃ molecule (purple circle marked in AIMD snapshots). Specifically, when U_RHE is −0.10 V (Fig. 3a), the proton attack leads to the weakening and breaking of the surface Au–S bond, however, it can only cause one Au–S bond to be disconnected and form the adsorbed HSCH₃ molecule, which proves that a relatively low bias potential is not sufficient to completely strip away the SCH₃ ligand. When the reduction potential is higher, −0.44 V (Fig. 3b) or −0.63 V (Fig. 3c), the –SCH₃ group can completely be stripped away from the bonding of surface and staple Au accompanied by the breaking of two Au–S bonds and desorb as HSCH₃ into the solution.

Fig. 3 Statistics of the relative distance between representative atoms during the equilibrated AIMD simulation at 300 K at (a) U_RHE = −0.10 V, (b) U_RHE = −0.44 V, and (c) U_RHE = −0.63 V for an acid system. The corresponding AIMD snapshot is shown on the right. The inset (left) is the corresponding local structures for Au¹⁶(surface)–S¹⁵ breaking and subsequent Au⁹(staple)–S¹⁵ breaking.

To capture more detailed dynamic information of the ligand etching behaviors, we focus on the AIMD region around the broken bond and label the key atoms around it (the detailed labeling can be found in Fig. S4c†). The Au₂₅(SCH₃)₁₈ NC can be viewed as a Au₁₃ icosahedron core protected by six Au₂(SCH₃)₃ staple motifs. The –S(CH₃) ligand coordinated to the icosahedra surface Au (labeled as Au¹⁶) and the staple Au (labeled Au⁹) is readily detached during the AIMD simulations. Fig. 3 shows the relative distance between representative atoms at different U_RHE. Notably, the S¹⁵ atom is first disconnected from the surface Au¹⁶: when U_RHE is −0.10 V, it takes about 2.78 ps (marked by the red star) to reach an equilibrium Au¹⁶⋯S¹⁵ distance of 4 Å that is considered to be completely disconnected (Fig. 3a), while when U_RHE is −0.44 and −0.63 V, the time scale needed for the Au¹⁶(surface)–S¹⁵ cleavage is dramatically reduced to 0.84 ps and 0.54 ps (marked by the first red star in Fig. 3b and c), respectively. Note that after the first Au¹⁶(surface)–S¹⁵ breaking, the other staple Au⁹ still has a strong interaction with S¹⁵ at the lower potential of −0.10 V. Interestingly, when the potential is increased to −0.44 V and −0.63 V, the Au⁹(staple)–S¹⁵ bond can be completely broken around 2.97 ps and 1.76 ps (marked by the second red star in Fig. 3b and c), respectively. This phenomenon emphasizes that the applied potential should be the most critical factor affecting the thiolate removal from Au₂₅ in the electrochemical process. The more negative the applied potential is, faster the kinetics in the proton attack onto S¹⁵ and easier the breaking of Au(surface)–S and Au(staple)–S bonds. For example, at the higher potential of −0.63 V, the proton can be transferred from H₃O⁺ in 0.36 ps and then stably attached to the S¹⁵ atom. After the detaching of a –SCH₃ ligand, two under-coordinated Au, Au⁹(staple) and Au¹⁶(surface), will be exposed, and the bond distance between them is shortened from the initial 3.4 Å to 2.7 Å. Note that our constant potential AIMD simulations did not observe a significant change in the S–C bond, indicating that the mild electrochemical potential can readily detach the –S(CH₃) group but is insufficient to strip away the –CH₃ tail moiety.

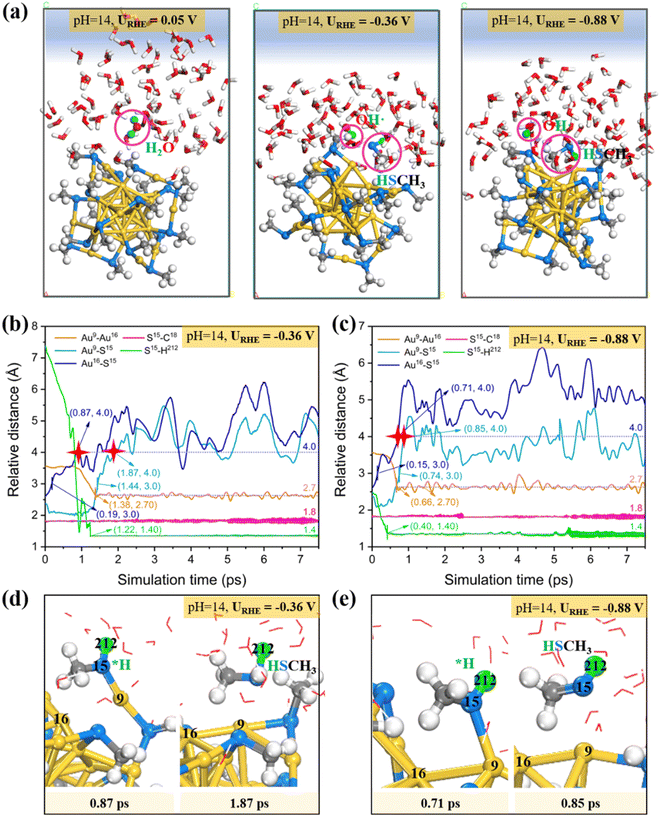
Likewise, we also studied the atomic structure evolution of the Au₂₅/water interface by performing the constant potential AIMD simulations under the alkaline conditions (pH = 14, Fig. S4b†), in which the proton source is provided by the water dissociation. Herein, 0e⁻, 2e⁻ and 4e⁻ were introduced which correspond to the electrode potentials (U_RHE) of 0.05 V, −0.36 V and −0.88 V, respectively. Fig. 4a shows the AIMD snapshots of Au₂₅(SCH₃)₁₈ NC exposed to liquid water at different potentials. Starting from the intact Au₂₅ cluster configuration, the Au–SCH₃ bonding does not go through dissociation during the ∼10 ps 300 K AIMD simulations at the ultralow potential U_RHE = 0.05 V (Fig. 4a (left)). Interestingly, if a more negative reduction potential is applied, the –SCH₃ group would readily collect a proton from the adjacent water molecule and quickly be transformed into a free HSCH₃ molecule (Fig. 4a (middle and right)) at ∼1.87 ps for U_RHE = −0.36 V (Fig. 4b) and ∼0.85 ps for U_RHE = −0.88 V (Fig. 4c). The formed hydroxide radical (OH˙) from water dissociation is not a static spectator, but then migrates further away from the Au₂₅ surface via proton exchange and hydrogen bonding with neighboring water molecules to propagate into the solution.

Fig. 4 (a) AIMD snapshots of the Au₂₅(SCH₃)₁₈ NC exposed to liquid water at three different potentials for pH = 14. Statistics of the relative distance between representative atoms during the equilibrated AIMD simulation (300 K) at (b) U_RHE = −0.36 V, and (c) U_RHE = −0.88 V for an alkaline system. Evolution of atomic structures for Au¹⁶(surface)–S¹⁵ breaking and subsequent Au⁹(staple)–S¹⁵ breaking at (d) U_RHE = −0.36 V, and (e) U_RHE = −0.88 V.

Our results for the alkaline conditions also show that decreasing the potential leads to faster kinetics for the Au–S bond breaking and formation of HSCH₃. Specifically, in the alkaline case (Fig. 4b and c), a proton produced by water dissociation is stably attached to the S¹⁵ atom accompanied by the weakening of the Au–S bond, and the S atom would be firstly detached from the surface Au¹⁶ and then dissociated from another staple Au⁹ to generate HSCH₃ (Fig. 4d and e; detailed atomic labeling can be found in Fig. S4d†). The two resultant under-coordinated Au¹⁶ and Au⁹ atoms are bonded closer with a shortened distance of 2.7 Å compared to that in the intact Au₂₅ (3.4 Å). The application of more negative potential will greatly accelerate the water splitting, for example, it only takes about 0.40 ps to complete H₂O dissociation and the resulting proton is stably adsorbed on S¹⁵ at U_RHE = −0.88 V. Similar to the acid case, we also did not observe significant elongation of the S–C bond during the entire dynamic simulations.

Therefore, our constant potential AIMD simulations indicate stronger dynamic preference in breaking the Au–S bond than stretching the S–C bond under either the acid or basic electrochemical conditions. That is to say, under a moderate electrochemical treatment, the Au₂₅ surface tends to detach the thiolate and then expose the under-coordinated Au sites. The kinetic origin of this unique etching behaviors can be understood from the following two aspects. Since the breaking of Au–S chemical bonds is triggered by the proton attack on the ligand, which has been ignored in conventional thermodynamic studies,^29,30,33 the first key affecting factor is whether there is accessible space for proton attack. As shown in Fig. S7,† the S site at the staple motifs has a large open space available to capture protons (green arrow), while the C atom from the –SCH₃ moiety is tightly wrapped by three H atoms (red circle), which makes it spatially difficult for protons to attack the C site due to the steric hindrance. Another key reason is the higher electronegativity and the presence of lone electrons of the S atom, which renders the S site with high affinity for capturing protons, facilitating the weakening of Au–S bonds and the liberation of an entire thiol group.

We further analyzed the Bader charge variation for the dethiolated bare Au atoms from the constant potential AIMD simulations (Fig. 5a and b). The naked under-coordinated Au atoms become negatively charged while the other thiolate-capped Au atoms show positive charges (Table S1†), indicating that the surface dethiolated Au tends to activate the reactants as active centers in electrocatalysis (e.g., CO₂ and O₂ species). What's more, despite the Au–S bond breaking, the structure of the singly dethiolated Au₂₅ NC, especially its metal frameworks, undergoes negligible distortion, indicating its excellent structural stability under mild electrochemical conditions. Further analysis of the radial distribution function (RDF) also verified this conclusion (Fig. 5c and d), and the average bond lengths of Au–Au, Au–S and S–C bonds are less effected between the singly dethiolated Au₂₅ and the intact one. Unsurprisingly, the electrochemical biasing is a desirable approach to selectively cleave the staple ligands without destroying the metal frameworks. However, an electrochemical biasing at an over excessively high potential may inevitably induce the structural destruction. To test this possibility, we intentionally investigated the structural evolution of Au₂₅ at a higher potential of −1.10 V. As shown in Fig. S8,† the constant potential AIMD simulations under the alkaline conditions demonstrated severe distortion of the Au₂₅ structure at U_RHE = −1.10 V, which is accompanied by the breaking of surface Au–Au bonds in addition to the Au–S bonds. This implies that the atomic structure of Au₂₅ NC is potential-dependent. By taking into account both the electrocatalytic activity and the cluster stability into consideration, an appropriate applied potential (not too high) is particularly critical for selectively stripping the thiolate ligands and in the meantime maintaining the structural integrity of the metal framework.

Fig. 5 Evolution of Bader charge on the under-coordinated bare Au atoms from dethiolated Au₂₅ NC at different potentials after AIMD simulations for the acid (a) and alkaline system (b). Radial distribution function (RDF) of Au–Au, Au–S and S–C bonds from the equilibrated AIMD trajectory in (c) acid and (d) alkaline systems.

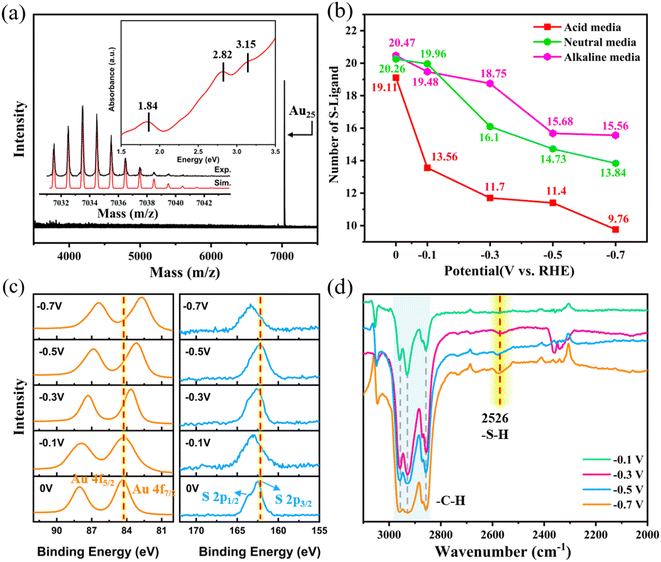
To further verify our theoretical predictions, we synthesized the Au₂₅ NCs and conducted key spectroscopic characterizations. As shown in the inset of Fig. 6a, the Au₂₅ clusters showed obvious absorption peaks at 1.84 eV, 2.82 eV, and 3.15 eV, which agree well with the previous reports.^9,51,52 In addition, electrospray ionization mass spectrometry (ESI-MS) showed a peak at m/z = 7033.48 Da, which can be assigned as the molecular ion (Cal: 7033.493 Da, deviation: 0.014 Da, Fig. 6a). The well-matched experimental and simulated isotope pattern further confirmed the assignment. Meanwhile, no obvious additional or fragmentation peaks was observed in the range of m/z = 3500–8000, indicating that the synthesized Au₂₅ cluster is of high purity.

Fig. 6 Experimental characterization of the Au₂₅(SR)₁₈⁻ NCs. (a) ESI-MS spectra, together with a comparison of the experimental and simulated isotope patterns, the inset in (a) is the absorption spectrum. (b) Remaining number of ligands in the Au₂₅ cluster after 1 h electrochemical activation at different potentials in different media. (c) XPS spectra for Au 4f and S 2p after 1 h reaction at different potentials in acidic medium. (d) FTIR spectra of the reaction solution at different test potentials in neutral medium.

Next, we studied the ligand stripping of Au₂₅ NCs after 1 h reaction at different potentials in different electrochemical media, similar to the catalyst activation treatment before the electrocatalytic reaction. The S-to-Au elemental ratio after the reaction was tested by XPS to calculate the average number of remaining ligands on the Au₂₅ cluster. As shown in Fig. 6b (note that as XPS may have error in accurately quantifying the internal composition of the sample, the measured Au : S ratio could be slightly overestimated than the real Au : S composition), when the potential goes more negative, less thiolate ligands remained, indicating that some ligands must have been stripped off the cluster. Interestingly, the number of stripped ligands follows the order of acidic medium > neutral medium > basic medium. These findings strongly validate the above derived theoretical results, indicating that Au–S bond cleavage should occur during the electrochemical reaction process. Since only the local solvent environment of finite units was considered, we did not trace the shedding of multiple –SR ligands in the theoretical simulation, but the shedding of multiple ligands is most likely to occur in the real electrochemical experiment.

Moreover, as shown in Fig. S9,† the binding energy of the S 2p_3/2 peak of intact Au₂₅(SR)₁₈ is at 162.88 eV.⁵³ The binding energy of the S 2p_3/2 peaks of the Au₂₅ cluster after 1 h reaction at different potentials is found to be in the range of 162.5–163.3 eV for acidic, neutral, and alkaline media (Fig. 6c, S10 and S11†). These observations indicate that after the electrochemical treatment, the chemical coordination environment of the retained S atom is almost unchanged, that is, still in the form of the Au–S–R motif. The absence of the characteristic S 2p_3/2 peak at ∼161.2 eV corresponding to gold-sulfide⁵⁴ supports the cleavage of the Au–S bond rather than the S–C bond. The Au 4f_7/2 peaks shift to the lower binding energy region in all electrolyte media, suggesting that some of the Au atoms become electron rich⁵⁵ due to dethiolation, which is also consistent with the DFT calculations.

To understand the nature of the stripped ligand in solution, using a neutral electrolyte system as an example, we performed the infrared spectroscopy of the organic matter in the reaction solution by extracting with DCM. As shown in Fig. 6d, the FTIR spectra at the potential of −0.3 V, −0.5 V, and −0.7 V showed a pronounced absorption band at 2526 cm⁻¹ and three apparent absorption peaks at ∼2900 cm⁻¹. By referring to the standard FTIR spectrum of hexyl mercaptan (Fig. S12†), the absorption bands of the DCM extract at 2526 and ∼2900 cm⁻¹ are attributed to the stretching vibrations of the S–H and C–H bonds, respectively. It can be noted that, at −0.1 V, only the stretching vibration of the C–H bond was observed, and no obvious band of S–H was present, indicating that only a few ligands stripped off at −0.1 V. When the applied potential goes more negative, the peaks at ∼2900 and 2526 cm⁻¹ are pronounced, indicating that more ligands stripped off from the clusters. From this, it is clear that the stripped off ligand (–SR) is converted into a free ligand molecule (RSH), which is in good agreement with our theoretical calculations. That is, with larger applied potentials, the H⁺ species becomes kinetically easier to be adsorbed onto the S atom of the ligand on the cluster, weakening the Au–S bond and eventually leading to the stripping off and formation of a free thiol molecule. Meanwhile, the proton formation from water dissociation and its subsequent attack on S of the cluster in the neutral or basic medium is kinetically slower as compared to those in the acidic medium, explaining why the number of remaining thiolate ligands on the cluster is less in an acid electrolyte at all tested potentials.

It is worth noting that regulating the pH is crucial in reaction design as it allows for the control and manipulation of catalytic species, thereby influencing the outcome of chemical reactions. Our current results showed that the electrochemical process on Au₂₅ NCs is accompanied by dethiolation, and the process is easier to drive in acidic environments, followed by the neutral and alkaline conditions. Thus, the initial electrochemical activation could be better done in an acidic solution to create as many active sites as possible. The atomically precise metal nanoclusters have been explored as electrocatalysts in various reactions such as the oxygen reduction reaction (ORR), hydrogen evolution reaction (HER), and carbon dioxide reduction reaction (CO₂RR). The HER and ORR are mainly investigated in the acid medium, while the CO₂RR is mainly operated under the near-neutral or alkaline conditions. Our current studies indicate that the pH value is an important factor in influencing the dethiolation dynamics of SR ligands (or the exposure of active Au sites), thus the electrocatalytic activity and selectivity of the above-mentioned reactions should be closely correlated with the pH conditions. However, thus far, the pH effect on the exact catalytic mechanisms and efficiency of these reactions has not been systematically explored in either theory or experiment, future experimental and theoretical investigations are expected to be closely interplayed to gain a deeper understanding of the pH-dependent electrocatalytic properties of nanoclusters and optimize their performance for specific electrocatalytic reactions.

Conclusions

In this work, we have explored the electrochemical etching kinetics of ligands in thiolate-protected Au NCs using the widely studied Au₂₅(SCH₃)₁₈ as the test candidate. We found that the oversimplified charge-neutral method based on the traditional CHE model was inaccurate to elucidate the thermodynamics and kinetics of the Au₂₅/water interface. The applications of constant potential calculations that explicitly include potential and solvation effects predict strong thermodynamic preference for –SR removal from Au₂₅. We further performed the constant potential AIMD simulations and uncovered for the first time the dynamic process of –SCH₃ detachment. Specifically, weakening of Au–S bonds is initiated by the selective attack of proton from H₃O⁺ (acidic conditions) or water dissociation (neutral or basic conditions) onto the S atom, which is followed by the breaking of the surface Au–S bond and subsequent breaking of the staple Au–S bond and finally form a free HSCH₃ molecule in solution. Our results highlight the kinetic origin of proton attack in facilitating the weakening and breaking of Au–S bonds, which was overlooked before. The strong proton affinity comes from the large spatial accessibility and the presence of lone pair electrons of the S site. Our predictions were further verified by the electrochemical activation experiments and XPS/FTIR characterizations. We observed a continuous decrease in the number of SR ligands and the increase in the vibrational intensity of S–H bonds with the increase of negative potential. Our work provides new atomic-level insights into the ligand etching dynamics of the Au₂₅(SR)₁₈ NC and resolve the debate over the real active site of thiolated metal nanoclusters. Particularly, the advanced constant-potential solvation dynamic model can be effectively applied to study the heterogeneous electrocatalysis of other size metal NCs protected by thiolates and other types of ligands.

Computational methods and experimental section

All spin-polarized density functional theory (DFT) calculations were implemented using the Vienna ab initio simulation package code (VASP5.4.4).⁵⁶ For the exchange-correlation energy, the Perdue–Burke–Ernzerhof (PBE) version of the generalized gradient approximation (GGA) was adopted.⁵⁷ The cutoff energy of the plane-wave basis was 400 eV in the relaxation, while 350 eV was used in the AIMD simulations, and the projected-augmented wave (PAW) pseudopotential was applied to describe the core electrons.⁵⁸ The Γ point only was used to sample the Brillouin zone; in addition, the Grimme's DFT + D3 method was utilized to accurately account for van der Waals correction.⁵⁹ The total energies and Hellmann–Feynman forces acting on atoms were converged below 10⁻⁵ eV per atom and smaller than 0.02 eV Å⁻¹, respectively. All atoms were unconstraint and fully relaxed during the simulation. Bader charges were obtained using the code developed by the Henkelman group.⁶⁰

Thermodynamics

For the thermodynamic calculations based on the computational hydrogen electrode (CHE) model, all the nanoclusters were placed in a cubic box (18 Å × 18 Å × 18 Å) and were optimized. The ligand removal free energy (ΔG) with an applied potential U and pH was calculated using CHE, which can be given by^38–40

ΔG(U_RHE, pH) = ΔG(U_CHE = 0, pH = 0) + neU_SHE + nK_BTpH × ln(10)

where ΔG(U_CHE = 0, pH = 0) is the change of Gibbs free energy for the ligand removal reaction at U = 0, pH = 0 and T = 298.15 K, which can be calculated from DFT; n is the number of electrons involved in the reaction; e is the numerical charge of an electron; k_B and T represent the Boltzmann constant and temperature, respectively (k_BT ln(10)=0.0592). With these results, the two bond breaking reactions' adhesion stability regions in pH-U_SHE space at T = 298.15 K can be written as follows:^38–40

However, to explicitly consider the electrode potential and solvation, we used the PBE + D3 with hybrid solvation in a bigger box (18 Å × 18 Å × 28 Å), labeled as the constant potential method (CPM). Here, we tuned the work function (Φ) of each model to match the applied potential U according to U_RHE = (Φ − Φ_SHE)/e + 0.0592 × pH,⁴⁷ where Φ_SHE is the work function of the standard hydrogen electrode (SHE; 4.44 V (ref. 61)). The Φ can be calculated with a standard approach, that is, according to the energy difference between the vacuum level (E_vac) and Fermi level (E_F). Thus, by introducing extra electrons to adjust the Fermi level of the system relative to the vacuum potential, the corresponding U can be obtained. For each modeled structure, calculations were performed at charges of 0e to 4e with decrements of 1e, that is, five potentials were considered respectively, and the potential-dependent free electrochemical energy can be obtained easily.³⁸ The free energy at the 5 charge values were then fitted with a quadratic function to obtain a continuous function with G as U, in the form⁶²

where U₀ is the potential of zero charge (PZC), E₀ is the corresponding free energy at PZC, and C is the capacitance of the surface. According to the fitted quadratic function, the change of the reaction energy with the potential can be further obtained.

Dynamics

To study the dynamics of the ligand removal process for Au₂₅ NCs under electrochemical conditions, we performed the AIMD simulations. The box size was set to be 18 × 18 × 35 ų, where 78H₂O molecules plus one H₃O⁺ were contained on the local surface of Au₂₅ NCs along the z-axis for the acid system, and 79H₂O molecules were added for the neutral or alkaline system. In a similar manner, the electrode potential was also determined via tuning the work function.^41,63 Given the fluctuations in the work function, at least 10 snapshots from the AIMD trajectories were extracted to determine the average work function (VASPsol with the inclusion of implicit water solvation was used in the calculations).^64,65 Each system was pre-optimized before carrying out the AIMD operation. All AIMD simulations were sampled in the NVT [constant number of atoms (N), constant volume (V), and constant temperature (T) of room temperature] ensemble employing Nose–Hoover thermostats with a time step of 0.5 fs at the target temperature of the canonical ensemble at 300 K.^66–70 Only one gamma-centered k-mesh was adopted in AIMD simulations.

Materials

Methanol, ethanol, methylene chloride (DCM), tetrahydrofuran (THF), dichloromethane (DCM), tetrachloroauric acid trihydrate (HAuCl₄·3H₂O), hexyl mercaptan, standard PBS buffer (pH = 7), phosphoric acid, tetraoctylammonium bromide (TOAB) and sodium borohydride (NaBH₄) were purchased from Energy Chemical (Shanghai, China). Water was supplied by the Barnstead Nanopure water system with a resistivity of 18.3 MΩ cm⁻¹. All chemicals were used as received without further treatment.

Instruments

UV-vis absorbance spectra were recorded using a Shimadzu UV-1800 spectrometer. The electrospray ionization mass spectra (ESI-MS) of NCs were acquired on a Bruker UItiMate3000 time-of-flight (TOF) system. ESI-MS instrumental parameters were maintained as: capillary voltage, −3.5 kV; dry temp., 200 °C; nebulizer, 0.6 bar; dry gas, 6.01 mL min⁻¹. The electrochemical test of the Au₂₅ cluster was evaluated on a CHI 710C electrochemical workstation. Fourier-transform infrared (FTIR) spectra were collected using KBr pellets in the range of 4000–650 cm⁻¹ with a Nicolet FTIR spectrometer. X-ray photoelectron spectroscopy (XPS) spectra were recorded on a Thermo Fisher Nexsa spectrometer. All binding energies were calibrated using the C 1s peak at 284.8 eV as the internal standard.

Synthesis of Au₂₅(SR)₁₈

The Au₂₅(SR)₁₈ NCs are synthesized by following a previous method with suitable modifications.³⁵ Firstly, 200 mg of HAuCl₄·3H₂O and 300 mg of TOAB were co-dissolved in 15 mL of THF. After stirring for 15 min, the solution turned clear orange-red. Then, hexyl mercaptan (320 μL) was added to the above solution. After stirring for 60 min, the solution became colorless. Subsequently, 190 mg of NaBH₄ dissolved in 5 mL ice water was quickly added to the above solution. After continuous stirring for 3 days, solvents were removed by rotatory evaporation and the precipitates were repeatedly washed with methanol/water solution (1 : 1) to remove all the impurities and get pure Au₂₅ NCs.

Preparation of the cathode material

Firstly, a DCM solution of Au₂₅ NCs (6.4 mg mL⁻¹) was prepared. The one-sided carbon cloth was accurately cut to the size of 1 cm², and then 50 μL of the above solution was dropped onto the conductive rubber surface of the one-sided carbon cloth. The solvent was allowed to completely volatilize.

The electrochemical test

Firstly, the standard PBS buffer with pH = 7 was prepared. NaOH (1 M) and phosphoric acid were added to adjust the pH value of the system to 11 and 3, respectively, to obtain alkaline and acidic electrolytes separately. With the H-type electrolytic cell as the reactor, 30 mL of the same electrolyte was added to the cathode and anode chambers, respectively. Next, the constant potential electrolysis measurements were conducted using an electrochemical workstation. The potentials were applied to the working electrode against a reference electrode, Ag/AgCl (1.0 M KCl). Electrode potentials measured on the Ag/AgCl scale (E_Ag/AgCl) were converted to the reversible hydrogen electrode (RHE) using the following equation:

E_RHE = E_Ag/AgCl + 0.210 + 0.059 × pH

The potential was set as −0.1, −0.3, −0.5, and −0.7 V (vs. RHE), and the cathode materials were collected and X-ray photoelectron spectroscopy tests were carried out after 1 h reaction in constant potential electrolysis.

X-ray photoelectron spectroscopy (XPS)

After each reaction, the side coated with Au₂₅ NCs on the carbon cloth was cut down and dried in the oven at 35 °C for 1 h. Then, the side coated with Au₂₅ NCs was directly characterized by XPS.

Fourier transform infrared spectrometer (FTIR) test method

After the electrolysis, the cathode chamber electrolyte was collected, and 0.2 mL DCM was added to extract the organic molecules. The DCM solution was collected and subjected to FTIR by using the liquid film method.

Data availability

All the data in this study are provided in the main text and ESI.†

Author contributions

Q. T. conceived the idea. F. S. developed the theoretical models and performed the theoretical calculation. L. Q. performed the experiment and analyzed the data under the guidance of Z. T. F. S. and L. Q. wrote the manuscript and with support from Z. W., T. H., G. D., M. B. and Q. T. finalized it. All authors discussed and commented on the manuscript.

Conflicts of interest

There are no conflicts to declare.

Acknowledgements

This work was supported by the National Natural Science Foundation of China (No. 21903008), the Chongqing Science and Technology Commission (cstc2020jcyj-msxmX0382), and the financial support from Guangdong Natural Science Funds (No. 2022A1515011840). Z. W. acknowledges the support by the National Key Research and Development Program of China (Nos 22090030, 52021004, 2021YFB4000300). T. H. acknowledges the financial support by the Research Center Program of the IBS (IBS-R006-D1) in Korea. M. S. B. acknowledges the IBS for the Young Scientist Fellowship (IBS-R006-Y2).

References

1. Y. Lu and W. Chen, Sub-nanometre sized metal clusters: from synthetic challenges to the unique property discoveries, Chem. Soc. Rev., 2012, 41, 3594–3623.
2. K. Kwak and D. Lee, Electrochemistry of Atomically Precise Metal Nanoclusters, Acc. Chem. Res., 2019, 52, 12–22.
3. G. Deng, J. Kim, M. S. Bootharaju, F. Sun, K. Lee, Q. Tang, Y. J. Hwang and T. Hyeon, Body-Centered-Cubic-Kernelled Ag₁₅Cu₆ Nanocluster with Alkynyl Protection: Synthesis, Total Structure, and CO₂ Electroreduction, J. Am. Chem. Soc., 2023, 145, 3401–3407.
4. H. Chang, N. S. Karan, K. Shin, M. S. Bootharaju, S. Nah, S. I. Chae, W. Baek, S. Lee, J. Kim, Y. J. Son, T. Kang, G. Ko, S.-H. Kwon and T. Hyeon, Highly Fluorescent Gold Cluster Assembly, J. Am. Chem. Soc., 2021, 143, 326–334.
5. W. Jing, H. Shen, R. Qin, Q. Wu, K. Liu and N. Zheng, Surface and Interface Coordination Chemistry Learned from Model Heterogeneous Metal Nanocatalysts: From Atomically Dispersed Catalysts to Atomically Precise Clusters, Chem. Rev., 2023, 123, 5948–6002.
6. C. M. Aikens, Electronic and Geometric Structure, Optical Properties, and Excited State Behavior in Atomically Precise Thiolate-Stabilized Noble Metal Nanoclusters, Acc. Chem. Res., 2018, 51, 3065–3073.
7. J. Yan, B. K. Teo and N. Zheng, Surface Chemistry of Atomically Precise Coinage-Metal Nanoclusters: From Structural Control to Surface Reactivity and Catalysis, Acc. Chem. Res., 2018, 51, 3084–3093.
8. C. Zeng, Y. Chen, K. Kirschbaum, K. J. Lambright and R. Jin, Emergence of hierarchical structural complexities in nanoparticles and their assembly, Science, 2016, 354, 1580–1584.
9. M. Zhu, C. M. Aikens, F. J. Hollander, G. C. Schatz and R. Jin, Correlating the Crystal Structure of A Thiol-Protected Au₂₅ Cluster and Optical Properties, J. Am. Chem. Soc., 2008, 130, 5883–5885.
10. X. Kang, Y. Li, M. Zhu and R. Jin, Atomically precise alloy nanoclusters: syntheses, structures, and properties, Chem. Soc. Rev., 2020, 49, 6443–6514.
11. R. Jin, Quantum sized, thiolate-protected gold nanoclusters, Nanoscale, 2010, 2, 343–362.
12. S. Yamazoe, S. Takano, W. Kurashige, T. Yokoyama, K. Nitta, Y. Negishi and T. Tsukuda, Hierarchy of bond stiffnesses within icosahedral-based gold clusters protected by thiolates, Nat. Commun., 2016, 7, 10414.
13. Y. Cao, T. Chen, Q. Yao and J. Xie, Diversification of Metallic Molecules through Derivatization Chemistry of Au₂₅ Nanoclusters, Acc. Chem. Res., 2021, 54, 4142–4153.
14. Y. Su, T. Xue, Y. Liu, J. Qi, R. Jin and Z. Lin, Luminescent metal nanoclusters for biomedical applications, Nano Res., 2019, 12, 1251–1265.
15. Z. Huang, F. Pu, Y. Lin, J. Ren and X. Qu, Modulating DNA-templated silver nanoclusters for fluorescence turn-on detection of thiol compounds, Chem. Commun., 2011, 47, 3487–3489.
16. Z.-J. Guan, J.-J. Li, F. Hu and Q.-M. Wang, Structural Engineering toward Gold Nanocluster Catalysis, Angew. Chem., Int. Ed., 2022, 61, e2022097.
17. T. Higaki, Y. Li, S. Zhao, Q. Li, S. Li, X.-S. Du, S. Yang, J. Chai and R. Jin, Atomically Tailored Gold Nanoclusters for Catalytic Application, Angew. Chem., Int. Ed., 2019, 58, 8291–8302.
18. F. Sun and Q. Tang, The ligand effect on the interface structures and electrocatalytic applications of atomically precise metal nanoclusters, Nanotechnology, 2021, 32, 352001.
19. F. Sun, C. Deng, S. Tian and Q. Tang, Oxygen Electrocatalysis by [Au₂₅(SR)₁₈]: Charge, Doping, and Ligand Removal Effect, ACS Catal., 2021, 11, 7957–7969.
20. F. Sun, Q. Tang and D.-E. Jiang, Theoretical Advances in Understanding and Designing the Active Sites for Hydrogen Evolution Reaction, ACS Catal., 2022, 12, 8404–8433.
21. R. Jin, G. Li, S. Sharma, Y. Li and X. Du, Toward Active-Site Tailoring in Heterogeneous Catalysis by Atomically Precise Metal Nanoclusters with Crystallographic Structures, Chem. Rev., 2021, 121, 567–648.
22. Y. Du, H. Sheng, D. Astruc and M. Zhu, Atomically Precise Noble Metal Nanoclusters as Efficient Catalysts: A Bridge between Structure and Properties, Chem. Rev., 2020, 120, 526–622.
23. M. Rambukwella, N. A. Sakthivel, J. H. Delcamp, L. Sementa, A. Fortunelli and A. Dass, Ligand Structure Determines Nanoparticles' Atomic Structure, Metal-Ligand Interface and Properties, Front. Chem., 2018, 6, 330.
24. H. Hakkinen, The gold-sulfur interface at the nanoscale, Nat. Chem., 2012, 4, 443–455.
25. P. Hu, L. Chen, X. Kang and S. Chen, Surface Functionalization of Metal Nanoparticles by Conjugated Metal-Ligand Interfacial Bonds: Impacts on Intraparticle Charge Transfer, Acc. Chem. Res., 2016, 49, 2251–2260.
26. S. Zhao, N. Austin, M. Li, Y. Song, S. D. House, S. Bernhard, J. C. Yang, G. Mpourmpakis and R. Jin, Influence of Atomic-Level Morphology on Catalysis: The Case of Sphere and Rod-Like Gold Nanoclusters for CO₂ Electroreduction, ACS Catal., 2018, 8, 4996–5001.
27. N. Austin, S. Zhao, J. R. McKone, R. Jin and G. Mpourmpakis, Elucidating the active sites for CO₂ electroreduction on ligand-protected Au₂₅ nanoclusters, Catal. Sci. Technol., 2018, 8, 3795–3805.
28. D. R. Alfonso, D. Kauffman and C. Matranga, Active sites of ligand-protected Au₂₅ nanoparticle catalysts for CO₂ electroreduction to CO, J. Chem. Phys., 2016, 144, 184705.
29. S. Li, D. Alfonso, A. V. Nagarajan, S. D. House and R. Jin, Monopalladium Substitution in Gold Nanoclusters Enhances CO₂ Electroreduction Activity and Selectivity, ACS Catal., 2020, 10, 12011–12016.
30. S. Li, A. V. Nagarajan, D. R. Alfonso, M. Sun, D. R. Kauffman, G. Mpourmpakis and R. Jin, Boosting CO₂ Electrochemical Reduction with Atomically Precise Surface Modification on Gold Nanoclusters, Angew. Chem., Int. Ed., 2021, 60, 6351–6356.
31. J. Akola, K. A. Kacprzak, O. Lopez-Acevedo, M. Walter and H. HäKkinen, Thiolate-Protected Au₂₅ Superatoms as Building Blocks: Dimers and Crystals, J. Phys. Chem. C, 2010, 114, 15986–15994.
32. D. R. Kauffman, D. Alfonso, C. Matranga, G. Li and R. Jin, Photomediated Oxidation of Atomically Precise Au₂₅(SC₂ H₄Ph)₁₈^– Nanoclusters, J. Phys. Chem. Lett., 2013, 4, 195–202.
33. J. McKay, M. J. Cowan, C. A. Morales-Rivera and G. Mpourmpakis, Predicting ligand removal energetics in thiolate-protected nanoclusters from molecular complexes, Nanoscale, 2021, 13, 2034–2043.
34. S. Li, A. V. Nagarajan, S. Zhao, G. Mpourmpakis and R. Jin, Understanding the Single Atom Doping Effects in Oxygen Reduction with Atomically Precise Metal Nanoclusters, J. Phys. Chem. C, 2021, 125, 24831–24836.
35. H. Seong, V. Efremov, G. Park, H. Kim, J. S. Yoo and D. Lee, Atomically Precise Gold Nanoclusters as Model Catalysts for Identifying Active Sites for Electroreduction of CO₂, Angew. Chem., Int. Ed., 2021, 60, 14563–14570.
36. H. Seong, Y. Jo, V. Efremov, Y. Kim, S. Park, S. M. Han, K. Chang, J. Park, W. Choi, W. Kim, C. H. Choi, J. S. Yoo and D. Lee, Transplanting Gold Active Sites into Non-Precious-Metal Nanoclusters for Efficient CO₂-to-CO Electroreduction, J. Am. Chem. Soc., 2023, 145, 2152–2160.
37. S. Chen, M. Li, S. Yu, S. Louisia, W. Chuang, M. Gao, C. Chen, J. Jin, M. B. Salmeron and P. Yang, Ligand removal of Au₂₅ nanoclusters by thermal and electrochemical treatments for selective CO₂ electroreduction to CO, J. Chem. Phys., 2021, 155, 051101.
38. F. Sun, F. Li and Q. Tang, Spin State as a Participator for Demetalation Durability and Activity of Fe-N-C Electrocatalysts, J. Phys. Chem. C, 2022, 126, 13168–13181.
39. T. Patniboon and H. A. Hansen, Acid-Stable and Active M-N-C Catalysts for the Oxygen Reduction Reaction: The Role of Local Structure, ACS Catal., 2021, 11, 13102–13118.
40. E. F. Holby, G. Wang and P. Zelenay, Acid Stability and Demetalation of PGM-Free ORR Electrocatalyst Structures from Density Functional Theory: A Model for “Single-Atom Catalyst” Dissolution, ACS Catal., 2020, 10, 14527–14539.
41. L. Yu, X. Pan, X. Cao, P. Hu and X. Bao, Oxygen reduction reaction mechanism on nitrogen-doped graphene: A density functional theory study, J. Catal., 2011, 282, 183–190.
42. R. Sundararaman, D. Vigil-Fowler and K. Schwarz, Improving the Accuracy of Atomistic Simulations of the Electrochemical Interface, Chem. Rev., 2022, 122, 10651–10674.
43. N. G. Hörmann, N. Marzari and K. Reuter, Electrosorption at metal surfaces from first principles, npj Comput. Mater., 2020, 6, 136.
44. D. Kim, J. Shi and Y. Liu, Substantial Impact of Charge on Electrochemical Reactions of Two-Dimensional Materials, J. Am. Chem. Soc., 2018, 140, 9127–9131.
45. J.-W. Chen, Z. Zhang, H.-M. Yan, G.-J. Xia, H. Cao and Y.-G. Wang, Pseudo-adsorption and long-range redox coupling during oxygen reduction reaction on single atom electrocatalyst, Nat. Commun., 2022, 13, 1734.
46. T. Cheng, L. Wang, B. V. Merinov and W. A. Goddard III, Explanation of dramatic pH-dependence of hydrogen binding on noble metal electrode: Greatly weakened water adsorption at high pH, J. Am. Chem. Soc., 2018, 140, 7787–7790.
47. K. Xie, F. Wang, F. Wei, J. Zhao and S. Lin, Revealing the Origin of Nitrogen Electroreduction Activity of Molybdenum Disulfide Supported Iron Atoms, J. Phys. Chem. C, 2022, 126, 5180–5188.
48. X. Zhao and Y. Liu, Origin of Selective Production of Hydrogen Peroxide by Electrochemical Oxygen Reduction, J. Am. Chem. Soc., 2021, 143, 9423–9428.
49. T. Giorgino, Computing 1-D atomic densities in macromolecular simulations: the Density Profile Tool for VMD, Comput. Phys. Commun., 2014, 185, 317–322.
50. K. T. Wikfeldt, M. Leetmaa, M. P. Ljungberg, A. Nilsson and L. G. M. Pettersson, On the Range of Water Structure Models Compatible with X-ray and Neutron Diffraction Data, J. Phys. Chem. B, 2009, 113, 6246–6255.
51. M. Zhu, E. Lanni, N. Garg, M. E. Bier and R. Jin, Kinetically Controlled, High-Yield Synthesis of Au₂₅ Clusters, J. Am. Chem. Soc., 2008, 130, 1138–1139.
52. Z. Wu, C. Gayathri, R. R. Gil and R. Jin, Probing the Structure and Charge State of Glutathione-Capped Au₂₅(SG)₁₈ Clusters by NMR and Mass Spectrometry, J. Am. Chem. Soc., 2009, 131, 6535–6542.
53. W. Fu, J. Fan and Q. Xiang, Ag₂S Quantum Dots Decorated on Porous Cubic-CdS Nanosheets-assembled Flowers for Photocatalytic CO₂ Reduction, Chin. J. Struct. Chem., 2022, 41, 2206039–2206047.
54. D. E. Weisshaar, M. M. Walczak and M. D. Porter, Electrochemically induced transformations of monolayers formed by self-assembly of mercaptoethanol at gold, Langmuir, 1993, 9, 323–329.
55. M. S. Bootharaju, C. W. Lee, G. Deng, H. Kim, K. Lee, S. Lee, H. Chang, S. Lee, Y.-E. Sung, J. S. Yoo, N. Zheng and T. Hyeon, Atom-Precise Heteroatom Core-Tailoring of Nanoclusters for Enhanced Solar Hydrogen Generation, Adv. Mater., 2023, 35, 2207765.
56. G. Kresse and J. Furthmuller, Efficient iterative schemes for ab initio total-energy calculations using a plane-wave basis set, Phys. Rev. B: Condens. Matter Mater. Phys., 1996, 54, 11169–11186.
57. J. P. Perdew, K. Burke and M. Ernzerhof, Generalized gradient approximation made simple, Phys. Rev. Lett., 1996, 77, 3865–3868.
58. P. E. Blochl, Projector Augmented-Wave Method, Phys. Rev. B: Condens. Matter Mater. Phys., 1994, 50, 17953–17979.
59. I. L. Garzon and A. PosadaAmarillas, Structural and vibrational analysis of amorphous Au₅₅ clusters, Phys. Rev. B: Condens. Matter Mater. Phys., 1996, 54, 11796–11802.
60. W. Tang, E. Sanville and G. Henkelman, A grid-based Bader analysis algorithm without lattice bias, J. Phys.: Condens. Matter, 2009, 21, 084204.
61. S. Trasatti, The absolute electrode potential: an explanatory note (recommendations 1986), Pure Appl. Chem., 1986, 58, 955–966.
62. Z. Duan and G. Henkelman, Surface Charge and Electrostatic Spin Crossover Effects in CoN₄ Electrocatalysts, ACS Catal., 2020, 10, 12148–12155.
63. X. Zhao and Y. Liu, Unveiling the Active Structure of Single Nickel Atom Catalysis: Critical Roles of Charge Capacity and Hydrogen Bonding, J. Am. Chem. Soc., 2020, 142, 5773–5777.
64. T. Cheng, L. Wang, B. V. Merinov and W. A. Goddard III, Explanation of Dramatic pH-Dependence of Hydrogen Binding on Noble Metal Electrode: Greatly Weakened Water Adsorption at High pH, J. Am. Chem. Soc., 2018, 140, 7787–7790.
65. T. Cheng, H. Xiao and W. A. Goddard III, Reaction Mechanisms for the Electrochemical Reduction of CO₂ to CO and Formate on the Cu(100) Surface at 298 K from Quantum Mechanics Free Energy Calculations with Explicit Water, J. Am. Chem. Soc., 2016, 138, 13802–13805.
66. N. Shuichi, A Unified Formulation of the Constant Temperature Molecular Dynamics Methods, J. Chem. Phys., 1984, 81, 511–519.
67. N. Shuichi, Constant Temperature Molecular Dynamics Methods, Prog. Theor. Phys. Suppl., 1991, 103, 1–46.
68. D. M. Bylander and L. Kleinman, Energy fluctuations induced by the Nosé thermostat, Phys. Rev. B: Condens. Matter Mater. Phys., 1992, 46, 13756–13761.
69. G. J. Martyna, M. L. Klein and M. Tuckerman, Nosé-Hoover chains: The canonical ensemble via continuous dynamics, J. Chem. Phys., 1992, 97, 2635–2643.
70. W. G. Hoover, Canonical dynamics: Equilibrium phase-space distributions, Phys. Rev. A: At., Mol., Opt. Phys., 1985, 31, 1695–1697.

---

Footnotes

† Electronic supplementary information (ESI) available: The relationships between the extra electrons and the electrode potential, free energies as a function of potential, theoretical model, water density, radial distribution function and integrated coordination number of O–O and O–H pairs, schematic illustration of proton attack, AIMD snapshot, XPS data, FTIR characterization and Bader charge analysis. See DOI: https://doi.org/10.1039/d3sc03018k

‡ F. S. and L. Q. contributed equally to this work.

---