Thermally activated delayed fluorescence in a mechanically soft charge-transfer complex: role of the locally excited state

Abstract

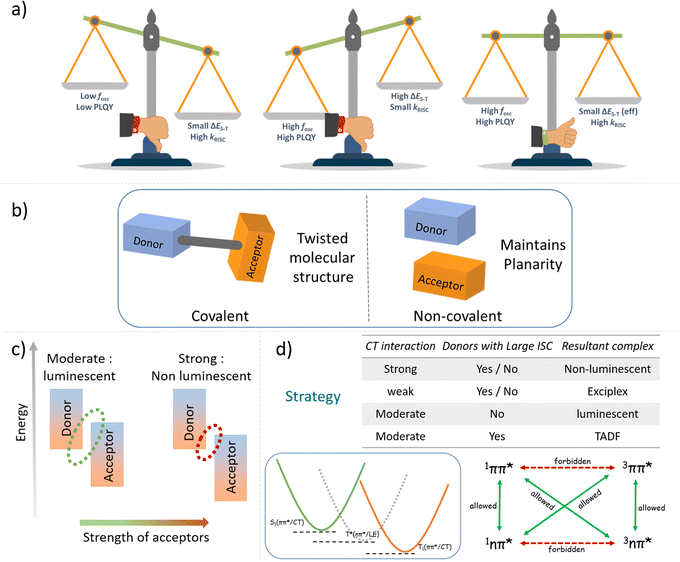
Molecular design for thermally activated delayed fluorescence (TADF) necessitates precise molecular geometric requirements along with definite electronic states to ensure high intersystem crossing (ISC) rate and photoluminescence quantum yield (PLQY). Achieving all these requirements synchronously while maintaining ease of synthesis and scalability is still challenging. To circumvent this, our strategy of combining a crystal engineering approach with basic molecular quantum mechanical principles appears promising. A holistic, non-covalent approach for achieving efficient TADF in crystalline materials with distinct mechanical properties is highlighted here. Charge transfer (CT) co-crystals of two carbazole-derived donors (ETC and DTBC) with an acceptor (TFDCNB) molecule are elaborated as a proof-of-concept. Using temperature-dependent steady-state and time-resolved photoluminescence techniques, we prove the need for a donor-centric triplet state (³LE) to ensure efficient TADF. Such intermediate states guarantee a naturally forbidden, energetically uphill reverse intersystem crossing (RISC) process, which is paramount for effective TADF. A unique single-crystal packing feature with isolated D–A–D trimeric units ensured minimal non-radiative exciton loss, leading to a high PLQY and displaying interesting mechanical plastic bending behaviour. Thus, a comprehensive approach involving a non-covalent strategy to circumvent the conflicting requirements of a small effective singlet–triplet energy offset and a high oscillator strength for efficient TADF emitters is achieved here.

---

Introduction

Since the discovery in 2012, TADF emitters and their organic light-emitting devices (OLEDs) have represented fascinating developments in lighting/display technologies. They require a delicate balance of various molecular features, such as the choice of the donor (D) and acceptor (A) units, the geometry of the molecule, the positioning of electronic states, etc., to achieve optimal TADF performances.^1–10 The conventionally followed geometric requisite of significant structural distortion between the D and A centre to attain a low singlet–triplet energy offset (ΔE_S–T) eventually results in low oscillator strength. Hence, achieving high PLQY in a conventional molecular design presents an inherent challenge.^11,12 Most traditional TADF systems reduce ΔE_S–T at the expense of oscillator strength, f_osc (Scheme 1a).^13–24 Therefore, the design of efficient TADF emitters relies on the subtle balance between these two antagonistic effects.

Scheme 1 (a) Graphical representation of conflicting requirements of simultaneously achieving a small effective singlet–triplet energy offset and a high oscillator strength for efficient TADF emitters; (b) simplified diagram representing our non-covalent donor–acceptor design strategy; (c) diagrammatic representation of the extent of the charge transfer interaction; (d) correlation of extent of CT interaction to the desired functional output and our hypothesis to facilitate ISC (RISC) via intermediate triplets of contrasting orbital symmetry.

Moreover, the synthetic complexity of obtaining TADF materials limits their commercial viability. As a result, developing cost-effective and scalable methods for efficient TADF emitters is still a challenge. Coupling mechanical softness to the single crystals of such materials would be an added advantage from the perspective of fundamental and applied functional aspects. Soft TADF crystalline materials would be highly suitable for mechanically flexible active layer channels for next-generation display technologies. The crystal engineering approach has been pivotal in tuning the mechanical properties of soft materials.²⁵ Moreover, there has been growing interest in flexible organic crystals as an advanced class of functional materials. Recent attempts to make dynamic, flexible organic crystals rather than conventional brittle crystals have increased due to their advantages in fabricating smart optoelectronic devices, waveguides and many other applications.^25–40 In this context, introducing flexibility in intermolecular TADF crystals with high PLQY will create new opportunities in the abovementioned applications.

This study focuses on developing mechanically compliant intermolecular CT co-crystal systems with small ΔE_S–T values for efficient TADF (Scheme 1b). Intermolecular D–A pair-mediated TADF offers distinct advantages over the traditional intramolecular pairs. Tedious and sophisticated synthetic steps to obtain various C–C and C—heteroatom bonds can be eliminated by using a bimolecular pair. Additionally, compared to the poor charge balancing issue in conventional host materials in OLED devices, the intrinsic charge transfer bipolarity of such bimolecular systems makes this design principle more attractive.^41–52 It is possible to achieve the desired combination of properties by mixing the right electron-rich and -deficient counterparts. Emphasis is placed on choosing donor and acceptor units of appropriate electron affinity (EA) and ionisation potential (IP) to obtain complexes with small ΔE_S–T values and higher RISC rates. It is known that the right balance of a D and A with an appropriate EA and IP is essential to ensure the radiative ¹CT state upon formation of the complex.^53,54

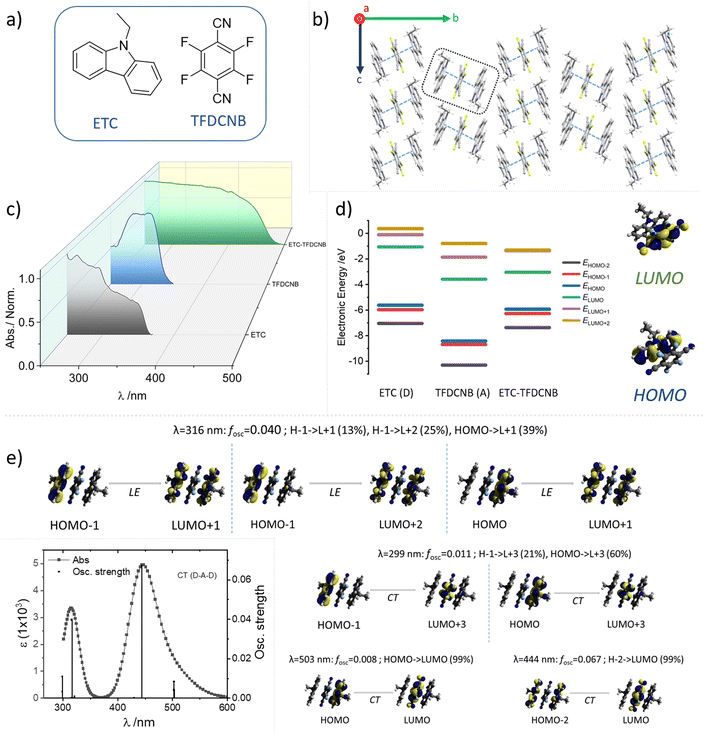
We have carefully screened a list of widely available small molecule D–A conjugates to condense our choice to a few of them to yield TADF (Fig. S1 and S2†). From the frontier energy levels of the D and A units and the intrinsic properties of the conformers, we narrowed down our choices to 9-ethylcarbazole (ETC) and 3,6-di-tert-butylcarbazole (DTBC) as donors and 2,3,5,6-tetrafluoroterephthalonitrile (TFDCNB) as the corresponding acceptors to obtain plausible TADF complexes. Emphasis is placed on the carbazole-derived donor unit because of its intrinsic low-lying triplet states and high intersystem crossing rate.⁵⁵ Later, the hypothesis is extended to other suitable pairs to obtain the desired complexes to further validate our proposed proof of concept (Schemes 1c, d and Fig. S3†).

Results and discussion

All the precursor materials and acceptor molecules used were procured from Sigma-Aldrich and used after recrystallisation. Carbazole was synthesised in the lab following a reported procedure; the detailed synthetic procedure and characterisation data are described in the ESI (Schemes S1, S2 and Fig. S4–S11†). As the optical signals of carbazole derivatives are known to be sensitive to any trace amounts of impurities present in the sample in the form of other structural isomers,⁵⁶ the purity was further confirmed by analytical HPLC to rule out all such possibilities. Fig. S11† depicts the HPLC trace analysis of the carbazole derivatives used in the present study.

The CT complexes were prepared using liquid-assisted grinding (LAG) (Fig. S12†). A detailed discussion of the preparation and structural characterisation of the CT complex using IR and powder X-ray diffraction (PXRD) (Fig. S13†), along with the single-crystal X-ray diffraction (SCXRD) analysis, is provided in the ESI.† Thermal analysis (TGA and DSC) was carried out to confirm the formation of the CT complexes and gauge their thermal stability, and is summarised in the ESI (Fig. S14 and S15†). Moreover, the drop-cast films are highly crystalline, retaining the CT character of the cocrystal evident from the microscopic data (see Fig. S16 and ESI for details†).

Crystallographic molecular packing and the relative orientation of the donor–acceptor pair of the CT complex in the unit cell are crucial in dictating the optical features of the sample (oscillator strength, reverse intersystem crossing rate, etc.). Hence, SCXRD analysis for ETC–TFDCNB was carefully carried out and is summarised in Fig. 1b and 4. The ETC–TFDCNB crystal belongs to the monoclinic P2₁/c space group, and both the D and the A motifs attained a planar geometry. Interestingly, a trimeric unit constituting two donors and one acceptor molecule interact strongly with each other in a face-to-face manner to form a D–A–D sandwich repeating unit, and the trimeric unit interacts weakly with another trimeric unit in an edge-to-face fashion along the b-axis (Fig. 1b and 4e). This packing significantly impacts the optical features (vide infra) by ensuring confined excitons within the stack of three molecules (2D:1A), enabling less exciton loss due to long-range excitonic migration in extended arrays. This unique molecular packing suggests additional interesting mechanical properties in the bulk crystals. Low-temperature (∼100 K) SCXRD experiments were also performed to identify any structural alteration upon lowering the sample temperature, which is vital in dictating the optical traits of these samples. No significant structural change was observed in the unit cell parameters or molecular stacking upon lowering the sample temperature (Table S1†).

Fig. 1 (a) Molecular structure of the donor ETC and the acceptor TFDCNB; (b) single-crystal molecular packing of the ETC–TFDCNB co-crystal along the a-axis; (c) UV-Visible absorption spectra (normalised at absorption maxima) of ETC, TFDCNB and the ETC–TFDCNB CT complex in the film state; (d) frontier molecular orbital (FMO) energy levels of ETC, TFDCNB and the ETC–TFDCNB CT complex; (e) TD-DFT simulated electronic absorption spectra of ETC–TFDCNB in D–A–D form, and the respective molecular orbitals involved in the transitions (the coordinates of the ETC–TFDCNB are obtained from the crystal structure).

The optical properties of these samples are also interesting. Dilute solutions of the CT crystals do not exhibit their resultant optical characteristics; individual monomeric absorption bands are visible rather than intermolecular charge transfer transitions, as expected due to the heavily solvated and dissociated CT pair. Thus, thin films prepared by drop-casting solutions of the obtained co-crystals were used to obtain the optical features of the CT forms. The optical absorption spectra of these thin films were recorded in transmission mode on a quartz substrate. They show distinctive new broad absorption and spectral bands originating from the hybrid states obtained between the HOMO of the donor and LUMO of the acceptor pair (Fig. 1c), highlighting the formation of the CT complex. It is to be noted that neither of the individual components of the CT complex have any characteristic optical transitions in the visible spectrum range, and, hence, they appear to be colourless in their solid state. For comparison, the absorption spectral profiles of ETC (donor), TFDCNB (acceptor) and ETC–TFDCNB (CT complex) are summarised in Fig. 1c.

Density functional theory (DFT) calculations were carried out to understand the electronic states of the CT complex pair. The frontier molecular orbital (HOMO, LUMO, etc.) energies and static dipole moment (SDM) were calculated using the geometry obtained from the X-ray crystal structure employing the B3LYP-D3/def2tzvp level of theory. The dispersion factor GD3 was used to account for the dispersive nature of π⋯π stacking. The energy levels and frontier orbitals of the CT complex and their corresponding conformers are shown in Fig. 1d. As expected, the highest occupied molecular orbital (HOMO) lies on the donor molecule, whereas the lowest unoccupied molecular orbital (LUMO) is localised on the acceptor. The calculated electronic energy diagram of the ETC–TFDCNB complex (Fig. 1d) proves that its HOMO (−5.92 eV) is energetically closer to the HOMO of ETC (−5.61 eV), and that its LUMO (−3.04 eV) is more comparable to that of TFDCNB (−3.58 eV). The calculated static dipole moment (SDM) for the ETC–TFDCNB complex is 2.63 Debye, indicating highly dipolar behaviour; the dipole moment vector aligning from the D to the A unit, which is a characteristic of such CT complexes (Fig. S17†). Time-dependent density functional theory (TD-DFT) calculations were performed using the ETC–TFDCNB geometry obtained from SCXRD at the TPSSh-GD3BJ/def2tzvp level of theory. The simulated optical absorption spectrum (Fig. 1e and S18†) is well harmonised with the experimental data. Based on TD-DFT analysis, two distinct electronic transitions are predicted: an intense lower-energy band centred at ∼443 nm with explicit CT character, and a less-intense band at a shorter wavelength (∼316 nm) with a significant donor-centric locally excited (LE) character.

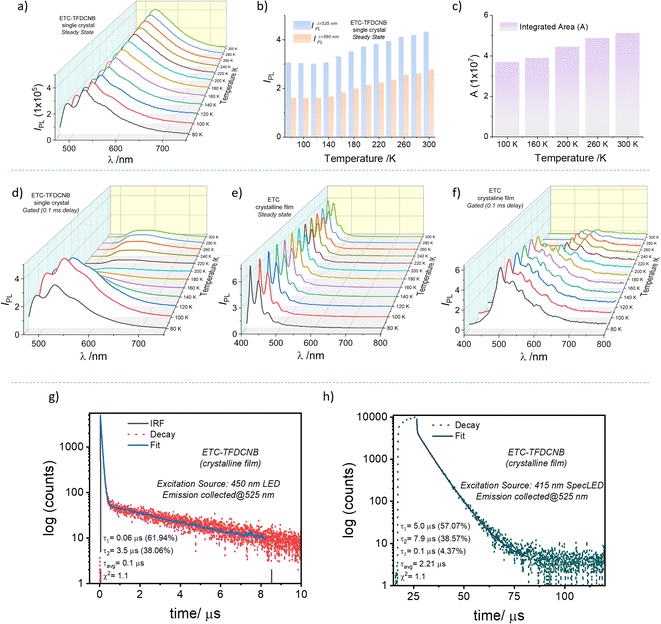
To probe the PL characteristics of the CT complex, solid-state samples, viz., pristine films, polymer-doped films and single-crystal samples, were used to record steady-state and gated PL spectra. At 300 K, a broad emission band ranging from 480 nm to 700 nm (λ_max = 530 nm) with a full-width half maximum (FWHM) of 3226 cm⁻¹, which is indicative of characteristic CT state emission, is observed from the single crystal upon excitation at 440 nm (Fig. S19†). The gated (0.1 ms initial delay) PL spectrum of the same crystal sample gives a very weak emission ranging from 510 nm to 720 nm (Fig. S22†). The gated emission spectral maximum (λ^Phos._max = 575 nm) is red-shifted compared to the steady-state PL emission maximum (λ^SS_max = 530 nm) (Fig. S19†). The energy offset (ΔE (S^CT₁ − T^CT₁)) at 300 K is found to be ∼0.15 eV from the corresponding emission spectral onsets. Fig. 2g and h shows the PL decay profiles of the pristine crystalline film. A biexponential decay with two distinct regimes, an initial prompt fluorescence decay (with τ^p = 60 ns) followed by a delayed component (with τ^d_avg = 2.2 μs), is evident. This observation leads us to envisage the possibility of a thermally activated delayed emission mechanism as preconceived by our design strategy (Scheme 1 and Fig. S3†). Moreover, homogeneously dispersed films of ETC–TFDCNB were prepared in polymer matrices of various dielectric constants. Even at a 10% (wt/wt) concentration, the complex retains its CT characteristics, as is evident from the absorption, PL emission and lifetime decay profile (Fig. S20†).

Fig. 2 (a) Temperature-dependent steady-state PL emission of an ETC–TFDCNB single crystal; (b) variation of the steady-state PL intensity with temperature at λ = 525 nm and λ = 590 nm; (c) variation of the integrated area of the steady-state PL band with temperature. Temperature-dependent (d) gated PL emission spectra (initial delay = 0.1 ms) of an ETC–TFDCNB single crystal; (e) steady-state and (f) gated (initial delay = 0.1 ms) PL emission spectra of ETC crystalline film; (g and h) lifetime decay profile of the ETC–TFDCNB film.

To better characterise the underlying photophysics of the delayed excited state phenomenon in the ETC–TFDCNB co-crystals, we analysed the steady-state and delayed emission spectral characteristics with varying sample temperatures and delay times (Fig. 2a and d). Interestingly, the emission spectra of the single-crystal and thick-crystalline-film (Fig. S21†) samples are firmly temperature-dependent. The temperature dependence of the steady state and delayed spectra were also found to be entirely different. In the case of the steady-state spectra, at 300 K, a PL band centred at 530 nm is noticed. The intensity (at λ_max) of this band steadily declines with the decrease of the sample temperature (Fig. 2b). The reduction in the integrated spectral area confirms the monotonic decline in PLQY with the lowering of the sample temperature (Fig. 2c). This observation is an evident characteristic of thermally activated up-conversion of the triplet excitons back to the singlet state. From the slope analysis, a thermal activation energy barrier of ∼0.3 meV is obtained, which is characteristic of the TADF mechanism (Fig. S22†).

Interestingly, at low temperatures (<100 K), an additional band centred at 480 (±5) nm appears in the steady-state spectrum upon 440 nm excitation. We hypothesised that the newly emerged band was the transition originating from the trapped-donor (ETC)-centric triplet states due to the lack of necessary activation energy below 100 K. To confirm this, we compared these emission features with the temperature-dependent steady-state and delayed PL spectra of the pure donor (ETC) sample (Fig. 2e and f). The phosphorescence band was invisible in the steady-state emission spectra (Fig. 2e). Still, the gated emission spectral profile (delay of 0.1 ms) proves the existence of an emission band centred at 440 nm (Fig. 2f). This band appeared to be similar to the high-energy band observed in the CT complex at <100 K (Fig. 2a). Moreover, the gated emission spectra of the ETC–TFDCNB further confirm the donor-centric transition at low temperature (Fig. 2d). As inferred from the phosphorescence spectra of the ETC sample at 80 K, we ensured that the higher energy band that appears for ETC–TFDCNB at low temperature is of ³LE character.

For TADF emitters, it is well accepted that the singlet to triplet energy gap (ΔE_S–T) is directly proportional to the electron exchange energy (J),^11,12 which is eventually related to the spatial overlap of the highest occupied molecular orbital (HOMO) and lowest unoccupied molecular orbital (LUMO). Thus, to achieve high (reverse) intersystem crossing rates, spatial separation of the HOMO and LUMO is essential to reduce J; this guideline has been followed in the conventional design strategy. In contrast, it is necessary to have sufficient wavefunction overlap to ensure high oscillator strength and excellent radiative decay rates (S₀ ← S₁). El Sayed's rules forbid direct T₁ and S₁ conversion in cases where the states have the exact orbital nature, as would be the case when both are pure CT states due to the predicted vanishing spin–orbit coupling.⁵⁷ Thus, the orbital nature of the singlet and triplet states (LE or CT) is an essential factor determining the efficiency of the ISC (and RISC) process.^5,35,57–62 We consider that for our system, the forbidden RISC (and ISC) are facilitated by the donor-centric locally excited triplet state ^(LE)T (Fig. 3). Thus, we propose that in the case of the ETC–TFDCNB co-crystal, a mechanism of sequential up-conversion (RISC) viz., ³CT → ³LE → ¹CT is followed. The schematic potential energy surfaces are illustrated in Fig. 3 according to the electronic energy levels of the different states involved. We suggest that simultaneous emission from both the LE and CT states is observed at sub-ambient temperatures (T < 100 K), as the thermally activated rate of RISC from ³LE → ¹CT is restricted (Fig. 3). The energy of the bridging ³LE state was estimated from the gated PL spectrum of the isolated donor alone, i.e., ETC. The donor's ³LE triplet state, which is sandwiched between the S₁(CT) and T₁(CT) states, is energetically in favour of ensuring effective RISC (or ISC). This process explains the high PLQY (ϕ ≈ 90% at room temperature and ambient pressure) for the ETC–TFDCNB crystal (Fig. 3). Similar photophysical behaviour is observed for the DTBC-TFDCNB pair (Fig. S23†). Intermediate donor-centric triplet emission from the donor (DTBC) also appeared at low temperatures. Moreover, we have extended this unique non-covalent approach to other suitable pairs to obtain the desired complexes (TADF, exciplex and fluorescent CT complexes), bolstering our proposed design strategy (Fig. S23–S26†).

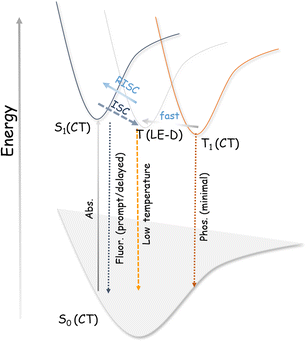Fig. 3 Simplified potential energy diagram of the electronic states involved in our designed TADF materials.

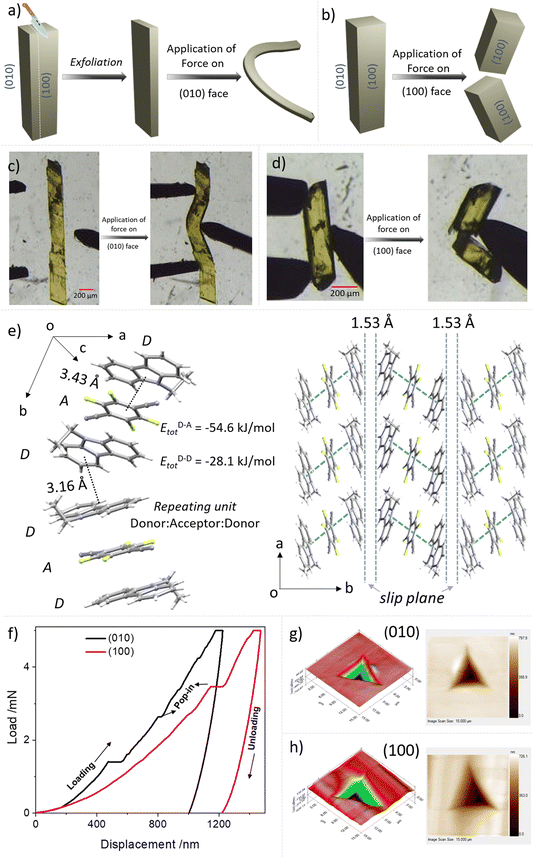
As a part of our continuous efforts to understand the mechanical properties of organic crystals with fascinating optoelectronic properties, we explored the properties of single crystals of DTBC-TFDCNB and ETC–TFDCNB by performing a sequence of mechanical operations.^35–38 A schematic representation and optical images of ETC–TFDCNB crystals under mechanical operations are summarised in Fig. 4a–d, S28 and the ESI Videos.† These qualitative tests at ambient temperature revealed that single crystals of DTBC-TFDCNB are brittle due to the absence of facile slip planes or any restorable interactions (Fig. S32†). On the other hand, ETC–TFDCNB crystals which grow along c-axis, can be easily exfoliated upon applying stress on the (100) or (001) faces using a metal needle, which results in thin crystals (Fig. S27†). Additionally, the delicate thin-needle shape crystals obtained by slicing the pristine crystal show remarkable plasticity upon application of stress on the (010) face, i.e., irreversible deformation (Fig. 4a, c, S28 and ESI Videos 1, 2†). The morphology and qualitative mechanical behaviour of the ETC–TFDCNB crystal before and after exfoliation are demonstrated in Fig. S28 and ESI Video 2.†

Fig. 4 (a) Schematic diagram representing exfoliation followed by bending on the (010) face for the ETC–TFDCNB crystal; (b) schematic diagram illustrating the brittle behaviour of the (100) face for the ETC–TFDCNB crystal; (c and d) optical images of plastic deformation and mechanical fracture upon application of force on the (010) and (100) face, respectively, for the ETC–TFDCNB crystal; (e) molecular packing of the ETC–TFDCNB crystal; quantitative nanomechanical tests: (f) load–displacement (P–h) curves of the (010) and (100) face of ambient crystals; in situ scanning probe 2D and 3D microscopic images of impressions after indentation at 5 mN loads on the (g) (010) face and (h) (100) face, respectively.

On the other hand, upon the application of mechanical stress on the (100) face, the crystal breaks in a brittle manner (Fig. 4b and d). To understand these distinct mechanical responses from different faces, we analysed the crystal structure from SCXRD studies. The SCXRD studies revealed that the monoclinic (P2₁/c space group) ETC–TFDCNB crystal has one ETC molecule and half a TFDCNB molecule in the asymmetric unit. One molecule of TFDCNB interacts with two molecules of ETC to form strong π-stacking interactions (D–A–D) with a centroid-to-centroid distance of 3.43 Å nearly along the b-axis (Fig. 4e). One ETC molecule from one D–A–D unit interacts with another ETC molecule of another D–A–D unit along the b-axis (Fig. 4e) via weak C–H⋯π interactions (d = 3.16 Å, θ = 110.42°). These weak interactions between two strongly interacting D–A–D units help to form a weak interacting plane, i.e., a slip plane, parallel to the (010) face with a layer separation of ∼1.53 Å. Applying mechanical stress perpendicular to the slip plane helps the crystal to bend plastically.^25,38

On the other hand, with mechanical stress on the (100) face, the crystal breaks in a brittle manner due to the absence of any facile slip plane perpendicular to this direction. The crystal was exfoliated when the force was applied by a needle on the (001) or (100) face due to the presence of a weak interacting plane parallel to the (010) face between two D–A–D units. To quantify the mechanical properties of the crystal, we performed nanoindentation⁶³ experiments on the (100) and (010) faces. Then, we analysed the extracted elastic modulus and hardness for both faces. The elastic modulus (E) and hardness (H) for the (010) face are 5.79 ± 0.27 and 0.18 ± 0.01, respectively, and for the (100) faces, 5.00 ± 0.31 and 0.12 ± 0.01, respectively, at a 5 mN load (Fig. 4f–h, S29 and S30†). The low elastic modulus and hardness for the plastically bendable (010) face indicate its soft nature and agree well with previously reported plastically bendable crystals.^63,64 However, for the (100) face, the values are even lower, which may be due to the indentation parallel to the weak interacting plane causing sudden slippage of the layers. In the loading curves, several pop-ins were observed in both faces (Fig. 4f). These pop-ins are generally seen when sudden penetration of the indenter tip at a constant load occurs due to a sudden burst of the microscopic elastically compressed layers upon reaching a critical load. To understand the mechanical behaviour of the crystal, we used pairwise energy framework calculations, which explain the anisotropic nature of the structure in ETC–TFDCNB (Fig. S31†). The analysis suggests that the total energy of the D–A pair is −54.6 kJ mol⁻¹, which is significantly higher than that of D–D interacting pairs (E_tot = −28.1 kJ mol⁻¹) on either side of the weakly interacting slip plane.

Conclusions

In summary, we have successfully demonstrated an efficient non-covalent molecular design strategy to yield efficient TADF in a set of CT co-crystals and solids. Selectively choosing the donor and acceptor pair ensured the forbidden singlet–triplet transitions facilitated through a fast ISC (or RISC) between ¹CT – ³LE sets of electronic states following El Sayed's rule. The relevance of the donor-centric local excited states is a prerequisite in donor selection. We also provide a plausible structural basis for designing efficient mechanically soft organic TADF materials. We believe this report will help in understanding the structural and electronic basis for designing mechanically flexible and efficient intermolecular TADF materials for future applications.

Data availability

The authors declare that all data supporting the findings of this study are available within the article, and ESI,† and raw data files are available from the authors upon reasonable request.

Author contributions

K. J. K. carried out the synthesis, crystallization, photophysical experiments and computational calculations. S. M. performed nanoindentation experiments and mechanical manipulation with the help of K. J. K. Experiments have been performed under the guidance of R. K. V., C. M. R. and K. J. K. wrote the initial draft. All the authors participated in the discussions and manuscript preparation and approved the article's final version.

Conflicts of interest

There are no conflicts to declare.

Acknowledgements

KJK thanks IISER K, and SM thanks CSIR-India for their fellowships. This work was supported by CRG/2021/006054. CMR thanks SERB for funding (CRG/2021/004992). KJK thanks Mr Subrata Das (CSS, IACS Kolkata) for the lifetime measurements.

Notes and references

1. H. Uoyama, K. Goushi, K. Shizu, H. Nomura and C. Adachi, Nature, 2012, 492, 234–238.
2. Z. Yang, Z. Mao, Z. Xie, Y. Zhang, S. Liu, J. Zhao, J. Xu, Z. Chi and M. P. Aldred, Chem. Soc. Rev., 2017, 46, 915–1016.
3. M. Y. Wong and E. Zysman-Colman, Adv. Mater., 2017, 29, 1605444.
4. Y. Liu, C. Li, Z. Ren, S. Yan and M. R. Bryce, Nat. Rev. Mater., 2018, 3, 18020.
5. D. Sasikumar, A. T. John, J. Sunny and M. Hariharan, Chem. Soc. Rev., 2020, 49, 6122–6140.
6. S. Ghosh, S. N. Ansari and S. J. George, in Energy Materials, World Scientific, 2022,  DOI:10.1142/9789811270956_0012.
7. S. Garain, B. C. Garain, M. Eswaramoorthy, S. K. Pati and S. J. George, Angew. Chem., Int. Ed., 2021, 60, 19720–19724.
8. L. Frédéric, A. Desmarchelier, L. Favereau and G. Pieters, Adv. Funct. Mater., 2021, 31, 2010281.
9. Y.-Z. Shi, H. Wu, K. Wang, J. Yu, X.-M. Ou and X.-H. Zhang, Chem. Sci., 2022, 13, 3625–3651.
10. C.-C. Yan, X.-D. Wang and L.-S. Liao, Adv. Sci., 2022, 9, 2200525.
11. X.-K. Chen, D. Kim and J.-L. Brédas, Acc. Chem. Res., 2018, 51, 2215–2224.
12. T. J. Penfold, F. B. Dias and A. P. Monkman, Chem. Commun., 2018, 54, 3926–3935.
13. N. Sharma, E. Spuling, C. M. Mattern, W. Li, O. Fuhr, Y. Tsuchiya, C. Adachi, S. Bräse, I. D. W. Samuel and E. Zysman-Colman, Chem. Sci., 2019, 10, 6689–6696.
14. S. Kuila, A. Ghorai, P. K. Samanta, R. B. K. Siram, S. K. Pati, K. S. Narayan and S. J. George, Chem.–Eur. J., 2019, 25, 16007–16011.
15. W. Li, Z. Li, C. Si, M. Y. Wong, K. Jinnai, A. K. Gupta, R. Kabe, C. Adachi, W. Huang, E. Zysman-Colman and I. D. W. Samuel, Adv. Mater., 2020, 32, 2003911.
16. D. Sun, E. Duda, X. Fan, R. Saxena, M. Zhang, S. Bagnich, X. Zhang, A. Köhler and E. Zysman-Colman, Adv. Mater., 2022, 34, 2110344.
17. X. Zhang, J. De, H. Liu, Q. Liao, S.-T. Zhang, C. Zhou, H. Fu and B. Yang, Adv. Opt. Mater., 2022, 10, 2200286.
18. B. Sk, E. Ravindran, U. Deori, N. Yadav, G. P. Nanda and P. Rajamalli, J. Mater. Chem. C, 2022, 10, 4886–4893.
19. D. Barman, K. Narang, R. Gogoi, D. Barman and P. K. Iyer, J. Mater. Chem. C, 2022, 10, 8536–8583.
20. S. Kuila, S. Garain, G. Banappanavar, B. C. Garain, D. Kabra, S. K. Pati and S. J. George, J. Phys. Chem. B, 2021, 125, 4520–4526.
21. H. Nakanotani, Y. Tsuchiya and C. Adachi, Chem. Lett., 2021, 50, 938–948.
22. S. Dey, M. Hasan, A. Shukla, N. Acharya, M. Upadhyay, S.-C. Lo, E. B. Namdas and D. Ray, J. Phys. Chem. C, 2022, 126, 5649–5657.
23. K. Thakur, B. van der Zee, G.-J. A. H. Wetzelaer, C. Ramanan and P. W. M. Blom, Adv. Opt. Mater., 2022, 10, 2101784.
24. L. Sun, W. Hua, Y. Liu, G. Tian, M. Chen, M. Chen, F. Yang, S. Wang, X. Zhang, Y. Luo and W. Hu, Angew. Chem., Int. Ed., 2019, 58, 11311–11316.
25. S. Saha, M. K. Mishra, C. M. Reddy and G. R. Desiraju, Acc. Chem. Res., 2018, 51, 2957–2967.
26. S. Hayashi, F. Ishiwari, T. Fukushima, S. Mikage, Y. Imamura, M. Tashiro and M. Katouda, Angew. Chem., Int. Ed., 2020, 59, 16195–16201.
27. S. Zhao, H. Yamagishi, O. Oki, Y. Ihara, N. Ichiji, A. Kubo, S. Hayashi and Y. Yamamoto, Adv. Opt. Mater., 2022, 10, 2101808.
28. M. Annadhasan, A. R. Agrawal, S. Bhunia, V. V. Pradeep, S. S. Zade, C. M. Reddy and R. Chandrasekar, Angew. Chem., Int. Ed., 2020, 59, 13852–13858.
29. W. M. Awad, D. W. Davies, D. Kitagawa, J. Mahmoud Halabi, M. B. Al-Handawi, I. Tahir, F. Tong, G. Campillo-Alvarado, A. G. Shtukenberg, T. Alkhidir, Y. Hagiwara, M. Almehairbi, L. Lan, S. Hasebe, D. P. Karothu, S. Mohamed, H. Koshima, S. Kobatake, Y. Diao, R. Chandrasekar, H. Zhang, C. C. Sun, C. Bardeen, R. O. Al-Kaysi, B. Kahr and P. Naumov, Chem. Soc. Rev., 2023, 52, 3098–3169.
30. T. Feiler, B. Bhattacharya, A. A. L. Michalchuk, S.-Y. Rhim, V. Schröder, E. List-Kratochvil and F. Emmerling, CrystEngComm, 2021, 23, 5815–5825.
31. Q. Di, L. Li, X. Miao, L. Lan, X. Yu, B. Liu, Y. Yi, P. Naumov and H. Zhang, Nat. Commun., 2022, 13, 5280.
32. T. Seki, N. Hoshino, Y. Suzuki and S. Hayashi, CrystEngComm, 2021, 23, 5686–5696.
33. K. Huang, L. Song, K. Liu, A. Lv, M. Singh, K. Shen, J. Shen, J. Wang, H. Wang, H. Shi, H. Ma, M. Gu, G. Sun, W. Yao, Z. An and W. Huang, npj Flexible Electron., 2021, 5, 21.
34. S. Bhandary, R. Van Deun, A. M. Kaczmarek and K. Van Hecke, Chem. Sci., 2022, 13, 10308–10314.
35. K. J. Kalita, S. Mondal, C. M. Reddy and R. K. Vijayaraghavan, Chem. Mater., 2023, 35, 709–718.
36. B. Bhattacharya, D. Roy, S. Dey, A. Puthuvakkal, S. Bhunia, S. Mondal, R. Chowdhury, M. Bhattacharya, M. Mandal, K. Manoj, P. K. Mandal and C. M. Reddy, Angew. Chem., Int. Ed., 2020, 59, 19878–19883.
37. R. Samanta, S. Das, S. Mondal, T. Alkhidir, S. Mohamed, S. P. Senanayak and C. M. Reddy, Chem. Sci., 2023, 14, 1363–1371.
38. G. R. Krishna, R. Devarapalli, G. Lal and C. M. Reddy, J. Am. Chem. Soc., 2016, 138, 13561–13567.
39. Y. Chen, Z. Chang, J. Zhang and J. Gong, Angew. Chem., Int. Ed., 2021, 60, 22424–22431.
40. S. Hayashi and T. Koizumi, Angew. Chem., Int. Ed., 2016, 55, 2701–2704.
41. Y. Yang, L. Silva de Moraes, C. Ruzié, G. Schweicher, Y. H. Geerts, A. R. Kennedy, H. Zhou, S. J. Whittaker, S. S. Lee, B. Kahr and A. G. Shtukenberg, Adv. Mater., 2022, 34, 2203842.
42. J. Gu, Z. Tang, H. Guo, Y. Chen, J. Xiao, Z. Chen and L. Xiao, J. Mater. Chem. C, 2022, 10, 4521–4532.
43. M. Sarma and K.-T. Wong, ACS Appl. Mater. Interfaces, 2018, 10, 19279–19304.
44. M. Zhang, C.-J. Zheng, H. Lin and S.-L. Tao, Mater. Horiz., 2021, 8, 401–425.
45. N. Li, F. Ni, X. Lv, Z. Huang, X. Cao and C. Yang, Adv. Opt. Mater., 2022, 10, 2101343.
46. S. K. Park, J. H. Kim, T. Ohto, R. Yamada, A. O. F. Jones, D. R. Whang, I. Cho, S. Oh, S. H. Hong, J. E. Kwon, J. H. Kim, Y. Olivier, R. Fischer, R. Resel, J. Gierschner, H. Tada and S. Y. Park, Adv. Mater., 2017, 29, 1701346.
47. G. Bolla, Q. Liao, S. Amirjalayer, Z. Tu, S. Lv, J. Liu, S. Zhang, Y. Zhen, Y. Yi, X. Liu, H. Fu, H. Fuchs, H. Dong, Z. Wang and W. Hu, Angew. Chem., Int. Ed., 2021, 60, 281–289.
48. Y. Huang, Z. Wang, Z. Chen and Q. Zhang, Angew. Chem., Int. Ed., 2019, 58, 9696–9711.
49. H. Méndez, G. Heimel, A. Opitz, K. Sauer, P. Barkowski, M. Oehzelt, J. Soeda, T. Okamoto, J. Takeya, J.-B. Arlin, J.-Y. Balandier, Y. Geerts, N. Koch and I. Salzmann, Angew. Chem., Int. Ed., 2013, 52, 7751–7755.
50. M. Madhu, R. Ramakrishnan, V. Vijay and M. Hariharan, Chem. Rev., 2021, 121, 8234–8284.
51. L. Fijahi, T. Salzillo, A. Tamayo, M. Bardini, C. Ruzié, C. Quarti, D. Beljonne, S. d'Agostino, Y. H. Geerts and M. Mas-Torrent, J. Mater. Chem. C, 2022, 10, 7319–7328.
52. Y. Yang, Y. Zhang, C. T. Hu, M. Sun, S. Jeong, S. S. Lee, A. G. Shtukenberg and B. Kahr, Chem. Mater., 2022, 34, 1778–1788.
53. S. Garain, S. N. Ansari, A. A. Kongasseri, B. Chandra Garain, S. K. Pati and S. J. George, Chem. Sci., 2022, 13, 10011–10019.
54. D. Veldman, S. C. J. Meskers and R. A. J. Janssen, Adv. Funct. Mater., 2009, 19, 1939–1948.
55. A. D. Nidhankar, Goudappagouda, V. C. Wakchaure and S. S. Babu, Chem. Sci., 2021, 12, 4216–4236.
56. C. Chen, Z. Chi, K. C. Chong, A. S. Batsanov, Z. Yang, Z. Mao, Z. Yang and B. Liu, Nat. Mater., 2021, 20, 175–180.
57. S. K. Lower and M. A. El-Sayed, Chem. Rev., 1966, 66, 199–241.
58. F. B. Dias, J. Santos, D. R. Graves, P. Data, R. S. Nobuyasu, M. A. Fox, A. S. Batsanov, T. Palmeira, M. N. Berberan-Santos, M. R. Bryce and A. P. Monkman, Adv. Sci., 2016, 3, 1600080.
59. P. K. Samanta, D. Kim, V. Coropceanu and J.-L. Brédas, J. Am. Chem. Soc., 2017, 139, 4042–4051.
60. R. Dhali, D. K. A. Phan Huu, F. Bertocchi, C. Sissa, F. Terenziani and A. Painelli, Phys. Chem. Chem. Phys., 2021, 23, 378–387.
61. M. Hariharan and G. D. Scholes, J. Phys. Chem. Lett., 2022, 13, 8365–8368.
62. M. Mondal and R. K. Vijayaraghavan, J. Phys. Chem. C, 2023, 127, 2398–2406.
63. S. Varughese, M. S. R. N. Kiran, U. Ramamurty and G. R. Desiraju, Angew. Chem., Int. Ed., 2013, 52, 2701–2712.
64. S. Das, A. Mondal and C. M. Reddy, Chem. Soc. Rev., 2020, 49, 8878–8896.

---

Footnote

† Electronic supplementary information (ESI) available: Synthesis, crystallography, photophysical studies and computational details. CCDC 2260509–2260514. For ESI and crystallographic data in CIF or other electronic format see DOI: https://doi.org/10.1039/d3sc03267a

---