Double-bond delocalization in non-alternant hydrocarbons induces inverted singlet–triplet gaps

Abstract

Molecules where the first excited singlet state is lower in energy than the first excited triplet state have the potential to revolutionize OLEDs. This inverted singlet–triplet gap violates Hund's rule and currently there are only a few molecules which are known to have this property. Here, we screen the complete set of non-alternant hydrocarbons consisting of 5-, 6-, 7-membered rings fused into two-, three- and four-ring polycyclic systems. We identify several molecules where the symmetry of the ground-state structure is broken due to bond-length alternation. Through symmetry-constrained optimizations we identify several molecular cores where the singlet–triplet gap is inverted when the structure is in a higher symmetry, pentalene being a known example. We uncover a strategy to stabilize the molecular cores into their higher-symmetry structures with electron donors or acceptors. We design several substituted pentalenes, s-indacenes, and indeno[1,2,3-ef]heptalenes with inverted gaps, among which there are several synthetically known examples. In contrast to known inverted gap emitters, we identify the double-bond delocalized structure of their conjugated cores as the necessary condition to achieve the inverted gap. This strategy enables chemical tuning and paves the way for the rational design of polycyclic hydrocarbons with inverted singlet–triplet gaps. These molecules are prospective emitters if their properties can be optimized for use in OLEDs.

---

1 Introduction

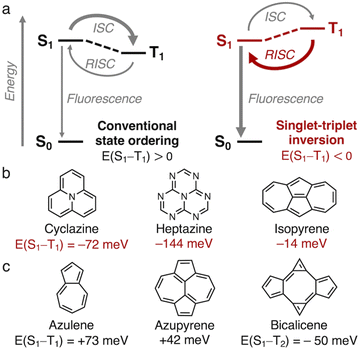
The efficiency of organic molecular emitters is limited by intersystem crossing (ISC) into low-lying non-emissive triplet states, which are favored over the emissive singlet states due to spin statistics.^1,2 The triplet states are furthermore favored energetically over singlets with the same electron configuration in accordance with Hund's rule, thereby making reverse ISC (RISC) less efficient (E(S₁–T₁) > 0, Fig. 1a).^3,4 Recently, it was discovered that the gap between the lowest excited singlet (S₁) and triplet (T₁) states of a class of azaphenalenes is inverted (E(S₁–T₁) < 0, Fig. 1a).^5–7 RISC is more efficient than ISC in cyclazine and heptazine because S₁ is thermodynamically favored over T₁, as shown in Fig. 1b.^7–9 Violations of Hund's rule can occur when the exchange interaction is minimized by reducing the overlap between the highest occupied and lowest unoccupied molecular orbitals (HOMO and LUMO).^5–8 As standard density functional theory-based methods struggle with Hund's rule violations,^6,9–16 azaphenalenes were only recently identified as inverted gap emitters using coupled cluster methods.^{5–7,17–19}

Fig. 1 (a) Simplified Jablonski diagrams of conventional and inverted state ordering. (b) Azaphenalenes and isopyrene with inverted singlet–triplet gaps. (c) Related non-alternant molecules; bicalicene is an example of a higher-lying Hund's rule violation. Computed at the EOM-CCSD/aug-cc-pVDZ//ωB97X-D/def2-TZVP level.

We recently used a high-throughput screening approach to uncover that the non-alternant hydrocarbon isopyrene (Fig. 1b) has an inverted gap of E(S₁–T₁) = −14 meV at the EOM-CCSD/aug-cc-pVDZ level.²⁰ We attributed the inverted gap to its D_2h-symmetry pentalene core, which ensures non-overlapping HOMO and LUMO.^20–23 Unlike pentalene, which distorts into C_2h-symmetry to alleviate antiaromaticity, the highly symmetric structure of isopyrene is aromatically stabilized by the pattern of 5- and 7-membered rings.²⁰ Isopyrene is an azulenoazulene (an azulene dimer), and a similar aromaticity pattern and symmetry are found in the heptalenic isomer azupyrene, which is shown in Fig. 1c alongside azulene, which has C_2v symmetry. However, they both have small positive singlet–triplet gaps.^20,24 In addition to isopyrene, we identified the D_2h-symmetry non-alternant hydrocarbon bicalicene, the trans-dimer of calicene,²⁵ which features an expanded pentalene core resulting in a higher-order Hund's rule violation. This occurs between S₁ and T₂, which are of the same electron configuration, while another lower energy triplet state is T₁ (Fig. S1†).

The exploration of molecules with inverted E(S₁–T₁) is essential for achieving a new generation of organic light-emitting diodes (OLEDs).^2,7–9 The molecules must have suitable excited-state dynamics and oscillator strengths to optimize the fluorescence rates. Combining these photophysical properties will be the key challenge in the years to come.^1,26–33 Here, we focus on establishing rational design rules for molecules with inverted singlet–triplet gaps by studying the vertical excitation energies. To expand the library of motifs of the non-alternant hydrocarbon class, we screen the complete set of up to four fused 5-, 6-, and 7-membered rings. This constitutes 187 molecular cores which have been enumerated by Balaban and Randić.³⁴ We uncover a substituent strategy that enables the stabilization of high-symmetry cores in pentalene, s-indacene and indeno[1,2,3-ef]heptalene, and several other non-alternant cores. We identify many new molecules with inverted singlet–triplet gaps (E(S₁–T₁) < 0) and higher-lying excited-state Hund's rule violations (E(S₁–T₂) < 0), among which several synthesized examples exist.

2 Methods

The 187 unsubstituted parent molecules were initially optimized to the tight criteria at the ωB97X-D/def2-TZVP level with the ultrafine integration grid as implemented in the Gaussian16 package.³⁵ Molecules with avoided symmetry in the ground-state structure were further optimized using explicit symmetry constraints at the same level of theory using the GAMESS 2016.1 code.³⁶ Finally, the selected substituted motifs were optimized without constraint using Gaussian16.³⁵ All unconstrained structures were verified to have no imaginary vibrational frequencies. Excited-state geometry optimizations were performed using Tamm–Dancoff-approximated time-dependent density functional theory (TDA-TDDFT) at the same level as the ground-state optimizations (ωB97X-D/def2-TZVP level).

Vertical excitation energies for all molecules were initially computed at the second-order approximate coupled-cluster level (CC2) using Turbomole 7.1.^37–39 CC2 provides a good compromise between computational accuracy and efficiency,^{5,10,11,16,30} which allows us to compute excitation energies of potentially thousands of molecules.²⁰ For molecules with negative gaps at the CC2 level, we further compute the excitation energies at the equations-of-motion coupled-cluster level (EOM-CCSD) with the QChem 5.1 package.^40,41 Depending on the size of the molecule, the aug-cc-pVDZ or cc-pVDZ basis set is applied.⁴² Based on molecules for which it is possible to compare both basis sets, the addition of augmented basis functions makes only a small difference in most cases (Fig. S2†).

Computational efficiency is a challenge as we study increasingly large substituted molecules. EOM-CCSD provides higher accuracy than CC2, but severely limits the number of tractable computations. CC2 appears to systematically underestimate the singlet–triplet gaps (Fig. S2†), which makes it suitable for screening given there will be few false negatives.²⁰ The singlet–triplet gaps we report will inherently be small, making accuracy essential. In this regard, even EOM-CCSD is a compromise, but EOM-CCSD seems to slightly overestimate the gaps towards more positive values. For example, we compute E(S₁–T₁) of azulene (Fig. 1c) to be +73 meV with EOM-CCSD/aug-cc-pVDZ and −5 meV with CC2/aug-cc-pVDZ. The experimentally determined value of +49 meV is between these.⁴³ Based on this offset with EOM-CCSD, azupyrene (Fig. 1c) is thus likely to be almost gapless. Here, we only report vertical excitation energies computed with EOM-CCSD as it provides a conservative estimate of singlet–triplet gaps. CC2 values are included in the ESI, Tables S1–S3.†

3 Results

Inspired by the non-alternant fused hydrocarbon structures of isopyrene and the near-gapless azulene and azupyrene, we screen the complete set of 187 non-alternant hydrocarbons that consist of up to four fused five-, six-, and seven-membered rings (Fig. 2, step 1, and Fig. S3).†³⁴ However, we find that at the EOM-CCSD level, the only molecule in this set that exhibits a Hund's rule violation is indeed isopyrene (Fig. 1c).

Fig. 2 Workflow for the generation of symmetric hydrocarbons with delocalized double bonds from a set of non-alternant hydrocarbons.

We notice that of the 187 molecules,³⁴ 27 are distorted into lower than expected symmetry in their ground-state geometry due to bond-length alternation, i.e., they have avoided symmetry. These include the known cases of pentalene and heptalene, which have inverted gaps in their D_2h structures.^20,21 We carry out symmetry-constrained optimizations of these 27 molecules to assess the excited-state energies at higher symmetries, which constitute low-energy transition states between the equivalent broken symmetry structures (Fig. S4†). As with pentalene and heptalene, we find that several of these higher energy structures exhibit excited-state violations of Hund's rule, step 2 in Fig. 2 and Table S2.†

A mechanism for the distortivity of π-systems was uncovered in seminal work by Shaik and co-workers using valence bond theory,^44,45 and by Heilbronner and co-workers using Hückel method calculations.^46–48 There is a balance between the σ-system's rigidity and the π-system's distortivity, which are both molecule-dependent. Pentalene is a textbook example of the distortion into a double-bond localized structure (from D_2h to C_2h symmetry), and its distortion correlates with a reduction in the antiaromaticity of the molecule.^21,49,50 The balance between π-distortivity and σ-rigidity can be pushed towards double-bond delocalization, and several substituted pentalenes and structurally analogous indacenes assume high symmetry in their crystal structures.^47,51–54 Several alternative explanations to double-bond delocalization in crystal structures have been suggested,^51,55–57 and the assignment of the correct global minimum structures continues to be a computational challenge when the energy difference is small.^57–59 Considering the ongoing challenge of assessing the true global minimum energies, our focus here is to assess excited-state energy ordering in substituted molecules where double-bond localization is minimized.

Yang and Heilbronner used a Hückel model to predict how bond localization is alleviated by electron-donating substituents at positions with large LUMO coefficients or by electron-withdrawing substituents at HOMO coefficient positions.⁴⁷ We apply this strategy using donor substituents at LUMO positions (step 3 in Fig. 2).^47,60 Yang and Heilbronner noted that electron-withdrawing substituents seem to have less effect in practice.⁴⁷ Our results agree with this, and we find primarily that electron-donating substituents at the LUMO positions have a notable effect on the bond-length alternation of the molecular core.

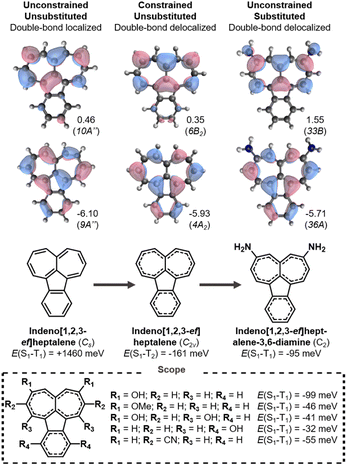
3.1 Pentalenes

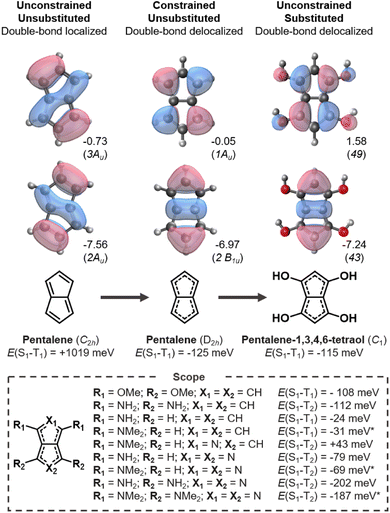
Pentalene is an archetypical antiaromatic molecule and the ground-state structure distorts into a C_2h symmetry geometry with significant bond-length alternation and positive E(S₁–T₁).^20,21,61 As shown in Fig. 3 (left), the large positive gap correlates with the overlapping HOMO and LUMO. When pentalene is constrained into a double-bond delocalized D_2h structure, the HOMO and LUMO become non-overlapping and consequently negative E(S₁–T₁) is achieved (Fig. 3, center).

Fig. 3 Singlet–triplet splittings of pentalene in its ground state (C_2h) and symmetry-constrained (D_2h) geometries, and substituted derivatives thereof. All energies and orbitals evaluated at the EOM-CCSD/aug-cc-pVDZ level (* = cc-pVDZ); eigenvalues in eV.

We carry out a series of substitutions at the LUMO positions, as shown in Fig. 3. Pentalene-1,3,4,6-tetraol has a double-bond delocalized ground-state structure with a negative E(S₁–T₁) = −115 meV (Fig. 3, right), which is very close to that of D_2h-constrained pentalene. Tetra-amino and -methoxy substituted pentalenes yield similar Hund's rule violations, albeit the amino-substituted case has a lower-lying T₁ state; that is, it constitutes a Hund's rule violation but the singlet–triplet gap is not inverted. When using strong donors, such as amine and dimethylamine, even the disubstituted cases result in inverted gaps. We also tested several electron withdrawing substituents at the 2,5-positions where the HOMO coefficients are large, but we found none with the desired bond delocalization nor inverted gaps.

The pentalene cores have double-bond delocalized quasi-D_2h symmetry in all the substituted molecules listed in Fig. 3. Still, their symmetry is lower than the D_2h-constrained pentalene. The slightly broken symmetry issuing from substituent geometries does not rule out inverted singlet–triplet gaps as the high local symmetry of the fused-ring core is preserved. However, all the gaps we report here are less negative than the −125 meV gap of the constrained parent pentalene.

Several donor-substituted pentalenes have been synthesized and there is thus promise that pentalenes can be appropriately functionalized for use as inverted gap emitters.^52,62 It is likely that the negative gap can be retained with larger donor substituents in combination with bulky substituents, tert-butyl (t-Bu) groups for example, to provide kinetic stability.^63,64 Here, we focus on small substituents due to the size limitations of the EOM-CCSD method.

Azapentalenes and diazapentalenes have also been reported in the literature.^65–67 Omar et al. recently identified an amine-substituted cyclopenta[c]pyrrole,⁶⁸ however, we find its E(S₁–T₂) to be +43 meV at the EOM-CCSD/aug-cc-pVDZ level. There are several substituted pyrrolo[3,4-c]pyrroles that exhibit Hund's rule violations between S₁ and T₂, which are listed in Fig. 3. The combination of larger substituents and reduced symmetry of the molecules holds great promise for the design of molecules with increased oscillator strengths between S₁ and S₀, which is essential for the molecules to be used as emitters.

3.2 Indacenes

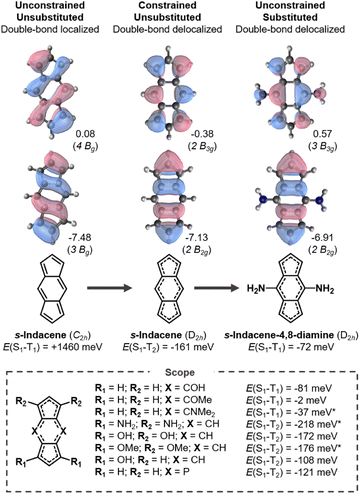
In an analogous fashion to pentalene, s-indacene distorts into a C_2h symmetry geometry with bond-length alternation to reduce antiaromaticity. Its HOMO and LUMO overlap and consequently its singlet–triplet gap is positive as shown in Fig. 4. When constrained into D_2h symmetry, pentalene-like HOMO and LUMO are achieved but the Hund's rule violation is between S₁ and T₂ in s-indacene. However, the singlet–triplet gap is inverted without a lower-lying triplet in several of the substituted indacenes.

Fig. 4 Singlet–triplet splittings of s-indacene in its ground state (C_2h) and symmetry-constrained (D_2h) geometries, and substituted derivatives thereof. All energies evaluated at the EOM-CCSD/aug-cc-pVDZ level (* = cc-pVDZ); eigenvalues in eV.

We substitute at positions with LUMO coefficients, which alleviates the antiaromaticity of the core (Fig. S5†) and stabilizes the double-bond delocalized structure as shown in Fig. 4. In the four cases where the central six-membered ring is substituted with donors (amine-, hydroxy-, methoxy-, dimethylamine-substituents) a negative E(S₁–T₁) is attained. Substituting instead at the five-membered rings yields more negative gaps, but between S₁ and T₂, which have the same electron configuration. Notably, E(S₁–T₂) is more negative in all the tetrasubstituted molecules than in the constrained parent s-indacene. From this, we conclude that substituted molecules can potentially achieve more negative gaps than its molecular core.

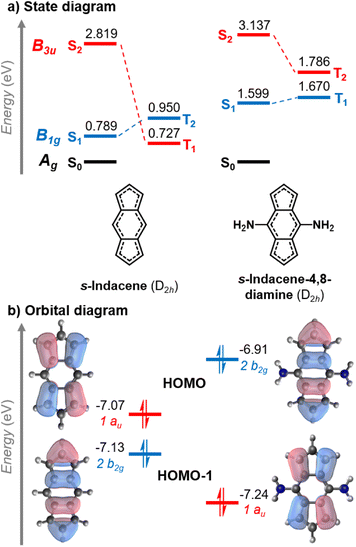
The change of the state ordering in the 4,8-disubstituted indacenes deserves attention. The two highest occupied MOs of D_2h-constrained s-indacene are quasi-degenerate, with a pentalene-like b_2g HOMO−1 and a benzene-like a_u HOMO shown in Fig. 5. The transitions involving the non-overlapping HOMO−1 and LUMO orbitals exhibit a Hund's rule violation (E(S₁–T₂) = −161 meV). However, the presence of the a_u HOMO that overlaps with the LUMO leads to a triplet state described by a HOMO → LUMO transition which is lower in energy, as marked in red in Fig. 5a. While the LUMO substituent patterns slightly raise the energy of the pentalene-like occupied 2b_2g orbital, it lowers the energy of the a_u orbital. As a result, the B_1g excited state that exhibits the singlet–triplet inversion is below the intruding B_3u triplet in the s-indacene-4,8-diamine. In three other 4,8-disubstituted cases, the B_3u triplet remains slightly below the B_1g triplet, but nonetheless the B_1g singlet is lower energy than both of them ensuring an inverted singlet–triplet gap, as listed in Fig. 4 and Table S3.† Substitution at the five-membered rings does not have this effect, and the state-ordering of the unsubstituted D_2hs-indacene remains. This finding highlights the importance of the substitution position on the excited-state ordering in s-indacene derivatives. We thus demonstrate that the states involved in the Hund's rule violation can be manipulated to be the lowest-lying excited states through appropriate substitution patterns that result in an inverted singlet–triplet gap.

Fig. 5 (a) State diagram of the lowest excited states of s-indacene in the symmetry-constrained (D_2h) geometry (left) and of s-indacene-4,8-diamine in the relaxed geometry (right). Energy levels not to scale. (b) Partial orbital diagram of the two highest occupied molecular orbitals (HOMO and HOMO−1) involved the transitions shown in (a), colored based on the excited states to which they contribute. All energies evaluated at the EOM-CCSD/aug-cc-pVDZ level; orbital and excited state energies in eV.

Many substituted indacenes have been synthesized due to their interest as model antiaromatic compounds. The excited-state properties of t-Bu-substituted s-indacenes have been studied in great detail.^{51,54,69–71} Recently, a number of phenyl-substituted indacenes were reported.⁷² Several donor-substituted s-indacenes were synthesized in the 1970s and 1980s, including 4,8-dimethylamine substituted analogues like the ones we report to have inverted gaps here.⁷³ Among many synthesized hetero-s-indacenes,^74–77 we find that a diphospa-s-indacene has a negative E(S₁–T₂) similar to that in D_2hs-indacene. The variety and tunability offered by the s-indacene motif holds great promise for the future design of inverted gap emitters.

3.3 Indeno[1,2,3-ef]heptalenes

The final molecule where we identify inverted S₁–T₁ gaps is indeno[1,2,3-ef]heptalene, which consists of a fused heptalene and indene as shown in Fig. 6. The unsubstituted molecule distorts into a C_s geometry with bond-length alternation and a positive singlet–triplet gap. When the molecule is constrained into the double-bond delocalized C_2v structure a Hund's rule violation between S₁ and T₂ is achieved. The key frontier MOs involved in the lowest excitations are heptalene-like and it is at the heptalene unit that substitution has the most significant effect.

Fig. 6 Singlet–triplet splittings of indeno[1,2,3-ef]heptalene in its ground state (C_s) and symmetry-constrained (C_2v) geometries, and substituted derivatives thereof. All energies evaluated at the EOM-CCSD/cc-pVDZ level; eigenvalues in eV.

As with s-indacene, the singlet–triplet gap can become inverted upon substitution. As shown in Fig. 6, we identify several indenoheptalene derivatives with a negative E(S₁–T₁). Donors at the 3,6 positions (R₁ in Fig. 6) provide the most negative gaps, but even disubstitution with hydroxyls at the six-membered ring (R₄) can cause the molecule to attain the necessary double-bond delocalization. Notably, we also succeed in finding an acceptor-substituted inverted gap molecule. In indeno[1,2,3-ef]heptalene, substituting with electron-withdrawing nitrile substituents at the 2,7-positions (R₂) has the same effect as donors at the LUMO positions. To the best of our knowledge, indeno[1,2,3-ef]heptalenes are yet to be synthesized.

3.4 Higher-lying Hund's rule violations

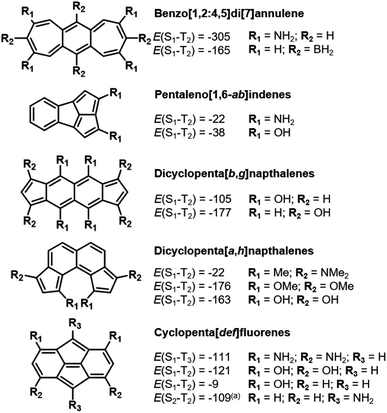
Similar to bicalicene (Fig. 1c) and the constrained D_2hs-indacene and C_2v indeno[1,2,3-ef]heptalene, our approach reveals several molecules with Hund's rule violations between the lowest excited singlet state and a higher-lying excited triplet state of the same electron configuration. The triplet state with the same electron configuration as the S₁ state is often not the T₁, as there can be intruding states with a different electron configuration that has lower energy, making those the first excited triplet state. While ideally we search for molecules with inverted singlet–triplet gaps, a Hund's rule violation is by definition one which occurs between electronic states with identical electron configuration.^3,4 Given the fundamental interest in such molecules, we highlight more examples of higher-lying Hund's rule violations that are achieved by stabilizing the double-bond delocalized structures through substitution, as shown in Fig. 7.

Fig. 7 Additional Hund's rule violations involving the lowest excited singlet state. All energies evaluated at the EOM-CCSD/cc-pVDZ level and shown in meV. (a) = this compound exhibits a triplet configuration of lower energy than the closed shell singlet.

The heptalenic analog of s-indacene, benzo[1,2:4,5]di[7]annulene, is stabilized in a high-symmetry structure by both electron-donating (amine) and electron-accepting (borane) groups at the LUMO and HOMO positions, respectively. This leads to large Hund's rule violations of −305 and −165 meV, respectively. While it is planar in the unsubstituted (C_2h) and amine-substituted (quasi-D_2h) forms, borane functionalization at the central 6-membered ring induces out-of-plane distortion to the ring system into C₂ symmetry. To our knowledge, benzo[1,2:4,5]di[7]annulenes have not been synthesized.

Pentaleno[1,6-ab]indene is the pentalene analog of indeno[1,2,3-ef]heptalene described above in Section 3.3. The three fused five-membered rings form a highly strained bowl shape which, to our knowledge, has not been synthesized. Through substitution at these rings with either amino or hydroxyl groups, a small S₁–T₂ inversion is achieved.

The next higher rectilinear analog of pentalene and indacene (Sections 3.1 and 3.2) is dicyclopenta[b,g]naphthalene, which has been synthesized.⁷⁸ As with indacene, substitution at both the six- and five-membered rings induces the requisite bond-length delocalization, which induces the Hund's rule violation. Unlike in s-indacene, we do not find a substituted molecule where the gap between S₁ and T₁ is inverted.

By repositioning the five-membered rings of dicyclopenta[b,g]naphthalene on the naphthalene core, we obtain dicyclopenta[a,h]naphthalene. Despite exhibiting out-of-plane bending due to steric congestion at the R₁ position, which leads to distortion of ∼7° in the bare molecule (R₁ = H) and ∼24° when R₁ = OMe, S₁–T₂ inversions are observed in the substituted molecules. Substituted dicyclopenta[b,g]naphthalenes have been reported as reaction intermediates.⁷⁹

Cyclopenta[def]fluorene is similar to our previously-reported isopyrene²⁰ (Fig. 1b) in that a pentalene core is flanked by symmetric fused ring systems. However, unlike isopyrene, whose planarity and bond-delocalization are enabled by push–pull aromaticity, cyclopenta[def]fluorene is bowl-shaped, exhibits bond-length alternation and is signficantly antiaromatic in the ground state (Fig. S5†). Through di- and tetra-substitution at the six-membered rings with electron-donating groups, the antiaromaticity of the ring systems is alleviated and inversions between the S₁ and T₂ are obtained due to the double-bond delocalized structures. To the best of our knowledge, cyclopenta[def]fluorene has not been synthetically reported.

In all the above molecules the intruding triplet state is much lower in energy (in most cases ∼1 eV) than the triplet state with the same electron configuration as S₁. In s-indacene the HOMO−1 and HOMO are near-degenerate which allows for fine-tuning of the excited state ordering with substituents. Still, in most cases the substituents we have used here do not change the frontier MO eigenvalues sufficiently to affect the state ordering.

4 Discussion

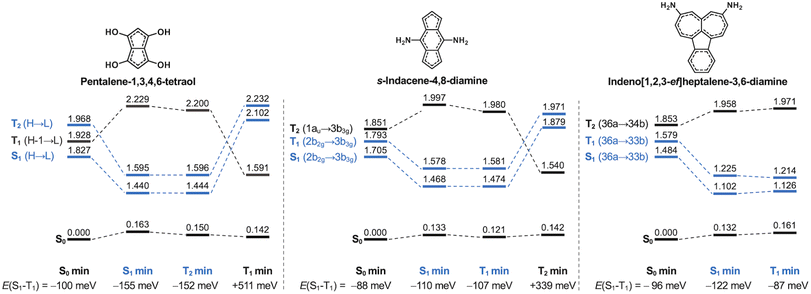
The molecules we have studied here are all highly (quasi-)symmetric, as the small substituents we use only slightly perturb the symmetry of the molecular cores. This severely limits the oscillator strengths of the S₁ transition because the HOMO–LUMO overlap is small. As listed in Tables S4 and S5,† none of the molecules achieve appreciable oscillator strengths from S₁, although some of the molecules are not far from potentially being in an experimentally measurable range.⁷ Consequently, many of them may not obey Kasha's rule, as is the case for s-indacene, azulene and pyrene.^70,80–83 The negligible oscillator strength associated with the transition to the S₁ state may lead to phosphorescence being the favoured decay pathway, as has been shown for other compounds with non-overlapping HOMO and LUMO orbitals.⁸⁴ The role of phosphorescence in compounds with inverted singlet–triplet gaps is, however, yet to be established.

To further evaluate their excited-state properties, we optimize the geometries of three featured molecules in their lowest-lying excited states using TDA-TDDFT and recompute the excited state energies with EOM-CCSD. The Hund's rule violations persist in pentalene-1,3,4,6-tetraol, s-indacene-4,8-diamine and indeno[1,2,3-ef]heptalene-3,6-diamine when the structures are relaxed into their singlet and triplet excited state minima (states marked in blue in Fig. 8). This indicates the inverted singlet–triplet gaps are persistent when the molecular structures may dynamically evolve in an excited state following the initial excitation.

Fig. 8 State diagram of the relaxed ground-state and excited-state structures of pentalene-1,3,4,6-tetraol (left), s-indacene-4,8-diamine (center), and indeno[1,2,3-ef]heptalene-3,6-diamine (right). States corresponding to Hund's rule violations are marked in blue. Note that for pentalene-1,3,4,6-tetraol, the triplet with the same configuration as S₁ is T₂ at the ground state minimum geometry. For each geometry, the next lowest excited state is ∼1 eV higher than the states shown. The relaxed T₂ geometry of indeno[1,2,3-ef]heptalene-3,6-diamine could not be located. Excited-state structures were optimized using TDA-TDDFT at the ωB97X-D/def2-TZVP level, and state energies were computed at the EOM-CCSD/cc-pVDZ level.

Future work must provide further analysis of the photophysical rates and vibrational contributions to develop molecules suitable as emitters. Non-alternant fused polycyclic hydrocarbons are a promising class of molecules that continue to attract attention for their antiaromatic and optical properties.^85–90 The new molecular motifs we have suggested provide many potential avenues to explore. A combined synthetic and computational screening effort was successful in identifying a heptazine-based emitter with inverted gap and significant oscillator strength from the emissive S₁ state.^7,9 Future screening efforts for synthesizable inverted gap molecules must apply this new conceptual understanding of substituent effects to optimize both the state-ordering and the oscillator strengths of the potential emitters.

In the previously-identified cases of azupyrene and bicalicene (Fig. 1), the requisite symmetry was induced by precise polycyclic push–pull ring motifs that enabled aromatic stabilization.²⁰ The structures described here correspond to a much simpler, robust and transferable design rule: the alleviation of antiaromaticity and concommitant double-bond delocalization through substituent effects. This relief of antiaromaticity stabilizes the substituted species, as indicated by homodesmotic and isodesmic reaction equations⁹¹ (Fig. S6†), which become almost non-aromatic in both their ground and excited states as judged from their NICS values in Fig. S5 and S7.† The scope and conceptual simplicity of this approach provide reason for optimism that perhaps larger substituents will be able to induce the same double-bond delocalization while enabling optically useful oscillator strengths.

5 Conclusions

We have identified several functionalized pentalenes, s-indacenes and indeno[1,2,3-ef]heptalenes with inverted lowest singlet and triplet excited state energy gaps. Furthermore, we find many molecules with higher-lying Hund's rule violations where the inversion is between S₁ and a higher triplet state of the same electron configuration, thus leaving the S₁–T₁ gap positive. This reveals that there is a broad structural diversity in the non-alternant hydrocarbon class of inverted gap emitters, similar to that seen in the azaphenalene class.

All the inverted gap molecules we have demonstrated here have double-bond delocalized structure with almost no bond-length alternation. This is achieved by systematically substituting the molecular cores with donors at positions with large LUMO coefficients, and, albeit to a lesser extent, with acceptors at positions with large HOMO coefficients. We thus provide a conceptual design strategy for achieving inverted singlet–triplet gaps. While the molecular cores all have high local symmetry within the ring systems, the overall molecular symmetry is often broken by the substituents. This highlights that double-bond delocalization in the conjugated molecular core is the underlying structural mechanism for inverted singlet–triplet gaps.

We have provided a significant expansion of the class of non-alternant hydrocarbons with inverted singlet–triplet gaps, which shows that excited-state Hund's rule violations are perhaps more common than first anticipated. Along with the azaphenalene class, a great variety of molecular motifs are now revealed to have this property, which will be of great technological importance if it can be applied in OLEDs. In this regard, it is urgent to establish further design rules for inverted gap emitters that also address emissive properties beyond state ordering along with experimental verification of the effect.

Data availability

The ESI contains additional figures, benchmarking results, and data tables. All optimized structures are provided separately as XYZ files.

Author contributions

M. H. G. and J. T. B. performed computations and analyzed the data. C. C. supervised the project. All authors discussed the results and contributed to the manuscript writing.

Conflicts of interest

There are no conflicts to declare.

Acknowledgements

The authors are grateful to the EPFL for financial support and the allocation of computational resources. J. T. B. and M. H. G. thank Dr Daniel Jana for technical assistance. M. H. G. is grateful for funding from the Carlsberg Foundation (CF21-0202).

References

1. J. Eng and T. J. Penfold, Commun. Chem., 2021, 4, 91.
2. J.-C. Sancho-García, Nature, 2022, 609, 473–475.
3. F. Hund, Z. Phys., 1925, 33, 345–371.
4. W. Kutzelnigg, Angew. Chem., Int. Ed. Engl., 1996, 35, 572–586.
5. J. Ehrmaier, E. J. Rabe, S. R. Pristash, K. L. Corp, C. W. Schlenker, A. L. Sobolewski and W. Domcke, J. Phys. Chem. A, 2019, 123, 8099–8108.
6. P. de Silva, J. Phys. Chem. Lett., 2019, 10, 5674–5679.
7. N. Aizawa, Y.-J. Pu, Y. Harabuchi, A. Nihonyanagi, R. Ibuka, H. Inuzuka, B. Dhara, Y. Koyama, K.-i. Nakayama and S. Maeda, et al. , Nature, 2022, 609, 502–506.
8. T. Won, K.-i. Nakayama and N. Aizawa, Chem. Phys. Rev., 2023, 4, 021310.
9. R. Pollice, P. Friederich, C. Lavigne, G. dos Passos Gomes and A. Aspuru-Guzik, Matter, 2021, 4, 1654–1682.
10. G. Ricci, E. San-Fabián, Y. Olivier and J. C. Sancho-García, ChemPhysChem, 2021, 22, 553–560.
11. J. C. Sancho-García, E. Brémond, G. Ricci, A. J. Pérez-Jiménez, Y. Olivier and C. Adamo, J. Chem. Phys., 2022, 156, 034105.
12. S. Ghosh and K. Bhattacharyya, J. Phys. Chem. A, 2022, 126, 1378–1385.
13. J. Li, Z. Li, H. Liu, H. Gong, J. Zhang, X. Li, Y. Wang and Q. Guo, Dyes Pigm., 2022, 203, 110366.
14. L. Tučková, M. Straka, R. R. Valiev and D. Sundholm, Phys. Chem. Chem. Phys., 2022, 24, 18713–18721.
15. D. Blasco, R. T. Nasibullin, R. R. Valiev and D. Sundholm, Chem. Sci., 2023, 14, 3873–3880.
16. R. Su and Z. Huang, Adv. Theory Simul., 2023, 6, 2200863.
17. W. Leupin and J. Wirz, J. Am. Chem. Soc., 1980, 102, 6068–6075.
18. W. Leupin, D. Magde, G. Persy and J. Wirz, J. Am. Chem. Soc., 1986, 108, 17–22.
19. D. Hwang and C. W. Schlenker, Chem. Commun., 2021, 57, 9330–9353.
20. J. T. Blaskovits, M. H. Garner and C. Corminboeuf, Angew. Chem., Int. Ed., 2023, 62, e202218156.
21. S. Koseki, T. Nakajima and A. Toyota, Can. J. Chem., 1985, 63, 1572–1579.
22. A. Toyota and T. Nakajima, J. Chem. Soc., Perkin Trans. 2, 1986, 1731–1734.
23. A. Toyota, Theor. Chim. Acta, 1988, 74, 209–217.
24. M. E. Sandoval-Salinas, G. Ricci, A. J. Pérez-Jiménez, D. Casanova, Y. Olivier and J. C. Sancho-García, Phys. Chem. Chem. Phys., 2023 10.1039/D3CP02465B.
25. S. Yonedo, M. Shibata, S. Kida, Z.-i. Yoshida, Y. Kai, K. Miki and N. Kasai, Angew. Chem., Int. Ed. Engl., 1984, 23, 63–64.
26. M. Rosenberg, C. Dahlstrand, K. Kilså and H. Ottosson, Chem. Rev., 2014, 114, 5379–5425.
27. Y. Olivier, J.-C. Sancho-Garcia, L. Muccioli, G. D'Avino and D. Beljonne, J. Phys. Chem. Lett., 2018, 9, 6149–6163.
28. J. Wagner, P. Zimmermann Crocomo, M. A. Kochman, A. Kubas, P. Data and M. Lindner, Angew. Chem., Int. Ed., 2022, 61, e202202232.
29. P. de Silva, C. A. Kim, T. Zhu and T. Van Voorhis, Chem. Mater., 2019, 31, 6995–7006.
30. A. L. Sobolewski and W. Domcke, J. Phys. Chem. Lett., 2021, 12, 6852–6860.
31. F. Dinkelbach, M. Bracker, M. Kleinschmidt and C. M. Marian, J. Phys. Chem. A, 2021, 125, 10044–10051.
32. L. E. de Sousa and P. de Silva, J. Chem. Theory Comput., 2021, 17, 5816–5824.
33. G. Ricci, J.-C. Sancho-García and Y. Olivier, J. Mater. Chem. C, 2022, 10, 12680–12698.
34. A. T. Balaban and M. Randić, J. Chem. Inf. Comput. Sci., 2004, 44, 1701–1707.
35. M. J. Frisch, G. W. Trucks, H. B. Schlegel, G. E. Scuseria, M. A. Robb, J. R. Cheeseman, G. Scalmani, V. Barone, G. A. Petersson, H. Nakatsuji, X. Li, M. Caricato, A. V. Marenich, J. Bloino, B. G. Janesko, R. Gomperts, B. Mennucci, H. P. Hratchian, J. V. Ortiz, A. F. Izmaylov, J. L. Sonnenberg, D. Williams-Young, F. Ding, F. Lipparini, F. Egidi, J. Goings, B. Peng, A. Petrone, T. Henderson, D. Ranasinghe, V. G. Zakrzewski, J. Gao, N. Rega, G. Zheng, W. Liang, M. Hada, M. Ehara, K. Toyota, R. Fukuda, J. Hasegawa, M. Ishida, T. Nakajima, Y. Honda, O. Kitao, H. Nakai, T. Vreven, K. Throssell, J. A. Montgomery Jr, J. E. Peralta, F. Ogliaro, M. J. Bearpark, J. J. Heyd, E. N. Brothers, K. N. Kudin, V. N. Staroverov, T. A. Keith, R. Kobayashi, J. Normand, K. Raghavachari, A. P. Rendell, J. C. Burant, S. S. Iyengar, J. Tomasi, M. Cossi, J. M. Millam, M. Klene, C. Adamo, R. Cammi, J. W. Ochterski, R. L. Martin, K. Morokuma, O. Farkas, J. B. Foresman and D. J. Fox, Gaussian 16, Revision A.03, Gaussian Inc., Wallingford, CT, 2016.
36. G. M. J. Barca, C. Bertoni, L. Carrington, D. Datta, N. De Silva, J. E. Deustua, D. G. Fedorov, J. R. Gour, A. O. Gunina, E. Guidez, T. Harville, S. Irle, J. Ivanic, K. Kowalski, S. S. Leang, H. Li, W. Li, J. J. Lutz, I. Magoulas, J. Mato, V. Mironov, H. Nakata, B. Q. Pham, P. Piecuch, D. Poole, S. R. Pruitt, A. P. Rendell, L. B. Roskop, K. Ruedenberg, T. Sattasathuchana, M. W. Schmidt, J. Shen, L. Slipchenko, M. Sosonkina, V. Sundriyal, A. Tiwari, J. L. Galvez Vallejo, B. Westheimer, M. Wloch, P. Xu, F. Zahariev and M. S. Gordon, J. Chem. Phys., 2020, 152, 154102.
37. O. Christiansen, H. Koch and P. Jørgensen, Chem. Phys. Lett., 1995, 243, 409–418.
38. R. Ahlrichs, M. Bär, M. Häser, H. Horn and C. Kölmel, Chem. Phys. Lett., 1989, 162, 165–169.
39. TURBOMOLE V7.4 2019, a development of University of Karlsruhe and Forschungszentrum Karlsruhe GmbH, TURBOMOLE GmbH, 1989−2007, since 2007, available from http://www.turbomole.com.
40. J. F. Stanton and R. J. Bartlett, J. Chem. Phys., 1993, 98, 7029–7039.
41. E. Epifanovsky, A. T. Gilbert, X. Feng, J. Lee, Y. Mao, N. Mardirossian, P. Pokhilko, A. F. White, M. P. Coons and A. L. Dempwolff, et al. , J. Chem. Phys., 2021, 155, 084801.
42. T. H. Dunning, J. Chem. Phys., 1989, 90, 1007–1023.
43. S. Vosskötter, P. Konieczny, C. M. Marian and R. Weinkauf, Phys. Chem. Chem. Phys., 2015, 17, 23573–23581.
44. S. S. Shaik, P. C. Hiberty, J. M. Lefour and G. Ohanessian, J. Am. Chem. Soc., 1987, 109, 363–374.
45. S. Shaik, A. Shurki, D. Danovich and P. C. Hiberty, Chem. Rev., 2001, 101, 1501–1540.
46. G. Binsch and E. Heilbronner, Tetrahedron, 1968, 24, 1215–1223.
47. E. Heilbronner and Z.-Z. Yang, Angew. Chem., Int. Ed. Engl., 1987, 26, 360–362.
48. E. Heilbronner, J. Chem. Educ., 1989, 66, 471.
49. T. K. Zywietz, H. Jiao, P. v. R. Schleyer and A. de Meijere, J. Org. Chem., 1998, 63, 3417–3422.
50. S. Zilberg and Y. Haas, J. Phys. Chem. A, 1998, 102, 10851–10859.
51. K. Hafner, B. Stowasser, H.-P. Krimmer, S. Fischer, M. C. Böhm and H. J. Lindner, Angew. Chem., Int. Ed. Engl., 1986, 25, 630–632.
52. R. Gompper and H.-U. Wagner, Angew. Chem., Int. Ed. Engl., 1988, 27, 1437–1455.
53. F. Closs, R. Gompper, H. Nöth and H.-U. Wagner, Angew. Chem., Int. Ed. Engl., 1988, 27, 842–845.
54. Y. Tobe, Top. Curr. Chem., 2018, 376, 12.
55. J. D. Dunitz, C. Krüger, H. Irngartinger, E. F. Maverick, Y. Wang and M. Nixdorf, Angew. Chem., Int. Ed. Engl., 1988, 27, 387–389.
56. S. Kozuch, RSC Adv., 2014, 4, 21650–21656.
57. R. H. Hertwig, M. C. Holthausen, W. Koch and Z. B. Maksić, Angew. Chem., Int. Ed. Engl., 1994, 33, 1192–1194.
58. I. García Cuesta, S. Coriani, P. Lazzeretti and A. M. J. Sánchez De Merás, ChemPhysChem, 2006, 7, 240–244.
59. L. J. Karas, S. Jalife, R. V. Viesser, J. V. Soares, M. M. Haley and J. I. Wu, Angew. Chem., Int. Ed., 2023, e202307379.
60. M. Kataoka, T. Ohmae and T. Nakajima, J. Org. Chem., 1986, 51, 358–362.
61. T. Bally, S. Chai, M. Neuenschwander and Z. Zhu, J. Am. Chem. Soc., 1997, 119, 1869–1875.
62. V. Thery, C. Barra, A. Simeoni, J. Pecaut, E. Tomás-Mendivil and D. Martin, Org. Lett., 2023, 25, 560–564.
63. B. Kitschke and H. J. Lindner, Tetrahedron Lett., 1977, 18, 2511–2514.
64. A. Falchi, C. Gellini, P. R. Salvi and K. Hafner, J. Phys. Chem. A, 1998, 102, 5006–5012.
65. S. Tanaka, K. Satake, A. Kiyomine, T. Kumagai and T. Mukai, Angew. Chem., Int. Ed. Engl., 1988, 27, 1061–1062.
66. F. Closs, R. Gompper, H. Nöth and H.-U. Wagner, Angew. Chem., Int. Ed. Engl., 1988, 27, 842–845.
67. M. Eckert-Maksić, R. Gleiter, K. Hafner and H. Kläs, Chem. Ber., 1988, 121, 1219–1223.
68. Ö. H. Omar, X. Xie, A. Troisi and D. Padula, J. Am. Chem. Soc., 2023 DOI:10.1021/jacs.3c05452.
69. R. Klann, R. J. Bäuerle, F. Laermer, T. Elsaesser, M. Niemeyer and W. Lüttke, Chem. Phys. Lett., 1990, 169, 172–178.
70. C. Gellini, P. R. Salvi and K. Hafner, J. Phys. Chem., 1993, 97, 8152–8157.
71. C. Gellini, L. Angeloni, P. R. Salvi and G. Marconi, J. Phys. Chem., 1995, 99, 85–93.
72. S.-J. Jhang, J. Pandidurai, C.-P. Chu, H. Miyoshi, Y. Takahara, M. Miki, H. Sotome, H. Miyasaka, S. Chatterjee, R. Ozawa, Y. Ie, I. Hisaki, C.-L. Tsai, Y.-J. Cheng and Y. Tobe, J. Am. Chem. Soc., 2023, 145, 4716–4729.
73. K. Hafner, Pure Appl. Chem., 1982, 54, 939–956.
74. T. S. Balaban, S. Schardt, K. Hafner and V. Sturm, Angew. Chem., Int. Ed. Engl., 1995, 34, 330–332.
75. S. Schardt and K. Hafner, Tetrahedron Lett., 1996, 37, 3829–3832.
76. D. Welideniya, M. R. K. Ramachandran, T. Kalisch and R. Streubel, Dalton Trans., 2021, 50, 9345–9366.
77. K. Hanida, J. Kim, N. Fukui, Y. Tsutsui, S. Seki, D. Kim and H. Shinokubo, Angew. Chem., Int. Ed., 2021, 60, 20765–20770.
78. T. Xu, Y. Han, Z. Shen, X. Hou, Q. Jiang, W. Zeng, P. W. Ng and C. Chi, J. Am. Chem. Soc., 2021, 143, 20562–20568.
79. T. J. Katz and W. Slusarek, J. Am. Chem. Soc., 1979, 101, 4259–4267.
80. M. Beer and H. C. Longuet-Higgins, J. Chem. Phys., 1955, 23, 1390–1391.
81. P. Geldof, R. Rettschnick and G. Hoytink, Chem. Phys. Lett., 1969, 4, 59–61.
82. T. Itoh, Chem. Rev., 2012, 112, 4541–4568.
83. J. Wang, F. G. Gámez, J. Marín-Beloqui, A. Diaz-Andres, X. Miao, D. Casanova, J. Casado and J. Liu, Angew. Chem., Int. Ed., 2023, 62, e202217124.
84. Y. Shoji, Y. Ikabata, I. Ryzhii, R. Ayub, O. El Bakouri, T. Sato, Q. Wang, T. Miura, B. S. B. Karunathilaka, Y. Tsuchiya, C. Adachi, H. Ottosson, H. Nakai, T. Ikoma and T. Fukushima, Angew. Chem., Int. Ed., 2021, 60, 21817–21823.
85. Y. Tobe, Chem. Rec., 2015, 15, 86–96.
86. A. Konishi and M. Yasuda, Chem. Lett., 2021, 50, 195–212.
87. Y. Fei and J. Liu, Adv. Sci., 2022, 9, 2201000.
88. P. Mathey, F. Lirette, I. Fernández, L. Renn, R. T. Weitz and J.-F. Morin, Angew. Chem., Int. Ed., 2023, 62, e202216281.
89. A. Diaz-Andres, J. Marín-Beloqui, J. Wang, J. Liu, J. Casado and D. Casanova, Chem. Sci., 2023, 14, 6420–6429.
90. A. Konishi, K. Horii and M. Yasuda, J. Phys. Org. Chem., 2023, 36, e4495.
91. S. E. Wheeler, K. N. Houk, P. v. R. Schleyer and W. D. Allen, J. Am. Chem. Soc., 2009, 131, 2547–2560.

---

Footnotes

† Electronic supplementary information (ESI) available: Additional figures and data tables. See DOI: https://doi.org/10.1039/d3sc03409g

‡ These authors contributed equally to this work.

---