Open Access Article
Open Access ArticleQMrebind: incorporating quantum mechanical force field reparameterization at the ligand binding site for improved drug-target kinetics through milestoning simulations†
Anupam Anand
Ojha
 a,
Lane William
Votapka
a,
Lane William
Votapka
 a and
Rommie Elizabeth
Amaro
a and
Rommie Elizabeth
Amaro
 *b
*b
aDepartment of Chemistry and Biochemistry, University of California San Diego, La Jolla, California 92093, USA
bDepartment of Molecular Biology, University of California San Diego, La Jolla, California 92093, USA. E-mail: ramaro@ucsd.edu
First published on 24th October 2023
Abstract
Understanding the interaction of ligands with biomolecules is an integral component of drug discovery and development. Challenges for computing thermodynamic and kinetic quantities for pharmaceutically relevant receptor–ligand complexes include the size and flexibility of the ligands, large-scale conformational rearrangements of the receptor, accurate force field parameters, simulation efficiency, and sufficient sampling associated with rare events. Our recently developed multiscale milestoning simulation approach, SEEKR2 (Simulation Enabled Estimation of Kinetic Rates v.2), has demonstrated success in predicting unbinding (koff) kinetics by employing molecular dynamics (MD) simulations in regions closer to the binding site. The MD region is further subdivided into smaller Voronoi tessellations to improve the simulation efficiency and parallelization. To date, all MD simulations are run using general molecular mechanics (MM) force fields. The accuracy of calculations can be further improved by incorporating quantum mechanical (QM) methods into generating system-specific force fields through reparameterizing ligand partial charges in the bound state. The force field reparameterization process modifies the potential energy landscape of the bimolecular complex, enabling a more accurate representation of the intermolecular interactions and polarization effects at the bound state. We present QMrebind (Quantum Mechanical force field reparameterization at the receptor–ligand binding site), an ORCA-based software that facilitates reparameterizing the potential energy function within the phase space representing the bound state in a receptor–ligand complex. With SEEKR2 koff estimates and experimentally determined kinetic rates, we compare and interpret the receptor–ligand unbinding kinetics obtained using the newly reparameterized force fields for model host–guest systems and HSP90-inhibitor complexes. This method provides an opportunity to achieve higher accuracy in predicting receptor–ligand koff rate constants.
1 Introduction
Receptor–ligand binding and unbinding is a crucial mechanism that governs a range of biological processes, including cellular signaling, enzymatic catalysis, and immunological responses.1–3 The interaction between the ligand and receptor enables cells to respond to environmental cues, transmit signals, and carry out essential physiological functions.4–6 A comprehensive understanding of the kinetic and thermodynamic properties of receptor–ligand interactions is essential for designing and optimizing therapeutic agents acting upon specific protein targets.7–11 Ligands with a higher residence time (or slow dissociation rates) tend to remain in the binding pocket of the receptor for an extended period, leading to prolonged pharmacological effects. On the other hand, ligands with a lower residence time (or fast dissociation rates) are less likely to produce pharmacological effects.12–17 Similarly, the thermodynamic parameters for receptor–ligand interaction, such as affinity, provide insights into the specificity and stability of receptor–ligand binding and unbinding.18–21 A complex interplay of kinetic and thermodynamic factors of receptor–ligand (un)binding determines the duration and strength of interaction between the two entities. Leveraging these factors could aid the development of novel therapeutics, leading to efficient drug discovery and development processes.With recent advancements in computing power and hardware, molecular dynamics (MD) simulations have emerged as a powerful tool for studying the kinetics and thermodynamics of molecular interactions.22,23 Despite such progress, MD simulations have limitations when studying complex biological processes, such as protein folding and unfolding,24–26 large protein conformational rearrangements,27,28 and receptor–ligand binding and unbinding due to the relatively long timescales needed to observe such events.29–31 These phenomena may occur on a timescale of milliseconds or longer, and it becomes increasingly difficult for MD simulations to rigorously characterize such events. Enhanced MD simulations accelerate the conformational search of the system, thereby allowing rare events to be observed within a reasonable computational time.32–34 Enhanced MD simulations can be roughly categorized into collective variable (CV) free and CV-based approaches. CV-based approaches include metadynamics,35–37 Markov state models (MSMs),38–40 variationally enhanced sampling,41–43 weighted ensemble,44–47 and umbrella sampling,48–50 while CV-free approaches include accelerated molecular dynamics (aMD),51–53 Gaussian accelerated molecular dynamics (GaMD),54–56 replica exchange molecular dynamics (REMD),57–59 and selective integrated tempering.60,61
Path sampling methods represent a class of enhanced sampling approaches that enable comprehensive exploration of the kinetic properties in biological systems, encompassing phenomena such as receptor–ligand binding and unbinding, protein folding and unfolding, and substantial conformational changes in complex biological systems. The Markovian milestoning with Voronoi tessellations (MMVT) approach in MD simulations partitions the phase space of the receptor–ligand complex into distinct regions called “Voronoi cells”.62–64 Independent and parallel MD simulations are carried out within each Voronoi cell, with the ligand incrementally displaced from the bound state. This approach is implemented in the computational software toolkit, Simulation Enabled Estimation of Kinetic Rates v.2 (SEEKR2),65–69 which is further discussed in Section 2.2. Estimation of drug-target residence times of pharmaceutically relevant biomolecular complexes remains difficult for MD-based approaches. However, SEEKR2 has recently succeeded in estimating close-to-experiment residence times for JAK2/STAT5 axis inhibitors with extended residence times (hours or longer) within the target.69,70
Enhanced MD simulations can be robust methods for investigating complex molecular systems. However, significant challenges are often encountered while predicting the kinetics and thermodynamics of receptor–ligand (un)binding. One such challenge is accurately representing non-covalent interactions at the binding site. While general force fields describe the potential energy landscape across a broad range of biomolecular configurations, incorporating quantum mechanics (QM) to tune the force field parameters can precisely describe non-covalent interactions at the binding site for the conformations examined with QM. Our approach focuses on reparameterizing the potential energy landscape of the receptor–ligand complex within the bound state conformation.
Despite the effectiveness of classical force fields in successfully replicating equilibrium properties and binding affinities, MD simulations face challenges in accurately predicting kinetic parameters.71,72 Recent investigations have extensively explored this issue, revealing noteworthy disparities between simulation results and experimental data and underscoring the growing realization that classical force fields might need to better capture the complexity of dynamics at transition states.73,74 Consequently, two promising avenues for improvement have surfaced. The first involves adopting polarizable force fields, a paradigm shift from traditional fixed-charge models.75–77 Secondly, quantum mechanics/molecular mechanics (QM/MM) simulations show promise to enhance rate prediction accuracy.77,78 In QM/MM simulations, specific regions (such as the ligand and binding site) are treated at the quantum mechanical level, allowing for precisely describing electronic properties during molecular events. These simulations have demonstrated their potential in modeling the complex kinetics of binding and unbinding processes.79–82 Furthermore, ongoing research efforts aim to refine parametrization strategies for classical force fields, integrating kinetic information and addressing polarization issues within fixed-charge schemes.83–85
In this study, we aim to recalibrate the charges of the ligand within the vicinity of its neighboring residues in the binding site, thereby facilitating an accurate representation of interactions between the drug and the target. Subsequently, the QM-enhanced force field parameters are employed in the SEEKR2 simulations to determine the unbinding kinetics of receptor–ligand complexes.
2 Methods
2.1 Quantum mechanical force field reparameterization at the receptor–ligand binding site (QMrebind)
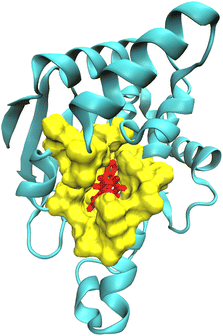
For computing kinetic and thermodynamic properties for receptor–ligand complexes, we have employed different theoretical frameworks to model certain regions of the biomolecular complex under study. Specifically, we applied a higher level of theory (i.e., high-level QM and low-level QM2) to model the active site of the complex and obtain optimized point charges of the ligand, while utilizing classical mechanics to model the remaining protein (Fig. 1). This multiscale approach allows for a more precise and efficient representation of the molecular system within the bound state, which may improve accuracy when modeling the binding and unbinding process. ORCA, a versatile quantum chemistry package that offers a wide range of electronic structure methods, enables the application of different theoretical frameworks for different regions of a molecular system.86–88 In its latest release, i.e., ORCA 5.0, new features include the three-layered (QM-QM2-MM) ONIOM method with electrostatic and mechanical embedding, covalent bond boundary definitions between the QM and QM2 regions, and automated detection of system topologies with link atoms.89–91 QMrebind integrates the ORCA QM engine for reparameterizing force field parameters for receptor–ligand complexes.The QMrebind method involves several steps to calculate the charges of the ligand at its binding site (see QMrebind protocol). Initially, a protein data bank (PDB) file of the receptor–ligand complex and its topology file are provided as inputs to the QMrebind software. The user defines a distance cut-off value, which delineates a region of receptor atoms encompassing the ligand within the cut-off distance, typically including only the residues in the binding site. Once the binding site is identified, the ligand is defined as the high-level QM region of the ONIOM method. Residues surrounding the ligand, containing any atom within the cut-off distance, are classified as the low-level QM2 region of the ONIOM method (Fig. 1). All the remaining residues of the receptor comprise the MM region. For the QM region, electronic structure methods such as the Hartree–Fock (HF), density functional theory (DFT), second-order Møller–Plesset perturbation (MP2), and coupled-cluster (CC) theories may be employed.92–94 A semi-empirical tight-binding method, GFN-XTB or GFN2-XTB, is employed in the QM2 region.95,96 The GFN2-XTB method accelerates the calculations of noncovalent interaction energies for complex molecular systems by accounting for anisotropic second-order density fluctuation effects.97,98
QMrebind protocol(1) Initialization• A structure (PDB) and topology file for the receptor–ligand complex with the ligand at its binding site is provided as an input. • The receptor-ligand complex is locally minimized (if not already minimized). • A user-defined distance cut-off value is defined to identify the receptor region (low-level QM2) surrounding the ligand (high-level QM). (2) Define QM, QM2, and MM regions within the multiscale ONIOM method • The ligand at the binding site is defined as the high-level QM region within the three-layered multiscale ONIOM method. • Residues surrounding the ligand containing any atoms within the cut-off distance are defined as low-level QM2 region within the ONIOM method. • All protein residues except those within the QM2 region are defined as the MM region. (3) Assign theories and methods to QM–QM2–MM regions • An appropriate electronic structure method (HF, DFT, MP2, etc.) and corresponding basis set for the high-level QM region are assigned to describe the quantum behavior of the system. • A semi-empirical tight-binding method (GFN-XTB/GFN2-XTB) is assigned for the QM2 region. • The MM region is treated with the generic force field provided in the original topology file. (4) Define QM–QM2 and (QM–QM2)–MM interactions • An additive scheme is employed to model (QM–QM2)–MM interactions, treating these regions as independent entities. • A subtractive scheme is employed to model QM–QM2 interaction, subtracting the contribution of the QM2 region from the total QM–QM2 interaction. • Electrostatic embedding is employed for QM–QM2 interactions, wherein the high-level QM region interacts with the atomic point charges of the low-level QM2 region. (5) Employ QM–QM2–MM calculations and charge-fitting schemes • QMrebind interfaces with ORCA to execute QM–QM2–MM calculations. • A self-consistent field (SCF) electronic structure calculation is performed for the QM–QM2–MM system. • Geometry-basis wavefunction (GBW) and the SCF electron density files are saved post-SCF convergence. • Charge-fitting methods are employed (CHELPG in this study, although Hirshfeld, Löwdin, etc. are available in QMrebind) that utilize the electron density distribution information to calculate charges for the ligand. (6) Integration of newly obtained ligand charges into a copy of the original parameter/topology file • Partial charges of the ligand are replaced in a copy of the original topology file with the newly obtained QM charges. • Tests are conducted using the OpenMM engine to validate the correctness of the reparameterized topology file. • After successful validation, the reparameterized receptor–ligand topology file can be used in SEEKR2 milestoning simulations. |
Two schemes are employed, i.e., subtractive and additive,90,99 to account for interactions between the QM, QM2, and MM regions. Let the three regions in the receptor–ligand complex be defined as the high-level QM region (H), the low-level QM region (M), and the MM region (L). The QM and QM2 regions employ a subtractive scheme, where the QM–QM2 interaction is calculated by subtracting the contribution of the QM2 region from the total QM–QM2 interaction to ensure the accuracy of the calculations. In a subtractive scheme, three separate energy calculations are performed, i.e., QM calculation for the high layer, (EQMH), QM2 calculation for the high and medium layer (EQM2HM), and a QM2 calculation for the high layer (EQM2H). The total energy for the subtractive scheme, EsubQM–QM2, is given by:
| EsubQM–QM2 = EQMH + EQM2HM − EQM2H | (1) |
An additive scheme models the (QM–QM2)–MM interaction. This scheme assumes the QM–QM2 and MM regions to be independent, and simple pairwise potentials describe their interactions. In an additive scheme, two energy calculations are performed, i.e., a subtractive QM–QM2 calculation for the QM–QM2 region (EsubQM–QM2) and a MM calculation, EMML–HM. The total energy for the additive scheme, Eadd(QM–QM2)–MM, is given by:
| Eadd(QM–QM2)–MM = EsubQM–QM2 + EMML–HM | (2) |
E MML–HM is defined as the sum of MM energy of the MM region (EMML) and the (QM–QM2)–MM interface energy (E(QM–QM2)–MML–HM) and is given by:
| EMML–HM = EMML + E(QM–QM2)–MML–HM | (3) |
Upon substituting the value of EsubQM–QM2 and EMML–HM in eqn (2), we get:
| Eadd(QM–QM2)–MM = EQMH + EQM2HM − EQM2H + EMML + E(QM–QM2)–MML–HM | (4) |
In subtractive QM–QM2 calculations, a high-level QM region interacts with a low-level QM2 region treated with the GFN-XTB/GFN2-XTB method. Since the QM2 method, i.e., GFN-XTB/GFN2-XTB, an extended semiempirical tight-binding model, is polarizable, the interaction with the high-level QM region is more accurate.100 The GFN-XTB method accounts for anisotropic second-order density fluctuation effects, allowing the QM2 region to adjust its electron density dynamically in response to external perturbations (electron distribution) in the QM region,95,101 allowing for a more realistic description of charge redistribution and electronic polarization during interactions between the high-level QM and low-level QM2 regions. Consequently, subtractive QM–QM2 methods, compared to additive methods, improve accuracy in energy calculations, geometry optimization, and interaction energies by accurately treating electron density differences.
By default, unless specified, ONIOM calculations in the ORCA engine employ the electrostatic embedding scheme, where the high-level QM region interacts with the atomic point charges of the low-level QM2 region. In the electrostatic embedding scheme, partial charges of QM2 atoms are incorporated directly into the Hamiltonian of the QM region, i.e., electrostatic interactions between the QM and QM2 regions are explicitly considered at the QM level. These point charges are determined based on a full system low-level (QM2) calculation, ensuring that they accurately represent the charge distribution of the QM2 atoms.
Different charge schemes implemented into the ORCA QM engine are available to calculate the charges of the ligand at the binding site, including the CHELPG (CHarge-Extra Loop and Gaussian Potentials), Hirshfeld, Löwdin, and Mulliken population analysis. The CHELPG algorithm was used exclusively in this study and involves fitting atomic charges to reproduce the molecular electrostatic potential at a set of grid points surrounding the molecule,102 subject to the constraint that the sum of charges of all the atoms equals the overall charge of the molecule. Other charge analysis schemes, such as the Hirshfeld, Mulliken and Löwdin population analysis, can also be employed within the framework. The CHELPG method is chosen for reparameterizing ligand charges for the two sets of receptor–ligand complexes in the present study due to its reliability in reproducing molecular electrostatic potentials (ESP). However, as discussed previously, other charge schemes could also be employed for ligand charge parameterization at the binding site. A self-consistent field (SCF) electronic structure calculation is performed for the QM–QM2–MM system to find the electronic wave function that minimizes the electronic energy of the system, accounting for the interactions between the QM and MM regions. Once the SCF calculation converges, necessary output files, including the geometry-basis wavefunction (GBW) and the SCF electron density file, are saved. These files contain information about the molecular structure, electronic structure, and electron density distribution. The CHELPG scheme then calculates the ESP using the data from the GBW and electron density files. It performs a charge fitting procedure to assign atomic charges to each atom in the molecule to best reproduce the calculated ESP at a set of grid points surrounding the molecule. These charges represent the electron density distribution within the molecule based on the electrostatic potential.
As a part of the QMrebind protocol, solvent molecules are not included in the charge calculation at the MM level. Numerous charge derivation methodologies in MD simulations exclude water or other solvent molecules,84,103,104 ensuring that derived charges are indicative of the inherent electronic properties of the system without being influenced by a liquid-phase, transient, high dielectric medium in its surroundings. Moreover, introducing water molecules into a charge calculation involves consideration of numerous complexities, such as selecting the number of water molecules, their respective orientations, and relative positions, which may introduce accounting for several parameters at once. It should also be noted that such decisions are made on a case-by-case basis and could introduce unnecessary degrees of arbitrariness in reparameterization processes. QMrebind automates the process of interfacing with the QM–QM2–MM multiscale calculation functionality within the ORCA simulation engine. Upon completion of the calculation, newly obtained QM charges for the ligand replace the charges in the initial topology file. Finally, a preliminary MD simulation is run to ensure the correctness of the reparameterized topology file. At this point, the reparameterized system is ready to be simulated with SEEKR2.
2.2 Simulation enabled estimation of kinetic rates v.2 (SEEKR2)
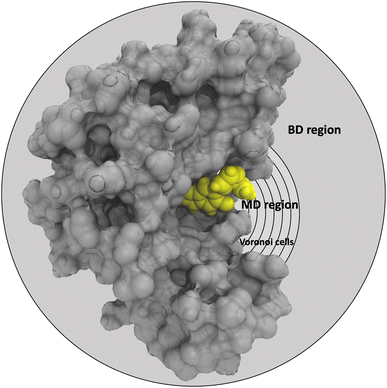
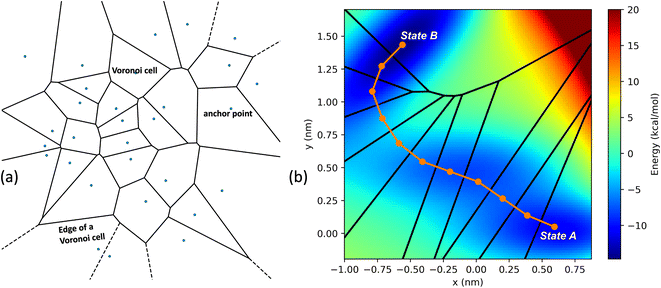
In the SEEKR2 algorithm, the phase space of the receptor–ligand complex is partitioned into two distinct regions based on the distance between the ligand and the binding site of the receptor, i.e., the MD region and the Brownian dynamics (BD) region (Fig. 2). SEEKR2 employs the OpenMM engine to run the MD simulations107,108 and the Browndye2 engine to run the BD simulations.109 The MD region is in close proximity to the binding site, where solvent effects and molecular flexibility predominantly mediate the receptor–ligand interactions. Consequently, fully atomistic MD simulations are required in this region to represent the molecular interactions accurately. A Voronoi tessellation approach partitions a given region into multiple smaller regions based on the proximity to a set of anchor points.110,111 In a Voronoi diagram, the boundaries of the cells corresponding to an anchor point are equidistant to adjacent anchor points, and the vicinity corresponding to the given anchor point is closer to that point than any other input point (Fig. 3a). Fig. 3b illustrates a Voronoi diagram for a simple Muller potential system transitioning between states A and B using a CV that follows a likely reaction pathway between states A and B. The CV is segmented into anchor points. Milestones are defined as surfaces that are equidistant between two adjacent anchor points. The spaces between milestones constitute the Voronoi cells. A Voronoi cell around a particular anchor point is the region in configuration space where every point within this cell is closer to that anchor point than any other. With the SEEKR approach on a biologically relevant receptor–ligand system, the MD region is partitioned into “Voronoi cells” based on the distance between the center of mass (COM) of the ligand and the COM of the alpha-carbon (α-C) atoms of the binding site residues of the receptor. Each Voronoi cell contains a copy of the system where the ligand is at varying distances from the binding site of the receptor, where independent MD simulations are carried out. To generate starting structures of the receptor–ligand complex in each Voronoi cell, steered molecular dynamics (SMD) simulations are propagated that facilitate the controlled movement of the ligand away from its binding site and into the solvent. This process involves gradually pulling the ligand out of the binding pocket with a moving harmonic restraint while maintaining the system in equilibrium and adding no significant stress. Each time the ligand crosses a milestone, a snapshot of the receptor–ligand complex is saved as a starting structure for that particular Voronoi cell for running SEEKR2 simulations. MD simulations with the Markovian milestoning scheme are then employed concurrently within individual Voronoi cells until convergence is reached.64,112 Reflective boundary conditions are implemented to confine the molecular trajectories within each cell. The mean free passage time (MFPT) is then calculated from the transition matrix, ![[Q with combining circumflex]](https://www.rsc.org/images/entities/b_char_0051_0302.gif) obtained from the MMVT-SEEKR2 simulations. Section 2.2.2 provides a comprehensive set of equations employed in the calculation of mean free passage time (MFPT) and the binding free energy profile (ΔGi) in the context of SEEKR2 simulations.
obtained from the MMVT-SEEKR2 simulations. Section 2.2.2 provides a comprehensive set of equations employed in the calculation of mean free passage time (MFPT) and the binding free energy profile (ΔGi) in the context of SEEKR2 simulations.
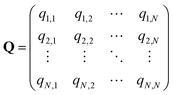 | (5) |
q ii and qij are the diagonal and off-diagonal elements, respectively, of the transition matrix, Q, Nij represents the number of transitions between the ith and jth milestone, and Ri is the time spent by a long-timescale trajectory having last touched the ith milestone, then qii and qij are represented by eqn (6) and (7) respectively.
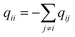 | (6) |
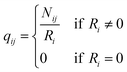 | (7) |
Let xα and vα be the position and velocity of an MMVT trajectory, at any time, t, in the Voronoi cell, Vα. The variables 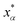 and
and 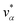 are the position and velocity of the trajectory at time, t + Δt, as predicted by the simulation time integrator algorithm (typically, the Langevin integrator). Reflective boundary conditions are employed to keep the trajectories within each Voronoi cell, as represented by eqn (8) and (9), respectively.
are the position and velocity of the trajectory at time, t + Δt, as predicted by the simulation time integrator algorithm (typically, the Langevin integrator). Reflective boundary conditions are employed to keep the trajectories within each Voronoi cell, as represented by eqn (8) and (9), respectively.
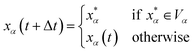 | (8) |
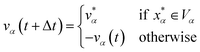 | (9) |
Let πα be the probability of an ensemble of unconstrained long-timescale trajectories being in a particular Voronoi cell when the system has reached equilibrium. For Voronoi cell Vα, let Tα be the total simulation time in that cell. A normalizing factor, T, is given by eqn (10).
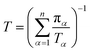 | (10) |
Let Nijα be the number of collisions during the MMVT trajectories with the ith milestone having last touched the jth milestone in Vα, then the total number of transitions between the ith and jth milestones, Nij is given by eqn (11).
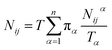 | (11) |
Let Riα be the simulation time in Voronoi cell Vα, having last touched the ith milestone. The time spent by the trajectory having last touched the ith milestone, Ri is given by eqn (12).
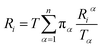 | (12) |
Let Nα,β be the number of MMVT trajectory collisions in Voronoi cell Vα against its boundary with Voronoi cell Vβ, and Nβ,α be the number of collisions in Voronoi cell Vβ against its boundary with Voronoi cell Vα. The equations to compute πα are to be found in eqn (13) and (14).
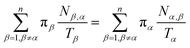 | (13) |
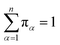 | (14) |
Let ![[Q with combining circumflex]](https://www.rsc.org/images/entities/b_char_0051_0302.gif) be the N-1 by N-1 matrix obtained from the upper left corner of Q, and 1 is a vector of ones, the mean free passage times from all states, TN is obtained by solving eqn (15).
be the N-1 by N-1 matrix obtained from the upper left corner of Q, and 1 is a vector of ones, the mean free passage times from all states, TN is obtained by solving eqn (15).
![[Q with combining circumflex]](https://www.rsc.org/images/entities/b_char_0051_0302.gif) TN = −1 TN = −1 | (15) |
Stationary probabilities of the milestones, p are obtained from solving eqn (16).
| Qp = p | (16) |
Let R be the gas constant, T be the temperature, pi and pref be the stationary probabilities of the ith and (arbitrary) reference milestone, respectively. The free energy profile of the ith milestone, ΔGi is given by eqn (17).
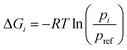 | (17) |
2.3 Applications to receptor–ligand complexes
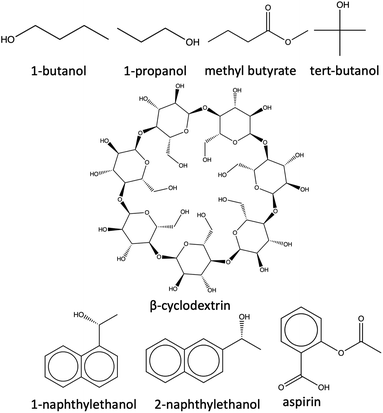
2.3.1.1 System preparation and simulation. The host molecule is initially parameterized using the q4md-CD force field,114 while the guest ligands are parameterized using the general Amber force field (GAFF).115 q4md-CD force field has been designed to accurately represent the geometrical, structural, dynamical, and hydrogen bonding aspects of heterogeneous cyclodextrin-based systems.114 q4md-CD force field incorporates geometrical parameters from the Amber99SB force field to describe protein residues and GLYCAM04 for carbohydrate and organic components (if available). Partial atomic charges are derived using the R.E.D. tools,116 while scaling factors of 1.2 and 2.0 are imposed for the 1–4 electrostatic and 1–4 van der Waals interactions, respectively. The q4md-CD force field has demonstrated better agreement with experimental findings compared to GAFF for cyclodextrin molecules.117,118
Subsequently, the complexes are solvated with the TIP3P water model and subjected to a non-bonded cut-off distance of 9 Å, and long-range electrostatic interactions were treated with the particle mesh Ewald (PME) method.119,120 The relatively smaller size of the host–guest complexes necessitates the division into two regions. We treated the ligand molecules quantum mechanically using the Becke-3-parameter-Lee–Yang–Parr (B3LYP) functional,121 and correlation consistent polarized valence triple zeta (cc-pVTZ)122 basis set in the QM region. The host molecule is assigned the QM2 region where the semi-empirical tight-binding method (GFN2-XTB) is employed. For each of the host–guest complexes, 14 CV-based milestones are defined as concentric spheres and are located at distances of 1.0, 2.0, 3.0, 4.0, 5.0, 6.0, 7.0, 7.0, 8.0, 9.0, 10.0, 11.0, 12.0, 13.0, and 14.0 Å respectively from the center of mass (COM) of the host. Starting structures for the SEEKR2 simulations are obtained using the steered molecular dynamics (SMD) simulations, where a moving harmonic restraint of 50![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 000 kJ mol−1 nm−2 is applied over the course of 50 ns. Identical CV definitions and milestone spacings have been implemented in the current study as in the previous SEEKR2 implementation,67 facilitating a comparison between the two methodologies.
000 kJ mol−1 nm−2 is applied over the course of 50 ns. Identical CV definitions and milestone spacings have been implemented in the current study as in the previous SEEKR2 implementation,67 facilitating a comparison between the two methodologies.
SEEKR2 simulations with the QMrebind-reparameterized force field parameters are run with same milestone spacings for all the complexes. A total of 50 ns of MD simulations are run within each Voronoi cell, totaling a simulation time of 700 ns for 14 Voronoi cells. To obtain statistically meaningful results and assess the reproducibility and robustness of the simulations, three replicas of SEEKR2 simulations are performed for each complex, totaling a simulation time of 2.1 μs. Experimental values for the unbinding rates for the seven host–guest complexes, along with the koff rates estimated by the SEEKR2 framework, with the QMrebind-reparameterized and generic force field parameters, are provided in ESI Table S1.†
N-Hsp90-inhibitor complexes pose challenges for MD simulations in a variety of ways. The binding and unbinding mechanism of N-Hsp90-inhibitor complexes is complicated and dynamic, involving multiple conformational states and high flexibility of the ATP binding site.133–135 These conformational changes may occur on timescales beyond the reach of current MD simulations, making it challenging to capture the entire binding/unbinding process accurately. Moreover, such (un)binding events typically involve long timescales, and MD simulations must be run for extended periods, often on the order of microseconds or milliseconds.30,136,137 Additionally, modeling the interactions between inhibitors and the binding site requires considering various factors, such as polarization at the bound state, complex receptor–ligand binding dynamics, choice of appropriate CVs, and initial starting states. To address such challenges, dividing the conformational space of the receptor–ligand complex into a series of discrete milestones implemented in SEEKR2 and an accurate representation of the non-covalent inhibitor–receptor interactions at the binding site through the QMrebind scheme allows for accurate and efficient sampling of rare events and a greater exploration the conformational space of the receptor–ligand complex.
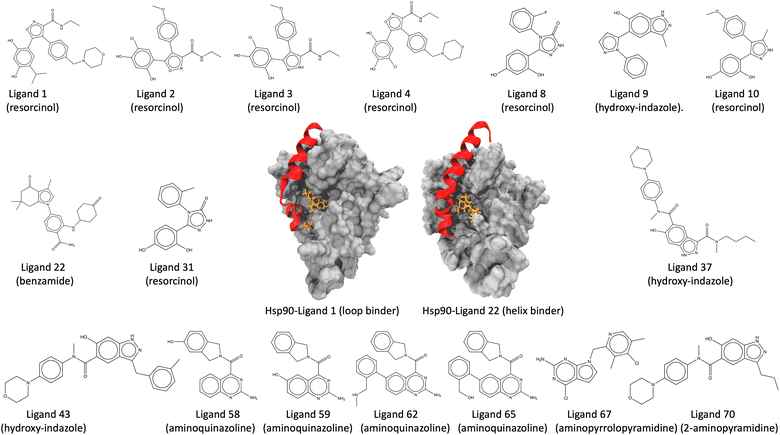
τ-Random acceleration molecular dynamics (τRAMD) is an enhanced sampling computational approach for exploring relevant biomolecular pathways and ranking drug candidates by estimated mean first passage times (MFPT).138 Recently, τRAMD has been used to observe the ligand unbinding pathway for a series of 70 N-Hsp90 inhibitors and ranked them according to their relative residence times. N-Hsp90 protein has been shown to acquire different conformations, namely the loop and the helix conformations.139 In the loop conformation, inhibitors bind solely to the ATP binding site, while in the helix conformation, inhibitors additionally occupy a hydrophobic transient subpocket situated between α-helix3 and the beta-strands, thereby stabilizing the α-helix3 domain (Fig. 5). This study chooses a subset of 17 inhibitors representing significant diversity in molecular scaffold among 70 inhibitors (Table 1). These inhibitors possess varying residence times within the protein, bind to either the loop or the helix conformation of the protein, and are classified into different groups, including resorcinol, hydroxy-indazole, benzamide, aminoquinazoline, aminopyrrolopyrimidine, and 2-aminopyramidine, based on their structural diversity, scaffold, and chemical motifs (Fig. 5). Absolute unbinding kinetics (koff) for eight of the 17 are calculated using the original force field parameters input directly into SEEKR2 and the QMrebind + SEEKR2 approach and are compared against the experimental values. PDB and topology files for the Hsp90-inhibitor complexes are obtained from the original study.138 In the same study, ligands were parameterized using the Antechamber program, and electrostatic potentials derived from ab initio calculations were employed to fit the restrained electrostatic potential (RESP) atomic partial charges140–142 at the HF level with a 6-31G*(1d) basis set. While the general Amber force field (GAFF) was applied to the ligands for all non-charge parameters, the protein was parameterized with the Amber14 force field.115,143
| Hsp90-inhibitor complex | Inhibitor group | Binding conformation |
|---|---|---|
| Hsp90-ligand 1 | Resorcinol | Loop |
| Hsp90-ligand 2 | Resorcinol | Loop |
| Hsp90-ligand 3 | Resorcinol | Loop |
| Hsp90-ligand 4 | Resorcinol | Loop |
| Hsp90-ligand 8 | Resorcinol | Loop |
| Hsp90-ligand 9 | Hydroxy-indazole | Loop |
| Hsp90-ligand 10 | Resorcinol | Helix |
| Hsp90-ligand 22 | Benzamide | Helix |
| Hsp90-ligand 31 | Resorcinol | Helix |
| Hsp90-ligand 37 | Hydroxy-indazole | Helix |
| Hsp90-ligand 43 | Hydroxy-indazole | Helix |
| Hsp90-ligand 58 | Aminoquinazoline | Helix |
| Hsp90-ligand 59 | Aminoquinazoline | Helix |
| Hsp90-ligand 62 | Aminoquinazoline | Helix |
| Hsp90-ligand 65 | Aminoquinazoline | Helix |
| Hsp90-ligand 67 | Aminopyrralopyrimidine | Helix |
| Hsp90-ligand 70 | 2-Aminopyramidine | Helix |
2.3.2.1 System preparation and simulation. PDB and topology files for the Hsp90-ligand complexes are obtained from the original study.138 Before initiating the QMrebind reparameterization process, structure files are subjected to energy minimization (using only MM) to ensure the stability and optimal conformation of the receptor–ligand complexes. In the reparameterization process, the Hsp90-inhibitor complexes are partitioned into three regions, the high-level QM region, the low-level QM2 region, and the MM region. The inhibitors comprise the QM region, where second-order Møller–Plesset perturbation (MP2) theory is implemented with the cc-pVTZ basis set. The binding site residues having any atoms within a cut-off distance of 5 Å comprise the QM2 region, where the semi-empirical tight-binding method, GFN2-XTB, is employed (refer to ESI Table S2† for an exhaustive list of binding site residues for Hsp90-inhibitor complexes). The rest of the protein comprises the MM region. CVs are defined based on the distance between the COM of the inhibitor and the α-carbon atoms of the residues at the binding site. For each of the Hsp90-inhibitor complexes, 20 CV-based milestones are defined as concentric spheres and are located at distances of 1.00, 1.50, 2.125, 2.875, 3.625, 4.375, 5.125, 5.875, 6.625, 7.375, 8.125, 8.875, 9.625, 10.50, 11.50, 12.50, 13.50, 14.50, 15.50, and 16.50 Å respectively from the COM of the α-C atoms of the binding site residues of the receptor. Starting structures for SEEKR2 simulations are obtained using the SMD simulations, where a moving harmonic restraint of 30
![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 000 kJ mol−1 nm−2 is applied over the course of 100 ns. A single set of SEEKR2 simulations with the reparameterized and generic force field parameters are run with the same milestone spacings for all the complexes. A total of 400 ns of MD simulations are run within each Voronoi cell, totaling a simulation time of 8 μs for 20 Voronoi cells. For a subset of eight of the Hsp90 inhibitors, the performance of QMrebind + SEEKR2 simulations is evaluated by comparing it with SEEKR2 simulations with generic force fields with the same simulation time, milestone spacings, and collective variable definitions for each of the Hsp90-inhibitor complexes.
000 kJ mol−1 nm−2 is applied over the course of 100 ns. A single set of SEEKR2 simulations with the reparameterized and generic force field parameters are run with the same milestone spacings for all the complexes. A total of 400 ns of MD simulations are run within each Voronoi cell, totaling a simulation time of 8 μs for 20 Voronoi cells. For a subset of eight of the Hsp90 inhibitors, the performance of QMrebind + SEEKR2 simulations is evaluated by comparing it with SEEKR2 simulations with generic force fields with the same simulation time, milestone spacings, and collective variable definitions for each of the Hsp90-inhibitor complexes.
3 Results and discussion
3.1 Host–guest complexes
The SEEKR2 and QMrebind + SEEKR2 methods reproduce the rank ordering for receptor–ligand unbinding rates for the seven host–guest complexes (Fig. 6). However, improved accuracies in estimating koff rates for the host–guest complexes are achieved with the QMrebind + SEEKR2 approach. SEEKR2 simulations with the generic force field tend to slightly overestimate the koff values for all host–guest complexes, while QMrebind helps to correct this overestimation, resulting in koff rates that are in closer agreement with experimental measurements (Fig. 6). Additionally, comparable convergences of koff rates for QMrebind + SEEKR2 simulations with reparameterized force fields and SEEKR2 simulations employing generic force fields are observed (ESI Fig. S1†). For all the seven host–guest complexes, QMrebind + SEEKR2 consistently outperformed SEEKR2 in estimating koff rates. Such improvements can likely be attributed to more accurate force field parameters for the ligand within the vicinity of the host molecule, as computed by the QMrebind software. There is a peculiar systematic error where the SEEKR2 and QMrebind + SEEKR2 approaches overestimate the experimental koff values for the host–guest systems. Similar overestimations have also been observed using weighted ensemble sampling144 and the Ligand Gaussian accelerated Molecular Dynamics (LiGaMD) method.145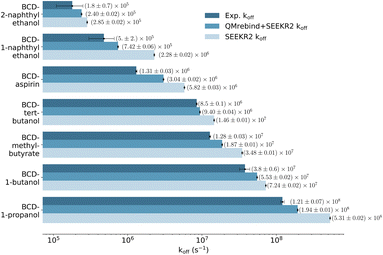 | ||
| Fig. 6 Unbinding rates or koff (s−1) for seven host–guest complexes obtained from experiments, QMrebind-reparameterized force field and the generic force field parameters employed in SEEKR2 simulations. Experimental koff rates for β-cyclodextrin complexed with naphthylethanols were measured using laser flash photolysis.146 For the other host–guest complexes, the ultrasonic absorption method was employed.147,148 The horizontal axis is represented in a logarithmic scale, allowing for better visualization of koff rates that span several orders of magnitude. | ||
3.2 Hsp90-inhibitor complexes
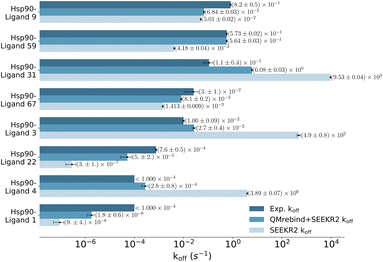
Unbinding rate estimates for the eight Hsp90-inhibitor complexes were substantially improved by the use of QMrebind, so that, while they do not match within experimental or theoretical error margins, they often fall within the single order of magnitude criteria for success67 and in almost all cases, at least within two orders of magnitude. While the QMrebind + SEEKR2 method has shown koff prediction accuracy for most of the Hsp90-inhibitor complexes, certain outliers underscore inherent challenges and limitations of this method. For the Hsp90-ligand 37 complex, the estimated koff of (3.82 ± 0.05) × 102 s−1 is significantly higher than the experimentally determined koff of (2.0 ± 0.2) × 10−3 s−1, and is essentially predicted by QMrebind + SEEKR2 to be a fast unbinder. We choose to define an outlier as any complex whose predicted koff is greater than two orders of magnitude distant from the experimental koff. For the outlier complex of ligand 37, reparameterizing partial charges of the ligand via QMrebind did not produce close-to-experiment koff. The inaccurate koff estimate for the Hsp90-ligand 37 complex can likely be attributed to other deficiencies within the model. In our assessment, it is possible that starting structures generated via SMD simulations do not always correctly sample the unbinding pathway. Unfortunately, attempts to pull the ligand more slowly out of the binding pocket via SMD simulations to generate starting structures to resolve the problem have not improved the kinetic estimates (data not shown). It is also possible that a better choice of CV, apart from the ligand-binding site COM–COM distance, would produce better kinetics, as it may lead to more extensive sampling within the Voronoi cells. Several attempts have been made to identify the exact causes of these discrepancies, but the solution has, so far, evaded us. Additional investigations, therefore, need to be undertaken to determine the exact causes to resolve such outlier kinetics estimates.
QMrebind-reparameterized SEEKR2 simulations predicted close-to-experimental koff rates for a majority of Hsp90-inhibitor complexes (Fig. 8). Linear fit and Kendall's tau analysis are performed to evaluate the predictive accuracy of QMrebind-reparameterized SEEKR2 simulations in estimating unbinding rates for a set of 17 Hsp90-Inhibitor complexes. The linear fit (R2 = 0.82) among the non-outliers demonstrated a strong correlation between the logarithm of experimental koff values and QMrebind + SEEKR2 estimated koff values, showing a good fit to the linear regression model (Fig. 9). Additionally, the computed Kendall's tau (τ = 0.79) displayed a positive and significant ordinal association between the experimental and QMrebind-reparameterized SEEKR2 estimated unbinding rates, supporting the agreement in ranking between both methods (Fig. 9). These analyses establish the improvement allowed by QMrebind-reparameterized SEEKR2 simulations in accurately predicting the unbinding rates for Hsp90-inhibitor complexes with high precision.
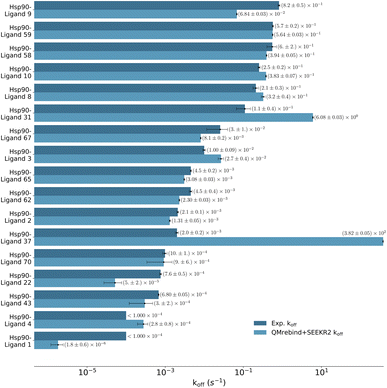 | ||
| Fig. 8 Unbinding rates or koff (s−1) for 17 Hsp90-inhibitor complexes obtained from experiments and QMrebind-reparameterized force field parameters employed in SEEKR2 simulations. The experimental koff rates were obtained using Surface Plasmon Resonance (SPR) measurements138,139,149 (refer to ESI Table S4† for a list of references for experimentally measured koff for each of the Hsp90-inhibitor complexes). The horizontal axis is represented in a logarithmic scale, allowing for better visualization of koff rates that span several orders of magnitude. | ||
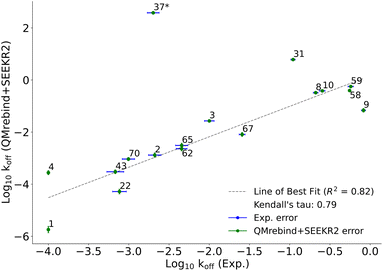 | ||
| Fig. 9 Scatter plot comparing the logarithm of experimental koff values against the QMrebind + SEEKR2 estimated koff values for Hsp90-inhibitor complexes. Each data point is labeled with its corresponding Hsp90-inhibitor complex ID, and error bars are shown for both data sets (refer to the ESI† of the SEEKR2 article67 for detailed analyses on milestoning error estimates). The plot displays a line of best fit to indicate the correlation between the experimental and theoretically calculated koff, with R2 values indicating the goodness of the fit and the computed Kendall's tau statistic, denoting the strength and direction of the ordinal association between the experimental koff and the QMrebind + SEEKR2 estimated koff values for 17 Hsp90-Inhibitor complexes. The QMrebind + SEEKR2 koff value for the Hsp90-ligand 37 complex deviates significantly from its experimental value and is considered an outlier. This complex is excluded from the linear fit and Kendall's tau analysis (refer to ESI Fig. S2† for the line of best fit and Kendall's tau statistics, including complex 37). | ||
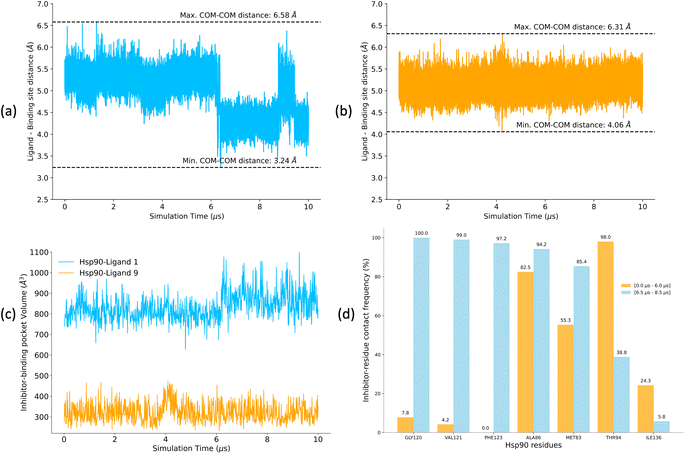
A low koff denotes an extended residence time for the ligand, characterizing it as a high-affinity binder (as observed for ligand 1). Conversely, ligand 9 exhibits a relatively higher koff as compared to ligand 1, indicating rapid dissociation from the binding site, classifying it as a low-affinity binder. To explain the variations in residence times, we computed the distances between the center of mass (COM) of the ligands and the COM of α-carbon atoms of the binding site residues for both the Hsp90-ligand 1 and Hsp90-ligand 9 complexes, as depicted in Fig. 10a and b. Changes in the ligand-binding site COM–COM distance during the simulation may suggest shifts in the interaction dynamics between the ligand and the receptor protein. In the context of the Hsp90-ligand 1 complex, a notable decrease in the COM–COM distance is evident at approximately 6 μs into the simulation, suggesting a modification in its interaction pattern with the binding site residues, as illustrated in Fig. 10a. This dynamic behavior could potentially contribute to an increased receptor–ligand interaction or efficient binding, contributing to a smaller koff. Conversely, the Hsp90-ligand 9 complex showed no significant changes in the ligand-binding site COM–COM distance throughout the simulation (Fig. 10b).
POVME2 (POcket Volume MEasurer 2) is a powerful computational tool designed to characterize and measure binding pockets within macromolecular and small-molecule complexes.154–156 POVME2 operates through a series of steps, including grid-based point generation, exclusion of points near receptor atoms, and optional removal of non-contiguous regions. We utilized the POVME2 algorithm to assess the binding pocket volumes for the two complexes for 10 μs of MD simulations. A 1.09 Å cutoff, corresponding to the van der Waals radius of the hydrogen atom, ensured the precise exclusion of non-pocket regions. Larger binding pocket volumes are observed for the Hsp90-ligand 1 complex compared to the Hsp90-ligand 9 complex (Fig. 10c). Ligand 1 possesses a larger and more voluminous molecular structure and is expected to adopt conformations that extend into the binding pocket more than ligand 9 (Fig. 5), leading to an increased volume estimate for the binding pocket. Consequently, the Hsp90-ligand 1 complex might exhibit a more expansive and accommodating binding pocket due to the specific interactions (Fig. 10d) and spatial arrangements between the ligand and the receptor, resulting in a larger calculated binding volume.
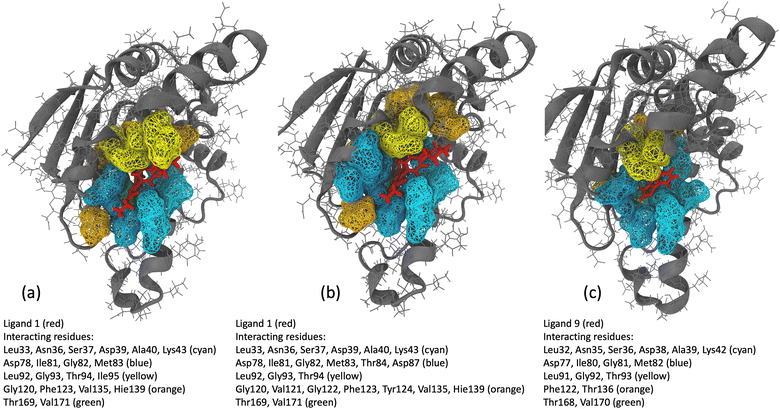
We analyzed interaction dynamics between ligand 1 and a set of key residues (within a cutoff distance of 4 Å) within the ligand-binding pocket of the Hsp90 receptor. Two distinct time intervals were selected (0 μs to 6.0 μs and 6.5 μs to 8.5 μs), where significant differences in the ligand-binding site distance were observed (Fig. 11a and b). More ligand-residue contacts were prevalent during the 6.5 μs to 8.5 μs simulation interval, indicating a dynamic shift in the binding interactions (Fig. 10d and ESI Table S5†). Residues such as Glu32, Ser35, Asn36, Asp39, and Gly80 consistently exhibited higher ligand-residue contact frequencies throughout both intervals (ESI Table S5†), indicating their key roles in maintaining robust interactions with the ligand. Conversely, residues such as Met83, Thr94, Gly120, Val121, and Phe123 displayed significant fluctuations in contact frequency between the two intervals, highlighting dynamic alterations in their binding patterns (Fig. 10d). Changes in receptor–ligand interactions are observed during the later simulation phase (6.5–8.5 μs), where a larger number of residues interacted with the ligand as compared to the initial 6 μs of simulation (Fig. 11a, b, and ESI Table S6†). Such a shift in the interaction landscape with a different ensemble of residues suggests a potential ligand rearrangement within the binding pocket, and a dynamicity of ligand 1 in the binding pocket of the receptor–ligand complex may contribute to an extended residence time of ligand 1. To interpret the binding strength and specificities of the two Hsp90-ligand complexes, residues interacting with the ligand within a cutoff distance of 4 Å were monitored at 0.4 ns intervals for the entire duration of the simulation. It is observed that ligand 1 interacted with a significantly higher number of residues than ligand 9 (Fig. 11a–c and ESI Table S6†). Interactions, such as hydrogen bonds, hydrophobic interactions, and van der Waals forces, potentially account for a higher residence time of ligand 1. On the contrary, reduced ligand-residue interactions for ligand 9 correlate well with its lower residence time, suggesting fewer constraints holding it in the binding pocket.
4 Conclusion
We have presented a novel approach to enhance the accuracy of SEEKR2 milestoning simulations of bimolecular complexes for predicting receptor–ligand unbinding rates through quantum mechanical reparameterization of the ligand charges at the binding site. The QMrebind force field reparameterization method may also be useful to simulate the binding–unbinding processes of receptor–ligand complexes using other enhanced sampling methods besides SEEKR2, such as RAMD, GaMD, etc. This method provides a multi-scale approach for force field parameterization through quantum mechanical treatment of the ligand at its binding site, thereby increasing the accuracy of simulations in estimating the unbinding rates of the ligands. To evaluate the effectiveness of our approach, we implemented this method within the SEEKR2 simulation framework to estimate the ligand-unbinding rates for seven host–guest complexes and 17 N-Hsp90-inhibitor complexes. Our results showed that the QMrebind-reparameterized force field within the SEEKR2 framework outperformed the generic force field in estimating the kinetic properties of receptor–ligand unbinding for most of the complexes. This comparison highlights the potential of the improved force field parameters to enhance the simulation accuracy. Integration of the QMrebind method into SEEKR2 is straightforward, and it can also be used as a standalone package for reparameterizing force field parameters for unbiased MD simulations and other enhanced MD simulation methods.Data availability
The QMrebind project is available at https://github.com/seekrcentral/qmrebind, and the SEEKR2 project is available at https://github.com/seekrcentral/seekr2. Data supporting the findings in this study are available as ESI at https://doi.org/10.6075/J09Z9545. The dataset includes SEEKR2 and QMrebind + SEEKR2 simulations for seven host–guest complexes and 17 Hsp90-inhibitor complexes, along with structural and topology files, simulation trajectories, and analysis scripts to obtain the receptor–ligand unbinding rate for each complex.Author contributions
A. A. O. and R. E. A. conceptualized the project. A. A. O. led the implementation and software development. A. A. O. conducted simulations, visualization, and analysis of the receptor–ligand complexes. A. A. O., L. W. V., and R. E. A. participated in data analysis and interpretation. A. A. O. led the writing, reviewing, and editing of the original draft. L. W. V. provided supporting contributions to the conceptualization, implementation, and software development and helped to write, review, and edit the original draft. R. E. A. provided funding and resource support and supervised the project while contributing to the writing, reviewing, and editing of the manuscript. All authors approved the final version of the manuscript.Conflicts of interest
The authors declare no conflicting interests.Acknowledgements
The authors express their gratitude to Eliseo Marin-Rimoldi (Molecular Sciences Software Institute), Shiksha Dutta (Université de Montréal), Diksha Pandey (Indian Institute of Science Education and Research Thiruvananthapuram), Adrian Mulholland (University of Bristol), Arnie Hagler (Valis Pharma), and Jeffrey Wagner (OpenFF) for their insightful and valuable discussions. A. A. O. acknowledges the support of the Molecular Sciences Software Institute (MolSSI) fellowship under NSF Grant OAC-1547580. R. E. A. acknowledges support from NSF Advanced Cyberinfrastructure Coordination Ecosystem: Services and Support (ACCESS) CHE060063 and NIH GM132826. All simulations were performed using the Popeye computing cluster at the San Diego Supercomputing Center (SDSC).References
- I. M. Klotz, Ligand–Receptor Energetics: A Guide for the Perplexed, John Wiley & Sons, 1997 Search PubMed.
- S. Majd, E. C. Yusko, Y. N. Billeh, M. X. Macrae, J. Yang and M. Mayer, Curr. Opin. Biotechnol., 2010, 21, 439–476 CrossRef CAS PubMed.
- Z. Cheng, B. Taylor, D. R. Ourthiague and A. Hoffmann, Sci. Signaling, 2015, 8, ra69 CrossRef PubMed.
- R. B. Bourret and A. M. Stock, J. Biol. Chem., 2002, 277, 9625–9628 CrossRef CAS PubMed.
- W. A. Lim, Nat. Rev. Mol. Cell Biol., 2010, 11, 393–403 CrossRef CAS PubMed.
- J. Z. Kechagia, J. Ivaska and P. Roca-Cusachs, Nat. Rev. Mol. Cell Biol., 2019, 20, 457–473 CrossRef CAS PubMed.
- D. J. Huggins, W. Sherman and B. Tidor, J. Med. Chem., 2012, 55, 1424–1444 CrossRef CAS PubMed.
- Y. Fang, Expert Opin. Drug Discovery, 2012, 7, 969–988 CrossRef CAS PubMed.
- R. A. Copeland, D. L. Pompliano and T. D. Meek, Nat. Rev. Drug Discovery, 2006, 5, 730–739 CrossRef CAS PubMed.
- K. C. Sivakumar, J. Haixiao, C. B. Naman and T. Sajeevan, Drug Dev. Res., 2020, 81, 685–699 CrossRef CAS PubMed.
- R. A. Copeland, Evaluation of Enzyme Inhibitors in Drug Discovery: A Guide for Medicinal Chemists and Pharmacologists, John Wiley & Sons, 2013 Search PubMed.
- F. Giordanetto and J. Kihlberg, J. Med. Chem., 2014, 57, 278–295 CrossRef CAS PubMed.
- B. R. Stockwell, Nature, 2004, 432, 846–854 CrossRef CAS PubMed.
- R. A. Copeland, Future Med. Chem., 2011, 3, 1491–1501 CrossRef CAS PubMed.
- S. Núñez, J. Venhorst and C. G. Kruse, Drug Discovery Today, 2012, 17, 10–22 CrossRef PubMed.
- P. J. Tummino and R. A. Copeland, Biochemistry, 2008, 47, 5481–5492 CrossRef CAS PubMed.
- R. A. Copeland, Nat. Rev. Drug Discovery, 2016, 15, 87–95 CrossRef CAS PubMed.
- M. R. Shirts, D. L. Mobley and S. P. Brown, Drug Des., 2010, 1, 61–86 Search PubMed.
- W. Liu, J. Jiang, Y. Lin, Q. You and L. Wang, J. Med. Chem., 2022, 65, 10809–10847 CrossRef CAS PubMed.
- Z. Tang, C. C. Roberts and A. C. Chia-en, Front. Biosci.-Landmark, 2017, 22, 960 CrossRef CAS PubMed.
- F. Feixas, S. Lindert, W. Sinko and J. A. McCammon, Biophys. Chem., 2014, 186, 31–45 CrossRef CAS PubMed.
- T. Hansson, C. Oostenbrink and W. van Gunsteren, Curr. Opin. Struct. Biol., 2002, 12, 190–196 CrossRef CAS PubMed.
- M. J. Harvey and G. De Fabritiis, Drug Discovery Today, 2012, 17, 1059–1062 CrossRef CAS PubMed.
- V. A. Voelz, G. R. Bowman, K. Beauchamp and V. S. Pande, J. Am. Chem. Soc., 2010, 132, 1526–1528 CrossRef CAS PubMed.
- T. J. Lane, D. Shukla, K. A. Beauchamp and V. S. Pande, Curr. Opin. Struct. Biol., 2013, 23, 58–65 CrossRef CAS PubMed.
- C. F. Miller, D. S. Kulyk, J. W. Kim and A. K. Badu-Tawiah, Analyst, 2017, 142, 2152–2160 RSC.
- D. Kern and E. R. Zuiderweg, Curr. Opin. Struct. Biol., 2003, 13, 748–757 CrossRef CAS PubMed.
- A. Sekhar, P. Vallurupalli and L. E. Kay, Proc. Natl. Acad. Sci. U. S. A., 2013, 110, 11391–11396 CrossRef CAS PubMed.
- S. Izrailev, S. Stepaniants, M. Balsera, Y. Oono and K. Schulten, Biophys. J., 1997, 72, 1568–1581 CrossRef CAS PubMed.
- S. Wolf, B. Lickert, S. Bray and G. Stock, Nat. Commun., 2020, 11, 2918 CrossRef CAS PubMed.
- F. Paul, C. Wehmeyer, E. T. Abualrous, H. Wu, M. D. Crabtree, J. Schöneberg, J. Clarke, C. Freund, T. R. Weikl and F. Noé, Nat. Commun., 2017, 8, 1095 CrossRef PubMed.
- L. Yang, C.-W. Liu, Q. Shao, J. Zhang and Y. Q. Gao, Acc. Chem. Res., 2015, 48, 947–955 CrossRef CAS PubMed.
- Y. I. Yang, Q. Shao, J. Zhang, L. Yang and Y. Q. Gao, J. Chem. Phys., 2019, 151, 070902 CrossRef PubMed.
- J. Debnath, M. Invernizzi and M. Parrinello, J. Chem. Theory Comput., 2019, 15, 2454–2459 CrossRef CAS PubMed.
- A. Barducci, M. Bonomi and M. Parrinello, Wiley Interdiscip. Rev.: Comput. Mol. Sci., 2011, 1, 826–843 CAS.
- G. Bussi and A. Laio, Nat. Rev. Phys., 2020, 2, 200–212 CrossRef.
- L. Sutto, S. Marsili and F. L. Gervasio, Wiley Interdiscip. Rev.: Comput. Mol. Sci., 2012, 2, 771–779 CAS.
- G. R. Bowman, V. S. Pande and F. Noé, An Introduction to Markov State Models and Their Application to Long Timescale Molecular Simulation, Springer Science & Business Media, 2013, vol. 797 Search PubMed.
- J. D. Chodera and F. Noé, Curr. Opin. Struct. Biol., 2014, 25, 135–144 CrossRef CAS PubMed.
- B. E. Husic and V. S. Pande, J. Am. Chem. Soc., 2018, 140, 2386–2396 CrossRef CAS PubMed.
- O. Valsson and M. Parrinello, Phys. Rev. Lett., 2014, 113, 090601 CrossRef CAS PubMed.
- P. Shaffer, O. Valsson and M. Parrinello, Proc. Natl. Acad. Sci. U. S. A., 2016, 113, 1150–1155 CrossRef CAS PubMed.
- L. Bonati, Y.-Y. Zhang and M. Parrinello, Proc. Natl. Acad. Sci. U. S. A., 2019, 116, 17641–17647 CrossRef CAS PubMed.
- D. M. Zuckerman and L. T. Chong, Annu. Rev. Biophys., 2017, 46, 43–57 CrossRef CAS PubMed.
- D. Bhatt, B. W. Zhang and D. M. Zuckerman, J. Chem. Phys., 2010, 133, 014110 CrossRef PubMed.
- S.-H. Ahn, A. A. Ojha, R. E. Amaro and J. A. McCammon, J. Chem. Theory Comput., 2021, 17, 7938–7951 CrossRef CAS PubMed.
- A. A. Ojha, S. Thakur, S.-H. Ahn and R. E. Amaro, J. Chem. Theory Comput., 2023 Search PubMed.
- J. Kästner, Wiley Interdiscip. Rev.: Comput. Mol. Sci., 2011, 1, 932–942 Search PubMed.
- P. Virnau and M. Müller, J. Chem. Phys., 2004, 120, 10925–10930 CrossRef CAS PubMed.
- A. Warmflash, P. Bhimalapuram and A. R. Dinner, J. Chem. Phys., 2007, 127, 114109 CrossRef PubMed.
- D. Hamelberg, J. Mongan and J. A. McCammon, J. Chem. Phys., 2004, 120, 11919–11929 CrossRef CAS PubMed.
- D. Perez, B. P. Uberuaga, Y. Shim, J. G. Amar and A. F. Voter, Annu. Rep. Comput. Chem., 2009, 5, 79–98 CAS.
- P. R. Markwick and J. A. McCammon, Phys. Chem. Chem. Phys., 2011, 13, 20053–20065 RSC.
- J. Wang, P. R. Arantes, A. Bhattarai, R. V. Hsu, S. Pawnikar, Y.-m. M. Huang, G. Palermo and Y. Miao, Wiley Interdiscip. Rev.: Comput. Mol. Sci., 2021, 11, e1521 CAS.
- Y. Miao, V. A. Feher and J. A. McCammon, J. Chem. Theory Comput., 2015, 11, 3584–3595 CrossRef CAS PubMed.
- A. Bhattarai and Y. Miao, Expert Opin. Drug Discovery, 2018, 13, 1055–1065 CrossRef CAS PubMed.
- Y. Sugita and Y. Okamoto, Chem. Phys. Lett., 1999, 314, 141–151 CrossRef CAS.
- K. Y. Sanbonmatsu and A. E. García, Proteins: Struct., Funct., Bioinf., 2002, 46, 225–234 CrossRef CAS PubMed.
- E. Rosta and G. Hummer, J. Chem. Phys., 2009, 131, 10B615 CrossRef PubMed.
- Y. I. Yang, J. Zhang, X. Che, L. Yang and Y. Q. Gao, J. Chem. Phys., 2016, 144, 094105 CrossRef PubMed.
- L. Yang and Y. Qin Gao, J. Chem. Phys., 2009, 131, 12B606 Search PubMed.
- Q. Du, V. Faber and M. Gunzburger, SIAM Rev., 1999, 41, 637–676 CrossRef.
- P. Májek and R. Elber, J. Chem. Theory Comput., 2010, 6, 1805–1817 CrossRef PubMed.
- E. Vanden-Eijnden and M. Venturoli, J. Chem. Phys., 2009, 130, 194101 CrossRef PubMed.
- L. W. Votapka, B. R. Jagger, A. L. Heyneman and R. E. Amaro, J. Phys. Chem. B, 2017, 121, 3597–3606 CrossRef CAS PubMed.
- B. R. Jagger, A. A. Ojha and R. E. Amaro, J. Chem. Theory Comput., 2020, 16, 5348–5357 CrossRef CAS PubMed.
- L. W. Votapka, A. M. Stokely, A. A. Ojha and R. E. Amaro, J. Chem. Inf. Model., 2022, 62, 3253–3262 CrossRef CAS PubMed.
- B. R. Jagger, L. W. Votapka and R. E. Amaro, Biophys. J., 2018, 114, 42a CrossRef.
- A. A. Ojha, A. Srivastava, L. W. Votapka and R. E. Amaro, J. Chem. Inf. Model., 2023, 63, 2469–2482 CrossRef CAS PubMed.
- A. A. Ojha, A. Srivastava, L. W. Votapka and R. E. Amaro, Data from: Selectivity and Ranking of Tight-Binding JAK-STAT Inhibitors using Markovian Milestoning with Voronoi Tessellations, 2022, DOI:10.6075/J01Z44MN.
- D. Petrov and B. Zagrovic, PLoS Comput. Biol., 2014, 10, e1003638 CrossRef PubMed.
- V. Gapsys, L. Pérez-Benito, M. Aldeghi, D. Seeliger, H. Van Vlijmen, G. Tresadern and B. L. De Groot, Chem. Sci., 2020, 11, 1140–1152 RSC.
- R. Capelli, W. Lyu, V. Bolnykh, S. Meloni, J. M. H. Olsen, U. Rothlisberger, M. Parrinello and P. Carloni, J. Phys. Chem. Lett., 2020, 11, 6373–6381 CrossRef CAS PubMed.
- K. Ahmad, A. Rizzi, R. Capelli, D. Mandelli, W. Lyu and P. Carloni, Front. Mol. Biosci., 2022, 9, 899805 CrossRef CAS PubMed.
- T. A. Halgren and W. Damm, Curr. Opin. Struct. Biol., 2001, 11, 236–242 CrossRef CAS PubMed.
- Z. Jing, C. Liu, S. Y. Cheng, R. Qi, B. D. Walker, J.-P. Piquemal and P. Ren, Annu. Rev. Biophys., 2019, 48, 371–394 CrossRef CAS PubMed.
- C. M. Baker, Wiley Interdiscip. Rev.: Comput. Mol. Sci., 2015, 5, 241–254 CAS.
- H. M. Senn and W. Thiel, Angew. Chem., Int. Ed., 2009, 48, 1198–1229 CrossRef CAS PubMed.
- R. Lonsdale, J. N. Harvey and A. J. Mulholland, Chem. Soc. Rev., 2012, 41, 3025–3038 RSC.
- A. Lodola, M. Mor, S. Rivara, C. Christov, G. Tarzia, D. Piomelli and A. J. Mulholland, Chem. Commun., 2008, 214–216 RSC.
- B. Raghavan, M. Paulikat, K. Ahmad, L. Callea, A. Rizzi, E. Ippoliti, D. Mandelli, L. Bonati, M. De Vivo and P. Carloni, J. Chem. Inf. Model., 2023, 63, 3647–3658 CrossRef CAS PubMed.
- S. T. Ngo, T. H. Nguyen, N. T. Tung, V. V. Vu, M. Q. Pham and B. K. Mai, Phys. Chem. Chem. Phys., 2022, 24, 29266–29278 RSC.
- J. Gao, S. Ma, D. T. Major, K. Nam, J. Pu and D. G. Truhlar, Chem. Rev., 2006, 106, 3188–3209 CrossRef CAS PubMed.
- J. W. Ponder, C. Wu, P. Ren, V. S. Pande, J. D. Chodera, M. J. Schnieders, I. Haque, D. L. Mobley, D. S. Lambrecht and R. A. DiStasio Jr, et al. , J. Phys. Chem. B, 2010, 114, 2549–2564 CrossRef CAS PubMed.
- K. Vanommeslaeghe and A. D. MacKerell Jr, J. Chem. Inf. Model., 2012, 52, 3144–3154 CrossRef CAS PubMed.
- F. Neese, F. Wennmohs, U. Becker and C. Riplinger, J. Chem. Phys., 2020, 152, 224108 CrossRef CAS PubMed.
- F. Neese, Wiley Interdiscip. Rev.: Comput. Mol. Sci., 2012, 2, 73–78 CAS.
- F. Neese, Wiley Interdiscip. Rev.: Comput. Mol. Sci., 2022, 12, e1606 Search PubMed.
- L. W. Chung, W. Sameera, R. Ramozzi, A. J. Page, M. Hatanaka, G. P. Petrova, T. V. Harris, X. Li, Z. Ke and F. Liu, et al. , Chem. Rev., 2015, 115, 5678–5796 CrossRef CAS PubMed.
- L. W. Chung, H. Hirao, X. Li and K. Morokuma, Wiley Interdiscip. Rev.: Comput. Mol. Sci., 2012, 2, 327–350 CAS.
- K. Morokuma, Bull. Korean Chem. Soc., 2003, 24, 797–801 CrossRef CAS.
- D. R. Bowler and T. Miyazaki, Rep. Prog. Phys., 2012, 75, 036503 CrossRef CAS PubMed.
- S. Goedecker, Rev. Mod. Phys., 1999, 71, 1085 CrossRef CAS.
- H. F. Schaefer, Methods of Electronic Structure Theory, Springer Science & Business Media, 2013, vol. 3 Search PubMed.
- C. Bannwarth, S. Ehlert and S. Grimme, J. Chem. Theory Comput., 2019, 15, 1652–1671 CrossRef CAS PubMed.
- L. Komissarov and T. Verstraelen, J. Chem. Inf. Model., 2021, 61, 5931–5937 CrossRef CAS PubMed.
- Z. Bodrog and B. Aradi, Phys. Status Solidi B, 2012, 249, 259–269 CrossRef CAS.
- C. Bannwarth, E. Caldeweyher, S. Ehlert, A. Hansen, P. Pracht, J. Seibert, S. Spicher and S. Grimme, Wiley Interdiscip. Rev.: Comput. Mol. Sci., 2021, 11, e1493 CAS.
- P. Tao and H. B. Schlegel, J. Comput. Chem., 2010, 31, 2363–2369 CrossRef CAS PubMed.
- F. Neese, et al., An Ab Initio, Density Functional and Semiempirical Program Package Version, 2009, vol. 2 Search PubMed.
- S. Grimme, C. Bannwarth and P. Shushkov, J. Chem. Theory Comput., 2017, 13, 1989–2009 CrossRef CAS PubMed.
- C. M. Breneman and K. B. Wiberg, J. Comput. Chem., 1990, 11, 361–373 CrossRef CAS.
- M. Zgarbová, M. Otyepka, J. Šponer, A. Mládek, P. Banáš, T. E. Cheatham III and P. Jurecka, J. Chem. Theory Comput., 2011, 7, 2886–2902 CrossRef PubMed.
- E. Harder, W. Damm, J. Maple, C. Wu, M. Reboul, J. Y. Xiang, L. Wang, D. Lupyan, M. K. Dahlgren and J. L. Knight, et al. , J. Chem. Theory Comput., 2016, 12, 281–296 CrossRef CAS PubMed.
- A. Ojha, L. Votapka, G. Huber, S. Gao and R. Amaro, An introductory tutorial to the SEEKR2 (Simulation enabled estimation of kinetic rates v. 2) multiscale milestoning software [Article v1. 0], 2023, DOI:10.26434/chemrxiv-2023-kd1wt.
- L. W. Votapka, A. M. Stokely, A. A. Ojha and R. E. Amaro, Data from: SEEKR2: Versatile Multiscale Milestoning Utilizing the OpenMM Molecular Dynamics Engine, 2022, DOI:10.6075/J0668DDR.
- P. Eastman, J. Swails, J. D. Chodera, R. T. McGibbon, Y. Zhao, K. A. Beauchamp, L.-P. Wang, A. C. Simmonett, M. P. Harrigan and C. D. Stern, et al. , PLoS Comput. Biol., 2017, 13, e1005659 CrossRef PubMed.
- P. Eastman and V. Pande, Comput. Sci. Eng., 2010, 12, 34–39 CAS.
- G. A. Huber and J. A. McCammon, Comput. Phys. Commun., 2010, 181, 1896–1905 CrossRef CAS PubMed.
- B. Boots, K. Sugihara, S. N. Chiu and A. Okabe, Spatial tessellations: concepts and applications of Voronoi diagrams, John Wiley & Sons, 2009 Search PubMed.
- F. Aurenhammer and R. Klein, Handbook of Computational Geometry, 2000, vol. 5, pp. 201–290 Search PubMed.
- A. E. Cardenas and R. Elber, J. Phys. Chem. B, 2016, 120, 8208–8216 CrossRef CAS PubMed.
- N. Morin-Crini, S. Fourmentin, É. Fenyvesi, E. Lichtfouse, G. Torri, M. Fourmentin and G. Crini, Environ. Chem. Lett., 2021, 19, 2581–2617 CrossRef CAS.
- C. Cézard, X. Trivelli, F. Aubry, F. Djedaïni-Pilard and F.-Y. Dupradeau, Phys. Chem. Chem. Phys., 2011, 13, 15103–15121 RSC.
- J. Wang, R. M. Wolf, J. W. Caldwell, P. A. Kollman and D. A. Case, J. Comput. Chem., 2004, 25, 1157–1174 CrossRef CAS PubMed.
- F.-Y. Dupradeau, A. Pigache, T. Zaffran, C. Savineau, R. Lelong, N. Grivel, D. Lelong, W. Rosanski and P. Cieplak, Phys. Chem. Chem. Phys., 2010, 12, 7821–7839 RSC.
- Z. Tang and C.-e. A. Chang, J. Chem. Theory Comput., 2018, 14, 303–318 CrossRef CAS PubMed.
- B. R. Jagger, C. T. Lee and R. E. Amaro, J. Phys. Chem. Lett., 2018, 9, 4941–4948 CrossRef CAS PubMed.
- U. Essmann, L. Perera, M. L. Berkowitz, T. Darden, H. Lee and L. G. Pedersen, J. Chem. Phys., 1995, 103, 8577–8593 CrossRef CAS.
- H. G. Petersen, J. Chem. Phys., 1995, 103, 3668–3679 CrossRef CAS.
- A. D. Beeke, J. Chem. Phys., 1993, 98, 5648–5652 CrossRef.
- D. G. Truhlar, Chem. Phys. Lett., 1998, 294, 45–48 CrossRef CAS.
- D. Picard, Cell. Mol. Life Sci., 2002, 59, 1640–1648 CrossRef CAS PubMed.
- A. D. Zuehlke, M. A. Moses and L. Neckers, Philos. Trans. R. Soc., B, 2018, 373, 20160527 CrossRef PubMed.
- C. Jolly and R. I. Morimoto, J. Natl. Cancer Inst., 2000, 92, 1564–1572 CrossRef CAS PubMed.
- V. Condelli, F. Crispo, M. Pietrafesa, G. Lettini, D. S. Matassa, F. Esposito, M. Landriscina and F. Maddalena, Cells, 2019, 8, 532 CrossRef PubMed.
- S. Messaoudi, J. Peyrat, J. Brion and M. Alami, Anti-Cancer Agents Med. Chem., 2008, 8, 761–782 CrossRef CAS PubMed.
- B. Tillotson, K. Slocum, J. Coco, N. Whitebread, B. Thomas, K. A. West, J. MacDougall, J. Ge, J. A. Ali and V. J. Palombella, et al. , J. Biol. Chem., 2010, 285, 39835–39843 CrossRef CAS PubMed.
- K. Richter, J. Reinstein and J. Buchner, J. Biol. Chem., 2002, 277, 44905–44910 CrossRef CAS PubMed.
- C. Prodromou, B. Panaretou, S. Chohan, G. Siligardi, R. O'Brien, J. E. Ladbury, S. M. Roe, P. W. Piper and L. H. Pearl, EMBO J., 2000, 19, 4383–4392 CrossRef CAS PubMed.
- P. Workman, Curr. Cancer Drug Targets, 2003, 3, 297–300 CrossRef CAS PubMed.
- K. Richter, S. Moser, F. Hagn, R. Friedrich, O. Hainzl, M. Heller, S. Schlee, H. Kessler, J. Reinstein and J. Buchner, J. Biol. Chem., 2006, 281, 11301–11311 CrossRef CAS PubMed.
- G. Vettoretti, E. Moroni, S. Sattin, J. Tao, D. A. Agard, A. Bernardi and G. Colombo, Sci. Rep., 2016, 6, 1–13 CrossRef PubMed.
- L. Li, L. Wang, Q.-D. You and X.-L. Xu, J. Med. Chem., 2019, 63, 1798–1822 CrossRef PubMed.
- J. Trepel, M. Mollapour, G. Giaccone and L. Neckers, Nat. Rev. Cancer, 2010, 10, 537–549 CrossRef CAS PubMed.
- A. Nunes-Alves, D. B. Kokh and R. C. Wade, Curr. Opin. Struct. Biol., 2020, 64, 126–133 CrossRef CAS PubMed.
- S. Wolf, B. Lickert, S. Bray and G. Stock, Biophys. J., 2021, 120, 77a CrossRef.
- D. B. Kokh, M. Amaral, J. Bomke, U. Gradler, D. Musil, H.-P. Buchstaller, M. K. Dreyer, M. Frech, M. Lowinski and F. Vallee, et al. , J. Chem. Theory Comput., 2018, 14, 3859–3869 CrossRef CAS PubMed.
- M. Amaral, D. Kokh, J. Bomke, A. Wegener, H. Buchstaller, H. Eggenweiler, P. Matias, C. Sirrenberg, R. Wade and M. Frech, Nat. Commun., 2017, 8, 2276 CrossRef CAS PubMed.
- J. Wang, W. Wang, P. A. Kollman and D. A. Case, J. Mol. Graphics Modell., 2006, 25, 247–260 CrossRef CAS PubMed.
- W. D. Cornell, P. Cieplak, C. I. Bayly and P. A. Kollman, J. Am. Chem. Soc., 2002, 115, 9620–9631 CrossRef.
- C. I. Bayly, P. Cieplak, W. Cornell and P. A. Kollman, J. Phys. Chem., 1993, 97, 10269–10280 CrossRef CAS.
- J. A. Maier, C. Martinez, K. Kasavajhala, L. Wickstrom, K. E. Hauser and C. Simmerling, J. Chem. Theory Comput., 2015, 11, 3696–3713 CrossRef CAS PubMed.
- S.-H. Ahn, B. R. Jagger and R. E. Amaro, J. Chem. Inf. Model., 2020, 60, 5340–5352 CrossRef CAS PubMed.
- Y. Miao, A. Bhattarai and J. Wang, J. Chem. Theory Comput., 2020, 16, 5526–5547 CrossRef CAS PubMed.
- T. C. Barros, K. Stefaniak, J. F. Holzwarth and C. Bohne, J. Phys. Chem. A, 1998, 102, 5639–5651 CrossRef CAS.
- T. Fukahori, S. Nishikawa and K. Yamaguchi, Bull. Chem. Soc. Jpn., 2004, 77, 2193–2198 CrossRef CAS.
- S. Nishikawa, T. Fukahori and K. Ishikawa, J. Phys. Chem. A, 2002, 106, 3029–3033 CrossRef CAS.
- D. A. Schuetz, L. Richter, M. Amaral, M. Grandits, U. Gradler, D. Musil, H.-P. Buchstaller, H.-M. Eggenweiler, M. Frech and G. F. Ecker, J. Med. Chem., 2018, 61, 4397–4411 CrossRef CAS PubMed.
- D. A. Case, H. M. Aktulga, K. Belfon, I. Ben-Shalom, S. R. Brozell, D. S. Cerutti, T. E. Cheatham III, V. W. D. Cruzeiro, T. A. Darden, R. E. Duke, et al., Amber 2021, University of California, San Francisco, 2021 Search PubMed.
- D. A. Case, T. E. Cheatham III, T. Darden, H. Gohlke, R. Luo, K. M. Merz Jr, A. Onufriev, C. Simmerling, B. Wang and R. J. Woods, J. Comput. Chem., 2005, 26, 1668–1688 CrossRef CAS PubMed.
- R. Salomon-Ferrer, D. A. Case and R. C. Walker, Wiley Interdiscip. Rev.: Comput. Mol. Sci., 2013, 3, 198–210 CAS.
- D. R. Roe and T. E. Cheatham III, J. Chem. Theory Comput., 2013, 9, 3084–3095 CrossRef CAS PubMed.
- J. D. Durrant, C. A. F. de Oliveira and J. A. McCammon, J. Mol. Graphics Modell., 2011, 29, 773–776 CrossRef CAS PubMed.
- J. D. Durrant, L. Votapka, J. Sørensen and R. E. Amaro, J. Chem. Theory Comput., 2014, 10, 5047–5056 CrossRef CAS PubMed.
- J. R. Wagner, J. Sørensen, N. Hensley, C. Wong, C. Zhu, T. Perison and R. E. Amaro, J. Chem. Theory Comput., 2017, 13, 4584–4592 CrossRef CAS PubMed.
Footnote |
| † Electronic supplementary information (ESI) available: The ESI file contains the experimentally determined and theoretically calculated unbinding rates for the seven host–guest and 17 Hsp90-inhibitor complexes. Convergence plots of ligand unbinding rates for the host–guest complexes are also provided in the ESI. See DOI: https://doi.org/10.1039/d3sc04195f |
| This journal is © The Royal Society of Chemistry 2023 |