Open Access Article
Open Access ArticleCreative Commons Attribution 3.0 Unported Licence
Machine learning based microfluidic sensing device for viscosity measurements†
Adil
Mustafa
 *abh,
Daniyal
Haider
c,
Arnab
Barua
d,
Melikhan
Tanyeri
*abh,
Daniyal
Haider
c,
Arnab
Barua
d,
Melikhan
Tanyeri
 *e,
Ahmet
Erten
f and
Ozlem
Yalcin
*g
*e,
Ahmet
Erten
f and
Ozlem
Yalcin
*g
aSchool of Life Sciences, University of Warwick, Coventry, UK. E-mail: adil.mustafa@warwick.ac.uk
bGraduate School of Biomedical Sciences and Engineering, Koç University, Istanbul, Turkey
cDepartment of Computer Technology, De Montfort University, Leicester, UK
dDivision of Computer Science and Software Engineering, Mälardalens University, Västerås, Sweden
eDepartment of Engineering, Duquesne University, Pittsburgh, USA. E-mail: tanyerim@duq.edu
fDepartment of Electronics and Communication Engineering, Istanbul Technical University, Istanbul, Turkey
gSchool of Medicine, Koç University, Istanbul, Turkey. E-mail: ozlemyalcin@ku.edu.tr
hDepartment of Biomedical Engineering, University of Bolton, Bolton, UK
First published on 30th August 2023
Abstract
A microfluidic sensing device utilizing fluid–structure interactions and machine learning algorithms is demonstrated. The deflection of microsensors due to fluid flow within a microchannel is analysed using machine learning algorithms to calculate the viscosity of Newtonian and non-Newtonian fluids. Newtonian fluids (glycerol/water solutions) within a viscosity range of 5–100 cP were tested at flow rates of 15–105 mL h−1 (γ = 60.5–398.4 s−1) using a sample volume of 80–400 μL. The microsensor deflection data were used to train machine learning algorithms. Two different machine learning (ML) algorithms, support vector machine (SVM) and k-nearest neighbour (k-NN), were employed to determine the viscosity of unknown Newtonian fluids and whole blood samples. An average accuracy of 89.7% and 98.9% is achieved for viscosity measurement of unknown solutions using SVM and k-NN algorithms, respectively. The intelligent microfluidic viscometer presented here has the potential for automated, real-time viscosity measurements for rheological studies.
Introduction
Investigating intriguing flow behaviour and rheological properties of industrially manufactured complex fluids and naturally occurring biofluids is of great importance in many fields of science and engineering.1–4 Dynamic viscosity is one of the most essential material properties of complex fluids.5 Robust viscosity measurements of Newtonian and non-Newtonian fluids using small sample volumes are crucial in many applications in health care,6 food processing,7 and pharmaceutical industries.8 Traditional viscometers employed to measure the viscosity of Newtonian and non-Newtonian fluids are typically categorized based on their operating principles. Major traditional viscosity measurement techniques include capillary viscometers,9,10 rotational viscometers,11 coaxial cylinder viscometers,12 falling ball viscometers,13,14 and vibrational viscometers.15 These traditional viscometers often use large sample volumes in the millilitre (mL) range to quantify the viscosity of fluids, which is highly undesirable for point of care applications.16 There is a growing demand for robust, portable platforms to rapidly and cost efficiently measure fluid viscosity at the point of need using sample volumes in the μL to nL range.17 Advancements in microfabrication, soft lithography and replica moulding in the past two decades have enabled researchers to design and fabricate microfluidic devices for viscosity measurements. Microfluidic devices inherently enable portable platforms that perform viscosity measurements in a fast and low-cost manner using small sample volumes. Microfluidic viscometers are commonly categorized based on their transduction mechanism, namely, flow rate sensing viscometers,18,19 pressure sensing viscometers,20 surface tension sensing viscometers,21 comparator viscometers,22 droplet-based viscometers,23 and microsensor-based viscometers.24,25Microsensor-based viscometers rely on determining the deflection of microsensor structures under external forces.26 Judith et al.27 reported a magnetically-actuated microsensor array to measure the viscosity of a fluid with a wide dynamic range (5–5000 cP) and a sensitivity of 1 cP. We recently developed a microsensor-based viscometer which relies on flow-induced deflection of microsensors, thereby eliminating the need for magnetic actuation.25 Our microfluidic viscometer comprises an array of microsensors arranged in a staggered or zigzag configuration to maximize fluid–structure interactions. The viscosity of sample fluids was determined by inserting the deflection of a microsensor tip into a 2nd order polynomial fit obtained from a calibration curve.25 While this method allows for viscosity measurements within a range of 2–100 cP and a sensitivity of 0.5 cP using minute amounts of sample, it also comes with certain limitations. First, it is an arduous task to construct an accurate analytical fluid–structure model which is consistent with experimental results. Second, extracting viscosity values of fluids using the raw deflection microsensor tip deflection data is a cumbersome process, as it requires post-processing hundreds of gigabytes of data. Indeed, a vast majority of the viscosity measurement methods discussed above require substantial mathematical modelling to accurately predict the viscosity of sample fluids. For microsensor-based viscometers, complex differential equations describing fluid dynamics and solid mechanics need to be coupled.25 Hence, we posit that new approaches such as machine learning could facilitate eliciting useful material properties such as viscosity without the need for extensive mathematical modelling.
Integration of machine learning with microfluidics and analytical chemistry in recent years has enabled an alternative route for continuous monitoring and dynamic control of microfluidic systems, extracting useful information by post-processing large amounts of raw data28–32 and eliminating the need for developing complex mathematical models representing the system under study. For instance, digital microfluidics for drug discovery is an emerging field where machine learning algorithms have been employed to improve the robustness of data analysis and the throughput of the systems.33 In addition, microfluidic systems for screening prostate and breast cancer based on high-content analysis of cell phenotype biomarkers have also been integrated with machine learning algorithms to overcome the shortcomings of conventional biomarker analysis.34 On-chip cell detection and quantification are of great importance for medical diagnosis. Deep neural networks (DNNs) can facilitate fast and efficient analysis of blood cells on microfluidic platforms to identify a toxic reaction or a viral infection towards point-of-care diagnostics.35 Machine learning can also be used to measure various fluidic properties. Hadikhani et al. used a neural network to extract these properties from images of water/alcohol droplets generated within a microfluidic device.36 A large number of droplet images are recorded and used to train deep neural networks (DNNs) to determine the concentration of each component (water/alcohol) in the mixture with 0.5% accuracy, and measure the flow rate of the same mixture with a resolution of 0.5 mL h−1. Moreover, the stability of emulsions inside a microfluidic chip can also be quantified based on the droplet shape descriptors using machine learning methods.37
In this study, we integrate our PDMS microsensor-based viscometer with machine learning algorithms to calculate the viscosity of both Newtonian and non-Newtonian fluids by analysing the deflection of PDMS microsensors by fluid flow. We also demonstrated a biomedical application where we identified various stages of clot formation during the coagulation process by classifying viscosity measurements for human whole blood samples using machine learning algorithms. Support vector machine (SVM) and k-nearest neighbour (k-NN) algorithms were used to extract viscosity values from raw experimental data. To the best of our knowledge, this is the first study where machine learning algorithms are used to calculate the viscosity of fluids by analysing deflection fluid–structure interactions within a microfluidic device. The SVM and k-NN algorithms presented in this study eliminate the need for developing complex mathematical models for measuring fluid viscosity. We show that ML methods can be easily integrated into measuring fluid viscosity using microfluidic devices. ML-based methods can be used to differentiate between data sets featuring similar characteristics and potentially accelerate the analysis time.
Materials and methods
Sample fluid preparation
The sample Newtonian fluids were prepared by mixing glycerol (PamReac Applichem, Barcelona, Spain) with deionized water (DI water) at different ratios to obtain a range of viscosities including 5, 10, 15, 25, 50, 75, and 100 cP. Whole blood samples were used as the non-Newtonian fluid following IRB: 001/2015 and approved by the Ethics Committee of Koç University School of Medicine and informed written consent was obtained from each subject participating in the study. The details of the device fabrication are given in ESI† S1.Experimental setup
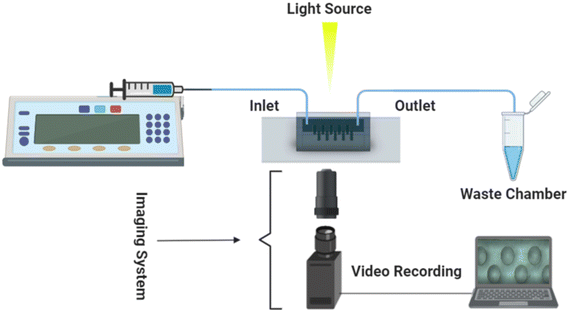
The experimental setup comprised a microfluidic viscometer chip, an inverted microscope for imaging (Nikon Eclipse TS100, Tokyo, Japan), a syringe pump (PHD Ultra 70-3007, Harvard Apparatus, Holliston, MA) to infuse the sample fluids into the microfluidic viscometer, a CCD camera (Point Grey Grasshopper3 USB3.0, Richmond, BC, Canada) and a computer for recording the experimental videos at 22 frames per second (fps) as shown in Fig. 1.Data acquisition
The recorded videos for each experiment were analysed using an in-house Matlab code to extract microsensor tip deflection as a function of time as shown in Fig. 2a. The initial 25 frames were acquired for the static conditions (no fluid infusion into the device) and the remaining frames were acquired for the dynamic conditions (fluid flow yielding microsensor deflection). The deflection of microsensors is quantified by comparing the initial position of the microsensor tip (first static frame) to each of the subsequent frames. Fig. 2a depicts microsensor deflection along the direction of fluid flow as a function of time for a single microsensor. We observed that deflection increases rapidly as the fluid is infused in the microchannel, and then reaches a plateau, depicting the maximum microsensor tip deflection. As soon as the fluid infusion is halted, the microsensor deflection decreases sharply. The duration of each recorded video was 15 seconds, captured at 22 fps, rendering a total of 330 frames for each measurement. The CCD camera was employed to record all experimental videos. The spatial resolution of the microfluidic viscometer device was determined by dividing the camera pixel size (5.68 μm) by the magnification (7×), resulting in a resolution of 0.81 μm per pixel. Following the Nyquist criterion and Shannon's sampling theorem, we set the sampling interval to two pixels, such that half the size of the smallest resolvable feature corresponds to a pixel. Using a sampling interval of two pixels, our setup yielded a spatial resolution of 1.62 μm. Microsensor deflection was monitored by continuous imaging of five microsensors at the centre of the channel as we observed that microsensor deflection near the entrance and exit of the channel was smaller compared to the centre. The microsensor with the maximum deflection value was chosen for further analysis. For each flow rate, the microsensor deflection was calculated by taking the average of all the tip deflection values in the plateau region. The subsequent decrease in deflection shown in Fig. 2a corresponds to no-flow (static) conditions where the microsensor tip relaxes back to its initial position. Fig. 2b is a collection of raw images depicting the top view of the device during fluid infusion (t = 0 s), maximum pillar deflection (t = 12 s) and finally an overlay of the two images. We can clearly observe that the microsensor tip deflection is at its maximum at t = 12 s. Fig. 2b illustrates the distance between two consecutive microsensor posts and the channel side walls is sufficiently large to minimize the effect of their mutual interactions on deflection.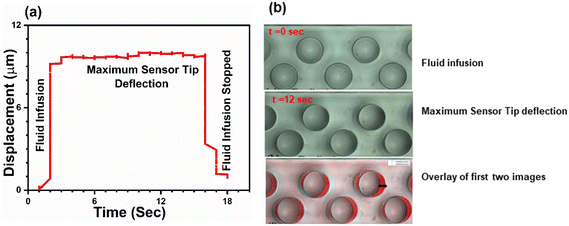 | ||
| Fig. 2 (a) Microsensor tip deflection as a function of time for a single microsensor with aqueous glycerol solution being infused. Tip deflection increases with time and the saturation region represents the average maximum microsensor tip deflection at a given flow rate. When the flow is stopped, the microsensor tip returns to its original position. (b) A collection of raw images depicting two stages of the microsensor tip deflection that is at t = 0 when there is no deflection and at t = 12 s when we have maximum deflection. An overlay of these two images is shown where we can clearly appreciate the microsensor deflection. The arrow indicates the amount the microsensor has moved from its mean position. See ESI† (a). | ||
Machine learning methods
Support vector machine (SVM)
Due to our small data set, we focused on machine learning (ML) algorithms that help build a non-biased model and avoid overfitting. We considered the most commonly used supervised learning algorithms including the decision tree (DT), naïve Bayes (NB), logistic regression (LR), k-nearest neighbour (k-NN) and support vector machine (SVM). We selected the SVM and k-NN as the primary ML method for our study based on their performance in avoiding data overfitting and their ability to build a non-biased model. The SVM, first introduced by Vapnik,38,39 is a supervised machine learning model that classifies nonlinearly separable data in a definite class. The SVM is known as a maximum margin classifier because it maximizes the geometrical margin and minimizes the empirical classification error. The SVM builds an area of spread vectors in a high dimensional space to create a maximum-margin separating hyperplane along with two parallel hyperplanes. The main task of the separating hyperplane is to expand the span of two parallel hyperplanes. The separating hyperplane (H) can be defined by eqn (1):| w·H + b = 0 | (1) |
The SVM performs the classification using different kernel functions such as polynomial, sigmoid, and radial basis function (rbf) for every nonlinear pattern. In our experiment, we used a nonlinear kernel, the rbf kernel function, which is defined by eqn (2):
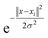 | (2) |
k-Nearest neighbour (k-NN)
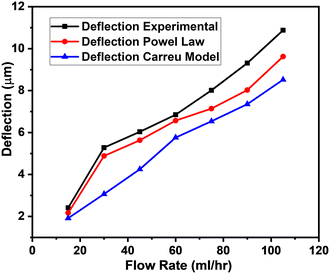
The k-NN is a simple non-parametric classification method utilized in classification and regression.42 The main idea of the k-NN is to memorize the training set and then predict the new sample based on its closest neighbours in the training set. Distance functions and metrics help to find the closest neighbours. Euclidian, Manhattan, Chebyshev etc. are examples of distance functions whereas Minkowski, Cosine, Hamming etc. are examples of distance metrics.43We used the Minkowski distance metric in this work, which handles continuous variables. Minkowski is a generalized distance metric that can be easily manipulated by changing its parameter value and is defined in eqn (3):
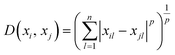 | (3) |
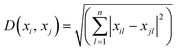 | (4) |
Results and discussion
Fluid infusion experiments
Experimental results for microsensor deflection were obtained for fluid flow rates ranging between 15 and 105 mL h−1 (γ = 60.5–398.4 s−1). A linear trend of increasing microsensor deflection was observed as the flow rate increases from 15 to 105 mL h−1 for all viscosities between 5 and 100 cP. The experimental results obtained for microsensor deflection were confirmed using computational fluid dynamic (CFD) studies as shown in Fig. 3, S2 and S3.† The microfluidic viscometer with a zigzag microsensor arrangement yields higher tip deflection compared to that with a straight microsensor arrangement due to enhanced fluid–structure interaction see ESI† S2. The microsensor in the middle of the array with the highest deflection values was chosen for data analysis (see ESI† S3).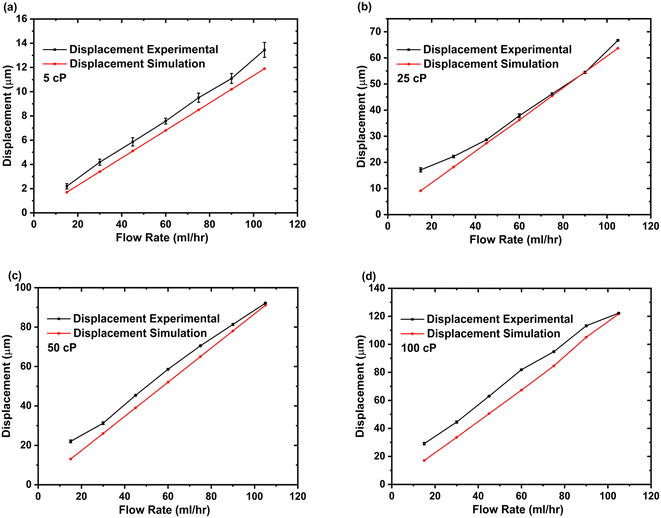 | ||
| Fig. 3 Comparison of experimental and CFD results for microsensor tip deflection due to fluid flow as a function of flow rate at various fluid viscosities. (a) 5 cP, (b) 25 cP, (c) 50 cP and (d) 100 cP. For each viscosity and flow rate value, a set of three experiments were performed (n = 3). The error bars for experiments with the 5 cP sample are clearly visible. However, at higher viscosity values, the measurements are more consistent, leading to much smaller error bars. Fig. S2(a–c)† show a comparison of additional experimental and CFD results for microsensor tip deflection at the following fluid viscosities: 10 cP, 15 cP and 75 cP. | ||
Fig. 3 presents results from a single microfluidic device with experiments performed at 7 different flow rates and 4 different viscosities with 3 measurements (n = 3) for each combination. The elasticity of PDMS microsensors, influenced by factors such as the base to curing agent ratio and baking temperature, remained unchanged throughout the experiments. We observed that the microsensors returned to their initial position once the fluid flow (shear stress) ceased, and repeated deflection cycles did not affect the maximum deflection, confirming the robustness of the microsensors where any changes in elasticity would compromise the consistency of the results.
The microfluidic viscometer was further tested using a non-Newtonian fluid (whole blood). To determine microsensor deflection, we adopted a method similar to the Newtonian fluid case, primarily recording videos as the blood was infused into the viscometer and then post-processing using the Matlab code. Similar to the Newtonian fluid case, an increasing trend for microsensor deflection with increasing flow rate was observed for whole blood samples as shown in Fig. 4. As we used the whole blood samples, it became increasingly difficult for our Matlab code to track the microsensor deflection especially at higher flow rates. The microsensor deflection response of our viscometer for whole blood samples was compared with CFD studies based on the power law and Carreu model for non-Newtonian fluid flow as shown in Fig. 4. The results indicate that the power law for non-Newtonian fluids more accurately models the microsensor deflection trend for our microfluidic viscometer when blood is used as the sample fluid. See ESI† S4 for simulation details. To illustrate the shear-dependent viscosity characteristics of non-Newtonian fluids, Fig. S4.3† presents a viscosity versus shear rate plot for a whole blood sample. The results reveal a shear-thinning behaviour, where the viscosity decreases with higher shear rates.
 | ||
| Fig. 4 Comparison of experimental and CFD results (power law and Carreu model) for microsensor tip deflection with whole blood as sample fluid flow as a function of flow rate. See ESI† (b). | ||
The sensitivity and dynamic range of the microfluidic viscometer depend on the device geometry (micropillar dimensions and aspect ratio) and the resolution of the imaging system. The viscometer sensitivity increases with the aspect ratio of the micropillars. The sensitivity can be increased by fabricating microsensors with higher aspect ratios, which was verified through CFD studies (see ESI† S5 for details). Increasing the resolution of the imaging system enhances the sensitivity of the microfluidic viscometer, but it also reduces the device's dynamic range. In our study, we determined the dynamic range to be 5–100 cP, as the micropillar tip displacement reached its maximum deflection beyond 100 cP, and the imaging system was unable to discern the small changes in displacement due to limited resolution. The microsensor deflection data discussed in this section was used to calculate the viscosity of unknown fluids using machine learning algorithms.
Viscosity calculations
The microfluidic viscometers reported in the literature employ internal flows for measuring fluid viscosity that requires mathematical modelling involving fluid dynamics governing equations. Modelling microfluidic systems with flexible structures and fluid flow is not trivial as it requires coupling of fluid dynamics and solid mechanics equations. We recently developed a facile microfluidic method to measure the fluid viscosity of both Newtonian and non-Newtonian fluids using elastomeric microsensors within a microchannel.25 Our method relies on deflection of the microsensors due to their interaction with impinging fluid flow. At a constant flow rate, the microsensor deflection increases with the fluid viscosity. Accurate modelling of the mechanical properties of flexible microposts and their interactions with the fluid flow is very challenging. Developing a rigorous model that closely matches experimental data by accurately coupling deformable solids (microposts) and an incompressible fluid requires precise viscoelastic characterization of the micropost material at the microscale and is the subject of ongoing research. To mitigate these challenges, we experimentally studied flexible microsensor deflection at various flow rates and fluid viscosities and obtained an empirical equation that correlates microsensor deflection to fluid viscosity. Using the microsensor deflection data for a number of reference fluids with known viscosities, we derived a calibration curve for the microfluidic viscometer. Specifically, we used a 2nd order polynomial fit to the fluid viscosity versus microsensor deflection data by using eqn (5):| η(x) = I + b1x + b2x2 | (5) |
The raw data were then divided into 1323 samples (known solution data) and were used to train our machine learning models. In the case of the SVM and k-NN, 926 of 1323 data samples (70% of total data) were used as the training data set, and 397 data samples (30% of the total data) were used for validation. The SVM and k-NN classified the data into 7 classes (viscosity solutions), i.e., 5, 10, 15, 20, 25, 50, 75, and 100 cP aqueous glycerol solutions. The confusion matrices provide an insight into the trained algorithm (Tables S2 and S3 in ESI† S6). The training and validation accuracies of the SVM and k-NN are shown in Table 1.
| Algorithms | Training accuracy | Validation accuracy | Test accuracy |
|---|---|---|---|
| SVM-rbf | 88.12% | 89.67% | 89.70% |
| k-NN3 | 97.94% | 98.48% | 98.90% |
The results were then validated by measuring three performance matrices: precision, recall and F1-score given by the following equations:
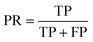 | (6) |
 | (7) |
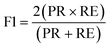 | (8) |
The precision matrix identifies the relevant instances (unknown solution viscosity data) among the retrieved instances (known solution viscosity data). The accuracy matrix on the other hand is a collection of correctly classified instances. The number of relevant instances which are retrieved from the total number of instances forms the recall matrix. The calculated results for the performance matrices are shown in ESI† S6. After validating the data from all known viscosities, experimental data (deflection vs. flow rate) from samples with unknown viscosity were classified. Four fluid samples with unknown viscosity, 5.74 cP (whole blood), 11.91 cP (decanol), 50 cP and 75 cP (aqueous glycerol solutions), were classified using the SVM. Reference viscosity measurements of the unknown samples were obtained either by using a conventional viscometer or from the commercial supplier. 596 data points were obtained for these fluid samples. Table 2 shows the confusion matrix for the fluid samples with unknown viscosity along with the corresponding performance matrices. The results show that the SVM classified the data with a test accuracy of 89.7%, yielding a similar result to the validation accuracy obtained during algorithm training.
| Classes | Predicted | Precision | Recall | F1 | |||||||
|---|---|---|---|---|---|---|---|---|---|---|---|
| 5 cP | 10 cP | 15 cP | 25 cP | 50 cP | 75 cP | 100 cP | |||||
| Actual | 5 cP | 149 | 0 | 0 | 0 | 0 | 0 | 0 | 0.91 | 1 | 0.95 |
| 10 cP | 13 | 127 | 9 | 0 | 0 | 0 | 0 | 1 | 0.85 | 0.92 | |
| 15 cP | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | |
| 25 cP | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | |
| 50 cP | 0 | 0 | 0 | 17 | 123 | 9 | 0 | 0.93 | 0.82 | 0.87 | |
| 75 cP | 0 | 0 | 0 | 0 | 8 | 135 | 5 | 0.93 | 0.91 | 0.92 | |
| 100 cP | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | |
As shown in Table 2, each sample was categorized based on the availability of the closest viscosity class. The whole blood sample, with a measured viscosity of 5.74 cP, was classified as a 5 cP solution, which represents the closest viscosity class available. Similarly, the decanol sample, with a measured viscosity of 11.91 cP, was classified as a 10 cP solution, again based on its closest matching viscosity class. Furthermore, the 50 and 75 cP aqueous glycerol solutions were accurately classified within their respective viscosity classes. The data presented in Table 2 suggest that the SVM provided the highest precision, equal to 1, when classifying decanol (11.91 cP). The 50 and 75 cP aqueous glycerol solutions both yielded a precision value of 0.93. The whole blood sample data (5.74 cP) resulted in a slightly lower precision value of 0.91.
To improve the data classification accuracy, the k-nearest neighbour (k-NN) classifier was used to calculate the viscosities of the unknown solutions. We set the value of k to be 3, where labels of 3 closest classes were checked. The trained k-NN algorithm was further validated by calculating performance matrices. The k-NN classified the data into 4 classes of 596 samples to find the viscosity of the unknown solutions. This algorithm yielded a test accuracy of 98.9%, which is significantly higher than the test accuracy of the SVM algorithm (89.7%). Table 3 provides the confusion matrix for the classification of the fluid samples with unknown viscosities along with the performance matrices. The results in Table 3 suggest that the k-NN also had the highest precision when classifying the decanol sample with a precision value of 1. Similarly, the 50 cP aqueous glycerol solution also achieved the same precision. The 75 cP aqueous glycerol solution and the whole blood sample resulted in a precision value of 0.98 and 0.90, respectively. By comparing the accuracy, precision values, recall and F-measure, we can safely conclude that the k-NN rendered more reliable values for these matrices and classified the data with higher accuracy in comparison with the SVM.
| Classes | Predicted | Precision | Recall | F1 | |||||||
|---|---|---|---|---|---|---|---|---|---|---|---|
| 5 cP | 10 cP | 15 cP | 25 cP | 50 cP | 75 cP | 100 cP | |||||
| Actual | 5 cP | 149 | 0 | 0 | 0 | 0 | 0 | 0 | 0.90 | 1 | 0.99 |
| 10 cP | 2 | 147 | 0 | 0 | 0 | 0 | 0 | 1 | 0.98 | 0.99 | |
| 15 cP | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | |
| 25 cP | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | |
| 50 cP | 0 | 0 | 0 | 0 | 146 | 3 | 0 | 1 | 0.97 | 0.98 | |
| 75 cP | 0 | 0 | 0 | 0 | 0 | 148 | 1 | 0.98 | 0.99 | 0.98 | |
| 100 cP | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | |
It is difficult to draw a direct quantitative comparison between ML methods and the traditional methods as the former are classification methods whereas the latter are based on determining a single viscosity value. To provide a quantitative comparison, we calculated the % error in viscosity measurements for our ML method using eqn (9).
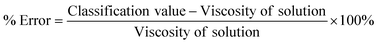 | (9) |
Real time monitoring of blood coagulation
To demonstrate the versatility of our ML-based viscosity measurement method, we performed blood coagulation studies and successfully identified various phases of clot formation. Viscoelastic haemostatic assays (VHAs) are blood tests which monitor various phases of blood coagulation by measuring viscoelastic properties of blood during clot formation and degradation. These tests typically measure blood viscosity (or clot firmness) as a function of time and classify viscosity values into distinct regions to determine phases of blood coagulation. In these tests, the duration of each phase and the transition time between phases reveal information about the coagulation process and are used for diagnosing bleeding disorders. We performed coagulation experiments with our microfluidic viscometer using human whole blood samples and employed our ML based method to classify viscosity values and identify different phases of clot formation. The purpose of these experiments was to predict time-dependent changes in blood viscosity during the coagulation process.44 The experiments were performed using a coagulation agent (5 mM CaCl2) at a continuous flow rate of 15 mL h−1 to mimic the physiological flow rate of the blood.45,46 The results shown in Fig. 5 represent the microsensor tip deflection as a function of time during blood coagulation. Overall, we observed that blood viscosity increases as a function of time where three distinct phases can be identified.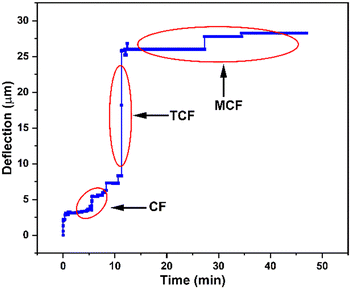 | ||
| Fig. 5 Identification of various stages of blood coagulation using the microfluidic viscometer and ML-based classification. We measured microsensor tip deflection as a function of time showing an overall increase in blood viscosity during clot formation. ML-based classification of this data reveals three distinct phases of coagulation as defined in rotational thromboelastometry (ROTEM), a conventional viscoelastic haemostatic assay: clot formation (CF), time to clot formation (TCF) and maximum clot firmness (MCF). See ESI† (c) for blood coagulation experiments. | ||
Using this plot, we identified various phases of blood coagulation by classifying microsensor tip deflection corresponding to the characteristic physiological processes taking place during clot formation (see the ESI† for videos on blood coagulation experiments). Specifically, we identified three distinct stages of clot formation, called clot formation (CF), time to clot formation (TCF), and maximum clot firmness (MCF), which are routinely determined in rotational thromboelastometry (ROTEM) tests, a conventional viscoelastic haemostatic assay. Between t = 0 and 12 min, the microsensor tip deflection remains between 2.5 and 5.5 μm. This period, defined as clot formation (CF), corresponds to the onset of thromboplastin activation and formation of first fibrins where the change in viscosity is relatively small. Between t = 12 and 15 min, the microsensor tip deflection rapidly increases to 21 μm. This period, called time to clot formation (TCF), represents the kinetics of thrombin formation and fibrin polymerization. After this point, the microsensor tip deflection enters a saturation region where blood viscosity remains stable. This coagulation phase, termed maximum clot firmness (MCF),47 indicates clot stabilization by fibrin polymerization. The shape of the curve in Fig. 5, representing various stages of blood clotting (CF, TCF and MCF), is used as a diagnostic tool for identifying congenital or acquired bleeding disorders in a clinical setting. The magnitude and length of the curve are correlated to the blood viscosity and the duration of a specific coagulation stage, respectively. Therefore, accurate classification of the coagulation stage is of utmost importance for clinicians for accurate and timely diagnosis. The ML method discussed above can be extended to viscosity measurements of blood samples from patients with coagulation disorders. With large training datasets from patients, we believe that our approach could facilitate rapid diagnosis of bleeding disorders in a clinical environment.
The classification of raw microsensor tip deflection data to identify each of the three blood coagulation stages shown in Fig. 5 is provided in Table 4. The microsensor tip deflection data were divided into three classes: 0–10 μm (class A), 11–20 μm (class B) and 21–30 μm (class C). Each class corresponds to a unique phase of coagulation (CF, TCF, MCF) during clot formation, as identified by conventional blood coagulation tests, with underlying physiological processes yielding a change in blood viscosity. To determine these viscosity values, a second classification step was performed to assign a viscosity value to each class. This was achieved by using classified data from Table S3 in the ESI† for all viscosity values (5–100 cP). The viscosities for the microsensor tip deflection data in classes A, B and C are 5–10 cP, 15–25 cP, and 50–75 cP, respectively. The viscosity ranges reported here for the three stages of coagulation process are comparable to those reported in the literature.48 Overall, our method has the potential to be utilized for determining blood viscosity to monitor stages of blood coagulation as a point-of-care diagnostic tool in biomedical applications.49,50
![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 867 data samples and performance matrices for blood coagulation
867 data samples and performance matrices for blood coagulation
| Classes | Class A | Class B | Class C | Total | Precision | Recall | F1 |
|---|---|---|---|---|---|---|---|
| CF (0–10 μm) | TCF (11–20 μm) | MCF (21–30 μm) | |||||
| 0–10 μm | 8112 | 0 | 0 | 8112 | 1 | 1 | 1 |
| 11–20 μm | 0 | 7 | 0 | 7 | 0.020 | 1 | 0.04 |
| 21–30 μm | 0 | 336 | 25![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 419 419 |
25![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 755 755 |
1 | 0.98 | 0.99 |
Our machine learning based approach for determining viscosity features several advantages over conventional methods. First, using machine learning algorithms to determine viscosity through unprocessed microsensor deflection data obviates the need to derive complex mathematical models and fit equations to calibration curves. Determination of viscosity for both Newtonian and non-Newtonian fluids with high classification accuracy, ease of classification and extracting useful information from raw data are distinctive advantages of our ML method over traditional counterparts. Second, the ML-based approach enables learning from additional data sets thereby reducing artifacts and improving accuracy. Third, our results suggest that this method provides the same level of accuracy in comparison with equation-based models with the potential for further improvement through acquisition of a refined training data set. Finally, our ML approach provides additional benefits for applications such as determining various stages of blood coagulation where a robust classification of viscosity is needed. However, our ML-based method comes with some limitations. First, raw data should be processed through a relatively slow algorithm, thereby limiting applications for real-time monitoring of fluid viscosity. Second, our method does not yield a specific viscosity value, therefore it is not suitable for applications where the viscosity behaviour is not known, or classification does not provide practical information.
Conclusion
The microsensor-based viscometer design was validated by performing experiments under continuous flow conditions within the range of 15–105 mL h−1. A computational fluid dynamics model was used to verify the microsensor bending for both Newtonian and non-Newtonian fluid samples. Viscosity values of four unknown solutions were determined with an average test accuracy of 89.7% (SVM) and 98.9% (k-NN) using two machine learning algorithms. We performed coagulation experiments with our microfluidic viscometer and determined three distinct stages of blood coagulation by classifying microsensor tip deflection as a measure of changing blood viscosity during clot formation.The method presented in this work can be expanded further for potential biomedical and clinical applications. For instance, ML-based methods could improve the accuracy of blood coagulation tests for different blood types where there are subtle differences among coagulation patterns.51 Moreover, for viscoelastic haemostatic assays, ML-based approaches can accelerate the analysis by eliciting additional features from the coagulation kinetics, thereby potentially reducing the test time. The ML-based approach discussed in this work would yield a high percentage error if the classification accuracy is low. The classification accuracy can be further improved with extended training data sets. However, obtaining large data sets may not be possible for many applications. Furthermore, ML classification is carried out for a set of predetermined viscosities, thereby limiting the precision of the measurement by the number of classes. Overall, while our method provides a convenient approach to measure viscosity, eliminating the need for accurate modelling of the underlying physical system, we should note that to improve the classification accuracy and reduce the % error of potential applications, an extended number of data sets for training would be required.
We anticipate that ML-based approaches would significantly improve performance for applications requiring classification of viscosity values. The microfluidic viscometer presented here can be modified by integrating multiple parallel channels with microsensor arrays on a single chip to enable simultaneous viscosity measurements of multiple (4–8) fluids using minute samples. A multichannel configuration can also be used to obtain replicate measurements from a sample, potentially improving measurement accuracy and device efficiency. The dynamic range of the microsensor-based microfluidic viscometer can be extended to measure viscosities beyond 100 cP by integrating a high precision imaging system.
Data availability
All data generated or analysed during this study are included in this published article and the ESI.†Ethical statement
This study was conducted under IRB: 001/2015 approved by the Ethics Committee of Koç University School of Medicine and informed written consent was obtained from each subject participating in the study.Author contributions
A. M. conducted the experiments; A. M. performed the data analysis; D. H. and A. B. developed the machine learning algorithms; A. M., D. H., and A. B. performed the viscosity measurements; M. T., A. E., and O. Y. supervised the experimental study design and interpretation; A. M., D. H., M. T., A. E. and O. Y. wrote the article; A. M., D. H., A. B., M. T., A. E., and O. Y. read and approved the final version of the manuscript.Conflicts of interest
The authors declare no potential conflict of interest.Acknowledgements
This study was supported by the Turkish Scientific and Technological Research Council grant SBAG-15S.References
- S. Ebnesajjad, Fabrication and Processing of Polytetrafluoroethylene Dispersions, in Introduction to Fluoropolymers, ed. S. Ebnesajjad, William Andrew Publishing, Oxford, 2nd edn, 2021, pp. 149–167, DOI:10.1016/B978-0-12-819123-1.00009-4.
- A. Taguet, Rheological characterization of compatibilized polymer blends, in Compatibilization of Polymer Blends, ed. R. A. Ajitha and S. Thomas, Elsevier, 2020, pp. 453–487, DOI:10.1016/B978-0-12-816006-0.00016-5.
- C. Verdier, J. Etienne, A. Duperray and L. Preziosi, Rheological properties of biological materials, C. R. Phys., 2009, 790–811 CrossRef CAS.
- J. Abraham, T. Sharika, R. K. Mishra and S. Thomas, Rheological characteristics of nanomaterials and nanocomposites, in Micro and Nano Fibrillar Composites (MFCs and NFCs) from Polymer Blends, ed. R. K. Mishra, S. Thomas and N. Kalarikkal, Woodhead Publishing, 2017, pp. 327–350, DOI:10.1016/B978-0-08-101991-7.00014-5.
- S. Gupta, W. S. Wang and S. A. Vanapalli, Microfluidic viscometers for shear rheology of complex fluids and biofluids, Biomicrofluidics, 2016, 10, 43402, DOI:10.1063/1.4955123.
- A. L. Coker, Point-of-Care (POC) Devices by Means of Advanced MEMS, Physiol. Behav., 2017, 176, 139–148, DOI:10.1016/j.physbeh.2017.03.040.
- R. Khnouf, D. Karasneh, E. Abdulhay, A. Abdelhay, W. Sheng and Z. H. Fan, Microfluidics-based device for the measurement of blood viscosity and its modeling based on shear rate, temperature, and heparin concentration, Biomed. Microdevices, 2019, 21(4), 80, DOI:10.1007/s10544-019-0426-5.
- B. Deng, J. De Ruiter and K. Schroën, Application of microfluidics in the production and analysis of food foams, Foods, 2019, 8(10), 476, DOI:10.3390/foods8100476.
- P. Kiełczyński, M. Szalewski, A. Balcerzak, A. J. Rostocki and D. B. Tefelski, Application of SH surface acoustic waves for measuring the viscosity of liquids in function of pressure and temperature, Ultrasonics, 2011, 51, 921–924, DOI:10.1016/j.ultras.2011.05.006.
- M. F. Khan, S. Schmid, P. E. Larsen, Z. J. Davis, W. Yan and E. H. Stenby, et al., Online measurement of mass density and viscosity of pL fluid samples with suspended microchannel resonator, Sens. Actuators, B, 2013, 185, 456–461, DOI:10.1016/j.snb.2013.04.095.
- R. Moreno, Rheology, in Encyclopedia of Materials: Science and Technology, ed. K. H. J. Buschow, R. W. Cahn, M. C. Flemings, B. Ilschner, E. J. Kramer and S. Mahajan, et al., Elsevier, Oxford, 2001, pp. 8192–8196, DOI:10.1016/B0-08-043152-6/01468-6.
- D. Ah-Moye, C. Davies, J. Goody, P. Hayward and R. Frewin, Introduction to haematology and transfusion science, in Clinical Biochemistry: Metabolic and Clinical Aspects, ed. W. J. Marshall, M. Lapsley, A. P. Day and R. M. Ayling, Churchill Livingstone, 3rd edn, 2014, pp. 497–514, DOI:10.1016/B978-0-7020-5140-1.00026-2.
- R. V. Stan, In Vitro Vascular Cell Culture Systems – Endothelial Cell Culture Systems, in Comprehensive Toxicology, ed. C. A. McQueen, Elsevier, Oxford, 2nd edn, 2010, pp. 97–111, DOI:10.1016/B978-0-08-046884-6.00727-2.
- P. M. Doran, Fluid Flow, in Bioprocess Engineering Principles, ed. P. M. Doran, Academic Press, London, 2nd edn, 2013, pp. 201–254, DOI:10.1016/B978-0-12-220851-5.00007-1.
- S. J. Shire, The molecular basis of high viscosity of monoclonal antibodies (mAbs) at high concentration, in Monoclonal Antibodies, ed. S. J. Shire, Woodhead Publishing, 2015, pp. 163–192, DOI:10.1016/B978-0-08-100296-4.00009-9.
- G. E. Miller, Biomedical Transport Processes, in Introduction to Biomedical Engineering, ed. J. D. Enderle and J. D. Bronzino, Academic Press, Boston, 3rd edn, 2012, pp. 937–993, DOI:10.1016/B978-0-12-374979-6.00014-9.
- A. Akpek, C. Youn and T. Kagawa, A Study on Vibrational Viscometers Considering Temperature Distribution Effect, JFPS Int. J. Fluid Power Syst., 2014, 7, 1–8, DOI:10.5739/jfpsij.7.1.
- A. Saluja and S. Kalonia, Vacuum Microbalance Techniques, AAPS PharmSciTech, 1966, 5, 193–205 Search PubMed.
- P. Guillot, P. Panizza, J. B. Salmon, M. Joanicot, A. Colin and C. H. Bruneau, et al., Viscosimeter on a microfluidic chip, Langmuir, 2006, 22, 6438–6445, DOI:10.1021/la060131z.
- Y. Jun Kang, J. Ryu and S. J. Lee, Label-free viscosity measurement of complex fluids using reversal flow switching manipulation in a microfluidic channel, Biomicrofluidics, 2013, 7, 19–21, DOI:10.1063/1.4816713.
- S.-G. Baek and J. J. Magda, Monolithic rheometer plate fabricated using silicon micromachining technology and containing miniature pressure sensors for N1 and N2 measurements, J. Rheol., 2003, 47, 1249–1260, DOI:10.1122/1.1595095.
- N. Srivastava and M. A. Burns, Analysis of non-Newtonian liquids using a microfluidic capillary viscometer, Anal. Chem., 2006, 78, 1690–1696, DOI:10.1021/ac0518046.
- Y. J. Kang, S. Y. Yoon, K. Lee and S. Yang, A Highly Accurate and Consistent Microfluidic Viscometer for Continuous Blood Viscosity Measurement, Artif. Organs, 2010, 34, 944–949, DOI:10.1111/j.1525-1594.2010.01078.x.
- S. E. Mena, Y. Li, J. McCormick, B. McCracken, C. Colmenero and K. Ward, A droplet-based microfluidic viscometer for the measurement of blood coagulation, Biomicrofluidics, 2020, 14(1), 014109, DOI:10.1063/1.5128255.
- A. Mustafa, A. Eser, A. C. Aksu, A. Kiraz, M. Tanyeri and A. Erten, A micropillar-based microfluidic viscometer for Newtonian and non-Newtonian fluids, Anal. Chim. Acta, 2020, 1135(0003-2670), 107–115, DOI:10.1016/j.aca.2020.07.039.
- S. Große and W. Schröder, The Micro-Pillar Shear-Stress Sensor MPS3 for turbulent flow, Sensors, 2009, 9, 2222–2251, DOI:10.3390/s90402222.
- R. M. Judith, B. Lanham, M. R. Falvo and R. Superfine, Microfluidic viscometry using magnetically actuated micropost arrays, PLoS One, 2018, 13(7), 1–17, DOI:10.1371/journal.pone.0200345.
- J. Riordon, D. Sovilj, S. Sanner, D. Sinton and E. W. K. Young, Deep Learning with Microfluidics for Biotechnology, Trends Biotechnol., 2019, 37, 310–324, DOI:10.1016/j.tibtech.2018.08.005.
- O. J. Dressler, P. D. Howes, J. Choo and A. J. Demello, Reinforcement Learning for Dynamic Microfluidic Control, ACS Omega, 2018, 3, 10084–10091, DOI:10.1021/acsomega.8b01485.
- A. Chu, D. Nguyen, S. S. Talathi, A. C. Wilson, C. Ye and W. L. Smith, et al., Automated detection and sorting of microencapsulation: Via machine learning, Lab Chip, 2019, 19, 1808–1817, 10.1039/c8lc01394b.
- Z. J. Baum, X. Yu, P. Y. Ayala, Y. Zhao, S. P. Watkins and Q. Zhou, J. Chem. Inf. Model., 2021, 61(7), 3197–3212, DOI:10.1021/acs.jcim.1c00619.
- B. Debus, H. Parastar, P. Harrington and D. Kirsanov, Deep learning in analytical chemistry, TrAC, Trends Anal. Chem., 2021, 0165–9936, DOI:10.1016/j.trac.2021.116459.
- S. Momtahen, F. Al-Obaidy and F. Mohammadi, Machine Learning with Digital Microfluidics for Drug Discovery and Development, 2019 IEEE Canadian Conference of Electrical and Computer Engineering CCECE, 2019, DOI:10.1109/CCECE.2019.8861842.
- M. S. Manak, J. S. Varsanik, B. J. Hogan, M. J. Whitfield, W. R. Su and N. Joshi, et al. , Nat. Biomed. Eng., 2018, 2(10), 761–772, DOI:10.1038/s41551-018-0285-z; M. S. Manak, J. S. Varsanik, B. J. Hogan, M. J. Whitfield, W. R. Su and N. Joshi, Live-cell phenotypic-biomarker microflu, Nat. Biomed. Eng., 2018, 47, 549–562, DOI:10.1097/CCM.0b013e31823da96d.Hydrogen.
- T. Xia, R. Jiang, Y. Q. Fu and N. Jin, Automated Blood Cell Detection and Counting via Deep Learning for Microfluidic Point-of-Care Medical Devices, IOP Conf. Ser.: Mater. Sci. Eng., 2019, 646, 012048, DOI:10.1088/1757-899X/646/1/012048.
- P. Hadikhani, N. Borhani, S. M. H. Hashemi and D. Psaltis, Learning from droplet flows in microfluidic channels using deep neural networks, Sci. Rep., 2019, 9, 1–7, DOI:10.1038/s41598-019-44556-x.
- J. W. Khor, N. Jean, E. S. Luxenberg, S. Ermon and S. K. Y. Tang, Using machine learning to discover shape descriptors for predicting emulsion stability in a microfluidic channel, Soft Matter, 2019, 15, 1361–1372, 10.1039/c8sm02054j.
- P. Prabhu, A. K. Karunakar, H. Anitha and N. Pradhan, Classification of gait signals into different neurodegenerative diseases using statistical analysis and recurrence quantification analysis, Pattern Recognit. Lett., 2020, 139, 10–16, DOI:10.1016/j.patrec.2018.05.006.
- V. N. Vapnik, Statistical learning theory, Wiley, 1998 Search PubMed.
- M. H. Afif and A. R. Hedar, Data classification using support vector machine integrated with scatter search method, Proceedings of the 2012 Japan-Egypt Conference on Electronics, Communications and Computers, JEC-ECC 2012, 2012, pp. 168–172, DOI:10.1109/JEC-ECC.2012.6186977.
- A. Barua, C. Dong, F. Al-Turjman and X. Yang, Edge Computing-Based Localization Technique to Detecting Behavior of Dementia, 2020, vol. 8, DOI:10.1109/ACCESS.2020.2988935.
- A. Barua, X. Yang, A. Ren, D. Fan, L. Guan and N. Zhao, et al., Gait signals classification and comparison, Int. J. Numer. Model.: Electron. Netw. Devices Fields, 2019, 32, 1–16, DOI:10.1002/jnm.2577.
- C. J. Pipe, T. S. Majmudar and G. H. McKinley, High shear rate viscometry, Rheol. Acta, 2008, 47, 621–642, DOI:10.1007/s00397-008-0268-1.
- G. M. Walker and D. J. Beebe, A passive pumping method for microfluidic devices, Lab Chip, 2002, 2, 131–134, 10.1039/b204381e.
- W. J. Lan, S. W. Li, J. H. Xu and G. S. Luo, Rapid measurement of fluid viscosity using co-flowing in a co-axial microfluidic device, Microfluid. Nanofluid., 2010, 8, 687–693, DOI:10.1007/s10404-009-0540-4.
- M. Ranucci, T. Laddomada, M. Ranucci and E. Baryshnikova, Blood viscosity during coagulation at different shear rates, Physiol. Rep., 2014, 2, 1–7, DOI:10.14814/phy2.12065.
- M. Klarhöfer, B. Csapo, C. Balassy, J. C. Szeles and E. Moser, High-resolution blood flow velocity measurements in the human finger, Magn. Reson. Med., 2001, 45, 716–719, DOI:10.1002/mrm.1096.
- X. Xu, J. Geng and X. Teng, Monitoring the blood coagulation process under various flow conditions with optical coherence tomography, J. Biomed. Opt., 2014, 19, 046021, DOI:10.1117/1.jbo.19.4.046021.
- M. Mohammadi Aria, A. Erten and O. Yalcin, Technology Advancements in Blood Coagulation Measurements for Point-of-Care Diagnostic Testing, Front. Bioeng. Biotechnol., 2019, 7, 1–18, DOI:10.3389/fbioe.2019.00395.
- S. D. Sahli, J. Rössler, D. W. Tscholl, J. D. Studt, D. R. Spahn and A. Kaserer, Point-of-care diagnostics in coagulation management, Sensors, 2020, 20, 1–21, DOI:10.3390/s20154254.
- C. Okeke, U. Okoro and A. Babatunde, Variations in activated partial thromboplastin time and prothrombin time in individuals of A, B, AB, and O blood groups, Iraqi J. Hematol., 2018, 7, 85, DOI:10.4103/ijh.ijh_11_18.
Footnote |
| † Electronic supplementary information (ESI) available. See DOI: https://doi.org/10.1039/d3sd00099k |
| This journal is © The Royal Society of Chemistry 2023 |