Open Access Article
Open Access ArticleCreative Commons Attribution 3.0 Unported Licence
Size-modified Poisson–Nernst–Planck approach for modeling a local electrode environment in CO2 electrolysis†
Esaar Naeem
Butt
 ,
Johan T.
Padding
,
Johan T.
Padding
 and
Remco
Hartkamp
and
Remco
Hartkamp
 *
*
Department of Process and Energy, Delft University of Technology, Leeghwaterstraat 39, 2628 CB, Delft, The Netherlands. E-mail: r.m.hartkamp@tudelft.nl; Tel: +31 15 27 86674
First published on 22nd November 2022
Abstract
Electrochemical reduction of CO2 heavily depends on the reaction conditions found near the electrode surface. These local conditions are affected by phenomena such as electric double layer formation and steric effects of the solution species, which in turn impact the passage of CO2 molecules to the catalytic surface. Most models for CO2 reduction ignore these effects, leading to an incomplete understanding of the local electrode environment. In this work, we present a modeling approach consisting of a set of size-modified Poisson–Nernst–Planck equations and the Frumkin interpretation of Tafel kinetics. We introduce a modification to the steric effects inside the transport equations which results in more realistic concentration profiles. We also show how the modification lends the model numerical stability without adopting any separate stabilization technique. The model can replicate experimental current densities and faradaic efficiencies till −1.5 vs. SHE/V of applied electrode potential. We also show the utility of this approach for systems operating at elevated CO2 pressures. Using Frumkin-corrected kinetics gels well with the theoretical understanding of the double layer. Hence, this work provides a sound mechanistic understanding of the CO2 reduction process, from which new insights on key performance controlling parameters can be obtained.
1 Introduction
Electrochemical reduction of CO2 (CO2ER) has emerged as one of the most promising technologies to mitigate the excessive amounts of CO2 in the atmosphere.1–3 Renewable electricity can be used to power the conversion of CO2 into different hydrocarbon molecules, which can then be utilized as fuels, energy storage media and chemicals for various industrial applications such as plastic production, preservatives and anti-freezing. However, there are several challenges for such a technology to be fully functional under industrially relevant operating conditions. A lot of these challenges stem from the gap in knowledge about the exact physicochemical phenomena taking place in the immediate environment of the catalyst surface. This local environment of a CO2ER catalyst is thought to be a vital ingredient determining the overall system performance.4The concentrations of the solution species found in the vicinity of the electrode end up affecting the properties of the catalyst and consequently the selectivities of the desired products.5,6 The buildup of cations on the surface of the electrode results in the formation of an electric double layer (EDL), which affects the mass transport of reactive CO2 as well as the driving force for the interfacial charge transfer reactions. Hence, it becomes essential to develop modeling approaches that can correctly resolve the mass transport as well as the electric field within the EDL, see Table 1. Most techniques used to model the CO2ER process ignore these EDL effects and are insufficient in their theoretical implementation. Modeling techniques based on atomistic calculations have been used a lot for modeling double layer effects,7,8 but atomistic simulations may not be the preferred approach to model reactions, capture the role of pH, and cover the range of length scales relevant to CO2ER. Continuum-based methods offer a more practical approach to model CO2ER, where the underlying physics is largely included in a mean-field way.
Out of the many approaches to model CO2ER transport, one of the most commonly used, is the reaction-diffusion model.9 This type of approach is based on the charge neutrality assumption and hence is not suitable for modeling mass transport inside the EDL.10–13 Another approach, rooted in dilute solution theory, uses a set of Poisson–Nernst–Planck (PNP) equations.14 This model specifically considers the migration of ions toward the catalyst surface. However, steric effects due to the finite size of solution species, are usually neglected. As a result, unphysically high ionic concentrations are typically predicted in the EDL region.15–17
Steric effects are predicted to play a significant role in dictating the local reaction conditions of an electrode.15,16,18 More recently, a set of generalized modified PNP (GMPNP) equations was adopted in the context of CO2ER by Bohra et al.17 This model highlighted the importance of steric effects in the EDL region, as it corrected for the high ionic concentrations predicted by the classical PNP models. This GMPNP modeling approach predicts extremely low CO2 concentration at the reaction plane for cathodic potentials of −0.9 vs. standard hydrogen electrode (SHE)/V for an Ag(111) catalyst surface. These low concentrations are a direct result of the introduction of steric effects leading to increased mass transfer limitations for CO2. However, it is known from experimental studies that CO2ER is not completely mass transfer limited (reaching limiting current density) at these electrode potentials,19 suggesting that there is an overestimation of steric effects experienced by a CO2 molecule in the GMPNP modeling approach. Because overcoming mass transfer limitations of CO2 is one of the primary challenges in the optimal design of a CO2ER system, it is essential to have models that can predict the CO2 concentration in the EDL region accurately. In this work, we propose a set of size-modified PNP equations (SMPNP) for modeling the mass transport in a CO2ER system, and we couple this transport model with Frumkin-corrected Tafel relations. Overall, the FBV-SMPNP model provides a unique methodology to better approximate the local electrode environment in a computationally tractable manner and can be easily implemented for a wide range of applications including the evaluation of optimal conditions under which maximum faradaic efficiencies can be attained. The SMPNP equations extend the GMPNP approach by explicitly including the influence of solvent (water) molecule size on the chemical potential of each solution species. The origin of this modification is rooted in a lattice model for the free energy and has been previously utilized in biomolecular systems.20,21 Another factor to consider is that most CO2ER models include the reaction rates as either fixed input to the system9,17,22 or use some formulation of Butler–Volmer (BV) or Tafel relations with experimentally fixed kinetics parameters to predict reaction rates.10,23 The latter approach is often used to validate the models against experimental data. This is not possible if the reaction rates are fixed input to the system. Another advantage of explicitly considering kinetics inside the model is that it allows for the prediction of current densities at elevated pressures by fixing the kinetics parameters at just one experimental pressure value.23 Working at elevated pressures allows one to offset the CO2 solubility limitations which can be a technological solution to attaining industrially relevant operating current densities. Morrison et al.23 used a Tafel relation to predict limiting current densities for a CO2 to HCOO− system at elevated pressures. However, a standard Tafel kinetics relation does not explicitly take into account the influence of surface charging on reactions that are determined by the rate of interfacial charge transfer, because it assumes the driving force for the reaction to be the potential difference between the electrode and the bulk of electrolyte. However, in the presence of an EDL, the driving force for an interfacial charge transfer reaction comes from the potential drop across the immobile Stern layer.24–26 This is the so-called Frumkin correction to Butler–Volmer kinetics (FBV).25,27 The addition of this correction incorporates double layer behavior in the form of altered electrode rate constants. Considering this type of kinetics description is also necessary because the local concentrations in the EDL affect the local electric field and consequently the driving force for the interfacial charge transfer reactions. In this study, we use the complete set of FBV-SMPNP equations to obtain the concentration profiles for all components in the solution near the electrode surface. We present comparisons for the concentration profiles using different modeling approaches summarized in Table 1 and highlight the advantages of using a SMPNP-type mass transport formulation. We focus on the concentration of CO2 in the EDL, which was previously a bottleneck in the GMPNP model. We present a comparison between both models based on the estimated concentrations and highlight the significance of considering the modification of steric effects as presented in the SMPNP equations. The model is then validated by comparing the partial current densities of reactions that are sensitive to CO2 concentration with experimental data. Finally, we make a case for using the Frumkin-corrected kinetics approach for its merits in predicting the hydrogen evolution current densities with great accuracy and for its theoretical consistency with the EDL formulation.
2 Reaction and mass transport modeling
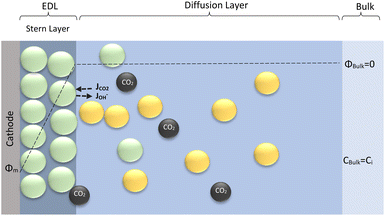
The electrochemical model is developed for a 1-D simulation domain stretching from the bulk of the electrolyte to the cathode. Only the cathodic side of the electrochemical cell is considered because the CO2ER reactions occurring at the cathode and the EDL are not influenced by the anodic section. The model also takes into account the so-called Nernst diffusion layer, sandwiched between the bulk electrolyte region and the EDL. It represents the charge-neutral layer of electrolyte where the concentrations of the species deviate from the bulk value because of the limited diffusivity of the solution species. Fig. 1 represents the complete simulation domain considered in this work. This study is based on potassium bicarbonate (KHCO3) electrolyte solution, which is one of the most commonly used electrolytes for CO2ER.28 The electrode material is assumed to be indium (In). The main product of CO2ER is HCOO−. The electrolyte solution is saturated with CO2 at high pressures. The following homogeneous carbonate equilibrium reactions occur in the electrolyte: | (1) |
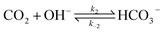 | (2) |
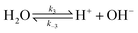 | (3) |
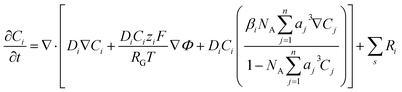 | (4) |
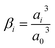 | (5) |
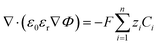 | (6) |
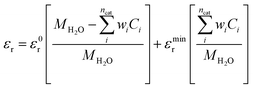 | (7) |
| CO2(aq) + H2O + 2e− ⇌ HCOO− + OH− | (8) |
| CO2(aq) + H2O + 2e− ⇌ CO(g) + 2OH− | (9) |
| 2H2O + 2e− ⇌ H2(g) + 2OH− | (10) |
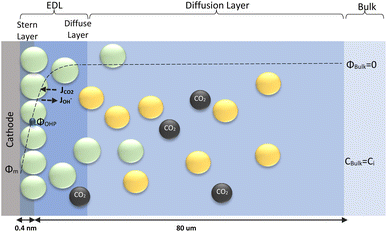 | ||
| Fig. 1 Schematic of mass transport regions for a CO2ER process. Stern layer composed mainly of K+. The plane of closest approach for the solution species is the outer Helmholtz plane (OHP). | ||
It is worth mentioning that eqn (8)–(10) represent the overall stoichiometric reaction and not the elementary electron transfer reactions. CO2 reduction reactions are complex multistep processes. In this work, the reaction mechanism is based on the work by Feaster et al.37 In the first step of CO2 reduction, one electron is transferred to form a radical anion CO2˙−. The radical anion may or may not be strongly adsorbed to the surface of the catalyst depending on the type of metal and the eventual product being produced.38 For HCOO− forming metals the CO2 binding occurs via the oxygen atoms resulting in intermediate *OCHO and for CO forming metals via the carbon atom resulting in intermediate *COOH.37 Regardless of the intermediate species, the final step involves the transfer of the second electron to the reactive intermediate to form the products (HCOO−, CO). The rate-determining step (RDS) is assumed to be the initial electron transfer to CO2 to form the radical anion.39,40 It is assumed that the adsorbed intermediate species do not influence or restrict CO2 to bind with the surface of the catalyst. This assumption has merit for catalyst surfaces such as indium, where at any time only small amounts of intermediate adsorbed species were found on the metal.38,41 Furthermore, experimental studies done at increasingly high CO2 pressures suggest an almost linear increase in limiting current densities, suggesting that even at high CO2 concentration, the adsorbed intermediates have negligible influence on the reaction rate.28 The flux of the species involved in the charge transfer reactions at the OHP (defined in our model as x = 0) and time t is given by:
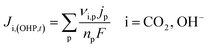 | (11) |
All other solution species are not taking part in charge transfer reactions, hence:
| Ji,(OHP,t) = 0, i = CO32−, K+, HCO3−, H+ | (12) |
The product species CO and H2 have very low solubility in water at room temperature hence it is assumed that they bubble out instantly from the system. HCOO− is assumed to not influence the overall transport of other solution species because it does not take part in homogeneous reactions23 and was found only in small amounts inside the system. νi,p is the stoichiometric coefficient of species i in reaction p (eqn (8)–(10)). np is the number of overall electrons transferred in reaction p. jp is the current density of the RDS involved in the overall reaction p. In many models, jp is assumed and given as input to the model alongside the applied electrode potential E. In reality, jp is influenced by local electric fields and the EDL environment until a steady state is reached. Therefore, in this work, only the electrode potential E is given as input to the model, and jp is evaluated at every time step, which in turn helps to inform the electrode flux boundary condition viaeqn (11). It is crucial to realize that because of the electrochemical reactions and formation of ions, the local environment at the surface of the electrode is in constant flux, with sharp gradients in species concentrations and electric potential. At relatively high applied electric potentials, we can therefore not assume local equilibrium conditions to apply. Because there is a practical interest in relatively high cathodic overpotentials, the backward reactions are ignored23 and the following Frumkin-corrected Tafel equation is used to evaluate current densities:24,25,42
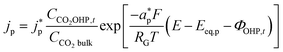 | (13) |
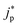 and
and 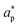 represent an effective exchange current density and charge transfer coefficient, respectively, and their values are calculated from Tafel plot data taken from the literature.28Eeq,p is the reference equilibrium potential for a reaction p according to standard potentials at pH = 7 (Table S6 in ESI†). ΦOHP,t is the electric potential at the reaction plane (OHP) and time t, modeled as:
represent an effective exchange current density and charge transfer coefficient, respectively, and their values are calculated from Tafel plot data taken from the literature.28Eeq,p is the reference equilibrium potential for a reaction p according to standard potentials at pH = 7 (Table S6 in ESI†). ΦOHP,t is the electric potential at the reaction plane (OHP) and time t, modeled as: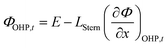 | (14) |
Eqn (14) is based on the idea that the Stern layer acts as a uniform dielectric film leading to a linear variation of the electric potential from the surface of the metal electrode to the OHP, with a continuous electric field at the OHP.27,43 Since the main reactant for the hydrogen evolution reaction in eqn (10) is H2O, there are no mass transfer limitations and the current density for HER becomes:
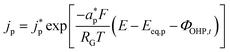 | (15) |
The significance of the Frumkin-corrected kinetics expressions eqn (13)–(15) is that the driving force for the elementary electron transfer is the potential difference between the metal electrode and the OHP. This correction accounts for the EDL by taking into consideration the variation of the apparent rate constants as a result of changing electric fields and local reaction environment.44,45 The concentration of the reactive species involved in the RDS is also evaluated at the OHP, which is the reaction plane in our model. This is in contrast to the standard BV formulation where the driving force is taken to be the potential difference between the metal electrode and the bulk region of the electrolyte. Furthermore, a standard BV formulation for kinetics is inconsistent with the Gouy–Chapman–Stern formulation of the EDL, as it ignores the influence of a diffuse layer. All potential values in the simulations are referenced with respect to the potential at the point of zero charge (PZC). The PZC value depends heavily on the material properties of the electrode as well as the electrolyte environment.46 Since we aim to recreate the experimental conditions, the value of PZC is fitted to data available in the literature.28Fig. 1 details the boundary conditions used in the model. Initially, all concentrations will be at bulk values and the electric potential value will be 0 throughout the simulation domain. The length of the diffusion layer is determined to be 80 μm based on the diffusion-limited current for such a system.23,28 Dirichlet boundary conditions for concentrations and potential are imposed on the right side of the simulation domain. At x = 0 (OHP), Neumann boundary conditions for the flux of the solution species are applied using eqn (11) and (12). Eqn (14) is used as a Robin boundary condition for the electric potential value at the OHP. Both Neumann and Robin boundary conditions are evaluated at every time step, making the model also suitable for transient and dynamic applications. The finite element package FEniCS is used to solve a weak formulation of the non-linear FBV-SMPNP equations. The complete set of equations (FBV eqn (11)–(15) and SMPNP eqn (4)–(7)) are solved self-consistently using a Newton solver. Spatial and temporal discretization is done using a finite element method and backward Euler scheme, respectively. The FBV-SMPNP model becomes less stable with increasing applied electrode potential. This is caused by the vastly different lengths and time scales required to model the different physicochemical processes. Hence the time step used in the first 7 milliseconds is 1 × 10−7 s and after that, a time step of 1 × 10−3 s is used until steady-state is reached. Similarly, a variable mesh spacing is used in the simulations, with a finer mesh near the OHP and a coarser mesh in the diffusion layer.
3 Results
In this section, we first present the resolved concentration profiles for various solution species in the vicinity of the electrode as a function of multiple applied electrode potentials (Fig. 2). The results are mainly centered around the first few nanometers because this is the region where most of the uncertainty with regard to concentrations of solution species exists. We show the effect of including the size ratio βi on the overall mass transfer. This effect is then validated against experimental partial current density values found in the literature (Fig. 4). The predictive power of the FBV-SMPNP model is tested by comparing partial current densities at elevated pressures of 40 bar (Fig. 5). We then show that using the FBV-type kinetics approach gives better estimates of HER partial current densities as compared to a standard BV-based kinetics model (Fig. 7).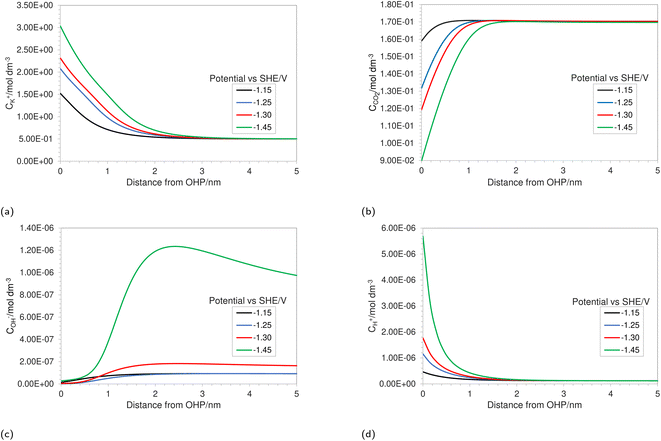 | ||
| Fig. 2 Concentration profiles in the EDL region for (a) K+, (b) CO2, (c) OH− and (d) H+ at varying applied electrode potentials for a 0.5 M KHCO3 solution at 5 bar CO2 pressure. | ||
Fig. 2a depicts the buildup of the cation K+ in the EDL region at increasing electrode potentials. Because the size of the solvated cations is explicitly considered in the model, there will be a limit on the maximum concentration of K+ ions at the OHP. Once this steric limit is reached, the thickness of the EDL profile increases. This results in the EDL behaving as a condensed layer of cations, rather than a diffuse layer. This in turn has implications for the CO2 reduction reaction, because now CO2 has to diffuse through a thicker dense layer of counter ions, leading to reduced access to the catalyst surface and, consequently, decrease in maximum attainable current density. Fig. 2b shows the decreasing CO2 concentration as the electrode potential is increased. This is correlated with the increasing K+ concentration and suggests that the rate of mass transfer is limiting the reaction. Fig. 2c depicts an almost complete depletion of OH− ions at the OHP. This is due to the negative charge associated with an OH− ion, resulting in increasing electrostatic repulsion near the OHP. This repulsion is taken into account by the migration term in eqn (4).
Similarly, an increase in the positively charged H+ ion concentration is observed with increasing electrode potential (Fig. 2d). The combined effect of OH− repulsion and H+ attraction leads to a significant drop in the local pH values. It is worth pointing out that not considering the volume exclusion effect will result in an unrealistically low pH.17 This is because, in the absence of the volume exclusion term in eqn (4), point-like species are assumed with no steric limits. For point-like species, the concentration of H+ at the OHP would be unrealistically high, whereas considering the size of hydrated H+ ions puts a steric limit to the maximum attainable concentration. It is also worth noting that the hydrated size of a H+ ion is considered since free protons generally do not exist in solution due to their lack of an electron cloud. Since pH is one of the more vital performance-controlling parameters experimentally,30 it becomes essential to consider size effects when modeling a CO2 reduction system. The general trend for concentration profiles as a function of applied potential is in agreement with the trends found by Bohra et al.17 using the GMPNP model but for different operating conditions of CO2 pressure, applied electrode potential and electrolyte concentration.
Fig. 3a shows the concentration profiles of K+ as predicted by different models at the same operating conditions. Each model differs in the level of complexity and physicochemical phenomena included in them (see Table 1). A reaction-diffusion type model (RD) predicts negligible cation concentration at the OHP as compared to other modeling approaches. This is because such an approach does not explicitly take into account the migration due to the assumption of charge neutrality. Consequently, such an approach might be only suitable for analyzing the mass transport behavior in the diffusion layer and for highly concentrated solutions where the entire double layer charge is carried inside the Stern layer, giving us a Helmholtz description of the EDL.
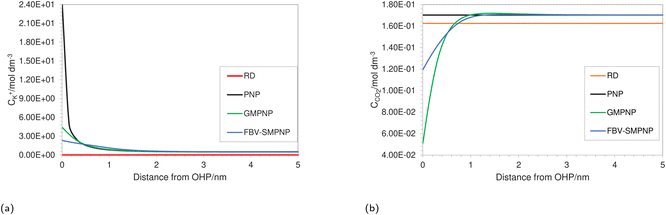 | ||
| Fig. 3 Comparison of (a) K+ and (b) CO2 concentration profiles in EDL using different approaches at an applied electrode potential of −1.3 vs. SHE/V for a 0.5 M KHCO3 solution at 5 bar CO2 pressure. | ||
The concentration of K+ predicted by the PNP model is extremely high (24 mol dm−3) at the OHP due to the absence of volume exclusion effects (dilute solution theory). The GMPNP model predicts lower concentration at the OHP owing to the excluded volume effects. As a result, a somewhat realistic concentration of 4.5 mol dm−3 can be seen. However, using the FBV-SMPNP approach, the observed concentration is approximately 50% lower than that predicted by GMPNP. This is due to the consideration of the βi ratio (ai3/a03) in eqn (4). Larger species encounter more steric repulsion as compared to smaller ones. In the GMPNP model, the underlying assumption is that βi is essentially 1 for all species. In the case of K+ transport, this would mean that hydrated K+ ions and H2O molecules have a similar size. The FBV-SMPNP model corrects this assumption by using the estimated sizes given in the ESI (Table S5).† As a result, the βi ratio is much larger than 1 for K+ ions, hence the steric effects on the cation are also enhanced, which can be clearly seen in Fig. 3a. Mathematically, the β factor acts as a hard limit on the maximum attainable concentration of K+ ions.
Since the buildup of cations in the vicinity of the electrode influences both the electric field strength and access to the catalyst for CO2, using the correct formulation for volume exclusion effects becomes essential. The study conducted by Bohra et al.17 using the GMPNP model, observed almost no CO2 concentration at the OHP beyond an electrode potential of −0.9 vs. SHE/V for a 1 bar CO2 pressure system at Ag(111) surface. As the authors noted, this is highly unrealistic because it is known experimentally that CO2ER has not reached the limiting current density at this potential. Applying the GMPNP approach to our system results in similarly lower CO2 concentrations (Fig. 3b), which are also inconsistent with the experimental current density data,28 suggesting an underestimation of CO2 concentration at the reaction plane. In contrast, the FBV-SMPNP model estimates a much higher concentration for CO2 at the OHP (Fig. 3b). The size of the unhydrated CO2 molecule is smaller than all other hydrated solution species including K+,47 and hence the steric effect experienced by a CO2 molecule is small relative to the other solution species. This in turn gives CO2 more space to diffuse toward the OHP. For both RD and PNP models, the concentration of CO2 remains close to the bulk values. This is because of the point species assumption in both RD and PNP approaches. The slightly lower concentration of CO2 in the RD model as compared to PNP is because, in the absence of migration, the RD model predicts a relatively more basic environment near the electrode surface, leading to the promotion of the CO32− forming reaction (1). To validate the effect of the βi ratio and the resulting CO2 concentration predicted at the OHP, we compare the partial current density data predicted by both FBV-SMPNP and GMPNP models with the experimental data from the literature.28
The simulations were performed assuming an indium catalyst and 5 bar of CO2 pressure, matching the experimental operating conditions. CO2 reduction on an In catalyst results in the formation of HCOO− and trace amounts of CO. The first step of the reduction process, namely the interfacial charge transfer reaction to form the intermediate radical anion (the rate-determining step) depends on the CO2 concentration at the reaction plane (OHP).48 Hence, a good match with experimental current densities would suggest an accurate estimation of CO2 concentration. The predicted HCOO− formation current density in Fig. 4a and the CO formation current density in Fig. 4c, using the FBV-SMPNP approach are in much better agreement with the experimental partial current densities as than a GMPNP model within a range of applied electrode potentials (up to ≈−1.5 vs. SHE/V). The FBV-SMPNP model requires the applied electrode potential and the fitted kinetics parameters as input to solve for the current densities using dynamic FBV kinetics as described by eqn (13). This is different from models such as GMPNP17 and RD,9 both of which take current density and applied electrode potential at a specific catalyst surface as input. The FBV-SMPNP approach is then used to analyze the current–voltage behavior and the resulting selectivities of all three electro-reduction products at elevated pressures of 5 (Fig. 4) and 40 bar (Fig. 5 and 7). At 5 bar pressure, within the applied potential range, HCOO− remains the dominant product with the highest faradaic efficiency of about 0.84 at −1.45 vs. SHE/V (Fig. 4d). Increasing the pressure of CO2 to 40 bar leads to a significant increase in the partial current density of HCOO− (Fig. 5a) with respect to the current density at 5 bar (Fig. 4a). Similarly, the partial current density of CO also increases with increasing CO2 pressure (Fig. 5bvs.4c).
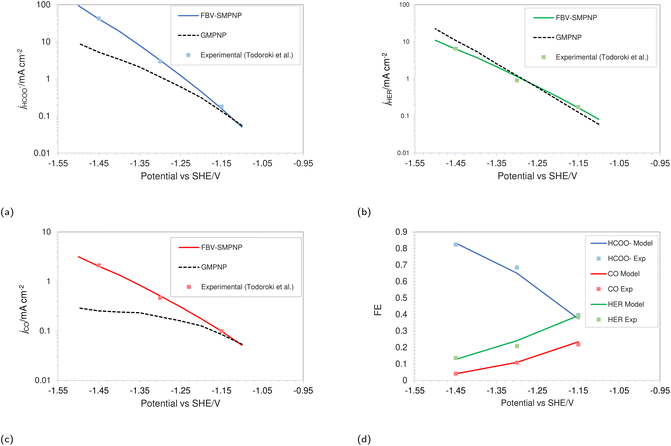 | ||
| Fig. 4 Comparison of partial current densities with experimental values using GMPNP and FBV-SMPNP methods (a–c). Comparison between faradaic efficiencies obtained from FBV-SMPNP model and experiments (d). The system is 0.5 M KHCO3 solution at 5 bar CO2 pressure based on an In catalyst. Experimental values are taken from the literature.28 | ||
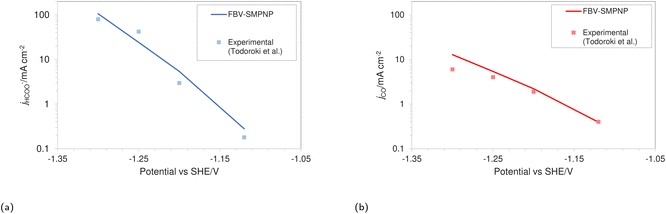 | ||
| Fig. 5 Comparison of (a) HCOO− and (b) CO formation current densities in a 0.5 M KHCO3 solution at 40 bar CO2 pressure based on an In catalyst. Experimental values used are taken from the literature.28 | ||
This is due to the increased amount of CO2 available in the system. The match with experimental faradaic efficiencies remains good even at high pressure of 40 bar as seen in Fig. 6. The current density data for HCOO− and CO formation will eventually start to diverge from the experimental values at higher applied electrode potentials. The experimental results in the literature suggest a faster consumption of CO2 at electrode potentials above −1.5 vs. SHE/V, compared to what is predicted by the FBV-SMPNP model. This leads to divergence between the predicted and experimental limiting current density values. This could be because the specific adsorption of intermediate species plays an increasingly important role in determining the rate of reaction (current densities) at high electrode potentials. In our model, this effect is not explicitly included. For further discussion see Section 4. Nevertheless, the match between experimental and predicted partial current densities remains extremely good up to −1.5 vs. SHE/V for all 3 products. The predictive power of the FBV-SMPNP model for the hydrogen evolution reaction is very good at both pressures (Fig. 4b and 7). HER varies directly with applied electrode potential and has no dependence on CO2 concentration at the OHP, hence the limitations found in the prediction of partial current densities for HCOO− and CO are practically non-existent.
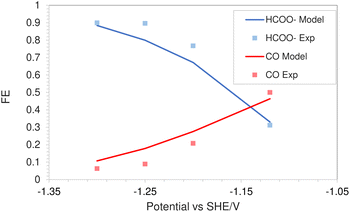 | ||
| Fig. 6 Comparison of faradaic efficiencies of CO2 based reduction products in a 0.5 M KHCO3 solution at 40 bar CO2 pressure based on an In catalyst. Experimental values used are taken from literature.28 | ||
Fig. 7 shows the comparison of HER partial current density predicted by the FBV-SMPNP model, the RD model and experimental values found in literature.28 Both models are compared to the same experimental study so that the difference in the predicted values can be associated with the difference in modeling methodology rather than possible variation in the experimental setup. A RD model that is based on the standard Tafel kinetics equations massively overpredicts the partial current density of HER. This is especially true at high applied electrode potentials. The partial current density at −1.86 vs. SHE/V using RD type model is approximately 400 mA cm−2, almost three times the actual experimental current density. Compared to the RD system, the FBV-SMPNP model performs exceptionally well in predicting the partial current densities of HER. This is because the Tafel relation in a RD model does not explicitly take into account the influence of varying OHP potentials on the rate constants. This effect is included in our model by employing the Frumkin correction within a Tafel relation.
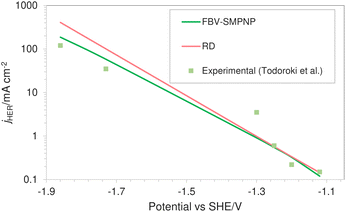 | ||
| Fig. 7 Comparison of HER partial current densities for CO2 reduction in a 0.5 M KHCO3 solution at 40 bar CO2 pressure based on an In catalyst. Experimental values used are taken from literature.28 | ||
It should be noted that a RD model based on the traditional Butler–Volmer relations can be interpreted as a theoretical limiting case of the FBV-SMPNP model. When the charge is carried entirely by the Stern layer, the EDL would consist almost entirely of densely packed cations, as shown in Fig. 8.
This is similar to the Helmholtz description of the EDL. This would mean that now the plane of closest approach for the solution species is at the edge of the EDL. As a result, the concentration of CO2 involved in at least the first step of the reduction process, will be the same as the bulk concentration of CO2 and the potential at reaction plane ΦOHP,t in eqn (13) becomes the same as the potential value in the bulk of electrolyte Φbulk, hence the Frumkin–Butler–Volmer equation (eqn (13)) gets reduced to a simple Tafel relation:
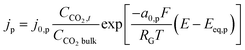 | (16) |
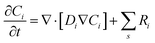 | (17) |
Hence using a standard Tafel kinetics equation, such as eqn (16), is implicitly tied to using a RD type transport equation eqn (17) and the EDL is described by the Helmholtz model. This type of formulation of EDL might be appropriate for high ionic strength systems but for the presented system, such a formulation is not sufficient, as the migration and steric effects inside the diffuse layer play a key role in the overall EDL dynamics and the charge transfer reactions.
4 Discussion
The presented continuum scale approach to model CO2 electrochemical reduction is extremely useful in analyzing the behavior of solution species in the EDL, while simultaneously being able to achieve practical current densities. Within a range of applied electrode potentials, this model can be used as a predictive tool for current–voltage analysis at elevated pressures. However, the model does find limitations at high applied electrode potentials, where we observed that the FBV-SMPNP model overpredicts the CO2 concentration at the OHP and consequently overestimates the partial current density for HCOO− and CO formation, as both these products depend heavily on CO2 concentration at the OHP. It is likely that at high applied electrode potentials, the first reduction step initiates beyond the condensed layer of counter ions.17 This would in turn imply an overestimation of CO2 in our current model at high electrode potentials. The kinetics model employed here is simplified by assuming that the specific adsorption of intermediate species and their lateral interactions do not significantly influence the interfacial charge transfer reactions. Explicitly accounting for these effects using DFT simulations might be necessary at these high electrode potentials since the coverage of metal surface and consequently the free space available for CO2 intermediates depends heavily on the applied electrode potentials. Another possible explanation could be that at higher electrode potentials the EDL becomes increasingly more condensed, which in turn decreases the local diffusivities of solution species, which are currently assumed to have constant (Fickian) values. In our model, we use a linear eqn (7) to evaluate the relative permittivity. This is done to avoid a high degree of nonlinearity that arises using more advanced approaches such as the Booth or Clausius–Mossotti equation.17,49,50 Furthermore, it is also worth mentioning that the molarity of water in eqn (7) is also assumed to be constant, however, the concentration of water would diminish near the electrode surface due to the presence of a condensed layer of solute species. We are currently exploring these effects as an extension for the FBV-SMPNP model.The continuum-scale approach provides a cost-effective alternative for the computationally expensive atomic-scale modeling of EDL. It can also be coupled with atomistic quantum models to provide the steady-state condition under which energetics are to be studied.17 A continuum scale approach does not account for the ion–ion interactions, which become relevant in concentrated electrolytes. Particle-based methods, such as molecular dynamics (MD), do account for such correlations. Giera et al. performed extensive MD simulations using a primitive model to successfully account for electrostatic correlations as well as steric interactions between ions.51 Also, MD simulations with explicit solvent have been widely used to compute the EDL at the interface between an electrolyte solution and a charged solid surface.7,52,53 However, the applicability of such an approach for a typical CO2ER process remains unexplored. This is primarily because a typical CO2ER process involves electrode reactions and homogenous reactions, and local pH plays an important role. These factors affect the EDL in a CO2ER system and are generally hard to simulate in MD. Moreover, the accuracy of an MD simulation is contingent on a good description of molecular interactions between all the fluid components and their interaction with the electrode.54 Since existing interaction potentials are typically optimized to reproduce bulk properties of single-component systems or dilute solutions, much caution is needed when using these potentials to simulate the interface between an electrode and a multicomponent concentrated solution as is relevant to CO2ER systems. Although MD would not be able to model every aspect of the electrochemical process, a tandem approach based on coupling MD simulations and continuum scale models could be a powerful way to leverage the complementary strengths of both approaches.
Another feature of the Frumkin-corrected kinetics approach is that it does not presuppose a fixed OHP potential. Rather it is evaluated at every time step. This would in turn determine the local electric field strength of the EDL, which eventually dictates the concentrations of different ionic species. This feature can be especially useful for dynamic CO2 reduction models, where the applied electrode potential is switched on and off (or high to low voltage) repeatedly to overcome diffusion limitations. Traditionally, it has been seen that solving (G)MPNP-type differential equations at relatively high applied electrode potentials, in an EDL-like environment leads to increased instability.17 Extremely small time steps and spatial discretizations, along with stabilization techniques such as the SUPG method, have to be adopted to get a tractable solution. Interestingly, using our FBV-SMPNP approach leads to a computationally much more efficient solution, without the need for any stabilization technique.
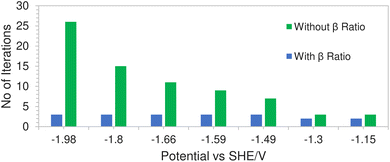
This is due to a hard concentration limit being enforced on the solution species near the electrode surface via the introduction of the βi ratio in the volume exclusion term resulting in less extreme potential gradients. Fig. 9 shows a comparison of the average number of iterations required (per time step) using Newton's method, with and without the inclusion of the βi ratio, as a function of applied electrode potential. In the case where the ratio was excluded from the model, the solution would not even converge at high electrode potentials. The number of iterations in the green bars represents the average number of iterations before the system fails to converge. However for the case where the ratio was included, not only does the solution converge but the number of iterations remained relatively stable throughout the range of applied electrode potentials.
5 Conclusions
In this work, we presented a CO2 reduction modeling approach based on a combination of size-modified Poisson–Nernst–Planck equations (SMPNP) for transport of the solution species and Frumkin-corrected Butler–Volmer type kinetics expression (FBV) to account for the interfacial reactions. By considering steric effects, we established the impact of the condensed layer of cations on the accessibility of the catalyst surface to the reacting CO2. We also observed a 50% decline in the estimated cation concentration at the reaction plane as compared to a GMPNP model.17 This is due to the inclusion of the molecular size (βi) ratio in the transport equations of our model. Perhaps its impact is most prominent in the estimation of CO2 concentration at the OHP, which was predicted to be extremely low in the GMPNP model. Using the βi ratio, we were able to rectify this problem and attain a much more realistic CO2 concentration at the OHP. We also validated the usage of this factor by matching the partial current density data for CO2 consuming products such as HCOO− and CO with the experimental Tafel plot data from the literature. The FBV-SMPNP model can also be used to make predictions for a high-pressure CO2 electrolyzer, which is of great industrial significance. Within a range of applied electrode potentials, we were able to predict the partial current densities of all 3 products with accuracy at elevated pressures of 5 and 40 bar, although the model does find limitations in predicting partial current densities for CO2 consuming products at high applied electrode potentials. We also observed that the model predicts the HER current densities much more accurately than a traditional RD model. This is due to the Frumkin-corrected kinetics formulation which assumes the driving force for interfacial charge transfer reactions to be the potential difference between the metal electrode and the OHP.Overall, the model provides a good approximation of the CO2 reaction environment which consists of several physicochemical phenomena occurring at vastly different lengths and time scales, in a computationally inexpensive manner. Gas diffusion electrodes (GDE) based CO2 electro-reduction systems are being studied extensively because of their advantage of reduced diffusion length for CO2 molecules. Such a system can also be incorporated within the FBV-SMPNP framework presented in this study. The model can also be useful in dynamic CO2 reduction systems, where step changes in the applied potential are used as a method to overcome diffusive limitations via the dispersion of the double layer.
Author contributions
Esaar Naeem Butt: conceptualization, methodology, software, validation, formal analysis, writing – original draft. Johan T. Padding: conceptualization, methodology, supervision, funding acquisition, writing – review. Remco Hartkamp: conceptualization, methodology, supervision, funding acquisition, writing – review.Conflicts of interest
There are no conflicts to declare.Acknowledgements
This work is part of the research programme Towards large-scale electroconversion systems (TOeLS) financed by Shell and the Topsectors Chemistry, HTSM and Energy.Notes and references
- X. Lu, D. Y. Leung, H. Wang, M. K. Leung and J. Xuan, ChemElectroChem, 2014, 1, 836–849 CrossRef CAS.
- W. A. Smith, T. Burdyny, D. A. Vermaas and H. Geerlings, Joule, 2019, 3, 1822–1834 CrossRef CAS.
- Z. Yan, J. L. Hitt, J. A. Turner and T. E. Mallouk, Proc. Natl. Acad. Sci. U. S. A., 2020, 117, 12558–12563 CrossRef CAS PubMed.
- G. O. Larrazábal, A. J. Martín and J. Pérez-Ramírez, J. Phys. Chem. Lett., 2017, 8, 3933–3944 CrossRef PubMed.
- M. Liu, Y. Pang, B. Zhang, P. D. Luna, O. Voznyy, J. Xu, X. Zheng, C. T. Dinh, F. Fan, C. Cao, F. P. G. D. Arquer, T. S. Safaei, A. Mepham, A. Klinkova, E. Kumacheva, T. Filleter, D. Sinton, S. O. Kelley and E. H. Sargent, Nature, 2016, 537, 382–386 CrossRef CAS PubMed.
- J. Resasco, L. D. Chen, E. Clark, C. Tsai, C. Hahn, T. F. Jaramillo, K. Chan and A. T. Bell, J. Am. Chem. Soc., 2017, 139, 11277–11287 CrossRef CAS PubMed.
- L. Scalfi, M. Salanne and B. Rotenberg, Annu. Rev. Phys. Chem., 2021, 72, 189–212 CrossRef CAS PubMed.
- M. F. Döpke, F. Westerbaan van der Meij, B. Coasne and R. Hartkamp, Phys. Rev. Lett., 2022, 128, 056001 CrossRef PubMed.
- N. Gupta, M. Gattrell and B. MacDougall, J. Appl. Electrochem., 2006, 36, 161–172 CrossRef CAS.
- C. Delacourt and J. Newman, J. Electrochem. Soc., 2010, 157, B1911 CrossRef CAS.
- D. Raciti, M. Mao and C. Wang, Nanotechnology, 2018, 29, 44001 CrossRef PubMed.
- H. Hashiba, L.-C. Weng, Y. Chen, H. K. Sato, S. Yotsuhashi, C. Xiang and A. Z. Weber, J. Phys. Chem. C, 2018, 122, 3719–3726 CrossRef CAS.
- S. Suter and S. Haussener, Energy Environ. Sci., 2019, 12, 1668–1678 RSC.
- J. Newman and K. Thomas-Alyea, Electrochemical Systems, John Wiley & Sons, 3rd edn, 2004 Search PubMed.
- M. S. Kilic, M. Z. Bazant and A. Ajdari, Phys. Rev. E: Stat., Nonlinear, Soft Matter Phys., 2007, 75, 021503 CrossRef PubMed.
- M. S. Kilic, M. Z. Bazant and A. Ajdari, Phys. Rev. E: Stat., Nonlinear, Soft Matter Phys., 2007, 75, 1–16 Search PubMed.
- D. Bohra, J. H. Chaudhry, T. Burdyny, E. A. Pidko and W. A. Smith, Energy and, Energy Environ. Sci., 2019, 12, 3380–3389 RSC.
- M. Z. Bazant, M. S. Kilic, B. D. Storey and A. Ajdari, Adv. Colloid Interface Sci., 2009, 152, 48–88 CrossRef CAS PubMed.
- T. Hatsukade, K. P. Kuhl, E. R. Cave, D. N. Abrama and T. F. Jaramillo, Phys. Chem. Chem. Phys., 2014, 13814–13819 RSC.
- B. Lu and Y. C. Zhou, Biophys. J., 2011, 100, 2475–2485 CrossRef CAS PubMed.
- K. Willems, D. Ruic, F. L. Lucas, U. Barman, N. Verellen, J. Hofkens, G. Maglia and P. V. Dorpe, Nanoscale, 2020, 12, 16775–16795 RSC.
- K. Wu, E. Birgersson, B. Kim, P. J. A. Kenis and I. A. Karimi, J. Electrochem. Soc., 2015, 162, F23–F32 CrossRef CAS.
- A. R. T. Morrison, V. van Beusekom, M. Ramdin, L. J. P. van den Broeke, T. J. H. Vlugt and W. de Jong, J. Electrochem. Soc., 2019, 166, E77–E86 CrossRef CAS.
- A. Frumkin, Z. Phys. Chem., 1933, 164, 121–133 CrossRef.
- M. van Soestbergen, Russ. J. Electrochem., 2012, 48, 570–579 CrossRef.
- S. Ringe, C. G. Morales-Guio, L. D. Chen, M. Fields, T. F. Jaramillon, C. Hahn and K. Chan, Nat. Commun., 2020, 33 CrossRef CAS PubMed.
- M. Rossi, T. Wallmersperger, S. Neukamm and K. Padberg-Gehle, Electrochim. Acta, 2017, 258, 241–254 CrossRef CAS.
- M. Todoroki, K. Hara, A. Kudo and T. Sakata, J. Electroanal. Chem., 1995, 394, 199–203 CrossRef.
- S. Weisenberger and A. Schumpe, AIChE J., 1996, 42, 298–300 CrossRef CAS.
- T. Burdyny, P. J. Graham, Y. Pang, C.-T. Dinh, M. Liu, E. H. Sargent and D. Sinton, ACS Sustainable Chem. Eng., 2017, 5, 4031–4040 CrossRef CAS.
- B. P. Sullivan and H. E. G. K. Krist, Electrochemical and Electrocatalytic Reactions of Carbon Dioxide, Elsevier Science, 1st edn, 1993 Search PubMed.
- M. Z. Bazant, K. T. Chu and B. J. Bayly, SIAM J. Appl. Math., 2005, 65, 1463–1484 CrossRef CAS.
- A. Bonnefont, F. Argoul and M. Z. Bazant, J. Electroanal. Chem., 2001, 500, 52–61 CrossRef CAS.
- H. Wang, A. Thiele and L. Pilon, J. Phys. Chem. C, 2013, 117, 18286–18297 CrossRef CAS.
- J. B. Hasted, D. M. Ritson and C. H. Collie, J. Chem. Phys., 1948, 16, 1–21 CrossRef CAS.
- J. Bockris and A. Reddy, Modern Electrochemistry, Springer, New York, 2nd edn, 1998 Search PubMed.
- J. T. Feaster, C. Shi, E. R. Cave, T. Hatsukade, D. N. Abram, K. P. Kuhl, C. Hahn, J. K. Nørskov and T. F. Jaramillo, ACS Catal., 2017, 7, 4822–4827 CrossRef CAS.
- Y. Hori, H. Wakebe, T. Tsukamoto and O. Koga, Electrochim. Acta, 1994, 1833–1839 CrossRef CAS.
- Y. Hori, Modern Aspects of Electrochemistry, Springer, New York, 2008, vol. 42, pp 89–189 Search PubMed.
- J. Li, M. Zhu and Y. F. Han, Eur. Soc. J. Catal., 2020, 514–531 Search PubMed.
- S. Kapusta and N. Hackerman, J. Electrochem. Soc., 1983, 607 CrossRef CAS.
- E. Itsicovich, A. A. Kornyshev and A. Vorotyntsev, Phys. Status Solidi A, 1977, 39, 229–238 CrossRef.
- P. M. Biesheuvel, M. van Soestbergen and M. Z. Bazant, Electrochim. Acta, 2009, 54, 4857–4871 CrossRef CAS.
- P. Delahay, Double Layer and Electrode Kinetics, Interscience, 2nd edn, 1965 Search PubMed.
- A. Bard and L. Faulkner, Electrochemical Methods: Fundamentals and Applications, Wiley, 2nd edn, 2002, vol. 38 Search PubMed.
- S. Trasatti and E. Lust, Mod. Aspects Electrochem., 2002, 1–215 Search PubMed.
- E. Nightingale, J. Phys. Chem., 1959, 1381–1387 CrossRef CAS.
- X. Zhu, J. Huang and M. Eikerling, ACS Catal., 2021, 14521–14532 CrossRef CAS.
- F. Booth, J. Chem. Phys., 1951, 391–394 CrossRef CAS.
- J. Daintith, A Dictionary of Chemistry, OUP Oxford, 2008, vol. 6 Search PubMed.
- B. Giera, N. Hanson, E. M. Kober and M. S. T. M. Squires, Langmuir, 2015, 3553–3562 CrossRef CAS PubMed.
- M. F. Döpke, J. Lützenkirchen, O. A. Moultos, B. Siboulet, J.-F. Dufrêche, J. T. Padding and R. Hartkamp, J. Phys. Chem. C, 2019, 123, 16711–16720 CrossRef.
- D. Biriukov, O. Kroutil and M. Předota, Phys. Chem. Chem. Phys., 2018, 20, 23954–23966 RSC.
- M. F. Döpke and R. Hartkamp, J. Chem. Phys., 2021, 154, 094701 CrossRef PubMed.
Footnote |
| † Electronic supplementary information (ESI) available. See DOI: https://doi.org/10.1039/d2se01262f |
| This journal is © The Royal Society of Chemistry 2023 |