Open Access Article
Open Access ArticleThe role of Mg dopant concentration in tuning the performance of the SnO2 electron transport layer in perovskite solar cells
Gennaro Vincenzo
Sannino
ab,
Adriana
Pecoraro
 bc,
Pasqualino
Maddalena
bc,
Pasqualino
Maddalena
 c,
Annalisa
Bruno
c,
Annalisa
Bruno
 de,
Paola Delli
Veneri
d,
Michele
Pavone
de,
Paola Delli
Veneri
d,
Michele
Pavone
 *ab and
Ana Belén
Muñoz-García
*ab and
Ana Belén
Muñoz-García
 *bc
*bc
aDepartment of Chemical Sciences, University of Naples Federico II, Napoli, Italy. E-mail: michele.pavone@unina.it
bINSTM-GISEL, National Interuniversity Consortium of Materials Science and Technology (INSTM), Florence, Italy. E-mail: anabelen.munozgarcia@unina.it
cDepartment of Physics “E. Pancini”, University of Naples Federico II, Napoli, Italy
dItalian National Agency for New Technologies, Energy and Sustainable Economic Development, (ENEA), Portici, (Na), Italy
eEnergy Research Institute @ NTU (ERI@N), Nanyang Technological University, Singapore
First published on 17th July 2023
Abstract
Recent experiments pointed out a beneficial role of moderate Mg doping in SnO2 for application as an electron transport layer (ETL) in perovskite solar cells. The high efficiencies obtained with Mg-doped SnO2 are driven by an improved open circuit potential (VOC), but the origin of this behaviour is still under debate. Some ascribe this enhancement to the improved quality of the thin ETL film, while others speculate it is due to an electronic structure rearrangement upon Mg doping. In this context, here we applied density functional theory calculations to uncover the changes in SnO2 structural, electronic, and defect properties induced by different percentages of Mg doping. Our predictions of conduction band minimum (CBM) variations provide new insights on the trend of different VOC values observed in experiments. We found that low Mg contents push up the SnO2 CBM increasing the VOC. In contrast, at high dopant concentration, interstitial Mg defects are more likely to occur, leading to lower VOC and to the formation of intra-gap band states, explaining the decrease of PSC performances at a high Mg doping ratio. These findings provide a new atomistic perspective on the positive/negative effects of Mg dopants for the application of SnO2 in last-generation solar cells, highlighting key structural and defect properties that can be easily tuned to obtain ETL materials with purposely tailored electronic features.
Introduction
Some metal oxides have the unique characteristic of being both electrically conductive and optically transparent in the visible region. Tin dioxide (SnO2) for example has attracted much attention for its applications as a transparent conducting oxide in different fields, such as solar cells,1,2 gas sensors,3,4 display devices,5 and lithium-ion batteries.6 SnO2 is intrinsically an n-type semiconductor due to the presence of native point defects7,8 and its optical band gap ranges from 3.6 to over 4.0 eV,9 ensuring a high optical transmittance (>80%) in the visible range.10 Noteworthily, it is also highly stable both thermally and chemically, and abundant in nature.The electronic and structural properties of SnO2 have been purposely tuned for different applications via doping with several possible elements. Donor dopants are widely used11,12 to increase the density of the majority carriers and produce an n-type SnO2 transparent electrode. Other dopants, such as Zn and Ni, are used to promote gas sensing properties13–15 and improve its performances as an electron transport layer (ETL) in perovskite solar cells (PSCs).16–19 Induction of ferromagnetic properties, a key feature for spintronic applications, has also been predicted via ab initio calculations and obtained experimentally with transition metal and non-magnetic doping elements.20–24 SnO2 can be doped instead with acceptor atoms but whether p-type conduction can be achieved in SnO2 using acceptor dopants is still an open question. Theoretical calculations considering different dopants (e.g., Al, Ga, In interstitial or substituting Sn, N substituting O and Li substituting Sn) indicate that different kinds of trapping states preclude SnO2 from having p-type character.25 On the other hand, p-type SnO2 films have already been fabricated, although with low conductivity. For example, In-doped SnO2 films with p-type conduction have been prepared and characterized in different studies,26–28 and Othmen et al.29 have demonstrated the applicability of p-type highly Fe-doped SnO2 thin films in homojunctions with non-doped SnO2. Several studies have reported the effects generated by Mg-doping in SnO2. Early studies by Li et al.30 have analyzed the morphological and optical properties of Mg-doped SnO2 thin films. He et al.31,32 have calculated the defect energy formation and the hole concentration indicating that Mg is suitable for doping of SnO2 and, recently, Fu and co-workers33 have developed a fabrication method to generate Mg-doped SnO2 film. Mg has also been reported to confer peculiar magnetic properties to SnO2 such as room-temperature ferromagnetism.23,34 Recent studies by Xiong et al.35 and Zhou et al.36 also pointed out the beneficial role of Mg doping in perovskite solar cell (PSC) performances. Indeed, doping with Mg2+ partially substituting Sn4+ ions has been reported to tune SnO2 properties without compromising its n-type character. Fabricated devices have reached higher efficiencies when Mg-doped SnO2 film has been used as the ETL compared to the pristine material. However, there is no consensus on the exact role of Mg in such improvement. Xiong et al. reported better quality of the Mg-doped film deposited via high-temperature treatment with respect to the undoped one and, consequently, suggest a better interfacial contact with the perovskite. In terms of performance, their PSCs are reported to attain the best power conversion efficiency (PCE) with a 7.5% Mg content, whilst higher doping percentages (10 and 20%) result in lower PCEs. Devices fabricated by Zhou have shown higher VOC, and a lower charge extraction ability for Mg-doped SnO2 films, which has been ascribed to a slight rise in SnO2 conduction band minimum potential upon Mg doping. These findings do not match the UPS measurements performed by Xiong, which reveal a lower CBM for doped films, not correlated with doping concentration and VOC values obtained from complete devices. This puzzling electronic behavior of Mg-doped SnO2 motivates the present work, which aims at assessing the effects of different Mg doping concentrations on the electronic properties of SnO2 as the ETL using atomistic simulations based on the density functional theory (DFT). In particular, we address the enhanced-to-thwarted performance switch of Mg-doped SnO2 as the ETL in PSCs when going from low to moderate doping degrees.
Since the band alignment between the ETL CBM and the perovskite CB is crucial in this kind of devices, any energy shift of the valence and/or conduction bands related to work function (WF) changes can affect the working mechanism and the solar cell parameters. After presenting (Mg-doped) SnO2 bulk properties, we exploit the surface-slab approach to calculate ΔCBM to explain, from an electronic point of view, the enhancement in performances and VOC reported in the literature35,36 for Mg-doped SnO2-based PSCs. In our models Sn4+ ions are substituted with Mg2+ but, given the limited solubility,23 we have considered both substitutional and interstitial Mg2+ ions at high doping concentrations. We want to emphasize that the wording “Mg-doped SnO2” denotes, from now on, the addition of Mg2+ acceptor defects in SnO2, preserving its n-type character.
Our study provides a fundamental understanding of the effective positive role of low dosage of Mg doping, which increases the CBM of the SnO2 providing higher VOC and enhances the PCE of PSCs and of the negative role of the high doping concentrations where Mg2+ occupy interstitial sites, which is detrimental for the PCE of the PSCs. Furthermore, our findings pave the way for a new structure-based approach for the design of doping for materials most used as ETLs.
Methods and computational details
Our first-principles spin-polarized DFT calculations have been performed within periodic boundary conditions and a plane wave/pseudopotential approach, as implemented in the Vienna ab initio simulation package (VASP, version 5.4.4) code.37–40 For structural optimizations and electronic structure calculations we applied Perdew, Burke, and Ernzerhof (PBE) GGA exchange–correlation density functional,41,42 as well as the Heyd–Scuseria–Ernzerhof (HSE06)43,44 hybrid functional. All atomic positions have been allowed to relax without imposing symmetry constraints until residual forces on each atom were smaller than 0.03 eV Å−1. All ionic cores have been represented by projector-augmented wave (PAW) potentials:45,46 2s22p4 electrons for O, 5s25p2 electrons for Sn, and 3s2 electrons for Mg were treated as valence electrons. Dispersion forces have been accounted for with Grimme's D3 (ref. 47) with the damping scheme by Becke and Johnson (D3BJ).48 We use the BJ damping to deal with dispersion interactions at short distances and mitigate the double-counting of electron correlation effects at intermediate distances. We chose an SCF energy threshold of 10−5 eV and a plane wave energy cut-off at 600 eV in all calculations. Γ-centered Monkhorst–Pack k-point grids of 6 × 6 × 9, 3 × 3 × 3, 3 × 5 × 1, and 2 × 3 × 1 have been used for the SnO2 bulk unit cell, (Mg-)SnO2 bulk supercell, and (Mg-)SnO2 slab models described below at PBE-D3BJ and HSE06-D3BJ levels of theory, respectively. These approaches have been widely exploited for several transition metal oxide bulk and surfaces.49–53Geometry optimization has been performed starting from experimental lattice constants and atomic parameters54 of the P42/mnm space group. The pristine bulk structure has been optimized at both PBE-D3BJ and HSE06-D3BJ levels of theory. A 96-atom supercell (32 f.u.) has been considered as the starting point to simulate different Mg concentrations in Mg-doped SnO2. Lattice constants of doped bulk supercells have been fixed to an integer multiple values of those PBE-D3BJ optimized for the undoped material since Mg2+ and Sn4+ ions in VI coordination have similar dimensions (∼0.7 Å).55 Subsequently, HSE06-D3BJ single point calculations have been performed on geometries optimized at the PBE-D3BJ level of theory.
Work functions have been computed from slab models of undoped and Mg-doped SnO2 surfaces. Our models have been built with the (110) surface termination, identified as the most stable surface.56,57 On the surface plane, our model consisted of a 3 × 1 supercell of the (110) unit cell. As for slab thickness, we employed five O–Sn–O tri-layers which ensured converged surface energy within 5 × 10−4 J m−2. This supercell and thickness choice resulted in 90-atom slabs. We used a vacuum layer >10 Å to avoid any interaction between images. The work function of pristine (0% Mg) and doped SnO2 has been calculated at the HSE06-D3BJ level of theory on PBE-D3BJ optimized geometries from the planar-average electrostatic potential (PAEP) of such slabs as follows:58
| WF(x%Mg) = Evac − EVB, x = 0, 3, 6, 10% |
Results and discussion
SnO2 pristine bulk structure has been analysed from the structural and electronic points of view with PBE-D3BJ and hybrid HSE06-D3BJ density functionals. Table 1 lists computed lattice parameters and eigenvalue gaps for both exchange–correlation functionals. As reported in other theoretical studies,56,57,59 lattice parameters predicted by PBE were overestimated within the expected error (∼1.2%). HSE06 hybrid functional provided slightly underestimated lattice constant values in better agreement with the experiments with percentage errors of ∼0.2% along all three lattice vectors.As expected, energy bandgap values extracted from these calculations are highly dependent on the used exchange–correlation functionals. The experimental band gap (3.6 eV)60 is underestimated by PBE (0.80 eV), consistently with other DFT studies on SnO2,61–63 whilst HSE06 functionals predicted a wider eigenvalue gap 3.04 eV, closer to the experimental value.
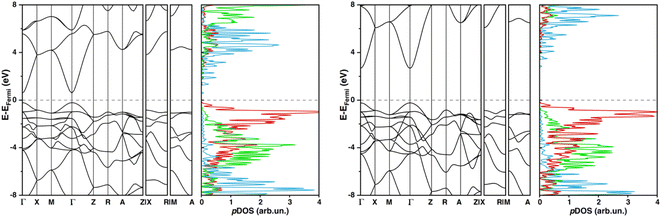
Computed band structures and pDOS plots of undoped SnO2 at PBE-D3BJ and HSE06-D3BJ levels of theory (depicted in Fig. 1) match what has been reported in previous studies.64,65 Except for the bandgap value itself, both levels of theory predicted qualitative identical pDOS and band structures, featuring a direct band gap at the Γ point, Oxygen p states are the main contributors to the edge of the valence band, and Sn s states to the bottom part of the CB.
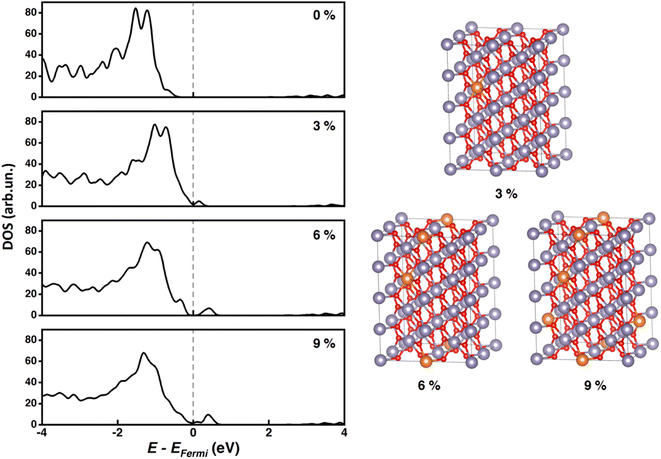
We adopted the supercell approach for Mg-doped SnO2 bulk at different doping levels. 1, 2, or 3 Sn atoms were replaced with Mg in the 96-atom supercell (32 f.u.) to reproduce 3, 6, or 9% doping percentages, respectively. For 6% and 9% cases, substituted atoms have been placed as far as possible from each other (minimum distance ∼ 5 Å) (Fig. 2). As reported in previous studies,66–68 replacement of Sn by Mg does not induce remarkable changes in optimized lattice parameters due to the very similar ionic radii of Sn4+ and Mg2+, respectively 0.69 and 0.72 Å.55 For this reason, we use the (scaled) lattice constants of pristine SnO2 also for the doped systems. Fig. 2 shows the total DOS calculated at the HSE06-D3BJ level of theory on PBE-D3BJ optimized geometries for all the considered doping percentages. We do not report spin-projected DOS as the discussion of magnetic properties is outside the scope of our work. The valence band (VB) crossed the Fermi level in doped bulks, pointing out the p-type behavior of the doped material.
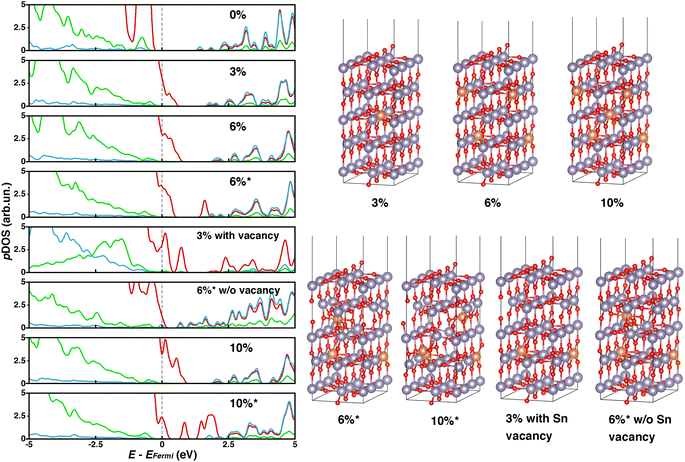
Starting from the 5L-(110) slab model containing 90 atoms (30 f.u.), 1, 2 or 3 inner Sn atoms were substituted with Mg to describe 3, 6, or 10% doping contents, respectively, as done for the bulk. Aiming at assessing the effect of substitutional vs. interstitial Mg doping, we have also considered two alternative 6% and 10% doped systems (labeled as 6%* and 10%*) where one and two Mg atoms, respectively, do not substitute Sn but fill interstitial lattice sites. In the 6%* and 10%* systems, a tin vacancy is associated with each interstitial Mg to keep the same stoichiometry as in 6% and 10%. For all these models, we have performed HSE06-D3BJ single point calculations on PBE-D3BJ optimized geometries, which are depicted in Fig. 3 together with the corresponding pDOS plots.
While the presence of Mg in the interstitial site is energetically unfavorable, the energy differences calculated between the “pure” substitutional slabs and the corresponding interstitial Mg counterparts are relatively small (0.15 and 0.21 eV f.u.−1 for 6% and 10%, respectively) so we can consider that both configurations are likely to occur.
While systems with substitutional doping presented p-type pDOS similar to those of bulk materials, the pDOS corresponding to interstitial Mg-doping featured intra-gap states that could promote undesired charge recombination processes and compromise the PCE of the PSC. Our calculations reveal that such intra-gap states can be ascribed mainly to oxygen atoms neighboring tin vacancies (Fig. 4 and 5), which are significantly displaced from their atomic positions in the pristine material. To determine whether such intragap states arise from the Sn vacancy or from the interstitial Mg itself, we have considered a substitutional 3% Mg-doped slab with one Sn vacancy (3%vac) and a 6%* system without Sn vacancy (6%*w/ovac). Computed pDOS of 3%vac (Fig. 3) revealed the presence of intra-gap 2p O states in line with those of 6%* and 10%* slabs, where a Sn vacancy is present. On the other hand, pDOS of 6%*w/ovac (Fig. 3) presented a smaller bandgap than the corresponding 6%* slab, but does not feature oxygen intra-gap states. These decoupled results confirmed that Sn vacancies play an active role in intra-gap state generation, due to the high structural distortion of neighboring oxygen atoms, while interstitial Mg decreased the bandgap but does not generate such states. Anyhow, both effects would jeopardize PSC performances, so, from this electronic point of view, our calculations predict that Mg may be beneficial only when it occupies regular Sn lattice sites.
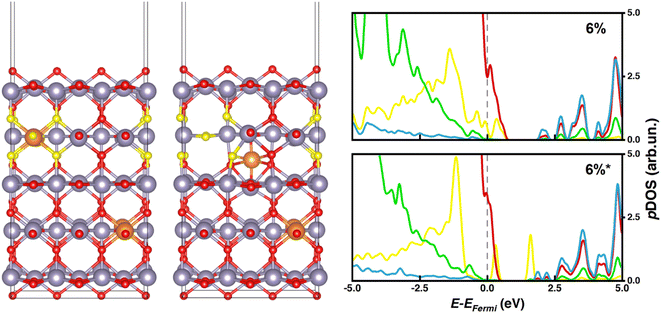 | ||
| Fig. 4 6% and 6%* doped slab models with oxygen atoms mainly responsible for generating intra-gap states colored in yellow; pDOS legend: O (p) – red or yellow, Sn (s) – blue, Sn (p) – green. | ||
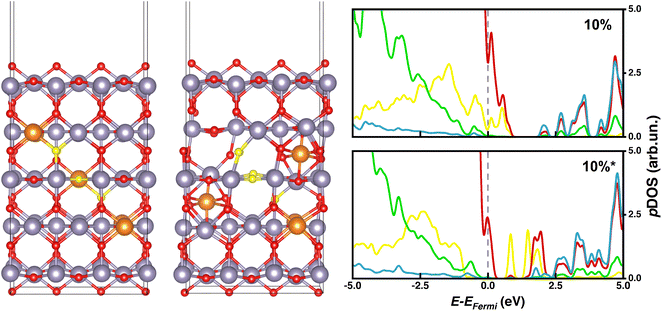 | ||
| Fig. 5 10% and 10%* doped slab models with oxygen atoms mainly responsible for generating intra-gap states colored in yellow; pDOS legend: O (p) – red or yellow, Sn (s) – blue, Sn (p) – green. | ||
Doping also brings structural changes to the SnO2 lattice. We have analyzed such distortions in terms of Pair Distribution Functions (PDFs) of Sn–O bond lengths for all doping degrees and types discussed above (Fig. 6). Besides the expected larger peak widths, substitutionally doped slabs present slightly shorter Sn–O distances than pristine material ones (in the range 1.95–2.15 Å vs. 2.00–2.17 Å in pure SnO2), but neither the shape nor the range of the PDF has been affected by increasing Mg content PDF (3%)–PDF (6%)–PDF (10%). We found similar PDF features for the other explored systems with Sn vacancies, e.g., 3%vac. This confirmed the negligible structural effects evinced experimentally between SnO2 and Mg-doped SnO2 with moderate Mg content, where Mg occupies only Sn sites. All systems with interstitial Mg (6%*, 10%*, and 6%*w/ovac) have broader PDFs ranging from 1.92 Å to 2.3 Å; Mg in interstitial sites also induces Sn–O bond elongations and overall larger distortions than substitutional Mg.
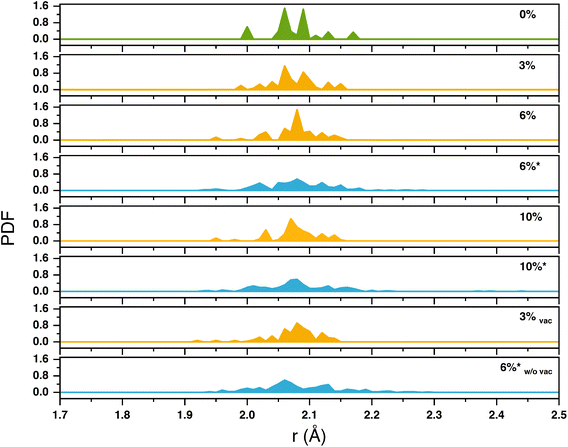 | ||
| Fig. 6 Pair distribution function analysis of Sn–O distances computed for pristine and Mg-doped slabs; * indicates the configuration with interstitial Mg. | ||
In a PSC the relative position of the CBM of the ETL and the VBM of the HTL plays a primary role in defining the VOC of the entire device. Lower ETL CBM potentials lead to lower VOC values.69,70 The trend of the WF is thus connected with the VBM potential and, in the approximation of the rigid band model, also with the CBM of the material. Therefore, we can assess the change in the CBM position from the shifts of the examined WFs of the SnO2 with different Mg doping concentrations and configurations. Briefly, lower WF values result in higher CBM potentials and, consequentially, higher VOC values.
For such a reason, we have computed work function values of doped materials from HSE06-D3BJ slab calculations and resulting ΔCBM values have been plotted with respect to pristine SnO2 in Fig. 7, and compared with experimental variations of VOC at different doping levels.35 Substitution of Mg ions in regular Sn sites produced an evident rise in CBM: higher the doping concentration, higher the CBM (Fig. 7, black dots). Interstitial Mg, instead, generates the opposite effect by lowering the CBM (Fig. 7, black stars). For this reason, the CBM of the 6% and 6*% configurations are higher/lower than that of 3% (substitutional doping). The 10*% WF value confirms this trend. These results, together with the experimental evidence of Mg occupying interstitial sites for concentrations around 8%,23 can explain the experimental VOC parameters obtained by Xiong et al.35 (Fig. 7): VOC increases with Mg doping reaching a maximum value at 5% and then starts to decrease.
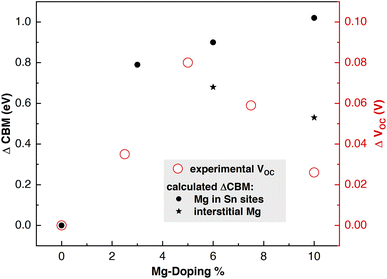 | ||
| Fig. 7 Trend in ΔCBM = (CBM(x%Mg) − CBM(0%Mg)) = – ΔWF as extracted from HSE06-D3BJ calculations at different Mg-doping percentages and the corresponding experimental ΔVOC.35 | ||
These results confirm that moderate amounts of Mg substituting Sn in regular lattice sites enhance the performances of SnO2 as the ETL material by pushing up the CBM and increasing the VOC without creating trap states or diminishing the bandgap. In contrast, higher Mg concentrations involving interstitial doping have a negative impact on such performances since the VOC decreases and internal structural distortions bring about undesired intra-gap states and band gap reduction.
Conclusions
In this work, we provided an atomistic characterization of Mg-ion doping effects on SnO2 structural, electronic, and work function features, aiming at uncovering the reasons behind the PCE improvement of PSC devices incorporating doped Mg:SnO2, which is not retained for higher-to-moderate doping degrees. Experimentally, it is found that low Mg doping of SnO2 as the ETL slightly improves the VOC of the PSC device. We ascribe this experimental evidence to electronic reasons. In particular, based on our computed work functions, we predict higher CBM for doped slabs and, consequently, an increase in VOC. However, Mg2+ ions start to occupy interstitial sites increasing the doping concentration so the CBM goes down and thus reduces the VOC. Furthermore, our analysis correlates higher structural distortions associated with interstitial Mg with bandgap reduction (due to interstitial Mg itself) and intra-gap states (due to Sn vacancies associated with interstitial Mg). Both effects could be responsible for undesired recombination processes in the PSC device and, hence, may further explain the drop in performances at high Mg doping concentrations. In conclusion, our work highlights the importance of doping effects on the electronic structure of ETL materials used in PSCs. Intra-gap states and band shifts are crucial features to be taken into account for boosting the PSC performances. We prove that intra-gap states can be fine-tuned with a proper evaluation from an atomistic/electronic structure perspective. Future investigations, exploring other dopants and ETL materials, will follow the main findings of this work to predict and design a priori the best dopant/ETL combination to maximize the features of PSC performance such as the VOC.Conflicts of interest
The authors declare there are no conflicts of interests.Acknowledgements
This work was supported by the Italian Ministry of Economic Development in the framework of the Operating Agreement with ENEA for Research on the Electric System. “The computing resources and the related technical support used for this work have been provided by the CRESCO/ENEAGRID High-Performance Computing infrastructure and its staff [F. Iannone et al.]. The CRESCO/ENEAGRID High-Performance Computing infrastructure is funded by ENEA, the Italian National Agency for New Technologies, Energy and Sustainable Economic Development and by Italian and European research programs (see https://www.cresco.enea.it/englishforinformation)”. The authors also wish to thank the National Research Foundation, Prime Minister's Office, Singapore under the Solar CRP (S18-1176-SCRP) for financial support.References
- Q. Jiang, Z. Chu, P. Wang, X. Yang, H. Liu, Y. Wang, Z. Yin, J. Wu, X. Zhang and J. You, Planar-Structure Perovskite Solar Cells with Efficiency beyond 21%, Adv. Mater., 2017, 29, 1703852 CrossRef PubMed.
- A. B. Muñoz-García, I. Benesperi, G. Boschloo, J. J. Concepcion, J. H. Delcamp, E. A. Gibson, G. J. Meyer, M. Pavone, H. Pettersson, A. Hagfeldt and M. Freitag, Dye-sensitized solar cells strike back, Chem. Soc. Rev., 2021, 50, 12450–12550 RSC.
- F. Schipani, D. R. Miller, M. A. Ponce, C. M. Aldao, S. A. Akbar, P. A. Morris and J. C. Xu, Conduction mechanisms in SnO2 single-nanowire gas sensors: An impedance spectroscopy study, Sens. Actuators, B, 2017, 241, 99–108 CrossRef CAS.
- V. B. Raj, A. T. Nimal, M. Tomar, M. U. Sharma and V. Gupta, Novel scheme to improve SnO2/SAW sensor performance for NO2 gas by detuning the sensor oscillator frequency, Sens. Actuators, B, 2015, 220, 154–161 CrossRef CAS.
- H. Kim and A. Piqué, Transparent conducting Sb-doped SnO2 thin films grown by pulsed-laser deposition, Appl. Phys. Lett., 2004, 84, 218–220 CrossRef CAS.
- Y. Idota, T. Kubota, A. Matsufuji, Y. Maekawa and T. Miyasaka, Tin-Based Amorphous Oxide: A High-Capacity Lithium-Ion-Storage Material, Science, 1997, 276, 1395–1397 CrossRef CAS.
- K. G. Godinho, A. Walsh and G. W. Watson, Energetic and Electronic Structure Analysis of Intrinsic Defects in SnO2, J. Phys. Chem. C, 2009, 113, 439–448 CrossRef CAS.
- Ç. Kılıç and A. Zunger, Origins of Coexistence of Conductivity and Transparency in SnO2, Phys. Rev. Lett., 2002, 88, 095501 CrossRef PubMed.
- L. Xiong, Y. Guo, J. Wen, H. Liu, G. Yang, P. Qin and G. Fang, Review on the Application of SnO2 in Perovskite Solar Cells, Adv. Funct. Mater., 2018, 28, 1802757 CrossRef.
- H. Kim, R. C. Y. Auyeung and A. Piqué, Transparent conducting F-doped SnO2 thin films grown by pulsed laser deposition, Thin Solid Films, 2008, 516, 5052–5056 CrossRef CAS.
- J. Ouerfelli, S. O. Djobo, J. C. Bernède, L. Cattin, M. Morsli and Y. Berredjem, Organic light emitting diodes using fluorine doped tin oxide thin films, deposited by chemical spray pyrolysis, as anode, Mater. Chem. Phys., 2008, 112, 198–201 CrossRef CAS.
- H. Toyosaki, M. Kawasaki and Y. Tokura, Electrical properties of Ta-doped SnO2 thin films epitaxially grown on TiO2 substrate, Appl. Phys. Lett., 2008, 93, 132109 CrossRef.
- K. Jain, R. P. Pant and S. T. Lakshmikumar, Effect of Ni doping on thick film SnO2 gas sensor, Sens. Actuators, B, 2006, 113, 823–829 CrossRef CAS.
- J. Kaur, R. Kumar and M. C. Bhatnagar, Effect of indium-doped SnO2 nanoparticles on NO2 gas sensing properties, Sens. Actuators, B, 2007, 126, 478–484 CrossRef CAS.
- Z. Lin, N. Li, Z. Chen and P. Fu, The effect of Ni doping concentration on the gas sensing properties of Ni doped SnO2, Sens. Actuators, B, 2017, 239, 501–510 CrossRef CAS.
- S. Akin, Hysteresis-Free Planar Perovskite Solar Cells with a Breakthrough Efficiency of 22% and Superior Operational Stability over 2000 h, ACS Appl. Mater. Interfaces, 2019, 11, 39998–40005 CrossRef CAS.
- E. Halvani Anaraki, A. Kermanpur, M. T. Mayer, L. Steier, T. Ahmed, S.-H. Turren-Cruz, J. Seo, J. Luo, S. M. Zakeeruddin, W. R. Tress, T. Edvinsson, M. Grätzel, A. Hagfeldt and J.-P. Correa-Baena, Low-Temperature Nb-Doped SnO2 Electron-Selective Contact Yields over 20% Efficiency in Planar Perovskite Solar Cells, ACS Energy Lett., 2018, 3, 773–778 CrossRef CAS.
- H. Ye, Z. Liu, X. Liu, B. Sun, X. Tan, Y. Tu, T. Shi, Z. Tang and G. Liao, 17.78% efficient low-temperature carbon-based planar perovskite solar cells using Zn-doped SnO2 electron transport layer, Appl. Surf. Sci., 2019, 478, 417–425 CrossRef CAS.
- G. V. Sannino, A. De Maria, V. La Ferrara, G. Rametta, L. V. Mercaldo, M. L. Addonizio, L. Lancellotti, A. Pecoraro, A. B. Muñoz-García, M. Pavone and P. Delli Veneri, Development of SnO2 Composites as Electron Transport Layer in Unencapsulated CH3NH3PbI3 Solar Cells, Solids, 2021, 2, 407–419 CrossRef CAS.
- L. Chouhan, S. K. Panda, S. Bhattacharjee, B. Das, A. Mondal, B. N. Parida, R. Brahma, M. K. Manglam, M. Kar, G. Bouzerar and S. K. Srivastava, Room temperature d0 ferromagnetism, zero dielectric loss and ac-conductivity enhancement in p-type Ag-doped SnO2 compounds, J. Alloys Compd., 2021, 870, 159515 CrossRef CAS.
- S. K. Srivastava, P. Lejay, B. Barbara, S. Pailhès, V. Madigou and G. Bouzerar, Possible room-temperature ferromagnetism in K-doped SnO2: X-ray diffraction and high-resolution transmission electron microscopy study, Phys. Rev. B: Condens. Matter Mater. Phys., 2010, 82, 193203 CrossRef.
- W. Wei, Y. Dai, M. Guo, K. Lai and B. Huang, Density functional study of magnetic properties in Zn-doped SnO2, J. Appl. Phys., 2010, 108, 093901 CrossRef.
- P. Wu, B. Zhou and W. Zhou, Room-temperature ferromagnetism in epitaxial Mg-doped SnO2 thin films, Appl. Phys. Lett., 2012, 100, 182405 CrossRef.
- W.-Z. Xiao, L.-L. Wang and Z. Tan, Unexpected magnetic properties in carbon-doped SnO2 from first-principles calculation, Comput. Mater. Sci., 2014, 83, 5–11 CrossRef CAS.
- D. O. Scanlon and G. W. Watson, On the possibility of p-type SnO2, J. Mater. Chem., 2012, 22, 25236–25245 RSC.
- C. E. Benouis, M. Benhaliliba, F. Yakuphanoglu, A. T. Silver, M. S. Aida and A. S. Juarez, Physical properties of ultrasonic sprayed nanosized indium doped SnO2 films, Synth. Met., 2011, 161, 1509–1516 CrossRef CAS.
- Z. Ji, Z. He, Y. Song, K. Liu and Z. Ye, Fabrication and characterization of indium-doped p-type SnO2 thin films, J. Cryst. Growth, 2003, 259, 282–285 CrossRef CAS.
- T. Le, H. P. Dang and V. H. Le, Determination of the optimum annealing temperature and time for Indium-doped SnO2 films to achieve the best p-type conductive property, J. Alloys Compd., 2017, 696, 1314–1322 CrossRef CAS.
- W. Ben Haj Othmen, Z. Ben Hamed, B. Sieber, A. Addad, H. Elhouichet and R. Boukherroub, Structural and optical characterization of p-type highly Fe-doped SnO2 thin films and tunneling transport on SnO2:Fe/p-Si heterojunction, Appl. Surf. Sci., 2018, 434, 879–890 CrossRef CAS.
- X. Li, R. Deng, Y. Li, B. Yao, Z. Ding, J. Qin and Q. Liang, Effect of Mg doping on optical and electrical properties of SnO2 thin films: An experiment and first-principles study, Ceram. Int., 2016, 42, 5299–5303 CrossRef CAS.
- H. He, Z. Xie, Q. Li, J. Li and Q. Zhang, Novel p-type conductivity in SnO2 thin films by Mg doping, J. Alloys Compd., 2017, 714, 258–262 CrossRef CAS.
- H. He, Z. Xie, Q. Li and H. Niu, On the possibility of p-type doping of SnO2 with Mg: A first-principles study, Comput. Mater. Sci., 2015, 101, 62–65 CrossRef CAS.
- W. Fu, M. Li, J. Li, G. Fang, P. Ye, E. Wentao, X. Xiao, H. Wei, B. Liu, Y. Lu and Y. He, Achieving p-type conductivity in wide-bandgap SnO2 by a two-step process, Appl. Phys. Lett., 2021, 118, 112102 CrossRef CAS.
- B. Chakraborty and L. M. Ramaniah, Exploring d0 magnetism in doped SnO2–a first principles DFT study, J. Magn. Magn. Mater., 2015, 385, 207–216 CrossRef CAS.
- L. Xiong, M. Qin, G. Yang, Y. Guo, H. Lei, Q. Liu, W. Ke, H. Tao, P. Qin, S. Li, H. Yu and G. Fang, Performance enhancement of high temperature SnO2-based planar perovskite solar cells: electrical characterization and understanding of the mechanism, J. Mater. Chem. A, 2016, 4, 8374–8383 RSC.
- N. Zhou, Q. Cheng, L. Li and H. Zhou, Doping effects in SnO2 transport material for high performance planar perovskite solar cells, J. Phys. D: Appl. Phys., 2018, 51, 394001 CrossRef.
- G. Kresse and J. Furthmüller, Efficient iterative schemes for ab initio total-energy calculations using a plane-wave basis set, Phys. Rev. B: Condens. Matter Mater. Phys., 1996, 54, 11169–11186 CrossRef CAS PubMed.
- G. Kresse and J. Furthmüller, Efficiency of ab-initio total energy calculations for metals and semiconductors using a plane-wave basis set, Comput. Mater. Sci., 1996, 6, 15–50 CrossRef CAS.
- G. Kresse and J. Hafner, Ab initio molecular dynamics for liquid metals, Phys. Rev. B: Condens. Matter Mater. Phys., 1993, 47, 558–561 CrossRef CAS PubMed.
- G. Kresse and J. Hafner, Ab initio molecular-dynamics simulation of the liquid-metal-amorphous-semiconductor transition in germanium, Phys. Rev. B: Condens. Matter Mater. Phys., 1994, 49, 14251–14269 CrossRef CAS.
- J. P. Perdew, K. Burke and M. Ernzerhof, Generalized Gradient Approximation Made Simple, Phys. Rev. Lett., 1996, 77, 3865–3868 CrossRef CAS PubMed.
- J. P. Perdew, K. Burke and M. Ernzerhof, Generalized Gradient Approximation Made Simple, Phys. Rev. Lett., 1996, 77, 3865 ( Phys. Rev. Lett. , 1997 , 78 , 1396 ) CrossRef CAS.
- J. Heyd, G. E. Scuseria and M. Ernzerhof, Hybrid functionals based on a screened Coulomb potential, J. Chem. Phys., 2003, 118, 8207–8215 CrossRef CAS.
- J. Heyd, G. E. Scuseria and M. Ernzerhof, Erratum: “Hybrid functionals based on a screened Coulomb potential”, J. Chem. Phys., 2003, 118, 8207 ( J. Chem. Phys. , 2006 , 124 , 219906 ) CrossRef CAS.
- P. E. Blöchl, Projector augmented-wave method, Phys. Rev. B: Condens. Matter Mater. Phys., 1994, 50, 17953–17979 CrossRef.
- G. Kresse and D. Joubert, From ultrasoft pseudopotentials to the projector augmented-wave method, Phys. Rev. B: Condens. Matter Mater. Phys., 1999, 59, 1758–1775 CrossRef CAS.
- S. Grimme, S. Ehrlich and L. Goerigk, Effect of the damping function in dispersion corrected density functional theory, J. Comput. Chem., 2011, 32, 1456–1465 CrossRef CAS PubMed.
- A. D. Becke and E. R. Johnson, A density-functional model of the dispersion interaction, J. Chem. Phys., 2005, 123, 154101 CrossRef PubMed.
- C. Baiano, E. Schiavo, C. Gerbaldi, F. Bella, G. Meligrana, G. Talarico, P. Maddalena, M. Pavone and A. B. Muñoz-García, Role of surface defects in CO2 adsorption and activation on CuFeO2 delafossite oxide, Mol. Catal., 2020, 496, 111181 CrossRef CAS.
- M. D'Arienzo, L. Gamba, F. Morazzoni, U. Cosentino, C. Greco, M. Lasagni, D. Pitea, G. Moro, C. Cepek, V. Butera, E. Sicilia, N. Russo, A. B. Muñoz-García and M. Pavone, Experimental and Theoretical Investigation on the Catalytic Generation of Environmentally Persistent Free Radicals from Benzene, J. Phys. Chem. C, 2017, 121, 9381–9393 CrossRef.
- A. B. Muñoz-García and M. Pavone, Structure and energy level alignment at the dye–electrode interface in p-type DSSCs: new hints on the role of anchoring modes from ab initio calculations, Phys. Chem. Chem. Phys., 2015, 17, 12238–12246 RSC.
- A. B. Muñoz-García, F. Sannino, G. Vitiello, D. Pirozzi, L. Minieri, A. Aronne, P. Pernice, M. Pavone and G. D'Errico, Origin and Electronic Features of Reactive Oxygen Species at Hybrid Zirconia-Acetylacetonate Interfaces, ACS Appl. Mater. Interfaces, 2015, 7, 21662–21667 CrossRef PubMed.
- B. Samanta, Á. Morales-García, F. Illas, N. Goga, J. A. Anta, S. Calero, A. Bieberle-Hütter, F. Libisch, A. B. Muñoz-García, M. Pavone and M. Caspary Toroker, Challenges of modeling nanostructured materials for photocatalytic water splitting, Chem. Soc. Rev., 2022, 51, 3794–3818 RSC.
- A. A. Bolzan, C. Fong, B. J. Kennedy and C. J. Howard, Structural Studies of Rutile-Type Metal Dioxides, Acta Crystallogr., Sect. B: Struct. Sci., 1997, 53, 373–380 CrossRef.
- R. Shannon, Revised effective ionic radii and systematic studies of interatomic distances in halides and chalcogenides, Acta Crystallogr., Sect. A: Cryst. Phys., Diffr., Theor. Gen. Crystallogr., 1976, 32, 751–767 CrossRef.
- J. Oviedo and M. J. Gillan, Energetics and structure of stoichiometric SnO2 surfaces studied by first-principles calculations, Surf. Sci., 2000, 463, 93–101 CrossRef CAS.
- Y. Duan, Electronic properties and stabilities of bulk and low-index surfaces of SnO in comparison with SnO2: A first-principles density functional approach with an empirical correction of van der Waals interactions, Phys. Rev. B: Condens. Matter Mater. Phys., 2008, 77, 045332 CrossRef.
- A. Pecoraro, A. De Maria, P. Delli Veneri, M. Pavone and A. B. Muñoz-García, Interfacial electronic features in methyl-ammonium lead iodide and p-type oxide heterostructures: new insights for inverted perovskite solar cells, Phys. Chem. Chem. Phys., 2020, 22, 28401–28413 RSC.
- G. Zhang, G. Qin, G. Yu, Q. Hu, H. Fu and C. Shao, Ab initio investigation on a promising transparent conductive oxide, Nb:SnO2, Thin Solid Films, 2012, 520, 5965–5970 CrossRef CAS.
- D. Fröhlich, R. Kenklies and R. Helbig, Band-Gap Assignment in SnO2 by Two-Photon Spectroscopy, Phys. Rev. Lett., 1978, 41, 1750–1751 CrossRef.
- P. D. Borges, L. M. R. Scolfaro, H. W. Leite Alves and E. F. da Silva, DFT study of the electronic, vibrational, and optical properties of SnO2, Theor. Chem. Acc., 2010, 126, 39–44 Search PubMed.
- X. Cai, P. Zhang and S.-H. Wei, Revisit of the band gaps of rutile SnO2 and TiO2: a first-principles study, J. Semicond., 2019, 40, 092101 Search PubMed.
- A. Stashans, P. Puchaicela and R. Rivera, DFT study of chromium-doped SnO2 materials, J. Mater. Sci., 2014, 49, 2904–2911 CrossRef CAS.
- M. Worsdale, A. Rabis, E. Fabbri, T. J. Schmidt and D. Kramer, Conductivity Limits of Extrinsically Doped SnO2 Supports, ECS Trans., 2015, 69, 1167–1178 CrossRef CAS.
- J. Xue, S. Ma, Q. Bi, X. Zhang, W. Guan and Y. Gao, Revealing the modification mechanism of La-doped Ti/SnO2 electrodes related to the microelectronic structure by first-principles calculations, J. Alloys Compd., 2018, 747, 423–430 CrossRef CAS.
- W. A. Farooq, S. M. Ali, J. Muhammad, S. D. Ali, M. H. Aziz, N.-u. Rehman and M. Hussain, Synthesis and characterization of Sn1Mg1−xO2 thin films fabricated by aero-sole assisted chemical vapor deposition, J. Mater. Sci.: Mater. Electron., 2013, 24, 5140–5146 CrossRef CAS.
- N. Mazumder, A. Bharati, S. Saha, D. Sen and K. K. Chattopadhyay, Effect of Mg doping on the electrical properties of SnO2 nanoparticles, Curr. Appl. Phys., 2012, 12, 975–982 CrossRef.
- B. Thomas and B. Skariah, Spray deposited Mg-doped SnO2 thin film LPG sensor: XPS and EDX analysis in relation to deposition temperature and doping, J. Alloys Compd., 2015, 625, 231–240 CrossRef CAS.
- K. Mahmood, S. Sarwar and M. T. Mehran, Current status of electron transport layers in perovskite solar cells: materials and properties, RSC Adv., 2017, 7, 17044–17062 RSC.
- B. A. Gregg and M. C. Hanna, Comparing organic to inorganic photovoltaic cells: Theory, experiment, and simulation, J. Appl. Phys., 2003, 93, 3605–3614 CrossRef CAS.
| This journal is © The Royal Society of Chemistry 2023 |