Tuning conformational asymmetry in particle-forming diblock copolymer alloys†
Logan J.
Case
,
Frank S.
Bates
 and
Kevin D.
Dorfman
and
Kevin D.
Dorfman
 *
*
Department of Chemical Engineering and Materials Science, University of Minnesota-Twin Cities, 421 Washington Ave SE, Minneapolis, Minnesota 55455, USA. E-mail: dorfman@umn.edu; Tel: +1 612 6245560
First published on 28th November 2022
Abstract
Self-consistent field theory is employed to compute the phase behavior of binary blends of conformationally asymmetric, micelle-forming diblock copolymers with miscible corona blocks and immiscible core blocks (a diblock copolymer “alloy”). The calculations focus on establishing conditions that promote the formation of Laves phases by tuning the relative softness of the cores of the two different Laves phase particles via independent control of their conformational asymmetries. Increasing the conformational asymmetry of the more spherical particles of the Laves structure has a stabilizing effect, consistent with the expectations of increased imprinting of the Wigner–Seitz cells on the core/corona interface as conformational asymmetry increases. The resulting phase diagram in the temperature-blend composition space features a more stable Laves phase field than that predicted for conformationally symmetric systems. The phase field closes at low temperatures in favor of macrophase separation between a hexagonally-packed cylinder (hex) phase and a body-centered cubic phase. Companion calculations, using an alloy whose components do not produce a hex phase in the neat melt state, suggest that the Laves phase field in such a blend will persist at strong segregation.
1 Introduction
Compositionally asymmetric diblock polymer melts produce particulate phases when cooled below the order-disorder transition (ODT). For linear AB diblock copolymers, the ordered state selection is governed by three parameters: (i) the segregation strength χN, where χ is the Flory–Huggins parameter and N is the total degree of polymerization; (ii) the minority block volume fraction fA = NA/N, where NA is the degree of polymerization of the minority block; and (iii) the conformational asymmetry εAB = bA/bB, where bi is the statistical segment length of block i.1–5 The classic theoretical diblock copolymer phase diagram focuses on systems with low conformational asymmetry (εAB ≈ 1),6–8 where the resulting micelles pack on a body-centered cubic (bcc) lattice,9–11 with a narrow region of close-packing near the ODT.7,12–14It is now recognized that increasing conformational asymmetry in compositionally asymmetric diblock copolymers gives rise to a different class of particle packings known as Frank–Kasper phases (Fig. 1a).15–19 In contrast to bcc, which has a single particle type arranged on a high symmetry lattice, Frank–Kasper phases are low-symmetry, tetrahedrally close-packed phases possessing multiple particle types,20,21 each with a distinct volume and, importantly, a distinct sphericity.5,22,23 Conformational asymmetry furnishes two synergistic effects that ultimately combine to stabilize Frank–Kasper phases relative to bcc. First, larger εAB shifts the order–order transitions to larger fA, delaying the onset of hexagonally packed cylinders (hex).1,22,24–27 Second, larger εAB produces softer micellar cores that can be partially imprinted by the Voronoi cells of the lattice,5,19,23,28–30 which introduces a tendency to prefer systems with a higher average sphericity of the constituent particles.23 Taken together, these two effects lead to Frank–Kasper phases possessing a better balance of chain stretching against interfacial area than bcc as conformational asymmetry increases.5,22,23 Among the 27 known Frank–Kasper phases in metallic alloys,31 only σ15,16,18,32–38 and A1518,36 are believed to be equilibrium states in neat diblock copolymer melts. Non-equilibrium C14 or C15 Laves phases can be accessed via thermal processing,17,35,39,40 but their emergence as equilibrium states is stymied by large particle volume asymmetry (Fig. 1b).37,41–44
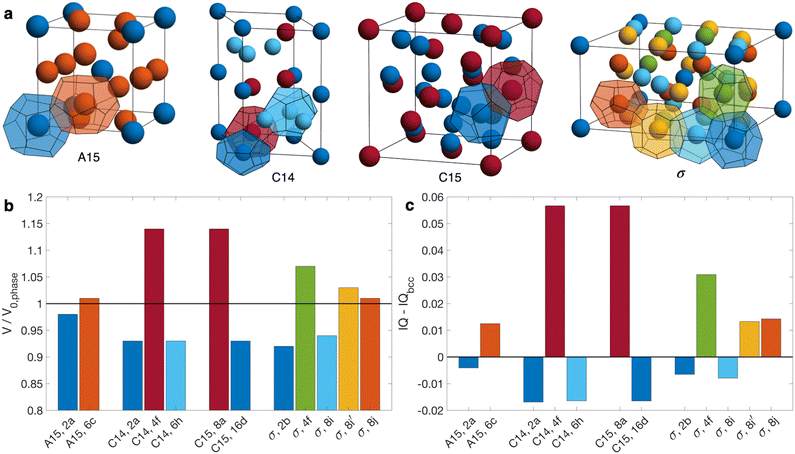 | ||
| Fig. 1 (a) Illustration of the Frank–Kasper σ, A15, C14, and C15 phases, highlighting the symmetry-inequivalent particle positions and associated Wigner-Seitz cells. (b) Volume of each particle type relative to the number-averaged particle volume for the structure, V0,phase. (c) Isoperimetric quotient IQ = 36πV2/S3 of each particle type as reported by Kim et al.,17 relative to that of bcc, where V is the particle volume and S is the particle surface area. Bar colors in (b and c) match the colors of the corresponding particles in (a). Particles are labeled in (b and c) according to phase and Wyckoff position. Structures in (a) are generated using a Matlab program developed by Lindsay et al.45 | ||
Since each particle type in a Frank–Kasper phase possesses a unique sphericity (Fig. 1c),5,22,23 fully elucidating the role of conformational asymmetry on the formation of Frank–Kasper phases is challenging in a neat diblock copolymer melt because there is but a single conformational asymmetry parameter, εAB. To understand more deeply how conformational asymmetry impacts ordered state selection, it is desirable to control each particle type's conformational asymmetry independently. One approach to access such control is going beyond a neat AB diblock copolymer melt to a diblock copolymer alloy consisting of two (or more) diblock copolymers with miscible majority blocks and immiscible minority blocks.46 The simplest such system is a binary alloy consisting of a blend of AB and B′C diblock copolymers,46 where the prime notation indicates a different degree of polymerization. To achieve this objective, the χ-parameter between blocks A and C must be large enough to prevent mixing of the particle cores.46 Such a binary blend possesses two conformational asymmetry parameters, εAB and εBC, which quantify the softness of the AB and B′C micelle cores, respectively.
In the present contribution, we use self-consistent field theory (SCFT)47,48 to investigate the ability of conformationally asymmetric block copolymer alloys to stabilize Laves phases. Laves phases are attractive for our purposes because they consist of two particles with disparate volumes and sphericities.17,23,49 As a result, this system is ideally suited for studying the tunability of the different types of particle cores enabled by binary block copolymer alloys. Prior work has already demonstrated from SCFT the potential for diblock copolymer alloys to address the challenge imposed by the volume asymmetry of a Laves phase (Fig. 1b).46 Here, we show that Laves phases can be further stabilized via differing conformational asymmetries in a polymer alloy, thereby providing a design strategy to address both volume asymmetry and sphericity asymmetry of the constituent particles, and clearly illustrating the power of controlling conformational asymmetry of each particle independently to enable the formation of complex particle packings in diblock copolymers.
2 Methods
Following prior work,46 we select highly compositionally asymmetric diblocks with equal core block fraction fA = fC = 0.20 to promote formation of quasi-spherical micelles at sufficiently high segregation strength. To simplify the ensuing analysis, we choose symmetric segregation strengths for the individual diblock copolymers, such that χABNAB = χBCNB′C = χN where χij is the Flory–Huggins interaction parameter between monomers i and j and NAB and NB′C are the degrees of polymerization of the AB and B′C chains, respectively. To enhance the immiscibility of A and C relative to A/B or B/C interactions, we select a larger Flory–Huggins parameter between monomers A and C such that χACNAB = 2(χN). In reporting our results, it is convenient to express the results in terms of temperature as well. To do so, we will assume that χ is purely enthalpic and set the reference temperature T0 to correspond to χN = 30.It is worthwhile to make a preliminary estimate here of where we might anticipate Laves phases to emerge in a conformationally asymmetric binary alloy, building on the prior analysis for conformationally symmetric systems.46 Stabilization of a Laves phase in this alloy system requires that (i) the AB and B′C form micelles with appropriate volume asymmetry α = VB′C/VAB and (ii) the chains are blended at a ratio which yields a particle stoichiometry of approximately 2![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1.46 If we choose the B′C diblock to form the larger micelles (the red particles in Fig. 1), the expected blend fraction for Laves phase formation is
1.46 If we choose the B′C diblock to form the larger micelles (the red particles in Fig. 1), the expected blend fraction for Laves phase formation is
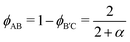 | (1) |
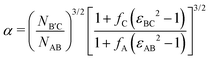 | (2) |
Our numerical analysis uses SCFT47,48 with a Gaussian chain model47,50,51 to predict the behavior of the alloy system. All calculations are performed using the C++ version of the open-source PSCF code using either the canonical or grand canonical ensembles.52–54 More details about the particular methodologies employed to analyze phase equilibria or compute phase boundaries are available in the ESI.†
3 Results
Our first objective is to understand how chain length and conformational asymmetry affect the stability of Laves phases, using the independent control over conformational asymmetry to adjust the softness of the AB and B′C micelle cores for different chain lengths. We thus consider systems with chain length asymmetries 0.5 ≤ NB′C/NAB ≤ 2.0 for conformational asymmetries of 1.00, 1.25, and 1.50 applied to (i) the AB diblock, (ii) the B′C diblock, and (iii) both the AB and B′C diblocks simultaneously. For each of these conditions, we performed canonical SCFT simulations of the C14 and C15 Laves phases and compared their free energies per chain of size NAB (denoted by F/nkBT) against potential macrophase separation via the common tangent construction.55 Among the three most common Laves phases (C14, C15, and C36),49 we consider only C14 and C15 because they are generally expected to be stable compared to C36,56 and are the only Laves phases observed in block polymer systems.17,35,37,39–41,57 Candidate phases for construction of the common tangent tie lines were face-centered cubic spheres (fcc), body-centered cubic spheres (bcc), and hexagonally-packed cylinders (hex), each with both AB-rich and B′C-rich varieties. At each condition, the common tangent representing macrophase separation for comparison to the Laves phases was taken to be the lowest-energy tangent among tangents formed by each (AB-rich, B′C-rich) phase pairing. In general, bcc–bcc macrophase separation is the relevant candidate to compare with the Laves phase, with the exception of a few cases of fcc–bcc macrophase separation. The analysis was performed at two segregation strengths, χN = 25 and χN = 28, chosen based on the neat diblock phase diagrams25 such that a neat diblock melt with block fraction fi = 0.2 and conformational asymmetry of εij = 1.0 or εij = 1.5, respectively, would be near the center of the bcc window. Details of this analysis are available in the ESI.†Fig. 2 depicts the lowest energy of the C14 Laves phase relative to macrophase separation at each of the conditions described above at χN = 28. Note that the Laves phases are nearly degenerate in free energy (see Fig. S3, ESI†) consistent with prior literature;17,39,46,56,58 thus selection of C14 over C15 for the analysis is inconsequential. At this segregation strength, the macrophase separation reference is dominated by coexistence of AB-rich and B′C-rich bcc morphologies; the only exceptions occur when B′C-rich fcc overtakes B′C-rich bcc at the highest conformational asymmetry condition (εij = 1.5) for very low NB′C/NAB, highlighted by the shaded regions in the figure.
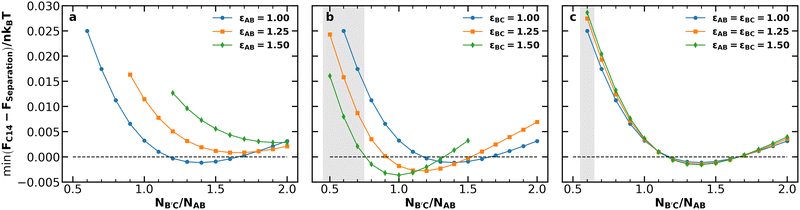 | ||
| Fig. 2 Minimum free energy of the C14 Laves phase relative to the macrophase separation tangent line at various conformational asymmetries for (a) the AB diblock, (b) the B′C diblock, or (c) both the AB and B′C diblocks for χABNAB = χBCNB′C = 28.0, χACNAB = 56.0, and fA = fC = 0.20. Shaded regions indicate those in which B′C-rich fcc is used in the macrophase separation tangent, rather than B′C-rich bcc, which only correspond to εBC = 1.5 in (b) or εAB = εBC = 1.5 in (c). The same analysis performed at χN = 25 exhibits similar results (see Fig. S2, ESI†). | ||
The data in Fig. 2 demonstrate the distinct effects of each conformational asymmetry on both the stability of the Laves phases and the chain length asymmetry most favorable to their formation. Increasing the conformational asymmetry of the AB diblock (Fig. 2a) generally destabilizes Laves phases while shifting the minima of the F vs. NB′C/NAB toward higher chain length asymmetry. If instead εBC is increased (Fig. 2b), the opposite effect is observed with the Laves phases becoming more stable with increasing conformational asymmetry and the minima of F vs. NB′C/NAB shifting to lower NB′C/NAB. Simultaneously increasing both εAB and εBC (Fig. 2c) leads to competition between these two opposing trends, resulting in only minimal changes to F vs. NB′C/NAB.
The stabilizing effect of εBC and the destabilizing effect of εAB both can be attributed to the softening of micelle cores and the resultant imprinting on the polyhedral Wigner–Seitz cell.5,19,23,28–30 As conformational asymmetry increases, faceting of the micelle core creates more interfacial area, but the thermodynamic cost, relative to micelle volume, is lower for more spherical polyhedra.5,22,23 In neat diblock systems, Frank–Kasper phases are proposed to form at higher conformational asymmetry because their particles are, on average, more spherical than in bcc.17,23 Critically, however, this does not mean that all Wigner-Seitz polyhedra in a Frank–Kasper phase are more spherical than those in bcc,17 as shown in Fig. 1c. Rather, the thermodynamic benefits of the polyhedra that are more spherical (the red Laves phase particles in Fig. 1) tend to outweigh the costs of those that are less spherical. In the Laves phases, the smaller micelles (AB) reside in domains that are less spherical than bcc, while the larger micelles (B′C) are in more spherical domains.17 Therefore, when increasing εAB, there is a thermodynamic cost (relative to bcc formation) incurred by deforming the small micelle cores without the larger domains as a counter-balance; likewise, increasing εBC creates a relative thermodynamic benefit without the opposing cost of the smaller micelles.
The observed shifts in the locations of the F vs. NB′C/NAB minima result from the effects of conformational asymmetry on the radius of gyration of a diblock copolymer. Increasing εij at fixed N increases the micelle volume. When increasing εAB, this swelling applies to the smaller particles in the Laves structure. Such changes reduce the volume asymmetry, making the Laves structure less stable. Increasing the chain length asymmetry compensates somewhat for the unfavorable swelling of AB micelles, resulting in the rightward shift of the curves. The reverse holds true for B′C: increasing εBC swells the larger particles for a given value of N, thus promoting excess volume asymmetry and demanding reduced length asymmetry in response to stabilize the Laves phase. In fact, the swelling induced by εBC = 1.50 is sufficient on its own to produce the requisite Laves volume asymmetry, with the observed minimum occurring at NB′C/NAB = 1.0.
Neither of these trends are evident in Fig. 2c, in which εBC and εAB are increased together. Instead, simultaneous changes to both conformational asymmetries obscure the competing effects described above, resulting in minimal changes to the free-energy curve. This condition is analogous to the single conformational asymmetry available in neat diblock melts obscuring the individual particle effects, and highlights the value of leveraging multiple conformational asymmetries. The same analysis as that in Fig. 2 was performed at χN = 25 and produced similar results (see Fig. S2, ESI†). For both values of χN, the Laves phases had their lowest relative free energy when εBC = 1.5 and NB′C/NAB = 1.0, so this condition was selected for further analysis.
Having established the impacts of simultaneously varying conformational asymmetry and chain length, we now investigate the applicability of the simple estimate for the optimal conditions for Laves phase stability in eqn (2). Fig. 3 compares the optimum NB′C/NAB at χN = 25 and χN = 28 from our SCFT results against values predicted by eqn (2) with varying conformational asymmetry. Predicting NB′C/NAB from eqn (2) requires a volume asymmetry α to use as a basis. For this basis, α = 1.48 is a good choice because the same value has appeared in prior work as (i) the best volume asymmetry observed from SCFT in conformationally symmetric diblock alloys,46 and (ii) the optimum volume asymmetry for Laves phases obtained from the unconstrained diblock foam model.23Fig. 3 reveals two shortcomings in this estimate. First, the model fails to capture the effects of χN, consistently underestimating the chain length asymmetry for χN = 28. Such a failure makes sense when considering that the chains' radii of gyration will deviate more strongly from the ideal Gaussian estimate used in our derivation as segregation strength increases. Second, the model significantly underestimates the impact of εAB. However, when varying εBC, the model shows reasonable agreement with the observed value. Overall, the simple model of eqn (2) captures the χN = 25 behavior in Fig. 3b and c, but fails to capture the effects of segregation strength or accurately reflect the behavior in Fig. 3a.
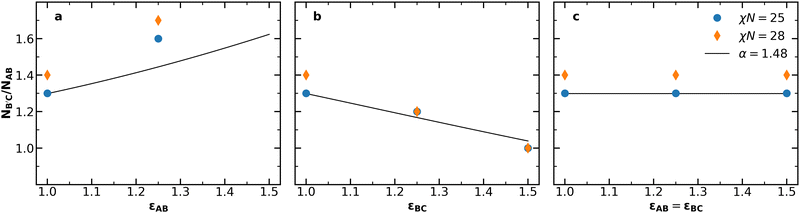 | ||
| Fig. 3 The chain length asymmetry NB′C/NAB at the F vs. NB′C/NAB minima at χN = 25 (Fig. S2, ESI†) and χN = 28 (Fig. 2), compared to the chain length asymmetry predicted by eqn (2) for α = 1.48 when (a) εAB is varied, (b) εBC is varied, and (c) εAB and εBC are varied together. In (a), no minimum could be clearly observed for εAB = 1.5, as the lowest observed free energy occurred at NB′C/NAB = 2.0, which was the highest value considered. | ||
We now continue our investigation with a thorough analysis of the phase behavior of the diblock alloy system with NB′C/NAB = 1.0, εAB = 1.0, and εBC = 1.5, identified prior to our discussion of eqn (2) as most effectively stabilizing the Laves phases amongst all of the systems we studied. To generate the phase diagram in Fig. 4, most phase boundaries were established first using the common-tangent construction55 and canonical ensemble SCFT calculations. In addition to the C14, C15, fcc, bcc, and hex phases already described, 15 additional competitors were included in these calculations. The competing phases are inspired by a 2014 study of B1AB2CB3 multiblock terpolymers by Xie et al.59 and are identical to those chosen by Magruder et al.46 for their block polymer alloys study. A list of all phases considered in the calculations is included in Table S1 (ESI†). Subsequent grand canonical calculations were used to resolve the region near each invariant point, where grand canonical ensemble's higher accuracy for problems involving macrophase separation53 substantially benefits the identification of the three-phase coexistence at these points. Grand canonical calculations were also used to map the phase boundaries near the ODT, where both canonical SCFT calculations and common tangent calculations started to suffer from failed convergence. C14 was used to represent the Laves phases while mapping the phase diagram. A detailed description of the canonical and grand canonical methodologies are included in the ESI.†
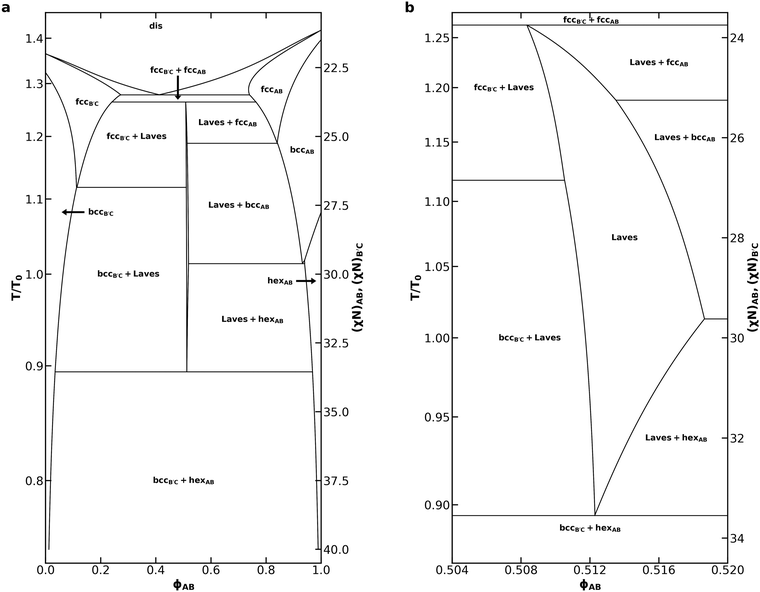 | ||
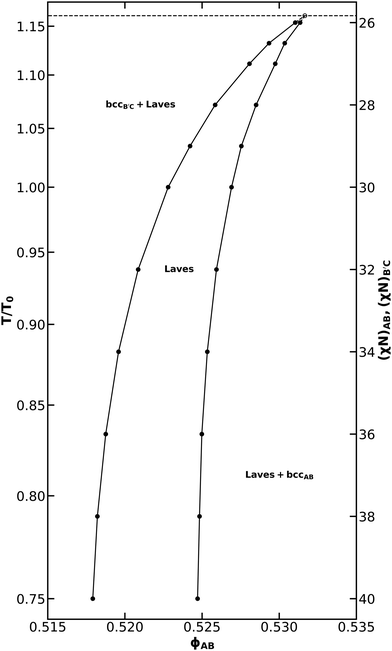
| Fig. 4 (a) Phase diagram for an AB/B′C alloy with NB′C/NAB = 1.0, fA = fC = 0.20, εAB = 1.0, εBC = 1.5, and assuming purely enthalpic χ values such that χACNAB = 2(χN) at all T and (b) a detailed view of the Laves phase field within that phase diagram. The reference temperature, T0, was chosen to correspond to χN = 30. Non-linear segments of the phase diagram are drawn using cubic splines fit to the sampled data. A companion phase diagram showing all of the points where SCFT calculations were performed is provided in Fig. S4 (ESI†). | ||
The phase diagram in Fig. 4a bears substantial qualitative resemblance to that presented by Magruder et al. for the conformationally symmetric case,46 with many characteristics reminiscent of metal alloy phase diagrams. In each case, the diblock alloys display a eutectic transition from a disordered liquid to coexistence between AB-rich and B′C-rich fcc phases, as well as a peritectoid transition to a Laves phase field upon cooling from coexistence of simple sphere phases (fcc or bcc). In the conformationally asymmetric case, however, the temperature difference between the eutectic and peritectoid points is greatly reduced when compared to prior results for a conformationally symmetric system.46 The peritectoid transitions of the two systems also differ on which simple sphere phase overtakes the Laves phase: bcc in the conformationally symmetric case,46 and fcc here. As also noted by Magruder et al.,46 experimental realization of this narrow eutectic to peritectoid transition is unlikely, given that fluctuation effects are expected to destroy the high-temperature regions of the diagram.
Below the peritectoid point, the Laves phase field widens as temperature decreases, and Laves coexistence with AB-rich and B′C-rich fcc phases is overtaken by coexistence with the corresponding bcc phases. At χN = 28, the highest segregation strength tested by Magruder et al.,46 we find a Laves phase field with a width of 0.006 in ϕAB. This exceeds the 0.002 width in ϕAB reported previously,46 consistent with the expectation that conformational asymmetry stabilizes Laves phases in the blend, while still possessing the narrow width characteristic of a phase field. The phase field reaches a maximum width at χN = 29.62 where the AB-rich bcc window closes, and the Laves phase starts to coexist with the AB-rich hex phase. At this segregation strength, the AB diblock would naturally form a hex phase in the neat melt. As the system is cooled further, conversion of the cylinder-forming AB diblock into spheres becomes increasingly unfavorable. The Laves phase field thus closes in a eutectoid transition to coexistence of B′C-rich bcc and AB-rich hex, which dominates the phase diagram at lower temperatures. The shape of the Laves phase field is difficult to resolve in Fig. 4a, so we include Fig. 4b to focus on the Laves window and help illuminate these details.
Compared to the neat melt conditions, both the AB-rich and B′C-rich fcc phase become stable over a much broader range of χN with the introduction of minority component. Aggregation of the minority component at the octahedral void spaces of the structure has been shown to stabilize the fcc phases,60,61 thus producing this effect. The difference in conformational asymmetry of the two diblocks results in substantial asymmetries in the phase diagram, particularly with regard to AB-rich and B′C-rich phase transitions. Conformational asymmetry shifts the phase boundaries of the neat B′C diblock relative to that of the AB diblock.1,22,24–27 These morphological differences between the neat diblock melts carry over into the blended behavior, resulting in the asymmetries observed in Fig. 4. Of particular interest is the absence of any B′C-rich hex formation. The presence of hex on the AB-rich side of the diagram results in a transition from a gradually broadening Laves phase field to a rapidly narrowing one.
The narrowing of the Laves phase field at the AB-rich bcc-hex transition suggests that, without competition from hex phases, conformationally asymmetric binary diblock alloys may exhibit a Laves phase field out to strong segregation. In order to test this speculation, we need to select a system in which neither diblock undergoes a transition to hex in the neat melt. From Fig. 2c, we see that when both diblocks have a conformational asymmetry of 1.5, the Laves phase remains stable when the ratio of the degrees of polymerization is used to induce volume asymmetry. We also know that a neat diblock with ε = 1.5 and f = 0.2 will not assemble into hex below χN = 40,25 which is an approximate upper bound for the ability to converge Frank–Kasper phase SCFT calculations with our software. Thus, we choose to further analyze an alloy system where εAB = εBC = 1.5 and NB′C/NAB = 1.4, which corresponds with the lowest relative free energy for Laves phases at the desired conformational asymmetry from our testing.
Using the same set of competing phases as for Fig. 4, the Laves phase field was mapped for this alloy. Canonical ensemble calculations were used in a common tangent analysis to identify the stable region for the Laves phase. As can be seen in Fig. 5, the Laves window remains open and continues to broaden up to χN = 40. The Laves window also shifts to lower ϕAB upon cooling, consistent with the trend seen in the work of Magruder et al. for conformationally symmetric alloys where NB′C/NAB was also used to create distinct particle sizes.46 It is also interesting to note that at the low-temperature end of Fig. 5, the AB-rich (right) side of the Laves window is much more nearly vertical than on the B′C-rich (left) side. Diblocks with the same block fraction and conformational asymmetry should exhibit the same phase behavior in the neat-melt limit; one might expect this symmetry to carry into the blending behavior and, likewise, into the Laves coexistence boundaries. However, both the deflection of the Laves window to lower ϕAB and the differing verticality of the coexistence boundaries demonstrate that this is not the case. This difference results from the asymmetry in chain length between the AB and B′C diblocks and resultant differences in their ability to pack in the interstitial sites of the bcc phases.
4 Conclusions
Using the Frank–Kasper Laves phases as a case study, we have demonstrated the ability of block polymer alloys to decouple the potentially competing effects of conformational asymmetry in different particle types, thereby probing the subtleties of its role in phase selection. In Laves phases, this decoupling revealed that increasing conformational asymmetry in the smaller, less spherical Laves particles has a detrimental effect on Laves phase stability, while increasing it in the larger, more spherical micelles is beneficial. The absence of significant changes to Laves stability when conformational asymmetry is simultaneously increased in both particles highlights how information can be obscured by competition when only a single conformational asymmetry is available such as in a neat diblock melt.Our results also demonstrate the value of independent conformational asymmetry control as a tool for designing self-assembling block polymer systems. We find that increasing conformational asymmetry in the large particles stabilizes the Laves phases. We also find that this effect is sufficient to produce the volume asymmetry required for Laves phase formation, without the need for asymmetry in the degrees of polymerization of the constituent chains, and results in a lower relative free energy for the Laves phases than was seen in the conformationally symmetric case. The phase diagram of this system bears a striking resemblance to that reported for the conformationally symmetric case,46 with a slightly broader Laves window and a greater variety of phases coexisting with the Laves phase. With increasing segregation strength, increasing preference for cylinder formation by one of the diblocks causes cylinders to rapidly out-compete the Laves phases, thus closing the Laves phase field. We are further able to leverage conformational asymmetry to avoid this cylinder formation and stabilize the Laves phases out to high segregation strength, suggesting the potential to extend the Laves phase field out to the strong segregation limit by balancing chain composition, degrees of polymerization, and conformational asymmetries.
Based on the results presented here, and in prior work,46 a substantial barrier to practical application of this methodology is likely to be the large windows of predicted macrophase separation. Introduction of some compatibilizing mechanism, such as hydrogen bonding between the corona blocks,62 to favor greater contact between the distinct micelle types may further stabilize the Laves phase in an alloy-type blend. Although the literature on diblock copolymer alloys has so far focused on Laves phases, the methodology will likely find utility tuning individual domains in other Frank–Kasper phases or other morphologies, particularly if mechanisms can be found to reduce the size of macrophase separation windows.
Author contributions
LJC, FSB, and KDD designed the research and edited the manuscript; LJC and KDD prepared the manuscript; LJC performed research and analyzed data.Conflicts of interest
There are no conflicts to declare.Acknowledgements
The authors thank Benjamin R. Magruder for helpful discussions and So Jung Park for valuable guidance regarding grand canonical ensemble methodologies. This work was supported by the National Science Foundation through DMR-1725272. Computational resources were provided in part by the Minnesota Supercomputing Institute.Notes and references
- S. T. Milner, Macromolecules, 1994, 27, 2333–2335 CrossRef CAS.
- F. S. Bates and G. H. Fredrickson, Macromolecules, 1994, 27, 1065–1067 CrossRef CAS.
- J. D. Vavasour and M. D. Whitmore, Macromolecules, 1993, 26, 7070–7075 CrossRef CAS.
- M. W. Matsen and M. Schick, Macromolecules, 1994, 27, 4014–4015 CrossRef CAS.
- G. M. Grason, Phys. Rep., 2006, 433, 1–64 CrossRef CAS.
- M. W. Matsen and M. Schick, Phys. Rev. Lett., 1994, 72, 2660–2663 CrossRef CAS PubMed.
- M. W. Matsen and F. S. Bates, Macromolecules, 1996, 29, 1091–1098 CrossRef CAS.
- E. W. Cochran, C. J. Garcia-Cervera and G. H. Fredrickson, Macromolecules, 2006, 39, 2449–2451 CrossRef CAS.
- L. Leibler, Macromolecules, 1980, 13, 1602–1617 CrossRef CAS.
- F. S. Bates, R. E. Cohen and C. V. Berney, Macromolecules, 1982, 15, 589–592 CrossRef CAS.
- E. L. Thomas, D. J. Kinning, D. B. Alward and C. S. Henkee, Macromolecules, 1987, 20, 2934–2939 CrossRef CAS.
- A. N. Semenov, Macromolecules, 1989, 22, 2849–2851 CrossRef CAS.
- Y.-Y. Huang, J.-Y. Hsu, H.-L. Chen and T. Hashimoto, Macromolecules, 2007, 40, 406–409 CrossRef CAS.
- N.-W. Hsu, B. Nouri, L.-T. Chen and H.-L. Chen, Macromolecules, 2020, 53, 9665–9675 CrossRef CAS.
- S. Lee, M. J. Bluemle and F. S. Bates, Science, 2010, 330, 349–353 CrossRef CAS PubMed.
- N. Xie, W. Li, F. Qiu and A.-C. Shi, ACS Macro Lett., 2014, 3, 906–910 CrossRef CAS PubMed.
- K. Kim, M. W. Schulze, A. Arora, R. M. Lewis, M. A. Hillmyer, K. D. Dorfman and F. S. Bates, Science, 2017, 356, 520–523 CrossRef CAS.
- M. W. Bates, J. Lequieu, S. M. Barbon, R. M. Lewis, K. T. Delaney, A. Anastasaki, C. J. Hawker, G. H. Fredrickson and C. M. Bates, Proc. Natl. Acad. Sci. U. S. A., 2019, 116, 13194–13199 CrossRef CAS.
- K. D. Dorfman, Macromolecules, 2021, 54, 10251–10270 CrossRef CAS.
- F. C. Frank and J. S. Kasper, Acta Crystallogr., 1958, 11, 184–190 CrossRef CAS.
- F. C. Frank and J. S. Kasper, Acta Crystallogr., 1959, 12, 483–499 CrossRef CAS.
- G. M. Grason, B. A. DiDonna and R. D. Kamien, Phys. Rev. Lett., 2003, 91, 1–4 CrossRef.
- A. Reddy, M. B. Buckley, A. Arora, F. S. Bates, K. D. Dorfman and G. M. Grason, Proc. Natl. Acad. Sci. U. S. A., 2018, 115, 10233–10238 CrossRef CAS.
- F. S. Bates, M. F. Schulz, A. K. Khandpur, S. Förster, J. H. Rosedale, K. Almdal and K. Mortensen, Faraday Discuss., 1994, 98, 7–18 RSC.
- M. W. Matsen and F. S. Bates, J. Polym. Sci. B: Polym. Phys., 1997, 35, 945–952 CrossRef CAS.
- M. W. Matsen, Macromolecules, 2012, 45, 2161–2165 CrossRef CAS.
- W. Li and Y.-X. Liu, J. Chem. Phys., 2021, 154, 014903 CrossRef CAS PubMed.
- P. D. Olmsted and S. T. Milner, Phys. Rev. Lett., 1994, 72, 936–939 CrossRef CAS PubMed.
- P. D. Olmsted and S. T. Milner, Macromolecules, 1998, 31, 4011–4022 CrossRef CAS.
- R. P. Collanton and K. D. Dorfman, Phys. Rev. Mater., 2022, 6, 015602 CrossRef CAS.
- M. Dutour Sikirić, O. Delgado-Friedrichs and M. Deza, Acta Crystallogr. A, 2010, 66, 602–615 CrossRef.
- S. Lee, C. Leighton and F. S. Bates, Proc. Natl. Acad. Sci. U. S. A., 2014, 111, 17723–17731 CrossRef CAS.
- T. M. Gillard, S. Lee and F. S. Bates, Proc. Natl. Acad. Sci. U. S. A., 2016, 113, 5167–5172 CrossRef CAS.
- M. W. Schulze, R. M. Lewis, J. H. Lettow, R. J. Hickey, T. M. Gillard, M. A. Hillmyer and F. S. Bates, Phys. Rev. Lett., 2017, 118, 207801 CrossRef PubMed.
- S. Jeon, T. Jun, S. Jo, H. Ahn, S. Lee, B. Lee and D. Y. Ryu, Macromol. Rapid Commun., 2019, 40, 1900259 CrossRef CAS.
- S. M. Barbon, J.-A. Song, D. Chen, C. Zhang, J. Lequieu, K. T. Delaney, A. Anastasaki, M. Rolland, G. H. Fredrickson, M. W. Bates, C. J. Hawker and C. M. Bates, ACS Macro Lett., 2020, 9, 1745–1752 CrossRef CAS.
- A. J. Mueller, A. P. Lindsay, A. Jayaraman, T. P. Lodge, M. K. Mahanthappa and F. S. Bates, ACS Macro Lett., 2020, 9, 576–582 CrossRef CAS.
- A. P. Lindsay, A. Jayaraman, A. J. Peterson, A. J. Mueller, S. Weigand, K. Almdal, M. K. Mahanthappa, T. P. Lodge and F. S. Bates, ACS Nano, 2021, 15, 9453–9468 CrossRef PubMed.
- K. Kim, A. Arora, R. M. Lewis, M. Liu, W. Li, A.-C. Shi, K. D. Dorfman and F. S. Bates, Proc. Natl. Acad. Sci. U. S. A., 2018, 115, 847–854 CrossRef CAS.
- B. Nouri, C.-Y. Chen, Y.-S. Huang, B. W. Mansel and H.-L. Chen, Macromolecules, 2021, 54, 9195–9203 CrossRef CAS.
- A. P. Lindsay, G. K. Cheong, A. J. Peterson, S. Weigand, K. D. Dorfman, T. P. Lodge and F. S. Bates, Macromolecules, 2021, 54, 7088–7101 CrossRef CAS.
- M. Liu, Y. Qiang, W. Li, F. Qiu and A.-C. Shi, ACS Macro Lett., 2016, 5, 1167–1171 CrossRef CAS PubMed.
- G. K. Cheong, F. S. Bates and K. D. Dorfman, Proc. Natl. Acad. Sci. U. S. A., 2020, 117, 16764–16769 CrossRef CAS PubMed.
- J. Xie and A.-C. Shi, Giant, 2021, 5, 100043 CrossRef CAS.
- A. P. Lindsay, A. J. Mueller, M. K. Mahanthappa, T. P. Lodge and F. S. Bates, Wigner-Seitz Cell generation and calculations in MATLAB, 2021, Retrieved from the Data Repository for the University of Minnesota.
- B. R. Magruder, S. J. Park, R. P. Collanton, F. S. Bates and K. D. Dorfman, Macromolecules, 2022, 55, 2991–2998 CrossRef CAS.
- E. Helfand, J. Chem. Phys., 1975, 62, 999–1005 CrossRef CAS.
- E. Helfand, Macromolecules, 1975, 8, 552–556 CrossRef.
- F. Stein and A. Leineweber, J. Mater. Sci., 2021, 56, 5321–5427 CrossRef CAS.
- M. W. Matsen, J. Phys.: Condens. Matter, 2002, 14, R21–R47 CrossRef CAS.
- G. H. Fredrickson, The Equilibrium Theory of Inhomogeneous Polymers, Oxford University Press, Oxford, United Kingdom, 2006 Search PubMed.
- G. K. Cheong, A. Chawla, D. C. Morse and K. D. Dorfman, Eur. Phys. J. E, 2020, 43, 15 CrossRef CAS.
- M. W. Matsen, Phys. Rev. Lett., 1995, 74, 4225–4228 CrossRef CAS PubMed.
- A. Shi, Variational Methods in Molecular Modeling, Springer Singapore, Singapore, 2017, pp. 155–180 Search PubMed.
- M. D. Whitmore and J. Noolandi, Macromolecules, 1985, 18, 2486–2497 CrossRef CAS.
- B. R. Magruder and K. D. Dorfman, Soft Matter, 2021, 17, 8950–8959 RSC.
- M. H. Uddin, C. Rodriguez, A. López-Quintela, D. Leisner, C. Solans, J. Esquena and H. Kunieda, Macromolecules, 2003, 36, 1261–1271 CrossRef CAS.
- M. Zhao and W. Li, Macromolecules, 2019, 52, 1832–1842 CrossRef CAS.
- N. Xie, M. Liu, H. Deng, W. Li, F. Qiu and A.-C. Shi, J. Am. Chem. Soc., 2014, 136, 2974–2977 CrossRef CAS PubMed.
- L. Chen, Y. Qiang and W. Li, Macromolecules, 2018, 51, 9890–9900 CrossRef CAS.
- M. W. Matsen, Phys. Rev. Lett., 2007, 99, 148304 CrossRef CAS.
- Q. Li, D. Woo, J.-K. Kim and W. Li, Macromolecules, 2022, 55, 6525–6535 CrossRef CAS.
Footnote |
| † Electronic supplementary information (ESI) available: Details of SCFT methodology; common tangent and grand canonical ensemble results; impact of conformational asymmetry; list of candidate phases and their properties; Laves phase degeneracy data; details of phase diagram calculations. See DOI: https://doi.org/10.1039/d2sm01332k |
| This journal is © The Royal Society of Chemistry 2023 |