Open Access Article
Open Access ArticleCreative Commons Attribution 3.0 Unported Licence
Morphology of vesicle triplets: shape transformation at weak and strong adhesion limits†
Toshikaze
Chiba
 a,
Yuka
Sakuma
a,
Yuka
Sakuma
 a,
Masayuki
Imai
a,
Masayuki
Imai
 *a and
Primož
Ziherl
*a and
Primož
Ziherl
 bc
bc
aDepartment of Physics, Tohoku University, Aoba, Sendai 980-8578, Japan. E-mail: imai@bio.phys.tohoku.ac.jp
bFaculty of Mathematics and Physics, University of Ljubljana, Jadranska 19, SI-1000 Ljubljana, Slovenia
cJožef Stefan Institute, Jamova 39, SI-1000 Ljubljana, Slovenia
First published on 16th May 2023
Abstract
We investigate the morphologies of adhering vesicle triplets as a function of volume-to-area ratio encoded by the reduced volume in strong and weak adhesion regimes. In the strong adhesion regime, the morphology change of the vesicle triplet depends on the arrangement of vesicles. By decreasing the reduced volume, a triangular triplet composed of three spherical caps with a trifurcated flat contact zone deformed to a compact spherical shape with a sigmoidal contact zone, whereas a linear vesicle triplet composed of pancake-shaped vesicles sandwiched between two spherical-cap vesicles with a flat contact zone deformed into a compact spherical shape with biconvex interfaces. The morphologies of vesicle triplets with flat contact zones are reproduced by the so-called two-tension model based on the total energy consisting of bending energy, adhesion energy and surface energy, where the surface tension in the noncontact zone is different from that in the contact zone. When the flat interface deforms, the two-tension model is no longer applicable. The compact spherical triplets with curved interfaces can be reproduced by introducing geometrical constraints requiring that the total area of the non-contact zones is minimal, thereby confining the aggregate to a spherical cavity; this is referred to as the cavity model. In the weak adhesion regime, vesicle triplets with either a triangular or linear topology deform into prolate-based triplets by decreasing the reduced volume.
1 Introduction
Cellular structures separated by closed membranes are frequently found around us. For example, a soap bubble is a spherical cellular structure partitioned by a thin water layer sandwiched between surfactant monolayers in the air. When a few soap bubbles meet, two adjacent layers at the contact zone merge, and they form characteristic multicellular patterns consisting of spherical caps and contact zones so as to minimize the surface energy, where the mean curvature is the same in each point of a given contact zone.1 The contact zones meet in threes at an angle of 120° to form an edge known as the Plateau border. The Plateau borders meet in fours at the tetrahedral angle so as to form a vertex. These geometrical laws governing soap bubble aggregates are called Plateau rules.2In contrast to a soap bubble, a vesicle—a closed surfactant bilayer suspended in water—shows a variety of shapes that minimize the bilayer bending energy at a given volume and area.3,4 A typical example of a vesicular structure is a mammalian red blood cell (RBC) which has a disklike biconcave shape with the reduced volume v ≈ 0.60 (v = 6π1/2V/A3/2, where A and V are the membrane area and the enclosed volume, respectively).5,6 The disklike biconcave shape agrees well with the prediction of the bending energy model.7,8 When a few RBCs form an aggregate, the contact zone shows a flat, concave, or sigmodal shape9,10 even in microcapillary flow.11–13 The static shape depends on the balance between the membrane bending energy and adhesion energy at the fixed reduced volume and adhesion strength.14–16 However, the morphology of RBC aggregates is strongly restricted by the constant reduced volume constraint. To release the constraint, we investigated the morphology of vesicle aggregates as a function of the reduced volume. For example, we studied the morphology of a vesicle doublet.17 As the reduced volume is decreased in the strong adhesion regime, the vesicle doublet with spherical caps and a flat contact zone deforms into a compact spherical doublet with the sigmoidal contact zone, whereas in the weak adhesion regime the vesicle doublet with spherical caps and a flat contact zone deforms into a parallel prolate doublet. Thus, our vesicle aggregates can present multicellular patterns which are not seen in aggregates of soap bubbles.
Morphological changes due to vesicle adhesion have been studied in many systems, such as vesicles adhering to other vesicles,17–19 substrates,20,21 and colloidal particles.22–26 In this study, we investigate the shapes of three adhering vesicles with varying reduced volume in both strong and weak adhesion regimes. We explore two triplet topologies, the triangle and the linear one. In the triangle topology, each of the three vesicles is in contact with the other two, whereas in the linear topology the middle vesicle is sandwiched by two end vesicles. We study typical morphological changes of both types of vesicle triplets at various reduced volumes and adhesion strengths. The obtained morphologies are examined using energy models composed of the bending energy, surface energy, and adhesion energy. The equilibrium shapes of triplets are computed by minimizing the total energy using the Surface Evolver package (hereafter abbreviated as SE)27 modified so as to apply to adhering vesicles.17 By combining systematic experiments and simulations, we reveal the various mechanisms that determine the morphology of vesicle triplets, especially focusing on the shape of the contact zone.
2 The model
2.1 Mechanical model of vesicle triplets: two-tension model
The total energy of the vesicle triplet Wtt is a sum of the local bending energy of vesicle i (i = 1, 2, 3),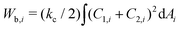 [kc is the bending rigidity and Cj,i (j = 1 or 2) is the principal curvature], the surface energy Wsuri = Ti|Ai − A0,i| (Ti is the surface tension, Ai is the actual vesicle area and A0,i is the preferred vesicle area), and the adhesion energy between vesicle i and j which reads Wadi,j = −ΓAci,j (Γ > 0 represents the adhesion strength and Aci,j is the contact area).17 First, we adopted the two-tension model where the surface tension in the non-contact zone (Tnc) is different from that in the contact zone (Tc), since the number density of lipid molecules in the contact zone is higher than that in the non-contact zone due to attractive inter-membrane interactions. In this case, the areas of vesicles in an aggregate are variable rather than fixed, and they are controlled by tensions. The total energy of the two-tension model is given by
[kc is the bending rigidity and Cj,i (j = 1 or 2) is the principal curvature], the surface energy Wsuri = Ti|Ai − A0,i| (Ti is the surface tension, Ai is the actual vesicle area and A0,i is the preferred vesicle area), and the adhesion energy between vesicle i and j which reads Wadi,j = −ΓAci,j (Γ > 0 represents the adhesion strength and Aci,j is the contact area).17 First, we adopted the two-tension model where the surface tension in the non-contact zone (Tnc) is different from that in the contact zone (Tc), since the number density of lipid molecules in the contact zone is higher than that in the non-contact zone due to attractive inter-membrane interactions. In this case, the areas of vesicles in an aggregate are variable rather than fixed, and they are controlled by tensions. The total energy of the two-tension model is given by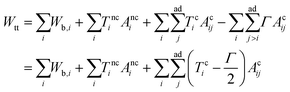 | (1) |
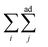 means summing over vesicles j adhering to vesicle i, and the constant term is disposed of. Here we assume that the contact-zone tensions are the same in all vesicles and so are the non-contact-zone tensions, i.e., Tnci = Tnc and Tci = Tc. We normalize the total energy Wtt by the bending energy of a spherical vesicle (equal to 8πkc) so that the dimensionless energy of the triplet reads
means summing over vesicles j adhering to vesicle i, and the constant term is disposed of. Here we assume that the contact-zone tensions are the same in all vesicles and so are the non-contact-zone tensions, i.e., Tnci = Tnc and Tci = Tc. We normalize the total energy Wtt by the bending energy of a spherical vesicle (equal to 8πkc) so that the dimensionless energy of the triplet reads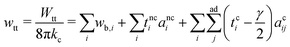 | (2) |
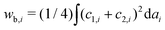 is the normalized bending energy; here cj,i = Cj,iRs,i (j = 1 or 2) is the dimensionless principal curvature scaled by a characteristic length
is the normalized bending energy; here cj,i = Cj,iRs,i (j = 1 or 2) is the dimensionless principal curvature scaled by a characteristic length 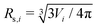 . Vi is the vesicle volume. Then the vesicle area is normalized to
. Vi is the vesicle volume. Then the vesicle area is normalized to 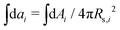 , anci = Anci/4πRs,i2, acij = 2Acij/4π(Rs,i2 + Rs,j2). The reduced surface tension for the non-contact and contact zone is defined by tk = TkRs,i2/2kc (k = nc or c). Similarly, the reduced adhesion strength between vesicle i and vesicle j reads γ = Γ(Rs,i2 + Rs,j2)/4kc. For convenience, we express wtt as
, anci = Anci/4πRs,i2, acij = 2Acij/4π(Rs,i2 + Rs,j2). The reduced surface tension for the non-contact and contact zone is defined by tk = TkRs,i2/2kc (k = nc or c). Similarly, the reduced adhesion strength between vesicle i and vesicle j reads γ = Γ(Rs,i2 + Rs,j2)/4kc. For convenience, we express wtt as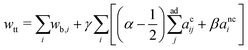 | (3) |
3 Materials and methods
3.1 Chemicals
The phospholipid, 1,2-dimyristoyl-sn-glycero-3-phosphocholine (DMPC) (purity > 99%), was purchased from Avanti Polar Lipids (Alabaster, AL) and used without further purification. The vesicles were labeled with a fluorescent phospholipid, Texas Red™ 1,2-dihexadecanoyl-sn-glycero-3-phosphoethanolamine (TR-DHPE), purchased from Thermo Fisher Scientific (Waltham, MA). The repulsive electrostatic interaction between DMPC vesicles was screened by adding potassium chloride (KCl) purchased from Wako Pure Chemicals Industries (Osaka, Japan). To adjust the osmolarity between the inside and outside of vesicles, we used fructose purchased from Sigma-Aldrich Japan (Tokyo, Japan). For the preparation of vesicle suspensions, we used ultrapure water purified with a Direct-Q 3 UV water purification system (Merck Millipore, Darmstadt, Germany).3.2 Vesicle preparation
Vesicles were prepared using the gentle hydration technique.28 First, 7 μL of a chloroform solution of DMPC (10 mg mL−1) and 0.15 μL of a chloroform solution of TR-DHPE (1 mg mL−1) were well mixed in a test tube with 50 μL of pure chloroform solution. Then we evaporated the organic solvent in a stream of nitrogen gas, and the obtained lipid film was kept under vacuum for one night to completely remove the remaining solvent. To adjust the osmolarity, the dried lipid film was hydrated with 1 mL of fructose solution having a desired concentration at 50 °C for half a day. During the hydration process, the lipid films spontaneously form a GUV suspension, where the diameters of the GUVs are 10–60 μm.3.3 Preparation of vesicle triplets
In general, DMPC vesicles show no spontaneous adhesion due to the repulsive electrostatic interaction.17 In this study, vesicle adhesion is attained by controlling the intermembrane interaction, which consists of van der Waals attraction, electrostatic repulsion, and undulation (Helfrich) repulsion. Vesicle aggregation is induced by enhancing the screening of electrostatic repulsion. The procedure for the preparation of vesicle triplets is as follows. First, the microscope observation chamber was filled with a KCl solution of the desired concentration (100 mM for weak adhesion and 200 mM for strong adhesion); KCl was chosen so as to minimize the effects of ion binding to the DMPC headgroup.29 Then, we picked up 10 or more spherical vesicles of diameters between 10 and 30 μm from the vesicle suspension using a micropipette with an inner diameter of 60 μm (Vacu Tip II; Eppendorf, Hamburg, Germany), and carefully transferred them into the KCl solution in the chamber. After the transfer, we sealed the chamber using a coverslip to avoid evaporation of water. The vesicles spontaneously formed doublets, triplets, and larger aggregates. Among them, triplets consisting of vesicles having the same size were selected and used for further examination.3.4 Observation of morphology changes of vesicle triplets with varying reduced volume
In this study, we investigated shapes of vesicle triplets with varying reduced volume, which is attained by thermal area expansion of the DMPC membrane.30 The thermal area expansion coefficients of the DMPC membrane in pure water, and 100 mM and 200 mM KCl solutions are 0.004, 0.011, and 0.0012 K−1, respectively.17 Using the thermal area expansion ε = A−1dA/dT (A: area of membrane), the temperature dependence of the reduced volume is expressed by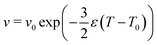 | (4) |
3.5 Analysis of triplet morphologies using Surface Evolver
The theoretical triplet shape was analyzed using the SE package. In SE, the surface of a vesicle is represented by a triangular mesh. To describe adhering vesicles, we imposed a geometrical constraint that fixes the distance between the adhesion zones of contacting vesicles.17 The equilibrium shapes were obtained by minimizing the total energy.4 Results
4.1 Shape transformation of vesicle triplet with triangular topology in strong adhesion regime
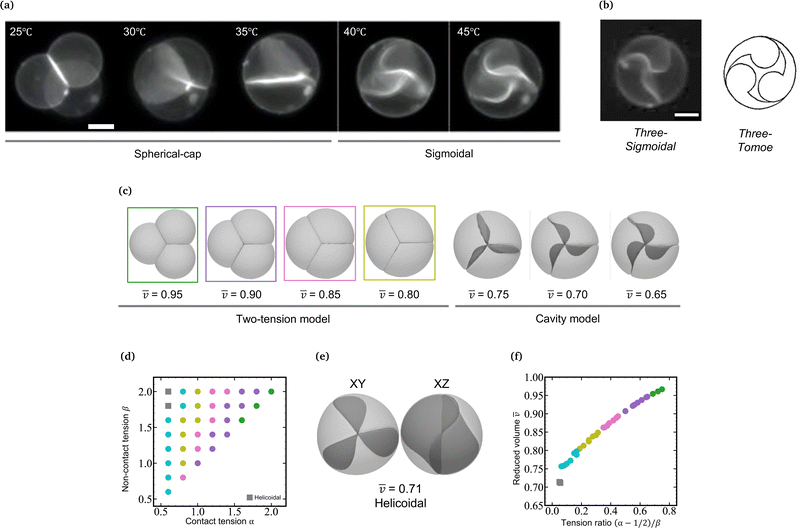
In a previous paper, we showed the shape transformation of vesicle doublets in the strong adhesion regime (KCl 200 mM) by increasing the temperature from 25 to 38 °C, where a vesicle doublet composed of spherical caps and a flat contact zone deforms into a compact sphere shape with a flat contact zone and then the flat contact zone transforms into a sigmoidal shape.17 When the vesicle aggregate changes from a doublet to a triplet, the topology plays an important role. Here we demonstrate the shape transformation of the triplet with a triangular topology in 200 mM KCl solution (strong adhesion regime) by heating from 25 to 45 °C as shown in Fig. 1a (Movie S1, ESI†). The initial triplet was composed of three spherical caps with a trifurcated flat contact zone (25 °C), where the three interfaces meet at an intersection with angles of 120°, similar to the Plateau rules. Upon increasing the temperature, the area of the contact zone increased while the zone itself remained flat, and the whole shape of the triplet transformed into a compact spherical shape (30 °C). Upon further heating, the flat contact zone bends to a half-wave shape (45 °C). In each vesicle, a pair of invaginating and protruding half-wave shapes adhered to other vesicles to form the so-called sigmoidal contact zone. Hereafter we refer to this structure as the “Three-Tomoe” pattern due to its similarity to the traditional Japanese emblem (Fig. 1b). In this sigmoid-contact triplet, the combined area of the contact zones is as large as possible due to the strong adhesion, resulting in a minimum area of the non-contact zone, i.e., the compact spherical shape with a sigmoidal contact zone. Note that at microscopic resolution, the compact triplet forms a notchless rim between the contact and non-contact zones. When we conducted the shape transformation in five different instances of vesicle triplets, three triplets showed the Three-Tomoe pattern, whereas the remaining two instances showed irregular curved contact zones. This is presumably because of the variation of the area, volume, and lamellarity across vesicles.4.2 Simulation using a two-tension model
The morphology change observed in the strongly-adhering triplet with a triangular topology (Fig. 1a) is analogous to that in the strongly-adhering doublet. To describe the vesicle triplet morphologies, we first adopted the two-tension model [eqn (3)] which was developed to describe the vesicle doublet (Section 2.1). The equilibrium shapes of triplets obtained by minimizing the total energy of the two-tension model are shown in Fig. 1c, where α is varied from 2.0 to 1.0 at β = 2.0 and γ = 100 (strong adhesion regime). The mean reduced volume of the triplet can be estimated by![[v with combining macron]](https://www.rsc.org/images/entities/i_char_0076_0304.gif) = (v1 + v2 + v3)/3 and is indicated at the bottom of each computed triplet shape. At α = 2.0 and β = 2.0 (
= (v1 + v2 + v3)/3 and is indicated at the bottom of each computed triplet shape. At α = 2.0 and β = 2.0 (![[v with combining macron]](https://www.rsc.org/images/entities/i_char_0076_0304.gif) = 0.95), the triplet consists of three spherical caps with a trifurcated flat contact zone, which describes well the observed triplet at 25 °C in Fig. 1a. As α decreases, the triplet develops into a compact shape with decreasing
= 0.95), the triplet consists of three spherical caps with a trifurcated flat contact zone, which describes well the observed triplet at 25 °C in Fig. 1a. As α decreases, the triplet develops into a compact shape with decreasing ![[v with combining macron]](https://www.rsc.org/images/entities/i_char_0076_0304.gif) , reaching a completely spherical shape with a trifurcated flat contact zone at α = 1.0 (
, reaching a completely spherical shape with a trifurcated flat contact zone at α = 1.0 (![[v with combining macron]](https://www.rsc.org/images/entities/i_char_0076_0304.gif) = 0.8), which well reproduces the observed morphology at 30 °C in Fig. 1a. To visualize the dependence of the triangular triplets on α and β dependence within the two-tension model, we constructed a phase diagram (Fig. 1d) where the triplets are represented using color-coded dots according to their mean reduced volume: green (0.95 ≤
= 0.8), which well reproduces the observed morphology at 30 °C in Fig. 1a. To visualize the dependence of the triangular triplets on α and β dependence within the two-tension model, we constructed a phase diagram (Fig. 1d) where the triplets are represented using color-coded dots according to their mean reduced volume: green (0.95 ≤ ![[v with combining macron]](https://www.rsc.org/images/entities/i_char_0076_0304.gif) < 1.00), violet (0.90 ≤
< 1.00), violet (0.90 ≤ ![[q with combining macron]](https://www.rsc.org/images/entities/i_char_0071_0304.gif) v < 0.95), pink (0.85 ≤
v < 0.95), pink (0.85 ≤ ![[v with combining macron]](https://www.rsc.org/images/entities/i_char_0076_0304.gif) < 0.90), dark yellow (0.80 ≤
< 0.90), dark yellow (0.80 ≤ ![[v with combining macron]](https://www.rsc.org/images/entities/i_char_0076_0304.gif) < 0.85), and light blue (0.75 ≤
< 0.85), and light blue (0.75 ≤ ![[v with combining macron]](https://www.rsc.org/images/entities/i_char_0076_0304.gif) < 0.80).
< 0.80).
It is interesting to note that the mean reduced volume lies on a master curve when we plot ![[v with combining macron]](https://www.rsc.org/images/entities/i_char_0076_0304.gif) against Tc/nc = (α − 1/2)/β [see eqn (3)] as shown in Fig. 1e. Considering that the tension ratio reads (α − 1/2)/β = (tc − γ/2)/tnc, the master curve in Fig. 1f indicates that the membrane area is determined by the force balance between the contact zone and non-contact zone. According to the Young-Dupré equation, the force balance between adhesion force and surface tension at the rim of the contact zone defines the contact angle. When it comes to the trifurcated flat contact zone in vesicle triplets, the contact angle determines the surface area of the vesicle, i.e., reduced volume, since the vesicle volume remains constant during morphological changes. It should be noted that if the normalized adhesion strength decreases to γ ≈ 10, the Young-Dupré equation is violated and the triplet morphology is dominated by the bending energy term in eqn (3). In this case, the triplet shape approaches the prediction of the model where the total energy is expressed by a sum of the vesicles' bending energies and adhesion energies with a constant vesicle surface area and volume constraints.
against Tc/nc = (α − 1/2)/β [see eqn (3)] as shown in Fig. 1e. Considering that the tension ratio reads (α − 1/2)/β = (tc − γ/2)/tnc, the master curve in Fig. 1f indicates that the membrane area is determined by the force balance between the contact zone and non-contact zone. According to the Young-Dupré equation, the force balance between adhesion force and surface tension at the rim of the contact zone defines the contact angle. When it comes to the trifurcated flat contact zone in vesicle triplets, the contact angle determines the surface area of the vesicle, i.e., reduced volume, since the vesicle volume remains constant during morphological changes. It should be noted that if the normalized adhesion strength decreases to γ ≈ 10, the Young-Dupré equation is violated and the triplet morphology is dominated by the bending energy term in eqn (3). In this case, the triplet shape approaches the prediction of the model where the total energy is expressed by a sum of the vesicles' bending energies and adhesion energies with a constant vesicle surface area and volume constraints.
As α is further decreased below 1.0, the contact zone of the compact spherical triplet is gradually deformed as shown in Fig. 1e (α = 0.6 and β = 2.0). A careful inspection of Fig. 1e reveals that this interface is a helicoidal shape rather than the sigmoidal shape observed in the experiments; the edge of the helicoidal contact zone is twisted. The compact spherical triplets with the helicoidal contact zone appear at small α and large β (gray squares: α = 0.6, β = 1.8 and 2.0 in Fig. 1d) and the flat-interface triplets transform into helicoidal-interface triplets discontinuously at Tc/nc ≈ 0.05 (Fig. 1f). In this theoretical framework, however, we cannot reproduce the compact vesicle triplet with a sigmoidal contact zone. Numerical energy minimization produced the same helicoidal equilibrium morphology even if the initial shape did have a sigmoidal contact zone. For comparison with another framework, the area-fixed model was introduced into the same reduced volume, resulting in oblate-based vesicle triplets (ESI:† Fig. S1).
4.3 Cavity model
In the compact sphere triplet region (![[v with combining macron]](https://www.rsc.org/images/entities/i_char_0076_0304.gif) < 0.8), the total area of non-contact zones should be equal to 4πRcav2, where
< 0.8), the total area of non-contact zones should be equal to 4πRcav2, where 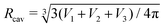 due to the strong tension at the non-contact zone (Tc/nc ≈ 0.05). Thus, the discontinuous decrease of the reduced volume observed in the two-tension model means abrupt expansion of the membrane area in the contact zone to minimize the adhesion energy in eqn (1). However, this abrupt expansion of the membrane area is unrealistic as the membrane cannot be stretched beyond a certain point. To construct a model of strongly adhering vesicles, we impose geometrical constraints that the total membrane area and volume of triplet vesicles are constant, and the total area of the non-contact zones is bounded by 4πRcav2 for the compact spherical triplets. This geometrical constraint for the non-contact zone is expressed by additional potential Ucav(r) = ∞ for |r| > Rcav otherwise Ucav(r) = 0. In SE, the vertices of the triangular mesh representing the vesicle surface are restricted to a sphere of radius Rcav. This effectively corresponds to an infinite potential at |r| > Rcav. The total energy of the cavity model for the vesicle triplet is given by
due to the strong tension at the non-contact zone (Tc/nc ≈ 0.05). Thus, the discontinuous decrease of the reduced volume observed in the two-tension model means abrupt expansion of the membrane area in the contact zone to minimize the adhesion energy in eqn (1). However, this abrupt expansion of the membrane area is unrealistic as the membrane cannot be stretched beyond a certain point. To construct a model of strongly adhering vesicles, we impose geometrical constraints that the total membrane area and volume of triplet vesicles are constant, and the total area of the non-contact zones is bounded by 4πRcav2 for the compact spherical triplets. This geometrical constraint for the non-contact zone is expressed by additional potential Ucav(r) = ∞ for |r| > Rcav otherwise Ucav(r) = 0. In SE, the vertices of the triangular mesh representing the vesicle surface are restricted to a sphere of radius Rcav. This effectively corresponds to an infinite potential at |r| > Rcav. The total energy of the cavity model for the vesicle triplet is given by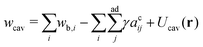 | (5) |
We minimize the total energy of the cavity model using SE as a function of ![[v with combining macron]](https://www.rsc.org/images/entities/i_char_0076_0304.gif) as shown in Fig. 1c (0.65 ≤
as shown in Fig. 1c (0.65 ≤ ![[v with combining macron]](https://www.rsc.org/images/entities/i_char_0076_0304.gif) < 0.75). Note that we set the adhesion strength at γ = 10, which is smaller than that of the two-tension model (γ = 100) due to the geometrical constraint. The cavity model reproduces well the compact spherical triplets with a sigmoidal contact zone observed in experiments. With a decrease in reduced volume, the magnitude of the sigmoidal deformation increases, which agrees well with the observed temperature dependence of the sigmoidal interface (40 and 45 °C in Fig. 1a). The switch from the two-tension model to the cavity model, corresponding to the transition from the flat interface to the sigmoidal interface, takes place between
< 0.75). Note that we set the adhesion strength at γ = 10, which is smaller than that of the two-tension model (γ = 100) due to the geometrical constraint. The cavity model reproduces well the compact spherical triplets with a sigmoidal contact zone observed in experiments. With a decrease in reduced volume, the magnitude of the sigmoidal deformation increases, which agrees well with the observed temperature dependence of the sigmoidal interface (40 and 45 °C in Fig. 1a). The switch from the two-tension model to the cavity model, corresponding to the transition from the flat interface to the sigmoidal interface, takes place between ![[v with combining macron]](https://www.rsc.org/images/entities/i_char_0076_0304.gif) = 0.80 and 0.75 (Fig. 1c). Note that the completely spherical triplet with a trifurcated flat contact zone has a mean reduced volume of
= 0.80 and 0.75 (Fig. 1c). Note that the completely spherical triplet with a trifurcated flat contact zone has a mean reduced volume of ![[v with combining macron]](https://www.rsc.org/images/entities/i_char_0076_0304.gif) ≈ 0.78. By combining the two-tension model with the cavity model, we can reproduce a series of morphological changes observed in the strongly-adhering vesicle triplets with a triangular topology.
≈ 0.78. By combining the two-tension model with the cavity model, we can reproduce a series of morphological changes observed in the strongly-adhering vesicle triplets with a triangular topology.
4.4 Shape transformation of triplets with a linear topology in the strong adhesion regime
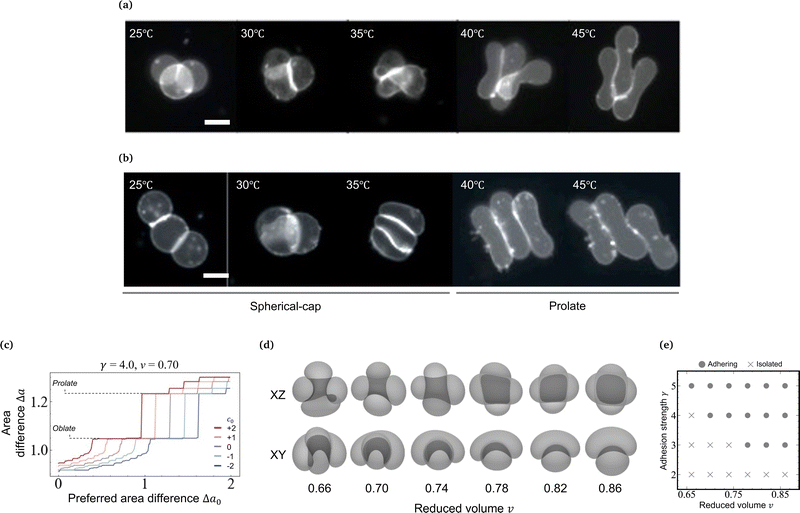
In the linear topology, triplets are composed of a pancake-shaped vesicle sandwiched by two spherical-cap vesicles. Thus, the middle vesicle is not identical to the end vesicles. Here we show the shape transformation of the vesicle triplet with a linear topology in 200 mM KCl solution (strong adhesion regime) by heating from 25 to 45 °C in Fig. 2a (Movie S2, ESI†). The initial triplet had parallel flat contact zones (25 °C). With an increase in temperature, the areas of the contact zones increased, and simultaneously the pancake-shaped middle vesicle became wedge-like (30 °C). At 35 °C, the triplet transformed into a compact, virtually spherical shape with two flat contact zones. Upon further heating, the middle vesicle assumed a biconvex shape (37 and 44 °C). We studied five instances of triplets, and all of them showed the reported shape transformation from a pancake-shaped vesicle sandwiched between two spherical-cap vesicles to a compact spherical shape with biconvex interfaces. Note that if the linear triplet is L-shaped, it undergoes a topological transition to a triangular triplet upon heating once and the contact between the two end vesicles is established (not shown).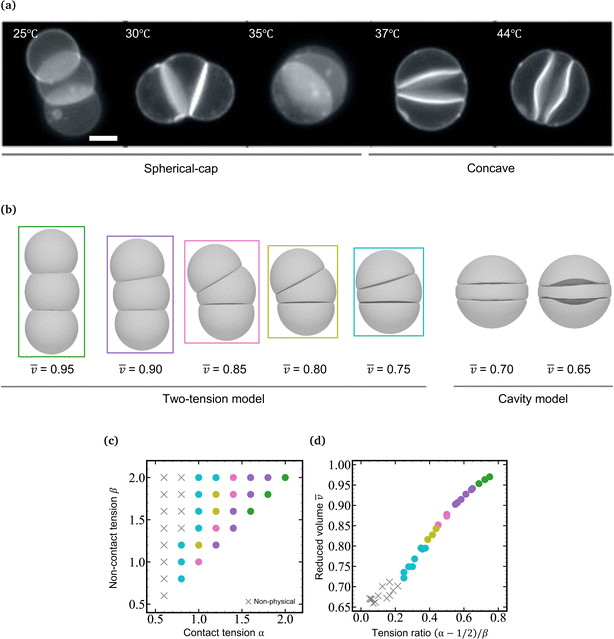 | ||
Fig. 2 Shape transformation of vesicle triplets with a linear topology in the strong adhesion regime. (a) Fluorescence microscopy images of vesicle triplets with a linear topology in KCl 200 mM solution upon heating from 25 °C to 44 °C. The deformation process is divided into the spherical-cap, flat-contact-zone triplet stage and the compact, biconvex-contact-zone triplet stage. (b) Shape change of vesicle triplets with a linear topology as a function of ![[v with combining macron]](https://www.rsc.org/images/entities/i_char_0076_0304.gif) , which are reproduced by numerical simulations using the Surface Evolver package; left: two-tension model, right: cavity model. (c) Phase diagram of the two-tension model in the (α,β) plane. Triplet shapes are color-coded like in Fig. 1d, with crosses indicating collapsed shapes. The triplet shapes in panel b are characterized by colored domains in the phase diagram in panel c. (d) Master curve of the mean reduced volume , which are reproduced by numerical simulations using the Surface Evolver package; left: two-tension model, right: cavity model. (c) Phase diagram of the two-tension model in the (α,β) plane. Triplet shapes are color-coded like in Fig. 1d, with crosses indicating collapsed shapes. The triplet shapes in panel b are characterized by colored domains in the phase diagram in panel c. (d) Master curve of the mean reduced volume ![[v with combining macron]](https://www.rsc.org/images/entities/i_char_0076_0304.gif) vs. (α − 1/2)/β, reconstructed from the phase diagram in panel c. Scale bars in microscopy images are 20 μm. vs. (α − 1/2)/β, reconstructed from the phase diagram in panel c. Scale bars in microscopy images are 20 μm. | ||
4.5 Simulations of two-tension and cavity models
The morphology of the linear triplets with flat contact zones is nicely reproduced by the two-tension model. Like in the triangular triplet, the numerical simulation using SE started at α = 2.0 and β = 2.0 (γ = 100 where the model predicts a![[v with combining macron]](https://www.rsc.org/images/entities/i_char_0076_0304.gif) = 0.95 linear triplet with parallel flat contact zones shown in Fig. 2b, which is geometrically consistent with experimental observations. As α is decreased at β = 2.0, the area of the flat contact zone increases, and at α = 1.4 (
= 0.95 linear triplet with parallel flat contact zones shown in Fig. 2b, which is geometrically consistent with experimental observations. As α is decreased at β = 2.0, the area of the flat contact zone increases, and at α = 1.4 (![[v with combining macron]](https://www.rsc.org/images/entities/i_char_0076_0304.gif) = 0.85 in Fig. 2b) the middle vesicle deforms into a wedge shape, which also agrees with observations (30 °C in Fig. 2a). By further decreasing α, the wedge angle of the middle vesicle decreases and the whole shape becomes more isometric and compact (α = 1.0,
= 0.85 in Fig. 2b) the middle vesicle deforms into a wedge shape, which also agrees with observations (30 °C in Fig. 2a). By further decreasing α, the wedge angle of the middle vesicle decreases and the whole shape becomes more isometric and compact (α = 1.0, ![[v with combining macron]](https://www.rsc.org/images/entities/i_char_0076_0304.gif) = 0.75). As α is further decreased below 1.0, the simulation gives collapsed self-intersecting non-physical shapes, indicating that the two-tension model is no longer applicable. To visualize the dependence of the flat-contact linear triplets on α and β, we construct a phase diagram (Fig. 2c), which is color-coded just like that of the triangular triplets in Fig. 1d. The morphology map for the linear triplet in the (α, β) plane is very similar to that for the triangular triplet (Fig. 1d). In the
= 0.75). As α is further decreased below 1.0, the simulation gives collapsed self-intersecting non-physical shapes, indicating that the two-tension model is no longer applicable. To visualize the dependence of the flat-contact linear triplets on α and β, we construct a phase diagram (Fig. 2c), which is color-coded just like that of the triangular triplets in Fig. 1d. The morphology map for the linear triplet in the (α, β) plane is very similar to that for the triangular triplet (Fig. 1d). In the ![[v with combining macron]](https://www.rsc.org/images/entities/i_char_0076_0304.gif) against Tc/nc plot, all points fall on a master curve (Fig. 2d), which has a slightly larger slope than that for the triangular triplet since the middle vesicle has a smaller reduced volume. The master curve terminates at Tc/nc = 0.23 (
against Tc/nc plot, all points fall on a master curve (Fig. 2d), which has a slightly larger slope than that for the triangular triplet since the middle vesicle has a smaller reduced volume. The master curve terminates at Tc/nc = 0.23 (![[v with combining macron]](https://www.rsc.org/images/entities/i_char_0076_0304.gif) = 0.75) where the two-tension triplets collapse. For comparison with another framework, the area-fixed model was introduced into the same reduced volume, resulting in oblate-based vesicle triplets (ESI:† Fig. S2).
= 0.75) where the two-tension triplets collapse. For comparison with another framework, the area-fixed model was introduced into the same reduced volume, resulting in oblate-based vesicle triplets (ESI:† Fig. S2).
From this point on, we switched to the cavity model which nicely reproduces compact triplets with a biconvex middle vesicle (![[v with combining macron]](https://www.rsc.org/images/entities/i_char_0076_0304.gif) = 0.65 in Fig. 2b). The transition from flat-contact triplets (reproduced by the two-tension model) to biconvex-contact triplets (reproduced by the cavity model) takes place at a mean reduced volume between
= 0.65 in Fig. 2b). The transition from flat-contact triplets (reproduced by the two-tension model) to biconvex-contact triplets (reproduced by the cavity model) takes place at a mean reduced volume between ![[v with combining macron]](https://www.rsc.org/images/entities/i_char_0076_0304.gif) = 0.70 and 0.65, which is consistent with the geometrical prediction of
= 0.70 and 0.65, which is consistent with the geometrical prediction of ![[v with combining macron]](https://www.rsc.org/images/entities/i_char_0076_0304.gif) ≈ 0.68 for a linear triplet which has a perfectly spherical external form and consists of vesicles of identical volumes with flat contact zones.
≈ 0.68 for a linear triplet which has a perfectly spherical external form and consists of vesicles of identical volumes with flat contact zones.
4.6 Morphology transition of vesicle triplets in the weak adhesion regime
Here we examine the morphology transition of vesicle triplets in the weak adhesion regime (KCl 100 mM). In the case of the triangular topology (Fig. 3a and Movie S3, ESI†), the initial morphology at 25 °C consists of three spherical caps with a trifurcated flat contact zone, identical to that observed in the strong adhesion regime. As the temperature increases, the triplets deformed into a compact shape with a trifurcated flat contact zone (30 °C). Upon further heating, however, each spherical-cap vesicle transformed into a prolate shape while keeping contact with the other two vesicles (35 °C), and eventually the triplet consisted of cigar-shaped vesicles (45 °C). For the linear topology in the weak adhesion regime (Fig. 3b and Movie S4, ESI†), the initial triplet shape at 25 °C was similar to that in the strong adhesion regime. With an increase in temperature, the middle vesicle deformed into a wedge shape and the linear arrangement transformed into an L-shaped arrangement (30 °C). On further heating, the vesicle shapes gradually became prolate (35 °C) until the triplet consisted of three parallel vesicles (40 and 45 °C). Like in the strong adhesion regime, we monitored the shape transformation in five linear and five triangular triplets in the weak adhesion regime, and all instances of each topology consistently showed the same shape transformation except for minor variations in the final state expected due to weak adhesion strength. In the triangular and linear topologies, each vesicle slid along the interface during the shape transformation and no separation of the vesicles was observed. Recalling that vesicle doublets in the weak adhesion regime transform into the parallel prolate morphology, we conclude that the stable shape of aggregates in the weak adhesion regime is based on prolate rather than on oblate vesicles.4.7 Theoretical interpretation of prolate-vesicle aggregates
As temperature increases, the undulation repulsion force increases (due to the increase of amplitude to membrane fluctuations), which results in a decrease of the adhesion strength.17 In the weak adhesion regime, however, since the membrane tension in the contact zone is weak, the excess membrane area produced by thermal expansion enhances the membrane fluctuations in the contact zone, which decreases the adhesion strength. Thus, the total energy in the weak adhesion regime is expressed by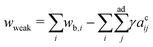 | (6) |
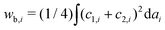 .31 However, when the total energy is dominated by the bending energy, an appropriate model for describing the morphology of a single vesicle is the area-difference elasticity (ADE) model,32–35 whose energy is expressed by the local-bending energy term and the non-local bending energy term
.31 However, when the total energy is dominated by the bending energy, an appropriate model for describing the morphology of a single vesicle is the area-difference elasticity (ADE) model,32–35 whose energy is expressed by the local-bending energy term and the non-local bending energy term 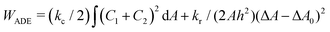 , where kr is the non-local bending modulus and h is the distance between the monolayers' neutral planes. Here
, where kr is the non-local bending modulus and h is the distance between the monolayers' neutral planes. Here 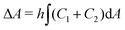 and ΔA0 = (N+ − N−)a are the area difference between the two monolayers and the preferred area difference, respectively, where N+ and N− are the number of lipid molecules in the outer and inner monolayers, and a is the cross-sectional area of a lipid. According to the ADE model, the vesicle shape is determined by the reduced volume v and the preferred area difference ΔA0. The ADE model predicts that in the 0.6 < v < 0.8 region, the stable vesicle shape is oblate. To stabilize the prolate vesicle, we have to adjust ΔA0 by introducing spontaneous curvature, which is expressed by area-difference-elasticity and spontaneous curvature (ADE-SC) model.36,37 The dimensionless energy of the ADE-SC model is given by
and ΔA0 = (N+ − N−)a are the area difference between the two monolayers and the preferred area difference, respectively, where N+ and N− are the number of lipid molecules in the outer and inner monolayers, and a is the cross-sectional area of a lipid. According to the ADE model, the vesicle shape is determined by the reduced volume v and the preferred area difference ΔA0. The ADE model predicts that in the 0.6 < v < 0.8 region, the stable vesicle shape is oblate. To stabilize the prolate vesicle, we have to adjust ΔA0 by introducing spontaneous curvature, which is expressed by area-difference-elasticity and spontaneous curvature (ADE-SC) model.36,37 The dimensionless energy of the ADE-SC model is given by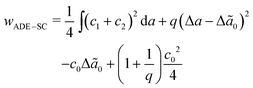 | (7) |
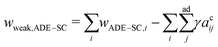 | (8) |
5 Discussion
Here we focus on curved interfaces observed in a compact spherical triplet (cavity model regime). In compact triplets, the non-contact zones form a spherical external surface, and the excess area produced by thermal expansion is used to deform the contact zones. The excess membrane forms a sigmoidal interface for triangular triplets (Fig. 1b), whereas a convex interface is observed for linear triplets (Fig. 2a). According to the cavity model [eqn (5)], the shape of the interface is governed by the bending energy under the constraints of a fixed vesicle volume and area.On the one hand, in the triangular triplets, all vesicles are identical and have two contact zones. There are two modes to deform the contact zone as the membrane expands upon heating. One is the sigmoidal mode where the edge of the contact zone is fixed, and the contact zone forms the half-wave shape (cavity model; Fig. 1c). Another one is the helicoidal mode where the edge of the contact zone is twisted and the contact zone forms a helicoid surface (two-tension model; Fig. 1e). In the experiments, we observe the sigmoidal mode as shown in Fig. 1a. The helicoidal mode appears in the two-tension model, where the reduced volume is discretely decreased (v = 0.75 to 0.71) at the flat to helicoid transition as shown in Fig. 1f. Since the volume of the vesicle is constant during the transition, this abrupt change in the reduced volume implies a discontinuous increase in the area of the vesicle membrane by 8.6%. However, due to the high area expansion modulus of the phospholipid membrane (∼250 mN m−1),43 such a drastic increase in the membrane area is not permitted. This membrane area constraint is imposed within the cavity model. Therefore, we observe the half-wave deformation of the contact zone as predicted by the cavity model. In addition, the volume change due to the half-wave deformation of the contact zone must be cancelled in each vesicle. This volume conservation results in a “Three-Tomoe” triplet, where each vesicle has a protruding contact zone and an invaginating contact zone (i.e., sigmoidal deformation) as shown in Fig. 1b.
On the other hand, in the linear triplets, the end vesicles have a single contact zone whereas the middle vesicle has two contact zones. In this case, the excess area used for the contact zone is different between the end vesicles and the middle vesicle. The excess area due to thermal expansion is the same in each vesicle, but in the end vesicles it is engaged in a single contact zone, whereas in the middle vesicle it is distributed between two of them. Therefore, in the contact zone, the excess area of the end vesicle is larger than that of the middle vesicle, which causes the membrane to protrude toward the end vesicle as shown in Fig. 2a. The middle vesicle deforms into a biconvex shape and the end vesicles deform into a stomatocyte shape while keeping their volume constant. It should be noted that in the linear topology, the edge of the contact zone is fixed as well.
In summary, the shape of the interface in compact doublets and triplets is determined under vesicle volume conservation conditions. For a single interface, the interface shape is governed by the area difference of the contact zone. If the contact area of each vesicle is the same, the contact zone is deformed into a sigmoidal shape, whereas if the contact zone has an area difference between the adhering vesicles, the contact zone protrudes toward the vesicle having a larger contact area. For connecting interfaces, each interface deforms into a half-wave shape and the overall shape of the interface is sigmoidal due to volume conservation.
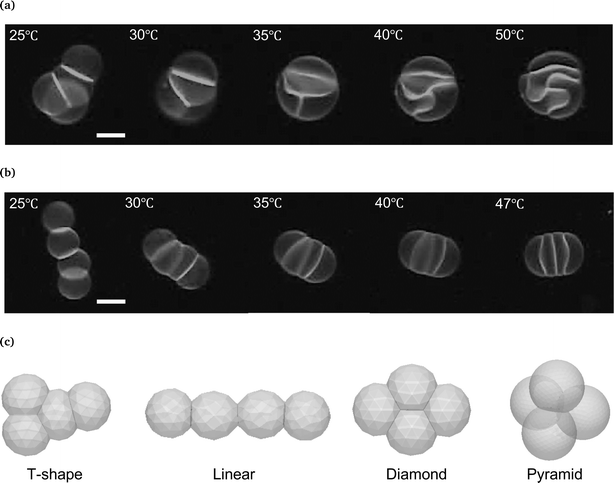
Based on the above deformation rule, we examined the interface shape of vesicle quartets having different topologies, i.e., T-shape and linear (Fig. 4a and b). In the T-shape vesicle quartet, one spherical cap vesicle adheres to the triangular triplet (Fig. 4c). Two spherical cap vesicles in the triangular part have two contact zones, the remaining one sandwiched vesicle in the triangular part has three contact zones, and an end vesicle has a single contact zone. At the initial stage (25 °C in Fig. 4a), all contact zones in the T-shape vesicle quartet are flat. Upon increasing the temperature, the three contact zones in the triangular part deform into the sigmoidal shape to keep the vesicle volume constant so as to form a “Three-Tomoe” pattern, whereas the interface between the “Tomoe” vesicle and end vesicle protrudes toward the end vesicle (40 and 50 °C in Fig. 4a). This interface pattern agrees with the deformation rule. The linear quartet is composed of two spherical end vesicles and two pancake vesicles (Fig. 4c). Two spherical end vesicles have one contact zone, and two pancake vesicles have two contact zones. By increasing the temperature to 47 °C (Fig. 4b), the interface between the end and pancake vesicles protrudes toward the end vesicle, whereas the interface between two pancake vesicles shows a flat contact zone since the two sandwiched vesicles are identical. Again, the observed interface shapes in the linear vesicle quartet are consistent with our deformation rule, although the whole shape of the non-contact zones of the quartet is not spherical.
It should be noted that vesicle quartets have two other interesting topologies, i.e., diamond and pyramid (Fig. 4c). In the diamond topology, two vesicles have three contact zones, and two vesicles have two contact zones, whereas the pyramid is composed of four identical vesicles with three contact zones. The three contact zones in a vesicle may produce frustrated interfaces to conserve the vesicle volume. Although we could not achieve these topologies experimentally, the deformations of vesicle quartets with topologies will reveal a geometrical law governing vesicle aggregates. To address these complex topologies, it might be practical to develop an efficient way for manufacturing vesicle aggregates by using optical tweezers or microfluidic devices.44,45
Finally, we mention that we also theoretically considered a wrapped topology where the inner vesicle is contained within two identical cup-like vesicles forming a shell.46 In the strong adhesion regime, this topology is energy-wise more favorable due to a large contact area but only if the reduced volumes of the three vesicles are quite different from each other: In the inner vesicle, v = 1 whereas in the other two v = 0.4. Given that in this work we focus on vesicles of identical sizes, we did not explore this shape further. At the same time, we note that the vesicle size polydispersity will significantly affect all vesicle aggregate topologies—and so would the existence of multiple contact zones between any two vesicles in an aggregate (here we tacitly restricted the discussion to single contact zones).
6 Conclusion
When comparing the present study of vesicle triplets with our past investigations of doublets, one can readily realize the increased complexity of the morphologies involved as well as the phenomena at work, which is of course anticipated—and in retrospect justifies our step-by-step approach to the physics of vesicle aggregates. Our experimental findings show that by controlling the adhesion strength, the vesicles can be steered so as to form either compact aggregates or non-compact ones. In the former, the contact zones show characteristic curved shapes that are never observed in soap bubbles, which is determined by the conservation of vesicle volume and area difference in the contact zone. Systematic studies for interface geometry of a few vesicle aggregates will lead to general rules for curved interfaces, such as the Plateau rules for planar interfaces. In the latter, the membrane bending energy evidently is very important, and this supports an interesting prospect of non-compact multivesicular aggregate morphologies such as shells. Whether these expectations will be confirmed remains to be seen, and it is unclear what may be the smallest number of vesicles in an aggregate where the morphological rather than topological classification will prevail.On the theoretical side, our study advances the understanding of the modeling of vesicle aggregates partly by providing additional support for the so-called two-tension model and partly by substituting it with the cavity model proposed here. Another important novelty stemming from the combination of the two models is that at least in the large-adhesion regime, the shape of vesicle aggregates is determined primarily by the reduced volume of the vesicles; in the cavity model, the reduced volume is the only control parameter whereas in the two-tension model it depends on the tensions. This finding may be helpful when further elaborating the theoretical description of the aggregates.
Altogether, the morphologies of vesicle triplets are governed by the reduced volume, the adhesion strength of vesicles and the topology of the triplets. The adhesion strength is determined by the balance of intermembrane interactions, i.e., the electrostatic repulsion, van der Waals attraction, and undulation repulsion, which produces the surface tensions in the contact and non-contact zones through the force balance. Therefore, the reported morphological changes in the vesicle triplets are general ones that would be observed in other phospholipid vesicle triplets.
Author contributions
P. Z., Y. S., and M. I. conceived the presented idea and designed the experiments. T. C. carried out the experiments. T. C. and P. Z. developed the theoretical formalism. T. C. wrote the manuscript with support from P. Z. and M. I.Conflicts of interest
There are no conflicts to declare.Acknowledgements
We acknowledge the financial support from the WISE Program for AI Electronics Tohoku University, JST SPRING (Grant Number JPMJSP2114), JSPS KAKENHI Grant-in-Aid for Challenging Exploratory Research (Grant Number JP20K20888), the Grant-in-Aid for Scientific Research on Innovative Areas: Aquatic Functional Materials (Grant Number JP20H05199) and the Slovenian Research Agency (research core funding No. P1-0055).References
- D. L. Weaire and S. Hutzler, The Physics of Foams, Clarendon Press, 1999 Search PubMed.
- J. Plateau, Statique expérimentale et théorique des liquides soumis aux seules forces moléculaires, Gauthier-Villars, 1873 Search PubMed.
- U. Seifert, K. Berndl and R. Lipowsky, Phys. Rev. A: At., Mol., Opt. Phys., 1991, 44, 1182–1202 CrossRef CAS PubMed.
- U. Seifert, Adv. Phys., 1997, 46, 13–137 CrossRef CAS.
- P. B. Canham, J. Theor. Biol., 1970, 26, 61–81 CrossRef CAS PubMed.
- S. Svetina and B. Žekš, Eur. Biophys. J., 1989, 17, 101–111 CrossRef CAS PubMed.
- H. J. Deuling and W. Helfrich, Biophys. J., 1976, 16, 861–868 CrossRef CAS PubMed.
- G. H. W. Lim, M. Wortis and R. Mukhopadhyay, Proc. Natl. Acad. Sci. U. S. A., 2002, 99, 16766–16769 CrossRef PubMed.
- D. Tilley, W. T. Coakley, R. K. Gould, S. E. Payne and L. A. Hewison, Eur. Biophys. J., 1987, 14, 499–507 CrossRef CAS PubMed.
- D. Flormann, O. Aouane, L. Kaestner, C. Ruloff, C. Misbah, T. Podgorski and C. Wagner, Sci. Rep., 2017, 7, 7928 CrossRef PubMed.
- J. L. McWhirter, H. Noguchi and G. Gompper, Proc. Natl. Acad. Sci. U. S. A., 2009, 106, 6039–6043 CrossRef CAS PubMed.
- G. Tomaiuolo, L. Lanotte, G. Ghigliotti, C. Misbah and S. Guido, Phys. Fluids, 2012, 24, 051903 CrossRef.
- M. Brust, O. Aouane, M. Thiébaud, D. Flormann, C. Verdier, L. Kaestner, M. W. Laschke, H. Selmi, A. Benyoussef, T. Podgorski, G. Coupier, C. Misbah and C. Wagner, Sci. Rep., 2014, 4, 4348 CrossRef CAS PubMed.
- P. Ziherl and S. Svetina, Proc. Natl. Acad. Sci. U. S. A., 2007, 104, 761–765 CrossRef CAS PubMed.
- S. Svetina and P. Ziherl, Bioelectrochemistry, 2008, 73, 84–91 CrossRef CAS PubMed.
- M. Hoore, F. Yaya, T. Podgorski, C. Wagner, G. Gompper and D. A. Fedosov, Soft Matter, 2018, 14, 6278–6289 RSC.
- K. Murakami, R. Ebihara, T. Kono, T. Chiba, Y. Sakuma, P. Ziherl and M. Imai, Biophys. J., 2020, 119, 1735–1748 CrossRef CAS PubMed.
- L. Parolini, B. M. Mognetti, J. Kotar, E. Eiser, P. Cicuta and L. Di Michele, Nat. Commun., 2015, 6, 5948 CrossRef CAS PubMed.
- L. Casas-Ferrer, A. Brisson, G. Massiera and L. Casanellas, Soft Matter, 2021, 17, 5061–5072 RSC.
- U. Seifert and R. Lipowsky, Phys. Rev. A: At., Mol., Opt. Phys., 1990, 42, 4768–4771 CrossRef CAS PubMed.
- J. Steinkühler, J. Agudo-Canalejo, R. Lipowsky and R. Dimova, Biophys. J., 2016, 111, 1454–1464 CrossRef PubMed.
- J. Agudo-Canalejo and R. Lipowsky, ACS Nano, 2015, 9, 3704–3720 CrossRef CAS PubMed.
- A. H. Bahrami, R. Lipowsky and T. R. Weikl, Soft Matter, 2016, 12, 581–587 RSC.
- Q. Yu, S. Othman, S. Dasgupta, T. Auth and G. Gompper, Nanoscale, 2018, 10, 6445–6458 RSC.
- H. T. Spanke, R. W. Style, C. François-Martin, M. Feofilova, M. Eisentraut, H. Kress, J. Agudo-Canalejo and E. R. Dufresne, Phys. Rev. Lett., 2020, 125, 198102 CrossRef CAS PubMed.
- E. J. Ewins, K. Han, B. Bharti, T. Robinson, O. D. Velev and R. Dimova, Chem. Commun., 2022, 58, 3055–3058 RSC.
- K. A. Brakke, Exp. Math., 1992, 1, 141–165 CrossRef.
- J. P. Reeves and R. M. Dowben, J. Cell. Physiol., 1969, 73, 49–60 CrossRef CAS PubMed.
- A. Cordom, O. Edholm and J. J. Perez, J. Phys. Chem. B, 2008, 112, 1397–1408 CrossRef PubMed.
- J. Käs and E. Sackmann, Biophys. J., 1991, 60, 825–844 CrossRef PubMed.
- W. Helfrich, Z. Naturforsch., C: Biochem., Biophys., Biol., Virol., 1973, 28, 693–703 CrossRef CAS PubMed.
- B. Božič, S. Svetina, B. Žekš and R. E. Waugh, Biophys. J., 1992, 61, 963–973 CrossRef PubMed.
- W. Wiese, W. Harbich and W. Helfrich, J. Phys.: Condens. Matter, 1992, 4, 1647 CrossRef.
- H.-G. Döbereiner, E. Evans, M. Kraus, U. Seifert and M. Wortis, Phys. Rev. E: Stat. Phys., Plasmas, Fluids, Relat. Interdiscip. Top., 1997, 55, 4458–4474 CrossRef.
- A. Sakashita, N. Urakami, P. Ziherl and M. Imai, Soft Matter, 2012, 8, 8569–8581 RSC.
- L. Miao, U. Seifert, M. Wortis and H. G. Döbereiner, Phys. Rev. E: Stat. Phys., Plasmas, Fluids, Relat. Interdiscip. Top., 1994, 49, 5389–5407 CrossRef CAS PubMed.
- T. Jimbo, Y. Sakuma, N. Urakami, P. Ziherl and M. Imai, Biophys. J., 2016, 110, 1551–1562 CrossRef CAS PubMed.
- S. Svetina and B. Žekš, Anat. Rec., 2002, 268, 215–225 CrossRef CAS PubMed.
- J. Majhenc, B. Božič, S. Svetina and B. Žekš, Biochim. Biophys. Acta, 2004, 1664, 257–266 CrossRef CAS PubMed.
- R. Lipowsky and H.-G. Döbereiner, EPL, 1998, 43, 219 CrossRef CAS.
- B. Różycki and R. Lipowsky, J. Chem. Phys., 2016, 145, 074117 CrossRef PubMed.
- T. Bhatia, S. Christ, J. Steinkühler, R. Dimova and R. Lipowsky, Soft Matter, 2020, 16, 1246–1258 RSC.
- W. Rawicz, K. C. Olbrich, T. McIntosh, D. Needham and E. Evans, Biophys. J., 2000, 79, 328–339 CrossRef CAS PubMed.
- G. Bolognesi, M. S. Friddin, A. Salehi-Reyhani, N. E. Barlow, N. J. Brooks, O. Ces and Y. Elani, Nat. Commun., 2018, 9, 1882 CrossRef PubMed.
- N. Yandrapalli and T. Robinson, Lab Chip, 2019, 19, 626–633 RSC.
- B. Kavčič, A. Sakashita, H. Noguchi and P. Ziherl, Soft Matter, 2019, 15, 602–614 RSC.
Footnote |
| † Electronic supplementary information (ESI) available. See DOI: https://doi.org/10.1039/d3sm00308f |
| This journal is © The Royal Society of Chemistry 2023 |