Open Access Article
Open Access ArticleImpact of process flexibility and imperfect forecasting on the operation and design of Haber–Bosch green ammonia†
Nicholas
Salmon
 and
René
Bañares-Alcántara
and
René
Bañares-Alcántara
 *
*
University of Oxford, Department of Engineering Science, Parks Road, Oxford, OX1 3PJ, UK. E-mail: rene.banares@eng.ox.ac.uk
First published on 24th April 2023
Abstract
Green ammonia is a promising energy storage vector which can provide back-up power when variable renewable energy sources (VREs) are not generating. However, it is generally agreed in the literature that the limited flexibility of the Haber–Bosch process required for ammonia synthesis increases its production cost. We assess the truth of this claim using two methods: firstly, a perfect forecasting design model based on Linear Programming (LP); and secondly, a model predictive control (MPC) approach which can estimate how the plant will operate with finite weather forecast information. This MPC approach is the first in the literature to demonstrate how islanded green ammonia plants can be operated without perfect forecasting. The LP approach demonstrates that, from a design perspective, there are diminishing marginal returns from improving HB flexibility; by 2050, there will be almost no benefit associated with reducing the HB MOR below 60%. The MPC approach supports this claim at a solar-dominated sites; however, at wind-dominated sites, the inability to perform long-distance forecasting means flexibility is an important lever for the plant to operate robustly.
Sustainability spotlightGreen ammonia is a liquid fuel which holds significant promise for decarbonising fertilisers, the maritime industry, and long-term energy storage; it is also well placed as a transport vector for green hydrogen. This research describes important techniques which need to be adopted in order to design green ammonia production affordably and sustainably; these techniques validate previously untested methods from the literature for plant design, and present a strategy for optimal plant operation. Ultimately, adopting these techniques will make this clean fuel cheaper. In doing so, the article advances our progress towards the UN SDG Goal 7 (affordable and clean energy), as well as Goal 13 (climate action). |
1 Introduction
As the world decarbonises, variable renewable energy (VRE) will need to be stored to meet demand during periods of low production.1 Chemical vectors such as green hydrogen, ammonia and methanol will play an important role in the overall mix of these technologies, offering reasonably priced storage on a months-to-years timescale,2 and the ability to transport renewable energy between resource-rich and resource-poor areas.3 Green ammonia has particular promise: it is more energetically dense on a volumetric basis than green hydrogen, and it does not require a carbon source for production (unlike synthetic hydrocarbons).4 The process of ammonia synthesis using the Haber–Bosch (HB) process is very well understood, having been in large scale use for over a century.5Despite its advantages, a major challenge for the industrialisation of green ammonia production is the partial inflexibility of the HB process. Using current technology, these plants will not be able to be switched off quickly. This has not affected production in the past, since conventional HB synthesis processes usually operate continuously at maximum rate (to extract the most benefit from the capital investment). However, green HB plants are unlikely to operate at their rated capacity at all times, and will instead adjust their production based on the current availability of VRE.6
This poses significant challenges for both the plant designer and the plant operator. The designer must install back-up energy storage technologies for periods of time when renewable power is not available,7 potentially at high costs; meanwhile, the operator must decide when to deploy those technologies, and when to cut production in order to maintain the storage inventory, despite having limited forecast information about future VRE generation.8 These factors are generally agreed to be responsible for increasing the cost of ammonia production.7,9,10 The purpose of this article is to assess precisely how inflexibility in the HB process impacts green ammonia plant design and operation, including consideration of the impacts of imperfect forecasting.
2 Methodology
This article adopts two methods for assessing the role of flexibility in green ammonia plants: Linear Programming (LP) for plant design, and Model Predictive Control (MPC) for plant operation. The former approach has been adopted in other analyses of green ammonia production,11–15 although a modification is proposed here to determine the extent to which cycling of storage units impacts on the ammonia price, and new sensitivity results are presented. The latter MPC approach is novel in its application to islanded green ammonia plants, and places guard rails around the results offered by the LP. The purpose of the MPC is not to design control loops which specifically determine the operating parameters of the ammonia plant (temperatures, pressures, feed ratios, etc.); rather, the MPC's purpose is to function as an algorithm which determines the set-point of the ammonia plant. In other words, the MPC presented here is analogous to the primary loop in a cascade-control arrangement, dictating the power allocation and ammonia production. For both models, weather data is sourced from ERA5, and converted into wind and solar data using a standard turbine curve13 and the PVLib module on Python.16There are a number of emerging technologies for producing green ammonia, such as direct electrochemical synthesis,5 and photochemical production.17 Rather than adopting those technologies, this article focusses on ammonia produced through using conventional HB synthesis for two reasons. Firstly, because emerging green ammonia projects globally, such as the Asian Renewable Energy Hub18 are targeting operation before 2030, and are therefore likely to rely on established technologies like HB. The development of operating strategies such as MPC that are applicable to green ammonia is therefore most pressing where HB is the synthesis process. Secondly, as new non-HB technologies advance, they will increasingly become more flexible, and will require less capital investment; if they overtake HB as the preferred synthesis technique, it will be because these traits enable ammonia production at lower costs. Therefore considering HB as the base-case for analysis provides the most conservative estimate of project cost.
2.1 Design approach
The design approach adopted for the ammonia plant uses a linear program to minimise the levelised cost of ammonia (which is the price at which ammonia must be sold in order to achieve a NPV of zero at the nominated discount rate). The model takes the renewable weather profile in a given location, and uses it to optimise the relative size of the plant equipment, which includes: fixed-axis solar panels, single-axis tracking solar panels, wind turbines, electrolysers, HB plants (including air separation), fuel cells, batteries, and hydrogen storage, as described in detail in earlier publications from the authors.13,19 Using an LP approach to design large plants is suitable as the majority of equipment in the green ammonia plant is modular, and its cost will not depend strongly on the scale of installation; the exception is the HB plant, but even for this module, the economies-of-scale are likely to break down at high production rates.The primary purpose of the LP model is to determine the extent to which ramping and flexibility impact on the ammonia cost. The ability of ammonia plants to operate flexibly is not well understood, but is likely to be constrained.
Flexibility constraints originate from the elevated temperature at which the HB process occurs. These temperatures are sustained by excess heat from the exothermic reaction; if production slows excessively, heat loss will exceed heat generation and the reaction will be quenched. Thermal expansion on start-up and shut-down has a damaging impact on equipment and catalysts, and therefore frequent cycling between an operating and quenched state is not possible. In order to prevent temperature hot spots inside the adiabatic catalyst bed reactors, rapid ramping of the production rate is also not generally considered practical.10,20 While technical solutions are emerging using innovative reactor designs,21 it is not likely that the HB process will be able to match its own operation to that of a variable renewable energy plant. The purpose of this article is not to determine the reactor designs and conditions which will best enable process flexibility; rather, it is to provide a techno-economic analysis which assesses whether these designs are beneficial in the first instance.
In order to meaningfully assess the role of plant flexibility, a large number of locations need to be considered, as the optimum plant design is highly dependent on the local weather profile. For that reason, 421 onshore sites were selected to analyse ramping and flexibility. The sites have a range of weather profiles and a range of latitudes (from 5°, near the equator, to 59°).
At each location, the model is solved under 13 different conditions: there are four different minimum operating rates (MORs) (20%, 40%, 60% and 80%) and three ramp rate factors (0.1, 1, and 10; these factors are applied to the base upward and downward rates of 5% and 20% respectively). The thirteenth case is an entirely inflexible plant, which operates continuously at 100% (in which instance consideration of ramping rates is obviously meaningless). The model is solved using costs for 2022 and for 2050; because of the rapidly falling prices of batteries and solar PV, future electrolyser plants will be differently designed and therefore may respond differently to flexibility limitations. Present costs of equipment were taken from IRENA22,23 and from Nayak-Luke et al.24 Future costs were estimated using Way et al.,25 who use a stochastic approach to determining cost forecasts, historical analysis of which has demonstrated to be highly accurate.
Calendar aging, and cycling aging in normal use, is incorporated in two ways: firstly, by accounting for equipment replacement costs, and secondly, by adjusting equipment efficiencies. Equipment replacement costs are accounted for by applying higher Operating and Maintenance (O&M) costs to units subject to degradation (i.e. assuming the replacement is carried out on a rolling basis, rather than en masse when equipment reaches end of life, although the impacts on NPV are the same). In previous published versions of the model, O&M has been set at a flat rate of 2% for all equipment; in this version, increased costs are applied to equipment subject to the degradation of the electrolysers, fuel cells and batteries. Because their membranes require replacement approximately every 50![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 000 operating hours, electrolysers and fuel cells are subject to a 3% O&M fraction, of which 1% would be allocated to annual operating costs (i.e. labour, insurance, etc.), and the remaining 2% would be allocated to membrane replacement. This has roughly the same impact on the NPV as reinvesting one-third of the electrolyser CAPEX every decade into membrane replacement at the nominated discount rate of 7% (i.e. if a plant were to replace all the membranes at once, rather than on a rolling basis). Meanwhile, batteries have comparatively short life spans (maximum 10 years) compared to the project as a whole (30 years); their O&M fraction is set at 3.5%. To again compare this annual maintenance cost with a decennial replacement of all the batteries, this is roughly equivalent to reinvesting half the CAPEX every decade (since only the battery itself needs to be re-installed; other components such as balance of plant electrical equipment do not). Equipment efficiencies are also adjusted to represent some degree of degradation; electrolyser efficiency for 2022 is set to 53 kW h kg−1, which is below the best market performance for a new electrolyser26 but includes a 3.5% degradation rate.27 For 2050, superior performance of 46 kW h kg−1 is assumed, which incorporates both overall improvements and a reduction in degradation rate.28 Battery charging/discharging efficiency is set at 95% for similar reasons.29
000 operating hours, electrolysers and fuel cells are subject to a 3% O&M fraction, of which 1% would be allocated to annual operating costs (i.e. labour, insurance, etc.), and the remaining 2% would be allocated to membrane replacement. This has roughly the same impact on the NPV as reinvesting one-third of the electrolyser CAPEX every decade into membrane replacement at the nominated discount rate of 7% (i.e. if a plant were to replace all the membranes at once, rather than on a rolling basis). Meanwhile, batteries have comparatively short life spans (maximum 10 years) compared to the project as a whole (30 years); their O&M fraction is set at 3.5%. To again compare this annual maintenance cost with a decennial replacement of all the batteries, this is roughly equivalent to reinvesting half the CAPEX every decade (since only the battery itself needs to be re-installed; other components such as balance of plant electrical equipment do not). Equipment efficiencies are also adjusted to represent some degree of degradation; electrolyser efficiency for 2022 is set to 53 kW h kg−1, which is below the best market performance for a new electrolyser26 but includes a 3.5% degradation rate.27 For 2050, superior performance of 46 kW h kg−1 is assumed, which incorporates both overall improvements and a reduction in degradation rate.28 Battery charging/discharging efficiency is set at 95% for similar reasons.29
Having accounted for the costs of calendar aging and a standard amount of cycling aging, the model then imposes constraints which prevent high frequency usage from degrading the batteries faster than anticipated. There are a number of metrics for battery usage that can impact the rate of degradation.29 We focus on two of these degradation metrics: total accumulated charge and depth of discharge. These parameters are related to each other: batteries which completely discharge on each cycle require replacement after around 6000 cycles;30 assuming a ten-year replacement cycle, this allows slightly less than 2 cycles per day. We assume a worst case scenario in which each cycle completely discharges, and limit the number of cycles using three constraints:
| λ(SC,t) ≥ λ(SC,t − 1) + (κ(SC,t) − κ(SC,t − 1)), ∀t ∈ St | (1) |
| λ(SC,t) ≥ λ(SC,t − 1), ∀t ∈ St | (2) |
| λ(SC,tfinal) ≤ GCL(SC) × CSC(SC) | (3) |
Eqn (1) and (2) count the total amount of charge which has flowed into the storage component (λ) as a function of time. If the state of charge of the storage component (κ) has increased (i.e. it is charging), then λ increases by that amount. If the equipment is discharging, then eqn (1) is inactive, but λ is prevented from decreasing by eqn (2). λ(0) is set to 0. The total number of cycles is constrained by eqn (3), in which the charge accumulation in the final time step (tfinal) must be less than the total allowable number of cycles (GCL), scaled according to the capacity of the storage component (CSC).
Although battery cycling is far more widely discussed in the literature, hydrogen stores may also degrade under cycling. The extent to which degradation occurs will depend on the mode of storage. Pressure vessels should be robust to cycling within design limits, but the integrity of salt caverns may degrade if they are subject to rapid and frequent pressure fluctuation,31 and hydrogen storage by adsorption onto alloys is known to degrade with cycling.32 We therefore include hydrogen storage cycling limits in order to understand how much they impact ammonia production costs.
2.2 Operating approach
A limitation of the design model, particularly from the perspective of operational flexibility, is that the design model operates with perfect forecasting across an entire year of data. This may enable them to operate safely through extended periods of poor renewable energy generation (so-called “dunkelflaute”) by curtailing ammonia production and prioritising hydrogen storage well before those dunkelflaute would have been visible to forecasters. On the flipside, they may discharge storage components completely with high frequency, knowing that they can be recharged in the near future; real plant operators may be less willing to do so with imperfect information.In the context of operating with imperfect forecasting, plant flexibility is important. A completely flexible plant which can ramp rapidly will be able to operate without risk of equipment damage or failure by determining the operating state solely based on the current energy availability. As plants become increasingly inflexible (both in the sense of ramping and the MOR), the further in advance of dunkelflaute they need to begin to adjust operation by winding down the HB plant to charge storage inventories.
There have been relatively few studies into the operation of green ammonia plants with a fixed design and finite forecasting information. Previous work from the authors has considered the role of changing the design year of weather data input to the LP model at a given location,19,33 describing how operation changed and plant design was adjusted. However, this work did not consider the role of uncertain forecasting. Similarly, Verleysen et al.34 also considered the role of uncertainty in changing design, although this work applied an uncertainty to wind inputs to determine a relationship between plant oversizing and robustness. Kelley et al.35 examined the role of ammonia plants in providing a demand response service, looking at process chemistry to determine if a grid-connected plant could ramp down quickly in response to high prices, although this was not focussed on using weather forecast information. Allman and Daoutidis36 adopted a rolling optimisation forecast to determine the operating state of their plant – this is similar to the MPC approach described here. However, they considered a grid-connected plant, which is simpler to operate since the inventories in the batteries and hydrogen storage do not need to be so carefully managed to account for dunkelflaute. Of the existing body of literature describing green ammonia, the authors are aware of none which considers solar PV, wind, batteries and fuel cells, and which considers the interplay between realistic plant operation and optimal plant design.
This research is better developed in the power-to-hydrogen space, although the control problem in that context is simpler since the largest complexity in ammonia production is the inflexibility of the HB process. In power-to-hydrogen, Model Predictive Controllers (MPCs)37 have been widely discussed as a possible approach to optimising plant operation given limited forecast information, and the same technique is adopted here. MPCs have been widely adopted for the operation of chemical processes globally, and are considered a useful tool for handling problems pertaining to variable operability.38
MPCs use an internal model to predict the behaviour of the plant over that time horizon. At each time step, they optimise the operation of the plant according to an objective function, and subject to constraints on the controlled variables and the state of the plant. The model takes the first step along the optimum path it has determined, and then re-evaluates a new optimum path and begins to progress along it. Here, the external disturbance is the varying weather pattern, and we consider the time horizon in the model to be equivalent to the forecast duration.
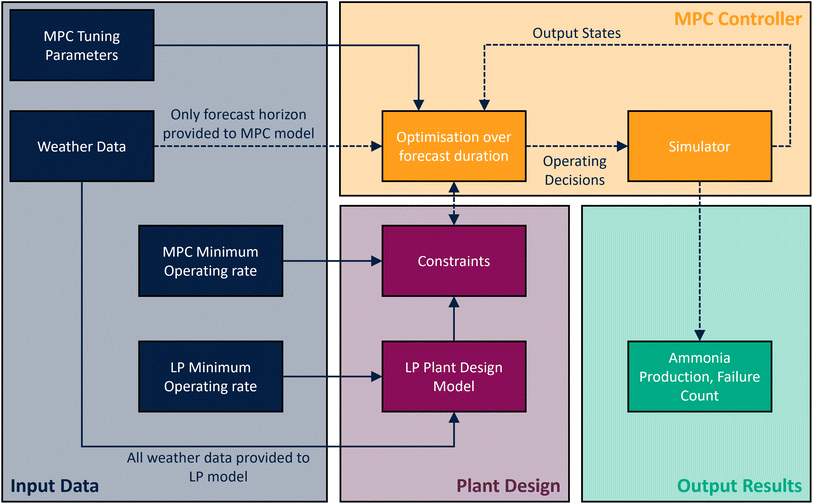
Fig. 1 explains the operation of the MPC model in this context. A year of weather data is used to determine an optimum design of the plant at a given location using the LP. The plant design creates the constraints on the MPC model, by setting the upper and lower bounds on the amount of power which can be sent to the various plant components. One particularly important constraint is the HB MOR, which is not necessarily the same between the LP and the MPC (see Section 3.2.1). Where we provide the LP model with a full year of weather data, the MPC is only provided with n hours at each time step, where n is the forecast horizon and takes values of 12, 24 and 48 in this analysis. The optimiser determines at each time step the optimum operating rate of each piece of equipment, which in turn determines the ammonia production; the plant state is then sent back to the optimiser, as it interacts with the constraints and the new weather pattern that emerges in the next time step. In general in this analysis, we use the same year of weather data for the LP and MPC models so they can be directly compared; however, in Section 3.4 we consider the impacts of using a weather dataset which spans a much greater time period for the MPC model than was provided to the LP model.
The MPC is implemented using the Python module Do-MPC,39 which modularises the process of building an MPC into a series of simple processes. The first process is constructing a model of plant operation, including state variables, model inputs and rate equations. Four state variables are considered: (i) the amount of hydrogen stored (xH); (ii) the amount of power stored in the battery (xB); (iii) the amount of ammonia produced in a given time step (xA); and (iv) the amount of electricity curtailed in a given time step (xC). These are dictated by the total renewable energy available to the plant at a given time (α) as well as five inputs, which are controlled by the MPC: (i) the power to the electrolyser (πE); (ii) the power to the HB plant (πHB); (iii) the power to the battery (βin); (iv) the power from the battery (βout); and (v) the power generated by the fuel cell (γ).
The inputs and disturbances are related to the states according to:
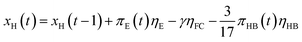 | (4) |
| xB(t) = [1 − εB]xB(t − 1) + ηBβin(t) − βout(t) | (5) |
| xA(t) = πHB(t)ηHB | (6) |
| xC(t) = α(t) + γ(t) + βout(t) − πE(t) − πHB(t) − βin(t) | (7) |
Eqn (4) and (5) are simple balance equations over the hydrogen storage and the battery storage respectively. ηE and ηB are the efficiencies of the electrolyser and battery, respectively; the same values are used in the MPC case as were used for the LP design model. In the case of the hydrogen, the state of the storage unit is given by the storage from the previous time step, plus any inflows from electrolyser production, minus outflows to the fuel cell or to the HB plant. The outflows to the HB plant are determined from the power consumption converted into tons of ammonia using the efficiency, and then into tons of hydrogen using the reaction stoichiometry. The battery equation is the same in principle, except a self discharge factor εB is included to display the gradual reduction in battery capacity. For the battery, the energy losses are imposed on the charging power as it enters the storage unit. Eqn (6) and (7) are then simple instantaneous balances over ammonia production and power respectively.
This model construction provides enough information for the plant to predict future behaviour. The MPC then needs to be provided with direction under an objective function and constraints to determine the operating process.
The objective function is given by:
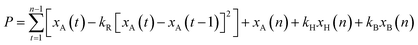 | (8) |
The goal of the MPC is to maximise P, the objective variable. This broadly corresponds to maximising the total amount of ammonia produced over the time horizon n, which is given by the first term inside the summation, and the first term outside the summation.
Three penalties need then to be imposed upon the optimisation model to ensure it acts as intended. The first is a penalty on ramping the ammonia plant, given by the quadratic term inside the summation, which is scaled by the tuning parameter kR. Without this term, the HB plant will change its operating rate significantly in each step; as kR grows, the rate of change of the HB plant is increasingly penalised. Because this penalty is quadratic, the model will prioritise slow ramping over sudden large steps, which is reflective of the slow ramping needed by the HB synloop. The second and third penalties are for depleting the storage inventories, which is represented by the final two terms, scaled by the tuning parameters kH (for hydrogen storage) and kB (for battery storage). In the absence of these terms, the model will attempt to maximise the ammonia produced at the expense of the storage inventories, which it will often plan to drain over the time horizon (since the low production or plant failure in the subsequent time horizon does not impact the optimisation). The parameters kH and kB are tuned depending on operator risk tolerance; as they grow, the plant is less likely to fail, because it will prioritise keeping the storage inventories full; however, doing so comes at the cost of ammonia production. To simplify the sensitivity modelling, the value of these parameters are set to be equal for this analysis, but specific tuning could be done on a site-by-site basis.
The MPC is constrained by the same limitations as the LP model. In general, these constrain all states and inputs to be greater than 0, and less than the capacity of the equipment in the pre-designed plant. The additional constraint is on the Haber–Bosch plant, which must maintain a MOR, which is measured as a fraction of the plant design size. The specific MOR is varied across different analyses in this research. The explicit constraint on plant ramping from the LP is removed; this is achieved by the ramping parameter kR described in the previous paragraph.
3 Results and discussion
3.1 Plant design
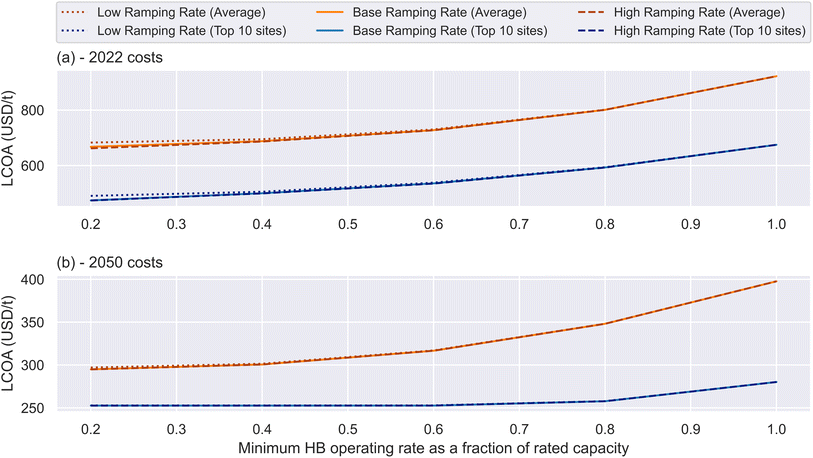
The most important observation in the figure is that there are diminishing marginal returns on increasing plant flexibility. In both 2022 and 2050, reducing the HB MOR from 60% to 20% achieves only one quarter of the cost reduction of reducing the HB MOR from 100% to 60% (for the average cases). For the cheapest sites in 2050, the results are even more stark, with almost no benefit gained whatsoever from reducing the HB MOR below 60% of rated capacity.
This is predominantly because the ammonia plant represents a significant capital expense, but its power draw is comparatively small. That means that the plant, for most of the year, receives relatively little benefit from turning down the ammonia plant to very low operating rates, since it can sustain operation using the battery and hydrogen storage units (and it is preferable to exploit the capital expense of that equipment to the greatest load factor possible). This may cause the state of charge in the batteries and hydrogen storage to cycle more (compared to a case in which the HB operating rate could be turned down further), but does not significantly increase their size. Therefore the increase in costs is fairly small, as there is no limit on cycling imposed in this section. The effect is even more pronounced in 2050, because solar electricity and battery storage are expected to fall in price so significantly, whereas the CAPEX of the ammonia plant is likely to remain fairly steady.
The overall process can operate the HB plant at high rates for most of the year by cycling the battery and hydrogen storage; this only becomes challenging during the deepest dunkelflaute. The model sustains the HB MOR through this period either by: (i) turning down the HB plant, (ii) increasing the size of energy storage equipment, or (iii) increasing the extent to which the renewable power generation is oversized. The results indicate that the benefits which accrue from using the lever of ammonia plant capacity tail off below 60% of the rated capacity, and that the model can adopt other strategies without significantly increasing cost.
Although there is some benefit to increasing plant flexibility, it is not as large as potential other sources of improvement to the plant. Firstly, site selection is evidently of great importance; in both 2022 and 2050, a completely inflexible site in the top 10 locations is roughly equivalent in performance to a highly flexible site in an average location. Secondly, potential improvements in equipment performance are bigger drivers of cost reduction than plant flexibility. In 2022, the largest improvement in ammonia cost with plant flexibility is in the order of 30%, but this falls to around 10% for the high quality sites in 2050. In contrast, equipment improvements unlock price reductions in the order of 50%. This suggests that, as long as Haber–Bosch production is partially flexible (down to a level of say, 60%), additional capital investment in more expensive but more flexible technologies (e.g. electrochemical ammonia synthesis) may not be justified.
A final relevant observation is that the impact of ramping rate on plant costs is small. In the low ramping cases, the plant ramps down at 2% per hour, and up at just 0.5% per hour; despite this quite significant constraint, the impact on plant performance is around 15 USD per tonne on average in 2022, and less in 2050, and only impacts results meaningfully when the plant has an MOR close to 1.
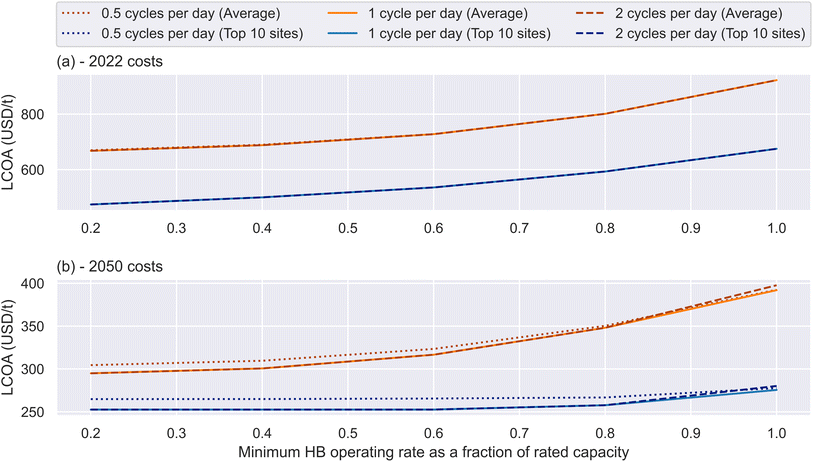
The most important observation in Fig. 3 is that cycling limitations are not likely to impact on the performance of ammonia plants at any degree of flexibility. The constraint has no impact on the LCOA when one or more cycles per day is allowed, which is well within the plausible operation of normal energy storage equipment. Even when only half a cycle per day is allowed, the impact on the LCOA is fairly minor (i.e. <5%).
The impacts in 2022 are particularly small because back-up power in 2022 is dominated by fuel cells. The LP model predicts that fuel cells are preferable in the short term because, compared to batteries, fuel cells connected to hydrogen storage have high power costs but relatively low stored energy costs (i.e. each additional MW of back-up power from a fuel-cell costs more than each additional MW from a battery, but each additional MWh of hydrogen storage is cheaper than each additional MWh of battery storage). Because the power demand of the HB plant at its MOR is a small fraction of the total power supplied around the plant, typically it is more costly to meet the energy storage requirements than the back-up power requirements, so the model opts for a fuel cell. Energy for the cases in 2022 therefore comes from cycling hydrogen storage, rather than batteries; this hydrogen storage can typically store enough energy for several days worth of production at the HB MOR, so it rarely needs to cycle quickly. In 2050, fuel cells are used less widely because the cost forecasting indicates that energy storage in batteries will become substantially cheaper.
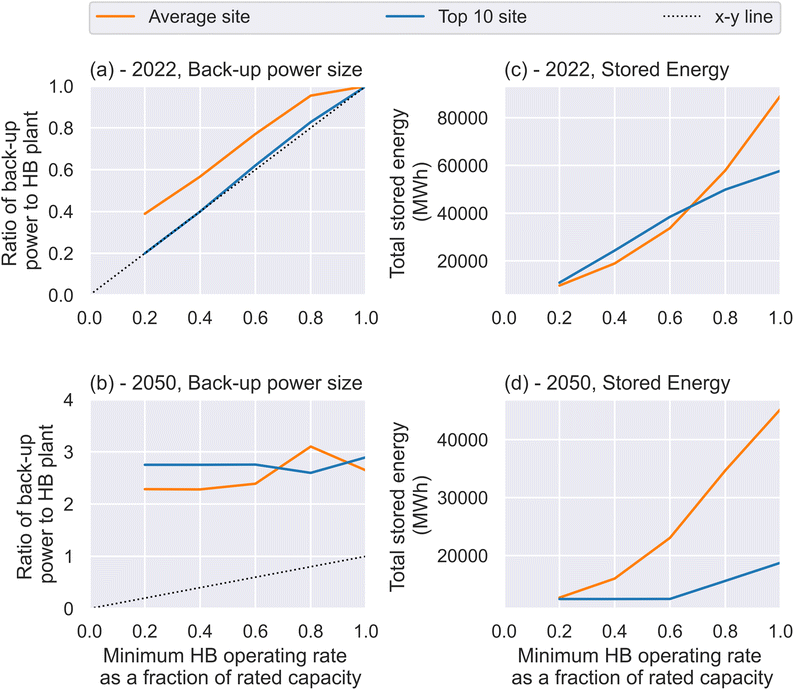
The cycling limitations tend to impact the HB plants which are more flexible, which is somewhat surprising, since cycling of the ammonia plant should reduce the need to cycle energy storage equipment. There are two factors which are responsible for this result; they are summarised in Fig. 4.
The first factor causing increased cycling of the battery in flexible plants in 2050 is a change in operating strategy over time. In 2022, the energy storage equipment is rated only to sustain operation of the HB plant; in the case of the top 10 sites, the back-up power capacity is almost exactly equal to the power draw of the HB plant at its minimum rate (i.e. in panel (a), the top-ten sites sit exactly on the x-y line). At the average sites, the total back-up power is slightly larger than the MOR. This is caused by the inability of the HB plant to ramp down sufficiently quickly.
By contrast, the back-up power in 2050 is significantly larger than the whole HB plant. Clearly, the role of back-up power in these plants is more than solely operating the HB plant during periods of low VRE output (if it were, the back-up power capacity would never exceed the power demand of the HB plant); it is partially to power the electrolyser. When the batteries are powering the electrolyser as well as the HB plant, they will tend to charge and discharge more frequently to maximise the amount of hydrogen produced. This change in behaviour is driven by the rapid fall in the cost of batteries.
Prices of solar panels will also fall, which will drive ammonia production towards Solar PV rather than wind. In a solar-driven system, the value of charging the electrolyser from the batteries is higher, since it otherwise sits unused during the night; in high quality wind sites, which will typically have a higher load factor, the electrolyser will be used more consistently. Again, this will drive increased cycling of batteries.
The second factor causing increased cycling of storage equipment in flexible plants in 2050 is simply that the storage equipment is smaller (see panel (d)). The total energy passing through the storage equipment is much higher in inflexible plants, but these plants have installed so much storage that the number of cycles remains relatively low.
3.2 Plant operation
Having designed the plants using the LP method (i.e. perfect forecasting), this section tests their operation under imperfect forecasting. In order to robustly consider the performance of the MPC, three sites were chosen from the >400 considered in the design cases. The three sites selected were chosen to offer a range of renewable profiles – one site is located in Algeria, and has excellent solar insolation; another in the United Kingdom is dominated by wind; a third in Morocco uses a hybrid of both. The figures displayed in this section on operation relate to production in 2022, when back-up energy is largely supplied by fuel cells; the ESI† includes equivalent figures for 2050, which demonstrates the applicability of the MPC method to batteries.Conventionally, ‘overdesign’ of a plant would involve applying some fixed factor to each piece of equipment, with larger factors applied to some, potentially less reliable, units. In this context, oversizing all equipment by the same amount would not improve reliability, since, although power generation grows, so too will the HB plant, necessitating a higher baseline power. Even scaling up all equipment except the HB plant is not sensible, as some equipment is not useful for supporting the plant during periods of low production (solar PV, for instance, should not be scaled up to correct an imbalance that occurs at nighttime or in winter). Instead, we design the plant using increasingly tight limitations on HB MOR in the LP, but then relax that constraint in the MPC, and allow the plant to operate at a lower minimum rate. This enables the oversizing to be concentrated on the equipment that enables flexible operation.
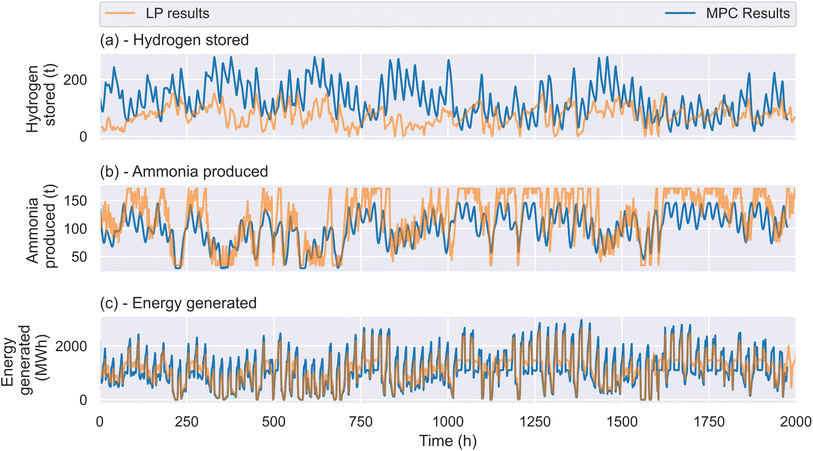 | ||
| Fig. 5 Comparison of hourly plant behaviour under in the operating mode, run by the MPC controller (blue), and the design mode optimised by the LP (orange) for a hybrid site containing both wind and solar in 2022. The MPC time horizon is 24 hours, and both tuning parameters are set to a value of 0.1, and the plant has been overdesigned using a Haber–Bosch minimum operating rate of 0.4 (compared to 0.2 for the LP). (a) – Top: compressed hydrogen in storage (a failure would be indicated by the storage level dropping below 0). Typically the tuning parameter which punishes low storage inventories keeps hydrogen stored by the MPC above hydrogen stored by the LP. (b) – Middle: ammonia produced in a given hour; note that due to the ramping parameter, the MPC makes fewer adjustments on an hourly basis than the LP. (c) – Bottom: total energy generated from all available renewable resources. Examples for the other two sites are provided in the ESI.† | ||
The most important result in this figure is that it demonstrates that a green ammonia plant can be operated using limited forecast information without exceeding the limits of the HB plant, provided the plant is adequately overdesigned. It is the first demonstration of this point for a HB plant that is not reliant on electricity grids.
There are a number of key differences between the LP results and the MPC results. Firstly, the MPC controller tends to store more hydrogen than the LP optimiser. This is partially because the overdesigned plant operated by the MPC has more hydrogen storage available than the LP plant; however, it is also encouraged to keep the storage full by the tuning parameter in the MPC optimisation function. The LP is only maximising ammonia production and is unconcerned by the storage inventory; for that reason, it more frequently allows the storage inventory to drop to 0, since it has enough forecast information to be confident that the hydrogen storage can be refilled.
Secondly, the LP model shows far more short-term variability in HB operation, which is most visible on panel (b). The LP model is constrained in how quickly it can ramp the operation of the HB plant (up at 5% of rated capacity/hour, down at 20% of rated capacity/hour). However, there are no limitations on how frequently it adjusts the HB rate of operation, so it makes changes almost at every time step. On the other hand, the MPC is not directly constrained to limit how quickly it can ramp the ammonia plant, but there is a general penalty for rapid ramping imposed upon the objective function. It therefore only changes operating rate if strictly necessary, and this results in ‘smoother’ operation, although it may sometimes surpass the ramping limits imposed on the LP. Less frequent cycling of the HB plant conditions reduces the risk of catalyst damage and is therefore likely to be advantageous, although some production may be sacrificed.
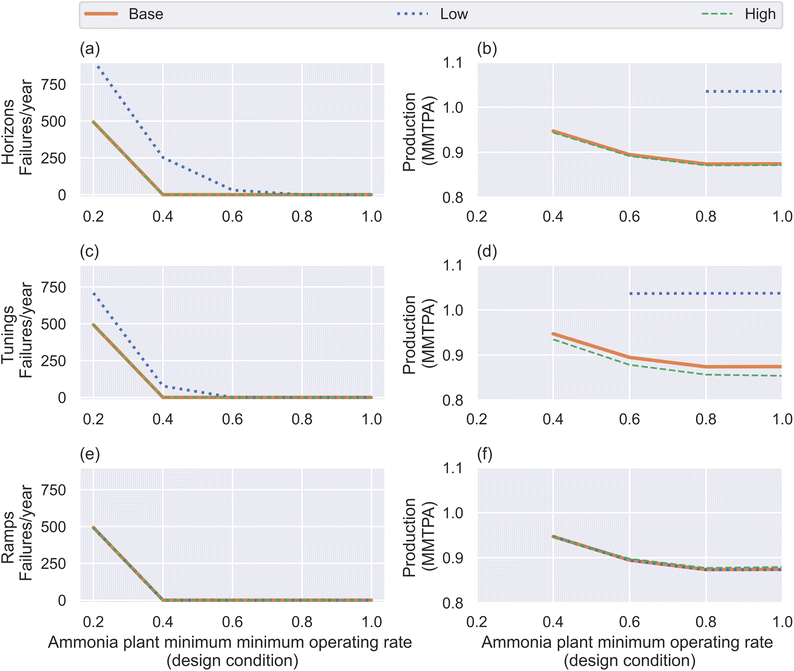 | ||
| Fig. 6 Plots of the failure frequency (left) and ammonia production (right) for a wind-dominated site in 2022. Different plots show the impact of varying different MPC parameters: forecast horizon (top), tuning parameters (middle) and ramping penalty (bottom). Each plot shows the impact of changing overdesign – in each case, the plant was operated with a minimum HB rate of 20% of rated capacity, but was designed with tighter constraints. Where the plant failed during operation, the design was considered untenable, and the associated production is excluded from the plots on the right. Examples for the hybrid and solar-only sites are provided in the ESI.† | ||
| Parameter | Low | Base | High | Units |
|---|---|---|---|---|
| Horizon | 12 | 24 | 48 | Hours |
| Tuning | 0.1 | 0.5 | 1 | — |
| Ramp | 0.05 | 0.1 | 0.5 | — |
Firstly, the figure demonstrates that, at this location, some plant oversizing is required in order to prevent plant failures. A ‘failure’ occurs when, given the forecast weather conditions, the model cannot keep all the state variables within their target bounds (i.e. a storage inventory falls below 0, the HB plant operates below its allowable MOR, or the plant curtails a negative amount of electricity). Given the relatively short time-frame of the input data used in this example (one year), even a single failure would represent a plant which is inadequately robust to weather variation. The need for oversizing differs between sites – at the wind dominated site, with no oversizing, there are hundreds of failures per year; this number falls to around 2 for the hybrid site (in 2022), and the solar-dominated site can operate without any oversizing (as can the hybrid site in 2050) – this result is discussed further in Section 3.3.
The amount of oversizing needed falls as the forecast horizon increases – see panel (a) – although increasing the length of the horizon would stretch the capacity of weather forecasters to make plausible predictions. With only 12 hours of forecasting, the number of failures is large because the system cannot adequately manage the storage inventory. Notably, however, if the plant can operate without failures using only 12 hours of forecasting, then the production rate is significantly higher – see panel (b).
Panels (c) and (d) shed light on why this occurs – when the tuning parameter is wound downwards, the effect is the same as using a shorter horizon. In other words, because the 12 hour forecast model has less information than the 24 hour version, it is more ‘reckless’, because it has less capacity to predict the consequences of increasing ammonia production on the storage inventory. This is only a suitable operating mode when the design is sufficiently oversized to guard against emptying the storage; however, when it is effective, it enables the plant to operate more like the LP. This emphasises the need for careful plant tuning; ideally, the plant will occupy the mode where production is maximised (and is essentially operating exactly as designed), but without tipping into a failure.
Interestingly, production tends to decline as oversizing increases. This is an artefact of the tuning parameter. As oversizing increases, the most significant changes to the plant design are to the hydrogen storage and battery capacities. The tuning penalty term is given by the product of the tuning parameter and the storage inventory; since the maximum value of the storage inventory has increased, the value of the penalty term also increases, and it therefore has more impact relative to the ammonia production terms. Maximising ammonia production is therefore weighted less heavily by the objective function. The exception is the site designed to be able to operate completely inflexibly. When the LP is solved for this mode, it oversizes components of the plant other than the storage only, which means the impact of the tuning penalty rebalances slightly in the other direction.
The role of the ramping parameter is less significant – within the range considered here, it does not affect the likelihood of plant failures, and it has a relatively small impact on overall production. This parameter therefore needs to be set such that the ammonia plant ramps at an adequate rate, ideally by introducing a cost function that depends on the impact of catalyst cycling, so that the optimal balance can be struck between preventing cycling and producing an adequate amount of ammonia.
Perhaps counter-intuitively, a higher ramping penalty (i.e. less ramping) increases the production rate. This is visible on Fig. 6(f), although the impact is more significant on the solar-dominated site in Algeria (see Fig. A1†). The ramping penalty drives up production by effectively overwhelming the tuning penalty, and therefore incentivising the HB loop to stay at maximum production, even if it draws down the inventory; provided this does not lead to plant failure, it increases production.
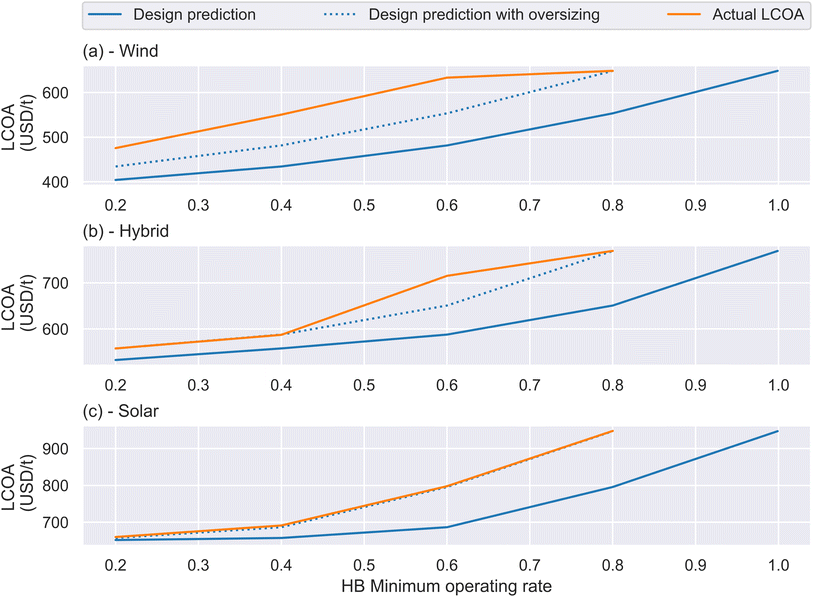
3.3 Actual LCOA
As is perhaps obvious, and also clear from the right-hand plots of Fig. 6, the plant operated with imperfect forecasting will produce less ammonia than was predicted in the design case by the LP, because it cannot manage its storage inventory as effectively.The MPC approach enables the true LCOA from each plant to be estimated by taking the product of the optimal design LCOA, and the ratio of the actual production and the design production. For this section, oversizing was enforced by considering a design case whose MOR was 20% larger than was allowed during operation (i.e. if the LP MOR used for plant design was 60%, the MPC MOR used for plant operation was 40%). The actual production was then determined by running the MPC using an array of parameters, and selecting the case with maximum production and no failures. To enable fair comparison of the LP and MPC controllers, MPC production was downrated by a factor of 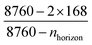 ; the discounting in the numerator relates to the two weeks of maintenance per year that are enforced on the LP, and the term in the denominator corrects for the hours at the end of the year which need to be excluded from the MPC's scope because there is inadequate forecast information. In both the MPC and the LP approaches, the discounting of production is conservatively applied to production over the whole year (rather than selecting a two week period in which production was likely to be low).
; the discounting in the numerator relates to the two weeks of maintenance per year that are enforced on the LP, and the term in the denominator corrects for the hours at the end of the year which need to be excluded from the MPC's scope because there is inadequate forecast information. In both the MPC and the LP approaches, the discounting of production is conservatively applied to production over the whole year (rather than selecting a two week period in which production was likely to be low).
Only 24 hours of forecast were allowed, over which range renewable forecasts tend to be highly accurate, because production estimates are required for bidding into day ahead electricity markets.40
Fig. 7 shows the results of this estimation approach. There are two sources of cost increase: oversizing costs (shown using the dotted line, which is simply the design prediction translated to the left by a value of 0.2), and reduced production. The solid red line on the figure shows the combined impact of plant oversizing and reduced production.
The results differ between the sites based on the primary source of energy. For the two sites with a large quantity of solar (the bottom two panels), actual production was almost equal to the design production in most cases – in other words, the MPC was able to replicate the performance of the LP model which had perfect foresight. This is an unsurprising result for a solar dominated plant in a high-quality location; because the renewable resource cycles on a 24 hour basis, optimising with a 24 hour forecast is broadly adequate. By contrast, the wind dominated site shown in the top panel fares far worse; because periods of low or high wind production may last for significantly longer than 24 hours, the MPC will not track the LP model as accurately.
For all locations, where the operating plant had very little HB flexibility (i.e. MOR > 80%), the production in the design and operating cases was very similar. Under these constraints, the degrees of freedom in plant operation is small, so both the design and operating cases will tend to behave in a similar way.
The exception to this rule is the performance of the hybrid site at an HB MOR of 60%, where the MPC production is around 10% less than the LP forecast, creating a significant spike in the LCOA on the figure. For the other cases, the optimal MPC production occurred when the tuning parameter took a value of 0.1; however, when this value for the tuning parameter was used in the case where the HB MOR was 60%, 97 plant failures were observed. This is a location-specific effect, indicating that for this case, the additional 20% oversizing was inadequate to run the MPC with a loose storage penalty parameter. For that specific case, therefore, the figure shows the next best production option which used a tighter value for the tuning parameter of 0.5. This tighter parameter prevented plant failures but at the cost of reduced production. Optimal design of the MPC would identify a tuning parameter between 0.1 and 0.5 that may strike a superior balance between these two goals. The effect is similar to that observed on panel (b) of Fig. 6 for the 12 hour horizon – achieving excellent production increases the risk of plant failure.
Reducing the actual LCOA requires (i) the plant oversizing to be reduced as much as possible, and (ii) the production from the MPC to be equal to the LP. For the solar plants, the latter goal has already been achieved; doing the same in wind plants will require superior forecasting and improved tuning, which may require machine learning to tune appropriately on a case-by-case basis. Achieving goal (i) is more complex, and is a useful area for further research. The approach used in this analysis used a fairly crude approach of using a plant designed with reduced flexibility; this could be improved at individual sites on a case-by-case basis by iteratively solving the design LP and the MCP in order to strike a tolerable balance between plant failure risk and meeting production goals. Additionally, less coarse steps in the HB MOR and in the MPC parameters would enable more precise tuning at a given location.
Fig. 7 presents a more complex view on plant flexibility than that presented using only the LP results (Fig. 2). In the case of the solar dominated plants, provided the MPC is well-tuned, the conclusions are broadly the same: there is some benefit to be gained from plant flexibility, but the majority of this benefit is associated with reducing the HB MOR to ∼60%, and not beyond it to a very low minimum ∼20%. Improving the estimate of the required plant oversizing (as discussed in the previous paragraph) would move the red line on Fig. 7 towards the solid green line, weakening the relationship between flexibility and LCOA yet further. However, in the case of predominantly wind-dominated plants, the difficulty of long-term forecasting means HB flexibility is a more useful lever for the plant to use while it is operating, and the LCOA continues to fall linearly as flexibility increases.
3.4 Long term operation
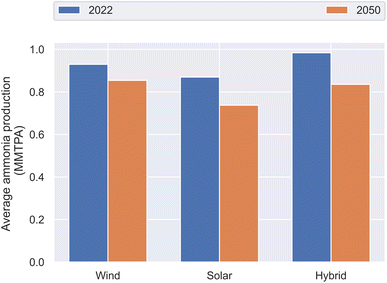
Until this point, this article has considered operation using weather data taken from the same year in which the plant was designed. To confirm that the parameters selected as optimum in the previous section enabled the plant to operate robustly across longer time periods, the model was operated using 12 years of historical weather data (from the start of 2010 to the end of 2021; this period includes the design year which was 2019). Note that the historical weather data is used for both the 2022 and 2050 cases, the primary difference between the cases relating to equipment efficiency and CAPEX. The MPC horizon was set to 24 hours, the ramping penalty was set to 0.1, and the tuning penalty was tuned based on the likelihood of failure observed in the sensitivity analysis: a tuning value of 1 was used for wind site, 0.5 for the hybrid site and 0.1 for the solar site. The plant design was selected by running the LP with a MOR of 40%; again, the MPC MOR was set to 20%.Under these conditions, no failures were observed across the 12 years of operation. The results are shown in Fig. 8. Evidently, the tuning of the MPC is best for the hybrid site, and may benefit from review in the other locations. However, in each 2022 case, production is within 10% of the design target, indicating that the MPC is robust when operated in unfamiliar weather profiles. For the 2050 cases, production is significantly less, indicating the tuning parameters are likely to be too conservative.
4 Conclusions
The general consensus in the literature is that enhanced flexibility is a prerequisite for affordable ammonia production. This article demonstrates that the true relationship between flexibility and green ammonia cost is more complex. While some flexibility is important, by 2050, reducing the MOR from 60% to 20% will improve the LCOA at the average site by less than 10%, even when constraints on storage equipment cycling are introduced; the benefits are even smaller at the best locations. It is therefore not likely that investing in more expensive technologies which enable more flexible operation (e.g. more robust catalysts or non-HB ammonia production technologies) will ultimately reduce the LCOA. There is significantly more to be achieved from (i) targeting reductions in equipment costs (particularly of Solar PV, which produces the cheapest ammonia in most production in the 2050 forecast), and (ii) improving the ability of operating plants to match the performance of optimally designed plants.The latter point is demonstrated through an MPC model which is the first to consider how weather forecast limitations impact the operation and design of green ammonia plants: in summary, using plausible forecast horizons, sufficient plant overdesign, and careful MPC parameter tuning can manage the risk of plant failure without sacrificing production. Production using imperfect forecasting at three locations as measured over a twelve year period was within 10% of the optimum production achievable using perfect forecasting; even better results may be achievable with more precise tuning. Only in circumstances where the VRE supply is less regular, such as a wind-dominated plant, is plant flexibility a useful lever for reducing ammonia costs. This study focused on detailed analysis of three sites; further research should consider whether the results are consistent in other locations.
There is significant room for further research. Firstly, this approach provided very limited forecast information to the MPC (only up to a horizon at which the predictions had a high degree of confidence). Performance may be improved by including longer-term but higher uncertainty weather forecasts; the possibility of doing so should be investigated. Secondly, different approaches to plant oversizing should be considered, perhaps by iterating the LP and the MPC models to design optimal, robust plants. This research used quite coarse steps between different values of the HB minimum operating rate when determining the extent to which the plant should be oversized, and there may be merit to considering finer steps in order to minimise the amount of overdesign required. Thirdly, the MPC approach should be extended to grid-connected plants, with a focus on the relationship between predictability of the grid cost and the opportunities posed by sector coupling. When a grid connection is used, plant flexibility may be more valuable than in the islanded case considered here, as it will enable the green ammonia plant to provide grid services. Fourthly, some of the 2050 cases produce considerably less ammonia in operating mode than targeted in design; more site-specific tuning studies should be conducted.
Abbreviations
| ASU | Air separation unit |
| CAPEX | Capital expenditures |
| HB | Haber–Bosch |
| LCOA | Levelised cost of ammonia |
| LP | Linear program |
| MMTPA | Million metric tonnes per annum |
| MOR | Minimum operating rate |
| MPC | Model predictive control |
| NPV | Net present value |
| O&M | Operating and maintenance costs |
| OPEX | Operating expenditures |
| USD | US dollars |
| VRE | Variable renewable energy |
List of symbols
| t | Time (h) |
| S t | The set of all times |
| α(t) | Total renewable energy available to the plant at time t in MWh |
| λ(SC,t) | Total charge accumulation in storage component SC at time t in MWh (design only) |
| κ(SC,t) | State of charge of a storage component SC at time t in MWh (design only) |
| x | State of plant in the MPC controller (operating approach only) |
| π E(t) | Total energy flow to the electrolyser at time t in MWh (MPC) |
| π HB(t) | Total energy flow to the HB plant (MPC) at time t in MWh |
| β in(t) | Energy flow to the battery at time t in MWh (MPC) |
| β out(t) | Energy flow from the battery at time t in MWh (MPC) |
| γ(t) | Energy flow from the fuel cell in MWh at time t(MPC) |
| η | Conversion efficiency |
| ε B | Battery hourly self discharge rate |
| SC | Storage component (a member of the set of storage components) |
| G CL | Maximum allowable number of battery cycles (design only) |
| C SC | Capacity of storage equipment in MWh |
| n | Forecast horizon of MPC controller (operating only) |
| k H | Hydrogen storage tuning parameter (operating only) |
| k B | Battery storage tuning parameter (operating only) |
| k R | Ramping tuning parameter (operating only) |
Conflicts of interest
There are no conflicts of interest to declare.Acknowledgements
The work here was supported financially by the Rhodes Trust. The use of Gurobi for the LP modelling was under a free academic license.References
- J. A. Dowling, K. Z. Rinaldi, T. H. Ruggles, S. J. Davis, M. Yuan, F. Tong, N. S. Lewis and K. Caldeira, Joule, 2020, 4, 1907–1928 CrossRef.
- Z. Cesaro, M. Ives, R. Nayak-Luke, M. Mason and R. Bañares-Alcántara, Appl. Energy, 2021, 282, 116009 CrossRef CAS.
- J. Schmidt, K. Gruber, M. Klingler, C. Klöckl, L. Ramirez Camargo, P. Regner, O. Turkovska, S. Wehrle and E. Wetterlund, Energy Environ. Sci., 2019, 12, 2022–2029 RSC.
- N. Salmon and R. Bañares-Alcántara, Sustainable Energy Fuels, 2021, 5, 2814–2839 RSC.
- D. MacFarlane, P. Cherepanov, J. Choi, B. R. Suryanto, R. Hodgetts, J. Bakker, F. Ferrero Vallana and A. Simonov, Joule, 2020, 4, 1186–1205 CrossRef CAS.
- R. Nayak-Luke and R. Bañares-Alcántara, Energy Environ. Sci., 2020, 13, 2957–2966 RSC.
- J. Armijo and C. Philibert, Int. J. Hydrogen Energy, 2020, 45, 1541–1558 CrossRef CAS.
- G. Wang, A. Mitsos and W. Marquardt, AIChE J., 2020, 66, e16947 CAS.
- T. Knight, C. Chen and A. Yang, in Embracing the era of renewable energy: model-based analysis of the role of operational flexibility in chemical production, ed. Y. Yamashita and M. Kano, Elsevier, 2022, vol. 49, pp. 1915–1920 Search PubMed.
- I. I. Cheema and U. Krewer, RSC Adv., 2018, 8, 34926–34936 RSC.
- O. Osman, S. Sgouridis and A. Sleptchenko, J. Cleaner Prod., 2020, 271, 121627 CrossRef CAS.
- M. Fasihi, R. Weiss, J. Savolainen and C. Breyer, Appl. Energy, 2021, 294, 116170 CrossRef CAS.
- N. Salmon and R. Bañares-Alcántara, Energy Environ. Sci., 2021, 6655–6671 RSC.
- N. Salmon and R. Bañares-Alcántara, Forthcoming PSE Conference, Kyoto, Japan, 2022 Search PubMed.
- G. Wang, A. Mitsos and W. Marquardt, AIChE J., 2017, 63, 1620–1637 CrossRef CAS.
- W. F. Holmgren, C. W. Hansen and M. A. Mikofski, J. Open Source Softw., 2018, 3, 884 CrossRef.
- H. Chen, F. Dong and S. D. Minteer, Nat. Catal., 2020, 3, 225–244 CrossRef.
- Asian Renewable Energy Hub, 2020, https://asianrehub.com/about/ Search PubMed.
- N. Salmon and R. Bañares-Alcántara, in Sector Coupling of Green Ammonia Production to Australia's Electricity Grid, ed. Y. Yamashita and M. Kano, Elsevier, 2022, vol. 49, pp. 1903–1908 Search PubMed.
- R. T. Zimmermann, J. Bremer and K. Sundmacher, Chem. Eng. J., 2020, 387, 123704 CrossRef CAS.
- C. Smith and L. Torrente-Murciano, Adv. Energy Mater., 2021, 11, 2003845 CrossRef CAS.
- International Renewable Energy Agency, Renewable Power Generation Costs in 2019, International Renewable Energy Agency, Abu Dhabi, 2019 Search PubMed.
- International Renewable Energy Agency, Hydrogen: a renewable energy perspective, 2019, https://www.irena.org/publications/2019/Sep/Hydrogen-A-renewable-energy-perspective Search PubMed.
- R. Nayak-Luke, R. Bañares-Alcántara and I. Wilkinson, Ind. Eng. Chem. Res., 2018, 57, 14607–14616 CrossRef CAS.
- R. Way, M. C. Ives, P. Mealy and J. D. Farmer, Joule, 2022, 6, 2057–2082 CrossRef.
- E. Taibi, H. Blanco, R. Miranda and M. Carmo, Green Hydrogen Cost Reduction, International renewable energy agency report, 2020 Search PubMed.
- M. J. Ginsberg, M. Venkatraman, D. V. Esposito and V. M. Fthenakis, Cell Rep. Phys. Sci., 2022, 3, 100935 CrossRef CAS.
- International Renewable Energy Agency, Making the breakthrough: Green hydrogen policies and technology costs, 2021, https://www.irena.org/-/media/Files/IRENA/Agency/Publication/2020/Nov/IRENA_Green_Hydrogen_breakthrough_2021.pdf?la=en%26hash=40FA5B8AD7AB1666EECBDE30EF458C45EE5A0AA6 Search PubMed.
- P. L. García-Miguel, J. Alonso-Martínez, S. Arnaltes Gómez, M. García Plaza and A. P. Asensio, Batteries, 2022, 8, 110 CrossRef.
- Y.-S. Cheng, Y.-H. Liu, H. C. Hesse, M. Naumann, C. N. Truong and A. Jossen, Energies, 2018, 11, 469 CrossRef.
- P. Berest, Thermomechanical Aspects of high frequency cycling in salt storage caverns, 2011, https://hal.archives-ouvertes.fr/hal-00654932/document Search PubMed.
- S. Nayebossadri and D. Book, Int. J. Hydrogen Energy, 2019, 44, 10722–10731 CrossRef CAS.
- N. Salmon and R. Bañares-Alcántara, in Importance of interannual renewable energy variation in the design of green ammonia plants, ed. Y. Yamashita and M. Kano, Elsevier, 2022, vol. 49, pp. 757–762 Search PubMed.
- K. Verleysen, D. Coppitters, A. Parente, W. De Paepe and F. Contino, Fuel, 2020, 266, 117049 CrossRef CAS.
- M. T. Kelley, T. T. Do and M. Baldea, AIChE J., 2022, 68, e17552 CrossRef CAS.
- A. Allman and P. Daoutidis, Chem. Eng. Res. Des., 2018, 131, 5–15 CrossRef CAS.
- M. J. Palys and P. Daoutidis, Comput. Chem. Eng., 2022, 165, 107948 CrossRef CAS.
- P. Daoutidis, J. H. Lee, I. Harjunkoski, S. Skogestad, M. Baldea and C. Georgakis, Comput. Chem. Eng., 2018, 115, 179–184 CrossRef CAS.
- S. Lucia, A. Tatulea-Codrean, C. Schoppmeyer and S. Engell, Control Eng. Pract., 2017, 60, 51–62 CrossRef.
- A. Nespoli, E. Ogliari, S. Leva, A. Massi Pavan, A. Mellit, V. Lughi and A. Dolara, Energies, 2019, 12, 9 CrossRef.
Footnote |
| † Electronic supplementary information (ESI) available. See DOI: https://doi.org/10.1039/d3su00067b |
| This journal is © The Royal Society of Chemistry 2023 |