Open Access Article
Open Access ArticleCreative Commons Attribution 3.0 Unported Licence
Stoichiometry matters: correlation between antisite defects, microstructure and magnetic behavior in the cathode material Li1−zNi1+zO2†
Damian
Goonetilleke‡§
 a,
Björn
Schwarz
a,
Björn
Schwarz
 b,
Hang
Li
b,
Francois
Fauth
b,
Hang
Li
b,
Francois
Fauth
 c,
Emmanuelle
Suard
c,
Emmanuelle
Suard
 d,
Stefan
Mangold
e,
Sylvio
Indris
d,
Stefan
Mangold
e,
Sylvio
Indris
 b,
Torsten
Brezesinski
b,
Torsten
Brezesinski
 a,
Matteo
Bianchini¶
a,
Matteo
Bianchini¶
 af and
Daniel
Weber§
af and
Daniel
Weber§
 *b
*b
aBattery and Electrochemistry Laboratory, Institute of Nanotechnology, Karlsruhe Institute of Technology (KIT), Hermann-von-Helmholtz-Platz 1, 76344 Eggenstein-Leopoldshafen, Germany
bInstitute for Applied Materials-Energy Storage Systems (IAM-ESS), Karlsruhe Institute of Technology (KIT), Hermann-von-Helmholtz-Platz 1, 76344 Eggenstein-Leopoldshafen, Germany. E-mail: daniel.weber3@kit.edu
cCELLS—ALBA Synchrotron, 08290 Cerdanyola del Vallès, Barcelona, Spain
dInstitut Laue-Langevin (ILL), BP 156, 71 Avenue des Martyrs, 38042 Grenoble, France
eInstitute for Photon Science and Synchrotron Radiation, Karlsruhe Institute of Technology (KIT), Hermann-von-Helmholtz-Platz 1, 76344 Eggenstein-Leopoldshafen, Germany
fBASF SE, Carl-Bosch-Strasse 38, 67056 Ludwigshafen, Germany
First published on 24th May 2023
Abstract
As contemporary battery applications such as electric vehicles demand higher energy densities, layered LiNiO2 (LNO) could contribute as the end-member of the LiNi1−x−yCoxMnyO2 (NCM) family with the highest extractable specific capacity in a practical voltage window. Achieving high capacities requires among other things a defect free crystal structure, which is not easily achieved due to the natural occurrence of Ni excess on the Li site (NiLi) and/or antisite defects where Ni and Li switch crystallographic sites. Here, we present a study of the evolution of point defects in a series of LNO samples varying from underlithiated to fully lithiated stoichiometry in layered Li1−zNi1+zO2 with −0.05 ≤ z ≤ 0.35. Using the high angular resolution of synchrotron X-ray diffraction complemented with the different elements contrast provided by neutron diffraction, we are able to identify two defect regimes. In the first regime, at the underlithiated end, both NiLi as well as Li on the Ni site (LiNi) defects are present. Inhibited crystal growth during synthesis is found to coincide with the presence of these LiNi defects for z ≥ 0.15. Upon decreasing z values and the vanishing of LiNi, the primary particle size distribution as well as average refined crystallite size increases. Investigation of the local structure by nuclear magnetic resonance reveals the presence of a Li environment not detected by diffraction methods at low z, the Li-rich end of the sample series. Finally, magnetometry data suggest the onset of the ferrimagnetic-to-antiferromagnetic transition in LNO correlates with the elimination of LiNi defects in the structure. The present study thus not only highlights the correlation between defect chemistry and physical properties, but also shows the relationship to crystal growth, a field highly relevant for industrial battery cathode materials engineering.
Introduction
Layered oxide cathode materials of the NCM family having a high Ni content have been widely adopted in applications requiring energy storage with a high energy density. To further improve gravimetric energy density, Ni-rich compositions have been developed with Ni content as high as 95%,1–3 effectively approaching the LiNiO2 (LNO) end-member. Despite being the NCM cathode active material with the highest specific capacity (≈245 mA h g−1 at 4.3 V vs. Li+/Li at 25 °C), key issues remain, as LNO is challenging to synthesize, suffers from both structural and surface instabilities in the pristine and de-lithiated state, as well as crystallographic defects hindering full delithiation.4 LiNiO2 has been the subject of numerous studies regarding its synthesis,5–9 crystallographic and electronic structures,10–14 and electrochemical behaviour,15–18 and the reader is directed to a recent review for a more comprehensive overview of the material.19 While current efforts yielded recipes for LNO with 1–2% of Ni2+ on the Li site (NiLi),20 the formation of defects, and thus possibility for their complete elimination, remains poorly understood in LNO.In a recent study, the LNO formation mechanism from the mixture of the industrial relevant reactants LiOH·H2O + Ni(OH)2 was elucidated by in situ diffraction.5 There, three steps were identified: (I) dehydration towards NiO + LiOH, (II) partial lithiation/oxidation of the Ni-containing phase towards cubic Ni1−xLixO (space group Fm![[3 with combining macron]](https://www.rsc.org/images/entities/char_0033_0304.gif) m) up to x ≈ 0.31 and even up to x ≈ 0.4 during the in situ lithiation, and (III) a final oxidation with a concomitant full lithiation towards stoichiometric LiNiO2. In the cubic, rock salt type phase, Ni and Li share a crystallographic site as well as an oxide anion polyhedron of the same volume. Once sufficient amounts of Ni2+ (r = 0.69 Å) are oxidized to Ni3+ (r = 0.56 Å), the difference of the average ionic radius of the nickel ions vs. the radius of 0.76 Å for Li+ becomes too large, inducing a phase transition towards layered, rhombohedral Li1−zNi1+zO2 (space group R
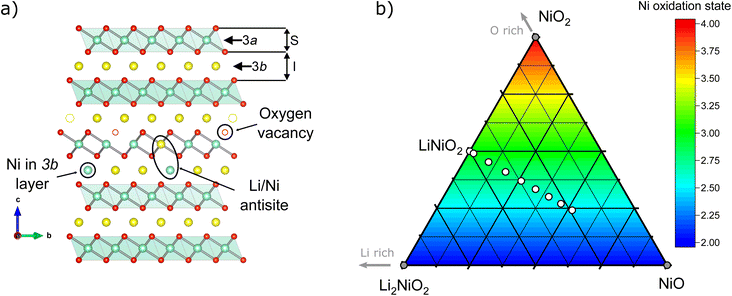
m) up to x ≈ 0.31 and even up to x ≈ 0.4 during the in situ lithiation, and (III) a final oxidation with a concomitant full lithiation towards stoichiometric LiNiO2. In the cubic, rock salt type phase, Ni and Li share a crystallographic site as well as an oxide anion polyhedron of the same volume. Once sufficient amounts of Ni2+ (r = 0.69 Å) are oxidized to Ni3+ (r = 0.56 Å), the difference of the average ionic radius of the nickel ions vs. the radius of 0.76 Å for Li+ becomes too large, inducing a phase transition towards layered, rhombohedral Li1−zNi1+zO2 (space group R![[3 with combining macron]](https://www.rsc.org/images/entities/char_0033_0304.gif) m). In ideal structure of LNO at z = 0, Ni3+, Li+ and O occupy the 3a, 3b and 6c site, as depicted in Fig. 1a. Hence, the oxygen ions remain in a cubic close packed (ccp) array similar to the rock salt phase, while Li and Ni separate into alternating layers along the c axis of the unit cell.
m). In ideal structure of LNO at z = 0, Ni3+, Li+ and O occupy the 3a, 3b and 6c site, as depicted in Fig. 1a. Hence, the oxygen ions remain in a cubic close packed (ccp) array similar to the rock salt phase, while Li and Ni separate into alternating layers along the c axis of the unit cell.
In real LNO materials though, nickel oxidation and thus separation of lithium and nickel into different crystallographic sites remains incomplete, leading to structural defects. The first such defect, excess of Ni on the Li site NiLi, is found in many studied materials and commonly referred to as “off-stoichiometry”. The defect originates from facile lithium losses during synthesis, even in samples of nearly perfect stoichiometry, and leads to a reduced, divalent oxidation state of Ni2+ in the Li site. The additional charges in the Li layer are compensated by the formation of charge defects in the NiO2− layer, i.e. [Li1−zNiz2+]3b[Niz2+Ni1−z3+]3a[O2]6c. As shown recently, with low temperature, ion exchange-based synthesis of LNO from NaNiO2 at around 320 °C instead of 700 °C, Li loss can be avoided.21 The NiLi defect is easily identified even in lab X-ray powder diffractometry due to the large additional electron density of nickel vs. lithium and thus routinely quantified in LNO studies. Another important defect, in which Ni and Li switch their crystallographic sites, i.e. [Li1−yNiy3+]3b[Liy+Ni1−y3+]3a[O2]6c, matches the definition of an antisite defect. In general, occupancy of Li+ in NiO2− slabs is highly unusual due to the difference in ionic radii. However, high temperatures may lead to the formation of such antisite defects, as has been reported in highly disordered Li0.92Ni1.08O2 ≡ (Li0.74Ni0.26)3a[Ni0.82Li0.18]3bO2 single crystals prepared at 900 °C.22 Another option to incorporate Li in the Ni site is to have a Li/Ni ratio higher than 1 and increasing the oxygen chemical potential at a lower T of around 550 °C, hence generating oxidized compounds until reaching Li2NiO3 (corresponding to an extended z range from −0.33 ≤ z ≤ 0.0).23 A recent combined synchrotron X-ray and neutron diffraction study in isostructural NCM materials by Yin et al.24 indicates that antisite defect concentrations increase with the volume of the transition metal oxide octahedron Ni1−x−yCoxMnyO6. There, the polyhedral volume is driven by the reduction of Ni3+ to Ni2+ in the presence of Mn4+ and thus strongly dependent on the stoichiometry. While a similar mechanism could be imagined in LNO due to the Ni2+ charge defect in the trivalent NiO2 layer induced by the off-stoichiometry NiLi defect, a similar correlation is not known. Moreover, the limited concentration and nature of antisite defects makes them difficult to probe with conventional characterisation techniques, for example X-ray scattering has low sensitivity for Li, or the relatively high electronic conductivity of LiNiO2 reduces its Raman scattering efficiency.25 Researchers have hence turned to more advanced methods, including neutron scattering,12,26 X-ray absorption spectroscopy,27 and solid-state nuclear magnetic resonance (NMR) spectroscopy28,29 to more precisely resolve the crystallographic, electronic, and magnetic structure of LiNiO2. In tandem with experimental studies, several authors have also adopted computational modelling to predict possible structures of LiNiO2.30–33 Yet, to date in most of the literature models of either antisite defects or off-stoichiometry are often chosen without a precise reasoning behind the choice of the models.
Using a comprehensive suite of characterisation techniques, we aim to resolve the relationship between material stoichiometry and the presence of site defects over a wide range of compositions with nominal stoichiometry Li1−zNi1+zO2 where −0.05 ≤ z ≤ 0.35, and the resulting consequences for the physical properties of the materials. The site occupancy defects of Li and Ni in the structure are quantitatively determined using combined Rietveld analysis of structural models against X-ray and neutron diffraction data to characterise the bulk average structure. Complementary solid-state NMR spectroscopy provides more detailed insight into the local environments of Li in the defective structures. Finally, we correlate the observed defect chemistry to the magnetic properties and particle size, which yields insights into growth dynamics highly relevant for industrial crystal engineering.
Results & discussion
To better understand the consequences of Li![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
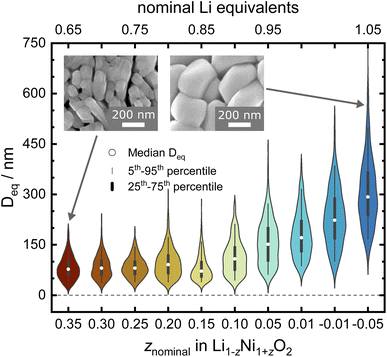
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) Ni stoichiometry for the micro- and crystal structure of LNO, a series of Li1−zNi1+zO2 samples with a nominal stoichiometry in the range of −0.05 ≤ z ≤ 0.35 were prepared via solid-state synthesis from commercially relevant hydroxide precursors LiOH·H2O and Ni(OH)2, see white dots in the ternary pseudo-phase diagram in Fig. 1b. Consistent with the studies mentioned above, a clear trend is seen in the evolution of the material's microstructure/morphology with changing nominal stoichiometry z, as shown in Fig. 2 and S1.† All the samples inherit a spherical secondary particle morphology from the Ni hydroxide precursor. However, an obvious change in the size of primary particles can be noticed among the different samples. To more accurately quantify the morphological changes, a semiautomated machine learning algorithm was used to measure the particle size distribution (PSD) from analysis of the electron microscopy images (further details are found in the Experimental section). The results are summarized in Fig. 2, including the median Deq, the 5th to 95th and 25th to 75th percentile of the PSD for each sample. The PSDs are multimodal and present some variation in their shape, which possibly originates from the counting statistics limited by the semiautomatic analysis workflow. Yet, an overall trend emerges: while the median Deq stagnates between approximately 77 and 90 nm for samples with z ≥ 0.15, the primary particle size steadily increases for samples with z ≤ 0.10 up to a median Deq of 308 nm. This observation indicates that the Li
Ni stoichiometry for the micro- and crystal structure of LNO, a series of Li1−zNi1+zO2 samples with a nominal stoichiometry in the range of −0.05 ≤ z ≤ 0.35 were prepared via solid-state synthesis from commercially relevant hydroxide precursors LiOH·H2O and Ni(OH)2, see white dots in the ternary pseudo-phase diagram in Fig. 1b. Consistent with the studies mentioned above, a clear trend is seen in the evolution of the material's microstructure/morphology with changing nominal stoichiometry z, as shown in Fig. 2 and S1.† All the samples inherit a spherical secondary particle morphology from the Ni hydroxide precursor. However, an obvious change in the size of primary particles can be noticed among the different samples. To more accurately quantify the morphological changes, a semiautomated machine learning algorithm was used to measure the particle size distribution (PSD) from analysis of the electron microscopy images (further details are found in the Experimental section). The results are summarized in Fig. 2, including the median Deq, the 5th to 95th and 25th to 75th percentile of the PSD for each sample. The PSDs are multimodal and present some variation in their shape, which possibly originates from the counting statistics limited by the semiautomatic analysis workflow. Yet, an overall trend emerges: while the median Deq stagnates between approximately 77 and 90 nm for samples with z ≥ 0.15, the primary particle size steadily increases for samples with z ≤ 0.10 up to a median Deq of 308 nm. This observation indicates that the Li![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) Ni ratio in the precursors mixture plays a crucial role in crystal growth, with a threshold between 0.10 ≤ z ≤ 0.15.
Ni ratio in the precursors mixture plays a crucial role in crystal growth, with a threshold between 0.10 ≤ z ≤ 0.15.
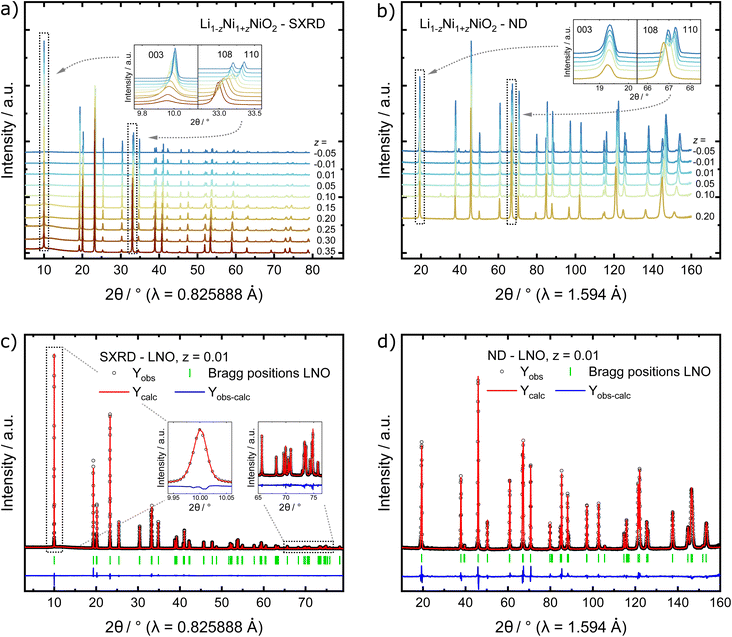
In order to find possible atomistic explanations for this observation and to quantitatively model the evolution of the crystal structure as a function of the nominal stoichiometry, synchrotron X-ray diffraction (SXRD) and neutron diffraction (ND) patterns were collected from the samples. The combination of both SXRD and ND is particularly useful for LNO and other layered cathode materials, as the high intensity and angular resolution coupled with negligible peak profile contributions of the instrument used in SXRD provides precise structural parameters. Neutrons on the other hand offer significantly improved sensitivity for Li and O in the presence of heavier transition metal elements for complementary accuracy of atomic parameters.34–36 The high-quality SXRD patterns feature narrow peak shapes in the best crystallized samples, allowing for more reliable deconvolution of the contribution to peak broadening due to crystallite size. A single structural model was simultaneously refined against both synchrotron and neutron data where both diffraction data sets were available. This allows for a more meaningful determination of the cation (especially Li) distribution among the 3a and 3b sites in the layered structure. Fig. 3a and b show diffraction patterns collected from the as-synthesised LNO materials. The peak positions of the 003 and 110 reflections, which depend on the c and a lattice parameter, respectively, shift towards higher 2θ values with decreasing z. This indicates that increasing Li content per sum formula is accompanied by a decrease in the unit cell volume. There is also considerable peak broadening of the full-width-at-half-maximum (FWHM) observed with decreasing Li content. Patterns of samples with small Li excess feature weak peaks corresponding to a minor LiOH impurity of 0.9(3) and 1.5(3) wt% for z of −0.01 and −0.05, respectively. Such LiOH impurities have been commonly observed on the surface of Ni-rich cathode materials.37,38 As we do not observe the 200 peak at about 2θ ≈ 23.0° (λ = 0.825888 Å), there is no evidence for the presence of a rock salt type side phase Ni1−xLixO (x ≤ 0.3).39
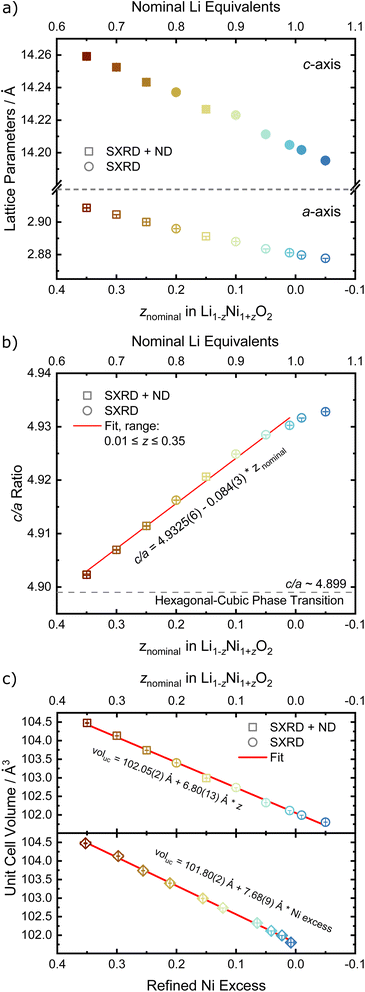
In order to quantify the trends observed in the diffraction patterns, structural models with space group R![[3 with combining macron]](https://www.rsc.org/images/entities/char_0033_0304.gif) m were refined against the diffraction patterns using Rietveld analysis. An example of the typical quality of fit by comparison of the observed vs. the calculated intensity including the difference curve is shown in Fig. 3c and d for SXRD and ND patterns of LNO with z = 0.01, and in Fig. S3† for the complete series of pattern. The resulting structural parameters are listed in Table 1 and their evolution with varying z or refined Ni excess is visualized in Fig. 4. LNO exhibits clear trends with decreasing Ni content (decreasing z), as summarized in Fig. 4a–c. The lattice parameters decrease from a = 2.90868(9) Å and c = 14.25917(6) Å in Li0.65Ni1.35O2 (z = 0.35) to a = 2.87771(9) Å and c = 14.19515(6) Å in nearly stoichiometric LNO (z = −0.05). The unit cell volume also decreases linearly with nominal z from 104.476(9) Å3 to 101.8037(8) Å3, as expected based on prior studies.19 This can be rationalized with the decreasing radii of the Ni-ions once oxidized from the di- to the trivalent state, with an accompanying reduction of the ionic radii from r(Ni2+) = 0.69 Å to r(Ni3+) = 0.56 Å.40 An increase in the c/a ratio from 4.9023 at z = 0.35, near the cubic c/a limit of 2√6 ≈ 4.8990, towards 4.9328 at z = −0.05 (near stoichiometric LNO) is a common indicator for low Li/Ni site disorder, good layering and the distortion observed in the trigonal space group.
m were refined against the diffraction patterns using Rietveld analysis. An example of the typical quality of fit by comparison of the observed vs. the calculated intensity including the difference curve is shown in Fig. 3c and d for SXRD and ND patterns of LNO with z = 0.01, and in Fig. S3† for the complete series of pattern. The resulting structural parameters are listed in Table 1 and their evolution with varying z or refined Ni excess is visualized in Fig. 4. LNO exhibits clear trends with decreasing Ni content (decreasing z), as summarized in Fig. 4a–c. The lattice parameters decrease from a = 2.90868(9) Å and c = 14.25917(6) Å in Li0.65Ni1.35O2 (z = 0.35) to a = 2.87771(9) Å and c = 14.19515(6) Å in nearly stoichiometric LNO (z = −0.05). The unit cell volume also decreases linearly with nominal z from 104.476(9) Å3 to 101.8037(8) Å3, as expected based on prior studies.19 This can be rationalized with the decreasing radii of the Ni-ions once oxidized from the di- to the trivalent state, with an accompanying reduction of the ionic radii from r(Ni2+) = 0.69 Å to r(Ni3+) = 0.56 Å.40 An increase in the c/a ratio from 4.9023 at z = 0.35, near the cubic c/a limit of 2√6 ≈ 4.8990, towards 4.9328 at z = −0.05 (near stoichiometric LNO) is a common indicator for low Li/Ni site disorder, good layering and the distortion observed in the trigonal space group.
| z | R Bragg/% | R wp/% | a/Å | c/Å | V/Å3 | D vol/nm | z O |
|---|---|---|---|---|---|---|---|
| 0.35 | 1.23 | 4.92 | 2.90868(9) | 14.2592(9) | 104.476(10) | 80(5) | 0.2556(3) |
| 0.30 | 1.71 | 4.94 | 2.90455(6) | 14.2525(6) | 104.130(6) | 78(5) | 0.2560(2) |
| 0.25 | 1.01 | 4.20 | 2.90003(6) | 14.2432(6) | 103.739(6) | 63(3) | 0.2569(2) |
| 0.20 | 1.89 | 5.01 | 2.89593(4) | 14.2371(3) | 103.402(3) | 80(3) | 0.25674(12) |
| 0.15 | 1.36 | 3.75 | 2.89122(3) | 14.2267(3) | 102.990(4) | 70(3) | 0.25710(15) |
| 0.10 | 1.95 | 4.92 | 2.88800(2) | 14.22304(15) | 102.735(2) | 116(3) | 0.25761(9) |
| 0.05 | 1.81 | 5.01 | 2.88350(2) | 14.21127(12) | 102.330(1) | 163(4) | 0.25799(9) |
| 0.01 | 1.73 | 5.56 | 2.88115(1) | 14.20480(9) | 102.117(1) | 219(5) | 0.25833(9) |
| −0.01 | 1.84 | 5.90 | 2.87971(1) | 14.20166(9) | 101.992(1) | 253(6) | 0.25839(9) |
| −0.05 | 1.69 | 5.87 | 2.87771(1) | 14.19515(6) | 101.804(1) | 316(8) | 0.25848(9) |
Rietveld analysis can also provide information about the materials' microstructure when instrumental and sample contributions to peak broadening are properly deconvoluted.41,42 Here, we first characterised the instrument contribution to peak broading by measuring Na2Ca3Al2F14 and performing a Rietveld analysis including a Thompson–Cox–Hastings (TCHZ) pseudo-Voigt peak shape and axial divergence. The obtained parameters for the TCHZ peak shape and axial divergence were included as fixed values in subsequent refinements. This approach allowed to deconvolute angle-dependent Gaussian and Lorentzian contributions to the peak shape broadening (FWHM), which were interpreted as either originating from the coherent diffracting domain size (FWHM ∼ cos(θ)−1) and microstrain (FWHM ∼ tan(θ)). We used the coherent diffracting domain size to estimate the crystallite size (Dvol), which initially remains relatively constant in the range of 70 to 75 nm for 0.15 ≤ z ≤ 0.35, see Fig. 5a and b. Upon z < 0.15, the defect regime changes as described in the upcoming paragraphs on site occupancies and the crystallites size grows rapidly with a higher amount of Li equivalents (decreasing z), cumulating in a size of 316(8) nm at z = −0.05. The microstrain displays high values for high z values (Ni-rich end), which is greatly reduced once the threshold at z < 0.15 towards low z values (Li-rich regime) is reached, see Fig. 5c. These results are supported by visual observations and quantification of the primary particle size over the whole sample series via SEM. Samples in the 0.15 ≤ z ≤ 0.35 regime feature small, intergrown primary particles, which then grow into larger, well crystallized primary particles beyond z ≤ 0.1, see Fig. 2. This indicates a threshold for crystal growth around z < 0.15.
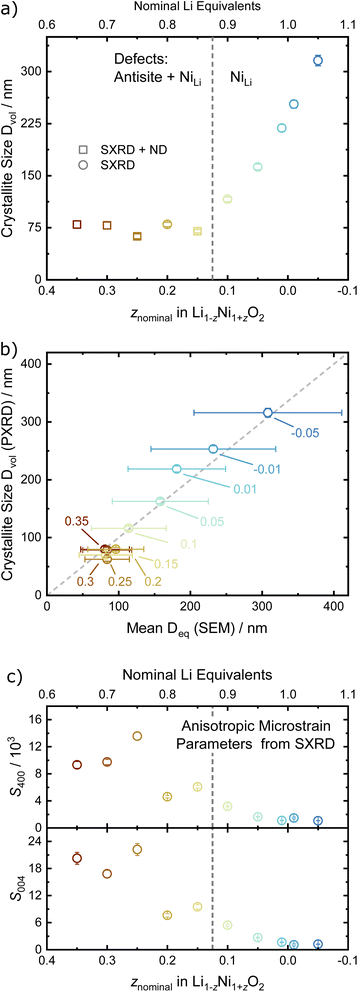 | ||
| Fig. 5 (a) Crystallite size Dvol in dependence of the off-stoichiometry parameter z, with the dashed line indicating a change in the defect regime as shown in Fig. 7a. (b) Comparison of the crystallite size Dvol from PXRD vs. the mean equivalent diameter Deq previously determined by SEM and (c) the S400 and S004 microstrain parameters from the Stephens model vs. z. If error bars not visible, they are smaller than the data symbol. | ||
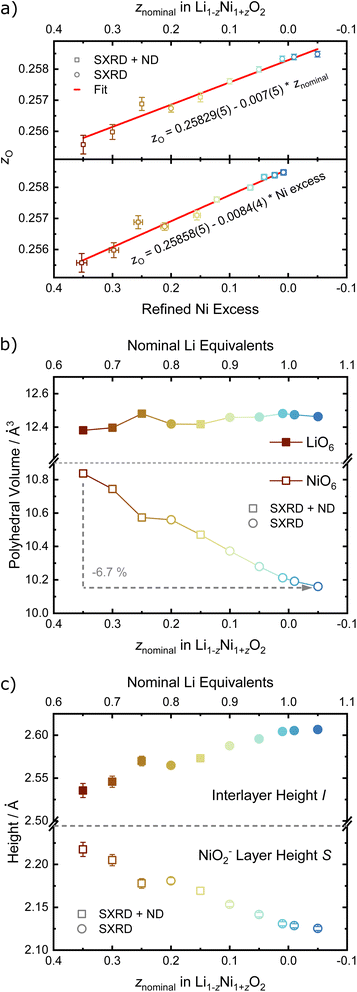
For the precise determination of atomic parameters, such as site occupancies, atomic coordinates, and atomic displacement parameters (ADPs), we utilize the complementary elemental contrast of SXRD and ND. The z-coordinate of oxygen, zO, is found to increase linearly with decreasing z, see Fig. 6a. In combination with the evolution of the lattice parameters, the change of zO affects the commonly used derived descriptors of the NiO2− layer height (S) and interlayer height (I), which are visualized in Fig. 1a, the bond distances d(Li–O) and d(Ni–O) as well as the volumes of the LiO6 and NiO6 polyhedra. The height of the NiO2− layer is defined as S = (2/3 − 2zO)c and decreases by about 0.1 Å from 2.22 Å for the sample Li0.65Ni1.35O2 (z = 0.35) to 2.12 Å in nearly stoichiometric LNO (z = −0.05). For the same sample range, the interlayer space I = (c/3 − S) accordingly increases from 2.54 to 2.62 Å. The descriptor S is highly correlated to the bond distance d(Ni–O) and the polyhedral volume NiO6, while I shows a weaker correlation to d(Li–O) and the polyhedral volume LiO6, as can be seen in Fig. 6b, c and Table 2. In general, the LiO6 polyhedral volume and Li–O distance barely change, while the NiO6 polyhedral volume and Ni–O distance strongly decrease, with d(Ni–O) starting at values close to NiO (d ≈ 2.09 Å (ref. 43)) and converging towards 1.97 Å with decreasing off-stoichiometry z due to the increasing average Ni oxidation state in nearly stoichiometric LNO. The trend in Ni oxidation state was detected via X-ray absorption spectroscopy on the Ni K edge (Fig. S4†), showing a successive oxidation of Ni with decreasing z in Li1−zNi1+zO2.
| z | d(Li–O)/Å | d(Ni–O)/Å | V(LiO6)/Å3 | V(NiO6)/Å3 | SOF NiLi (3b) | SOF LiNi (3a) | B iso Li (3b)/Å2 | B iso Ni (3a)/Å2 | B iso O (6c)/Å2 |
|---|---|---|---|---|---|---|---|---|---|
| 0.35 | 2.104(2) | 2.012(2) | 12.4626 | 10.1605 | 0.466(5) | 0.113(8) | 0.29(4) | 0.23(2) | 0.77(6) |
| 0.30 | 2.105(2) | 2.007(2) | 12.4734 | 10.1915 | 0.374(4) | 0.076(7) | 0.44(3) | 0.279(17) | 0.87(5) |
| 0.25 | 2.1106(17) | 1.9973(15) | 12.4805 | 10.2122 | 0.300(3) | 0.044(7) | 0.38(4) | 0.268(15) | 0.79(5) |
| 0.20 | 2.1072(11) | 1.9961(10) | 12.4602 | 10.2798 | 0.245(2) | 0.034(6) | 0.49(3) | 0.272(12) | 0.82(4) |
| 0.15 | 2.1075(13) | 1.9907(11) | 12.4574 | 10.3726 | 0.179(2) | 0.023(6) | 0.54(4) | 0.290(11) | 0.86(4) |
| 0.10 | 2.1105(8) | 1.9848(7) | 12.417 | 10.4698 | 0.1333(14) | 0.011(5) | 0.62(4) | 0.2957(8) | 0.78(3) |
| 0.05 | 2.1109(7) | 1.9794(7) | 12.4184 | 10.5599 | 0.0764(13) | 0.012(5) | 0.75(5) | 0.2882(8) | 0.81(3) |
| 0.01 | 2.1125(7) | 1.9754(6) | 12.4795 | 10.5735 | 0.0505(12) | 0.010(5) | 0.81(6) | 0.296(8) | 0.80(3) |
| −0.01 | 2.1122(7) | 1.9741(6) | 12.3961 | 10.7439 | 0.0372(12) | 0.014(5) | 0.88(7) | 0.307(8) | 0.83(3) |
| −0.05 | 2.1116(7) | 1.9722(6) | 12.3802 | 10.8367 | 0.0237(12) | 0.016(5) | 0.92(7) | 0.306(7) | 0.82(3) |
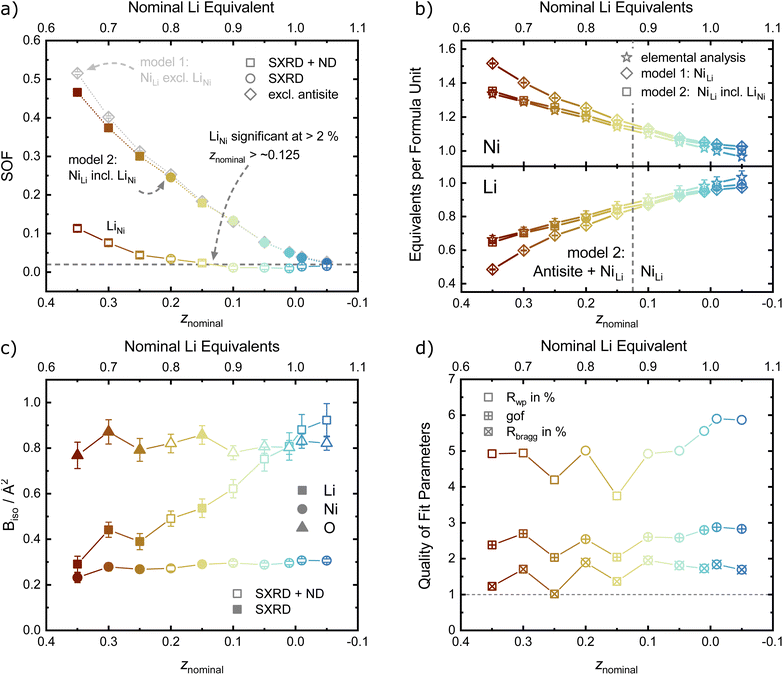
For the site occupancies of the Ni (3a), Li (3b) and O (6c) sites, different hypothesis were implemented and evaluated based on improvement of figure of merit parameters (Rwp, goodness of fit as gof, RBragg),41 number of parameters used per refinement and chemical reasoning. The free refinement of the oxygen site occupancy was also tested, and was found to converge towards 1 within the refinement error in all samples, suggesting the absence of any oxygen vacancies in these materials. The oxygen occupancy was thus set to 1 for all other refinement models in order to reduce the number of free parameters, and the metal sites were assumed to be fully occupied. For the occupancy of the metal sites, two defect models were compared in order to introduce a Ni excess in the unit cell with increasing z. The first model describes a fully occupied Ni site on 3a and a NiLi defect occupancy on the Li site (the so-called off-stoichiometry). The occupancy of Li on the 3b site was modelled as LiLi = 1 − NiLi and a shared atomic displacement parameter was used. This is the most commonly encountered model in published literature on LNO and similar compounds. In the second model, additional Ni was allowed on the Li site (LiLi = 1 − NiLi) as well as Li on the Ni site (NiNi = 1 − LiNi), so that the two occupancy defect parameters NiLi and LiNi were freely refined in parallel. In general, antisite defects appear when two different, neighboring atoms or ions exchange their lattice sites. Thus, the amount of LiNi matched by an equal amount of NiLi represents antisite defects in Li1−zNi1+zO2. Excess Ni is defined as Niexcess = NiLi − LiNi, which should approximately correspond to z as found by elemental analysis. In both models, NiLi increases with increasing off-stoichiometry z, as displayed in Fig. 7a. Yet, model 1 leads to unphysically low or even negative atomic displacement parameters on the Li site, hinting at issues with NiLi as the sole defect model. Upon inclusion of antisite defects by refinement of the LiNi occupancy on the Ni (3a) site, the Rwp and RBragg values for the data sets of z ≥ 0.15 decrease, indicating a better fit of the model. The effect is not significant in models with antisite defects below the limit of LiNi ≈ 2% (z < 0.15). This indicates that the inclusion of a single additional parameter is not responsible for the drop in R-values, but rather that there is a resolution limit to the refinement despite the availability of an additional scattering contrast from the neutron data sets. To further test this hypothesis, we compared the elemental composition obtained from the two refinement models with the composition obtained from chemical analysis, see Fig. 7b. A high correlation of the Ni and Li content obtained from inductively coupled plasma-optical emission spectroscopy (ICP-OES) and refinement model 2 (NiLi incl. LiNi) can be observed. Model 1 with only the NiLi occupancy defect on the other hand shows highly divergent behaviour at higher z values, which is hard to reconcile with quantities of elemental amounts found in our samples. Our results regarding antisite defects, the absence of oxygen vacancies, and the refinement improvement by using combined synchrotron X-ray and neutron data are aligned with a report by Yin et al. for a variety of isostructural Li1−zNi1−x−y+zCoxMnyO2 materials, as well as with the seminal study of Pouillerie et al.26,34 From this, we could confirm that a certain minimum amount of Ni2+ (z ≥ 0.15) is needed to sufficiently enlarge the Ni layer and allow a measurable amount of LiNi to be present. In addition to the described parameters, we also refined the atomic displacement parameters Biso, which are shown in Fig. 7c for Li, Ni and O. The values are fairly stable between Biso ≈ 0.23 to 0.3 Å2 for Ni and Biso ≈ 0.77 to 0.82 Å2 for O over the range of −0.05 ≤ z ≤ 0.35. The atomic displacement parameters of Li decrease with increasing z from around Biso ≈ 0.92 Å2 at z = −0.05 towards Biso ≈ 0.29 Å2 in Li0.65Ni1.35O2 (z = 0.35). This evolution is chemically intuitive, as increasing z statistically places additional, heavier Ni-ions (MWNi = 58.693 g mol−1vs. MWLi = 6.938 g mol−1) on the Li site, thus leading to an average lower displacement from the site at the same temperature. Overall, the observed values are physically meaningful and close to other values obtained in similar studies utilizing combined refinements against synchrotron X-ray and neutron data sets.34,35
Combining the observations from X-ray and neutron diffraction with SEM imaging points towards a correlation of LiNi defects with inhibited crystallite and particle growth and a high degree of microstrain in the lattice. The role of LiNi in the impeded layer growth could be rationalised thanks to LiNi acting as an observable for the average oxidation state of Ni in the NiO2 layer. In this hypothesis, LiNi can only reside in the Ni site (resolution limit ≤ 2 wt%) when the lattice has a minimum volume of the NiO6 octahedra at ≈10.4 Å3, which corresponds to a polyhedral volume ratio of 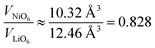 . In this case, the shrinkage of the NiO6 polyhedral volume with increasing oxidation state would allow to indirectly quantify LiNi. Additionally, one could rationalize the presented observations in a similar manner to the established Cabrera–Vermilyea theory on crystal growth inhibition.44 There, impurities act as stoppers by impinging step growth. Viewing the results of our studies through this lens, LiNi defects present for z ≥ 0.15 act as a growth inhibitor for the NiO2− layer based on the ionic Li–O bond disrupting the formation of hybridized Ni–O bonds. On the other hand, one may also recognize that Li ions are likely to be the more mobile cations during the synthesis, hence samples with high z and little Li content have less ion diffusion hence less crystal growth. Either way, these findings also point to the importance of choosing the appropriate Li/Ni ratio when tailoring the size of the particles, in particular in two-steps synthesis aiming at preparing single crystalline cathode materials.45,46
. In this case, the shrinkage of the NiO6 polyhedral volume with increasing oxidation state would allow to indirectly quantify LiNi. Additionally, one could rationalize the presented observations in a similar manner to the established Cabrera–Vermilyea theory on crystal growth inhibition.44 There, impurities act as stoppers by impinging step growth. Viewing the results of our studies through this lens, LiNi defects present for z ≥ 0.15 act as a growth inhibitor for the NiO2− layer based on the ionic Li–O bond disrupting the formation of hybridized Ni–O bonds. On the other hand, one may also recognize that Li ions are likely to be the more mobile cations during the synthesis, hence samples with high z and little Li content have less ion diffusion hence less crystal growth. Either way, these findings also point to the importance of choosing the appropriate Li/Ni ratio when tailoring the size of the particles, in particular in two-steps synthesis aiming at preparing single crystalline cathode materials.45,46
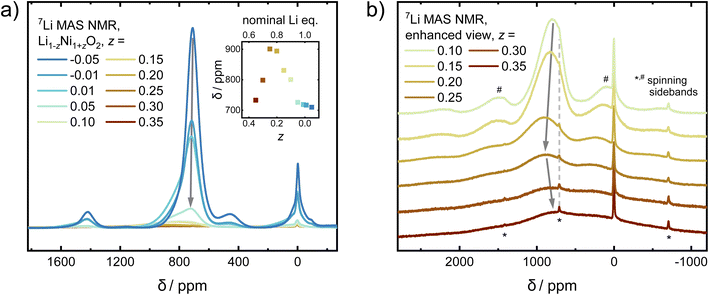
In order to probe changes to the local environment, ex situ7Li MAS NMR spectra of the Li1−zNi1+zO2 sample series were measured and are displayed in Fig. 8a and b. For ideal LiNiO2, there is only one Li+ local environment, i.e. Li+ is surrounded by 12 Ni3+ (3d7, S = 1/2) within the two neighbouring NiO2− layers. Six of them are linked to Li+via 90° oxygen bonds and the other six via 180° oxygen bonds.47 In off-stoichiometric Li1−zNi1+zO2, Ni2+ also resides on the Li site, leading to potentially more than 12 Ni surrounding a Li+ ion and an increased number of 90° Ni–O–Li bonds. Changing the oxidation state from Ni3+ to Ni2+ (3d8, S = 1; increasing z) creates different, statistically distributed local environments, which leads to Ni–O–Li bond angle dependent peak shift and broadening of the signal. The hyperfine shifts and thus peak position are sensitive to the Ni–O–Li bond angle and Ni oxidation state. The values for the shift contributions were determined for the model compound LiNi0.02Co0.96Mn0.02O2 with highly diluted Ni and Mn ions by Zeng et al.48 and are useful to explain trends in Ni-rich NCM compositions, as observed by Märker et al. for LiNi0.8Co0.1Mn0.1O2.49 When one Ni3+ at 180° Ni–O–Li bond (+110 ppm) is replaced by one Ni2+ (+170 ppm), the original signal will move to higher ppm positions by 60 ppm. In the 90° Ni–O–Li bond, reducing Ni3+ (−15 ppm) to Ni2+ (−30 ppm) only provides a minor contribution of −15 ppm to the peak shifts. In our sample series, corresponding shifts in the peak positions can be observed. From −0.05 ≤ z ≤ 0.20, the peaks shift towards higher ppm values, as 180° Ni–O–Li bonds dominate. As more and more Ni2+ resides in the Li+ layer, Li+ should be influenced by Ni–O–Li 90° bonds with increasing NiLi. This hypothesis could explain the strong decrease in the ppm values for samples in the range of 0.25 ≤ z ≤ 0.35.
In addition to changes in the peak position, there is a correlation of the peaks' FWHM and the stoichiometry of the samples. Different ratios of Ni![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) Li on the local scale give rise to various possible environments. The FWHM is expected to be narrow for a uniform environment, which in the present case is a single Li+ ion surrounded by 12 Ni3+. Once samples are less stoichiometric (increasing z), there is a statistical distribution of signals arising from Li+ ions from the various sites and environments. With an increasing z, the distribution becomes broader, leading to a massive increase in FWHM. This is what we observe in our samples, where the broadest peaks observed for 0.25 ≤ z ≤ 0.35 cover the range of approximately 2000 to −1000 ppm.
Li on the local scale give rise to various possible environments. The FWHM is expected to be narrow for a uniform environment, which in the present case is a single Li+ ion surrounded by 12 Ni3+. Once samples are less stoichiometric (increasing z), there is a statistical distribution of signals arising from Li+ ions from the various sites and environments. With an increasing z, the distribution becomes broader, leading to a massive increase in FWHM. This is what we observe in our samples, where the broadest peaks observed for 0.25 ≤ z ≤ 0.35 cover the range of approximately 2000 to −1000 ppm.
Aside from the main peaks, some other, minor bands can be observed in the NMR spectra. There is also a small, broad peak observed at 450 ppm, which carries 5.6%, 3.0%, and 2.5% of the intensity of the main peak for z = −0.05, −0.01, and 0.01, respectively, before completely diminishing. There are two common, yet opposing explanations found in the literature regarding its origin. A recent study argues that Li+ in the Ni layer close to Ni4+ (3d6, S = 0) would produce such a shift.23 The most extreme cases were described for a system Li1−zNi1+zO2 from 0 ≤ z ≤ −0.33. There, ordering of Li+ in the Ni layer increases closer to z = −0.33, leading to peak shifts from 450 ppm in z ≈ 0 towards about 250–300 ppm in z = −0.33 (Li1.33Ni0.66O2 ≡ Li2NiO3). As our diffraction data does not indicate a well-ordered structure with a high amount of Li+ in the Ni layer, the signal could originate from a small amount of a solid solution of LiNiO2–Li2NiO3−δ with ≤2% Li+ excess on the local scale, which would be below the resolution limit of our diffraction study. This hypothesis is further strengthened by the fact that the NMR data from LiNiO2 prepared by low temperature ion exchange from well-ordered NaNiO2 (no Li+ in the Ni layer) does not show a peak at 450 ppm.21 The second explanation for the 450 ppm peak commonly encountered in the literature assumes the presence of a Ni1−xLixO, rock salt type phase with a large amount of Ni2+.50 If present, the prominent cubic phase reflection 200 would be expected at 2θ ≈ 23.0° (e.g. Ni0.8Li0.2O)39 at the wavelengths utilized in this study (λ = 0.825888 Å). However, as no peaks are observed in that region, we exclude the presence of a rock salt type phase. The last remaining, sharp and narrow peak at 0 ppm originates from diamagnetic impurities such as LiOH, which were also found via X-ray and neutron diffraction in this and others studies.51
Overall, there are three regimes which give rise to different observations via NMR: the highly off-stoichiometric Li1−zNi1+zO2 regime (I) from z = 0.35 to 0.25, where 90° Ni–O–Li bonds dominate the signal and lead to a decreasing peak position as well as strongly increasing line width of the main NMR signal with increasing z. In the slightly off-stoichiometric Li1−zNi1+zO2 regime (II) with z reaching from 0.2 to 0.05, Li+ ions within LNO are surrounded by an increasingly uniform environment with decreasing z. There, 180° Ni–O–Li bonds dominate and lead to a decrease in the peak position and a sharpening of the FWHM with lower off-stoichiometry. In the nearly stoichiometric regime (III) from z = 0.01 to −0.05, peak intensity and FWHM are at their maximum and minimum, respectively, as the environment of the Li+ ions is the most homogeneous. In addition, a secondary peak arises which increases in intensity with increasing Li content.
Another possible probe, highly sensitive to structural order and inhomogeneities in battery materials, is the study of magnetic properties, which have been intensely reported in LiNiO2.52–55 Nearly stoichiometric Li1−zNi1+zO2 has been described as a glassy antiferromagnet, which features ferromagnetic intralayer coupling and weakly antiferromagnetic coupling between different NiO2− layers.56 With increasing off-stoichiometry, Ni2+ resides on the Li site, leading to local magnetic coupling between neighboring layers via small ferrimagnetic clusters. In order to characterise our samples, we measure the cusp in the magnetic susceptibility vs. T curve as a proximate to the magnetic ordering transition and the low-temperature magnetization as a function of an applied magnetic field. The magnetic transition temperature measured under zero field cooled conditions changes with composition, ranging from 10 to 247 K in our data, very similar to the data of Barton et al. as displayed in Fig. 9.53 In a simplified picture, it was assumed that increasing the amount of NiLi beyond a critical threshold leads to the formation of ferrimagnetic clusters.52 Prior studies hypothesized that long-range antiferromagnetic ordering in a composition of the [LixNi1−x]Li[Ni]NiO2 type is superseded by short-range, strongly ferrimagnetic behavior in disordered [Lix/2Ni(1−x)/2]Li[Lix/2Ni(1−x)/2]NiO2 at 0.1 ≤ z ≤ 0.15 (ref. 53) based on the change in the remanent magnetization MR. We investigated the low-temperature magnetization behavior at 2 K between −7 T ≤ μ0H ≤ 7 T and observe hysteresis loops, indicating the behavior suggested by Barton et al. The resulting data are presented as an inset in Fig. 9, with the raw data hysteresis loops displayed in the ESI Fig. S4 and S5.† In our samples, a similar correlation between composition, remanent magnetization and magnetic transition temperature has been observed. The high angular resolution X-ray and neutron diffraction data indicates that the bulk presence of NiLi as well as antisite defects ≥2% coincides with the transition to a strongly ferrimagnetic coupled material as postulated by B. T. Barton et al.53 The stoichiometry dependent peak in the remanent magnetization also matches the maximum of the predicted magnetization per ion found by J. B. Goodenough et al. at x ≈ 0.43 for LixNi1−2x2+Nix3+O (z ≈ 0.14 in Li0.86Ni1.14O2).55 Thus, our diffraction results hint at a possible mechanistic explanation and map the border for the transition of the bulk structure: the ordered regime exists until z ≥ 0.15 (x ≤ (1 − z)/2 ≈ 0.425). Afterwards, the Li incorporates into the Ni layer, which possibly separates the ferrimagnetic clusters. The presented data points towards a possible starting point of future studies for enhancing the understanding of Li1−zNi1+zO2 fundamental magnetic properties.
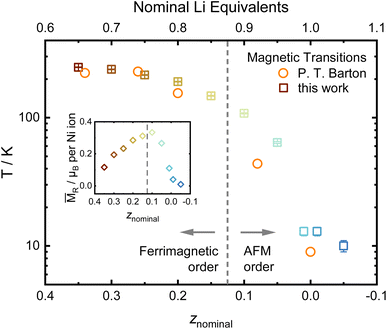 | ||
| Fig. 9 Evolution of the magnetic ordering temperature determined from the maxima in ZFC curves and data from P. T. Barton et al.,53 including the remanent magnetization MRvs. composition as an inset. | ||
Conclusion
Our study maps the rhombohedral phase space of the Li-ion battery cathode active material Li1−zNi1+zO2 with −0.05 ≤ z ≤ 0.35 and reports the correlation of stoichiometry, observed crystal defects, particle growth and magnetic properties. The increase in crystallite size strongly correlates with an increasing LiOH![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) Ni(OH)2 ratio once the off-stoichiometry parameter z is <0.15, as shown by SEM and SXRD. This suggests the presence of LiNi defects for z ≥ 0.15 coincides with an inhibited growth of NiO2 layer and LNO crystallization in general. The high angular resolution of SXRD with complementary ND indicates a continuous evolution of lattice parameters and derived metrics, yet delivers new information on the occupancies based on the difference in scattering factor for X-rays and neutrons. Specifically, we observe that the physical meaningful model includes NiLi occupancy defects as well as antisite defects for z ≥ 0.15. While the former is often included in refinement models observed in the literature, the antisite defects are not. However, the difference between the two models is only significant for z ≥ 0.15, while below that value both models accurately reproduce the diffraction data within error of the refinement. Our results suggest that Li deficiency leads to an incomplete separation of lithium and nickel into different crystallographic sites during the transition from cubic Ni1−xLixO to layered Li1−zNi1+zO2, leading to antisite defects and NiLi for z ≥ 0.15. On the local level, NMR suggests the existence of three regimes: (I) a highly disordered, Ni2+ rich environment (0.25 ≤ z ≤ 0.35), (II) a single-phase regime with increasing order around Li+ (0.05 ≤ z ≤ 0.2) and (III) a two-phase environment in the highly stoichiometric regime (−0.05 ≤ z ≤ 0.01), hinting at the presence of a small amount of highly disordered LiNiO2–Li2NiO3 solid solution. Finally, the threshold of LiNi defects also coincides with the transition from antiferromagnetic behavior in low z LNO to strong ferrimagnetism in disordered LNO. Hence, LiNi defects could play a role in localizing magnetic interactions within the NiO2 layer. Our detailed examination of the correlation between stoichiometry, defects, crystal growth, and related properties in rhombohedral Li1−zNi1+zO2 thus opens new avenues for manipulating and improving the cathode materials LNO and its Co- and Mn-containing derivatives.
Ni(OH)2 ratio once the off-stoichiometry parameter z is <0.15, as shown by SEM and SXRD. This suggests the presence of LiNi defects for z ≥ 0.15 coincides with an inhibited growth of NiO2 layer and LNO crystallization in general. The high angular resolution of SXRD with complementary ND indicates a continuous evolution of lattice parameters and derived metrics, yet delivers new information on the occupancies based on the difference in scattering factor for X-rays and neutrons. Specifically, we observe that the physical meaningful model includes NiLi occupancy defects as well as antisite defects for z ≥ 0.15. While the former is often included in refinement models observed in the literature, the antisite defects are not. However, the difference between the two models is only significant for z ≥ 0.15, while below that value both models accurately reproduce the diffraction data within error of the refinement. Our results suggest that Li deficiency leads to an incomplete separation of lithium and nickel into different crystallographic sites during the transition from cubic Ni1−xLixO to layered Li1−zNi1+zO2, leading to antisite defects and NiLi for z ≥ 0.15. On the local level, NMR suggests the existence of three regimes: (I) a highly disordered, Ni2+ rich environment (0.25 ≤ z ≤ 0.35), (II) a single-phase regime with increasing order around Li+ (0.05 ≤ z ≤ 0.2) and (III) a two-phase environment in the highly stoichiometric regime (−0.05 ≤ z ≤ 0.01), hinting at the presence of a small amount of highly disordered LiNiO2–Li2NiO3 solid solution. Finally, the threshold of LiNi defects also coincides with the transition from antiferromagnetic behavior in low z LNO to strong ferrimagnetism in disordered LNO. Hence, LiNi defects could play a role in localizing magnetic interactions within the NiO2 layer. Our detailed examination of the correlation between stoichiometry, defects, crystal growth, and related properties in rhombohedral Li1−zNi1+zO2 thus opens new avenues for manipulating and improving the cathode materials LNO and its Co- and Mn-containing derivatives.
Experimental
Synthesis
Li1−zNi1+zO2 was synthesized from the starting materials Ni(OH)2 (D50 = 11.8 μm, BASF SE, Germany), LiOH·H2O (BASF SE, Germany) in a high-temperature reaction under gas flow with z values ranging from −0.05 to 0.35. The reactants were dry mixed in a laboratory blender for 30 min under Ar atmosphere in the required ratios with a 1 mol% excess of LiOH·H2O. The reactant mixtures were calcined in an alumina crucible under an O2 flow of two volume exchanges per hour in a tube furnace (Nabertherm P330) with heating and cooling ramps of 3 K min−1. The samples were annealed at 700 °C for 6 h, and the furnace was then allowed to cool naturally.Diffraction
Synchrotron XRD data were collected on the BL04-MSPD beamline at the ALBA Synchrotron, Spain.57,58 Powder patterns were collected in Debye–Scherer mode geometry using the one-dimensional silicon-based position-sensitive detector MYTHEN, enabling fast data acquisition with excellent statistics and high angular resolution. Data were collected in the angular range 0.4° < 2θ < 57° (Q range 0.0708–9.671 Å−1) at a wavelength of λ = 0.825888(3) Å. The wavelength was determined using a NIST Si 640c SRM. The instrumental contribution to the peak broadening was determined by measuring a crystalline Na2Ca3Al2F14:CaF2 (NAC) sample as a line broadening reference in a 0.5 mm diameter borosilicate capillary and modelled via Thompson–Cox–Hastings pseudo-Voigt functions. An overall acquisition time of 5 minutes was used to measure each sample, which were packed in 0.5 mm diameter borosilicate glass capillaries. Neutron diffraction (ND) data were acquired on the D2B high-resolution powder diffractometer of the Institute Laue-Langevin (Grenoble, France), at a wavelength of 1.594 Å, calibrated with a Na2Ca3Al2F14 reference.59 Samples were loaded into cylindrical vanadium cans of diameter 10 mm and data were collected in the 10° < 2θ < 160° angular range. Rietveld refinement was performed using Topas v6 (Bruker AXS). Combined refinements against the X-ray and neutron data were performed for samples with z = −0.05, −0.01, 0.01, 0.05, 0.1 and 0.2, the remaining samples were investigated using synchrotron X-ray data only. The measured intensities of X-ray and neutron data were weighted according to their experimental uncertainties with 1/σ(Yobs).2 The background was fitted to the data using a Chebyshev polynomial function with 11 terms for X-ray and 7 terms for neutron data. During combined refinements, the lattice parameters, size broadening and microstrain contributions were refined vs. X-ray data, while the unit cell content (atomic coordinates, SOFs and ADPs) were refined vs. X-ray and neutron data. For refinements, scale factor, zero shift, crystallite size and anisotropic strain broadening parameters based on the Stephens model60 were allowed to vary. In the structural model, the unit cell parameters, the oxygen z coordinate, site occupancy factors (SOFs) and the isotropic atomic displacement parameters Biso for each site were refined. Two site occupancy defects, Ni occupancy on the Li site and antisite defects were refined. Atoms occupying the same site were constrained to have the same Biso, and SOFs were constrained such that each site remained fully occupied. Previous studies have shown that systematic errors in refinement of XRD data from layered cathode materials can be corrected by choosing specific form factors34 or representing them as linear combinations of a charged and uncharged state.35 In our refinements, we chose the form factors of Li+, Ni2+ and O2− in order to represent the electron density in the unit cell.Peak shapes were modelled in a double Voigt approach including Gaussian and Lorentzian contributions. The width of the peaks in the synchrotron data evolving with 2θ as cos(θ)−1 were interpreted as crystallite size broadening. Crystallite size is reported as the volume-weighted average column height (Dvol) calculated via 1/integral breadth (Gaussian & Lorentzian contribution).41 Broadening contributions with Voigt components that follow a tan(θ) evolution were interpreted as microstrain and analyzed via the phenomenological model described by Stephens.60 The model allows the description of anisotropic strain parameters Shkl, which are symmetry restricted and related to the variance of the spacing of lattice planes along certain hkl directions. Thus, a higher number of local defects on certain hkl lattice planes increases Shkl. Both crystallite size and microstrain broadening contributions were determined from the X-ray data during initial LeBail fits, fixed and re-refined towards the end of the refinement process. Critical parameters affecting the intensity apart from the choice of the structure factor are the oxygen z-coordinate (zO), occupancy of excess Ni2+ on the Li site NiLi, antisite defect concentration as well as the isotropic atomic displacement parameters Biso and were refined in this order from X-ray and neutron data, where neutron data was available. Antisite defects are defined as an exchange of a pair of Li and Ni ions from their respective layers into the other layer.24 The average antisite defect occupancy was modelled by a free, parallel refinement of defect occupancies of Li+ on the Ni site (LiNi) and Ni2+ on the Li site (NiLi) and evaluated by the reduction in Rwp and the comparison of the overall composition to values measured in elemental analysis.
Elemental analysis
The Li, Ni, and O content of the samples was determined via inductively coupled plasma-optical emission spectroscopy (ICP-OES) using a Thermo Fischer Scientific iCAP 7600 DUO. The mass fraction was determined from three independent measurements. About 10 mg of the samples was dissolved in 6 mL of hydrochloric acid and 2 mL of nitric acid at 353 K for 4 h in a graphite oven. The digestions were diluted, and analysis of the elements was accomplished with four different calibration solutions and an internal standard (Sc). The range of the calibration solutions did not exceed a decade. Two or three wavelengths of elements were used for calculation. The O content was analyzed by carrier gas hot extraction (CGHE) using a commercial oxygen/nitrogen analyser TC600 (LECO). The O concentration was calibrated with the certified standard KED 1025, a steel powder from ALPHA. The standards and samples were weighed with a mass in the range from 1–2 mg together with 5 mg of graphite in Sn crucibles (9–10 mm) and wrapped. Together with a Sn pellet, the wrapped samples were put into a Ni crucible and loaded in an outgassed (6300 W) double-graphite crucible. The measurements took place at 5800 W. The evolving gases, CO2 and CO, were swept out by He as inert carrier gas and measured by infrared detectors.Nuclear magnetic resonance
7Li magic-angle spinning (MAS) NMR experiments were conducted on a Bruker Avance 200 MHz spectrometer at a magnetic field of 4.7 T. Spectra were acquired at a Larmor frequency of 77.8 MHz with 1.3 mm rotors and spinning at 55 kHz. A rotor-synchronized Hahn-echo pulse sequence (90°–τ–180°–τ–acquisition) was used with a 90° pulse length of 0.85 μs and a recycle delay of 1 s. The 7Li NMR shifts were referenced using an aqueous 1 M LiCl solution (0 ppm). All spectra were normalized with respect to sample mass and the number of scans.Electron microscopy
The morphology of the samples was investigated utilizing a Merlin thermal field emission scanning electron microscope (FESEM, Carl Zeiss). Prior to the measurements, samples were glued onto conductive carbon pads and coated with an approximately 5 nm layer of Au0.8Pd0.2 using an EM ACE 600 coater (Leica). Images were segmented using the trainable WEKA segmentation algorithm in order to count the number of particles and measure their areas using Image2 (Fiji).61,62 Each segmentation was visually crosschecked in order to avoid counting artefacts. In this manner, at least three secondary particles and approximately 380 to 530 individual primary particles were characterized for good counting statistics. Pixel-count areas were transformed into physical units via magnification based calibration factors from the image metadata. Only particles of an area of at least 500 nm2 and a circularity (defined as 4πA/[perimeter]2) of ≥0.5 were used for counting statistics, similarly to a procedure described in the literature.20 The areas A of the particles with a circularity ≥0.5 were transformed into an equivalent diameter Deq of a circle of the same area using the formula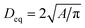 .
.
Magnetometry
DC magnetometry was measured using a Physical Property Measurement System (PPMS) DynaCool from Quantum Design equipped with a vibrating sample magnetometry (VSM) option. LNO powder was filled into polypropylene sample capsules (Quantum Design QDS-4096-388) in an Ar-filled glove box and transferred to the device. Zero-field cooled (ZFC) and field-cooled (FC) magnetization vs. temperature was measured at a magnetic field of 500 Oe from 2 to 390 K in temperature settle mode from 2 to 25 K and in sweep mode with 2 K min−1 from 25 to 390 K. The signal was averaged over 10 seconds for each measurement. Magnetization vs. field scans with maximum field of μ0H = ±7 T were measured at 2 K by first cooling the sample to 2 K in zero field before measuring a full loop (4 quadrants) starting at 7 T. For samples with z = −0.05 and −0.01, which included small amounts of diamagnetic impurity phases, only the LNO phase has been considered for data evaluation. Diamagnetic corrections were applied to all data, with −7.71 × 10−9 emu Oe−1 for the sample capsule and values for the atomic electronic closed shells by the incremental method as described by Lueken.63X-ray absorption spectroscopy
X-ray absorption spectroscopy (XAS) was performed at the XAS beamline of the KIT synchrotron in transmission mode with the IC Spec ionisation chamber. The measurements were undertaken inside a vacuum chamber to avoid contact with air/moisture and to maximize the signal-to-noise ratio. The samples were transferred with a sample transfer system. The position of the absorption edge was determined via the maximum in the first derivative.Conflicts of interest
There are no conflicts to declare.Acknowledgements
This work was partially supported by BASF SE. The authors acknowledge MSPD and the ALBA synchrotron for the beamtime awarded under proposal 2020094478 and D2B at Institut Laue-Langevin for neutron beamtime awarded under proposals 1-04-232 (https://doi.org/10.5291/ILL-DATA.1-04-232). We thank Dr Anna-Lena Hansen and Dr Marie Duffiet for insightful discussions. Bettina Hunzinger is acknowledged for acquisition of the SEM images. We thank Dr Thomas Bergfeldt (KIT's IAM-AWP-CA) and his group for elemental analysis.Notes and references
- Y. Luo, H. Wei, L. Tang, Y. Huang, Z. Wang, Z. He, C. Yan, J. Mao, K. Dai and J. Zheng, Nickel-Rich and Cobalt-Free Layered Oxide Cathode Materials for Lithium Ion Batteries, Energy Storage Mater., 2022, 50, 274–307, DOI:10.1016/j.ensm.2022.05.019.
- J. H. Yang, H. Kim and G. Ceder, Insights into Layered Oxide Cathodes for Rechargeable Batteries, Molecules, 2021, 26(11), 3173, DOI:10.3390/molecules26113173.
- W. Li, E. M. Erickson and A. Manthiram, High-Nickel Layered Oxide Cathodes for Lithium-Based Automotive Batteries, Nat. Energy, 2020, 5(1), 26–34, DOI:10.1038/s41560-019-0513-0.
- Q. Xie, Z. Cui and A. Manthiram, Unveiling the Stabilities of Nickel-Based Layered Oxide Cathodes at an Identical Degree of Delithiation in Lithium-Based Batteries, Adv. Mater., 2021, 33(32), 2100804, DOI:10.1002/adma.202100804.
- M. Bianchini, F. Fauth, P. Hartmann, T. Brezesinski and J. Janek, An in Situ Structural Study on the Synthesis and Decomposition of LiNiO2, J. Mater. Chem. A, 2020, 8(4), 1808–1820, 10.1039/C9TA12073D.
- C.-C. Chang and P. N. Kumta, Mechanochemical Synthesis of LiNiO2, Mater. Sci. Eng., B, 2005, 116(3), 341–345, DOI:10.1016/j.mseb.2004.05.042.
- D. Goonetilleke, A. Mazilkin, D. Weber, Y. Ma, F. Fauth, J. Janek, T. Brezesinski and M. Bianchini, Single Step Synthesis of W-Modified LiNiO2 Using an Ammonium Tungstate Flux, J. Mater. Chem. A, 2022, 10(14), 7841–7855, 10.1039/D1TA10568J.
- P. Kurzhals, F. Riewald, M. Bianchini, S. Ahmed, A. M. Kern, F. Walther, H. Sommer, K. Volz and J. Janek, Deeper Understanding of the Lithiation Reaction during the Synthesis of LiNiO2 Towards an Increased Production Throughput, J. Electrochem. Soc., 2022, 169(5), 050526, DOI:10.1149/1945-7111/ac6c0b.
- A. Mesnier and A. Manthiram, Synthesis of LiNiO2 at Moderate Oxygen Pressure and Long-Term Cyclability in Lithium-Ion Full Cells, ACS Appl. Mater. Interfaces, 2020, 12(47), 52826–52835, DOI:10.1021/acsami.0c16648.
- A. N. Mansour, Characterization of LiNiO2 by XPS, Surf. Sci. Spectra, 1994, 3(3), 279–286, DOI:10.1116/1.1247757.
- Y. Koyama, T. Mizoguchi, H. Ikeno and I. Tanaka, Electronic Structure of Lithium Nickel Oxides by Electron Energy Loss Spectroscopy, J. Phys. Chem. B, 2005, 109(21), 10749–10755, DOI:10.1021/jp050486b.
- J.-H. Chung, T. Proffen, S. Shamoto, A. M. Ghorayeb, L. Croguennec, W. Tian, B. C. Sales, R. Jin, D. Mandrus and T. Egami, Local Structure of LiNiO2 Studied by Neutron Diffraction, Phys. Rev. B: Condens. Matter Mater. Phys., 2005, 71(6), 064410, DOI:10.1103/PhysRevB.71.064410.
- M. E. Arroyo y de Dompablo and G. Ceder, On the Origin of the Monoclinic Distortion in LixNiO2, Chem. Mater., 2003, 15(1), 63–67, DOI:10.1021/cm020239+.
- J. N. Reimers, J. R. Dahn, J. E. Greedan, C. V. Stager, G. Liu, I. Davidson and U. Von Sacken, Spin Glass Behavior in the Frustrated Antiferromagnetic LiNiO2, J. Solid State Chem., 1993, 102(2), 542–552, DOI:10.1006/jssc.1993.1065.
- Y. Ma, J. H. Teo, D. Kitsche, T. Diemant, F. Strauss, Y. Ma, D. Goonetilleke, J. Janek, M. Bianchini and T. Brezesinski, Cycling Performance and Limitations of LiNiO2 in Solid-State Batteries, ACS Energy Lett., 2021, 6(9), 3020–3028, DOI:10.1021/acsenergylett.1c01447.
- V. Bianchi, S. Bach, C. Belhomme, J. Farcy, J. P. Pereira-Ramos, D. Caurant, N. Baffier and P. Willmann, Electrochemical Investigation of the Li Insertion–Extraction Reaction as a Function of Lithium Deficiency in Li1-xNi1+xO2, Electrochim. Acta, 2001, 46(7), 999–1011, DOI:10.1016/S0013-4686(00)00681-2.
- R. Kanno, H. Kubo, Y. Kawamoto, T. Kamiyama, F. Izumi, Y. Takeda and M. Takano, Phase Relationship and Lithium Deintercalation in Lithium Nickel Oxides, J. Solid State Chem., 1994, 110(2), 216–225, DOI:10.1006/jssc.1994.1162.
- H. Li, N. Zhang, J. Li and J. R. Dahn, Updating the Structure and Electrochemistry of LixNiO2 for 0 ≤ x ≤ 1, J. Electrochem. Soc., 2018, 165(13), A2985, DOI:10.1149/2.0381813jes.
- M. Bianchini, M. Roca-Ayats, P. Hartmann, T. Brezesinski and J. Janek, There and Back Again - The Journey of LiNiO2 as a Cathode Active Material, Angew. Chem., Int. Ed., 2019, 58(31), 10434–10458, DOI:10.1002/anie.201812472.
- F. Riewald, P. Kurzhals, M. Bianchini, H. Sommer, J. Janek and H. A. Gasteiger, The LiNiO2 Cathode Active Material: A Comprehensive Study of Calcination Conditions and Their Correlation with Physicochemical Properties Part II. Morphology, J. Electrochem. Soc., 2022, 169(2), 020529, DOI:10.1149/1945-7111/ac4bf3.
- L. Karger, D. Weber, D. Goonetilleke, A. Mazilkin, H. Li, R. Zhang, Y. Ma, S. Indris, A. Kondrakov, J. Janek and T. Brezesinski, Low-Temperature Ion Exchange Synthesis of Layered LiNiO2 Single Crystals with High Ordering, Chem. Mater., 2023, 35(2), 648–657, DOI:10.1021/acs.chemmater.2c03203.
- J. Akimoto and Y. Gotoh, Single Crystal Growth, Structure and Physical Property of LiCoO2 and LiNiO2, Mol. Cryst. Liq. Cryst. Sci. Technol., Sect. A, 2000, 341(2), 143–146, DOI:10.1080/10587250008026131.
- M. Bianchini, A. Schiele, S. Schweidler, S. Sicolo, F. Fauth, E. Suard, S. Indris, A. Mazilkin, P. Nagel, S. Schuppler, M. Merz, P. Hartmann, T. Brezesinski and J. Janek, From LiNiO2 to Li2NiO3: Synthesis, Structures and Electrochemical Mechanisms in Li-Rich Nickel Oxides, Chem. Mater., 2020, 32(21), 9211–9227, DOI:10.1021/acs.chemmater.0c02880.
- L. Yin, Z. Li, G. S. Mattei, J. Zheng, W. Zhao, F. Omenya, C. Fang, W. Li, J. Li, Q. Xie, E. M. Erickson, J.-G. G. Zhang, M. S. Whittingham, Y. S. Meng, A. Manthiram and P. G. Khalifah, Thermodynamics of Antisite Defects in Layered NMC Cathodes: Systematic Insights from High-Precision Powder Diffraction Analyses, Chem. Mater., 2020, 32(3), 1002–1010, DOI:10.1021/acs.chemmater.9b03646.
- P. Kalyani and N. Kalaiselvi, Various Aspects of LiNiO2 Chemistry: A Review, Sci. Technol. Adv. Mater., 2005, 6(6), 689, DOI:10.1016/j.stam.2005.06.001.
- C. Pouillerie, E. Suard and C. Delmas, Structural Characterization of Li1−z−xNi1+zO2 by Neutron Diffraction, J. Solid State Chem., 2001, 158(2), 187–197, DOI:10.1006/jssc.2001.9092.
- R. J. Green, H. Wadati, T. Z. Regier, A. J. Achkar, C. McMahon, J. P. Clancy, H. A. Dabkowska, B. D. Gaulin, G. A. Sawatzky and D. G. Hawthorn, Evidence for Bond-Disproportionation in LiNiO2 from X-Ray Absorption Spectroscopy, arXiv November 12, 2020, DOI:10.48550/arXiv.2011.06441.
- D. Carlier, M. Ménétrier, C. P. Grey, C. Delmas and G. Ceder, Understanding the NMR Shifts in Paramagnetic Transition Metal Oxides Using Density Functional Theory Calculations, Phys. Rev. B: Condens. Matter Mater. Phys., 2003, 67(17), 174103, DOI:10.1103/PhysRevB.67.174103.
- C. Chazel, M. Ménétrier, L. Croguennec and C. Delmas, 6/7Li NMR Study of the Li1-zNi1+zO2 Phases, Magn. Reson. Chem., 2005, 43(10), 849–857, DOI:10.1002/mrc.1639.
- M. E. Arroyo y de Dompablo, A. Van der Ven and G. Ceder, First-Principles Calculations of Lithium Ordering and Phase Stability on LixNiO2, Phys. Rev. B: Condens. Matter Mater. Phys., 2002, 66(6), 064112, DOI:10.1103/PhysRevB.66.064112.
- M. E. Arroyo y de Dompablo and G. Ceder, First-Principles Calculations on LixNiO2: Phase Stability and Monoclinic Distortion, J. Power Sources, 2003, 119–121, 654–657, DOI:10.1016/S0378-7753(03)00199-X.
- J. Kang and B. Han, First-Principles Study on the Thermal Stability of LiNiO2 Materials Coated by Amorphous Al2O3 with Atomic Layer Thickness, ACS Appl. Mater. Interfaces, 2015, 7(21), 11599–11603, DOI:10.1021/acsami.5b02572.
- S. Sicolo, M. Mock, M. Bianchini and K. Albe, And Yet It Moves: LiNiO2, a Dynamic Jahn–Teller System, Chem. Mater., 2020, 32(23), 10096–10103, DOI:10.1021/acs.chemmater.0c03442.
- L. Yin, G. S. Mattei, Z. Li, J. Zheng, W. Zhao, F. Omenya, C. Fang, W. Li, J. Li, Q. Xie, J. G. Zhang, M. S. Whittingham, Y. S. Meng, A. Manthiram and P. G. Khalifah, Extending the Limits of Powder Diffraction Analysis: Diffraction Parameter Space, Occupancy Defects, and Atomic Form Factors, Rev. Sci. Instrum., 2018, 89(9) DOI:10.1063/1.5044555.
- H. Liu, H. Liu, S. H. Lapidus, Y. S. Meng, P. J. Chupas and K. W. Chapman, Sensitivity and Limitations of Structures from X-Ray and Neutron-Based Diffraction Analyses of Transition Metal Oxide Lithium-Battery Electrodes, J. Electrochem. Soc., 2017, 164(9), A1802–A1811, DOI:10.1149/2.0271709jes.
- V. K. Peterson and G. J. Kearley, Neutron Applications in Materials for Energy: An Overview, in Neutron Applications in Materials for Energy, ed. G. J. Kearley and V. K. Peterson, Neutron Scattering Applications and Techniques, Springer International Publishing, Cham, 2015, pp. 1–9, DOI:10.1007/978-3-319-06656-1_1.
- D. Pritzl, T. Teufl, A. T. S. Freiberg, B. Strehle, J. Sicklinger, H. Sommer, P. Hartmann and H. A. Gasteiger, Washing of Nickel-Rich Cathode Materials for Lithium-Ion Batteries: Towards a Mechanistic Understanding, J. Electrochem. Soc., 2019, 166(16), A4056, DOI:10.1149/2.1351915JES.
- Y. Kim, H. Park, J. H. Warner and A. Manthiram, Unraveling the Intricacies of Residual Lithium in High-Ni Cathodes for Lithium-Ion Batteries, ACS Energy Lett., 2021, 6(3), 941–948, DOI:10.1021/acsenergylett.1c00086.
- I. Davidson, J. E. Greedan, U. von Sacken, C. A. Michal and J. R. Dahn, Structure of 1T-Li2NiO2 from Powder Neutron Diffraction, Solid State Ionics, 1991, 46(3), 243–247, DOI:10.1016/0167-2738(91)90222-W.
- R. D. Shannon, Revised Effective Ionic Radii and Systematic Studies of Interatomic Distances in Halides and Chalcogenides, Acta Crystallogr., Sect. A: Cryst. Phys., Diffr., Theor. Gen. Crystallogr., 1976, 32(5), 751–767, DOI:10.1107/S0567739476001551.
- R. E. Dinnebier, A. Leineweber and J. S. O. Evans, Rietveld Refinement - Practical Powder Diffraction Pattern Analysis Using TOPAS, De Gruyter, 2018, DOI:10.1515/9783110461381.
- J. A. Kaduk and J. Reid, Typical Values of Rietveld Instrument Profile Coefficients, Powder Diffr., 2011, 26(1), 88–93, DOI:10.1154/1.3548128.
- S. Sasaki, K. Fujino and Y. Takéuchi, X-Ray Determination of Electron-Density Distributions in Oxides, MgO, MnO, CoO, and NiO, and Atomic Scattering Factors of Their Constituent Atoms, Proc. Jpn. Acad., Ser. B, 1979, 55(2), 43–48, DOI:10.2183/pjab.55.43.
- N. Cabrera, D. Vermilyea, R. Doremus, B. Roberts and D. Turnbull, Growth and Perfection of Crystals, New York, 1958, p. 393 Search PubMed.
- A. Liu, N. Zhang, J. E. Stark, P. Arab, H. Li and J. R. Dahn, Synthesis of Co-Free Ni-Rich Single Crystal Positive Electrode Materials for Lithium Ion Batteries: Part I. Two-Step Lithiation Method for Al- or Mg-Doped LiNiO2, J. Electrochem. Soc., 2021, 168(4), 040531, DOI:10.1149/1945-7111/abf7e8.
- A. Liu, N. Zhang, J. E. Stark, P. Arab, H. Li and J. R. Dahn, Synthesis of Co-Free Ni-Rich Single Crystal Positive Electrode Materials for Lithium Ion Batteries: Part II. One-Step Lithiation Method of Mg-Doped LiNiO2, J. Electrochem. Soc., 2021, 168(5), 050506, DOI:10.1149/1945-7111/abf9c2.
- C. P. Grey and N. Dupré, NMR Studies of Cathode Materials for Lithium-Ion Rechargeable Batteries, Chem. Rev., 2004, 104(10), 4493–4512, DOI:10.1021/cr020734p.
- D. Zeng, J. Cabana, J. Bréger, W.-S. Yoon and C. P. Grey, Cation Ordering in Li[NixMnxCo(1–2x)]O2-Layered Cathode Materials: A Nuclear Magnetic Resonance (NMR), Pair Distribution Function, X-Ray Absorption Spectroscopy, and Electrochemical Study, Chem. Mater., 2007, 19(25), 6277–6289, DOI:10.1021/cm702241a.
- K. Märker, P. J. Reeves, C. Xu, K. J. Griffith and C. P. Grey, Evolution of Structure and Lithium Dynamics in LiNi0.8Mn0.1Co0.1O2 (NMC811) Cathodes during Electrochemical Cycling, Chem. Mater., 2019, 31(7), 2545–2554, DOI:10.1021/acs.chemmater.9b00140.
- U.-H. H. Kim, D.-W. W. Jun, K.-J. J. Park, Q. Zhang, P. Kaghazchi, D. Aurbach, D. T. Major, G. Goobes, M. Dixit, N. Leifer, C. M. Wang, P. Yan, D. Ahn, K.-H. H. Kim, C. S. Yoon and Y.-K. K. Sun, Pushing the Limit of Layered Transition Metal Oxide Cathodes for High-Energy Density Rechargeable Li Ion Batteries, Energy Environ. Sci., 2018, 11(5), 1271–1279, 10.1039/C8EE00227D.
- H. Li, W. Hua, X. Liu-Théato, Q. Fu, M. Desmau, A. Missyul, M. Knapp, H. Ehrenberg and S. Indris, New Insights into Lithium Hopping and Ordering in LiNiO2 Cathodes during Li (De)Intercalation, Chem. Mater., 2021, 33(24), 9546–9559, DOI:10.1021/acs.chemmater.1c02680.
- D. Mertz, Y. Ksari, F. Celestini, J. M. Debierre, A. Stepanov and C. Delmas, Magnetic Cluster Formation in LixNi1-xO Compounds: Experiments and Numerical Simulations, Phys. Rev. B: Condens. Matter Mater. Phys., 2000, 61(2), 1240–1245, DOI:10.1103/PhysRevB.61.1240.
- P. T. Barton, Y. D. Premchand, P. A. Chater, R. Seshadri and M. J. Rosseinsky, Chemical Inhomogeneity, Short-Range Order, and Magnetism in the LiNiO2-NiO Solid Solution, Chem.–Eur. J., 2013, 19(43), 14521–14531, DOI:10.1002/chem.201301451.
- N. A. Chernova, G. M. Nolis, F. O. Omenya, H. Zhou, Z. Li and M. Stanley Whittingham, What Can We Learn about Battery Materials from Their Magnetic Properties?, J. Mater. Chem., 2011, 21(27), 9865–9875, 10.1039/C1JM00024A.
- J. B. Goodenough, D. G. Wickham and W. J. Croft, Some Magnetic and Crystallographic Properties of the System Lix+Ni1−2x++Nix+++O, J. Phys. Chem. Solids, 1958, 5(1–2), 107–116, DOI:10.1016/0022-3697(58)90136-7.
- E. Chappel, M. D. Núñez-Regueiro, S. de Brion, G. Chouteau, V. Bianchi, D. Caurant and N. Baffier, Interlayer Magnetic Frustration in Quasistoichiometric Li1-xNi1+xO2, Phys. Rev. B: Condens. Matter Mater. Phys., 2002, 66(13), 132412, DOI:10.1103/PhysRevB.66.132412.
- F. Fauth, I. Peral, C. Popescu and M. Knapp, The New Material Science Powder Diffraction Beamline at ALBA Synchrotron, Powder Diffr., 2013, 28(S2), S360–S370, DOI:10.1017/S0885715613000900.
- F. Fauth, R. Boer, F. Gil-Ortiz, C. Popescu, O. Vallcorba, I. Peral, D. Fullà, J. Benach and J. Juanhuix, The Crystallography Stations at the Alba Synchrotron, Eur. Phys. J. Plus, 2015, 130(8), 160, DOI:10.1140/epjp/i2015-15160-y.
- G. Courbion and G. Ferey, Na2Ca3Al2F14: A New Example of a Structure with “Independent F-” - A New Method of Comparison between Fluorides and Oxides of Different Formula, J. Solid State Chem., 1988, 76(2), 426–431, DOI:10.1016/0022-4596(88)90239-3.
- P. W. Stephens, Phenomenological Model of Anisotropic Peak Broadening in Powder Diffraction, J. Appl. Crystallogr., 1999, 32(2), 281–289, DOI:10.1107/S0021889898006001.
- I. Arganda-Carreras, V. Kaynig, C. Rueden, K. W. Eliceiri, J. Schindelin, A. Cardona and H. Sebastian Seung, Trainable Weka Segmentation: A Machine Learning Tool for Microscopy Pixel Classification, Bioinformatics, 2017, 33(15), 2424–2426, DOI:10.1093/bioinformatics/btx180.
- J. Schindelin, I. Arganda-Carreras, E. Frise, V. Kaynig, M. Longair, T. Pietzsch, S. Preibisch, C. Rueden, S. Saalfeld, B. Schmid, J.-Y. Tinevez, D. J. White, V. Hartenstein, K. Eliceiri, P. Tomancak and A. Cardona, Fiji: An Open-Source Platform for Biological-Image Analysis, Nat. Methods, 2012, 9(7), 676–682, DOI:10.1038/nmeth.2019.
- H. Lueken, C. Elschenbroich, F. Hensel and H. Hopf, Magnetochemie, Teubner Studienbücher Chemie, Vieweg+Teubner Verlag, Wiesbaden, 1999, DOI:10.1007/978-3-322-80118-0.
Footnotes |
| † Electronic supplementary information (ESI) available. See DOI: https://doi.org/10.1039/d3ta01621h |
| ‡ Current Affiliation: Corporate Research and Development, Umicore, Watertorenstraat 33, 2250 Olen, Belgium. |
| § Equal author contribution. |
| ¶ Current affiliation: University of Bayreuth, Bavarian Center for Battery Technology (BayBatt), Universitätsstrasse 30, 95447 Bayreuth, Germany. |
| This journal is © The Royal Society of Chemistry 2023 |