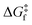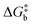Understanding kinetically controlled spin transitions in bistable spin crossover materials

Abstract

Spin crossover (SCO) materials can be kinetically trapped in a photo-excited metastable state in the so-called LIESST and reverse-LIESST processes. Under these conditions, SCO molecules are excellent light-responsive bistable molecular switches. However, above a certain temperature (T_LIESST and T_r-LIESST, respectively), the relaxation to the ground state becomes favorable and their bistability is suppressed. Understanding the mechanism of these processes, and being able to predict their kinetics, is key to designing SCO switches that are able to operate at room temperature. Herein, we reveal the mechanism of thermally induced spin transitions of the [Fe^II(1-bpp)₂]²⁺ SCO complex, and we predict its T_LIESST (as well as its T_1/2) with unprecedented accuracy. This is possible here thanks to the efficient reconstruction of the low-spin (LS, S = 0), high-spin (HS, S = 2) and intermediate (IS, S = 1) state Free energy surfaces (FESs) with ab initio and machine-learning methods, and the characterization of the minimum energy crossing points (MECPs) connecting those FESs. This approach paves the way for the systematic investigation of molecular features determining the mechanism of kinetically controlled transitions in SCO materials, as well as their temperature-dependent rate constants.

---

1. Introduction

The characterization and exploitation of the spin crossover (SCO) phenomenon has been one of the main adventures in chemistry in the last 30 years.^1–9 It refers to a reversible spin transition between states of different spin multiplicity, and is regarded as a molecular switch able to significantly modify the physical properties of the molecule (or crystal). Consequently, it has been exploited in multiple applications including displays, memories, sensors, detectors, contrast agents, refrigerators, and actuators,^10–14 and is currently investigated for their use in barocalorics,^15,16 thermal damping¹⁷ and explosives.¹⁸ Typically (but not exclusively^19–22), SCO materials are based on transition metals with Fe^II being the most common spin bearer.^1,5 The SCO transition can be triggered using several stimuli with temperature²³ and light^24,25 being the most widely employed (among others^26,27). In the first case, temperature exploits the larger entropy of the high spin (HS) state to revert the stability of relative states at T_1/2 (see Scheme 1). In the second case, light irradiation is applied to the most stable state (the low-spin state, LS) to trigger an isothermal SCO transition (green arrow, Scheme 1). When the metal is both the chromophore and the spin center, the process is called LIESST (Light-Induced Excited Spin State Trapping),^{23,25,28–30} and the transition to the HS state usually occurs in less than a picosecond.^31,32 This process, thus, combines a fast and selective input (i.e. light), with a potentially fast readout (e.g. magnetism), and hence could be applied in ultrafast data manipulation.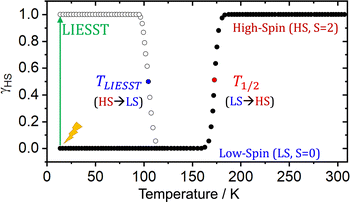

Scheme 1 Scheme of the thermally driven spin transition (LS → HS) characterized by T_1/2, and the LIESST (HS → LS) thermal relaxation characterized by T_LIESST, of a hypothetical SCO material.

The main fundamental problem for the exploitation of the LIESST transition in technological applications is that the bistability region exists only at very low temperatures. Above the so-called T_LIESST temperature, which is typically below 120 K,³³ the molecule relaxes back to its most stable LS state (see Scheme 1). Such a low temperature hinders the exploitation of the LIESST in technological applications. In recent years, the so-called “hidden” SCO materials have been identified as an alternative avenue to reach a bistable switch at higher temperatures.^34–36 In this class of materials, the HS is the most stable state along the whole range of temperatures, and a reverse-LIESST process can be induced upon light irradiation to populate the LS state. While in traditional SCO materials the LS state is extremely short-lived at moderate temperatures, hidden SCO materials can trap the metastable LS state for longer, effectively achieving a persistent switch that can be interconverted by light of different wavelengths. The maximum temperature at which this process can operate is the so-called reverse-LIESST temperature (T_r-LIESST).

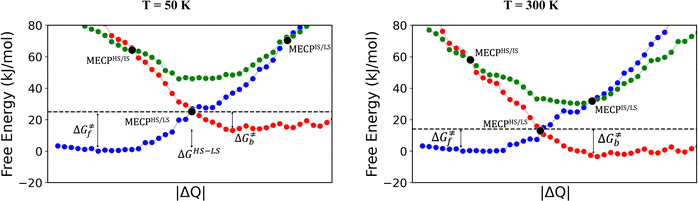
The rationale behind all these spin transitions (e.g. T_1/2, T_LIESST and T_r-LIESST) lies in the temperature evolution of the Free Energy Surfaces (FESs) of the states involved (see Fig. 1). T_1/2 can be understood as the lowest temperature at which both thermodynamic (ΔG^HS–LS < 0) and kinetic (surmountable 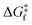) criteria are fulfilled, while T_LIESST and T_r-LIESST are the lowest temperature at which the kinetics (i.e., a surmountable 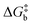or 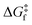) are fast enough so the relaxation (assuming favourable thermodynamics) can be recorded under predefined temperature and scan rates.³⁷ The standard procedure for T_LIESST characterization is irradiation at 10 K and a warming mode of 0.3 K min⁻¹.^25,30,38,44

Fig. 1 Computed free-energy surface (FES) of the (red) HS, (green) IS and (blue) LS states of 1 at (left) 50 K and (right) 300 K. For the sake of clarity, the FES along the complex n-dimensional space (n = 147) of Q values is projected into the norm of Q (|ΔQ|) connecting the LS and HS minima in the PES. The barriers associated with the forward (LS-to-HS) and backward (HS-to-LS) spin transitions for the direct pathway are shown as and , respectively.

The thermodynamic picture can be routinely evaluated with computations of the LS and HS minima, both in solution and solid state.^39–41 However, the incorporation of kinetic considerations is much more challenging (see below). As a result, these have been typically neglected when predicting or explaining SCO transitions, or when discussing the pathways and the barriers involved in those processes. This is a burden to understand the relationship between T_1/2 and T_LIESST beyond empirical relationships,^30,42–45 to make computational predictions of T_LIESST or T_r-LIESST, and ultimately, to design SCO materials with long-lived metastable spin states at room temperature.

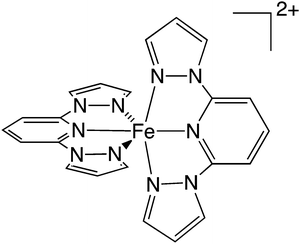
Herein, we solve this important shortcoming by incorporating kinetics into the description of SCO transitions. This enables us to characterize the thermal LS-to-HS SCO transition beyond the limited thermodynamic perspective and, most importantly, to gain access to the understanding and prediction of T_LIESST (or T_r-LIESST) in SCO materials. A protocol is described and applied here, as a proof of concept, to predict with great accuracy both T_1/2 and T_LIESST of the SCO complex [Fe^II(1-bpp)₂]²⁺ (1) (see Scheme 2). Our protocol (i) establishes the structure and energy of the Minimum Energy Crossing Points (MECPs) in the FES, (ii) identifies the states involved in the different spin transition mechanisms (thermal and LIESST), and (iii) defines the temperature regimes at which these transitions are thermodynamically and kinetically favoured. Overall, this protocol maps the macroscopic behaviour of SCO materials to the fundamental features in their spin state FES, thus enabling the rational design of systems with optimal spin transition temperatures.

Scheme 2 Representation of [Fe^II(1-bpp)₂]²⁺ (1)

2. Methodology

In adiabatic chemical reactions, the kinetics can be evaluated very accurately with transition state theory (TST), using the energies of the minima and of the transition state (TS).^46,47 In spin-forbidden reactions such as SCO transitions, TST can be directly applied only when the spin orbit coupling (SOC) is very strong.^48,49 When not, the concept of TS is replaced by the MECP, which are points where the two FESs cross or become nearly degenerate. At the MECP, the probability of hopping between FESs (p_sh) is maximum, and depends on several factors related to the topology of the two crossing FESs, and the strength of the SOC. In practice, p_sh behaves as a temperature-independent pre-factor to the TST expressions applied in chemical reactions.⁴⁸ Another practical simplification of studying adiabatic chemical reactions is that both the minima and the TS are zero-gradient points of the same potential energy surface (PES). Thus, search algorithms can be applied, and few computations suffice to identify those points, and to add thermal corrections to retrieve their free energies. In contrast, the computation of MECP leads to two associated problems. First, while constrained optimization algorithms have been designed to search for MECP^48,50 or conical intersections^51,52 connecting PESs, no equivalent exists (to the best of our knowledge) to search in FESs. However, working on the FES instead of the PES is key to capture the temperature-dependence of the minima (ΔG^HS–LS) and of the energy barriers (ΔG^‡) in SCO transitions. Second, given that MECPs are not zero-gradient points, it is not clear how the thermal corrections can be incorporated. Thus, estimating the kinetics of SCO transitions requires solving the fundamental problem of how to add thermal corrections outside zero-gradient points, and the more practical challenge of evaluating a sufficiently broad region of the multi-dimensional FES to identify the MECP.

In the proposed protocol, the FES of the LS, intermediate (IS) and HS states of 1 have been evaluated in the geometrical space between their minima. The 147-dimensional vibrational space of the LS state is compressed into a 5-dimensional grid. The four vibrational normal modes (VNM) that contribute more towards the stabilization of the HS and IS minima are selected as individual dimensions of the grid, and the 143 remaining VNM as an effective mode are included in a single dimension. This follows the philosophy of the effective-mode representation for the Linear Vibronic Coupling (LVC) model,⁵³ in which the full vibrational space is decomposed into a small number of relevant modes, and an additional residual mode.⁵⁴ In the case of 1, the relevant modes are (i) and (ii), two bending modes in which the tridentate ligands undergo the typical Jahn–Teller distortion reported in bpp-based SCO systems (ν^LS₁ and ν^LS₂),^55–58 (iii) a breathing mode in which all Fe–N distances are elongated (ν^LS₈), and (iv) a stretching mode involving the pyridine rings and the associated Fe–N(pyr) distances (ν^LS₂₄). The modes ν^LS₈ and ν^LS₂₄ have frequencies of 117 and 366 cm⁻¹, which lie in the energy range of the vibrational modes that drive the photoinduced LIESST in [Fe(bpy)₃]²⁺,^31,32 while ν^LS₁ and ν^LS₂ are mostly ligand-dependent and thus may play a different role in other SCO systems.

Initially, 1323 structures of the FES were generated. Each point of the grid is associated with one Q displacement coordinate for each VNM (Q_i). For each structure, the electronic enthalpy of the three states (H^l_elec, l = HS, IS, LS) is computed using ab initio methods (see Section S1, ESI†). Despite a large number of points (1323), this grid is too sparse to identify the MECP and, thus, to provide reliable estimates on the reaction kinetics (see Section S5, ESI†). Thus, a second grid is built, which encompasses the same dimensions and space as the first one but is much denser with a total of 26 208 points. At each point of this second grid, H^l_elec is evaluated using a machine learning (ML) model trained on the ab initio electronic enthalpies computed on the first grid (see the Computational details section) with a mean absolute error (MAE) below 1 kJ mol⁻¹. ML applications to PES predictions are increasingly common,^59,60 although not to describe spin transitions. After the evaluation of the second grid, we obtain a very detailed picture of the LS, IS and HS PES in the space where their free energies are likely to cross (see Section S6, ESI†).

On top of these PESs, the FESs are built by incorporating thermal corrections. These are based on the quantum harmonic oscillator expressions for the vibrational enthalpy (H^l_vib) and entropy (H^l_vib), which are usually applied only at zero-gradient points of the PES (e.g. minima). Instead, here we apply these corrections along the entire PES. To do so, the contribution of each VNM to the vibrational enthalpy (H^l_vib,i) is weighted by a factor (f^l_i) that depends on Q_i (see Section S1, ESI†), and the vibrational frequencies obtained at the minima (ν^l_i) are replaced by geometry-dependent effective frequencies (ν^l_eff,i) that account for anharmonicity deviations, with which the H^l_vib,i and S^l_vib contributions are evaluated (see Section S1, ESI†). Once the FES is built for the LS, IS and HS states, the points where the FESs cross are identified, and the MECP are used to compute the energy barrier (ΔG^‡) associated with the direct (HS ↔ LS) and indirect (HS ↔ IS ↔ LS) pathways. The barriers are then used to evaluate the rate constants using TST (k_D or k_I, respectively) and the associated half-life times, assuming a first-order reaction (τ_D and τ_I) (see Section S7, ESI† for a discussion on the selected parameters within TST). That is, the dependence of ΔG^‡ on temperature is converted into half-life times through the rate constants to obtain the temperature-evolution of τ_D and τ_I. The lowest temperatures at which τ_D or τ_I is less than 1 second (and have favourable thermodynamics) are considered as T_1/2 and T_LIESST. Notice that in this model T_LIESST is defined using a time scale, similar to the temperature scan rates used in the experimental setup.^25,30,38,44

3. Results and discussion

Minimum energy geometries

Existing protocols to obtain T_1/2 are typically based on the evaluation of the electronic and vibrational enthalpy (H_elec and H_vib) and entropy (S_elec and H_vib) contributions at the HS and LS minima. At the B3LYP*-D3BJ/Def2-SVP level, the difference in H_elec between the 1^HS and 1^IS minima with respect to 1^LS is 24.0 kJ mol⁻¹ and 44.5 kJ mol⁻¹, respectively (ΔH^HS–LS_elec and ΔH^IS–LS_elec). Using these values, together with the vibrational contributions and ΔS^HS–LS_elec = 13.4 J K⁻¹ mol⁻¹, we obtain that the thermal SCO transition of 1 (LS-to-HS) occurs at T_1/2 = 283 K, not far from the range of experimental T_1/2 reported for this complex in solution⁷⁷ (248 K) and in crystals based on 1 (ca. 259 K),⁶¹ and within the common error of T_1/2 predictions.^41,62,63 Considering that crystal packing effects are not significant for this compound (see Section S2, ESI†),^40,64,77 the good agreement between the gas-phase estimation of T_1/2 reported here and the experimental value is a genuine success of the electronic structure method. With this standard protocol, energy barriers are not evaluated, and thus a prediction of T_LIESST is not possible. To include kinetic effects in the picture, we now proceed to evaluate the FES in the region between the LS, IS, and HS state minima. As explained above, we search for the MECP at which the FES of the relevant states either cross or become nearly degenerate.

FES computation

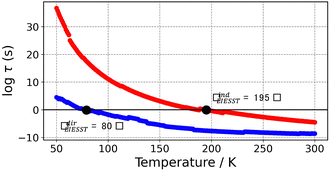
To visualize the multi-dimensional free energy surfaces, we projected them in one simplified dimension that mainly corresponds to the Fe–N breathing mode but incorporates all other VNM (Fig. 1). It can be seen that higher temperatures lead to a progressive stabilization of both the HS state and MECP^HS/LS, as well as an increase of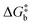 from ca. 15 kJ mol⁻¹ at T_LIESST, to 18 kJ mol⁻¹ at T_1/2 (i.e. 254 K), and up to ca. 25 kJ mol⁻¹ at 300 K. Despite such energy barrier increase, the direct LIESST mechanism has faster kinetics at higher temperatures due to the larger thermal energy, as described by TST. In comparison, the MECPs associated with the indirect LIESST mechanism (MECP^HS/IS and MECP^IS/LS) are located above ca. 30 kJ mol⁻¹ for the whole range of temperatures (see Fig. 1). Finally, the MECP^HS/LS also changes with temperature, moving towards more LS-like structures at higher temperatures, but retaining a structure that highly resembles the IS state minimum, albeit slightly more distorted (see Section S3, ESI† for details).

Thermal SCO transition

Using our protocol, which is summarized in the methodology section and detailed in Section S1 (ESI†), we retrieve T_1/2 ≈ 254 K for the forward spin transition (LS-to-HS), even closer to experimental values than with the standard protocol (283 K). The reason for the different T_1/2, prediction is that in the standard protocol, the thermal corrections are added to the enthalpy minimum, meaning that the FES and PES minima of a given state always coincide. In the new protocol, however, deviations from the harmonic oscillator behaviour slightly displace the FES minima with respect to the PES minima (average Fe–N distance changes of about 0.05 Å), which leads to a different T_1/2, prediction for 1. When it comes to the kinetics, the forward transition is kinetically accessible above 130 K for the direct pathway (LS → HS), and above 210 K for the indirect pathway (LS → IS → HS). However, given that the thermodynamics are not favourable until 254 K, the thermal SCO transition of 1 is delayed until this temperature (thermodynamic control). Interestingly, it must be noted that SCO systems typically display T_1/2 > 130 K. One potential explanation (if the computed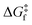 for 1 at 130 K could be extrapolated to other systems) is that the thermal LS-to-HS SCO transitions could be kinetically impeded at lower temperatures in some complexes. More investigations are necessary to confirm this point.

LIESST thermal relaxation

The thermal LIESST relaxation is explored starting at 50 K, above the low-temperature tunnelling regime.⁴³ At this temperature, our estimation is that the relaxation to the LS state would occur in ca. 10 hours (ca. 10⁴ seconds, see Fig. 2). As expected, faster kinetics are predicted as the temperature increases, until the second timescale is reached at 80 K. Thus, the protocol retrieves T_LIESST ≈ 80 K for the direct pathway (HS → LS), much lower than the ca. 195 K obtained for the indirect pathway (HS → IS → LS) (see Fig. 2). As mentioned before, these estimates are obtained using the same probability of surface hopping (p_sh = 1) for both pathways. Certainly, the two hops involved in the indirect pathway should both have a larger SOC (ca. 50–100 cm⁻¹) than the single hop of the direct pathway (1 cm⁻¹).⁶⁵ However, as discussed in Section S7 (ESI†), this difference does not overcome the 100 K difference in T_LIESST between both mechanisms. Therefore, our results indicate that the LIESST thermal relaxation of 1 proceeds from the HS to the LS state in a single step, without the intervention of the triplet IS. Interestingly, this is in contrast with the ultrafast LIESST relaxation after photo-excitation, for which experiments have unveiled the participation of the IS state.^78,79 In this case, the system is in an excited singlet state (LS*), with enough energy to access the manifold of triplet states and then decay to the HS (LS* → IS → HS). This extra energy is lacking in the thermal relaxation process, and hence the IS manifolds become inaccessible, and the direct mechanism (HS → LS) is chosen instead. Quantitatively, our estimation of T_LIESST ≈ 80 K under the direct pathway compares very well with the range of experimental T_LIESST reported for eight hydrated and anhydrous salts based on 1 (between 40 and 110 K, with most being around 75 K),³⁸ as well as for isopropyl-sulfanyl derivatives (80–95 K).⁶⁶

Fig. 2 Temperature-evolution of the half-life times associated with the direct (τ_D, blue) and indirect (τ_I, red) pathways for the HS-to-LS LIESST thermal relaxation. The T_LIESST associated with each pathway is defined as the temperature at which τ reaches the second timescale (i.e. the black line at log τ = 0).

Relationship between T_1/2 and T_LIESST

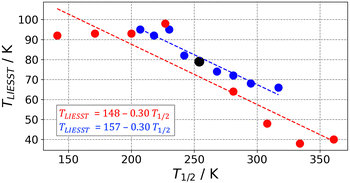
SCO complexes able to undergo LIESST have been classified in different linear T_1/2vs. T_LIESST empirical relationships depending on the denticity of their ligands.^30,44 This suggests that the origin of these so-called T₀ lines must be mainly molecular. To explain the molecular contribution to the T₀ lines, the rigidity of the coordination sphere has been proposed, and it has been related to the frequency of the breathing VNM.⁶⁷ This is in agreement with our results that the Fe–N breathing mode is the most important VNM to find the MECP. What remains to be seen is whether the rigidity depends exclusively on the ligand denticity or if any other ligand properties play a role. In other words, do different ligands with the same denticity always induce a similar amount of rigidity? This is a relevant question, as it would clarify whether different families of SCO systems with ligands of the same denticity should belong to the same T₀ line or not.

With the protocol presented here, it is possible to investigate the T_1/2vs. T_LIESST response of families of SCO systems. Within a given family, one would expect the individual complexes to have a very similar FES, with only small perturbations between them caused by chemical functionalization. Herein, we simulated these perturbations as a relative energy shift that is applied on top of the computed FES of the HS and IS states (the LS state FES is taken as a reference and remains unaffected). Two types of energy shifts have been considered, (i) a constant shift that applies to the whole FES, and simulates changes in the ligand-field strength, and (ii) a variable shift whose magnitude decreases linearly with |ΔQ| as it moves away from the respective H_elec minimum (i.e. it vanishes away from the minimum), thus simulating structure-dependent interactions such as crystal-packing effects. Notice that the main difference is that the latter type allows a shift in the position of the minima (i.e. a change of structure) as a response to the perturbation.

The application of each type of perturbation leads to two linear T_1/2vs. T_LIESST relationships (Fig. 3) with very similar parameters to the T₀ line expected for tri-dentate ligands (T₀ = 150 K and a = 0.3). Therefore, both the constant and variable shift strategies capture the expected relationship between the characteristic SCO temperatures, and thus the modulation of the MECP in response to energy changes. However, the validity of the T_1/2vs. T_LIESST linear relationships is questionable as in both the experimental and simulated correlations the deviation from linearity is noticeable, and the appearance of outliers is remarkable.²⁵ Particularly interesting is the change of the slope when applying a positive vs. negative constant perturbation (red points in Fig. 3). The stabilization of the HS surface rapidly brings T_LIESST to a maximum value of ca. 90 K that remains constant under stronger perturbations. This could be associated with the lack of SCO complexes with tridentate ligands displaying T_1/2 < 200 K and T_LIESST > 100 K reported in the literature.^25,30 Also, it highlights the difficulty to anticipate the displacement of MECP upon perturbation when high-dimension FES are explicitly considered. Further investigations are needed to determine whether the break of linearity and the T_LIESST saturation are common features of SCO complexes. Finally, the role of molecular and crystal packing effects in modulating the T_1/2vs. T_LIESST relationships beyond the linear trend is still under debate,^25,30 so it is not clear to what extent our molecular view connects with previous solid-state experimental measurements. Further work is needed to fully understand these relationships, and we expect the current protocol to help in this regard.

Fig. 3 Relationship between T_1/2 and T_LIESST under the application of a (red) constant or (blue) variable external perturbation on HS PES. From left to right, the points are obtained by applying a perturbation ranging from −8 to +8 kJ mol⁻¹ in steps of 2 kJ mol⁻¹. In black is the value without external perturbation. The dashed-lines indicate the best linear fits to each dataset, obtained with the inset parameters.

4. Conclusions

In summary, we have developed a computational protocol to incorporate kinetics into the description of spin transitions in SCO systems. This protocol consists of the explicit evaluation of the PESs of the LS, IS, and HS states in the region between their minima, and the approximate incorporation of thermal corrections to retrieve the FESs. The protocol is applied here to the SCO complex [Fe^II(1-bpp)₂]²⁺ (1) in the gas-phase, and predicts T_1/2 (254 K) and T_LIESST (80 K) that are extremely close to the range of experimental values commonly obtained for materials based on 1 (e.g. for [Fe(bpp)₂][BF₄]₂ these are 260 and 81 K).^{38,66,68–70} As expected, the LS-to-HS SCO transition is driven by thermodynamics. Interestingly, the reaction becomes kinetically accessible only above 130 K under a more favourable direct pathway (LS-to-HS). This suggests that for some SCO systems the thermal SCO transition might be kinetically blocked at low temperatures. Similarly, the indirect pathway becomes accessible at 210 K, which implies that both the direct and indirect pathways are accessible and potentially competitive above this temperature. Finally, our results indicate that the LIESST thermal relaxation (HS-to-LS) of 1 occurs through the direct pathway, without the intervention of the intermediate triplet state, since the MECPs connecting the triplet with the other spin states are much higher in energy.

Certainly, the combination of DFT methods and machine learning models offers a computationally affordable strategy to detect MECP, and obtain a reliable characterization of T_1/2 and T_LIESST (or T_r-LIESST) values for a series of SCO compounds, provided that their HS, IS and LS minima can be described within the same space of VNM. Thus, our protocol will enable the computational analysis of the inverse energy gap, the factors controlling it, and how to design better SCO systems. In addition, the possibility to disentangle kinetic and thermodynamic contributions is important to identify exotic SCO systems (e.g. class III systems in ref. 25). Overall, the combination of advanced physical models,⁶⁷ and atomistic approaches on real systems such as this one, will enable a better understanding of the T_1/2vs. T_LIESST empirical relationships governing SCO complexes. Particularly, to understand how the different T₀ lines are related to the MECP, and how this MECP relates to the VNM of complexes with different structures, chemical compositions, and denticities.

5. Computational details

The grid has been generated using the structure, frequencies and Hessian from the HS (S = 2), IS (S = 1) and LS (S = 0) minima of 1 computed at the B3LYP*-D3BJ/Def2-SVP level using Gaussian 16 (G16). The computation on H^l_elec at each point of the grid has been carried out at the same level. The B3LYP* functional is a modification of the B3LYP in which the HF-exchange percentage is reduced from 20% to 15%, and is specifically parametrized to model HS–LS energy differences (ΔH^HS–LS_elec) in Fe^II-based SCO systems.^71,72 While the accuracy of this functional to compute individual H^l_elec values is difficult to evaluate, the value of ΔH^HS–LS_elec is similar to the ones obtained in the past with other reliable computational methods (see Table S2, ESI†).^40,64 The same holds for the vibrational terms calculated from the VNM using eqn (S6) and (S7) (ESI†).

ML models have been trained separately for each spin state (l = HS, IS, and LS) using the geometries and the computed H^l_elec values of the ab initio grid. To that purpose, we have employed the Kernel Ridge Regression (KRR)⁷³ and the SLATM representation⁷⁴ as implemented in QML.⁷⁵ The model hyper-parameters (Kernel width, σ, and regularizer, λ) were determined on the training set using the Nelder–Mead optimization algorithm implemented in the SciPy library.⁷⁶ The error associated with the ML prediction of the relative spin state energies ΔH^HS–LS_elec and ΔH^IS–LS_elec is 0.5 and 0.6 kJ mol⁻¹, respectively (see Section S6, ESI†).

Conflicts of interest

There are no conflicts to declare.

Acknowledgements

S.V. and M.F. acknowledge funding from Beatriu de Pinós Projects 2020 BP 00043 and 2020 BP 00050, respectively. C.S. has been supported by the Spanish Ministerio de Ciencia y Universidades (MICIUN) (grant RTI2018-095460-B-I00), the Excellence María de Maeztu Program (grant MDM-2017-0767), and the Generalitat de Catalunya (grant 2017SGR13). The IQCTUB and the University of Barcelona are also acknowledged for computational resources.

Notes and references

1. P. Gütlich, Y. Garcia and H. A. Goodwin, Spin crossover phenomena in Fe(II) complexes, Chem. Soc. Rev., 2000, 29(6), 419–427,  10.1039/b003504l.
2. D. J. Harding, P. Harding and W. Phonsri, Spin crossover in iron(III) complexes, Coord. Chem. Rev., 2016, 313, 38–61,  DOI:10.1016/j.ccr.2016.01.006.
3. K. Senthil Kumar and M. Ruben, Emerging trends in spin crossover (SCO) based functional materials and devices, Coord. Chem. Rev., 2017, 346, 176–205,  DOI:10.1016/j.ccr.2017.03.024.
4. A. B. Gaspar and M. Seredyuk, Spin crossover in soft matter, Coord. Chem. Rev., 2014, 268, 41–58,  DOI:10.1016/j.ccr.2014.01.018.
5. G. Aromí, L. A. Barrios, O. Roubeau and P. Gamez, Triazoles and tetrazoles: Prime ligands to generate remarkable coordination materials, Coord. Chem. Rev., 2011, 255(5), 485–546,  DOI:10.1016/j.ccr.2010.10.038.
6. M. A. Halcrow, Structure: Function relationships in molecular spin-crossover complexes, Chem. Soc. Rev., 2011, 40(7), 4119–4142.
7. R. W. Hogue, S. Singh and S. Brooker, Spin crossover in discrete polynuclear iron(II) complexes, Chem. Soc. Rev., 2018, 47(19), 7303–7338,  10.1039/C7CS00835J.
8. A. Bousseksou, G. Molnar, L. Salmon and W. Nicolazzi, Molecular spin crossover phenomenon: Recent achievements and prospects, Chem. Soc. Rev., 2011, 40(6), 3313–3335,  10.1039/c1cs15042a.
9. L. Cambi and L. Szegö, Über die magnetische susceptibilität der komplexen verbindungen, Ber. Dtsch. Chem. Ges. A and B, 1931, 64(10), 2591–2598,  DOI:10.1002/cber.19310641002.
10. C. Lefter, V. Davesne, L. Salmon, G. Molnár, P. Demont, A. Rotaru and A. Bousseksou, Charge transport and electrical properties of spin crossover materials: Towards nanoelectronic and spintronic devices, Magnetochemistry, 2016, 2(1), 18.
11. G. Molnár, S. Rat, L. Salmon, W. Nicolazzi and A. Bousseksou, Spin crossover nanomaterials: From fundamental concepts to devices, Adv. Mater., 2018, 30(5), 1703862,  DOI:10.1002/adma.201703862.
12. H. J. Shepherd, I. A. Gural'skiy, C. M. Quintero, S. Tricard, L. Salmon, G. Molnár and A. Bousseksou, Molecular actuators driven by cooperative spin-state switching, Nat. Commun., 2013, 4,  DOI:10.1038/ncomms3607.
13. E. Resines-Urien, E. Burzurí, E. Fernandez-Bartolome, M. Á. García García-Tuñón, P. de la Presa, R. Poloni, S. J. Teat and J. S. Costa, A switchable iron-based coordination polymer toward reversible acetonitrile electro-optical readout, Chem. Sci., 2019, 10(27), 6612–6616,  10.1039/C9SC02522G.
14. R. N. Muller, L. van der Elst and S. Laurent, Spin transition molecular materials: Intelligent contrast agents for magnetic resonance imaging, J. Am. Chem. Soc., 2003, 125(27), 8405–8407,  DOI:10.1021/ja0349599.
15. K. G. Sandeman, Research update: The mechanocaloric potential of spin crossover compounds, APL Mater., 2016, 4(11), 111102,  DOI:10.1063/1.4967282.
16. S. P. Vallone, A. N. Tantillo, A. M. dos Santos, J. J. Molaison, R. Kulmaczewski, A. Chapoy, P. Ahmadi, M. A. Halcrow and K. G. Sandeman, Giant barocaloric effect at the spin crossover transition of a molecular crystal, Adv. Mater., 2019, 31(23), 1807334,  DOI:10.1002/adma.201807334.
17. K. Ridier, Y. Zhang, M. Piedrahita-Bello, C. M. Quintero, L. Salmon, G. Molnár, C. Bergaud and A. Bousseksou, Heat capacity and thermal damping properties of spin-crossover molecules: A new look at an old topic, Adv. Mater., 2020, 32(21), 2000987,  DOI:10.1002/adma.202000987.
18. T.-A. D. Nguyen, J. M. Veauthier, G. F. Angles-Tamayo, D. E. Chavez, E. Lapsheva, T. W. Myers, T. R. Nelson and E. J. Schelter, Correlating mechanical sensitivity with spin transition in the explosive spin crossover complex [Fe(Htrz)₃]_n[ClO₄]2_n, J. Am. Chem. Soc., 2020, 142(10), 4842–4851,  DOI:10.1021/jacs.9b13835.
19. K. Lekin, H. Phan, S. M. Winter, J. W. L. Wong, A. A. Leitch, D. Laniel, W. Yong, R. A. Secco, J. S. Tse, S. Desgreniers, P. A. Dube, M. Shatruk and R. T. Oakley, Heat, pressure and light-induced interconversion of bisdithiazolyl radicals and dimers, J. Am. Chem. Soc., 2014, 136(22), 8050–8062,  DOI:10.1021/ja502753t.
20. J. M. Rawson and J. J. Hayward, Spin Crossover Materials: Properties and Applications, Wiley, 2013.
21. R. G. Hicks, Switchable materials: A new spin on bistability, Nat. Chem., 2011, 3(3), 189–191.
22. L. Norel, J.-B. Rota, L.-M. Chamoreau, G. Pilet, V. Robert and C. Train, Spin transition and exchange interaction: Janus visions of supramolecular spin coupling between face-to-face verdazyl radicals, Angew. Chem., Int. Ed., 2011, 50(31), 7128–7131,  DOI:10.1002/anie.201101190.
23. P. Gütlich, A. Hauser and H. Spiering, Thermal and optical switching of iron(II) complexes, Angew. Chem., Int. Ed. Engl., 1994, 33(20), 2024–2054,  DOI:10.1002/anie.199420241.
24. W. Zhang, R. Alonso-Mori, U. Bergmann, C. Bressler, M. Chollet, A. Galler, W. Gawelda, R. G. Hadt, R. W. Hartsock, T. Kroll, K. S. Kjær, K. Kubiček, H. T. Lemke, H. W. Liang, D. A. Meyer, M. M. Nielsen, C. Purser, J. S. Robinson, E. I. Solomon, Z. Sun, D. Sokaras, T. B. van Driel, G. Vankó, T.-C. Weng, D. Zhu and K. J. Gaffney, Tracking excited-state charge and spin dynamics in iron coordination complexes, Nature, 2014, 509(7500), 345–348,  DOI:10.1038/nature13252.
25. G. Chastanet, C. Desplanches, C. Baldé, P. Rosa, M. Marchivie and P. Guionneau, A Critical review of the T(LIESST) temperature in spin crossover materials – what it is and what it is not, Chem. Sq., 2018, 2, 2,  DOI:10.28954/2018.csq.07.001.
26. S. Dhers, A. Mondal, D. Aguilà, J. Ramírez, S. Vela, P. Dechambenoit, M. Rouzières, J. R. Nitschke, R. Clérac and J.-M. Lehn, Spin State chemistry: Modulation of ligand pK_a by spin state switching in a [2 × 2] iron(II) grid-type complex, J. Am. Chem. Soc., 2018, 140(26), 8218–8227,  DOI:10.1021/jacs.8b03735.
27. G. D. Harzmann, R. Frisenda, H. S. J. van der Zant and M. Mayor, Single-molecule spin switch based on voltage-triggered distortion of the coordination sphere, Angew. Chem., Int. Ed., 2015, 54(45), 13425–13430,  DOI:10.1002/anie.201505447.
28. J. J. McGravey and I. Lawthers, Photochemically-induced perturbation of the 1A ⇌ 5T equilibrium in Fe¹¹ complexes by pulsed laser irradiation in the metal-to-ligand charge-transfer absorption band, J. Chem. Soc., Chem. Commun., 1982, 16, 906–907,  10.1039/C39820000906.
29. S. Decurtins, P. Gütlich, C. P. Köhler, H. Spiering and A. Hauser, Light-induced excited spin state trapping in a transition-metal complex: The hexa-1-propyltetrazole-iron(II) tetrafluoroborate spin-crossover system, Chem. Phys. Lett., 1984, 105(1), 1–4,  DOI:10.1016/0009-2614(84)80403-0.
30. J.-F. Letard, Photomagnetism of iron(II) spin crossover complexes-the T(LIESST) approach, J. Mater. Chem., 2006, 16(26), 2550–2559,  10.1039/B603473J.
31. G. Auböck and M. Chergui, Sub-50-Fs photoinduced spin crossover in [Fe(bpy)₃]²⁺, Nat. Chem., 2015, 7(8), 629–633,  DOI:10.1038/nchem.2305.
32. C. Sousa, C. de Graaf, A. Rudavskyi, R. Broer, J. Tatchen, M. Etinski and C. M. Marian, Ultrafast deactivation mechanism of the excited singlet in the light-induced spin crossover of [Fe(2,2′-bipyridine)₃]₂⁺, Chem. – Eur. J., 2013, 19(51), 17541–17551,  DOI:10.1002/chem.201302992.
33. G. Chastanet, M. Lorenc, R. Bertoni and C. Desplanches, Light-induced spin crossover—solution and solid-state processes, C. R. Chim, 2018, 21(12), 1075–1094,  DOI:10.1016/j.crci.2018.02.011.
34. P. Chakraborty, R. Bronisz, C. Besnard, L. Guénée, P. Pattison and A. Hauser, Persistent bidirectional optical switching in the 2D high-spin polymer {[Fe(bbtr)₃](BF₄)₂}_∞, J. Am. Chem. Soc., 2012, 134(9), 4049–4052,  DOI:10.1021/ja211897t.
35. E. Milin, V. Patinec, S. Triki, E. E. Bendeif, S. Pillet, M. Marchivie, G. Chastanet and K. Boukheddaden, Elastic frustration triggering photoinduced hidden hysteresis and multistability in a two-dimensional photoswitchable hofmann-like spin-crossover metal–organic framework, Inorg. Chem., 2016, 55(22), 11652–11661,  DOI:10.1021/acs.inorgchem.6b01081.
36. T. Boonprab, S. J. Lee, S. G. Telfer, K. S. Murray, W. Phonsri, G. Chastanet, E. Collet, E. Trzop, G. N. L. Jameson, P. Harding and D. J. Harding, The first observation of hidden hysteresis in an iron(III) spin-crossover complex, Angew. Chem., Int. Ed., 2019, 131(34), 11937–11941,  DOI:10.1002/ange.201907619.
37. Notice that, in the LIESST thermal relaxation, the final LS state is more stable than the metastable HS state. Therefore, the thermodynamic criterion is always fulfilled.
38. S. Marcén, L. Lecren, L. Capes, H. A. Goodwin and J.-F. Létard, Critical temperature of the LIESST effect in a series of hydrated and anhydrous complex salts [Fe(Bpp)₂]X₂, Chem. Phys. Lett., 2002, 358(1), 87–95,  DOI:10.1016/S0009-2614(02)00590-0.
39. H. Paulsen, V. Schünemann and J. A. Wolny, Progress in electronic structure calculations on spin-crossover complexes, Eur. J. Inorg. Chem., 2013,(5–6), 628–641,  DOI:10.1002/ejic.201201289.
40. S. Vela, M. Fumanal, J. Cirera and J. Ribas-Arino, Thermal spin crossover in Fe(II) and Fe(III). Accurate spin state energetics at the solid state, Phys. Chem. Chem. Phys., 2020, 22(9), 4938–4945,  10.1039/D0CP00162G.
41. J. Cirera and E. Ruiz, Computational modeling of transition temperatures in spin-crossover systems, Comments Inorg. Chem., 2019, 39(4), 216–241,  DOI:10.1080/02603594.2019.1608967.
42. A. Hauser, C. Enachescu, M. L. Daku, A. Vargas and N. Amstutz, Low-Temperature lifetimes of metastable high-spin states in spin-crossover and in low-spin iron(II) compounds: The rule and exceptions to the rule, Coord. Chem. Rev., 2006, 250(13), 1642–1652,  DOI:10.1016/j.ccr.2005.12.006.
43. A. Hauser, Intersystem Crossing in Fe(II) Coordination Compounds, Coord. Chem. Rev., 1991, 111, 275–290,  DOI:10.1016/0010-8545(91)84034-3.
44. J.-F. Létard, L. Capes, G. Chastanet, N. Moliner, S. Létard, J.-A. Real and O. Kahn, Critical temperature of the LIESST effect in iron(II) spin crossover compounds, Chem. Phys. Lett., 1999, 313(1–2), 115–120,  DOI:10.1016/S0009-2614(99)01036-2.
45. J.-F. Létard, P. Guionneau, O. Nguyen, J. S. Costa, S. Marcén, G. Chastanet, M. Marchivie and L. Goux-Capes, A Guideline to the design of molecular-based materials with long-lived photomagnetic lifetimes, Chem. – Eur. J., 2005, 11(16), 4582–4589,  DOI:10.1002/chem.200500112.
46. K. J. Laidler and M. C. Klng, The Development of Transition-State Theory, 1983, vol. 87.
47. J. L. Bao and D. G. Truhlar, Variational transition state theory: Theoretical framework and recent developments, Chem. Soc. Rev., 2017, 7548–7596,  10.1039/c7cs00602k.
48. J. N. Harvey, Understanding the kinetics of spin-forbidden chemical reactions, Phys. Chem. Chem. Phys., 2007, 9(3), 331–343,  10.1039/B614390C.
49. R. Poli and J. N. Harvey, Spin forbidden chemical reactions of transition metal compounds. new ideas and new computational challenges, Chem. Soc. Rev., 2003, 1–8,  10.1039/b200675h.
50. N. Aizawa, Y. Harabuchi, S. Maeda and Y. J. Pu, Kinetic Prediction of reverse intersystem crossing in organic donor–acceptor molecules, Nat. Commun., 2020, 11(1), 3909,  DOI:10.1038/s41467-020-17777-2.
51. B. G. Levine, J. D. Coe and T. J. Martínez, Optimizing conical intersections without derivative coupling vectors: Application to multistate multireference second-order perturbation theory (MS-CASPT2), J. Phys. Chem. B, 2008, 112(2), 405–413,  DOI:10.1021/jp0761618.
52. M. J. Bearpark, M. A. Robb and H. Bernhard Schlegel, A direct method for the location of the lowest energy point on a potential surface crossing, Chem. Phys. Lett., 1994, 223(3), 269–274,  DOI:10.1016/0009-2614(94)00433-1.
53. W. Popp, M. Polkehn, K. H. Hughes, R. Martinazzo and I. Burghardt, Vibronic coupling models for donor–acceptor aggregates using an effective-mode scheme: Application to mixed frenkel and charge-transfer excitons in oligothiophene aggregates, J. Chem. Phys., 2019, 150(24), 244114,  DOI:10.1063/1.5100529.
54. E. Gindensperger and L. S. Cederbaum, Quantum dynamics in macrosystems with several coupled electronic states: Hierarchy of effective hamiltonians, J. Chem. Phys., 2007, 127(12), 124107,  DOI:10.1063/1.2778682.
55. J. Elhaik, D. J. Evans, C. A. Kilner and M. A. Halcrow, A Structural, magnetic and mossbauer spectroscopic study of an unusual angular Jahn–Teller distortion in a series of high-spin iron(II) complexes, Dalton Trans., 2005, 1693–1700,  10.1039/b502175h.
56. C. Carbonera, C. A. Kilner, J.-F. Letard and M. A. Halcrow, Anion doping as a probe of cooperativity in the molecular spin-crossover compound [FeL₂][BF₄]₂ (L = 2,6-di{pyrazol-1-yl}pyridine), Dalton Trans., 2007, 1284–1292,  10.1039/b618480d.
57. J. M. Holland, J. A. McAllister, C. A. Kilner, M. Thornton-Pett, A. J. Bridgeman and M. A. Halcrow, Stereochemical effects on the spin-state transition shown by salts of [FeL₂]²⁺ [L = 2,6-di(pyrazol-1-yl)pyridine], Dalton Trans., 2002, 548–554,  10.1039/b108468m.
58. S. Vela, J. J. Novoa and J. Ribas-Arino, Insights into the crystal-packing effects on the spin crossover of [Fe^II(1-bpp)]²⁺-based materials, Phys. Chem. Chem. Phys., 2014, 16(48), 27012–27024,  10.1039/c4cp03971h.
59. G. Schmitz, I. H. Godtliebsen and O. Christiansen, Machine learning for potential energy surfaces: An extensive database and assessment of methods, J. Chem. Phys., 2019,(24), 244113,  DOI:10.1063/1.5100141.
60. P. O. Dral, A. Owens, A. Dral and G. Csányi, Hierarchical machine learning of potential energy surfaces, J. Chem. Phys., 2020, 152(20), 204110,  DOI:10.1063/5.0006498.
61. J. M. Holland, J. A. McAllister, Z. Lu, C. A. Kilner, M. Thornton-Pett and M. A. Halcrow, An unusual abrupt thermal spin-state transition in [FeL₂][BF₄]₂ [L = 2,6-di(pyrazol-1-yl)pyridine, Chem. Commun., 2001, 577–578,  10.1039/b100995h.
62. J. Cirera and F. Paesani, Theoretical prediction of spin-crossover temperatures in ligand-driven light-induced spin change systems, Inorg. Chem., 2012, 51(15), 8194–8201,  DOI:10.1021/ic300750c.
63. A. Rudavskyi, C. Sousa, C. de Graaf, R. W. A. Havenith and R. Broer, Computational approach to the study of thermal spin crossover phenomena, J. Chem. Phys., 2014, 140(18), 184318,  DOI:10.1063/1.4875695.
64. S. Vela, M. Fumanal, J. Ribas-Arino and V. Robert, Towards an accurate and computationally-efficient modelling of Fe(II)-based spin crossover materials, Phys. Chem. Chem. Phys., 2015, 17, 16306–16314,  10.1039/C5CP02502H.
65. C. Sousa, A. Domingo and C. de Graaf, Effect of second-order spin–orbit coupling on the interaction between spin states in spin-crossover systems, Chem. – Eur. J., 2018, 24(20), 5146–5152,  DOI:10.1002/chem.201704854.
66. R. Kulmaczewski, E. Trzop, E. Collet, S. Vela and M. A. Halcrow, Structure: Function relationships for thermal and light-induced spin-crossover in isomorphous molecular materials, J. Mater. Chem. C, 2020, 8(25), 8420–8429,  10.1039/d0tc02174a.
67. M. Nadeem, J. Cruddas, G. Ruzzi and B. J. Powell, Toward high-temperature light-induced spin-state trapping in spin-crossover materials: The interplay of collective and molecular effects, J. Am. Chem. Soc., 2022, 144(20), 9138–9148,  DOI:10.1021/jacs.2c03202.
68. V. A. Money, I. Radosavljevic Evans, M. A. Halcrow, A. E. Goeta and J. A. K. Howard, Light induced excited high spin-state trapping in [FeL₂](BF₄)₂ (L = 2,6-di(pyrazol-1-yl)pyridine, Chem. Commun., 2003, 158–159,  10.1039/B210146G.
69. M. A. Halcrow, Iron(II) complexes of 2,6-di(pyrazol-1-yl)pyridines—A versatile system for spin-crossover research, Coord. Chem. Rev., 2009, 253(21–22), 2493–2514,  DOI:10.1016/j.ccr.2009.07.009.
70. G. A. Craig, O. Roubeau and G. Aromí, Spin state switching in 2,6-bis(pyrazol-3-yl)pyridine (3-Bpp) based Fe(II) complexes, Coord. Chem. Rev., 2014, 269, 13–31,  DOI:10.1016/j.ccr.2014.02.002.
71. M. Reiher, Theoretical study of the Fe(phen)₂(NCS)₂ spin-crossover complex with reparametrized density functionals, Inorg. Chem., 2002, 41(25), 6928–6935,  DOI:10.1021/ic025891l.
72. M. Reiher, O. Salomon and B. Artur Hess, Reparameterization of hybrid functionals based on energy differences of states of different multiplicity, Theor. Chem. Acc., 2001, 107(1), 48–55,  DOI:10.1007/s00214-001-0300-3.
73. Z. Yuchen, D. John and W. Martin, Divide and Conquer Kernel Ridge Regression; PMLR, 2013, pp. 592–617.
74. A. S. Christensen, L. A. Bratholm, F. A. Faber and O. A. von Lilienfeld, FCHL revisited: Faster and more accurate quantum machine learning, J. Chem. Phys., 2020, 152(4), 44107,  DOI:10.1063/1.5126701.
75. A. S. Christensen, F. A. Faber, B. Huang, L. Bratholm, A. Tkatchenko, K.-R. Müller and O. von Lilienfeld, QML: A Python Toolkit for Quantum Machine Learning, 2017.
76. P. Virtanen, R. Gommers, T. E. Oliphant, M. Haberland, T. Reddy, D. Cournapeau, E. Burovski, P. Peterson, W. Weckesser, J. Bright, S. J. van der Walt, M. Brett, J. Wilson, K. J. Millman, N. Mayorov, A. R. J. Nelson, E. Jones, R. Kern, E. Larson, C. J. Carey, İ. Polat, Y. Feng, E. W. Moore, J. VanderPlas, D. Laxalde, J. Perktold, R. Cimrman, I. Henriksen, E. A. Quintero, C. R. Harris, A. M. Archibald, A. H. Ribeiro, F. Pedregosa, P. van Mulbregt, A. Vijaykumar, A. P. Bardelli, A. Rothberg, A. Hilboll, A. Kloeckner, A. Scopatz, A. Lee, A. Rokem, C. N. Woods, C. Fulton, C. Masson, C. Häggström, C. Fitzgerald, D. A. Nicholson, D. R. Hagen, D. v Pasechnik, E. Olivetti, E. Martin, E. Wieser, F. Silva, F. Lenders, F. Wilhelm, G. Young, G. A. Price, G. L. Ingold, G. E. Allen, G. R. Lee, H. Audren, I. Probst, J. P. Dietrich, J. Silterra, J. T. Webber, J. Slavič, J. Nothman, J. Buchner, J. Kulick, J. L. Schönberger, J. V. de Miranda Cardoso, J. Reimer, J. Harrington, J. L. C. Rodríguez, J. Nunez-Iglesias, J. Kuczynski, K. Tritz, M. Thoma, M. Newville, M. Kümmerer, M. Bolingbroke, M. Tartre, M. Pak, N. J. Smith, N. Nowaczyk, N. Shebanov, O. Pavlyk, P. A. Brodtkorb, P. Lee, R. T. McGibbon, R. Feldbauer, S. Lewis, S. Tygier, S. Sievert, S. Vigna, S. Peterson, S. More, T. Pudlik, T. Oshima, T. J. Pingel, T. P. Robitaille, T. Spura, T. R. Jones, T. Cera, T. Leslie, T. Zito, T. Krauss, U. Upadhyay, Y. O. Halchenko and Y. Vázquez-Baeza, SciPy 1.0: Fundamental algorithms for scientific computing in python, Nat Methods, 2020, 17(3), 261–272,  DOI:10.1038/s41592-019-0686-2.
77. M. Halcrow, I. Capel Berdiall, C. Pask and R. Kulmaczewski, Relationship between the molecular structure and switching temperature in a library of spin-crossover molecular materials, Inorg. Chem., 2019, 58(15), 9811–9821,  DOI:10.1021/acs.inorgchem.9b00843.
78. G. Auböck and M. Chergui, Sub-50 fs photoinduced spin crossover in [Fe(bpy)₃]²⁺, Nat. Chem., 2015, 7(8), 629–633,  DOI:10.1038/nchem.2305.
79. C. Sousa, C. de Graaf, A. Rudavskyi, R. Broer, J. Tatchen, M. Etinski and C. M. Marian, Ultrafast deactivation mechanism of the excited singlet in the light-induced spin crossover of [Fe(2,2′-bipyridine)₃]²⁺, Chem. – Eur. J., 2013, 19(51), 17541–17551,  DOI:10.1002/chem.201302992.

---

Footnote

† Electronic supplementary information (ESI) available. See DOI: https://doi.org/10.1039/d2tc04266e

---