Density functional theory study of hydrophobic zeolites for the removal of triclosan from aqueous solution

Abstract

The chlorinated biphenyl ether triclosan (TCS), used as a disinfectant in health care settings and in various personal care products, is an emerging organic contaminant of significant concern. Adsorption-based methods have been proposed as one potential pathway for the removal of TCS from wastewaters. Hydrophobic high-silica zeolites could constitute suitable adsorbent materials for such applications. In order to gauge the impact of pore size, topology, and framework composition, the adsorption of TCS in six different all-silica zeolites (AFI, BEA, CFI, FAU, IFR, MOR frameworks) and two highly siliceous protonated zeolites (H-FAU, H-MOR) was investigated using dispersion-corrected density functional theory (DFT). While pore size was found to affect the interaction strength, the rather flexible TCS molecule can adjust to different pore shapes, resulting in very similar adsorption energies for most all-silica zeolites. Although the interaction with TCS is enhanced in protonated zeolites, the affinity towards water increases even more. In DFT-based molecular dynamics simulations of TCS and water co-adsorption, H₂O molecules quickly replace TCS in the vicinity of the framework protons, deprotonating the framework and forming positively charged clusters. In addition to delivering atomic-level insights into TCS adsorption, the calculations indicate that a fine-tuning of pore size with a concurrent maximization of hydrophobicity should constitute a promising strategy to develop optimized zeolite adsorbents for TCS removal.

---

Environmental significance

Triclosan is widely employed as a disinfectant, antiseptic, and preservative agent. Besides uses in healthcare, TCS is also contained in a variety of consumer products, including soaps, deodorants, and toothpastes, as well as being incorporated in some textiles and household items. In an environmental context, TCS is considered as an emerging contaminant of concern. In addition to potential toxic and endocrine-disrupting effects to aquatic organisms, it may also contribute to the development of microbial resistance, with possible negative consequences for human health. TCS can enter the environment through various pathways, with reported removal efficiencies of conventional wastewater treatment facilities varying widely. As a result, TCS is frequently detected in surface, ground, and drinking water. The present study illustrates how state-of-the-art electronic structure calculations can help to understand the interaction of emerging contaminants with highly siliceous zeolites, which could find use in adsorption-based TCS removal.

Introduction

Pharmaceuticals and personal care products (PPCPs) have attracted considerable attention as emerging environmental contaminants.^1–3 Within this very diverse group of species with varying physico- and biochemical properties, the chlorinated biphenyl ether triclosan (C₁₂H₇Cl₃O₂, 5-chloro-2-(2,4-dichlorophenoxy)phenol, abbreviated to TCS or, less frequently, TCL) is often named as one species of particular concern.^4–7 Due to its antimicrobial and antifungal properties, TCS is not only used as a disinfectant in health care settings, but also in a large variety of personal care products, such as soaps, deodorants, or toothpastes, and as a preservative in household items.^7–9 Since potential risks to human health, including reproductive problems and enhanced risk of asthma and allergies, have been identified, the use of TCS in consumer products has been restricted in several countries.^7,9 Given the persistence of TCS, which is stable to hydrolysis at near-neutral pH values, it comes as no surprise that it is commonly found in wastewaters.^3,10–13 Incomplete removal of TCS by wastewater treatment facilities results in a significant discharge into the environment: in a global survey by the German Environment Agency (Umweltbundesamt), triclosan was listed among the 20 PPCP contaminants that were most frequently detected in surface water, groundwater, or drinking water.¹⁴ In the European Union, it has recently been proposed to add triclosan to a list of priority water pollutants requiring more stringent control measures (EU legislative procedure 2022/0344/COD).

A number of possible effects contribute to the environmental hazard potential of TCS. These include acute toxicity to aquatic organisms (however, at concentrations that are typically not reached in real-world scenarios¹⁵), chronic toxicity, and endocrine-disrupting effects.⁵ Moreover, the antimicrobial TCS may contribute to selection processes that are responsible for the development of antibiotic-resistant bacteria.^5,8,16 Due to the frequent presence of relatively low levels of antibiotics and disinfectants in wastewaters and wastewater treatment plants (WWTPs), these have been identified as “hot spots” for the development of microbial resistance.¹⁷ Hence, the occurrence of TCS in such environments should be a cause for concern, not only due to its potential environmental impact, but also with regard to possible, more indirect consequences for human health. Non-negligible amounts of TCS can also be found in soils amended with biosolids from wastewater treatment plants. Here, TCS and its degradation product methyltriclosan, formed during the wastewater treatment process, may accumulate in terrestrial organisms like earthworms.¹⁸ Other relevant degradation products include highly toxic chlorinated dioxins and chlorophenols, which are produced through photolytic degradation of TCS.^5,19

Starting with the work of McAvoy et al.,¹⁰ several authors have measured TCS concentrations in WWTP influents and effluents, and the results have been compiled in review articles^3,12 and databases.^14,20 While concentrations in effluents remain usually below 1 μg L⁻¹, a few studies reported values above 10 μg L⁻¹.¹¹ The reported removal efficiencies of conventional WWTPs also vary widely, ranging from removal rates below 50% to essentially complete removal.^12,13,21 Several advanced treatment methods that are under consideration for PPCP removal in general have also been studied for TCS removal in particular, including adsorption-based methods, advanced oxidation processes, and biodegradation. The advantages and drawbacks of individual methods have been discussed in recent reviews.^22,23

Due to the lipophilicity of TCS (log(K_ow) of 4.76 ²⁴), hydrophobic adsorbents appear as the most promising materials for the adsorption-based removal of TCS from aqueous solution. Activated carbons^25,26 and other carbon-based adsorbents like biochars²⁷ have been shown to exhibit high TCS removal efficiencies. Although hydrophobic high-silica zeolites are more expensive to produce than these materials, they possess some advantages, such as high thermal and chemical stability, allowing for regeneration under fairly harsh conditions,²⁸ reduced co-adsorption of natural organic matter,²⁹ and high affinities towards species that fit well into the ordered pore system of the zeolite.³⁰

Rossner et al. studied the removal of a “cocktail” of 25 organic contaminants, including TCS with an initial concentration of about 0.6 μg L⁻¹, from spiked lake water by two high-silica zeolites.²⁵ Whereas high-silica mordenite (MOR framework type³¹) showed essentially complete removal of TCS (along with various other species), FAU-type zeolite Y removed only about 45%. Since the FAU-type sample should be more hydrophobic due to its higher Si/Al ratio (Si/Al ≈ 400 as compared to Si/Al ≈ 110 for MOR), this difference cannot be attributed to the zeolite composition, but is more likely related to differences in pore size and topology: both zeolites have pore apertures outlined by 12-membered rings (12MRs) of tetrahedrally coordinated atoms, but the MOR framework possesses 1D channels with a diameter of about 6.5 Å, whereas the pore system of FAU consists of large supercages (diameter about 11 Å) connected by 12MR windows. More recently, Jiang et al. measured TCS adsorption isotherms (aqueous solution, concentrations ranging from ∼200 to ∼6000 μg L⁻¹) using zeolites with four different framework types:³² In addition to FAU- and MOR-type zeolites, zeolite beta (BEA framework, 12MR pore openings) and ZSM-5 (MFI framework, 10MR pore openings) were considered, and samples with different Si/Al ratios were compared for FAU, BEA, and MFI. Only negligible uptake was observed for MFI-type samples, indicating that the sizeable TCS molecules cannot diffuse through the 10MR windows. Among the other three zeolites, the highest TCS uptake of 378 mg g⁻¹ was observed for the most Si-rich FAU sample (Si/Al ≈ 400), and both maximum uptake and affinity towards TCS, determined via a Langmuir–Freundlich fit, decreased with decreasing Si/Al ratio. While still being appreciable, uptakes and affinities of BEA-type zeolites (Si/Al ratios from ∼80 to ∼300) and a MOR-type sample (Si/Al ≈ 110) were lower. In addition to these investigations of synthetic zeolites, TCS adsorption experiments were also performed on natural zeolites (clinoptilolites) modified with organic surfactants, which could be cheaper to produce.^33,34 It is, however, worth noting that maximal TCS loadings and affinities towards TCS reported in those works were considerably lower than for the best-performing high-silica zeolites studied by Jiang et al.³²

Computational modelling has become a very widely used tool in zeolite science.³⁵ Atomistic simulations at different levels of theory have been exploited for various purposes, e.g., to develop a deeper understanding of experimental observations, or to predict properties that were so far not characterized experimentally. With regard to PPCP removal, force field (FF) simulations were employed to compute the adsorption energies of 21 contaminants, including TCS, in all-silica MOR and FAU.³⁶ Despite the simplistic description of the interatomic interactions, a good correlation between FF adsorption energies and experimental removal efficiencies reported by Rossner et al.²⁵ was observed. This indicates that such simulations could be employed to predict zeolite adsorbents having a high affinity towards a given PPCP prior to an experimental characterization. Subsequently, the adsorption energies were recomputed using periodic electronic structure calculations in the framework of dispersion-corrected density functional theory (DFT) with the purpose of identifying suitable DFT approaches for the study of functional organic molecules in zeolites.³⁷ Several earlier DFT studies employed cluster models cut out from the zeolite structure in order to reduce the computational expense, with examples including investigations of sulfonamide antibiotics in all-silica FAU^38,39 and of salicylic acid, carbamazepine, and ciprofloxacin in cation-exchanged FAU.⁴⁰ With ongoing hardware and software developments, periodic calculations are now routinely feasible for unit cells of typical zeolites. A recent DFT investigation studied the adsorption of carbamazepine (CBZ) in eleven all-silica zeolites.⁴¹ In addition to the optimization of CBZ@Zeo adsorption complexes, DFT-based ab initio molecular dynamics (AIMD) simulations were carried out for selected zeolites to analyze the influence of temperature. Moreover, the role of guest–guest interactions was evaluated through an investigation of adsorbed CBZ dimers.

The present work addresses the adsorption of TCS in zeolites, employing, by and large, a similar approach as this previous study. As for CBZ, the investigation is restricted to zeolites having 12MR or 14MR pore openings, as experimental findings indicate that zeolites with smaller pores do not adsorb appreciable amounts of TCS.³² A somewhat smaller number of purely siliceous zeolite is considered here, including six, rather than eleven, frameworks. Apart from studying a different guest molecule, the present study goes beyond the previous work in the following respects: first, preliminary FF-based simulations are used to corroborate that TCS can diffuse through the pores of these zeolites. Second, the focus is no longer exclusively on all-silica zeolites, but models of highly siliceous, protonated zeolites are also considered for FAU and MOR topologies. Third, the co-adsorption of water, neglected in the previous study, is investigated for selected systems. In addition to providing atomic-level insights into TCS adsorption, the calculations allow predictions how pore size, pore shape, and framework composition affect the performance of hydrophobic zeolites as adsorbents for TCS removal.

Computational details

Structure of guest molecules

The molecular structure of TCS was taken from a previous X-ray diffraction study.⁴² In the crystal structure, the TCS hydroxyl groups simultaneously act as hydrogen bond donors and acceptors, resulting in one-dimensional chains of hydrogen-bonded TCS molecules. Moreover, the phenyl rings of neighboring molecules interact through π–π stacking interactions. Since it can be expected that the equilibrium molecular structure will be considerably different in the absence of intermolecular interactions, a conformational screening was carried out, using the Materials Studio (MS) Conformer module and the pcff force field⁴³ (see ESI, Table S1† for pcff parameters). Local energy minima were re-optimized using DFT calculations with the CP2K code (see subsection on DFT calculations for further details). In the lowest-energy conformer identified on the basis of these calculations, the hydroxyl group forms an intramolecular hydrogen bond to the central oxygen atom O_c (Fig. 1, r(H_h⋯O_c) = 2.181 Å). A vibrational calculation confirmed the absence of imaginary frequencies. The DFT-calculated electrostatic potential (bottom panel of Fig. 1) shows the comparatively strong positive polarization of the H_h proton of the hydroxyl group, which exceeds that of other positively polarized areas of the molecule (aromatic protons). This TCS conformer was used as reference for the calculation of adsorption energies and as starting point for the generation of TCS@Zeo adsorption complexes.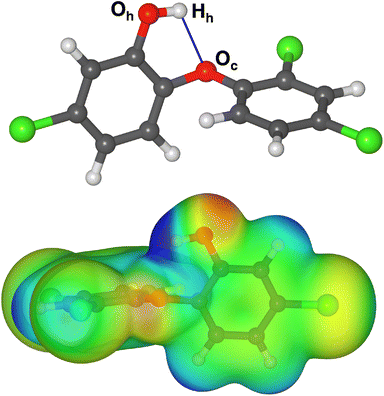

Fig. 1 (Top) DFT-optimized structure of triclosan (color code: red = O, grey = C, green = Cl, white = H). Labels of atoms that are of particular relevance in the analysis of hydrogen bonds are given, and the intramolecular hydrogen bond is shown as blue line. (Bottom) DFT-computed electrostatic potential plotted on a DFT electron density isosurface. The TCS molecule is rotated with respect to the top panel to better visualize key features of the ESP. Structure figures were prepared using VESTA.⁴⁶

The structure of the H₂O molecule was first optimized using pcff and then re-optimized with DFT, using the same settings as for TCS. As discussed in more detail in the Results section, there is little point in comparing adsorption energies obtained for single water molecules to those of one TCS molecule per cell due to the vast difference in molecular size. For the case of protonated zeolites, experimental results and prior DFT studies indicate that an adsorption of clusters of several H₂O molecules, which are large enough to deprotonate the framework, is energetically favored over the adsorption of single H₂O molecules at the framework protons.^44,45 Therefore, calculations aimed at a comparison of TCS and water adsorption considered clusters of eight H₂O molecules. To study energetic trends among (H₂O)_N clusters of different size, additional calculations were done for models with N = 1, 4, and 12.

Zeolite structures

The structures of the six all-silica zeolites (BEA, FAU, AFI, IFR, MOR, CFI frameworks, represented by the framework type codes [FTC] assigned in the structure database of the International Zeolite Associations IZA³¹) are the same as in previous work (Table 1).⁴¹ Sources of the experimental structure data and the corresponding cell parameters are given in the ESI (Table S2†). As described in more detail in previous work, short AIMD simulations were run for all zeolite structures (NVT ensemble, T = 298 K, timestep 1 fs, total duration 12.5 ps). The average structure from the production stage of the AIMD simulation (10 ps) was then subjected to a symmetry search and DFT-optimized.

Table 1 Zeolites considered in this study. Cell content refers to the supercell used in the calculations. FD corresponds to the framework density. The last column reports the diameters of the largest included sphere d_LIS and the largest diffusing sphere d_LDS, taken from the IZA database³¹

	Material	Pore system	Cell content	FD [T atoms per 1000 Å^3]	d LIS/dLDS [Å]
BEA	Pure-silica beta^47,48	12MR, 3D	Si256O512	15.6	6.7/6.0
FAU	Siliceous zeolite Y^49	12MR, 3D	Si192O384	13.5	11.2/7.4
AFI	SSZ-24 ^50	12MR, 1D	Si144O288	17.8	8.3/7.4
IFR	ITQ-4 ^51	12MR, 1D	Si192O384	17.0	7.2/6.4
MOR	High-silica mordenite^52,53	12MR, 1D	Si144O288	17.6	6.7/6.5
CFI	CIT-5 ^54	14MR, 1D	Si256O512	18.3	7.5/7.3
H-FAU	Dealuminated Y^55	12MR, 3D	HAlSi191O384 (Si/Al = 191)	13.5	11.2/7.4
H-MOR	Dealuminated mordenite^53	12MR, 1D	HAlSi143O288 (Si/Al = 143)	17.6	6.7/6.5

---

Models of the protonated zeolites H-FAU and H-MOR were constructed by introducing one Al atom and one charge-balancing proton per unit cell/1 × 1 × 3 supercell, respectively. Due to the low amount of framework Al atoms, the same (experimental) cell parameters as for the all-silica systems were used.^49,53 As there is only one type of T site in FAU, only one Al position was considered. Structure models with protons attached to each of the four surrounding oxygen atoms were constructed and DFT-optimized. Among the four models, the H@O₂ case was found to be lowest in energy (Table S3†, the labelling of T and O atoms in FAU and MOR follows the IZA database³¹). However, the H@O₂ proton points across a 6MR in an inaccessible area of the structure (the 6MR links a double six-membered ring and a sodalite cage, both of which are inaccessible for most guest molecules). In the H@O1 model, which is only 5 kJ mol⁻¹ higher in energy (second lowest), the proton points into a 12MR, thus being accessible to guests accommodated in the supercages that are linked by these windows. This is also the most occupied proton site according to experimental investigations on protonated FAU samples with lower Si/Al ratios.^56,57 The H-FAU(H@O1) model was hence used in all further calculations. In MOR, the increased complexity of the framework, with 4 non-equivalent T sites in the aristotype, is exacerbated by the symmetry reduction to space group P2₁2₁2₁ in the structure model obtained from the AIMD simulations.⁴¹ To limit the number of possible Al + H arrangements, only those cases where the proton points (approximately) into the 12MR channels were considered: under this constraint, the framework proton can be attached to the O1, O4, O7, or O10 atoms, and the Al atom, which should be at a neighboring T site, can be located at the T1, T2, or T4 sites. Due to the aforementioned symmetry reduction, some of these sites are split into up to 4 non-equivalent sites, resulting in a total of 22 distinct arrangements. Models for these arrangements were constructed in a 1 × 1 × 3 supercell of the MOR unit cell and DFT-optimized. All models are listed in the ESI (Table S4 and Fig. S2†). Among them, the model dubbed H-MOR(Al@T1_4,H@O4_4) was found to be lowest in energy and used in all following calculations on H-MOR. A previous DFT study of protonated MOR also delivered a model with Al@T1, H@O4 as lowest-energy case, in line with this result.⁵⁸ As for the all-silica models, AIMD simulations (NVT ensemble, T = 298 K, timestep 0.5 fs, total duration 12.5 ps) were run for H-FAU and H-MOR. The average structures from the 10 ps production part of the trajectory were optimized again. These calculations converged to the same minima as the initial optimizations.

Force field simulations

In order to generate adsorption complexes of TCS, water ((H₂O)_N), or both TCS and water in different zeolites, a combination of Monte Carlo (MC) and molecular dynamics (MD) simulations was used, employing parameters from the pcff force field.^43,59 The typical protocol consisted of fixed-loading MC simulations using the MS Sorption module, from which five low-energy snapshots were extracted for each combination of guest and zeolite. To enhance the sampling, MD-based simulated annealing runs using the MS Forcite module were then carried out, starting from the five snapshots, with each run consisting of 20 annealing cycles. The configurations from the end of each annealing cycle were optimized. Out of the 100 configurations obtained via this procedure, five low-energy configurations were selected as starting points for the DFT optimizations. These configurations were labelled as “guest@Zeo, ConfigX”, where “guest” represents TCS or H₂O, “Zeo” corresponds to the zeolite framework type, and “X” is a running index from 1 to 5, assigned according to the pcff total energy. For co-adsorption of TCS and H₂O, labels of the format “guest2(guest1@Zeo)” were assigned, where “guest1” is the species that was added first, and “guest2” the species that was added subsequently. Detailed settings of the force field simulations are provided in the ESI.†

Additional MD simulations were carried out to assess whether TCS can diffuse through the pores of the six all-silica zeolites. These simulations, which started from low-energy TCS@Zeo configurations, also used pcff parameters. Unlike in the MC and simulated annealing simulations, the zeolite frameworks were treated as flexible. Self-diffusion coefficients D_s were determined from a least-square fitting to mean square displacements computed for the individual MD trajectories using the Einstein relation.⁶⁰

DFT calculations

DFT calculations and AIMD simulations used the electronic structure module Quickstep of the CP2K package, version 9.1, which uses the Gaussian and plane wave method.^61,62 The rev-vdW-DF2 exchange-correlation functional was used in all calculations,⁶³ in line with earlier studies addressing the interaction of sizeable organics with zeolites.^37,41 Core electrons were represented using Goedeker–Teter–Hutter (GTH) pseudopotentials devised by Krack.⁶⁴ In the DFT structure optimizations, all atomic positions were relaxed using a BFGS algorithm, whereas cell parameters were held fixed at the experimental values compiled in Table S2†. The optimizations employed Gaussian basis sets of double-zeta quality (DZVP-MOLOPT-SR⁶⁵) and a plane wave cutoff of 600 Ry. A maximal residual force of 5 × 10⁻⁶ Ha bohr⁻¹ and a maximal displacement of 2 × 10⁻⁵ bohr between steps were used as convergence criteria. After successful optimizations, total energies were recomputed using larger triple-zeta basis sets (TZVP-MOLOPT) and a plane wave cutoff of 900 Ry. For a given configuration, the adsorption energy was then calculated as:

ΔE_ads = E_guest@Zeo − E_Zeo − N·E_guest (1)

The terms on the right-hand side represent the total energies of the adsorption complex, the guest-free zeolite framework, and the guest molecule in a cubic box with an edge length of 20 Å (N = 1 for TCS and N = 1, 4, 8, 12 for H₂O; for the case of water, adsorption energies are either reported for the entire cluster or per H₂O molecule, depending on context). Adsorption energies for systems containing co-adsorbed TCS and water were calculated accordingly, subtracting the total energies of both guests.

Single-point calculations using TZVP basis sets were also carried out for fragments of the optimized structures, permitting the calculation of the deformation energies:

ΔE_deform,Zeo = E_Zeo,config − E_Zeo (2)

ΔE_deform,TCS = E_TCS,config − E_TCS (3)

Here, the first term on the right-hand side corresponds to the total energy of the zeolite framework/TCS molecule extracted from the DFT-optimized adsorption complex, from which the total energy of the DFT-optimized system is subtracted. The deformation energy is always positive. For adsorption of a (H₂O)₈ cluster, an analogous calculation would correspond to:

ΔE_{guest–guest,H2O} = E_H2O,config − 8ΔE_H2O (4)

Here, the term E_H2O,config contains both attractive H₂O–H₂O interactions and energy “penalties” arising from deformations of the adsorbed molecules. In the light of the ability of the H₂O molecule to act as hydrogen bond donor and acceptor, it can be expected that the former contribution will typically outweigh the latter, and that the overall term will hence be negative.

DFT-based AIMD simulations

Like the DFT calculations described in the preceding subsection, DFT-based AIMD simulations made use of the CP2K package, also using the rev-vdW-DF2 exchange-correlation functional, GTH pseudopotentials, and double-zeta basis sets. The AIMD simulations were carried out in the NVT ensemble for T = 298 K, using a Nosé–Hoover thermostat^66,67 (time constant 50 fs). Trajectories were calculated for a total duration of 12.5 ps, using a time step of 0.5 fs (25 000 steps). Unless otherwise noted, the final 10 ps of each AIMD trajectory were taken as production part that was used in the analysis. The AIMD simulations usually started from DFT-optimized structures (exception: simulations of TCS and H₂O co-adsorption in protonated zeolites, discussed in more detail in the Results section). For each structure considered, three independent 12.5 ps simulations were run. After completing AIMD simulations for a given TCS@Zeo configuration, the zeolite framework alone, and TCS in a box, the internal energy of adsorption was calculated as:

ΔU_ads,298K = 〈Ē_TCL@Zeo〉_3tr,298K − 〈Ē_Zeo〉_3tr,298K − 〈Ē_TCS〉_3tr,298K (5)

Here, the terms in brackets correspond to the averages over the total energies (sum of potential and kinetic energy) obtained from the production stages of the AIMD simulations. The index “3tr” highlights that these averages were computed over the three independent trajectories. To have a measure of the uncertainty in the internal energies of adsorption, ΔU_ads,298K was recalculated using only subsets of two trajectories in the calculations of the averages in eqn (5), considering all possible permutations. The resulting estimated boundary values of ΔU_ads,298K are reported as ΔU_min and ΔU_max, respectively. For relevant combinations of atoms/group of atoms, radial distribution functions (RDFs) were calculated using the VMD code, version 1.9.4.⁶⁸ With one exception, discussed in the Results section, the presented RDFs always correspond to averages over three trajectories. Furthermore, angles between the planes defined by the two TCS phenyl rings ω_phenyl were measured using the TRAVIS code, both for lowest-energy configurations and as averages over the AIMD trajectories.^69,70

Results and discussion

Preliminary investigation: diffusion of TCS in all-silica zeolites

As a first step, FF-based MD simulations were used to evaluate whether TCS could diffuse through the pores of the six all-silica zeolites chosen for this study. For each zeolite, five trajectories were calculated, starting from the TCS@Zeo configurations that were also used as starting points for the DFT optimizations. Table 2 gives the average self-diffusion coefficients D_s,aver (averaged over five trajectories) as well as the minimal and maximal individual values of D_s. As it should be expected, the trend in the self-diffusion coefficients follows the evolution of diameters of the largest diffusing sphere. A fairly large scatter in individual values, which span almost one order of magnitude in the most extreme case, is evident. It is, however, not the purpose of these calculations to deliver accurate predictions of D_s, but rather to determine whether a diffusion of TCS can be expected at all. This is clearly the case for FAU, AFI, MOR, and CFI, with self-diffusion coefficients on the order of 20 to 2000 × 10⁻⁸ cm² s⁻¹. Values in this range are typical for sizeable organic molecules in zeolites with 12MR windows (e.g., 9550/573 × 10⁻⁸ cm² s⁻¹ computed for benzene/para-xylene in FAU at 300 K^71,72). While diffusion is distinctly slower in IFR, it can be inferred that the TCS molecule is still able to move through the pores. No diffusion on the nanosecond timescale occurs for BEA, where TCS remains in the vicinity of its initial location during all 50 ns simulations. This finding disagrees with the experimental observation of a significant TCS uptake from aqueous solution in zeolite beta samples having different Si/Al ratios.³² Although the difference between the idealized all-silica BEA model used in the calculations and real zeolite beta samples, which exhibit stacking disorder of the tetragonal beta layers along the [001] direction,⁴⁸ could be responsible for this discrepancy, other explanations cannot be ruled out. Altogether, the findings for BEA indicate that the MD simulations make a rather conservative estimate of the diffusion behavior, giving confidence in the prediction that TCS can diffuse through the pore systems of the other zeolites.

Table 2 Self-diffusion coefficients averaged over five trajectories D_s,aver and minimal/maximal values obtained for individual trajectories

FTC (dLDS)	D s,aver [×10^−8 cm^2 s^−1]	D s,min/Ds,max [×10^−8 cm^2 s^−1]
BEA (6.0 Å)	—	—/—
FAU (7.4 Å)	226	170/298
AFI (7.4 Å)	1284	690/1848
IFR (6.4 Å)	4.25	1.57/10.6
MOR (6.5 Å)	38.4	23.5/53.1
CFI (7.3 Å)	189	69.6/283

---

Adsorption energies of TCS@Zeo complexes

All-silica zeolites. For the six all-silica zeolites, Boltzmann-weighted adsorption energies ΔĒ_ads,298K as well as adsorption and deformation energies of the lowest-energy TCS@Zeo configurations are compiled in Table 3 (results for all configurations are given in Table S5†). With the exception of FAU, the adsorption energies of the other five all-silica zeolites fall in a relatively narrow range from −153 to −160 kJ mol⁻¹. While the weaker interaction in FAU can be explained with the much larger pore diameter, resulting in reduced dispersion interactions between TCS and the pore walls, there is no apparent correlation of the adsorption energy with pore diameter and/or framework density for the remaining systems. The deformation energies are always small, with the sum of the two ΔE_deform terms amounting to less than 5% of the total adsorption energy in all zeolites except MOR (where it reaches 6.5%). Rather different observations were made in the earlier DFT study of CBZ adsorption, where the sum of the deformation energies exceeded 10% of the total adsorption energies for some zeolites, notably BEA and MOR.⁴¹ Whereas the CBZ molecule is rather rigid, containing a tricyclic aromatic system, TCS can adjust much more easily to different pore environments because the two phenyl rings can rotate essentially independently. The flexibility manifests in the variation of the angle ω_phenyl, which amounts to 89.0° in the crystal structure of triclosan at 150 K.⁴² This angle is reduced to 75.9° in the DFT-optimized structure of isolated TCS, and ω_phenyl values varying from 53.9 to 92.5° occur in the lowest-energy TCS@Zeo complexes. There is no apparent correlation with the magnitude of the ΔE_deform,TCS term (Table 3).

Table 3 Results for TCS in all-silica zeolites. (Top) Boltzmann-averaged adsorption energies ΔĒ_ads,298K, adsorption energies and deformation energies of lowest-energy configurations. (Bottom) Selected interatomic distances and angles of lowest-energy configurations

	ΔĒads,298K [kJ mol^−1]	ΔEads,lowest [kJ mol^−1]	ΔEdeform,Zeo [kJ mol^−1]	ΔEdeform,TCS [kJ mol^−1]
BEA	−155.8	−156.2	1.8	2.6
FAU	−122.9	−124.1	2.7	1.4
AFI	−155.4	−156.2	1.5	1.6
IFR	−159.9	−160.4	3.7	3.0
MOR	−154.4	−155.3	5.4	4.6
CFI	−152.9	−153.8	1.7	2.0

---

	r(Oh–Hh) [Å]	r(Hh⋯Oc) [Å]	r(Hh⋯OZeo) [Å]	ω phenyl [°]
Free TCS	0.981	2.181	—	75.9
BEA	0.984	2.154	2.332	55.4
FAU	0.982	2.133	2.302	92.5
AFI	0.983	2.166	2.113	74.5
IFR	0.981	2.120	>3	79.1
MOR	0.982	2.094	2.475	53.9
CFI	0.982	2.174	2.252	91.5

---

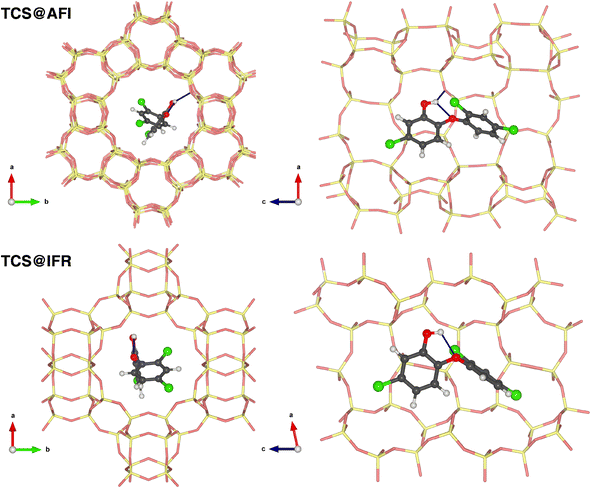
As discussed above, the DFT-optimized lowest-energy TCS conformer possesses an intramolecular hydrogen bond from the hydroxyl group to the central oxygen atom. This bond remains present in all of the lowest-energy TCS@Zeo complexes, and an evaluation of the hydrogen bond distances reveals a certain shortening of the distance r(H_h⋯O_c) with respect to free TCS in all zeolites. This shortening is most pronounced in MOR and IFR, the two zeolites where the ΔE_deform,TCL term is largest. The elongation of the covalent O_h–H_h bond remains negligible. Additional hydrogen bonds to framework oxygen atoms can be found in all zeolites except IFR, with distances r(H_h⋯O_Zeo) varying from 2.11 Å in AFI to 2.48 Å in MOR. As the adsorption energies are not correlated with the hydrogen bond distance, it can be concluded that hydrogen bonds make only a minuscule contribution to the total zeolite–TCS interaction. To illustrate typical adsorption complexes with and without hydrogen bonds, the lowest-energy TCS@AFI and TCS@IFR configurations are visualized in Fig. 2.

Fig. 2 Lowest-energy TCS@AFI (top) and TCS@IFR (bottom) configurations. Atoms of the all-silica zeolite frameworks are shown in pale yellow (Si) and pale red (O). Panels on the left show the full channel in a projection along the channel axis, those on the right show only the vicinity of the adsorbed TCS molecule.

Protonated zeolites. Table 4 compiles the results for protonated zeolites H-FAU and H-MOR in a largely analogous fashion to Table 3 (full results are given in Table S5†). The adsorption energies are distinctly more negative than for the corresponding all-silica zeolites, with the differences amounting to −31 kJ mol⁻¹ (corresponding to a change by −25%) for FAU and to −36 kJ mol⁻¹ (−23%) for MOR. This increase in interaction strength can be straightforwardly attributed to the formation of a hydrogen bond from the framework proton to the TCS O_h atom, visualized in the lowest-energy configurations shown in Fig. 3. With a bond length of 1.49/1.63 Å in H-FAU/H-MOR, these bonds are much shorter than the H_h⋯O_Zeo hydrogen bonds that are formed in all-silica zeolites. As a result, the O_Zeo–H_Zeo bond is elongated significantly, explaining the increased ΔE_deform,Zeo term. Moreover, the H_Zeo⋯O_h hydrogen bond withdraws some electron density from the O_h atom, leading to a weakening of the O_h–H_h bond and, concurrently, a shortening of the intramolecular H_h⋯O_c hydrogen bond. These changes in the molecular structure can serve to explain the relatively large TCS deformation energies. For TCS@H-MOR, the pronounced rotation of the rings (ω_phenyl = 37.4°) probably also contributes to ΔE_deform,TCS. Due to steric reasons, the hydroxyl group of TCS does not form any additional hydrogen bonds to framework oxygen atoms in the lowest-energy TCS@H-FAU/H-MOR complexes.

Table 4 Results for TCS in protonated zeolites. (Top) Boltzmann-averaged adsorption energies ΔĒ_ads,298K, adsorption energies and deformation energies of lowest-energy configurations. (Bottom) Selected interatomic distances and angles of lowest-energy configurations. In guest-free H-FAU/H-MOR, d(O_Zeo–H_Zeo) amounts to 0.981 Å

	ΔĒads,298K [kJ mol^−1]	ΔEads,lowest [kJ mol^−1]	ΔEdeform,Zeo [kJ mol^−1]	ΔEdeform,TCS [kJ mol^−1]
H-FAU	−153.5	−153.7	19.5	5.5
H-MOR	−190.6	−191.4	11.1	12.6

---

	r(Oh−Hh) [Å]	r(Hh⋯Oc) [Å]	r(OZeo–HZeo) [Å]	r(HZeo⋯Oh) [Å]	ω phenyl [°]
H-FAU	0.988	2.034	1.050	1.488	89.9
H-MOR	0.988	2.013	1.022	1.628	37.4

---

Fig. 3 Lowest-energy configurations of TCS in protonated zeolites H-FAU and H-MOR. The framework Al atoms are shown as turquoise spheres.

AIMD simulations

AIMD simulations for all-silica FAU and MOR as well as H-FAU and H-MOR started from the lowest-energy TCS@Zeo configurations. Internal energies of adsorption were computed according to eqn (5), using the results from three independent trajectories computed for the TCS@Zeo complex, the zeolite alone, and TCS in a box. The first column of Table 5 gives the internal energies of adsorption as well as the upper and lower boundary values obtained by using averages over two, rather than three, trajectories. On this basis, the uncertainties in the reported values can be estimated to be on the order of ±8 kJ mol⁻¹ for the all-silica zeolites and ±13 kJ mol⁻¹ for the protonated zeolites. As the AIMD simulations used DZVP basis sets, the ΔU_ads,298K values are not directly comparable to the Boltzmann-weighted adsorption energies ΔĒ_ads,298K computed with TZVP basis sets. To allow such a comparison, the ΔU_ads,298K values were rescaled using scaling factor s_Zeo, which was calculated as the ratio of the Boltzmann-weighted TZVP and DZVP adsorption energies, i.e., s_Zeo = ΔĒ_ads,298K(TZVP)/ΔĒ_ads,298K(DZVP). The scaling factors fall in a fairly narrow range (Table 5), indicating that this is a suitable strategy to extrapolate the DZVP internal energies of adsorption to larger basis sets.

Table 5 Results of AIMD simulations: unscaled and scaled internal energies of adsorption, including boundary values obtained by considering subsets of trajectories. Boltzmann-weighted adsorption energies ΔĒ_ads,298K are given for comparison

	ΔUads,298K (ΔUmin/ΔUmax) [kJ mol^−1]	s Zeo	ΔUads,298K,scaled (ΔUmin/ΔUmax) [kJ mol^−1]	ΔĒads,298K^a [kJ mol^−1]	ΔUads,298K,scaled/ΔĒads,298K
a From TZVP single-point calculations (same values as in Tables 3 and 4).
FAU	−118.0 (−110.5/−125.7)	0.828	−97.7 (−91.5/−104.1)	−122.9	0.795
MOR	−166.9 (−159.7/−175.1)	0.830	−138.6 (−132.6/−145.4)	−154.4	0.898
H-FAU	−152.8 (−141.6/−168.3)	0.842	−128.7 (−119.3/−141.8)	−153.5	0.838
H-MOR	−206.4 (−195.5/−219.2)	0.859	−177.2 (−167.9/−188.2)	−190.6	0.930

---

Comparing the scaled internal energies of adsorption ΔU_{ads,298K,scaled} to the ΔĒ_ads,298K values, it is clear that the AIMD-computed values are systematically less negative. The relative difference can be evaluated through the ratio of both quantities, given in the last column of Table 5. The largest deviation of about 20% occurs for all-silica FAU, followed by H-FAU (16%), whereas the differences for all-silica MOR (10%) and H-MOR (7%) are significantly smaller. As observed in the previous study of CBZ adsorption, where FAU, IFR, and MOR were compared,⁴¹ the deviation between “dynamic” and “static” results is directly correlated with the guest molecule's freedom of motion in the zeolite pores: much more pronounced oscillations are possible in the large cages of FAU than in the comparatively narrow channels of MOR. This results in a larger impact of thermal motion on the internal energy of adsorption in the former system. In the protonated zeolites, the formation of a relatively strong hydrogen bond further reduces the freedom of motion.

The AIMD trajectories were further analyzed to investigate the evolution of the hydrogen bonds during the simulation. Although this analysis remains limited to the picosecond timescale, it can permit some conclusions on the stability/lability of these bonds. For MOR, H-FAU, and H-MOR, average RDFs over the three trajectories were used as basis for the analysis, because differences among the individual trajectories were primarily of a statistical nature. For FAU, however, a distinct behavior was observed in one of the three trajectories (labelled as “Traj1”), which will be discussed in more depth at the end of this section. Therefore, the average RDFs for FAU were calculated only over the other two trajectories. Fig. 4a shows the RDFs of the intramolecular hydrogen bond of TCS, including the cumulative RDFs that correspond to the number of interatomic contacts within a given distance range. Both in free TCS and in the adsorption complexes, the intramolecular hydrogen bond persists during the AIMD simulations, with 97.5 to 99% of the distances r(H_h⋯O_c) remaining below 2.5 Å. While the maxima in the RDFs of free TCS and of the TCS@FAU and TCS@MOR complexes are very close to the DFT-optimized bond distances tabulated in Table 2, those computed for TCS in protonated zeolites are shifted towards somewhat higher distances.

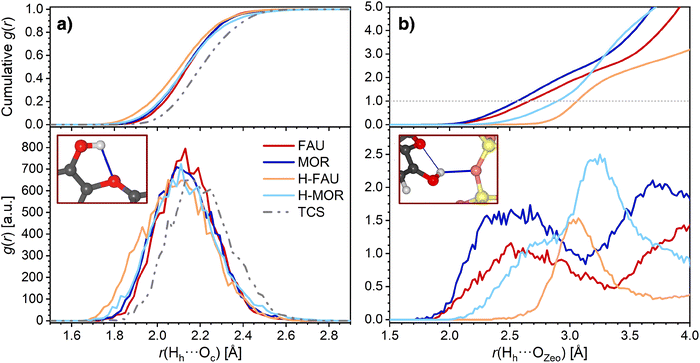Fig. 4 Radial distribution functions (RDFs) obtained from AIMD simulations. (a) Intramolecular hydrogen bonds of TCS, (b) H_h⋯O_Zeo hydrogen bonds. Top panels show the cumulative RDFs.

The RDFs corresponding to contacts from the TCS hydroxyl proton H_h to framework oxygen atoms are shown in Fig. 4b. It is worth noting that the RDFs cover all O atoms of the framework, not only the atom to which a hydrogen bond is formed in the initial, DFT-optimized structure. The RDFs of all-silica FAU and MOR exhibit a pronounced increase in the distance range above 2.1 Å, and a cumulative RDF of 1 is reached at distances of 2.56 Å and 2.66 Å, respectively (this means that there is, on average, one H_h⋯O_Zeo contact within this distance throughout the AIMD simulation). Distances below 2.6 Å are rarely found for H-FAU, corroborating the absence of H_h⋯O_Zeo hydrogen bonds that was already observed in the DFT optimizations. H-MOR takes a somehow intermediate position, with H_h being within 2.5 Å of a framework O atom for about 20% of the simulation time. This observation points to the formation of transient, relatively long and weak H_h⋯O_Zeo hydrogen bonds in the channels of H-MOR. In contrast, the H_Zeo⋯O_h RDFs for the protonated zeolites, visualized in Fig. 5, show that the short, strong hydrogen bonds from the framework proton to the TCS O_h atom are too stable to be broken by thermal motion at 298 K. The difference in the distance r(H_Zeo⋯O_h) between H-FAU and H-MOR that was observed in the DFT-optimized structures also persists.

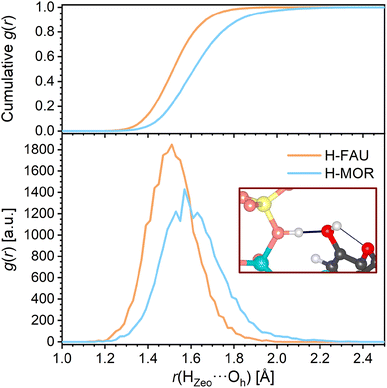Fig. 5 Radial distribution functions (RDFs) of H_Zeo⋯O_h hydrogen bonds in protonated zeolites. The top panel shows the cumulative RDFs.

A further analysis of the AIMD trajectories can give insights into the formation of additional short contacts between framework oxygen atoms and the H and Cl atoms that are bonded to the phenyl rings of TCS. The corresponding RDFs are shown in Fig. S4.† The sum of the van der Waals radii amounts to 2.70 Å for H_phenyl⋯O_Zeo contacts and to 3.32 Å for Cl⋯O_Zeo contacts.⁷³ Although shorter contacts occur in all systems, they account only for a relatively small fraction, and cumulative RDFs of 1 are reached at distances that exceed the respective sums of the van der Waals radii. The more frequent occurrence of relatively short contacts in MOR-type systems in comparison to FAU-type systems is related to the narrower channel dimensions of the former framework. The internal dynamics of the TCS molecule do not appear to be strongly affected by the confinement, as oscillations of the angle between the TCS phenyl rings, expressed by the standard deviations in ω_phenyl computed over individual trajectories (Table S11†), do not exhibit any systematic trends.

Finally, as already mentioned above, the different evolution of one of the three TCS@FAU trajectories (Traj1) warrants a separate discussion. In this particular case, an inspection of the H_h⋯O_Zeo RDF shows that the first maximum at about 2.5 Å, well visible for the other two TCS@FAU trajectories, is absent, indicating that the hydrogen bond to the framework has been broken during the AIMD simulation (Fig. S5†). Moreover, the maximum in the H_h⋯O_h RDF is also shifted to longer distances by about 0.15 Å. A visualization of the last frames of the three trajectories (Fig. S6†) shows that the TCS molecule remains in a very similar position as in the DFT-optimized structure in Traj2 and Traj3, with the central part of the molecule located at one side of the 12MR pore opening. In contrast, TCS has moved away from this location in Traj1, with the central area now being closer to the center of the 12MR ring, not forming any H_h⋯O_Zeo hydrogen bond. Interestingly, the breaking of the hydrogen bond does not incur a pronounced change in the average potential energy, which remains within the typical uncertainty range of the AIMD energies of about 10 kJ mol⁻¹. Even though the importance of an observation made for one particular trajectory only should not be overestimated, this implies that hydrogen bonds formed between TCS and all-silica framework are relatively labile. If AIMD simulations covering much longer timescales were possible, one would likely observe an equilibrium between hydrogen-bonded and non-bonded configurations, with hydrogen bonds breaking and re-forming over time.

Adsorption of water and co-adsorption of TCS and water

The calculations presented up to this point made the simplifying assumption that no co-adsorption of water occurs when adsorbing TCS from aqueous solution. While this simplification might appear reasonably justified for all-silica zeolites, which are known to be highly hydrophobic,^74,75 the introduction of framework Al atoms and charge-balancing protons will increase the hydrophilicity. The relative affinity towards water and organic molecules such as phenol has sometimes been evaluated by comparing interaction energies computed for adsorption complexes of individual molecules.⁷⁶ However, when looking at molecules of vastly different size, adsorption energies obtained for single molecules will (in almost all cases) be much less negative for water, simply because the contribution of dispersion interactions is much larger for a bulky organic molecule like TCS. For this reason, it appears to be more plausible to compare TCS adsorption energies to those obtained for a cluster of water molecules that is similar in size to TCS. An estimation of the molecular volumes based on the crystal structures delivered molecular volumes of 32.5 ų for H₂O (hexagonal ice⁷⁷) and 302 ų for TCS,⁴² corresponding to a ratio of about 1 : 9.3. Moreover, experimental investigations on protonated zeolites have shown that the typical size of water clusters in the vicinity of the acid sites (framework protons) is in the range of eight H₂O molecules (for MFI-type ZSM-5 ⁴⁵). For these reasons, an adsorption of eight water molecules per simulation cell was assumed in calculations aimed at a comparison of TCS and H₂O adsorption energies and in studies of TCS + H₂O co-adsorption. Additional results obtained for 1, 4, and 12H₂O molecules per cell were evaluated to investigate the impact of cluster size on the adsorption energy.

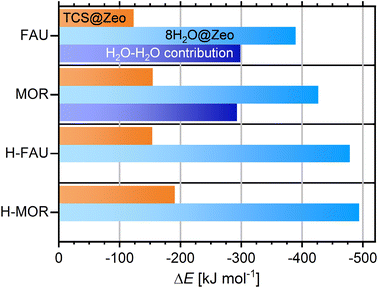
For the FAU- and MOR-type all-silica zeolites as well as H-FAU and H-MOR, five configurations containing different arrangements of eight H₂O molecules per cell were DFT-optimized, and the Boltzmann-weighted adsorption energies were computed in an analogous fashion as for TCS. Fig. 6 shows the total adsorption energies and compares them to the TCS adsorption energies (full results for individual configurations are given in Table S6†). Even for the two all-silica zeolites, the total adsorption energies for the cluster are much more negative than for TCS, amounting to −389 and −427 kJ mol⁻¹, respectively. However, a calculation of the guest–guest contribution shows that the larger part of the adsorption energy stems from H₂O–H₂O interactions, which are on the order of −295 kJ mol⁻¹ for both zeolites. The remaining host–guest contribution is about 20 to 30 kJ mol⁻¹ smaller than the TCS adsorption energies, indicating a preference for TCS over H₂O. On a per molecule basis, the H₂O adsorption energies correspond to −48.7/−53.3 kJ mol⁻¹ for all-silica FAU/MOR. As guest–guest interactions are virtually identical, the more negative value for MOR can be attributed to stronger interactions with the framework in the narrower channels. It has to be noted that these values are not directly comparable to thermodynamically measurable quantities that represent the intermolecular interactions in liquid water, specifically the enthalpy of vaporization (44 kJ mol⁻¹ at 298 K). For a semi-quantitative estimation, however, they can be compared to the intermolecular contribution to the total energy obtained in DFT optimizations of a box of water molecules using the same approach. Calculations for four different boxes containing 256H₂O molecules (DFT-optimized density ≈ 1.06 g cm⁻³) delivered energies on the order of −60 kJ mol⁻¹ per H₂O molecule. In other words, the DFT calculations correctly predict the interaction to be weaker in the all-silica zeolites than in liquid water, in line with the experimentally observed hydrophobicity of the materials. The hydrophobic nature is confirmed when adsorption energies computed for clusters of different size (1, 4, 8, 12H₂O molecules) are compared (Fig. S3†): the interaction with a single H₂O molecule is very weak, with adsorption energies of −25.1/−38.2 kJ mol⁻¹ for FAU/MOR. The computed adsorption energies per molecule become increasingly negative with increasing cluster size, with the most prominent change occurring when moving from one to four molecules per cell. Differences between (H₂O)₈ and (H₂O)₁₂ clusters are relatively modest, amounting to 3.5/1.5 kJ mol⁻¹ per molecule. This indicates that the stability of adsorbed water clusters in this size range does not depend strongly on the exact number of molecules involved.

Fig. 6 Boltzmann-averaged adsorption energies obtained for (H₂O)₈ clusters adsorbed in FAU- and MOR-type zeolites (central columns). TCS adsorption energies are given for comparison (top columns). For all-silica zeolites, the contribution of H₂O–H₂O interactions is also shown (bottom columns).

Unsurprisingly, the water adsorption energies obtained for protonated zeolites are considerably more negative, amounting to −479 kJ mol⁻¹ (−59.8 kJ mol⁻¹ per molecule) for H-FAU and −494 kJ mol⁻¹ (−61.7 kJ mol⁻¹ per molecule) for H-MOR. For these systems, computations for clusters of different size deliver the most negative value for adsorption of a single H₂O molecule at the framework proton (∼−86 kJ mol⁻¹), with decreasing interaction strength upon increasing cluster size. As for the all-silica zeolites, the adsorption energies for (H₂O)₈ and (H₂O)₁₂ clusters are within 3 kJ mol⁻¹ (per molecule). An inspection of the DFT-optimized structures shows that the interaction of 4, 8, or 12 water molecules with the framework proton results in framework deprotonation and formation of a H₃O⁺(H₂O)_N−1 cluster. This finding agrees with experimental observations⁴⁵ and previous DFT results.⁴⁴ The framework deprotonation precludes a simple calculation of the contribution of H₂O–H₂O interactions as done for the all-silica zeolites. However, it is apparent from Fig. 6 that the increase in interaction strength when moving from an all-silica zeolite to its protonated counterpart is much more pronounced for water than for TCS. The occurrence of framework deprotonation upon water adsorption, and its absence during TCS adsorption, also confirm the notion of a stronger interaction with water.

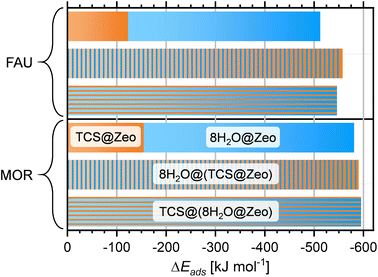
It is clear that calculations addressing the individual adsorption of either TCS molecules or H₂O clusters can only deliver indirect insights into the relative affinity towards the two species. In particular, the magnitude of the adsorption energy of a (H₂O)_N cluster that competes with TCS will depend on the cluster size, limiting the quantitative interpretation. To obtain insights into the co-adsorption of TCS and water, the simultaneous interaction of both species with FAU- and MOR-type zeolites was investigated. For all-silica FAU and MOR, an approach based on DFT optimizations was employed: starting from DFT-optimized low-energy TCS@Zeo and 8H₂O@Zeo configurations, the other species (eight H₂O molecules/one TCS molecule) was added using MC simulations. After a simulated annealing of the MC snapshots, five configurations for each case were extracted and DFT-optimized. Fig. 7 shows the Boltzmann-averaged adsorption energies for the 8H₂O@(TCS@Zeo) and TCS@(8H₂O@Zeo) complexes. First of all, it is worth noting that the adsorption energies are very close, regardless of whether H₂O molecules were added to a TCS@Zeo complex or vice versa. Second, the total adsorption energies are more negative than the sum of the individual adsorption energies computed for TCS and water, indicating that H₂O-TCS interactions during co-adsorption of both species are, overall, attractive. The difference is larger for FAU than for MOR, which can be understood when looking at exemplary low-energy configurations (Fig. 8): in the spacious cages of FAU, the water molecules not only form hydrogen bonds to each other and to framework oxygen atoms, but also to the hydroxyl group of TCS, which simultaneously acts as hydrogen bond donor and acceptor. In MOR, the water cluster occupies a different channel section than the TCS molecule, limiting the possibility of guest–guest interactions.

Fig. 7 Boltzmann-averaged adsorption energies obtained for all-silica FAU and MOR with co-adsorbed TCS and water. Sums of the adsorption energies of individual guest molecules are shown for comparison (top columns).

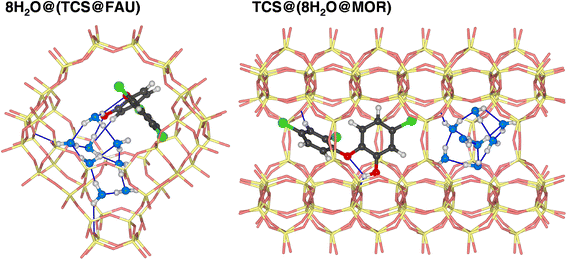Fig. 8 Lowest-energy configurations of co-adsorbed TCS and water in all-silica zeolites FAU and MOR. Oxygen atoms of H₂O molecules are shown in blue.

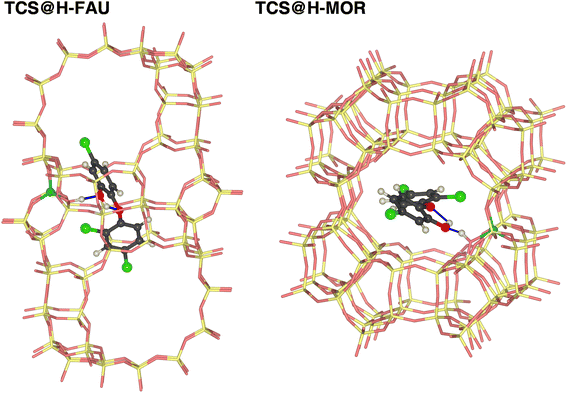
For the protonated zeolites, it is most interesting to elucidate what happens to a TCS molecule that is adsorbed at a framework proton in the presence of water at finite temperature. To investigate this, 8H₂O@(TCS@Zeo) configurations were generated for H-FAU and H-MOR using MC simulations. Subsequently, three AIMD simulations starting from different MC-generated configurations were run for each zeolite. In these cases, the first 2.5 ps of the trajectories were not discarded, but included in the analysis, since the most significant structural changes were typically found to occur during the very initial stages of the simulations. An inspection of the temperature evolution of the individual simulations showed that no significant “overshoot” in temperature occurred during this initial phase. Although a qualitative interpretation could be based on the visualization of individual frames from the AIMD trajectories alone, a more comprehensive picture can be obtained by looking at the evolution of relevant interatomic distances over time. As analogous observations were made for all three trajectories for H-FAU and H-MOR, a representative example trajectory is discussed here for each zeolite, and additional results are shown in the ESI (Fig. S7 to S12†).

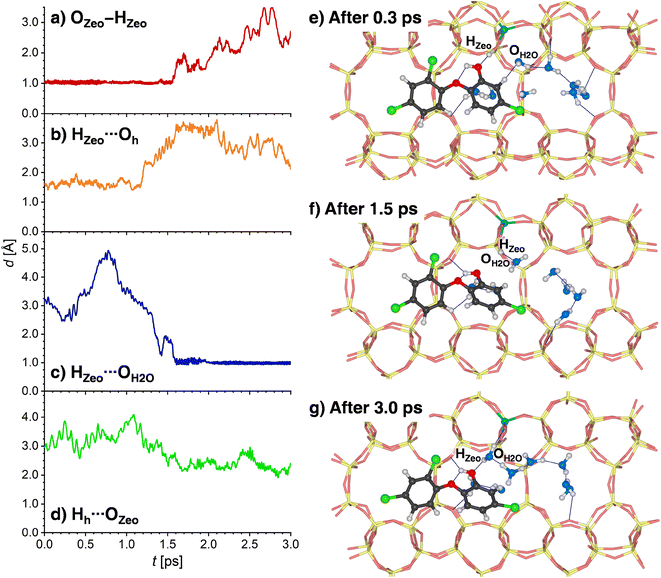
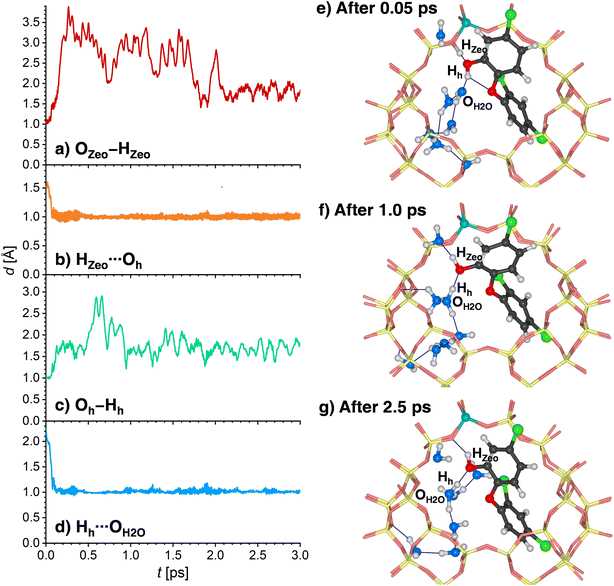
Since the behavior of H-MOR is somewhat simpler, the results for this zeolite are presented first. Fig. 9a and b shows the time evolution of the O_Zeo–H_Zeo and H_Zeo⋯O_h distances during the first 3 ps of the simulation. For a time of about 1.2 ps, the framework proton remains bonded to the framework, and hydrogen-bonded to the TCS molecule. This situation is depicted in Fig. 9e, which shows a snapshot from the initial phase of the simulation. After this period, a breaking of the H_Zeo⋯O_h hydrogen bond occurs, and a transient hydrogen bond to a water molecule is formed (Fig. 9f). After about 1.6 ps, the covalent O_Zeo–H_Zeo bond is broken, with the distance r(O_Zeo–H_Zeo) quickly increasing to values above 2 Å. A visualization of a simulation frame obtained after this period (Fig. 9g) shows that the proton is now bonded to the H₂O molecule that participated in the transient hydrogen bond. It remains bonded to the same H₂O oxygen atom for the remainder of the simulation, as is visible from the time evolution of the corresponding H_Zeo⋯O_H2O distance (while Fig. 9c shows only the first 3 ps, the full 12.5 ps are visualized in Fig. S10†). After the framework deprotonation, further proton transfers between water molecules occur, as evidenced by the fact that the hydronium ion that is present after 3 ps is not the same molecule that deprotonated the framework (Fig. 9g). The TCS molecule moves away from the framework Al atom after the H_Zeo⋯O_h hydrogen bond is broken, now acting as a donor through formation of a new H_h⋯O_Zeo hydrogen bond (Fig. 9d). This bond is formed to a framework oxygen atom that does not neighbor the Al atom (Fig. 9g).

Fig. 9 (a)–(d) Evolution of selected interatomic distances during the first 3 ps of one AIMD trajectory (Traj1) computed for 8H₂O@(TCS@H-MOR), (e)–(g) environment of the framework Al atom at different stages of the simulation.

A somewhat different chain of events unfolds in the AIMD simulations for 8H₂O@(TCS@H-FAU). Here, two concerted proton transfers occur during the very initial stages of the AIMD simulation (completed within 0.1 to 0.4 ps): the H_Zeo proton leaves its position at the framework oxygen atom and moves to the O_h atom of TCS, whereas the H_h proton, initially bonded to O_h, is transferred to a water molecule, forming a hydronium ion (Fig. 10a to d). Although both transfers happen almost at the same time, the time evolution of the distances indicates that the framework deprotonation precedes the TCS → H₂O proton transfer. After moving towards the TCS molecule, the H_Zeo proton may form a hydrogen bond to the O_Zeo atom to which it was originally attached or to a water molecule in the vicinity. While Fig. 10e shows a simulation frame at the very beginning of the simulation (after 0.05 ps), prior to deprotonation of the framework, Fig. 10e (after 1.0 ps) and Fig. 10f (after 2.5 ps) exemplify the consecutive formation of H_Zeo⋯O_H2O and H_Zeo⋯O_Zeo hydrogen bonds after completion the proton transfer. Similar alternations can be observed in the other two trajectories. Furthermore, the H_h proton, now part of a hydronium ion, forms a hydrogen bond to the O_h atom of TCS.

Fig. 10 (a)–(d) Evolution of selected interatomic distances during the first 3 ps of one AIMD trajectory (Traj1) computed for 8H₂O@(TCS@H-FAU), (e)–(g) environment of the framework Al atom at different stages of the simulation. Not all eight H₂O molecules are visible in the portion of the cage shown in the figure.

To compute the adsorption energy in a way that is comparable to the calculations for all-silica zeolites, described above, the following approach was used: for both H-FAU and H-MOR, the last 5 ps of each trajectory were analyzed to identify the frame having the lowest potential energy. This frame was then optimized with DZVP basis sets, and the total energy recomputed using TZVP basis sets. For 8H₂O@(TCS@H-FAU), a Boltzmann-averaged adsorption energy of −613.5 kJ mol⁻¹ was obtained. This value is 17.5 kJ mol⁻¹ less negative than the sum of the adsorption energies computed for TCS and for eight H₂O molecules, which amount to −153.5 and −478.5 kJ mol⁻¹, respectively. For H-MOR, on the other hand, the ΔĒ_ads,298K value computed from three optimized AIMD frames of −686.8 kJ mol⁻¹ is about 2.5 kJ mol⁻¹ more negative than the sum of the individual values (TCS: −190.6 kJ mol⁻¹, (H₂O)₈: −493.7 kJ mol⁻¹). Given the limited sampling of only a few frames, these observations should not be overinterpreted in a quantitative way. Qualitatively, however, it seems reasonable to surmise that the contribution of attractive TCS–H₂O interactions is offset by a reduced ability of TCS to interact with the framework proton in the presence of water as compared to the water-free system.

Conclusions

Calculations of the adsorption energies for TCS in all-silica zeolites delivered very similar adsorption energies in the range of −153 to −160 kJ mol⁻¹ for five of the six frameworks, with a weaker interaction being observed only for FAU, which possesses large supercages. This is a notably different finding compared to the previous DFT study of CBZ adsorption, where adsorption energies obtained for these five zeolites varied between −122 kJ mol⁻¹ for BEA and −172 kJ mol⁻¹ for IFR.⁴¹ This qualitative difference can be attributed to the higher flexibility of TCS, which allows it to adjust in a way that the interaction with the pore walls in differently shaped pores is maximized. At first glance, it might appear that the low affinity of FAU disagrees with the findings of Jiang et al., who observed the highest affinity towards TCS in a FAU-type sample.³² However, it has to be taken into account that this sample also had the highest Si/Al ratio among the zeolites with 12MR pore systems, thus being most hydrophobic. Moreover, all isotherm points reported in that study correspond to loadings of at least eight TCS molecules per unit cell (the maximal reported loading is close to two TCS in every supercage, i.e., 16 per FAU unit cell). At such high loadings, attractive guest–guest interactions will contribute to the overall affinity. Such interactions can be expected to be stronger in the supercages of FAU, where the adsorbed molecules have space to reorient in a way that maximizes guest–guest interactions, in comparison to frameworks with narrower pores or channels.⁴¹ For a more direct comparison between experiment and DFT, it would be required to measure TCS adsorption in the Henry regime.

The stronger interaction of TCS with protonated zeolites can be attributed to the formation of hydrogen bonds between the framework proton and the O_h atom of TCS, which, unlike the weak H_h⋯O_Zeo hydrogen bonds found in all-silica zeolites, are too stable to be broken at room temperature. However, calculations including the co-adsorption of water showed that the stronger interaction would not necessarily translate into higher removal efficiencies: The H_Zeo⋯O_h hydrogen bond is not strong enough to remain stable in the presence of a cluster of water molecules, and framework deprotonation with concurrent formation of a hydronium ion in the pores is energetically favored. Thus, it appears unlikely that a bonding of TCS to framework protons could be realized in real systems, where these more hydrophilic areas of the structure will be occupied by clusters of H₂O molecules. In such a material, TCS could still be adsorbed in the more hydrophobic areas of the pore system, meaning that the presence of some framework Al atoms and charge-balancing protons will not necessarily have a completely detrimental effect on the removal efficiency. However, it can be inferred that the removal efficiency will deteriorate with decreasing Si/Al ratio, as indeed observed experimentally.³²

Putting together the findings outlined above, it appears that the hydrophobicity should be maximized in order to develop adsorbents with maximal TCS removal efficiency. Since smaller pores afford stronger dispersion interactions with the pore walls, the pores of an “ideal” adsorbent should, of course, be large enough to accommodate TCS and allow its diffusion, but not much larger. However, there appears to be little scope to optimize specific features of the pore shape. Although the present work looked exclusively at high-silica zeolites, it seems likely that these general criteria could also be applied to adsorbents from other classes. Furthermore, similar relationships should be valid for organic molecules of similar hydrophobicity and flexibility. In contrast, the shape and size of the pores have a much larger impact on the affinity towards more rigid molecules like CBZ. This difference highlights that guest molecule flexibility should be taken into account when searching for suitable adsorbents.

Conflicts of interest

There are no conflicts of interest to declare.

Acknowledgements

This research was funded by the Deutsche Forschungsgemeinschaft (German Research Foundation, DFG) through a Heisenberg fellowship (project no. 455871835). The author gratefully acknowledges the computing time granted by the Resource Allocation Board and provided on the supercomputer Lise and Emmy at NHR@ZIB and NHR@Göttingen as part of the NHR infrastructure. The calculations for this research were conducted with computing resources under the project hbc00062. The author is grateful to Jakob Brauer for comments on different versions of the manuscript.

References

1. S. D. Richardson and S. Y. Kimura, Emerging environmental contaminants: Challenges facing our next generation and potential engineering solutions, Environ. Technol. Innovation, 2017, 8, 40–56.
2. A. J. Ebele, M. Abou-Elwafa Abdallah and S. Harrad, Pharmaceuticals and personal care products (PPCPs) in the freshwater aquatic environment, Emerging Contam., 2017, 3, 1–16.
3. M. Patel, R. Kumar, K. Kishor, T. Mlsna, C. U. Pittman and D. Mohan, Pharmaceuticals of emerging concern in aquatic systems: Chemistry, occurrence, effects, and removal methods, Chem. Rev., 2019, 119, 3510–3673.
4. R. Loos, G. Locoro, S. Comero, S. Contini, D. Schwesig, F. Werres, P. Balsaa, O. Gans, S. Weiss, L. Blaha, M. Bolchi and B. M. Gawlik, Pan-European survey on the occurrence of selected polar organic persistent pollutants in ground water, Water Res., 2010, 44, 4115–4126.
5. A. B. Dann and A. Hontela, Triclosan: Environmental exposure, toxicity and mechanisms of action, J. Appl. Toxicol., 2011, 31, 285–311.
6. J. M. Brausch and G. M. Rand, A review of personal care products in the aquatic environment: Environmental concentrations and toxicity, Chemosphere, 2011, 82, 1518–1532.
7. M. Milanović, L. Đurić, N. Milošević and N. Milić, Comprehensive insight into triclosan—from widespread occurrence to health outcomes, Environ. Sci. Pollut. Res., 2023, 30, 25119.
8. H. P. Schweizer, Triclosan: A widely used biocide and its link to antibiotics, FEMS Microbiol. Lett., 2001, 202, 1–7.
9. L. M. Weatherly and J. A. Gosse, Triclosan exposure, transformation, and human health effects, J. Toxicol. Environ. Health, Part B, 2017, 20, 447–469.
10. D. C. McAvoy, B. Schatowitz, M. Jacob, A. Hauk and W. S. Eckhoff, Measurement of triclosan in wastewater treatment systems, Environ. Toxicol. Chem., 2002, 21, 1323–1329.
11. A. Agüera, A. R. Fernández-Alba, L. Piedra, M. Mézcua and M. J. Gómez, Evaluation of triclosan and biphenylol in marine sediments and urban wastewaters by pressurized liquid extraction and solid phase extraction followed by gas chromatography mass spectrometry and liquid chromatography mass spectrometry, Anal. Chim. Acta, 2003, 480, 193–205.
12. P. Verlicchi, M. Al Aukidy and E. Zambello, Occurrence of pharmaceutical compounds in urban wastewater: Removal, mass load and environmental risk after a secondary treatment-A review, Sci. Total Environ., 2012, 429, 123–155.
13. S. Mohan and P. Balakrishnan, Triclosan in Treated Wastewater from a City Wastewater Treatment Plant and its Environmental Risk Assessment, Water, Air, Soil Pollut., 2019, 230, 69.
14. S. Graumnitz and D. Jungmann, Report No. FB000627/ENG: the database ‘Pharmaceuticals in the Environment’ Update for the period 2017–2020, 2021, https://www.umweltbundesamt.de/sites/default/files/medien/479/publikationen/texte_163-2021_the_database_pharmaceuticals_in_the_environment.pdf.
15. D. R. Orvos, D. J. Versteeg, J. Inauen, M. Capdevielle, A. Rothenstein and V. Cunningham, Aquatic toxicity of triclosan, Environ. Toxicol. Chem., 2002, 21, 1338–1349.
16. A. D. Russell, Whither triclosan?, J. Antimicrob. Chemother., 2004, 53, 693–695.
17. A. Karkman, T. T. Do, F. Walsh and M. P. J. Virta, Antibiotic-Resistance Genes in Waste Water, Trends Microbiol., 2018, 26, 220–228.
18. A. Macherius, D. R. Lapen, T. Reemtsma, J. Römbke, E. Topp and A. Coors, Triclocarban, triclosan and its transformation product methyl triclosan in native earthworm species four years after a commercial-scale biosolids application, Sci. Total Environ., 2014, 472, 235–238.
19. K. Aranami and J. W. Readman, Photolytic degradation of triclosan in freshwater and seawater, Chemosphere, 2007, 66, 1052–1056.
20. T. aus der Beek, F.-A. Weber, A. Bergmann, S. Hickmann, I. Ebert, A. Hein and A. Küster, Pharmaceuticals in the environment-Global occurrences and perspectives, Environ. Toxicol. Chem., 2016, 35, 823–835.
21. M. K. Shahid, A. Kashif, A. Fuwad and Y. Choi, Current advances in treatment technologies for removal of emerging contaminants from water – A critical review, Coord. Chem. Rev., 2021, 442, 213993.
22. Z. Luo, Y. He, D. Zhi, L. Luo, Y. Sun, E. Khan, L. Wang, Y. Peng, Y. Zhou and D. C. W. Tsang, Current progress in treatment techniques of triclosan from wastewater: A review, Sci. Total Environ., 2019, 696, 133990.
23. B. Quan, X. Li, H. Zhang, C. Zhang, Y. Ming, Y. Huang, Y. Xi, X. Weihua, L. Yunguo and Y. Tang, Technology and principle of removing triclosan from aqueous media: A review, Chem. Eng. J., 2019, 378, 122185.
24. S. Kim, J. Chen, T. Cheng, A. Gindulyte, J. He, S. He, Q. Li, B. A. Shoemaker, P. A. Thiessen, B. Yu, L. Zaslavsky, J. Zhang and E. E. Bolton, PubChem in 2021: new data content and improved web interfaces, Nucleic Acids Res., 2021, 49, D1388–D1395.
25. A. Rossner, S. A. Snyder and D. R. U. Knappe, Removal of emerging contaminants of concern by alternative adsorbents, Water Res., 2009, 43, 3787–3796.
26. A. A. Sharipova, S. B. Aidarova, N. E. Bekturganova, A. Tleuova, M. Schenderlein, O. Lygina, S. Lyubchik and R. Miller, Triclosan as model system for the adsorption on recycled adsorbent materials, Colloids Surf., A, 2016, 505, 193–196.
27. Y. Tong, B. K. Mayer and P. J. McNamara, Triclosan adsorption using wastewater biosolids-derived biochar, Environ. Sci.: Water Res. Technol., 2016, 2, 761–768.
28. I. Braschi, S. Blasioli, E. Buscaroli, D. Montecchio and A. Martucci, Physicochemical regeneration of high silica zeolite Y used to clean-up water polluted with sulfonamide antibiotics, J. Environ. Sci., 2016, 43, 302–312.
29. D. J. De Ridder, J. Q. J. C. Verberk, S. G. J. Heijman, G. L. Amy and J. C. Van Dijk, Zeolites for nitrosamine and pharmaceutical removal from demineralised and surface water: Mechanisms and efficacy, Sep. Purif. Technol., 2012, 89, 71–77.
30. N. Jiang, R. Shang, S. G. J. Heijman and L. C. Rietveld, High-silica zeolites for adsorption of organic micro-pollutants in water treatment: A review, Water Res., 2018, 144, 145–161.
31. C. Baerlocher and L. B. McCusker, Database of Zeolite Structures, 2022, http://www.iza-structure.org/databases/.
32. N. Jiang, R. Shang, S. G. J. Heijman and L. C. Rietveld, Adsorption of triclosan, trichlorophenol and phenol by high-silica zeolites: Adsorption efficiencies and mechanisms, Sep. Purif. Technol., 2020, 235, 116152.
33. C. Lei, Y. Y. Hu and M. Z. He, Adsorption characteristics of triclosan from aqueous solution onto cetylpyridinium bromide (CPB) modified zeolites, Chem. Eng. J., 2013, 219, 361–370.
34. S. Alvarez-Garciá, G. MacEdo-Miranda, S. Martínez-Gallegos, E. Ordoñez-Regíl, J. López-Castillo and E. Aguirre-Miranda, Removal of triclosan by CTAB-modified zeolite-rich tuff from aqueous solutions, MRS Adv., 2020, 3257–3264.
35. V. Van Speybroeck, K. Hemelsoet, L. Joos, M. Waroquier, R. G. Bell and C. R. A. Catlow, Advances in theory and their application within the field of zeolite chemistry, Chem. Soc. Rev., 2015, 44, 7044–7111.
36. M. Fischer, Simulation-based evaluation of zeolite adsorbents for the removal of emerging contaminants, Mater. Adv., 2020, 1, 86–98.
37. M. Fischer, Studying the adsorption of emerging organic contaminants in zeolites with dispersion-corrected density functional theory calculations: From numbers to recommendations, ChemRxiv, 2022, preprint,  DOI:10.26434/chemrxiv-2022-nz7rz.
38. I. Braschi, G. Gatti, G. Paul, C. E. Gessa, M. Cossi and L. Marchese, Sulfonamide antibiotics embedded in high silica zeolite Y: A combined experimental and theoretical study of host–guest and guest-guest interactions, Langmuir, 2010, 26, 9524–9532.
39. I. Braschi, G. Paul, G. Gatti, M. Cossi and L. Marchese, Embedding monomers and dimers of sulfonamide antibiotics into high silica zeolite Y: An experimental and computational study of the tautomeric forms involved, RSC Adv., 2013, 3, 7427–7437.
40. X. Wei, Y. Wang, A. J. Hernández-Maldonado and Z. Chen, Guidelines for rational design of high-performance absorbents: A case study of zeolite adsorbents for emerging pollutants in water, Green Energy Environ., 2017, 2, 363–369.
41. M. Fischer, Adsorption of Carbamazepine in All-Silica Zeolites Studied with Density Functional Theory Calculations, ChemPhysChem, 2023, 24, e202300022.
42. A. I. Ramos, S. S. Braga and F. A. Almeida Paz, Triclosan, Acta Crystallogr., Sect. C: Cryst. Struct. Commun., 2009, 65, o404–o405.
43. H. Sun, S. J. Mumby, J. R. Maple and A. T. Hagler, An ab Initio CFF93 All-Atom Force Field for Polycarbonates, J. Am. Chem. Soc., 1994, 116, 2978–2987.
44. M. V. Vener, X. Rozanska and J. Sauer, Protonation of water clusters in the cavities of acidic zeolites: (H₂O)_n·H-chabazite, n = 1–4, Phys. Chem. Chem. Phys., 2009, 11, 1702–1712.
45. S. Eckstein, P. H. Hintermeier, R. Zhao, E. Baráth, H. Shi, Y. Liu and J. A. Lercher, Influence of Hydronium Ions in Zeolites on Sorption, Angew. Chem., Int. Ed., 2019, 58, 3450–3455.
46. K. Momma and F. Izumi, VESTA 3 for three-dimensional visualization of crystal, volumetric and morphology data, J. Appl. Crystallogr., 2011, 44, 1272–1276.
47. M. A. Camblor, A. Corma and S. Valencia, Spontaneous nucleation and growth of pure silica zeolite-beta free of connectivity defects, Chem. Commun., 1996, 2365–2366.
48. J. B. Higgins, R. B. LaPierre, J. L. Schlenker, A. C. Rohrman, J. D. Wood, G. T. Kerr and W. J. Rohrbaugh, The framework topology of zeolite beta, Zeolites, 1988, 8, 446–452.
49. J. A. Hriljac, M. M. Eddy, A. K. Cheetham, J. A. Donohue and G. J. Ray, Powder Neutron Diffraction and ²⁹Si MAS NMR Studies of Siliceous Zeolite-Y, J. Solid State Chem., 1993, 106, 66–72.
50. R. Bialek, W. M. Meier, M. Davis and M. J. Annen, The synthesis and structure of SSZ-24, the silica analog of AlPO₄-5, Zeolites, 1991, 11, 438–442.
51. P. A. Barrett, M. A. Camblor, A. Corma, R. H. Jones and L. A. Villaescusa, Structure of ITQ-4, a New Pure Silica Polymorph Containing Large Pores and a Large Void Volume, Chem. Mater., 1997, 9, 1713–1715.
52. W. Kolodziejski, P. J. Barrie, H. He and J. Klinowski, Two-dimensional J-scaled ²⁹Si NMR COSY of highly siliceous mordenite, J. Chem. Soc., Chem. Commun., 1991, 961–962.
53. R. Fantini, R. Arletti, S. Quartieri, M. Fabbiani, S. Morandi, G. Martra, F. Di Renzo and G. Vezzalini, Thermal behavior of high silica mordenite, Microporous Mesoporous Mater., 2020, 294, 109882.
54. P. Wagner, M. Yoshikawa, M. Lovallo, K. Tsuji, M. Taspatsis and M. E. Davis, CIT-5: a high-silica zeolite with 14-ring pores, Chem. Commun., 1997, 2179–2180.
55. L. Leardini, S. Quartieri, G. Vezzalini and R. Arletti, Thermal behaviour of siliceous faujasite: Further structural interpretation of negative thermal expansion, Microporous Mesoporous Mater., 2015, 202, 226–233.
56. M. Czjzek, H. Jobic, A. N. Fitch and T. Vogt, Direct determination of proton positions in D-Y and H-Y zeolite samples by neutron powder diffraction, J. Phys. Chem., 1992, 96, 1535–1540.
57. K. Suzuki, N. Katada and M. Niwa, Detection and quantitative measurements of four kinds of OH in HY zeolite, J. Phys. Chem. C, 2007, 111, 894–900.
58. A. J. Jones and E. Iglesia, The Strength of Brønsted Acid Sites in Microporous Aluminosilicates, ACS Catal., 2015, 5, 5741–5755.
59. J. R. Hill and J. Sauer, Molecular mechanics potential for silica and zeolite catalysts based on ab initio calculations. 1. Dense and microporous silica, J. Phys. Chem., 1994, 98, 1238–1244.
60. M. P. Allen and D. J. Tildesley, Computer Simulation of Liquids, Oxford University Press, Oxford, UK, 1st edn, 2017, vol. 1.
61. J. VandeVondele, M. Krack, F. Mohamed, M. Parrinello, T. Chassaing and J. Hutter, Quickstep: Fast and accurate density functional calculations using a mixed Gaussian and plane waves approach, Comput. Phys. Commun., 2005, 167, 103–128.
62. T. D. Kühne, M. Iannuzzi, M. Del Ben, V. V. Rybkin, P. Seewald, F. Stein, T. Laino, R. Z. Khaliullin, O. Schütt, F. Schiffmann, D. Golze, J. Wilhelm, S. Chulkov, M. H. Bani-Hashemian, V. Weber, U. Borštnik, M. Taillefumier, A. S. Jakobovits, A. Lazzaro, H. Pabst, T. Müller, R. Schade, M. Guidon, S. Andermatt, N. Holmberg, G. K. Schenter, A. Hehn, A. Bussy, F. Belleflamme, G. Tabacchi, A. Glöβ, M. Lass, I. Bethune, C. J. Mundy, C. Plessl, M. Watkins, J. VandeVondele, M. Krack and J. Hutter, CP2K: An electronic structure and molecular dynamics software package – Quickstep: Efficient and accurate electronic structure calculations, J. Chem. Phys., 2020, 152, 194103.
63. I. Hamada, van der Waals density functional made accurate, Phys. Rev. B: Condens. Matter Mater. Phys., 2014, 89, 121103.
64. M. Krack, Pseudopotentials for H to Kr optimized for gradient-corrected exchange-correlation functionals, Theor. Chem. Acc., 2005, 114, 145–152.
65. J. VandeVondele and J. Hutter, Gaussian basis sets for accurate calculations on molecular systems in gas and condensed phases, J. Chem. Phys., 2007, 127, 114105.
66. S. Nosé, A unified formulation of the constant temperature molecular dynamics methods, J. Chem. Phys., 1984, 81, 511–519.
67. W. G. Hoover, Canonical dynamics: Equilibrium phase-space distributions, Phys. Rev. A: At., Mol., Opt. Phys., 1985, 31, 1695–1697.
68. W. Humphrey, A. Dalke and K. Schulten, VMD: Visual molecular dynamics, J. Mol. Graphics, 1996, 14, 33–38.
69. M. Brehm and B. Kirchner, TRAVIS – A Free Analyzer and Visualizer for Monte Carlo and Molecular Dynamics Trajectories, J. Chem. Inf. Model., 2011, 51, 2007–2023.
70. M. Brehm, M. Thomas, S. Gehrke and B. Kirchner, TRAVIS—A free analyzer for trajectories from molecular simulation, J. Chem. Phys., 2020, 152, 164105.
71. R. Rungsirisakun, T. Nanok, M. Probst and J. Limtrakul, Adsorption and diffusion of benzene in the nanoporous catalysts FAU, ZSM-5 and MCM-22: A molecular dynamics study, J. Mol. Graphics Modell., 2006, 24, 373–382.
72. D. Zhai, L. Zhao, J. Gao and C. Xu, Effect of temperature on the diffusion mechanism of xylene isomers in a FAU zeolite: a molecular dynamics study, Phys. Chem. Chem. Phys., 2012, 14, 7296–7303.
73. S. Alvarez, A cartography of the van der Waals territories, Dalton Trans., 2013, 42, 8617–8636.
74. S. Kulprathipanja, Zeolites in Industrial Separation and Catalysis, Wiley-VCH Verlag GmbH & Co. KGaA, Weinheim, Germany, 2010.
75. Y. G. Bushuev, G. Sastre, J. V. de Julián-Ortiz and J. Gálvez, Water–Hydrophobic Zeolite Systems, J. Phys. Chem. C, 2012, 116, 24916–24929.
76. H. Jabraoui, I. Khalil, S. Lebègue and M. Badawi, Ab initio screening of cation-exchanged zeolites for biofuel purification, Mol. Syst. Des. Eng., 2019, 4, 882–892.
77. S. W. Peterson and H. A. Levy, A single-crystal neutron diffraction study of heavy ice, Acta Crystallogr., 1957, 10, 70–76.

---

Footnote

† Electronic supplementary information (ESI) available: Associated material includes a PDF document with additional computational details, tables (Tables S1 to S11) and figures (Fig. S1 to S12). See DOI: https://doi.org/10.1039/d3va00078h. ZIP archives containing results of preliminary calculations for H-FAU and H-MOR (01_H-FAU_H-MOR_models.zip), results of TZVP single-point calculations (02_TZVP_results.zip), and AIMD trajectories (in separate archives, labels starting with 03_ and 04_) can be retrieved from: https://doi.org/10.26434/chemrxiv-2023-c5q6w-v2.

---