Lower limit characterization of segregation degree for large-size low-alloy steel
Xiaofen
Zhang
ab,
Yunhai
Jia
 *a,
Zhigang
Yang
*c,
Liang
Sheng
a,
Baibing
Li
b,
Yong
Lyu
ab,
Shanshan
Xu
b,
Chunyan
Zhang
c and
Zhihao
Tang
c
*a,
Zhigang
Yang
*c,
Liang
Sheng
a,
Baibing
Li
b,
Yong
Lyu
ab,
Shanshan
Xu
b,
Chunyan
Zhang
c and
Zhihao
Tang
c
aBeijing Advanced Innovation Center for Materials Genome Engineering, Central Iron and Steel Research Institute, Beijing, 100081, China. E-mail: jiayunhai@ncschina.com
bUniversity of Science and Technology Beijing, Beijing, 100083, China
cBeijing Key Laboratory of Metal Materials Characterization, The NCS Testing Technology Co., Ltd., Beijing, 100081, China. E-mail: yangzhigang@ncschina.com
First published on 12th December 2023
Abstract
Based on the original position statistic distribution analysis technique, the characterization method of segregation for large-size metal materials gives significant guidance to the research of material properties and production. However, random errors are inevitably brought into the calculation of segregation degree for materials characterization by the Spark Mapping Analysis for Large Sample (SMALS) technique, resulting in a misguide of the segregation degree. In this paper, we present the lower limit of segregation degree (Ds(L)) method to distinguish the random error from metal material segregation for large-size samples over the SMALS method. The random error of standard material in the 95% confidence interval was utilized as Ds(L) and the method has been applied for macro-segregation quantitative analysis. The precision correlation between Spark Atomic Emission Spectrometry (Spark-AES) and SMALS was established. Furthermore, the functional relationship between the Ds(L) and element content C can be obtained in the SMALS method. The Ds(L) method as the criterion can be used to not only characterize the minimum limit of the segregation degree but also the segregation existence for large-size samples. Applying to low-alloy steel can illustrate the effective performance of the Ds(L) method. Results on both spark mapping analysis and Spark-AES verify the substantial consistency.
1 Introduction
Elemental segregation1–5 is an inevitable phenomenon in the production process of billet and has a great impact on the properties of steel. The properties are closely related to the structure and composition of the material. Mortazavi et al.6,7 undertook simulations and calculations to confirm the mechanical and optoelectronic properties of 2D materials based on atomic structure by first-principles. The different solidification rate of elements leads to homogeneous distribution of chemical components. The quantitative evaluation of segregation degree is crucial for product parameter improvement and subsequent process setting. The Original Position Statistic Distribution Analysis (OPA) technique8–10 was proposed and used to study the internal characteristics and material properties over the past two decades. This technology quantitatively determines the composition distribution of different elements for large-scale metal materials. The Spark Mapping Analysis for Large Sample (SMALS) technique11 was designed and developed to map super-large-scale samples for full-surface analysis in 2022. The analytical techniques adopt no preignition, continuous scanning excitation, and single spark discharge, which are distinct from Spark Atomic Emission Spectrometry (Spark-AES).12–14 SMALS and OPA techniques can qualitatively and quantitatively characterize the element homogeneity of metal materials, and accurately express the segregation degree of each element for the large-size material.OPA and SMALS methodologies have been introduced to obtain better analytical results.15–18 For example, Wang15 used the OPA technique to carry out statistical distribution analysis for low-alloy steel continuous casting billets and calculate the maximum segregation degree. The difference between an equiaxed sample and a columnar sample was quantitatively compared. Sheng11 characterized the multiple elements composition distribution of high-speed rail axle casting billets in 1000 mm × 250 mm by SMALS, and compared with other characterization methods, which proved the accuracy of SMALS results. However, the evaluation criteria of segregation degree for large-size samples are rarely studied. Wang19 proposed two judgment models: the total weight ratio of carbon contents within the permissive content range (C0 ± R) of statistical distribution and the confidence extension ratio of the median value (K) at 95% of the confidence limit of the weight ratio, which characterize the segregation degree of continuous casting quality billets by OPA. Zhang20 proposed a segregation degree evaluation method for large-size metal materials using the SMALS technique, which formulates the upper limit equation of segregation degree by the 95% prediction interval limit of the regression equation of permissible deviation and element content. However, there is almost no research on the lower limit of segregation degree for large-size samples by SMALS.
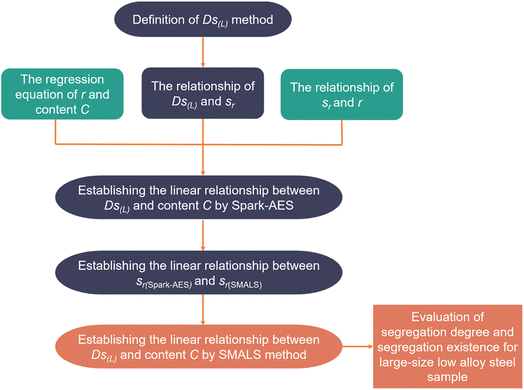
Firstly, the reference material normally contains no segregation because of better homogeneity but still shows a small segregation value due to the random error in detection. This random fluctuation has an impact on the results of segregation degree using calculation methods for the segregation degree. Next, the two-dimensional or three-dimensional contour map uses a color scale for qualitative judgment of sample segregation in most studies. Due to no definite specification for setting the color scale, visual error and misjudgment possibly are caused by color difference. Therefore, it is necessary to introduce the Ds(L) as the criterion for large-size sample by SMALS, and the random error limit of the reference material can be set as the low segregation limit. Fig. 1 shows the derivation process of the Ds(L) formula based on SMALS. SMALS and Spark-AES were used to analyze carbon steel and low-alloy steel. The correlation between the two methods was investigated, and the Ds(L) equation about the content of each element was obtained based on the SMALS method.
2 Experimental section
2.1 Equipment
The SMALS analyzer was used, and the X and Y axes of SMALS control the movement of the low-alloy steel sample platform. The full surface processing of the samples was carried out, and the sample platform was moved to the spark stand in the lower part of the spectrometer. The steel samples were moved along the planned path to realize full-scale surface analysis.2.2 Sample preparation and instrument parameters
The milling system adopts cooling compressed air with water and oil filtered. The parallelism error of the upper and bottom surfaces is less than 0.015 mm. The roughness is less than 3.2 μm, the speed is 800 rpm, and the scanning speed is 1 mm s−1. The relevant working parameters of the SMALS system are shown in Table 1. The working parameters of the Spark-AES method are the same as SMALS.| Item | Value |
|---|---|
| Spark excitation frequency/Hz | 500 |
| Excitation capacitance/μF | 7.0 |
| Pre-burning voltage/V | 360 |
| Integration voltage/V | 190 |
| Argon flow rate/L min−1 | 8 |
| Tungsten electrode | Diameter 6 mm with sharp end 90° |
| Wavelength range/nm | 160 to 650 |
| PMT diameter/mm | 13 |
| PMT sensitivity/μA lm−1 | 40 |
2.3 Sample analysis
Homogeneous samples of carbon steel or low-alloy steel were selected as test objects to eliminate the impact of segregation on random error. The chemical compositions of 6 square standard samples with side lengths of 60 mm are shown in Table 2.| 1 | 2 | 3 | 4 | 5 | 6 | |
|---|---|---|---|---|---|---|
| C | 0.215 | 0.424 | 0.082 | 0.634 | 0.008 | 0.036 |
| Si | 0.135 | 0.244 | 0.487 | 0.333 | 0.643 | 0.786 |
| Mn | 0.268 | 0.139 | 0.435 | 0.652 | 1.281 | 1.739 |
| P | 0.017 | 0.026 | 0.049 | 0.037 | 0.006 | 0.041 |
| S | 0.006 | 0.03 | 0.025 | 0.037 | 0.024 | 0.014 |
| Cr | 0.76 | 0.369 | 1.451 | 0.991 | 0.119 | 1.71 |
| Ni | 0.977 | 1.595 | 0.692 | 1.383 | 0.444 | 0.136 |
| Mo | 1.06 | 0.501 | 1.192 | 0.141 | 1.16 | 0.70 |
| Cu | 0.236 | 0.054 | 0.433 | 0.138 | 0.182 | 0.319 |
| V | 0.298 | 0.407 | 0.077 | 0.231 | 0.526 | 0.069 |
| Nb | 0.209 | 0.045 | 0.096 | 0.284 | 0.15 | 0.219 |
| Al | 0.055 | 0.536 | 0.099 | 0.259 | 0.381 | 0.007 |
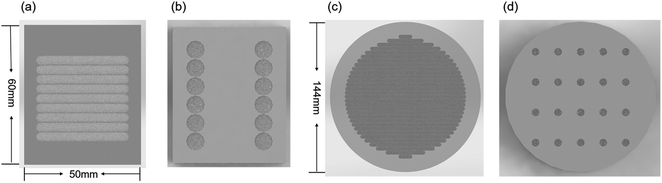
The six standard samples were analyzed by SMALS and Spark-AES, as shown in Fig. 2(a) and (b). The SMALS mapping area is 36 mm × 36 mm, and the effective excitation spot is 4 mm. A total of 12 spectral analyses were performed by Spark-AES on every sample surface. A large-size low-alloy steel sample was selected as the application sample. The steel was taken for SMALS full-scale surface analysis, where the mapping diameter is 124 mm (Fig. 2(c)). 20 spectral analyses were performed at uniformly distributed locations on the sample surface by Spark-AES (Fig. 2(d)).
3 Results and discussion
3.1 Establishing the lower limit of segregation degree for Spark-AES
Segregation (SE) is the phenomenon of smelted components differing from finished components. Degree of segregation (Ds) is defined as the ratio of segregation to the overall average value. The total mean of the element content in the sample is taken as the melting component, and the content in a position or an area of the sample is taken as the finished component.The segregation value of the finished product is the content of a position (x, y) or the average content of an area C minus the total average content of the finished product 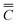 , eqn (1) as follows:
, eqn (1) as follows:
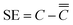 | (1) |
The segregation degree is divided into positive segregation degree (Ds(P)) and negative segregation degree (Ds(N)), as shown in eqn (2) and (3).
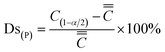 | (2) |
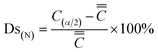 | (3) |
Any analysis method will have a random error, and the random error cannot be corrected, and increasing the number of parallel experiments may reduce the random error fluctuation. At the same time, the random error in testing from the instrument cannot be regarded as material segregation, so the composition change introduced by segregation must be greater than the random testing error of the standard material, otherwise measurement error will be confused with segregation. The random error has a normal distribution, and the absolute value of the error will not exceed a certain limit under a certain confidence probability (where α = 0.05). This limit value can be used as the lower limit of segregation degree of large-size metal materials. The lower limit value of segregation can be expressed by formula (4):
| Ds(L) = 1.96sr/C | (4) |
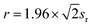 | (5) |
The functional relationship between Ds(L) and r can be obtained by substituting sr derived from formula (5) into formula (4). Moreover, the precision data in ASTM E415-15 Standard Test Method for Analysis of Carbon and Low-Alloy Steel by Spark Atomic Emission Spectrometry gave the values corresponding to the repeatability limits r and content C of each element in carbon steel and low-alloy steel measured by Spark Atomic Emission Spectrometry. Since the contents of several standard materials of V and Al exceeded the content range given by ASTM E415-15, the precision equations of GB/T 11170-2008 Stainless steel—Determination of multi-element contents-Spark discharge atomic emission spectrometric method were added. The regression equations of the repeatability limits r of each element by Spark-AES to content C were calculated, as shown in Table 3.
| Element | Content range C/% | Repeatability limit r/% | R 2 |
|---|---|---|---|
| C | 0.02–1.1 | r = 0.0133C + 0.0036 | 0.926 |
| Si | 0.02–1.54 | r = 0.0147C + 0.0005 | 0.921 |
| Mn | 0.03–2.0 | r = 0.0186C − 0.0016 | 0.849 |
| P | 0.006–0.085 | r = 0.1478C + 0.0017 | 0.916 |
| S | 0.001–0.055 | r = 0.1581C − 0.0003 | 0.867 |
| Cr | 0.007–8.14 | r = 0.0089C + 0.0004 | 0.967 |
| Ni | 0.006–5.0 | r = 0.0133C + 0.0004 | 0.982 |
| Mo | 0.007–1.3 | lg![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) r = 0.854 r = 0.854![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) lg lg![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) C − 1.648 C − 1.648 |
0.968 |
| V | 0.003–0.3 | r = 0.0248C + 0.0006 | 0.989 |
| 0.04–2.5 | r = 0.0222C + 0.0028 | ||
| Al | 0.006–0.093 | r = 0.0724C − 0.0001 | 0.87 |
| 0.02–2.0 | r = 0.0305C + 0.002 | ||
| Ti | 0.001–0.2 | r = 0.0809C − 0.00004 | 0.975 |
| Cu | 0.006–0.5 | r = 0.0823C + 0.000006 | 0.915 |
| Nb | 0.003–0.12 | r = 0.0879C + 0.00008 | 0.95 |
| Sb | 0.006–0.027 | r = 0.0699C + 0.0007 | 0.912 |
| N | 0.01–0.055 | r = 0.035C + 0.0007 | 0.888 |
| Zr | 0.01–0.05 | r = 0.2448C + 0.00006 | 1 |
| As | 0.003–0.1 | r = 0.1041C + 0.0004 | 0.996 |
| Sn | 0.005–0.061 | r = 0.0767C − 0.0003 | 0.919 |
The linear functional relationship between r and C of repeatability limits of C, Si, Mn, P, S, Cr, Ni, Mo, V, Al, Ti, Cu, Nb, Sb, N, Zr, As, Sn elements and the logarithmic function relation of Mo element are obtained in ASTM E415-15. The correlation coefficient R0.05,11 = 0.553 was used to check the significance for the regression equation of each element, and the R for all elements was greater than R0.05,11, indicating that the regression line determined was meaningful.
Because the repeatability limit was measured by standard materials, sr is the measurement error of Spark-AES. According to the relationship between Ds(L) and r, the functional relationship between the lower limit of segregation degree Ds(L) and the content C of each element can be obtained, and the results are shown in Table 4.
| Element | Content range (quality score) C/% | Ds(L) |
|---|---|---|
| C | 0.02–1.1 | Ds(L) = 0.0025/C + 0.0094 |
| Si | 0.02–1.54 | Ds(L) = 0.0004/C + 0.0104 |
| Mn | 0.03–2.0 | Ds(L) = 0.0011/C + 0.0132 |
| P | 0.006–0.085 | Ds(L) = 0.0012/C + 0.1045 |
| S | 0.001–0.055 | Ds(L) = 0.0002/C + 0.1118 |
| Cr | 0.007–8.14 | Ds(L) = 0.0003/C + 0.0063 |
| Ni | 0.006–5.0 | Ds(L) = 0.0003/C + 0.0094 |
| Mo | 0.007–1.3 | Ds(L) = 0.0159C−0.146 |
| V | 0.003–0.3 | Ds(L) = 0.0004/C + 0.0175 |
| 0.04–2.5 | Ds(L) = 0.0020/C + 0.0157 | |
| Al | 0.006–0.093 | Ds(L) = −0.00007/C + 0.0512 |
| 0.02–2.0 | Ds(L) = 0.0014/C + 0.0216 | |
| Ti | 0.001–0.2 | Ds(L) = 0.00003/C + 0.0572 |
| Cu | 0.006–0.5 | Ds(L) = 0.000004/C + 0.0582 |
| Nb | 0.003–0.12 | Ds(L) = 0.00006/C + 0.0622 |
| Sb | 0.006–0.027 | Ds(L) = 0.0005/C + 0.0494 |
| N | 0.01–0.055 | Ds(L) = 0.0005/C + 0.0247 |
| Zr | 0.01–0.05 | Ds(L) = 0.00004/C + 0.1731 |
| As | 0.003–0.1 | Ds(L) = 0.0003/C + 0.0736 |
| Sn | 0.005–0.061 | Ds(L) = 0.0002/C + 0.0542 |
The lower limit segregation equation is for the Spark-AES method and applies only to carbon and low-alloy steels. The content ranges are listed in Table 4, with Ds(L) corresponding to each content. If the maximum positive and negative segregation of the sample measured by Spark-AES is less than Ds(L), it indicates no segregation or the segregation is so small as to be negligible. The correlation of the standard deviation sr between the SMALS method and the Spark-AES method will be established. The lower limit of segregation degree will be used as the criterion to judge segregation existence in the sample for the SMALS method. If the positive and negative segregation degree of an element in a large sample is less than the Ds(L), no segregation of the element in the sample will occur.
3.2 Establishing of the lower limit of segregation degree for the SMALS method
The standard deviations of the SMALS results of C, Si, Mn, P, S, Cr, Ni, Mo, V, Al elements with 6 standard samples and the standard deviations of Spark-AES were calculated, and the correlation between them was established. The standard deviation S(SMALS) of the SMALS of C, Si, Mn, P, S, Cr, Ni, Mo, V, Al elements was taken as the y-axis, and the standard deviation of the Spark-AES results S(Spark-AES) of each element was taken as the x-axis, and linear regression was fitted. At the same time, the regression equation of Mo element lg![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) S(SMALS) to lg
S(SMALS) to lg![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) S(Spark-AES) was calculated, as shown in Fig. 3.
S(Spark-AES) was calculated, as shown in Fig. 3.
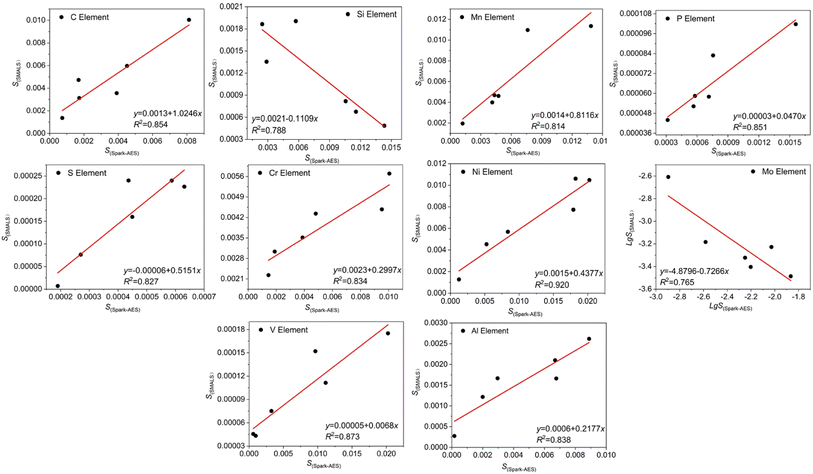 | ||
| Fig. 3 Standard deviation fitting curves of the Spark-AES method and the SMALS method for elements C, Si, Mn, P, S, Cr, Ni, Mo, V and Al. | ||
The linear regression equation and determination coefficient R2 of the standard deviation of the SMALS results and Spark-AES results of a series of large-size standard samples are shown in Fig. 3. The correlation coefficient R0.05,4 = 0.811 was used to conduct significance tests for the regression equations of C, Si, Mn, P, S, Cr, Ni, Mo, V, Nb and Al elements. The correlation coefficient R of all elements was greater than R0.05,4, indicating that the regression line determined was meaningful.
The regression equations obtained from standard deviations of C, Si, Mn, P, S, Cr, Ni, Mo, V, Al and the functional relationship between the Ds(L) and C of Spark-AES are substituted into the formula (4) to obtain the functional relationship between the Ds(L) and C of SMALS for each element, as shown in Table 5.
| Element | Content range (quality score) C/% | Ds(L) |
|---|---|---|
| C | 0.02–1.1 | Ds(L) = 0.0052/C + 0.0096 |
| Si | 0.02–1.54 | Ds(L) = 0.0042/C − 0.0012 |
| Mn | 0.03–2.0 | Ds(L) = 0.0037/C + 0.0107 |
| P | 0.006–0.085 | Ds(L) = 0.00006/C + 0.0049 |
| S | 0.001–0.055 | Ds(L) = −0.00002/C + 0.0576 |
| Cr | 0.007–8.14 | Ds(L) = 0.0047/C + 0.0019 |
| Ni | 0.006–5.0 | Ds(L) = 0.0031/C + 0.0041 |
| Mo | 0.007–1.3 | lg![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) Ds(L) = −0.6205 Ds(L) = −0.6205![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) lg lg![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) C −3.054 C −3.054 |
| V | 0.04–2.5 | Ds(L) = 0.0001/C + 0.0001 |
| Al | 0.02–2.0 | Ds(L) = 0.0015/C + 0.0047 |
3.3 Application to large-size low-alloy steel
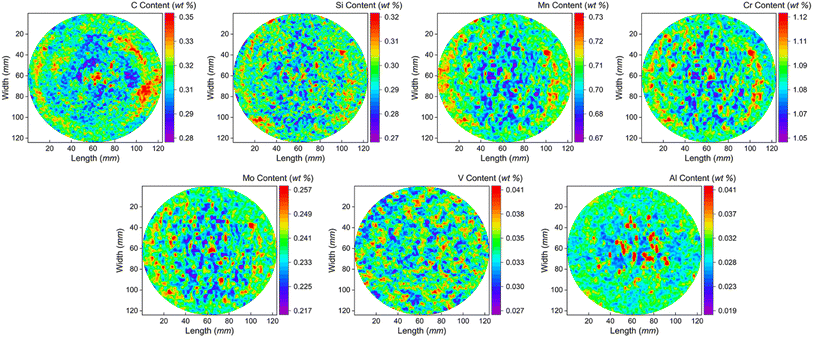
The low-alloy steel matrix is a tempered sorbite structure, containing alloying elements such as Cr, Ni and Mo. The crystal structure is body-centered cubic with a lattice constant of 2.879 nm. The function relationships of C, Si, Mn, Cr, Ni, Mo, V, Al elements between Ds(L,SMALS) and Ds(L,Spark-AES) are applied to the sample of the large-size low-alloy steel. The two-dimensional content distribution maps of C, Si, Mn, Cr, Mo, V and Al elements of the low-alloy steel sample are shown in Fig. 4. Each content value corresponds to a different position on the surface of the sample, and the intensity of each signal reflects the chemical composition information of the original position. In the distribution map, the horizontal axis is sample length and the vertical axis is sample width, and the color scale from blue to red indicates the increase in element content gradually.The C, Si, Mn, Cr, Mo, V and Al composition content distributions are heterogeneous at the surface, and C, Si, Mn, Cr, Mo have pattern segregation. The phenomenon's main reason may be that in the condensation process of the ingot, the surface temperature is lower than the interior, the outer region cooling speed is fast. Alloying elements such as Mn, Cr, Mo, V solidified too late to diffuse at 3/4 R (scanning diameter is R), resulting in the formation of columnar crystal and negative segregation in the interior region. During the cooling process, Fe and a large number of alloying elements form a solid solution or interstitial solid solution with C and Si elements. Therefore, the location of segregation behavior of C and Si elements is consistent with that of heavy metals. The internal heat is dissipated at the surface through diffusion, and the internal cooling rate is slower, then forming coarse equiaxed crystals. The outer columnar crystals of crystallization growth pushes the unsolidified low-melting point segregation elements and impurities to the central region. As the temperature of the molten steel in the core tends to be uniform and drops below the supercooling temperature, coarse equiaxed crystals form in the central region. Al has low solid solubility in steel, and most Al exists in the form of inclusions. Under the condition that the crystallization process is sufficient, it cannot exist between the cells and moves to the liquid phase until the core part is completely solidified and remains in the center, so these elements are mainly distributed in the center of the sample. Al elements form a large number of point segregations in the center, indicating central segregation. The formation of this non-uniform layered structure is closely related to the compositional segregation during its thermal processing.
The total amount of single sparks was 1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 562
562![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 298 by mapping the section surface of large-size low-alloy steel. These over of thousands of spectral signals can picture the probability density statistical distribution map of the element content in each original position and determine the element segregation through the peak pattern. Moreover, given the content of elements, the calculated repeatability limit r of each element is converted to repeatability standard deviation sr by formula (5), obtaining the probability density of normal distribution for each element content, which is the normal distribution for analyzing the random error of standard samples (non-segregation). According to the definition of the lower limit of segregation degree, the content value of the standard sample random error sr under 95% confidence is exceeded which illustrates element segregation existence.
298 by mapping the section surface of large-size low-alloy steel. These over of thousands of spectral signals can picture the probability density statistical distribution map of the element content in each original position and determine the element segregation through the peak pattern. Moreover, given the content of elements, the calculated repeatability limit r of each element is converted to repeatability standard deviation sr by formula (5), obtaining the probability density of normal distribution for each element content, which is the normal distribution for analyzing the random error of standard samples (non-segregation). According to the definition of the lower limit of segregation degree, the content value of the standard sample random error sr under 95% confidence is exceeded which illustrates element segregation existence.
As shown in Fig. 5, the probability density statistical distribution diagrams of elements C, Si, Mn, Cr and Al for the applied samples all have peak shape widths that exceed the 95% confidence interval of normal distribution of the standard samples, with negative segregation on the left and positive segregation on the right.
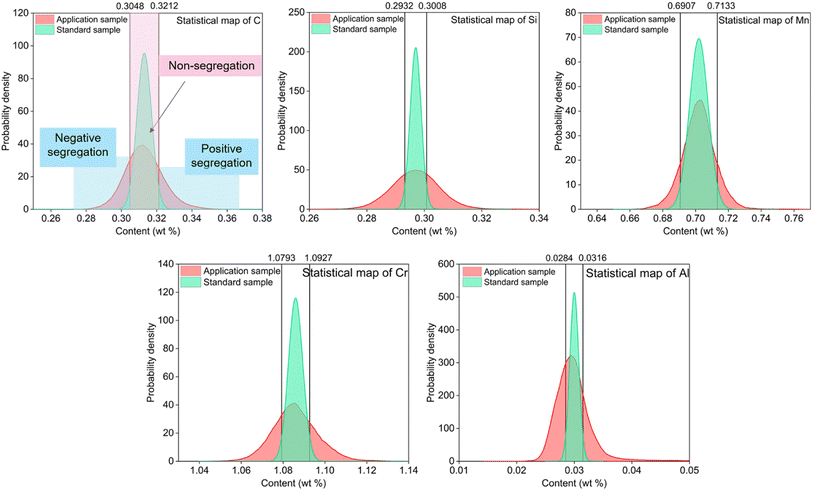 | ||
| Fig. 5 Probability density statistical maps of C, Si, Mn, Cr, Al elements in the low-alloy steel by the SMALS method. | ||
The Ds(L) of the SMALS method was used as the evaluation method for segregation existence, and the average contents of elements C, Si, Mn, Cr, Ni, Mo, Cu, V and Al were substituted into the Ds(L,SMALS) equation of each element. The analysis statistical results are shown in Table 6.
| Element | Content average wt/% | 95% confidence interval of content wt/% | Ds(N-max)/% | Ds(P-max)/% | Ds(L)/% | |
|---|---|---|---|---|---|---|
| C | 0.313 | 0.2931 | 0.336 | −6.36 | 7.35 | 2.61 |
| Si | 0.297 | 0.2811 | 0.3134 | −5.35 | 5.52 | 1.28 |
| Mn | 0.702 | 0.6819 | 0.7218 | −2.86 | 2.82 | 1.60 |
| Cr | 1.086 | 1.0649 | 1.1089 | −1.94 | 2.11 | 0.62 |
| Ni | 1.09 | 0.924 | 1.2319 | −15.23 | 13.02 | 0.70 |
| Mo | 0.237 | 0.2236 | 0.2509 | −5.65 | 5.86 | 0.22 |
| Cu | 0.048 | 0.0446 | 0.0514 | −7.08 | 7.08 | 0.23 |
| V | 0.034 | 0.0208 | 0.0471 | −38.82 | 38.53 | 0.30 |
| Al | 0.03 | 0.0251 | 0.0382 | −16.33 | 27.33 | 5.42 |
The maximum positive and negative segregation degrees of C, Si, Mn, Cr, Ni, Mo, Cu, V and Al are all greater than the Ds(L,SMALS) in Table 6, indicating that segregation exists in the sample. Moreover, the two-dimensional composition distribution of each element shows the segregation behavior. The calculated results are consistent with the content distribution diagram and probability density statistical map.
The large-size low-alloy steel was analyzed at 20 points by Spark-AES, which was evenly distributed on the full surface. The probability density distribution of each element content was obtained by Gaussian fitting of these spectral points. The average contents and sr with ASTM E415-15 of C, Si, Mn, Cr, Ni, Mo, Cu and Al were used to picture the normal distribution in Fig. 6.
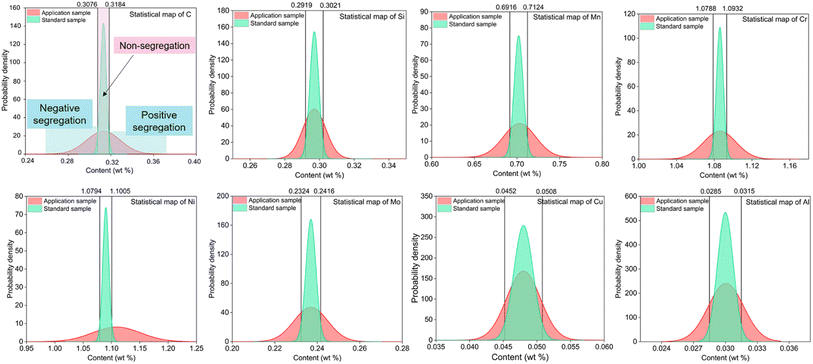 | ||
| Fig. 6 Probability density statistical maps of C, Si, Mn, Cr, Ni, Mo, Cu, Al elements in the low-alloy steel by the Spark-AES method. | ||
Compared with the statistical distribution maps of the two methods, the different peak shapes of the applied samples have two main reasons. One is the unequal analysis areas, the failure in full-scale scanning with Spark-AES, and the original position information of materials cannot be completely obtained. Another one is a different excitation pattern for two methods, Spark-AES adopts preignition for 10 s and integrates for 10 s. However, the peak width on both sides of the probability density statistical distribution diagram of elements C, Si, Mn, Cr, Ni, Mo, Cu, and Al of the applied sample exceeds the 95% confidence interval of normal distribution of the standard sample, indicating that segregation exists in the sample. The results of the SMALS method are consistent with the results of the Spark-AES method. Therefore, it has further demonstrated that Ds(L) can quantitatively determine the minimum limit of segregation degree and segregation existence using the SMALS technique.
4 Conclusion
The segregation value of elements should exceed the value of the 95% confidence coefficient of random error with the standard material. We propose the Ds(L) method as an important criterion that quantitatively characterizes the minimum limit of the segregation degree for large metal materials using the SMALS technique. Based on precision data from ASTM E415-15, the values of repeatability limit r and content C of each element in carbon steel and low-alloy steel are fitted in Spark-AES to obtain the functional relationship of each element. By establishing the functional relationship between Ds(L) and content C, we obtain the Ds(L) equation for carbon steel and low-alloy steel using Spark-AES. The correlation of precision between the SMALS and Spark-AES was established with standard deviation of non-segregation material, leading to a functional relationship of the SMALS method between the repeatability limit r and the content C of each element in carbon and low-alloy steel. Finally, we obtain the Ds(L) equation about content C using the SMALS technique.The effectiveness of the Ds(L) equations was demonstrated through successful application to low-alloy steel with the SMALS methods. The two-dimensional content distributions of C, Si, Mn, Cr, Ni, Mo, Cu elements indicate pattern segregation and center segregation of Al. In mapping data, the Ds(L) of SMALS is less than the maximum segregation in the sample which is consistent with Spark-AES data, meaning that the Ds(L) equation can be a criterion of the segregation degree and segregation existence.
Moreover, combined with the upper limit of the segregation degree equation, the Ds(L) is proposed to improve the segregation evaluation system for SMALS. Due to the Ds(L) analytical method, the qualitative analysis of the segregation for large-size samples is upgraded to quantitative characterization, and each content has a corresponding Ds(L) value one by one. This method can be used as a reference for advanced characterization technology and other steels.
Author contributions
Conceptualization: Xiaofen Zhang and Yunhai Jia; data curation and validation: Xiaofen Zhang, Baibing Li, Shanshan Xu, Yong Lyu and Zhihao Tang; writing – original draft: Xiaofen Zhang and Yunhai Jia; visualization: Xiaofen Zhang, Chunyan Zhang and Zhigang Yang; writing – reviewing and editing: Xiaofen Zhang, Yunhai Jia and Liang Sheng; project administration: Yunhai Jia and Zhigang Yang; funding acquisition and supervision: Yunhai Jia and Zhigang Yang. All authors have read and agree to the published version of the manuscript.Conflicts of interest
The authors declare that they have no known competing financial interests or personal relationships that could have appeared to influence the work reported in this paper.Acknowledgements
This work was supported by the National Key Scientific Instrument and Equipment Development Project of China (2017YFF0106200).References
- D. Manova, A. Lotnyk and S. Mändl, et al., CrN precipitation and elemental segregation during the decay of expanded austenite, Mater. Res. Express, 2016, 3, 066502, DOI:10.1088/2053-1591/3/6/066502.
- T. Michler, Y. Lee and R. P. Gangloff, et al., Influence of macro segregation on hydrogen environment embrittlement of SUS 316L stainless steel, Int. J. Hydrogen Energy, 2009, 34, 3201–3209, DOI:10.1016/j.ijhydene.2009.02.015.
- S. G. Zheng, C. Davis and M. Strangwood, Elemental segregation and subsequent precipitation during solidification of continuous cast Nb–V–Ti high-strength low-alloy steels, Mater. Charact., 2014, 95, 94–104, DOI:10.1016/j.matchar.2014.06.008.
- M. Amirthalingam, E. M. Van Der Aa and C. Kwakernaak, et al., Elemental segregation during resistance spot welding of boron containing advanced high strength steels, Weld. World, 2015, 59, 743–755, DOI:10.1007/s40194-015-0250-3.
- F. Boué-Bigne, Simultaneous characterization of elemental segregation and cementite networks in high carbon steel products by spatially-resolved laser-induced breakdown spectroscopy, Spectrochim. Acta, Part B, 2014, 96, 21–32, DOI:10.1016/j.sab.2014.03.011.
- B. Mortazavi, B. Javvaji, F. Shojaei, T. Rabczuk, A. V. Shapeev and X. Zhuang, Exceptional piezoelectricity, high thermal conductivity and stiffness and promising photocatalysis in two-dimensional MoSi2N4 family confirmed by first-principles, Nano Energy, 2021, 82, 105716, DOI:10.1016/j.nanoen.2020.105716.
- B. Mortazavi, M. Silani, E. V. Podryabinkin, T. Rabczuk, X. Zhuang and A. V. Shapeev, First-principles multiscale modeling of mechanical properties in graphene/borophene heterostructures empowered by machine-learning interatomic potentials, Adv. Mater., 2021, 33, 2102807, DOI:10.1002/adma.202102807.
- H. Z. Wang, Original position statistic distribution analysis (original position analysis), Sci. China, Ser. B: Chem., 2003, 46, 119–123, DOI:10.1360/03yb9017.
- H. Z. Wang, L. Zhao, Y. H. Jia, D. L. Li, L. X. Yang, Y. H. Lu, G. Feng and W. H. Wan, State-of-the-art review of high-throughput statistical spatial-mapping characterization technology and its applications, Engineering, 2020, 6, 621–636, DOI:10.1016/j.eng.2020.05.005.
- H. Z. Wang, Original position statistic distribution analysis (OPA)-novel statistic characterization method of different chemical compositions and its states of the materials, Mater. Sci. Forum, 2007, 539–543, 4446–4451, DOI:10.4028/www.scientific.net/MSF.539-543.4446.
- L. Sheng, L. J. Yuan, Y. H. Jia, L. Zhao, X. F. Zhang, L. Yu, Q. C. Zhang and H. Z. Wang, Full-scale spark mapping of elements and inclusions of a high-speed train axle billet, J. Anal. At. Spectrom., 2022, 37, 1522–1534, 10.1039/D2JA00009A.
- D. N. Bock and V. A. Labusov, Determination of nonmetallic inclusions in metal alloys by the method of spark atomic emission spectroscopy (review), Inorg. Mater., 2019, 55, 1415–1427, DOI:10.1134/S0020168519140012.
- R. Meilland and L. Dosdat, Rapid characterization of inclusionary cleanliness in steels by PDA-OES mapping, Rev. Metall., 2002, 99, 373–382, DOI:10.1051/metal:2002128.
- A. Bengtson, Laser Induced Breakdown Spectroscopy compared with conventional plasma optical emission techniques for the analysis of metals – A review of applications and analytical performance, Spectrochim. Acta, Part B, 2017, 134, 123–132, DOI:10.1016/j.sab.2017.05.006.
- H. Z. Wang, P. Zhao, J. W. Chen, M. L. Li, Z. J. Yang and C. Wu, Original position statistic distribution analysis study of low alloy steel continuous casting billet, Sci. China, Ser. E: Technol. Sci., 2005, 48, 104–115, DOI:10.1360/04ye0208.
- S. Carter, A. Fisher, B. Gibson, J. Marshall, B. Russell and I. Whiteside, Atomic spectrometry update: review of advances in the analysis of metals, chemicals and materials, J. Anal. At. Spectrom., 2017, 32, 2068–2117, 10.1039/C7JA90046E.
- J. H. Liu, Y. P. Bao, X. Dong, T. Q. Li, Y. Ren and S. Zhang, Distribution and segregation of dissolved elements in pipeline slab, J. Univ. Sci. Technol. Beijing, 2007, 14, 212–218, DOI:10.1016/S1005-8850(07)60041-3.
- D. L. Li, L. Zhao, X. J. Shen and H. Z. Wang, Study of inclusion characterization method in IF steel based on the spark source original position statistic distribution analytical technology (in Chinese), Spectrosc. Spectral Anal., 2020, 40, 1710–1715, DOI:10.3964/j.issn.1000-0593(2020)06-1710-06.
- H. Z. Wang, M. L. Li, J. W. Chen and C. Wu, Original position statistic distribution analysis (OPA) study on the quality of billet, Eng. Sci., 2003, 10, 34–42 Search PubMed.
- X. F. Zhang, Y. H. Jia, L. Sheng, L. J. Yuan and J. Q. Li, Characterization of segregation degree for large size metal component and application on high-speed train wheel, Anal. Chim. Acta, 2022, 1203, 339719, DOI:10.1016/j.aca.2022.339719.
| This journal is © The Royal Society of Chemistry 2024 |