Metal-free negative linear compressibility (NLC) material – the cocrystal of 1,2-bis(4-pyridyl)ethane and fumaric acid

Abstract

Materials that show significant negative linear compressibility (NLC) reported so far suffer from a number of shortcomings that affect their applicability. The cocrystal of 1,2-bis(4-pyridyl)ethane and fumaric acid, which exhibits exceptional NLC behaviour, overcomes these problems and sets the foundation for the development of environmentally friendly metal-free NLC materials.

---

Negative linear compressibility (NLC) is a rare behaviour where crystals respond to compression by expanding along one principal axis.¹ Although such a response to external stress can appear counterintuitive, it is thermodynamically possible as long as a decrease in volume is achieved by sufficient compression along the remining principal axes. Such materials can mimic the work of muscle tissue¹ and have possible applications as optical sensors and telecommunication systems that need to function under high pressure (e.g. deep in the ocean).² From this point of view, materials with large, persistent NLC, present in the industrially relevant pressure range, i.e. up to 1 and 2 GPa,^1,3 would be of the highest interest.

NLC materials reported in the literature differ in their chemical nature, NLC mechanism, as well as the magnitude and pressure range of the negative compressibility.¹ Many can be characterized by small or moderate negative compressibility, reaching only a couple of TPa⁻¹.¹ Meanwhile, cases of significant NLC are rather scarce, with the most impressive effects observed for Ag₃[Co(CN)₆] phase I (K = −76(9) TPa⁻¹; pressure range 0–0.19 GPa),⁴ InH(BCD)₂ (K = −62.4 TPa⁻¹; pressure range 0–0.53 GPa),⁵ Zn[Au(CN)₂]₂ phase I (K = −42(5) TPa⁻¹; pressure range 0–1.8 GPa)⁶ and recently a giant NLC was uncovered by density functional theory for a 3D covalent organic framework NPN-3 (K = −42.04 TPa⁻¹; pressure range 0–0.9 GPa).⁷ In 2020 Zhao et al. reported a study on a porous organic salt crystal (CPOS-1), where the most negative compressibility of −91 TPa⁻¹ was achieved at ca. 2.3 GPa, when the dried crystal was compressed in the pressure range of 1.02–2.32 GPa.⁸ However, the unusual changes in the unit-cell volume observed between 1.4 and 2.3 GPa raise some questions about the validity of this observation (see Comment sections of Table S9, ESI†).

Although these examples show exceptional NLC behaviour,^4–6,8 they are not free of deficiencies. Their synthesis can be considered cumbersome and environmentally unfriendly,^5,6 and/or they are built of expensive^6,8 and toxic^6,9 compounds. At the same time, porous NLC crystals are susceptible to sorption of small molecules (especially ubiquitous water) that can affect their performance, as observed for CPOS-1.⁸

In this work we introduce an organic cocrystal¹⁰ as an alternative to metal-containing and porous materials so far associated with the most significant NLC effects. We have discovered that a cocrystal (ETYFUM) composed of 1,2-bis(4-pyridyl)ethane (ETY) and fumaric acid (FUM), shown in Fig. 1, exhibits significant NLC, in many aspects exceptional compared to other NLC materials. It can be grown in the form of single crystals of good quality (Fig. S1–S3, ESI†) from relatively simple and inexpensive organic coformers via evaporation from hot methanol, or be synthesised in an environmentally friendly manner using solvent-assisted ball milling (Fig. S4, ESI†).

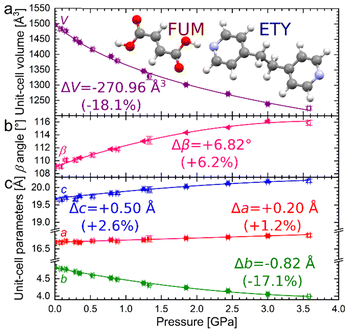Fig. 1 Pressure dependence of unit-cell volume (a), β angle (b), and unit-cell parameters (c) for ETYFUM. Full symbols: data for sample crystal A (Fig. S1, ESI†), half full: sample crystal C (left-side full: compression run 1; right-side full: compression run 2; Fig. S3, ESI†), empty: sample crystal B (Fig. S2, ESI†). For some data points, error bars are smaller than symbols. In panes (b) and (c) lines are for guiding the eye only, for volume the line represents 3rd order Birch–Murnaghan EOS¹¹ (Table S3, ESI†). The insert in pane (a) shows molecular structures of ETY and FUM.

ETYFUM crystallises in the monoclinic system, space group C2/c¹² (here discussed in an alternative setting of space group I2/a), and no phase transition was detected on its compression up to 3.6 GPa. However, an increase in two lattice parameters, a and c, is observed (by 1.2 and 2.6%, respectively), accompanied by an increase in the β angle, and a drastic decrease in lattice parameter b (by 17.1%), see Fig. 1. This leads to an overall volume reduction of more than 18%. Changes in the lattice parameters a and c (Fig. 1 and Table S1, ESI†) reflect the NLC along the principal axis roughly aligned along the 0.73a–0.68c direction (Table S2 and Fig. S5, ESI†).

The NLC effect is significant, with a median compressibility K = −24(1) TPa⁻¹/0.1 MPa–3.6 GPa range (Table S2–S6, ESI†), the most negative value of −36(6) TPa⁻¹ (at 0.1 MPa), and the least negative of −11(2) TPa⁻¹ (at 3.58(2) GPa). At the same time, a large positive linear compressibility (PLC) was recorded for the principal axis aligned with the axis b (median of 68(2) TPa⁻¹, maximum: 109(6) TPa⁻¹/0.1 MPa).

The mechanism behind NLC in ETYFUM is topological in nature and can be related to the wine rack motif (a motif widely associated with NLC^1,2,13–15), that is formed by the O–H⋯N bonded chains of alternating molecules ETY and FUM (Fig. 2 and GIF S1, ESI†). As there are no traditional hinges in the form of metal centres (present in coordination polymers), ETYFUM resembles (μ₂-1,4-di-isocyanobenzene)-bis(pentafluorophenyl)-di-gold (JOHGIX),¹⁶ for which a hingeless NLC mechanism was observed. However, in JOHGIX, molecules aggregate to form a harmonica motif not a wine rack. Instead of the hinge, a hinge point (point at which pivoting of the chains takes place) can be assigned at the oxygen atom O1 of FUM interlocked between two carbon atoms (C4, C5) of the pyridine ring of adjacent ETY (Fig. 2 and Fig. S6, ESI†), with the position being enforced by the formation of weak C–H⋯O bonds (Table S34, ESI†).

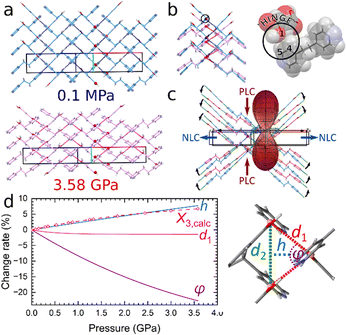Fig. 2 Part (a): structure of ETYFUM at 0.1 MPa/298 K (blue) and 3.58 GPa/298 K (pink) with selected oxygen atoms involved in hinge points shown as balls. Part (b): overlapped fragments of ETYFUM structures with the triangle motif marked by navy blue centroids and dashed lines (0.1 MPa) and red centroids and dashed lines (3.58 GPa). The black circle points to the hinge point (magnified on the right). Part (c): the superposition of fragments of ETYFUM structures overlapped with the indicatrix plot produced with PASCal^17,18 (green dashed lines – hydrogen bonds; black arrows – the direction of movement of the chains on compression; red and blue arrows – directions of PLC and NLC, respectively). Part (d): change rate for the parameters d₁, h and φ (solid lines) of a triangle, formed by centroids acting as hinge points (shown on the right), and for the length of the principal axis X₃ calculated with PASCal^17,18 (X_3,calc, dashed line and open symbols). The change rate for the parameters d₁, h and φ was obtained for the values calculated based on functions fitted to the experimental data (Fig. S7 and Tables S32, S33, ESI†).

To describe pressure-induced changes in the geometry of the wine rack, the motif can be simplified to a triangle formed by three hinge points (each represented by a centroid calculated for the triad of atoms O1, C4, and C5) positioned closest to one another (Fig. 2 and Fig. S7, ESI†). The height of the triangle is approximately aligned with the 0.73a–0.68c direction. As compression progresses, the base of triangle (d₂) becomes significantly shorter (Fig. S7, ESI†), with the decrease corresponding to the crystal compression along the direction [010]. Meanwhile, the parameter d₁ (side of the triangle) remains almost unchanged (Fig. 2d and Fig. S7, ESI†). As the crystal is compressed and the wine rack progressively flattened, the angle φ between the sides of the triangle (Fig. 2d) becomes more acute with pressure, decreasing by more than 22% on compression to 3.58 GPa. Consequently, the height of the triangle (blue dashed line in Fig. 2d) increases, as it can be linked to the parameter d₁ and φ angle in the following manner: h = d₁·cos(φ/2). As d₁ remains almost constant throughout the compression, the height of the triangle will strongly depend on the φ angle, and the smaller its value, the larger the height. We can observe that height changes at a similar rate to the change of the length of the principal axis X₃ (an NLC axis; Fig. 2d) that was calculated using PASCal^17,18 (Table S5, ESI†), directly linking deformation of the wine rack to the NLC of the crystal.

For materials of the wine rack topology, a significant NLC can be achieved by a combination of soft metal centres (e.g. those showing Jahn–Teller distortion¹⁹) and rigid ligands that would allow a large compressibility of the angle φ and a small compressibility of the parameter d₁.⁵ Such approach can be applied to ETYFUM to some degree. Instead of incorporating a soft metal hinge, it is completely removed, eliminating any restriction coming from the coordination geometry of the metal cation. Meanwhile, long H-bonded chains built of conformationally rigid coformers can be considered as very long linkers (acting as struts) that cannot be non-destructively modified by stress in other manner than by moving as a whole, with little to no change in the conformation of the chain.

The median NLC recorded for ETYFUM already puts it closer to the framework materials exhibiting significant NLC, than to most organic NLC crystals¹ (Fig. S8 and Table S7, ESI†). However, the median is not an ideal reflection of the NLC effects, as information on how the compressibility changes with pressure is lost, and its value is susceptible to many factors (see NLC comparison section in ESI†). Although it remains a good indicator to signal the potential for the material to be exceptional in terms of its NLC, a much more reliable and informative parameter is the compressibility capacity χ_K.¹ It is defined by equation 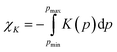, where K(p) is pressure dependence of the linear compressibility. By choosing suitable pressure limits (p_min, p_max) for integral evaluation, it is possible to determine which material exhibits the most significant NLC, i.e., for which χ_K is higher over the selected pressure range. For the moderate NLC χ_K oscillates at ca. 1%, and only in exceptional cases it gets closer to 10%,¹ bearing in mind that the wider the pressure range the higher the χ_K value. To provide a reliable function for integration, compressibility should be evaluated based on at least 10 data points.¹ Insufficient data affect the ESDs of the reported values, hinders error estimation, or leads to values lacking physical sense.

To put the NLC behaviour of ETYFUM in a broader context, its χ_K was compared with selected NLC materials in the following categories: (i) over the entire pressure range NLC persists in; (ii) for specific pressure ranges of different width with p_min set at 0.1 MPa (provided material was investigated in a given pressure range); (iii) for selected Δp bins to include materials not exhibiting NLC in ambient phases (for details, see sections: NLC comparison and Compressibility capacity calculations, Tables S8–S31 and Fig. S9, S10 in ESI†).

For the first criterion, χ_K of ETYFUM reaches 6.8% (for the range of 0.1 MPa–3.58 GPa, Fig. 3 and Fig. S9–S11, ESI†), putting it very close to Zn[Au(CN)₂]₂ I and II of χ_K = 7.6(9)% over 0–1.8 GPa and χ_K = 7(4)% over 1.8–14.2 GPa, respectively (values cited after data from the literature^1,6). However, in the case of Zn[Au(CN)₂]₂ II such a high χ_K is achieved over a span of more than 12 GPa, and the χ_K values calculated by us were lower (plausibly due to the smaller pressure ranges used in the calculations). For MIL-53(Al) χ_K of 8.5% (0–3 GPa range) was reported¹ for the experimental data of Serra–Crespo et al.²⁰ which puts it higher than ETYFUM in terms of χ_K. However, more precise data provided by Jiang et al.²¹ gave lower χ_K value (2.74%/0.1 MPa–1.8 GPa range). Despite, χ_K being calculated for a narrower pressure range (limited by the availability of data), the trend of the χ_K change with pressure makes it highly doubtful it would exceed χ_K of ETYFUM, if data up to 2.7 GPa were available to us (Fig. S10 and S11, ESI†).

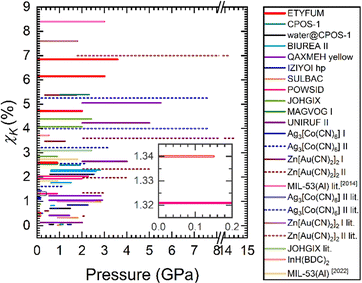Fig. 3 The compressibility capacity (χ_K) of selected NLC materials (horizontal lines) for selected pressure bins. The length of the line corresponds to the pressure range χ_K was calculated for (several lines are shown for the same material). Solid lines: values calculated in this work, double lines: data from the literature. Different phases of the same compound are marked in the same colour, but the high-pressure phases are shown with dashed lines. See Fig. S11 (ESI†) for details on sample and phase nomenclature.

The most exceptional NLC effects will be those characterised by the highest χ_K over the narrowest pressure range. Hence, it is more appropriate to consider the same pressure conditions for all materials that are being compared. If ambient pressure is selected as the p_min, we reduce the number of materials with which ETYFUM can be contrasted, as cases where NLC is triggered in the high-pressure phases will be excluded. For 0.1 MPa–0.15 GPa range ETYFUM exhibits moderate NLC (χ_K = 0.52%), and is surpassed by Ag₃[Co(CN)₆] I (χ_K = 1.10%), InH(BDC)₂ (χ_K = 1.34%), and JOHGIX (0.89%). However, in the last case, there is a significant difference in the accuracy of calculated K values at 0.1 MPa: K_ETYFUM = −36(6) TPa⁻¹ and K_JOHGIX = −76(37) TPa⁻¹. When p_max is increased to 0.9 GPa, difference in χ_K between ETYFUM and JOHGIX decreases (2.6 vs. 2.9%, respectively). For both ranges discussed so far, ETYFUM surpasses one of the material described as exhibiting giant NLC, [Ag(en)]NO₃ (refcode MAGVOG²²) phase I (Fig. 3 and Fig. S11, ESI†). For the extended industrially relevant pressure range (0.1 MPa–2 GPa) ETYFUM gives the field only to Zn[Au(CN)₂]₂ I, which χ_K is higher despite being calculated in a smaller pressure range (0.35–1.8 GPa; Table S22, ESI†) due to phase transition.

To include materials in which NLC is triggered in high-pressure phases, pressure bins of the same width, but with the p_min moved to the lowest pressure NLC behaviour begins, were considered. For Δp = 0.15 GPa, ETYFUM is additionally surpassed by deuterated biurea II (BIUREA II)²³ (χ_K =0.83%). However, its K at the lowest pressure (0.62 GPa) is accompanied by significant ESD, K = −117(83) TPa⁻¹ (Table S12, ESI†). NLC is also recorded for the ambient-pressure phase (BIUREA I), but the ESDs are a couple times higher than the values themselves (Table S11, ESI†), making analysis of the data unreliable.

For Δp = 0.9 GPa, χ_K of ETYFUM becomes significantly higher than that of BIUREA II, and only after considering the wider range of Δp = 1.32 GPa, dry CPOS-1 surpasses ETYFUM and Zn[Au(CN)₂]₂ I, in terms of χ_K (Fig. S11, ESI†). However, due to the low number of data points for CPOS-1 estimation of errors was hindered, impeding confirmation of the accuracy of the compressibility values and the fitting.

As we show, the exceptionality of the NLC behaviour of ETYFUM is four-fold: (i) its median compressibility and χ_K is comparable to those of Zn[Au(CN)₂]₂ I, when considering the entire pressure range investigated and the industrially relevant pressure range (0.1 MPa–2 GPa); (ii) it shows significant NLC starting at ambient pressure, making it suitable for applications at pressure close to 0.1 MPa; (iii) although its compressibility decreases with pressure, the rate of change is mild and even above 3 GPa compressibility remains significant; (iv) for the 0.1 MPa–2 GPa range it surpasses all other organic and non-framework materials that exhibit NLC in this entire range. What is important, ETYFUM can be easily obtained with minimal amounts of solvent in time-efficient manner using solvent-assisted ball-milling, while substrates can be recycled by dissolving the cocrystal. Hence, ETYFUM as a NLC material can overcome downsides that can limit the application of benchmark materials reported so far in the literature: (i) the expensive and cumbersome synthesis (Ag₃[Co(CN)₆]I⁹ and Zn[Au(CN)₂]₂I⁶); (ii) small pressure range in which significant NLC is exhibited (Ag₃[Co(CN)₆]I,⁴ InH(BDC)₂⁵); (iii) lack of NLC in 0.1 MPa–1 GPa pressure range (CPOS-1⁸); (iv) vulnerability to the presence of small molecules capable of being adsorbed in pores (CPOS-1⁸). This makes ETYFUM an environmentally friendly alternative to framework materials.

The discovery of NLC in ETYFUM can set a foundation for the development of a crystal engineering approach to the design of NLC materials. By selecting linear, conformationally rigid molecules capable of forming straight or almost straight H-bonded chains, stress-resistant struts can be created. Meanwhile, weaker interactions and hydrogen bonds that would not disrupt the main aggregation motif can be employed to form hinge points. As a result, we could ultimately bypass the requirement for metal centres to be present to act as hinges, eliminating the restrictions imposed by their coordination spheres, and still construct materials of significant NLC.

We also wish to highlight the need for a unified manner in which NLC is investigated and reported, including: (i) providing a number of data points sufficient for reliable calculation of compressibility; (ii) reporting information on the way in which compressibility was calculated (including list of used parameters); (iii) clearly stating what values are compared and reported (maximum or median). Adherence to those guidelines will enable assessment of NLC materials in a manner that allows more reliable selection of the most exceptional cases.

E. P.-K.: conceptualisation, investigation, formal analysis, resources, data curation, writing (original draft, review and editing), visualisation, supervision, project administration, funding acquisition; M. K.: software, data curation, writing- review and editing, visualisation.

This study was financed by the National Science Center Poland, grant number 2020/39/D/ST4/00260.

Data availability

Crystallographic data has been deposited in the CSD (CCDC: 2340674-2340687) and can be accessed at https://www.ccdc.cam.ac.uk/structures/, and at zenodo.org (https://doi.org/10.5281/zenodo.12080893).

Conflicts of interest

There are no conflicts to declare.

Notes and references

1. A. B. Cairns and A. L. Goodwin, Phys. Chem. Chem. Phys., 2015, 17, 20449–20465.
2. R. H. Baughman, S. Stafström, C. Cui and S. O. Dantas, Science, 1998, 279, 1522–1524.
3. K. W. Chapman, G. J. Halder and P. J. Chupas, J. Am. Chem. Soc., 2009, 131, 17546–17547.
4. A. L. Goodwin, D. A. Keen and M. G. Tucker, Proc. Natl. Acad. Sci. U. S. A., 2008, 105, 18708–18713.
5. Q. Zeng, K. Wang and B. Zou, J. Am. Chem. Soc., 2017, 139, 15648–15651.
6. A. B. Cairns, J. Catafesta, C. Levelut, J. Rouquette, A. van der Lee, L. Peters, A. L. Thompson, V. Dmitriev, J. Haines and A. L. Goodwin, Nat. Mater., 2013, 12, 212–216.
7. M. Erkartal, J. Phys. Chem. C, 2024, 128, 588–596.
8. Y. Zhao, C. Fan, C. Pei, X. Geng, G. Xing, T. Ben and S. Qiu, J. Am. Chem. Soc., 2020, 142, 3593–3599.
9. A. L. Goodwin, M. Calleja, M. J. Conterio, M. T. Dove, J. S. O. Evans, D. A. Keen, L. Peters and M. G. Tucker, Science, 2008, 319, 794–797.
10. S. Aitipamula, R. Banerjee, A. K. Bansal, K. Biradha, M. L. Cheney, A. R. Choudhury, G. R. Desiraju, A. G. Dikundwar, R. Dubey, N. Duggirala, P. P. Ghogale, S. Ghosh, P. K. Goswami, N. R. Goud, R. R. K. R. Jetti, P. Karpinski, P. Kaushik, D. Kumar, V. Kumar, B. Moulton, A. Mukherjee, G. Mukherjee, A. S. Myerson, V. Puri, A. Ramanan, T. Rajamannar, C. M. Reddy, N. Rodriguez-Hornedo, R. D. Rogers, T. N. G. Row, P. Sanphui, N. Shan, G. Shete, A. Singh, C. C. Sun, J. A. Swift, R. Thaimattam, T. S. Thakur, R. Kumar Thaper, S. P. Thomas, S. Tothadi, V. R. Vangala, N. Variankaval, P. Vishweshwar, D. R. Weyna and M. J. Zaworotko, Cryst. Growth Des., 2012, 12, 2147–2152.
11. F. Birch, Phys. Rev., 1947, 71, 809–824.
12. K. F. Bowes, G. Ferguson, A. J. Lough and C. Glidewell, Acta Crystallogr., Sect. B: Struct. Sci., 2003, 59, 100–117.
13. W. Li, M. R. Probert, M. Kosa, T. D. Bennett, A. Thirumurugan, R. P. Burwood, M. Parinello, J. A. K. Howard and A. K. Cheetham, J. Am. Chem. Soc., 2012, 134, 11940–11943.
14. Y. Yan, A. E. O’Connor, G. Kanthasamy, G. Atkinson, D. R. Allan, A. J. Blake and M. Schröder, J. Am. Chem. Soc., 2018, 140, 3952–3958.
15. Q. Zeng, K. Wang and B. Zou, ACS Mater. Lett., 2020, 2, 291–295.
16. C. H. Woodall, C. M. Beavers, J. Christensen, L. E. Hatcher, M. Intissar, A. Parlett, S. J. Teat, C. Reber and P. R. Raithby, Angew. Chem., Int. Ed., 2013, 52, 9691–9694.
17. M. J. Cliffe and A. L. Goodwin, J. Appl. Crystallogr., 2012, 45, 1321–1329.
18. M. Lertkiattrakul, M. L. Evans and M. J. Cliffe, J. Open Source Softw., 2023, 8, 5556.
19. C. J. McMonagle, P. Comar, G. S. Nichol, D. R. Allan, J. González, J. A. Barreda-Argüeso, F. Rodríguez, R. Valiente, G. F. Turner, E. K. Brechin and S. A. Moggach, Chem. Sci., 2020, 11, 8793–8799.
20. P. Serra-Crespo, A. Dikhtiarenko, E. Stavitski, J. Juan-Alcañiz, F. Kapteijn, F.-X. Coudert and J. Gascon, CrystEngComm, 2014, 17, 276–280.
21. D. Jiang, T. Wen, Y. Guo, J. Liang, Z. Jiang, C. Li, K. Liu, W. Yang and Y. Wang, Chem. Mater., 2022, 34, 2764–2770.
22. W. Cai and A. Katrusiak, Nat. Commun., 2014, 5, 4337.
23. C. L. Bull, N. P. Funnell, C. J. Ridley, C. R. Pulham, P. L. Coster, J. P. Tellam and W. G. Marshall, CrystEngComm, 2019, 21, 5872–5881.

---

Footnote

† Electronic supplementary information (ESI) available: Experimental details; principal axis strain calculations results; figures of sample crystals; PXRD patterns; results of the CSD data mining and additional figures of molecular aggregation. CCDC 2340674–2340687. For ESI and crystallographic data in CIF or other electronic format see DOI: https://doi.org/10.1039/d4cc02183e

---