Nitro group and K⁺-based secondary building units for the self-assembly of 3D coordination polymers built on dinuclear dianionic helicate connectors

Abstract

Two 3D coordination polymers based on dinuclear dianionic helicates, K₂[M^II₂(L)₃] M = Mn^II (1) and Ni^II (2), were obtained by slow liquid–liquid diffusion of solutions of 2-hydroxy-5-nitrobenzaldehyde, 4,4′-methylenedianiline, KOtBu and the metal salt at room temperature. The resulting dianionic triply stranded helicates self-assemble into novel 3D coordination polymers, in which the helicate units act as connectors. The assembly is promoted by the phenolate bridging ability and the coordination of the pre-organized NO₂ groups to K–(O–N–O)₄–K nodes, resulting in robust paramagnetic materials. SC-XRD shows that the metal centers are located 11.257(2) and 11.264(1) Å apart. The Mn–L bond lengths correspond to the high-spin (HS, S = 5/2) state for 1. The magnetic behavior for both complexes shows weak magnetic exchange, as expected due to the spin carrier separation, and the confirmation of the HS-sate for the Mn^II centers. For complex 1, an antiferromagnetic exchange is detected, whereas for complex 2, a mixture of intramolecular antiferromagnetic and intermolecular ferromagnetic exchanges are detected. Thus, we demonstrated that nitro groups can be used for the stabilization of anionic complexes because coordination to K⁺ results in stable intricate architectures.

---

Introduction

Triply stranded dimetallic helicates¹ have received considerable attention as they can offer interesting physicochemical properties such as chirality,² act as hosts for molecules,³ magnetism,⁴ and luminescence.⁵

The ligand design is fundamental for obtaining helicate complexes; therefore, two approaches can be followed: a designer approach in which a polydentate multinucleated ligand can be synthesized (investing serious time and effort) or a self-assembly approach, in which in situ formation of the ligand and the helicate complex occurs, due to the right match of subcomponents, e.g., ligands bite angle, metal ion geometry, and angle between coordination pockets. Therefore, the latter approach is commonly used due to mild reaction conditions, and the possibility of using commercially available motifs.

Imine-based ligands are some of the choices for the self-assembly of dinuclear helicates because the formation of the ligand is metal-directed by simply mixing a diamine, containing both NH₂ at an angle smaller than 180° using a flexible linker and two equivalents of a monoaldehyde; the latter should contain, at least, a donor moiety. Most of the imine-based helicates are derived from N-heterocycle monoaldehydes, although there are very few examples known based on cathecolatealdehyde-⁶ and, to a much less extent, hydroxybenzaldehyde-synthons.^7,8 These phenolate groups are known to act as bridging ligands, with a M₁–O_Ph–M₂ motif, forming discrete or polynuclear homo- and hetero-metallic complexes.⁹

However, the use of helicates as metalloligands is not common,¹⁰ and even fewer examples are found for the construction of more complex 1D-^7,11,12 or 3D structures.¹³ The ligands in this type of structure contain secondary assembly instruction sites that permit the 1D or 3D growth; to date, only pyridine or carboxylate groups have been used. In fact, the majority of metalloligands that are used for the synthesis of intricate designer heterometallic architectures such as metal–organic frameworks (MOF), coordination networks and polymers, contain N or O-functional groups for secondary assembly instruction,¹⁴i.e., the interconnections with the second metal synthon are formed using N-heterocycles, amides, amines, imines, and/or carboxylate groups. Due to the robustness and coordination versatility of the latter group, it has been widely used for the generation of such architectures.¹⁵

Thus, we have decided to explore the formation of dinuclear helicates based on 2-hydroxy-5-nitrobenzaldehyde and 4,4′-methylenedianiline as the diamine moiety. The resulting imine ligand (H₂L) comprises two bidentate (N and O donors) coordination pockets. Thus, upon deprotonation of the OH groups, three ligand strands could wrap two metal centers, resulting in a N₃O₃ coordination sphere (Fig. 1). The latter coordination sphere could impart interesting magnetic properties for Mn complexes, e.g., spin crossover (SCO).¹⁶ Moreover, the ligand contains nitro groups that can be used as secondary assembly instruction because it has been observed that this group can coordinate alkali and alkaline earth metal counter ions (see ESI†) in anionic complexes.

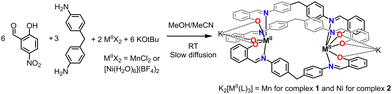Fig. 1 Synthesis of triply stranded dianionic dimetallic helicates K₂[M₂(L)₃], M = Mn²⁺ and Ni²⁺, under mild reaction conditions.

Experimental

General

All reactions were carried out in an argon atmosphere using standard Schlenk techniques. The solvents were degassed just before use. Elemental analyses were performed on a Thermo-Finnigan Flash 1112 elemental analyzer at the Chemistry Department CINVESTAV. Infrared (IR) spectra were obtained on a Varian 640-IR spectrometer using a diamond attenuated total reflectance (ATR) method. The spectral data were obtained in a spectral window of 4000–550 cm⁻¹. X-ray diffraction measurements were collected on a Bruker D8 VENTURE diffractometer (PHOTON 100 detector), using a multilayer mirror monochromator and MoKα source (λ = 0.71073 Å).

Synthesis

Synthesis of K₂[Mn^IIL₃]·MeOH (1). A Schlenk flask under an argon atmosphere was charged with anhydrous manganese(II) chloride (30.5 mg, 0.24 mmol, 2 equiv.) and 3 mL of methanol. The MnCl₂ salt was partially soluble. A yellow solution of 2-hydroxy-5-nitrobenzaldehyde (121.1 mg, 0.72 mmol, 6 equiv.) in 3 mL of acetonitrile was added to this solution. To the resulting mixture, 6 mL of acetonitrile was carefully layered over without mixing, and then a colorless solution of potassium tert-butoxide (82 mg, 0.72 mmol, 6 equiv.) in 3 mL of methanol was layered dropwise without mixing. A further layer of 6 mL of acetonitrile was added without mixing and finally a colorless solution of 4,4′-methylenedianiline (72 mg, 0.36 mmol, 3 equiv.) in 3 mL acetonitrile was layered over without mixing. The Schlenk flask was kept isolated from disturbance for a few days, during which time the five layers were mixed by slow liquid–liquid diffusion, obtaining red crystals suitable for SC-XRD. The crystals were washed with distilled water and acetonitrile and subsequently dried under vacuum, obtaining 85 mg of red solid (0.049 mmol, 40.8%). IR-ATR v (cm⁻¹): 1614.5, 1593.7, 1543.7, 1481.9, 1296, 1245.2, 1169.2, 1099.2, 828.7, 681.9, 635.8. Elemental analysis (%): calculated for K₂[Mn₂(C₈₁H₅₄O₁₈N₁₂)]·(MeOH)·(H₂O)₃ C: 56.04, H: 3.67, N: 9.56; found: C: 55.56, H: 2.99, N: 9.09.

Synthesis of K₂[Ni^IIL₃]·MeCN (2). A Schlenk flask under argon atmosphere was charged with [Ni^II(H₂O)₆](BF₄)₂ (40 mg, 0.12 mmol, 2 equiv.), 2-hydroxy-5-nitrobenzaldehyde (59 mg, 0.35 mmol, 6 equiv.), 3 mL of methanol and 3 mL of acetonitrile, and this mixture was stirred until a green solution was obtained. The resulting mixture was layered dropwise first with 10 mL of acetonitrile without mixing, and then with a colorless solution of potassium tert-butoxide (39.3 mg, 0.35 mmol, 6 equiv.) in 3 mL of methanol. A whitish suspension was formed, which was deposited at the interface between the first and second layers. An additional layer of 6 mL of acetonitrile and finally a colorless solution of 4,4′-methylenedianiline (35 mg, 0.18 mmol, 3 equiv.) in 4 mL of acetonitrile was added. The Schlenk flask was kept isolated from disturbance for a week, during which time the five layers were mixed by slow liquid–liquid diffusion, obtaining greenish-yellow crystals suitable for SC-XRD. The crystals were washed with distilled water and acetonitrile and subsequently dried under vacuum, obtaining 20 mg of a green solid (0.012 mmol, 19.8%). IR-ATR v (cm⁻¹): 1614.2, 1595.1, 1543.5, 1485.6, 1399.5, 1291.8, 1246.2, 1181.2, 1099.6, 831.3, 683.5, 643.5. Elemental analysis (%): calculated for K₂[Ni₂(C₈₁H₅₄O₁₈N₁₂)] C: 57.94, H: 3.24, N: 10.01; found: C: 57.47, H: 3.24, N: 9.60.

Surface area analysis. The total pore volume and specific surface area of complex K₂[Mn^IIL₃]·MeOH (1) were measured through N₂ adsorption isotherms at 77 K and calculated with the Brunauer–Emmett–Teller (BET) method, using a Micromeritics Gemini 2340 surface area analyzer. The powder sample was previously degassed at 80 °C overnight under vacuum conditions. The BET-surface area value was 0.1915 m² g⁻¹, with a negligible total pore volume (1 × 10⁻⁴ cm³ g⁻¹). The results indicate that no N₂ adsorption occurs in complex 1, and a similar behavior would be expected for complex 2.

Results

Synthesis and characterization

The attempted architecture was a neutral helicate, where the metal centers would have a 3+ oxidation state. In many cases, coordination of phenolate ligands to low oxidation state metal ions results in metal oxidation. Therefore, the synthesis of the helicates (see Experimental section) was attempted by employing MnCl₂ under inert conditions, followed by crystallization in the air for spontaneous oxidation of the metal center. The synthesis of the complexes was achieved by two methods, one in which all the components were mixed in a refluxing solvent resulting in the precipitation of solids, which were insoluble in most of the common solvents, except for DMF or DMSO that partially dissolved the complexes. Therefore, a second method was used, a liquid–liquid slow diffusion method resulted in crystals suitable for single-crystal X-ray diffractometry (SCXRD, see below). Surprisingly, SCXRD showed the formula K₂[Mn^II₂(L)₃]·MeOH (1), which is a triply-stranded dianionic dimetallic helicate in which the metal ion is found in a +2 oxidation state. To prove that the dianionic helicates were stable, [Ni^II(H₂O)₆](BF₄)₂ was used as the metal source under similar conditions, obtaining K₂[Ni^II₂(L)₃]·MeCN (2) according to SCXRD, thus confirming the dianionic nature of the helicates.

Both complexes were characterized as solids by IR and microanalysis. It is possible to observe in the IR spectra the characteristic υ for the NO₂ group at 1593 and 1296 cm⁻¹ for 1 and 1595 and 1292 cm⁻¹ for 2. The imine υ_N=C is found at 1614 cm⁻¹ for both complexes. Due to the lack of solubility, it was not possible to further characterize the complexes by other techniques.

Single crystal X-ray diffractometry

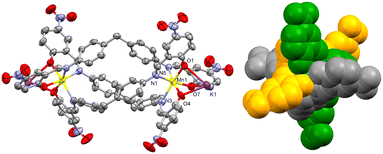
SCXRD measurements were performed at RT for 1 and 2. Crystal data and refinement parameters are given in Table 1, while Table 2 shows some selected structural parameters. Both metal complexes are isostructural, crystallizing in the C2/c space group, Fig. 2 and S1.† The asymmetric unit consists of one half helicate dianion, one MeOH molecule disordered over two positions for 1, but one half MeCN solvent molecule for 2, and one K⁺; the rest of the helicate, the second K⁺ and the solvent molecule are generated by a C₂ rotation axis. The N₃O₃ coordination sphere for the only symmetry-independent metal center, for both complexes, is formed by three N_imine and three O_phenolate in a fac mode, in a distorted octahedral geometry. Complex 1 exhibits a greater degree of distortion compared to 2, based on the values for the ∑_Oh parameter^17,18 (63.75° and 46.67°, respectively, Table 2 and S3†).

Table 1 Crystal data and structure refinement for complexes 1 and 2

Complex	1	2
Empirical formula	C83H62K2Mn2N12O20	C83H57K2N13Ni2O18
Formula weight	1735.52	1720.03
Temperature	298(2) K	296(2) K
Wavelength	0.71073 Å	0.71073 Å
Crystal system	Monoclinic	Monoclinic
Space group	C2/c	C2/c
Unit cell dimensions	a = 16.080(3) Å	a = 15.7610(11) Å
	α = 90°	α = 90°
	b = 14.472(3) Å	b = 14.5644(9) Å
	β = 100.611(8)°	β = 97.921(2)°
	c = 37.326(8) Å	c = 36.558(3) Å
	γ = 90°	γ = 90°
Volume	8537(3) Å^3	8311.7(10) Å^3
Z	4	4
Density (calculated)	1.350 Mg m^−3	1.375 Mg m^−3
Absorption coefficient	0.469 mm^−1	0.629 mm^−1
F(000)	3568	3536
Crystal size	0.350 × 0.260 × 0.100 mm^3	0.384 × 0.217 × 0.056 mm^3
Theta range for data collection	2.221 to 27.195°	2.250 to 25.026°
Index ranges	−20 ≤ h ≤ 20, −18 ≤ k ≤ 18, −47 ≤ l ≤ 47	−18 ≤ h ≤ 18, −17 ≤ k ≤ 17, −42 ≤ l ≤ 43
Reflections collected	126 744	204 178
Independent reflections	9469 [R(int) = 0.1708]	7322 [R(int) = 0.1132]
Completeness to theta = 25.242°	99.70%	99.60%
Absorption correction	Semi-empirical from equivalents	Semi-empirical from equivalents
Max. and min. transmission	0.7455 and 0.4820	0.7452 and 0.6704
Refinement method	Full-matrix least-squares on F^2	Full-matrix least-squares on F^2
Data/restraints/parameters	9469/36/558	7322/0/551
Goodness-of-fit on F^2	1.026	1.066
Final R indices [I > 2sigma(I)]	R 1 = 0.0737, wR2 = 0.1871	R 1 = 0.0642, wR2 = 0.1671
R indices (all data)	R 1 = 0.1797, wR2 = 0.2480	R 1 = 0.1076, wR2 = 0.1879
Largest diff. peak and hole	0.851 and −0.356 e Å^−3	0.795 and −0.267 e Å^−3

---

Table 2 Average bond lengths (Å) and angles (°), and ∑_Oh parameter for 1 and 2

Complex	1	2
a The octahedral distortion parameter, ∑Oh, is the sum of the absolute deviation values of the twelve cis angles to 90°. ∑Oh = 0 for a perfect octahedron. b X is a methanol O-atom for complex 1, while an acetonitrile N-atom for complex 2.
M–N [Å]	2.293(4)	2.124(3)
M–O [Å]	2.116(3)	2.040(3)
M–M [Å]	11.257(2)	11.264(1)
K–Ophenolate [Å]	2.829(3)	2.803(3)
K–Onitro [Å]	2.951(5)	2.983(5)
K–Xsolvent^b [Å]	3.999(7)	3.448(19)
cis O–M–O [°]	87.07(14)	85.56(12)
cis N–M–N [°]	99.19(13)	97.44(13)
cis O–M–N [°]	86.67(13)	88.16(13)
trans O–M–N [°]	168.68(13)	171.19(12)
∑Oh^a	63.75(46)	46.67(43)

---

Fig. 2 Left: perspective view of 1, 40% probability level ellipsoids. Solvent molecules and H-atoms are omitted. Right: side view of 2 in a space-fill model, each ligand strand is colored differently to highlight the wrapping of the ligands around the metal centers.

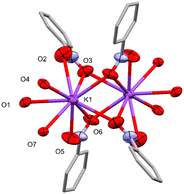
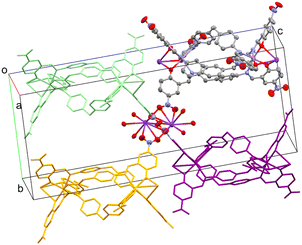
The three O_phenolate groups are found in the external face away from the helicate cavity, which permits the O to act as a bridging ligand to a K⁺. The latter is found in a nine-coordination sphere comprising three O_phenolate and six O coming from four NO₂ groups of neighboring complexes, similar to the acetate paddle wheel structures. All the NO₂ groups act as μ^1,1 and μ^1,3-bridging ligands connecting to a symmetry-generated K⁺ possessing the same coordination environment, promoting the formation of dinuclear potassium units (Fig. 3) interconnecting the dinuclear helicates in three dimensions (Fig. 4).

Fig. 3 Numbering scheme of the symmetry-independent atoms and coordination sphere of the two K⁺ metal centers interconnected by μ¹-μ^1,3-bridging NO₂ ligands. Dangling oxygen atoms correspond to O_phenolate moieties. The rest of the dinuclear unit, solvent molecule, H-atoms are omitted.

Fig. 4 Perspective view of the three-dimensional growth of (1), promoted by the NO₂ groups and K⁺. The dinuclear K unit is drawn with ellipsoids at 30% probability level. The coordinated NO₂ to the K dinuclear node come from different helicate units, highlighted in different colors and in a capped stick style. Solvent molecules and H-atoms are omitted for the sake of clarity.

Mn–O_phenolate (2.116(3) Å) and Mn–N_imine (2.293(4) Å) bond lengths of complex 1 agree with the values reported for high spin (S = 5/2) six-coordinate Mn^II complexes with salicylamide-based ligands (2.073–2.196 Å and 2.185–2.273 Å, respectively).^19–22 However, these examples correspond to complexes with discrete (0-D) or one-dimensional arrangements and, in most cases complexes that contain co-ligands/anions/solvent molecules to complete the coordination sphere. In this sense, 1 is a novel example of a 3D homoleptic Mn^II coordination polymer. For complex 2, the Ni–O_phenolate (2.040(3) Å) and Ni–N_imine (2.124(3) Å) bond lengths also agree with values previously reported for analogous complexes (1.978–2.083 Å and 1.988–2.064 Å, respectively).^28–31 In Fig. S2,† the ligands used in the examples mentioned above are shown. In both cases, the M–N_imine length is slightly higher than the range found, possibly due to the effects of the internal triple-stranded structure. This relatively long bond is unusual, as examples of helicates or mesocates of Mn^II and Ni^II with Schiff base-derived ligands show shorter M–N_imine lengths compared to 1 and 2.^23–26 Only one example showed a Ni–N_imine bond length (2.179 Å), even higher than that reported in complex 2.²⁷ Moreover, both complexes 1 and 2 have the peculiarity of containing the M^II metal centers in a dinuclear anionic species, which had not been reported (as far as we know) for Mn^II and Ni^II complexes with salicylimine-based-ligands.

Although the K⁺ center is nine-coordinated, KO₉, the solvent molecules also interact with it in a non-covalent manner. In 1, the K–O_MeOH distance is 3.999(7) Å (Fig. S3a†), which is close to the previously reported K–O_MeOH distances in a highly-coordinated potassium complex (3.913 Å).²⁸ However, this O_MeOH cannot be considered as part of the K⁺ coordination sphere. A search in the CSD database (update June 2023) shows at least 158 crystal structures with ten-coordinated potassium, KO₁₀, where the K–O distances range from 2.574 to 3.389 Å (see histogram in Fig. S4†), suggesting that the K–O_MeOH interaction in 1 is weak. Furthermore, there is an H-bond between the methanol –OH group (H donor) and the O_phenolate (H acceptor) atom (Fig. S5†), which could favor the orientation of O_MeOH towards K⁺. Complex 2 shows a weak K–N_MeCN interaction, with a distance of 3.448(19) Å (Fig. S3b†). Crystal structures that present ten-coordinated potassium atoms in an N₁O₉ coordination sphere are rare since only seven examples were found (based on the CSD database, updated in June 2023), of which only one structure presents MeCN as a ligand.²⁹ K–N bond lengths are found in a range of 3.008 to 3.160 Å, which are smaller than the value found for 2. This suggests, as in 1, a weak K–N_MeCN interaction.

Thus, the K atom is found in a distorted nine-coordinate sphere. The average K–O_phenolate bond length is 2.828(3) and 2.803(3) Å for 1 and 2, respectively, Table 2, which are notably higher than the average Mn^II/Ni^II–O_phenolate of 2.116(3) and 2.040(3) Å, respectively, due to a more covalent interaction between the latter atoms compared to K–O_phenolate. The Mn^II–K and Ni^II–K heterometallic intramolecular distances are 3.555(1) and 3.564(1) Å, while the homometallic (M–M) distances are 11.257(2) and 11.264(1) Å, respectively.

Interestingly, the shortest M–M distance is not the intramolecular one, i.e., within a helicate molecular unit. Fig. S6–S8† show the five shortest M–M distances, in a range between 10.73 and 13.05 Å (Table S4†). The shortest M–M distance is the one parallel to the ab plane, 10.817(2) Å for 1 and 10.730(1) Å for 2, while the longest is the one parallel to the ac plane, 13.050(2) Å for 1 and 12.535(1) Å for 2.

As mentioned above, dinuclear K units act as nodes between adjacent metal helicates due to K–O_nitro bonds. Each coordinated NO₂ group comes from a different helicate unit, as shown in Fig. 4. This allows the growth of the structure through the three axes, forming the 3D network (Fig. S9†). The phenolate oxygen atoms coordinated to the K⁺ center form O–K–O angles of approximately 59–63°, while the angles formed by the O_nitro are ca. 40°. These O–K–O angle values are close to those previously reported in similar complex structures involving metalloligands.^28,30 The 3D topology for both complexes is a pcu; 6/4/c1; sqc1, in a cluster representation, according to TopCryst.³¹ The CSD occurrence of the pcu; 6/4/c1; sqc1 topology in a cluster representation (all nodes and single node) is 3541 structures.

There is another non-covalent interaction that promotes the 3D growth of the crystal structure, that is, the intermolecular π–π stacking between two aromatic rings of terminal nitrophenolate groups, as shown in Fig. S10.† This interaction is an off-centered parallel stacking with an interplanar angle of 0.0°. There is an interplanar normal distance of approximately 3.51–3.53 Å and a horizontal displacement (offset) of 2.30–2.39 Å (Fig. S11 and S12†). Both normal and offset distances agree with the range of typical distances reported in other π–π stacking systems.^32,33 These π–π interactions, together with the coordinated K atoms, promote the structural growth of zigzag-type chains along the c axis, Fig. S13.† Furthermore, intramolecular C–H/π interactions occur in complexes 1 and 2, where a C(sp²)–H of a benzene ring from diphenylmethane moiety is directed towards the benzene center of the adjacent ligand strand (Fig. S14 and S15†). Both aromatic rings of a single diphenylmethane moiety act as the C–H/π acceptor, while the remaining two ligands act as the donors. The C–H/π distances are 3.640 and 3.503 Å for complexes 1 and 2, respectively. The interplanar angles are close to 90° (87.27° and 88.89°), and the C–H– π α angle ranges from 167.46° to 168.80°, both parameters indicate a quasi-perpendicular interaction (Fig. S16†).

Magnetic and N₂ adsorption properties

The magnetic properties of crystalline samples for both complexes 1 and 2 were obtained in the 5–300 K temperature range under a 0.1 T external magnetic field, Fig. 5. In the case of complex 1, the room temperature χ_MT = 9.30 cm³ mol⁻¹ K is in good agreement for two non-interacting Mn²⁺ in the high-spin state (S = 5/2), spin only χ_MT value of 8.75 cm³ mol⁻¹ K. The value slightly decreases upon cooling reaching 8.24 cm³ mol⁻¹ K at 50 K. The best fit for the data using PHI,³⁴Ĥ_ex = −2JS₁·S₂, indicates a negligible antiferromagnetic coupling J = −0.0029 cm⁻¹, g = 1.954, TIP = 414 × 10⁻⁶ cm³ mol⁻¹, monomeric impurity of 0.07 and a residual error R = 0.92.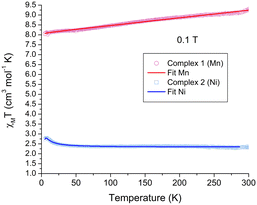

Fig. 5 χ _M T vs. T magnetic behavior for complexes 1 and 2. The solid lines represent the best fit for both complexes.

In the case of the complex 2, χ_MT = 2.37 cm³ mol⁻¹ K at RT, which is slightly higher than the expected spin-only value for two S = 1 systems, 2.00 cm³ mol⁻¹ K, and is maintained relatively constant down to 50 K, χ_MT = 2.40 cm³ mol⁻¹ K. Below this temperature, an increase is observed reaching a maximum at 7.2 K of χ_MT = 2.80 cm³ mol⁻¹ K, on cooling, this value decreases again. The latter behavior indicates two types of exchange interactions, as seen for other dinuclear Ni complexes.³⁵ The best fit using PHI³⁷ affords an antiferromagnetic intramolecular interaction between Ni centers J = −0.92 cm⁻¹, a ferromagnetic intermolecular interaction zJ = 0.44 cm⁻¹, g = 2.15, a ZFS D parameter of 2.7 cm⁻¹, TIP = 94.8 × 10⁻⁶ cm³ mol⁻¹ and R = 0.38, which are in good agreement for dinuclear Ni complexes containing O-based ligands, previously reported.³⁶ The small exchange coupling values for both systems are consistent with distant metal centers found in the helicate units.

In addition, the total pore volume and specific surface area of complex 1 were measured through N₂ adsorption isotherms at 77 K. The BET-surface area value found is 0.1915 m² g⁻¹, with a negligible total pore volume (1 × 10⁻⁴ cm³ g⁻¹). The results indicate that no N₂ adsorption occurs in complex 1, and a similar behavior would be expected for complex 2.

Discussion

Dinuclear anionic triply stranded helicates are rare species. In fact, to the best of our knowledge, there are only a few examples: polymeric Ti⁴⁺ or V⁴⁺ helicates^37,38 based on catecholate-imine ligands, 2D coordination polymers of Ni²⁺,^39,40 containing pyridine-carboxamide or polyoxamate-type ligands, and two coordination polymers based on Fe³⁺ and catecholamide or salicylic acid–carboxamide ligand.^41,42 In some of these compounds, the helicates act as metalloligands to alkali metal cations, Fig. 6, and the polymeric growth occurs thanks to the O-donors, coming from the catecholate, amide and/or carboxylate groups, that coordinate to an alkali metal counterion. In our case, the ligand is a salicyl-imine derivative, which provides an unusual N₃O₃ donor set that stabilizes the metal ions in the low oxidation state (M²⁺). In addition, it is important to emphasize that the nitro group functions as a secondary assembly instruction, coordinating to the K⁺ nodes and none of the reported structures contain nitro groups, see Fig. 6. Thus, our structures are a new class of anionic [M₂L₃]²⁻ helicates, which, in general, have been little explored.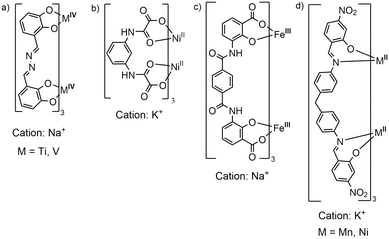

Fig. 6 a–c) Structures reported in the literature of triple-stranded anionic dinuclear helicates that form coordination polymers mediated by alkali metal cations. d) This work.

The coordination of nitro group to alkali or alkaline earth metal ions and some other transition metal centers has been previously observed. A search in the CSD database (update June 2023) shows at least 88 crystal structures of aromatic nitro groups coordinated to metal ions. However, it is important to mention that only six out of the 88 structures are based on anionic metalloligands, in which the nitro groups coordinate to the countercation, and from those only four self-assemble in polymeric coordination structures, the rest of the structures correspond to deprotonated ligands counterbalanced by the metal cation. The metal cations observed in the 88 structures correspond to alkali (77), alkaline-earth (8) and transition metals (5), forming discrete (0D), 1D, 2D and 3D structures (Table S5†). The analysis shows that the nitro groups are responsible for the n-dimensional growth (n = 1, 2, 3) of these structures, behaving as μ,¹-μ^1,3and -μ₃¹ bridging ligands (Fig. S17†). None of the discrete (0-D) structures present the NO₂ as a bridging ligand, but only in a mono- and bidentate mode. It is observed that alkali metal ions dominate the list, with the K atom being the most frequent (34 structures), mainly based in homometallic 3D networks. However, as previously mentioned, the presence of metalloligands in this type of nitro-mediated 3D-coordination polymers is very unusual, with few examples similar to those reported in this work.^28,43,44 Furthermore, most structures contain less than four nitro groups per metal cation (67 structures), therefore, a high NO₂/[M⁺] ratio is relatively uncommon (21 structures).

Conclusions

We have shown that it is possible to synthesize, under ambient conditions, triply stranded dinuclear helicates, which act as connectors for the self-assembly construction of intricate 3D structures, by harnessing the potential of nitro groups as ligands for K⁺. The pre-organization and the spatial disposition of the NO₂ attached to the aromatic groups, coming from the helicate, permits the use of the latter as connectors, which to the best of our knowledge is an unseen type of building units for the 3D structures. Moreover, the use of NO₂ groups as ligands to K⁺ (and other metal cations) could be used for the stabilization of anionic complexes, without the need to use expensive crown ether type of ligands for the cation, and thus permitting the crystallization and stabilization of the pair by choosing nitro-containing synthons, which are commercially available. The resulting compounds are robust and insoluble in most common solvents, which could be used for the development of novel materials. We are investigating the incorporation of other metal ions to produce interesting magnetic materials, for example, Fe²⁺ and Co²⁺ for SCO. In addition, we are exploring other cations as connectors to try to improve the porosity of this type of material.

Author contributions

R. Mendoza-Báez and A. Molina-Renteria: investigation, methodology. R. Mendoza-Báez and J. Olguín: formal analysis, data curation, writing – original draft. J. Olguín: conceptualization, funding acquisition, supervision, and writing – review and editing.

Conflicts of interest

There are no conflicts to declare.

Acknowledgements

We thank Cinvestav for financial support, Dr. Agustin Conde-Gallardo (Departamento de Física, Cinvestav) for access to the PPMS and measurements, Conahcyt for a PhD scholarship to R. M.-B., Marco A. Leyva Ramírez for X-ray diffractometry, to Naytzé Ortiz Pastrana for microanalysis, and Dr. Omar Solorza for access to surface area analyzer.

References

1. C. Piguet, G. Bernardinelli and G. Hopfgartner, Chem. Rev., 1997, 97, 2005–2062.
2. H. Miyake and H. Tsukube, Chem. Soc. Rev., 2012, 41, 6977–6991.
3. J. Jiao, J. Dong, Y. Li and Y. Cui, Angew. Chem., 2021, 133, 16704–16711.
4. L. A. Barrios, R. Diego, M. Darawsheh, J. I. Martínez, O. Roubeau and G. Aromí, Chem. Commun., 2022, 58, 5375–5378.
5. F. Stomeo, C. Lincheneau, J. P. Leonard, J. E. O'Brien, R. D. Peacock, C. P. McCoy and T. Gunnlaugsson, J. Am. Chem. Soc., 2009, 131, 9636–9637.
6. M. Albrecht, I. Janser and R. Fröhlich, Chem. Commun., 2005, 157–165.
7. X. Xi, Y. Fang, T. Dong and Y. Cui, Angew. Chem., Int. Ed., 2011, 50, 1154–1158.
8. S. Fernández-Fariña, I. Velo-Heleno, M. Martínez-Calvo, M. Maneiro, R. Pedrido and A. M. González-Noya, Int. J. Mol. Sci., 2023, 24, 8654.
9. M. Andruh, Dalton Trans., 2015, 44, 16633–16653.
10. M. Albrecht, X. Chen and D. Van Craen, Chem. – Eur. J., 2019, 25, 4265–4273.
11. H. Yoo, J. Lee, P. Kang and M.-G. Choi, Dalton Trans., 2015, 44, 14213–14216.
12. P. Cucos, L. Sorace, C. Maxim, S. Shova, D. Patroi, A. Caneschi and M. Andruh, Inorg. Chem., 2017, 56, 11668–11675.
13. Y. Liu, X. Xi, C. Ye, T. Gong, Z. Yang and Y. Cui, Angew. Chem., Int. Ed., 2014, 53, 13821–13825.
14. G. Kumar and R. Gupta, Chem. Soc. Rev., 2013, 42, 9403–9453.
15. M. Eddaoudi, D. B. Moler, H. Li, B. Chen, T. M. Reineke, M. O'Keeffe and O. M. Yaghi, Acc. Chem. Res., 2001, 34, 319–330.
16. J. Olguín, Coord. Chem. Rev., 2020, 407, 213148.
17. M. G. B. Drew, C. J. Harding, V. McKee, G. G. Morgan and J. Nelson, J. Chem. Soc., Chem. Commun., 1995, 1035–1038.
18. F. A. Deeney, C. J. Harding, G. G. Morgan, V. McKee, J. Nelson, S. J. Teat and W. Clegg, J. Chem. Soc., Dalton Trans., 1998, 1837–1844.
19. M. Mikuriya, K. Nakadera and T. Tokii, Inorg. Chim. Acta, 1992, 194, 129–131.
20. M. Mikuriya, T. Fujii, S. Kamisawa, Y. Kawasaki, T. Tokii and H. Oshio, Chem. Lett., 1990, 19, 1181–1184.
21. B. Mabad, P. Cassoux, J. P. Tuchagues and D. N. Hendrickson, Inorg. Chem., 1986, 25, 1420–1431.
22. J. Adhikary, A. Chakraborty, S. Dasgupta, S. K. Chattopadhyay, R. Kruszynski, A. Trzesowska-Kruszynska, S. Stepanović, M. Gruden-Pavlović, M. Swart and D. Das, Dalton Trans., 2016, 45, 12409–12422.
23. J. R. Pioquinto-Mendoza, J. A. Rosas-Ortiz, R. Reyes-Martínez, P. Conelly-Espinosa, R. A. Toscano, J. M. Germán-Acacio, A. Avila-Sorrosa, O. Baldovino-Pantaleón and D. Morales-Morales, Inorg. Chim. Acta, 2015, 438, 146–152.
24. S. D. Reid, C. Wilson, C. I. De Matteis and J. B. Love, Eur. J. Inorg. Chem., 2007, 2007, 5286–5293.
25. J. Sanmartín, A. M. García-Deibe, M. R. Bermejo, F. Novio, D. Navarro and M. Fondo, Eur. J. Inorg. Chem., 2003, 2003, 3905–3913.
26. Z. Xu, L. K. Thompson, D. O. Miller, H. J. Clase, J. A. K. Howard and A. E. Goeta, Inorg. Chem., 1998, 37, 3620–3627.
27. J. Mayans, M. Font-Bardia, L. Di Bari, L. Arrico, F. Zinna, G. Pescitelli and A. Escuer, Chem. – Eur. J., 2018, 24, 7653–7663.
28. G. W. Bates, P. A. Gale, M. E. Light, M. I. Ogden and C. N. Warriner, Dalton Trans., 2008, 4106–4112.
29. T. Han and C.-F. Chen, J. Org. Chem., 2008, 73, 7735–7742.
30. V. K. Bhardwaj, Dalton Trans., 2015, 44, 8801–8804.
31. A. P. Shevchenko, A. A. Shabalin, I. Y. Karpukhin and V. A. Blatov, Sci. Technol. Adv. Mater.: Methods, 2022, 2, 250–265.
32. C. R. Martinez and B. L. Iverson, Chem. Sci., 2012, 3, 2191–2201.
33. D. P. Malenov and S. D. Zarić, Coord. Chem. Rev., 2020, 419, 213338.
34. N. F. Chilton, R. P. Anderson, L. D. Turner, A. Soncini and K. S. Murray, J. Comput. Chem., 2013, 34, 1164–1175.
35. A. Patra, L. M. Carrella, P. Vojtíšek, E. Rentschler and S. C. Manna, Polyhedron, 2022, 226, 116098.
36. K. Matelková, R. Boča, L'. Dlháň, R. Herchel, J. Moncol, I. Svoboda and A. Mašlejová, Polyhedron, 2015, 95, 45–53.
37. M. Albrecht, I. Janser, H. Houjou and R. Fröhlich, Chem. – Eur. J., 2004, 10, 2839–2850.
38. M. Albrecht, S. Kamptmann and R. Fröhlich, Polyhedron, 2003, 22, 643–647.
39. M. A. Palacios, A. Rodríguez-Diéguez, A. Sironi, J. M. Herrera, A. J. Mota, J. Cano and E. Colacio, Dalton Trans., 2009, 8538–8547.
40. C. A. Simosono, R. M. R. da Silva, N. R. De Campos, M. A. R. Silva, A. C. Doriguetto, L. S. Flores, C. C. Correa, T. R. G. Simões, A. K. S. M. Valdo, F. T. Martins, F. Garcia, G. P. Guedes, B. R. L. Galvão, J. Cancino-Bernardi, R. D. dos Reis, H. O. Stumpf, D. D. Justino, P. F. R. Ortega, W. D. do Pim, M. Julve and M. V. Marinho, Molecules, 2023, 28, 2086.
41. J.-L. Do, H. M. Titi, L. A. Cuccia and T. Friščić, Chem. Commun., 2021, 57, 5143–5146.
42. E. J. Enemark and T. D. P. Stack, Inorg. Chem., 1996, 35, 2719–2720.
43. S. Samanta, S. Mukhopadhyay, D. Mandal, R. J. Butcher and M. Chaudhury, Inorg. Chem., 2003, 42, 6284–6293.
44. W. Zhang and J. Zhao, Inorg. Chem. Commun., 2006, 9, 397–399.

---

Footnote

† Electronic supplementary information (ESI) available: Crystallographic and characterization data. CCDC 2326580 and 2326581. For ESI and crystallographic data in CIF or other electronic format see DOI: https://doi.org/10.1039/d4ce00255e

---