Open Access Article
Open Access ArticleCreative Commons Attribution 3.0 Unported Licence
A model analysis of centimeter-long electron transport in cable bacteria†
Jasper R.
van der Veen
 *ab,
Stephanie
Valianti
a,
Herre S. J.
van der Zant
*ab,
Stephanie
Valianti
a,
Herre S. J.
van der Zant
 a,
Yaroslav M.
Blanter
a,
Yaroslav M.
Blanter
 a and
Filip J. R.
Meysman
a and
Filip J. R.
Meysman
 *bc
*bc
aKavli Institute of Nanoscience, Delft University of Technology, Lorentzweg 1, Delft, 2628CJ, The Netherlands. E-mail: j.r.vanderveen@tudelft.nl
bDepartment of Biotechnology, Delft University of Technology, Van der Maasweg 9, Delft, 2629HZ, The Netherlands
cExcellence center for Microbial Systems Technology, University of Antwerp, Universiteitsplein 1, Wilrijk, 2610, Belgium. E-mail: filip.meysman@uantwerpen.be
First published on 8th January 2024
Abstract
The recent discovery of cable bacteria has greatly expanded the known length scale of biological electron transport, as these multi-cellular bacteria are capable of mediating electrical currents across centimeter-scale distances. To enable such long-range conduction, cable bacteria embed a network of regularly spaced, parallel protein fibers in their cell envelope. These fibers exhibit extraordinary electrical properties for a biological material, including an electrical conductivity that can exceed 100 S cm−1. Traditionally, long-range electron transport through proteins is described as a multi-step hopping process, in which the individual hopping steps are described by Marcus electron transport theory. Here, we investigate to what extent such a classical hopping model can explain the conductance data recorded for individual cable bacterium filaments. To this end, the conductive fiber network in cable bacteria is modelled as a set of parallel one-dimensional hopping chains. Comparison of model simulated and experimental current(I)/voltage(V) curves, reveals that the charge transport is field-driven rather than concentration-driven, and there is no significant injection barrier between electrodes and filaments. However, the observed high conductivity levels (>100 S cm−1) can only be reproduced, if we include much longer hopping distances (a > 10 nm) and lower reorganisation energies (λ < 0.2 eV) than conventionally used in electron relay models of protein structures. Overall, our model analysis suggests that the conduction mechanism in cable bacteria is markedly distinct from other known forms of long-range biological electron transport, such as in multi-heme cytochromes.
1 Introduction
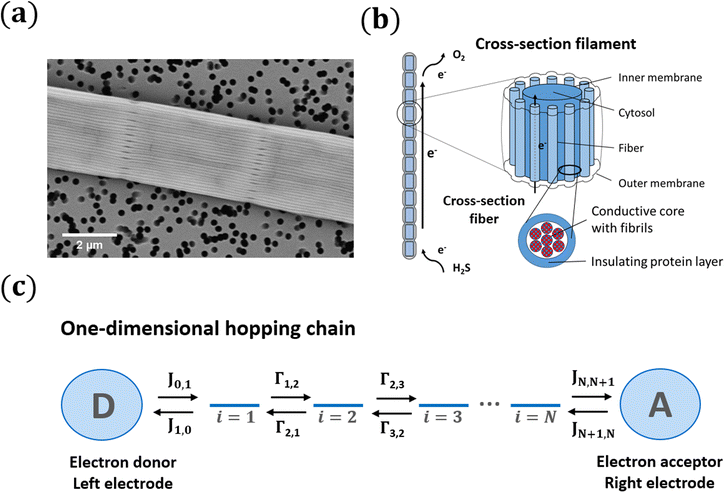
Electron flow through proteins is central to the functioning of living organisms, as it connects the sites where oxidation and reduction half-reactions occur that support vital biochemical processes.1 The best studied systems in terms of biological electron transport are the membrane complexes that enable photosynthesis in chloroplasts or respiration in mitochondria.2,3 These protein structures incorporate a series of non-protein cofactors (e.g., hemes, FeS clusters) that act as relay centres for electron transport. Electrons migrate through the electrically insulating protein medium by quantum-mechanical tunneling from one center to the next. As the tunneling rate exponentially decreases with distance, cofactors must be closely spaced (<1.4 nm apart) to allow for sufficiently fast rates (>103 s−1 time scale) that can sustain metabolism.3 Typically, electron transport chains incorporate up to 10–20 cofactors, and so the overall length scale of conduction is limited to <20 nm. This has fueled the idea that biological electron transport takes place at the nanometer scale, and so, any electron current exceeding 3 nm in biology is generally referred to as “long-range electron transport”.2The recent discovery that cable bacteria can channel electrical currents across centimeter distances,4i.e. 106 times further, thus gives a radically new meaning to the concept of “long-range electron transport”.5 Cable bacteria are long, motile, filamentous bacteria that thrive in the surface sediments of rivers, lakes, and oceans.6–9 Their respiratory metabolism couples the oxidation of free sulfide (H2S) to the reduction of oxygen (O2), which is an energetically favorable reaction.10,11 The remarkable feature is that these two half-reactions are carried out by different parts of the long filaments, and so the sites of oxidation and reduction can be millimetres to centimetres apart.4 To ensure that the redox half-reactions remain electrically coupled, electrons are internally conveyed through the cable bacterium filaments.12–14
To mediate this centimeter-scale electron transport, cable bacteria harbor an electrical grid consisting of thin protein fibers embedded in the cell envelope13 (Fig. 1a). Recent studies have resolved the intricate architecture of this highly organized fiber network15–17 (see Fig. 1b and discussion below). Additionally, it has been shown that these protein fibers display extraordinary electrical properties for a biological material. Electrical measurements demonstrate that the fiber conductivity can reach up to 100 S cm−1, which is comparable to that of highly doped conductive polymers.13,18 Because of this, the protein fibers are regarded as a promising new material for bio-based electronics.13 Such technological application however necessitates the resolution of some fundamental questions. What mechanism allows for such highly efficient centimeter-scale conduction in proteins? Does the electron transport in cable bacteria bear any similarity to the mechanisms seen in the well-studied protein systems of photosynthesis and respiration?
At present, the molecular structure of the fiber network remains unresolved, and as a result, the conduction mechanism remains elusive. Model analysis, however, allows us to explore potential mechanisms. Nanoscale electron transport across proteins, as seen in multi-heme cytochromes, is conventionally described by the multistep hopping formalism.19 Here, we investigate whether this same model formalism can describe the highly efficient, centimeter-scale electron transport in cable bacteria. In the multi-hopping picture, it is assumed that charges are temporarily localized at particular sites, and that electron transport occurs by incoherent “hopping” between consecutive sites along a chain. The electron transfer during a single hop is described by Marcus theory, which requires that the reorganization energy, λ, is significantly larger than electronic coupling, H, so that localized charge carriers form in the initial and final states.20 These Marcus-type hopping models comprise the default modelling approach for biological conduction, and have been used previously to describe nanometer scale electron transport in multi-heme cytochromes21 and protein-based molecular junctions,22–24 as well as micrometer scale electron transport in the nanowires of metal-reducing bacteria.25–27
The distance over which electron transport occurs in cable bacteria is however very different from the length scale for which the Marcus multi-stepping model has been originally developed. To test the validity of the Marcus formalism, we describe the conductive fiber network in cable bacteria as a set of parallel one-dimensional hopping chains. This is the most parsimonious model description, given that the molecular structure of the fibers still remains unresolved. The model describes the electron transport through the hopping chains when a voltage bias is imposed by connecting electrodes (Fig. 1). In our analysis, we simulate the site occupancy along the chain as well as the resulting current/voltage response, and investigate the relationship between the hopping rate and the electrical conductivity. The model output is compared to an experimental dataset that was recently obtained by detailed electrical characterization of individual fiber networks of cable bacteria.28
2 Model framework
2.1 The conductive structure in cable bacteria
Cable bacteria possess a set of NF fibre structures in their cell envelope, which are arranged in parallel and run continuously along the whole length of the centimeter-long cable bacterium filaments (Fig. 1a and b). These fibres consist of a conductive core (diameter dF = 26 nm), surrounded by an electrically insulating shell,17 and always appear to have a similar geometry.15 Thicker cable bacteria simply embed more parallel fibers in the cell envelope (NF ranges from 15 to 7515). Here, we adopt NF = 60 as a reference value, which is a characteristic value for Electrothrix gigas, the larger strain of cable bacteria29 that was used in our electrical characterization experiments.The large ratio of the fiber length (107 nm) to the fiber diameter (26 nm) suggests that charge transport in the fibers is largely one-dimensional. Still, the fiber core diameter is considerably larger than the typical spacing between charge carrier sites in metalloproteins3 (≈1 nm). Hence, there could be multiple conduction channels acting in parallel in a single fiber. Here, we assume that each conductive fiber core consists of NC parallel conduction paths, each dC = 2 nm in diameter (Fig. 1b). Assuming a hexagonal packing of cylinders, this implies that each fiber embeds NC = 125 parallel conduction channels. This large number of conduction channels can be regarded as an upper limit, thus providing a conservative estimate for the conductivity estimated by the model. If less channels are present, then the conductivity of individual channels must be higher. We disregard electron transport between channels, and so the total electrical current through a single bacterial filament is due to electron transport in NP = NF·NC = 7500 parallel one-dimensional conduction channels (see Table 1).
| Parameter | Symbol | Units | Value |
|---|---|---|---|
| Fibre diameter | d F | nm | 26 |
| Number of fibres | N F | — | 60 |
| Conduction channel diameter | d C | nm | 2 |
| Number of conduction channels per fibre | N C | — | 125 |
| Total number of parallel conduction channels | N P | — | 7500 |
2.2 Electron flow in a one-dimensional hopping chain
Each conduction channel is described as a one-dimensional chain of charge carrier sites that spans a length L. From a biological perspective, a charge carrier site can be interpreted as a electron-carrying cofactor embedded in a non-conductive protein matrix. Electrons are assumed to be solely transported by hopping, i.e., sequential tunneling through the protein matrix from one cofactor to the next. A site can be in two states: uncharged (carrying no electron; Xi) or charged (carrying an electron; Xi−). The resulting electron transfer can be represented by a biomolecular self-exchange reaction between electron carriers| Xi− + Xj → Xi + Xj−. | (1) |
When the energies of the departure and destination sites differ (Ui ≠ Uj), energy must be exchanged with the environment during the electron transfer from i to j to ensure energy conservation. If this energy is dissipated to an environment at constant temperature T (heat bath), the ratio of the transition rates must follow the detailed balance relation:31,32
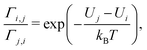 | (2) |
| Ji,j = Γi,jpi(1 − pj). | (3) |
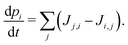 | (4) |
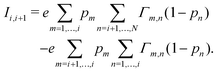 | (5) |
2.3 Nearest neighbour hopping
Electron tunneling in protein structures is known to have a strong exponential dependence on distance.33–36 Therefore, the chance that an electron hops to a remote site in the chain is improbable. We can implement this by only allowing transitions between adjacent sites, i.e., nearest neighbour hopping. Moreover, when the protein structure that forms the conduction channel is highly regular, all charge carriers will be identical, and the interdistance and site energy (without an imposed electrical field) will show little variation. As a result, the transition rates between neighbouring sites will be identical throughout the whole chain (Γi,i+1 = ΓR and Γi+1,i = ΓL). Assuming nearest neighbour hopping in a regular chain with identical sites, the net chain current (eqn (5)) simplifies to:| I = eΓRpi(1 − pi+1) − eΓLpi+1(1 − pi). | (6) |
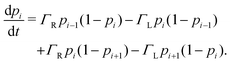 | (7) |
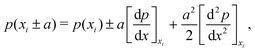 | (8) |
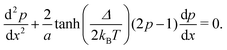 | (9) |
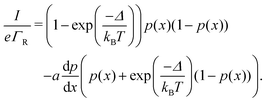 | (10) |
2.4 Charge transfer to and from the chain
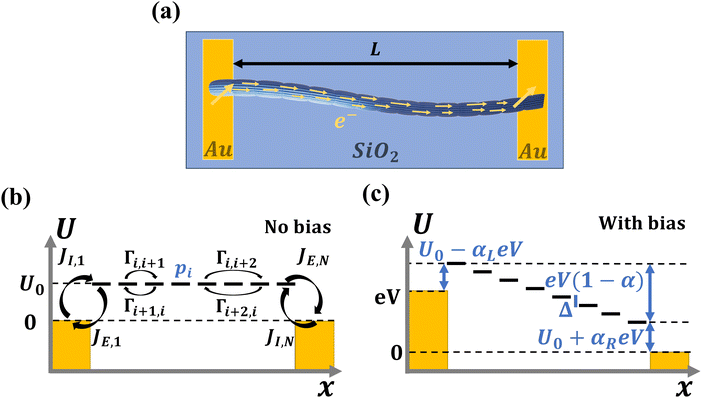
The site occupancy equation (eqn (9)), which governs the electron transport within the hopping chain, requires suitable boundary conditions. For this, we need to consider how electrons are either injected or ejected from the chain at the left and right boundaries. Two different situations can be considered: the metabolic operation of cable bacteria under in vivo conditions (in which electrons are supplied and removed through redox half-reactions; Fig. S2 in the ESI†), and the situation under which cable bacteria are electrically investigated in the laboratory (in which electrons are exchanged with electrodes; Fig. 2). The latter will be the focus of our analysis here, as it represents the situation under which the conductance data are collected.In the laboratory, the conductance of cable bacteria is studied by connecting individual filaments to metal electrodes.13,18,28 A bias voltage, V, is applied to the two terminal electrode contacts, and the electrical current, I, that flows through the cable bacterium segment is recorded (operation of the electrode set-up is illustrated in Fig. 2a). If charge injection from the electrode is non-limiting (J ≫ ΓR,L; see Fig. S3 and additional derivations in ESI†), the occupation probability at the edges reads:
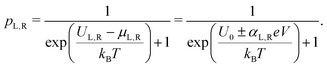 | (11) |
2.5 Marcus hopping rate
Semi-classical Marcus theory provides the following expression for the electron transfer rate between two sites in the hopping chain:20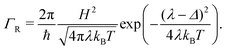 | (12) |
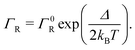 | (13) |
2.6 Numerical approach
The solution of the occupancy balance equation (eqn (4)) with suitable boundary conditions (eqn (11)) fully describes the electron transport through the hopping chain. To solve this differential equation, we implemented a numerical solution procedure (see ESI†) that calculates the site occupancy profile, p(x), as a function of the position along the chain x and the applied bias voltage V. Subsequently the normalized chain current I/(eΓR) is calculated, and this is then combined with the Marcus expression (eqn (12)) to simulate the full I(V) curve (see Fig. S1, ESI†). We also derived a set of analytical expressions for the occupancy profile and normalized chain current for the case when there's a symmetric voltage drop at the electrodes (αL = αR). Expressions are derived for the absence (U0 = 0) or presence (U0 > 0) of an injection barrier. These analytical expressions allow to identify how different end-member transport regimes influence the shape of the I/V curve. The details of the derivations are given in the ESI† and the resulting expressions are summarized in Tables S1 and S2.3 Results
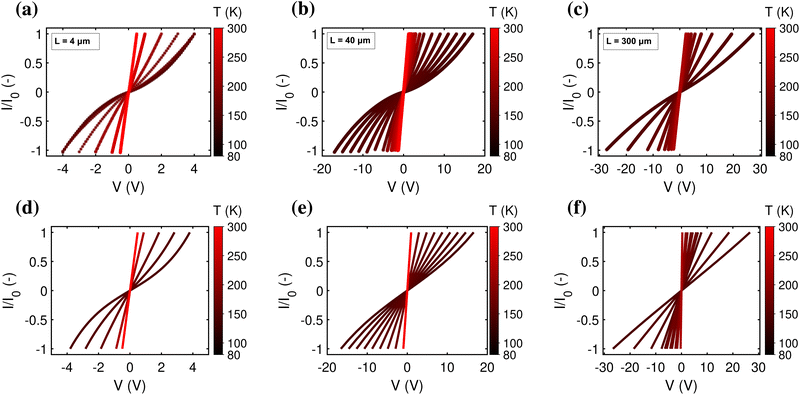
The mapping of the electrical current, I, as a function of the applied bias voltage, V, forms a key analysis in the electrical characterisation of materials. As a baseline and reference situation, we simulated a hopping chain with following parameters: N = 200, transport is predominantly field-driven (α = 0.2), resides in the resonant regime (U0 = 0), and has a reorganisation energy, λ = 200 meV, and electronic coupling, H = 16 meV. Subsequently, we systematically varied each parameter individually to verify its impact on the I(V) curve. We also compared the output of the model simulations to an extensive experimental dataset, consisting of I(V) curves collected at different temperatures (T = 80–300 K) for cable bacterium filaments of different length. The data collection procedure is presented in detail elsewhere.28Fig. 5 displays relevant I(V) curves for three segments of different length (L = 4, 40, 300 μm).3.1 Concentration-driven versus field-driven regime
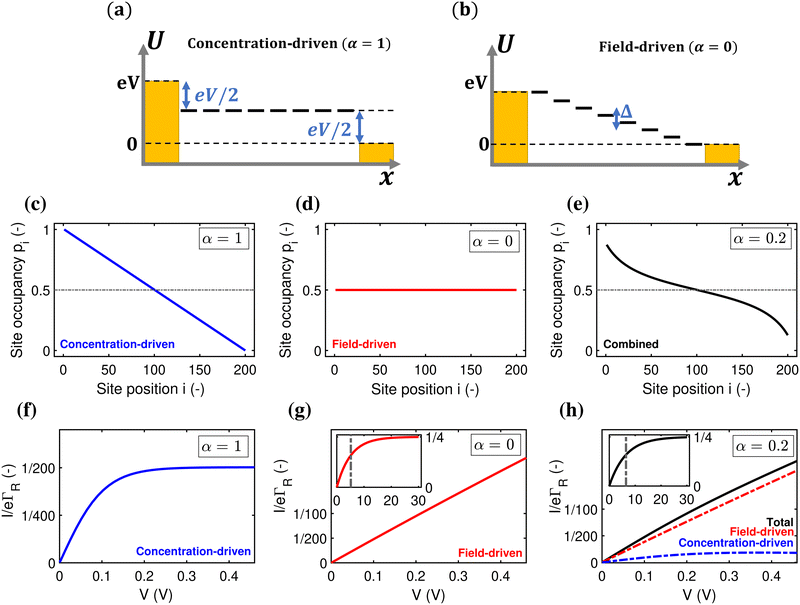
A first question is whether the electron transport in cable bacteria is concentration-driven or field-driven. These regimes correspond to two limiting cases for the behaviour of the electrical field at the electrode interfaces (see Fig. 3): either the applied voltage completely drops over the electrode interfaces (α = 1), or there is no voltage drop at the electrodes (α = 0). In our simulations, we assume that the voltage drop is similar at both electrodes (αL = αR = α/2).When the current is exclusively concentration-driven, the entire voltage drop occurs at the interface of the electrodes (α = 1, Fig. 3a), and there is no electric field or electric potential gradient present in the hopping chain (Δ = 0). As a result, all sites reside at the same site energy, and the detailed balance relation (eqn (2)) implies that the forward and backward transition rates must be equal. In this regime, the electron transport is purely “diffusive”, i.e., driven by the difference in site occupation probability along the chain. The differential equation describing the occupancy profile (eqn (9)), becomes the stationary diffusion equation and has a linear solution (Fig. 3c):
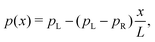 | (14) |
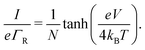 | (15) |
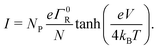 | (16) |
Oppositely, when the current is exclusively field-driven (α = 0, Fig. 3b), the site occupancy does not show a gradient (pi = 1/2, Fig. 3d). In this field-driven scenario, electron transport is solely “drift” based, i.e., it is driven by the difference in the forward and backward transition rates. The normalized chain current becomes (Fig. 3g, derivation in ESI†):
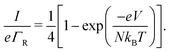 | (17) |
When the voltage bias is sufficiently small compared to the reorganization energy (eV/N < λ), we can use the Marcus rate expression, eqn (13), and so the I/V curve attains the form:
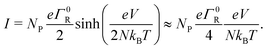 | (18) |
When α = 0.2, the site occupancy profile adopts a non-linear shape, which lies in between the linear concentration-driven and flat field-driven profile (Fig. 3e). Likewise, it can be shown that the resulting I(V) curve can be decomposed into the sum of a field-driven and a concentration-driven contribution (Fig. 3h; see derivation in ESI†). At higher voltages, the field-driven current becomes dominant (Fig. S5, ESI†).
3.2 Resonant versus off-resonant transport
A second question is whether the electron transport in the conductive fibers of cable bacteria is affected by an injection barrier, U0, or not. When the charge transport is not hampered by the barrier, it resides in the resonant regime. Oppositely, when the injection barrier is slowing down the transport, it is off-resonant. Fig. 4 shows the transition from the off-resonant to resonant transport regime for the reference parameters, but with U0 = 0.1 eV instead of zero. Analytical expressions can be derived for the occupancy profile and the normalized chain current (see ESI†). For low bias voltages, transport is off-resonant (αLeV < U0), and the site occupancy stays low throughout the chain (Fig. 4a). As the bias voltage increases, the conduction enters the resonant regime when αLeV = U0 and the occupancy profile evolves towards a static tangent-shaped profile (Fig. 4a, similar to that displayed in Fig. 3e). The normalized I(V) curve shows the transition from off-resonant to resonant transport, which occurs at V = U0/(eαL) (Fig. 4b). At low bias, in the off-resonant regime, the normalized chain current is non-linear, while in the resonant regime, the current increases linearly with the applied voltage bias.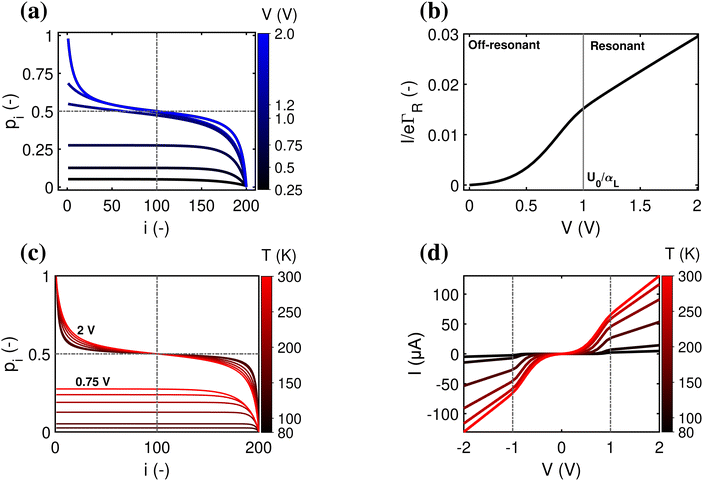 | ||
| Fig. 4 Resonant and off-resonant electron transport in a hopping with an injection barrier. Model parameters are: N = 200, U0 = 0.1 eV, α = 0.2, T = 300 K. (a) Simulated occupancy profile for six different voltages (as indicated by numbers next to the colour bar). The dashed lines indicate the crossing at pN/2 = 1/2. (b) Normalized chain current, I/eΓR, plotted as a function voltage bias, V. The transition from off-resonant to resonant occurs at eV = U0/αL = 1 V. (c) Occupancy profile at two fixed voltages (off-resonant V = 0.75 V and resonant V = 2 V) for six different temperatures (indicated by numbers next to the colour scale). (d) Simulated current–voltage response for six different temperatures, using the Marcus rate (eqn (12)) with parameters H = 16 meV and λ = 0.2 eV. | ||
In the off-resonant regime, the temperature has a large effect on the site occupancy profile, and induces an overall decrease of the site occupancy upon cooling. In contrast, in the resonant regime, the occupancy profile is only marginally influenced by the temperature (Fig. 4c). Overall, the full I(V) curves show the same strong non-linear shape as the normalized I(V) (Fig. 4d). The experimental I(V) curves do not display this strong non-linearity (Fig. 5). This indicates that there is no significant injection barrier present, when the cable bacterium filaments are interfaced to gold electrodes.
3.3 Length dependence of the I(V) curve
A third aspect relates to the impact of the hopping chain length on the I(V) curve. As clearly seen in the experimental data (Fig. 5a–c), the shape of the I(V) curve becomes more linear as the length of the investigated segment increases. This phenomenon is well represented by eqn (18), which predicts that the I(V) curve becomes more linear as the number of sites N increases (simulated I/V curves are displayed in Fig. 5d–f). The explanation is rather straight forward: as the number of sites N decreases, the site energy difference Δ = eV/N increases at a given fixed voltage. When Δ increases, the expression for the normalized current (eqn (17)) becomes non-linear, while also the Marcus rate (eqn (13)) adds to the non-linearity. As a result, the full I(V) curve becomes increasingly hyperbolic, when the temperature decreases and/or the segment length decreases (Fig. 5).3.4 Conductivity
Overall, the multistep hopping model appears to adequately simulate the experimental I(V) curves, in the field-driven regime with no significant injection barrier. Therefore, a prominent question is whether the model can also reproduce the conductivity of the cable bacteria fibers, which is extremely high for a biological system (reaching up to >100 S cm−1 at room temperature). To this end, we now investigate the relationship between the hopping rate and the electrical conductivity.Assuming a suitably long chain (such that the low-bias limit eV/N ≪ kBT holds), and adopting field-driven transport (α = 0) and no injection barrier (U0 = 0), we can use eqn (18) to express the conductivity of a fiber of length L and cross-section A:
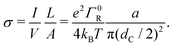 | (19) |
Eqn (19) provides a direct relation between the hopping rate and the conductivity, and readily illustrates the problem of explaining the high conductance in cable bacteria. If we assume that multistep hopping in cable bacteria occurs over a similar length scale as in multi-heme cytochromes,21 the center-to-center distance between sites would be a ∼ 1 nm. Using this value in eqn (19), the required hopping rate for a conductivity of 100 S cm−1 becomes ΓR ≈ 2 × 1013 s−1. This value exceeds by far the fastest hopping rate reported in literature for a biological protein structure (109 s−1).39,40 More problematically, it also exceeds the typical relaxation rate of vibrational modes in cofactors, ∼1013 s−1, which is considered as a “speed limit” for hopping conduction.41 The relaxation rate of vibrational modes must be higher than the hopping rate itself, so that the electron has time to dissipate energy before hopping onwards (see ESI:† ‘Non-adiabatic constraint’ for further detail).
To examine the maximum conductivity that a hopping model for cable bacteria can support, we can evaluate the theoretical limits of the Marcus rate expression eqn (12). Marcus theory requires that the inter-site electronic coupling H is weak,20 so that it remains small with respect to the reorganisation energy (H ≪ λ). When H ≈ λ or beyond, the electron will no longer be localised on the hopping site.37,38,42 To quantitatively evaluate the maximum conductivity allowed by the Marcus formalism, we adopt the working assumption that the maximum electronic coupling is Hmax = 0.1λ (see ESI† for additional discussion of this ‘weak coupling’ constraint).
As a result, the conductivity in eqn (19) only varies with the reorganisation energy λ and the center-to-center distance a. The resulting model simulations are shown in Fig. 6a. For parameters representing electron transport through multi-heme cytochromes21 (λ = 0.8 eV, a = 1 nm), a hopping rate of 5 × 1010 s−1 and a conductivity level of 0.2 S cm−1 form the theoretical maximum within the Marcus framework. Note however that this conductivity limit is based upon an unrealistically high electronic coupling, H ≈ λ/10 = 80 meV. As known from experimental and theoretical assessments, H = 10 meV is already on the high side for multi-heme cytochromes.21 Adopting the latter value lowers the maximum allowed conductivity to 4 mS cm−1 (hopping rate: 8 × 108 s−1).
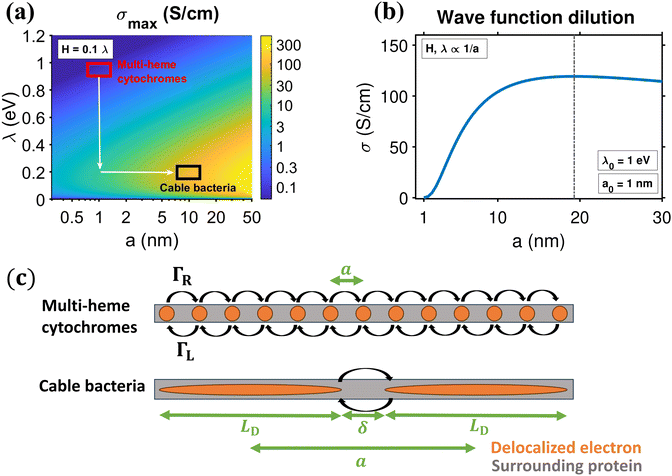 | ||
| Fig. 6 Idealized hopping conductivity and mobility within the one-dimensional hopping chain, using Marcus rates (eqn (12)). (a) Conductivity colour map, under the constraint H = 0.1λ, as a function of reorganisation energy λ and center-to-center distance between hopping sites a. The red and black square are indicators for the typical reorganisation energy and center-to-center distance in hemes and cable bacteria, respectively (see panel (c)). Directions for increased conductivity compared to cytochromes are drawn in white. (b) Conductivity, σ, as a function of center-to-center hopping distance, a, for a biological system that improves on heme-to-heme hopping with distance a0 = 1 nm, reorganisation λ0 = 1 eV and electronic coupling H0 = 0.1λ0 = 100 meV, by wave function dilution (H, λ ∝ 1/a). (c) Scheme of heme-to-heme transport (red) and the proposed hopping mechanism in cable bacteria (black), with center-to-center distance, a, between regions in which is the electron is unobstructed (orange, zero resistance) with repetitive surrounding protein structure (grey). Electrons hop between repeated structures with hopping rates ΓR,L. | ||
We conclude that a multi-step hopping model with cytochrome-like parameters cannot explain the conductivities measured in cable bacteria. As illustrated in Fig. 6a, there are two ways to achieve a higher conductivity. A first way is to reduce the reorganisation energy, and effectively, cable bacteria appear to do this. Recent studies18,28 indicate that the reorganisation energy of conductance in cable bacteria is remarkably low (λ = 0.2 eV), i.e., a factor 4 lower compared to heme-to-heme transport in multi-heme cytochromes.
Still, a reduction of the reorganization energy alone is not enough to explain the high conductivity in cable bacteria. With λ = 0.2 eV and a = 1 nm, we can only reach a hopping rate of 2 × 1012 s−1 and a conductivity level of 10 S cm−1 (vertical arrow in Fig. 6a). Therefore, a second way is to increase increase conductivity is to increase the center-to-center distance a, thus lowering the number of hopping steps. To attain a conductivity of σ = 100 S cm−1 as reported for cable bacterium fibers, we need to increase the hopping distance to a ≈ 10 nm, under the constraint Hmax = 0.1λ with λ = 0.2 eV (horizontal arrow in Fig. 6a). This provides a hopping rate 2.2 × 1012 s−1, which is still high, but below the “speed limit” for hopping conduction.41 For more stringent constraints with lower H/ratios, higher a values are required (see Fig. S10 and additional results in ESI†).
The predicted electron mobility accompanying λ = 0.2 eV and a = 10 nm is μ = 80 cm2 V−1 s−1 (Fig. S10, ESI†). This mobility value is high and similar to that of metals (∼50 cm2 V−1 s−1). Metals are highly conductive because many electrons contribute to transport (n ≈ 1022 cm−3), but their charge carrier mobilities are not exceptionally high, since electrons frequently collide with the crystal lattice. The predicted charge carrier density in the one-dimensional hopping chain model with a = 10 nm, is n = 1/(4aπ(dC/2)2) ≈ 8 × 1018 cm−3, which is much lower than for metals, thus explaining why the conductivity in cable bacteria is 4 orders of lower than in metals.
4 Discussion and conclusions
We have developed a one-dimensional hopping model to describe the extremely long-range electron transport in the periplasmic fiber network of cable bacteria. When filaments are connected to metal electrodes, we propose that the edge occupation probabilities in the hopping chain can be treated as if they were part of the electrode (see eqn (11)). This allows simplified analytical expressions to be derived for the current–voltage characteristics in the field- and concentration-driven regimes (Tables S1 and S2, ESI†). For more general cases, I/V curves can be numerically simulated.The conductive fiber network in cable bacteria has been shown to consist of a metalloprotein that incorporates a nickel cofactor.17 Yet, the detailed molecular structure of this cofactor remains unresolved, and consequently, any model of charge transport in cable bacteria remains somehow speculative. Still, the model analysis here allows to exclude certain transport models, while at the same time, it provides guidance for further experimental investigations and theoretical developments.
4.1 The shape of the I/V curve
When cable bacterium filaments are connected to electrodes and electrically investigated at room temperature, the resulting I/V curves are conspicuously linear.13,18,28 Comparison of our model results to these experimentally recorded I/V curves, shows that the model adequately reproduces the impact of segment length and temperature on the shape of the I/V curve, provided that we adopt a field-driven regime with no significant injection barrier (Fig. 5).The linearity is explained by the fact that the filaments investigated are long, and so the charge transfer involves a large number of charge transfer steps N. As a result, the driving force Δ = eV/N remains small compared to the thermal energy scale (Δ ≪ kBT and so eqn (17) becomes valid). Moreover, the driving force also stays well below the reorganization energy (Δ ≪ λ), implying that the electron transfer rate ΓR remains largely independent of the applied voltage bias (see eqn (12)). These conditions generate linear I/V curves near room temperature, which become increasingly non-linear (sinus hyperbolic) for lower temperatures and shorter segments, as seen in the experimental data (Fig. 5). Note that the condition (Δ ≪ λ) also implies that the charge transport well remains within the normal Marcus regime (and hence does not enter into the inverted regime).
When using gold electrodes, there appears to be no injection barrier involved in the charge transport. This absence of an injection barrier is intriguing, and requires further experimental examination. The work function, which directly influences the barrier, varies among metals (the energy to bring an electron from the electrode to vacuum of the electrode).43,44 Therefore, it could be that for electrode materials other than gold, there is a sizable injection barrier.
4.2 Impact of reorganization on conductivity
Our model analysis demonstrates that a low reorganization energy is key to achieving a high conductivity in cable bacteria (Fig. 6a). Recent studies have shown that the reorganisation energy in cable bacteria is indeed considerably lower than in other conductive protein systems.18,28 Yet at present, the molecular structure of the conductive fibers in cable bacteria remains largely unresolved, and therefore, it is not understood why the reorganisation energy of cable bacteria is so small. One potential explanation could be delocalization along the electron transport path, as would result from an ordered aggregation or tight stacking of cofactors. Recently, an extension of Marcus theory has been developed that accounts for charge transfer between so-called donor and acceptor “aggregates”, in which the charge is no longer localized on a single cofactor, but delocalized across a cluster of multiple cofactor molecules.45 It was shown that such delocalization can substantially reduce the reorganization energy below what is possible with a single donor and a single acceptor. For example, for a donor aggregate with a fully delocalized state of N identical donors, the reorganisation energy is decreased N-fold.45 For example, if we assume that the reorganization energy λ between a single donor and a single acceptor would be similar to that between consecutive hemes in multi-heme cytochromes, the observed 4 times reduction in λ for cable bacteria as compared to multi-heme cytochromes18,28 then would imply a delocalization of the charge across ∼4 cofactor molecules. Yet, to verify whether such a delocalization mechanism is truly at play, we need a better insight into the actual identity and structure of the cofactor molecules in cable bacteria.4.3 A tentative model of charge transport in cable bacteria
Our model analysis reveals that the high conductivity recorded in the conductive fibers of cable bacteria (>100 S cm−1) can only be explained by a Marcus-type hopping model, unless the number of hopping steps is substantially reduced and the center-to-center distance a becomes very large (Fig. 6a). Clearly, a hopping distance of a ≈ 10 nm exceeds by far the known hopping distances in metalloproteins such as multi-heme cytochromes. If electrons are transported by quantum mechanical tunneling, the center-to-center distance a must be lower than 1.4 nm to attain metabolically relevant electron transport rates (see Moser et al.3). How can such a large value for a be reached?A tentative model is depicted in Fig. 6c. The key difference with classical hopping models of biological transport (e.g. heme-based electron transport) is the amount of delocalization, as reflected by the size of the charge carrier sites. Instead of being localized on a small cofactor molecule, electrons are delocalized across wide “relay segments” (distance LD ∼ 10 nm) that are connected through small non-conductive bridges (distance δ). The electron transport through this protein connection is the rate limiting process, and follows a Marcus-type hopping mechanism. In contrast, the electron transport in the delocalized segments is very fast, and needs to have a far higher mobility than the hopping transport. These relay segments could either be large conjugated molecules, as seen in pi-conjugated polymers and graphene nanoribbons,46 or alternatively, they could involve sets of tightly stacked cofactor molecules that induce electron delocalization (the donor and acceptor “aggregates” discussed above).
This model immediately provokes the question of how biology can synthesize such a structure. Clearly, to ensure high charge transport rates, the “relay segments” should be carefully positioned and oriented, which hence requires a precise coordination by ligating proteins. Furthermore, it is known that delocalized regions are particularly sensitive to disorder effects, as impurities and defects will induce Anderson localisation of electrons,47 and hence reduce the conductivity. Effectively, the latter phenomenon may help explaining the observation that the conductivity in cable bacteria fibers is variable (ranging from 0.1 to >100 S cm−1; see ref. 13). Differences in levels of defects/impurities may induce variability in conductance between filaments.
4.4 Impact of delocalization on conductivity
As detailed above, the conductivity can be increased by lowering the reorganization energy and increasing the center-to-center distance (Fig. 6a). To quantitatively assess the conjoint impact of both factors, we can introduce reference values for the hopping distance (a0 ∼ 1 nm) and reorganization energy (λ0 ∼ 1 eV) for conventional biological electron transport. We can now increase a while keeping δ constant, thus simulating the process of wave function dilution (Fig. 6c). When a becomes much larger than a0, we can approximate the delocalization length LD ≈ a and write the reorganisation energy as λ = λ0(a0/a) and the electronic coupling as H = H0(a0/a), where λ0 is the original reorganisation energy and H0 the original electronic coupling. With these constraints, the ratio between H and λ stays constant, and so the transport remains within the Marcus regime. Moreover, the conductivity can be calculated as a sole function of the center-to-center distance: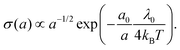 | (20) |
4.5 Hopping versus band transport?
In our model analysis, we described the electron transport in cable bacteria as thermally assisted hopping, as this is the default modelling approach employed to describe long-range biological conduction. Is there a possibility that the charge transport is not due to hopping, but rather acts as a form of band transport? In a hopping regime, the charge carrier is localized on a single molecule whereas in the band regime, the charge carrier (wave function) is delocalized over the entire system. In order to achieve a band regime, one must have a highly ordered structure with only a few defects or impurities, and a large electronic coupling between adjacent sites. In highly purified molecular single crystals such as pentacene, transport at low temperature can be described within a band picture.48 However, at higher temperatures, the charge carriers get localized over single polymer strands and transport operates by a thermally activated hopping mechanism between adjacent polymer chains.49As impurities, disorder and structural defects seem hard to avoid in the cm-long fiber structures in cable bacteria, a hopping regime is expected to operate at room temperature, as in organic crystals. Nevertheless, the models investigated here consider only one electronic state in a given “relay segment”. This leaves the possibility that there is more than one electronic state in a given “relay segment”. Recall that the driving force behind localisation in our model is a weak electronic coupling at the edge of the hopping site (H < λ). If a relay segment would be composed of N tightly stacked molecules, these must all be strongly coupled with an interaction energy, t > λ, if not, the electron would localise in a smaller region.37 According to the tight binding model, this results in multiple electronic states lying in an energy band of width 4t.26,50 Within a 10 nm wide “relay segment”, and assuming a stacking distance of 0.35 nm (a typical intermolecular distances in organic conjugated crystals and films), each molecule (N = 30) would add a single state to an energy band with an expected level spacing 4t/N ∼ 4λ/N ≈ 27 meV. At room temperature, the majority of states would contribute to the conductance (thermal window kBT ≈ 25 meV). Therefore, while pure band transport is not expected in the conductive fiber network of cable bacteria, future studies should consider more elaborate model approaches that allow the existence of multiple electronic states within “relay segments”.
Author contributions
J. R. V. performed numerical simulations and model analysis. Y. M. B., H. S. J. Z., F. J. R. M. and J. R. V. conceptualized the model analysis, and S. V. validated the simulation approach. J. R. V. and F. J. R. M. wrote the manuscript, with additional input from H. S. J. Z., Y. M. B. and S. V.Conflicts of interest
There are no conflicts to declare.Acknowledgements
We acknowledge Damian Bouwmeester for suggesting that the occupancy profile can be approximated with an ordinary differential equation. S. V. thanks the Kavli Institute of Science in Delft for the KIND Postdoctoral fellowship support. J. R. V. and F. J. R. M. were financially supported by the Netherlands Organization for Scientific Research (VICI grant 016.VICI.170.072). F. J. R. M. was additionally supported by Science Foundation Flanders (FWO-SBO grant S004523N). F. J. R. M. and H. S. J. Z. received support from the EIC Pathfinder project PRINGLE.Notes and references
- D. Becker, R. Banerjee, M. Dickman, V. Gladyshev and S. Ragsdale, Redox biochemistry, John Wiley & Sons, 2007 Search PubMed.
- H. B. Gray and J. R. Winkler, Biochim. Biophys. Acta, Bioenerg., 2010, 1797, 1563–1572 CrossRef CAS PubMed.
- C. C. Moser, J. R. Anderson and P. L. Dutton, Biochim. Biophys. Acta, Bioenerg., 2010, 1797, 1573–1586 CrossRef CAS PubMed.
- C. Pfeffer, S. Larsen, J. Song, M. Dong, F. Besenbacher, R. L. Meyer, K. U. Kjeldsen, L. Schreiber, Y. A. Gorby and M. Y. El-Naggar, et al. , Nature, 2012, 491, 218–221 CrossRef CAS PubMed.
- F. J. Meysman, Trends Microbiol., 2018, 26, 411–422 CrossRef CAS PubMed.
- S. Y. Malkin, A. M. Rao, D. Seitaj, D. Vasquez-Cardenas, E.-M. Zetsche, S. Hidalgo-Martinez, H. T. Boschker and F. J. Meysman, ISME J., 2014, 8, 1843–1854 CrossRef CAS PubMed.
- N. Risgaard-Petersen, M. Kristiansen, R. B. Frederiksen, A. L. Dittmer, J. T. Bjerg, D. Trojan, L. Schreiber, L. R. Damgaard, A. Schramm and L. P. Nielsen, Appl. Environ. Microbiol., 2015, 81, 6003–6011 CrossRef CAS PubMed.
- L. D. Burdorf, A. Tramper, D. Seitaj, L. Meire, S. Hidalgo-Martinez, E.-M. Zetsche, H. T. Boschker and F. J. Meysman, Biogeosciences, 2017, 14, 683–701 CrossRef CAS.
- V. V. Scholz, B. C. Martin, R. Meyer, A. Schramm, M. W. Fraser, L. P. Nielsen, G. A. Kendrick, N. Risgaard-Petersen, L. D. Burdorf and I. P. Marshall, New Phytol., 2021, 232, 2138–2151 CrossRef CAS PubMed.
- N. M. Geerlings, C. Karman, S. Trashin, K. S. As, M. V. Kienhuis, S. Hidalgo-Martinez, D. Vasquez-Cardenas, H. T. Boschker, K. De Wael and J. J. Middelburg, et al. , Proc. Natl. Acad. Sci. U. S. A., 2020, 117, 5478–5485 CrossRef CAS PubMed.
- S. Scilipoti, K. Koren, N. Risgaard-Petersen, A. Schramm and L. P. Nielsen, Sci. Adv., 2021, 7, eabe1870 CrossRef CAS PubMed.
- J. T. Bjerg, H. T. Boschker, S. Larsen, D. Berry, M. Schmid, D. Millo, P. Tataru, F. J. Meysman, M. Wagner and L. P. Nielsen, et al. , Proc. Natl. Acad. Sci. U. S. A., 2018, 115, 5786–5791 CrossRef CAS PubMed.
- F. J. Meysman, R. Cornelissen, S. Trashin, R. Bonné, S. H. Martinez, J. van der Veen, C. J. Blom, C. Karman, J.-L. Hou and R. T. Eachambadi, et al. , Nat. Commun., 2019, 10, 1–8 CrossRef CAS PubMed.
- R. Thiruvallur Eachambadi, R. Bonné, R. Cornelissen, S. Hidalgo-Martinez, J. Vangronsveld, F. J. Meysman, R. Valcke, B. Cleuren and J. V. Manca, Adv. Biosyst., 2020, 4, 2000006 CrossRef PubMed.
- R. Cornelissen, A. Bøggild, R. Thiruvallur Eachambadi, R. I. Koning, A. Kremer, S. Hidalgo-Martinez, E.-M. Zetsche, L. R. Damgaard, R. Bonné and J. Drijkoningen, et al. , Front. Microbiol., 2018, 9, 3044 CrossRef PubMed.
- Z. Jiang, S. Zhang, L. H. Klausen, J. Song, Q. Li, Z. Wang, B. T. Stokke, Y. Huang, F. Besenbacher and L. P. Nielsen, et al. , Proc. Natl. Acad. Sci. U. S. A., 2018, 115, 8517–8522 CrossRef CAS PubMed.
- H. T. Boschker, P. L. Cook, L. Polerecky, R. T. Eachambadi, H. Lozano, S. Hidalgo-Martinez, D. Khalenkow, V. Spampinato, N. Claes and P. Kundu, et al. , Nat. Commun., 2021, 12, 1–12 CrossRef PubMed.
- R. Bonné, J.-L. Hou, J. Hustings, K. Wouters, M. Meert, S. Hidalgo-Martinez, R. Cornelissen, F. Morini, S. Thijs and J. Vangronsveld, et al. , Sci. Rep., 2020, 10, 1–8 CrossRef PubMed.
- J. Blumberger, Chem. Rev., 2015, 115, 11191–11238 CrossRef CAS PubMed.
- R. A. Marcus and N. Sutin, Biochem. Biophys. Acta, 1985, 811, 265–322 CAS.
- M. Breuer, K. M. Rosso and J. Blumberger, Proc. Natl. Acad. Sci. U. S. A., 2014, 111, 611–616 CrossRef CAS PubMed.
- N. Amdursky, D. Marchak, L. Sepunaru, I. Pecht, M. Sheves and D. Cahen, Adv. Mater., 2014, 26, 7142–7161 CrossRef CAS PubMed.
- S. Valianti, J.-C. Cuevas and S. S. Skourtis, J. Phys. Chem. C, 2019, 123, 5907–5922 CrossRef CAS.
- N. Amdursky, L. Sepunaru, S. Raichlin, I. Pecht, M. Sheves and D. Cahen, Adv. Sci., 2015, 2, 1400026 CrossRef PubMed.
- S. M. Strycharz-Glaven, R. M. Snider, A. Guiseppi-Elie and L. M. Tender, Energy Environ. Sci., 2011, 4, 4366–4379 RSC.
- N. F. Polizzi, S. S. Skourtis and D. N. Beratan, Faraday Discuss., 2012, 155, 43–61 RSC.
- S. Pirbadian, S. E. Barchinger, K. M. Leung, H. S. Byun, Y. Jangir, R. A. Bouhenni, S. B. Reed, M. F. Romine, D. A. Saffarini and L. Shi, et al. , Proc. Natl. Acad. Sci. U. S. A., 2014, 111, 12883–12888 CrossRef CAS PubMed.
- J. R. van der Veen, S. H. Martinez, A. Wieland, M. De Pellegrin, R. Verweij, Y. M. Blanter, H. S. van der Zant and F. J. Meysman, arXiv, 2023, preprint, arXiv:2308.09560 DOI:10.48550/arXiv.2308.09560.
- J. S. Geelhoed, C. A. Thorup, J. J. Bjerg, L. Schreiber, L. P. Nielsen, A. Schramm, F. J. Meysman and I. P. Marshall, Microbiol. Spectrum, 2023, e00538 Search PubMed.
- J. Cottaar and P. Bobbert, Phys. Rev. B: Condens. Matter Mater. Phys., 2006, 74, 115204 CrossRef.
- R. Egger, C. Mak and U. Weiss, J. Chem. Phys., 1994, 100, 2651–2660 CrossRef CAS.
- Y. V. Nazarov and Y. M. Blanter, Quantum transport: introduction to nanoscience, Cambridge University Press, 2009 Search PubMed.
- Y. A. Berlin, A. L. Burin and M. A. Ratner, J. Am. Chem. Soc., 2001, 123, 260–268 CrossRef CAS PubMed.
- S. Pirbadian and M. Y. El-Naggar, Phys. Chem. Chem. Phys., 2012, 14, 13802–13808 RSC.
- D. Monroe, Phys. Rev. Lett., 1985, 54, 146 CrossRef CAS PubMed.
- S. Lindsay, Life, 2020, 10, 72 CrossRef CAS PubMed.
- S. Fratini, D. Mayou and S. Ciuchi, Adv. Funct. Mater., 2015, 26, 2292–2315 CrossRef.
- S. Giannini, A. Carof, M. Ellis, H. Yang, O. G. Ziogos, S. Ghosh and J. Blumberger, Nat. Commun., 2019, 10, 1–12 CrossRef CAS PubMed.
- X. Jiang, Z. Futera, M. E. Ali, F. Gajdos, G. F. von Rudorff, A. Carof, M. Breuer and J. Blumberger, J. Am. Chem. Soc., 2017, 139, 17237–17240 CrossRef CAS PubMed.
- J. H. van Wonderen, K. Adamczyk, X. Wu, X. Jiang, S. E. Piper, C. R. Hall, M. J. Edwards, T. A. Clarke, H. Zhang and L. J. Jeuken, et al. , Proc. Natl. Acad. Sci. U. S. A., 2021, 118, e2107939118 CrossRef CAS PubMed.
- A. Troisi, Org. Electron., 2011, 12, 1988–1991 CrossRef CAS.
- Y. V. Nazarov and J. Danon, Advanced Quantum Mechanics: A Practical Guide, Cambridge University Press, 2013 Search PubMed.
- J. Hwang, A. Wan and A. Kahn, Mater. Sci. Eng., R, 2009, 64, 1–31 CrossRef.
- J. M. Beebe, V. B. Engelkes, L. L. Miller and C. D. Frisbie, J. Am. Chem. Soc., 2002, 124, 11268–11269 CrossRef CAS PubMed.
- N. B. Taylor and I. Kassal, Chem. Sci., 2018, 9, 2942–2951 RSC.
- K. I. Bolotin, K. Sikes, Z. Jiang, M. Klima, G. Fudenberg, J. Hone, P. Kim and H. L. Stormer, Solid State Commun., 2008, 146, 351–355 CrossRef CAS.
- F. Evers and A. D. Mirlin, Rev. Mod. Phys., 2008, 80, 1355 CrossRef CAS.
- V. Coropceanu, J. Cornil, D. A. da Silva Filho, Y. Olivier, R. Silbey and J.-L. Brédas, Chem. Rev., 2007, 107, 926–952 CrossRef CAS PubMed.
- J.-L. Brédas, J. P. Calbert, D. da Silva Filho and J. Cornil, Proc. Natl. Acad. Sci. U. S. A., 2002, 99, 5804–5809 CrossRef PubMed.
- F. C. Grozema and L. D. Siebbeles, Int. Rev. Phys. Chem., 2008, 27, 87–138 Search PubMed.
Footnote |
| † Electronic supplementary information (ESI) available. See DOI: https://doi.org/10.1039/d3cp04466a |
| This journal is © the Owner Societies 2024 |