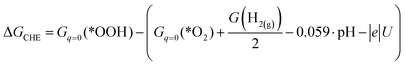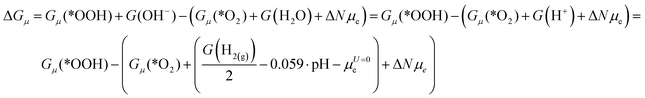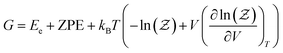Revision of the oxygen reduction reaction on N-doped graphenes by grand-canonical DFT†
Vitaliy A.
Kislenko
 ab,
Sergey V.
Pavlov
ab,
Sergey V.
Pavlov
 b,
Victoria A.
Nikitina
b,
Victoria A.
Nikitina
 a and
Sergey A.
Kislenko
a and
Sergey A.
Kislenko
 *b
*b
aSkolkovo Institute of Science and Technology (Skoltech), Bolshoy Boulevard 30, bld. 1, Moscow, 121205, Russian Federation
bJoint Institute for High Temperatures of the Russian Academy of Sciences, Izhorskaya 13/2, Moscow, 125412, Russian Federation. E-mail: kislenko@ihed.ras.ru
First published on 23rd November 2023
Abstract
Nitrogen-doped graphenes were among the first promising metal-free carbon-based catalysts for the oxygen reduction reaction (ORR). However, data on the most efficient catalytic centers and their catalytic mechanisms are still under debate. In this work, we study the associative mechanism of the ORR in an alkaline medium on graphene containing various types of nitrogen doping. The free energy profile of the reaction is constructed using grand-canonical DFT at a constant electrode potential in combination with an implicit electrolyte model. It is shown that the reaction mechanism differs from the generally accepted one and depends on the surface potential and doping type. In particular, as the potential decreases, coupled electron–proton transfer changes to sequential electron and proton transfer, and the potential at which this occurs depends on the doping type. It has been shown that oxygen chemisorption is the limiting step. The electrocatalytic mechanism of the nitrogen dopants involves reducing the oxygen chemisorption energy. Calculations predict that, at different potentials, different types of nitrogen impurities most effectively catalyze the ORR.
1 Introduction
The oxygen reduction reaction is the most sluggish reaction in fuel cells and its catalysis is critical to developing efficient devices.1 The most efficient electrocatalysts for the ORR are the platinum group metals. However, due to the high cost and degradation problems, the development of cheaper and more durable electrocatalysts is required.A promising alternative is chemically modified graphene (see ref. 2–4). To date, the electrocatalytic activity of various heteroatoms incorporated into graphene has been identified, including B, S, P, Cl, and many others.4 However, this effect was first demonstrated for nitrogen heteroatoms.5,6 Therefore, carbon materials doped with nitrogen are the most studied. It was shown that nitrogen doping reduces the ORR overpotential7–9 and directs the reaction via a four-electron mechanism.8,10
N-doped carbon materials exhibit electrocatalytic properties in both alkaline and acidic media. However, their effectiveness is higher in an alkaline medium.11,12 In addition, in alkali, N-doped graphenes exhibit higher electrochemical stability and durability, outperforming Pt electrocatalysts.9,13,14
There are three chemical forms of nitrogen in graphene-like materials – pyridine, pyrrole, and graphitic nitrogen atoms. However, experimental data on electrocatalytic centers are extremely contradictory. It was stated in ref. 13 that graphitic nitrogen atoms catalyze the ORR. In contrast, in ref. 15, pyridine N atoms were defined as catalytic centers. It is believed in ref. 8, that both pyridine and graphitic nitrogen accelerate the ORR. In ref. 10, authors came to the conclusion that graphitic N increases the limiting diffusion current and pyridine N reduces the overpotential of the reaction. The interpretation of such contradictory experimental data and the determination of the catalytic mechanism of nitrogen require the involvement of theory and modeling.
The use of DFT calculations in such research is widespread. It was shown that the nitrogen dopants make the chemisorption of the O2 molecule energetically more favorable.16 It was also found that a single substituting nitrogen atom on the graphene edge significantly reduces the O2 adsorption barrier.17 In the later work, the free energy profile of the ORR was constructed in an acidic medium.18 The exothermic nature of each elementary step of the four-electron mechanism is shown. However, the calculations were performed for an electrically neutral cluster system, while the ORR half-wave potential is about 0.7–0.9 V (vs. SHE),7,19 which means a significant positive surface charge.
The most widely used method for studying electrocatalytic reactions is the computational hydrogen electrode (CHE) model proposed by Norskov et al.20 This method makes it possible to calculate the free energy profile of a multistage electrochemical reaction at a given potential. This approach was used in ref. 21 to calculate the ORR thermodynamics on N-doped graphene in an alkaline medium. It was shown that the associative mechanism is more favorable than the dissociative one. It should be noted, however, that the CHE method is based on a number of assumptions and simplifications that are not necessarily fulfilled in real systems.22 One of the drawbacks of the method is the calculation at a fixed surface charge (most often at zero charge) with subsequent non-self-consistent corrections to the free energy, including those related to the surface potential. At the same time, in a real system, the ORR proceeds at a constant electrode potential, while the surface charge is generally non-zero and non-constant. The recently developed modeling approach at a fixed potential23 gives particularly noticeable differences from the CHE method for two-dimensional materials, in which the Fermi level shifts relative to the band structure during charging due to the low density of electronic states.24–26 For instance, simulation of the oxygen evolution reaction on Ni- and Co-doped graphene at a fixed potential predicts a different limiting step compared to the traditional CHE.27
In this work, using the grand canonical (GC) DFT simulation at a fixed electrode potential, the thermodynamics of the oxygen reduction reaction under alkaline conditions on the graphene surface containing various types of nitrogen doping is calculated for the first time. For comparison, the energy profiles of the reaction for defect-free graphene are given, which were not previously presented in the literature. The emphasis of the work is on the study of the associative mechanism of the ORR and those refinements to it that the GC-DFT provides. We determined the limiting step of the ORR and the catalytic mechanism of nitrogen heteroatoms and also analyzed the differences in predictions given by GC-DFT and the CHE method.
2 Computational details
2.1 Details of DFT calculations
Spin-polarized DFT calculations were performed using the JDFTx software package.28 The CANDLE continuum solvation model was used.29 The implicit aqueous electrolyte with 1 M K+ and 1 M Cl− was applied. The GGA-PBE exchange–correlation functional was used. The DFT-D3 correction was applied for the correct prediction of the van der Waals interaction.30 Ultrasoft GBRV-type pseudopotentials were used.31 The cutoff energy for wave functions and electron density was 28 and 140 Hartree, respectively. A gamma-centered 5 × 5 × 1 k-point grid was used. The energy convergence criterion during the self-consistent step was 10−8 Hartree. Ionic optimization was carried out until the difference between successive steps did not exceed 10−6 Hartree in energy and the mean root square of the force acting on the atoms did not exceed 5 × 10−5 Hartree Bohr−1. The computational cell was represented by a rectangular single-layer graphene 12.8 Å × 12.3 Å in size with a distance of 15 Å in the direction perpendicular to the graphene plane.2.2 Associative mechanism of the ORR
The following associative four-electron mechanism of oxygen reduction in an alkaline medium was considered:32| O2 + * → *O2 | (1) |
| *O2 + H2O + e → *OOH + OH− | (2) |
| *OOH + e → *O + OH− | (3) |
| *O2 + H2O + e → *OH + OH− | (4) |
| *OH + e → * + OH− | (5) |
| *OOH + e → * + OOH− | (3′) |
Previous works suggest that an associative mechanism is more likely for N-doped graphenes, but a dissociative mechanism cannot be completely excluded. For instance, it was shown that barriers of dissociation of O2 are quite high both on the surface of pristine graphene33 and N-doped graphene.34–36 DFT calculations with explicit water solvent also show that the associative mechanism is more favourable than the dissociative mechanism35 on graphene surfaces doped with graphitic nitrogen. However, Tai et al. suggested that the ORR can proceed with a dissociative mechanism in the presence of pyrrole nitrogen.37 Some insights into the possibility of the dissociative pathway on pristine graphene and graphene containing nitrogen, pyridine, and pyrrole defects will also be presented in the Results and discussion section. However, a comprehensive study of this mechanism is beyond the scope of our study.
2.3 Calculating the free energy of elementary steps
Let us consider the method for calculating the free energy of the ORR elementary steps using a particular example of reaction (2):| *O2 + H2O + e → *OOH + OH− |
| ΔGCHE = Gq=0(*OOH) + G(OH−) − (Gq=0(*O2) + G(H2O) + μe) |
| ΔGCHE = Gq=0(*OOH) − (Gq=0(*O2) + G(H+) + μe) |
where U is the electrode potential referenced to the SHE, and G(H2(g)) is the free energy of hydrogen gas.
Calculations at a constant potential (as opposed to calculations at a constant charge) assume that the system is not closed and exchanges electrons with the reservoir. This leads to the fact that the change in the number of electrons ΔN in reaction (2), generally speaking, is different from unity:
| *O2 + H2O + ΔN·e → *OOH + OH− |
Thus, the reaction energy in the grand canonical ensemble takes the form:24,27
| μe = μU=0e − |e|U |
The free energy of the OH− ion in reactions (3) and (5) was calculated from the equation:38
| G(H+) + G(OH−) = G(H2O) |
| G(OOH−) + G(H+) = G(H2O2) |
The free energy of a water molecule and H2O2 in solution was obtained directly from DFT calculations.
The free energy of the studied systems was calculated using the following equation:
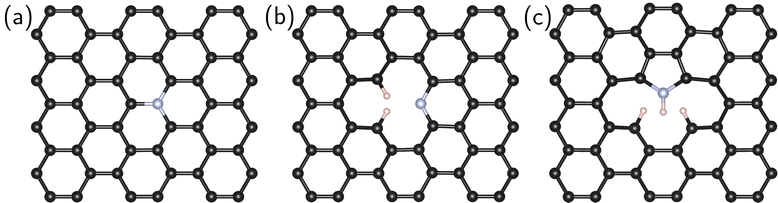
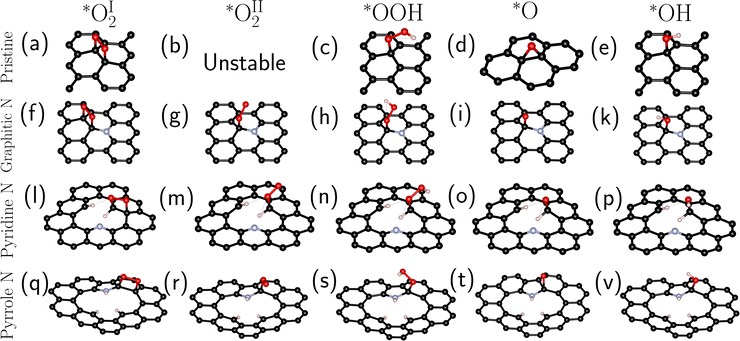
Four systems were studied in this work: pristine (defect-free) graphene and graphene containing an impurity nitrogen atom in three different forms: graphitic N, pyridine N, and pyrrole N (Fig. 1).
3 Results and discussion
3.1 Active sites
In the first stage, we searched for the most energetically favorable configurations of chemisorbed intermediates (*O2, *OOH, *O, and *OH) on the surfaces under study. The search was carried out at zero surface potential vs. SHE, which corresponds to the onset potential of the ORR for N-doped graphenes.6,10 The initial adsorption site and the orientation of the intermediates were varied. Then the systems were optimized. Fig. 2 shows the most favorable configurations of intermediates for all investigated types of doping.For graphitic and pyrrole nitrogen atoms, the intermediates prefer to form a chemical bond with the carbon atom adjacent to the impurity nitrogen atom. In general, the fact that the active sites are C atoms adjacent to nitrogen is consistent with previous works.16,18,21 Particularly, for graphitic nitrogen, the same active site was found in works with different theory levels: planewave DFT with ultrasoft pseudopotential in a vacuum37,40 and PBE0/6-31+G(d) in a vacuum.41 For the pyridine nitrogen atom, the active site is a carbon atom that has a bond with hydrogen, which differs, for instance, from that in the study in ref. 37, where such a site was not considered.
Two types of chemisorption are possible for the O2 molecule on the selected site. In the first type (denoted by the symbol I), O2 forms two C–O bonds with the surface (Fig. 2a, f, l, and q). The O–O bond is parallel to the surface (Fig. 2a, f and q) except for the pyridine nitrogen (Fig. 2l). The π bond in graphene breaks, and the carbon atoms bound to O pass into the sp3 hybridized state. This type of chemisorption was shown earlier in certain studies.16,35 In the second (II) type of chemisorption, one C–O bond is formed (Fig. 2g, m, and r); the O–O bond is at an angle to the surface. A similar configuration was shown in ref. 21, where the explicit solvent (water) was taken into account. On the pristine graphene and the pyridine N atom, this type of chemisorption is unstable at U = 0 V vs. SHE. Note also that atomic oxygen near the pyrrole N forms an epoxy group (C–O–C), while when near the graphitic and pyridine nitrogen atoms, atomic oxygen forms only one bond with the surface.
The configurations in Fig. 2 were used as initial ones for further optimization at non-zero surface potentials. Changes in geometry during these optimizations were small, except for non-stable configurations, which are described below.
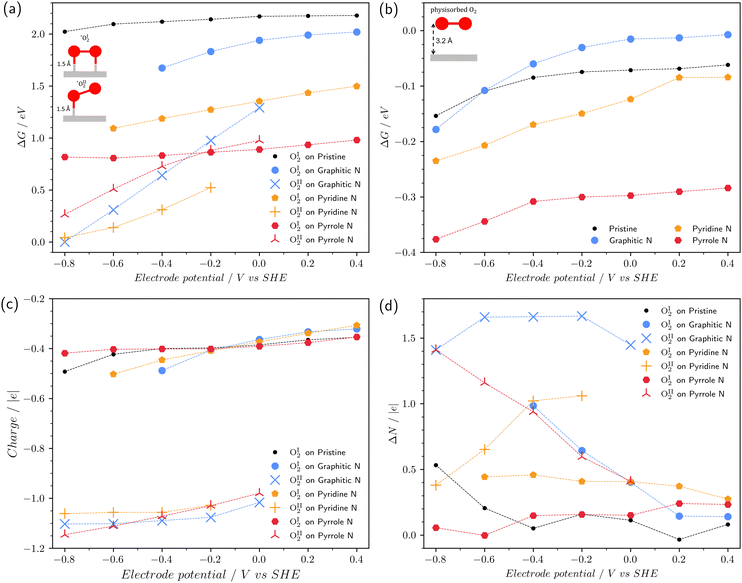
3.2 Effect of potential on O2 chemisorption
Fig. 3a displays the chemisorption free energy of the reaction (1) for both types of chemisorbed O2: type I and type II with two and one C–O bonds with the surface, respectively. We found out that some of the chemisorbed configurations are not stable at a certain range of the electrode potential, for instance, OI2 on graphitic nitrogen for potentials less than −0.4 V vs. SHE (herein and across the following manuscript, the electrode potential is referenced to the SHE). Due to this reason, points corresponding to the several pairs of the electrode potential/defect type are absent in the figure. The range of considered potentials is from −0.8 V to 0.4 V, which corresponds to the electrochemical window of water at pH 14.Fig. 3a exhibits that in all cases, the chemisorption energy is positive. This is due to the fact that chemisorbed oxygen is metastable.16,42 For the type I of chemisorption, all considered nitrogen impurities stabilize the chemisorbed state. Such an effect was shown previously for an uncharged surface.16 In this respect, the pyrrole nitrogen is the most effective, which reduces the chemisorption energy of OI2 by more than 1 eV. The interaction strength with the surface increases in the series: pristine graphene < graphitic N < pyridine N < pyrrole N. Also, it should be noted that this type of chemisorption is unstable at U < −0.4 V on graphitic nitrogen and U < −0.6 V on pyridine nitrogen.
Type II of chemisorption is unstable at positive surface potentials on graphitic and pyrrole nitrogen atoms; on the pyridine N, the stability region is at U ≤ −0.2 V. This type of chemisorption is characterized by a strong decrease in the chemisorption energy with decreasing potential, which cannot be predicted by the standard CHE method. It is important to note that type II chemisorption on graphitic and pyridine nitrogen atoms is energetically more favorable than type I. The free energy difference depends on the potential and is at least 0.6 eV. With such a large difference, one can speak of a change in the type of chemisorption at a potential of 0 V for graphitic N and a potential of −0.2 V for pyridine N. On pyrrole nitrogen at U = −0.2 V, both types of chemisorption coexist due to the closeness of ΔG values. On pristine graphene, the type II of chemisorption is not observed in the entire studied potential range.
Fig. 3b shows the dependence of the free energy of physisorption of the O2 molecule on the potential. Physisorbed O2 molecules were obtained from the chemisorbed configurations of type I by slightly increasing the C–O bond length followed by geometric optimization. After optimization, the distance from O2 to the surface increased to ∼2.9–3.2 Å. It can be seen that the free energy of physisorption, contrary to the chemisorption, weakly depends on the potential and is endothermic. For the pyrrole nitrogen, the ΔG values are 0.2–0.3 eV less than for the other doping types, which indicates that pyrrole nitrogen is the most favorable defect for the physical adsorption of the oxygen molecule.
Fig. 3c shows the charge of a chemisorbed O2 molecule as a function of the potential. The charge of O2 and other chemisorbed intermediates in this work was determined by DDEC6 atomic population analysis.43 Note that in the type I chemisorption with two C–O bonds, the charge of the O2 molecule is closer to zero, while the type II chemisorption with one C–O bond demonstrates the O2 charge close to −1. Fig. 3d shows the change in the number of electrons ΔN in the system during chemisorption due to exchange with an external reservoir. It can be seen that chemisorption to type II is accompanied by the transfer of a significant number of electrons from the external circuit. For example, for graphitic nitrogen ΔN∼1.5 e at negative potentials, for pyridine nitrogen ΔN ∼ 1 e at potentials of −0.2 and −0.4 V and it decreases at more negative potentials. For pyrrole nitrogen, ΔN increases from 0.5 e to 1.5 e when the potential changes from 0 to −0.8 V. Thus, generalizing and somewhat simplifying the picture, we can conclude that doping with nitrogen leads to potential-dependent chemisorption of O2. At positive potentials, chemisorption leads to the formation of two C–O bonds and is not accompanied by electron transfer. At negative potentials, O2 chemisorption leads to the formation of one bond with the surface and is accompanied by electron transfer: * + O2 + e → *O2−. Note that the CHE method assumes a priori that O2 chemisorption occurs without electron transfer, which our calculations in the grand canonical ensemble do not confirm.
3.3 Aspects of the dissociative mechanism
One of the important aspects of the ORR on defective graphene that we want to pay attention to is the stability of the defect and the possibility of the dissociative mechanism through the following reaction:| *O2 + H2O + e → *O + *OH + OH− | (2′) |
We discovered that on the pristine graphene the reaction (2′) does not occur spontaneously. Instead, OOH is formed, which is desorbed from the surface for all considered initial hydrogen positions. It means that only “good” geometric *OOH configurations that are placed in the local potential well are able to preserve the chemisorbed state through the optimization procedure. This is consistent with our reaction energy diagrams that show the absence of the stable chemisorbed OOH at potentials lower than 0.0 V. Also, it is indirect evidence of the preference of the 2e-mechanism on pristine graphene.
Graphitic and pyridine nitrogen atoms stabilize the *OOH intermediate compared to the pristine graphene which leads to the formation of chemisorbed OOH without dissociation through reaction (2′) and desorption. Thus, we did not take into account the dissociative mechanism on these types of defects.
The pyrrole nitrogen demonstrates the most nontrivial behavior, the reconstruction of which we observed. Fig. S1 (ESI†) shows two possible final geometries of the pyrrole defect after the optimization depending on close to which oxygen the hydrogen atom is placed in the initial configuration. Such reconstruction results in the transformation of the pyrrole defect to the new one since oxygen is incorporated into the graphene structure by the formation of edge epoxy and ketone groups with relatively large binding energy.44
However, the approach of hydrogen atom to the OII2 always results in *OOH formation. Since type II of chemisorbed oxygen is more favorable at U ≤ −0.4 V in the case of pyrrole N, we consider that the associative mechanism is relevant for pyrrole nitrogen at least under large negative potentials.
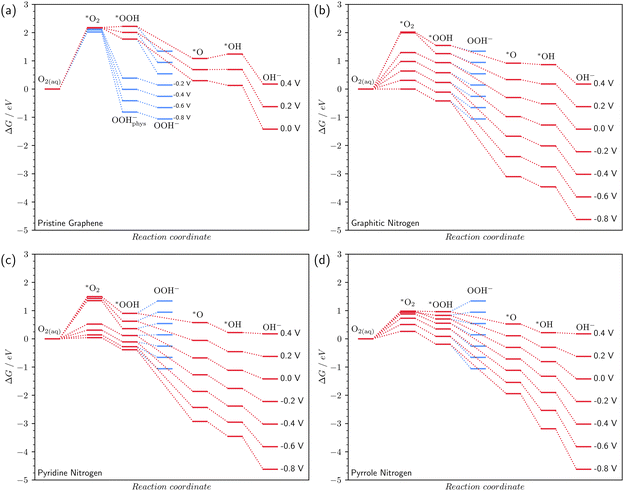
3.4 Free energy profile of the ORR
Fig. 4 shomws the free energy profile of the oxygen reduction reaction in an alkaline medium (pH 14) at various surface potentials. For N-doped surfaces in Fig. 4b–d, considering the step of O2 chemisorption, we chose the most favorable type of O2 chemisorption at a given potential for constructing the energy profiles.In the case of pristine graphene, the reduction reaction is hindered (Fig. 4a). The first chemisorption reaction is endothermic with a large thermodynamic barrier of more than 2 eV. This barrier almost does not decrease even at high reaction overpotentials. The poor catalytic properties of graphene, which does not contain impurity atoms, are confirmed experimentally.6,15,45 It is important to note that at U ≤ −0.2 V, the *OOH radical becomes unstable. The C–O bond with the surface is broken and a physically adsorbed ion OOH−phys is formed (Fig. S2 in the ESI†). The subsequent desorption of OOH−phys corresponds to reaction (3′), which means that at potentials U ≤ −0.2 V, the ORR on defect-free graphene proceeds via the two-electron mechanism, which also agrees with the experiment.6
In the case of graphitic nitrogen, the O2 chemisorption energy decreases rapidly with overpotential (Fig. 4b), which should lead to an acceleration of the ORR compared to pristine graphene. Note that the graphitic N also stabilizes all other intermediates.
For a more complete analysis, Fig. 5 and 6 show the change in the number of electrons in the system for each of the elementary steps and the charges of the intermediates, respectively, depending on the applied potential. The generally accepted mechanism suggests that reactions (2)–(5) are accompanied by the transfer of one electron, while reaction (1) proceeds without electron transfer. Calculations in the grand canonical ensemble show that the picture is more complex and depends on the doping type (Fig. 5 and 6).
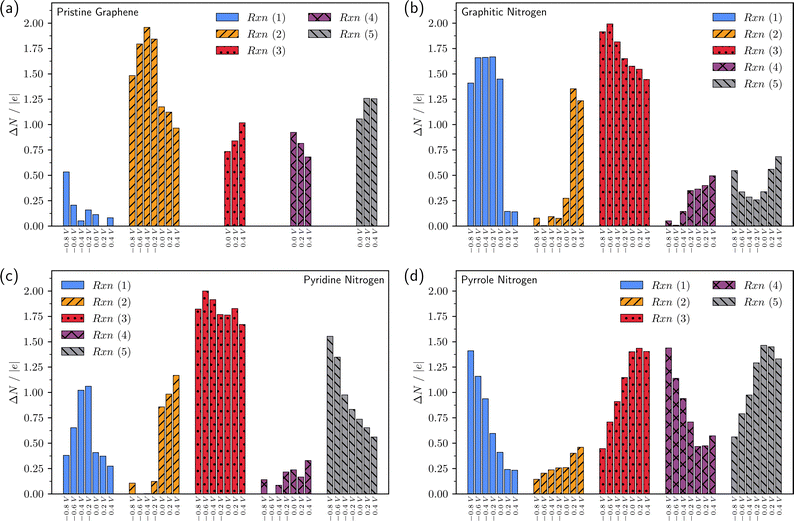 | ||
| Fig. 5 Change in the number of electrons in the system due to exchange with an external reservoir in reactions (1)–(5) at different potentials vs. SHE. (a)–(d) are data for pristine graphene, graphitic N, pyridine N, and pyrrole N, respectively. | ||
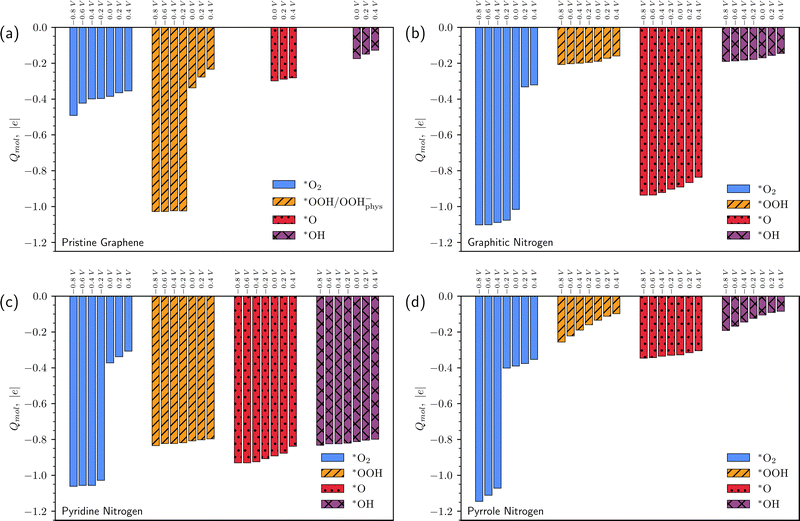 | ||
| Fig. 6 Charges of *O2, *OOH, *O, and *OH on pristine graphene (a), graphitic N (b), pyridine N (c), and pyrrole N (d) as a function of surface potential vs. SHE. | ||
Let us once again focus on the fact that on graphitic nitrogen *O2 acquires a charge of ca. −1 at U ≤ 0 V (Fig. 6b), while ∼1.5 electrons enter the system from the external circuit (Fig. 5b). Thus, the reaction (1) of O2 chemisorption is accompanied by electron transfer. At the same time, reaction (2) is not accompanied by electron transfer at U ≤ 0 V (Fig. 5b) but is a purely chemical reaction of proton transfer from a water molecule. Thus, the coupled electron–proton transfer in reaction (2), most often assumed in the literature, is divided into two sequential steps of electron and proton transfer. In the reaction (3) of breaking the O–O bond, the value of ΔN changes from ∼1.5 at U = 0 V to ΔN ∼ 2 at U ∼ −0.8 V; the charge of the *O radical is close to −1. Therefore, reaction (3) is accompanied by two electron transfers. Thus, the first three reactions on graphitic nitrogen in the refined ORR mechanism at U ≤ 0 V have the form:
| O2 + * + e → *O2 |
| *O2− + H2O → *OOH + OH− |
| *OOH + 2e → *O− + OH− |
The pyridine and pyrrole nitrogen atoms also stabilize *O2 compared to pristine graphene (Fig. 4c and d). The experimental potential range at which the ORR occurs on N-doped graphenes is usually U ≤ 0 V vs. SHE.6,10 In our calculations, at a potential U = 0 V, the lowest thermodynamic barrier of O2 chemisorption is observed for pyrrole nitrogen. At potentials of −0.6 ≤ U ≤ −0.2 V, the lowest O2 chemisorption energy is achieved on pyridine nitrogen; at U = −0.8 V – on graphite nitrogen. Thus, our calculations show that at different potentials, different types of nitrogen doping exhibit the best catalytic properties. Probably, this fact explains the extremely contradictory data on the most efficient catalytic centers in experiments.8,10,13,15
The pyridine and pyrrole nitrogen atoms stabilize the *OOH radical more efficiently than the graphitic one, which leads to the fact that the last reaction (3′) of the two-electron mechanism proceeds with energy consumption at potentials of −0.2 ≤ U ≤ 0.4 V on pyridine nitrogen (Fig. 4c) and 0.2 V ≤ U ≤ 0.4 V on pyrrole nitrogen (Fig. 4d). Therefore, in these potential ranges, these types of defects inhibit the parasitic two-electron mechanism. Preference of the four-electron mechanism of the ORR on pyridine and pyrrole N-doped graphene was also found in non-periodical DFT previously46 and confirmed experimentally.6,10
Note also that the charge of chemisorbed intermediates depends significantly on the doping type. On graphitic nitrogen, the *OOH and *OH charges are close to zero, while the *O charge is about −1 regardless of the potential (Fig. 6b). On pyridine nitrogen *OOH, *O, and *OH intermediates, regardless of the potential, have a charge close to −1 (Fig. 6c), while on pyrrole nitrogen, in contrast, the charge of the intermediates is close to zero (Fig. 6d). For a chemisorbed O2 molecule, the charge jumps from 0 to −1. However, the potential at which this happens is different for all types of defects.
To compare the CHE method with calculations at constant potential, we calculated the free energy differences using both methods for each elementary step of the ORR for 4e and 2e− mechanisms (Fig. S3 and S4 in the ESI†). The four-electron mechanism does not show a difference between the two methods of more than 0.2 eV for pristine graphene. For N-doped graphenes, the difference in free energies strongly depends on the potential and can reach ∼1.5 eV. Furthermore, in Fig. S3b, c, S4b and c (ESI†) one can see that the difference between ΔGCPM and ΔGCPE is experiencing a huge and non-smooth change for reactions (1) and (2) in the case of nitrogen and pyridine nitrogen, the origin of which is potential-dependent chemisorbed *O2 geometry that cannot be predicted in the CHE model. In the case of pyrrole nitrogen (Fig. S3d and S4d, ESI†) there is no such step due to the smooth transition between OI2 and OII2 in terms of reaction free energy (Fig. 3a). Fig. S4a (ESI†) demonstrates an abrupt increase/decrease of dependencies for reactions (2) and (3′) between −0.2 V and 0.0 V, due to the barrier-free detachment of *OOH on pristine graphene at negative potentials that, also, cannot be predicted in the CHE model.
Summing up the result, we note that for the associative reaction mechanism, our calculations in the grand canonical ensemble using the CANDLE implicit model of the electrolyte show that oxygen chemisorption is the limiting step. The electrocatalytic mechanism of nitrogen dopants is to reduce the chemisorption energy of the oxygen molecule. Due to the fact that chemisorbed O2 is the metastable state, from our point of view, ORR mechanisms that proceed through the physical adsorption of O2 or do not require O2 adsorption deserve attention. An example of such a mechanism is the mechanism proposed by Schmikler et al. for an alkaline environment on the surface of metals that weakly interact with oxygen, such as gold and silver.47–49 Indeed, on the pristine graphene and near the graphitic/pyridine nitrogen at positive potentials, the physisorption energy is close to zero (Fig. 3b). For these cases, probably the first ORR reaction may be an outer-sphere electron transfer to a completely solvated O2 molecule, as suggested in previous studies.47–49 It can also be assumed that the mechanism considered by us in Section 2.2 is formally carried out, however, it proceeds not through the stage of chemisorption, but the physisorption of O2. In this case, reaction (2) has the form O2phys + H2O + e → *OOH + OH−, and formally assumes the implementation of three elementary processes: electron transfer, proton transfer from a water molecule, and formation of a chemical bond with the surface. The answer to the question of whether such a reaction is possible in principle, or whether it can be implemented as several sequential elementary steps, is beyond the scope of this work and requires a separate study.
4 Conclusions
The thermodynamics of the oxygen reduction reaction in an alkaline medium on the graphene surface was studied using grand canonical DFT calculations with the CANDLE solvation model.It is shown that on pristine graphene the reaction proceeds according to the two-electron mechanism due to the instability of the *OOH intermediate, which desorbs as an OOH− ion at reaction potentials. Doping with nitrogen catalyzes the four-electron mechanism. The catalytic mechanism consists of a decrease in the free energy of O2 chemisorption, which is the limiting step. The energy of O2 chemisorption rapidly decreases with decreasing potential on N-doped graphenes, which cannot be predicted within the framework of the computational hydrogen electrode. At different potentials, various forms of nitrogen impurities have the best catalytic properties. At U = 0 V pyrrole nitrogen dominates, at −0.6 V ≤ U −0.2 V pyridine nitrogen, and at U = −0.8 V graphitic nitrogen.
Calculations at a constant potential showed that the associative reaction mechanism depends on the potential and type of doping and differs significantly from the generally accepted one. In particular, as the potential decreases, a chemisorbed oxygen molecule loses one C–O bond with the surface and acquires a charge of −1. This leads to the decoupling of the first electron–proton transfer. The difference between the free energies of elementary steps obtained at a constant potential and a constant charge depends in a complex way on the potential and the type of doping and can reach ∼1.5 eV.
In this way, the presented work takes a step towards an accurate accounting of the electrode potential applying the continuum model of the solvent. It should also be noted that for confident conclusions about the mechanism of the ORR, it is necessary to take into account the barriers of all elementary steps.35,50 It is also worth mentioning that it would be promising to improve the solvent model in used joint DFT, which could be done within the framework of classical DFT liquids with an atomic-scale structure.51 Another option is to use ab initio molecular dynamics simulations;35,52 however, it is still computationally costly and very tricky to fix the surface potential, which as was shown plays an important role.
Author contributions
V. Kislenko: investigation, methodology, software, visualization, and writing – review & editing; S. Pavlov: investigation; V. Nikitina: supervision; S. Kislenko: conceptualization, project administration, supervision, and writing – original draft.Conflicts of interest
There are no conflicts to declare.Acknowledgements
The work was supported by a grant from the Russian Science Foundation (project no. 22-23-00535). The research was carried out using the Skoltech supercomputer Zhores53 and supercomputers at Joint Supercomputer Center of the Russian Academy of Sciences (JSCC RAS).54Notes and references
- T. B. Ferriday and P. H. Middleton, Alkaline fuel cell technology - A review, Int. J. Hydrogen Energy, 2021, 46, 18489–18510 CrossRef CAS.
- R. Ma, G. Lin, Y. Zhou, Q. Liu, T. Zhang, G. Shan, M. Yang and J. Wang, A review of oxygen reduction mechanisms for metal-free carbon-based electrocatalysts, npj Comput. Mater., 2019, 5, 78 CrossRef.
- L. Zhang, C.-Y. Lin, D. Zhang, L. Gong, Y. Zhu, Z. Zhao, Q. Xu, H. Li and Z. Xia, Guiding Principles for Designing Highly Efficient Metal-Free Carbon Catalysts, Adv. Mater., 2019, 31, 1805252 CrossRef PubMed.
- B. Wang, B. Liu and L. Dai, Non-N-Doped Carbons as Metal-Free Electrocatalysts, Adv. Sustainable Syst., 2021, 5, 2000134 CrossRef CAS.
- K. Gong, F. Du, Z. Xia, M. Durstock and L. Dai, Nitrogen-Doped Carbon Nanotube Arrays with High Electrocatalytic Activity for Oxygen Reduction, Science, 1979, 323, 760–764 CrossRef PubMed.
- L. Qu, Y. Liu, J.-B. Baek and L. Dai, Nitrogen-Doped Graphene as Efficient Metal-Free Electrocatalyst for Oxygen Reduction in Fuel Cells, ACS Nano, 2010, 4, 1321–1326 CrossRef CAS PubMed.
- Y. Jia, L. Zhang, L. Zhuang, H. Liu, X. Yan, X. Wang, J. Liu, J. Wang, Y. Zheng, Z. Xiao, E. Taran, J. Chen, D. Yang, Z. Zhu, S. Wang, L. Dai and X. Yao, Identification of active sites for acidic oxygen reduction on carbon catalysts with and without nitrogen doping, Nat. Catal., 2019, 2, 688–695 CrossRef CAS.
- H. Begum, M. S. Ahmed and Y.-B. Kim, Nitrogen-rich graphitic-carbon@graphene as a metal-free electrocatalyst for oxygen reduction reaction, Sci. Rep., 2020, 10, 12431 CrossRef CAS PubMed.
- H. Tabassum, R. Zou, A. Mahmood, Z. Liang and S. Guo, A catalyst-free synthesis of B, N co-doped graphene nanostructures with tunable dimensions as highly efficient metal free dual electrocatalysts, J. Mater. Chem. A, 2016, 4, 16469–16475 RSC.
- L. Lai, J. R. Potts, D. Zhan, L. Wang, C. K. Poh, C. Tang, H. Gong, Z. Shen, J. Lin and R. S. Ruoff, Exploration of the active center structure of nitrogen-doped graphene-based catalysts for oxygen reduction reaction, Energy Environ. Sci., 2012, 5, 7936–7942 RSC.
- K. Wan, Z. Yu, X. Li, M. Liu, G. Yang, J. Piao and Z. Liang, pH Effect on Electrochemistry of Nitrogen-Doped Carbon Catalyst for Oxygen Reduction Reaction, ACS Catal., 2015, 5, 4325–4332 CrossRef CAS.
- M. Rauf, Y.-D. Zhao, Y.-C. Wang, Y.-P. Zheng, C. Chen, X.-D. Yang, Z.-Y. Zhou and S.-G. Sun, Insight into the different ORR catalytic activity of Fe/N/C between acidic and alkaline media: Protonation of pyridinic nitrogen, Electrochem. Commun., 2016, 73, 71–74 CrossRef CAS.
- H. Bin Yang, J. Miao, S.-F. Hung, J. Chen, H. B. Tao, X. Wang, L. Zhang, R. Chen, J. Gao, H. M. Chen, L. Dai and B. Liu, Identification of catalytic sites for oxygen reduction and oxygen evolution in N-doped graphene materials: Development of highly efficient metal-free bifunctional electrocatalyst, Sci. Adv., 2016, 2, e1501122 CrossRef PubMed.
- I. T. Kim, M. J. Song, Y. B. Kim and M. W. Shin, Microwave-hydrothermal synthesis of boron/nitrogen co-doped graphene as an efficient metal-free electrocatalyst for oxygen reduction reaction, Int. J. Hydrogen Energy, 2016, 41, 22026–22033 CrossRef CAS.
- D. Guo, R. Shibuya, C. Akiba, S. Saji, T. Kondo and J. Nakamura, Active sites of nitrogen-doped carbon materials for oxygen reduction reaction clarified using model catalysts, Science, 1979, 2016(351), 361–365 Search PubMed.
- Y. Okamoto, First-principles molecular dynamics simulation of O2 reduction on nitrogen-doped carbon, Appl. Surf. Sci., 2009, 256, 335–341 CrossRef CAS.
- T. Ikeda, M. Boero, S.-F. Huang, K. Terakura, M. Oshima and J. Ozaki, Carbon Alloy Catalysts: Active Sites for Oxygen Reduction Reaction, J. Phys. Chem. C, 2008, 112, 14706–14709 CrossRef CAS.
- L. Zhang and Z. Xia, Mechanisms of Oxygen Reduction Reaction on Nitrogen-Doped Graphene for Fuel Cells, J. Phys. Chem. C, 2011, 115, 11170–11176 CrossRef CAS.
- J. Shui, M. Wang, F. Du and L. Dai, N-doped carbon nanomaterials are durable catalysts for oxygen reduction reaction in acidic fuel cells, Sci. Adv., 2022, 1, e1400129 CrossRef PubMed.
- J. K. Nørskov, J. Rossmeisl, A. Logadottir, L. Lindqvist, J. R. Kitchin, T. Bligaard and H. Jónsson, Origin of the Overpotential for Oxygen Reduction at a Fuel-Cell Cathode, J. Phys. Chem. B, 2004, 108, 17886–17892 CrossRef.
- L. Yu, X. Pan, X. Cao, P. Hu and X. Bao, Oxygen reduction reaction mechanism on nitrogen-doped graphene: A density functional theory study, J. Catal., 2011, 282, 183–190 CrossRef CAS.
- H. Oberhofer, Handbook of Materials Modeling, Springer International Publishing, Cham, 2018, pp. 1–33 Search PubMed.
- R. Sundararaman, W. A. Goddard and T. A. Arias, Grand canonical electronic density-functional theory: Algorithms and applications to electrochemistry, J. Chem. Phys., 2017, 146, 114104 CrossRef PubMed.
- D. Kim, J. Shi and Y. Liu, Substantial Impact of Charge on Electrochemical Reactions of Two-Dimensional Materials, J. Am. Chem. Soc., 2018, 140, 9127–9131 CrossRef CAS PubMed.
- V. A. Kislenko, S. V. Pavlov and S. A. Kislenko, Influence of defects in graphene on electron transfer kinetics: The role of the surface electronic structure, Electrochim. Acta, 2020, 341, 136011 CrossRef CAS.
- S. V. Pavlov, V. A. Kislenko and S. A. Kislenko, Fast method for calculating spatially resolved heterogeneous electron-transfer kinetics and its application to graphene with defects, J. Phys. Chem. C, 2020, 124, 18147–18155 CrossRef CAS.
- G. Gao and L.-W. Wang, Substantial potential effects on single-atom catalysts for the oxygen evolution reaction simulated via a fixed-potential method, J. Catal., 2020, 391, 530–538 CrossRef CAS.
- R. Sundararaman, K. Letchworth-Weaver, K. A. Schwarz, D. Gunceler, Y. Ozhabes and T. A. Arias, JDFTx: Software for joint density-functional theory, SoftwareX, 2017, 6, 278–284 CrossRef PubMed.
- R. Sundararaman and W. A. Goddard, The charge-asymmetric nonlocally determined local-electric (CANDLE) solvation model, J. Chem. Phys., 2015, 142, 064107 CrossRef PubMed.
- S. Grimme, J. Antony, S. Ehrlich and H. Krieg, A consistent and accurate ab initio parametrization of density functional dispersion correction (DFT-D) for the 94 elements H-Pu, J. Chem. Phys., 2010, 132, 154104 CrossRef PubMed.
- K. F. Garrity, J. W. Bennett, K. M. Rabe and D. Vanderbilt, Pseudopotentials for high-throughput DFT calculations, Comput. Mater. Sci., 2014, 81, 446–452 CrossRef CAS.
- K. Kakaei, M. D. Esrafili and A. Ehsani, in Graphene Surfaces, ed. K. Kakaei, M. D. Esrafili and A. Ehsani, Elsevier, 2019, vol. 27, pp. 203–252 Search PubMed.
- H. J. Yan, B. Xu, S. Q. Shi and C. Y. Ouyang, First-principles study of the oxygen adsorption and dissociation on graphene and nitrogen doped graphene for Li-air batteries, J. Appl. Phys., 2012, 112, 104316 CrossRef.
- H. J. Yan, B. Xu, S. Q. Shi and C. Y. Ouyang, First-principles study of the oxygen adsorption and dissociation on graphene and nitrogen doped graphene for Li-air batteries, J. Appl. Phys., 2012, 112, 104316 CrossRef.
- L. Yu, X. Pan, X. Cao, P. Hu and X. Bao, Oxygen reduction reaction mechanism on nitrogen-doped graphene: A density functional theory study, J. Catal., 2011, 282, 183–190 CrossRef CAS.
- M. Yang, L. Wang, M. Li, T. Hou and Y. Li, Structural stability and O2 dissociation on nitrogen-doped graphene with transition metal atoms embedded: A first-principles study, AIP Adv., 2015, 5, 067136 CrossRef.
- S.-H. Tai and B. K. Chang, Effect of nitrogen-doping configuration in graphene on the oxygen reduction reaction, RSC Adv., 2019, 9, 6035–6041 RSC.
- D. Gunceler, K. Letchworth-Weaver, R. Sundararaman, K. A. Schwarz and T. A. Arias, The importance of nonlinear fluid response in joint density-functional theory studies of battery systems, Modell. Simul. Mater. Sci. Eng., 2013, 21, 74005 CrossRef.
- S. J. Blundell and K. M., Blundell Concepts in Thermal Physics, OUP, Oxford, 2nd edn, 2010 Search PubMed.
- N. Wang, B. Lu, L. Li, W. Niu, Z. Tang, X. Kang and S. Chen, Graphitic Nitrogen Is Responsible for Oxygen Electroreduction on Nitrogen-Doped Carbons in Alkaline Electrolytes: Insights from Activity Attenuation Studies and Theoretical Calculations, ACS Catal., 2018, 8, 6827–6836 CrossRef CAS.
- J. Vazquez-Arenas, A. Galano, D. U. Lee, D. Higgins, A. Guevara-García and Z. Chen, Theoretical and experimental studies of highly active graphene nanosheets to determine catalytic nitrogen sites responsible for the oxygen reduction reaction in alkaline media, J. Mater. Chem. A, 2016, 4, 976–990 RSC.
- D. C. Sorescu, K. D. Jordan and P. Avouris, Theoretical Study of Oxygen Adsorption on Graphite and the (8,0) Single-walled Carbon Nanotube, J. Phys. Chem. B, 2001, 105, 11227–11232 CrossRef CAS.
- T. A. Manz and N. G. Limas, Introducing DDEC6 atomic population analysis: Part 1. Charge partitioning theory and methodology, RSC Adv., 2016, 6, 47771–47801 RSC.
- G. Lee and K. Cho, Electronic structures of zigzag graphene nanoribbons with edge hydrogenation and oxidation, Phys. Rev. B: Condens. Matter Mater. Phys., 2009, 79, 165440 CrossRef.
- J. Liang, Y. Jiao, M. Jaroniec and S. Z. Qiao, Sulfur and Nitrogen Dual-Doped Mesoporous Graphene Electrocatalyst for Oxygen Reduction with Synergistically Enhanced Performance, Angew. Chem., Int. Ed., 2012, 51, 11496–11500 CrossRef CAS PubMed.
- L. Zhang and Z. Xia, Mechanisms of Oxygen Reduction Reaction on Nitrogen-Doped Graphene for Fuel Cells, The, J. Phys. Chem. C, 2011, 115, 11170–11176 CrossRef CAS.
- A. Ignaczak, R. Nazmutdinov, A. Goduljan, L. M. de Campos Pinto, F. Juarez, P. Quaino, E. Santos and W. Schmickler, A scenario for oxygen reduction in alkaline media, Nano Energy, 2016, 29, 362–368 CrossRef CAS.
- A. Ignaczak, R. Nazmutdinov, A. Goduljan, L. M. de Campos Pinto, F. Juarez, P. Quaino, G. Belletti, E. Santos and W. Schmickler, Oxygen Reduction in Alkaline Media—a Discussion, Electrocatalysis, 2017, 8, 554–564 CrossRef CAS.
- A. Ignaczak, E. Santos and W. Schmickler, Oxygen reduction reaction on gold in alkaline solutions – The inner or outer sphere mechanisms in the light of recent achievements, Curr. Opin. Electrochem., 2019, 14, 180–185 CrossRef CAS.
- A. Kulkarni, S. Siahrostami, A. Patel and J. K. Nørskov, Understanding Catalytic Activity Trends in the Oxygen Reduction Reaction, Chem. Rev., 2018, 118, 2302–2312 CrossRef CAS PubMed.
- R. Sundararaman and T. A. Arias, Atomic-Scale Modelling of Electrochemical Systems, 2021, pp. 139–172 Search PubMed.
- Y. Okamoto, First-principles molecular dynamics simulation of O2 reduction on nitrogen-doped carbon, Appl. Surf. Sci., 2009, 256, 335–341 CrossRef CAS.
- I. Zacharov, R. Arslanov, M. Gunin, D. Stefonishin, A. Bykov, S. Pavlov, O. Panarin, A. Maliutin, S. Rykovanov and M. Fedorov, “Zhores”—Petaflops supercomputer for data-driven modeling, machine learning and artificial intelligence installed in Skolkovo Institute of Science and Technology, Open Eng., 2019, 9, 512–520 CrossRef.
- G. I. Savin, B. M. Shabanov, P. N. Telegin and A. V. Baranov, Joint Supercomputer Center of the Russian Academy of Sciences: Present and Future, Lobachevskii J. Math., 2019, 40, 1853–1862 CrossRef.
Footnote |
| † Electronic supplementary information (ESI) available. See DOI: 10.1039/d3cp04517j |
| This journal is © the Owner Societies 2024 |