A confinement-regulated (H₃C–NH₃)⁺ ion as a smallest dual-wheel rotator showing bisected rotation dynamics

Abstract

On the basis of variable-temperature single-crystal X-ray diffraction, rotational energy barrier analysis, variable-temperature/frequency dielectric response, and molecular dynamics simulations, here we report a new crystalline supramolecular rotor (CH₃NH₃)(18-crown-6)[CuCl₃], in which the (H₃C–NH₃)⁺ ion functions as a smallest dual-wheel rotator showing bisected rotation dynamics, while the host 18-crown-6 macrocycle behaves as a stator that is not strictly stationary. This study also provides a helpful insight into the dynamics of ubiquitous –CH₃/–NH₃ groups confined in organic or organic–inorganic hybrid solids.

---

Introduction

Over the past few decades, molecular rotors have attracted increasing attention due to their potential applications in molecular machines, sensing, energy conversion, and data storage at the molecular scale.^1–21 Crystalline supramolecular rotors refer to the self-assembled rotatable components within a supramolecular system, which are periodically arranged in the solid state.^22–28 Compared with molecular rotors, supramolecular rotors usually exhibit higher dynamism, which facilitates the rotors to possess a higher degree of freedom for diverse rotations and external stimulus responses.

Among various types of supramolecular rotors, crown-ether-based rotors are of particular interest, which have been intensively studied from time to time.^29–40 In confined space, the conformationally flexible crown ethers are capable of forming stable supramolecular complexes with primary ammonium (R-NH₃)⁺ ions through multiple O⋯H–N hydrogen bonds, which bind and/or semi-encapsulate the primary ammonium ions, providing a confined environment for their rotation. Following this strategy, a series of crown-ether-based supramolecular rotors had been prepared merely by a one pot self-assembly method, without intricate chemical processes. However, to our surprise, research on the (H₃C–NH₃)⁺ ion as a smallest rotator within these unique systems has long been neglected, although some related compounds have been prepared and documented.^41–43 In fact, considering the possibility of the rotation of the bisected –CH₃ and –NH₃ fragments around the rotatable “C–N” axis, this basic model can also be viewed as a smallest double-wheel rotator with different confinement-regulated rotation dynamics at both ends (Chart 1). Studies on this model rotator may provide a further insight into the confinement-regulated molecular dynamics and the inherent rotation mechanism of the crown-ether-based host–guest systems.

Chart 1 Conception of the (H₃C–NH₃)⁺ ion functioning as a smallest double-wheel rotator with different confinement-regulated rotation dynamics at both ends. The N, C and H atoms are shaded in blue, grey and green, respectively.

Herein, to address the above-mentioned issue, we prepare and study such a new model compound, namely (CH₃NH₃)(18-crown-6)[CuCl₃] (1), in which the (CH₃NH₃)⁺ ion functions as a smallest dual-wheel rotator showing bisected rotation dynamics, while the host 18-crown-6 macrocycle behaves as a supramolecular stator that is not strictly stationary. The inherent molecular dynamics of the rotator was uncovered by the variable-temperature crystal structure analysis, rotational energy barrier analysis, variable-temperature/frequency dielectric response, and molecular dynamics simulations.

Results and discussion

Compound 1 was synthesized as red block-shaped crystals by evaporation of the mixed aqueous solution of 18-crown-6, CuCl₂ and CH₃NH₃Cl in a dry environment (for details, see ESI†). Thermogravimetric analysis shows that it decomposes at ca. 150 °C under a nitrogen atmosphere (Fig. S1, ESI†). Single-crystal X-ray diffraction revealed that 1 crystallizes in the low-symmetry space group P1̄ (Table S1, ESI†). The asymmetric unit of 1 contains a unique Cu²⁺ cation, three crystallographically independent Cl⁻ anions, one 18-crown-6 molecule, and a (CH₃NH₃)⁺ cation (Fig. 1). The crystal structure features a discrete [Cu₂Cl₆]²⁻ dimer related by an inversion center, which is fused by the bridging of a pair of bidentate Cl⁻ ligands. The coordination geometry around the Cu²⁺ ion can be described as a severely distorted tetrahedron. The Cu–Cl distances at 293 K [2.1972(9)–2.323(1) Å] are in the normal range (Table S1, ESI†). On the other hand, the (CH₃NH₃)⁺ ion in 1 is hydrogen bonded to 18-crown-6 to form a discrete [(CH₃NH₃)(18-crown-6)]⁺ cationic complex, which as a whole exhibits two-fold disorder.

Fig. 1 ORTEP representation (at 30% probability) for the selected unit of 1 at 150 K (a) and 293 K (b), respectively. For clarity, C-bound H atoms have been omitted, and one set of disordered 18-crown-6 molecules and one set of N-bound disordered H atoms are shaded in transparent colors. Symmetry code for the generated atoms: (A) 1 − x, −y, 2 − z.

A comparative inspection of the variable-temperature structures of 1 (Fig. 1a and b) showed that the thermal ellipsoid for the N1 atom in the (CH₃NH₃)⁺ ion is nearly spherical at 293 K, but becomes anisotropic at 150 K. This suggests that the N1 atom is dynamically rotating around the C–N axis at 293 K and turns frozen at 150 K. To further evaluate the rotation dynamics of the (CH₃NH₃)⁺ ion as a dual-wheel rotator, on the basis of the crystal structure of 1 at 293 K, we performed the density functional theory (DFT) calculations of the rotational energy changes as a function of the rotation angles of the –CH₃ and –NH₃ fragments around the C–N axis, respectively. The quantum chemical calculation, by using the DMol3 module of Materials Studio,⁴⁴ is on the basis of the generalized gradient functionals with Perdew–Burke–Ernzerhof correlation. The treatment of core electrons is replaced by a single effective potential. The convergence threshold for the maximum energy change during the geometry optimization is 1.0 × 10⁻⁵ Ha. As shown in Fig. 2a, the rotation energy barrier (E_a) for the –CH₃ fragment (∼0.24 eV) is somewhat smaller than that (∼0.28 eV) for the –NH₃ fragment (note: based on the relatively stable intermediate state present at the rotation angle of 45° for the –NH₃ fragment, its rotation dynamics proceeds in a stepwise manner, with an E_a of 0.28 eV in the first step and an E_a of 0.16 eV in the second step. See the red curve in Fig. 2a). The intermolecular interaction surrounding the (CH₃NH₃)⁺ ion can also be vividly displayed in its Hirshfeld surface map⁴⁵ and the corresponding 2D fingerprint plot that distinguishes different elements (Fig. 2b and Fig. S2, ESI†). The fingerprint plot mainly consists of three types of intermolecular interactions, i.e., H_i⋯O_e, H_i⋯H_e, and H_i⋯Cl_e, respectively. The N–H⋯O hydrogen bonds are represented by the spike at the lower-left area, which accounts for the major contribution to the intermolecular interactions.

Fig. 2 (a) The calculated relative potential energy diagram for 1 at 293 K, as a function of the rotation angles of three C-bound and N-bound H atoms of the (CH₃NH₃)⁺ cation that rotate around the C–N bond (plotted as grey and red, respectively), showing the varied energies from 0° to 360° in a step of 15°. (b) Front and back views of the Hirshfeld surface of one (CH₃NH₃)⁺ ion in 1 at 293 K, displaying the relative strength of the intermolecular interactions surrounding the (CH₃NH₃)⁺ ion. The blue, white, and red regions represent molecular contacts longer than, equal to, and shorter than the van der Waals distance, respectively.

The three-dimensional self-assembly of the [Cu₂Cl₆]²⁻ dimers and [(CH₃NH₃)(18-crown-6)]⁺ cationic complexes in 1, mainly through the Coulomb interaction and van der Waals interaction, leads to a relatively loose stacking structure (Fig. 3), with the adjacent staggered 18-crown-6 molecules being arranged in an anti-parallel orientation. The O–C–C–O torsion angles of the annular crown ether all are close to ±60° at 153 K and 293 K (Fig. S3, ESI†), with a pattern of g⁺g⁻g⁺g⁻g⁺g⁻ (beginning at O1 and increasing clockwise, labeled as g⁺ if the angle is 60° ± 60°, and labeled as g⁻ when the angle is −60° ± 60°),⁴⁶ showing a nearly planar conformation for the macrocycle (Fig. S4a, ESI†). The subtle change in the torsions at different temperatures (Fig. S3a and b, ESI†) reveals that the conformation of the 18-crown-6 molecule in 1 is flexible and variable under external thermal stimulation.

Fig. 3 View of the three-dimensional supramolecular structure of 1 down the b-axis. For clarity, H atoms of 18-crown-6 molecules have been omitted, and one set of disordered 18-crown-6 molecules and one set of N-bound disordered H atoms are shaded in transparent colors.

It is worth noting that the “N–C” rotation axis is not strictly fixed when the flipping or rotation of the N-bound H atoms occurs, which is accompanied by a synergistic quivering of the 18-crown-6 macrocycle. Consequently, the dynamic rotation of the (H₃C–NH₃)⁺ cation as a whole manifests a variable orientation of its dipole. This can lead to an active dielectric response under AC electric field, which is often sensitive to changes in temperature and AC frequency.^47–49 Thus, to further experimentally probe into the dynamics of the (H₃C–NH₃)⁺ ion at the molecular level, the complex permittivity ε* (ε′ − iε′′, where ε′ and ε′′ are the real and imaginary parts, respectively) of 1 was recorded over a frequency range from 0.5 to 1000 kHz (Fig. 4). Owing to dielectric relaxation of the (H₃C–NH₃)⁺ cation, the ε′ and ε′′ both show notable frequency dispersion. The dielectric constants ε′ at all test AC frequencies increase continuously upon heating, and dielectric constants ε′′ all exhibit a peak-shaped transition. The peak maxima of ε′′ appear at the increasing temperatures (T_peak) from 165 to 243 K for the corresponding frequencies from 0.5 to 1000 kHz.

Fig. 4 Temperature-dependent ε′ and ε′′ of 1 at various ac frequencies.

To deeply analyze the frequency-dependent dielectric signal, the ε* was measured against AC frequencies at a series of constant temperatures (Fig. 5). In the low-frequency region, where the molecular motion is faster than the reversal of the electric field, the molecular dipole can follow the switching of the electric field, with a full contribution to the dielectric constant. At high frequencies, where the molecular reorientation is not fast enough to follow the changing electric field, the molecular dipole is relatively stationary on the time scale, which contributes little to the value of dielectric constant. At intermediate frequencies, where the time scales of frequency and molecular reorientation are comparable, molecular reorientation occurs with some delay, causing dielectric loss. This loss is displayed as peaks in the plot of ε′′ against frequency, and the relaxation time (τ) of molecular reorientation can be estimated from the Havriliak–Negami equation:⁵⁰ε* = ε_∞ + Δε/{[1 + (iωτ)^(1−α)]^β} (0 ≤ α, β ≤ 1), where ω = 2πf, α/β are related to the distribution of τ, and Δε = ε_s − ε_∞ (ε_s and ε_∞ are the low/high-frequency limits of dielectric permittivity, respectively). By fitting the experimental data of both the real and imaginary parts, the resultant fitted parameters (Table S4, ESI†) and fitted curves (Fig. 5) match well with the experimental data. The parameter ε_∞, as the contribution of ionic polarization apart from electronic polarization, increases slightly upon heating, indicating that the electrostatic binding force between the [(CH₃NH₃)(18-crown-6)]⁺ complex and [Cu₂Cl₆]²⁻ dimer loosens lightly with rising temperature. At the testing temperatures from 160 to 230 K, the relaxation occurs over a wide frequency range of 10³–10⁶ Hz. Apparently, as the temperature increases, the molecular thermal motion turns more active and accordingly the relaxation time decreases. The τ calculated at the testing temperatures obeys the Arrhenius equation (Fig. S4, ESI†): 1/τ = ω₀ exp[−E_a/(k_BT)], where ω₀ is the pre-exponential factor, E_a is the activation energy, and k_B is the Boltzmann constant. By linear fitting of the plots of 1000/T vs. ln(τ), an ω₀ of 5.0 × 10¹² s⁻¹ and an E_a of 0.28 eV were obtained. Such a value is quite consistent with the theoretically calculated E_a for the rotation of the three N-bound H atoms (Fig. 2a).

Fig. 5 Frequency-dependent ε′ and ε′′ for 1 at several selected temperatures (a), and the Cole–Cole diagrams are plotted as a series of arcs to show the relationship between ε′ and ε′′ (b). Solid curves represent the fit of the experimental data to the Debye equation.

As well known, molecular dynamics simulation can serve as an effective method for elucidating the microscopic molecular motion processes, such as vibrational, translational or rotational, as a function of time and/or temperature. To further gain a direct insight into the distinct rotational dynamics of the –CH₃ and –NH₃ fragments in 1, we performed molecular dynamics simulations using the Dreiding force field, based on the crystal structures of 1 at 150/293 K (keeping volume constant), respectively. As shown in Fig. 6a and Fig. S5 (ESI†), at a simulation temperature (T_S) of 150 K, all the atoms except those of the –CH₃ fragment are frozen and show no translation or rotation, further supporting that the disorder about 18-crown-6 at 150 K is static in essence, in accordance with the results of structural analysis and low-temperature dielectric spectroscopy. When the T_S is raised to 330 K based on the crystal structure of 1 at 293 K, both of the –CH₃ and –NH₃ fragments in 1 actively rotate, which is accompanied by a slight-amplitude quivering of the “N–C” axis (Fig. 6b and Fig. S6, ESI†).

Fig. 6 Overlapping maps of six snapshots for a [(CH₃NH₃)(18-crown-6)]⁺ cationic complex in 1, by NVT dynamic simulation of 1 at T_S values of 150 K (a) and 300 K (b), respectively, showing orientation changes over the simulation times from 500 to 2500 ps (in an increasing step of 400 ps). The specified H and O atoms are represented as balls.

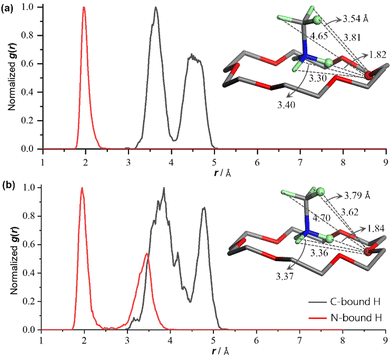
To statistically identify the locations of the N/C-bound H atoms of the (CH₃NH₃)⁺ ion within 1, the radial distribution functions (RDF)⁵¹ derived from the molecular dynamics simulations were calculated using the equation g_ij(r) = 〈ΔN_ij(r, r + Δr)〉V/(4πr²ΔrN_iN_j), where r is the distance between species i and j, 〈ΔN_ij(r, r + Δr)〉 is the ensemble-averaged number of species j around i within a shell from r to r + Δr, V is the system volume, and N_i and N_j are the numbers of species i and j. Thus, the g(r) values of the specific N/C-bound H atoms around the designated O atom of 18-crown-6 at T_S values of 150 and 330 K are shown in Fig. 7a and b, respectively. At a T_S of 150 K, the one sharp peak of the red H⋯O curve and the two closely adjacent peaks of the black H⋯O curve show that the highlighted N-bound H atom is roughly fixed at one site without rotation, whereas the highlighted C-bound H atom rotates apparently. At a T_S of 330 K, the two discrete peaks of the red H⋯O curve suggest that the highlighted N-bound H atom can hop among three relatively stable sites (see the three different H⋯O distances of 1.84, 3.36 and 3.37 Å in the inset map of Fig. 7b, two of which are very close); on the other hand, the two overlapped peaks of the black H⋯O curve show that the highlighted C-bound H atom rotates in a greater degree of random distribution in comparison with that at a T_S of 150 K. Overall, the RDF analysis coincides well with the structural and dielectric analyses.

Fig. 7 RDF profiles of the specific N/C-bound H atoms about the specified O atom of 18-crown-6 (highlighted in the inset image) in 1, derived from molecular dynamics simulations of 1 at T_S values of 150 K (a) and 330 K (b), respectively.

Experimental

Materials and methods

All chemicals were obtained from commercial sources and used without further purification. The FT-IR spectrum was recorded on a Nicolet 6700 FT-IR spectrometer using KBr pellets from 4000 to 400 cm⁻¹. The powder X-ray diffraction (PXRD) pattern (Cu-Kα) was collected on a Rigaku MiniFlex600 θ–2θ diffractometer. Thermogravimetric analysis (TGA) was carried out on a TA Q50 system at a heating rate of 10 °C min⁻¹ under a nitrogen atmosphere. The complex permittivity was measured under a nitrogen atmosphere, using a Tonghui TH2838 LCR meter in a Mercury iTC cryogenic environment controller from Oxford Instruments, and the tested sample was ground and pressed into a tablet under a pressure of ca. 3 MPa.

Synthesis

A mixture of CuCl₂·2H₂O (1.0 mmol), 18-crown-6 (1.0 mmol), and (CH₃NH₃)Cl (1.0 mmol) was dissolved in an aqueous solution (3 mL). The resultant clear solution was allowed to stand at room temperature in a dry environment. Two days later, colorless column-shaped red crystals of 1 were deposited from the solution, in ca. 85% yield based on Cu. The PXRD pattern of bulky crystals indicated that the experimental pattern matches well with the simulated one (Fig. S7, ESI†). IR data (KBr, cm⁻¹): 3447(m), 3165(m), 3108(s), 3026(m), 2903(s), 2822(m), 2746(m), 2522(m), 1965(m), 1616(m), 1469(m), 1351(s), 1285(m), 1249(m), 1099(vs), 960(s), 837(m), 528(m).

Single-crystal X-ray crystallography

The variable-temperature single-crystal X-ray diffraction intensities of 1 were collected on a Rigaku synergistic diffractometer equipped with a graphite-monochromated Mo-Kα radiation (λ = 0.71073 Å) source, at the temperatures of 150(2) and 293(2) K, respectively. Absorption corrections were applied by using the multi-scan program CrysAlisPro.⁵² The structures were solved by direct methods and refined using the full-matrix least-squares technique with the SHELX program package.⁵³ All hydrogen atoms were generated geometrically. Crystallographic data and structural refinements for 1 at five different temperatures are summarized in Table S1 (ESI†). Selected bond lengths are listed in Table S2 (ESI†). More details about the crystallographic data have been deposited as ESI.†

Classical molecular dynamics simulations

The classical molecular dynamics simulations of 1 were performed using the Forcite program implemented in Materials Studio.⁴⁴ For retaining the chemical environments of all the molecular fragments, all the molecular dynamics simulations were performed for the solid-state by using periodic models based on the experimental crystal data. Besides, except for fixing the unit-cell parameters, all the atoms and coordinates were set in free motion during simulation processes. The constant–volume and temperature (NVT) ensemble was used to simulate the dynamic processes at specific simulation temperature. The partial atomic charges of all the atoms were estimated through the charge equilibration method,⁵⁴ and the force field parameters of C, H, N, O and Cl are taken from the Dreiding force field, while that of Cu can be adopted from the universal force field. The electrostatic interactions and the van der Waals interactions were evaluated by the Ewald summation method, with a buffer width of 0.5 Å. The total simulation time was 2500 ps, with a time step of 1.0 fs.

Conclusions

In summary, this research has focused on the (CH₃NH₃)⁺ ion that functions as a smallest dual-wheel rotator within a crown-ether-based supramolecular rotor. Through a comprehensive investigation involving variable-temperature crystal structure analysis, rotational energy barrier analysis, variable-temperature/frequency dielectric response, and molecular dynamics simulations, we unveiled the bisected rotation dynamics inherent to this supramolecular rotor, offering a valuable perspective on the dynamics of ubiquitous –CH₃/–NH₃ groups confined in organic or organic–inorganic hybrid solids. Further research will be extended to investigate the confinement molecular dynamics of the (CH₃NH₃)⁺ ion trapped in other crystalline systems.

Author contributions

Z.-Y. Du conceived the study. W. Li and M. Xie conducted the synthesis of the material and characterization methods such as PXRD, TGA, IR spectroscopy, and dielectric measurement. S.-Y. Zhang performed crystal data collection and structural analysis. C.-H. Zeng, C.-T. He and Z.-Y. Du performed DFT calculations, MD simulations and related analyses. Z.-Y. Du wrote the paper with contributions from all the authors.

Conflicts of interest

There are no conflicts to declare.

Acknowledgements

This work was supported by the Natural Science Foundation of China (21971091, 22161002) and the Natural Science Foundation of Jiangxi Province (20224ACB203002).

Notes and references

1. N. Koumura, R. W. Zijlstra, R. A. van Delden, N. Harada and B. L. Feringa, Light-driven monodirectional molecular rotor, Nature, 1999, 401, 152–155.
2. G. S. Kottas, L. I. Clarke, D. Horinek and J. Michl, Artificial molecular rotors, Chem. Rev., 2005, 105, 1281–1376.
3. C. S. Vogelsberg and M. A. Garcia-Garibay, Crystalline molecular machines: function, phase order, dimensionality, and composition, Chem. Soc. Rev., 2012, 41, 1892–1910.
4. A. Comotti, S. Bracco and P. Sozzani, Molecular rotors built in porous materials, Acc. Chem. Res., 2016, 49, 1701–1710.
5. S. Bracco, M. Beretta, A. Cattaneo, A. Comotti, A. Falqui, K. Zhao, C. Rogers and P. Sozzani, Dipolar rotors orderly aligned in mesoporous fluorinated organosilica architectures, Angew. Chem., Int. Ed., 2015, 54, 4773–4777.
6. J. Kaleta, J. Chen, G. Bastien, M. Dracinsky, M. Masat, C. T. Rogers, B. L. Feringa and J. Michl, Surface inclusion of unidirectional molecular motors in hexagonal tris(o-phenylene)cyclotriphosphazene, J. Am. Chem. Soc., 2017, 139, 10486–10498.
7. C. S. Vogelsberg, F. J. Uribe-Romo, A. S. Lipton, S. Yang, K. N. Houk, S. Brown and M. A. Garcia-Garibay, Ultrafast rotation in an amphidynamic crystalline metal organic framework, Proc. Natl. Acad. Sci. U. S. A., 2017, 114, 13613–13618.
8. M. Inukai, M. Tamura, S. Horike, M. Higuchi, S. Kitagawa and K. Nakamura, Storage of CO₂ into porous coordination polymer controlled by molecular rotor dynamics, Angew. Chem., Int. Ed., 2018, 57, 8687–8690.
9. A. Colin-Molina, D. P. Karothu, M. J. Jellen, R. A. Toscano, M. A. Garcia-Garibay, P. Naumov and B. Rodríguez-Molina, Thermosalient amphidynamic molecular machines: motion at the molecular and macroscopic scales, Matter, 2019, 1, 1033–1046.
10. M. Jin, S. Yamamoto, T. Seki, H. Ito and M. A. Garcia-Garibay, Anisotropic thermal expansion as the source of macroscopic and molecular scale motion in phosphorescent amphidynamic crystals, Angew. Chem., Int. Ed., 2019, 58, 18003–18010.
11. D. Dattler, G. Fuks, J. Heiser, E. Moulin, A. Perrot, X. Yao and N. Giuseppone, Design of collective motions from synthetic molecular switches, rotors, and motors, Chem. Rev., 2020, 120, 310–433.
12. J. Perego, S. Bracco, M. Negroni, C. X. Bezuidenhout, G. Prando, P. Carretta, A. Comotti and P. Sozzani, Fast motion of molecular rotors in metal-organic framework struts at very low temperatures, Nat. Chem., 2020, 12, 845–851.
13. J. Dong, V. Wee, S. B. Peh and D. Zhao, Molecular-rotor-driven advanced porous materials, Angew. Chem., Int. Ed., 2021, 60, 16279–16292.
14. A. Gonzalez-Nelson, S. Mula, M. Simenas, S. Balciu Nas, A. R. Altenhof, C. S. Vojvodin, S. Canossa, J. R. Banys, R. W. Schurko, F. X. Coudert and M. A. van der Veen, Emergence of coupled rotor dynamics in metal-organic frameworks via tuned steric interactions, J. Am. Chem. Soc., 2021, 143, 12053–12062.
15. M. Jin, R. Ando, M. J. Jellen, M. A. Garcia-Garibay and H. Ito, Encapsulating N-heterocyclic carbene binuclear transition-metal complexes as a new platform for molecular rotation in crystalline solid-state, J. Am. Chem. Soc., 2021, 143, 1144–1153.
16. J. Perego, C. X. Bezuidenhout, S. Bracco, G. Prando, L. Marchio, M. Negroni, P. Carretta, P. Sozzani and A. Comotti, Cascade dynamics of multiple molecular rotors in a MOF: benchmark mobility at a few kelvins and dynamics control by CO₂, J. Am. Chem. Soc., 2021, 143, 13082–13090.
17. Y. S. Su, E. S. Lamb, I. Liepuoniute, A. Chronister, A. L. Stanton, P. Guzman, S. Perez-Estrada, T. Y. Chang, K. N. Houk, M. A. Garcia-Garibay and S. E. Brown, Dipolar order in an amphidynamic crystalline metal-organic framework through reorienting linkers, Nat. Chem., 2021, 13, 278–283.
18. A. Dhamija, C. K. Das, Y. H. Ko, Y. Kim, R. D. Mukhopadhyay, A. Gunnam, X. J. Yu, I. C. Hwang, L. V. Schafer and K. Kim, Remotely controllable supramolecular rotor mounted inside a porphyrinic cage, Chem, 2022, 8, 543–556.
19. X. W. Liu, W. Zhao, Y. Wu, Z. Meng, Z. He, X. Qi, Y. Ren, Z. Q. Yu and B. Z. Tang, Photo-thermo-induced room-temperature phosphorescence through solid-state molecular motion, Nat. Commun., 2022, 13, 3887.
20. A. Mondal, R. Toyoda, R. Costil and B. L. Feringa, Chemically driven rotatory molecular machines, Angew. Chem., Int. Ed., 2022, 61, e202206631.
21. A. D. Nicola, A. Correa, S. Bracco, J. Perego, P. Sozzani, A. Comottic and G. Milanod, Collective dynamics of molecular rotors in periodic mesoporous organosilica: a combined solid-state 2H-NMR and molecular dynamics simulation study, Phys. Chem. Chem. Phys., 2022, 24, 666–673.
22. D. Jose and A. Datta, Molecular rotor inside a phosphonate cavitand: Role of supramolecular interactions, J. Phys. Chem. Lett., 2010, 1, 1363–1366.
23. Y. M. You, W. Q. Liao, D. Zhao, H. Y. Ye, Y. Zhang, Q. Zhou, X. Niu, J. Wang, P. F. Li, D. W. Fu, Z. Wang, S. Gao, K. Yang, J. M. Liu, J. Li, Y. Yan and R. G. Xiong, An organic-inorganic perovskite ferroelectric with large piezoelectric response, Science, 2017, 357, 306–309.
24. H. Y. Ye, Y. Y. Tang, P. F. Li, W. Q. Liao, J. X. Gao, X. N. Hua, H. Cai, P. P. Shi, Y. M. You and R. G. Xiong, Metal-free three-dimensional perovskite ferroelectrics, Science, 2018, 361, 151–155.
25. X. Jiang, H. B. Duan, M. J. Jellen, Y. Chen, T. S. Chung, Y. Liang and M. A. Garcia-Garibay, Thermally activated transient dipoles and rotational dynamics of hydrogen-bonded and charge-transferred diazabicyclo [2.2.2]octane molecular rotors, J. Am. Chem. Soc., 2019, 141, 16802–16809.
26. S. Perez-Estrada, B. Rodriguez-Molina, E. F. Maverick, S. I. Khan and M. A. Garcia-Garibay, Throwing in a monkey wrench to test and determine geared motion in the dynamics of a crystalline one-dimensional (1D) columnar rotor array, J. Am. Chem. Soc., 2019, 141, 2413–2420.
27. I. Liepuoniute, M. J. Jellen and M. A. Garcia-Garibay, Correlated motion and mechanical gearing in amphidynamic crystalline molecular machines, Chem. Sci., 2020, 11, 12994–13007.
28. R. Ando, A. Sato-Tomita, H. Ito and M. Jin, Giant crystalline molecular rotors that operate in the solid state, Angew. Chem., Int. Ed., 2023, 31, e202309694.
29. W. Li, C. T. He, Y. Zeng, C. M. Ji, Z. Y. Du, W. X. Zhang and X. M. Chen, Crystalline supramolecular gyroscope with a water molecule as an ultrasmall polar rotator modulated by charge-assisted hydrogen bonds, J. Am. Chem. Soc., 2017, 139, 8086–8089.
30. R. K. Huang, Z. F. Xiao, D. X. Liu, W. X. Zhang and X. M. Chen, Unprecedented water-controlled rotator-stator conversion of supramolecular rotors in crystals, Chem. Commun., 2019, 55, 7159–7162.
31. W. Li, Y. Zeng, X. Shu, C. T. He, Z. Y. Du, W. X. Zhang and X. M. Chen, Isostructural phase transition and tunable water rotation within a unique solid rotor system, J. Mater. Chem. C, 2019, 7, 13176–13181.
32. Y. F. Gao, Z. X. Zhang, T. Zhang, C. Y. Su, W. Y. Zhang and D. W. Fu, Regulated molecular rotor in phase transition materials with switchable dielectric and SHG effect, Mater. Chem. Front., 2020, 4, 3003–3012.
33. R. K. Huang, X. X. Chen, Z. F. Xiao, D. X. Liu, W. X. Zhang and X. M. Chen, Enhancing switchable dielectric property for crystalline supramolecular rotor compounds by adding polar components, Chem. Commun., 2020, 56, 4114–4117.
34. X. J. Song, T. Zhang, Z. X. Gu, Z. X. Zhang, D. W. Fu, X. G. Chen, H. Y. Zhang and R. G. Xiong, Record enhancement of Curie temperature in host-guest inclusion ferroelectrics, J. Am. Chem. Soc., 2021, 143, 5091–5098.
35. S. N. Du, D. Su, Z. Y. Ruan, Y. Q. Zhou, W. Deng, W. X. Zhang, Y. Sun, J. L. Liu and M. L. Tong, Reversible switchability of magnetic anisotropy and magnetodielectric effect induced by intermolecular motion, Angew. Chem., Int. Ed., 2022, 61, e202204700.
36. W. Li, D. X. Liu, W. Y. Hu, Q. Y. Liu, Z. Y. Du, C. T. He, W. X. Zhang and X. M. Chen, A crystalline supramolecular rotor functioned by dual ultrasmall polar rotators, Chin. J. Chem., 2022, 40, 1917–1923.
37. L. P. Miao, N. Ding, N. Wang, C. Shi, H. Y. Ye, L. Li, Y. F. Yao, S. Dong and Y. Zhang, Direct observation of geometric and sliding ferroelectricity in an amphidynamic crystal, Nat. Mater., 2022, 21, 1158–1164.
38. S. Y. Ge, R. K. Huang, J. B. Wu, K. Takahashi, C. S. Lee and T. Nakamura, Planar positive-zero-negative thermal expansion transition in crystalline supramolecular rotors, Chem. Mater., 2023, 35, 4311–4317.
39. M. M. Lun, C. Y. Su, Q. Q. Jia, Z. X. Zhang, J. Li, H. F. Lu, Y. Zhang and D. W. Fu, Remarkable enhancement of optical and electric properties by temperature-controlled solid-phase molecular motion, Inorg. Chem. Front., 2023, 10, 5026–5034.
40. S. Mandal, T. K. Mukhopadhyay and A. Datta, Role of momentum matching in increasing the Curie temperature for ferroelectricity in host-guest complexes, J. Phys. Chem. C, 2023, 127, 18206–18212.
41. K. N. Trueblood, C. B. Knobler, D. S. Lawrence and R. V. Stevens, Structures of the 1:1 complexes of 18-crown-6 with hydrazinium perchlorate, hydroxylammonium perchlorate, and methylammonium perchlorate, J. Am. Chem. Soc., 1982, 104, 1355–1362.
42. H. Nagata, H. Nishi, M. Kamigauchi and T. Ishida, Guest-dependent conformation of 18-crown-6 tetracarboxylic acid: Relation to chiral separation of racemic amino acids, Chirality, 2008, 20, 820–827.
43. Y. Jin, Methylammonium tetrafluoridoborate 18-crown-6 clathrate, Acta Cryst., 2012, E68, o225.
44. Accelrys, Materials Studio Getting Started, release 5.5, Accelrys Software, Inc., San Diego, CA, 2009.
45. M. Turner, J. McKinnon, S. Wolff, D. Grimwood, P. Spackman, D. Jayatilaka and M. Spackman, CrystalExplorer17, University of Western Australia, 2017.
46. P. Auffinger and G. Wipff, High temperature annealed molecular dynamics simulations as a tool for conformational sampling. Application to the bicyclic “222” cryptand, J. Comput. Chem., 1990, 11, 19–31.
47. F. Kremer and A. Schönhals, Broadband dielectric spectroscopy, Springer Science & Business Media, Berlin, Germany, 2002.
48. K. C. Kao, Dielectric phenomena in solids, Elsevier, Cambridge, MA, 2004.
49. J. Harada, M. Ohtani, Y. Takahashi and T. Inabe, Molecular motion, dielectric response, and phase transition of charge-transfer crystals: acquired dynamic and dielectric properties of polar molecules in crystals, J. Am. Chem. Soc., 2015, 137, 4477–4486.
50. S. Havriliak and S. Negami, A complex plane representation of dielectric and mechanical relaxation processes in some polymers, Polymer, 1967, 8, 161–210.
51. R. Babarao and J. W. Jiang, Upgrade of natural gas in rhozeolite-like metal–organic framework and effect of water: a computational study, Energy Environ. Sci., 2009, 2, 1088–1093.
52. CrysAlisPro, Rigaku Oxford Diffraction, The Woodlands, TX, 2015.
53. G. M. Sheldrick, Crystal structure refinement with SHELXL, Acta Crystallogr., Sect. C: Struct. Chem., 2015, 71, 3–8.
54. S. Ramachandran, T. Lenz, W. Skiff and A. Rappé, Toward an understanding of zeolite Y as a cracking catalyst with the use of periodic charge equilibration, J. Phys. Chem., 1996, 100, 5898–5907.

---

Footnote

† Electronic supplementary information (ESI) available: Experimental details and characterization. CCDC 2302601 and 2302602. For ESI and crystallographic data in CIF or other electronic format see DOI: https://doi.org/10.1039/d3cp05406c

---