Elastic and electronically inelastic scattering of electrons by the pyrazine molecule
Murilo O.
Silva
 *a,
Giseli M.
Moreira
*a,
Giseli M.
Moreira
 b,
Jaime
Rosado
b,
Jaime
Rosado
 c,
Francisco
Blanco
c,
Francisco
Blanco
 c,
Gustavo
García
c,
Gustavo
García
 d,
Márcio H. F.
Bettega
d,
Márcio H. F.
Bettega
 a and
Romarly F.
da Costa
a and
Romarly F.
da Costa
 *e
*e
aDepartamento de Física, Universidade Federal do Paraná, Caixa Postal 19044, 81531-980 Curitiba, Paraná, Brazil
bDepartamento de Física, Universidade Estadual do Centro-Oeste, 85040-167 Guarapuava, Paraná, Brazil
cDepartamento de Estructura de la Materia, Física Térmica y Electrónica e IPARCOS, Universidad Complutense de Madrid, 28040 Madrid, Spain
dInstituto de Física Fundamental, Consejo Superior de Investigaciones Científicas, 28006 Madrid, Spain
eCentro de Ciências Naturais e Humanas, Universidade Federal do ABC, 09210-580 Santo André, São Paulo, Brazil. E-mail: romarly.costa@ufabc.edu.br; roma.ifi@unicamp.br
First published on 21st November 2023
Abstract
We report on elastic and electronically inelastic integral and differential cross sections as well as ionization and total cross sections for electron collisions with the pyrazine molecule. The Schwinger multichannel method is applied in calculations carried out according to the minimal orbital basis for single configuration interactions strategy from the 1-channel up to 139-channels close-coupling level of approximation. With these calculations we have obtained integral and differential cross sections as well as excitation functions for elastic electron scattering and, also, integral and differential cross sections for electronic excitation from the ground state to the 3B1u, 3B2u, 3B3u, 1B1u, 1B2u and 1B3u excited states of pyrazine by electron impact. By summing the total ionization cross section obtained by means of the binary-encounter-Bethe model to these elastic and electronically inelastic contributions, we provided an estimate for the total cross section describing the electron-pyrazine interaction process. The independent atom model with the screening-corrected additivity rule plus interference terms method was also used in the present study to determine elastic integral and differential as well as ionization and total cross sections for electron collisions from pyrazine. The present results were, whenever possible, critically compared to the experimental and theoretical data available in the literature. In general, the overall agreement between the present results and the experiment is quite encouraging.
1 Introduction
The pyrazine molecule and its derivatives are widely found in natural as well as synthetic compounds, with the pyrazine core being a crucial component in the pharmaceutical industry due to its biologically active nature.1 Pyrazine, a simpler analogue of the pyrimidinic nucleobases, has been considered as a good model for investigating electron collisions with DNA and RNA constituents. In fact, due to specific properties such as its high symmetry (it has D2h symmetry) and non-polarity, this system has become the object of interest in many studies reported in the literature.2 This molecule is an aza-derivative of benzene, where two C–H groups are replaced by nitrogen atoms and, along with pyrimidine and pyridazine, form the chemical group known as diazines.Pioneer investigations concerning electron collisions by pyrazine were conducted by Nenner and Schulz.3 In their study these authors observed three π* resonances in the elastic cross section, which they interpreted as two shape resonances arising from the capture of the incident electron into an empty π* orbital of the target and one resonance that was tentatively attributed to have a mixed shape and core-excited character. Theoretical work later performed by Winstead and McKoy4,5 by using the Schwinger multichannel (SMC) method at the static-exchange (SE) and static-exchange plus polarization (SEP) approximations have addressed the formation of resonances in the elastic scattering of electrons by pyrazine and provided strong evidence for the mixed (shape and core-excited) character of the third π* resonance, thus giving support to the conjecture proposed by Nenner and Schulz. The assignments (positions and character) for these low-lying resonances were further confirmed by the R-matrix calculations from Mašín and Gorfinkiel,6,7 who also reported the presence of a number of core-excited resonances above the energy of 4.8 eV. The discussion about the nature of these resonances were complemented by differential (DCS) and integral (ICS) elastic cross sections and by total inelastic cross sections and the cross sections for the individual excitation into the two lowest excited states of pyrazine. Experimental investigation on elastic electron scattering from pyrazine were carried out by Palihawadana et al.8 using a crossed electron–molecular beam spectrometer combined with the relative flow technique. Measured DCSs and ICS obtained in that work were in good agreement with available R-matrix and SMC-SEP calculations for energies below around 20 eV. At higher energies, however, the SMC-SE results overestimate the DCS measurements, especially at middle and backward angles and the reason for the difference remained unclear. In subsequent investigations, Sanz et al.2 and Fuss et al.9 presented experimental total cross sections (TCSs) for electron scattering from pyrazine determined by using a new magnetically confined electron transmission-beam apparatus. These measurements were complemented by theoretical differential and integral elastic as well as integral inelastic cross sections calculated by means of the independent atom with screening corrected additivity rule (IAM-SCAR) method covering a wide range of incident electron energies. The level of accord between measured and calculated cross sections reported in that work and also with previous R-matrix and SMC results was, in general, good. Disagreement between theoretical and experimental cross sections observed for angles below 20°, a region dominated by the dipole interaction, were understood as a side effect of the finite angular resolution of the experimental apparatus in the forward direction. More recently, Graves and Gorfinkiel10 revisited the problem of electron collisions against pyrazine by carrying out calculations with the R-matrix method at the SEP and close-coupling (CC) levels of approximation in order to assess the role of polarization and correlation effects. From that investigation, which also involves the study of positron scattering by pyrazine, the authors concluded that, for electron scattering, the discrepancies observed between the calculated integral cross sections and the experimental data below 3 eV should be attributed to the extrapolations made in the measured differential cross sections in order to obtain the integral cross section. This hypothesis was reinforced by the fact that the DCSs calculated by means of the R-matrix method showed a much better agreement with the measurements. In order to address some of the discrepancies observed in the comparison of previous experimental and theoretical cross sections and to put some light into the discussion we have performed elastic and electronically inelastic calculations for the electron scattering by pyrazine using the Schwinger multichannel method with pseudopotentials (SMCPP)11 and the independent atom model with screening corrected additivity rule plus interference terms (IAM-SCAR + I) method.12 In the SMCPP calculations the scattering amplitude was obtained within the scope of the minimal orbital basis for single configuration interactions (MOB-SCI)13 strategy taking into account from 1-channel up to 139-channels. Differential and integral cross sections as well as excitation functions for elastic electron scattering by pyrazine were obtained and compared with prior measurements and calculations with focus on analysing the influence of polarization and multichannel coupling effects. Electronic excitation involving the transitions from the ground state to the 3B1u, 3B2u, 3B3u, 1B1u, 1B2u and 1B3u electronically excited states of pyrazine driven by electron impact are also reported and compared to the R-matrix results from Mašín and Gorfinkiel,6 when available. We also obtained the total ionization cross section for the pyrazine molecule using the binary-encounter-Bethe (BEB) model, which next was summed to the SMCPP elastic and electronically inelastic cross sections to estimate the total cross section. Finally, by means of the IAM-SCAR+I calculations, we have obtained elastic integral and differential cross sections and, also, ionization and total cross sections.
The remainder of this paper is structured as follows. Theoretical and computational details of present calculations are described in Section 2. In Section 3, the cross sections obtained by means of the SMCPP and IAM-SCAR+I methods are presented and critically compared to previous calculations and measurements. Finally, our conclusions are summarized in Section 4.
2 Theory and computational details
2.1. Schwinger multichannel method
Part of the results presented in this work were obtained with the Schwinger multichannel method14,15 within its implementation with norm-conserving pseudopotentials,11 where the effective potentials proposed by Bachelet et al.16 were used to represent the nuclei and the core electrons of the heavy atoms.The SMC method is a variational approach for the scattering amplitude and has been recently reviewed in ref. 17. Here we will only discuss the aspects of the method that are relevant to the present calculations. The working expression for the scattering amplitude obtained in the SMC method is given by:
 | (1) |
| dmn = 〈χm|A(+)|χn〉, | (2) |
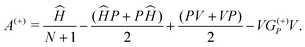 | (3) |
 is an eigenstate of the unperturbed Hamiltonian H0 = HN + TN+1 and it is given by the product of a target state and a plane wave with
is an eigenstate of the unperturbed Hamiltonian H0 = HN + TN+1 and it is given by the product of a target state and a plane wave with  representing the momentum of the free incident (scattered) electron. In the definition of H0, HN represents the target Hamiltonian and TN+1 corresponds to the kinetic energy operator of the incident electron; V is the interaction potential between the incident electron and the target's electrons and nuclei; Ĥ = E − H, where E is the total collision energy and H is the (N + 1)-electron Hamiltonian in the fixed nuclei approximation; G(+)P = PG(+)0 is the free-particle Green's function projected into the P-space and P is a projection operator onto the open-channel space of the target, which is given by:
representing the momentum of the free incident (scattered) electron. In the definition of H0, HN represents the target Hamiltonian and TN+1 corresponds to the kinetic energy operator of the incident electron; V is the interaction potential between the incident electron and the target's electrons and nuclei; Ĥ = E − H, where E is the total collision energy and H is the (N + 1)-electron Hamiltonian in the fixed nuclei approximation; G(+)P = PG(+)0 is the free-particle Green's function projected into the P-space and P is a projection operator onto the open-channel space of the target, which is given by: | (4) |
 | (5) |
 is the antisymmetrization operator, |Φ01〉 represents the target ground state obtained at the Hartree–Fock level and |Φsm〉 (m ≥ 2) represents a N-electron Slater determinant obtained by performing single excitations of the target from the valence occupied (hole) orbitals of the ground (reference) state to a set of unoccupied (particle) orbitals with spin s (s = 0 for singlet or s = 1 for triplet states), where |ϕn〉 is a scattering orbital.
is the antisymmetrization operator, |Φ01〉 represents the target ground state obtained at the Hartree–Fock level and |Φsm〉 (m ≥ 2) represents a N-electron Slater determinant obtained by performing single excitations of the target from the valence occupied (hole) orbitals of the ground (reference) state to a set of unoccupied (particle) orbitals with spin s (s = 0 for singlet or s = 1 for triplet states), where |ϕn〉 is a scattering orbital.
The molecular geometry of pyrazine was optimized in the D2h point group through the second-order Møller–Plesset perturbation theory (MP2) with the aug-cc-pVDZ basis set by using the GAMESS18 computational package. The ball and stick model of pyrazine is shown in Fig. 1 (generated with MacMolPlt19). The ground state was described at the Hartree–Fock level while the excited states were obtained through the full single configuration interaction (FSCI) technique. The valence electrons of carbon and nitrogen atoms are described by a set of 5s5p2d uncontracted Cartesian Gaussian (CG) functions generated according to the procedure described in ref. 20 and the exponents of these CG functions are shown in Table 1. To describe the hydrogen atoms we employed the 4s/3s basis set of Dunning21 increased by one p-type function with the exponent equal to 0.75.
 | ||
| Fig. 1 Ball and stick model of the pyrazine molecule generated with MacMolPlt.19 | ||
| Type | C | N |
|---|---|---|
| s | 12.49628 | 17.56734 |
| s | 2.470286 | 3.423615 |
| s | 0.614028 | 0.884301 |
| s | 0.184028 | 0.259045 |
| s | 0.039982 | 0.055708 |
| p | 5.228869 | 7.050692 |
| p | 1.592058 | 1.910543 |
| p | 0.568612 | 0.579261 |
| p | 0.210326 | 0.165395 |
| p | 0.072250 | 0.037192 |
| d | 0.603592 | 0.403039 |
| d | 0.156753 | 0.091192 |
The calculations in the present work were performed as follows: (i) Using the improved virtual orbitals22 to represent the particle and scattering orbitals, we run a FSCI calculation, which provided a total number of 3015 states; (ii) From the energy spectrum obtained through the FSCI we selected the 80 lowest excited states of the target (5 singlet and 5 triplet states of each irreducible symmetry of the D2h point group) to be described by using 69 hole–particle pairs and then we used these pairs to construct the MOB-SCI13 strategy. In choosing the hole–particle pairs for the MOB-SCI scheme we ensure that the energy values obtained according to this strategy would maintain at least 90% of agreement with the FSCI ones.
Tables 2 and 3 show the vertical excitation energies for the first eight triplet and the first eleven singlet electronic excited states of pyrazine. The energies obtained from the MOB-SCI calculation show a degree of agreement going from very good (a difference in energy less than 0.1 eV) to reasonable (a difference in energy of at most 1.0 eV) as compared to the FSCI energies, even though an inversion in the ordering of some states is observed. As previously discussed, ensuring good equivalence with the energies of the FSCI calculation (taken as our reference) is an important step in the application of the MOB-SCI strategy. Comparison to theoretical6,23–28 and experimental29–31 results found in the literature denotes a level of agreement ranging from excellent to acceptable, as can be seen in Tables 2 and 3. A schematic representation for the complete MOB-SCI spectrum of the pyrazine molecule used in the present calculations is presented in Fig. 3 and the different channel coupling schemes (from 1 up to 139 open channels) used in the scattering calculations are specified by the color lines.
| State | FSCI | MOB-SCI | Ref. 6 | Ref. 23 | Ref. 24 | Ref. 24 | (UV-IR/EEL29) |
|---|---|---|---|---|---|---|---|
| 13B1u | 3.20 | 3.60 | 3.86 | 4.25 | 4.15 | 4.33 | —/4.04 |
| 13B2u | 3.89 | 3.98 | 4.81 | 4.12 | 4.39 | 4.63 | —/4.40 |
| 13B3u | 3.97 | 4.55 | 4.16 | 3.82 | 3.24 | 3.93 | 3.2625/3.26 |
| 23B1u | 5.00 | 5.21 | 5.10 | 5.14 | 5.04 | 5.43 | —/5.50–6.00 |
| 13B2g | 5.22 | 5.94 | 5.28 | 5.39 | 4.84 | 5.32 | 4.5927/4.60 |
| 13Au | 6.67 | 7.19 | 5.95 | 5.34 | 4.42 | 5.32 | —/4.20 |
| 13B1g | 6.99 | 7.13 | 7.09 | —/5.50–6.00 | |||
| 33B2u | 7.06 | 7.30 |
| State | FSCI | MOB-SCI | Ref. 6 | Ref. 23 | Ref. 26 | Ref. 28 | Ref. 28 | (VUV/EEL)29 |
|---|---|---|---|---|---|---|---|---|
| 11B3u | 5.03 | 5.39 | 4.80 | 4.25 | 3.95 | 4.12 | 4.42 | 3.8330/— |
| 11B2u | 5.79 | 6.16 | 4.88 | 4.84 | 4.64 | 4.85 | 5.14 | 4.8030/4.80 |
| 11B1u | 6.45 | 7.28 | 8.59 | 6.68 | 6.58 | 6.89 | 7.18 | 6.50/6.50 |
| 11B2g | 6.57 | 7.04 | 5.84 | 6.04 | 5.57 | 5.68 | 6.02 | 5.1927/— |
| 11Au | 6.92 | 7.32 | 6.00 | 5.24 | 4.81 | 4.70 | 5.29 | —/5.00 |
| 11B1g | 7.15 | 7.26 | 7.24 | 6.62 | 6.41 | 7.13 | 5.50/6.00 | |
| 21B3u | 8.06 | 8.25 | 9.96 | 7.61 | 7.49 | 6.75/— | ||
| 21B2u | 8.22 | 8.27 | 9.94 | 7.67 | 7.14 | 7.65 | 8.29 | 7.07/— |
| 21Au | 8.22 | 8.31 | 11.17 | |||||
| 21B1u | 8.45 | 9.49 | 10.46 | 8.24 | 7.72 | 7.79 | 8.34 | 6.84/— |
| 21Ag | 8.68 | 8.85 | 8.25 | 7.07 | 6.53 | 8.61 | 9.55 | 6.3031/— |
The same 69 hole–particle pairs used to construct the active space in the MOB-SCI strategy were employed in the construction of the CSF space. The number of CSFs obtained for each symmetry was: 3466 for Ag, 3338 for Au, 3396 for B1g, 3399 for B2g, 3410 for B3g, 3326 for B1u, 3453 for B2u and 3416 for B3u. In this work, the scattering calculations were performed at different channel coupling levels. This means that, depending on the energy of the incident electron, a different number of electronically excited states of the target (all those that become energetically allowed) were treated as open in the definition of the P operator given by eqn (4). However, here we will present only the cross sections associated with the best level of channel coupling in each energy. Although we chose not to present the comparison between the different levels of channel coupling, we observed that as more states become allowed to the molecular target, the magnitude of the cross section decreases due to the flux competition among all energetically accessible electronic target states. Such an outcome is consistent with the results observed in previous studies that we have carried out by using the MOB-SCI strategy.32–35 In order to distinguish the different levels of channel coupling in the calculations, we adopted the nomenclature already used in previous works (see, for instance, ref. 36)Nopench, where Nopen is the number of open channels entering in the definition of the P operator in eqn (4). Then, following the strategy schematized in Fig. 2, the scattering calculations were carried out at the 2ch, 3ch, 4ch, 8ch, 16ch, 47ch, 68ch, 88ch, 126ch, 130ch, 135ch, 136ch and 139ch levels of channel coupling.
 | ||
| Fig. 3 Integral cross section for elastic electron scattering by pyrazine. Solid green line, present SMCPP results considering all channels energetically accessible to the molecular target up to 50 eV. The region of formation of the resonances (in which all channels energetically accessible up to 7 eV were included) is highlighted as an inset frame in the figure; black dashed-dotted line, present IAM-SCAR+I results; solid dark green line, SMC results obtained by Winstead and McKoy;5 solid black line, IAM-SCAR results obtained by Sanz et al.;2 blue dashed line, R-matrix results obtained by Graves and Gorfinkiel10 (calculated in ref. 6); violet circles, experimental measurements performed by Palihawadana et al.8 | ||
To obtain the TCS, in addition to elastic and electronically inelastic contributions, it is necessary to calculate the ionization cross section. The SMC method does not take the ionization channel into account. In view of that, we computed the total ionization cross section (TICS) by using the BEB model,37 which provides a simple analytical formula for the electron-impact ionization cross section of atoms and molecules. In this model, the ionization cross section for the ith molecular orbital is given by:
 | (6) |
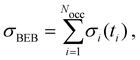 | (7) |
2.2. Independent atom model with the screening-corrected additivity rule plus interference terms method
We employed the IAM-SCAR+I method to obtain differential and integral elastic cross sections as well as ionization and total cross sections. This method has been described in detail40 and its reliability for impact energies above 15 eV has been thoroughly verified.41–43 Briefly, the molecular target is considered as an aggregate of its individual atoms. Each atom is represented by an “ab initio” optical potential, where the real part accounts for elastic scattering, while the imaginary part represents the inelastic processes, considered as the “absorption part”.44 The differential scattering cross sections are obtained from the atomic data by the screening corrected additivity rule (SCAR) procedure, incorporating interference (I) corrections45 by summing all the atomic amplitudes, where the phase coefficients are included. Then, by integrating over all the scattered angular range, the integral scattering cross sections are obtained.3 Results and discussion
In Fig. 3 we present our SMCPP and IAM-SCAR+I ICS results for the elastic electron scattering by pyrazine for energies from 0 to 50 eV and compare them with the data available in the literature. As highlighted in the inset of this figure, the SMCPP curve obtained according to the 1-channel up to 139-channels level of calculation displays the presence of three resonant structures peaked at 0.561 , 0.92
, 0.92  and 4.60 eV
and 4.60 eV 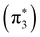 . Our assignments for these structures as resonances of shape
. Our assignments for these structures as resonances of shape  and mixed shape and core-excited
and mixed shape and core-excited  character are consistent with remarks previously reported by Winstead and McKoy5 and by Mašín and Gorfinkiel.6 With respect to the position of the resonant peaks, current and earlier results are summarized in Table 4. In short, our
character are consistent with remarks previously reported by Winstead and McKoy5 and by Mašín and Gorfinkiel.6 With respect to the position of the resonant peaks, current and earlier results are summarized in Table 4. In short, our 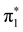 resonance is located above the theoretical predictions reported in ref. 5 and 6 and the experimental determination provided by Nenner and Schulz3 by about 0.4 eV and 0.5 eV, respectively. On the other hand, in the case of the
resonance is located above the theoretical predictions reported in ref. 5 and 6 and the experimental determination provided by Nenner and Schulz3 by about 0.4 eV and 0.5 eV, respectively. On the other hand, in the case of the  resonance, our result is placed below previous SMC and R-matrix results by around 0.4–0.2 eV but is in very good agreement with the experimental data from ref. 3. Finally, in our SMCPP model, the
resonance, our result is placed below previous SMC and R-matrix results by around 0.4–0.2 eV but is in very good agreement with the experimental data from ref. 3. Finally, in our SMCPP model, the  resonance is located in between the positions assigned by the other two theoretical methods and again nearly by 0.5 eV above the measurements from Nenner and Schulz. Above 5 eV, i.e. outside the region where resonant structures appear, the overall agreement (in terms of general dependence on the incident energy and magnitude) of present SMCPP ICS with the measurements from Palihawadana et al.8 is quite good, except at 10 and 20 eV where our curve underestimates the experimental data. In spite of that it is worth noting that, even in these two specific cases, the magnitude of our SMCPP ICS is within the confidence interval established by the experimental error bars. The discrepancy in terms of magnitude observed between present and previous SMC results is already expected since the calculations performed by Winstead and McKoy5 do not take into account the flux stealing due to the inclusion of channel coupling effects. From 10 eV, the agreement between the present SMCPP and previous IAM-SCAR starts at fair and improves until it is very good as the energy increases from 30 eV on, as was also expected. Current IAM-SCAR+I ICS overestimates all theoretical curves in the whole energy interval, but displays reasonable agreement with the experimental data for the energies between 10 and 20 eV. The discrepancies observed for energies above 20 eV are unexpected considering that the reliability of the IAM-SCAR+I method for impact energies above 15 eV has been thoroughly verified in previous applications,41–43 as mentioned before. Although unforeseen, the reason for this result remains unclear. Finally, it is worth noting that even though Winstead and McKoy5 and Mašín and Gorfinkiel6 reported the appearance of a Ramsauer–Townsend (RT) minimum in the cross section for the Ag symmetry, present SMCPP ICS curve shows no sign of the presence of such a minimum. As it is already known, an accurate representation of the target polarization is crucial in the explicit demonstration of a RT minimum. So, in order to check this point, we have performed a second round of calculations (only for the Ag symmetry) in which the description of the polarization effects was modified by increasing the number of single excitations used to build the configuration space from 69 to 148 hole–particle pairs. With this choice, it was possible to obtain a suitable description of the polarization effects while keeping the general behavior and magnitude of the present SMCPP ICS unchanged. As can be seen in Fig. 5, through the analysis of the s-wave cross section (top panel) and the corresponding eigenphase (bottom panel) we identify the presence of the RT minimum at 0.28 eV, thus giving support to the findings previously reported in ref. 5 and 6.
resonance is located in between the positions assigned by the other two theoretical methods and again nearly by 0.5 eV above the measurements from Nenner and Schulz. Above 5 eV, i.e. outside the region where resonant structures appear, the overall agreement (in terms of general dependence on the incident energy and magnitude) of present SMCPP ICS with the measurements from Palihawadana et al.8 is quite good, except at 10 and 20 eV where our curve underestimates the experimental data. In spite of that it is worth noting that, even in these two specific cases, the magnitude of our SMCPP ICS is within the confidence interval established by the experimental error bars. The discrepancy in terms of magnitude observed between present and previous SMC results is already expected since the calculations performed by Winstead and McKoy5 do not take into account the flux stealing due to the inclusion of channel coupling effects. From 10 eV, the agreement between the present SMCPP and previous IAM-SCAR starts at fair and improves until it is very good as the energy increases from 30 eV on, as was also expected. Current IAM-SCAR+I ICS overestimates all theoretical curves in the whole energy interval, but displays reasonable agreement with the experimental data for the energies between 10 and 20 eV. The discrepancies observed for energies above 20 eV are unexpected considering that the reliability of the IAM-SCAR+I method for impact energies above 15 eV has been thoroughly verified in previous applications,41–43 as mentioned before. Although unforeseen, the reason for this result remains unclear. Finally, it is worth noting that even though Winstead and McKoy5 and Mašín and Gorfinkiel6 reported the appearance of a Ramsauer–Townsend (RT) minimum in the cross section for the Ag symmetry, present SMCPP ICS curve shows no sign of the presence of such a minimum. As it is already known, an accurate representation of the target polarization is crucial in the explicit demonstration of a RT minimum. So, in order to check this point, we have performed a second round of calculations (only for the Ag symmetry) in which the description of the polarization effects was modified by increasing the number of single excitations used to build the configuration space from 69 to 148 hole–particle pairs. With this choice, it was possible to obtain a suitable description of the polarization effects while keeping the general behavior and magnitude of the present SMCPP ICS unchanged. As can be seen in Fig. 5, through the analysis of the s-wave cross section (top panel) and the corresponding eigenphase (bottom panel) we identify the presence of the RT minimum at 0.28 eV, thus giving support to the findings previously reported in ref. 5 and 6.
DCSs for elastic electron scattering by pyrazine are shown in Fig. 4 at the selected energies of 6, 10, 15, 20, 30 and 50 eV. At higher scattering angles the accord between present SMCPP and IAM-SCAR+I cross sections is good and the level of agreement between them improves as the impact energy increases, as already anticipated in the discussion of the ICS results. Particularly, for the energy of 30 eV at angles above 90° and for the energy of 50 eV at angles above 60°, the agreement between current SMCPP and IAM-SCAR+I is quite good. In the region of small angles, the curve corresponding to the calculation performed by using the SMCPP method presents a more pronounced minimum located approximately at 60° for the energy of 10 eV and at around 30° for the energies of 15, 20, 30 and 50 eV. The occurrence of this minimum is not reproduced in the DCS curves obtained according to the IAM-SCAR+I method. The same sort of agreement is also observed in the comparison of present SMCPP DCSs with previous IAM-SCAR results obtained by Sanz et al.2 On the other hand, the overall agreement between the SMCPP results and those obtained by Mašín and Gorfinkiel6 is, in general, very good. However, it is worth noting that there are small differences between the magnitudes of the SMCPP and R-matrix DCSs at intermediate angles, more precisely, between 35° and 90° for the energies of 10 and 15 eV and at backward angles (from 120° on) for the energy of 6 eV. Despite the discrepancies observed between the different theoretical results, it is noteworthy that the agreement between SMCPP DCSs and the experimental data measured by Palihawadana et al.8 is excellent at all energies considered here. Such an outcome provides an indication that the calculations performed by using the SMCPP method have a good enough balance both in terms of choosing the set of basis functions used in the description of the molecular target and the strategies for including the effects of polarization and multichannel coupling in the description of the electron-pyrazine elastic scattering process. The fairly good level of accord between the present IAM-SCAR+I and the experimental DCSs for angles typically above 90° should also be noticed. As the pyrazine molecule is an aza-derivative of benzene, we compare our present DCSs with the experimental data obtained by Cho et al.,46 Sanches et al.47 and Kato et al.48 We notice a remarkable agreement between the current theoretical results and the experimental data, where the behavior and magnitude of the DCSs indicate that, at these energies, the electron does not recognize the differences caused by the substitution of two C–H groups by two nitrogen atoms in the benzene ring.
 | ||
| Fig. 4 Differential cross sections for elastic electron scattering by pyrazine at the impact energies of 6, 10, 15, 20, 30 and 50 eV. Solid green line, present SMCPP results obtained according to the best multichannel coupling scheme (4ch at 6 eV, 47ch at 10 eV, 126ch at 15 eV, 135ch at 20 eV and 139ch at 30 and 50 eV); black dashed-dotted line, present IAM-SCAR+I results; solid black line, IAM-SCAR results obtained by Sanz et al.;2 dashed blue line, R-matrix results from Mašín and Gorfinkiel;6 violet circles, experimental measurements reported by Palihawadana et al.;8 measured data for the benzene molecule: orange squares, results reported by Cho et al.;46 red up triangles, results reported by Sanches et al.;47 brown diamonds, results reported by Kato et al.48 | ||
 | ||
| Fig. 5 s-Wave cross section (top frame) and s-wave eigenphase (bottom frame) for elastic electron scattering by the pyrazine molecule. Solid green line, present SMCPP results. | ||
In Fig. 6 we show the excitation functions (that is, the differential cross section at a specific scattering angle as a function of energy) for elastic electron scattering from pyrazine at the angles of 60°, 90° and 120°. Present excitation functions, obtained by means of the SMCPP method considering all 126 states energetically accessible to the molecular target up to 15 eV as open channels, are compared with the measurements performed by Palihawadana et al.8 and the R-matrix results obtained within the SEP and CC levels of approximation as reported by Graves and Gorfinkiel.10 As it would be expected, our results are in better agreement with the R-matrix CC results than with the R-matrix SEP ones. In fact, the inclusion of the multichannel coupling effects in the present SMCPP and in the R-matrix CC calculations gives rise to smoother excitation functions in nice agreement with the measurements from Palihawadana et al.,8 while the R-matrix SEP curves are affected by a number of pseudoresonances and have a magnitude that, in general, overestimates the experimental data for energies above 5 eV. As in the case of the elastic ICS, in the low-energy regime, our elastic excitation functions at 60°, 90° and 120° are dominated by the presence of resonant structures. Below 1.5 eV, all three curves display a clear signature of the first and second low-energy π* resonances. The positions of the peak of these structures are consistent with those observed in the R-matrix results, though slightly shifted to the left and to the right in the case of resonances  and
and  , respectively. The higher lying resonance (around 4.6 eV) is clearly visible in our excitation functions at the angles of 90° and 120°, in line with what was observed by Graves and Gorfinkiel.10 Finally, other structures discerned in the present excitation functions above 5 eV are possibly related to threshold effects due to channels that are energetically accessible to the electron–molecule system during the collision.
, respectively. The higher lying resonance (around 4.6 eV) is clearly visible in our excitation functions at the angles of 90° and 120°, in line with what was observed by Graves and Gorfinkiel.10 Finally, other structures discerned in the present excitation functions above 5 eV are possibly related to threshold effects due to channels that are energetically accessible to the electron–molecule system during the collision.
 | ||
| Fig. 6 Excitation functions for elastic electron scattering from pyrazine at the angles of 60°, 90° and 120°. Solid green line, present SMCPP results; brown squares, experimental data from Palihawadana et al.;8 violet circles, angular DCS measurements taken at discrete energies in the range of interest reported by Palihawadana et al.;8 dashed blue and dotted-dashed cyan lines, R-matrix results of Graves and Gorfinkiel10 (calculated in ref. 6) computed by using the SEP and CC models, respectively. | ||
Fig. 7 and 8 show the electronically inelastic integral cross sections involving the transition from ground state to the first three triplet excited states (3B1u, 3B2u and 3B3u) and to the first three singlet excited states (1B3u, 1B2u and 1B1u) of the pyrazine molecule by electron impact, respectively. These ICSs were obtained according to the 1-channel up to 139-channels calculation carried out by means of the SMCPP method, with the best level of channel coupling used at a given energy range being defined according to the criteria presented in Fig. 2. As a general feature in common, all curves exhibit a steep rise from the opening threshold, reaching a maximum intensity typically between 4 and 10 eV, followed by a rapid decrease in terms of magnitude. Due to the high density of electronically excited states that appear in our calculation below 15 eV, present SMCPP results are strongly affected by a number of structures in this energy range. Some of them were possibly related to the thresholds of the upcoming channels as indicated by the arrows included in the figures. Unfortunately, our efforts to provide the assignment for these structures (Feshbach or core-excited shape type and the corresponding parent states) through inspection of the orbitals involved in the capture of the incident electron were not conclusive and, because of this, no signature for the character of the resonant structures will be supplied here. As can be seen in the left panel of Fig. 7, our ICS for the 1Ag → 3B1u electronic transition is in reasonable agreement with the results reported by Mašín and Gorfinkiel.6 In particular, the weak shoulder appearing in the R-matrix cross section at the energy of 4.6 eV (ascribed by the authors as a resonance with partial core-excited character) is also observed in our ICS as a more defined structure with a peak centered at the energy of 4.66 eV. In addition, we believe that the two structures that appear in our results around the energies of 6.00 and 6.30 eV are, in fact, a single structure affected by a dip due to a singlet state with an opening threshold at 6.16 eV in the MOB-SCI calculation (see Table 3). This feature, commonly referred to as a Wigner cusp in the literature,50 is equally observed in the energy range corresponding to the elastic ICS, albeit with a smaller magnitude. This being the case, such a structure may correspond to the broad peak observed at the energy of 5.7 eV in the R-matrix results provided by Mašín and Gorfinkiel6 and assigned by these authors as a core-excited resonance arising from the B1g symmetry with the parent states 13?B1u and 1?B2u, where the use of the question mark indicates that the authors were not able to characterize completely these states. In the case of the 1Ag → 3B3u electronic transition, the agreement between present SMCPP and previous R-matrix results is poor, especially for energies above 5 eV. However, the structure present in the ICS obtained by Mašín and Gorfinkiel at the energy of 4.6 eV (arising from contributions from two resonances observed in the B2g symmetry) is clearly seen in the present SMC curve centered at around 4.5 eV.
 | ||
| Fig. 7 Integral cross sections for the excitation from the ground state to the 13B1u (3.60 eV), 13B2u (3.98 eV) and 13B3u (4.55 eV) excited states of pyrazine by electron impact. Solid green line, present SMCPP results; dashed blue line, R-matrix results from Mašín and Gorfinkiel.6 | ||
TICS for electron scattering by the pyrazine molecule calculated by using the IAM-SCAR+I method and the BEB model are presented in Fig. 9, for energies ranging from the first ionization thresholds to 1000 eV. Despite some differences, the curves basically show the same energy dependency, namely, a cross section that grows in magnitude from the ionization threshold with a maximum around 70 and 85 eV for the calculations performed with the IAM-SCAR+I methos and with the BEB model, respectively, followed by a smooth decay with increasing energy. The good agreement between these results, added to the fact that BEB model provides TICSs within 10% or more agreement with experimental data,49 gives us confidence that the combination of the BEB TICS with the elastic and inelastic cross sections obtained with the SMCPP method will provide a good estimate of the TCS for electron scattering by the pyrazine molecule.
 | ||
| Fig. 9 Ionization cross sections for electron scattering by the pyrazine molecule. Solid orange line, present BEB result; solid black line, present IAM-SCAR+I result. | ||
In Fig. 10 we present the TCS for electron scattering by the pyrazine molecule. For energies below 15 eV, the contributions coming from elastic and electronically inelastic cross sections to the SMCPP TCS are prevalent, as can be noticed from the comparison with the curve (ICS elastic + inelastic) that represents the sum of these two contributions. Above this energy, the contribution coming from the ionization cross section obtained via BEB model causes an increase in the magnitude of the TCS obtained from the SMCPP method which, with this, now displays a better agreement with present IAM-SCAR+I TCS. However, both SMCPP and IAM-SCAR+I TCS results show a greater magnitude than the theoretical and experimental data reported by Sanz et al.2 in the entire energy range considered in this study. Although the origin for this discrepancy is not apparent, in the case of the SMCPP TCS, a possible explanation is that the TICS was introduced in an ad hoc manner for the TCS estimation and therefore does not compete for flux with the other channels.
 | ||
| Fig. 10 Total cross sections for electron scattering by the pyrazine molecule. Solid brown line, present SMCPP ICS elastic + inelastic; dashed red line, present SMCPP TCS elastic + inelastic + BEB result; solid black line, present IAM-SCAR+I result; dotted orange line, IAM-SCAR result from ref. 2; red triangles, measurements from ref. 2. | ||
4 Conclusions
Elastic and electronically inelastic ICSs and DCSs for electron scattering by the pyrazine molecule were obtained with the SMCPP method within the MOB-SCI approach from 1 up to 139 open channels and with the IAM-SCAR+I method.For the elastic channel, in the results obtained with the SMCPP method, three π* resonances were identified with assignments (character and positions) in good agreement with those previously reported in the literature.3–7 In the energy region below approximately 8 eV, the elastic SMCPP ICS shows good agreement compared to the other theoretical results obtained using the SMC,4,5 R-matrix6,10 and IAM-SCAR2 methods. For energies above 10 eV, the ICS curve obtained by means of the SMCPP method lies consistently below the previous one reported by Winstead and McKoy4,5 (obtained through the SMC method by considering only the elastic channel as open) but displays a good agreement with the experimental data.8 These findings highlight the importance of the inclusion of the multichannel coupling effects in the description of the scattering process as the energy of the incident electron increases. On the other hand, the comparison between present SMCPP and IAM-SCAR+I ICSs did not agree well. In the SMC ICS we identified an RT minimum at 0.28 eV, which was also observed by the previous calculations carried out with the SMC and R-matrix methods. The comparison between the elastic DCSs presented here (obtained with the SMCPP and IAM-SCAR+I methods) and those reported in the literature showed a good agreement. As expected, the inclusion of more channels in the scattering calculations obtained with the SMCPP method reduced the magnitude of the cross section, thus improving the agreement with the experiment8 and with the recent results calculated with the IAM-SCAR+I. In addition, we noticed an excellent agreement in the comparison between the DCSs obtained in this study and the experimental data of the benzene molecule46–48 for energies from 10 to 50 eV. This finding provides an indication that at these energies the incident electron it is not sensitive to the replacement of two C–H groups in the benzene ring by two nitrogen atoms in the para position in pyrazine. Particularly noteworthy is the level of accord with the experimental data. We also observed an excellent agreement when comparing the elastic excitation functions obtained by the SMCPP method and those previously reported in the literature.5,6,10
The ICSs corresponding to the excitation from the ground state to the first three singlet and triplet electronically excited states were also reported using the SMCPP method. We compared the present ICS for the first and third triplet excited states with those calculated via R-matrix method and observed the occurrence of some similar structures. Using previous works obtained with the SMC4,5 and R-matrix6 methods as a reference, we believe that a structure centered at 4.66 eV in the ICS for the 13B1u state to be the contribution of the mixed resonance that we also identified in the elastic case.
The comparison between the total ionization cross section estimated with the BEB model compared to that obtained with the IAM-SCAR+I method are in good agreement with each other. The TCS was also estimated by summing the elastic and electronically inelastic cross sections obtained with the SMCPP method and the total ionization cross section (obtained with the BEB model). Although present SMCPP and IAM-SCAR+I TCS are in reasonable agreement with each other, both overestimate the experimental and theoretical data reported by Sanz et al.2
In summary, the present results show the importance of the multichannel coupling effects in order to provide cross sections for the elastic channel in excellent agreement with the experiment.
Author contributions
M. O. S.: data curation, formal analysis, investigation, methodology, validation, writing – original draft; G. M. M.: data curation, formal analysis, methodology, validation, writing – original draft, writing – review & editing; J. R.: formal analysis, investigation, methodology; F. B.: formal analysis, investigation, methodology; G. G.: conceptualization, formal analysis, investigation, resources, writing – review & editing; M. H. F. B.: conceptualization, formal analysis, investigation, resources, supervision, writing – review & editing; R. F. da C.: conceptualization, formal analysis, investigation, resources, supervision, writing – original draft, writing – review & editing.Conflicts of interest
There are no conflicts to declare.Acknowledgements
M. O. S. and M. H. F. B. acknowledge support from the Brazilian Agency Coordenação de Aperfeiçoamento de Pessoal de Nível Superior (CAPES). R. F. da C. and M. H. F. B. acknowledge support from Conselho Nacional de Desenvolvimento Científico e Tecnológico (CNPq). The authors acknowledge computational support from Professor Carlos M. de Carvalho at LFTC-DFis-UFPR and at LCPAD-UFPR and from Centro Nacional de Processamento de Alto Desempenho em São Paulo (CENAPAD-SP). J. R., F. B. and G. G. acknowledge partial financial support from the Spanish Ministry of Science and Innovation (Project PID2019-104727RB) and the EURAMET project 21GRD02 BIOSPHERE.Notes and references
- M. Juhás and J. Zitko, J. Med. Chem., 2020, 63, 8901 CrossRef.
- A. G. Sanz, M. C. Fuss, F. Blanco, J. D. Gorfinkiel, D. Almeida, F. Ferreira da Silva, P. Limão-Vieira, M. J. Brunger and G. García, J. Chem. Phys., 2013, 139, 184310 CrossRef CAS.
- I. Nenner and G. J. Schulz, J. Chem. Phys., 1975, 62, 1747 CrossRef CAS.
- C. Winstead and V. McKoy, Phys. Rev. Lett., 2007, 98, 113201 CrossRef PubMed.
- C. Winstead and V. McKoy, Phys. Rev. A: At., Mol., Opt. Phys., 2007, 76, 012712 CrossRef.
- Z. Mašín and J. D. Gorfinkiel, J. Chem. Phys., 2011, 135, 144308 CrossRef PubMed.
- Z. Mašín and J. D. Gorfinkiel, J. Chem. Phys., 2012, 137, 204312 CrossRef.
- P. Palihawadana, J. P. Sullivan, S. J. Buckman and M. J. Brunger, J. Chem. Phys., 2012, 137, 204307 CrossRef CAS PubMed.
- M. C. Fuss, A. G. Sanz, F. Blanco, J. C. Oller, P. Limão-Vieira, M. J. Brunger and G. García, J. Phys.: Conf. Ser., 2014, 488, 012048 CrossRef CAS.
- V. Graves and J. D. Gorfinkiel, Eur. Phys. J. D, 2022, 76, 43 CrossRef CAS.
- M. H. F. Bettega, L. G. Ferreira and M. A. P. Lima, Phys. Rev. A: At., Mol., Opt. Phys., 1993, 47, 1111 CrossRef CAS PubMed.
- F. Blanco and G. García, Chem. Phys. Lett., 2015, 635, 321 CrossRef CAS.
- R. F. da Costa, F. J. da Paixão and M. A. P. Lima, J. Phys. B: At., Mol. Opt. Phys., 2005, 38, 4363 CrossRef CAS.
- K. Takatsuka and V. McKoy, Phys. Rev. A: At., Mol., Opt. Phys., 1981, 24, 2473 CrossRef CAS.
- K. Takatsuka and V. McKoy, Phys. Rev. A: At., Mol., Opt. Phys., 1984, 30, 1734 CrossRef CAS.
- G. B. Bachelet, D. R. Hamman and M. Schlüter, Phys. Rev. B: Condens. Matter Mater. Phys., 1982, 26, 4199 CrossRef CAS.
- R. F. da Costa, M. T. do, N. Varella, M. H. F. Bettega and M. A. P. Lima, Eur. Phys. J. D, 2015, 69, 159 CrossRef.
- G. M. J. Barca, C. Bertoni, L. Carrington, D. Datta, N. De Silva, J. E. Deustua, D. G. Fedorov, J. R. Gour, A. O. Gunina, E. Guidez, T. Harville, S. Irle, J. Ivanic, K. Kowalski, S. S. Leang, H. Li, W. Li, J. J. Lutz, I. Magoulas, J. Mato, V. Mironov, H. Nakata, B. Q. Pham, P. Piecuch, D. Poole, S. R. Pruitt, A. P. Rendell, L. B. Roskop, K. Ruedenberg, T. Sattasathuchana, M. W. Schmidt, J. Shen, L. Slipchenko, M. Sosonkina, V. Sundriyal, A. Tiwari, J. L. Galvez Vallejo, B. Westheimer, M. Wloch, P. Xu, F. Zahariev and M. S. Gordon, J. Chem. Phys., 2020, 152, 154102 CrossRef CAS.
- B. M. Bode and M. S. Gordon, J. Mol. Graphics Modell., 1998, 16, 133 CrossRef CAS PubMed.
- M. H. F. Bettega, A. P. P. Natalense, M. A. P. Lima and L. G. Ferreira, Int. J. Quantum Chem., 1996, 60, 821 CrossRef CAS.
- T. H. Dunning Jr., J. Chem. Phys., 1970, 53, 2823 CrossRef.
- W. J. Hunt and W. A. Goddard III, Chem. Phys. Lett., 1969, 3, 414 CrossRef CAS.
- Y. Li, J. Wan and X. Xu, J. Comput. Chem., 2007, 28, 1658 CrossRef CAS.
- P. Weber and J. R. Reimers, J. Phys. Chem. A, 1999, 103, 9821 CrossRef CAS.
- G. Fischer, Chem. Phys. Lett., 1981, 3, 573 CrossRef.
- J. E. D. Bene, J. D. Watts and R. J. Bartlett, J. Chem. Phys., 1997, 106, 6051 CrossRef.
- Y. Okuzawa, M. Fujii and M. Ito, Chem. Phys. Lett., 1990, 171, 341 CrossRef CAS.
- M. Schreiber, M. R. Silva-Junior, S. P. A. Sauer and W. Thiel, J. Chem. Phys., 2008, 128, 134110 CrossRef.
- I. C. Walker and M. H. Palmer, Chem. Phys., 1991, 153, 169 CrossRef CAS.
- A. Bolovinos, P. Tsekeris, J. Philis, E. Pantos and G. Andritsopoulos, J. Mol. Spectrosc., 1984, 103, 240 CrossRef CAS.
- R. E. Turner, V. Vaida, C. A. Molini, J. O. Berg and D. H. Parker, Chem. Phys., 1978, 28, 47 CrossRef CAS.
- D. B. Jones, G. B. da Silva, R. F. C. Neves, H. V. Duque, L. Chiari, E. M. de Oliveira, M. C. A. Lopes, R. F. da Costa, M. T. do, N. Varella, M. H. F. Bettega, M. A. P. Lima and M. J. Brunger, J. Chem. Phys., 2014, 141, 074314 CrossRef CAS PubMed.
- R. F. da Costa, M. T. do N. Varella, M. H. F. Bettega, R. F. C. Neves, M. C. A. Lopes, F. Blanco, G. García, D. B. Jones, M. J. Brunger and M. A. P. Lima, J. Chem. Phys., 2016, 144, 124310 CrossRef PubMed.
- R. F. da Costa, J. C. Ruivo, F. Kossoski, M. T. do, N. Varella, M. H. F. Bettega, D. B. Jones, M. J. Brunger and M. A. P. Lima, J. Chem. Phys., 2018, 149, 174308 CrossRef CAS PubMed.
- R. F. da Costa, M. H. F. Bettega and M. A. P. Lima, Phys. Rev. A: At., Mol., Opt. Phys., 2008, 77, 042723 CrossRef.
- G. M. Moreira, M. H. F. Bettega and R. F. da Costa, J. Appl. Phys., 2021, 129, 203301 CrossRef CAS.
- Y. Kim and M. E. Rudd, Phys. Rev. A: At., Mol., Opt. Phys., 1994, 50, 3954 CrossRef CAS.
- D. M. P. Holland, A. W. Potts, L. Karlsson, M. Stener and P. Decleva, Chem. Phys., 2011, 390, 25 CrossRef CAS.
- Computational Chemistry Comparison and Benchmark DataBase, https://cccbdb.nist.gov/acessed in April 02, 2023.
- F. Blanco and G. García, Phys. Lett. A, 2004, 330, 230 CrossRef CAS.
- A. García-Abenza, A. I. Lozano, L. Álvarez, J. C. Oller, F. Blanco, P. Stokes, R. D. White, J. de Urquijo, P. Limão-Vieira, D. B. Jones, M. J. Brunger and G. García, Eur. Phys. J. D, 2021, 75, 303 CrossRef.
- M. C. Fuss, A. G. Sanz, F. Blanco, J. C. Oller, P. Lim, M. J. Brunger and G. García, Phys. Rev. A: At., Mol., Opt. Phys., 2013, 88, 042702 CrossRef.
- A. I. Lozano, F. F. da Silva, F. Blanco, P. Limão-Vieira and G. García, Chem. Phys. Lett., 2018, 706, 533 CrossRef CAS.
- F. Blanco and G. García, Phys. Rev. A: At., Mol., Opt. Phys., 2003, 67, 022701 CrossRef.
- F. Blanco, L. Ellis-Gibbings and G. García, Chem. Phys. Lett., 2016, 645, 71 CrossRef CAS.
- H. Cho, R. J. Gulley, K. Sunohara, M. Kitajima, L. J. Uhlmann, H. Tanaka and S. J. Buckman, J. Phys. B: At., Mol. Opt. Phys., 2001, 34, 1019 CrossRef CAS.
- I. P. Sanches, R. T. Sugohara, L. Rosani, M.-T. Lee and I. Iga, J. Phys. B: At., Mol. Opt. Phys., 2008, 41, 185202 CrossRef.
- H. Kato, M. C. Garcia, T. Asahina, M. Hoshino, C. Makochekanwa and H. Tanaka, Phys. Rev. A: At., Mol., Opt. Phys., 2009, 79, 62703 CrossRef.
- Y.-K. Kim, W. Hwang, N. M. Weinberger, M. A. Ali and M. E. Rudd, J. Chem. Phys., 1997, 106, 1026 CrossRef CAS; M. A. Ali, Y.-K. Kim, W. Hwang, N. M. Weinberger and M. E. Rudd, J. Chem. Phys., 1997, 106, 9602 CrossRef; H. Nishimura, W. M. Huo, M. A. Ali and Y.-K. Kim, J. Chem. Phys., 1999, 110, 3811 CrossRef.
- E. P. Wigner, Phys. Rev., 1948, 73, 1002 CrossRef CAS.
| This journal is © the Owner Societies 2024 |





