Economical quasi-Newton unitary optimization of electronic orbitals†
Samuel A.
Slattery
 a,
Kshitijkumar A.
Surjuse
a,
Kshitijkumar A.
Surjuse
 a,
Charles C.
Peterson
b,
Deborah A.
Penchoff
a,
Charles C.
Peterson
b,
Deborah A.
Penchoff
 c and
Edward F.
Valeev
c and
Edward F.
Valeev
 *a
*a
aDepartment of Chemistry, Virginia Tech, Blacksburg, VA 24061, USA. E-mail: efv@vt.edu
bOffice of Advanced Research Computing, University of California, Los Angeles, CA 90095, USA
cUT Innovative Computing Laboratory, University of Tennessee, Knoxville, TN 37996, USA
First published on 19th December 2023
Abstract
We present an efficient quasi-Newton orbital solver optimized to reduce the number of gradient evaluations and other computational steps of comparable cost. The solver optimizes orthogonal orbitals by sequences of unitary rotations generated by the (preconditioned) limited-memory Broyden–Fletcher–Goldfarb–Shanno (L-BFGS) algorithm equipped with trust-region step restriction. The low-rank structure of the L-BFGS inverse Hessian is exploited when solving the trust-region problem. The efficiency of the proposed “Quasi-Newton Unitary Optimization with Trust-Region” (QUOTR) solver is compared to that of the standard Roothaan–Hall approach accelerated by the Direct Inversion of Iterative Subspace (DIIS), and other exact and approximate Newton solvers for mean-field (Hartree–Fock and Kohn–Sham) problems.
1 Introduction
Orbital optimization is a fundamental ingredient of the electronic structure methods at all levels of approximation, from 1-body models (Hartree–Fock (HF), Kohn–Sham density functional theory (KS DFT), collectively known as the self-consistent field (SCF) method1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) ‡), to many-body methods (e.g., multiconfiguration self-consistent field (MCSCF)). Despite the long history of innovation,2–29 development of improved orbital optimizers continues to this day.30–35 Although the relevant functionals of the orbitals are nonconvex, and global and local nonconvex optimization is NP-hard,36,37 it is known that many practical orbital optimization problems are easily solved using existing heuristics. For the crucial HF/KS SCF use case, the most popular solvers in the molecular context are based on the Roothaan–Hall (RH) iterative diagonalization of the Fock matrix2,38 augmented by convergence accelerators such as Anderson mixing39 or the closely related direct inversion in the iterative subspace (DIIS) method,10,13,40,41 as well as others.42 However, several issues plague the efficient RH/DIIS heuristics:
‡), to many-body methods (e.g., multiconfiguration self-consistent field (MCSCF)). Despite the long history of innovation,2–29 development of improved orbital optimizers continues to this day.30–35 Although the relevant functionals of the orbitals are nonconvex, and global and local nonconvex optimization is NP-hard,36,37 it is known that many practical orbital optimization problems are easily solved using existing heuristics. For the crucial HF/KS SCF use case, the most popular solvers in the molecular context are based on the Roothaan–Hall (RH) iterative diagonalization of the Fock matrix2,38 augmented by convergence accelerators such as Anderson mixing39 or the closely related direct inversion in the iterative subspace (DIIS) method,10,13,40,41 as well as others.42 However, several issues plague the efficient RH/DIIS heuristics:
• for systems with complex electronic structure (such as molecules far from equilibrium, open-shell systems,32,43 and systems with small HOMO–LUMO gaps28) convergence will be slow,30 erratic, or nonexistent,31,44
• the use of diagonalization produces canonical orbitals whose lack of localization makes them incompatible with fast algorithms for the Fock matrix construction (e.g., using local or sparse density fitting45–47),
• applications to large systems and/or in non-LCAO representations can be bottlenecked by the
• locating non-Aufbau (e.g., excited state) solutions is possible48 but is not robust, and
• even in favorable cases the convergence rate is linear49,50 (i.e., the error is reduced by approximately the same factor each iteration) or perhaps slightly better when accelerated with DIIS;51 this is slower than the quadratic convergence exhibited by, e.g., the Newton method.52
The lack of convergence guarantees is probably the most severe of these in practice. Extensions of the standard RH/DIIS heuristics have been devised to improve the robustness40,53,54 but for challenging cases the user is expected to control the many heuristic solver control parameters that help the convergence (level shift, damping, etc.).
Orbital optimizer solvers that rely on direct energy minimization can address some/all of these concerns and thus have a long history of development.3,5,6,8,9,11,12,14–19,21–29,55 In the molecular mean-field context direct minimization SCF solvers have long been employed as the recommended alternative in the case of convergence problems, used in combination with RH/DIIS to gain superlinear convergence, and to enable reduced-scaling SCF approaches.26,28 Nevertheless, RH/DIIS remains the default SCF solver, not due to its formal advantages, but due to its superior efficiency. This may be puzzling since direct minimization solvers are often demonstrated to converge in as few as (or fewer) iterations than RH/DIIS.21,35 However, the number of iterations is a misleading figure since each update of the orbitals or density matrix may involve multiple energy/gradient evaluations or solving similarly expensive subproblems (such as multiplication of a trial orbital rotation by the orbital Hessian). In other words, the number of gradient evaluations (Fock build equivalents, NF) in a direct minimization solver is typically significantly greater than the number of iterations (NI), whereas in RH/DIIS they are equal. Thus the latter typically involves significantly fewer Fock matrix evaluations, which in most practical applications determines the overall cost.
The objective of this work is to design a quasi-Newton orbital optimizer that minimizes the number of gradient evaluations (and its equivalents) to be as competitive with RH/DIIS as possible, and as robust as possible without the need to adjust the control parameters. Our “Quasi-Newton Unitary Optimization with Trust-Region” (QUOTR) solver uses preconditioned limited-memory Broyden–Fletcher–Goldfarb–Shanno (L-BFGS) algorithm53 step-restricted by trust-region (TR) and leverages the inverse L-BFGS Hessian's low-rank structure to efficiently solve the trust-region update problem.56
The rest of the manuscript is structured as follows. In Section 2 we briefly review the general classes of SCF solvers before describing the theoretical aspects of QUOTR. Next, the implementation of QUOTR is discussed in Section 3. In Section 4 we display solver performance statistics for a standard set of chemical systems and make a comparison to a method that uses information from the “exact” Hessian. Additionally, in Section 4 we illustrate the utility of QUOTR for several prototypical problems where RH/DIIS and other SCF solvers struggle, such as a system with vanishing HOMO–LUMO gap as well as select d- and f-element containing systems. In Section 5 we summarize our findings.
2 Formalism
2.1 Overview of SCF solver approaches
All SCF methods attempt to iteratively minimize the electronic energy E(x) or its Lagrangian counterpart, where x is a set of independent parameters defining the particular method. In practice the minimum is determined by using the energy, its gradient g, and optionally the Hessian B. Starting with an initial (guess) set of parameters x(0) SCF solvers construct improved parameter values using the current energy and its derivatives, (optionally) their values from previous iterations (histories), as well as any optional additional parameters and their histories:| x(k+1) = f({x(k)}, {E(k)}, {g(k)},…) | (1) |
![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) ) is an algorithm, not a simple function. Thus here we only focus on essential common elements of all SCF solvers.
) is an algorithm, not a simple function. Thus here we only focus on essential common elements of all SCF solvers.
Most solvers split the update problem (1) into 2 subproblems by defining the parameter update,
| s(k) ≡ x(k+1) − x(k) = α(k)p(k) | (2) |
| p(k) = g({x(k)}, {E(k)}, {g(k)},…), | (3) |
| α(k) = h({x(k)}, {E(k)}, {g(k)},…). | (4) |
The simplest “2-step” solver is the steepest descent (SD) method3 in which the search direction p(k) is opposite to the current gradient g(k):
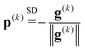 | (5) |
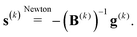 | (6) |
![[g with combining tilde]](https://www.rsc.org/images/entities/b_char_0067_0303.gif) (k) ≡ (B(k)1e)−1g(k). (k) ≡ (B(k)1e)−1g(k). | (7) |
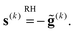 | (8) |
Although some solvers compute the step length separately from the direction, more sophisticated approaches fuse step restriction deeper into the step computation. Indeed, when an underlying quadratic model of the energy exists, it is not natural to simply perform a line search toward the (unrestricted) minimum of the model, considering that the model is known to be locally accurate in all directions. The alternative concept of searching for the minimum of a model in all directions, but restricting the step size to some maximum value, is the key idea of the trust-region (TR) method.23–26,28,31,55,62,63 Two important aspects of any TR method are: how the trust-region is updated between iterations, and how the trust-region problem is solved for the step. The update method that is commonly used is based on an algorithm developed by Fletcher,64 and one of the first true TR applications in quantum chemistry used it in the context of MCSCF.62 A common occurrence of the TR problem in quantum chemistry is within the framework of the AH method; due to the use of full (level-shifted) Hessian in AH the cost of the TR solve is similar to the cost of the unrestricted step.31 Here we use the TR method in the context of the L-BFGS method which allows us to exploit the low-rank structure of the L-BFGS Hessian to essentially eliminate the extra cost of using the TR method.56
2.2 QUOTR: quasi-Newton unitary optimization with trust-region
Our direct minimization SCF solver is a preconditioned quasi-Newton (L-BFGS) solver with TR step restriction. Although its aspects are similar to prior SCF solvers, there are several novel elements:• The optimization is parameterized with a consistent “reference” (epoch) MO basis allowing use of the exact gradient with minimal computation after the Fock matrix is constructed.
• The preconditioner is updated only on some iterations, and it is regularized in a simple way to ensure a positive definite Hessian.
• The low-rank structure of the L-BFGS Hessian is exploited when solving for the quasi-Newton step on the TR boundary.
The QUOTR algorithm is described in Algorithm 1, and its user-controllable parameters are listed in Table 1. The parameters listed have been divided into three groups: free user choice, convergence tweaking, and expert-only controls. The two convergence criteria for the solver can be chosen however the user wishes, within reason. The next three parameters could be adjusted in cases that convergence is not as fast as desired. Finally, the remaining parameters are not recommended to be adjusted. Below we elaborate on each key aspect of the solver.
| Algorithm 1 QUOTR SCF solver | ||
|---|---|---|
| 1: | function QUOTR (C(0)) | |
| 2: | k ← 0, Staken ← false, Rhist ← false, Uepoch ← 1, {E(k), FAO} ← FOCK(C(k)) | |
| 3: | g(k) ← GRAD(FAO, C(k), Uepoch) | ▷eqn (14) |
| 4: | B0 ← PRECONDITIONER(FAO, C(k)) | ▷eqn (24) |
| 5: | while RMS(g(k)) > tcg AND (k = 0 OR ΔE(k) > tce) do | |
| 6: | ifStakenthen | |
| 7: | s(k−1) ← B−1/20![[s with combining tilde]](https://www.rsc.org/images/entities/b_char_0073_0303.gif) (k−1) (k−1) |
|
| 8: | if y(k−1)·s(k−1) > th‖y(k−1) ‖‖s(k−1)‖ then | |
| 9: | ỹ(k−1) ← B−1/20y(k) | |
| 10: | ![[S with combining tilde]](https://www.rsc.org/images/entities/b_char_0053_0303.gif) ← APPEND( ← APPEND(![[S with combining tilde]](https://www.rsc.org/images/entities/b_char_0053_0303.gif) , , ![[s with combining tilde]](https://www.rsc.org/images/entities/b_char_0073_0303.gif) (k−1)), (k−1)), ![[S with combining tilde]](https://www.rsc.org/images/entities/b_char_0053_0303.gif) ← TRIM( ← TRIM(![[S with combining tilde]](https://www.rsc.org/images/entities/b_char_0053_0303.gif) , m), Ỹ ← APPEND(Ỹ, ỹ(k−1)), Ỹ ← TRIM(Ỹ, m) Ṽ ← CONCAT( , m), Ỹ ← APPEND(Ỹ, ỹ(k−1)), Ỹ ← TRIM(Ỹ, m) Ṽ ← CONCAT(![[S with combining tilde]](https://www.rsc.org/images/entities/b_char_0053_0303.gif) , Ỹ) , Ỹ) |
▷update history |
| 11: | end if | |
| 12: | end if | |
| 13: | Rhist ← Δ(k) < tt OR ‖g(k)‖∞ > tb | |
| 14: | if NOT Rhistthen | |
| 15: | ![[g with combining tilde]](https://www.rsc.org/images/entities/b_char_0067_0303.gif) (k) ← B−1/20g(k) (k) ← B−1/20g(k) |
|
| 16: | ifk > 0 AND Ṽ not empty then | ▷BFGS |
| 17: | ![[s with combining tilde]](https://www.rsc.org/images/entities/b_char_0073_0303.gif) (k) ← L-BFGS( (k) ← L-BFGS(![[g with combining tilde]](https://www.rsc.org/images/entities/b_char_0067_0303.gif) (k),Ṽ) (k),Ṽ) |
▷eqn (27) and (29) |
| 18: | if ‖![[s with combining tilde]](https://www.rsc.org/images/entities/i_char_0073_0303.gif) (k)‖> Δ(k)then (k)‖> Δ(k)then |
|
| 19: | ![[s with combining tilde]](https://www.rsc.org/images/entities/b_char_0073_0303.gif) (k) ← TRSTEP(Δ(k), (k) ← TRSTEP(Δ(k), ![[g with combining tilde]](https://www.rsc.org/images/entities/b_char_0067_0303.gif) (k), (k), ![[s with combining tilde]](https://www.rsc.org/images/entities/b_char_0073_0303.gif) (k), Ṽ) (k), Ṽ) |
▷Algorithm 2 |
| 20: | end if | |
| 21: | q(k) ← eqn (38), Rhist ← q(k) > 0 | ▷energy increase predicted |
| 22: | else | |
| 23: | ![[s with combining tilde]](https://www.rsc.org/images/entities/b_char_0073_0303.gif) (k) ← − (k) ← −![[g with combining tilde]](https://www.rsc.org/images/entities/b_char_0067_0303.gif) (k) (k) |
▷steepest descent |
| 24: | end if | |
| 25: | end if | |
| 26: | ifRhistthen | ▷new epoch |
| 27: | if not Stakenthen | |
| 28: | {E(k), FAO} ← FOCK(C(k)) | |
| 29: | end if | |
| 30: | Ṽ ← {![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) }, Uepoch ← 1, B0 ← PRECONDITIONER(FAO, C(k)), g(k) ← GRAD(FAO, C(k), Uepoch) }, Uepoch ← 1, B0 ← PRECONDITIONER(FAO, C(k)), g(k) ← GRAD(FAO, C(k), Uepoch) |
▷steepest descent |
| 31: |
![[g with combining tilde]](https://www.rsc.org/images/entities/b_char_0067_0303.gif) (k) ← B−1/20g(k),
(k) ← B−1/20g(k), ![[s with combining tilde]](https://www.rsc.org/images/entities/b_char_0073_0303.gif) (k) ← − (k) ← −![[g with combining tilde]](https://www.rsc.org/images/entities/b_char_0067_0303.gif) (k) (k) |
|
| 32: | end if | |
| 33: | ifk = 0 OR Ṽ is empty then | ▷line search |
| 34: | α(k) ← LINESEARCH(![[s with combining tilde]](https://www.rsc.org/images/entities/b_char_0073_0303.gif) (k)) (k)) |
▷Section 2.2.4 |
| 35: | ![[s with combining tilde]](https://www.rsc.org/images/entities/b_char_0073_0303.gif) (k) ← α(k) (k) ← α(k)![[s with combining tilde]](https://www.rsc.org/images/entities/b_char_0073_0303.gif) (k)/‖ (k)/‖![[s with combining tilde]](https://www.rsc.org/images/entities/b_char_0073_0303.gif) (k)‖, Δ(k) ← α(k) (k)‖, Δ(k) ← α(k) |
|
| 36: | end if | |
| 37: | Staken ← true, s(k) ← B−1/20![[s with combining tilde]](https://www.rsc.org/images/entities/b_char_0073_0303.gif) (k) (k) |
▷attempt step |
| 38: | U(k) ← UNITARYSTEP (s(k), Uepoch) | ▷eqn (16) and (12) |
| 39: | C(k+1) ← C(k)U(k), {E(k+1), FAO} ← FOCK(C(k+1)), ΔE(k) ← E(k+1) − E(k) | |
| 40: | ifk > 0 AND Ṽ not empty then | |
| 41: | ρ(k) ← ΔE(k)/q(k) | |
| 42: | Staken ← ρ(k) ≥ τ1 OR ΔE(k) ≤ t0 | |
| 43: | ifρ(k) < τ2then | |
| 44: | Δ(k+1) ← MIN(η1Δ(k), η2‖![[s with combining tilde]](https://www.rsc.org/images/entities/i_char_0073_0303.gif) (k)‖) (k)‖) |
|
| 45: | else if (ρ(k) > τ3 AND ‖![[s with combining tilde]](https://www.rsc.org/images/entities/i_char_0073_0303.gif) (k)‖ > η3Δ(k)) then (k)‖ > η3Δ(k)) then |
|
| 46: | Δ(k+1) ← η4Δ(k) | |
| 47: | end if | |
| 48: | else | |
| 49: | Staken ← ΔE(k) ≤ t0 | |
| 50: | ifStakenthen | |
| 51: | Δ(k+1) ← ‖![[s with combining tilde]](https://www.rsc.org/images/entities/b_char_0073_0303.gif) (k)‖ (k)‖ |
|
| 52: | end if | |
| 53: | end if | |
| 54: | ifStakenthen | |
| 55: | k ← k + 1, Uepoch ← UepochU(k−1), g(k) ← GRAD(FAO, C(k), Uepoch), y(k−1) ← g(k) − g(k−1) | ▷accept step |
| 56: | else | |
| 57: | Δ(k) ← Δ(k+1) | ▷reject step, change TR |
| 58: | end if | |
| 59: | end while | |
| 60: | return C(k) | |
| 61: | end function | |
| Description | Symbol | Value |
|---|---|---|
| Energy convergence threshold | t ce | 10−9 |
| Gradient convergence threshold | t cg | 10−5 |
| L-BFGS start threshold | t b | 0.1 |
| Max history size | m | 8 |
| Regularizer threshold | t r | 0.25 |
| History keep threshold | t h | 10−5 |
| Exponential tolerance | t e | 10−15 |
| Compare zero threshold | t 0 | 10−11 |
| Line search fitting range shrink factor | α fit,shrink | 1/2 |
| Minimum TR tolerance | t t | 10−10 |
| TR step accept threshold | τ 1 | 0 |
| TR shrink threshold | τ 2 | 0.25 |
| TR expand threshold | τ 3 | 0.75 |
| TR shrink factor | η 1 | 0.25 |
| TR shrink by step factor | η 2 | 0.5 |
| TR expand check factor | η 3 | 0.8 |
| TR expand by factor | η 4 | 2.0 |
We seek a unitary matrix, Ū, that transforms the initial (guess) set of orthonormal orbitals, C(0), into the target solution, ![[C with combining macron]](https://www.rsc.org/images/entities/b_char_0043_0304.gif) .
.
![[C with combining macron]](https://www.rsc.org/images/entities/b_char_0043_0304.gif) = C(0)Ū = C(0)Ū | (9) |
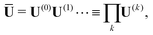 | (10) |
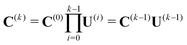 | (11) |
| U(k) = exp(σ(k)), | (12) |
It is important to express both the gradients and parameter updates for each iteration in the same coordinate frame (basis). In the context of the DIIS methods this is usually done by working in the AO basis (e.g., as noted by Pulay in ref. 13 “In order to be useful for extrapolation purposes, [the Fock] matrices (one in each iteration step) must be transformed to a common basis, e.g., to the original AO basis set.”). Here the working frame is defined by the initial orthogonal MO basis for each epoch (namely, the sequence of iterations whose history is used to construct the current approximation to the Hessian). The gradient of the energy evaluated with orbitals C(k) with respect to their arbitrary rotation σ(k) has the familiar form when expressed in terms of C(k):
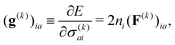 | (13) |
| g(k)epoch ≡ 2ni[F(k)epoch, P(k)epoch]. | (14) |
| P(k)epoch = U(k)epochP(U(k)epoch)T, | (15) |
Note that σ(k) is a matrix, but only some of its elements can be varied independently. It is also traditional in applied mathematics literature to arrange the parameters of multivariate functions into vectors. Thus it is appropriate to comment on the detailed relationship of σ(k) and the corresponding step vector s(k). Due to the antihermiticity of σ, σpq = − σqp, hence for real orbitals (which we assume here without any loss of generality) only the lower elements are independent. Although for 1-body SCF methods considered here elements of the gradient matrix are nonzero only between occupied and unoccupied orbitals, hence one would think that only (σ)ia elements need to be independently varied, this is only true for σ expressed in the current MO basis (i.e., the basis defining the density). To be able to work in an arbitrary (e.g., epoch) basis all lower-triangular elements of σ thus must be considered independent. For an MO basis with no orbitals, this means that the number of independent parameters is n ≡ no (no − 1)/2, assuming no additional symmetries are taken into account. In the spin-unrestricted case, the sigma elements for the separate alpha and beta spin MOs are simply concatenated into one vector. Notice that the gradient matrix in eqn (14) is also antihermitian, with the same structure as σ. Thus, we can map the matrix elements of the gradient to a vector in exactly the same way as for the matrix elements of σ, using only the lower (or upper) triangle. We use the symbol s(k) for the vector version of σ(k); for the gradient henceforth only its vector form, g(k), is used.
The steps and gradient differences are the ingredients for the L-BFGS update to the Hessian and its inverse. All quantities throughout each epoch (see below) are kept in the epoch “reference” basis to make application of L-BFGS and TR consistent. However, when a new step s(k) is proposed, to convert it to the unitary rotation viaeqn (12) it must be transformed to the current MO basis, via
| σ(k) = U(k−1)Tepochσ(k)epochU(k−1)epoch. | (16) |
| B(k)BFGS = B0 − V(k)B(W(k))−1V(k)TB | (17) |
| H(k)BFGS = H0 + V(k)HM(k)V(k)TH | (18) |
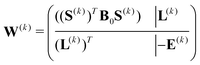 | (19) |
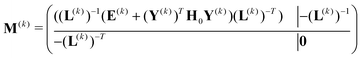 | (20) |
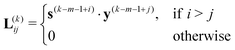 | (21) |
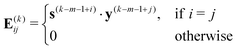 | (22) |
The quasi-Newton step, s(k) = −H(k)BFGSg(k), is calculated by multiplying the inverse L-BFGS Hessian of eqn (18) with the negative of the gradient. Thus, the factorized form of eqn (18) makes the task of calculating the quasi-Newton step simply a matter of a few matrix-vector multiplications. Note that although we only need the inverse Hessian to compute the quasi-Newton step, the Hessian is used to compute the energy decrease predicted by the quadratic model. This is needed for determining how the TR is to be updated between iterations as described in Section 2.2.3.
As is well known, due to the large (and increasing with the basis) condition number of the Hessian it is important to use a preconditioner to achieve competitive convergence.18,19,21 Since the orbital Hessian is often diagonally dominant and its 1-electron (Fock) contributions are cheap to evaluate, we define B0 in terms of the diagonal elements of the 1-electron component of the exact Hessian, B1e, whose unique nonzero elements in the current MO basis are
| (B1e)(ia)(jb) = 2ni(Fabδij − Fijδab). | (23) |
| (B0)(ia)(ia) = 2nir(Faa − Fii); | (24) |
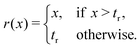 | (25) |
An alternative and perhaps more conventional view of the preconditioner is that it is a basis transformation that makes the diagonal part of the L-BFGS Hessian or its inverse closer to an identity matrix. To see how this view relates to the diagonal Hessian, consider the following transformation of the quasi-Newton equation: s = −Hg (omitting iteration index). Multiply both sides of the equation by B01/2 and insert 1 = B01/2B−1/20 (which is clearly acceptable because the diagonal matrix B0 is guaranteed to be positive definite due to the regularizer) between the inverse Hessian and the gradient, to get an equivalent equation.
| B01/2s = − (B01/2HB01/2)B0−1/2g. | (26) |
![[s with combining tilde]](https://www.rsc.org/images/entities/b_char_0073_0303.gif) ≡ B01/2s,
≡ B01/2s, ![[g with combining tilde]](https://www.rsc.org/images/entities/b_char_0067_0303.gif) ≡ B0−1/2g, and
≡ B0−1/2g, and ![[H with combining tilde]](https://www.rsc.org/images/entities/b_char_0048_0303.gif) ≡ B01/2HB01/2 identified as the step, gradient, and inverse Hessian, respectively, in the “preconditioned” basis (henceforth denoted by the tilde), the Newton step (eqn (26)) becomes
≡ B01/2HB01/2 identified as the step, gradient, and inverse Hessian, respectively, in the “preconditioned” basis (henceforth denoted by the tilde), the Newton step (eqn (26)) becomes![[s with combining tilde]](https://www.rsc.org/images/entities/char_0073_0303.gif) = − = −![[H with combining tilde]](https://www.rsc.org/images/entities/b_char_0048_0303.gif) ![[g with combining tilde]](https://www.rsc.org/images/entities/b_char_0067_0303.gif) . . | (27) |
![[B with combining tilde]](https://www.rsc.org/images/entities/b_char_0042_0303.gif) BFGS ≡ B0−1/2BBFGSB0−1/2 = 1 − Ṽ(W)−1ṼT, BFGS ≡ B0−1/2BBFGSB0−1/2 = 1 − Ṽ(W)−1ṼT, | (28) |
![[H with combining tilde]](https://www.rsc.org/images/entities/b_char_0048_0303.gif) BFGS ≡ B01/2HBFGSB01/2 = 1 + ṼMṼT, BFGS ≡ B01/2HBFGSB01/2 = 1 + ṼMṼT, | (29) |
| Ṽ ≡ B01/2VH = B0−1/2VB. | (30) |
![[s with combining tilde]](https://www.rsc.org/images/entities/b_char_0073_0303.gif) (k).
(k).
Here is probably a good place to summarize the steps to obtain the unitary rotation at iteration k, since there are now quite a few layers.
![[s with combining tilde]](https://www.rsc.org/images/entities/b_char_0073_0303.gif) (k) → s(k)→ σ(k)epoch→ σ(k)→ U(k) (k) → s(k)→ σ(k)epoch→ σ(k)→ U(k) | (31) |
| s(k)·y(k) > th‖s(k)‖‖y(k)‖. | (32) |
![[s with combining tilde]](https://www.rsc.org/images/entities/b_char_0073_0303.gif) (k), ỹ(k)} are not added to the history. Here we used th = 10−5.
(k), ỹ(k)} are not added to the history. Here we used th = 10−5.
![[s with combining tilde]](https://www.rsc.org/images/entities/b_char_0073_0303.gif) (k) is TR-acceptable if
(k) is TR-acceptable if‖![[s with combining tilde]](https://www.rsc.org/images/entities/b_char_0073_0303.gif) (k)‖ ≤ Δ(k), (k)‖ ≤ Δ(k), | (33) |
When the quasi-Newton step does not satisfy eqn (33), we solve for the optimal step that is within the TR, which must be on the TR boundary: ‖![[s with combining tilde]](https://www.rsc.org/images/entities/b_char_0073_0303.gif) (k)‖ = Δ(k). This is done by finding an optimal level-shift, σ, which satisfies the two conditions:56
(k)‖ = Δ(k). This is done by finding an optimal level-shift, σ, which satisfies the two conditions:56
(![[B with combining tilde]](https://www.rsc.org/images/entities/b_char_0042_0303.gif) BFGS + σ1) BFGS + σ1)![[s with combining tilde]](https://www.rsc.org/images/entities/b_char_0073_0303.gif) (k) = − (k) = −![[g with combining tilde]](https://www.rsc.org/images/entities/b_char_0067_0303.gif) (k) (k) | (34a) |
‖![[s with combining tilde]](https://www.rsc.org/images/entities/b_char_0073_0303.gif) (k)‖ = Δ(k). (k)‖ = Δ(k). | (34b) |
| Description | Symbol | Value |
|---|---|---|
| Initial guess σ | σ init | 0.0 |
| Convergence criterion 1 | T 1 | 10−4 |
| Convergence criterion 2 | T 2 | 10−7 |
| Maximum iterations | i max | 500 |
| Sigma modify factor | F 0 | 1.1 |
The TR solver in QUOTR is based on the solver described by Burdakov et al.56 that leverages the low-rank structure of the L-BFGS Hessian. The advantage of this approach is that the cost of each TR solver iteration is trivial compared to the conventional TR formulation with exact Hessian in which each iteration has a cost similar to that of the gradient evaluation. The TR solver algorithm is outlined in Algorithm 2 and its user-controllable parameters are given in Table 2. Although the parameters for the TR solver could be adjusted, we recommend keeping them as listed. The initial guess for σ is best kept at zero, as this will help convergence in cases where the optimal level shift is a very small value. Changing parameters T1,2 only impacts when the TR problem is considered solved, and tightening the values given is not expected to have a significant impact on QUOTR overall.
| Algorithm 2. Trust-region step update | ||
|---|---|---|
| 1: |
function TRSTEP (Δ, ![[g with combining tilde]](https://www.rsc.org/images/entities/b_char_0067_0303.gif) , , ![[s with combining tilde]](https://www.rsc.org/images/entities/b_char_0073_0303.gif) , Ṽ) , Ṽ) |
|
| 2: | σ ← σinit, C ← false, F ← F0 | ▷initialize |
| 3: | G ← ṼTṼ | |
| 4: | {R, R−1} ← ORTHOGONALIZE(G) | ▷eqn (37) |
| 5: | R−1W−1(R−1)T = UΛUT | ▷diagonalize |
| 6: | P‖ = ṼRU | ▷eqn (12)57 |
| 7: | ![[g with combining tilde]](https://www.rsc.org/images/entities/b_char_0067_0303.gif) ‖ = (P‖)T ‖ = (P‖)T![[g with combining tilde]](https://www.rsc.org/images/entities/b_char_0067_0303.gif) |
|
| 8: | rmax = dim(![[g with combining tilde]](https://www.rsc.org/images/entities/b_char_0067_0303.gif) ‖) ‖) |
|
| 9: | ‖![[g with combining tilde]](https://www.rsc.org/images/entities/b_char_0067_0303.gif) ⊥‖2 = ‖ ⊥‖2 = ‖![[g with combining tilde]](https://www.rsc.org/images/entities/b_char_0067_0303.gif) ‖2− ‖ ‖2− ‖![[g with combining tilde]](https://www.rsc.org/images/entities/b_char_0067_0303.gif) ‖‖2 ‖‖2 |
▷eqn (25)57 |
| 10: | i = 0 | |
| 11: | while not C AND i < imaxdo | |
| 12: | ṽ‖ ← − (Λ + σ1)−1![[g with combining tilde]](https://www.rsc.org/images/entities/b_char_0067_0303.gif) ‖ ‖ |
▷eqn (16)57 |
| 13: | ‖ṽ‖ ← (‖ṽ‖‖2 + ‖![[g with combining tilde]](https://www.rsc.org/images/entities/b_char_0067_0303.gif) ⊥‖2/(1 + σ)2)1/2 ⊥‖2/(1 + σ)2)1/2 |
▷eqn (20)57 |
| 14: | vtemp ← − ‖![[g with combining tilde]](https://www.rsc.org/images/entities/b_char_0067_0303.gif) ⊥‖2/(1 + σ)3 ⊥‖2/(1 + σ)3 |
▷eqn (21)57 |
| 15: | r ← 0 | |
| 16: | whiler < rmaxdo | |
| 17: | vtemp ← vtemp− (![[g with combining tilde]](https://www.rsc.org/images/entities/b_char_0067_0303.gif) ‖[r])2/ (1 + σ)3 ‖[r])2/ (1 + σ)3 |
▷eqn (21)57 |
| 18: | r ← r + 1 | |
| 19: | end while | |
| 20: | 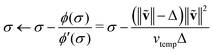 |
▷eqn (19)57 |
| 21: | ifσ ∈ {σ−1, σ−2, σ−3, σ−4} then | ▷stabilize |
| 22: | 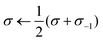 |
|
| 23: | end if | |
| 24: | {σ−1, σ−2, σ−3, σ−4} ← {σ, σ−1, σ−2, σ−3} | |
| 25: | if ‖|ṽ‖−Δ| ≤ min (T1 Δ, T2) then | ▷converged? |
| 26: | ifσ < 0 then | ▷wrong sign? |
| 27: | σ ← −σF | ▷reset σ |
| 28: | F ← FF0 | |
| 29: | C = false | |
| 30: | else ifσ ≥ 0 then | |
| 31: | C = true | ▷converged |
| 32: | end if | |
| 33: | end if | |
| 34: | i ← i + 1 | |
| 35: | end while | |
| 36: | ṽ‖ ← −(Λ + σ1)−1![[g with combining tilde]](https://www.rsc.org/images/entities/b_char_0067_0303.gif) ‖ ‖ |
▷eqn (16)57 |
| 37: | ![[s with combining tilde]](https://www.rsc.org/images/entities/b_char_0073_0303.gif) = P‖(ṽ‖ + (1 + σ)−1 = P‖(ṽ‖ + (1 + σ)−1![[g with combining tilde]](https://www.rsc.org/images/entities/b_char_0067_0303.gif) ‖) − (1 + σ)−1 ‖) − (1 + σ)−1![[g with combining tilde]](https://www.rsc.org/images/entities/b_char_0067_0303.gif) |
▷eqn (27)57 |
| 38: | ifi ≥ imaxthen | |
| 39: | ![[s with combining tilde]](https://www.rsc.org/images/entities/b_char_0073_0303.gif) ← ← ![[s with combining tilde]](https://www.rsc.org/images/entities/b_char_0073_0303.gif) given given |
▷use original step |
| 40: | end if | |
| 41: | return ![[s with combining tilde]](https://www.rsc.org/images/entities/b_char_0073_0303.gif) |
|
| 42: | end function | |
We have modified the algorithm of ref. 56 in several ways. First, the use of rank-revealing Cholesky decomposition in ref. 56 (see text around their eqn (9)) is replaced by the use of Löwdin canonical orthogonalization.70 Inserting eqn (28) in eqn (34a) produces
((1 + σ) 1 − Ṽ(W)−1ṼT)![[s with combining tilde]](https://www.rsc.org/images/entities/b_char_0073_0303.gif) (k) = − (k) = −![[g with combining tilde]](https://www.rsc.org/images/entities/b_char_0067_0303.gif) (k). (k). | (35) |
| RTGR = 1 | (36) |
| G = UgUT, gi > ε | (37a) |
| R = Ug−1/2 | (37b) |
| R−1 = (Ug1/2)T | (37c) |
• we enforce σ > 0,
• we prevent some infinite loops by averaging σ with the previous value if that value of σ occurred in the last four iterations,
• we simplify convergence criteria to merely check that step size is within a threshold difference of Δ.
Once a TR-compliant step has been determined energy (and gradient) is evaluated at the displaced geometry and compared to the quadratic model estimate
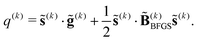 | (38) |
Note that the TR problem is always solved in the preconditioned epoch basis; this is yet another reason to use the same basis throughout the epoch. When a new epoch starts and the preconditioner and the epoch basis change we cannot simply carry over the TR value between epochs. Thus, however, since each epoch starts with a line search step, this produces a fresh initial estimate of the trust-radius valid in that epoch's preconditioned basis.
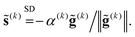 | (39) |
| E(α) ≈ Efit(α) = aα3 + bα2 + cα + d | (40) |
Choosing αfit is crucial for the success of the line search. Due to the fact that the exponential parametrization of the unitary is periodic, it is straightforward to estimate the shortest period of oscillation by finding the largest (magnitude) eigenvalue ωmax of the σ matrix (or matrices, for the unrestricted case) corresponding to the SD direction −![[g with combining tilde]](https://www.rsc.org/images/entities/b_char_0067_0303.gif) (k)/‖
(k)/‖![[g with combining tilde]](https://www.rsc.org/images/entities/b_char_0067_0303.gif) (k)‖.71 This results in
(k)‖.71 This results in
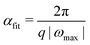 | (41) |
The minimum of Efit(α) is found by solving the quadratic equation dEfit/dα = 0. Each of its two solutions, αmin, is checked for sanity in turn; it is expected to be real, positive, resulting in a decrease of energy (i.e., Efit(αmin) < Efit(0)), and the second derivative of Efit at αmin should be positive. Since a 3rd-order polynomial can have at most one local minimum, the solution with the smallest positive α is checked whether it satisfies all of these criteria. The failure to meet these conditions indicates a poor quality of the fit, and in such case the polynomial fit is recomputed with αfit scaled by αfit,shrink = 1/2. Note that the energy decrease criterion is checked only after building the new Fock matrix, while the other conditions can be checked immediately after solving the quadratic equation.
Here's a brief recap of all situations that cause history reset:
• The gradient is too large (‖g(k)‖∞ > tb)
• The TR is too small (Δ(k) < tt)
• The quadratic model predicts energy increase (q(k) > 0)
The first 2 of these situations are detected before the L-BFGS step is constructed, allowing the solver to skip this step to go directly to re-building the preconditioner and on to perform the line search. The last situation is only determined after the L-BFGS step is calculated.
3 Technical details
The QUOTR solver was implemented in a developmental version of the Massively Parallel Quantum Chemistry (MPQC) version 4 program package.77 The default values for parameters in Tables 1 and 2 were used throughout, unless noted. The orbital bases sets used were 6-31G*,78–84 6-31G**,80 6-311++G**,85–88 def2-TZVPP,89 cc-pVTZ-DK,90 and cc-pVTZ-X2C.91 Density fitting, where noted, used the def2-universal-J basis.92 The extended Hückel initial guess was constructed in the Huzinaga MINI basis,93 then projected onto the orbital basis. Calculations on the f-element containing system in Section 4.2.3 did not use the extended Hückel guess to avoid the uncertainties about its quality in such heavy systems. Instead, we use a superposition of minimal atomic basis guess densities to construct the initial Fock matrix in the orbital basis (without projection), followed by diagonalization. The minimal AO basis used the corresponding subset of the ANO-DK3 basis94 on Fm atom and the MINI AO basis on the other atoms. The same minimal bases were used to compute the atomic charges in Section 4.2.3, using the pseudoinverse method described in ref. 95. The orbital bases used in the relativistic calculations employed cc-pVTZ-X2C on the Fm atom, and cc-pVTZ-DK on all other atoms.Hartree–Fock calculations were performed in Section 4.1 for the G2 set,96 the geometries for which were obtained from the Gaussian output files on the NIST website97 with the exception of four systems that were not available with the correct method (MP2 = FULL/6-31G*). For the four systems that were not available from NIST (acetamide, furan, SiH2-triplet and 2-butyne) Gaussian 0998 was used to obtain the geometry. The G2-1 set consists of 55 systems and is a subset of G2-2, which consists of a total of 148 systems.96
Henceforth RH/DIIS will be denoted simply by DIIS. Unless explicitly mentioned, DIIS results were obtained with its implementation in MPQC using the default parameters: keeping the 5 most recent pairs of Fock matrix and error vectors for the extrapolation, and no damping applied.
The KS DFT implementation in MPQC uses GauXC99 (which uses LibXC100) for calculation of the exchange–correlation potentials and energies. The integration grid used for the 1PLW calculations in Section 4.2.1 was the “ultrafine” grid (99 radial Mura–Knowles101 points, 590 angular Lebedev–Laikov102 points). All other KS DFT calculations used the “superfine” grid which has 250 radial points and 974 angular points for all atoms except hydrogen, which has 175 radial points. The particular parameterization we use for LDA is Slater Exchange103 with VWN RPA.104 For the B3LYP calculations on the Cr systems in Section 4.2.2, we use VWN3 for the local correlation functional104 to match PySCF. The structure of the neuropeptide, 1PLW,105 was obtained from the Protein Data Bank (PDB).106
Calculations using KDIIS53 for SCF acceleration on the CrC and Cr2 systems in Section 4.2.2 were performed with the Orca program system, version 5.0.4.107 Additionally, the DIIS implementation from Orca was also used for these systems instead of the MPQC version. The bond length used for both of these diatomic systems is 2 angstrom, as has been used in previous studies.20,31 Orbitals were plotted for Cr2 with Jmol; due to its inability to read in Molden files with l = 4 (g) AOs, the calculations (only for the visualizations) were performed with def2-TZVPP with g-type AOs removed.
Full (2-component) and spin-free (1-component) 1-electron X2C Hamiltonians were implemented in MPQC using the standard formalism.108,109 No empirical scaling was utilized to emulate the mean-field effects on the Dirac Hamiltonian. For the sake of comparison with the results of ref. 110 only the spin-free X2C Hamiltonian was used here.
4 Results and discussion
4.1 Easy testset: G2 data set
Performance of QUOTR was first assessed for converging Hartree–Fock wave functions (RHF and UHF for closed- and open-shell systems, respectively) and compared to DIIS, as well as published literature data for three second-order solvers, GDM,21 ETDM,33 and CIAH.30 The computations where convergence was not achieved in 256 iterations (333 for ETDM, 50 macroiterations for CIAH) were removed from the statistical values and aggregated in the “no convergence” row. The number of “local minima” for each solver was determined by comparing converged energies to the lowest energy that we obtained, except for the GDM and ETDM results (which are the numbers reported by the respective publications). All calculations with QUOTR and DIIS used the extended Hückel guess with perturbed valence orbitals. Although we attempted to compare solvers as faithfully as possible, due to lack of direct access to the source code and/or implementation of GDM and ETDM this was not always possible (see below).Table 3 reports the number of Fock matrix evaluations NF (“Fock builds”) and the number of solver iterations NI. Due to the different performance statistics reported in the literature for GDM and ETDM, three different sets of G2 calculations were performed.
| G2-1/6-311++G** | G2-2/6-31G** | G2-2/6-31G* | |||||||
|---|---|---|---|---|---|---|---|---|---|
| DIIS | QUOTR | GDMa | DIIS | QUOTR | ETDMb | DIIS | QUOTR | CIAHc | |
| a Geometric direct minimization.21 b Exponential transformation direct minimization.33 c Co-iterative augmented Hessian.30 | |||||||||
| N F: mean | 15.2 | 26.8 | — | 13.6 | 20.5 | (17) | 15.3 | 19.4 | 34.5 |
| N F: median | 14 | 20 | — | 12 | 17 | (17) | 12 | 16 | 30 |
| N F: max | 40 | 136 | — | 64 | 107 | 72 | 234 | 69 | 77 |
| N I: mean | 15.2 | 20.5 | 16.3 | 13.6 | 15.3 | — | 15.3 | 14.2 | 2.9 |
| N I: median | 14 | 15 | — | 12 | 12 | — | 12 | 12 | 3 |
| N I: max | 40 | 107 | 42 | 64 | 96 | — | 234 | 55 | 5 |
| Local minima | 3 | 0 | 5 | 5 | 0 | — | 8 | 0 | 4 |
| No convergence | 2 | 0 | 0 | 2 | 0 | 0 | 1 | 0 | 1 |
To make the comparison with GDM as faithful as possible, we used the same orbital basis set and convergence criteria (1 × 10−10Eh for the energy difference between iterations and 1 × 10−7 for the RMS of the unique gradient elements). Our initial guess orbitals were likely similar; however, we did apply a random unitary perturbation to the valence orbitals, which was not done by GDM. The average number of iterations taken by QUOTR is about 4 more than GDM, and it has a higher max at 107 for NO followed by P2 at 66 iterations. Notice, though, that GDM found 5 local minima relative to the lowest energy that they could obtain in any of their calculations. Thus, while the convergence with QUOTR takes more iterations, QUOTR appears to be more robust than GDM. Unfortunately, the number of Fock builds used by GDM was not reported in ref. 21. The computational cost of QUOTR is fairly competitive with DIIS, with a median number of Fock builds being 20 and 14, respectively; note that the latter is close to the reported performance of DIIS in the GDM paper.21 The only systems that did not converge for DIIS in 256 iterations were HCO and Si2. There were no local minima found by QUOTR (relative to the DIIS solution) but for 3 systems (CN, O2 and CH singlet) QUOTR got a significantly lower energy than DIIS. Also note that for 5 systems GDM landed on local minima too.21 Thus for the G2-1/6-311++G** test set QUOTR was found to be more robust than DIIS and GDM, albeit with a slightly worse performance.
Comparison to ETDM was less precise for a few reasons. The data presented in Table 3 for ETDM used KS DFT (PBE) and a different basis (double-zeta polarized numerical atomic orbital basis equipped with projector augmented wave (PAW) for the inner region). Here we performed all-electron SCF in the 6-31G** Gaussian AO basis, because it is a double-zeta basis with polarization functions on all atoms, so should be similar to the basis used by ETDM. Also, the open-shell KS DFT implementation in MPQC is not yet finalized, hence we are comparing QUOTR HF SCF to ETDM PBE SCF. Lastly, QUOTR set m = 3 to make the comparison with ETDM as faithful as possible. The average number of iterations (unclear if it is mean or median) reported for ETDM was 17, which compares well with the median of QUOTR at 17. Therefore, we conclude that QUOTR is roughly equivalent in computational cost to ETDM. Notice also that 5 of the DIIS solutions are local minima relative to QUOTR.
With access to the implementation of CIAH in PySCF111 we were able to perform a direct comparison with QUOTR (Table 3). Note that the number of iterations is sometimes used35 to compare the cost of the AH-based methods to that of RH/DIIS and quasi-Newton approaches; such comparison is misleading. Each iteration of the AH approach, in addition to the evaluation of the gradient, involves iteratively solving an eigenproblem defining the optimal shift; thus the cost of each iteration is determined by the cost of multiplying a trial step vector by the (exact) Hessian times the number of iterations of the eigensolver. The cost of applying exact Hessian to the trial step is comparable to the cost of the Fock matrix evaluation (in fact many programs will use the same machinery for both). Thus the performance assessment of CIAH and other AH-based methods will report the number of Fock build equivalents, NF. For CIAH the total number of Fock build equivalents is the sum of the key frames (KF) and coulomb/exchange (JK) calls, with the former accounting for the cost of the exact evaluation of the gradient and the latter the cost of Hessian-step products.30
The convergence statistics in Table 3 indicate that the median NF for QUOTR is roughly half of the median NF for CIAH. QUOTR was also more robust: for one system (HCl) CIAH did not converge as it could not reduce the gradient norm below 1.2 × 10−6 and failed to make progress until the maximum number of iterations was reached (50). In four other systems (CH, O2, NO2 and Si2) CIAH landed on a local minimum, as indicated by the substantially lower energies obtained with QUOTR. For the rest of the systems, CIAH and QUOTR agreed within 1 × 10−9Eh. The systems that took the most Fock build equivalents to converge with QUOTR and CIAH were Si2 and NF3, respectively, requiring 69 and 77.
As expected, RH/DIIS is on average slightly faster than QUOTR, but is far less robust, with 8 local minima and 1 system where converged solution could not be obtained. This demonstrated proliferation of incorrect solutions found with DIIS for even such “easy” chemical systems as those in the G2 test set has significant implications. How could high-throughput screening be performed with confidence using such a solver? We expect that other programs that default to using the RH solver will also have similar issues. And, as demonstrated in ref. 21, second-order solvers are not a panacea.
Even with direct access to the CIAH implementation it was difficult to compare methods fairly. Some differences were minor, such as the convergence tests. Both solvers use magnitudes of energy change and gradient for convergence monitoring. For the former threshold was set to 1 × 10−9Eh, but the CIAH gradient criterion (1 × 10−6) is defined in terms of the gradient norm rather than the RMS value used by QUOTR (1 × 10−5). Some differences were more significant, like the choice of the guess orbitals. The QUOTR data in Table 3 was obtained with its default guess (perturbed extended Hückel) that differs from the default minimal AO guess used for CIAH calculations. To elucidate the impact of the guess differences we performed additional tests with (unperturbed) core Hamiltonian guess implemented identically in MPQC and PySCF to ensure that the initial energies matched to better than 9 digits between the two programs. The convergence criteria for QUOTR were changed to match the criteria of CIAH, using 1 × 10−6 norm of the unique elements of the gradient, and the criterion on energy change was kept at 1 × 10−9Eh. The results for RHF computations of 10 small molecules in the G2 set are displayed in Table 4. In all cases, CIAH and QUOTR found the same solution but the former required on average 3 times more Fock build equivalents.
| System | CIAH | QUOTR | ||
|---|---|---|---|---|
| KF | JK | N F | N F | |
| CH4 | 9 | 35 | 44 | 14 |
| CO | 17 | 70 | 87 | 22 |
| F2 | 7 | 24 | 31 | 12 |
| H2 | 3 | 7 | 10 | 5 |
| H2O | 11 | 43 | 54 | 14 |
| HF | 12 | 48 | 60 | 13 |
| Li2 | 6 | 18 | 24 | 10 |
| LiH | 5 | 15 | 20 | 10 |
| N2 | 9 | 34 | 43 | 13 |
| NH3 | 12 | 53 | 65 | 19 |
| Median | 9 | 34.5 | 43.5 | 13 |
| Mean | 9.1 | 34.7 | 43.8 | 13.2 |
| Max | 17 | 70 | 87 | 22 |
A deeper breakdown of QUOTR's convergence statistics for the G2-2/6-31G* set is presented in Table 5, where “Before L-BFGS” refers to the line search iterations before the first use of a quasi-Newton step, and “Line Search” refers to all instances of line search (including those occurring later in the SCF process e.g. due to the gradient becoming too large again). On average 7 Fock builds are needed before the gradient is sufficiently reduced to start quasi-Newton steps. This is consistent with the average of 3 line search iterations before stating L-BFGS because each line search takes two Fock builds and we need one initial Fock build. These results are mostly an indication of the quality of the initial guess and the relative simplicity of the electronic structure in this test set. The data in Table 5 also illustrates the efficiency of the L-BFGS/TR combination used in QUOTR since almost half (8.8) of the total number of Fock builds (19.4) are spent in performing steps that ultimately use line searches. The negligible difference between “Line Search” and “Before L-BFGS” statistics indicates that in most cases there is no need for line search after starting L-BFGS/TR steps.
| Median | Max | Mean | ||
|---|---|---|---|---|
| N F | Cumulative | 16 | 69 | 19.4 |
| Before L-BFGS | 7 | 21 | 7.8 | |
| Line search | 7 | 27 | 8.8 | |
| N I | Cumulative | 12 | 55 | 14.2 |
| Before L-BFGS | 3 | 10 | 3.4 | |
| Line search | 3 | 13 | 3.9 | |
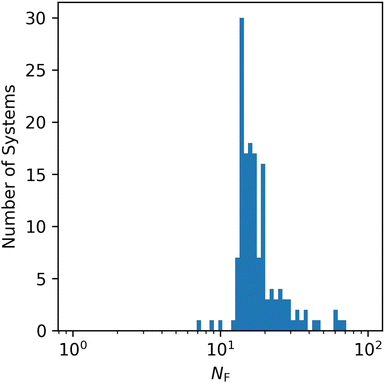
Although the G2-2 test set is composed of systems with relatively simple electronic structure, there is substantial variance within the set, as illustrated in Fig. 1. Although for most systems convergence is achieved in fewer than 30 Fock builds, there are more than 10 systems for which more Fock builds were required.
Quality of the initial guess unfortunately matters even with very robust solvers. Specifically, the need for random perturbation of the initial guess orbitals was found to be crucial for some systems with geometric symmetry. In particular, we found for AlCl3 that without breaking the symmetry of the extended Hückel orbitals, a local minimum at −1619.598631Eh was obtained by QUOTR. However, when the perturbation was applied, a solution at −1620.576010Eh was consistently found. To examine how the random perturbations to the initial guess impact convergence, we ran AlCl3 with 50 different seeds for the random number generator. The plot in Fig. 2 shows that when the minimum solution is accessible by symmetry, then QUOTR is robust in converging to the solution.
4.2 Challenging tests
We have now shown that QUOTR is competitive with standard RH/DIIS and competitive or superior to the representative quasi-Newton SCF solvers for the relatively easy test problems (G2 test set). To test the robustness of QUOTR we considered several prototypes of systems where the standard (RH/DIIS) usually fails outright, and even representative quasi-Newton heuristics struggle. We selected 3 types of problems where convergence difficulties often occur: (a) systems with small or vanishing HOMO–LUMO gap, (b) transition metal-containing systems, and (c) f-element containing systems.| HF | LDA | PBE | PBE0 | B3LYP | |
|---|---|---|---|---|---|
| HOMO | −6.38 | −3.26 | −2.53 | −2.70 | −2.75 |
| LUMO | 0.86 | −3.25 | −2.52 | −2.34 | −2.47 |
| Gap | 7.24 | 0.01 | 0.01 | 0.36 | 0.28 |
The sizeable 7.24 eV gap found for HF nearly vanished with the hybrid DFT functionals (PBE0, B3LYP), with all values within 0.01 eV of the values found in ref. 44. For the LDA and PBE functionals, for which solutions could not be located in ref. 44, QUOTR produced converged solutions with a nearly zero HOMO–LUMO gap! The origin of the vanishing gap in this and other similar biopolymers will be elaborated elsewhere, but we emphasize that the vanishing gap solution is the unphysical but “correct” solution, and QUOTR successfully located it. A key motivation for the development of QUOTR was the need to understand the origin of such unphysical solutions.
Fig. 3 illustrates how the HF and KS LDA energies converge with QUOTR and RH/DIIS solvers. The two panels in the figure illustrate the impact of the starting orbitals on the solver convergence. While the ultimate outcome—RH/DIIS did not converge for LDA, the rest of the combinations converged—did not depend on whether the starting orbitals were perturbed or not, it took twice as many iterations for QUOTR to converge to the LDA solution without perturbation than with. Note that the perturbation in these cases is applied to all orbitals, not just valence. Both solvers converge at a similar rate for the HF case where the HOMO–LUMO gap is large, with approximately 20 or fewer iterations sufficient for microhartree accuracy. With unperturbed guess the number of Fock builds for RH/DIIS and QUOTR are 17 and 43, respectively; with perturbed guess the corresponding counts are 28 and 34.
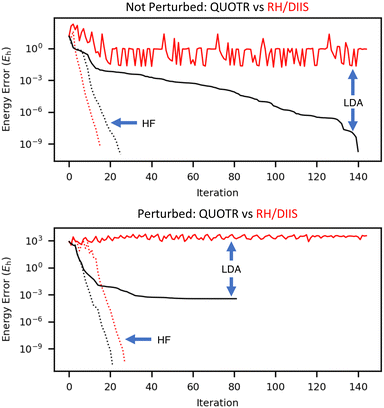 | ||
| Fig. 3 Convergence of HF and KS DFT for the 1PLW polypeptide (displayed energy error relative to the lowest energy obtained for each method). | ||
While QUOTR manages to locate the LDA solution correctly, its rate of convergence can be relatively slow. We identify regularization of the preconditioner as the likely culprit. Since at the converged KS LDA solution the HOMO–LUMO gap is zero (see Table 6) and the condition number of the exact Hessian is large and grows with the system size, the exact Hessian (hence, the preconditioner) can vary significantly as the solution is approached. The last iteration where the preconditioner was recomputed was 51 (with non-perturbed guess) and 32 (with perturbed guess).
Table 7 reports the number of Fock builds necessary to converge HF and KS DFT using a variety of solvers. The first set of comparisons juxtaposes QUOTR (implemented in MPQC) against a quasi-Newton TRAH solver (implemented in the Orca program) and 2 variants of DIIS (both implemented in Orca). These computations used the core Hamiltonian initial guess throughout and the default convergence criteria of Orca: 5 × 10−5 for the gradient norm, 1 × 10−6Eh for the energy difference between iterations. Although the core Hamiltonian initial guess is known to be poor, it was chosen to make sure that the same initial orbital set was used to bootstrap computations in MPQC and Orca. The choice of such a poor starting point makes the job of the orbital optimizer even more difficult. It should be noted that TRAH uses a random number in one of the Davidson diagonalization start vectors which helps break symmetry, while for QUOTR we apply a small random unitary rotation to the initial guess (all orbitals, not just valence) with a maximum σ element of 0.01 for these systems. Thus, the initial guess for QUOTR differs from the others by this perturbation, and the QUOTR initial guess is usually higher in energy (approx. 1–2Eh for CrC and 4–4.5Eh for Cr2).
| QUOTR | TRAH | DIISb | KDIISb | QUOTRc | CIAHc | |
|---|---|---|---|---|---|---|
| a N F are reported for each solver. The core Hamiltonian eigenstates were used as the initial guess, unless noted. The def2-TZVPP basis used throughout. b As implemented in ORCA. c Initial guess: hcore + 1 Fock build and diagonalize. d Local minimum. | ||||||
| CrC | ||||||
| RHF | 162 | 377 | 44d | 47d | 205 | 164d |
| LDA | 148 | 202 | — | 320d | 107 | 208 |
| B3LYP | 129 | 300 | 25d | 440d | 91 | 240 |
| Cr2 | ||||||
| RHF | 249 | 295 | 26d | — | 472 | 160d |
| LDA | 208 | 233 | 20 | 113d | 144 | 478d |
| B3LYP | 123 | 267 | 18d | 201d | 169 | 330 |
Comparing QUOTR to TRAH, we see that in all cases QUOTR requires fewer Fock builds. The largest error in converged energies for QUOTR was for CrC with B3LYP, which was higher than TRAH by 1.1 × 10−6Eh. This error is reasonable since the energies were only converged to 1 × 10−6Eh.
The results for DIIS and KDIIS look promising according to the number of Fock builds; however, local minima are very common, so the rapid convergence is deceiving. Only in the LDA case for Cr2 was DIIS able to find a solution that is not a local minimum relative to QUOTR's solution.
The second batch of comparisons juxtaposes QUOTR (in MPQC) against the CIAH solver (in PySCF) using the custom variant of core Hamiltonian (hcore) guess in PySCF, namely the standard hcore guess followed up by a single RH iteration. The first thing to notice is that QUOTR takes more Fock builds than CIAH for RHF, but fewer Fock builds for the other two methods. However, CIAH converges to a local minimum for both systems when using RHF, indicating that QUOTR is more robust and/or faster than CIAH in both cases.
The very large number of Fock builds for Cr2 with RHF merits further investigation. While QUOTR does converge to the lowest energy solution that we could find, it does so at a cost of 249 Fock builds (or 472 for the comparison with PySCF hcore guess). However, this difficulty is not unique to QUOTR, as TRAH also takes nearly 300 Fock builds to achieve the same solution. This is in contrast to the LDA solution, which seems to be generally easier to converge. Fig. 4 provides some insight into why RHF for Cr2 is a difficult case. Namely, the RHF solution located by QUOTR lacks cylindrical symmetry, in contrast to LDA.
 | ||
| Fig. 4 The valence orbitals viewed along the bond axis and the matching orbital energies (eV) for RHF and LDA singlet ground states of Cr2. | ||
To summarize: for CrC and Cr2 QUOTR was able to locate the lowest-energy solution (unlike DIIS and CIAH) and was faster than TRAH.
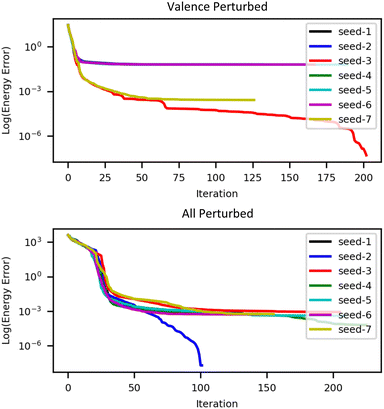
We used QUOTR with superposition of atomic densities guess orbitals, constructed as described in Section 3. Due to the complex optimization landscape in this system, it was necessary to explore the landscape of solutions by varying the initial guess. Thus the entire set of guess orbitals, or just their valence subset, was perturbed by pseudorandom unitaries generated using seven different integers (between 123 and 129) as the random engine seed. The results are displayed in Table 8 and Fig. 5. The column labeled “energy error” is relative to the lowest energy solution that we obtained, which was for seed 2 with all orbitals perturbed (total energy −35![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 045.703224Eh). As can be seen, two types of solutions were found; the lower energy one has a formal +2 charge on Fm, and the other, roughly 40 kcal mol−1 higher in energy, has a +3 charge on Fm. The ground state energy agreed quite well with the value located by Penchoff et al. in ref. 110 using Molpro's RH/DIIS SCF solver using complicated guess obtained by merging converged fragment MOs (in fact, the ground state energy located by QUOTR is slightly lower in energy). Unfortunately, it was only possible to obtain 10 significant digits of precision in the energy, due to the impact of roundoff errors and the non-determinism of the Fock matrix construction in MPQC. As we did for 1PLW, we ran separate calculations to check the orthogonality of the converged orbitals. Again, we found errors on the order of 1 × 10−12 in all cases. Clearly, all electron computations in heavy element systems with Gaussian AO bases that have high condition numbers will be increasingly untenable in double precision.
045.703224Eh). As can be seen, two types of solutions were found; the lower energy one has a formal +2 charge on Fm, and the other, roughly 40 kcal mol−1 higher in energy, has a +3 charge on Fm. The ground state energy agreed quite well with the value located by Penchoff et al. in ref. 110 using Molpro's RH/DIIS SCF solver using complicated guess obtained by merging converged fragment MOs (in fact, the ground state energy located by QUOTR is slightly lower in energy). Unfortunately, it was only possible to obtain 10 significant digits of precision in the energy, due to the impact of roundoff errors and the non-determinism of the Fock matrix construction in MPQC. As we did for 1PLW, we ran separate calculations to check the orthogonality of the converged orbitals. Again, we found errors on the order of 1 × 10−12 in all cases. Clearly, all electron computations in heavy element systems with Gaussian AO bases that have high condition numbers will be increasingly untenable in double precision.
| Seed | Valence perturbed | All perturbed | ||||||
|---|---|---|---|---|---|---|---|---|
| N I | N F | ΔE | Q | N I | N F | ΔE | Q | |
| 1 | 124 | 189 | 40.19 | 2.70 | 131 | 201 | 0.58 | 1.81 |
| 2 | 132 | 199 | 40.13 | 2.70 | 102 | 168 | 0 | 1.81 |
| 3 | 203 | 274 | 0.76 | 1.81 | 205 | 295 | 0.54 | 1.81 |
| 4 | 136 | 191 | 40.16 | 2.70 | 225 | 307 | 0.04 | 1.81 |
| 5 | 189 | 262 | 40.16 | 2.70 | 209 | 290 | 0.25 | 1.81 |
| 6 | 167 | 229 | 40.34 | 2.70 | 144 | 215 | 0.34 | 1.81 |
| 7 | 126 | 170 | 0.92 | 1.82 | 155 | 243 | 0.35 | 1.81 |
There are clearly many outstanding challenges suggested by the computational experiments on this actinide-containing complex. In particular, the sensitivity of the final solution to the initial guess suggests that various global (e.g., stochastic35) approaches to the orbital optimization should be considered.
5 Summary
We have presented a state-of-the-art solver for quasi-Newton unitary optimization that combines the preconditioned L-BFGS orbital update with the trust-region step restriction method. The exploitation of the low-rank structure of the L-BFGS Hessian, including in solving the trust-region (sub) problem, makes the QUOTR solver remarkably efficient, approaching the efficiency of the mainstream RH/DIIS heuristics when applied to problems with easy optimization landscapes (like the standard G2 test set). When applied to problems with complex optimization landscapes (problems with vanishing HOMO–LUMO gaps, d- and f-element containing molecules) QUOTR matches or exceeds the robustness of representative quasi-Newton solvers, all at a significantly lower computational cost due to avoiding the exact Hessian evaluation.While QUOTR guarantees convergence to a local stationary point, it is not able to guarantee global convergence due to the nonconvexity of the energy. However, its efficiency makes it a robust building block for even sophisticated solvers that combine efficient local minimum search with global (e.g., stochastic) landscape traversal.
Conflicts of interest
There are no conflicts to declare.Acknowledgements
This work was supported by the U.S. Department of Energy via award DE-SC0022327.Notes and references
- D. R. Hartree, Rep. Prog. Phys., 1947, 11, 113–143 CrossRef
.
- C. C. J. Roothaan, Rev. Mod. Phys., 1951, 23, 69–89 CrossRef CAS
.
- R. McWeeny, Proc. R. Soc. Lond. A, 1956, 235, 496–509 CAS
.
- B. Levy and G. Berthier, Int. J. Quantum Chem., 1968, 2, 307–319 CrossRef
.
- I. H. Hillier and V. R. Saunders, Proc. R. Soc. Lond. A, 1970, 320, 161–173 CAS
.
- I. H. Hillier and V. R. Saunders, Int. J. Quantum Chem., 1970, 4, 503–518 CrossRef CAS
.
- B. Levy, Chem. Phys. Lett., 1973, 18, 59–62 CrossRef CAS
.
- R. Seeger and J. A. Pople, J. Chem. Phys., 1976, 65, 265–271 CrossRef CAS
.
- J. Douady, Y. Ellinger, R. Subra and B. Levy, J. Chem. Phys., 1980, 72, 1452–1462 CrossRef CAS
.
- P. Pulay, Chem. Phys. Lett., 1980, 73, 393–398 CrossRef CAS
.
- G. B. Bacskay, Chem. Phys., 1981, 61, 385–404 CrossRef CAS
.
- G. B. Bacskay, Chem. Phys., 1982, 65, 383–396 CrossRef CAS
.
- P. Pulay, J. Comput. Chem., 1982, 3, 556–560 CrossRef CAS
.
- M. Head-Gordon and J. A. Pople, J. Phys. Chem., 1988, 92, 3063–3069 CrossRef CAS
.
- T. H. Fischer and J. Almlof, J. Phys. Chem., 1992, 96, 9768–9774 CrossRef CAS
.
- R. Shepard, Theor. Chim. Acta, 1993, 84, 343–351 CrossRef
.
- A. P. Rendell, Chem. Phys. Lett., 1994, 229, 204–210 CrossRef CAS
.
- A. T. Wong and R. J. Harrison, J. Comput. Chem., 1995, 16, 1291–1300 CrossRef CAS
.
- G. Chaban, M. W. Schmidt and M. S. Gordon, Theor. Chim. Acta, 1997, 97, 88–95 CAS
.
- A. D. Daniels and G. E. Scuseria, Phys. Chem. Chem. Phys., 2000, 2, 2173–2176 RSC
.
- T. Van Voorhis and M. Head-Gordon, Mol. Phys., 2002, 100, 1713–1721 CrossRef CAS
.
- J. VandeVondele and J. Hutter, J. Chem. Phys., 2003, 118, 4365–4369 CrossRef CAS
.
- L. Thøgersen, J. Olsen, D. Yeager, P. Jørgensen, P. Sałek and T. Helgaker, J. Chem. Phys., 2004, 121, 16 CrossRef PubMed
.
- L. Thøgersen, J. Olsen, A. Köhn, P. Jørgensen, P. Sałek and T. Helgaker, J. Chem. Phys., 2005, 123, 074103 CrossRef PubMed
.
- C. Yang, J. C. Meza and L.-W. Wang, SIAM J. Sci. Comput., 2007, 29, 1854–1875 CrossRef
.
- P. Sałek, S. Høst, L. Thøgersen, P. Jørgensen, P. Manninen, J. Olsen, B. Jansík, S. Reine, F. Pawłowski, E. Tellgren, T. Helgaker and S. Coriani, J. Chem. Phys., 2007, 126, 114110 CrossRef PubMed
.
- V. Weber, J. Vande Vondele, J. Hutter and A. M. N. Niklasson, J. Chem. Phys., 2008, 128, 084113 CrossRef PubMed
.
- S. Høst, J. Olsen, B. Jansík, L. Thøgersen, P. Jørgensen and T. Helgaker, J. Chem. Phys., 2008, 129, 124106 CrossRef PubMed
.
- K. Baarman and J. VandeVondele, J. Chem. Phys., 2011, 134, 244104 CrossRef PubMed
.
- Q. Sun, arXiv, 2017, preprint, arXiv:161008423 Phys DOI:10.48550/arXiv.1610.08423.
- B. Helmich-Paris, J. Chem. Phys., 2021, 154, 164104 CrossRef CAS PubMed
.
- T. Nottoli, J. Gauss and F. Lipparini, Mol. Phys., 2021, 119, e1974590 CrossRef
.
- A. V. Ivanov, E. Ö. Jónsson, T. Vegge and H. Jónsson, Comput. Phys. Commun., 2021, 267, 108047 CrossRef CAS
.
- C. Seidl and G. M. J. Barca, J. Chem. Theory Comput., 2022, 18, 4164–4176 CrossRef CAS PubMed
.
- L. B. Dittmer and A. Dreuw, J. Chem. Phys., 2023, 159, 134104 CrossRef CAS PubMed
.
-
S. Vavasis, Nonlinear Optimization: Complexity Issues, Oxford University Press, 1991 Search PubMed
.
- N. Boumal, P.-A. Absil and C. Cartis, IMA J. Numer. Anal., 2019, 39, 1–33 CrossRef
.
- G. G. Hall, Proc. R. Soc. Lond. A, 1951, 205, 541–552 CAS
.
- D. G. Anderson, J. ACM, 1965, 12, 547–560 CrossRef
.
- K. N. Kudin, G. E. Scuseria and E. Cancès, J. Chem. Phys., 2002, 116, 8255–8261 CrossRef CAS
.
- A. J. Garza and G. E. Scuseria, J. Chem. Phys., 2012, 137, 054110 CrossRef PubMed
.
- R. J. Harrison, J. Comput. Chem., 2004, 25, 328–334 CrossRef CAS PubMed
.
- C. Kollmar, J. Chem. Phys., 1996, 105, 8204–8212 CrossRef CAS
.
- E. Rudberg, J. Phys.: Condens. Matter, 2012, 24, 072202 CrossRef PubMed
.
- C. Köppl and H.-J. Werner, J. Chem. Theory Comput., 2016, 12, 3122–3134 CrossRef PubMed
.
- C. A. Lewis, J. A. Calvin and E. F. Valeev, J. Chem. Theory Comput., 2016, 12, 5868–5880 CrossRef CAS PubMed
.
- X. Wang, C. A. Lewis and E. F. Valeev, J. Chem. Phys., 2020, 153, 124116 CrossRef CAS PubMed
.
- A. T. B. Gilbert, N. A. Besley and P. M. W. Gill, J. Phys. Chem. A, 2008, 112, 13164–13171 CrossRef CAS PubMed
.
- R. E. Stanton, J. Chem. Phys., 1981, 75, 3426–3432 CrossRef CAS
.
- R. Fletcher, Mol. Phys., 1970, 19, 55–63 CrossRef
.
- M. Chupin, M.-S. Dupuy, G. Legendre and É. Séré, ESAIM: Math. Modell. Numer. Anal., 2021, 55, 2785–2825 CrossRef
.
-
J. Nocedal and S. J. Wright, Numerical Optimization, Springer, New York, 2nd edn, 2006 Search PubMed
.
- C. Kollmar, Int. J. Quantum Chem., 1997, 62, 617–637 CrossRef CAS
.
- X. Hu and W. Yang, J. Chem. Phys., 2010, 132, 054109 CrossRef PubMed
.
- J. B. Francisco, J. M. Martínez and L. Martínez, J. Chem. Phys., 2004, 121, 10863 CrossRef CAS PubMed
.
- O. Burdakov, L. Gong, S. Zikrin and Y.-x Yuan, Math. Prog. Comp., 2017, 9, 101–134 CrossRef
.
- T. A. Claxton and N. A. Smith, Theor. Chim. Acta, 1971, 22, 399–402 CrossRef CAS
.
- D. H. Sleeman, Theor. Chim. Acta, 1968, 11, 135–144 CrossRef CAS
.
- J. Olsen and P. Jørgensen, J. Chem. Phys., 1982, 77, 6109–6130 CrossRef CAS
.
- D. A. Kreplin, P. J. Knowles and H.-J. Werner, J. Chem. Phys., 2019, 150, 194106 CrossRef PubMed
.
- Y. Yao and C. J. Umrigar, J. Chem. Theory Comput., 2021, 17, 4183–4194 CrossRef CAS PubMed
.
- P. Jo/rgensen and J. Simons, J. Chem. Phys., 1983, 79, 334–357 CrossRef
.
- H.-J. A. Jensen and P. Jørgensen, J. Chem. Phys., 1984, 80, 1204–1214 CrossRef CAS
.
-
R. Fletcher, Practical Methods of Optimization, Wiley, New York, 1980, vol. 1 Search PubMed
.
- D. Thouless, Nucl. Phys., 1960, 21, 225–232 CrossRef CAS
.
- B. Levy, Chem. Phys. Lett., 1969, 4, 17–19 CrossRef CAS
.
-
T. Helgaker, P. Jørgensen and J. Olsen, Molecular Electronic-Structure Theory, John Wiley & Sons, Ltd, Chichester, UK, 1st edn, 2000 Search PubMed
.
- C. Moler and C. Van Loan, SIAM Rev., 1978, 20, 801–836 CrossRef
.
- R. H. Byrd, J. Nocedal and R. B. Schnabel, Math. Program., 1994, 63, 129–156 CrossRef
.
- P.-O. Löwdin, Adv. Phys., 1956, 5, 1–171 CrossRef
.
- T. Abrudan, J. Eriksson and V. Koivunen, Signal Process., 2009, 89, 1704–1714 CrossRef
.
- R. Hoffmann, J. Chem. Phys., 1963, 39, 1397–1412 CrossRef CAS
.
- J. H. Ammeter, H. B. Buergi, J. C. Thibeault and R. Hoffmann, J. Am. Chem. Soc., 1978, 100, 3686–3692 CrossRef CAS
.
- S. Lehtola, J. Chem. Theory Comput., 2019, 15, 1593–1604 CrossRef CAS PubMed
.
- P. Norman and H. J. A. Jensen, Chem. Phys. Lett., 2012, 531, 229–235 CrossRef CAS
.
- C. F. Fischer, At. Data Nucl. Data Tables, 1972, 4, 301–399 CrossRef CAS
.
- C. Peng, C. A. Lewis, X. Wang, M. C. Clement, K. Pierce, V. Rishi, F. Pavošević, S. Slattery, J. Zhang, N. Teke, A. Kumar, C. Masteran, A. Asadchev, J. A. Calvin and E. F. Valeev, J. Chem. Phys., 2020, 153, 044120 CrossRef CAS PubMed
.
- R. Ditchfield, W. J. Hehre and J. A. Pople, J. Chem. Phys., 1971, 54, 724–728 CrossRef CAS
.
- W. J. Hehre, R. Ditchfield and J. A. Pople, J. Chem. Phys., 1972, 56, 2257–2261 CrossRef CAS
.
- P. C. Hariharan and J. A. Pople, Theor. Chim. Acta, 1973, 28, 213–222 CrossRef CAS
.
- J. D. Dill and J. A. Pople, J. Chem. Phys., 1975, 62, 2921–2923 CrossRef CAS
.
- J. S. Binkley and J. A. Pople, J. Chem. Phys., 1977, 66, 879–880 CrossRef CAS
.
- M. S. Gordon, J. S. Binkley, J. A. Pople, W. J. Pietro and W. J. Hehre, J. Am. Chem. Soc., 1982, 104, 2797–2803 CrossRef CAS
.
- M. M. Francl, W. J. Pietro, W. J. Hehre, J. S. Binkley, M. S. Gordon, D. J. DeFrees and J. A. Pople, J. Chem. Phys., 1982, 77, 3654–3665 CrossRef CAS
.
- R. Krishnan, J. S. Binkley, R. Seeger and J. A. Pople, J. Chem. Phys., 1980, 72, 650–654 CrossRef CAS
.
- A. D. McLean and G. S. Chandler, J. Chem. Phys., 1980, 72, 5639–5648 CrossRef CAS
.
- T. Clark, J. Chandrasekhar, G. W. Spitznagel and P. V. R. Schleyer, J. Comput. Chem., 1983, 4, 294–301 CrossRef CAS
.
- G. W. Spitznagel, T. Clark, P. von Ragué Schleyer and W. J. Hehre, J. Comput. Chem., 1987, 8, 1109–1116 CrossRef CAS
.
- F. Weigend and R. Ahlrichs, Phys. Chem. Chem. Phys., 2005, 7, 3297 RSC
.
- W. A. de Jong, R. J. Harrison and D. A. Dixon, J. Chem. Phys., 2001, 114, 48 CrossRef CAS
.
- R. Feng and K. A. Peterson, J. Chem. Phys., 2017, 147, 084108 CrossRef PubMed
.
- F. Weigend, Phys. Chem. Chem. Phys., 2006, 8, 1057 RSC
.
- K. L. Schuchardt, B. T. Didier, T. Elsethagen, L. Sun, V. Gurumoorthi, J. Chase, J. Li and T. L. Windus, J. Chem. Inf. Model., 2007, 47, 1045–1052 CrossRef CAS PubMed
.
- T. Tsuchiya, M. Abe, T. Nakajima and K. Hirao, J. Chem. Phys., 2001, 115, 4463–4472 CrossRef CAS
.
- M. C. Clement, X. Wang and E. F. Valeev, J. Chem. Theory Comput., 2021, 17, 7406–7415 CrossRef CAS PubMed
.
- L. A. Curtiss, K. Raghavachari, P. C. Redfern and J. A. Pople, J. Chem. Phys., 1997, 106, 1063–1079 CrossRef CAS
.
- R. D. Johnson, Computational Chemistry Comparison and Benchmark Database, NIST Standard Reference Database 101, 2002.
-
M. J. Frisch, G. W. Trucks, H. B. Schlegel, G. E. Scuseria, M. A. Robb, J. R. Cheeseman, G. Scalmani, V. Barone, B. Mennucci, G. A. Petersson, H. Nakatsuji, M. Caricato, X. Li, H. P. Hratchian, A. F. Izmaylov, J. Bloino, G. Zheng, J. L. Sonnenberg, M. Hada, M. Ehara, K. Toyota, R. Fukuda, J. Hasegawa, M. Ishida, T. Nakajima, Y. Honda, O. Kitao, H. Nakai, T. Vreven, J. A. Montgomery Jr., J. E. Peralta, F. Ogliaro, M. Bearpark, J. J. Heyd, E. Brothers, K. N. Kudin, V. N. Staroverov, T. Keith, R. Kobayashi, J. Normand, K. Raghavachari, A. Rendell, J. C. Burant, S. S. Iyengar, J. Tomasi, M. Cossi, N. Rega, J. M. Millam, M. Klene, J. E. Knox, J. B. Cross, V. Bakken, C. Adamo, J. Jaramillo, R. Gomperts, R. E. Stratmann, O. Yazyev, A. J. Austin, R. Cammi, C. Pomelli, J. W. Ochterski, R. L. Martin, K. Morokuma, V. G. Zakrzewski, G. A. Voth, P. Salvador, J. J. Dannenberg, S. Dapprich, A. D. Daniels, O. Farkas, J. B. Foresman, J. V. Ortiz, J. Cioslowski and D. J. Fox, Gaussian 09, Gaussian, Inc., 2013 Search PubMed
.
- A. Petrone, D. B. Williams-Young, S. Sun, T. F. Stetina and X. Li, Eur. Phys. J. B, 2018, 91, 169 CrossRef
.
- S. Lehtola, C. Steigemann, M. J. Oliveira and M. A. Marques, SoftwareX, 2018, 7, 1–5 CrossRef
.
- M. E. Mura and P. J. Knowles, J. Chem. Phys., 1996, 104, 9848–9858 CrossRef CAS
.
- V. I. Lebedev and D. N. Laikov, Dokl. Math., 1999, 59, 477–481 Search PubMed
.
- P. A. M. Dirac, Math. Proc. Cambridge Philos. Soc., 1930, 26, 376–385 CrossRef CAS
.
- S. H. Vosko, L. Wilk and M. Nusair, Can. J. Phys., 1980, 58, 1200–1211 CrossRef CAS
.
- I. Marcotte, F. Separovic, M. Auger and S. M. Gagné, Biophys. J., 2004, 86, 1587–1600 CrossRef CAS PubMed
.
- H. M. Berman, Nucleic Acids Res., 2000, 28, 235–242 CrossRef CAS PubMed
.
- F. Neese, Wiley Interdiscip. Rev.: Comput. Mol. Sci., 2022, 12, e1606 Search PubMed
.
- W. Liu and D. Peng, J. Chem. Phys, 2009, 131, 031104 CrossRef PubMed
.
- D. Peng, N. Middendorf, F. Weigend and M. Reiher, J. Chem. Phys, 2013, 138, 184105 CrossRef PubMed
.
- D. A. Penchoff, C. C. Peterson, M. S. Quint, J. D. Auxier, G. K. Schweitzer, D. M. Jenkins, R. J. Harrison and H. L. Hall, ACS Omega, 2018, 3, 14127–14143 CrossRef CAS PubMed
.
- Q. Sun, X. Zhang, S. Banerjee, P. Bao, M. Barbry, N. S. Blunt, N. A. Bogdanov, G. H. Booth, J. Chen, Z.-H. Cui, J. J. Eriksen, Y. Gao, S. Guo, J. Hermann, M. R. Hermes, K. Koh, P. Koval, S. Lehtola, Z. Li, J. Liu, N. Mardirossian, J. D. McClain, M. Motta, B. Mussard, H. Q. Pham, A. Pulkin, W. Purwanto, P. J. Robinson, E. Ronca, E. R. Sayfutyarova, M. Scheurer, H. F. Schurkus, J. E. T. Smith, C. Sun, S.-N. Sun, S. Upadhyay, L. K. Wagner, X. Wang, A. White, J. D. Whitfield, M. J. Williamson, S. Wouters, J. Yang, J. M. Yu, T. Zhu, T. C. Berkelbach, S. Sharma, A. Y. Sokolov and G. K.-L. Chan, J. Chem. Phys., 2020, 153, 024109 CrossRef CAS PubMed
.
Footnotes |
| † Electronic supplementary information (ESI) available: Geometries (xyz format), convergence statistics and converged energies for most calculations. See DOI: https://doi.org/10.1039/d3cp05557d |
| ‡ Sometimes SCF is also used to denote a specific class of solvers to the Hartree–Fock/Kohn–Sham equations, which goes counter to the original use of the term. |
| This journal is © the Owner Societies 2024 |