Investigation of the stability of D5SIC-DNAM-incorporated DNA duplex in Taq polymerase binary system: a systematic classical MD approach†
Tanay
Debnath
 a and
G. Andrés
Cisneros
a and
G. Andrés
Cisneros
 *ab
*ab
aDepartment of Physics, University of Texas at Dallas, Richardson, Texas 75080, Dallas, USA. E-mail: andres@utdallas.edu
bDepartment of Chemistry and Biochemistry, University of Texas at Dallas, Richardson, Texas 75080, Dallas, USA
First published on 8th February 2024
Abstract
DNA polymerases are fundamental enzymes that play a crucial role in processing DNA with high fidelity and accuracy ensuring the faithful transmission of genetic information. The recognition of unnatural base pairs (UBPs) by polymerases, enabling their replication, represents a significant and groundbreaking discovery with profound implications for genetic expansion. Romesberg et al. examined the impact of DNA containing 2,6-dimethyl-2H-isoquiniline-1-thione: D5SIC (DS) and 2-methoxy-3-methylnaphthalene: DNAM (DN) UBPs bound to T. aquaticus DNA polymerase (Taq) through crystal structure analysis. Here, we have used polarizable and nonpolarizable classical molecular dynamics (MD) simulations to investigate the structural aspects and stability of Taq in complex with a DNA duplex including a DS–DN pair in the terminal 3′ and 5′ positions. Our results suggest that the flexibility of UBP-incorporated DNA in the terminal position is arrested by the polymerase, thus preventing fraying and mispairing. Our investigation also reveals that the UBP remains in an intercalated conformation inside the active site, exhibiting two distinct orientations in agreement with experimental findings. Our analysis pinpoints particular residues responsible for favorable interactions with the UBP, with some relying on van der Waals interactions while other on Coulombic forces.
Introduction
The precise synthesis and repair of DNA1 within cells relies extensively on a complex network of proteins of which DNA polymerases are key players.2–5 In biological process, DNA polymerases are specific towards four nucleotides (A, T, G, C) and two base-pairings (A–T and G–C).1–6 The concept of incorporating synthetic molecules as base pairs, termed Unnatural Base-Pairs (UBPs),7–42 depends upon a crucial prerequisite: these synthetic entities must undergo a thorough selection process orchestrated by polymerase enzymes.43–50 In essence, the viability of these synthetic molecules as base pairs is contingent upon the polymerase's ability to discriminate and incorporate them into the growing DNA strand with a high degree of accuracy and efficiency. This selectivity is essential to ensure that the resulting DNA sequence maintains fidelity and stability, akin to the natural base pairs (nBPs), and to avoid introducing errors or disruptions that could compromise the biological function of DNA. As a result, successful recognition and incorporation of unnatural bases by DNA polymerases is fundamental to their potential utilization in various biotechnological and genetic engineering applications.Several potential UBPs have been synthesized in recent years30–42 among them d5SICS (DS)-dNaM (DN) have emerged as one of the proficiently replicated unnatural base pairs.30,31 Previous reported work revealed that DS–DN form unconventional structures inside a DNA duplex. Bertz et al. reported two crystal structures of a DNA polymerase in complex with DNA containing a DS–DN incorporation.30,31 The first report involves a crystal structure of DNA polymerase I from T. aquaticus (Taq) in a closed ternary complex with DN in the templating position, and DS- triphosphate (DSTP) as substrate (PDB ID: 3SV3).30 In this structure, DN and DSTP exhibit Watson–Crick–Franklin (WCF) like parallelly stacked geometry.
Later they also reported the binary complex of Taq with the artificial base pair DS–DN in the post-insertion site. Crystal structures showed that in the binary complex of the polymerase, DS–DN forms two distinct intercalated non-Watson–Crick–Franklin (nWCF) structures in the terminal position of the DNA duplex. In one structure (PDB ID: 4C8L),31 the primer-DS is located externally with respect to the substrate-DS; whereas in another (PDB ID: 4C8O)31 the positioning becomes opposite.
Different computational techniques have been employed to predict the impact of DS–DN inside DNA in aqueous solvent, which predict both WCF and nWCF structures of the UBP inside DNA without polymerase systems.51–58 Our another theoretical work51 suggests that the inclusion of a DS–DN pair at the terminal position of DNA increases the flexibility of these bases, with occasional mispairing and fraying.
Romesberg et al. further reported individual residue contacts between Taq and the UBP-incorporated DNA based on the X-ray crystal structures.31 Although this investigation provided valuable insights into possible molecular interactions, a comprehensive interplay between Taq and UBP-incorporated-DNA including their dynamic characteristics, remains a subject yet to be thoroughly investigated. The full scope of how a polymerase orchestrates the interactions, and the dynamic nature of these connections remains an unsolved avenue for further exploration and scientific inquiry.
Here, we have employed classical molecular dynamics simulation with both AMOEBA and AMBER force fields to investigate the dynamical characteristics of UBP-incorporated DNA in binary complex with Taq and the molecular level interactions of UBP incorporated DNA with Taq. The reminder of the paper is organized as follows: The next section describes the setup of the simulation systems, simulation procedures, and analyses. Subsequently, analysis of the MD simulations is presented and discussed, followed by concluding remarks. This work is intended to provide novel insights on the DNA polymerase-bound behaviour of DNA that incorporates an experimentally synthesized and tested UBP that can be replicated, translated and transcribed in vitro. Our results uncover the specific drivers for the stabilization and selectivity of specific pairing of the UBP in the active site, which can help drive the field of synthetic biology forward.
Computational methods
System setup
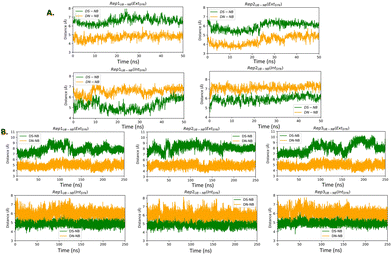
We have considered two types of binary complexes of Taq with a DS–DN UBP in the post-insertion site. In one case PDB ID: 4C8L has been used to generate a model where DS is externally placed with respect to DN designated as EXT. Additionally, the INT structure has been generated by using the PDB ID: 4C8O crystal structure where DS is placed below DN (Fig. 1). These EXT and INT structures are linked through the inter-strand flipping process of the UBP. In both cases the UBP adopts an intercalated configuration with the sulfur and methoxy groups in the same phase (SYN). We have also considered ANTI structures for both EXT and INT where the sulfur and methoxy groups are on opposite sides. All together four structures have been considered: EXTSYN, EXTANTI, INTSYN, INTANTI. Both the EXTSYN and INTSYN have been simulated in two ways; (i) UBP-incorporated DNA with one single overhang base and (ii) truncated UBP-incorporated DNA. We have considered one single orientation of the glycosidic bond as reported in the crystal structures. The Taq fragment consists of 541 amino acid residues with residue numbers from 292 to 832. The residue numbers of DNA base-pairs are from 833 to 855 with DS and DN located in positions 843 and 846 respectively. The distance between DS and DN is designated as dDS–DN. The distance between the UB and its adjacent NB is designated as dDS–DC and dDN–DG respectively. The <DS–P–DC and <DN–P–DG have been also calculated as depicted in Fig. S1 (ESI†). Parameters for the DS and DN bases were obtained with the PYRED program59 for AMBER.60–62 For the required AMOEBA parameters63–66 we have used TINKER67 and GDMA 2.3.68 All new parameters are included as electronic ESI.†AMBER setup
The LEaP module69 in AMBER2070 was used to set up the simulation box with Taq with UBP-incorporated DNA systems. The PROPKA software is adopted to protonate the amino acids of the Taq.71,72 Adding the hydrogen atoms to the systems, neutralization of the system with the required number of counterions (Na+), and solvation of the system in a cubic box filled with TIP3P water,60 extending at least 12 Å from the protein–DNA complex was done with the LEAP module from AMBER. The MD simulations were performed via AMBER20 pmemd.cuda using ff14SB AMBER force field61 for protein OL15 for nucleic acid.62 Seven minimization steps were done with decreasing restraint (10.0–0.0 kcal mol−1 Å−2) on the solute's heavy atoms. In each stage, the system was minimized within 5000 cycles of minimization via the steepest descent algorithm, continuing with 5000 cycles via the conjugated gradient algorithm. In the next step, each system was heated to 300 K using Langevin dynamics with a collision frequency of 2 ps−1 followed by 7 ns of NVT equilibration with decreasing restraint (10.0–0.0 kcal mol−1 Å−2) on the protein's heavy atoms. The production calculations for each system were accomplished in 250 ns of NPT ensemble without restraints in triplicate for a total of 750 ns of production simulation for each system. Production was run in the NPT ensemble using a Langevin thermostat and Berendsen barostat. Temperature was held constant at 300 K and pressure at 1.0 bar with a 2 fs time step. The SHAKE method73 has been employed for the bonds with hydrogen atoms, and for long-range Coulomb interactions, the smooth particle mesh Ewald approach74 was used with a 10 Å cutoff for nonbonded interactions. The CPPTRAJ module75 in AMBER20 was used to analyze production dynamics, i.e., RMSD, RMSF, correlation, normal mode analysis and geometrical parameters. In addition, Python libraries NumPy,76 Matplotlib,77 Pandas,78 were also employed for further data processing and graphing. A total of 12![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 500 frames have been extracted from the entire trajectory of each replicate for the analysis. Energy decomposition analysis (EDA) has been employed to investigate the intermolecular interactions between the UBP and residues of the rest of the systems for the entire trajectory using 12
500 frames have been extracted from the entire trajectory of each replicate for the analysis. Energy decomposition analysis (EDA) has been employed to investigate the intermolecular interactions between the UBP and residues of the rest of the systems for the entire trajectory using 12![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 500 frames for two replicates. As both the replicates show similar outcomes, the rest of the analysis has been done for one replicate. Amber-EDA was employed to calculate the nonbonded intermolecular interaction energies.79
500 frames for two replicates. As both the replicates show similar outcomes, the rest of the analysis has been done for one replicate. Amber-EDA was employed to calculate the nonbonded intermolecular interaction energies.79
AMOEBA setup
All polarizable AMOEBA (Atomic Multipole Optimized Energetics for Biomolecular)63–66 simulations were performed with TINKER-HP.67 The simulation box with the protein–DNA system was built with the help of packmol software.80 Initially, the Taq and UBP-incorporated DNA duplex complex was minimized using the BFGS nonlinear optimization algorithm with a convergence criterion (RMS gradient) of 0.1 Å. Subsequently molecular dynamics simulations in vacuum followed by implicit water with the GBSA model for 2 ns were carried out to relax the system. The resulting system was solvated using 72![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 000 AMOEBA water molecules and neutralized using Na+ in the center of the box with volume 90 × 90 × 90 Å3 using packmol. After that, the system was heated to 300 K in 4 simulation steps (2 ns each) with an NVT ensemble removing all positional restrains (100.0–0.0 kcal Å−1). After the equilibration step, MD simulations were carried out for 50 ns in an NPT ensemble (1 atm and 300 K). The Monte Carlo barostat and the Bussi thermostat were used to keep the pressure and temperature fixed respectively. The duration of the time step was 2 fs using RESPA integrator. The smooth particle mesh Ewald (sPME) method81 was used in the calculation of charge, atomic multipole, and polarization interactions. A value of 10 Å was used for the cutoff distance value for van der Waals potential energy interactions and the real-space distance cutoff in the Ewald summation.82 Geometry sampling was done every 5 ps, which led to generate total 10
000 AMOEBA water molecules and neutralized using Na+ in the center of the box with volume 90 × 90 × 90 Å3 using packmol. After that, the system was heated to 300 K in 4 simulation steps (2 ns each) with an NVT ensemble removing all positional restrains (100.0–0.0 kcal Å−1). After the equilibration step, MD simulations were carried out for 50 ns in an NPT ensemble (1 atm and 300 K). The Monte Carlo barostat and the Bussi thermostat were used to keep the pressure and temperature fixed respectively. The duration of the time step was 2 fs using RESPA integrator. The smooth particle mesh Ewald (sPME) method81 was used in the calculation of charge, atomic multipole, and polarization interactions. A value of 10 Å was used for the cutoff distance value for van der Waals potential energy interactions and the real-space distance cutoff in the Ewald summation.82 Geometry sampling was done every 5 ps, which led to generate total 10![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 000 frames.
000 frames.
Results and discussion
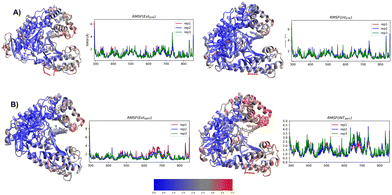
The results for the EXTSYN conformer systems (Fig. 1) simulated using the AMBER force field suggest that the DS–DN pair maintains an intercalated orientation in the DNA duplex for the entire 250 ns duration in all three replicates. No deviation from the intercalated structure of the DS–DN pair inside the DNA duplex were observed from the simulation with AMOEBA force field for 50 ns in two replicates. The low RMSD value (Table 1 and Fig. S2, ESI†) suggests that the system is stable throughout the simulation. This indicates that the flexibility of the UBP in DNA observed in aqueous solution as previously reported51 is arrested by the polymerase, which is also consistent with the per-residue RMSF values (Fig. 3).| RMSD/STDV | |||
|---|---|---|---|
| Rep1 | Rep2 | Rep3 | |
| AMOEBA | |||
| EXTSYN | 2.71/0.37 | 1.56/0.23 | |
| INTSYN | 2.17/0.29 | 2.23/0.24 | |
| AMBER | |||
| EXTSYN | 2.11/0.26 | 2.40/0.28 | 2.21/0.30 |
| INTSYN | 2.58/0.30 | 2.40/0.31 | 2.58/0.41 |
| INTANTI | 2.65/0.40 | 2.29/0.23 | 2.72/0.46 |
| EXTANTI | 2.87/0.40 | 2,93/0.39 | 2.79/0.45 |
The distance between DS and DN (dDS–DN) (Table 2 and Fig. S3, ESI†) based on both AMOEBA and AMBER simulation, indicating a reduced distance compared to that of a nBP of ∼10.5 Å. We have also measured the distance (Fig. 2) and angles (Fig. S4, ESI†) of UBs with respect to their adjacent nBP. It has been found that throughout the simulation the gap between dDS–DC and dDN–DG is always positive indicating the asymmetric nature of the DNA strand with external intercalation of DS and DN (Fig. 2). From angle analysis the asymmetric nature of DNA is also observed since <DS–P–DC is found to be greater than <DN–P–DG throughout entire trajectory of the simulation. In the crystal structure a similar trend for the UB–NB and <UB–P–NB have been observed.
| Distance/STDV | |||
|---|---|---|---|
| Rep1 | Rep2 | Rep3 | |
| AMOEBA | |||
| EXTSYN | 8.08/0.45 | 8.10/0.38 | |
| INTSYN | 9.10/0.32 | 7.52/0.62 | |
| AMBER | |||
| EXTSYN | 8.60/0.77 | 8.86/0.87 | 7.89/1.13 |
| INTSYN | 9.63/0.44 | 9.67/0.47 | 9.71/0.38 |
| INTANTI | 9.06/0.73 | 9.07/0.76 | 9.19/0.86 |
Similar to AMBER, simulations with the AMOEBA force field for 50 ns for EXTSYN also result in an intercalated DS–DN structure with no conformational change and no significant distortion inside the polymerase. Here also, the DS–DN distance is found to be shorter than that of nBPs. AMOEBA also predicts greater dDS–DC and <DS–P–DC than dDN–DG and <DN–P–DG (Fig. 2 and Fig. S4, ESI†) and throughout the simulations supporting an external intercalation of the UBP leading to the maintenance of an asymmetric DNA strand structure. From the AMBER and AMOEBA simulations, it becomes apparent that both yield mostly similar results in terms of RMSD values and related geometric parameters. Furthermore, the simulations show minimal deviations from the actual crystal structures, suggesting that the molecular dynamics (MD) simulations align closely with the experimental observation of binary Taq with UBP-incorporated DNA. Interestingly, with no-overhang DNA, the simulation with AMBER also predicts similar stability and structural features indicating an overhanging base doesn’t significantly impact UBP stability when the dsDNA is in complex with Taq. The associated RMSD, RMSF and geometrical parameters are presented in Fig. S6 (ESI†).
The INT structure has been obtained through inter-strand flipping of the UBP in the EXT conformer (Fig. 4). For the INTSYN conformer, the intercalation of DS–DN was also maintained during the entire simulation with both force fields, with low RMSD value (average RMSD for each replicate <2.6 Å for AMBER) (Table 1 and Fig. S2, ESI†). RMSF values obtained from the AMBER simulated system indicates that the fluctuation of all the residues including UBP are low. Similar to EXTSYN, the INTSYN system exhibits no conformational change and no significant distortion, suggesting that in this case the flexibility of the UBP has also been prevented by Taq. It is also evident (Fig. 3) that along with most of the protein–DNA residues, DS and DN also display low RMSF values confirming the relatively low fluctuating nature of the UBP.
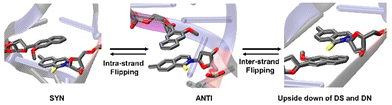 | ||
| Fig. 4 Conformational change through Intra- and Inter-strand flipping observed during the MD simulations. (Figure taken from preprint with permission51). | ||
The pattern of fluctuations of the polymerase residues as observed from the RMSF analysis is similar to EXTSYN, suggesting that a conformational change of the UBP doesn’t influence the characteristics of the system. In this case also the calculated dDS–DN distance, derived from both AMOEBA and AMBER force fields, is found to be lower than that of nBPs. Asymmetricity of the DNA duplex is reflected in the associated uneven dUB–NB (Fig. 2) and <UB–P–NB (Fig. S4, ESI†) obtained from both AMOEBA and AMBER simulations. It is observed that here dDS–DC and <DS–P–DC are found to be lower than dDN–DG and <DN–P–DG respectively, which is in agreement with the crystal structure. Comparing these geometrical parameters between EXTSYN and INTSYN, contrasting trajectories have been observed from which two conformers can be distinguished. Here also there is no significant deviations between the AMBER and AMOEBA results as both predict similar structural behaviour. We have further simulated no-overhang INTSYN system with the AMBER force field from which it is evident that in absence of hanging base pair also UBP can stabilize an intercalated structure with low RMSD values and similar RMSF and geometrical parameters (Fig. S7, ESI†). It also suggests that hanging base pair has no significant influence on the formation of nWCF UBP-incorporated DNA strand in Taq.
Despite the conformational dissimilarities between EXTSYN and INTSYN, they exhibit mostly similar RMSF pattern (ΔRMSF∼0). (Fig. S5, ESI†) This is further supported by the cross-correlation analyses for both systems (Fig. S8, ESI†), which demonstrates similar correlation patterns among the residues for both EXTSYN and INTSYN. Normal mode analysis also indicates that exclusive dominance of the 1st normal mode has been observed with similar vibration pattern (ESI†).
To investigate the effect of conformational change on Taq, we have generated the EXTANTI system via an intra-strand flipping of the DS in the EXTSYN structure where the sulfur of DS and methoxy group of DN are on opposite sides. As discussed in our previous article,51 the UBP can stay in both SYN and ANTI forms within DNA in aqueous solution with spontaneous intra-strand flipping. As depicted in Fig. 5, O–S distance for INTSYN is lower than INTANTI. But simulations of UBP-intercalated DNA bound to Taq suggests that the EXTANTI conformer of UBP inside the DNA duplex is disfavored, leading to a non-pairing between DS and DN inside the DNA duplex (Fig. 1). From all three replicates it has been found that DS–DN fails to generate an intercalated structure, and rather DS is flanked out from the DNA duplex. Comparatively higher RMSD value (Table 1 and Fig. S2, ESI†) suggests that EXTANTI induces larger structural changes compared with the SYN conformation. Notably, some specific polymerase residues mainly from the finger region of the polymerase exhibit higher RMSF (ΔRMSF(SYN-ANTI) > 0) values (Fig. S5, ESI†). From cross-correlation analysis also, significant deviation of movement correlation among the polymerase residues has been observed between SYN and ANTI conformation (Fig. S8, ESI†).
 | ||
| Fig. 5 O–S distance for INTSYN and INTANTI conformers obtained from AMBER simulation. O–S distance of crystal structure of INTSYN is 7.4 Å. Distance value are in Å. | ||
INTSYN is further reoriented through intra-strand flipping the DS which leads to the production of INTANTI structure (Fig. 1). Despite the conformational change, this UBP conformation results in an intercalated structure in Taq with low RMSD value throughout the simulation (Fig. S2, ESI†). RMSF analysis suggests that apart from terminal residues, the fluctuation of most polymerase residues is below 4.5 Å, indicating low degree of flexibility. Here also it is observed that for ANTI conformer, polymerase residues from finger region fluctuate more compared to SYN indicating perturbation arises on conformational change on the finger region. Average DS–DN distance is found to be ∼9.1 Å, indicating minor reduction of the distance as obtained from SYN conformer (Table 2). The persistence of intercalated geometry of the UBP suggests that, unlike EXT, the INT conformer doesn’t result in mispairing through intra-strand flipping, indicating that both SYN and ANTI orientations are tolerated by Taq for INT UB conformers.
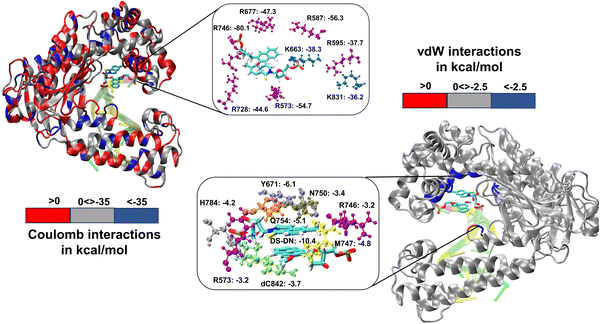
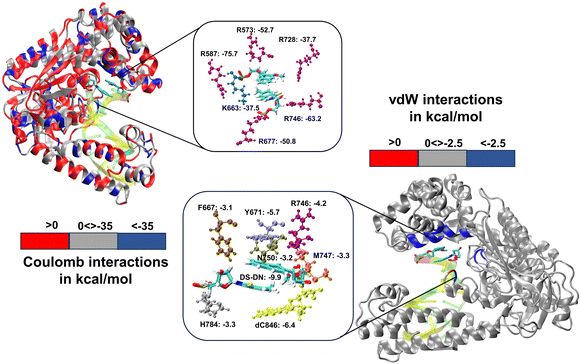
We have further performed EDA analysis to identify and quantify individual interactions between individual protein residues and the UBP (Fig. S9 and S10, ESI†). It has been observed that attractive Coulomb interactions (ECoul) arise mostly from positively charged residues. Arg and Lys, from all three polymerase subdomains (Fig. 6 and 7). For all the conformers, R587 and R746 exhibit the highest ECoul with the UBP through interactions with the phosphate backbone of 3′-DS and 5′-DN respectively. Interestingly, these two residues are identified in the interacting zone with the phosphate backbone of DS and DN from the crystal structure analysis of 4C8L (EXTSYN) but not for 4C8O (INTSYN) by Romesberg et al. R573 is also found to be strongly interacting with the UBs having higher negative ECoul for all the conformers but only reported for EXTSYN from crystal structure analysis. These findings lead to create a scope to extend the experimental investigation through mutagenesis techniques to identify the Taq residues that interact with UBP in different conformers. EDA also predicts that residues residing in the finger region of Taq interacting with the UBP through vdW interactions. Tyr671 is known as the steric gate, which is crucial for rNTP discrimination. Interestingly, in the case of UBPs, Tyr671 exhibits stabilizing vdW interactions with the exposed UBs (DS for EXTSYN and DN for INTSYN) which is also in agreement with the findings from crystal structure analysis. Nevertheless, a disparity between experimental observations and our EDA results becomes evident concerning Glu615. While crystal structure analysis propose that Glu615 forms attractive interactions with DS, our EDA findings indicate that while the van der Waals interaction is indeed attractive, the Coulombic interaction is significantly repulsive in nature and consequently the total non-covalent interaction energy between DS and Glu615 becomes positive. This is consistent with the fact that Glu615, being a negatively charged residue in physiological pH exhibits repulsive Coulombic interactions with the phosphate backbone of the UBP.
Comparing the EDA results of Taq-UBP-incorporated DNA with the 3.2 Å resolution mapped structures of Taq-nB-DNA83 it is observed that interaction profile (EvdW) looks mostly similar for both the cases. A notable distinction observed is that, in the case of nBP, Tyr671 and Phe667 form interactions with the 5'- and 3'-BP positions, respectively. In contrast, when the UBP is incorporated into DNA, significant interactions primarily occur between the exposed UBs (3'-DS for EXTSYN and 5'-DN INTSYN) and Tyr671. Additionally, in the INTSYN scenario, instead of the Phe667-5'-BP interaction, we observed EvdW interaction between Phe667 and the 3'-DS.
We have further calculated the total inter-molecular interaction (interaction between UBP and sum of all the Taq residues) differences (ΔETot) between different conformers. The difference in total interaction energy ΔETot between EXTSYN and INTSYN is found to be insignificant (−3.5 kcal mol−1) suggesting the similar stability of the UBP inside Taq for both of these conformers. However, EXTANTI displays a significant increase of ΔETot as compared to EXTSYN (ΔETot = 70.4 kcal mol−1) implying intra-strand flipping is not favored for EXT conformer, which is consistent with this conformation not being structurally stabilized. For INT, ΔETot between SYN and ANTI is found to be −12.4 kcal mol−1 indicating despite energetic difference INTANTI is also significantly stabilized inside Taq.
Mutation of R660S of the homologous E. coli DNA polymerase I (Klenow fragment, KF) conducted by Yosida et al. revealed a reduction in transitions from T to C.84 Thompson et al. reported changes in fidelity by mutating 26 amino acids in the KF, and found that DNA mismatches are recognized by two important factors; free energy difference for the partitioning of the DNA primer terminus (i) between the polymerase and exonuclease sites for several mispairs, (ii) between the residues near the active site and the mismatched pairs.46 They concluded that residues N845 and R668 are required for recognition of correct mispairs. Singh and Modak also reported that residues N845, Q849, R668, H881, and Q677 are part of a hydrogen bond track. Computational studies have also been done to investigate the effect of mutation of DNA polymerase I towards mispairing of the base pairs in the terminal positions.49,85
Collectively, previous studies confirmed that mutation of KF residues R668, R682, E710 and N845 (R573, R587, E615 and Asn750 for Taq) are the key residues controlling the fidelity within the KF84–87 whereas E742 and A743 are found to be crucial for the elongation activity.87 Our studies also identified similar residues with significant interactions (E) with UBP particularly for EXTSYN, INTSYN and INTANTI. Interestingly these residues also exhibit significant difference in interactions (ΔE) on conformational change. It has been observed that Coulomb interaction profile (ECoul) almost looks similar apart from few residues (R573, R587, E615 and R746) displaying significant altered interactions (ΔECoul ≠ 0) from EXTSYN to INTSYN. (Fig. 8) Similar vdW interaction profile (EvdW) has also been observed for these two conformers with few residues exhibiting altered vdW interactions (ΔEvdW ≠ 0) on finger region. Intra-strand flipping between SYN and ANTI also leads to minimal perturbation of Coulomb and vdW interaction between UBP and Taq (Fig. 9). The difference in inter-molecular interactions between the different UBP orientations results in almost all residues exhibiting similar (de)stabilizing roles, albeit there are some exceptions, among them R573, R587, E615, E742 and R746 are significant. However, the difference of interaction profile is prominent between SYN and ANTI for EXT with several residues showing altered interactions indicating the EXTANTI is not stabilized by Taq, leading to non-pairing of the UBP. The extent of non-covalent interactions between DS and DN is also obtained from EDA. Interaction between DS and DN is found to be highest for EXTSYN (EvdW = −10.4 kcal mol−1) followed by INTSYN (EvdW = −9.9 kcal mol−1) and INTANTI (EvdW = −9.2 kcal mol−1) and least for EXTANTI (EvdW = −3.5 kcal mol−1) indicating apart from EXTANTI intercalation persist for all three conformers. During the examination of adjacent nBP interactions, EDA analysis indicates that the neighboring base pair exhibits relatively lower stability when contrasted with other base pairs, which suggest that the structure and stability of adjacent BP have been affected by the presence of the unconventional orientation of UBP.
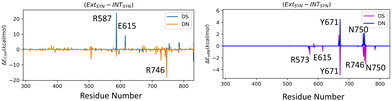 | ||
| Fig. 8 Difference in interaction profiles (ΔECoul and ΔEvdW) between EXTSYN and INTSYN. Energy values are in kcal mol−1. | ||
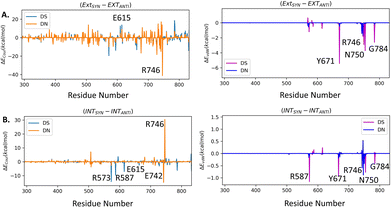 | ||
| Fig. 9 Difference in interaction profiles (ΔECoul and ΔEvdW) between (A) EXTSYN and EXTANTI, (B) (A) INTSYN and INTANTI. Energy values are in kcal mol−1. | ||
Conclusions
Our research delved into the structural characteristics and conformational orientations of UBP-incorporated DNA within the binary Taq. Further, we conducted an in-depth analysis to predict the interaction profile between UBP and Taq through Coulombic and vdW interactions. Both the AMOEBA and AMBER force fields employed in this study produce consistent results that agree with experimental outcomes. Our simulated results predict that flexibility of the UBP- incorporated DNA, observed in the solution, is arrested by the polymerase. This stabilization leads to a stable intercalated form of the UBP that is conducive to DNA polymerization with unnatural bases. It has been observed that inter-strand flipping from EXT to INT leads to the generation of minimal perturbation of the stabilization of the UBP within Taq, whereas intra-strand flipping from SYN to ANTI leads to the generation of a non-pairing structure of the UBP with significant perturbations in the polymerase residues specifically for EXT conformers. Further EDA analysis established the interaction profiles between UBP and polymerase residues which also depicts minor differences of interactions during inter-strand flipping and intra-strand flipping for INT. Lack of pairing of DS–DN in EXTANTI leads to change the interaction profiles significantly. Unlike nBP-polymerase interactions, Tyr671 interacts with both 3′ and 5′-UB depending on the exposure of the UB in the conformers. Overall, our systematic MD simulation associated with EDA analysis portrayed the structural properties, effect of conformational changes and interaction profiles of binary system of Taq in complex with a DNA duplex including an intercalated DS–DN pair.Conflicts of interest
There are no conflicts to declare.Acknowledgements
This work was supported by NIH R01GM108583 and Fulbright-Nehru postdoctoral Scholarship. Computing time from UNT CASCaM funded by NSF Grant No. CHE1531468 and OAC-2117247 is gratefully acknowledged. Tanay Debnath is a USIEF postdoctoral fellow (Fulbright-Nehru postdoctoral Scholarship). Computational time for this project was provided by the University of North Texas CASCaM CRUNTCh3 and 4 high-performance cluster and the University of Texas at Dallas, Cyberinfrastructure and Research Services, Ganymede and Titan HPC clusters and NCSA DELTA at University of Illinois Urbana-Champaign. The authors thank the reviewers for their constructive comments, which have helped improve our manuscript.References
- J. D. Watson and F. H. C. Crick, Nature, 1953, 171, 737–738 CrossRef CAS PubMed.
- P. S. Freemont, J. M. Friedman, L. S. Beese, M. R. Sanderson and T. A. Steitz, Proc. Natl. Acad. Sci. U. S. A., 1988, 85, 8924–8928 CrossRef CAS PubMed.
- L. S. Beese, J. M. Friedman and T. A. Steitz, Biochemistry, 1993, 32, 14095–14101 CrossRef CAS PubMed.
- R. D. Kuchta, P. Benkovic and S. J. Benkovic, Biochemistry, 1988, 27, 6716–6725 CrossRef CAS PubMed.
- K. Singh and M. J. Modak, Biochemistry, 2005, 44, 8101–8110 CrossRef CAS PubMed.
- J. Gouge, C. Ralec, G. Henneke and M. Delarue, J. Mol. Biol., 2012, 423, 315–336 CrossRef CAS.
- K. H. Lee, K. Hamashima, M. Kimoto and I. Hirao, Curr. Opin. Biotechnol, 2018, 51, 8–15 CrossRef CAS.
- D. A. Malyshev and F. E. Romesberg, Angew. Chem., Int. Ed., 2015, 54, 11930–11944 CrossRef CAS PubMed.
- S. Hoshika, N. A. Leal, M.-J. Kim, M.-S. Kim, N. B. Karalkar, H.-J. Kim, A. M. Bates, N. E. Watkins, H. A. SantaLucia, A. J. Meyer, S. DasGupta, J. A. Piccirilli, A. D. Ellington, J. SantaLucia, M. M. Georgiadis and S. A. Benner, Science, 2019, 363, 884–887 CrossRef CAS PubMed.
- T. P. Hettinger, Proc. Natl. Acad. Sci. U. S. A., 2017, 114, E6476–E6477 CrossRef CAS PubMed.
- R. Yamashige, M. Kimoto, Y. Takezawa, A. Sato, T. Mitsui, S. Yokoyama and I. Hirao, Nucleic Acids Res., 2012, 40, 2793–2806 CrossRef CAS PubMed.
- M. Manandhar, E. Chun and F. E. Romesberg, J. Am. Chem. Soc., 2021, 143, 4859–4878 CrossRef CAS PubMed.
- D. A. Malyshev, K. Dhami, H. T. Quach, T. Lavergne, P. Ordoukhanian, A. Torkamani and F. E. Romesberg, Proc. Natl. Acad. Sci. U. S. A., 2012, 109, 12005–12010 CrossRef CAS PubMed.
- K. Hashimoto, E. C. Fischer and F. E. Romesberg, J. Am. Chem. Soc., 2021, 143, 8603–8607 CrossRef CAS PubMed.
- N. Tarashima, Y. Komatsu, K. Furukawa and N. Minakawa, Chemistry, 2015, 21, 10688–10695 CrossRef CAS PubMed.
- M. Kimoto, R. Yamashige, K.-I. Matsunaga, S. Yokoyama and I. Hirao, Nat. Biotechnol., 2013, 31, 453–457 CrossRef CAS PubMed.
- N. R. Jena and P. Das, J. Biomol. Struct. Dyn., 2023, 41, 366–376 CrossRef CAS PubMed.
- N. Beiranvand, M. Freindorf and E. Kraka in Hydrogen Bonding in Natural and Unnatural Base Pairs—A Local Vibrational Mode Study, vol. 26, 2021 Search PubMed.
- J. Riedl, Y. Ding, A. M. Fleming and C. J. Burrows, Nat. Commun., 2015, 6, 8807 CrossRef CAS PubMed.
- M. M. Georgiadis, I. Singh, W. F. Kellett, S. Hoshika, S. A. Benner and N. G. J. Richards, J. Am. Chem. Soc., 2015, 137, 6947–6955 CrossRef CAS PubMed.
- R. Dörrenhaus, P. K. Wagner and S. Kath-Schorr, Biol. Chem., 2023, 404, 883–896 CrossRef PubMed.
- M. Kimoto and I. Hirao, ACS Synth. Biol., 2017, 6, 1944–1951 CrossRef.
- I. Hirao and M. Kimoto, Proc. Jpn. Acad., Ser. B, 2012, 88, 345–367 CrossRef CAS PubMed.
- T. Lavergne, D. A. Malyshev and F. E. Romesberg, Chem. – Eur. J., 2012, 18, 1231–1239 CrossRef CAS PubMed.
- S. Ochoa and V. T. Milam in Modified Nucleic Acids: Expanding the Capabilities of Functional Oligonucleotides, vol. 25, 2020 Search PubMed.
- A. Ambrogelly, S. Palioura and D. Söll, Nat. Chem. Biol., 2007, 3, 29–35 CrossRef CAS.
- I. Hirao, M. Kimoto and R. Yamashige, Acc. Chem. Res., 2012, 45, 2055–2065 CrossRef CAS.
- M. P. Ledbetter, R. J. Karadeema and F. E. Romesberg, J. Am. Chem. Soc., 2018, 140, 758–765 CrossRef CAS PubMed.
- C. Kaul, M. Müller, M. Wagner, S. Schneider and T. Carell, Nat. Chem., 2011, 3, 794–800 CrossRef CAS PubMed.
- K. Betz, D. A. Malyshev, T. Lavergne, W. Welte, K. Diederichs, T. J. Dwyer, P. Ordoukhanian, F. E. Romesberg and A. Marx, Nat. Chem. Biol., 2012, 8, 612–614 CrossRef CAS PubMed.
- K. Betz, D. A. Malyshev, T. Lavergne, W. Welte, K. Diederichs, F. E. Romesberg and A. Marx, J. Am. Chem. Soc., 2013, 135, 18637–18643 CrossRef CAS PubMed.
- A. Marx and K. Betz, Chem. – Eur. J., 2020, 26, 3446–3463 CrossRef CAS PubMed.
- D. A. Malyshev, K. Dhami, T. Lavergne, T. Chen, N. Dai, J. M. Foster, I. R. Corrêa and F. E. Romesberg, Nature, 2014, 509, 385–388 CrossRef CAS PubMed.
- F. E. Romesberg in Unnatural Base Pairs to Expand the Genetic Alphabet and Code, ed N. Sugimoto, Springer Nature Singapore, Singapore, 2022, pp. 1–21 Search PubMed.
- A. W. Feldman, V. T. Dien, R. J. Karadeema, E. C. Fischer, Y. You, B. A. Anderson, R. Krishnamurthy, J. S. Chen, L. Li and F. E. Romesberg, J. Am. Chem. Soc., 2019, 141, 10644–10653 CrossRef CAS PubMed.
- L. Sun, X. Ma, B. Zhang, Y. Qin, J. Ma, Y. Du and T. Chen, RSC Chem. Biol., 2022, 3, 1173–1197 RSC.
- A. W. Feldman and F. E. Romesberg, Acc. Chem. Res., 2018, 51, 394–403 CrossRef CAS PubMed.
- A. W. Feldman and F. E. Romesberg, J. Am. Chem. Soc., 2017, 139, 11427–11433 CrossRef CAS PubMed.
- M. Kimoto and I. Hirao, Chem. Soc. Rev., 2020, 49, 7602–7626 RSC.
- E. C. Fischer, K. Hashimoto, Y. Zhang, A. W. Feldman, V. T. Dien, R. J. Karadeema, R. Adhikary, M. P. Ledbetter, R. Krishnamurthy and F. E. Romesberg, Nat. Chem. Biol., 2020, 16, 570–576 CrossRef CAS PubMed.
- J. Oh, J. Shin, I. C. Unarta, W. Wang, A. W. Feldman, R. J. Karadeema, L. Xu, J. Xu, J. Chong, R. Krishnamurthy, X. Huang, F. E. Romesberg and D. Wang, Nat. Chem. Biol., 2021, 17, 906–914 CrossRef CAS PubMed.
- S. A. Mukba, P. K. Vlasov, P. M. Kolosov, E. Y. Shuvalova, T. V. Egorova and E. Z. Alkalaeva, Mol. Biol., 2020, 54, 475–484 CrossRef CAS.
- T. D. Christian, L. J. Romano and D. Rueda, Proc. Natl. Acad. Sci. U. S. A., 2009, 106, 21109–21114 CrossRef CAS PubMed.
- V. Khare and K. A. Eckert, Mutat. Res., Fundam. Mol. Mech. Mutagen., 2002, 510, 45–54 CrossRef CAS PubMed.
- K. A. Johnson, Biochim. Biophys. Acta, Proteins Proteomics, 2010, 1804, 1041–1048 CrossRef CAS PubMed.
- E. H. Z. Thompson, M. F. Bailey, E. J. C. van der Schans, C. M. Joyce and D. P. Millar, Biochemistry, 2002, 41, 713–722 CrossRef CAS PubMed.
- S. K. Jozwiakowski, B. J. Keith, L. Gilroy, A. J. Doherty and B. A. Connolly, Nucleic Acids Res., 2014, 42, 9949–9963 CrossRef CAS.
- A. R. Walker and G. A. Cisneros, Chem. Res. Toxicol., 2017, 30, 1922–1935 Search PubMed.
- A. A. Elias and G. A. Cisneros, Adv. Protein Chem. Struct. Biol., 2014, 96, 39–75 Search PubMed.
- L. Aravind and E. V. Koonin, Nucleic Acids Res., 1998, 26, 3746–3752 CrossRef CAS PubMed.
- G. A. C. Tanay Debnath, Phys. Chem. Chem. Phys., 2024 10.1039/D3CP05572H.
- I. Negi, P. Kathuria, P. Sharma and S. D. Wetmore, Phys. Chem. Chem. Phys., 2017, 19, 16365–16374 RSC.
- R. Galindo-Murillo and J. Barroso-Flores, Phys. Chem. Chem. Phys., 2017, 19, 10571–10580 RSC.
- R. Galindo-Murillo and J. Barroso-Flores, J. Biomol. Struct. Dyn., 2020, 38, 4098–4106 CrossRef CAS PubMed.
- L. Eberlein, F. R. Beierlein, N. J. R. van Eikema Hommes, A. Radadiya, J. Heil, S. A. Benner, T. Clark, S. M. Kast and N. G. J. Richards, J. Chem. Theory Comput., 2020, 16, 2766–2777 CrossRef CAS PubMed.
- S. Jahiruddin and A. Datta, J. Phys. Chem. B, 2015, 119, 5839–5845 CrossRef CAS PubMed.
- S. Jahiruddin, N. Mandal and A. Datta, ChemPhysChem, 2018, 19, 67–74 CrossRef CAS PubMed.
- H. Wang, L. Wang, N. Ma, W. Zhu, B. Huo, A. Zhu and L. Li, ACS Synth. Biol., 2022, 11, 334–342 CrossRef CAS PubMed.
- https://upjv.q4md-forcefieldtools.org/REDServer-Development/overview.php .
- P. Mark and L. Nilsson, J. Phys. Chem. A, 2001, 105, 9954–9960 CrossRef CAS.
- C. Tian, K. Kasavajhala, K. A. A. Belfon, L. Raguette, H. Huang, A. N. Migues, J. Bickel, Y. Wang, J. Pincay, Q. Wu and C. Simmerling, J. Chem. Theory Comput., 2020, 16, 528–552 CrossRef PubMed.
- M. Zgarbová, J. Šponer, M. Otyepka, T. E. Cheatham, III, R. Galindo-Murillo and P. Jurečka, J. Chem. Theory Comput., 2015, 11, 5723–5736 CrossRef PubMed.
- P. Ren and J. W. Ponder, J. Comput. Chem., 2002, 23, 1497–1506 CrossRef CAS PubMed.
- P. Ren and J. W. Ponder, J. Phys. Chem. B, 2003, 107, 5933–5947 CrossRef CAS.
- P. Ren and J. W. Ponder, J. Phys. Chem. B, 2004, 108, 13427–13437 CrossRef CAS.
- P. Ren, C. Wu and J. W. Ponder, J. Chem. Theory Comput., 2011, 7, 3143–3161 CrossRef CAS PubMed.
- L. Lagardère, L.-H. Jolly, F. Lipparini, F. Aviat, B. Stamm, Z. F. Jing, M. Harger, H. Torabifard, G. A. Cisneros, M. J. Schnieders, N. Gresh, Y. Maday, P. Y. Ren, J. W. Ponder and J.-P. Piquemal, Chem. Sci., 2018, 9, 956–972 RSC.
- A. J. Stone, J. Chem. Theory Comput., 2005, 1, 1128–1132 CrossRef CAS PubMed.
- C. Schafmeister, W. Ross and V. Romanovski, LEAP, University of California, San Francisco, 1995 Search PubMed.
- D. A. Case, K. Belfon, I. Y. Ben-Shalom, S. R. Brozell, D. S. Cerutti, T. E. Cheatham, III, V. W. D. Cruzeiro, T. A. Darden, R. E. Duke, G. Giambasu, M. K. Gilson, H. Gohlke, A. W. Goetz,R. Harris, S. Izadi, S. A. Izmailov, K. Kasavajhala, A. Kovalenko, R. Krasny, T. Kurtzman, T. S. Lee, S. LeGrand, P. Li, C. Lin, J. Liu, T. Luchko, R. Luo, V. Man, K. M. Merz, Y. Miao, O. Mikhailovskii, G. Monard, H. Nguyen, A. Onufriev, F. Pan, S. Pantano, R. Qi, D. R. Roe, A. Roitberg, C. Sagui, S. Schott-Verdugo, J. Shen, C. L. Simmerling, N. R. Skrynnikov, J. Smith, J. Swails, R. C. Walker, J. Wang, L. Wilson, R. M. Wolf, X. Wu, Y. Xiong, Y. Xue, D. M. York and P. A. Kollman, AMBER 2020, University of California, San Francisco, 2020 Search PubMed.
- M. H. M. Olsson, C. R. Søndergaard, M. Rostkowski and J. H. Jensen, J. Chem. Theory Comput., 2011, 7, 525–537 CrossRef CAS PubMed.
- C. R. Søndergaard, M. H. M. Olsson, M. Rostkowski and J. H. Jensen, J. Chem. Theory Comput., 2011, 7, 2284–2295 CrossRef PubMed.
- J.-P. Ryckaert, G. Ciccotti and H. J. C. Berendsen, J. Comput. Phys., 1977, 23, 327–341 CrossRef CAS.
- R. Salomon-Ferrer, A. W. Götz, D. Poole, S. Le Grand and R. C. Walker, J. Chem. Theory Comput., 2013, 9, 3878–3888 CrossRef CAS PubMed.
- D. R. Roe and T. E. Cheatham, III, J. Chem. Theory Comput., 2013, 9, 3084–3095 CrossRef CAS PubMed.
- S. Van Der Walt, S. C. Colbert and G. Varoquaux, Comput. Sci. Eng., 2011,(13), 22–30 Search PubMed.
- J. D. Hunter, Comput. Sci. Eng., 2007, 9, 90–95 Search PubMed.
- W. McKinney, In Data Structures for Statistical Computing in Python, Proceedings of the 9th Python in Science Conference, Austin, TX, 2010, vol. 445, pp. 51–56 Search PubMed.
- E. Leddin, Cisneros Research Group and G. Andres Cisneros, 2021, CisnerosResearch/AMBER-EDA: First Release (v0.1). Zenodo. https://zenodo.org/records/4469902 Search PubMed.
- L. Martínez, R. Andrade, E. G. Birgin and J. M. Martínez, J. Comput. Chem., 2009, 30, 2157–2164 CrossRef PubMed.
- U. Essmann, L. Perera, M. L. Berkowitz, T. Darden, H. Lee and L. G. Pedersen, J. Chem. Phys., 1995, 103, 8577–8593 CrossRef CAS.
- P. J. Steinbach and B. R. Brooks, J. Comput. Chem., 1994, 15, 667–683 CrossRef CAS.
- S. H. Eom, J. Wang and T. A. Steitz, Nature, 1996, 382, 278–281 CrossRef CAS PubMed.
- K. Yoshida, A. Tosaka, H. Kamiya, T. Murate, H. Kasai, Y. Nimura, M. Ogawa, S. Yoshida and M. Suzuki, Nucleic Acids Res., 2001, 29, 4206–4214 CrossRef CAS PubMed.
- K. Singh and M. J. Modak, J. Biol. Chem., 2003, 278, 11289–11302 CrossRef CAS PubMed.
- S. E. Graham, F. Syeda and G. A. Cisneros, Biochemistry, 2012, 51, 2569–2578 CrossRef CAS PubMed.
- T. Yamagami, S. Ishino, Y. Kawarabayasi and Y. Ishino, Front. Microbiol., 2014, 5, 461 Search PubMed.
Footnote |
| † Electronic supplementary information (ESI) available: Additional details of MD, EDA (PDF). Additional ESI for the initial coordinates and parameters for all of the studied systems (ESI-1.zip) (ZIP). NMA movies of all the conformers (NMA.zip) (ZIP). See DOI: https://doi.org/10.1039/d3cp05571j |
| This journal is © the Owner Societies 2024 |