The heterointerface effect to boost the catalytic performance of single atom catalysts for sulfur conversion in lithium–sulfur batteries†
Haikuan
Liang
,
Zhihao
Zeng
 ,
Zhengping
Qiao
,
Zhengping
Qiao
 *,
Yan
Li
*,
Yan
Li
 * and
Chengxin
Wang
* and
Chengxin
Wang

State key Laboratory of Optoelectronic Materials and Technologies, School of Materials Science and Engineering, Sun Yat-sen (Zhongshan) University, Guangzhou 510275, People's Republic of China. E-mail: cesqzp@mail.sysu.edu.cn; liyan266@mail.sysu.edu.cn
First published on 20th January 2024
Abstract
Lithium–sulfur (Li–S) batteries are considered as one of the promising next-generation energy storage devices due to their characteristics of high energy density and low cost. However, the shuttle effect and sluggish conversion of lithium polysulfide (LiPs) have hindered their commercial applications. To address these issues, in our previous works, we have screened several highly efficient single atom catalysts (SACs) (MN4@G, M = V, Mo and W) with atomically dispersed transition metal atoms supported by nitrogen doped graphene based on high throughput calculations. Nevertheless, they still suffer from low loading of metal centers and unsatisfactory capability for accelerating the reaction kinetics. To tackle such problems, based on first-principles calculations, we systematically investigated the heterointerface effect on the catalytic performance of such three MN4@G toward sulfur conversion upon forming heterostructures with 5 typical two-dimensional materials of TiS2, C3N4, BN, graphene and reduced graphene oxide. Guided by efficient descriptors proposed in our previous work, we screened VN4@G/TiS2, MoN4@G/TiS2 and WN4@G/TiS2 possessing low Li2S decomposition barriers of 0.54, 0.44 and 0.41 eV, respectively. They also possess enhanced capabilities for catalyzing the sulfur reduction reaction as well as stabilizing soluble LiPs. More interestingly, the heterointerface can enhance the capability of the carbon atoms far away from the metal centers for trapping LiPs. This work shows that introducing a heterointerface is a promising strategy to boost the performance of SACs in Li–S batteries.
1. Introduction
To reduce the greenhouse gas emission caused by the consumption of fossil fuels stimulates great interest from researchers to develop high-performance energy storage devices. Among these state-of-the-art energy storage devices, lithium–sulfur (Li–S) batteries have garnered significant attention in recent years owing to their high theoretical specific capacity of 1675 mA h g−1 and high energy density of 2600 W h kg−1.1–5 However, certain issues still exist, weakening the performance of Li–S batteries and thus impeding their commercial applications. The most significant issue among them is the occurrence of the ‘shuttle effect’. During the discharge process, lithium polysulfides (LiPs) formed on the cathode can dissolve into the electrolyte, diffuse through the separator, and accumulate on the lithium anode. This phenomenon leads to a decrease in the Coulombic efficiency and capacity degradation of the batteries, thus hindering their cycle performance.6,7 Moreover, the intrinsic insulation properties of sulfur (5 × 10−30 S cm−1) and Li2S (10−13 S cm−1) hinder the efficient transfer of electrons, resulting in sluggish electrochemical reactions.8 Therefore, the rational design of catalysts exhibiting suitable adsorption capability for LiPs and superior catalytic performance for accelerating the reaction kinetics of sulfur redox in Li–S batteries has attracted increasing research attention in recent years.9–12Among the efficient catalysts, carbonaceous materials supported single atom catalysts (SACs) have been widely explored due to their superior catalytic performance for sulfur redox and LiP stabilization.10,13–15 Nevertheless, the performances of SACs for catalyzing sulfur redox, particularly the sulfur evolution reaction (SER), are still unsatisfactory. Therefore, to further enhance their catalytic performance toward the sulfur conversion is of importance, which might be realized by tailoring the electronic and structural properties of the central metals of SACs. In this regard, significant research efforts have been devoted to the design of SACs with transition metal atoms possessing various coordination environments, which involve graphene,13,14 C2N10 and g-C3N415 as the supports. In addition to doping strategies, the introduction of heterointerfaces has also been proved to be an efficient strategy to enhance the catalytic performance of electrochemical catalysts for energy storage and conversion, which can be realized by assembling two-dimensional (2D) materials into van der Waals heterostructures.16 These heterostructures are formed by chemical bonding or physical combination of two or more 2D materials. In recent years, this concept has also been adopted to design electrocatalysts for Li–S batteries, which will incorporate the merits of individual components to neutralize the shortcomings of each building block17–22 of the heterointerfaces. Nevertheless, there have been no reports on exploring the heterointerface effect on the catalytic performance of SACs for sulfur chemistry.
Up to now, various materials have been investigated for use as electrodes including 2D carbonaceous materials,23,24 metal sulfides,25,26 metal oxides27,28 and Mxenes.29,30 This implies that the combination of SACs with such materials will give rise to a huge number of heterostructures given the various metal centers of SACs. In this regard, to explore the catalytic performance particularly the SER performance of such heterostructures will be very time consuming, which accordingly requires an efficient descriptor guiding the systematic investigation. In our previous work, we have systematically investigated the descriptors of the Li2S decomposition energy barrier on MN4@G (typical configuration of SACs containing pyridine-N coordinated transition-metal atoms) and found that some properties could serve as universal descriptors for the rational design of SACs giving rise to a low Li2S decomposition barrier, which could predict the activity of the catalyst quickly.14
Here, we investigated systematically the performance of heterostructures for sulfur chemistry, which are built by combining SACs with 5 typical 2D materials. For SACs, we utilized three MN4@G (M = V, Mo and W) with the highest catalytic activity for Li2S decomposition screened in our previous work.14 The other 5 types of 2D materials are TiS2,31 C3N4,32 BN,33 graphene (G)34 and reduced graphene oxide (rGO).35 After examining the extendibility, we selected ΔE (energy difference before and after the Li2S decomposition) as the efficient descriptor for screening several heterostructures with enhanced catalytic performance for Li2S decomposition, which were then further explored for their performance for catalyzing SRR and stabilizing LiPs. Our work will pave a new way for designing electrocatalysts for sulfur chemistry in alkaline metal sulfide batteries.
2. Computational details
The DFT simulations were carried out by using the Vienna Ab initio Simulation Package (VASP).36,37 Additionally, the Perdew–Burke–Ernzerhof functional38,39 within the generalized gradient approximation (GGA-PBE)40 was employed to calculate the exchange–correlation energy and the projector augmented wave (PAW) method was used to describe the electron–ion interactions.41,42 We employed the DFT-D2 scheme to take the van der Waals interactions into account.43 To avoid the interaction between two neighboring surfaces, we set the vacuum space to be larger than 20 Å. In all of the calculations, the plane-wave cutoff energy was set to be 520 eV. All the calculations were carried out with the force and energy thresholds of 0.02 eV Å−1 and 10−4 eV, respectively. Self-consistent field (SCF) calculations were performed to obtain the energy of the optimized structure while non-self-consistent field (NSCF) calculations were used to gain the electronic density of states (DOS). Three different k-point meshes of 2 × 2 × 1, 3 × 3 × 1 and 7 × 7 × 1 were employed in the structural optimizations, and SCF and NSCF calculations. For the Li2S decomposition, the minimum energy path (MEP) profiles are obtained by using the climbing image nudged elastic band (CI-NEB) method.44,45 The formulas for calculating binding energy of heterostructure materials, lattice mismatch of the heterostructure materials, adsorption energy, zero vibration energy, charge density difference and Gibbs free energy changes are labeled as eqn (1)–(10).The binding energy of heterostructures were calculated according to
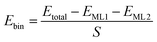 | (1) |
| |a − ah|/ah × 100% | (2) |
The adsorption energy (Eads) is calculated based on the following formula:
| Eads = Etotal − Esubstrate − Eadsorbate | (3) |
The Gibbs free energy of LiPs and S8 on substrates are calculated by
| G = EDFT + Ezpe − TS | (4) |
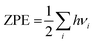 ; here h and νi are the Planck constant and vibrational frequencies, respectively. S is the entropy, the entropies of molecules we utilized were acquired from experimental values in the NIST database,46 while those of the absorbed intermediates were set to zero; T is the room temperature and is set at 298.15 K.
; here h and νi are the Planck constant and vibrational frequencies, respectively. S is the entropy, the entropies of molecules we utilized were acquired from experimental values in the NIST database,46 while those of the absorbed intermediates were set to zero; T is the room temperature and is set at 298.15 K.
The elementary reaction steps for sulfur reduction in lithium–sulfur (Li–S) batteries are considered as
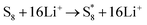 | (5) |
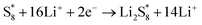 | (6) |
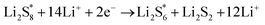 | (7) |
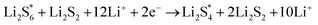 | (8) |
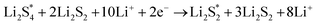 | (9) |
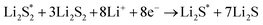 | (10) |
The linear correlations between Eb and three descriptors ΔE, ΔE(*LiS) and ICOHP were identified in our previous work.14
| Eb = 1.07 × ΔE + 0.16 | (11) |
| Eb = 0.87 × ΔE(*LiS) + 0.38 | (12) |
| Eb = −1.30 × ICOHP − 3.49 | (13) |
| ΔE = E(*Li + *LiS) − E(*Li2S) | (14) |
| ΔE(*LiS) = E(*LiS) + E(Li)bcc − E(*Li2S) | (15) |
3. Results and discussion
3.1 Structure and electronic properties of heterostructures
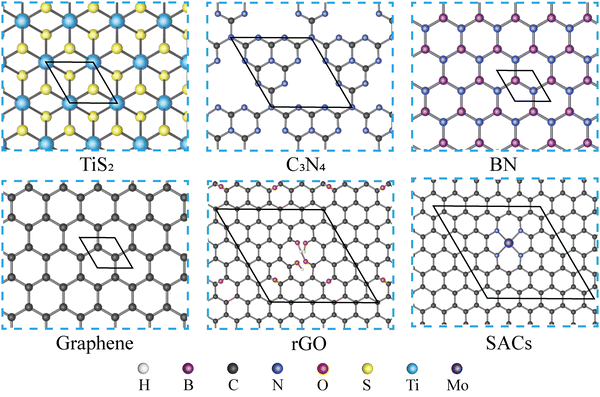
As shown in Fig. 1, five types of monolayers, which are TiS2, g-C3N4, BN, graphene, and rGO, are selected and combined with MN4@G to build heterostructures. Due to the different lattice parameters of those monolayers, various supercells are set up for TiS2, g-C3N4, BN, graphene and rGO to guarantee a small lattice mismatch in the heterostructure. The primitive cell parameters, corresponding supercells, lattice mismatches and the total number of atoms contained in the simulation box of the heterostructures are listed in Table S1 (ESI†). Regarding the model of rGO and MN4@G, they are built using a 6 × 6 × 1 supercell of graphene. rGO is then achieved by introducing two kinds of oxygen-containing defects in the graphene lattice. One type refers to the vacancy defects with hydroxyl saturating the dangling bonds of carbon atoms and the other type includes the epoxide functional groups adsorbed on the carbon atoms while the MN4@G are modeled by locating the TM atoms in the N doped graphene with the central metal atoms coordinated with four N atoms, which are accordingly labeled as MN4@G. The largest lattice mismatch is 2.354% between TiS2 and MN4@G, and the others are lower than 2% when MN4@G forms heterostructures with g-C3N4(1.777%), BN(1.749%), graphene(0.000%) and rGO(1.211%). In order to distinguish those various heterostructures, we named them MN4@G/ML (ML = TiS2, C3N4, BN, G, rGO), as shown in Fig. S1 (ESI†). Moreover, MN4@G/ML (ML = TiS2, C3N4, G and rGO) and G/BN prefer AB stacking, while the configuration of MN4@G/BN possesses a mixture of AB- and AA-stacking.The interaction strength between the components of the heterostructures can be evaluated by the binding energy (Ebin), which is calculated by eqn (1) in the ESI.† As listed in Table S2 (ESI†), the Ebin values for different heterostructures are between −13 and −21 meV Å−2 and close to that for van der Waals interaction,48 which can also be confirmed by the interlayer distance of 3.20–3.96 Å. Among them, the largest and smallest Ebin are −26.39 meV Å−2 (WN4@G/BN) and −7.49 meV Å−2 (MoN4@G/C3N4), respectively. Moreover, MN4@G can bind more strongly with BN than with other monolayers, while the binding strength of MN4@G with TiS2 and C3N4 are relatively weak. Among MN4@G/TiS2 or MN4@G/BN, the interaction strength of monolayers as M = V is stronger than that when M = Mo and W, due to the fact that V atom tends to sit between the two monolayers by forming chemical bond with two components of the heterostructures, as shown in Fig. S1 (ESI†). Note that heterostructures of MN4@G/rGO have significantly larger interlayer distances than the others due to the presence of functional groups on the surface of rGO.
The formation of heterostructures also induces the charge redistribution in the components, i.e. MN4@G loses charges to the adjacent layers leading to the metal centers more positively charged compared to that in the monolayer of MN4@G. The diagram of charge density difference of various heterostructures are illustrated in Fig. S1 (ESI†). In general, the charge transfer occurs mainly around the MN4 moiety and the specific values of charge transfer are listed in Table S2 (ESI†). However, for MN4@G/TiS2, there is a uniform charge redistribution throughout the interface. In general, the charge transfer between the monolayers in MN4@G/TiS2 and MN4@G/C3N4 is more pronounced than that in MN4@G/BN and MN4@G/G as illustrated in Table S2 (ESI†). Moreover, for MN4@G/TiS2 and MN4@G/C3N4, M = V gives rise to more charge transfer than M = Mo and W. Taking MN4@G/TiS2 as an example, the charge transfer in MN4@G/TiS2 is 1.48 e per cell, which is more than those in MoN4@G/TiS2 (1.11 e per cell) and WN4@G/TiS2 (1.11 e per cell). Although the total amount of charge transfer for MN4@G/BN is less than that for MN4@G/TiS2, the interaction between the monolayers is still stronger in MN4@G/BN than that in MN4@G/TiS2. This is attributed to the fact that the charge redistribution only occurs around the MN4 in the former case while there is wider range of charge redistribution for the rest case.
3.2 Catalytic performance of MN4@G/ML for SER
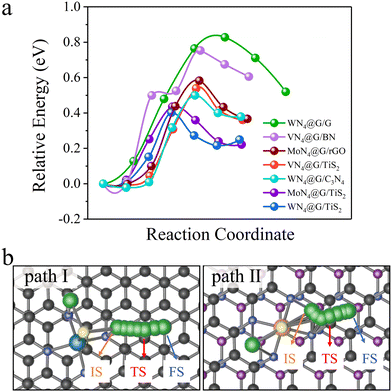
We next explored the catalytic performance of the heterostructures for SER. In the charging cycles of Li–S batteries, the decomposition of Li2S is a crucial step for SER requiring efficient electrocatalysts to accelerate the reaction kinetics. This is usually evaluated by the energy barrier (Eb) of Li2S decomposition, which can be achieved based on the nudged elastic band (NEB) method.14We selected some heterostructures as representatives and explored the decomposition of Li2S on them. The energy profiles of Li2S decomposition on WN4@G/G, VN4@G/BN, MoN4@G/rGO, WN4@G/C3N4, MoN4@G/TiS2 and WN4@G/TiS2 with the energetically preferable decomposition pathways are illustrated in Fig. 2. It can be seen from Fig. 2a that the Eb of Li2S decompositions on all heterostructures are lower than 1.0 eV. The lowest and the highest Eb are observed on WN4@G/TiS2 (0.41 eV) and WN4@G/G (0.83 eV), respectively. The catalytic performances of the heterostructures for the Li2S decomposition follow the order WN4@G/TiS2 > MoN4@G/TiS2 > WN4@G/C3N4 > VN4@G/TiS2 > MoN4@G/rGO > VN4@G/BN > WN4@G/G, and the corresponding Eb values are 0.41, 0.44, 0.50, 0.54, 0.58, 0.75 and 0.83 eV respectively. It should be noted that those heterostructures possess more enhanced capability for catalyzing SER than individual MN4@G, such as VN4@G (Eb = 0.70 eV), MoN4@G (Eb = 0.58 eV), WN4@G (Eb = 0.55 eV) and CoN4@G (Eb = 1.37 eV).13,14 Overall, the catalytic performance of MN4@G for the SER will be significantly improved when forming the heterostructures with C3N4, TiS2 and rGO. Moreover, due to the different adsorption configurations of Li2S, two different Li2S decomposition pathways are identified as shown in Fig. 2b. And the cleavage of the Li–S bond on WN4@G/G is along the path I, while for the rest cases it follows the relatively short path II.
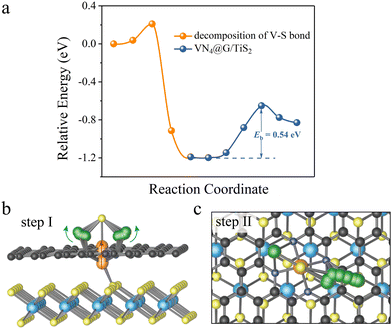
It should be noted that the decomposition of Li2S on VN4@G/TiS2 is a bit complex as reflected by the energy profiles of Li2S decomposition (see Fig. 3a). This is due to the specific structural configuration of VN4@G/TiS2, for which the V atom sits between the graphene layer and TiS2 (see Fig. 3b). This further leads to the weak interaction between Li2S and the V atom upon the adsorption of Li2S on VN4@G/TiS2 since the S atom of Li2S cannot form a chemical bond with the V atom with only the Li atoms binding to N/C atoms from the N doped graphene. Overall, the whole process of Li2S decomposition on VN4@G/TiS2 can be divided into two subprocesses. Firstly, before the breakage of Li–S bonds in adsorbed Li2S, the V atom moves back to the center of the N edged hole and binds to the S atom of adsorbed Li2S, leaving the V–S (S from TiS2) bond broken (see Fig. 3b). This process just requires overcoming a very small energy barrier of 0.21 eV as shown in Fig. 3a. Meanwhile, the angle of Li–S–Li bond gradually increases from 85.01° to 139.29° and the bond length of Li–S also expands from 2.25 Å to 2.39 Å. It is then followed by the second subprocess of Li2S decomposition accompanied by the Li–S bond breakage as shown in Fig. 3c (consistent with the decomposition pathway II in Fig. 2b), which necessitates surmounting an energy barrier of 0.54 eV.
It is time-consuming to calculate directly the Eb values for 15 heterostructures using the CI-NEB method. In our previous works, we have identified three descriptors ΔE, ΔE(*LiS) and ICOHP correlating well with Eb for MN4@G, where ΔE refers to the energy difference between the initial and final states of the Li2S decomposition, ΔE(*LiS) stands for the reaction energy of the Li2S decomposition and ICOHP means the integral value of the crystal orbital Hamilton population for evaluating the binding strength of Li–S in adsorbed Li2S.14 And the corresponding functions describing the linear correlations between Eb and ΔE, ΔE(*LiS), ICOHP are shown in the computational details. Among them, ΔE performs the best in predicting Eb values. Based on the available data from the current study, we next explored the predictive capability of ΔE, ΔE(*LiS), ICOHP for determining Eb and then to screen high performance MN4@G/ML for Li2S decomposition. As shown in Fig. 4a, all the data points of Eb fall near the line, implying the robustness of the functional of Eb = 1.07 × ΔE + 0.16 proposed in our previous work.14 The minimum percentage error of Eb between the ΔE–Eb prediction and the CI-NEB calculation occurs in VN4@G/TiS2, which is only 2.22%. The largest percentage error is observed in WN4@G/C3N4, reaching 14%, but the specific difference is only 0.07 eV. The percentage errors of the predicted values with respect to those obtained from CI-NEB calculations for the remaining structures are all below 10%. In contrast, the ΔE(*LiS)−Eb and ICOHP−Eb relationships from the current study do not follow the trend described by those linear functions obtained from previous works (see Fig. 4b and c). The corresponding data of predicted Eb values based on ΔE, ΔE(*LiS) and ICOHP are listed in Table S3 (ESI†). Overall, these results show that ΔE can serve as the best descriptor and provide efficient theoretical guidance for fast screening of active MN4@G/ML toward Li2S decomposition based on the equation of Eb = 1.07 × ΔE + 0.16.
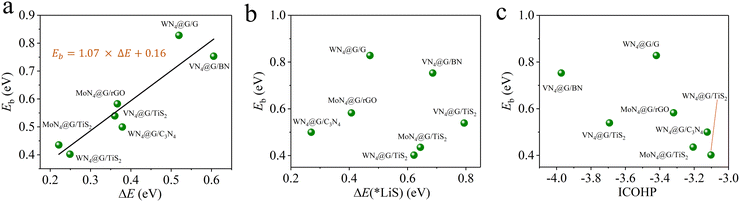 | ||
| Fig. 4 Calculated values of Eb using the CI-NEB method (green balls) for representative heterostructures as a function of ΔE (a), ΔE(*LiS) (b) and ICOHP (c). In (a), the linear relationship (black lines), obtained in our previous works for graphene supported SACs was included for comparison.14 | ||
As listed Table S3 (ESI†), the Eb values are predicted based on the linear function Eb = 1.07 × ΔE + 0.16 for 15 heterostructures which are built by combining 3 MN4@G with 5 monolayers. Among them, MoN4@G/TiS2 and WN4@G/TiS2 give rise to significantly low Eb values of 0.40 and 0.43 eV, which are accordingly highly efficient for catalyzing the SER. In contrast, the worst SER performance is found for VN4@G/C3N4 with Eb = 2.24 eV since the V center does not participate in activating the Li–S bond. As shown in Fig. 5a, in VN4@G/C3N4 the V atom tends to sit between the graphene and C3N4 monolayers leading to the absence of S–V bonds upon the Li2S deposition indicating that there is no direct interaction between Li2S and the V center. Moreover, this holds for the whole process of Li2S decomposition. Therefore, the catalytic performance of VN4@G/C3N4 for Li2S decomposition is rather worse compared to the rest of the heterostructures. It should be noted that, in the VN4@G/TiS2 the V atom remains between graphene and TiS2 monolayers after the Li2S adsorption. However, during the Li2S decomposition the V atom can move back the N-edged hole and form a chemical bond with S from Li2S by overcoming a low energy barrier of 0.21 eV (see Fig. 2a). This S–V bond even remains when the Li–S bond is eventually broken as shown in Fig. 5b. Therefore, VN4@G/TiS2 still shows efficient SER performance by giving rise to a low Eb of 0.54 eV.
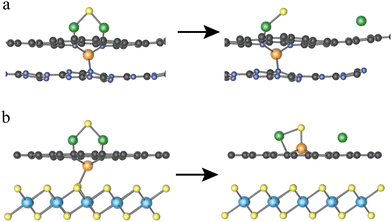 | ||
| Fig. 5 Initial and final structures of Li2S decomposition on VN4G/C3N4 (a) and VN4@G/TiS2 (b). The orange, yellow, green spheres represent the V, S and Li atoms. | ||
We next analyzed the heterointerface effect on the catalytic performance of MN4@G for SER. To this end, three SACs of WN4@G, MoN4@G, and VN4@G, screened by our previous work14 were considered to explore the changes of Eb before and after forming the heterointerfaces. Table 1 shows a comparison of Eb values between MN4@G and MN4@G/ML (M = V, Mo and W; ML = TiS2, C3N4, BN, G and rGO). The energy barriers of Li2S decomposition over MN4@G are decreased when forming the heterostructures with TiS2, C3N4 and rGO. Among them, TiS2 provides the best effect on surface regulation leading to enhanced SER performance of MN4@G by giving rise to Eb of 0.41, 0.44 and 0.54 for WN4@G/ML, MoN4@G/TiS2 and VN4@G/TiS2, respectively, while the effect of C3N4 and rGO on enhancing the catalytic activity for SER was significantly weak. In contrast, BN and G actually increased the Eb on VN4@G and WN4@G, respectively, indicating decreased SER performances. Note that the VN4@G/C3N4 gives rise to the Eb value of 2.24 eV significantly larger than that of 0.70 eV given by VN4@G. This is due to the fact that the V atom does not participate in catalyzing the Li2S decomposition. As shown in Fig. 5a, during the whole process of Li2S decomposition, no chemical bond is formed between the Li2S cluster and the atomically dispersed V atom sitting between VN4@G and C3N4.
| Heterostructures | MN4@G | |
|---|---|---|
| a E b values obtained based on the NEB method. b E b values predicted by the Eb–ΔE relationship. | ||
| WN4@G/TiS2 | 0.41a | 0.55 |
| MoN4@G/TiS2 | 0.44a | 0.58 |
| VN4@G/TiS2 | 0.54a | 0.70 |
| WN4@G/C3N4 | 0.50a | 0.55 |
| MoN4@G/C3N4 | 0.57b | 0.58 |
| VN4@G/C3N4 | 2.24b | 0.70 |
| WN4@G/BN | 0.62b | 0.55 |
| MoN4@G/BN | 0.63b | 0.58 |
| VN4@G/BN | 0.75a | 0.70 |
| WN4@G/rGO | 0.54b | 0.55 |
| MoN4@G/rGO | 0.58a | 0.58 |
| VN4@G/rGO | 0.79b | 0.70 |
| MoN4@G/G | 0.74b | 0.55 |
| WN4@G/G | 0.83a | 0.58 |
| VN4@G/G | 0.79b | 0.70 |
3.3 Heterointerface effect on the performance of MN4@G for catalyzing SRR and stabilizing LiPs
Since the catalytic performance of SCAs for catalyzing Li2S decomposition will be significantly enhanced when being combined with TiS2, we next chose the heterostructures of MN4@G/TiS2 to further investigate their binding strengths to LiPs and S8 as well as their SRR performance, which are also crucial for suppressing the shuttle effect as well. In this regard, both sides of the heterostructures were explored. To indicate the specific surface where the adsorbates locate, it is necessary to redefine the nomenclature for the heterostructures. The bilayer consisting of monolayers of ML1 and ML2 can be named ML1/ML2 or ML2/ML1, representing the adsorbate being adsorbed on the side of the ML1 or ML2. For example, MoN4@G/TiS2 means that MoN4 provides the active sites for adsorbing the LiPs and S8 while it means the opposite when it is represented by TiS2/MoN4@G.As shown in Fig. 6a and Table S4 (ESI†), the adsorption energies of LiPs on MN4@G/TiS2 (M = Mo and W) are both below −3.00 eV, which are lower than those on the organic electrolyte molecules such as 1,3-dioxynaphthenes (DOL) and 1,2-dimethoxy ethane (DME) within the range of −1.00 to −0.80 eV.49 This implies the advantages of such heterointerfaces in suppressing the shuttle effect because the host material exhibits stronger adsorption performance than the organic electrolyte molecules. Moreover, WN4@G/TiS2 possesses more enhanced capability in trapping LiPs than MoN4@G/TiS2. In detail, the adsorption energies of LiPs (Li2Sx, x = 1, 2, 4, 6, 8) and S8 on the WN4@G/TiS2 interface are −5.21, −5.15, −4.17, −4.17, −4.33 and −2.52 eV, respectively. They are lower than the corresponding values on MoN4@G/TiS2, which are −4.67, −3.72, −3.71, −3.35, −3.28 and −2.11 eV, respectively. Note that the adsorption energies on individual TiS2 and MN4@G are higher than those on the heterostructures as shown in Table S4. Therefore, the capabilities of MoN4@G and WN4@G in stabilizing LiPs are generally enhanced when combined with TiS2. In contrast, the adsorption strength of VN4@G/TiS2 to LiPs and S8 are weaker than that for MN4@G/TiS2 (M = Mo and W). The lowest adsorption energy observed on VN4@G/TiS2 is merely −1.73 eV for Li2S adsorption, which means that the adsorption strength of VN4@G to LiPs is significantly weakened upon forming a heterointerface with TiS2. This can be attributed to the formation of V–S bonds in the interlamination of VN4@G/TiS2. When the reaction intermediates are adsorbed on VN4@G/TiS2, the lack of V atoms on the surface of VN4@G/TiS2 leads to the absence of chemical bond between V atoms and LiPs/S8, indicating a relatively weak interaction strength between the heterostructure and LiPs/S8.
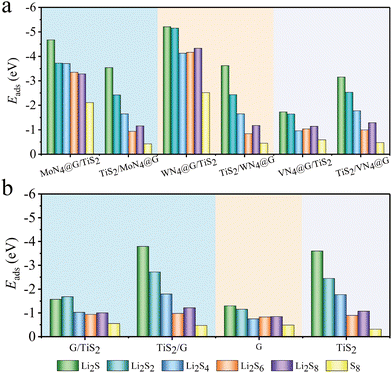 | ||
| Fig. 6 The bar chart of adsorption energies of LiPs and S8 on MN4@G/TiS2 (a), G/TiS2, graphene (G) and TiS2 (b). ML1/ML2 indicates the adsorption site is on ML1. | ||
We also considered the binding strength of TiS2 of three heterostructures to the adsorbates and found that the adsorption energies of various clusters on TiS2/MN4@G (M = V, Mo and W) are very similar. Furthermore, the values are comparable to the adsorption on pure TiS2, suggesting that MN4@G has a tiny impact on the adsorption performance of TiS2 in heterostructures.
The application of MN4@G is often constrained by the low loading density of metal atoms and heterogeneous distribution of doping sites. In the region without dopants, the local structure of MN4@G retains the carbon lattice of pure graphene. Therefore, we set up a model of G/TiS2 in order to further examine the regulatory role of TiS2 on the performance of such carbon atoms far away from the metal centers. As shown in Fig. 6b and Table S4, G/TiS2 possesses enhanced trapping capabilities for LiPs with respect to G. Moreover, the adsorption energies of Li2S4, Li2S6 and Li2S8 on G/TiS2 are −1.03, −0.94 and −1.01 eV, respectively, which are lower than those for organic electrolyte (−1.00 to −0.80 eV). Therefore, combining with TiS2 can enhance the adsorption performance of the entire region of MN4@G monolayers for LiPs, which will help overcome the disadvantages of low loading of atomically dispersed atoms in MN4@G.
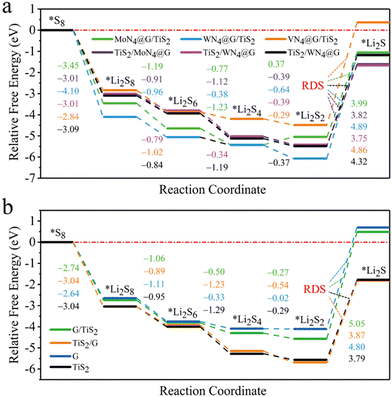
We have also investigated the SRR performance of those heterostructures by calculating the Gibbs free energy changes (ΔG) profile as depicted in Fig. 7. For MoN4@G/TiS2 and WN4@G/TiS2 (see Fig. 7a), the ΔG values of overall SRR are −1.06 and −1.19 eV, respectively, which are lower than those of −0.41 and −0.33 eV for MoN4@G and WN4@G, respectively. Moreover, the ΔG of rate-determining step (ΔGRDS) for the transition from Li2S2 to Li2S are 3.99 and 4.89 eV, lower than the corresponding values of 4.25 and 4.36 eV for individual MoN4@G and WN4@G, respectively. These results imply the positive effect of heterointerface on enhancing the SRR performance of MN4@G (M = Mo and W). In contrast, the overall ΔG of SRR on VN4@G/TiS2 is 0.37 eV, which is larger than −0.82 eV for VN4@G. Such an increase of ΔG can be attributed to the structural feature of VN4@G/TiS2 with the V atom located between VN4@G and TiS2 and formation of the V–S bond. It means that the single V atom in VN4@G/TiS2 will not participate in forming chemical bonds with LiPs and S8 during the SRR process leading to decreased SRR performance compared to individual VN4@G. When it turns to TiS2/MN4@G (M = Mo, W and V), the overall ΔG of SRR are −1.61, −1.66, and −1.17 eV, respectively, while the related ΔGRDS values are 3.82, 3.75 and 4.32 eV. These values are comparable to the corresponding values for individual TiS2. This shows that the heterointerface effect on the SRR performance of TiS2 is relatively weak. Regarding G and G/TiS2, they exhibit even worse performance for SRR, as reflected by the ΔG values of 0.69 and 0.48 eV for the overall SRR, respectively (see Fig. 7b). This also implies that the SRR performance of carbon atoms far away from the metal centers in MN4@G/TiS2 (M = Mo, W and V) is relatively worse, which is still better than that for pristine graphene. Nevertheless, based on the above analysis, we believe that both sides of MN4@G/TiS2 possess promising performance for SRR. Overall, MN4@G/TiS2 (M = Mo and W) show good performance in stabilizing LiPs and accelerating the kinetics of SER/SRR as confirmed by the low values of adsorption energies for LiPs/S8, ΔG for overall SRR, ΔGRDS and Eb for Li2S decomposition, which demonstrate that they are promising candidates electrocatalysts for sulfur chemistry in Li–S batteries.
4. Conclusions
Using DFT calculations, we explored the heterointerface effect on the catalytic performance SACs toward sulfur conversion in Li–S batteries. To this end, 15 heterostructures were constructed by combining MN4@G (M = Mo, W and V) with 5 different 2D materials of TiS2, C3N4, BN, graphene and rGO. We then investigated their electronic properties, adsorption capabilities for LiPs/S8 and catalytic activities for sulfur redox. Using previously proposed descriptors of ΔE, we firstly screened three heterointerfaces MN4@G/TiS2 (M = Mo, W and V) due to their low values of Eb of 0.54, 0.44, and 0.41 eV, respectively, indicating the enhanced SER performance of MN4@G caused by the interface effect. This effect also induces the increased binding strength to LiPs/S8 beneficial for suppressing the shuttle effect as reflected by the low adsorption energies. Moreover, our DFT calculations demonstrate that both sides of MN4@G/TiS2 (M = Mo and W) possess enhanced SRR performance compared to the individual components of heterostructures. These can be confirmed by those competitive values of low values of adsorption energies for soluble LiPs (<∼−3 eV), ΔG for the overall SRR (−1.66 to 0.37) and ΔGRDS (3.82 to 4.89). Interestingly, the interface effect even strengthens the binding strength of the carbon atoms far away from the metal centers and soluble LiPs, which will probably address the issue of low loading rate of atomically dispersed metal atoms. This study paves a new way of designing novel electrocatalyst for sulfur chemistry for Li–S batteries and even other alkali-ion-chalcogen batteries.Author contributions
H. Liang and Z. Zeng performed the calculations and the data analysis and H. Liang prepared the draft of the manuscript. Z. Qiao and Y. Li initialize the project and proposed the supervision. All authors have given approval to the final version of the manuscript.Conflicts of interest
The authors declare no competing financial interest.Acknowledgements
This work was financially supported by the National Natural Science Foundation of China (Grants No. 52372254 and 91963210) and the Key Research and Development Program of Guangdong Province (No. 2020B0101690001). The calculations were carried out using supercomputers ‘Tianhe-2’ at NSCC Guangzhou.References
- X. Hong, R. Wang, Y. Liu, J. Fu, J. Liang and S. Dou, Recent advances in chemical adsorption and catalytic conversion materials for Li–S batteries, J. Energy Chem., 2020, 42, 144–168 CrossRef
.
- Y. Song, W. Cai, L. Kong, J. Cai, Q. Zhang and J. Sun, Rationalizing Electrocatalysis of Li–S Chemistry by Mediator Design: Progress and Prospects, Adv. Energy Mater., 2020, 10(11), 1901075 CrossRef CAS
.
- L. Zhou, D. L. Danilov, R.-A. Eichel and P. H. L. Notten, Host Materials Anchoring Polysulfides in Li–S Batteries Reviewed, Adv. Energy Mater., 2021, 11(15), 2001304 CrossRef CAS
.
- Z. W. Seh, Y. Sun, Q. Zhang and Y. Cui, Designing high-energy lithium–sulfur batteries, Chem. Soc. Rev., 2016, 45(20), 5605–5634 RSC
.
- Q. Pang, X. Liang, C. Y. Kwok and L. F. Nazar, Advances in lithium–sulfur batteries based on multifunctional cathodes and electrolytes, Nat. Energy, 2016, 1(9), 16132 CrossRef CAS
.
- Q. Shao, Z.-S. Wu and J. Chen, Two-dimensional materials for advanced Li–S batteries, Energy Storage Mater., 2019, 22, 284–310 CrossRef
.
- J. Xu, W. Zhang, H. Fan, F. Cheng, D. Su and G. Wang, Promoting lithium polysulfide/sulfide redox kinetics by the catalyzing of zinc sulfide for high performance lithium-sulfur battery, Nano Energy, 2018, 51, 73–82 CrossRef CAS
.
- H.-J. Peng, J.-Q. Huang and Q. Zhang, A review of flexible lithium–sulfur and analogous alkali metal–chalcogen rechargeable batteries, Chem. Soc. Rev., 2017, 46(17), 5237–5288 RSC
.
- Y. Huang, L. Lin, C. Zhang, L. Liu, Y. Li, Z. Qiao, J. Lin, Q. Wei, L. Wang, Q. Xie and D.-L. Peng, Recent Advances and Strategies toward Polysulfides Shuttle Inhibition for High-Performance Li–S Batteries, Adv. Sci., 2022, 2106004 CrossRef CAS PubMed
.
- Z. Liang, D. Yang, P. Tang, C. Zhang, J. Jacas Biendicho, Y. Zhang, J. Llorca, X. Wang, J. Li, M. Heggen, J. David, R. E. Dunin-Borkowski, Y. Zhou, J. R. Morante, A. Cabot and J. Arbiol, Atomically dispersed Fe in a C2N Based Catalyst as a Sulfur Host for Efficient Lithium–Sulfur Batteries, Adv. Energy Mater., 2021, 11(5), 2003507 CrossRef CAS
.
- W. Ren, W. Ma, S. Zhang and B. Tang, Recent advances in shuttle effect inhibition for lithium sulfur batteries, Energy Storage Mater., 2019, 23, 707–732 CrossRef
.
- L. Zhang, D. Liu, Z. Muhammad, F. Wan, W. Xie, Y. Wang, L. Song, Z. Niu and J. Chen, Single Nickel Atoms on Nitrogen-Doped Graphene Enabling Enhanced Kinetics of Lithium–Sulfur Batteries, Adv. Mater., 2019, 31(40), 1903955 CrossRef CAS PubMed
.
- Z. Du, X. Chen, W. Hu, C. Chuang, S. Xie, A. Hu, W. Yan, X. Kong, X. Wu, H. Ji and L.-J. Wan, Cobalt in Nitrogen-Doped Graphene as Single-Atom Catalyst for High-Sulfur Content Lithium–Sulfur Batteries, J. Am. Chem. Soc., 2019, 141(9), 3977–3985 CrossRef CAS PubMed
.
- Z. Zeng, W. Nong, Y. Li and C. Wang, Universal-Descriptors-Guided Design of Single Atom Catalysts toward Oxidation of Li2S in Lithium–Sulfur Batteries, Adv. Sci., 2021, 8(23), 2102809 CrossRef CAS PubMed
.
- S. Wu, C. Wang, H. Liang, W. Nong, Z. Zeng, Y. Li and C. Wang, High-Throughput Calculations for Screening d- and p-Block Single-Atom Catalysts toward Li2S/Na2S Decomposition Guided by Facile Descriptor beyond Brønsted–Evans–Polanyi Relationship, Small, 2023, 2305161 Search PubMed
.
- J. Mei, T. Liao and Z. Sun, 2D/2D Heterostructures: Rational Design for Advanced Batteries and Electrocatalysis, Energy Environ. Mater., 2022, 5(1), 115–132 CrossRef CAS
.
- Y. Li, J. Zhang, Q. Chen, X. Xia and M. Chen, Emerging of Heterostructure Materials in Energy Storage: A Review, Adv. Mater., 2021, 33(27), 2100855 CrossRef CAS PubMed
.
- S. Huang, Z. Wang, Y. Von Lim, Y. Wang, Y. Li, D. Zhang and H. Y. Yang, Recent Advances in Heterostructure Engineering for Lithium–Sulfur Batteries, Adv. Energy Mater., 2021, 11(10), 2003689 CrossRef CAS
.
- Y. Song, H. Zhou, X. Long, J. Xiao, J. Yang, N. Wu, Z. Chen, P. Li, C. Chen, J. Liao and M. Wu, Dual-heterostructures decorated interweaved carbon nanofibers sulfur host for high performance lithium-sulfur batteries, Chem. Eng. J., 2021, 418, 129388 CrossRef CAS
.
- Y. Xue, D. Luo, N. Yang, G. Ma, Z. Zhang, J. Hou, J. Wang, C. Ma, X. Wang, M. Jin, Z. Chen and L. Shui, Engineering checkerboard-like heterostructured sulfur electrocatalyst towards high-performance lithium sulfur batteries, Chem. Eng. J., 2022, 440, 135990 CrossRef CAS
.
- W. Yang, Y. Wei, Q. Chen, S. Qin, J. Zuo, S. Tan, P. Zhai, S. Cui, H. Wang, C. Jin, J. Xiao, W. Liu, J. Shang and Y. Gong, A MoO3/MoO2-CP self-supporting heterostructure for modification of lithium–sulfur batteries, J. Mater. Chem. A, 2020, 8(31), 15816–15821 RSC
.
- J. Qin, R. Wang, P. Xiao and D. Wang, Engineering Cooperative Catalysis in Li–S Batteries, Adv. Energy Mater., 2023, 2300611 CrossRef CAS
.
- H. X. Dang, A. J. Sellathurai and D. P. J. Barz, An ion exchange membrane-free, ultrastable zinc-iodine battery enabled by functionalized graphene electrodes, Energy Storage Mater., 2023, 55, 680–690 CrossRef
.
- X. Xia, J. Yang, Y. Liu, J. Zhang, J. Shang, B. Liu, S. Li and W. Li, Material Choice and Structure Design of Flexible Battery Electrode, Adv. Sci., 2023, 10(3), 2204875 CrossRef CAS PubMed
.
- Y. V. Lim, X. L. Li and H. Y. Yang, Recent Tactics and Advances in the Application of Metal Sulfides as High-Performance Anode Materials for Rechargeable Sodium-Ion Batteries, Adv. Funct. Mater., 2021, 31(10), 2006761 CrossRef CAS
.
- M. Yang, X. Chang, L. Wang, X. Wang, M. Gu, H. Huang, L. Tang, Y. Zhong and H. Xia, Interface Modulation of Metal Sulfide Anodes for Long-Cycle-Life Sodium-Ion Batteries, Adv. Mater., 2023, 35(13), 2208705 CrossRef CAS PubMed
.
- B. Li, Y. Wang, N. Jiang, L. An, J. Song, Y. Zuo, F. Ning, H. Shang and D. Xia, Electrolytic-anion-redox adsorption pseudocapacitance in nanosized lithium-free transition metal oxides as cathode materials for Li-ion batteries, Nano Energy, 2020, 72, 104727 CrossRef CAS
.
- Y. Pei, Q. Chen, M. Wang, P. Zhang, Q. Ren, J. Qin, P. Xiao, L. Song, Y. Chen, W. Yin, X. Tong, L. Zhen, P. Wang and C.-Y. Xu, A medium-entropy transition metal oxide cathode for high-capacity lithium metal batteries, Nat. Commun., 2022, 13(1), 6158 CrossRef CAS PubMed
.
- Y. Wang, T. Guo, E. Alhajji, Z. Tian, Z. Shi, Y.-Z. Zhang and H. N. Alshareef, MXenes for Sulfur-Based Batteries, Adv. Energy Mater., 2023, 13(4), 2202860 CrossRef CAS
.
- F. Ming, H. Liang, G. Huang, Z. Bayhan and H. N. Alshareef, MXenes for Rechargeable Batteries Beyond the Lithium-Ion, Adv. Mater., 2021, 33(1), 2004039 CrossRef CAS PubMed
.
- M. Telkhozhayeva, B. Hirsch, R. Konar, E. Teblum, R. Lavi, M. Weitman, B. Malik, E. Moretti and G. D. Nessim, 2D TiS2 flakes for tetracycline hydrochloride photodegradation under solar light, Appl. Catal., B, 2022, 318, 121872 CrossRef CAS
.
- J. Wang and S. Wang, A critical review on graphitic carbon nitride (g-C3N4)-based materials: Preparation, modification and environmental application, Coord. Chem. Rev., 2022, 453, 214338 CrossRef CAS
.
- L. Liu, J. Park, D. A. Siegel, K. F. McCarty, K. W. Clark, W. Deng, L. Basile, J. C. Idrobo, A.-P. Li and G. Gu, Heteroepitaxial Growth of Two-Dimensional Hexagonal Boron Nitride Templated by Graphene Edges, Science, 2014, 343(6167), 163–167 CrossRef CAS PubMed
.
- Y. Zheng, H. Li, H. Yuan, H. Fan, W. Li and J. Zhang, Understanding the anchoring effect of Graphene, BN, C2N and C3N4 monolayers for lithium−polysulfides in Li−S batteries, Appl. Surf. Sci., 2018, 434, 596–603 CrossRef CAS
.
- R. Jain, P. Hundekar, T. Deng, X. Fan, Y. Singh, A. Yoshimura, V. Sarbada, T. Gupta, A. S. Lakhnot, S. O. Kim, C. Wang and N. Koratkar, Reversible Alloying of Phosphorene with Potassium and Its Stabilization Using Reduced Graphene Oxide Buffer Layers, ACS Nano, 2019, 13(12), 14094–14106 CrossRef CAS PubMed
.
- J. Hafner, Ab-initio simulations of materials using VASP: Density-functional theory and beyond, J. Comput. Chem., 2008, 29(13), 2044–2078 CrossRef CAS PubMed
.
- G. Kresse and J. Furthmüller, Efficient iterative schemes for ab initio total-energy calculations using a plane-wave basis set, Phys. Rev. B: Condens. Matter Mater. Phys., 1996, 54(16), 11169–11186 CrossRef CAS PubMed
.
- J. P. Perdew, J. A. Chevary, S. H. Vosko, K. A. Jackson, M. R. Pederson, D. J. Singh and C. Fiolhais, Atoms, molecules, solids, and surfaces: Applications of the generalized gradient approximation for exchange and correlation, Phys. Rev. B: Condens. Matter Mater. Phys., 1992, 46(11), 6671–6687 CrossRef CAS PubMed
.
- J. P. Perdew and Y. Wang, Accurate and simple analytic representation of the electron-gas correlation energy, Phys. Rev. B: Condens. Matter Mater. Phys., 1992, 45(23), 13244–13249 CrossRef PubMed
.
- J. P. Perdew, K. Burke and M. Ernzerhof, Generalized Gradient Approximation Made Simple, Phys. Rev. Lett., 1996, 77(18), 3865–3868 CrossRef CAS PubMed
.
- P. E. Blöchl, Projector augmented-wave method, Phys. Rev. B: Condens. Matter Mater. Phys., 1994, 50(24), 17953–17979 CrossRef PubMed
.
- G. Kresse and D. Joubert, From ultrasoft pseudopotentials to the projector augmented-wave method, Phys. Rev. B: Condens. Matter Mater. Phys., 1999, 59(3), 1758–1775 CrossRef CAS
.
- S. Grimme, Semiempirical GGA-type density functional constructed with a long-range dispersion correction, J. Comput. Chem., 2006, 27(15), 1787–1799 CrossRef CAS PubMed
.
- G. Henkelman and H. Jónsson, Improved tangent estimate in the nudged elastic band method for finding minimum energy paths and saddle points, J. Chem. Phys., 2000, 113(22), 9978–9985 CrossRef CAS
.
- G. Henkelman, B. P. Uberuaga and H. Jónsson, A climbing image nudged elastic band method for finding saddle points and minimum energy paths, J. Chem. Phys., 2000, 113(22), 9901–9904 CrossRef CAS
.
- III, R. D. J., NIST Computational Chemistry Comparison and Benchmark Database. https://cccbdb.nist.gov.
- Q. He, B. Yu, H. Wang, M. Rana, X. Liao and Y. Zhao, Oxygen defects boost polysulfides immobilization and catalytic conversion: First-principles computational characterization and experimental design, Nano Res., 2020, 13(8), 2299–2307 CrossRef CAS
.
- T. Björkman, A. Gulans, A. V. Krasheninnikov and R. M. Nieminen, van der Waals Bonding in Layered Compounds from Advanced Density-Functional First-Principles Calculations, Phys. Rev. Lett., 2012, 108(23), 235502 CrossRef PubMed
.
- Y. Qie, J. Liu, S. Wang, S. Gong and Q. Sun, C3B monolayer as an anchoring material for lithium-sulfur batteries, Carbon, 2018, 129, 38–44 CrossRef CAS
.
Footnote |
| † Electronic supplementary information (ESI) available: Computational details; structure information of heterostructure materials; additional figures and tables. See DOI: https://doi.org/10.1039/d3cp05883b |
| This journal is © the Owner Societies 2024 |