Open Access Article
Open Access ArticleCreative Commons Attribution 3.0 Unported Licence
Combining low-cost electronic structure theory and low-cost parallel computing architecture†
Pit
Steinbach
 and
Christoph
Bannwarth
and
Christoph
Bannwarth
 *
*
Institute for Physical Chemistry, RWTH Aachen University, Melatener Str. 20, 52074 Aachen, Germany. E-mail: bannwarth@pc.rwth-aachen.de
First published on 20th May 2024
Abstract
The computational efficiency of low-cost electronic structure methods can be further improved by leveraging heterogenous computing architectures. The software package TeraChem has been developed since 2008 to make use of graphical processing units (GPUs), particularly their strong single-precision performance, for the acceleration of quantum chemical calculations. Here, we present the implementation of three low-cost methods, namely HF-3c, PBEh-3c, and the recently introduced ωB97X-3c. We show that these can benefit in terms of performance when combined with “consumer grade” GPUs by leveraging the mixed precision integral handling in TeraChem. The current limitation of the latter's GPU integral library is that Gaussian integrals only for functions with angular momentum l < 3 can be computed, which generally restricts the achievable accuracy in terms of the one-particle basis set. Particularly, the implementation of the ωB97X-3c method now enables higher accuracy with this setting which, in turn, provides the most efficient implementation accessible with consumer-grade hardware. We furthermore show that the implemented 3c methods can be combined with the hh-TDA formalism. This gives new and efficient low-cost multi-configurational excited states methods, which are benchmarked for the description of lowest vertical excitation energies in this work. All in all, the combination of these efficient electronic structure theory methods with affordable highly parallelized computing hardware provides an optimal computational and monetary cost to accuracy ratio.
1 Introduction
When attempting the computation of chemical properties with high accuracy, considering the flexibility of the investigated molecules is essential.1–3 This task usually involves the computation of energies and gradients for many geometries to explore the configurational space.4,5 For this exploratory phase usually semi-empirical or classical methods are used.6–8 This choice of theory level often leads to a lack in accuracy of the corresponding energies, making a precise determination of the lowest-lying conformers difficult. For this purpose, an ab initio method with reasonable energy description at low computational cost is beneficial. An additional field of application for such methods, would be the computation of thermochemical properties for large molecules.9 For transition state geometry searches, efficient methods are also of interest since many singlepoint, gradient and even Hessian matrix calculations are necessary. For such situations, Grimme and coworkers pioneered the development of “low-cost” ab initio methods, with HF-3c.10 The so-called “3c methods” are characterized by small basis sets and empirical correction schemes,11–13 specially fitted for this combination of method and basis set. This concept was successfully adapted to density functional theory (DFT), for example, with PBEh-3c and and the recently introduced ωB97X-3c.9,14–16 Details about the components of the aforementioned composite methods are discussed later on in this work.Variants without Fock exchange may benefit from significant speed-up if combined with the resolution-of-the-identity approximation for Coulomb integrals (RIJ).17 This has then enabled the use of basis sets with somewhat larger cardinal numbers (triple-zeta), providing larger variational flexibility than achievable with minimal and double-zeta basis sets. The previously published B97-3c15 and r2SCAN-3c16 methods are the representatives of this 3c method subset. In combination with the RIJ approximation, these have become very popular in well-established CPU-based quantum chemistry packages like ORCA18,19 or TURBOMOLE.20,21 The small basis set 3c methods with Fock exchange, however, may be favored in situations when the DFT-related self interaction error becomes relevant, e.g., in polar systems or for the calculation of excited states. Particularly, the most recent variant, ωB97X-3c,9 also holds promise for delivering reasonable ground state energetics with very compact basis sets. By far, the rate-determining step remains the computation of the Fock exchange in this method, as well as in the HF-3c and PBEh-3c methods. Acceleration of this component is less straightforward than for Coulomb integrals: here, the formal scaling with the system size cannot be reduced via a resolution-of-the-identity scheme.22 Instead, the formal scaling can be reduced from quartic to cubic only by introduction of a seminumerical integration scheme.23–27 These are particularly effective for large basis sets with cardinal number of three or higher. For small basis sets (minimal and double-zeta), however, using schemes that provide a lower formal scaling are expected to be less significant, as reducing the effective scaling, e.g., through Schwarz screening,28 can already lead to more significant speed-ups. For example, the standard GPU-accelerated integral library in the quantum chemistry program TeraChem29,30 makes no use of any formal scaling reduction scheme (like resolution-of-the-identity or seminumerical integration) but strongly reduces the effective scaling through efficient prescreening of necessary ERIs to be computed. In the present work, we take the subset of Fock exchange-inclusive 3c methods with small basis sets (HF-3c, PBEh-3c, and ωB97X-3c) and implement them into the quantum chemistry program TeraChem.
Here, the effective wall time can be further reduced by using heterogeneous computing architecture like graphical processing units (GPUs). GPUs represent highly parallel computing architectures that are well suited for single instruction operations performed on multiple data points. Electronic structure theory is, in principle, a prime application for GPU acceleration, due to the large number of integral evaluations and linear algebra operations to be performed.31–39 Leveraging GPUs in scientific computing was particularly enabled through the release of NVIDIA's Compute Unified Device Architecture (CUDA) toolchain for general purpose GPU computing in 2007.40 During the advent of CUDA, the idea for the TeraChem29,30 software package emerged. The initial focus was the computation of the electron repulsion integrals (ERIs), which marks the computational bottleneck for most methods.41–44 An initial limitation of GPUs in electronic structure theory calculations was the availability and performance of double-precision floating point (FP64) operations. FP64 describes the use of 64 bits to store floating point numbers, which leads to a precision of 15–17 significant digits.45,46 This high precision is generally necessary in quantum chemical calculations, since usually large total electronic energies or large energy terms of opposing sign need to be stored. However, the net energy changes relevant for chemistry are often much smaller, such that these can be expressed sufficiently well within single-precision floating point (FP32) arithmetic. Consequently, by using reformulations of the self-consistent field (SCF)47 method like incremental SCF techniques, and clever handling of ERIs,29,48 the majority of operations may be carried out with FP32 numbers, while the number of costly FP64 operations can be reduced considerably. This is realized in the so-called “mixed-precision” (MP) scheme48 in TeraChem, which enables precision errors nearly as low as a full FP64 ERI handling, but at a computational cost much closer to an FP32 treatment. The corresponding integral routines became the core of the TeraChem codebase and are encapsulated into the IntBox library.30 Hence, all electronic structure theory implementations inherit the speed of those fundamental routines by using Fock matrix components from this library.
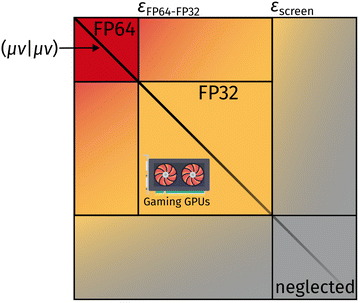
While the need of algorithms leveraging good FP32 performance may have been mitigated with the advent of FP64 capable GPUs (e.g., from the Tesla family), so-called “consumer-grade” or “gaming” GPUs still show significant efficiency drops (1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 64), when it comes to computations executed in double-precision (FP64). At the same time, “consumer-grade” GPUs are often cheaper by about a factor of 2–10. Hence, the availability of MP schemes in electronic structure theory remains of great importance in order to leverage this kind of low-priced computing hardware. Furthermore, the total memory capactiy of consumer-grade GPUs (<24 GB) remains a limiting factor. The implication for quantum chemistry is that most GPU-based integral implementations are only available, at least with superior performance, for Gaussian basis functions with angular momentum of l < 3 (i.e., s, p, and d functions).29,37,39
64), when it comes to computations executed in double-precision (FP64). At the same time, “consumer-grade” GPUs are often cheaper by about a factor of 2–10. Hence, the availability of MP schemes in electronic structure theory remains of great importance in order to leverage this kind of low-priced computing hardware. Furthermore, the total memory capactiy of consumer-grade GPUs (<24 GB) remains a limiting factor. The implication for quantum chemistry is that most GPU-based integral implementations are only available, at least with superior performance, for Gaussian basis functions with angular momentum of l < 3 (i.e., s, p, and d functions).29,37,39
In this this work, we want to put the focus on combining such low-cost heterogeneous computing architecture with the low-cost Fock exchange-inclusive 3c methods. To further highlight our implementation of those methods in TeraChem, we present a new field of application for the 3c methods arising from their availability in TeraChem and choose to focus on excited states. Especially in the realm of simulation of energy conversion materials, an ongoing need for efficient excited states methods applicable to molecular complexes exists. A promising candidate in this regard is the recently suggested variation of hole–hole Tamm–Dancoff Approximation (hh-TDA).49,50 This relatively inexpensive multi-configuration framework can be coupled with the 3c methods in the quantum chemistry package TeraChem. Ultimately, this combination and use of MP enables robust and fast exploratory excited-state potential energy surface calculations. We focus on benchmarking vertical excitations in this work, but conical intersections are also accessible with hh-TDA, as shown before.49,50 A short theoretical introduction to hh-TDA will be given in the Section 1.1.
1.1 Hole–hole Tamm–Dancoff approximation
We give a short overview on hh-TDA, starting from the non-Hermitian eigenvalue problem of the particle–particle random phase approximation:49,51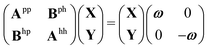 | (1) |
| AhhY = Yωhh | (2) |
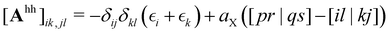 | (3) |
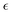 denotes the orbital energy, ijkl denotes occupied spin orbitals. The response kernel is scaled according to the amount of Fock-exchange aX used in the density functional approximation (DFA).49 In the case of a range-separated DFA, a modified Coulomb operator is used, which is not further discussed in this work. For a comprehensive derivation, we refer the reader to ref. 49. Instead of the double anionic reference proposed in the original work,49 later work50 proposed a more robust variant using fractionally occupied molecular orbitals (FOMO) of an N electron system with the occupied space spanning all orbitals required to describe the double anionic (N + 2) system. This variant will be used for benchmarking in this work.
denotes the orbital energy, ijkl denotes occupied spin orbitals. The response kernel is scaled according to the amount of Fock-exchange aX used in the density functional approximation (DFA).49 In the case of a range-separated DFA, a modified Coulomb operator is used, which is not further discussed in this work. For a comprehensive derivation, we refer the reader to ref. 49. Instead of the double anionic reference proposed in the original work,49 later work50 proposed a more robust variant using fractionally occupied molecular orbitals (FOMO) of an N electron system with the occupied space spanning all orbitals required to describe the double anionic (N + 2) system. This variant will be used for benchmarking in this work.
1.2 Low-cost 3c composite methods with Fock exchange
For implementation in TeraChem, we favored those 3c methods with Fock exchange since the efficient exchange matrix build of the former can be leveraged.29 Therefore, the HF-3c, PBEh-3c, and ωB97X-3c are added to the TeraChem software suite. Table 1 gives an overview of the components of the implemented methods.Due to the missing London dispersion in Hartree–Fock (HF), a specially fitted dispersion correction based on the DFT-D3 model12 (with Becke–Johnson damping)53 is used. The basis set incompleteness error and basis set superposition error (BSSE) are reduced by corrections applied using the geometrical counterpoise correction (gCP)11 and a short-range bond correction. These three corrections lead to the original naming scheme with the “3c” suffix.
As a successor, PBEh-3c also includes dispersion and BSSE corrections fitted for the use with the high amount of non-local Fock exchange (42%). Different from HF-3c, three-body Axilrod-Teller_Muto (ATM) dispersion terms12 are included and a modified, short-ranged damped gCP correction is used. The def2-mSVP basis is mainly derived from the def2-SVP,54 but was modified for various elements.14 This composite method also involves changes to the parameters of the PBE0 exchange and correlation functionals.55,56
The latest addition to this family of composite methods is ωB97X-3c.9 Here, Grimme and coworkers developed a new double zeta basis set with large-core effective core potentials (ECPs). A large number of primitive Gaussian functions is used for every contracted Gaussian, allowing a good description with a small number of basis set coefficients. The basis set is constructed such that the BSSE is relatively low compared to basis sets with the same cardinal number.9 A correction using a fitted gCP model is thereby not necessary for this method. The parameters for the functional and range-separated exchange are unchanged to those in the parent ωB97X-V method.57 In the following section, we will further go into the details of the integral handling in TeraChem.
1.3 Computation of electron repulsion integrals and mixed precision scheme in TeraChem
Hybrid DFT methods use a combination of exact Fock exchange combined with a density-based exchange functional. Inclusion of Fock exchange increases the computational cost, however, it is essential when considering excited states, e.g., via time-dependent DFT (TD-DFT)58 or through the hh-TDA framework. Furthermore, it was shown to improve the thermochemistry of reactions.59 We can leverage the GPU-based Fock exchange build routine in TeraChem to speed-up this costly process. All integrals within TeraChem are computed in an effectively low-scaling integral-direct fashion,30 while approximations such as the resolution-of-the-identity (RI)17 are not employed. We will outline the steps used to reduce the number of FP64 operations and, thereby, improve the performance with consumer-grade GPUs.48To estimate the numerical value of off-diagonal elements in ERI tensors, TeraChem employs a density-weighted Schwarz bound:28,30,47,48
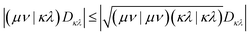 | (4) |
Here, (μν|κλ) are ERI integrals in the non-orthogonal atomic orbital (AO) basis and Dκλ is the density matrix element for the AOs κ and λ. We are simplifying the mathematical approach here slightly, as the actual implementation performs the screening based on primitives and uses the largest density matrix element of a shell–shell pair for screening.30 The density-weighted ERI tensor elements are then sorted according to the value estimated by eqn (4). Based on a threshold εscreen, values are screened-out and neglected for computation. Due to the performance difference between FP32 and FP64 operations, a further sorting of values is beneficial. The εFP64–FP32 threshold determines if single or double precision is used for the calculation of those elements. This value can remain constant during the self-consistent field (SCF), yielding the “mixed precision” scheme proposed by Luehr et al.48 The change of this value with the SCF cycles gives the “dynamic precision” scheme.48 A graphical representation of this tiered precision scheme for ERI tensors can be seen in Fig. 1.
As already suggested by Almlöf et al.,47 density-based screening approaches are more effective when combined with an incremental build of the Fock Matrix F (shown here for the closed-shell case):
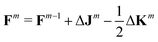 | (5) |
Combining the mixed-precision scheme and incremental Fock builds reduces the number of FP64 operations required and thus speeds-up the computation, especially on “gaming” GPUs. However, the GPU-based implementation also comes with a drawback. Currently, the TeraChem software package can only handle integrals up to an angular momentum of l = 2 (d-functions) and ECP potentials with an angular momentum up to l = 4 (g-functions). This is the prime reason why we did not consider the B97-3c and r2SCAN-3c schemes. But also for the chosen 3c methods, this restricts the elements for which the implemented 3c methods are available.
After introducing the computational details of our work, we will go over some implementation details and give an overview on the elements available in our implementation. Next, the average wall time per SCF cycle of our implementation compared to state-of-the-art CPU quantum chemical packages, ORCA18,19 and TURBOMOLE20,21 is discussed. We will also compare the performance for GPUs of various retail prices to carefully assess the price to performance ratio for the GPUs in our compute cluster. Lastly we will benchmark the 3c methods with the hh-TDA scheme for their ability to compute vertical excitations for organic molecules.
2 Computational details
To assess the correctness of our implementation, the ORCA18,19 and TURBOMOLE20,21 programs were used as reference. These codes were also used to compare the performance of our presented GPU implementation to existing and well-performing CPU implementations. The ORCA18,19 calculations were performed with version 5.0.4 using defgrid3, all other parameters were kept as per default unless specified otherwise. TURBOMOLE20,21 version 7.6.1 was used, the dynamic grid m4 was used. No symmetry is exlpoited in any of our calculations. Furthermore, generation of the guess computed by the define program (via an extended Hückel scheme) is not included in the timings. The TeraChem29,30 calculations are performed with a development version based on release 1.9. All TeraChem calculations are performed using dftgrid1 and the superposition of atomic densities (SAD) guess (without purification) unless stated otherwise.We also would like to share the hardware details used for the timings. A small number of identical HPZ workstations are used to compute the timings for ORCA, TURBOMOLE, and TeraChem (with one RTX 3070 GPU per node). This workstation contains an Intel i7-11700 CPU running at 2.50 GHz base-clock. Eight CPU threads are used for all calculations. The system has 32 GB of CPU RAM, and an NVIDIA GeForce RTX 3070 GPU with 8 GB VRAM. The systems used for the Quadro RTX 5000 and 3080Ti timings feature an Intel Xeon W-2255 CPU @ 3.70GHz and 64 GB of CPU RAM. TeraChem is built with compilers and linked against libraries from the CUDA v11.6 release, the Intel Classic Compiler, and its Math Kernel Library (Intel oneAPI 2023.0). During timings no other user controlled workloads are executed, and the systems are kept in a climate controlled room at 22 °C.
For the hh-TDA benchmark set taken from ref. 49, a regular single point calculation is performed first. The coefficients from this calculation are then used as a guess for the subsequent hh-TDA calculation with fractionally occupied molecular orbitals (FOMO). The detailed input is given in the ESI.† For the intermolecular charge transfer subset, the number of computed states had to be increased to 10 roots to find the charge transfer state, mainly for ωB97X-3c.
3 Results and discussion
3.1 Implementation details and element availability
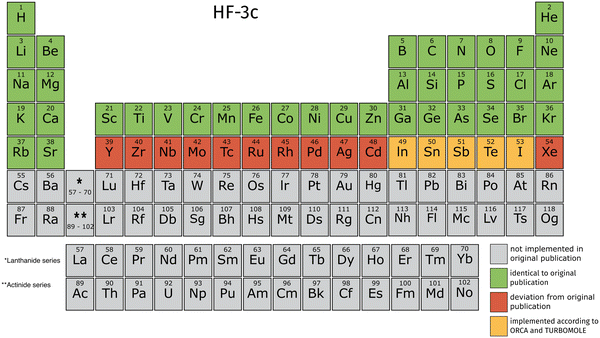
TeraChem's current integral library is limited to angular momenta l < 3 (spd-functions) for the explicit treatment of electrons. The ECPs provide angular momenta up to g. These limitations lead to a restricted availability of elements for the 3c methods in TeraChem. We validate our implementation against those in ORCA and TURBOMOLE, by computing energies and gradients for small molecules containing all implemented elements. The validation thresholds are detailed in the ESI.† We employed large grids for the DFT calculations in all software programs to compare absolute energy and gradient values. In TeraChem, “dftgrid5” is used, “defgrid3” in ORCA and “grid m4” in TURBOMOLE. In the following Fig. 2–4, we will give an overview on which elements are available according to their original publication.9,10,14For HF-3c, we encountered some inconsistencies comparing the original publication and the implementation in ORCA and TURBOMOLE. We found that the elements from Y to Xe use the def2-SVP basis set instead of def2-SV(P). Additionally, the ECPs vary between transition metals and main group elements. From Y to Cd, the def2-ECPs60 are used, whereas the def-ECPs (modified version of ref. 61) are used for the main group elements from In to Xe. Due to the angular momentum limitation, the transition metals from Y to Cd can't be computed according to the ORCA and TURBOMOLE implementation. For In to I, we adopt the ORCA and TURBOMOLE implementation, which differs from the original publication, hence a different color is used.
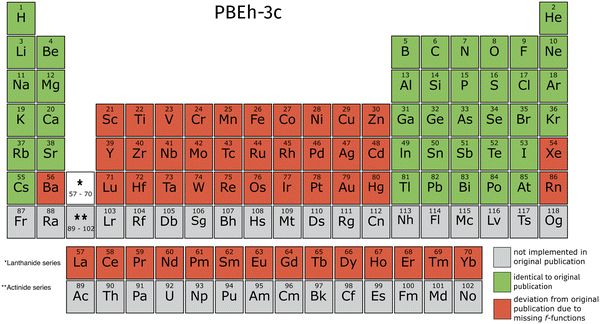
For PBEh-3c, elements with atomic number Z > 10, the def2-SVP basis set is used in the def2-mSVP basis (despite a typographical error in the original publication indicating the use of def2-SV(P)).14 Therefore, transition metals and lanthanides in addition to Xe, Ba, and Rn deviate from the original publication due to the missing implementation of f-functions.
Since ωB97X-3c was not available to us in TURBOMOLE when preparing this work, we only compared against ORCA for this composite method. The ωB97X-3c composite method relies less on f-functions for transition metals, making its implementation in TeraChem very appealing. The sixth period (likewise, Kr and Xe) use ECPs with very high angular momenta, i.e. up to h, which is not supported in TeraChem. Despite this restriction, ωB97X-3c is the composite method available for the largest number of elements out of the selection covered in this work.
The geometric counterpoise correction model is added to the software package as Fortran code,62 enabling compatibility to the C code base through the iso c binding module. The DFT-D4 model is accessed via the C API of the corresponding Fortran project,63 whereas the D3 model (including three-body terms) had been reimplemented in TeraChem by one of us previously, based on the available Fortran code.
The GMTKN5559 benchmark set is used to assess the numerical accuracy of the mixed precision (MP) scheme in TeraChem compared to double precision (DP) in TeraChem and to ORCA. Since the ωB97X-3c method has the largest collection of available elements, we choose it to compare those computation schemes. The GMTKN55 database is a collection of 55 benchmark sets grouped into 5 subsets, dedicated to various properties. We will not focus on comparing the results of this benchmark to other methods or DFAs, since it is well covered in the original ωB97X-3c publication.9 The detailed comparison of mean absolute deviation (MAD) values according to the weighted MAD (WTMAD-2) scheme59 for the subcategories in GMTKN55 can be found in Table 2.
| Program (numerical precision) | MAD of subcategories weighted according to WTMAD-2 [kcal mol−1] | |||||
|---|---|---|---|---|---|---|
| Basic properties | Reaction energies | Barrier heights | Intermol. NCIs | Intramol. NCIs | GMTKN52 | |
| ORCA DP | 4.749 | 7.933 | 5.154 | 4.887 | 5.698 | 5.480 |
| TeraChem DP | 4.745 | 7.935 | 5.154 | 4.883 | 5.701 | 5.479 |
| TeraChem MP | 4.746 | 7.934 | 5.153 | 4.883 | 5.703 | 5.479 |
| Program (numerical precision) | WTSTD-2: STD of subcategories weighted according to WTMAD-2 [kcal mol−1] | |||||
|---|---|---|---|---|---|---|
| Basic properties | Reaction energies | Barrier heights | Intermol. NCIs | Intramol. NCIs | GMTKN52 | |
| ORCA DP | 5.180 | 7.471 | 5.963 | 4.766 | 5.515 | 5.608 |
| TeraChem DP | 5.184 | 7.475 | 5.963 | 4.762 | 5.518 | 5.609 |
| TeraChem MP | 5.184 | 7.475 | 5.963 | 4.762 | 5.519 | 5.610 |
We can observe at most a deviation 0.005 kcal mol−1 in the intermolecular non-covalent interactions subset between both TeraChem schemes and ORCA. To even emphasize potential single outliers, we also show the Bessel corrected standard deviation (STD) for each subset, weighted accordingly to the WTMAD-2. For the WTSTD-2, we can also observe a deviation of at most 0.004 kcal mol−1 between ORCA and TeraChem. Again, the WTSTD-2 values are mostly indistinguishable for both numerical accuracy schemes in TeraChem.
The small deviations observed are absolutely negligible and are likely due to different settings in the analytical ERI and numerical DFT integral evaluation alongside different SCF thresholds in both programs, but not due to precision errors arising from the MP scheme in TeraChem. Therefore, the MP ERI evaluation scheme can be used safely for a large variety of molecules without any noticeable accuracy penalty.
Additionally, we would like to point out that with ωB97X-3c implemented, more accurate but fast thermochemistry calculations become available with consumer-grade GPUs. Usually such good performance for thermochemistry is only accessible with large basis sets including polarization functions. However, these basis sets contain functions with high angular momenta (l > 2), not available in TeraChem (and not well-performing in other GPU codes). With ωB97X-3c and its specifically parametrized basis set, we are now able to come closer to the good results of DFAs such as ωB97X-D464 with quadruple-zeta basis sets. We would like to highlight this using the C60ISO65 benchmark set, a subset of the GMTKN55. For this set, ωB97X-3c (as implemented with TeraChem) scores an MAD of 14.64 kcal mol−1 compared to 14.17 kcal mol−1 for ωB97X-D4/def2-QZVP.64 Calculations with the latter DFA and basis set require significantly more computational resources and, due to the basis set, cannot be carried out with existing GPU implementations at all, while the former has now become accessible with high efficiency (see below) through the ωB97X-3c implementation in TeraChem. Hence, through the implementation of this low-cost composite DFT method, fairly accurate thermochemistry calculations are possible on consumer-grade GPUs with the TeraChem program package. This leads to a considerable speed-up as demonstrated in the following section.
3.2 Comparing SCF wall times for implemented 3c methods
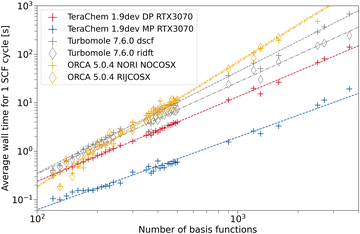
To assess the speed-up associated with the use of GPUs, we compare the average wall time per SCF cycle. This measure comes with the advantage, that varying numerical convergence thresholds and different implementations of convergence accelerators are not influencing the results. Rather, the average build of the Fock matrix and solving the eigenvalue problem are compared on fair grounds. Modern inexpensive workstations usually feature at least 8 CPU threads, hence, we also use 8 CPU threads in our comparison to provide a fair setup. ORCA and TURBOMOLE feature various approximations such as the resolution of the identity approximation for the Coulomb Matrix build (RI-J)17,28,66–68 and chain of spheres approximation for the exchange (COSX)24,69,70 (ORCA only). We use the cefine71 tool distributed by the Grimme group to prepare TURBOMOLE calculations. This tool sets a couple of default values for HF-3c and PBEh-3c. For both composite methods, g angular momentum functions are removed from the auxiliary basis set. TeraChem features no such low-scaling integral approximations, therefore we give timings with and without these acceleration methods for the other programs. For every program and integral setting, we obtain the wall time per SCF cycle from the wall time required for performing a full singlepoint energy calculation (including program startup and potential overheads) divided by the number of SCF cycles performed.The dependence on system size is evaluated using a set containing 164 carbon nanotubes taken from ref. 72. The geometries are used as given in the database. For all structures with the same system size, we average the wall time per SCF cycle over all those structures. In Fig. 5, the timings for the HF-3c composite method are shown. The missing datapoints for large fullerenes (larger than 1600 basis functions) can be explained by large disk space requirements in the default program settings. The workstations used for timings only possess 500 GB of disk space, restricting the number of ERI intermediates to be saved. In the regime with fewer basis functions, we can observe a seemingly less regular behavior for the mean wall time in ORCA. This may be caused by different program overheads (RIJ and COSX setup) details of the SCF algorithm in ORCA, which switches between various acceleration schemes. As expected, the use of the RI approximation does not lead to a significant speed-up for any program due the minimal basis set in HF-3c. When computing in full FP64, a speed-up of the TeraChem implementation compared to the CPU programs can be observed. However, reducing the number of FP64 operations in the MP scheme greatly decreases the average wall time per SCF cycle on this consumer-grade GPU. For small system sizes (160–200 basis functions), we can see a nearly constant wall time with the MP scheme in TeraChem. This effect can be rationalized by the time overhead to setup the GPU. These steps become significant to the overall wall time for small system sizes and fast methods. Despite this overhead associated to GPU calculations, we can achieve a significant speed-up (1 order of magnitude) for the HF-3c composite method with our TeraChem implementation.
Next we will evaluate the wall time per SCF cycle for the PBEh-3c hybrid DFT composite method. Due to the grid dependence of DFT functionals, additional complexity is added to the timing. However for hybrid DFT functionals, the exact Fock exchange computation is expected to be the dominant contributor to the overall computational cost. This should partially offset the grid dependence on the computational wall time. For PBEh-3c, the cefine tool adds the following parameter to the TURBOMOLE control file “$extol 2.5”. This parameter is an additive term to the exponents of varying numerical thresholds within the exact Fock exchange computation routine in TURBOMOLE's ridft program.73 It has been used as a default in many PBEh-3c calculations in TURBOMOLE. To assess the influence of this parameter on wall time, we show timings with and without the addition of this parameter in Fig. 6. For calculations performed in ORCA, the calculation failed at different stages for fullerenes larger than C260 (3900 basis functions). We expect that disk space on our test node became the limiting factor here, since certain intermediates are written to hard disk during the calculations.
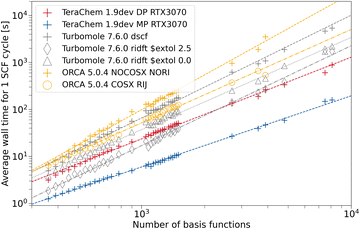 | ||
| Fig. 6 Average wall time per SCF cycle for the PBEh-3c composite method as a function of the number of basis functions. For TeraChem, the mixed precision (MP) and double precision (DP) computation schemes are considered. For TURBOMOLE and ORCA, single point calculations with and without the low scaling ERI approximations (RIJ and RIJCOSX, respectively) are shown. “$extol” is a parameter that is added to the exponential value of screening parameters in the Fock build routine of ridft.73 An NVIDIA RTX 3070 GPU is used. | ||
Similar wall times are measured for ORCA and TURBOMOLE in Fig. 6 when no integral approximations are used, analogous to the observations in Fig. 5. TeraChem's DP scheme is again faster than the CPU programs without approximations, but with more significant speed-up when using the MP scheme. It can be seen that the RIJ approximation (cf. ridft vs. dscf) reduces the computational cost to some degree. Still, the computation of Fock exchange dominates the overall computational cost, as expected. As such, we can observe that additionally employing the COSX approximation (ORCA) or changing the screening threshold by means of the extol-parameter (TURBOMOLE) is very effective. For “$extol 2.5”, TURBOMOLE RI-approximated calculations become faster than TeraChem with the DP scheme for the systems with <2000 basis functions. When applying default screening thresholds, TeraChem DP is faster than both CPU codes, which become very similar in this case. The better performance of TURBOMOLE's ridft with “$extol 0.0” compared to ORCA may be, at least partially, a result from using a smaller auxiliary basis set in the former. The TURBOMOLE ridft “$extol 2.5” variant approaches the speed of TeraChem with the MP scheme for small system sizes. Nevertheless, the GPU-accelerated MP scheme clearly yields the fastest computation method evaluated in this work.
For ωB97X-3c, we compare TeraChem to ORCA in Fig. 7. With our setup, we were not able to compute singlepoints for fullerenes larger than 100 carbon atoms (1300 basis functions). Mostly, the calculation failed during the setup of the model potential for the guess calculation. For larger systems, disk space limitations may also factor in. ORCA with RIJ and COSX approximation presents about the same average wall time as the DP scheme in TeraChem. COSX and RIJ appear to be more effective for ωB97X-3c compared to the previously discussed 3c methods. This is probably due to the deeper contraction scheme used in the vDZP basis set compared to the MINIX and def2-mSVP basis sets. Again, the MP scheme in TeraChem outperforms all other ERI implementations and assures a significant speed-up by about an order of magnitude compared to formally low scaling integral approximations (cf. ORCA with RIJCOSX).
In the following section, we are investigating how the wall time varies with GPU models and how their price relates to the performance.
3.3 Price-to-performance comparison of GPU models
In the previous section, we showed timings recorded with an NVIDIA RTX 3070 GPU, the manufacturer's suggested retail price (MSRP) for this card is $499.74 We will refer to the MSRP when discussing GPU prices for the remainder of this work, regardless of current market prices. The GPUs compared in this section vary by number of cores and type of such cores as well as the available memory. We also have access to the NVIDIA Quadro RTX 5000 GPU in our group-internal cluster. These cards are generally more expensive workstation cards with more memory and often a better FP64 performance relative to the number of cores installed. The theoretical floating point operations per second (FLOPS) of consumer grade (GeForce) cards for FP64 operations is 1/64th of their FP32 performance.74 For Quadro series cards, this ratio shifts to 1/3274 as shown in Table 3.| GPU | Theoretical performance | |
|---|---|---|
| FP64 [GFLOPS] | FP32 [TFLOPS] | |
| GeForce RTX 3070 | 317.4 | 20.31 |
| GeForce RTX 3080Ti | 532.8 | 34.10 |
| Quadro RTX 5000 | 348.5 | 11.15 |
In our computing cluster, we do not have access to the more pricey high-end cards of the Tesla family, which generally outmatch the Quadro cards in terms of memory and FP64 performance (1/2 FP64:FP32 performance for the V100 card at an estimated price of about $10![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 000). However, we expect the trends observed for the GeForce and Quadro cards to be translatable to the Tesla family as well.
000). However, we expect the trends observed for the GeForce and Quadro cards to be translatable to the Tesla family as well.
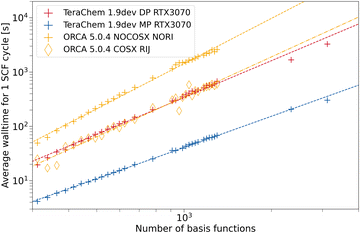
In Fig. 8, we examine how the theoretical performance of these GPUs translates to wall time differences for TeraChem calculations. We employ the same structures as in the previous section, to assess the average wall time per SCF cycle for the MP and DP scheme. In our computing cluster, the systems with RTX 3080Tis and Quadro RTX 5000 cards don't use the same CPUs as the ones with RTX 3070s. However, we assume that the GPU has a superior influence on the wall time and varying CPU models can be neglected. We present the values for PBEh-3c, while the plots for the other composite methods implemented in this work can be found in the SI.
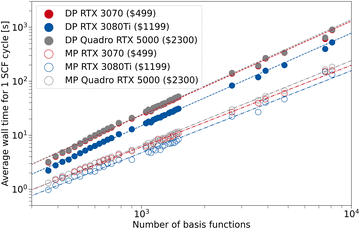 | ||
| Fig. 8 Average wall time for 1 SCF cycle for the composite method PBEh-3c as a function of the number of basis set functions. For TeraChem, the mixed precision (MP) and double precision (DP) computation schemes are compared for different GPU models. The indicated prices are MSRP according to ref. 74. | ||
In general, the resulting average wall time for the RTX 3070 and Quadro RTX 5000 are fairly similar throughout the investigated basis set sizes and precision schemes. Although for the MP scheme, the 3070 has a perceivable advantage over the Quadro card, which is more evident for larger system sizes. This can be rationalized by the better FP32 performance of the 3070 compared to the Quadro card. Hence, the low-priced GeForce card can offer the same (or better) performance if combined with the MP scheme in TeraChem. The RTX 3080Ti shows a clear advantage in average SCF wall time over the other GPUs, both in MP and DP scheme. However, the costs associated with this GPU are more than twice that of the RTX 3070. Therefore, it depends on the target deployment and usage, whether investing in a single 3080 Ti card or two 3070 cards is preferable. We can conclude from our work that the use of so-called “consumer-grade” GPUs for quantum chemical calculations is absolutely sufficient, especially when combined with a mixed precision scheme. Given that such “consumer-grade” cards are comparable in price to modern CPU chips, while providing much better performance in electronic structure calculations (by a factor of ∼10 with the MP scheme, see Section 3.2), one can expect roughly a five-fold speed-up in the calculations per invested dollar. As such, this provides the perfect setup for the small basis set 3c methods that were implemented in the present work.
3.4 Benchmarking 3c methods for their use with FOMO-hh-TDA
In this section, we will investigate the ability of the 3c-methods to describe excited states using the hh-TDA formalism. To allow comparison across a larger set of density functional approximations (DFA), we choose to use the same benchmark set as in the original publication,49 while focussing only on the lowest vertical excitations. The reference values are either “best estimate” values from Thiel's benchmark ref. 75 or, otherwise, are (spin-component-scaled) simplified coupled-cluster singles and doubles (CC2) values with mostly triple-zeta basis sets76,77 (see ref. 49 for details). In the charge-transfer (CT) subset, the CT states may not be the lowest when using different DFAs in hh-TDA. Therefore, among the computed excitations, we selected the lowest for which the static dipole moment changes by at least 8 Debye.The FOMO-hh-TDA study by Yu et al.50 also contained most of the parent methods, based on which the 3c methods discussed in this work have been build. For HF-3c, we compare with HF and for PBEh-3c with PBE0. The ωB97X-3c method is based on the exchange correlation functional parameters from ωB97X-V, however this DFA is not implemented in TeraChem. We compare against ωB97X-D3 instead. Prior studies49,50 have shown that high amounts of Fock exchange are beneficial for computation of singlet excitations with the hh-TDA scheme and BHLYP was one of the best performing DFAs. Hence, BHLYP is added to our comparison. The def2-SV(P) basis set is used throughout for the calculation with the parent methods.
In Fig. 9, the vertical excitation errors for different DFAs and composite methods are shown. The composite methods implemented in this work are shown in full lines, whereas their “parent” methods are shown in dotted lines.
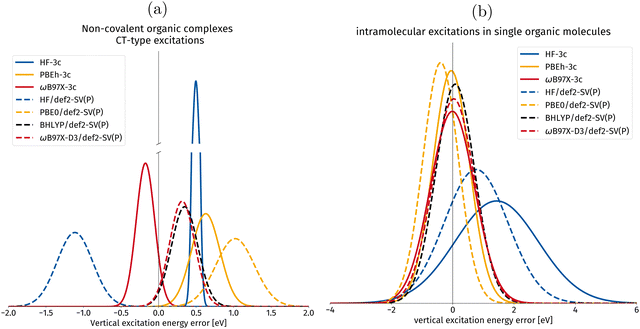 | ||
| Fig. 9 Gaussian error distribution functions for hh-TDA with different density functional approximations in the calculation of vertical excitation energies. Comparing the implemented 3c-methods with their parent methods with the spherical def2-SV(P)54 basis set. The values for the parent methods are taken from ref. 50. BHLYP/def2-SV(P) is added as it is one of the best performing density functionals in the original publication.49,50 The centers of the Gaussians correspond to the mean deviation (MD), whereas the width of the Gaussian corresponds to the standard deviation (SD), both in eV. (a) Excitations of non-covalently bound molecular complexes with intermolecular charge transfer (CT) character are shown in this subset. (b) Intramolecular excitations of local-excitation and push–pull type character. | ||
In Fig. 9a, vertical excitation errors in intermolecular CT excitations in non-covalently bound organic complexes are presented. For this subset, PBEh-3c is the only composite method for which the mean deviation shows the same sign as for its parent method. PBEh-3c shows a narrower error distribution and a smaller mean deviation compared to PBE0/def2-SV(P). This tendency could be explained by the higher amount of exact Fock exchange in PBEh-3c (42%) compared to PBE0 (25%). However, the mean deviation of PBEh-3c is larger than for BHLYP, making BHLYP the best choice for global hybrids among the compared DFAs for CT intermolecular excitations in organic complexes.
For HF-3c, we observe a narrow error distribution with a systematic overestimation by 0.50 eV. ωB97X-3c has the smallest MD among the considered DFAs for this intermolecular CT set. Hence, we can recommend its use for computing intermolecular valence CT excitations. We mention at this point, that the incorporation of large-core ECPs in ωB97X-3c prevents the calculation of core-excited states that can, in principle, be computed with hh-TDA (cf. ref. 78).
In Fig. 9b, the local and push–pull-type excitation subsets are combined into one set for statistical evaluation. The individual subset plots can be found in the ESI.† For this joined set, PBEh-3c shows again better results than its parent DFA PBE056 with a smaller MD of −0.05 eV compared to 0.39 eV. Primarily, we expect this to be an effect of the larger amount of Fock exchange in PBEh-3c (42%), as BHLYP (50%) is known to be one of the best DFAs for hh-TDA.50 ωB97X-3c improves on the already excellent MD of ωB97X-D3 with −0.01 eV relative to 0.03 eV, both show wider error distributions than the global hybrids presented in this work.
In summary, we find that PBEh-3c works very well for the lowest vertical valence excitations, though somewhat less so for intermolecular CT excitations. The range separated composite method ωB97X-3c is, overall, better suited for describing intramolecular and intermolecular excitations. However, the computational cost associated with this method is slightly higher than with PBEh-3c (cf.Fig. 6 and 7) due to the deeper contraction scheme in the vDZP basis set.
4 Conclusions & outlook
In this work, we presented the implementation of the 3c composite methods in the GPU-accelerated software package TeraChem. We could demonstrate that our implementation offers a considerable speed-up in average SCF wall time compared to CPU-based implementations across the implemented 3c methods. When using consumer-grade GPUs, the use of the mixed precision scheme is best suited, it offers an exceptional speed-up with virtually no deficit in numerical accuracy. We found that mid-tier consumer GPUs, such as the RTX 3070, present an excellent price to performance ratio, which could lead to wider use of these heterogeneous architectures throughout the community. Some elements cannot be handled with the current implementation, due to missing high angular momentum functions in the corresponding basis sets or ECPs. This is less severe for the most accurate ωB97X-3c model, where this almost exclusively affects the row 6 elements of the periodic table. With this method, it has now become possible to achieve high accuracy in quantum chemistry calculations, comparable to DFT calculations with quadruple zeta basis sets, with extremely low computational times on consumer-grade GPUs.This work also assessed the performance of the 3c methods for their use in excited states calculations within the FOMO-hh-TDA scheme. Using a benchmark set for small organic molecules, we found that PBEh-3c is a great choice for a density functional approximation (DFA) for local vertical excitations, while less so for intermolecular charge-transfer excitations. The DFA ωB97X-3c also shows very good performance with an overall better balance in the error between local and charge-transfer excitations. The combination with FOMO-hh-TDA allows fast exploration of photochemical reactions, which will be important for simulations in energy conversion materials. The combinations of 3c methods with this scheme will be used in the future for studies of photoinduced processes in large molecules and aggregates.
Conflicts of interest
There are no conflicts to declare.Acknowledgements
We thank Prof. Todd J. Martínez for granting access to the TeraChem code base and supporting our implementational work. The authors would like to thank Dr Uwe Huniar for answering questions about the TURBOMOLE software package and its screening parameters. The authors would also like to thank Mike Pauls for the talks and discussions throughout this work. This project has been funded by the Ministry of Culture and Science of the German State of North Rhine-Westphalia (MKW) via the NRW Rückkehrprogramm.References
- T. Kratz, P. Steinbach, S. Breitenlechner, G. Storch, C. Bannwarth and T. Bach, J. Am. Chem. Soc., 2022, 144, 10133–10138 CrossRef CAS PubMed
.
- S. Grimme, C. Bannwarth, S. Dohm, A. Hansen, J. Pisarek, P. Pracht, J. Seibert and F. Neese, Angew. Chem., Int. Ed., 2017, 56, 14763–14769 CrossRef CAS PubMed
.
- P. Pracht and S. Grimme, J. Phys. Chem. A, 2021, 125, 5681–5692 CrossRef CAS PubMed
.
- P. Pracht, F. Bohle and S. Grimme, Phys. Chem. Chem. Phys., 2020, 22, 7169–7192 RSC
.
- S. Grimme, J. Chem. Theory Comput., 2019, 15, 2847–2862 CrossRef CAS PubMed
.
- S. Grimme, C. Bannwarth and P. Shushkov, J. Chem. Theory Comput., 2017, 13, 1989–2009 CrossRef CAS PubMed
.
- C. Bannwarth, S. Ehlert and S. Grimme, J. Chem. Theory Comput., 2019, 15, 1652–1671 CrossRef CAS PubMed
.
- C. Bannwarth, E. Caldeweyher, S. Ehlert, A. Hansen, P. Pracht, J. Seibert, S. Spicher and S. Grimme, Wiley Interdiscip. Rev.: Comput. Mol. Sci., 2021, 11, e1493 CAS
.
- M. Müller, A. Hansen and S. Grimme, J. Chem. Phys., 2023, 158, 014103 CrossRef PubMed
.
- R. Sure and S. Grimme, J. Comput. Chem., 2013, 34, 1672–1685 CrossRef CAS PubMed
.
- H. Kruse and S. Grimme, J. Chem. Phys., 2012, 136, 154101 CrossRef PubMed
.
- S. Grimme, J. Antony, S. Ehrlich and H. Krieg, J. Chem. Phys., 2010, 132, 154104 CrossRef PubMed
.
- E. Caldeweyher, S. Ehlert, A. Hansen, H. Neugebauer, S. Spicher, C. Bannwarth and S. Grimme, J. Chem. Phys., 2019, 150, 154122 CrossRef PubMed
.
- S. Grimme, J. G. Brandenburg, C. Bannwarth and A. Hansen, J. Chem. Phys., 2015, 143, 054107 CrossRef PubMed
.
- J. G. Brandenburg, C. Bannwarth, A. Hansen and S. Grimme, J. Chem. Phys., 2018, 148, 064104 CrossRef PubMed
.
- S. Grimme, A. Hansen, S. Ehlert and J.-M. Mewes, J. Chem. Phys., 2021, 154, 064103 CrossRef CAS PubMed
.
- O. Vahtras, J. Almlöf and M. Feyereisen, Chem. Phys. Lett., 1993, 213, 514–518 CrossRef CAS
.
- F. Neese, Wiley Interdiscip. Rev.: Comput. Mol. Sci., 2012, 2, 73–78 CAS
.
- F. Neese, Wiley Interdiscip. Rev.: Comput. Mol. Sci., 2018, 8, e1327 Search PubMed
.
- S. G. Balasubramani, G. P. Chen, S. Coriani, M. Diedenhofen, M. S. Frank, Y. J. Franzke, F. Furche, R. Grotjahn, M. E. Harding, C. Hättig, A. Hellweg, B. Helmich-Paris, C. Holzer, U. Huniar, M. Kaupp, A. Marefat Khah, S. Karbalaei Khani, T. Müller, F. Mack, B. D. Nguyen, S. M. Parker, E. Perlt, D. Rappoport, K. Reiter, S. Roy, M. Rückert, G. Schmitz, M. Sierka, E. Tapavicza, D. P. Tew, C. van Wüllen, V. K. Voora, F. Weigend, A. Wodynski and J. M. Yu, J. Chem. Phys., 2020, 152, 184107 CrossRef CAS PubMed
.
- Y. J. Franzke, C. Holzer, J. H. Andersen, T. Begušić, F. Bruder, S. Coriani, F. Della Sala, E. Fabiano, D. A. Fedotov, S. Fürst, S. Gillhuber, R. Grotjahn, M. Kaupp, M. Kehry, M. Krstić, F. Mack, S. Majumdar, B. D. Nguyen, S. M. Parker, F. Pauly, A. Pausch, E. Perlt, G. S. Phun, A. Rajabi, D. Rappoport, B. Samal, T. Schrader, M. Sharma, E. Tapavicza, R. S. Treß, V. Voora, A. Wodynski, J. M. Yu, B. Zerulla, F. Furche, C. Hättig, M. Sierka, D. P. Tew and F. Weigend, J. Chem. Theory Comput., 2023, 19, 6859–6890 CrossRef CAS PubMed
.
- F. Weigend, Phys. Chem. Chem. Phys., 2002, 4, 4285–4291 RSC
.
- R. A. Friesner, Chem. Phys. Lett., 1985, 116, 39–43 CrossRef CAS
.
- F. Neese, F. Wennmohs, A. Hansen and U. Becker, J. Chem. Phys., 2009, 356, 98–109 CAS
.
- P. Plessow and F. Weigend, J. Comput. Chem., 2012, 33, 810–816 CrossRef CAS PubMed
.
- F. Liu and J. Kong, Chem. Phys. Lett., 2018, 703, 106–111 CrossRef CAS
.
- H. Laqua, T. H. Thompson, J. Kussmann and C. Ocsenfeld, J. Chem. Theory Comput., 2020, 16, 1456–1468 CrossRef CAS PubMed
.
- J. L. Whitten, J. Chem. Phys., 1973, 58, 4496–4501 CrossRef CAS
.
- S. Seritan, C. Bannwarth, B. S. Fales, E. G. Hohenstein, C. M. Isborn, S. I. L. Kokkila-Schumacher, X. Li, F. Liu, N. Luehr, J. W. Snyder Jr., C. Song, A. V. Titov, I. S. Ufimtsev, L.-P. Wang and T. J. Martínez, Wiley Interdiscip. Rev.: Comput. Mol. Sci., 2021, 11, e1494 CAS
.
- S. Seritan, C. Bannwarth, B. S. Fales, E. G. Hohenstein, S. I. L. Kokkila-Schumacher, N. Luehr, J. Snyder, W. James, C. Song, A. V. Titov, I. S. Ufimtsev and T. J. Martínez, J. Chem. Phys., 2020, 152, 224110 CrossRef CAS PubMed
.
- K. Yasuda, J. Chem. Theory Comput., 2008, 4, 1230–1236 CrossRef CAS PubMed
.
- K. Yasuda, J. Comput. Chem., 2008, 29, 334–342 CrossRef CAS PubMed
.
- A. Asadchev, V. Allada, J. Felder, B. M. Bode, M. S. Gordon and T. L. Windus, J. Chem. Theory Comput., 2010, 6, 696–704 CrossRef CAS PubMed
.
- K. A. Wilkinson, P. Sherwood, M. F. Guest and K. J. Naidoo, J. Comput. Chem., 2011, 32, 2313–2318 CrossRef CAS PubMed
.
- X. Wu, A. Koslowski and W. Thiel, J. Chem. Theory Comput., 2012, 8, 2272–2281 CrossRef CAS PubMed
.
- Y. Miao and K. M. J. Merz, J. Chem. Theory Comput., 2013, 9, 965–976 CrossRef CAS PubMed
.
- Y. Miao and K. M. J. Merz, J. Chem. Theory Comput., 2015, 11, 1449–1462 CrossRef CAS PubMed
.
- J. Kussmann and C. Ochsenfeld, J. Chem. Theory Comput., 2017, 13, 3153–3159 CrossRef CAS PubMed
.
- J. Kalinowski, F. Wennmohs and F. Neese, J. Chem. Theory Comput., 2017, 13, 3160–3170 CrossRef CAS PubMed
.
- https://docs.nvidia.com/cuda/cuda-c-programming-guide/index.html, (last accessed 21.11.2023).
- I. S. Ufimtsev and T. J. Martínez, Comput. Sci. Eng., 2008, 10, 26–34 CAS
.
- I. S. Ufimtsev and T. J. Martínez, J. Chem. Theory Comput., 2008, 4, 222–231 CrossRef CAS PubMed
.
- I. S. Ufimtsev and T. J. Martinez, J. Chem. Theory Comput., 2009, 5, 1004–1015 CrossRef CAS PubMed
.
- I. S. Ufimtsev and T. J. Martinez, J. Chem. Theory Comput., 2009, 5, 2619–2628 CrossRef CAS PubMed
.
- IEEE Computer Society Standards Committee. Working group of the Microprocessor Standards Subcommittee and American National Standards Institute. IEEE standard for binary floating-point arithmetic, 1985, vol. 754.
- IEEE Standard for Floating-Point Arithmetic, IEEE Standard, 2008, vol. 754 DOI:10.1109/IEEESTD.2008.4610935.
- J. Almlöf, K. Faegri Jr. and K. Korsell, J. Comput. Chem., 1982, 3, 385–399 CrossRef
.
- N. Luehr, I. S. Ufimtsev and T. J. Martínez, J. Chem. Theory Comput., 2011, 7, 949–954 CrossRef CAS PubMed
.
- C. Bannwarth, J. K. Yu, E. G. Hohenstein and T. J. Martínez, J. Chem. Phys., 2020, 153, 024110 CrossRef PubMed
.
- J. K. Yu, C. Bannwarth, E. G. Hohenstein and T. J. Martínez, J. Chem. Theory Comput., 2020, 16, 5499–5511 CrossRef CAS PubMed
.
- D. Peng, H. van Aggelen, Y. Yang and W. Yang, J. Chem. Phys., 2014, 140, 18A522 CrossRef PubMed
.
- Y. Yang, L. Shen, D. Zhang and W. Yang, J. Phys. Chem. Lett., 2016, 7, 2407–2411 CrossRef CAS PubMed
.
- S. Grimme, S. Ehrlich and L. Goerigk, J. Comput. Chem., 2011, 32, 1456–1465 CrossRef CAS PubMed
.
- F. Weigend and R. Ahlrichs, Phys. Chem. Chem. Phys., 2005, 7, 3297–3305 RSC
.
- J. P. Perdew, K. Burke and M. Ernzerhof, Phys. Rev. Lett., 1996, 77, 3865–3868 CrossRef CAS PubMed
.
- C. Adamo and V. Barone, J. Chem. Phys., 1999, 110, 6158–6170 CrossRef CAS
.
- N. Mardirossian and M. Head-Gordon, Phys. Chem. Chem. Phys., 2014, 16, 9904–9924 RSC
.
- A. Dreuw and M. Head-Gordon, Chem. Rev., 2005, 105, 4009–4037 CrossRef CAS PubMed
.
- L. Goerigk, A. Hansen, C. Bauer, S. Ehrlich, A. Najibi and S. Grimme, Phys. Chem. Chem. Phys., 2017, 19, 32184–32215 RSC
.
- D. Andrae, U. Haeussermann, M. Dolg, H. Stoll and H. Preuss, Theor. Chim. Acta, 1990, 77, 123–141 CrossRef CAS
.
- A. Bergner, M. Dolg, W. Küchle, H. Stoll and H. Preuß, Mol. Phys., 1993, 80, 1431–1441 CrossRef CAS
.
- https://github.com/grimme-lab/gcp, (last accessed 21.11.2023).
- https://github.com/dftd4/dftd4, (last accessed 21.11.2023).
- A. Najibi and L. Goerigk, J. Comput. Chem., 2020, 41, 2562–2572 CrossRef CAS PubMed
.
- R. Sure, A. Hansen, P. Schwerdtfeger and S. Grimme, Phys. Chem. Chem. Phys., 2017, 19, 14296–14305 RSC
.
- K. Eichkorn, O. Treutler, H. Öhm, M. Häser and R. Ahlrichs, Chem. Phys. Lett., 1995, 242, 652–660 CrossRef CAS
.
- K. Eichkorn, F. Weigend, O. Treutler and R. Ahlrichs, Theor. Chem. Acc., 1997, 97, 119–124 Search PubMed
.
- F. Neese, J. Comput. Chem., 2003, 24, 1740–1747 CrossRef CAS PubMed
.
- B. Helmich-Paris, B. de Souza, F. Neese and R. Izsák, J. Chem. Phys., 2021, 155, 104109 CrossRef CAS PubMed
.
- R. Izsák, F. Neese and W. Klopper, J. Chem. Phys., 2013, 139, 094111 CrossRef PubMed
.
- https://github.com/grimme-lab/cefine, (last accessed 21.11.2023).
- D. Tomanek and N. Frederick, https://nanotube.msu.edu/fullerene/fullerene-isomers.html, (last accessed: 21.11.2023).
- U. Huniar, Private Commun., 2023 Search PubMed
.
- https://www.techpowerup.com/, (last accessed: 21.11.2023).
- M. Schreiber, M. R. Silva-Junior, S. P. A. Sauer and W. Thiel, J. Chem. Phys., 2008, 128, 134110 CrossRef PubMed
.
- T. Risthaus, A. Hansen and S. Grimme, Phys. Chem. Chem. Phys., 2014, 16, 14408–14419 RSC
.
- S. Grimme and C. Bannwarth, J. Chem. Phys., 2016, 145, 054103 CrossRef PubMed
.
- E. G. Hohenstein, J. K. Yu, C. Bannwarth, N. H. List, A. C. Paul, S. D. Folkestad, H. Koch and T. J. Martínez, J. Chem. Theory Comput., 2021, 17, 7120–7133 CrossRef CAS PubMed
.
Footnote |
| † Electronic supplementary information (ESI) available. See DOI: https://doi.org/10.1039/d3cp06086a |
| This journal is © the Owner Societies 2024 |