Effect of trimethylamine-N-oxide on the phase separation of aqueous polyethylene glycol-600-Dextran-75 two-phase systems

Abstract

The emergence of phase separation in both intracellular biomolecular condensates (membrane-less organelles) and in vitro aqueous two-phase systems (ATPS) relies on the formation of immiscible water-based phases/domains. The solvent properties and arrangement of hydrogen bonds within these domains have been shown to differ and can be modulated with the addition of various inorganic salts and osmolytes. The naturally occuring osmolyte, trimethylamine-N-oxide (TMAO), is well established as a biological condensate stabilizer whose presence results in enhanced phase separation of intracellular membrane-less compartments. Here, we show the unique effect of TMAO on the mechanism of phase separation in model PEG-600-Dextran-75 ATPS using dynamic and static light scattering in conjunction with ATR-FTIR and solvatochromic analysis. We observe that the presence of TMAO may enhance or destabilize phase separation depending on the concentration of phase forming components. Additionally, the behavior and density of mesoscopic polymer agglomerates, which arise prior to macroscopic phase separation, are altered by the presence and concentration of TMAO.

---

Introduction

Liquid–liquid phase separation (LLPS) is a universal process that drives the formation of numerous membrane-less intracellular compartments, such as stress-granules, Cajal bodies, P-bodies, and centrosomes,^1–9 which can be found in the nucleus, cytoplasm, and mitochondria/chloroplasts of eukaryotic cells, as well as within bacteria and archaea. These compartmentalized cellular bodies (foci, puncta, membrane-less organelles, or biomolecular condensates) contain vastly different protein/RNA/macromolecule concentrations compared to the surrounding cytosol, nucleosol or mitochondrial matrix despite the absence of a lipid boundary. LLPS is one of the fundamental mechanisms for organizing intracellular space, but currently different models of the mechanism behind LLPS formation are debated.^10–14 However, there seems to be an agreement that water, specifically the structure and strength of its interactions, plays an important role in the cellular LLPS processes.^15–22

Aqueous two-phase systems (ATPSs) have been proposed as the simplest in vitro model system for analyzing the governing principles behind the emergence of LLPS.²³ ATPSs are formed from mixtures of two polymers or a single polymer and inorganic/organic salt or other low molecular weight organic compounds, ionic liquids, surfactants, proteins, polysaccharides, etc. in water.^23–25 When the concentrations of phase-forming solutes exceed a particular threshold (e.g., binodal line in Fig. 1), the mixture separates into two phases containing predominantly one of the phase-forming solutes, a small concentration of the other solute, and water at a concentration approximately in the range of 80–90 mol%.

Fig. 1 Phase diagram of Dextran-75-PEG-8000 ATPS in 0.15 M NaCl/0.01 M Na-phosphate buffer (NaPB), pH 7.4. A₀, A₁, and A₂ represent systems with the three different volume ratios lying on a straight tie-line between compositions of the coexisting phases represented by points D (lower, Dextran-rich phase) and P (upper, PEG-rich phase). C represents the critical point determined by extrapolation through the midpoints of several tie-lines. Data taken from ref. 31.

An example of a typical two-dimensional phase diagram for ATPSs formed with two polymers (Dextran-75 and PEG-8000) is presented in Fig. 1. The curved, binodal line separates two regions of polymer compositions. All compositions below the binodal line correspond to a visually homogeneous single-phase region, while those above the binodal line correspond to the region of two-phase systems. Points representing the compositions of the upper and lower phases lie on the binodal curve. The line connecting the compositions of the two coexisting phases and the overall composition of the system is called a tie line. The length of the tie line decreases as the concentrations of the two polymers in a given ATPS is reduced. At a certain point called the critical point (point C in Fig. 1) the compositions of the two coexisting phases are identical.

It is well established that the solvent properties of aqueous media in the phases of ATPSs are different and depend upon the specific composition of the phases.^18,26–28 The solvent properties of water in individual phases of ATPSs can be characterized using the Kamlet–Taft solvatochromic comparison method, allowing for the estimation of a solvent's ability to participate in dipole–dipole and dipole-induced-dipole interactions (solvent dipolarity/polarizability, π*), donate a hydrogen bond (hydrogen bond donor (HBD) acidity, α), and accept a hydrogen bond (solvent hydrogen bond acceptor (HBA) basicity, β). The partition behavior of various solutes between the phases of an ATPS are governed by these solvent properties.^18,26–30

The differences in solvent properties between phases have been suggested to originate from the rearrangement of water hydrogen bonds (H-bonds).³² The arrangement of H-bonds can be estimated by analyzing the OH-stretch band (4000–2500 cm⁻¹) of aqueous solutions. We have previously established a model based on the decomposition of the OH-stretch band into four Gaussian components assigned to different subpopulations of water.³² Components at lower optical frequencies are generally assigned to water molecules forming strong, ice-like, H-bonds, while those at higher frequencies are assigned to water molecules in an environment with weaker and/or distorted H-bonds. We have recently established that the arrangement of H-bonds in the two phases of ATPS are different and strongly correlate with the solvent properties of the individual phases.^32,33 A theoretical model has been proposed, in which different water domains with dissimilar solvent properties are formed, and both their size and difference amplify with the increase of polymer concentrations, leading to emergence of interfacial tension and the formation of two aqueous phases.^20,22 We have previously found that at concentrations below the threshold of phase separation, the arrangement of H-bonds in water abruptly changes, and agglomerates of one of the polymers in the mixture are formed.²¹ We suggest that the underlying principles of this agglomerate formation and phase separation in ATPS are comparable to those governing LLPS in the formation of membrane-less biocondensates.²¹

Solvent properties also strongly correlate with changes in protein and nucleic acid stability with the addition of osmolytes.²⁶ Osmolytes are a critical component of LLPS as they affect cellular homeostasis in aqueous solution by countering external changes in osmotic pressure, resulting in enhanced phase separation of membrane-less compartments.^34,35 The osmolyte, trimethylamine-N-oxide (TMAO), has been shown to stabilize biological condensate droplets and protect proteins and nucleic acids from denaturation.^34,36–39 This stabilizing effect of TMAO has been suggested to occur via strengthening of the H-bond network via reorganization of H-bonds in aqueous solution.^35,39–42 It has also been suggested that the direct stabilization of proteins by TMAO is less significant than TMAO's indirect stabilizing effect via TMAO–water complexes.⁴³ Here, we examine in detail the effects of TMAO on phase separation, agglomerate formation and structure, and H-bond arrangement in model ATPS formed by two nonionic polymers (polyethylene glycol and Dextran).

Materials and methods

Materials

Polymers. Polyethylene glycol (PEG-600, lot. 1KD0658) with an average molecular weight of 600 g mol⁻¹ was obtained by Spectrum Chemical Mfg. Corp. (New Brunswick, NJ, USA). Dextran-75 (lot. 119945) with an average molecular weight of 75 000 was obtained by USB Corporation (Cleveland, OH, USA).

Organic compounds and other chemicals. Trimethylamine N-oxide (TMAO) and 4-nitrophenol of the highest purity grade were purchased from Sigma-Aldrich and used without further purification. 4-Nitroanisole (GC, >99%) was supplied by Acros organic (New Jersey, USA). Reichardt's carboxylated betaine dye sodium (2,6-diphenul-4-[4-(4-carboxylato-phenyl)-2,6-diphenylpyridinium-1-yl)phenolate] was synthesized as previously described.⁴⁴ Ultrapure water (18.5 mΩ) purified using a Milli-Q® lab water system (EMD Millipore Sigma, Burlington, MA, USA) was used for the preparation of all solutions.

Methods

Aqueous two-phase systems (ATPS). ATPS were prepared by mixing appropriate amounts of the aqueous stock solutions for PEG-600 (90 wt%), Dextran-75 (42 wt%), TMAO (5.0 M), 3 M NaCl in 0.2 M sodium phosphate buffer (NaPB), pH 7.4, and water. Separate stock solutions of 0.15 M NaCl/0.01 M NaPB, pH 7.4 with no TMAO, 2 wt% TMAO and 7.2 wt% TMAO were prepared and used as the diluents for mixed ATPS of the same TMAO concentration. ATPS compositions used in this study are listed below in Table 1.

Table 1 Compositions of ATPS used in this study

ATPS	PEG-600 (wt%)	Dextran-75 (wt%)	TMAO (wt%)	Buffer
1	18.5	8.5	—	0.15 M NaCl in 0.01 M NaPB, pH 7.4
2	20	8.5	2	0.15 M NaCl in 0.01 M NaPB, pH 7.4
3	20	8.5	7.2	0.15 M NaCl in 0.01 M NaPB, pH 7.4

---

Solutions were mixed vigorously and allowed to settle at room temperature (20–23 °C). For ATR-FTIR, DLS, and SLS analysis each system was vigorously mixed, quickly aliquoted and diluted with 0.15 M NaCl in 0.01 M NaPB, pH 7.4, with or without the addition of TMAO, to ∼50, 70, 80, 90, 95, and 97 wt% of the initial ATPS. For experiments requiring an isolated phase of an ATPS, the mixture was centrifuged, and aliquots of the individual phases were withdrawn and diluted with 0.15 M NaCl in 0.01 M NaPB, pH 7.4, with or without the addition of TMAO, to ∼50, 70, 80, 90, 95, 97, and 100 wt% of each phase. Actual wt% varied from these exact values and were calculated to 0.1 wt%.

Solvatochromic studies. The solvatochromic probes 4-nitroanisole, 4-nitrophenol, and Reichardt's carboxylated betaine dye were used to determine the solvent dipolarity/polarizability π*, H-bond acceptor (HBA) basicity β, and H-bond donor (HBD) acidity α of the media in the separated phases of the PEG-Dextran-(TMAO) ATPS as previously described.^18,45

Spinning drop tensiometry. ATPS were prepared as described above and individual phases were removed and stored separately for testing. SDT measurements were conducted by Krüss Scientific (Charlotte, NC, USA). The bottom, denser phase was aspirated into a glass sample holder with a Teflon plug. A 1.0 μL drop of the top, less dense phase was dispensed into the glass sample holder containing the bottom phase and capped with the Teflon plug. The sample holder was then placed into the SDT and spun at 4500 rpm at 25 °C for 60 minutes. The liquid–liquid boundary of the drop was imaged in real time using a high-resolution camera and fit using the intelligence image evaluation algorithm software, ADVANCE. Drop shape was evaluated using the standard Vonnegut method,⁴⁶ and the average of three independent experiments was reported.

Analysis of TMAO concentration in the phases of ATPS. Identical systems to those listed in Table 1 were prepared along with a 20 wt% PEG-600/8.5 wt% Dextran-75/0.15 M NaCl in 0.01 M NaPB, pH 7.4 ATPS. Systems were centrifuged and individual phases were withdrawn and diluted to a dilution factor of 2, 5, 10, 12, 15, 18, and/or 20 with water. TMAO concentrations in the phases were measured by total nitrogen assay with chemiluminescent nitrogen detector (CLND) by Analiza Inc. (Cleveland, OH, USA) as previously described.⁴⁷

Fourier transform infrared (FTIR) spectroscopy analysis. ATR-FTIR spectra for each sample were measured in two separately prepared solutions using an Alpha II FT-IR spectrometer (Bruker) equipped with Platinum single reflection ATR single reflection diamond ATR module (Bruker Scientific, LLC, Billerica, MA, USA). All measurements were performed at ambient temperature (approximately 23 °C) using 24 scans for each sample and 24 scans for background in the spectral range of 4000–1000 cm⁻¹ with resolution of 4 cm⁻¹. The spectra were reproducible to better than 1 cm⁻¹.

ATR-FTIR spectra were analyzed using custom software written in Wolfram Mathematica and run under version 12. Details on the software and protocol used can be found in ref. 21.

Dynamic and static light scattering measurements. An Argon gas laser (Spectra Physics, Stabilite 2017) with a wavelength of 488 nm and output power of 250 mW was used as the light source for both DLS and SLS measurements. A photomultiplier tube (BI DS2) attached to a goniometer (BI 200SM) was used to take measurements at different angles. The data was analyzed by BI 9000 digital correlator. All samples were filtered (with 0.45 μm filter) into borosilicate glass test tubes and submerged in decalin vat to minimize reflection from the glass. All samples were kept at 25 °C during SLS/DLS experiments by a bath circulator (NesLab RTE-111). DLS data was analyzed using the spectral time moment analysis following.⁴⁸

For SLS measurements, the scattering intensities were measured at 13 angles at a range of 60–120° in increments of 5°. Each sample was measured at the same angles twice and the intensity values were averaged for the Zimm analysis.⁴⁹ Details described further in (ESI†). Proper SLS measurements require determination of the specific refractive index increment (dn/dc) for the samples studied. The dn/dc values were directly measured using a Brice–Phoenix refractometer (BPR) and the procedure described in ref. 50. The concentrations used to measure dn/dc in BPR mirror the ones used for SLS experiments. Since no wavelength dependence of dn/dc was observed across three wavelengths (436, 546, and 589 nm), an average value of those measurements was taken as dn/dc for each system.

Sample concentrations for SLS centered around 10 wt%, the lowest concentration used for each system in DLS, were used in SLS. DLS measurements used concentrations of 10, 30, 50, 60, 70, and 80 wt% across three systems. For DLS, three 2–3 min measurements were taken at each of the five scattering angles, 60, 75, 90, 105, 120°.

Additional details regarding DLS and SLS analysis can be found in ESI.†

Results

Phase diagrams of Dextran-75-PEG-600 in 0.15 M NaCl and 0.01 M sodium phosphate buffer (NaPB), pH 7.4 ATPSs with varying concentrations of TMAO are presented in Fig. 2. The upward shift of the left side of the binodal line in the presence of 7.2 wt% TMAO (blue curve), relative to that for the same ATPS containing 2 wt% TMAO (red curve), implies the hindrance of phase separation with increasing TMAO concentration. However, the downward shift of the right side of the binodal line for systems containing 7.2 wt% TMAO indicates the enhancement of phase separation in comparison to the 2 wt% TMAO-containing systems. The binodal line for systems in absence of TMAO (black curve) is provided as a reference, in which the presence of TMAO diminishes phase separation overall. The most commonly observed trend for ATPSs formed by two nonionic polymers with additives of inorganic salts is either the downward or upward shift of the binodal line (see in ref. 23) with the most pronounced difference in the central part of the binodal line.

Fig. 2 Binodal lines for aqueous Dextran-75-PEG-600 two-phase systems in the absence of TMAO (black, dotted curve); in the presence of 2 wt% TMAO (red, solid curve) and 7.2 wt% TMAO (blue, dashed curve). Additional detailed phase diagrams for the same systems are presented in Fig. S1 and S2 in ESI.†

The only example of the binodal change in the manner shown in Fig. 2 to the authors’ knowledge was observed when comparing the binodal lines for the systems formed by polypropylene glycol (PPG) with a molecular weight of 725 Da and sodium citrate⁵¹ and by Ucon (copolymer of ethylene glycol and propylene glycol) with a molecular weight of 4 kDa and the same salt.⁵² A much less pronounced, but similar effect was observed when 2 mol kg⁻¹ urea was added to ATPSs formed by Dextran-75 and polyvinyl alcohol.²³ We have also previously shown²⁷ that PEG-600 and TMAO, in the absence of Dextran, phase separate in 0.01 M NaPB at relatively high concentrations.

Empirically, we have observed a similar trend for the effects of TMAO addition to ATPSs formed with a higher molecular weight PEG (35 000 g mol⁻¹) and bovine serum albumin (BSA), shown in Fig. 3. In this case, we observed again a variable effect of TMAO on the formation of ATPS, which appears to be dependent upon the total amount of TMAO in a given system. To further illustrate this point, an ATPS formed with 10 wt% PEG-35K, 10 wt% BSA, and 0.15 M NaCl in 0.01 M NaPB, pH 7.4 was prepared. This system was well mixed, and 100 μL was dispensed on a glass slide and imaged using an Olympus BX51 microscope under 20× magnification. Small droplets of one phase within the other can be observed in Fig. 4A. However, when an aliquot of 40 μL of 4 M TMAO in 0.15 M NaCl and 0.01 M NaPB, pH 7.4 was added to this slide, all small droplets were removed (Fig. 4B), suggesting the diminishment of phase separation. In order to ensure that this was not just due to dilution of the system, the same process was repeated but with water in place of 4 M TMAO (Fig. 4C).

Fig. 3 Binodal lines for aqueous bovine serum albumin (BSA)-PEG-35 000 two-phase systems in the absence of TMAO (black, dotted curve); in the presence of 2 wt% TMAO (red, solid curve) and 7.2 wt% TMAO (blue, dashed curve).

Fig. 4 Microscope images of a mixed ATPS formed with 10 wt% bovine serum albumin (BSA) and 10 wt% PEG-35 000 alone (A), with the addition of 40 μL 4 M TMAO (B), or with the addition of 40 μL water (C).

The distribution of TMAO between the phases of these ATPSs is characterized as a ratio of the TMAO concentration in the upper, PEG-rich phase to that in the lower, Dextran-rich phase. The function of the distribution of TMAO concentrations in the top and bottom phases of the systems measured here are presented in Fig. S3 (ESI†). It is well documented²³ that salt additives in ATPS formed by two nonionic polymers generally distribute between the phases differently. The distribution ratio for these additives may be described as:

Log(D_salt) = b_salt × D[polymer_i] (1)

where D_salt is the ratio of the salt concentrations in the top and bottom phases; D[polymer_i] is the difference between the polymer i concentrations in the same phases; and b_salt is a constant with the value depending on the type of polymers and on the type and concentration of salt additive.

It follows from eqn (1) that the linear dependence of Log(D_salt) = 0 when D[polymer_i] = 0, implying that in the ATPS composition corresponding to the critical point of phase diagram (when compositions of both phases are identical), the salt additive distributes evenly between the phases, with distribution ratio of 1. In the case of TMAO, its distribution behavior differs from that of salt additives and may be described as:

Log(D_TMAO) = a_TMAO + b_TMAO × D[PEG-600] (2)

where D_TMAO is the ratio of the TMAO concentrations in the top and bottom phases; D[PEG-600] is the difference between the PEG-600 concentrations in the same phases; a_TMAO and b_TMAO are coefficients which depend on the TMAO concentration in ATPSs formed by Dextran-75 and PEG-600.

Listed in Table 2 are the solvent properties measured via Kamlet–Taft solvatochromic analysis of these systems, where we see an increase in solvent dipolarity/polarizability, π*, and reduction in HBA basicity, β, with increasing in TMAO concentration across all systems.

Table 2 Compositions and solvent properties of aqueous media in the phases of examined ATPSs. Compositions for each ATPS are as follows: 1–18.5 wt% PEG-600/8.5 wt% Dextran-75; 2–20 wt% PEG-600/8.5 wt% Dextran-75/2 wt% TMAO; 3–20 wt% PEG-600/8.5 wt% Dextran-75/7.2 wt% TMAO. All ATPS contain 0.15 M NaCl in 0.01 M NaPB, pH 7.4

ATPS	Top phase		Bottom phase		Δπ*	Δα	Δβ	γ (μN m^−1)
	PEG	Dextran	PEG	Dextran
1	21.40%	1.10%	13.80%	22.10%	−0.057 ± 0.004	0.024 ± 0.005	−0.007 ± 0.004	3.361 ± 0.392
2	25.20%	0.35%	11.10%	23.10%	−0.032 ± 0.004	0.022 ± 0.003	−0.010 ± 0.004	—
3	24.40%	0.05%	11.00%	26.40%	−0.008 ± 0.003	0.048 ± 0.003	−0.041 ± 0.005	14.154 ± 3.815

---

We have previously reported²¹ that the arrangement of H-bonds in mixtures of polymers in water abruptly changes prior to macroscopic phase separation. For studying the H-bond arrangement of aqueous solutions, we analyze the OH-stretch band using Attenuated Total Reflection-Fourier Transfer Infrared spectroscopy (ATR-FTIR) and the previously reported model.^21,32 This simple model is based on the decomposition of the OH-stretch band into four Gaussian components assigned to different subpopulations of water.³² The positions of the Gaussian curves are fixed for pure water as well as for aqueous solutions of individual compounds and their mixtures. In our model, the four Gaussian components are assigned to the following subpopulations: water with four tetrahedrally arranged H-bonds (3080 cm⁻¹), water with four distorted H-bonds (3230 cm⁻¹), water with loosely arranged three or four H-bonds (3400 cm⁻¹), and water with three, two, or one H-bond(s) (3550 cm⁻¹). Although the estimated relative contributions of these components depend on the solute type and concentration, the physical dimensions of each subpopulation remain unknown. Therefore, our assignment of the Gaussian components is only a rough approximation of the complex H-bond network existing in water.^33,52 The fractions of these subpopulations have been shown³⁰ to change with the type and concentration of a solute in aqueous solution.

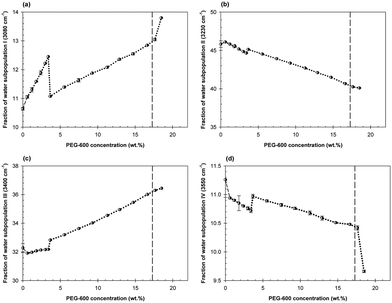
The concentration dependences of the fractions of the water subpopulations in the mixtures of Dextran-75 and PEG-600 with the Dextran/PEG ratio of 0.459 are shown in Fig. 5a–d. The first abrupt change in the concentration dependences of each water subpopulation is observed at the PEG-600 concentration of 0.6 wt% followed by that at the PEG-600 concentration of 3.25 wt%.

Fig. 5 Concentration dependences of the water subpopulation fractions represented by the relative contribution of Gaussian components I (a), II (b), III (c), IV (d) on dilutions of mixed ATPS consisting of 18.5 wt% PEG-600/8.5 wt% Dextran-75 in 0.15 M NaCl/0.01 M NaPB, pH 7.4 (black circles connected by dotted line). The vertical dashed line represents the estimated disruption point of this system according to its phase diagram.

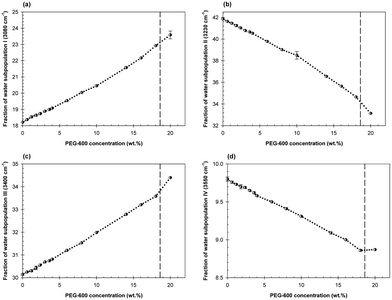
Qualitatively similar, but quantitatively quite distinct, concentration dependences of the fractions of the water subpopulations in the mixtures of Dextran-75 and PEG-600 with the Dextran/PEG ratio of 0.425 in the presence of 2 wt% TMAO are shown in Fig. 6a–d. Here again, the first abrupt change in the concentration dependences of each water subpopulation is observed at the PEG-600 concentration of 0.6 wt%.

Fig. 6 Concentration dependences of the water subpopulation fractions represented by the relative contribution of Gaussian components I (a), II (b), III (c), IV (d) on dilutions of mixed ATPS consisting of 20 wt% PEG-600/8.5 wt% Dextran-75/2 wt% TMAO in a diluent consisting of 0.15 M NaCl/2 wt% TMAO/0.01 M NaPB, pH 7.4 (black circles connected by dotted line). The vertical dashed line represents the estimated disruption point of this system according to its phase diagram.

Concentration dependencies of the water subpopulations’ fractions in the mixtures of Dextran-75 and PEG-600 with the Dextran/PEG ratio of 0.425 in the presence of 7.2 wt% TMAO are shown in Fig. 7a–d. These dependencies also demonstrate abrupt changes in the H-bonds arrangement at the same PEG-600 concentration of 0.6 wt%. However, this initial abrupt change appears to be less drastic than that observed in the presence of 2 wt% TMAO or in the absence of TMAO.

Fig. 7 Concentration dependences of the water subpopulation fractions represented by the relative contribution of Gaussian components I (a), II (b), III (c), IV (d) on dilutions of mixed ATPS consisting of 20 wt% PEG-600/8.5 wt% Dextran-75/7.2 wt% TMAO in a diluent consisting of 0.15 M NaCl/7.2 wt% TMAO/0.01 M NaPB, pH 7.4 (black circles connected by dotted line). The vertical dashed line represents the estimated disruption point of this system according to its phase diagram.

It is well established that TMAO as a protective osmolyte does not interact directly with proteins, but rather increases their stability through H-bond reorganization.^{30,34,35,39,41,43} We decided, however, to explore potential TMAO interactions with the nonionic polymers used in this study as we have previously observed changes in the H-bond rearrangement of polymer solutions dissolved in water compared to those dissolved in 0.15 M NaCl in 0.01 M NaPB, pH 7.4 (data not shown). The relative contributions of the Gaussian components I–IV aqueous solutions of 25 wt% PEG-600 and 25 wt% Dextran-75 alone and in the presence of 7.2 wt% of TMAO are shown in Fig. 8a–d and 9a–d, respectively.

Fig. 8 Concentration dependences of the water subpopulation fractions represented by the relative contribution of Gaussian components I (a), II (b), III (c), and IV (d) for 25 wt% PEG-600 in 0.15 M NaCl/0.01 M NaPB, pH 7.4 alone (open circles) versus with the addition of 7.2 wt% TMAO (filled black circles).

Fig. 9 Concentration dependences of the water subpopulation fractions represented by the relative contribution of Gaussian components I (a), II (b), III (c), and IV (d) for 25 wt% Dextran-75 in 0.15 M NaCl/0.01 M NaPB, pH 7.4 alone (open circles) versus with the addition of 7.2 wt% TMAO (filled black circles).

The difference between each water subpopulation fraction for a given polymer in the presence of TMAO and that in the solution of the same polymer in the absence of TMAO was calculated. Since the experiments in the solutions of each polymer in the absence and the presence of TMAO were performed at slightly different concentrations, the differences were calculated between the curves, fitting the experimental data with correlation coefficients exceeding 0.99 in each case and evaluating with identical intervals of 0.25.

The estimated differences are listed for each polymer in Table S1 (ESI†). The differences for each water subpopulation of both polymers were very close, amounting to 8.28 ± 0.039 for water subpopulation I; −4.69 ± 0.024 for water subpopulation II; −2.14 ± 0.010 for water subpopulation III; and −1.444 ± 0.007 for water subpopulation IV. The difference between the fractions of the different water subpopulations in 0.15 M NaCl and 0.01 M NaPB, pH 7.4 alone versus with the addition of 7.2 wt% TMAO amounts to 7.46 ± 0.25 for water subpopulation I; −4.24 ± 0.45 for water subpopulation II; −1.89 ± 0.34 for water subpopulation III; and −1.33 ± 0.15 for water subpopulation IV. These data confirm that TMAO does not interact directly with either polymer used in this study, and that the TMAO effect on the arrangement of H-bonds in aqueous solutions of both polymers is identical and additive to that of each polymer.

The previously observed abrupt changes in the H-bond arrangement of water in dilute ATPS mixtures, formed with PEG-polymer and PEG-Na₂SO₄, have been suggested to arise from the formation of PEG agglomerates prior to macroscopic phase separation.²¹ Here, we performed static and dynamic light scattering (SLS and DLS, respectively) experiments to examine the PEG agglomerates formed in the dilute ATPS mixtures used in this study.

The hydrodynamic radii (R_h) measured with DLS, calculated by the Stokes–Einstein equation (further described in ESI†), of the three PEG-600/Dextran-75/(TMAO) ATPS are presented as a function of total system wt% in Table 3 and as a function of PEG-600 concentration in Fig. 10. For monodisperse particles with spherical geometry, the intercept of spectral decay rate to scattering vector, Γ(q²), should be close to zero. This trend is largely followed by all three systems, Γ(q²) shown in Fig. S4 in ESI.† However, as seen from Table 3 for all three ATPSs, the relative intercept of Γ vs. q² decreases as ATPS concentration increases. Correspondingly, the agreement between the calculated diffusion coefficient (D_T) from the Γ(q²) slope and the D_T measurements at each angle increases with increasing ATPS mixture concentration. Therefore, we observe more diffusive particles that as the concentration of the ATPS mixture increases toward the binodal in all three systems.

Table 3 The slopes and intercepts of Γ vs. q² at each concentration for all three systems. Ratios compare the intercept to the largest gamma of each run. D_T values from the Γ vs. q² and resulting R_h values are also shown. Compositions of each system at 100 wt% are as follows: ATPS #1 – 18.5 wt% PEG-600/8.5 wt% Dextran-75; ATPS #2 – 20 wt% PEG-600/8.5 wt% Dextran-75/2 wt% TMAO; ATPS #3 – 20 wt% PEG-600/8.5 wt% Dextran-75/7.2 wt% TMAO. all ATPS contain 0.15 M NaCl in 0.01 M NaPB, pH 7.4

Dilute ATPS	ATPS #1				ATPS #2				ATPS #3
	Intercept (μs^−1)	Int/Γ ratio	D T (nm^2 μs^−1)	R h (nm)	Intercept (μs^−1)	Int/Γ ratio	D T (nm^2 μs^−1)	R h (nm)	Intercept (μs^−1)	Int/Γ ratio	D T (nm^2 μs^−1)	R h (nm)
10%	−1.19 × 10^−3	−3.88 × 10^−2	35.64	6.89	−2.52 × 10^−3	−7.01 × 10^−2	35.95	6.83	−1.24 × 10^−3	−5.47 × 10^−2	26.84	9.15
30%	−9.85 × 10^−4	−3.75 × 10^−2	30.32	8.1	−1.12 × 10^−3	−4.79 × 10^−2	27.61	8.90	−5.14 × 10^−4	−2.77 × 10^−2	21.44	11.46
50%	−2.01 × 10^−4	−1.25 × 10^−2	18.44	13.32	−5.28 × 10^−4	−3.47 × 10^−2	17.44	14.08	−3.01 × 10^−4	−2.53 × 10^−2	13.90	17.67
60%	−2.85 × 10^−4	−2.15 × 10^−2	15.51	15.84	—	—	—	—	—	—	—	—
70%	—	—	—	—	−1.76 × 10^−4	−2.29 × 10^−2	8.90	27.60	−6.47 × 10^−5	−1.03 × 10^−2	7.04	34.89
80%	−3.07 × 10^−5	−4.60 × 10^−3	7.47	32.88	—	—	—	—	−8.54 × 10^−5	−2.33 × 10^−2	4.22	58.21

---

Fig. 10 Hydrodynamic radius (R_h) as a function of PEG-600 concentration in mixed dilutions of 18.5 wt% PEG-600/8.5 wt% Dextran-75 in 0.15 M NaCl/0.01 M NaPB, pH 7.4 (black circles), 20 wt% PEG-600/8.5 wt% Dextran-75/2% TMAO in 0.15 M NaCl/2 wt% TMAO/0.01 M NaPB, pH 7.4 (red circles), and 20 wt% PEG-600/8.5 wt% Dextran-75/7.2 wt% TMAO in 0.15 M NaCl/7.2 wt% TMAO/0.01 M NaPB, pH 7.4 (blue circles).

The hydrodynamic radius of detected agglomerates appears to increase non-linearly with increasing ATPS and PEG-600 concentration for all systems, in line with our previous findings.²¹ As PEG concentration increases from 2 to 16 wt%, R_h from 7–9 to 33–58 nm depending on the system. This increase in R_h corresponds to increase in volume by a factor of at least 65 and as much as 250. R_h of these agglomerates also appears to increase substantially with the addition of 7.2 wt% TMAO. Agglomerate sizes are similar across the systems at low ATPS concentration, less than a factor of 1.4 at 10 wt%, and the difference becomes more pronounced at higher ATPS concentrations, ∼factor of 1.8 at 80 wt%.

A summary of SLS analysis for observed agglomerates at concentrations near 10 wt% of each ATPS (∼2 wt% PEG-600) can be found in Table 4. Assuming spherical particles, R_h values determined via DLS at 10 wt% total ATPS concentration were used to find the volume of the particle. Molecular weight (M_w) and apparent density decrease dramatically (almost two orders of magnitude) when TMAO is introduced. Addition of more of TMAO (7.2 wt% as opposed to 2 wt%), leads to a further decrease of Mw and density but to a lesser extent. R_g also decreases with the addition of 2 wt% TMAO but slightly increases with the addition of 7.2 wt% TMAO.

Table 4 Compositions and SLS results of observed agglomerates in each examined ATPS: (1 – 18.5 wt% PEG-600; 8.5 wt% Dextran-75; 2 – 20 wt% PEG-600; 8.5 wt% Dextran-75; 2 wt% TMAO; 3 – 20 wt% PEG-600; 8.5 wt% Dextran-75; 7.2 wt% TMAO; all ATPS contain 0.01 M NaPB, pH 7.4)

ATPS	PEG-600 conc. (wt%)	Dextran-75 conc. (wt%)	M w (g mol^−1)	A 2 (cm^3 mol g^−2)	R g (nm)	R h (nm)	Density (g cm^−3)
1	18.5	8.5	1.44 × 10^6	9.36 × 10^−2	82.9 ± 539.0	6.89 ± 0.24	1.75 × 10^0
2	20	8.5	3.03 × 10^4	5.90 × 10^−4	12.85 ± 17.0	6.83 ± 0.16	3.77 × 10^−2
3	20	8.5	1.93 × 10^4	4.87 × 10^−4	15.3 ± 4.3	9.15 ± 0.15	9.99 × 10^−3

---

Discussion

Here, our ATR-FTIR data shows that the addition of TMAO decreases both the amount and intensity of abrupt changes in water H-bond arrangement. We have previously reported evidence of an abrupt rearrangement of H-bonds in aqueous mixtures of two phase-forming polymers or a single polymer and inorganic salt prior to phase separation. We have also shown that in polymer-polymer and polymer–salt ATPS, agglomerates of one of the polymers in the mixture are formed at concentrations below the threshold of phase separation.²¹ The results reported here suggest that the agglomerates which form in Dextran-75/PEG-600/(TMAO) systems follow the same trend as previously described, but that the addition of TMAO changes the behavior and density of the observed agglomerates. These data also suggest that TMAO can either enhance or inhibit phase separation in Dextran-75/PEG-600 ATPSs depending on the specific ratio of the phase forming components.

The DLS results reported here indicate that these agglomerates are largely diffusive, with the diffusive nature of these clusters increasing as ATPS concentration increases. However, for all three systems, samples with low ATPS concentration showed noticeable non-zero intercept of Γ(q²) and an increase in D_T with increasing q. This behavior can be due to geometrical anisotropy of samples (where a rotational diffusion is added to translational), significant polydispersity of samples (with large particles scattering significantly less at high angles), or sampling apparent internal motion.⁵³ Agglomerates in samples at higher ATPS concentration exhibit behavior similar to that of monodisperse spheres, with D_T being independent of q and Γ(q²) having small intercept, particularly for the system without TMAO. The DLS data also show that the hydrodynamic radius, R_h, of the clusters increases more dramatically with increasing ATPS concentration in the presence of TMAO, specifically at 7.2 wt% where the hydrodynamic volume of the particles over the range the range of concentrations grew by a factor of about 250.

The apparent density determined from SLS-measured Mw and DLS-measured hydrodynamic volume, V_h, decreases with the addition of TMAO, indicating that in the presence of this osmolyte, PEG agglomerates are also less dense. Therefore, the combined DLS and SLS results suggest that at lower ATPS concentrations, the apparent densities of the observed agglomerates significantly decrease with the addition of TMAO at both 2 wt% and 7.2 wt%. These changes in density are not correlated with changes in agglomerate volume. The apparent radius of gyration decreases with the addition of TMAO, suggesting the possibility that in the absence of this osmolyte, PEG clusters are non-spherical and upon the addition of TMAO these agglomerates become more sphere-like. The second virial coefficient (A₂ in Table 4) is positive for all three ATPS with this force being larger in the presence of TMAO, indicating a presence of repulsive force between pairs of chains in the PEG clusters. Mandalaparthy & Noid⁵⁴ recently showed that when the concentration of TMAO in an aqueous mixture increases, its interfacial preference decreases due to repulsive interactions with other TMAO molecules, which is in agreement with our findings here.

Conclusions

Phase separation in aqueous solutions is dependent on multiple complex, dynamic mechanisms including direct interactions of the solutes themselves, water–solute interactions, and modification of water properties by the solute. In polymer-polymer ATPS, the two polymers form different polymer-specific water H-bond network domains, which have dissimilar solvent properties. There are two types of domains that exist in the polymer mixtures until the polymer concentrations exceed a threshold beyond which the domains become immiscible, at which point the emerging interfacial tension leads to the formation of micro-droplets, eventually coalescing into separate layers controlled by the density of the phases.²¹ It is well established that phase separation takes place in the miscibility gap composed of both metastable and unstable regions. Micro-droplet coalescence describes phase separation via nucleation and growth which occurs in metastable regions, where the continuous change of phase is stable from small fluctuations (i.e., temperature, pressure, etc.), but is unstable to large fluctuations.^55,56 There also exists an unstable region in which phase separation is driven by spinodal decomposition which has a drastically different density profile compared to that of droplet nucleation and growth.

Based on the results presented here, we hypothesize that we are potentially seeing spinodal decomposition, i.e. elongation of agglomerates, in PEG-600/Dextran-75/TMAO systems, and that this may in part be controlled by TMAO. Studies on the dynamics of aqueous TMAO solutions focusing on the interaction of water with the hydrophilic N–O group observed a pronounced asymmetric broadening toward lower wavenumbers for the O–H stretch band of water.^43,57 The commonly accepted argument is that the TMAO–water molecule bonds are stronger than the mean water–water bonds in aqueous solutions containing TMAO.⁵⁷ TMAO has also been shown to counteract droplet dissolution by pressure due to these strong interactions.⁵⁵ This is in agreement with the biological effect of TMAO, which is to regulate the volume of cells by counteracting external osmotic pressure. It has been suggested that this occurs via TMAO reducing the activity of water inside a cell and thus reducing the activity gradient along the cell membrane.⁴³

Author contributions

Conceptualization, B. Y. Z., K. A. S., V. N. U.; methodology A. R. T., P. H., P. P. M.; validation, A. R. T., K. A. S., P. P. M.; investigation, A. R. T., K. A. S., P. H., P. P. M.; writing – original draft preparation, A. R. T., B. Y. Z., K. A. S., P. H.; writing – review and editing, P. P. M., V. N. U.; visualization, A. R. T., B. Y. Z., K. A. S., P. H.; supervision, B. Y. Z., K. A. S.; project administration, B. Y. Z. All authors have read and agree to the published version of the manuscript.

Conflicts of interest

The authors declare no conflict of interest. The funders had no role in the design of this study; in the collection, analysis, or interpretation of the data; in the writing of this manuscript; or in the decision to publish these results.

Acknowledgements

P. H. acknowledges the Undergraduate Summer Research Award from the Cleveland State University for support of the project. P. P. M. acknowledges the University of Aveiro, CICECO-Aveiro Institute of Materials for funding in the framework of the project UIDB/5011/2020, UIDP/50011/2020 & LA/P/0006/2020, financed by national funds through the FCT/MCTES (PIDDAC). This work is funded by national funds (O. E.) through FCT – Fundação para a Ciência e a Tecnologia, I. P., in the scope of the framework contract foreseen in the numbers 4, 5 and 6 of article 23, of the Decree-Law 57/2016, of August 29, changed by Law 57/2017, of July 19.

References

1. E. P. Bentley, B. B. Frey and A. A. Deniz, Physical Chemistry of Cellular Liquid-Phase Separation, Chem. – Eur. J., 2019, 25(22), 5600–5610.
2. J. Berry, C. P. Brangwynne and M. Haataja, Physical principles of intracellular organization via active and passive phase transitions, Rep. Prog. Phys., 2018, 81(4), 046601.
3. H. Falahati and A. Haji-Akbari, Thermodynamically driven assemblies and liquid–liquid phase separations in biology, Soft Matter, 2019, 15(6), 1135–1154.
4. A. A. Hyman and K. Simons, Cell biology. Beyond oil and water--phase transitions in cells, Science, 2012, 337(6098), 1047.
5. A. A. Hyman, C. A. Weber and F. Julicher, Liquid-liquid phase separation in biology, Annu. Rev. Cell Dev. Biol., 2014, 30, 39–58.
6. W. Stroberg and S. Schnell, On the origin of non-membrane-bound organelles, and their physiological function, J. Theor. Biol., 2017, 434, 42–49.
7. J. Wang, et al., A Molecular Grammar Governing the Driving Forces for Phase Separation of Prion-like RNA Binding Proteins, Cell, 2018, 174(3), 688–699.
8. H. Yoo, C. Triandafillou and D. A. Drummond, Cellular sensing by phase separation: Using the process, not just the products, J. Biol. Chem., 2019, 294(18), 7151–7159.
9. Y. Shin and C. P. Brangwynne, Liquid phase condensation in cell physiology and disease, Science, 2017, 357(6357), eaaf4382.
10. S. Alberti and D. Dormann, Liquid–liquid phase separation in disease, Annu. Rev. Genet., 2019, 53, 171–194.
11. X. Ge, et al., In Vivo Formation of Protein Based Aqueous Microcompartments, J. Am. Chem. Soc., 2009, 131(25), 9094–9099.
12. A. F. Harrison and J. Shorter, RNA-binding proteins with prion-like domains in health and disease, Biochem. J., 2017, 474(8), 1417–1438.
13. N. Martin, Dynamic synthetic cells based on liquid–liquid phase separation, ChemBioChem, 2019, 20(20), 2553–2568.
14. A. Patel, et al., A Liquid-to-Solid Phase Transition of the ALS Protein FUS Accelerated by Disease Mutation, Cell, 2015, 162(5), 1066.
15. J. Ahlers, et al., The key role of solvent in condensation: Mapping water in liquid-liquid phase-separated FUS, Biophys. J., 2021, 120(7), 1266–1275.
16. P. Azzari and R. Mezzenga, LLPS vs. LLCPS: analogies and differences, Soft Matter, 2023, 19(10), 1873–1881.
17. S. Bielskutė, et al., Low amounts of heavy water increase the phase separation propensity of a fragment of the androgen receptor activation domain, Protein Sci., 2021, 30(7), 1427–1437.
18. L. A. Ferreira, et al., Solvent properties of water in aqueous solutions of elastin-like polypeptide, Int. J. Mol. Sci., 2015, 16(6), 13528–13547.
19. S. Pezzotti, et al., Liquid–Liquid Phase Separation? Ask the Water!, J. Phys. Chem. Lett., 2023, 14(6), 1556–1563.
20. A. R. Titus, et al., Interfacial tension and mechanism of liquid-liquid phase separation in aqueous media, Phys. Chem. Chem. Phys., 2020, 22(8), 4574–4580.
21. A. R. Titus, et al., Mechanism of phase separation in aqueous two-phase systems, Int. J. Mol. Sci., 2022, 23(22), 14366.
22. B. Y. Zaslavsky, L. A. Ferreira and V. N. Uversky, Driving Forces of Liquid–Liquid Phase Separation in Biological Systems, Biomolecules, 2019, 473.
23. B. Y. Zaslavsky, Aqueous two-phase partitioning: physical chemistry and bioanalytical applications, CRC press, 1994.
24. E. Andersson and B. Hahn-Hägerdal, Bioconversions in aqueous two-phase systems, Enzyme Microb. Technol., 1990, 12(4), 242–254.
25. R. Hatti-Kaul, Aqueous two-phase systems, Mol. Biotechnol., 2001, 19(3), 269–277.
26. L. A. Ferreira, et al., Effects of osmolytes on solvent features of water in aqueous solutions, J. Biomol. Struct. Dyn., 2017, 35(5), 1055–1068.
27. L. A. Ferreira, V. N. Uversky and B. Y. Zaslavsky, Phase equilibria, solvent properties, and protein partitioning in aqueous polyethylene glycol-600-trimethylamine N-oxide and polyethylene glycol-600-choline chloride two-phase systems, J. Chromatogr. A, 2018, 1535, 154–161.
28. P. P. Madeira, et al., Salt effects on solvent features of coexisting phases in aqueous polymer/polymer two-phase systems, J. Chromatogr. A, 2012, 1229, 38–47.
29. N. R. da Silva, et al., Analysis of partitioning of organic compounds and proteins in aqueous polyethylene glycol-sodium sulfate aqueous two-phase systems in terms of solute–solvent interactions, J. Chromatogr. A, 2015, 1415, 1–10.
30. N. R. da Silva, et al., Linear Relationships between Partition Coefficients of Different Organic Compounds and Proteins in Aqueous Two-Phase Systems of Various Polymer and Ionic Compositions, Polymers, 2020, 12(7), 1452.
31. P. A. P. Madeira, Protein partitioning in polymer/polymer aqueous two-phase systems, 2008, Universidade do Porto.
32. N. da Silva, et al., Effects of different solutes on the physical chemical properties of aqueous solutions via rearrangement of hydrogen bonds in water, J. Mol. Liq., 2021, 335, 116288.
33. N. Kitadai, et al., Effects of ions on the OH stretching band of water as revealed by ATR-IR spectroscopy, J. Solution Chem., 2014, 43, 1055–1077.
34. A. Pica and G. Graziano, A Rationalization of the Effect That TMAO, Glycine, and Betaine Exert on the Collapse of Elastin-like Polypeptides, Life, 2022, 12(2), 140.
35. Q. Zou, et al., The molecular mechanism of stabilization of proteins by TMAO and its ability to counteract the effects of urea, J. Am. Chem. Soc., 2002, 124(7), 1192–1202.
36. K.-J. Choi, et al., A chemical chaperone decouples TDP-43 disordered domain phase separation from fibrillation, Biochemistry, 2018, 57(50), 6822–6826.
37. H. Cinar, et al., Temperature, hydrostatic pressure, and osmolyte effects on liquid–liquid phase separation in protein condensates: physical chemistry and biological implications, Chem. – Eur. J., 2019, 25(57), 13049–13069.
38. H. Cinar, et al., Effects of cosolvents and crowding agents on the stability and phase transition kinetics of the SynGAP/PSD-95 condensate model of postsynaptic densities, J. Phys. Chem. B, 2022, 126(8), 1734–1741.
39. R. Sarma and S. Paul, Exploring the molecular mechanism of trimethylamine-N-oxide's ability to counteract the protein denaturing effects of urea, J. Phys. Chem. B, 2013, 117(18), 5691–5704.
40. M. Gao, et al., Modulation of human IAPP fibrillation: cosolutes, crowders and chaperones, Phys. Chem. Chem. Phys., 2015, 17(13), 8338–8348.
41. L. Larini and J.-E. Shea, Double resolution model for studying TMAO/water effective interactions, J. Phys. Chem. B, 2013, 117(42), 13268–13277.
42. Y. Rezus and H. Bakker, Destabilization of the hydrogen-bond structure of water by the osmolyte trimethylamine N-oxide, J. Phys. Chem. B, 2009, 113(13), 4038–4044.
43. J. Hunger, et al., Complex formation in aqueous trimethylamine-N-oxide (TMAO) solutions, J. Phys. Chem. B, 2012, 116(16), 4783–4795.
44. C. Reichardt, E. Harbusch-Görnert and G. SchWäfer, Über Pyridinium-N-phenolat-Betaine und ihre Verwendung zur Charakterisierung der Polarität von Lösungsmitteln, XI. Herstellung und UV/VIS-spektroskopische Eigenschaften eines wasserlöslichen Carboxylat-substituierten Pyridinium-N-phenolat-Betainfarbstoffs, Liebigs Ann. Chem., 1988, 839–844.
45. P. P. Madeira, et al., Salt effects on solvent features of coexisting phases in aqueous polymer/polymer two-phase systems, J. Chromatogr. A, 2012, 1229, 38–47.
46. B. Vonnegut, Rotating bubble method for the determination of surface and interfacial tensions, Rev. Sci. Instrum., 1942, 13(1), 6–9.
47. A. Kestranek, et al., Chemiluminescent nitrogen detection (CLND) to measure kinetic aqueous solubility, Curr. Protoc. Chem. Biol., 2013, 5(4), 269–280.
48. K. A. Streletzky, J. T. McKenna and R. Mohieddine, Spectral time moment analysis of microgel structure and dynamics, J. Polym. Sci., Part B: Polym. Phys., 2008, 46(8), 771–781.
49. P. S. Russo, et al., Characterization of polymers by static light scattering, Molecular Characterization of Polymers, Elsevier, 2021, pp. 499–532.
50. P. Herron, et al., Measuring dn/dc for Polysaccharide Microgels of Varying Crosslinking Density, J. Undergrad. Res. Phys. Astron., 2023, 32(1), 30–34.
51. M.-K. Shahbazinasab and F. Rahimpour, Liquid–liquid equilibrium data for aqueous two-phase systems containing PPG725 and salts at various pH values, J. Chem. Eng. Data, 2012, 57(7), 1867–1874.
52. G. Tubio, et al., Liquid–liquid equilibrium of the Ucon 50-HB5100/sodium citrate aqueous two-phase systems, Sep. Purif. Technol., 2009, 65(1), 3–8.
53. P. S. Russo, et al., Characterization of polymers by dynamic light scattering, Molecular Characterization of Polymers, Elsevier, 2021, pp. 441–498.
54. V. Mandalaparthy and W. Noid, A simple theory for interfacial properties of dilute solutions, J. Chem. Phys., 2022, 157(3), 034703.
55. H. Cinar and R. Winter, The effects of cosolutes and crowding on the kinetics of protein condensate formation based on liquid–liquid phase separation: A pressure-jump relaxation study, Sci. Rep., 2020, 10(1), 17245.
56. E. Favvas and A. C. Mitropoulos, What is spinodal decomposition, J. Eng. Sci. Technol. Rev., 2008, 1(1), 25–27.
57. M. Freda, G. Onori and A. Santucci, Infrared study of the hydrophobic hydration and hydrophobic interactions in aqueous solutions of tert-butyl alcohol and trimethylamine-N-oxide, J. Phys. Chem. B, 2001, 105(51), 12714–12718.

---

Footnote

† Electronic supplementary information (ESI) available. See DOI: https://doi.org/10.1039/d3cp06200g

---