Evolution of the atomic and electronic structures of CuO clusters: a comprehensive study using the DFT approach

Abstract

One of the most fundamental aspects of cluster science is to understand the structural evolution at the atomic scale. In this connection, here we report a comprehensive study of the atomic and electronic structures of (CuO)_n clusters for n = 1 to 12 using DFT-based formalisms. Both the plane wave-based pseudo-potential approach and LCAO-MO-based method have been employed to obtain the ground state geometries of neutral, cation and anion copper oxide clusters. The results reveal that neutral copper oxide clusters favor a planar ring structure up to heptamer and from octamer onwards they adopt a three-dimensional motif with (CuO)₉ and (CuO)₁₂ forming a barrel-shaped layered structure. Detailed electronic structure analysis reveals that the transition of the atomic structure from 2D to 3D is guided by the energy balance of the Cu–O (d–p) and Cu–Cu (d–d) bonds. The removal of one electron from the cluster (cation) results in slightly stretched bonds while the addition of one electron (anion) showed compression in the overall geometries. The thermodynamic and electronic stability of these clusters has been analyzed by estimating their binding energy, ionization energy and electron affinity as a function of size. Remarkably, among these clusters, the octamer (CuO)₈ and dodecamer (CuO)₁₂ show higher binding energy and electron affinity (∼6.5 eV) with lower ionization energy (5.5–6.0 eV). This unique feature of the octamer and dodecamer indicates that they are very promising candidates for both oxidizing and reducing agents in different important chemical reactions.

---

1. Introduction

Transition metal oxide clusters and in particular late transition metal oxide clusters of 3d elements are least understood due to their complicated electronic structure and the large number of competing atomic structures. In recent times, various transition metal oxide clusters such as FeO,^1–4 NiO,^5,6 CoO,^7,8 ZnO,^9–11etc. have been investigated to understand their role in the field of catalysis, supercapacitors, semiconductors, fuel cells, sensors, etc. Copper oxide is one such important metal oxide, which has immense utility in different fields of research, such as catalysis,¹² gas sensors,¹³ energy materials,¹⁴ batteries,¹⁵ superconductors,¹⁶ environmental protection, energy storage and conversion,¹⁷etc. Moreover, it is important to note that bulk CuO shows deviations in the structural motif as compared to its neighboring oxides. For example, while the equilibrium crystal structures of MnO, FeO, CoO and NiO show rock salt structure, CuO deviates to the monoclinic structure with lower symmetry.¹⁸ Thus, it is of interest to explore the structural evolution of CuO at the ultra-small scale (cluster) as this will provide an opportunity to understand the role of electronic structure in the structural evolution of CuO nanoparticles.

Experimentally, copper oxide clusters are prepared by laser ablation/sputtering of metallic copper or CuO powder in the gas phase and characterization of the structure, composition and stability is carried out by mass spectrometry.^19–23 On the basis of the reports available, it is seen that generally these clusters are produced with non-stoichiometric compositions i.e., either in oxygen deficient form (Cu_nO_m: n > m) or in oxygen rich conditions (Cu_nO_m: n < m).^19,20 Mafune and co-workers studied the thermal and chemical stability of copper oxide clusters at elevated temperature where oxygen deficient clusters (n : m = 3 : 2) are found to be more stable due to the release of oxygen.²¹ Also, reactions of different molecules such as CO and NO with oxygen deficient clusters were studied, which leads to the formation of O₂ and NO₂, respectively.^22,23 Studies were extended to oxygen rich clusters (CuO_m: m ≤ 6) where photoelectron spectroscopy of the neutral and anion clusters was explored.^24–27 Theoretical studies compliment these studies by predicting the structural motifs of the oxygen rich clusters.^28–32 Thus, oxygen rich and oxygen deficient clusters are reasonably well investigated; however, there are fewer reports on stoichiometric clusters. Matsuda et al. observed stoichiometric clusters under single photon ionization conditions (118 nm) where the clusters undergo the least fragmentation in the laser ionization process.³³ Bae and co-workers studied the structure and electronic property of stoichiometric clusters (CuO)_n using density functional theory, where non-planar structures are found to be the most stable isomer for n > 4.^34,35 Though there are few experimental and theoretical works on stoichiometric copper oxide clusters, a systematic study on the evolution of atomic and electronic structure is still missing. Understanding the stoichiometric clusters is even more requisite as the bulk CuO is stoichiometric in nature.

In the present work, a systematic study of the structure and electronic property of copper oxide clusters (CuO)_n (n = 1–12) has been carried out using density functional theory. Neutral clusters are optimized using the plane wave-based method, where two exchange correlation functionals, namely Perdew–Burke–Ernzerhof (PBE) and hybrid functional (HSE06), have been employed to understand the influence of bonding and correlation between electronic structure and atomic structure. Several new isomers have been established for copper oxide clusters (CuO)_n, which have not been reported earlier.³⁴ Based on the most stable isomers, structural transition from two dimensional (2D) to three dimensional (3D) has been observed in copper oxide clusters. Moreover, a few ground state structures of the clusters assume a nano-barrel structure. Previously, a nano-barrel structure has been reported for copper oxide where the nano-sheet is folded to form a barrel-like structure for very large clusters (top-down approach).³⁶ In the present work, we have established the structural transformation from a nano-ring to nano-barrel structure in copper oxide clusters in the small size regime (bottom-up approach). A detailed study of the projected density of states (PDOS) explains how the p-orbitals of oxygen and d-orbitals of the Cu atom influence the structural transformation of the (CuO)_n cluster from 2D to 3D. The structures of the cations and anions were also optimized using the linear combination of atomic orbitals approach and they were compared with the neutral counterpart. Based on the energetics of the neutral, cation and anion clusters, the binding energy, ionization energy and electron affinity of the copper oxide clusters have been calculated as a function of size. Using these values, the thermodynamic stability and reactivity of these clusters in chemical reactions has been explored.

2. Theoretical methods

All calculations of neutral clusters are performed within the density functional theory using the plane wave-pseudopotential approach as implemented in the Vienna Ab initio Simulation Package (VASP).^37–39 The electron–ion interaction is described by the all-electron projector augmented wave (PAW) method.⁴⁰ The spin polarized generalized gradient approximation has been used to calculate the exchange–correlation energy under PBE formalism.^41,42 The energy cut off for the plane wave basis set has been fixed at 500 eV for assuming a good energy convergence. To balance the accuracy and calculation effort and time, the lowest energy isomer of each cluster was found in two steps; (i) first we have optimized several initial configurations using the Perdew–Burke–Ernzerhof (PBE) functional; (ii) in the second step, we have further optimized a few low-lying isomers with the hybrid exchange correlation functional (HSE06) where exchange is a mixture of 20% HF exchange and 80% PBE exchange (HFSCREEN = 0.2) and correlation is described in GGA (PBE).^43,44 The ionic optimization has been carried out using the conjugate gradient scheme and the forces on each ion are minimized to 5 meV Å⁻¹. A suitable simulation box of size 20 × 20 × 20 Å has been considered for all calculations. The k-point sampling in the Brillouin zone (BZ) is treated with the Monkhorst–Pack scheme using the gamma point (Γ) only. To generate the initial structures for various cluster sizes, several methods like the Generic algorithm, molecular dynamic simulation method, and evolution algorithm are available in the literature. However, in the present work, for small clusters, we have used chemical intuition, i.e., educated guess structures are used. A large number of initial structures are generated and the total energy has been calculated and compared to locate the ground state isomer for a particular size. For all possible isomers of different size clusters, we have carried out spin polarized calculation to remove the spin contamination. Moreover, we have checked the effect of London dispersion correction and spin–orbit coupling on the total energy of the ground state isomer of the copper oxide clusters. As the change in the variation in total energy is minimal for these effects, we have not considered London dispersion correction and spin–orbit coupling in our calculation.

The stability or binding energy of each cluster is calculated with respect to the CuO monomer as a unit following equation (i). In addition, we have also calculated the relative stability (equation ii) of each cluster with respect to its nearest neighbor. The binding energy (BE) of the copper oxide monomer has been calculated by using the energy of the CuO monomer Cu and O.

BE(CuO)_n = [n·E(CuO) − E(CuO)_n]/n (i)

Δ²E = 2E(CuO)_n − E(CuO)_n−1 − E(CuO)_n+1 (ii)

In order to underscore the accuracy of the pseudopotentials of the Cu and O atoms, first we have optimized the CuO bulk (monoclinic) using both PBE and the hybrid exchange correlation functional (HSE06) where the Brillouin zone (BZ) is sampled with a 5 × 5 × 5 k-point grid. Both functionals show similar Cu–O bond length and Cu–O–Cu bond angle. The bulk CuO with a monoclinic unit cell has a square planar CuO₄ unit arranged in an eclipsed fashion. In the axial/perpendicular directions of the CuO₄ square planar, the Cu-atoms are connected to each other via Cu–Cu bonds. Using both PBE and the hybrid functional (HSE06), the lattice parameters (a = 4.52, b = 3.57, c = 5.11 and α = 90°, β = 97°, γ = 90°) are found to be in good agreement with the literature value.⁴⁵

For calculations of the cation and anion of the most stable isomer of the copper oxide clusters, the linear combination of atomic orbitals-molecular orbitals (LCAO-MO) approach is used as implemented in GAMESS.⁴⁶ Here, the LCAO-MO approach is used over the plane wave-based approach as it provides better accuracy for charged species. First, we have evaluated several basis sets (i.e., 6-31, 6-31 (d, p), 6-311, 6-311(d, p), LANL2DZ) and methods (i.e., B3LYP, B3PW91) for the calculation of cations and anions. Out of these, the LANL2DZ basis set in the B3LYP method is found to produce results with reasonable accuracy. In addition, it is worth mentioning that as the calculations of neutral clusters were performed using the pseudopotential approach in VASP, we felt that using the LANL2DZ basis set, based on frozen core approximation, is appropriate for comparing the results of neutral, cation and anion clusters.

3. Results & discussion

3.1 Structural evolution of copper oxide clusters

3.1.1 Atomic structure of neutral copper oxide clusters. The optimized CuO monomer shows a bond length of 1.70 Å using the PBE functional (Tables S1 and S2 in ESI†) which is in agreement with the experimental value (1.72 Ų⁴). Using the hybrid functional (HSE06), the Cu–O bond length was found to be marginally stretched to 1.73 Å (Fig. 1). From dimer onwards, since both Cu–O and Cu–Cu interactions are present in the cluster, we have compared these two interactions as a function of size. In general, the Cu–O interaction is much stronger than the Cu–Cu interaction and the bond length varies between 1.7–2.0 Å for Cu–O and 2.2–2.6 Å for Cu–Cu. (Table S3, ESI†). The interatomic separation of more than 2.3 Å and 3.0 Å for the Cu–O and Cu–Cu bonds, respectively, is assumed to have negligible interaction. To obtain the lowest energy isomer of the copper oxide dimer (CuO)₂, various initial structures are optimized such as rhombus, square planar, linear etc. The energetics of different isomeric structures are listed in the ESI† (Table S1, ESI†). Out of these, the rhombus structure is found to be the energetically most stable isomer. Bond angle and bond length details of the structure are listed in Table S2 (ESI†) (PBE functional) and Table 1 (Hybrid functional (HSE06)). For copper oxide trimer (CuO)₃, a planar cyclic structure is found to be the most stable isomer (Fig. 1). For the tetramer cluster, the lowest energy isomer shows a planar ring structure (Table S1, ESI†). Previously, a non-planar seven membered ring-type structure has been reported for (CuO)₄, which is the smallest cluster having a three dimensional structure.³⁴ We have compared the three-dimensional isomer (Structure 4b of Table S1, ESI†) with our present finding of a planar isomer. However, the planar structure is found to be ∼1.5 eV more stable. For the pentamer (CuO)₅, the lowest energy isomer forms a planar pentagonal ring structure. In a previous study by Bae et al., the most stable structure of the pentamer of CuO was reported to be a non-planar isomer (similar to Structure 5c of Table S1, ESI†) over the planar isomer.³⁴ However, our calculation shows that the non-planar structure is energetically less stable as compared to the planar pentagon structure by ∼0.75 eV of energy. In the case of hexamer (CuO)₆, the hexagonal planar ring structure is found to be the most stable isomer over various non-planar structures as listed in Table S1 (ESI†). In this context, it may be noted that using the hybrid functional (HSE06), the lowest energy isomer of the (CuO)₆ hexamer becomes pseudo-planar with zig-zag orientations of the Cu and O atoms. For the heptamer, the ground state isomer is found to be a planar ring structure similar to that obtained for smaller clusters. If we compare the Cu–O bond length from dimer to heptamer, it is in the range of 1.72–1.83 Å; however, the Cu–Cu distance increases gradually from 2.30–3.21 Å with cluster size (Table 1). Also, the Cu–O–Cu bond angle is found to increase from 78° to 138° as the diameter of the nano-ring increases (Table 1). These findings of a planar ring structure for larger size suggests that larger nano-rings are stabilized by the stronger Cu–O interaction, while the Cu–Cu interaction has a negligible effect on the planar structure.

Table 1 Cu–O and Cu–Cu interatomic distances and Cu–O–Cu bond angles of the lowest energy isomers of the copper oxide clusters (n = 1–12). For comparison, the geometrical parameters of the 3D-(CuO)₄, planar (CuO)₈ and bulk CuO are also included

Cluster size (n)	Hybrid functional (HSE06)
	Cu–O		Cu–Cu		Average Cu–O–Cu bond angle (degree)
	Avg. interatomic distance (Å)	No of bonds	Avg. interatomic distance (Å)	No of bonds
a Cu–Cu interatomic distance up to 3 Å is considered as a bond.
1	1.73	1	—	—	—
2	1.83	4	2.30	1	78.0
3	1.78	6	2.45	3	86.9
4	1.75	8	2.88	4	111.3
4-3D	1.96	12	2.55	6	79.6
5	1.75	10	3.00	5	121.5
6	1.72	12	3.15		132.2
7	1.72	14	3.21		138.0
8	1.95	24	2.55, 3.00	16	84.0, 110.0
8-Planar	1.72	16	3.35		132.0
9	1.90	27	2.65, 4.00	18	90.0, 126.0
10	1.84	30	2.55	10	83.2, 120.4
11	1.91	33	2.60	13	84.3, 103.0, 112.0, 136.9, 146.6
12	1.84, 1.96, 2.06	40	2.65, 2.90	24	103.4, 138.8
Bulk	1.94	4	2.88	4	102.7, 119.0

---

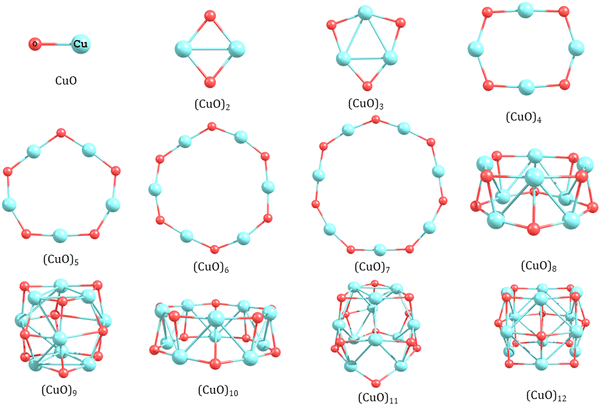Fig. 1 The lowest energy isomers of copper oxide clusters (n = 1–12) using the hybrid functional (HSE06).

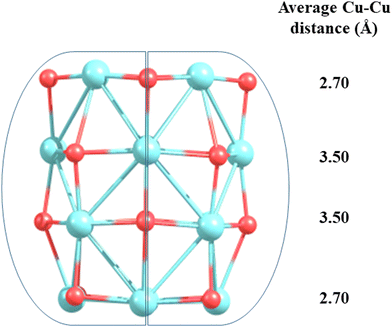
The lowest energy isomers of CuO clusters show a three-dimensional motif from octamer onwards. For (CuO)₈, a bilayer structure consisting of two tetramer units of (CuO)₄ arranged in a staggered fashion is found to be the most stable isomer. In comparison to a planar ring isomer of (CuO)₈, the 3D layered isomer is ∼0.75 eV more stable (Table S1, ESI†). Thus, a significant structural transition from a planar ring to a three dimensional (3D) stacked layer structure is observed from n = 7 to n = 8. This result is different from previous literature where the transition of the planar structure to a non-planar structure is reported from trimer to tetramer.³⁴ In line with the structural transition, we also find a significant change in the trend of Cu–O and Cu–Cu bond length. The Cu–O bond length is longer (1.95 Å) in the 3D layered structure than the 2D planar structure (1.72 Å) of the octamer. In contrast to this trend, the Cu–Cu bond length (2.55 Å) is shorter in the 3D layered structure than the 2D planar isomer (3.35 Å). Thus, 2D to 3D structural transition of CuO clusters strengthens the Cu–Cu bond (3.35 to 2.55 Å) at the cost of weakening the Cu–O bond (elongation from 1.73 to 1.95 Å). This also corroborates with the change in the Cu–O–Cu bond angle, which reduces from ∼132° to ∼98°. In addition, the planar to 3D transition is governed by energy economy of the Cu–O bond and Cu–Cu bonds. For the planar ring isomers up to n = 7, while the number of strong Cu–O bond increases systematically, the Cu–Cu interaction decreases because of larger separation between them. Since Cu–O bonds are stronger than Cu–Cu bonds, the planar structures could sustain by energy gain arising from the limited number of Cu–O bonds. However, at the size n = 8, the larger ring could not get stabilized itself by the Cu–O bonds only and it turned to a 3D structure as it could provide weaker (longer) but a larger number of Cu–O bonds assisted by a good number of Cu–Cu interactions in the bonding range (∼2.3 Å). It is clear from the above discussion that the structure of the (CuO)_n cluster is the net result of energy economy achieved by adjusting the number of stronger Cu–O bonds along with simultaneous formation of an appropriate amount of relatively weaker Cu–Cu bonds in the given structure.

For higher clusters, the trend of stacked layer structure continues. The lowest energy isomer of (CuO)₉ forms by stacking three trimer units of (CuO)₃ in a staggered fashion. The average Cu–O and Cu–Cu bond distances are 1.90 and 2.65 Å, respectively. In the middle layer, the Cu–O bond distance was found to be similar to the upper and lower layer; however, the Cu–Cu distance increases drastically to ∼4 Å leading to elongation at the middle of the tubular structure. Thus, the three-dimensional stacked layer structure adopts a barrel-like structure. The barrel form of the nonamer (CuO)₉ is not reported in the literature. For decamer (CuO)₁₀, the lowest energy isomer follows a layer growth motif where one monomer unit is attached on top of a nonamer unit (Structure 10a in Table S1, ESI†). However, when the hybrid energy functional (HSE06) is used, a symmetric layer-type structure consisting of two pentamer units in a staggered fashion is found to be the most stable isomer for (CuO)₁₀ as shown in Fig. 1. It may be noted here that although the most stable isomers obtained using the PBE and hybrid functional (HSE06) are apparently different, both isomers inherently follow the layer growth motif. This layer growth motif continues for (CuO)₁₁ where the most stable isomer is obtained upon optimizing one trimer unit on the octamer structure in a staggered configuration (4 × 4 × 3 configuration). For the dodecamer of copper oxide (CuO)₁₂, a large number of initial structures have been optimized. The lowest energy isomer forms a barrel-type structure where three tetramer units of (CuO)₄ are stacked in a staggered fashion and the Cu–O and Cu–Cu bonds in the middle layer are slightly elongated as compared to the top and bottom layer. Thus, we call it a 4 × 4 × 4 layer structure with a barrel shape. For comparison, we have also optimized other layer structures like 3 × 3 × 3 × 3 tetra-layer and 6 × 6 bi-layer. The results show that they are 0.93 and 2.0 eV higher in energy, respectively. Here it is worth mentioning that we have carried out the calculation of vibrational frequency for all the optimized structures of CuO clusters (n = 1–12), which shows no imaginary frequency (Table S4 in ESI†) indicating that the structures are not at a saddle point.

After establishing the equilibrium geometries of the (CuO)_n clusters (n = 1–12) using both the PBE and hybrid functional (HSE06) it may be worth discussing the differences in the structures obtained. It is noted that the Cu–O and Cu–Cu bond length of the optimized structure in the two functionals are similar; however, the Cu–O–Cu bond angles are more in the hybrid functional (HSE06) leading to a more open structure of the ground state isomer.

3.1.2 Atomic structure of the cations and anions of the copper oxide clusters. The optimization of the cations and anions was carried out using the LCAO-MO method. Before optimizing the charged species, the structure of the neutral ground state isomer of the copper oxide clusters was further optimized using the LCAO-MO method. The optimized geometries are shown in Table S5 (in ESI†) and the structural parameters are tabulated in Table 2. In general, the trend in geometrical parameters of the optimized isomers suggests that the LCAO-MO method results in more relaxation and the bonds are slightly stretched as compared to the structure obtained using plane wave-based calculation. The overall structural pattern of the most stable isomer of the copper oxide clusters is similar in both the methods (compare Fig. 1 and Table S5, ESI†). These isomers were further optimized after removal of one electron. For cation clusters, the Cu–O–Cu bond angle is more as compared to their neutral counterpart, indicating a relatively open structure for the cation compared to the neutral cluster. However, when the neutral clusters are optimized after incorporating one electron (i.e., anion), the Cu–O–Cu bond angle decreases, which indicates a contracted structure as compared to the neutral cluster.

Table 2 Structural parameters of CuO clusters (CuO)_n (n = 1–12) optimized using the LCAO-MO approach

Species	Neutral			Cation			Anion
	Avg. interatomic distance		Avg. Cu–O–Cu bond angle (°)	Avg. interatomic distance		Avg. Cu–O–Cu bond angle (°)	Avg. interatomic distance		Avg. Cu–O–Cu bond angle (°)
	Cu–O (Å)	Cu–Cu (Å)		Cu–O (Å)	Cu–Cu (Å)		Cu–O (Å)	Cu–Cu (Å)
CuO	1.80	—	—	1.90	—	—	1.74	—	—
(CuO)2	1.91	2.48	81.1	1.97	2.75	88.8	1.93	2.35	75.4
(CuO)3	1.85	2.87	101.9	1.84	3.17	119.6	1.86	2.67	91.6
(CuO)4	1.83	3.01	110.4	1.82	3.29	130.0	1.84	2.77	98.1
(CuO)5	1.81	3.17	122.5	1.80	3.34	135.4	1.80	3.09	118.6
(CuO)6	1.79	3.27	131.5	1.80	3.38	140.6	1.79	3.20	127.2
(CuO)7	1.79	3.33	137.8	1.79	3.40	145.6	1.79	3.27	132.3
(CuO)8	1.98	2.60, 3.17	82.2, 113.6	1.95	2.75, 3.32	89.1, 121.1	1.96	2.67, 3.13	84.2, 111.1
(CuO)9	2.05	2.83, 4.31	93.2, 129.9	1.98	2.81, 4.05	92.7, 147.6	2.00	2.76, 3.96	90.7, 123.4
(CuO)10	1.93	3.37	87.1, 125.7	1.93	3.42	90.3, 130.2	1.95	3.30	86.1, 122.4
(CuO)11	1.95	3.2	88.2, 112.9, 141.9	1.94	3.22	93.3, 116.2, 142.6	1.97	3.13	87.4, 110.1, 133.1
(CuO)12	1.94	3.02, 3.83	106.1, 143.4	1.96	3.11, 4.01	110.5, 141.4	1.97	3.03, 3.96	105.9, 137.7

---

3.1.3 Finding the building block of copper oxide clusters. One of the most important aspects of cluster studies is to search for a building block that can further assemble to grow larger clusters. In the present work, we have optimized copper oxide clusters from monomer to dodecamer. From n = 1–7, a planar ring-like structure is found to be the most stable isomer while from octamer to dodecamer, a non-planar layer structure has been observed. Furthermore, if we analyze the non-planar structure of the CuO clusters, it is observed that the building blocks constituting the larger clusters are mostly trimer and tetramer. For example, the octamer is composed of two tetramer units (4 × 4) while the dodecamer is composed of three tetramer units (4 × 4 × 4). In the case of the nonamer, three trimer units (3 × 3 × 3) are stacked in a staggered fashion. In (CuO)₁₁, both trimer and tetramer units are stacked in a (4 × 4 × 3) configuration. In order to further resolve the issue of whether a trimer or tetramer is the building block, we have considered the Cu₁₂O₁₂ cluster in detail. To optimize the structure of Cu₁₂O₁₂, three units of tetramer (4 × 4 × 4) and four units of trimer (3 × 3 × 3 × 3) were explored. The isomer comprising four units of trimer (3 × 3 × 3 × 3) is found to be ∼1 eV higher in energy as compared to the isomer that consists of three tetramer units (4 × 4 × 4). This result clearly implies that the tetramer is a more suitable building block than the trimer in the size regime. In order to further validate this inference, we have optimized the layered isomer of the (CuO)₁₆ cluster. Fig. 2 represents the structure of (CuO)₁₆ where the Cu–Cu interatomic distance of the top and bottom layer is 2.7 Å, while it increases to 3.5 Å for two middle layers. Elongation of the Cu–Cu interatomic distance in the two middle layers of the stacked structure helps to presume the structure as a nano-barrel. This structure is distinctly different from (CuO)₈ where the Cu–Cu interatomic distance is found to be similar in both the layers. Curvature in the barrel structure of (CuO)₁₆ helps it to interact differently as compared to the simple layer structure. In the literature, various barrel structures have been synthesized for encapsulation of important chemicals like proteins, C₆₀etc.^47–49 In future, this kind of nano-barrel structure can be explored for different chemical reactions, catalysis, gas sensing, etc.

Fig. 2 Nano-barrel structure of (CuO)₁₆ clusters where 4 tetramer units are stacked in a staggered fashion.

3.2 Electronic structure of copper oxide clusters

The physico-chemical properties of any material have a strong correlation with the electronic structure. In order to elucidate the electronic structure of the (CuO)_n cluster, we have analyzed the projected density of states (PDOS) of these clusters as shown in Fig. S1 of the ESI.† Strong chemical interactions between Cu and O atoms are observed leading to overlap among the energy states of the oxygen and Cu atoms, giving hybrid character to the energy states, especially near the Fermi level. The electronic charge distribution between the Cu and O atoms was analyzed through Bader charge distribution.⁵⁰ In general, the trend showed that electronic charge transfer took place from the Cu to O atoms. The details of the charge on the Cu atom in each cluster are tabulated in Table S6 in the ESI.† In line with the magnetic moment of the individual clusters, the spin polarization for the up and down spin states was visible in the PDOS [except for the (CuO)₈ and (CuO)₁₂ clusters since they have zero magnetic moment]. Importantly, spin polarization is synchronal on both the Cu and O energy states. For the smallest monomer unit of CuO, the Fermi level is dominated by d_xz, d_yz and p-states of oxygen atoms, while d_z² and d_x²−y² states remain almost unaffected. For the (CuO)₂ dimer unit, where the Cu–Cu interactions comes into the picture, the d_yz and d_xy of Cu and p-states of oxygen atoms appear at the Fermi level and the d_z² and d_x²−y² states remain deep. A similar trend continues for the trimer (CuO)₃ cluster along with more states appearing between −6.5 eV and the Fermi level. The spin polarized nature of the tetramer cluster (CuO)₄ is apparent in PDOS, as the energy states with down and up spin differ substantially. The d_xz and d_yz states of Cu and p-states of oxygen atoms form the Fermi energy level. The d_z² and d_x²−y² states appear around the −3 eV energy region. The larger size clusters, viz., (CuO)₅, (CuO)₆ and (CuO)₇, also have fewer energy states near the Fermi level, followed by a higher number of states around 3–4 eV and again fewer states at lower energy. The PDOS pattern changes significantly from octamer onwards as the structure becomes three dimensional. Since the (CuO)₈ cluster has zero spin polarization, the up and down spin states are exact mirror images of each other. The variation in the intensity of PDOS across the energy scale reduces and more states appear at the Fermi energy level. A similar trend continues for larger size clusters as (CuO)₉, (CuO)₁₀, (CuO)₁₁ and (CuO)₁₂ clusters show broader dispersion along with higher energy states around the Fermi level.

On the basis of the previous description on the lowest energy isomers of (CuO)_n clusters, it is felt that both tetramer and octamer clusters need additional discussion as the first one is being used as a building block and the latter one shows onset of a three-dimensional structure. In order to correlate the electronic structure with atomic structure, an in-depth analysis of PDOS for the (CuO)₄ and (CuO)₈ clusters has been carried out. In particular, the nature of the PDOS has been viewed from the perspective of bonding, and dimensionality. In Fig. 3, we have shown a comparison of the PDOS pattern between the 2D and 3D isomers of the (CuO)₄ and (CuO)₈ clusters. The planar structure of (CuO)₄ shows shorter Cu–O (∼1.75 Å) and longer Cu–Cu (∼2.9 Å) bonds in the molecular plane. In contrast, the 3D isomer of (CuO)₄ (structure 4d in Table S1, ESI†), which is 2.49 eV higher in energy, shows a decrease in the Cu–Cu bond (from 2.9 to 2.6 Å) and increase in the Cu–O bond (1.75 to 1.93 Å) (Table 1). Thus, the higher energy 3D isomer has greater Cu–Cu interactions. This leads to enhanced d–d mixing across the energy scale. Noticeably, all five d-orbitals contribute to the Fermi level along with the oxygen states for the 3D tetramer unit. In contrast, the ground state planar isomer has a smaller Cu–Cu interaction and larger Cu–O interaction in the molecular plane leading to a lower extent of d–d mixing across the energy scale and only the d_yz and d_xy states contribute to the Fermi level along with the p-states of the oxygen atoms. The Cu–O bond strength (∼1.22 eV per atom) is higher than the Cu–Cu bond strength (∼1.03 eV) (Table S3, ESI†). Therefore, it is expected that Cu–O interaction will influence the extent of mixing of Cu and O atom energy states/orbitals more in comparison to Cu–Cu interaction (d–d mixing). Indeed, the same is visible in the (CuO)₄ tetramer unit. Moreover, the planar tetramer has fewer states at the Fermi level than at the deeper energy scale. As the size increases, a similar trend continues up to heptamer (n = 7), i.e., limited d–d mixing across the energy scale and Fermi level has smaller energy states with a major contribution from d-states of Cu and p-states of oxygen. These observations are in line with the fact that (CuO)₅, (CuO)₆ and (CuO)₇ have a lower number of Cu–Cu interactions with a longer Cu–Cu distance (∼3 Å or more). However, at n = 8, as the dimensionality of the cluster switches from planar to 3D, two major changes are observed; (i) the Cu–O bond length increases from 1.73 Å to 1.96 Å and (ii) the number of Cu–Cu bonds as well as their strength increases (i.e., Cu–Cu interatomic distance around 2.5–2.9 Å). A larger number of Cu–Cu bonds along all dimensions leads to a significant increase in the extent of d–d mixing across the energy scale. For (CuO)₈, all five d-orbitals contribute to the Fermi level with a substantial increase in the DOS along with oxygen p-states.

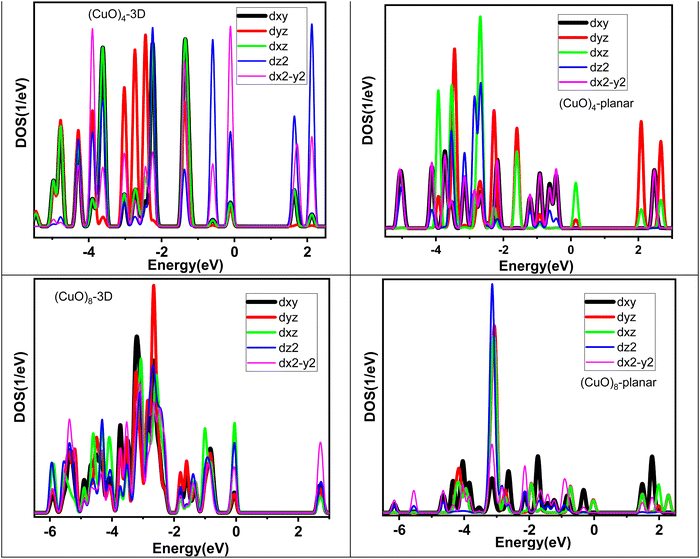Fig. 3 Projected density of states (PDOS) of planar and 3D (CuO)₄ and (CuO)₈ clusters as a function of energy.

The bulk CuO has a central Cu atom in the square planar configuration where each Cu atom forms four Cu–O bonds (bond distance ∼1.9 Å) and four long Cu–Cu bonds (bond distance ∼2.9 Å). Thus, each Cu atom in CuO is under a strong ligand field of four oxide ions and weak/very weak interactions with other neighboring Cu atoms. Stronger Cu–O bonds in a square planar arrangement do not favor uniform contributions from the five d-orbitals having different shapes due to geometrical constraints/dimensionality and hence they are not expected to mix uniformly while interacting with the oxide ligand (Fig. 4). This feature was indeed manifested in the PDOS (Fig. S1, ESI†), as the d_yz, d_xy and d_xz states have wide dispersion from the Fermi level to −8 eV, while the d_z² and d_x²−y² states are primarily dispersed in a narrow region around −4 eV. Stronger Cu–O interaction and weaker Cu–Cu interaction in CuO bulk (with square planar CuO₄ arrangements) results in less d–d mixing, which resembles the electronic structure of smaller cluster CuO (n = 3–7) having a planar configuration.

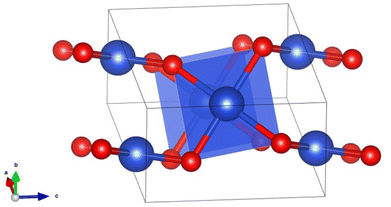Fig. 4 A square planar motif in the structure of CuO bulk where blue and red balls indicate Cu and O atoms, respectively.

Thus, based on the above discussion, it is clear that in general the atomic structure of (CuO)_n clusters is governed by energy economy between Cu–O and Cu–Cu bonds, which correlates with their electronic structure. The 2D planar structure, with stronger Cu–O and weaker Cu–Cu interactions, shows poor d–d mixing and fewer states at the Fermi level. On the other hand, the compactness of the 3D structure quantitatively increases the Cu–Cu interaction along with a decent bond strength of the Cu–O bonds. Hence, the electronic structure of these clusters observes significant d–d mixing and substantial energy states at the Fermi level. Thus, the strong correlation between the atomic structure and electronic structure of the (CuO)_n clusters is demonstrated based on a systematic evolution of the growth pattern vis-à-vis their electronic structure analysis.

3.3 Binding energy, ionization energy and electron affinity of copper oxide clusters

In this section, the energetics of the neutral and charged clusters are described. In Table 3, the binding energy of the neutral copper oxide clusters is listed. These are also plotted as a function of size as shown Fig. 5. It is evident that the binding energy increases with cluster size. As the cluster size increases up to five, the average binding energy increases sharply. This is due to the formation of a greater number of Cu–O bonds and Cu–Cu bonds. On further increase of the size, the Cu–O bond length increases marginally along with a decrease in the Cu–Cu bond length. As a result, the average binding energy increased marginally from n = 5 to n = 7. For n = 8, the average binding energy increased significantly. This is attributed to the formation of a greater number of Cu–O bonds and Cu–Cu bonds during structural transition to a 3D motif. Afterwards, the binding energy increase systematically with cluster size and for dodecamer (CuO)₁₂, the binding energy is −3.46 eV per CuO unit. Importantly, even though the bulk has four coordination number with respect to oxygen, the ultra-small cluster has a coordination number with respect to oxygen of 2 or 3 but for the dodecamer (CuO)₁₂ cluster, the middle layer Cu atom connects with four oxygen atoms. The binding energy of copper oxide clusters (CuO)_n has also been calculated using the PBE method and the results are presented in Table 2. From the results, it is evident that the binding energy increases with cluster size and finally saturates. Though the trend of binding energy is similar in the two methods, the PBE functional overestimates the binding energy as compared to the hybrid functional (HSE06).

Table 3 Binding energy/CuO unit, second derivative of energy and magnetic moment for (CuO)_n clusters (n = 1–12) using the hybrid functional (HSE06). Binding energy/CuO unit of different clusters using the PBE functional are mentioned in brackets in column 2

Cluster size	Binding energy/CuO unit (eV)	Δ^2E (eV)	Mag. Mom.
1	—	—	1.00
2	1.46 (1.82)	1.18	2.00
3	2.34 (2.72)	−0.53	3.00
4	2.64 (3.07)	−0.50	2.00
5	2.73 (3.20)	0.29	3.00
6	2.83 (3.26)	−0.47	6.00
7	2.84 (3.27)	2.66	7.00
8	3.18 (3.38)	−1.98	0.00
9	3.22 (3.43)	0.25	1.00
10	3.28 (3.46)	−0.55	2.00
11	3.29 (3.54)	2.10	3.00
12	3.46 (3.64)	—	0.00

---

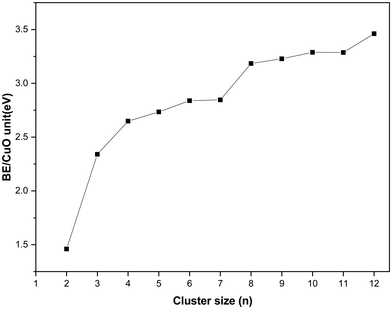Fig. 5 Binding energy of the copper oxide cluster/CuO unit as a function of cluster size. All energy values are derived from total energy calculations using the hybrid functional (HSE06).

In order to understand the relative stability of a cluster with respect to the nearest neighbor, the second derivative of energy (Δ²E) has been calculated and listed in Table 3 and plotted as a function of cluster size in Fig. 6. It shows that among different clusters, trimer, tetramer, hexamer, octamer and decamer have negative Δ²E value. Negative Δ²E value indicates stability of these clusters as compared to the nearest neighbor. The octamer has the most negative Δ²E value, which is attributed to the non-planar structure of (CuO)₈ where the number of Cu–O bonds increases drastically along with more Cu–Cu bonds as compared to the linear structure of the heptamer.

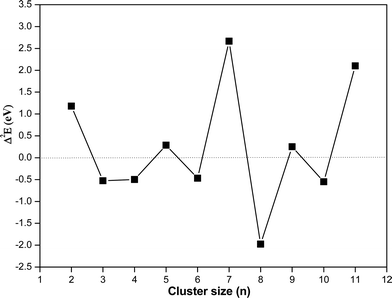Fig. 6 Second derivative energy value (Δ²E) of the copper oxide clusters as a function of cluster size using the hybrid functional (HSE06).

On the basis of the energetics of the neutral and cation clusters, the ionization energy of the copper oxide clusters has been calculated and listed in Table 4. From this table it is evident that the adiabatic ionization energy lies in the range of 8–9 eV except for the octamer and dodecamer. The octamer and dodecamer show exceptionally low ionization energy in the range of 5.5–6 eV, which is very close to the work function (5.3 eV) of CuO bulk.⁵¹ The observation of a low ionization energy for (CuO)₈ and (CuO)₁₂ makes them a potential reducing agent in a chemical reaction. To estimate the electron affinity of these clusters, we have optimized the anionic clusters. It is seen that the electron affinity increases with cluster size and most of the cluster species have a very high electron affinity, which is in the range of 3.2–4.2 eV, indicating their ability as strong oxidizing agents. Most interestingly, for (CuO)₈ and (CuO)₁₂, the electron affinity is found to be much higher as compared to the other clusters and it is in the range of ∼6.5 eV. As the electron affinity of these species exceeds that of chlorine, which has the highest electron affinity (3.7 eV) in the periodic table, these species can be termed as ‘super-halogens’ and can be used as a potential oxidizing agent.

Table 4 Adiabatic ionisation energy (AIE) and electron affinity (EA) of copper oxide clusters (CuO)_n (n = 1–12) using the LCAO-MO method

Species	AIE (in eV)	EA (in eV)
CuO	9.13	1.24
(CuO)2	8.77	2.14
(CuO)3	8.70	3.23
(CuO)4	8.53	3.82
(CuO)5	8.51	3.93
(CuO)6	8.10	3.98
(CuO)7	7.75	3.99
(CuO)8	5.62	6.43
(CuO)9	8.30	4.18
(CuO)10	7.68	3.96
(CuO)11	8.17	4.17
(CuO)12	5.97	6.54

---

4. Conclusions

In the present work, the ground state structures of ultra-small clusters of copper oxide have been studied using density functional theory. From monomer to heptamer (n = 1–7), the planar cyclic ring structure is found to be the most stable while from octamer to dodecamer (n = 8–12), a three-dimensional layer structure is found to be energetically most favored. Among these layer structures, the nonamer and dodecamer assume the nano-barrel structure where the Cu–Cu interatomic distance increases in the middle layer as compared to the top and bottom layer. To date, there is no report of a nano-barrel structure for such small copper oxide clusters. In order to understand the evolution of cluster growth and transition from a two-dimensional nano-ring structure to a three-dimensional layer structure, geometrical aspects (bond length, bond angle) and the electronic structure of the optimized isomer have been investigated. Detailed analysis reveals that in the smaller cluster regime (n = 1–7), the Cu–O bond dominates and poor d–d mixing stabilizes the planar structure. On the contrary, at higher cluster size (n = 8–12), weaker Cu–O bonds followed by significant mixing of the d–d orbitals substantiates a three-dimensional layer structure. The ionization energy of the clusters is calculated as a function of size, where the octamer and dodecamer have the lowest ionization energy in the range of 5.5–6 eV. The electron affinity of most of the clusters lies in the range of ∼3.5 eV, while (CuO)₈ and (CuO)₁₂ show very high values of ∼6.5 eV. The higher value of electron affinity of the octamer and dodecamer indicates their super-halogen nature. Therefore, the octamer and dodecamer clusters exhibit noteworthy features in the small size regime and they can be used as potential oxidizing agents as well as reducing agents.

Conflicts of interest

There are no conflicts to declare.

References

1. G. L. Gutsev, S. N. Khanna, B. K. Rao and P. Jena, J. Phys. Chem. A, 1999, 103, 5812–5822.
2. M. Ju, J. Lv, X. Kuang, L. Ding, C. Lu, J. Wang, Y. Jin and G. Maroulis, RSC Adv., 2015, 5, 6560–6570.
3. M. F. A. Hendrickx and K. R. Anam, J. Phys. Chem. A, 2009, 113, 8746–8753.
4. G. L. Gutsev, K. G. Belay, L. G. Gutsev and B. R. Ramachandran, Comput. Mat. Sci., 2017, 137, 134–143.
5. S. Srirama, R. Chandiramouli, D. Balamurugan, K. Ravichandran and A. Thayumanavan, J. At. Mol. Sci., 2013, 4, 336–348.
6. G. L. Gutsev, K. G. Belay, K. V. Bozhenko, L. G. Gutsev and B. R. Ramachandran, Phys. Chem. Chem. Phys., 2016, 18, 27858–27867.
7. E. L. Uzunova, G. S. Nikolov and H. Mikosch, J. Phys. Chem. A, 2002, 106, 4104–4114.
8. C. N. van Dijk, D. R. Roy, A. Fielicke, T. Rasing, A. C. Reber, S. N. Khanna and A. Kirilyuk, Eur. Phys. J. D, 2014, 68, 357.
9. D. C. Perera and J. C. Rasaiah, ACS Omega, 2022, 15, 12556–12569.
10. S. A. Aravindh, I. S. Roqan and H. Alawadhi, J. Cluster Sci., 2021, 32, 55–62.
11. E. V. Trushin, I. L. Zilberberg and A. V. Bulgakov, Phys. Solid State, 2012, 54, 859–865.
12. J. B. Reitz and E. I. Solomon, J. Am. Chem. Soc., 1998, 120, 11467–11478.
13. A. Aslani and V. Oroojpour, Phys. B, 2011, 406, 144–149.
14. J. Meng, Z. Yang, L. Chen, H. Qin, F. Cui, Y. Jiang and X. Zeng, Mater. Today Energy, 2020, 15, 100370.
15. P. Wang, X. Gou, S. Xin and F. Cao, New J. Chem., 2019, 43, 6535–6539.
16. X. Zhang, W. Shi, J. Zhu, D. J. Kharistal, W. Zhao, B. S. Lalia, H. H. Hng and Q. Yan, ACS Nano, 2011, 5, 2013–2019.
17. A. Mittiga, E. Salza, F. Sarto, M. Tucci and R. Vasanthi, Appl. Phys. Lett., 2006, 88, 163502.
18. W. Siemons, G. Koster, D. H. A. Blank, R. H. Hammond, T. H. Geballe and M. R. Beasley, Phys. Rev. B: Condens. Matter Mater. Phys., 2009, 79, 195122.
19. J. R. Gord, R. J. Bemish and B. S. Freiser, Int. J. Mass Spectrom. Ion Processes, 1990, 102, 115–132.
20. M. A. Latif, J. W. J. Wu, R. Moriyama, M. Nakano, K. Ohshimo and F. Misaizu, ACS Omega, 2018, 3, 18705–18713.
21. K. Morita, K. Sakuma, K. Miyajima and F. Mafune, J. Phys. Chem. A, 2013, 117, 10145–10150.
22. S. Hirabayashi and M. Ichihashi, J. Phys. Chem. A, 2014, 118, 1761–1768.
23. F. Mafune, K. Miyajima and K. Morita, J. Phys. Chem. C, 2015, 119, 11106–11113.
24. M. L. Polak, M. K. Gilles, J. Ho and W. C. Lineberger, J. Phys. Chem., 1991, 95, 3460–3463.
25. H. Wu, S. R. Desai and L. S. Wang, J. Chem. Phys., 1995, 103, 4363–4366.
26. H. Wu, S. R. Desai and L. S. Wang, J. Phys. Chem. A, 1997, 101, 2103–2111.
27. L. S. Wang, H. Wu, S. R. Desai and L. Lou, Phys. Rev. B: Condens. Matter Mater. Phys., 1996, 53, 8028–8031.
28. K. Deng, J. Yang and Q. Zhu, J. Chem. Phys., 2000, 113, 7867–7873.
29. C. Massobrio and Y. Pouillon, J. Chem. Phys., 2003, 119, 8305–8310.
30. Y. Pouillon and C. Massobrio, Chem. Phys. Lett., 2002, 356, 469–475.
31. Y. Pouillon and C. Massobrio, Appl. Surf. Sci., 2004, 226, 306–312.
32. G. Bae, Comput. Theor. Chem., 2021, 1204, 113377.
33. Y. Matsuda, D. N. Shin and E. R. Bernstein, J. Chem. Phys., 2004, 120, 4165–4171.
34. G. Bae, B. Dellinger and R. W. Hall, J. Phys. Chem. A, 2011, 115, 2087–2095.
35. J. Baek and G. Bae, J. Korean Chem. Soc., 2020, 64, 61–66.
36. H. H. Farrell and R. D. Parra, J. Vac. Sci. Technol., B, 2011, 29, 061806.
37. G. Kresse and J. Furthmuller, Phys. Rev. B: Condens. Matter Mater. Phys., 1996, 54, 11169–11186.
38. D. Vanderbilt, Phys. Rev. B: Condens. Matter Mater. Phys., 1990, 41, 7892–7895.
39. G. Kresse and J. Furthmuller, Comput. Mater. Sci., 1996, 6, 15–50.
40. P. E. Blochl, Phys. Rev. B: Condens. Matter Mater. Phys., 1994, 50, 17953–17979.
41. J. P. Perdew, J. A. Chevary, S. K. Vosko, K. A. Jackson, M. R. Pederson, D. J. Singh and C. Fiolhias, Phys. Rev. B: Condens. Matter Mater. Phys., 1992, 46, 6671–6687.
42. J. P. Perdew, K. Burke and M. Ernzerhof, Phys. Rev. Lett., 1996, 77, 3865–3868.
43. J. Heyd, G. E. Scuseria and M. Ernzerhof, J. Chem. Phys., 2003, 118, 8207–8215.
44. J. Heyd and G. E. Scuseria, J. Chem. Phys., 2004, 121, 1187–1192.
45. A. Zivkovic, A. Roldan and N. H. de Leeuw, Phys. Rev. B, 2019, 99, 035154.
46. M. W. Schmidt, K. K. Baldridge, J. A. Boatz, S. T. Elbert, M. S. Gordon, J. H. Jensen, S. Koseki, N. Matsunaga, K. A. Nguyen, S. Su, T. L. Windus, M. Dupuis and J. A. Montgomery Jr., J. Comput. Chem., 1993, 14, 1347–1363.
47. Y. Chen, C. Zeng, C. Liu, K. Kirschbaum, C. Gayathri, R. R. Gil, N. L. Rosi and R. Jin, J. Am. Chem. Soc., 2015, 137, 10076–10079.
48. J. Song, N. Aratani, H. Shinokubo and A. Osuka, J. Am. Chem. Soc., 2010, 132, 16356–16357.
49. S. Bera, S. Das, M. Melle-Franco and A. Mateo-Alonso, Angew. Chem., 2023, 62, e202216540.
50. R. Bader, Atoms in Molecules: A Quantum Theory, Oxford University Press, New York, 1990.
51. F. P. Koffyberg and F. A. Benko, J. Appl. Phys., 1982, 53, 1173–1177.

---

Footnote

† Electronic supplementary information (ESI) available. See DOI: https://doi.org/10.1039/d3cp06235j

---