Open Access Article
Open Access ArticleSignatures of s-wave scattering in bound electronic states
Robin E.
Moorby
 *ab,
Valentina
Parravicini
*ab,
Valentina
Parravicini
 a,
Maristella
Alessio
a,
Maristella
Alessio
 a and
Thomas-C.
Jagau
a and
Thomas-C.
Jagau
 *a
*a
aDepartment of Chemistry, KU Leuven, Celestijnenlaan 200F, B-3001 Leuven, Belgium. E-mail: robin.moorby@kuleuven.be; thomas.jagau@kuleuven.be
bDepartment of Chemistry, University of Durham, South Road, Durham, DH1 3LE, UK
First published on 31st January 2024
Abstract
We compute EOM-EA-CCSD and EOM-EA-CCSDT potential energy curves and one-electron properties of several anions at bond lengths close to where these states become unbound. We compare the anions of HCl and pyrrole, which are associated with s-wave scattering, with N2 and H2, which correspond to resonances. For HCl and pyrrole, we observe, on inclusion of diffuse basis functions, a pronounced bending effect in the anionic potential energy curves near the crossing points with their corresponding neutral molecules. Additionally, we observe that the Dyson orbital and second moment of the electron density become extremely large in this region; for HCl, the size of the latter becomes 5 orders of magnitude larger over a range of 5 pm. This behaviour is not observed in H2 or N2. Our work thus shows that bound state electronic-structure methods can distinguish between anions that turn into electronic resonances and those associated with s-wave scattering states.
1 Introduction
The attachment of electrons to neutral molecules can lead to bound or unbound molecular anions. If the electron affinity of a molecule is positive, the attachment of the excess electron is permanent, and the anions can be treated theoretically with conventional Hermitian quantum-chemical methods. One can distinguish between valence anions, in which the additional electron resides in a rather compact orbital close to the molecule, and non-valence anions, where the additional electron resides in a diffuse orbital and is bound by either the molecular dipole moment, quadrupole moment, or dispersion effects.1–6 For the computational treatment of non-valence anions in particular, large basis sets are mandatory to capture the enormous extent of the wave function. Also, correlated wave function theory is often necessary to compute accurate electron affinities and, in some cases, an anion is not bound at all at the Hartree–Fock (HF) level of theory. Furthermore, it is notable that corrections to the energy from nuclear contributions can be largely different for the anionic and neutral molecules.1,7In cases where the anion is unbound at the equilibrium geometry of the neutral molecule, a non-zero angular momentum of the incoming electron can introduce a centrifugal barrier behind which the electron is temporarily trapped allowing for the formation of metastable electronic states, known as shape resonances.1,8,9 The energy of electronic resonances places them within a continuum of elastically scattered states, meaning that they can decay via electron loss due to their coupling with the continuum.10–12 Such shape resonances are widespread, two well-characterised examples are the anions of H2 and N2. Besides shape resonances, there are Feshbach resonances which decay by a two electron process. A simple case of this type of state is the (σg)1(σu)2 excited state of H2− at stretched bond lengths.13–15
In the case of s-wave scattering, however, there is no centrifugal barrier. Temporary electron-attached states near the continuum threshold have been termed virtual states in s-wave scattering and, while also unbound, are distinct from resonances.8,9,16,17 Virtual states have been associated with anions in molecules such as CO2,3,18–22 (CN)2,23 Fe(CO)5,24 HCl25–27 and pyrrole.28
The asymptotic behaviour of unbound electronic states means that they cannot be treated with bound-state quantum chemical methods which fail to impose the correct boundary conditions. For electronic resonances, non-Hermitian quantum chemistry offers an elegant solution to this problem: the energies are calculated as complex-valued eigenvalues of a non-Hermitian Hamiltonian.10–12 Methods in this regard include complex scaling,29–31 where the coordinates of the Hamiltonian are rotated into the complex plane; complex basis functions, where the exponents of basis functions are rotated into the complex plane;32 and complex absorbing potentials,33,34 where a complex potential is applied to absorb the tails of the wave function. Alternatively, resonance positions can be determined using stabilisation and extrapolation techniques.35–38 Analytical continuation of such methods is necessary to additionally calculate resonance decay widths.39,40
These techniques can be integrated into bound-state quantum chemistry enabling a treatment of electronic resonances in analogy to that of bound states. However, their applicability to s-wave scattering and virtual states is questionable, which means that one must resort to more traditional methods based on scattering theory.9 The combination of the latter approaches with bound-state methods is still very challenging, even for diatomics such as HCl,26,27,41,42 which often necessitates the use of relatively low-level electronic-structure methods.
It is thus desirable to identify and characterise anions that correspond to virtual states and distinguish them from other anions that correspond to electronic resonances. To this end, we investigate in this work the anions of HCl and pyrrole both of which are relevant to s-wave scattering and contrast them with H2− and N2− as prototypical examples of resonances. While these anions all are unbound at the equilibrium structures of the respective neutral molecules, they become bound upon bond stretching. We show in this work that close to the point at which an anion becomes unbound, bound states turning into resonances and s-wave scattered states, respectively, exhibit different behaviour in terms of potential energy curves and one-electron properties.
2 Computational details
We conduct coupled-cluster singles and doubles (CCSD) calculations43,44 on the ground states of the neutral HCl, N2, H2, and pyrrole molecules and equation-of-motion electron-attachment CCSD (EOM-EA-CCSD) calculations45,46 to access the corresponding anions. We construct customised basis sets from the aug-cc-pVTZ basis47–49 with additional diffuse functions obtained by recursively dividing the exponent of the most diffuse s and p shell by a factor of 2. A basis set labelled aug-cc-pVTZ+nsnp indicates that we have added n additional s and p shells to all atoms according to this even-tempered manner. In the largest basis sets used, aug-cc-pVTZ+15s15p, the smallest exponent, corresponding to an s function on hydrogen, is of the order of 10−7. The molecular geometry of pyrrole is taken from ref. 50.For all systems but pyrrole, we also carry out coupled-cluster singles, doubles and triples (CCSDT)51,52 and equation-of-motion electron-attachment CCSDT (EOM-EA-CCSDT) calculations.53,54 Our EOM-EA-CCSDT calculations make use of the continuum orbital method:55 a basis function with an exponent of 10−10, which effectively does not interact with the rest of the basis set, is included in the calculation and two electrons are placed in the resulting orbital when solving the restricted HF (RHF) equations. In a subsequent EOM excitation energy CCSDT (EOM-EE-CCSDT) calculation, one electron can then be excited from the continuum orbital into a target orbital allowing for the calculation of EOM-EA-CCSDT states using an EOM-EE-CCSDT implementation.
Additionally, for HCl− and N2−, we compute the second moments of the electron density and the Dyson orbital of the anionic states at the EOM-EA-CCSD level. Dyson orbitals can be viewed as transition density matrices between neutral and electron-attached states and characterise electron attachment without invoking a mean-field approximation.56–58 The frozen-core approximation is used in all CC calculations. For HCl, we also compute the energy of the anion at the unrestricted HF (UHF) level of theory and by applying Koopmans' theorem to the virtual orbitals of the neutral molecule. All CCSD, EOM-EA-CCSD, and UHF calculations were performed using the Q-Chem software, version 6.0.2.59 All CCSDT and EOM-EA-CCSDT calculations were performed using the CFOUR software, version 2.1.60
3 Results
3.1 Potential energy curve of HCl−
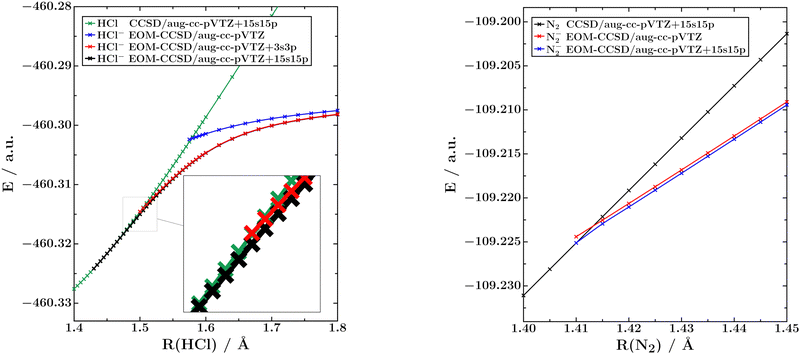
In the left panel of Fig. 1 we show potential energy curves of neutral HCl and of the 2Σ+ ground state of HCl− computed using CCSD and EOM-EA-CCSD, respectively, and three different basis sets: aug-cc-pVTZ, aug-cc-pVTZ+3s3p and aug-cc-pVTZ+15s15p. To illustrate the special character of these potential energy curves, we show in the right panel of the same figure the corresponding curves for neutral N2 and the 2Πg ground state of N2− computed with the same methods and basis sets.Fig. 1 demonstrates that the inclusion of diffuse shells in the basis set has a much bigger effect on HCl− than on N2−. In the unmodified aug-cc-pVTZ basis, both anionic potential energy curves behave similarly, but upon the addition of diffuse shells the HCl− curve bends downwards and crosses the curve of the neutral molecule at a much shorter H–Cl distance.
The crossing points between the neutral and anionic HCl potential energy curves computed with different methods and basis sets can be found in Table 1. It is seen that this point moves by 0.143 Å at the EOM-EA-CCSD level when going from the standard aug-cc-pVTZ basis to aug-cc-pVTZ+15s15p. In fact, we cannot assure that the value of 1.434 Å computed in the largest basis is converged with respect to basis-set size because the inclusion of 15 diffuse s and p shells represents a technical limit of our implementation. In contrast, the crossing point between the N2 and N2− curves in the right panel of Fig. 1 is nearly invariant and only moves from 1.413 Å to 1.412 Å upon the inclusion of 15 diffuse s and p shells. We also note that the basis-set dependence of the HCl− curve is only significant near the crossing point. At H–Cl bond lengths of 1.8 Å, the differences between the basis sets are negligible.
| Basis set | KT | ΔHF | CCSD | CCSDT |
|---|---|---|---|---|
| aug-cc-pVTZ | 1.735 | 1.639 | 1.577 | 1.569 |
| aug-cc-pVTZ+3s3p | 1.682 | 1.630 | 1.502 | 1.498 |
| aug-cc-pVTZ+5s5p | 1.664 | 1.630 | 1.475 | 1.474 |
| aug-cc-pVTZ+10s10p | 1.642 | 1.630 | 1.445 | |
| aug-cc-pVTZ+15s15p | 1.631 | 1.630 | 1.434 |
To confirm the validity of the EOM-EA-CCSD approximation for the HCl− anion, we conducted EOM-EA-CCSDT calculations, which are documented in Table 1 as well. This illustrates that the crossing point moves to slightly shorter bond distances as compared to EOM-EA-CCSD but the bending effect remains similar in magnitude. However, due to technical limitations, we could not run EOM-EA-CCSDT calculations with more than 5 diffuse s and p shells. For N2−, differences between EOM-EA-CCSDT and EOM-EA-CCSD are very similar to those observed for HCl−, which corroborates that the bending feature observed for HCl− is well captured by EOM-EA-CCSD and not related to an insufficient treatment of electron correlation.
To further investigate the nature of HCl−, we also conducted UHF calculations on this anion and we also applied Koopmans' theorem to the lowest-lying virtual orbital of neutral HCl. The resulting potential energy curves are shown in Fig. 2, and the corresponding crossing points are available in Table 1. It is seen that UHF does not recover the bending effect and basis-set dependence visible in the EOM-CC potential energy curves from Fig. 1, while Koopmans' theorem does. At the HF level of theory, the inclusion of 15 diffuse s and p shells in the basis set moves the crossing point by only 0.009 Å, whereas that value amounts to 0.104 Å with Koopmans' theorem.
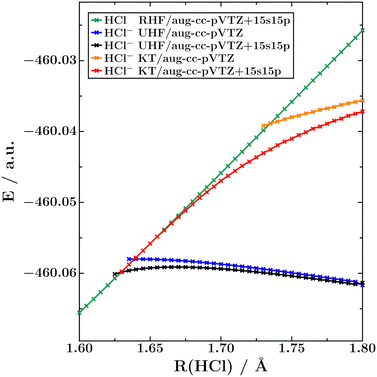 | ||
| Fig. 2 Potential energy curves of the 1Σ+ ground state of HCl and the 2Σ+ ground state of HCl− computed with HF theory and Koopmans' theorem at 1.6 < R(HCl) < 1.8 Å. | ||
We add that there is a region of ca. 0.2 Å, from 1.63 Å to 1.434 Å, where HCl− is only bound at correlated levels of theory. At these H–Cl distances, the energy of the anionic UHF potential curve lies above the RHF neutral potential curve, while the EOM-EA-CCSD anionic potential curve lies below the CCSD neutral potential curve. Also this behaviour is qualitatively different from N2−, which is bound already at shorter distances at the HF level of theory (R(NN) ≈ 1.33 Å) than at the EOM-EA-CCSD level of theory (R(NN) ≈ 1.41 Å).11
We note that the dipole moment of HCl, computed with CCSD/aug-cc-pVTZ+15s15p, amounts to 1.48 D and 1.24 D at R(H–Cl) = 1.8 Å and 1.434 Å, respectively. This is substantially below the critical value needed to form a dipole-bound anion,1 meaning that the polarity of HCl is not the critical difference to N2. However, the same bending effect shown for HCl− in Fig. 1 and 2 has also been observed in EOM-EA-CCSD calculations along the bending coordinate of CO2− and connected to s-wave scattering.20 A further interesting parallel can be drawn to correlation-bound anions such as C6F6−61 and C60−:62 also for these electronic states, a description based on a UHF wave function of the anion yields poor results, while EOM-EA-CC calculations based on an orbital manifold optimised for the neutral molecule perform much better.
3.2 Second moment of the electron density of HCl−
To further characterise the HCl− anion, we computed second moments of the electron density (〈r2〉) with EOM-EA-CCSD and different basis sets. The results are reported in Table 2. At 1.8 Å where HCl− is in all basis sets bound in terms of Koopmans' theorem, 〈r2〉 is around 18 Å2. Increasing the number of diffuse shells has only a small impact on 〈r2〉 at this bond length. At 1.60 Å, where HCl− is bound at the EOM-EA-CCSD level but already unbound at the HF level, the basis-set dependence of 〈r2〉 is already more pronounced; 3 additional diffuse s and p shells on top of aug-cc-pVTZ lead to an increase by 50%. However, even more diffuse shells only become relevant at shorter distances: At 1.50 Å, the value of 〈r2〉 has increased to 255 Å2 and 10 diffuse s and p shells are needed to capture it. At 1.434 Å i.e., the crossing point in our largest basis set (aug-cc-pVTZ+15s15p), we obtain a value of 647![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 000 Å2 for 〈r2〉, which corresponds to an average distance of ca. 800 Å. Moreover, we cannot say whether this value is actually converged with respect to basis-set size.
000 Å2 for 〈r2〉, which corresponds to an average distance of ca. 800 Å. Moreover, we cannot say whether this value is actually converged with respect to basis-set size.
| Basis set | Crossing point | 1.45 Å | 1.50 Å | 1.55 Å | 1.60 Å | 1.80 Å |
|---|---|---|---|---|---|---|
| aug-cc-pVTZ | 20.3 (1.577 Å) | 19.8 | 17.5 | |||
| aug-cc-pVTZ+3s3p | 71.4 (1.502 Å) | 48.6 | 31.4 | 18.0 | ||
| aug-cc-pVTZ+5s5p | 250.1 (1.475 Å) | 170.9 | 61.8 | 32.3 | 18.0 | |
| aug-cc-pVTZ+10s10p | 6897.8 (1.445 Å) | 5507.7 | 255.2 | 62.5 | 32.4 | 18.6 |
| aug-cc-pVTZ+15s15p | 647![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 195.1 (1.434 Å) 195.1 (1.434 Å) |
449![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 047.1 047.1 |
255.7 | 62.5 | 32.4 | 18.4 |
The explosion of 〈r2〉 by a factor of more than 2 × 105 over a range of less than 0.2 Å explains the pronounced basis-set dependence of the HCl− potential energy curve in Fig. 1, but it is by no means typical of molecular anions. As a counterexample, we present in Table 3 〈r2〉 values for N2−. For this anion, the second moment is nearly invariant with respect to basis-set changes and, in fact, decreases somewhat when approaching the crossing point.
| Basis set | Crossing point | 1.6 Å | 1.8 Å |
|---|---|---|---|
| aug-cc-pVTZ | 17.3 | 19.5 | 22.1 |
| aug-cc-pVTZ+3s3p | 17.7 | 19.5 | 22.1 |
| aug-cc-pVTZ+5s5p | 17.8 | 19.5 | 22.1 |
| aug-cc-pVTZ+10s10p | 17.9 | 19.5 | 22.1 |
| aug-cc-pVTZ+15s15p | 17.7 | 19.5 | 22.1 |
3.3 Dyson orbital of HCl−
The extremely diffuse nature of the EOM-EA-CCSD wave function of HCl− near the crossing point with the neutral potential curve is also captured by the corresponding Dyson orbital, which is displayed in Fig. 3. Plotted at R(H–Cl) = 1.434 Å and an isovalue of 5 × 10−5 (left panel of Fig. 3), the orbital resembles a σ* orbital between hydrogen s and chlorine p atomic orbitals with a node in the centre of the bond. On reducing the isovalue to 3 × 10−5 (middle panel of Fig. 3), the character of the orbital changes and it becomes more akin to a σ orbital with a larger amplitude on the side of the hydrogen atom. At R(H–Cl) = 1.8 Å (right panel of Fig. 3), the σ-character of the Dyson orbital is preserved but its spatial extent is considerably smaller consistent with the trend seen in 〈r2〉 in Table 2.Similar to the second moment, the behaviour of the Dyson orbital of HCl− is by no means typical of molecular anions as illustrated by Fig. 4, which shows the Dyson orbital of N2−. In contrast to HCl−, the Dyson orbital of N2− remains compact and of π* character independent of the isovalue and also when the N–N bond length is decreased from 1.8 Å to 1.413 Å, where the potential curves of N2− and N2 cross. In fact, this orbital becomes slightly less diffuse when the bond becomes shorter. With non-Hermitian techniques, it is possible to evaluate a complex-valued Dyson orbital in the unbound region at R(NN) < 1.413 Å as well;57 the real part of such an orbital looks very similar to those displayed in Fig. 4.
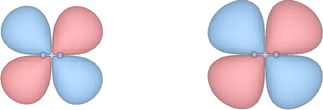 | ||
| Fig. 4 Dyson orbital of the 2Πg ground state of N2− computed with EOM-EA-CCSD/aug-cc-pVTZ+15s15p and plotted at an isovalue of 0.001 at internuclear distances of 1.413 Å (left) and 1.800 Å (right). | ||
The Dyson orbital of HCl− shown in Fig. 3 is, however, similar to what one observes for correlation-bound anions.3,6,61,62 In C6F6−, for example, the EOM-EA-CC natural orbital hosting the excess electron has a spatial extent much larger than the nuclear framework.61
3.4 Anions of H2
There are two bound doublet states of H2−: a 2Σ+u state, which is bound at bond lengths above ca. 1.6 Å, and a 2Σ+g state, which is bound at bond lengths above ca. 2.7 Å. The configuration of the first state is (σg)2(σu)1, while that of the second state is (σg)1(σu)2. The first state turns into a shape resonance at shorter bond lengths, whereas the second state is first a Feshbach resonance and then becomes a shape resonance as soon as the 3Σ+u state of H2 is lower in energy.15 As H2− has only three electrons, both states can be treated exactly within a given basis set by means of EOM-EA-CCSDT calculations. Particularly relevant in the context of the present work is that the electron emitted in the decay of the 2Σ+g state of H2− has to have zero angular momentum, meaning it represents an s-wave.The potential curves of both anionic states computed with full EOM-EA-CC in different basis sets are shown in Fig. 5; the corresponding crossing points with the potential energy curve of neutral H2 are summarised in Table 4. Fig. 5 shows that none of the two H2− states show the bending effect observed in HCl−. Also, the position of the crossing point between the neutral and anionic potential curves depends much less on the basis set than in the case of HCl−.
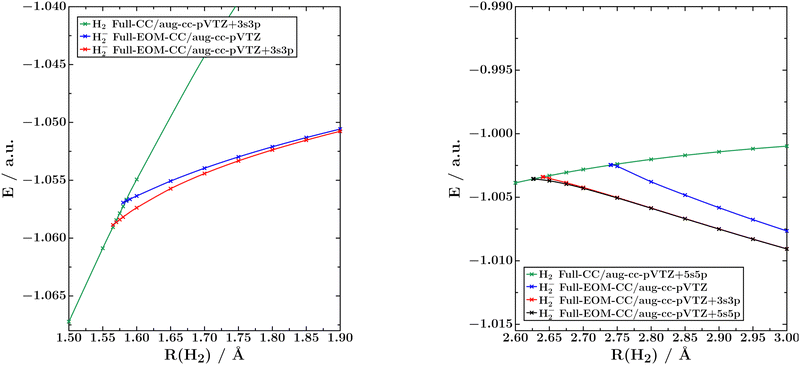 | ||
| Fig. 5 Potential energy curves of the 2Σ+u (left) and 2Σ+g (right) states of H2− computed with full EOM-EA-CC. The 1Σ+g ground state of H2 is also shown. | ||
| Basis set | 2Σ+u | 2Σ+g | ||
|---|---|---|---|---|
| CCSD | CCSDT | CCSD | CCSDT | |
| aug-cc-pVTZ | 1.613 | 1.585 | 2.760 | 2.741 |
| aug-cc-pVTZ+3s3p | 1.594 | 1.570 | 2.672 | 2.641 |
| aug-cc-pVTZ+5s5p | 1.593 | 2.668 | 2.627 | |
| aug-cc-pVTZ+10s10p | 1.593 | 2.668 | ||
| aug-cc-pVTZ+15s15p | 1.593 | 2.668 | ||
For the 2Σ+u state, the position of the crossing point is converged in the aug-cc-pVTZ+3s3p basis, where it differs by only 0.02 Å from the position in the aug-cc-pVTZ basis. The crossing point of the 2Σ+g state does vary more than that of the ungerade state when diffuse shells are added to the basis, but the position is converged within the aug-cc-pVTZ+5s5p basis and additional diffuse shells make no impact. We note that at much longer bond distances of 4.0 and 5.0 Å the potential curves obtained in the aug-cc-pVTZ and aug-cc-pVTZ+5s5p basis sets continue to run parallel.
This indicates that the aug-cc-pVTZ basis is insufficient to describe the 2Σ+g state at any bond length and the discrepancy in the position of the crossing points is not reflective of the bending effect observed in HCl−, for which diffuse shells make very little impact at long bond distances. We finally note that the differences between EOM-EA-CCSD and EOM-EA-CCSDT are for both states of H2− similar to those observed for HCl− and N2−.
3.5 Pyrrole anion
To demonstrate the relevance of our findings beyond diatomic molecules, we investigated the 2A1 state of the pyrrole anion. Pyrrole does not support a bound anion at its equilibrium structure but has a rich electron-induced chemistry.28,50,63–65 While the nature of two π* resonances is not debated, it is less clear if the low-lying totally symmetric anionic state, which is also present in pyrrole, should be interpreted as virtual state or rather as σ* resonance.28,50,65 Independent of the nature of the latter state, there are indications that non-adiabatic transitions66 between the π* resonances and the totally symmetric state mediate dissociative electron attachment, which has implications for similar processes in more complex molecules.1,17For a comprehensive investigation of the pyrrole anion, the full-dimensional potential energy surface would need to be studied. By means of analytic gradient techniques,67–69 this is, in principle, possible also in the unbound regions as recent applications illustrated.50 However, here we concentrate on the bound regions of the potential energy surface and furthermore limit ourselves to the N–H stretching coordinate.
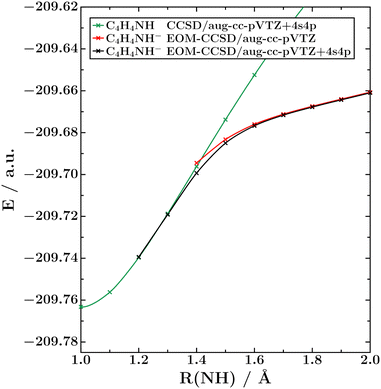
As Fig. 6 illustrates, the bound part of the potential energy curve of the 2A1 state of the pyrrole anion shows the same bending effect and basis-set dependence that we documented for HCl− in Fig. 1 and that was previously observed in CO2−.20 At the EOM-EA-CCSD level, the 2A1 state is bound at R(NH) > 1.2 Å in the aug-cc-pVTZ+4s4p basis, but only at R(NH) > 1.4 Å in the unmodified aug-cc-pVTZ basis. Similar to HCl−, the diffuse functions make no substantial impact at larger N–H distances of around 2 Å. This strongly suggests that the 2A1 state turns into a virtual state in the unbound region and not a σ* resonance.
4 Conclusions
We have investigated the bound anions of HCl, pyrrole, N2, and H2 using the EOM-EA-CCSD and EOM-EA-CCSDT methods at molecular structures close to where they become unbound. The 2Σ+ state of HCl− and the 2A1 state of pyrrole anion, both of which are connected to s-wave scattering, show a number of features that are not present in N2− and H2−: close to the crossing point with the parent neutral state, the spatial extent of the anionic wave function increases exponentially, which renders the potential energy curve extremely sensitive to diffuse functions in the basis set. For HCl−, the inclusion of 15 diffuse s and p shells with exponents down to 10−7 on top of the aug-cc-pVTZ basis set yields a value of 647![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 000 Å2 for the second moment of the electron density and moves the crossing point with the potential energy curve of neutral HCl by 0.143 Å compared to aug-cc-pVTZ. Likely, these values are not yet converged with respect to the size of the basis set. Also, they do not take into account effects beyond the Born–Oppenheimer approximation. In contrast, the 2Πg state of N2− and the 2Σ+u state of H2−, which are associated with d-wave scattering and p-wave scattering, respectively, are not sensitive to diffuse basis functions as their spatial extent does not change by a lot along the potential energy curve. Interestingly, the totally-symmetric 2Σ+g state of H2−, which is subject to a two-electron decay process past the crossing point, also does not show the features observed in HCl− and the anion of pyrrole.
000 Å2 for the second moment of the electron density and moves the crossing point with the potential energy curve of neutral HCl by 0.143 Å compared to aug-cc-pVTZ. Likely, these values are not yet converged with respect to the size of the basis set. Also, they do not take into account effects beyond the Born–Oppenheimer approximation. In contrast, the 2Πg state of N2− and the 2Σ+u state of H2−, which are associated with d-wave scattering and p-wave scattering, respectively, are not sensitive to diffuse basis functions as their spatial extent does not change by a lot along the potential energy curve. Interestingly, the totally-symmetric 2Σ+g state of H2−, which is subject to a two-electron decay process past the crossing point, also does not show the features observed in HCl− and the anion of pyrrole.
We note that the sensitivity of the potential energy curve towards diffuse basis functions was also observed for CO2−,20 another state associated with s-wave scattering. The unusual character of the HCl− anion is also visible in the Dyson orbital, which, close to the crossing point, acquires an extremely diffuse character that is akin to correlation-bound anions of, for example, C60 or C6F6, which have been related to s-wave scattering as well.3,61,62
Importantly, the non-totally symmetric states of H2− and N2−, which turn into electronic shape resonances at shorter bond lengths, can be treated by means of non-Hermitian techniques such as complex basis functions or complex absorbing potentials in the unbound region.70 The same applies to the totally-symmetric 2Σ+g state of H2−, which turns into a Feshbach resonance.15
In contrast, the totally-symmetric anions of HCl, CO2, pyrrole, and similar molecules likely should not be considered as electronic resonances in the unbound region. Instead, the term “virtual state” has been coined for them. Whether these virtual states are amenable to a treatment in terms of complex absorbing potentials or complex basis functions, or how to integrate them by other techniques into bound-state electronic-structure theory, is not clear at present and we hope that our work stimulates further research in this direction.
Conflicts of interest
There are no conflicts to declare.Acknowledgements
R. E. M. acknowledges the European Union for mediating a bilateral exchange from the University of Durham to KU Leuven as a part of the Erasmus+ program. This work has been supported by a Marie Skłodowska-Curie Actions fellowship to M. A. (Grant Agreement No. 101062717). T.-C. J. gratefully acknowledges funding from the European Research Council (ERC) under the European Unions Horizon 2020 research and innovation program (Grant Agreement No. 851766) and the KU Leuven internal funds (Grant No. C14/22/083).Notes and references
- J. Simons, J. Phys. Chem. A, 2008, 112, 6401–6511 CrossRef CAS PubMed.
- J. M. Herbert, Rev. Comp. Chem., 2015, 28, 391–517 CAS.
- V. K. Voora, A. Kairalapova, T. Sommerfeld and K. D. Jordan, J. Chem. Phys., 2017, 147, 214114 CrossRef PubMed.
- J. P. Rogers, C. S. Anstöter and J. R. R. Verlet, Nat. Chem., 2018, 10, 341–346 CrossRef CAS PubMed.
- J. Simons, J. Phys. Chem. A, 2023, 127, 3940–3957 CrossRef CAS PubMed.
- G. P. Paran, C. Utku and T.-C. Jagau, Phys. Chem. Chem. Phys., 2024, 26, 1809–1818 RSC.
- S. Gulania, T.-C. Jagau, A. Sanov and A. I. Krylov, Phys. Chem. Chem. Phys., 2020, 22, 5002–5010 RSC.
- K. McVoy, Nucl. Phys. A, 1968, 115, 481–494 CrossRef CAS.
- J. R. Taylor, Scattering theory: the quantum theory of nonrelativistic collisions, John Wiley & Sons, Inc., Hoboken, NJ, 1972 Search PubMed.
- N. Moiseyev, Non-Hermitian Quantum Mechanics, Cambridge University Press, 2011 Search PubMed.
- T.-C. Jagau, K. B. Bravaya and A. I. Krylov, Annu. Rev. Phys. Chem., 2017, 68, 525–553 CrossRef CAS PubMed.
- T.-C. Jagau, Chem. Commun., 2022, 58, 5205–5224 RSC.
- J. N. Bardsley and J. S. Cohen, J. Phys. B: At., Mol. Opt. Phys., 1978, 11, 3645 CrossRef CAS.
- D. T. Stibbe and J. Tennyson, J. Phys. B: At., Mol. Opt. Phys., 1998, 31, 815 CrossRef CAS.
- A. F. White, E. Epifanovsky, C. W. McCurdy and M. Head-Gordon, J. Chem. Phys., 2017, 146, 234107 CrossRef PubMed.
- W. Domcke, Phys. Rep., 1991, 208, 97–188 CrossRef.
- H. Hotop, M.-W. Ruf, M. Allan and I. Fabrikant, Adv. At., Mol., Opt. Phys., 2003, 49, 85–216 CAS.
- M. A. Morrison, Phys. Rev. A, 1982, 25, 1445–1449 CrossRef CAS.
- H. Estrada and W. Domcke, J. Phys. B: At. Mol. Phys., 1985, 18, 4469–4479 CrossRef CAS.
- T. Sommerfeld, J. Phys. B: At., Mol. Opt. Phys., 2003, 36, L127 CrossRef CAS.
- J. Dvořák, M. Rankovič, K. Houfek, P. Nag, R. Čurík, J. Fedor and M. Čížek, Phys. Rev. Lett., 2022, 129, 013401 CrossRef PubMed.
- J. Dvořák, K. Houfek and M. Čížek, Phys. Rev. A, 2022, 105, 062821 CrossRef.
- P. Nag, R. Čurík, M. Tarana, M. Polášek, M. Ehara, T. Sommerfeld and J. Fedor, Phys. Chem. Chem. Phys., 2020, 22, 23141–23147 RSC.
- M. Allan, M. Lacko, P. Papp, Š. Matejčík, M. Zlatar, I. I. Fabrikant, J. Kočišek and J. Fedor, Phys. Chem. Chem. Phys., 2018, 20, 11692–11701 RSC.
- R. K. Nesbet, J. Phys. B: At. Mol. Phys., 1977, 10, L739 CrossRef CAS.
- M. Čížek, J. Horáček and W. Domcke, Phys. Rev. A, 1999, 60, 2873–2881 CrossRef.
- J. Fedor, C. Winstead, V. McKoy, M. Čížek, K. Houfek, P. Kolorenč and J. Horáček, Phys. Rev. A: At., Mol., Opt. Phys., 2010, 81, 042702 CrossRef.
- T. P. Ragesh Kumar, P. Nag, M. Ranković, T. F. M. Luxford, J. Kočišek, Z. Mašín and J. Fedor, Coupling of distant parts of pyrrole molecule through virtual and resonant states, arXiv, 2022, preprint, arXiv:2208.13539 DOI:10.48550/arXiv.2208.13539.
- J. Aguilar and J. M. Combes, Commun. Math. Phys., 1971, 22, 269–279 CrossRef.
- E. Balslev and J. M. Combes, Commun. Math. Phys., 1971, 22, 280–294 CrossRef.
- B. Simon, Commun. Math. Phys., 1972, 27, 1–9 CrossRef.
- C. W. McCurdy and T. N. Rescigno, Phys. Rev. Lett., 1978, 41, 1364–1368 CrossRef CAS.
- G. Jolicard and E. J. Austin, Chem. Phys. Lett., 1985, 121, 106–110 CrossRef CAS.
- U. V. Riss and H.-D. Meyer, J. Phys. B: At., Mol. Opt. Phys., 1993, 26, 4503–4535 CrossRef CAS.
- B. Nestmann and S. D. Peyerimhoff, J. Phys. B: At. Mol. Phys., 1985, 18, 615–626 CrossRef CAS.
- B. M. Nestmann and S. D. Peyerimhoff, J. Phys. B: At. Mol. Phys., 1985, 18, 4309–4319 CrossRef CAS.
- H. S. Taylor, in Models, Interpretations, and Calculations Concerning Resonant Electron Scattering Processes in Atoms and Molecules, John Wiley & Sons, Ltd, 1970, pp. 91–147 Search PubMed.
- A. U. Hazi and H. S. Taylor, Phys. Rev. A, 1970, 1, 1109–1120 CrossRef.
- J. Simons, J. Chem. Phys., 1981, 75, 2465–2467 CrossRef CAS.
- J. Simons, J. Phys. Chem. A, 2021, 125, 7735–7749 CrossRef CAS PubMed.
- W. Domcke and C. Mündel, J. Phys. B: At. Mol. Phys., 1985, 18, 4491–4509 CrossRef CAS.
- M. Allan, M. Čízek, J. Horáček and W. Domcke, J. Phys. B: At., Mol. Opt. Phys., 2000, 33, L209–L213 CrossRef CAS.
- G. D. Purvis III and R. J. Bartlett, J. Chem. Phys., 1982, 76, 1910–1918 CrossRef.
- I. Shavitt and R. J. Bartlett, Many-Body Methods in Chemistry and Physics: MBPT and Coupled-Cluster Theory, Cambridge University Press, Cambridge, UK, 2009 Search PubMed.
- J. F. Stanton and R. J. Bartlett, J. Chem. Phys., 1993, 98, 7029–7039 CrossRef CAS.
- M. Nooijen and R. J. Bartlett, J. Chem. Phys., 1995, 102, 3629–3647 CrossRef CAS.
- T. H. Dunning, J. Chem. Phys., 1989, 90, 1007–1023 CrossRef CAS.
- R. A. Kendall, T. H. Dunning and R. J. Harrison, J. Chem. Phys., 1992, 96, 6796–6806 CrossRef CAS.
- D. E. Woon and T. H. Dunning, J. Chem. Phys., 1993, 98, 1358–1371 CrossRef CAS.
- M. Mukherjee, T. P. Ragesh Kumar, M. Ranković, P. Nag, J. Fedor and A. I. Krylov, J. Chem. Phys., 2022, 157, 204305 CrossRef CAS PubMed.
- J. Noga and R. J. Bartlett, J. Chem. Phys., 1987, 86, 7041–7050 CrossRef CAS.
- J. Noga and R. J. Bartlett, J. Chem. Phys., 1988, 89, 3401 CrossRef CAS.
- S. A. Kucharski, M. Włoch, M. Musiał and R. J. Bartlett, J. Chem. Phys., 2001, 115, 8263–8266 CrossRef CAS.
- Y. J. Bomble, K. W. Sattelmeyer, J. F. Stanton and J. Gauss, J. Chem. Phys., 2004, 121, 5236–5240 CrossRef CAS PubMed.
- J. F. Stanton and J. Gauss, J. Chem. Phys., 1999, 111, 8785–8788 CrossRef CAS.
- C. Melania Oana and A. I. Krylov, J. Chem. Phys., 2007, 127, 234106 CrossRef PubMed.
- T.-C. Jagau and A. I. Krylov, J. Chem. Phys., 2016, 144, 054113 CrossRef PubMed.
- A. I. Krylov, J. Chem. Phys., 2020, 153, 080901 CrossRef CAS PubMed.
- E. Epifanovsky, A. T. B. Gilbert, X. Feng, J. Lee, Y. Mao, N. Mardirossian, P. Pokhilko, A. F. White, M. P. Coons, A. L. Dempwolff, Z. Gan, D. Hait, P. R. Horn, L. D. Jacobson, I. Kaliman, J. Kussmann, A. W. Lange, K. U. Lao, D. S. Levine, J. Liu, S. C. McKenzie, A. F. Morrison, K. D. Nanda, F. Plasser, D. R. Rehn, M. L. Vidal, Z.-Q. You, Y. Zhu, B. Alam, B. J. Albrecht, A. Aldossary, E. Alguire, J. H. Andersen, V. Athavale, D. Barton, K. Begam, A. Behn, N. Bellonzi, Y. A. Bernard, E. J. Berquist, H. G. A. Burton, A. Carreras, K. Carter-Fenk, R. Chakraborty, A. D. Chien, K. D. Closser, V. Cofer-Shabica, S. Dasgupta, M. de Wergifosse, J. Deng, M. Diedenhofen, H. Do, S. Ehlert, P.-T. Fang, S. Fatehi, Q. Feng, T. Friedhoff, J. Gayvert, Q. Ge, G. Gidofalvi, M. Goldey, J. Gomes, C. E. González-Espinoza, S. Gulania, A. O. Gunina, M. W. D. Hanson-Heine, P. H. P. Harbach, A. Hauser, M. F. Herbst, M. Hernández Vera, M. Hodecker, Z. C. Holden, S. Houck, X. Huang, K. Hui, B. C. Huynh, M. Ivanov, Á. Jász, H. Ji, H. Jiang, B. Kaduk, S. Kähler, K. Khistyaev, J. Kim, G. Kis, P. Klunzinger, Z. Koczor-Benda, J. H. Koh, D. Kosenkov, L. Koulias, T. Kowalczyk, C. M. Krauter, K. Kue, A. Kunitsa, T. Kus, I. Ladjánszki, A. Landau, K. V. Lawler, D. Lefrancois, S. Lehtola, R. R. Li, Y.-P. Li, J. Liang, M. Liebenthal, H.-H. Lin, Y.-S. Lin, F. Liu, K.-Y. Liu, M. Loipersberger, A. Luenser, A. Manjanath, P. Manohar, E. Mansoor, S. F. Manzer, S.-P. Mao, A. V. Marenich, T. Markovich, S. Mason, S. A. Maurer, P. F. McLaughlin, M. F. S. J. Menger, J.-M. Mewes, S. A. Mewes, P. Morgante, J. W. Mullinax, K. J. Oosterbaan, G. Paran, A. C. Paul, S. K. Paul, F. Pavošević, Z. Pei, S. Prager, E. I. Proynov, Á. Rák, E. Ramos-Cordoba, B. Rana, A. E. Rask, A. Rettig, R. M. Richard, F. Rob, E. Rossomme, T. Scheele, M. Scheurer, M. Schneider, N. Sergueev, S. M. Sharada, W. Skomorowski, D. W. Small, C. J. Stein, Y.-C. Su, E. J. Sundstrom, Z. Tao, J. Thirman, G. J. Tornai, T. Tsuchimochi, N. M. Tubman, S. P. Veccham, O. Vydrov, J. Wenzel, J. Witte, A. Yamada, K. Yao, S. Yeganeh, S. R. Yost, A. Zech, I. Y. Zhang, X. Zhang, Y. Zhang, D. Zuev, A. Aspuru-Guzik, A. T. Bell, N. A. Besley, K. B. Bravaya, B. R. Brooks, D. Casanova, J.-D. Chai, S. Coriani, C. J. Cramer, G. Cserey, A. E. DePrince III, R. A. DiStasio, Jr, A. Dreuw, B. D. Dunietz, T. R. Furlani, W. A. Goddard III, S. Hammes-Schiffer, T. Head-Gordon, W. J. Hehre, C.-P. Hsu, T.-C. Jagau, Y. Jung, A. Klamt, J. Kong, D. S. Lambrecht, W. Liang, N. J. Mayhall, C. W. McCurdy, J. B. Neaton, C. Ochsenfeld, J. A. Parkhill, R. Peverati, V. A. Rassolov, Y. Shao, L. V. Slipchenko, T. Stauch, R. P. Steele, J. E. Subotnik, A. J. W. Thom, A. Tkatchenko, D. G. Truhlar, T. Van Voorhis, T. A. Wesolowski, K. B. Whaley, H. L. Woodcock III, P. M. Zimmerman, S. Faraji, P. M. W. Gill, M. Head-Gordon, J. M. Herbert and A. I. Krylov, J. Chem. Phys., 2021, 155, 084801 CrossRef CAS PubMed.
- D. A. Matthews, L. Cheng, M. E. Harding, F. Lipparini, S. Stopkowicz, T.-C. Jagau, P. G. Szalay, J. Gauss and J. F. Stanton, J. Chem. Phys., 2020, 152, 214108 CrossRef CAS PubMed.
- V. K. Voora and K. D. Jordan, J. Phys. Chem. A, 2014, 118, 7201–7205 CrossRef CAS PubMed.
- V. K. Voora, L. S. Cederbaum and K. D. Jordan, J. Phys. Chem. Lett., 2013, 4, 849–853 CrossRef CAS PubMed.
- A. Modelli and P. D. Burrow, J. Phys. Chem. A, 2004, 108, 5721–5726 CrossRef CAS.
- E. M. de Oliveira, M. A. P. Lima, M. H. F. Bettega, S. d’A. Sanchez, R. F. da Costa and M. T. do N. Varella, J. Chem. Phys., 2010, 132, 204301 CrossRef PubMed.
- S. A. Pshenichnyuk, I. I. Fabrikant, A. Modelli, S. Ptasińska and A. S. Komolov, Phys. Rev. A, 2019, 100, 012708 CrossRef CAS.
- K. Chatterjee, Z. Koczor-Benda, X. Feng, A. I. Krylov and T.-C. Jagau, J. Chem. Theory Comput., 2023, 19, 5821–5834 CrossRef CAS PubMed.
- Z. Benda and T.-C. Jagau, J. Chem. Phys., 2017, 146, 031101 CrossRef PubMed.
- Z. Benda, K. Rickmeyer and T.-C. Jagau, J. Chem. Theory Comput., 2018, 14, 3468–3478 CrossRef CAS PubMed.
- Z. Benda and T.-C. Jagau, J. Chem. Theory Comput., 2018, 14, 4216–4223 CrossRef CAS PubMed.
- T.-C. Jagau and A. I. Krylov, J. Phys. Chem. Lett., 2014, 5, 3078–3085 CrossRef CAS PubMed.
| This journal is © the Owner Societies 2024 |