Open Access Article
Open Access ArticleCreative Commons Attribution 3.0 Unported Licence
Dispersion, ionic bonding and vibrational shifts in phospho-aluminosilicate glasses†
Thilo
Grammes
 a,
Dominique
de Ligny
a,
Dominique
de Ligny
 b,
Dintu
Mathew
a,
Kristin
Griebenow
a,
Franziska
Scheffler
a,
Florian
Lindner
c,
Claudia
Aichele
c,
Jan
Dellith
c,
Leo
van Wüllen
d,
Efstratios I.
Kamitsos
b,
Dintu
Mathew
a,
Kristin
Griebenow
a,
Franziska
Scheffler
a,
Florian
Lindner
c,
Claudia
Aichele
c,
Jan
Dellith
c,
Leo
van Wüllen
d,
Efstratios I.
Kamitsos
 *e and
Delia S.
Brauer
*e and
Delia S.
Brauer
 *a
*a
aOtto Schott Institute of Materials Research, Friedrich Schiller University Jena, Lessingstr. 12 (AWZ), 07743 Jena, Germany. E-mail: delia.brauer@uni-jena.de
bInstitute of Glass and Ceramics, Department of Materials Science and Engineering, Friedrich Alexander University Erlangen Nuremberg, Martensstr. 5, 91058 Erlangen, Germany
cLeibniz Institute of Photonic Technology, Albert-Einstein-Straße 9, 07745 Jena, Germany
dInstitute of Physics, Augsburg University, Universitätsstr. 1, 86159 Augsburg, Germany
eTheoretical and Physical Chemistry Institute, National Hellenic Research Foundation, 48 Vassileos Constantinou Avenue, 11635 Athens, Greece. E-mail: eikam@eie.gr
First published on 17th April 2024
Abstract
Understanding the relationships between structure and properties of aluminosilicate glasses is of interest in magmatic studies as well as for glass applications as mechanical or optical components. Glass properties may be tailored by the incorporation of additional elements, and here we studied the effect of phosphate incorporation on refractive index and the degree of ionic bonding in aluminosilicate glasses. The studied glasses in the system SiO2–Al2O3–Na2O–P2O5 had a metaluminous composition (Al:Na = 1) with the content of SiO2 ranging from 50 to 70 mol% and of P2O5 from 0 to 7.5 mol%. Refractive index was measured at four wavelengths from visible to near-infrared and found to decrease both with increasing P2O5 content (at the expense of NaAlO2) and with increasing SiO2 content (by substitution of SiO4 for AlO4 groups). This trend correlated with a decrease in density while, additionally, the formation of Al–O–P bonds with an SiO2-like structure may account for this change. The degree of ionic bonding, assessed via optical basicity and oxygen polarisability, decreased with increasing P2O5 and SiO2 content. Despite the complexity of the studied glasses, oxygen polarisability and optical basicity were found to follow Duffy's empirical equation for simple oxide glasses. In the high frequency infrared and Raman spectra, band shifts were observed with increasing P2O5 and SiO2 content. They indicated changing average bond strength of the glass network and showed a linear correlation with optical basicity.
1 Introduction
Understanding the structure of aluminosilicate glasses is of great importance both in geological sciences and materials science. Magmas are melts of aluminosilicate composition,1–6 and aluminosilicate glasses are used in a variety of applications such as reinforcement fibres in composites,7–10 the entrapment of radioactive waste,11,12 as optical components such as photonic waveguides and optical amplifiers13,14 and as host media for high power lasers.15,16 A detailed knowledge of the structure–property relationships in such glasses is key to tailoring mechanical and optical properties. The addition of new components, such as phosphate, enables manipulation of glass structure and properties.The presence of P2O5 as a third network former besides SiO2 and Al2O3 is known to inhibit crystallisation of aluminosilicate melts, an observation that has been explained by the formation of Al–O–P bonds.17 In previous studies, we found the presence of phosphate to reduce glass transition temperature and elastic moduli, owing to decreases in polymerisation and packing density.18,19 Additionally, our previous structural analysis by Raman and NMR spectroscopy supports the presence of Al–O–P bonds.19,20 In the literature, the formation of these bonds has been correlated with a change in refractive index in high-silica (>77 mol% SiO2) SiO2–Al2O3–P2O5 glasses.21 The relationship between phosphate content and refractive index in lower silica content sodium aluminosilicate glasses still requires investigation.
Phosphate associates not only with aluminate but also with alkali cations,22–28 iron29 and rare elements.30,31 The interaction of phosphate with metal cations not only is of geological interest for the identification of deposits, but it also affects the structure of phosphate-containing aluminosilicate glasses. We have recently identified a competition between aluminate and phosphate groups for charge-balancing sodium in such glasses,19 and such ionic interactions we are now investigating further by studying the degree of ionic bonding. The overall bonding in multi-component oxide glasses reflects a mixture of covalent and ionic interactions. While the average degree of ionic bonding in some glasses is higher, or more ionic, e.g. in glasses involving fluorides,32 other glasses, such as vitreous silica,33 show a lower average degree of ionic bonding, meaning the average bonding is more covalent. The average degree of ionic bonding therefore provides an additional means for interpreting the structure–property relationships in glasses.
For this study, phosphate-containing sodium aluminosilicate glasses of metaluminous composition (Al:Na = 1) in the system SiO2–Al2O3–Na2O–P2O5 were investigated, with SiO2 contents ranging from 50 to 70 mol% and P2O5 contents up to 7.5 mol%, including phosphate-free reference glasses. The refractive index was measured and the degree of ionic bonding was assessed by determining the optical basicity as well as oxygen polarisability. In addition, we investigated the relationship between the degree of ionic bonding and the average bond strength in these glasses, as manifested by their high frequency infrared and Raman band shifts.
2 Experimental
2.1 Glass design and synthesis
Three series of melt-derived metaluminous (Al:Na = 1) aluminosilicate glasses (SiO2–Al2O3–Na2O–P2O5, Table 1) were prepared as described previously.18 In Series i, the silica content was kept constant and P2O5 substituted for NaAlO2, while in Series ii and iii, the silica content was increased (by substituting SiO4 tetrahedra for Na+[AlO4]−) while the phosphate content was kept fixed at 0 or 7.5 mol% P2O5, respectively. As an EDX compositional analysis revealed no critical deviation from nominal values,18 all calculations here are based on nominal composition. For further analysis, samples were cut and polished to optical grade.| Series | Glass | SiO2 | P2O5 | Al2O3 | Na2O |
|---|---|---|---|---|---|
| i | Si60P0 | 60 | — | 20 | 20 |
| Si60P2.5 | 60 | 2.5 | 18.75 | 18.75 | |
| Si60P5 | 60 | 5 | 17.5 | 17.5 | |
| Si60P6.25 | 60 | 6.25 | 16.875 | 16.875 | |
| Si60P7.5 | 60 | 7.5 | 16.25 | 16.25 | |
| ii | Si50P0 | 50 | — | 25 | 25 |
| Si60P0 | 60 | — | 20 | 20 | |
| Si70P0 | 70 | — | 15 | 15 | |
| iii | Si50P7.5 | 50 | 7.5 | 21.25 | 21.25 |
| Si55.5P7.5 | 55.5 | 7.5 | 18.5 | 18.5 | |
| Si60P7.5 | 60 | 7.5 | 16.25 | 16.25 | |
| Si70P7.5 | 70 | 7.5 | 11.25 | 11.25 |
For analysis of optical basicity, glasses Si60P0, Si60P5 and Si60P7.5 were doped with lead ions.34 80 g batches of glasses were prepared. For this purpose, high purity powders (Fe content <10 ppm) of aluminium hydroxide, quartz, sodium carbonate and ammonium hydrogen phosphate (NH4H2PO4) were mixed by stirring with a spoon and then by shaking for five minutes after placing an alumina ball inside the batch. Then, Pb2+ was introduced into the batch as PbCO3 (about 100 ppm) by first mixing the lead carbonate with one spoonful of the batch, and afterwards adding another spoonful of the batch and mixing again. This process was repeated until the entire batch was added and mixed with lead carbonate.
Subsequently, the batches were placed into alumina crucibles and heated from room temperature first to 1000 °C at a heating rate of 5 K min−1 in a high-temperature electrical furnace (HTK 16/17 FL, Thermconcept, Bremen, Germany) and kept at this temperature for one hour to allow for evaporation of gases from the mixtures. In a second step, the batch was heated to 1650 °C at 5 K min−1 and held at this temperature (3 hours for Si60P0_Pb and Si60P5_Pb and overnight, about 7 to 10 hours, for Si60P7.5_Pb). After quenching in air for a minute, the crucibles containing the glass melts were moved to an annealing furnace heated to Tg + 20 K, held there for three hours and allowed to cool to room temperature inside the furnace afterwards. Since casting of the melts was not possible owing to their high viscosity, glass samples were retrieved by breaking off the alumina crucible walls. For UV-vis measurements, glass samples were cut into small square pieces (about 1–2 mm in thickness) and polished.
Doped glasses were analysed by wavelength-dispersive X-ray spectrometry (WDX) using a microprobe analyser (JXA-8800 L, JEOL, Tokyo, Japan). Samples were coated with a thin carbon layer of approximately 10 nm to avoid charging effects. As sodium ion diffusion is a known issue, the electron beam was defocused to a diameter of 100 μm (to lower the dose and consequently the sample stress) and the stability of the generated Na-Kα intensity checked for a given time. The analyses were performed as fully quantitative (standard-related) measurements on four different positions along a line on the samples. Reference materials used for the analysis were sodium chloride (for Na), sapphire (for Al), gallium phosphide, GaP (for P) and SiO2 (for Si). The accumulation time was 60 s for the characteristic peaks of each element and 2 × 30 s to measure the corresponding background radiation. The energy of the exciting electrons was 10 keV and the beam current was 200 nA. Analysed compositions are shown in Table 3.
Lead contents were analysed by digesting about 100 mg of glass powder with a mixture of 2 mL of 65% nitric acid, 3 mL of 40% hydrofluoric acid and 3 mL of 70% per chloric acid in TFM-modified PTFE containers in a pressure digestion system (DAS, PicoTrace, Bovenden, Germany). Samples were heated to 180 °C over 6 hours, held at that temperature for 12 hours and cooled down. Acids were removed by heating to 180 °C over four to five hours in a special evaporating hood and holding that temperature for 14 hours. After cooling to room temperature, solids were dissolved in a mixture of 2 mL nitric acid, 0.6 mL hydrochloric acid and 7 mL of pure water at 150 °C over eight hours. After cooling to room temperature, samples were transferred to 25 mL volumetric flasks, filled to 25 mL with pure water and analysed using inductively coupled plasma mass spectroscopy (ICP-MS). Analyses were performed in triplicate.
2.2 Refractive index and dispersion
The refractive index was measured at 480, 546.1, 632.8 and 1300 nm to cover the range from the visible to the NIR regime. For refractive index determination at 632.8 and 1300 nm, a prism coupler (2010/M Prism Coupler, Metricon, Pennington, USA) was used with lasers of the respective wavelengths. Presented refractive indices at 632.8 and 1300 nm are arithmetic mean values from three to four measurements at different spots on the samples; errors are given as standard deviations (Table 2). The indices at 480 and 546.1 nm were measured by Pulfrich refractometry (PR2, VEB Carl Zeiss, Jena, Germany) with an experimental uncertainty of ±0.001, using a cadmium lamp for 480 nm (F′ line) and a mercury lamp for 546.1 nm (e line).| Series | Glass | n 480 | n 546.1 | n 632.8 | n 1300 |
|---|---|---|---|---|---|
| Series i (Pb) | Si60P0 | 1.5109 ± 0.0005 | 1.5066 ± 0.0005 | 1.5036 ± 0.0001 | 1.4925 ± 0.0008 |
| (1.504 ± 0.001) | (1.492 ± 0.001) | ||||
| Si60P2.5 | 1.5048 ± 0.0005 | 1.5007 ± 0.0005 | 1.4967 ± 0.0005 | 1.4857 ± 0.0001 | |
| Si60P5 | 1.4985 ± 0.0003 | 1.4944 ± 0.0003 | 1.4913 ± 0.0001 | 1.4810 ± 0.0004 | |
| (1.493 ± 0.002) | (1.483 ± 0.001) | ||||
| Si60P6.25 | 1.4954 ± 0.0005 | 1.4912 ± 0.0005 | 1.4884 ± 0.0002 | 1.4780 ± 0.0003 | |
| Si60P7.5 | 1.4924 ± 0.0005 | 1.4885 ± 0.0005 | 1.4864 ± 0.0007 | 1.4756 ± 0.0006 | |
| (1.489 ± 0.003) | (1.480 ± 0.004) | ||||
| Series ii | Si50P0 | 1.5212 ± 0.0005 | 1.5166 ± 0.0005 | 1.5130 ± 0.0001 | 1.5012 ± 0.0002 |
| Si60P0 | 1.5109 ± 0.0005 | 1.5066 ± 0.0005 | 1.5036 ± 0.0001 | 1.4925 ± 0.0008 | |
| Si70P0 | 1.5007 ± 0.0005 | 1.4966 ± 0.0005 | 1.4944 ± 0.0001 | 1.4836 ± 0.0001 | |
| Series iii | Si50P7.5 | 1.5018 ± 0.0003 | 1.4976 ± 0.0003 | 1.4953 ± 0.0008 | 1.4842 ± 0.0011 |
| Si55.5P7.5 | 1.4966 ± 0.0005 | 1.4926 ± 0.0005 | 1.4898 ± 0.0002 | 1.4792 ± 0.0001 | |
| Si60P7.5 | 1.4924 ± 0.0005 | 1.4885 ± 0.0005 | 1.4864 ± 0.0007 | 1.4756 ± 0.0006 | |
| Si70P7.5 | 1.4824 ± 0.0010 | 1.4788 ± 0.0010 | 1.4773 ± 0.0020 | 1.4663 ± 0.0013 |
The dispersion of the glasses was determined by fitting the refractive index data over the four wavelengths with a two-term Sellmeier approximation.35
 | (1) |
 | (2) |
2.3 Optical basicity and oxygen polarisability
To measure the optical basicity, Pb2+ was incorporated into the glasses as probe ions. Experimental optical basicity was then assessed via UV-visible absorption spectroscopy by measuring the Pb2+ absorption in the UV region due to the 1S0 → 3P1 transition. Discs of Pb2+ doped glass samples were analysed in the range of 200 to 800 nm using a double beam spectrophotometer (Cary 5000 UV-Vis-NIR spectrophotometer, Agilent, Waldbronn, Germany). Measurements were performed at room temperature with two light sources: deuterium lamp (for UV) and halogen bulb (for VIS). Experimental optical basicity (Λexp) was calculated using the equation given below:
 | (3) |
![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 700 cm−1), vglass is the frequency of Pb2+ ions measured in the glass, and νCaO is the Pb2+ ion frequency in calcium oxide (29
700 cm−1), vglass is the frequency of Pb2+ ions measured in the glass, and νCaO is the Pb2+ ion frequency in calcium oxide (29![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 700 cm−1).34
700 cm−1).34
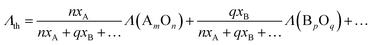 | (4) |
We complemented the optical basicity with another measure of the degree of ionic bonding, which was derived from experimental data: the (partial molar) oxygen polarisability, αO2−. A high oxygen polarisability indicates large electron density around the oxygen, which is then closer to being an O2− anion, i.e. the glass has a higher degree of ionic bonding. To derive αO2−, one first needs to calculate the molar electronic polarisability, αm, from measured values of refractive index and density. This was done using the Lorentz–Lorenz relationship.37
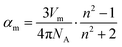 | (5) |
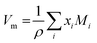 . The molar electronic polarisability represents a sum of the partial molar polarisabilities of all constituent ions, weighted with respect to their respective molar fractions, Fi37
. The molar electronic polarisability represents a sum of the partial molar polarisabilities of all constituent ions, weighted with respect to their respective molar fractions, Fi37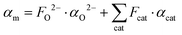 | (6) |
2.4 Vibrational spectroscopy
The high frequency Raman spectra were deconvoluted to investigate band shifts. Prior to deconvolution, spectra were normalised to the maximum of the high frequency envelope. The number of deconvoluted bands (three for phosphate-free glasses, five for phosphate-containing glasses) was chosen to match the number of bands identified by parallel-polarised and cross-polarised Raman spectra published previously.19 Fitting of Gaussian bands was carried out with the Levenberg–Marquardt algorithm implemented in the software package Origin (OriginLab, Northampton, USA). Except for manually choosing starting position and amplitude, no further constraints were applied to the Gaussian fitting parameters. Output band positions were evaluated; error bars show standard errors.
3 Results and discussion
3.1 Refractive index
The dependency of refractive index (Table 2) on wavelength, i.e. the dispersion, was similar for all studied glasses and showed the typical non-linear increase of refractive index towards shorter wavelengths (exemplified in Fig. 1 for the series with increasing P2O5 content; for other series refer to Fig. S1, ESI†). The dispersion relation between 480 and 1300 nm was determined for all glasses using a two-term Sellmeier approximation (eqn (3), dashed lines in Fig. 1 and Fig. S1, ESI†), which yielded good fits of the data (R2 > 0.98) for all glasses, see Table S1 (ESI†).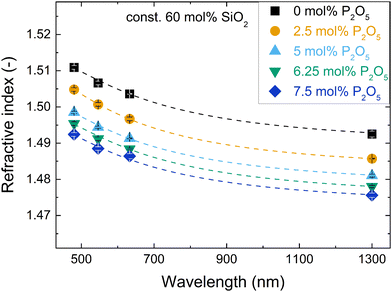 | ||
| Fig. 1 Changes in refractive index with wavelength for the glass series with increasing P2O5 content and constant 60 mol% SiO2. Dashed lines are fits with a two-term Sellmeier approximation (details in ESI†). | ||
In the literature, the only comparable glass compositions with reported refractive index are phosphate-free metaluminous aluminosilicate glasses (indicated by + and × in Fig. 2b).42–44 Their reported refractive indices are in good agreement with the present study.
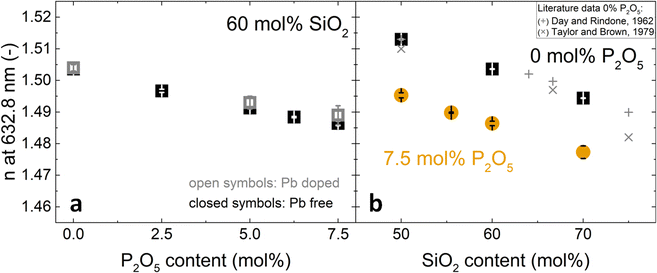 | ||
| Fig. 2 Changes in refractive index at 632.8 nm with (a) increasing P2O5 content and constant 60 mol% SiO2 and (b) increasing SiO2 content and constant P2O5 contents of 0 mol% (black squares) or 7.5 mol% (orange circles). Literature values (+, ×) for 0 mol% P2O5 glasses are shown for comparison: (+),42 (×).43,44 In (a), closed symbols refer to Pb-free glasses and open symbols to Pb-doped glasses. | ||
The compositional trends of the refractive index were similar for all tested wavelengths, shifting the dispersion curves in a uniform fashion. The trends are exemplarily shown for 632.8 nm in Fig. 2. The refractive index decreased both with increasing phosphate content (substitution of P2O5 for NaAlO2, Fig. 2a) and with increasing silica content (substitution of SiO4 for Na+[AlO4]− tetrahedra, Fig. 2b). This decrease matched with a simultaneous decrease in packing density that was published elsewhere.18 A decrease in packing density can be expected to cause a decrease in the average electron density of the glasses; this will subsequently affect the refractive index, since refraction is based on the interaction of light with the electrons of matter.45 In compositional terms, the decrease of refractive index with increasing silica content (Fig. 2b) may be explained by it approaching the lower refractive index value of vitreous silica, which for the studied wavelengths ranges from 1.44 to 1.46.46 As these metaluminous glasses by design share a near-fully polymerised network structure with vitreous silica, the increasing silica content simply implies replacing SiO4 for Na+[AlO4]− tetrahedra with no major structural changes disturbing the refractive index trend. This is supported by earlier findings on these glasses by solid-state NMR, showing that the network forming elements silicon, phosphorus and aluminium all maintain a fourfold coordination.20,47 For aluminium we confirmed this by X-ray absorption spectroscopy.19
A composition-based explanation for the decreasing refractive index upon increasing phosphate content (Fig. 1 and 2a) may be found in a study by DiGiovanni et al. who investigated the refractive index of glasses in the system SiO2–Al2O3–P2O5.21 For constant silica content and Al/P ratio approaching unity, their refractive indices decreased to values approaching that of vitreous silica. These conditions match the compositional trend of Fig. 2a, i.e. Al/P ratio slowly approaching unity, despite the lack of sodium in their glasses. DiGiovanni et al. have ascribed the decreasing refractive index to the formation of Al–O–P bonds,21 with the resulting AlPO4 units having the same structure as SiO2, and thus similar refractive properties. Such Al–O–P bonds were also found for the glasses studied here by means of solid-state NMR20 and Raman spectroscopy.19 The NMR analysis on these glasses revealed that with increasing phosphate content the relative amount of fully polymerised phosphate groups similar to those in AlPO4 increased with regard to depolymerised phosphate groups.20 Advanced solid-state NMR approaches by 27Al{31P}-REDOR and 31P{27Al}-REAPDOR NMR indicated that in average each aluminate tetrahedron is connected to at least one phosphate tetrahedron and each phosphate tetrahedron to 2.5 aluminate tetrahedra.20 There is no phase separation to be expected either, as 29Si{27Al}-REAPDOR NMR indicated an average of 2.5 Al neighbours for each Si. We therefore conclude that the presence of Al–O–P bonds with a structure similar to SiO2 explains the decreasing refractive index upon increasing phosphate content.
A question remaining is whether metaphosphate groups (QP2; where in the notation QTi the T marks the element at the centre of a tetrahedral group and i is the number of bridging oxygen bonds of this group) which are not bound to aluminium may have a major contribution to the decreasing refractive index upon increasing phosphate content. The refractive index of pure sodium metaphosphate glass (NaPO3) at 546.1 nm is 1.4859,48 just below the value measured for glass Si60P7.5 (1.4885). Given the much lower phosphate content in glass Si60P7.5, the contribution of metaphosphate groups to the overall refractive index decrease is therefore assumed to be small compared to the Al–O–P contribution.
Looking again at the dispersion curves from a wider structural viewpoint (Fig. 1 and Fig. S1, ESI†), it is interesting to note that their shift to lower refractive indices is linked to a change in distance between the UV and IR absorption edges.35 The IR absorption edge corresponds to the highest frequency of the infrared absorption bands. As will be discussed later, these infrared absorption bands shift to higher frequency with increasing P2O5 and SiO2 contents, thus slightly reducing the gap between IR and UV absorption edge. The simultaneous dispersion shift to lower refractive indices therefore correlates with the vibrational shifts discussed later on.
3.2 Optical basicity and oxygen polarisability
The measured Pb2+ absorption band, due to the 1S0 → 3P1 electronic transition, is shown in Fig. 3 for the three Pb2+-doped glasses of Series i. An increase in the phosphate content caused the shift of this band maximum (vglass in eqn (3)) to higher frequencies (Fig. 3). This leads to lower values of the experimental optical basicity (Λexp) as shown in Fig. 4a, and listed also in Table S2 (ESI†). The measurement of optical basicity by UV-vis spectroscopy is cumbersome since it requires additional preparation of lead-doped glasses. Here, this was only done for three glass compositions (0, 5 and 7.5 mol% SiO2). The analysed compositions are shown in Table 3. Similar lead concentrations have been obtained for all three compositions. The concentrations of the other components are in agreement with an earlier compositional analysis on the lead-free glasses.18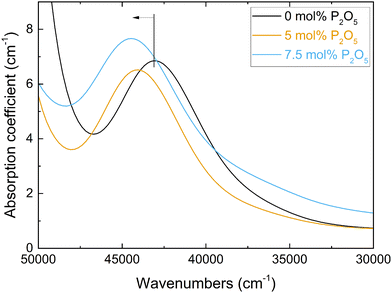 | ||
| Fig. 3 Spectra of the UV-vis absorption coefficient for the three Pb-doped glasses with 0 to 7.5 mol% P2O5 (Series i, Table S2, ESI†). The blue shift of the Pb2+ 1S0 → 3P1 absorption band with increasing P2O5 content, and thus changing optical basicity, is indicated. | ||
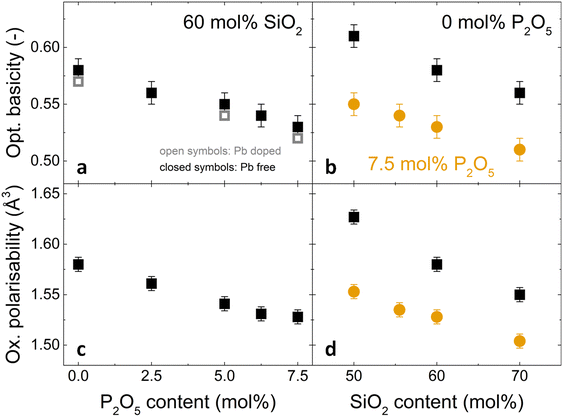 | ||
| Fig. 4 Changes in (a,b) optical basicity and (c,d) oxygen polarisability with (a,c) increasing P2O5 content and constant 60 mol% SiO2 and (b,d) increasing SiO2 content and constant P2O5 contents of 0 mol% (black squares) or 7.5 mol% (orange circles). In (a), closed symbols refer to Pb-free glasses (Λtheor calculated from eqn (4)) and open symbols to Pb-doped glasses (experimental values, Λexp). | ||
| Glass | SiO2 | P2O5 | Al2O3 | Na2O | Pb |
|---|---|---|---|---|---|
| Si60P0_Pb | 60.8 ± 0.1 | 0.0054 ± 0.007 | 20.9 ± 0.4 | 18.3 ± 0.6 | 58.8 ± 6.1 |
| Si60P5_Pb | 62.7 ± 1.1 | 5.1 ± 1.0 | 16.6 ± 0.9 | 15.6 ± 0.4 | 63.4 ± 5.9 |
| Si60P7.5_Pb | 57.5 ± 2.6 | 6.5 ± 1.5 | 19.8 ± 2.0 | 16.1 ± 0.7 | 61.6 ± 5.9 |
The measured basicities can be compared to calculated optical basicity which bears the underlying assumption of additivity of the basicities of the simple oxide components. The measured optical basicity values are systematically slightly lower than the calculated ones but within the error bar. The good agreement with the theoretical value is here confirmed.
At this point one should remark that theoretical and measured optical basicity are not necessarily identical. The theoretical optical basicity represents an average value calculated from the glass composition, whereas the UV-vis measurement probes the electronic state of Pb2+ ions which are only available in trace amounts and which do not necessarily track all available oxygen configurations. Looking at size and charge first, Pb2+ ions have an ionic radius and field strength comparable to that of alkaline earth elements.49,50 They might therefore occupy sites different from the modifier Na+ used in the present glasses. Indeed, Pb2+ ions have been found earlier to exhibit bonding preferences or create new sites of their own,51 as was confirmed in alkali borate glasses.52 In mixed fluoride-phosphate glasses, Pb2+ probe ions were indicating higher than average optical basicity, caused by preferential association with highly depolymerised phosphate groups.40 In borosilicate glasses that were investigated for optical basicity by using Mn2+ probe ions, the Mn2+ was found to prefer borate sites over silicate sites.53 As pointed out by Möncke et al.,54 the probe ions show a bonding preference to groups with more non-bridging oxygen, i.e. sites with a higher local optical basicity. Using the definition of group basicity by Duffy and Ingram,34 the calculated group basicities for the network forming tetrahedral groups are Λ(QAl4) = 0.70, Λ(QSi4) = 0.48, Λ(QP4) = 0.25 and Λ(QP2) = 0.50. Based on that, one may expect a preference of Pb2+ for depolymerised QP2 groups over fully polymerised QP4 groups, yet the more abundant groups QSi4 and QAl4 offer local basicities that are comparable or even higher. Silicate and aluminate groups were found earlier to be evenly distributed within the present glasses.20 Given this, Pb2+ ions may also be expected to probe multiple of the glasses’ potential sites. This is supported by the good agreement between measured and calculated optical basicity. The slightly lower measured values might rather indicate some preference of Pb2+ for phosphate over silicate or aluminate, but the deviation from calculated basicities is within error. As shown further below, the oxygen polarisability, based on experimental values for density and refractive index, also agrees well with the calculated optical basicity values. The coefficients used provided a good approximation in this extrapolated chemical composition domain. The calculated optical basicities are therefore considered reliable.
Optical basicity and oxygen polarisability decreased with increasing phosphate content (Fig. 4a, c and Table S2, ESI†) as well as with increasing silica content (Fig. 4b and d). This decrease corresponds to a shift in average chemical bonding character from ionic to covalent. For increasing silica content, this increasing covalency is caused by the substitution of SiO4 for Na+[AlO4]− tetrahedra. An increase in P2O5 content by 7.5 mol% resulted in a comparable decrease in optical basicity as an increase in silica content by about 20 mol% (Fig. 4a and b). This cannot be explained by a replacement of Al3+ and Na+ ions by P2O5 alone, and an additional factor may be the strong Lewis acid character of P5+ cations. As strong electron acceptors, they withdraw electron density from the surrounding bridging oxygen atoms. Since the charge density available to oxide anions in glasses is variable depending on the degree of ionic bonding, an oxide anion bonded to a highly positively charged cation like P5+ will have an effective charge that differs from the ideal ionic case of −2. The bridging oxygen bond involving such an oxygen anion is therefore more covalent.55
Oxygen polarisability and optical basicity are two different means of probing the average degree of ionic bonding, and Duffy, one of the creators of the optical basicity concept,34,37–39,56 found an empirical, nonlinear relationship between the two properties:57
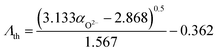 | (7) |
This relationship was first shown to exist for binary calcium silicate glasses57 and later for more oxide glass systems,58,59 including simple aluminosilicate glasses,60 but it is not valid for all glass systems. Especially when oxygen is no longer the only present anionic species, e.g. in oxyfluoride or oxynitride glasses, more elaborated relationships between optical basicity and oxygen polarisability have to be applied.40,54 For the glasses reported here, however, the relationship matches well as shown in Fig. 5. The deviation from eqn (7) (green dash-dotted line in Fig. 5) is minor and can only be seen under magnification (inset of Fig. 5). This adherence to eqn (7), despite the phospho-aluminosilicate glasses’ complexity in composition and structure when compared to simple (alumino-)silicate glasses, reflects the all-oxidic nature of the studied glasses. With the validity of eqn (7) and with the good agreement between the measured and calculated optical basicities (Fig. 4), we are confident that the calculated theoretical optical basicities represent a valid measure of the average degree of ionic bonding, on which we will build when interpreting vibrational shifts further below.
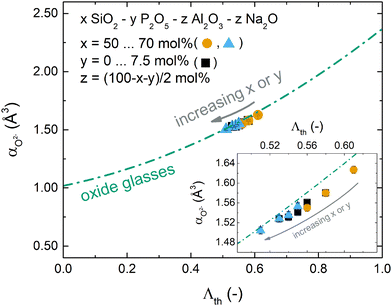 | ||
| Fig. 5 Relationship between oxygen polarisability and optical basicity for the studied glasses. Compositional changes are indicated by the grey arrow. The green dash-dotted line represents eqn (7) as reported by Duffy57 for simple oxide glasses. The inset shows a magnification of the studied compositional range. (Black squares: increasing P2O5 content and const. 60 mol% SiO2; orange circles: increasing SiO2 content and const. 0 mol% P2O5; blue triangles: increasing SiO2 content and const. 7.5 mol% P2O5.) | ||
3.3 Vibrational spectroscopy
The shift of the individual bands was further investigated by deconvolution of the Raman spectra (Fig. S3 and S4 (ESI†) and Fig. 6). The three bands used for deconvolution of phosphate-free glasses were interpreted as the T2s, QSi/Al4,low and QSi/Al4,high modes (Fig. S3, ESI†). Here the notation QSi/Al4,high and QSi/Al4,low indicates stretching of QSi/Al4 units with larger and smaller intertetrahedral angles, respectively, while T2s corresponds to the stretching of Q4 units where two oxygens move toward the tetrahedral centre and the other two move away from it, regardless of their intertetrahedral angle.19 The two additional bands used for deconvolution of phosphate-containing glasses were assigned to the symmetric and asymmetric stretching of QP2 units, νs(QP2) and νas(QP2), respectively (Fig. S4, ESI†). All deconvolutions showed a good agreement between experimental data and fitted models. The residuals remained low, below 3% of the maximum spectral intensity. They were more random for the phosphate-containing glasses than for the phosphate-free ones. This is probably caused by their larger number of fitted bands. The largest non-randomness of the residual was found for glass Si50P0, and it is probably caused by luminescence observed for this glass.
The deconvolution of the phosphate-free glasses is in agreement with earlier studies,1,61–63 including similarly low residuals and a similar remaining non-randomness of the residuals. With increasing P2O5 content, the three aluminosilicate bands gradually decreased in intensity while the phosphate bands, especially νs(QP2), increased in intensity in line with the incorporation of the new component. All deconvoluted bands were found to shift to higher wavenumbers with increasing SiO2 and P2O5 content (Fig. 6). However, the positions of the fitted and the experimental band only agreed for the maximum band of each individual spectrum, even though positions of all bands were known experimentally from cross-polarisation Raman spectra.19 As the remaining bands were hidden in the unpolarised spectra used for deconvolution, the fitting process converged to different positions because no constraints were applied on the position parameter of the fits. Considering these uncertainties, no further analysis of relative band areas will be attempted here. The results of the deconvolution shown in Fig. 6 are consistent with the observation that the high frequency Raman envelopes shift to higher wavenumbers with increasing SiO2 and P2O5 content.
In the literature, such a shift of the high frequency vibrational bands of phosphate-free metaluminous aluminosilicate glasses and crystals has been related to a change in Al/Si ratio.1,62,64,65 As Al–O bonds are weaker than Si–O bonds,42,66,67 the average bond strength within the glasses increases with increasing SiO2 content. The continuity of the shift has been taken as evidence of random mixing between Al and Si units, and this argument has been supported by X-ray scattering experiments.43 However, in the phosphate-containing glasses studied here, a change in Al/Si ratio may not be the only reason for shifting bands, as an increase in P2O5 content may also affect the shifts, owing to P–O bonds being even stronger than Si–O or Al–O bonds.25,68,69 Shifts of phosphate-related bands do indicate changes in P–O bond strength caused by interaction with neighbouring groups.68 Here, the shift of phosphate-related Raman bands with SiO2 content (i.e. Al/Si ratio) at constant P2O5 content (e.g. main band in Fig. S2f, ESI†) suggests that phosphate groups are linked to the aluminosilicate network and are, thus, affected by changes of vibrational frequency within the aluminosilicate network. This is supported by our solid-state NMR and vibrational analyses published earlier where we found Al–O–P bond formation.19,20 The weak shift of the phosphate-related Raman maximum in Fig. S2b (ESI†) may also be caused by changes in P2O5 content.
Note that not all bands shifted equally. For example, the phosphate-related main band shifted much less (about 25 cm−1; Fig. S2f, ESI†) with SiO2 content than the aluminosilicate-related main band (about 80 cm−1; Fig. S2d, ESI†). Such a pronounced difference is likely to have additional reasons besides small variations in Al/Si ratio between phosphate-containing and phosphate-free glasses. Presumably, owing to the reduced connectivity of QP2 units to the network, frequency shifts of neighbouring aluminosilicate units may have less influence on the vibrational frequency of the phosphate band. In addition, a previous depolarisation Raman analysis of these glasses indicated a preference of phosphate to bind to aluminate groups situated in smaller rings of the glass network structure.19 Structural changes in the larger rings may therefore have less effect on the shifting of phosphate bands.
Even in phosphate-free glasses not all bands shifted equally. The Raman high frequency maximum (shift of about 80 cm−1; Fig. S2d, ESI†) was affected much more by Al/Si ratio than the IR maximum (shift of about 40 cm−1; Fig. S2c, ESI†). As the Raman high-frequency envelope corresponds mainly to symmetric stretching vibrations and the IR envelope to asymmetric ones, symmetric stretching vibrations seem to have been more affected by changes in Al/Si ratio than the asymmetric ones. It is possible that not all vibrational modes equally reflect the bonding between the different network formers. Cicconi et al.61 suggested that aluminate tetrahedra in sodium aluminosilicate glasses rather have a more pronounced tendency to turn into QAl4,low units (smaller inter-tetrahedral bond angle) than QAl4,high units. Their Raman analysis was supported by previous molecular orbital calculations and X-ray scattering experiments,70 and showed that an increase in aluminium content in a metaluminous system decreases the average inter-tetrahedral bond angle. While the Raman band maximum (Fig. S2d, ESI†) corresponds to QSi/Al4,low units, the IR band maximum (Fig. S2c, ESI†) corresponds to a different vibration. This may explain why the IR maximum shifted less with Al/Si ratio.
| ωeff = (fHωH2 + fLωL2)1/2 | (8) |
| ωeff = α + βΛth | (9) |
In principle, the above approach could be applied to calculate effective frequencies ωeff for the high frequency IR and Raman envelopes based on the results of fitting with three (Fig. S3, ESI†) or five (Fig. S4, ESI†) component bands. However, consideration of more than two component bands in the fitting process introduces uncertainties in the position ωi and the relative integrated intensity fi of the component bands and, thus, uncertainties in the determination of ωeff since ωeff = (Σfiωi2)1/2, where i = 3 (Fig. S3, ESI†) or 5 (Fig. S4, ESI†). To overcome this problem, we determine here an effective frequency ωeff by calculating the centre of gravity (COG) of the high frequency envelope, after prior subtraction of a linear baseline from the integrated region.
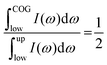 | (10) |
In order to check whether this COG calculation is justified and does not oversimplify the band shift analyses, the COG shift needs to be compared with an independent measure of average bond strength. A simple correlation of the COG shift with Al/Si ratio would neglect contributions by P and Na. In order to take all glass components into account, the theoretical optical basicity Λth was chosen as an alternative measure of average bond strength as was done previously.58,76,78 The relationship of Λth with the degree of ionic bonding in glass allows us to relate it to the measured changes in vibrational frequency. Decreasing optical basicity indicates a higher degree of covalent bonding37 and, since covalent bonds are more directional, the bond strength along the bond axis would increase.79 Therefore, the average bond strength of the glass network should increase with decreasing optical basicity, resulting in higher frequency of the stretching vibration modes in the high frequency IR/Raman spectra. This reasoning is supported by the good correlation between theoretical optical basicity and the high frequency COG (in cm−1) of the IR and Raman spectra for the three glass series studied here (Fig. 7).
| COG = γ − δΛth | (11) |
The trends of IR/Raman COG versus optical basicity of all three glass series studied here appear to form a single straight line (indicated by the dash-dotted lines in Fig. 7), as compared to different COG trends versus composition demonstrated in Fig. S5 (ESI†). Still, several limitations are to be taken into account when assuming a linear correlation between optical basicity and bond stretching vibrational frequency. First, a direct correlation between the changing average bond strength and the shifts of vibrational frequencies may only be true in the absence of network polymerisation changes. The only major depolymerisation here was found for increasing P2O5 content;19 however, depolymerisation would shift the high frequency envelope to lower wavenumbers81–85 rather than to higher wavenumbers as observed here. The increasing average bond strength caused by phosphate incorporation seems to outweigh the influence of depolymerisation on the vibrational frequency. Depolymerisation may, however, be responsible for the deviation of the Raman COG shift from the straight line in Fig. 7b, as expressed by the lower R2 value. Another potential influence may come from the different Raman scattering powers of the three network former species, especially the larger polarisability of the non-bridging oxygen containing metaphosphate species, QP2, as compared to the bridging oxygen containing silicate and aluminate species (QSi/Al4). The scattering power affects Raman band intensities, so that metaphosphate bands have larger relative contribution to COG calculations than contributions from aluminosilicate bands. This, too, may explain why the Raman data (Fig. 7b) showed a lower R2 value (i.e. larger deviation from the straight line) than the IR data (Fig. 7a). The optical basicity may also be influenced by changes in coordination number of the network formers.34,77,86,87 However, here, no coordination changes were detected by solid-state NMR and XANES spectroscopy.19,20
The linear correlation between the high frequency COG over optical basicity for the three glass series studied here requires further investigation especially in simpler binary glass systems such as silicate and phosphate glasses, where network polymerisation and network former coordination are well known. This may provide deeper insights into how the degree of covalent/ionic bonding affects various aspects of glass structure.
4 Conclusions
Here, we have investigated refractive index, degree of ionic bonding and vibrational shifts in metaluminous (Al:Na = 1) phospho-aluminosilicate glasses SiO2–Al2O3–Na2O–P2O5 with SiO2 content between 50 and 70 mol% and P2O5 content varying from 0 to 7.5 mol%. The results indicated changes towards a more covalent bonding character within the glass network with increasing SiO2 or P2O5 contents. Despite the complexity of the studied glass system, the relationship between optical basicity and oxygen polarisability was found to agree well with Duffy's empirical equation established for simple oxide glasses. Vibrational shifts in the high frequency infrared and Raman spectra were interpreted in terms of changing glass composition. Here we observed also that not all component bands shifted equally upon compositional changes. In case of phosphate-related bands this was explained by metaphosphate QP2 groups being less connected to the surrounding network than the QSi/Al4 groups. The averaged shift of the high frequency IR and Raman spectra, obtained by calculating their centre of gravity, showed linear correlation with the theoretical optical basicity. This implies that, in the absence of other factors, the degree of covalent/ionic bonding and the average bond strength in such glasses may be estimated in a simple approach by vibrational spectroscopy. These results highlight that in case of glass and melts, such a simple approach is sufficient to predict many properties. We see clearly that the optical basicity and the internal modes frequencies are linear with the chemical composition. In this last case, the shown correlation of the high frequency vibration is in good agreement with the additivity of heat capacity at high temperature of the glasses and the melts.88Author contributions
DSB, DdL and LvW: conceptualisation; TG, DM, FL, CA and JD: investigation; TG: formal analysis, visualisation, writing – original draft; DSB, EIK, KG, FS: supervision; DSB, DdL, EIK, TG: writing – review & editing.Conflicts of interest
There are no conflicts to declare.Acknowledgements
Financial support by the German Research Foundation (DFG, grant BR 4608/5 within priority programme SPP 1594) is gratefully acknowledged. The authors would like to thank Christian Zeidler and Thomas Kittel (Otto Schott Institute of Materials Research, University of Jena) for refractive index measurements, Dirk Merten (Institute of Geoschiences, University of Jena) for analyses of lead content and Dimitrios Palles (National Hellenic Research Foundation, Athens) for assistance with IR measurements and discussions on data evaluation.References
- C. LeLosq and D. R. Neuville, Chem. Geol., 2013, 346, 57–71 CrossRef.
- S. Matthes, Mineralogie, Springer, 2nd edn, 1987 Search PubMed.
- P. F. McMillan, B. T. Poe, P. Gillet and B. Reynard, Geochim. Cosmochim. Acta, 1994, 58, 3653–3664 CrossRef CAS.
- B. O. Mysen, Am. Mineral., 2011, 96, 1636–1649 CrossRef CAS.
- B. O. Mysen and P. Richet, Developments in Geochemistry Volume 10 - Silicate Glasses and Melts, Elsevier, 1st edn, 2005 Search PubMed.
- M. J. Toplis, D. B. Dingwell and T. Lenci, Geochim. Cosmochim. Acta, 1997, 61, 2605–2612 CrossRef CAS.
- M. Botev, H. Betchev, D. Bikiaris and C. Panayiotou, J. Appl. Polym. Sci., 1999, 74, 523–531 CrossRef CAS.
- A. T. DiBenedetto, Mater. Sci. Eng., A, 2001, 302, 74–82 CrossRef.
- G. Nkurunziza, A. Debaiky, P. Cousin and B. Benmokrane, Prog. Struct. Eng. Mater., 2005, 7, 194–209 CrossRef.
- T. P. Sathishkumar, S. Satheeshkumar and J. Naveen, J. Reinf. Plast. Compos., 2014, 33, 1258–1275 CrossRef CAS.
- D. R. Neuville, L. Cormier, B. Boizot and A.-M. Flank, J. Non-Cryst. Solids, 2003, 323, 207–213 CrossRef CAS.
- J. S. J. van Deventer, J. L. Provis, P. Duxson and G. C. Lukey, J. Hazard. Mater., 2007, 139, 506–513 CrossRef CAS PubMed.
- M. P. Hehlen, N. J. Cockroft and T. R. Gosnell, Phys. Rev. B: Condens. Matter Mater. Phys., 1997, 56, 9302–9318 CrossRef CAS.
- A. D. Sontakke, K. Biswas and K. Annapurna, J. Lumin., 2009, 129, 1347–1355 CrossRef CAS.
- M. Engholm, L. Norin and D. Åberg, Opt. Lett., 2007, 32, 3352–3354 CrossRef CAS PubMed.
- S. Yoo, C. Basu, A. J. Boyland, C. Sones, J. Nilsson, J. K. Sahu and D. Payne, Opt. Lett., 2007, 32, 1626–1628 CrossRef CAS PubMed.
- P. Glatz, M. Comte, L. Cormier, L. Montagne, B. Doumert and G. G. Moore, J. Non-Cryst. Solids, 2018, 493, 48–56 CrossRef CAS.
- T. Grammes, R. Limbach, S. Bruns, L. van Wüllen, D. de Ligny, E. I. Kamitsos, K. Durst, L. Wondraczek and D. S. Brauer, Front. Mater., 2020, 7, 115 CrossRef.
- T. Grammes, D. de Ligny, F. Scheffler, A. Nizamutdinova, L. van Wüllen, E. I. Kamitsos, J. Massera and D. S. Brauer, J. Phys. Chem. B, 2022, 126, 9911–9926 CrossRef CAS PubMed.
- A. Nizamutdinova, T. Uesbeck, T. Grammes, D. S. Brauer and L. van Wüllen, J. Phys. Chem. B, 2020, 124, 2691–2701 CrossRef CAS PubMed.
- D. J. DiGiovanni, J. B. MacChesney and T. Y. Kometani, J. Non-Cryst. Solids, 1989, 113, 58–64 CrossRef CAS.
- R. Dupree, D. Holland, M. G. Mortuza, J. A. Collins and M. W. G. Lockyer, J. Non-Cryst. Solids, 1989, 112, 111–119 CrossRef.
- H. Gan and P. C. Hess, Am. Mineral., 1992, 77, 495–506 CAS.
- B. O. Mysen and G. Cody, Geochim. Cosmochim. Acta, 2001, 65, 2413–2431 CrossRef CAS.
- F. J. Ryerson and P. C. Hess, Geochim. Cosmochim. Acta, 1980, 44, 611–624 CrossRef CAS.
- F. J. Ryerson and P. C. Hess, Geochim. Cosmochim. Acta, 1978, 42, 921–932 CrossRef CAS.
- M. J. Toplis and D. B. Dingwell, Geochim. Cosmochim. Acta, 1996, 60, 4107–4121 CrossRef CAS.
- M. J. Toplis and T. Schaller, J. Non-Cryst. Solids, 1998, 224, 57–68 CrossRef CAS.
- J. L. Knipping, L. D. Bilenker, A. C. Simon, M. Reich, F. Barra, A. P. Deditius, M. Wälle, C. A. Heinrich, F. Holtz and R. Munizaga, Geochim. Cosmochim. Acta, 2015, 171, 15–38 CrossRef CAS.
- Y. Tang, H. Zhang and B. Rao, Am. Mineral., 2016, 101, 415–422 CrossRef.
- J. D. Webster, R. Thomas, D. Rhede, H.-J. Förster and R. Seltmann, Geochim. Cosmochim. Acta, 1997, 61, 2589–2604 CrossRef CAS.
- D. Ehrt, M. Leister and A. Matthai, Phys. Chem. Glasses, 2001, 42, 231–239 CAS.
- K. Rao, Structural Chemistry of Glasses, Elsevier, 2002 Search PubMed.
- J. A. Duffy and M. D. Ingram, J. Non-Cryst. Solids, 1976, 21, 373–410 CrossRef CAS.
- H. Bach and N. Neuroth, The properties of optical glass, Springer, Berlin, Heidelberg, 1998 Search PubMed.
- W. Vogel, Glass chemistry, Springer, Berlin, Heidelberg, New York, London, 2nd edn, 1994 Search PubMed.
- J. A. Duffy, Geochim. Cosmochim. Acta, 1993, 57, 3961–3970 CrossRef CAS.
- J. A. Duffy and M. D. Ingram, J. Am. Chem. Soc., 1971, 93, 6448–6454 CrossRef CAS.
- J. A. Duffy and M. D. Ingram, J. Inorg. Nucl. Chem., 1975, 37, 1203–1206 CrossRef CAS.
- L. L. Velli, C. P. E. Varsamis, E. I. Kamitsos, D. Möncke and D. Ehrt, Phys. Chem. Glasses, 2008, 49, 182–187 CAS.
- I. Efthimiopoulos, D. Palles, S. Richter, U. Hoppe, D. Möncke, L. Wondraczek, S. Nolte and E. I. Kamitsos, J. Appl. Phys., 2018, 123, 233105 CrossRef.
- D. E. Day and G. E. Rindone, J. Am. Ceram. Soc., 1962, 45, 489–496 CrossRef CAS.
- M. Taylor and G. E. Brown, Geochim. Cosmochim. Acta, 1979, 43, 1467–1473 CrossRef CAS.
- M. Taylor and G. E. Brown, Geochim. Cosmochim. Acta, 1979, 43, 61–75 CrossRef CAS.
- E. Hecht, Optics, Pearson Education, 5th edn, 2016 Search PubMed.
- J. H. Wray and J. T. Neu, J. Opt. Soc. Am., 1969, 59, 774–776 CrossRef CAS.
- T. Grammes, Dr-Ing. Doctoral thesis, Friedrich-Schiller-Universität Jena, 2020.
- D. Ehrt, Phys. Chem. Glasses: Eur. J. Glass Sci. Technol., Part B, 2015, 56, 217–234 Search PubMed.
- V. Dimitrov and S. Sakka, J. Appl. Phys., 1996, 79, 1736–1740 CrossRef CAS.
- R. D. Shannon, Acta Crystallogr., 1976, A32, 751–767 CrossRef CAS.
- V. Dimitrov and T. Komatsu, J. Chem. Technol. Metall., 2010, 45, 219–250 CAS.
- E. I. Kamitsos, G. D. Chryssikos, A. P. Patsis and J. A. Duffy, J. Non-Cryst. Solids, 1996, 196, 249–254 CrossRef CAS.
- D. Möncke, D. Ehrt and E. I. Kamitsos, Phys. Chem. Glasses: Eur. J. Glass Sci. Technol., Part B, 2013, 54, 42–51 Search PubMed.
- D. Möncke, S. Ali, B. Jonson and E. I. Kamitsos, Phys. Chem. Chem. Phys., 2020, 22, 9543–9560 RSC.
- J. A. Duffy, Bonding, energy levels and bands in inorganic solids, Longman Scientific & Technical, New York, 1990 Search PubMed.
- J. A. Duffy and M. D. Ingram, J. Chem. Soc., Chem. Commun., 1973, 635–636 RSC.
- J. A. Duffy, J. Non-Cryst. Solids, 2002, 297, 275–284 CrossRef CAS.
- E. I. Kamitsos, Y. D. Yiannopoulos and J. A. Duffy, J. Phys. Chem. B, 2002, 106, 8988–8993 CrossRef CAS.
- A. Winterstein-Beckmann, D. Möncke, D. Palles, E. I. Kamitsos and L. Wondraczek, J. Phys. Chem. B, 2015, 119, 3259–3272 CrossRef CAS PubMed.
- J. A. Duffy, Phys. Chem. Glasses, 2003, 44, 388–392 CAS.
- M. R. Cicconi, D. R. Neuville, W. Blanc, J.-F. Lupi, M. Vermillac and D. de Ligny, J. Non-Cryst. Solids, 2017, 475, 85–95 CrossRef CAS.
- D. R. Neuville and B. O. Mysen, Geochim. Cosmochim. Acta, 1996, 60, 1727–1737 CrossRef CAS.
- A. N. Novikov, D. R. Neuville, L. Hennet, Y. Gueguen, D. Thiaudiere, T. Charpentier and P. Florian, Chem. Geol., 2017, 461, 115–127 CrossRef CAS.
- R. G. Milkey, Am. Mineral., 1960, 45, 990–1007 CAS.
- B. O. Mysen, F. J. Ryerson and D. Virgo, Am. Mineral., 1981, 66, 106–117 CAS.
- E. I. Kamitsos, J. A. Kapoutsis, H. Jain and C. H. Hsieh, J. Non-Cryst. Solids, 1994, 171, 31–45 CrossRef CAS.
- C. I. Merzbacher and W. B. White, J. Non-Cryst. Solids, 1991, 130, 18–34 CrossRef CAS.
- D. Palles, I. Konidakis, C. P. E. Varsamis and E. I. Kamitsos, RSC Adv., 2016, 6, 16697–16710 RSC.
- A. Varshneya, Fundamentals of Inorganic Glasses, Academic Press, 1994 Search PubMed.
- A. Navrotsky, K. Geisinger, P. McMillan and G. Gibbs, Phys. Chem. Miner., 1985, 11, 284–298 CrossRef CAS.
- E. I. Kamitsos, M. A. Karakassides and G. D. Chryssikos, J. Phys. Chem., 1987, 91, 5807–5813 CrossRef CAS.
- G. D. Chryssikos, L. P. Liu, C. P. Varsamis and E. I. Kamitsos, J. Non-Cryst. Solids, 1998, 235, 761–765 CrossRef.
- E. I. Kamitsos, A. P. Patsis and G. D. Chryssikos, J. Non-Cryst. Solids, 1993, 152, 246–257 CrossRef CAS.
- C. I. Merzbacher and W. B. White, Am. Mineral., 1988, 73, 1089–1094 CAS.
- E. I. Kamitsos, Y. D. Yiannopoulos, H. Jain and W. C. Huang, Phys. Rev. B: Condens. Matter Mater. Phys., 1996, 54, 9775–9783 CrossRef CAS PubMed.
- J. A. Duffy, E. I. Kamitsos, G. D. Chryssikos and A. P. Patsis, Phys. Chem. Glasses, 1993, 34, 153–157 CAS.
- Y. D. Yiannopoulos, G. D. Chryssikos and E. I. Kamitsos, Phys. Chem. Glasses, 2001, 42, 164–172 CAS.
- E. I. Kamitsos and G. D. Chryssikos, Solid State Ionics, 1998, 105, 75–85 CrossRef CAS.
- S. de Wispelaere, D. Cabaret, C. Levelut, S. Rossano, A.-M. Flank, P. Parent and F. Farges, Chem. Geol., 2004, 213, 63–70 CrossRef CAS.
- F. Seifert, B. O. Mysen and D. Virgo, Am. Mineral., 1982, 67, 696–717 CAS.
- B. O. Mysen, Contrib. Mineral. Petrol., 1998, 133, 38–50 CrossRef CAS.
- B. O. Mysen, L. Finger, D. Virgo and F. Seifert, Am. Mineral., 1982, 67, 686–695 CAS.
- B. O. Mysen, D. Virgo and F. Seifert, Rev. Geophys. Space Phys., 1982, 20, 353–383 CrossRef CAS.
- S.-H. Shim and K. Catalli, Earth Planet. Sci. Lett., 2009, 283, 174–180 CrossRef CAS.
- E. Stavrou, D. Palles, E. I. Kamitsos, A. Lipovskii, D. Tagantsev, Y. Svirko and S. Honkanen, J. Non-Cryst. Solids, 2014, 401, 232–236 CrossRef CAS.
- N. Chukanov and A. Chervonnyi, Infrared Spectroscopy of Minerals and Related Compounds, Springer, 2016 Search PubMed.
- N. S. Tagiara, D. Palles, E. D. Simandiras, V. Psycharis, A. Kyritsis and E. I. Kamitsos, J. Non-Cryst. Solids, 2017, 457, 116–125 CrossRef CAS.
- P. Richet and D. de Ligny, in Encyclopedia of Glass Science, Technology, History, and Culture, ed. P. Richet, Wiley, Hoboken, New Jersey, 2021, ch. 3.6, pp. 313–330 DOI:10.1002/9781118801017.
Footnote |
| † Electronic supplementary information (ESI) available. See DOI: https://doi.org/10.1039/d4cp00685b |
| This journal is © the Owner Societies 2024 |