Understanding and fine tuning the propensity of ATP-driven liquid–liquid phase separation with oligolysine

Abstract

Liquid–liquid phase separation (LLPS) plays a pivotal role in the organization and functionality of living cells. It is imperative to understand the underlying driving forces behind LLPS and to control its occurrence. In this study, we employed coarse-grained (CG) simulations as a research tool to investigate systems comprising oligolysine and adenosine triphosphate (ATP) under conditions of various ionic concentrations and oligolysine lengths. Consistent with experimental observations, our CG simulations captured the formation of LLPS upon the addition of ATP and tendency of dissociating under high ionic concentration. The electrostatic interaction between oligolysine and ATP is of great importance in forming LLPS. An in-depth analysis on the structural properties of LLPS was conducted, where the oligolysine structure remained unchanged with increased ionic concentration and the addition of ATP led to a more pronounced curvature, aligning with the observed enhancement of α-helical secondary structure in experiments. In terms of the dynamic properties, the introduction of ATP led to a significant reduction in translational and vibrational degrees of freedom but not rotational degrees of freedom. Through keeping the total number of charged residues constant and varying their entropic effects, we constructed two systems of similar biochemical significance and further validated the entropy effects on the LLPS formation. These findings provide a deeper understanding of LLPS formation and shed lights on the development of novel bioreactor and primitive artificial cells for synthesizing key chemicals for certain diseases.

---

1 Introduction

Liquid–liquid phase separation (LLPS) is a ubiquitous phenomenon observed frequently in our daily life, evident in instances ranging from the formation of water and oil droplets to the origin of life.¹ Recent studies have highlighted its association with the organization and regulation of cellular functions, especially in the process of amyloid aggregation related proteins, such as α-synuclein,^2–4 tau,^5–7 the islet amyloid polypeptide (IAPP),⁸ and so on. Recognizing its significance, considerable experimental and theoretical efforts have been directed towards understanding the underlying mechanisms in this field.^9–12 However, the intricate interactions between various co-solutes, such as ions, lipid vesicles, and macromolecular crowders, within the real cell further blur the primary driving forces behind this phenomenon. Therefore, systems that are simple but still biologically significant warrant focused attention.

Oligolysine (K_n) paired with adenosine triphosphate (ATP) stands out not only for their simplicity and ability of spontaneous microdroplet formation under varied conditions but also their role in prebiotic context.^13–16 Most importantly, its composition is well defined and limited. Oligolysine consists solely of lysine (K) residue, which are positively charged under physiological conditions and it role in the field of biological phase separation has been well recognized.^17,18 ATP is well-known for its role as an energy currency. Its high abundance in the cytosol, along with its biphasic regulatory effects on protein stability, solubility, and aggregation propensity, renders it a promising species.^19–23

As a consensus has been reached that the principles governing biomolecular phase separation should guide the development of innovative liquid-based organelles and therapeutics, numerous studies addressing the tunable predisposition to LLPS and fibrillization and controllable pathway and dynamics of liquid condensates have been reported.^24–30 To manipulate the amyloidogenic pathway, chimeric peptides merging highly amyloidogenic fragment of insulin's A-chain^31,32 with oligolysine were proposed. With the addition of ATP, such amyloidogenic pathway could be altered by varying the length of oligolysine. Fibrillization was observed directly with short oligolysine lengths. However, with longer ones, fibrils formed after LLPS intermediates.^24,30 Similarly, amphiphilic peptides combining features of fibrillar assembly domain (LVFFA) and coacervation factors (oligoarginine and ATP) enabled the coexistence of fibrous assembly inside liquid coacervates upon fine tuning the ratio of ATP and oligoargine.²⁶ Regarding tuning the dynamics of liquid condensates, the contribution of polymer length, stoichiometry, and differences between lysine and arginine residues was explored.²⁵ Furthermore, the impacts of the polypeptides sequence and charge patterning were examined, concluding that charge-rich long sequence exhibit more robust charge interactions compared to patterns featuring less contiguous runs of the same charge.²⁹

Despite significant advancements in fine-tuning LLPS properties, a comprehensive understanding of how these factors contribute to the underlying mechanism is still lacking at molecular level. In this work, considering both the simplicity and biological significance, we picked the oligolisine-ATP system and conducted coarse-grained (CG) simulations under varied conditions, including different oligolysine chain lengths and ionic strengths, to dissect the underlying mechanism of LLPS formation. Comprehensive analyses were performed and chimeric systems were built, revealing that electrostatic interactions play important roles in LLPS formation, but as oligolysine length increases, entropic effects become substantial. Subsequent entropy manipulation further emphasized its role in LLPS propensity. Our findings bring forth a novel strategy for modulating LLPS properties and set the stage for innovative bioreactor and drug delivery system designs.

2 Computational details

The initial all-atom structures of oligolysine (K_n where n = 4, 8, 16, 24, 32, 40) were generated by LEaP, a program embedded in AMBER 20 software.³³ Subsequently, these structures were solvated in a pre-equilibrated TIP3P³⁴ water box, maintaining a buffer of 12 Å between the outermost atoms of oligolysine and the box edge. Counter ions were added to neutralize the system. To fully relax the side chains of oligolysine, 2 ns simulations were performed under isothermal–isobaric (NPT) ensemble, following 5000 steps minimization and canonical (NVT) simulations where the temperature was heated to 298.15 K within 100 ps. Throughout the simulations, constraints were solely applied to atom Cα of backbone, using a force constant of 5 kcal mol⁻¹ Å⁻². In the NVT simulation, temperature maintained at 298.15 K was achieved using Berendsen coupling algorithm,³⁵ with a time constant of 2 ps. In the NPT simulation, temperature was hold at 298.15 K by Langevin dynamics with a collision frequency of 3 ps⁻¹, while pressure was kept at 1 atm through isotropic position scaling. The ff14SB³⁶ force field was for oligolysine, and all bonds involving hydrogen were constrained using the SHAKE algorithm³⁷ to increase the time step to 2 fs. Short-range electrostatic and van der Waals interactions used an 8 Å cutoff, while long-range electrostatic interactions were handled by the Particle-Mesh Ewald method (PME).³⁸

Coordinates of oligolysine extracted from the last frame of all-atom simulations served as the initial structure for subsequent coarse-grained (CG) simulations. Here, the MARITINI coarse-grained model (version 2.2)³⁹ was employed for oilgolysine, where the main-chain beads at the N and C terminals were assigned positive and negative charges, respectively.(Detailed information can be found in Table S1, ESI†). For adenosine triphosphate (ATP), initial coordinates and parameters were directly retrieved from the literature.⁴⁰ The molar ratio of oligolysine and ATP was fixed at 1 : 1 throughout this work, unless otherwise specified. Both the effects of ATP and ionic concentration were taken into consideration. Initially, 20 oligolysines were randomly placed in a cubic box measuring 132 × 132 × 132 ų with the help of packmol.⁴¹ For simulations investigating the effect of ATP, 20 ATP molecules were subsequently inserted into the previously constructed boxes (Fig. 1). These boxes were then filled with water beads. The influence of finite-size effects was further explored by performing simulations that increase the number of oligolysines and ATPs up to 100 while maintaining similar peptide concentrations and ratios.⁴² To neutralize the entire system and establish the ion concentration, adequate numbers of Na⁺ and Cl⁻ ions were added. Four categories of ionic concentrations, namely, 0.15 M, 0.50 M, 0.75 M, and 1.00 M were studied. In the coarse-grained simulations, the initial structures were first equilibrated under the NPT ensemble for 200 ns, with temperature maintained at 300 K using velocity rescaling⁴³ and pressure kept at 1 bar using Berendsen.³⁵ For the production run, the entire system remained under the NPT ensemble for 8 μs, with pressure treated by employing the Parrinello–Rahman approach.^44,45 Throughout all CG simulations, electrostatic and van der Waals (vdW) interactions were treated with the reaction field method⁴⁶ and the cut-off⁴⁷ method, respectively, where the cutoff distances were both set to 11 Å. All coarse-grained simulations were performed using the Gromacs 2023 package suite⁴⁸ and each simulation was repeated three times. A detailed summary of the systems we studied is provided in Table S2 (ESI†). All analyses conducted in this work were implemented with homemade tool command language (TCL) scripts under the framework of visual molecular dynamics (VMD),⁴⁹ and tools provided by Gromacs.⁴⁸

Fig. 1 Schematic representation of key species utilized in this work. Although oligolysines of different lengths (n = 4, 8, 16, 24, 32, 40) were examined, only the oligolysine with a length of 4 (K₄) is depicted. For clarity, ions and water molecules are not shown. Oligolysines are represented as sphere with backbone colored in pink and side chains in yellow. ATPs are portrayed in stick form, segmented into three regions: adenine (blue), ribose (marine), and phosphate group (light blue). Inserted on the right is a zoom-in view of oligolysine with four consecutive lysine. Additionally illustrated are the orientation angle (θ_rot) between the dipole moment (m) of a single oligolysine and the Z-axis of the simulation box and dihedral (SC1-BB-BB-SC1) between two adjacent residues.

3 Results and discussions

3.1 Validation of MARTINI force field

Although great success has been achieved in various fields by MARTINI force fields,^50–52 their limitations should be kept in mind.^53–55 Consequently, it is imperative to evaluate their performance on oligolysine paired ATP systems prior to discovering the underlying mechanism of LLPS formation. For a comprehensive assessment, two distinct properties, namely, macroscopic and microscopic properties were employed here.

3.1.1 Macroscopic property. Two parameters, namely, the number of clusters and the maximum size of a single cluster, were introduced in this work to quantify the propensity for aggregation. To this end, oligolysines were classified within the same cluster when the minimum distance between any atoms of paired oligolysines was smaller than 8 Å. The number of oligolysines within a single cluster denotes the size of that cluster. The rationale for adopting this criterion is detailed in ESI.† (Fig. S5, ESI†).

As illustrated in Fig. 2(a) and (b), taking oligolysine with a length of four (K₄) as an example, in the absence of ATP, the number of cluster approaches 20, indicating the dispersion of oligolysines (upper left panel of Fig. 2(a)) as per our initial random placed structure. (cf. Section 2) Upon the inclusion of ATPs, aggregation occurred, resulting in the reduction of the number of clusters to nearly one (Fig. 2(a)) and an increase in the maximum cluster size to 20 (Fig. 2(b)). Given that our simulation included only 20 ATPs and oligolysines, both the number of clusters and the maximum cluster size indicate that all oligolysines assembled into a single droplet. (upper right panel of Fig. 2(a)) When increasing the oligolysine length while maintaining a constant ratio between oligolysine and ATP, the difference in the propensity for aggregation with and without ATP diminished, but a turning point was observed at the oligolysine length of 24. It should be noted that the peptide we studied contains only oligolysine segments, and difference can exist between our simulations and chimeric peptides.²⁴ However, the inflection point aligns with observations in chimeric peptide systems, where oligolysine of length 24 serves as a turning point altering the pathway of fibrillization through intermediates of LLPS²⁴ and unusual fibril → droplet transition can only be observed in chimeric peptide of longer oligolysine (K_n) chain (n = 24, 40) incubated with proteinase K.³⁰ As shown in the upper panel of Fig. 2(b), fewer differences could be observed in terms of structure with and without the addition of ATP. Same conclusion could be drawn from the number of clusters and the maximum cluster size. Similar trends and behaviors can be observed in large systems containing 100 oligolysines and ATPs, indicating that results derived from systems of 20 oligolysines are robust. (Fig. S10 and S11, ESI†) The propensity for forming LLPS is further supported by the analysis of the solvent-accessible surface area (SASA) of oligolysines, as shown in Fig. S7 (ESI†). Upon the addition of ATPs, the SASA values notably decreased, particularly for oligolysine of length 4, 8, and 16. However, the values overlapped with each other in the system with oligolysines of length 40.

Turning our attention to the effects of the ionic concentrations, a gradual reduction in aggregation capability becomes evident with increasing ionic concentrations, spanning from 0.15 to 1.00 M. As depicted in Fig. 2(c) and (d), corresponding trends were observed, including an increase in the number of clusters and a decrease in maximum cluster size. From a structural perspective, we further analyzed the radial distribution function between oligolysines of different lengths and ions. As depicted in Fig. S2 and S3 (ESI†), with increasing ionic concentrations, the coordinated ions within the first spherical shell increased, while the peak between the oligolysines and ions remained unaltered. These increased ions, particularly chloridion (Cl⁻), may compete with negatively charged ATPs, attenuating the attractions necessary for LLPS formation. A similar phenomenon has been experimentally observed in biomolecular condensates and was rationalized by the shortened decay length¹⁴ based on the classic Debye–Hückel theory.⁵⁶

3.1.2 Microscopic property. In examining the microscopic properties, we focused on estimating both structural and static bulk properties. Within the realm of structural properties, the radius of gyration (r_gyr²) and static permittivity were utilized to evaluate the performance of MARTINI. The r_gyr² metric describes the extent of global structure curling, and is complementary to the local structure detected by short distance-range techniques such as circular dichroism (CD) and nuclear magnetic resonance (NMR).⁵⁷ A decreasing value indicates an increasingly coiled structure. The definition of radius of gyration is provided belowwhere r (i) denotes the position of the ith bead, and r̄ represents the center of the entire molecule, taking the weight of each bead (ω(i)) into consideration. Since the masses of the beads employed in this work are same, the weight ω(i) is set to be 1.

As summarized in Table 1, the radius of gyration consistently increases with the length of oligolysine, regardless of the presence of ATP. Little difference is observed in r_gyr² for short oligolysine peptides when considering the presence of ATP. For instance, taking both K₄ and K₈ as examples, the averaged values of r_gyr² are nearly identical: 5.34 for K₄, both with and without ATP, and 7.10 (with ATP) versus 7.12 (without ATP) for K₈. Nonetheless, the inclusion of ATP tends to yield slightly reduced average values or standard deviations, especially as oligolysine length increases. A notable case is K₄₀, where r_gyr² is 17.78 with ATP, distinctly lower than its counterpart value of 19.34 without ATP. To provide local structural changes, distribution of dihedral (SC1-BB-BB-SC1) formed between two adjacent residues using side chain bead (SC1) and backbone bead (BB) was analyzed. (cf.Fig. 1 and Fig. S1, ESI†) As shown in Fig. S1 (ESI†), with the addition of ATPs, the dihedral population ranging from −60° to 60° increases a lot compared to the one without ATPs and fall in the range of standard helix structures. These trends in the changes of global and local structures align with experimental observations where helical secondary structure is promoted in the droplets formed in polylysine paired with ATP system.¹³ This stabilization of secondary structure formation can be attributed to the local stacking of ATP species.^13,14 Corresponding structural insights will be discussed in the following sections. These trends persist when increasing the ionic concentration from 0.15 to 1.00 M. Detailed results can be found in Table S3 (ESI†).

Table 1 Summary of radii of gyration (r_gyr²) for oligolysine of different lengths, both with and without the addition of ATP, at the ionic concentration of 0.15 M. Standard deviations are provided in parentheses. Detailed analysis of radii of gyration over different ionic concentrations can be found in Table S3 (ESI)

Oligolysine	r gyr ^2 (Å^2)
	w/o ATP	w ATP
K4	5.34 (0.32)	5.34 (0.31)
K8	7.12 (0.54)	7.10 (0.50)
K16	10.52 (1.02)	10.00 (1.04)
K24	13.77 (1.44)	12.76 (1.71)
K32	16.68 (1.91)	15.27 (2.38)
K40	19.34 (2.42)	17.78 (2.84)

---

Relative permittivity (ε) is another static property utilized here to further validate the performance of the MARTINI force field. Given the prevailing consensus regarding the issue of artificial acceleration in the coarse-grained models,^58–60 the emphasis shifted to the relative disparities between systems, specifically those with and without ATPs. The fluctuation of the dipole moment was employed here for the estimation of relative permittivity,^61,62

Here, V represents the volume of the bulk systems, k_B is the Boltzmann constant, and T is the temperature. 〈|M|²〉 − |〈M〉|² denotes the dipole moment fluctuation of the species under consideration. For both systems, whether including ATP or not, we only consider water and oligolysine for the calculation of dipole moment fluctuation.

As indicated in Table 2, when ATP is mixed with oligolysine, the relative permittivity decreases in all the systems we studied. For example, when the oligolysine length was set to 4, the relative permittivity decreased from 2.21 to 1.88 upon the addition of ATP. Referring to the assembled structure formed between oligolysine (K₄) and ATP (upper right panel of Fig. 2(a)), this decrease suggests that the interior of such aggregation tends to behave more like hydrophobic functional groups compared to that dissolved in the solvent. A more direct method that characterizes the hydrophobicity through the presence of water was conducted. As shown in Fig. 3, the radial distribution function (RDF) formed between oligolysine and water beads was estimated. The position of the first peak between oligolysines and water beads remained constant regardless of ATP addition. However, the peak height decreases significantly with the addition of ATPs, indicating a lower probability of water presence in such a region. The integration over the first shell is the average number of coordinated water beads and drops a lot when ATPs were included. (Fig. 3 and Table 2) For example, when the oligolysine length is set to be 4, the number of water beads coordinated with oligolysine within the first shell was 4.53 and 8.88 with and without ATPs, respectively. The water mainly comes from the outermost oligolysine of the formed cluster in the presence of ATPs. These results suggest that oligolysines tend to repel water from their adjacent spherical shell once mixed with ATPs. Both Table 2 and Fig. 3 show that incorporating ATPs reduces the probabilities of encountering water in the first shell, thereby increasing hydrophobicity. Both permittivity estimated from dipole moment fluctuation and water presence are in line with certain experimental observations. For instance, specific hydrophobic molecules, such as porphyrins, are selectively sequestered into microdroplets formed by oligolysines and ATPs, which serve as platform for catalytic reactions.¹³ Conversely, a clear increase in relative permittivity was observed when the length of oligolysine was increased. For example, with and without the addition of ATP, the relative permittivity increased from 2.21 and 1.88 to 51.11 and 42.21 for K₄ and K₄₀, respectively. This increase is mainly a result of the total dipole moment increaseing as the length of oligolysine grows. Furthermore, with an increase in the oligolysine length, more degrees of freedom are allowed, leading to a much more frequent fluctuation of dipole moment and interaction with water beads. By juxtaposing the macroscopic and microscopic properties as predicted by the MARTINI force field, it can be confidently asserted that the MARTINI force field is sufficient for elucidating the fundamental forces driving LLPS formation between oligolysine and ATP.

Table 2 Comparison of permittivity (ε) and number of water beads within the first shell across various oligolysine lengths, with and without the addition of ATP, at the ionic concentration of 0.15 M

Oligolysine	ε		# wat bead
	w/o ATP	w ATP	w/o ATP	w ATP
K4	2.21	1.88	8.88	4.53
K8	4.83	4.32	7.94	4.96
K16	16.11	13.55	7.38	6.00
K24	30.88	24.96	7.20	6.37
K32	44.30	39.43	7.08	6.45
K40	51.11	42.21	6.98	6.47

---

Fig. 2 Effects of ATPs and ionic concentrations on the propensity to form LLPS. The effect of ATP exerts on (a) the number of clusters and (b) the maximum cluster size over systems of different oligolysine lengths (K_n), keeping the ionic concentration constant at 0.15 M; the effect of different ionic concentrations caused on (c) the number of clusters and (d) the maximum cluster size in the systems of oligolysines paired with ATPs. Four exemplary snapshots for K₄ and K₄₀, with and without ATPs, are shown in the top panel. Here, oligolysine is represented as spheres, while ATP is illustrated as blue sticks. To enhance visual clarity, beads of water and counterions are omitted.

Fig. 3 The radial distribution function between oligolysines of different lengths ((a)–(f) represent K₄, K₈, K₁₆, K₂₄, K₃₂, and K₄₀, respectively) and water beads (W), with (red line) or without (black line) the addition of ATPs at the ionic concentration of 0.15 M. Together shown are their corresponding integrations in dashed lines and the number of water beads in the first shell.

3.2 Driving force underlying LLPS of oligolysine/ATP system

The driving force underlying the LLPS formation in the oligolysine/ATP system was analyzed from two aspects: enthalpic and entropic contributions.

3.2.1 Enthalpic effects. To investigate the enthalpic effects, interactions formed between proteins and proteins (P–P), proteins and ions (P–I), and proteins and ATPs (P–ATP) were extracted and scrutinized. As depicted in Fig. S8 (ESI†), the electrostatic interaction formed between proteins and ATPs (P–ATP) is more pronounced than that between proteins and ions (P–I) when oligolysine length is less than 24. This indicates that proteins prefer to interact more strongly with ATPs than ions. Consequently, the entropy associated with ions release should be lower among short oligolysines.⁶³ However, for a straightforward but not rigorous observation, artificial systems were meticulously constructed with parameters inherited from the previous set, except for the electrostatic-related parameters of oligolysine. In the previous simulation, the side chains of oligolysines were all treated as positively charged, according to biochemical conditions. Here, the charge states of the side chains were set to be neutral, and the ionic concentration was fixed at 0.15 M. As depicted in Fig. 4, electrostatic interactions had a significant impact on the ability to form LLPS when oligolysines were mixed with ATP. From Fig. 4(a) and (b), notable differences in the number of clusters and maximum cluster size were observed between oligolysine systems where side chains are positively charged and neutral. This distinction was particularly noteworthy when the length of oligolysines shorter than 16. However, when extended to 40, the disparity diminishes. For instance, when the oligolysine length is set to 4, there was a notable difference in the number of clusters, with approximately 13 being observed, whereas with oligolysine length of 40, only 2 can be achieved. Examining the radial distribution functions (RDFs) formed between charged oligolysines and ions Na⁺ and Cl⁻, while accounting for the presence of ATPs, provides additional evidence of the prevailing enthalpic effects. As shown in Fig. S4 (ESI†), the height of first peak formed between oligolysines and ions Na⁺ and Cl⁻ with addition of ATPs is larger than the case without ATPs. Such phenomenon is more significant over oligolysines of short lengths and vanishes when oligolysines are of length 40. For instance, when oligolysines are of length 4, higher values of radial distribution function mean more ions could be accommodated within first spherical shell.

Fig. 4 Effects of electrostatic interactions on the ability of LLPS formation between oligolysine and ATP: (a) the number of clusters and (b) the maximum cluster size. The ionic concentration was fixed at 0.15 M.

Since increasing the oligolysine length inherently increased entropy, both phenomena observed above indicate that a competition between electrostatic interaction and entropy does exist in these systems. Moreover, it is compelling to note that among the neutral oligolysines, both the number of clusters and maximum cluster size remain relatively stable when the length of oligolysine increases from 4 to 24, but exhibit a pronounced decline when the oligolysine length reached 40. (Fig. 4) This inflection point around 24 again coincided well with the one observed in the charged oligolysine system and experimental observations.²⁴

3.2.2 Entropic effects. In this section, entropic effects were explored by decomposing them into three distinct components: translational (trans.), rotational (rot.), and vibrational (vib.) degrees of freedom. To assess the translational degree of freedom, a bulk property, namely, diffusion coefficient (D), was employed here, which is defined as belowHere, 〈⋯〉 denotes the ensemble average, 6 accounts for the dimension of particle motions, and r(t) and r(0) represent the particle positions at time t and 0, respectively.

Both Fig. 5 and Table 3 illustrate that the diffusion coefficient linearly decreases with increasing oligolysine length when ATP is absent. This trend coincides with the intuitive notion that diffusion coefficient is inversely related to molecular size or weight.⁶⁴ Such an observation suggests that oligolysine, in isolation, can not undergo LLPS since the size and weight pertain to singular molecule. A linear relationship plot correlating the diffusion coefficient with oligolysine length is illustrated in Fig. S6 (ESI†). For oligolysine of short lengths, increasing the ionic concentration reduces the associated diffusion coefficient. At low ionic concentrations, positively charged oligolysines repel each other and behave as individual molecules. Conversely, at high ionic concentrations, repulsion among oligolysines decreases, and side chains may promote LLPS to lower the diffusion constant. A similar effect of salinity on LLPS has been reported for polyarginine peptide series.⁶⁵ However, subtle changes are observed for longer oligolysines, such as K₂₄ and K₄₀. Additionally, with the addition of ATP, the diffusion coefficient significantly decreases in systems capable of forming LLPS. For instance, the diffusion coefficient of K₄ is 0.295 × 10⁻⁵ cm² s⁻¹, but when mixed with ATP, it drops to 0.068 × 10⁻⁵ cm² s⁻¹. These results indicate that translational degrees of freedom are restricted when ATPs are present. Intriguingly, no significant change in the diffusion coefficients was observed in the mixture of ATPs and different oligolysine lengths, except for K₄₀. For example, the diffusion coefficients were consistently around 0.065 × 10⁻⁵ cm² s⁻¹. A somewhat large decrease in oligolysine of length 40 might be attributed to its reduced ability of forming LLPS. (Table 3 and Fig. S6, ESI†) It is worth noting that owing to the nature of coarse-grain models, the presented diffusion coefficients are qualitative measurements.

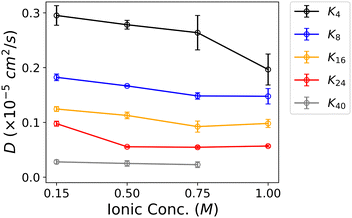Fig. 5 Diffusion coefficient of oligolysine with varying lengths as a function of the ionic concentration of NaCl when ATPs are absent.

Table 3 Comparison of diffusion coefficient (D) of oligolysine with and without ATP at an ionic concentration of 0.15 M

Oligolysine	D (× 10^−5 cm^2 s^−1)
	w/o ATP	w ATP
K4	0.295 ± 0.018	0.068 ± 0.016
K8	0.182 ± 0.006	0.067 ± 0.008
K16	0.124 ± 0.005	0.076 ± 0.001
K24	0.098 ± 0.005	0.062 ± 0.006
K40	0.028 ± 0.004	0.046 ± 0.005

---

The distribution of orientation angle (θ_rot) formed between the dipole moment (μ) of each oligolysine and the Z-axis was employed to estimate the degree of rotational freedom. A schematic illustration of the rotational angle can be found in Fig. 1. Both effects of ATPs and ionic concentrations were took into considerations. As depicted in Fig. 6(a)–(e), little change in the overall distribution shape of the rotational angle (θ_rot) was detected among systems with or without ATPs. These changes were primarily reflected in the shift of the peak position in systems composed of longer oligolysines. For example, in systems of shorter oligolysines, such as K₄ and K₈, the distributions with and without ATPs almost overlapped with each other. This indicates that oligolysine behavior in the resulting LLPS closely resembles its isolated form concerning rotational freedom. However, for longer oligolysines, a peak increase around 20° suggests that their rotational freedom was somewhat constrained upon the addition of ATPs. In comparison to the influence exerted by ATPs, the effects resulting from different ionic concentrations were subtle. Even in the case of longer oligolysines, their distributions closely aligned with each other. (Fig. 6(f)–(j)).

Fig. 6 Distribution of orientation angle (θ_rot) between the dipole moment of oligolysines (K_n) of different lengths and the Z-axis of the simulation box, considering different factors: (a)–(e) with and without the addition of ATP at the ionic concentration of 0.15 M; (f)–(j) at varying ionic strengths in the presence of ATPs.

Focusing exclusively on vibrational freedom, we delved into the analysis of vibrational entropy, relying on the root-mean-square fluctuation (RMSF). As shown in Fig. 7, the inclusion of ATPs significantly impacts the RMSF of oligolysine, affecting both its mean value and standard deviation. This effect on the mean value is particularly pronounced in the case of short-length oligolysine, such as K₄ and K₈, where the RMSF decreases markedly upon mixing with ATPs. This decrease mainly arises from the interactions formed between ATPs and oligolysines. Energy decomposition into interactions formed between oligolysine (P), ions (I), water (W), and ATPs further demonstrates it. As depicted in Fig. S8(a)–(f) (ESI†), the inclusion of ATPs weakens the electrostatic interactions formed between oligolysines–oligolysines (P–P), oligolysines–ions (P–I), and van der Waals (vdW) interactions between oligolysines–ions (P–I), and oligolysines–water (P–W), while strengthening the vdW interaction formed between P–P. These trends can be rationalized by the strong interactions formed between oligolysines and ATPs. ATPs compete with negatively charged species, such as ions, and attract positively charged oligolysines. Consequently, the electrostatic and vdW interactions between oligolysines and ions (P–I) decreased. The reduction in the vdW interactions of P–W mainly results from the lower probabilities of finding water beads within the adjacent spherical shell. (Fig. 3) The shortened distance between oligolysines due to the attractive force of ATPs accounts for the weakened electrostatic interactions and increased vdW interactions. Fig. 7(a) features a representative snapshot depicting π–π stacking between two adjacent ATPs, occurring in both parallel and T-shape configurations. This phenomenon stems from the unique structure of ATP, which possesses both hydrophobic (adenine) and hydrophilic (phosphate groups, cf.Fig. 1) components at its ends. Such interactions have also been observed using all-atom simulations.^15,66 Furthermore, since ATPs form π–π stacking and orient their phosphate groups outward, the predominant interactions between ATPs and oligolysine occur at the side chains of oligolysines and the phosphate groups, which carry positive and negative charges, respectively. (Fig. 7(b)) Delving deeper into the interactions formed between ATPs and oligolysines, we further decomposed these interactions into terms involving the backbone (BB_P) and side chain (SC_P) of oligolysines, and the phosphate group (PO4_ATP) and side chains (SC_ATP) of ATPs. As listed in Table 4, the electrostatic interactions primarily arise from the side chain of oligolysine (SC_P) and the phosphate groups of ATPs (PO4_ATP). The mode of interaction coincides well with the one depicted in Fig. 7(a) and (b). As the length of oligolysine increases to 16, the difference in RMSF between oligolysine with and without ATPs diminishes but remains observable. This observation finds further support in the structural context. As depicted in Fig. 7(c), most oligolysines exhibit interactions with ATPs, except for a few isolated oligolysines. These interactions between oligolysines and ATPs continue to restrict the fluctuations of oligolysine. This result is in line with the conclusions we draw from Fig. 2(a), where oligolysines of length 16 can still form LLPS. However, when the oligolysine length increases to both 24 and 40, the difference between systems with ATPs and without ATPs vanishes. (Fig. 7(d) and (e)) A snapshot inserted in Fig. 7(d) reveals that most oligolysines are isolated, behaving similarly to those without ATPs. This observation provides an explanation for the superposition of RMSF in the presence or absence of ATPs.

Fig. 7 Root-mean-square fluctuation (RMSF) of oligolysine (K_n) across different lengths, presented with linear ATP (red circle) and ATP with constrained entropy (blue circle) and without ATP (black circle). Panels (a)–(e) correspond to K₄, K₈, K₁₆, K₂₄, and K₄₀, respectively. Insets showcase representative snapshots extracted from simulations, with ATP depicted as sticks and oligolysine as spheres. The π–π stacking observed between two adjacent ATPs is highlighted by a dashed yellow line, and details are magnified in panels (a) and (b).

Table 4 Interaction energies between the side chain of oligolysine (SC_P), the backbone of the oligolysine (BB_P), the side chain of ATPs (SC_ATP), and the phosphate groups of ATPs (PO4_ATP) were decomposed into Coulomb and Lennard-Jones (LJ) terms, respectively. Standard deviations are provided in parentheses and expressed in the unit of kJ mol⁻¹

		K4	K8	K16	K24	K32	K40
Elec	SCP–PO4ATP	−1948.2(61.0)	−2534.6(57.2)	−2615.9(85.6)	−2478.1(70.2)	−2522.3(71.4)	−2622.8(71.4)
	SCP–SCATP	0.0(0.0)	0.0(0.0)	0.0(0.0)	0.0(0.0)	0.0(0.0)	0.0(0.0)
	BBP–PO4ATP	−508.2(38.1)	−447.9(30.5)	−186.0(38.0)	−150.1(23.5)	−135.6(34.9)	−70.7(27.6)
	BBP–SCATP	0.0(0.0)	0.0(0.0)	0.0(0.0)	0.0(0.0)	0.0(0.0)	0.0(0.0)
LJ	SCP–PO4ATP	−1370.8(44.1)	−1747.6(45.0)	−1798.9(57.3)	−1696.9(51.9)	−1730.9(51.0)	−1797.6(53.8)
	SCP–SCATP	−1206.3(49.5)	−1362.2(47.0)	−1397.6(61.6)	−1350.0(51.6)	−1367.7(54.1)	−1439.0(54.9)
	BBP–PO4ATP	−728.5(45.7)	−872.2(49.2)	−754.1(61.0)	−696.3(68.9)	−727.8(65.4)	−778.3(62.8)
	BBP–SCATP	−955.1(55.0)	−1279.8(57.4)	−1595.3(63.8)	−1457.2(68.1)	−1537.9(75.0)	−1532.7(71.4)

---

Instead of solely focusing on the mean value of RMSF, a compelling trend becomes evident when examining the standard deviation. Notably, these elevated standard deviations predominantly dwell in regions characterized by high fluctuations. For instance, in system K₄, high standard deviations primarily occur at terminal residues. In the case of oligolysine with a length greater than 8, pronounced standard deviations are present not only in terminal regions but also within central regions where fluctuations remain considerable. This outcome is reminiscent of a previous conclusion suggesting that ATPs can enhance protein thermal stability by favoring regions with high flexibility and an abundance of charged residues.⁶⁷ To delve deeper into the preference for areas of high flexibility, oligolysines were further categorized into high and low flexibility region. Detailed categorizations for oligolysines of varying lengths can be found in Fig. S9 (ESI†). As the interactions primarily occur between the phosphate groups of ATPs and side chains of oligolysine, (cf. structure inserted in Fig. 7(b)) radial distribution functions (RDFs) for the phosphate groups of ATPs and oligolysine in high and low flexibility regions were analyzed. As indicated in Fig. S7(a)–(e) (ESI†), the first peak of distance between the phosphate group (PO4_ATP) and oligolysine remains consistent. However, the height of the interaction between high flexibility regions (solid line) and the integrated area under it (dashed line) is greater than that of the low flexibility one. This further substantiates that ATPs exhibit a preference for interacting with highly flexible regions.

3.3 Regulating the tendency of forming LLPS through entropy

At this point, a conclusion has been reached that both enthalpy and entropy significantly contribute to the formation of LLPS in the system where oligolysine is paired with ATPs. As the length of oligolysines increases, the effects of entropy become dominant and cannot be ignored. Consequently, this prompts us to explore the possibility of finely tuning the propensity for LLPS formation by achieving a delicate balance between entropy and enthalpy contributions. In this system, the enthalpy effect mainly comes from electrostatic interactions, where oligolysine should be positively charged under physiological conditions. In order to simulate realistic physiological conditions and minimize artificial effects, we preserved the charge states and focused on the impact of entropy. Although both translational and vibrational entropy affect the formation of LLPS, fine−tuning vibrational entropy appears to be a more straightforward approach both theoretically and experimentally. Here, the vibrational entropy was restrained by creating a closed-loop structure based on a linear peptide. This structure, termed as cyclic peptide, has garnered notable success in drug discovery, structural biology, and therapeutic development.^68–70 As depicted in Fig. 7(e) and 8, the formation of a bond was between the ends of the linear peptide restricted the internal freedom and incurred a significant decrease in fluctuation. Notably, only the entropy was altered while other variables such as temperature and inner energies were held constant. According to the thermodynamic free energy principles, the free energies prefer to ascend, thereby reducing the propensity for forming LLPS. As shown in Fig. 8(a) and (b), diminishing internal freedom results in a larger number of clusters and a small maximum cluster size compared with the system comprising linear oligolysine and ATPs.

Fig. 8 Propensity of forming LLPS in the system of linear and cyclic oligolysine mixed with ATPs at the ionic concentration of 0.15 M: distribution of (a) the number of clusters and (b) the maximum cluster size.

In another trial, entropy increased by breaking a long linear oligolysine (K₄₀) into 10 short oligolysines (K₄). Again, both the electrostatic interaction and temperature were maintained. As anticipated, the propensity for forming LLPS increased. A representative snapshot is available in Fig. S13 (ESI†). Both in terms of the number of clusters and maximum cluster size, ATPs could absorb more oligolysines than required to neutralize its own charge into a single cluster. This phenomenon coincides with experimental observations that droplets can still form beyond the boundary of charge neutralization.¹⁵ These trends regarding the propensity of LLPS formation through constraining and releasing entropy were also validated in large-size systems. (Fig. S12 and S14, ESI†).

4 Conclusions

In this work, we conducted a comprehensive investigation into the driving force underlying the LLPS formation between the oligolysine and ATPs using coarse grained simulations. We explored two key factors, namely, oligolysine length and ionic concentrations, which may influence the propensity for LLPS formation. First and foremost, we assessed the performance of the MARTINI force field in reproducing both macroscopic and microscopic properties. Predictions of LLPS propensity under different oligolysine lengths and ionic concentrations closely matched experimental observations. Next, we constructed an artificial system in which the side chains of oligolysine were treated as neutral to elucidate the enthalpic contribution to LLPS. For oligolysines of short length, enthalpy was identified as the dominant driving force. However, as oligolysine length increased, the contribution of entropy became increasingly significant. The entropic effect was further dissected into contributions from translational, rotational, and vibrational degrees of freedom. Upon the addition of ATPs, substantial changes were observed in both translational and vibrational degree of freedom, except for rotational freedom. A detailed structural analysis revealed that ATPs exhibited a preference for forming π–π stacking interactions using adenine regions, while leaving phosphate groups pointing toward oligolysine. Additionally, ATPs exhibited a higher frequency of interaction with oligolysine in regions characterized by high fluctuation. Finally, we validated our hypotheses by designing two distinct systems: one involved the creation of cyclic oligolysine to decrease the entropy, while the other entailed breaking the long oligolysine into shorter segments to increase the entropy. As expected, the propensity for LLPS formation increased when entropy was enhanced and decreased in the case of cyclic oligolysine. The findings presented in this study provide valuable insights into strategies for modulating LLPS propensity, with implications for the design of drug delivery systems and bioreactors.

Author contributions

Qiang Zhu: conceptualization, validation, visualization, investigation, formal analysis, and writing – original draft preparation; Yongxian Wu: investigation, validation, visualization, and writing – reviewing and editing; Ray Luo: conceptualization, supervision, projection administration, funding acquisition, and writing – reviewing and editing.

Conflicts of interest

There are no conflicts to declare.

Acknowledgements

The authors gratefully acknowledge the research support from NIH (GM130367 to R. L.).

Notes and references

1. A. I. Oparin and S. Morgulis, The Origin of Life, 1938, Macmillan, New York, p. 270.
2. S. Ray, N. Singh, R. Kumar, K. Patel, S. Pandey, D. Datta, J. Mahato, R. Panigrahi, A. Navalkar and S. Mehra, et al. , Nat. Chem., 2020, 12, 705–716.
3. S. Mukherjee, A. Sakunthala, L. Gadhe, M. Poudyal, A. S. Sawner, P. Kadu and S. K. Maji, J. Mol. Biol., 2023, 435, 167713.
4. A. S. Sawner, S. Ray, P. Yadav, S. Mukherjee, R. Panigrahi, M. Poudyal, K. Patel, D. Ghosh, E. Kummerant and A. Kumar, et al. , Biochemistry, 2021, 60, 3676–3696.
5. Y. Lin, Y. Fichou, A. P. Longhini, L. C. Llanes, P. Yin, G. C. Bazan, K. S. Kosik and S. Han, J. Mol. Biol., 2021, 433, 166731.
6. S. Ambadipudi, J. Biernat, D. Riedel, E. Mandelkow and M. Zweckstetter, Nat. Commun., 2017, 8, 275.
7. S. Wegmann, B. Eftekharzadeh, K. Tepper, K. M. Zoltowska, R. E. Bennett, S. Dujardin, P. R. Laskowski, D. MacKenzie, T. Kamath and C. Commins, et al. , EMBO J., 2018, 37, e98049.
8. L. Pytowski, C. F. Lee, A. C. Foley, D. J. Vaux and L. Jean, Proc. Natl. Acad. Sci. U. S. A., 2020, 117, 12050–12061.
9. C. P. Brangwynne, P. Tompa and R. V. Pappu, Nat. Phys., 2015, 11, 899–904.
10. J. R. Simon, N. J. Carroll, M. Rubinstein, A. Chilkoti and G. P. López, Nat. Chem., 2017, 9, 509–515.
11. Y. Shin, J. Berry, N. Pannucci, M. P. Haataja, J. E. Toettcher and C. P. Brangwynne, Cell, 2017, 168, 159–171.
12. L. Tang, Nat. Methods, 2019, 16, 18.
13. S. Koga, D. S. Williams, A. W. Perriman and S. Mann, Nat. Chem., 2011, 3, 720–724.
14. Z. Fetahaj, L. Ostermeier, H. Cinar, R. Oliva and R. Winter, J. Am. Chem. Soc., 2021, 143, 5247–5259.
15. D. Kota, R. Prasad and H.-X. Zhou, bioRxiv, 2023, 2023-08.
16. S. Mann, Angew. Chem., Int. Ed., 2013, 52, 155–162.
17. J. C. Ferreon, A. Jain, K.-J. Choi, P. S. Tsoi, K. R. MacKenzie, S. Y. Jung and A. C. Ferreon, Int. J. Mol. Sci., 2018, 19, 1360.
18. M. Saito, D. Hess, J. Eglinger, A. W. Fritsch, M. Kreysing, B. T. Weinert, C. Choudhary and P. Matthias, Nat. Chem. Biol., 2019, 15, 51–61.
19. A. Patel, L. Malinovska, S. Saha, J. Wang, S. Alberti, Y. Krishnan and A. A. Hyman, Science, 2017, 356, 753–756.
20. J. Kang, L. Lim and J. Song, Commun. Biol., 2019, 2, 223.
21. J. Mehringer, T.-M. Do, D. Touraud, M. Hohenschutz, A. Khoshsima, D. Horinek and W. Kunz, Cell Rep. Phys. Sci., 2021, 2, 100343.
22. M. Zalar, J. Bye and R. Curtis, J. Am. Chem. Soc., 2023, 145, 929–943.
23. C. Exley, NeuroReport, 1997, 8, 3411–3414.
24. R. Dec, M. W. Jaworek, W. Dzwolak and R. Winter, J. Am. Chem. Soc., 2023, 145, 4177–4186.
25. R. S. Fisher and S. Elbaum-Garfinkle, Nat. Commun., 2020, 11, 4628.
26. A. Jain, S. Kassem, R. S. Fisher, B. Wang, T.-D. Li, T. Wang, Y. He, S. Elbaum-Garfinkle and R. V. Ulijn, J. Am. Chem. Soc., 2022, 144, 15002–15007.
27. A. M. Tayar, F. Caballero, T. Anderberg, O. A. Saleh, M. Cristina Marchetti and Z. Dogic, Nat. Mater., 2023, 1–8.
28. Y. Xing, N. Andrikopoulos, Z. Zhang, Y. Sun, P. C. Ke and F. Ding, Biomacromolecules, 2022, 23, 4179–4191.
29. L.-W. Chang, T. K. Lytle, M. Radhakrishna, J. J. Madinya, J. Vélez, C. E. Sing and S. L. Perry, Nat. Commun., 2017, 8, 1273.
30. R. Dec, W. Dzwolak and R. Winter, J. Am. Chem. Soc., 2024, 146, 6045–6052.
31. M. Piejko, R. Dec, V. Babenko, A. Hoang, M. Szewczyk, P. Mak and W. Dzwolak, J. Biol. Chem., 2015, 290, 5947–5958.
32. R. Dec and W. Dzwolak, Langmuir, 2020, 36, 12150–12159.
33. D. A. Case, H. M. Aktulga, K. Belfon, I. Ben-Shalom, S. R. Brozell, D. S. Cerutti, T. E. Cheatham III, V. W. D. Cruzeiro, T. A. Darden and R. E. Duke, et al., Amber 2020, University of California, San Francisco, 2020.
34. W. L. Jorgensen, J. Chandrasekhar, J. D. Madura, R. W. Impey and M. L. Klein, J. Chem. Phys., 1983, 79, 926–935.
35. H. J. Berendsen, J. v Postma, W. F. Van Gunsteren, A. DiNola and J. R. Haak, J. Chem. Phys., 1984, 81, 3684–3690.
36. J. A. Maier, C. Martinez, K. Kasavajhala, L. Wickstrom, K. E. Hauser and C. Simmerling, J. Chem. Theory Comput., 2015, 11, 3696–3713.
37. J.-P. Ryckaert, G. Ciccotti and H. J. Berendsen, J. Comput. Phys., 1977, 23, 327–341.
38. T. Darden, D. York and L. Pedersen, J. Chem. Phys., 1993, 98, 10089–10092.
39. D. H. de Jong, G. Singh, W. D. Bennett, C. Arnarez, T. A. Wassenaar, L. V. Schafer, X. Periole, D. P. Tieleman and S. J. Marrink, J. Chem. Theory Comput., 2013, 9, 687–697.
40. C. F. Schroer, L. Baldauf, L. van Buren, T. A. Wassenaar, M. N. Melo, G. H. Koenderink and S. J. Marrink, Proc. Natl. Acad. Sci. U. S. A., 2020, 117, 5861–5872.
41. L. Martnez, R. Andrade, E. G. Birgin and J. M. Martnez, J. Comput. Chem., 2009, 30, 2157–2164.
42. Y. Tang, S. Bera, Y. Yao, J. Zeng, Z. Lao, X. Dong, E. Gazit and G. Wei, Cell Rep. Phys. Sci., 2021, 2, 100579.
43. G. Bussi, D. Donadio and M. Parrinello, J. Chem. Phys., 2007, 126, 014101.
44. M. Parrinello and A. Rahman, J. Appl. Phys., 1981, 52, 7182–7190.
45. S. Nosé and M. Klein, Mol. Phys., 1983, 50, 1055–1076.
46. I. G. Tironi, R. Sperb, P. E. Smith and W. F. van Gunsteren, J. Chem. Phys., 1995, 102, 5451–5459.
47. D. H. De Jong, S. Baoukina, H. I. Ingólfsson and S. J. Marrink, Comput. Phys. Commun., 2016, 199, 1–7.
48. M. J. Abraham, T. Murtola, R. Schulz, S. Páll, J. C. Smith, B. Hess and E. Lindahl, SoftwareX, 2015, 1, 19–25.
49. W. Humphrey, A. Dalke and K. Schulten, J. Mol. Graphics, 1996, 14, 33–38.
50. R. Alessandri, F. Grünewald and S. J. Marrink, Adv. Mater., 2021, 33, 2008635.
51. P. C. Souza, R. Alessandri, J. Barnoud, S. Thallmair, I. Faustino, F. Grünewald, I. Patmanidis, H. Abdizadeh, B. M. Bruininks and T. A. Wassenaar, et al. , Nat. Methods, 2021, 18, 382–388.
52. S. J. Marrink, H. J. Risselada, S. Yefimov, D. P. Tieleman and A. H. De Vries, J. Phys. Chem. B, 2007, 111, 7812–7824.
53. X. Periole and S.-J. Marrink, Biomolecular simulations: Methods and protocols, 2013, pp. 533–565.
54. S. O. Yesylevskyy, L. V. Schäfer, D. Sengupta and S. J. Marrink, PLoS Comput. Biol., 2010, 6, e1000810.
55. Z. Jarin, J. Newhouse and G. A. Voth, J. Chem. Theory Comput., 2021, 17, 1170–1180.
56. J. N. Israelachvili, The Handbook of Surface Imaging and Visualization, CRC Press, 2022, pp. 793–816.
57. B. Zagrovic, G. Jayachandran, I. S. Millett, S. Doniach and V. S. Pande, J. Mol. Biol., 2005, 353, 232–241.
58. S. Bag, M. K. Meinel and F. Müller-Plathe, J. Chem. Theory Comput., 2022, 18, 7108–7120.
59. C. A. Lemarchand, M. Couty and B. Rousseau, J. Chem. Phys., 2017, 146, 074904.
60. C.-C. Fu, P. M. Kulkarni, M. S. Shell and L. G. Leal, J. Chem. Phys., 2013, 139, 094107.
61. S. W. de Leeuw, J. W. Perram and E. R. Smith, Proc. R. Soc. London, Ser. A, 1980, 373, 27–56.
62. M. Neumann, Mol. Phys., 1983, 50, 841–858.
63. Z. Ou and M. Muthukumar, J. Chem. Phys., 2006, 124, 154902.
64. D. P. Valencia and F. J. González, Electrochem. Commun., 2011, 13, 129–132.
65. Y. Wang, D. Xiang, S. Chen and G. Yang, Molecules, 2023, 28, 6707.
66. R. Dec, W. Puławski and W. Dzwolak, J. Mater. Chem. B, 2021, 9, 8626–8630.
67. X. Ou, Y. Lao, J. Xu, Y. Wutthinitikornkit, R. Shi, X. Chen and J. Li, JACS Au, 2021, 1, 1766–1777.
68. D. J. Craik, D. P. Fairlie, S. Liras and D. Price, Chem. Biol. Drug Des., 2013, 81, 136–147.
69. M. J. Rybin, H. O’Brien, I. B. L. Ramiro, L. Azam, J. M. McIntosh, B. M. Olivera, H. Safavi-Hemami and D. Yoshikami, Toxins, 2020, 12, 197.
70. E. Lenci and A. Trabocchi, Chem. Soc. Rev., 2020, 49, 3262–3277.

---

Footnote

† Electronic supplementary information (ESI) available: System summary; radius of gyration under different ionic concentrations; radial distribution function on the effect of ATPs and ionic concentrations; determination of the threshold distance; diffusion coefficient; solvent accessible surface area; investigation of the preference for high flexibility; propensity of LLPS formation when releasing entropy; all data and scripts are available from the corresponding author upon reasonable request. See DOI: https://doi.org/10.1039/d4cp00761a

---