Photochemical formation of the elusive Dewar isomers of aromatic systems: why are substituted azaborines different?

Abstract

Photochemical reactions enabling efficient transformation of aromatic systems into energetic but stable non-aromatic isomers have a long history in organic chemistry. One recently discovered reaction in this realm is that where derivatives of 1,2-azaborine, a compound isoelectronic with benzene in which two adjacent C atoms are replaced by B and N atoms, form the non-hexagon Dewar isomer. Here, we report quantum-chemical calculations that explain both why 1,2-azaborine is intrinsically more reactive toward Dewar formation than benzene, and how suitable substitutions at the B and N atoms are able to increase the corresponding quantum yield. We find that Dewar formation from 1,2-azaborine is favored by a pronounced driving force that benzene lacks, and that a large improvement in quantum yield arises when the reaction of substituted 1,2-azaborines proceeds without involvement of an intermediary ground-state species. Overall, we report new insights into making photochemical use of the Dewar isomers of aromatic compounds.

---

Introduction

In 1929, Lonsdale used X-ray diffraction to corroborate August Kekulé's proposal some 60 years earlier that benzene adopts a structure in which the six C atoms are arranged to form a regular hexagon, with each C atom bonded to a H atom.¹ Interestingly, some of the alternative proposals from the same era, including Ladenburg's prismane structure and Dewar's bicyclo[2.2.0]hexadiene structure (subsequently called Dewar benzene), were many years later (starting in 1968) found as products of benzene photolysis.^2–5 Specifically, these isomers (see Fig. 1a), which are commonly referred to as valence-bond isomers of benzene,⁶ were formed upon irradiation of benzene using vacuum UV light, albeit with very low quantum yields.^2–5 Around the same time and later, these findings triggered the search for valence-bond isomers of other aromatic and heteroaromatic compounds, leading to the detection of Dewar isomers of pyridines,^7–10 naphthalenes¹¹ and anthracenes¹² as photolysis products of their corresponding parent compounds.

Fig. 1 (a) Structures of valence-bond isomers of benzene identified in photolysis experiments. (b) Structures of azaborine (left) and its Dewar isomer (right).

Beginning in the 1990s, the Dewar isomers of different aromatic and heteroaromatic compounds started attracting attention from computational chemists, who used quantum-chemical methods to study their ground-state properties.^13–17 For example, it was shown that these and all other valence-bond isomers are highly energetic, typically lying more than 200 kJ mol⁻¹ above their parent compounds.^13–17 Despite their high energy content, many Dewar species are predicted to be reasonably stable, as they are separated from the parent compounds by large energy barriers.^18–20 As for the possibility to pursue photochemical synthesis of Dewar species, quantum-chemical modelling has also shown that the photoisomerization reactions through which they are formed proceed in singlet excited states,^18,20 as originally suggested for Dewar benzene.³ Thus, if such synthesis is attempted, addition of triplet sensitizers or removal of triplet quenchers is not required. However, any potential application of Dewar species that involves their photochemical formation is challenged by the fact that these processes generally exhibit rather low quantum yields. For example, for Dewar benzene and Dewar pyridine, the quantum yields are as low as 0.006² and 0.07,⁷ respectively. Hence, for applications, other arenes or heteroarenes should likely be considered.

1,2-Dihydro-1,2-azaborine, from now on azaborine, is a well-known compound^21,22 isoelectronic with benzene in which two adjacent C atoms are replaced by B and N atoms (see Fig. 1b). Prior to 2009, most efforts to synthesize azaborines focused on 1,2-disubstituted derivatives, as these positions had to be prefunctionalized to achieve the desired reactivity.^23–25 Then, in 2009, Dixon and Liu and their co-workers presented the first synthetic route giving access to the pristine compound, which turned out to be stable (consistent with substantial aromatic character) and showed no appreciable degradation when subjected to high-temperature conditions for several days.²⁶ These researchers also compared the electronic properties of azaborine to those of benzene and borazine (another benzene-isoelectronic compound in which all six C atoms are replaced by alternating B and N atoms) through measurements of UV-vis absorption spectra in pentane. Relative to these systems, the absorption of azaborine is strongly red-shifted, with the most intense bands peaking at 269 (azaborine), 208 (benzene) and 203 nm (borazine), respectively.²⁶

Shortly thereafter, in 2012, the first photolysis experiments of azaborine were reported.²⁷ Using low-temperature Ne/Ar/Xe matrices and a low-pressure Hg lamp (254 nm), conversion of azaborine into a photoproduct was observed within 105 minutes.²⁷ By comparing the IR spectrum of the photoproduct with calculated IR spectra of potential structures, the photoproduct was identified as the Dewar isomer of azaborine featuring a single bond between the C₃ and C₆ atoms (those adjacent to the B and N atoms, see Fig. 1b).²⁷ A few years later, Liu and Bettinger and their co-workers presented two azaborine derivatives, bearing a silyl group at the N atom and a mesityl group or Cl atom at the B atom, capable of achieving high quantum yields (up to 0.46) for Dewar formation.²⁸ Combined with the finding that both of the corresponding Dewar isomers show sizable barriers for the thermal ring-opening reaction back to the parent isomer, these results point to the possibility of using azaborines for future applications in solar-energy storage.²⁸

In this context, molecular photoswitches tailored to convert solar energy into chemical energy and then back into heat are often referred to as molecular solar thermal energy (MOST) systems.^29–32 However, despite the existence of several promising MOST systems (based on, e.g., azobenzene, norbornadiene and dihydroazulene photoswitches),³⁰ it has proven very difficult for any single one of them to simultaneously meet all photophysical and thermochemical requirements for viable applications in solar-energy storage.^30,31,33,34 Besides showing a high quantum yield for the photoisomerization that produces the energy-storing isomer and a large barrier for the thermal back-reaction (so as to enable long storage times), other desirable characteristics include a high energy density, UV-vis absorption in the violet-blue regime, and minimal spectral overlap between the parent and energy-storing isomers.^31,32

Given the fundamental importance of an efficient photoisomerization step for the utility of a MOST system, optimizing azaborines for such applications will likely require a better understanding of their photochemistry than currently available. Based on quantum-chemical calculations, it has been found that the photoisomerization of azaborine in the first singlet excited state (S₁) that produces the C₃–C₆ bond is more favorable than photoisomerizations forming a N–C₄ or B–C₅ bond.³⁵ Furthermore, it has been shown that azaborine features an easily accessible conical intersection (CI) between the S₁ and ground S₀ states, which is connected to both the parent species and a prefulvene-like structure containing a B–C₆ bond.³⁶ The latter structure is quite unstable, and can evolve through small energy barriers to either the parent species or the C₃–C₆ Dewar isomer.³⁶ Recently, these results were corroborated by means of non-adiabatic molecular dynamics (NAMD) simulations, from which it was concluded that the prefulvene-like structure is indeed a key mechanistic element for the photochemistry of azaborine, mediating both the regeneration of the parent species and the formation of the Dewar isomer.³⁷ However, the quantum yield for Dewar formation extractable from these simulations appears much too low (only a few percent³⁷) compared to the experimental observations.²⁷

Despite the many insights provided by the aforementioned studies, a more thorough appreciation of the unique photochemistry of azaborines and their potential for future applications will require resolving a number of fundamental issues, which are yet to be explored. Firstly, it is crucial to understand exactly how and why the photochemistry of azaborine is different from that of archetypal benzene with respect to Dewar formation. Secondly, it is equally important to explain the origin of the favorable (for Dewar azaborine formation) substituent effects observed by Liu and Bettinger in 2018.²⁸ As a first step towards filling these gaps, we here present a detailed comparison of the photochemistry of benzene, azaborine and their 1-silyl-2-chloro-substituted counterparts (see Fig. 2) in the S₁ state using both static quantum-chemical calculations and semi-classical NAMD simulations^38,39 based on time-dependent density functional theory (TD-DFT).⁴⁰ Moreover, the TD-DFT modelling is complemented by calculations based on complete active space self-consistent field (CASSCF) theory.⁴¹ Through these endeavors, we are able to identify key electronic and structural features that make azaborine more prone than benzene to form the Dewar isomer, and allow substituted azaborines to attain much higher quantum yields for Dewar formation than the parent species.

Fig. 2 Molecules studied in this work (from left to right and from top to bottom): benzene, azaborine, 1-silyl-2-chlorobenzene and 1-silyl-2-chloroazaborine. The atom-numbering schemes displayed are used throughout the paper. 1-Silyl-2-chloroazaborine is very similar to one of the substituted azaborines studied by Liu and Bettinger,²⁸ except that it harbors the simplest possible silyl group (SiH₃) instead of a tert-butyldimethylsilyl group for computational expedience. We do not expect the neglected alkyl groups to have any significant impact on the formation of the Dewar isomer.

Results and discussion

UV-vis absorption spectra

In order to assess the accuracy of the adopted DFT-based computational methodology relative to both previous modelling studies and experimental data, our first task was to calculate vertical transition energies for the five lowest singlet excited states of each of the four molecules in Fig. 2. As can be seen from Table 1, all transitions lie in the UV-C regime (<280 nm, >4.43 eV), with the S₀ → S₁ transition for the two azaborines being red-shifted by ca. 0.35 eV relative to the S₀ → S₁ transition for their benzene counterparts. Furthermore, from the corresponding oscillator strengths, it is clear that whereas the S₀ → S₁ transition is strongly allowed for the C_s-symmetric azaborines, it is forbidden for the benzenes (D_6h and C_s). Notably, the S₀ → S₁ energy of 5.18 eV obtained for the plain azaborine agrees very well with previous high-level, ab initio calculations, which have yielded values of 5.15 (using the multireference configuration interaction method³⁶) and 5.16 eV (using the equation-of-motion coupled cluster singles and doubles method³⁷) for this transition.

Table 1 Calculated vertical transition energies (ΔE and λ, in eV and nm, respectively) and oscillator strengths (f) for the molecules studied in this work

Transition	Benzene			1-Silyl-2-chlorobenzene			Azaborine			1-Silyl-2-chloroazaborine
	ΔE	λ	f	ΔE	λ	f	ΔE	λ	f	ΔE	λ	f
S0 → S1	5.53	224	0.00	5.24	237	0.01	5.18	239	0.16	4.90	253	0.15
S0 → S2	6.24	199	0.00	5.84	212	0.05	6.20	200	0.08	6.12	203	0.06
S0 → S3	7.55	164	0.00	6.56	189	0.00	6.45	192	0.00	6.39	194	0.00
S0 → S4	7.55	164	0.00	6.70	185	0.74	6.66	186	0.00	6.42	193	0.00
S0 → S5	7.94	156	0.00	6.76	183	0.37	7.47	166	0.00	7.26	171	0.00

---

Next, in order to also evaluate the computational methodology relative to experimental data,²⁶ we calculated the UV-vis absorption spectra of the four molecules by describing their nuclear motion around the respective S₀ minimum through Wigner sampling from harmonic vibrational frequencies.^42,43 The resulting spectra, shown in Fig. 3, reveal that the breaking of planar symmetry allows some forbidden transitions to take place. For benzene and azaborine, the absorption maxima occur at 208 and 246 nm, respectively, which are reasonably close to the positions of 208 and 269 nm recorded experimentally in a pentane solvent²⁶ (notwithstanding the fact that we have here chosen to not include solvent effects in the modelling). For 1-silyl-2-chloroazaborine, the absorption maximum is further red-shifted to 262 nm, which reflects the observation in Table 1 that the silyl group and Cl atom exert a red-shifting effect on each of the five lowest excited states. Notably, owing to the molecular motion, 1-silyl-2-chloroazaborine is even predicted to exhibit some residual absorption in the UV-B regime (280–315 nm).

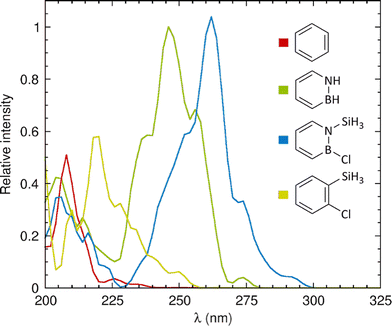Fig. 3 Calculated UV-vis absorption spectra of the molecules studied in this work. Intensities are given relative to that of the main band of azaborine (whose intensity is set to 1).

NAMD simulations

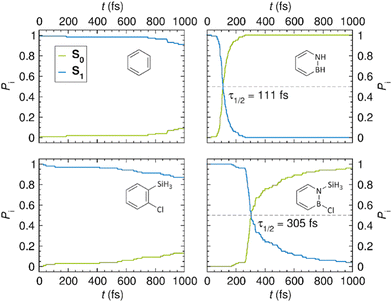
As noted in the Introduction, a central goal of this work is to gain an understanding of why the S₁ state of azaborines is more reactive towards Dewar formation than the S₁ state of benzene. Thus, we are concerned with identifying key features of this state, and its interplay with the ground S₀ state, that promote Dewar formation. For this reason, all modelling performed to address these issues focused exclusively on the S₁ and S₀ states, so as to ensure a balanced comparison of the four systems under study. Although such an approach does not account for the proposal that Dewar benzene might be formed from the second singlet excited state (S₂),³ this incongruence is of no consequence given the very low quantum yield (0.006) with which Dewar benzene is produced.² That this approach is sound is also attested by the many previous studies devoted to investigating the photochemical reactivity of aromatic compounds in the S₁ state.⁴⁴

Having tested the performance of the DFT-based computational methodology, we then proceeded to model the photodynamics of the four systems by means of NAMD simulations. For each system, the simulations were run for ca. 1 ps with 100 different initial nuclear geometries and velocities starting from the vertically excited S₁ Franck–Condon (FC) points of these geometries. At any given time during the simulations, the classical populations P₀ and P₁ of the S₀ and S₁ states were obtained (following the usual convention) as the proportions of trajectories evolving in the respective state at that particular time. From these populations, the S₁ lifetime – denoted τ_1/2 – was estimated as the time it takes before the two states become equally populated.

For each system, Fig. 4 plots the time evolution of the classical populations of the S₀ and S₁ states predicted by the NAMD simulations. Interestingly, from these results, it can be inferred that the photophysical behavior of the azaborines is rather different from that of their benzene counterparts. As for the latter, only 9 (benzene) and 13% (1-silyl-2-chlorobenzene) of the trajectories have decayed back to the S₀ state after 1 ps of simulation. In sharp contrast, the former show full (100%, azaborine) or almost full (96%, 1-silyl-2-chloroazaborine) S₀ recovery within the same time frame. Furthermore, from the observation of a rather substantial difference in the S₁ lifetimes of azaborine (111 fs) and 1-silyl-2-chloroazaborine (305 fs), the photophysical behavior of the plain azaborine appears more controllable through functionalization than what is the case for benzene.

Fig. 4 Time evolution of the classical populations (P_i) of the S₀ and S₁ states of benzene (top left), azaborine (top right), 1-silyl-2-chlorobenzene (bottom left) and 1-silyl-2-chloroazaborine (bottom right) predicted by the NAMD simulations. For azaborine and 1-silyl-2-chloroazaborine, the grey-dashed line indicates equal populations of the S₀ and S₁ states.

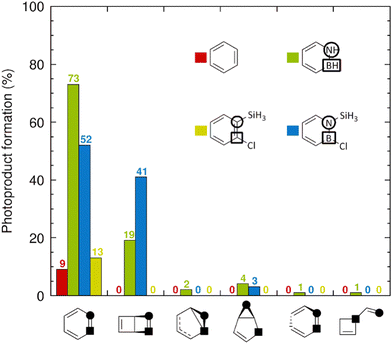
Next, we analyzed the distributions of species formed upon internal conversion (IC) to the S₀ state. The corresponding results are shown as histograms in Fig. 5, in which each molecule is represented by a specific color. After 1 ps, all 9 trajectories (= 9% of the trajectories) for benzene (red) and all 13 trajectories for 1-silyl-2-chlorobenzene (yellow) that did decay to the S₀ state have reformed the parent benzene and 1-silyl-2-chlorobenzene species, respectively, without producing Dewar or other photoproducts. Loosely, the complete absence of Dewar photoproducts in the simulations of these compounds is consistent with the minuscule quantum yield assigned to Dewar benzene in benzene photolysis.² Contrarily, among the 96 trajectories for 1-silyl-2-chloroazaborine that decayed to the S₀ state, 41 of them formed the corresponding Dewar photoproduct. Notably, this result corroborates the finding by Liu and Bettinger that 1,2-disubstituted azaborines can achieve rather high quantum yields for Dewar formation (e.g., 0.46 for an azaborine bearing a tert-butyldimethylsilyl group at the N atom and a mesityl group at the B atom).²⁸ Among the remaining 96 − 41 = 55 trajectories, 52 reformed the parent 1-silyl-2-chloroazaborine species, whereas only 3 formed another photoproduct (a dihydroborole derivative) than the Dewar one.

Fig. 5 Photoproduct distributions after 1 ps of NAMD simulations. The photoproduct structures represented by the different bins are given below the bins (the leftmost bin is for the parent species, the second leftmost bin is for the Dewar photoproduct, and the other bins are for alternative photoproducts). For each system, the percentage of trajectories that remain in the S₁ state is obtained by subtracting the sum of all photoproduct percentages from 100%.

Turning to the unsubstituted azaborine in Fig. 5, among the 100 trajectories (= 100% of the trajectories) that underwent comparatively faster (than in 1-silyl-2-chloroazaborine) S₀ recovery, 19 of them formed the Dewar photoproduct. Thereby, the associated quantum yield can be estimated to be about two-fold lower than that for 1-silyl-2-chloroazaborine. Moreover, for the unsubstituted azaborine, the proportion of alternative (to Dewar) photoproducts produced is higher (8 vs. 3% for 1-silyl-2-chloroazaborine), with four such photoproducts detected. Taken together, the NAMD results in Fig. 5 support two main conclusions that are consistent with experimental observations.^27,28 First, whereas photoexcitation to the S₁ state does not promote formation of Dewar benzene, photoisomerization of azaborine into Dewar azaborine is possible in this state and occurs with non-negligible quantum yield.²⁷ Second, this quantum yield can be improved by introducing suitable substituents at the B and N atoms.²⁸ However, the NAMD simulations provide no rationale for these findings. Therefore, in the next section, we will present electronic and structural factors, identified from S₀ and S₁ potential energy surfaces (PESs) calculated with static DFT methods, that do explain these results.

Potential energy surfaces

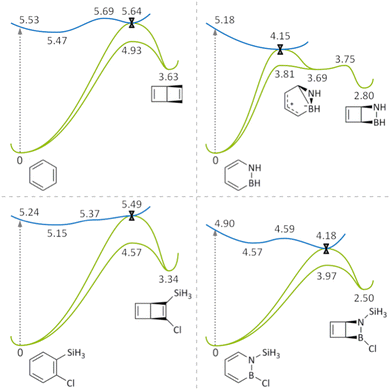
Fig. 6 summarizes the regions of the S₀ and S₁ PESs of benzene, azaborine, 1-silyl-2-chlorobenzene and 1-silyl-2-chloroazaborine relevant for the photoisomerization reactions into their Dewar forms. Given that Dewar formation is indeed the central focus of this work, Fig. 6 does not include any of the alternative reaction pathways that are possible for these molecules following IC to the S₀ state, as evidenced by the appearance of other (than Dewar) photoproducts in the NAMD simulations. Nonetheless, for the case of the unsubstituted azaborine, we will return to a discussion of such pathways below. Besides Fig. 6, results from complementary CASSCF-based calculations (which corroborate the results in Fig. 6) are presented in Section S1 of the ESI.†

Fig. 6 Calculated S₀ (green) and S₁ (blue) PESs of benzene (top left), azaborine (top right), 1-silyl-2-chlorobenzene (bottom left) and 1-silyl-2-chloroazaborine (bottom right), with dashed vertical lines indicating photoexcitation to the respective S₁ FC point and local maxima corresponding to transition structures (TSs). S₁/S₀ CIs are indicated with hourglass symbols. For each system, electronic energies of the relevant structures (stationary points, the S₁ FC point, and the S₁/S₀ CI) are given in eV relative to the corresponding S₀ global minimum.

Starting with benzene and 1-silyl-2-chlorobenzene, their PESs are qualitatively very similar (Fig. 6, left column). Following photoexcitation to the respective S₁ FC point, in both systems subsequent relaxation populates a planar S₁ minimum slightly below the FC point (0.06 eV below for benzene and 0.09 eV below for 1-silyl-2-chlorobenzene). Furthermore, in both systems, reaching the S₁/S₀ CI that acts as a funnel for the formation of the S₀ Dewar isomer from the S₁ minimum is an energetically uphill process. In fact, for benzene/1-silyl-2-chlorobenzene, this funnel lies 0.17/0.34 eV above the S₁ minimum and 0.11/0.25 eV above the S₁ FC point. For this reason, photoexcitation to the S₁ state does not seem to provide sufficient energy for accessing these structures, which explains the observation from the NAMD simulations that the benzenes are unlikely to form the S₀ Dewar isomer from this state (see Fig. 5). The actual geometries of the CIs (including those for azaborine and 1-silyl-2-chloroazaborine) are shown in Section S2 of the ESI.† While the reaction coordinates leading to the CIs are multidimensional, which is generally the case in photochemistry⁴⁵ and explains why no particular reaction coordinate is specified in Fig. 6, Section S2 of the ESI† also presents some data for assessing relevant structural changes along the respective coordinate.

Continuing with the azaborines, their PESs (Fig. 6, right column) show a major difference relative to the benzenes in that the S₁/S₀ CI now lies well below the S₁ FC point (1.03 eV below for azaborine and 0.72 eV below for 1-silyl-2-chloroazaborine), and thus is much more easily accessible. This difference provides a rationale why the likelihood of Dewar formation in the NAMD simulations is so much higher for the azaborines than for the benzenes (see Fig. 5). As for the unsubstituted azaborine, the S₁/S₀ CI is reached in a barrierless fashion, which is consistent with its short S₁ lifetime of 111 fs (see Fig. 4). This CI is connected to a prefulvene-like S₀ minimum (at 3.69 eV) in one direction, and to the S₀ parent species in the other. The prefulvene-like minimum, which was also found in previous studies,^36,37 can evolve through a small energy barrier to either the S₀ Dewar isomer (barrier of 0.06 eV) or the S₀ parent species (0.12 eV). Accordingly, this minimum is a sort of pivotal point steering the competition between these two pathways. Taken together, these results identify a route through which formation of the S₀ Dewar isomer from the S₁ state of an unsubstituted azaborine is an energetically favorable process. Altogether, the S₀ dynamics following IC at the S₁/S₀ CI has at least three different components (formation of the Dewar isomer through the prefulvene-like minimum, formation of the parent species through the prefulvene-like minimum, and direct formation of the parent species), which are further discussed in terms of calculated NAMD trajectories in Section S3 of the ESI.†

As for the 1-silyl-2-chloroazaborine, its substituents have two effects on the calculated PESs in Fig. 6 relative to those of the unsubstituted azaborine. The first effect is the appearance of a minimum on the S₁ PES, 0.33 eV below the FC point. Featuring a slight ring puckering at the N atom, this minimum is not equivalent to the aforementioned planar minima on the S₁ PESs of benzene and 1-silyl-2-chlorobenzene. Furthermore, being separated from the S₁/S₀ CI by an energy barrier of just 0.02 eV, this minimum is very shallow and does not appear to have a negative influence on Dewar formation, as judged by the fact that the number of NAMD trajectories forming the Dewar isomer are about twice as many for 1-silyl-2-chloroazaborine than for azaborine (see Fig. 5). However, albeit tiny, this barrier may be responsible for the longer S₁ lifetime (305 vs. 111 fs) shown by 1-silyl-2-chloroazaborine. The second effect attributable to the substituents of 1-silyl-2-chloroazaborine is the disappearance of the prefulvene-like minimum on the S₀ PES (in fact, all attempts to locate such a minimum produced the Dewar isomer). In the absence of such a minimum, the S₁/S₀ CI is instead connected directly to the Dewar isomer in one reaction channel, and to the parent species in the other. This direct route to the Dewar isomer, combined with the fact that the absence of a prefulvene-like minimum also eliminates an alternative reaction channel back to the parent species, offers a simple explanation why 1-silyl-2-chloroazaborine shows a much higher quantum yield for Dewar formation than the unsubstituted azaborine (see Fig. 5).

Given that our work focuses on photoconversion of benzene, azaborine, 1-silyl-2-chlorobenzene and 1-silyl-2-chloroazaborine into their Dewar isomers, the PESs in Fig. 6 do not include any of the alternative reaction pathways that are possible for these molecules following IC to the S₀ state. However, for the case of the unsubstituted azaborine, Fig. 7 illustrates the regions of the S₀ PES that, starting from the prefulvene-like minimum (labeled I1), describe such pathways for the formation of alternative (to Dewar) photoproducts detected by the NAMD simulations. Here, for reference, the pathway leading to the Dewar isomer (labeled P1) and the pathway leading back to the parent azaborine (labeled S₀ FC), which were shown already in Fig. 6, are displayed in black color, whereas the alternative pathways are displayed in red, green and blue colors, respectively. Notably, the I1 → P1 reaction is indeed the kinetically preferred pathway, having an energy barrier that is smaller (0.06 eV) than that for the I1 → S₀ FC (0.12 eV) process and those for all other competing pathways. Furthermore, the high (0.95 eV) barrier for the P1 → I1 back-reaction ensures that the Dewar isomer is stable. As a complement to Fig. 7, the optimized geometries of the potential-energy minima along the different pathways are shown in Section S4 of the ESI.†

Fig. 7 Calculated S₀ PES of azaborine comparing different reaction pathways starting from the I1 prefulvene-like minimum formed upon IC at the S₁/S₀ CI. Electronic energies of stationary points (minima and TSs) are given in eV relative to the S₀ global minimum (labeled S₀ FC).

Besides the I1 → P1 and I1 → S₀ FC reactions in Fig. 7, a third pathway is that producing the P2 5,6-E-azaborine, which is displayed in red color in Fig. 7 and has a barrier of 0.32 eV. However, even if formed, this structure appears to be rather unstable, reverting back to I1via a very small barrier of 0.05 eV. A fourth pathway is the formation of the P3 dihydroborole, which is shown in green color in Fig. 7 and proceeds in two steps. In the first, a N–C₅ bond is formed to produce the benzvalene-like I2 intermediate through a barrier of 0.43 eV. This intermediate is then cleaved to yield P3 in a nearly barrierless (0.01 eV) process. The fifth and final pathway considered is the four-step formation of the P4 dihydroborete represented in blue color in Fig. 7. In the first step, the C₅–C₆ bond of I1 is cleaved to form the singlet-biradical I3 intermediate via a very large barrier of 2.84 eV. Rotation of the B–C₃ bond and cleavage of the B–N bond subsequently produce, through a barrier of 0.15 eV, the linear singlet-biradical I4 intermediate, which evolves to the closed-shell I5 intermediate by means of hydrogen migration (barrier of 0.44 eV). Finally, the P4 dihydroborete is furnished by an electrocyclic ring-closure reaction (barrier of 0.13 eV). However, because of the considerable barrier for the first step, the likelihood that the P4 species is formed should be very small, which is also what the NAMD simulations in Fig. 5 of the main text predict (1%). Altogether, then, the results in Fig. 7 suggest that the two predominant reaction channels originating from the I1 prefulvene-like minimum are those producing the Dewar isomer (I1 → P1) or the parent azaborine (I1 → S₀ FC), which, again, is consistent with the NAMD results in Fig. 5 (indeed, 92% of the NAMD trajectories form either P1 or S₀ FC).

Finally, we also sought to provide a further explanation for the difference between the azaborines and the benzenes in their reactivity towards Dewar formation rooted in the principle of least motion. First proposed by Rice and Teller in 1938, this principle asserts that “there shall be least change in atomic position and least change in electronic configuration during an elementary reaction”.⁴⁶ Refined throughout the years,^47,48 this principle has remained a fruitful framework for rationalizing chemical reactivity.^49–54 Here, as we have explored one and the same reaction, the changes in atomic positions along the pathways mapped out by the calculated PESs are very similar. For this reason, we instead focused on changes in electron density. Specifically, using densities calculated with TD-DFT, we evaluated the changes in S₁ natural bond orbital (NBO) charges⁵⁵ at the atomic positions along the S₁ PESs of the four systems, as they evolve from the FC point to the CI. Using the corresponding NBO charges at the FC point as reference, these results are presented in Fig. 8, in which a red color indicates an increase in electron density (i.e., a decrease in atomic charge) and a green color indicates a decrease in electron density (i.e., an increase in atomic charge).

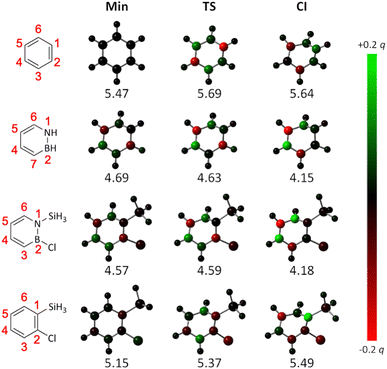Fig. 8 Changes in S₁ NBO charges along the S₁ PESs in Fig. 6 (below each structure is given its electronic energy in eV relative to the corresponding S₀ global minimum). A red color indicates an increase in electron density (i.e., a decrease in atomic charge) and a green color indicates a decrease in electron density (i.e., an increase in atomic charge) at that position relative to the electron density at the S₁ FC point. As the S₁ PES of azaborine does not feature any minimum or TS (see Fig. 6), structures obtained by replacing the silyl group and Cl atom at the minimum and the TS on the S₁ PES of 1-silyl-2-chloroazaborine with two H atoms (and reoptimizing just the positions of these H atoms) were considered for the corresponding calculations.

Interestingly, it can be seen that the changes in NBO charges are very different in the two groups of molecules. For the azaborines, the changes are largely monotonous, as exemplified by the decrease in electron density at the C₄ and C₆ positions (these positions go from being black/dark-green-colored to being bright-green-colored as the CI is approached), and the increase in electron density at the C₅ position (this position goes from being black/dark-red-colored to being bright-red-colored as the CI is approached). In striking contrast, for the benzenes, the changes are much more variable and show no uniform trends, with some positions exhibiting a decrease/increase in electron density at one stage of the reaction and an increase/decrease at the next. Qualitatively, this means that the limited accessibility to the CI mediating Dewar formation experienced by the benzenes (as compared to the azaborines, see Fig. 6) can indeed be understood in terms of the principle of least motion.

Conclusions

In summary, using a combination of static quantum-chemical calculations and semi-classical NAMD simulations, we have investigated the S₁ photochemistry of benzene, azaborine and their 1-silyl-2-chloro-substituted counterparts, with two particular goals. The first is to explain the experimental observation that azaborine, as opposed to benzene, is able to form the Dewar isomer with a non-negligible quantum yield.²⁷ Notably, this observation is reproduced by the NAMD simulations in that 19 (azaborine) vs. 0% (benzene) of the calculated trajectories furnish the Dewar species. The second goal is to, similarly, rationalize the experimental observation that the quantum yield can be increased through suitable substitutions at the B and N atoms of azaborine,²⁸ which the NAMD simulations also account for by showing that the fraction of trajectories forming the Dewar isomer is appreciably larger for 1-silyl-2-chloroazaborine (41%) than for azaborine (19%).

As for the first goal, the higher propensity of azaborine to form the Dewar isomer can be explained by the finding that the associated S₁/S₀ CI occurs well below (by 1.03 eV) the S₁ FC point of the parent species, which provides a considerable driving force for reaching the former structure upon photoexcitation. For benzene, on the other hand, the corresponding S₁/S₀ CI lies above (by 0.11 eV) the S₁ FC point. As for the second goal, the improvement in quantum yield achieved by 1,2-disubstituted azaborines can be rationalized by the absence of the prefulvene-like minimum that is present on the S₀ PES of the unsubstituted azaborine. Rather than being linked to such a minimum, the S₁/S₀ CI is instead connected directly to the Dewar isomer, which is clearly advantageous for the formation of this species. Furthermore, the absence of this minimum also eliminates an undesirable reaction channel back to the parent 1,2-disubstituted azaborine. All in all, these results help identify strategies for tailoring the efficiency of a well known photochemical reaction for possible applications in solar-energy storage.

Computational details

S₀ and S₁ PESs were mapped by performing DFT and TD-DFT calculations, respectively, with the CAM-B3LYP range-separated hybrid density functional.⁵⁶ While potential-energy minima, TSs and minimum-energy S₁/S₀ CIs were calculated with the cc-pVDZ basis set,⁵⁷ more accurate electronic energies of the corresponding structures were obtained through single-point calculations with the larger cc-pVTZ basis set.⁵⁷ By calculating harmonic vibrational frequencies at the CAM-B3LYP/cc-pVDZ level of theory, all potential-energy minima and TSs were characterized as stationary points having only real frequencies or one imaginary frequency along the relevant normal mode, respectively. Moreover, in order to further ensure that the located TSs do indeed connect the associated reactant and product species, intrinsic reaction coordinate calculations⁵⁸ were also carried out at this level of theory. As a means to verify the TD-DFT results, single-point calculations were additionally performed with the multistate complete active space second-order perturbation theory (MS-CASPT2)^59,60 method. These calculations also employed the cc-pVTZ basis set, and were based on CASSCF⁴¹ reference wave functions optimized in a state-average fashion, utilizing equal weights for the S₀ and S₁ states. For each of the four molecules studied, the active space for the CASSCF calculations was chosen so as to include the full π-system (i.e., 6 electrons in 6 orbitals).

Vertical transition energies (at S₀ molecular geometries) and their oscillator strengths were calculated at the TD-CAM-B3LYP/cc-pVTZ level of theory. In order to model UV-vis absorption spectra, for each molecule, 100 different molecular geometries around the respective S₀ minimum were generated by means of Wigner sampling. Accordingly, as thoroughly described by Barbatti and Sen,⁴³ the nuclear phase-space is assumed to follow a Wigner distribution⁴² of S₀ harmonic vibrational frequencies, from which normal modes can be sampled and converted to Cartesian coordinates. For each of the 100 sampled sets of nuclear geometries, vertical transition energies and oscillator strengths were calculated for the five lowest singlet excited states. Based on these results, the UV-vis absorption spectrum for each individual geometry was then derived by convoluting the transitions with Gaussian functions having a half-width of 0.05 eV. Finally, by summing the resulting spectra for all geometries, the spectra shown in Fig. 3 were obtained.

NAMD simulations were carried out at the TD-CAM-B3LYP/cc-pVDZ level of theory (CAM-B3LYP/cc-pVDZ in the S₀ state) using Tully's fewest-switches surface hopping algorithm⁶¹ as implemented in TURBOMOLE.^62,63 For each system, the simulations were started from the S₁ FC points of the 100 different nuclear geometries obtained through the aforementioned Wigner sampling. For each of these geometries, initial nuclear velocities were generated randomly from a Maxwell–Boltzmann distribution at 298 K. For the classical propagation of the nuclei in Tully's method, the leapfrog Verlet algorithm⁶⁴ was used to integrate Newton's equations of motion with a fixed time step of 40 a.u. (ca. 1 fs). Propagating the nuclear trajectories through 1024 steps, the total simulation time was ca. 1 ps. For the quantum mechanical description of the electrons in Tully's method, full technical details are provided in the original literature^61–63 or in recent applications of the method.^65,66

The CASSCF and MS-CASPT2 calculations were performed with the OpenMolcas 19.11 suites of programs.⁶⁷ The NAMD simulations were carried out with the TURBOMOLE 7.5 suites of programs.⁶³ CIs were optimized with a penalty-function approach⁶⁸ as implemented in the SHARC 2.0 package⁶⁹ interfaced with the ORCA 4.2.1⁷⁰ and Gaussian 16⁷¹ packages. All other calculations were done with Gaussian 16.

Data availability

All data supporting this article are available in the main text or the ESI.†

Author contributions

E. M. A. contributed to conceptualization, formal analysis, investigation, methodology and writing – original draft. S. S. contributed to formal analysis, funding acquisition, methodology and writing – review and editing. B. D. contributed to conceptualization, formal analysis, funding acquisition, methodology, resources, supervision and writing – review and editing.

Conflicts of interest

There are no conflicts to declare.

Acknowledgements

B. D. acknowledges financial support from the Swedish Research Council (grant 2019-03664), the Olle Engkvist Foundation (grant 204-0183) and the Carl Trygger Foundation (grant CTS 20:102). S. S. acknowledges financial support from the Swedish Research Council (grant 2022-06442). The computations were enabled by resources provided by the National Academic Infrastructure for Supercomputing in Sweden (NAISS) and the Swedish National Infrastructure for Computing (SNIC) at the National Supercomputer Centre partially funded by the Swedish Research Council (grants 2022-06725 and 2018-05973).

Notes and references

1. K. Lonsdale, The structure of the benzene ring in C₆(CH₃)₆, Proc. R. Soc. Lond. A, 1929, 123, 494–515.
2. H. R. Ward and J. S. Wishnok, The vacuum ultraviolet photolysis of benzene, J. Am. Chem. Soc., 1968, 90, 5353–5357.
3. D. Bryce-Smith, A. Gilbert and D. A. Robinson, Direct transformation of the second excited singlet state of benzene into Dewar-benzene, Angew. Chem., Int. Ed. Engl., 1971, 10, 745–746.
4. L. Kaplan, D. J. Rausch and K. E. Wilzbach, Photosolvation of benzene. Mechanism of formation of bicyclo[3.1.0]hex-3-en-2-yl and of bicyclo[3.1.0]hex-2-en-6-yl derivatives, J. Am. Chem. Soc., 1972, 94, 8638–8640.
5. W. Albert Noyes Jr. and K. E. Al-Ani, The photochemistry of some simple aromatic molecules in the gaseous state, Chem. Rev., 1974, 74, 29–43.
6. E. E. Van Tamelen, Valence bond isomers of aromatic systems, Acc. Chem. Res., 1972, 5, 186–192.
7. K. E. Wilzbach and D. J. Rausch, Photochemistry of nitrogen heterocycles. Dewar pyridine and its intermediacy in photoreduction and photohydration of pyridine, J. Am. Chem. Soc., 1970, 92, 2178–2179.
8. D. E. Johnstone and J. R. Sodeau, Matrix-controlled photochemistry of benzene and pyridine, J. Phys. Chem., 1991, 95, 165–169.
9. J. W. Pavlik, N. Kebede, M. Thompson, A. Colin Day and J. A. Barltrop, Vapor-phase photochemistry of dimethylpyridines, J. Am. Chem. Soc., 1999, 121, 5666–5673.
10. S. Kudoh, M. Takayanagi and M. Nakata, Dewar pyridine studied by matrix isolation infrared spectroscopy and DFT calculation, J. Photochem. Photobiol. A: Chem., 1999, 123, 25–30.
11. W. L. Mandella and R. W. Franck, Photoisomerization of peri-di-tert-butylnaphthalenes, J. Am. Chem. Soc., 1973, 95, 971–972.
12. M. A. Meador and H. Hart, Substituent effects on the photoisomerization of anthracenes to their 9,10-Dewar isomers, J. Org. Chem., 1989, 54, 2336–2341.
13. D. W. Rogers, F. J. McLafferty, W. Fang and Y. Qi, Molecular enthalpies 3: ground-state thermodynamic and computed enthalpies of the valence isomers of benzene, Struct. Chem., 1993, 4, 161–166.
14. Y.-S. Cheung, C.-K. Wong and W.-K. Li, Ab initio calculations of the heats of formation for (CH)₆ isomers, J. Mol. Struct. Theochem., 1998, 454, 17–24.
15. U. Deva Priyakumar, T. C. Dinadayalane and G. Narahari Sastry, An ab initio and DFT study of the valence isomers of pyridine, Chem. Phys. Lett., 2001, 337, 361–367.
16. T. C. Dinadayalane, U. Deva Priyakumar and G. Narahari Sastry, Exploration of C₆H₆ potential energy surface: a computational effort to unravel the relative stabilities and synthetic feasibility of new benzene isomers, J. Phys. Chem. A, 2004, 108, 11433–11438.
17. J. R. B. Gomes and M. A. V. Ribeiro da Silva, Gas-phase enthalpies of formation of the fluorobenzenes family and their Dewar isomers from ab initio calculations, J. Mol. Struct. Theochem., 2006, 778, 77–84.
18. S. Grimme and S. D. Peyerimhoff, Theoretical study of the valence isomerization of anthracene and 9-tert-butylanthracene to their Dewar forms in ground and excited states, J. Phys. Chem., 1994, 98, 12927–12932.
19. R. P. Johnson and K. J. Daoust, Electrocyclic ring opening modes of Dewar benzenes: ab initio predictions for Möbius benzene and trans-Dewar benzene as new C₆H₆ isomers, J. Am. Chem. Soc., 1996, 118, 7381–7385.
20. M.-D. Su, Model study on the pyridine-Dewar pyridine and some related photoisomerization reactions, J. Phys. Chem. A, 2007, 111, 971–975.
21. G. C. Culling, M. J. S. Dewar and P. A. Marr, New heteroaromatic compounds. XXIII. Two analogs of triphenylene and a possible route to borazarene, J. Am. Chem. Soc., 1964, 86, 1125–1127.
22. A. J. Fritsch, Borazaromatic compounds, in Chemistry of Heterocyclic Compounds, ed. A. Weissberger and E. C. Taylor, John Wiley & Sons, 1977, vol. 30, pp. 381–440.
23. A. J. Ashe III and X. Fang, A synthesis of aromatic five- and six-membered B–N heterocycles via ring closing metathesis, Org. Lett., 2000, 2, 2089–2091.
24. A. J. Ashe III, X. Fang, X. Fang and J. W. Kampf, Synthesis of 1,2-dihydro-1,2-azaborines and their conversion to tricarbonyl chromium and molybdenum complexes, Organometallics, 2001, 20, 5413–5418.
25. J. Pan, J. W. Kampf and A. J. Ashe III, The preparation and crystal structures of η¹-derivatives of 2-phenyl-1,2-azaboratabenzene, Organometallics, 2008, 27, 1345–1347.
26. A. J. V. Marwitz, M. H. Matus, L. N. Zakharov, D. A. Dixon and S.-Y. Liu, A hybrid organic/inorganic benzene, Angew. Chem., Int. Ed., 2009, 48, 973–977.
27. S. A. Brough, A. N. Lamm, S.-Y. Liu and H. F. Bettinger, Photoisomerization of 1,2-dihydro-1,2-azaborine: a matrix isolation study, Angew. Chem., Int. Ed., 2012, 51, 10880–10883.
28. K. Edel, X. Yang, J. S. A. Ishibashi, A. N. Lamm, C. Maichle-Mössmer, Z. X. Giustra, S.-Y. Liu and H. F. Bettinger, The Dewar isomer of 1,2-dihydro-1,2-azaborinines: isolation, fragmentation, and energy storage, Angew. Chem., Int. Ed., 2018, 57, 5296–5300.
29. A. Lennartson, A. Roffey and K. Moth-Poulsen, Designing photoswitches for molecular solar thermal energy storage, Tetrahedron Lett., 2015, 56, 1457–1465.
30. Z. Wang, P. Erhart, T. Li, Z.-Y. Zhang, D. Sampedro, Z. Hu, H. A. Wegner, O. Brummel, J. Libuda, M. B. Nielsen and K. Moth-Poulsen, Storing energy with molecular photoisomers, Joule, 2021, 5, 3116–3136.
31. A. E. Hillers-Bendtsen, J. L. Elholm, O. B. Obel, H. Hölzel, K. Moth-Poulsen and K. V. Mikkelsen, Searching the chemical space of bicyclic dienes for molecular solar thermal energy storage candidates, Angew. Chem., Int. Ed., 2023, 62, e202309543.
32. E. M. Arpa and B. Durbeej, In silico design of dihydroazulene/vinylheptafulvene photoswitches for solar-energy storage guided by an all-around performance descriptor, Chem. Methods, 2023, 3, e202200060.
33. M. B. Nielsen, Molecular solar thermal energy systems and absorption tuning, ChemPhotoChem, 2019, 3, 168–169.
34. C.-L. Sun, C. Wang and R. Boulatov, Applications of photoswitches in the storage of solar energy, ChemPhotoChem, 2019, 3, 268–283.
35. M.-D. Su, Mechanistic investigations on the photoisomerization reactions of 1,2-dihydro-1,2-azaborine, Chem. – Eur. J., 2013, 19, 9663–9667.
36. J. Kim, J. Moon and J. S. Lim, Theoretical investigation of the reaction mechanism of the photoisomerization of 1,2-dihydro-1,2-azaborine, Chem. Phys. Chem., 2015, 16, 1670–1675.
37. S. Jeong, E. Park, J. Kim and K. H. Kim, Ultrafast photoisomerization mechanism of azaborine revealed by nonadiabatic molecular dynamics simulations, Phys. Chem. Chem. Phys., 2023, 25, 17230–17237.
38. M. Barbatti, Nonadiabatic dynamics with trajectory surface hopping method, Wiley Interdiscip. Rev.: Comput. Mol. Sci., 2011, 1, 620–633.
39. E. Tapavicza, G. D. Bellchambers, J. C. Vincent and F. Furche, Ab initio non-adiabatic molecular dynamics, Phys. Chem. Chem. Phys., 2013, 15, 18336–18348.
40. M. E. Casida and M. Huix-Rotllant, Progress in time-dependent density-functional theory, Annu. Rev. Phys. Chem., 2012, 63, 287–323.
41. B. O. Roos, P. R. Taylor and P. E. M. Siegbahn, A complete active space SCF method (CASSCF) using a density matrix formulated super-CI approach, Chem. Phys., 1980, 48, 157–173.
42. E. Wigner, On the quantum correction for thermodynamic equilibrium, Phys. Rev., 1932, 40, 749–759.
43. M. Barbatti and K. Sen, Effects of different initial condition samplings on photodynamics and spectrum of pyrrole, Int. J. Quantum Chem., 2016, 116, 762–771.
44. See, for example, most recently: J. Jara-Cortés, J. A. Pérez-Pimienta, J. W. Park and J. Hernández-Trujillo, ChemPhotoChem, 2024, 8, e202300291.
45. F. Bernardi, M. Olivucci and M. A. Robb, Potential energy surface crossings in organic photochemistry, Chem. Soc. Rev., 1996, 25, 321–328.
46. F. O. Rice and E. Teller, The role of free radicals in elementary organic reactions, J. Chem. Phys., 1938, 6, 489–496.
47. J. Hine, The principle of least nuclear motion, Adv. Phys. Org. Chem., 1977, 15, 1–61.
48. M. L. Sinnott, The principle of least nuclear motion and the theory of stereoelectronic control, Adv. Phys. Org. Chem., 1988, 24, 113–204.
49. C.-M. Cheung, F. W. Goldberg, P. Magnus, C. J. Russell, R. Turnbull and V. Lynch, An expedient formal total synthesis of (–)-diazonamide A via a powerful, stereoselective O-aryl to C-aryl migration to form the C10 quaternary center, J. Am. Chem. Soc., 2007, 129, 12320–12327.
50. S. Jautze, S. Diethelm, W. Frey and R. Peters, Diastereoselective bis-cyclopalladation of ferrocene-1,1′-diyl bis-imidazolines: translation of central via axial into planar chirality, Organometallics, 2009, 28, 2001–2004.
51. K. Troshin and H. Mayr, Electrofugalities of 1,3-diarylallyl cations, J. Org. Chem., 2013, 78, 2649–2660.
52. S. R. Chidipudi, D. J. Burns, I. Khan and H. W. Lam, Enantioselective synthesis of spiroindenes by enol-directed rhodium(III)-catalyzed C–H functionalization and spiroannulation, Angew. Chem., Int. Ed., 2015, 127, 14181–14185.
53. C. G. Seitz, H. Zhang, Y. Mo and J. M. Karty, Why do enolate anions favor O-alkylation over C-alkylation in the gas phase? The roles of resonance and inductive effects in the gas-phase S_N2 reaction between the acetaldehyde enolate anion and methyl fluoride, J. Org. Chem., 2016, 81, 3711–3719.
54. M. E. Alikhani and B. Silvi, Isomerism in secondary bonded complexes: do structural rules apply?, Int. J. Quantum Chem., 2022, 122, e26670.
55. J. P. Foster and F. Weinhold, Natural hybrid orbitals, J. Am. Chem. Soc., 1980, 102, 7211–7218.
56. T. Yanai, D. P. Tew and N. C. Handy, A new hybrid exchange-correlation functional using the Coulomb-attenuation method (CAM-B3LYP), Chem. Phys. Lett., 2004, 393, 51–57.
57. T. H. Dunning Jr., Gaussian basis sets for use in correlated molecular calculations. I. The atoms boron through neon and hydrogen, J. Chem. Phys., 1989, 90, 1007–1023.
58. H. P. Hratchian and H. B. Schlegel, Accurate reaction paths using a Hessian based predictor-corrector integrator, J. Chem. Phys., 2004, 120, 9918–9924.
59. K. Andersson, P.-Å. Malmqvist and B. O. Roos, Second-order perturbation theory with a complete active space self-consistent field reference function, J. Chem. Phys., 1992, 96, 1218–1226.
60. J. Finley, P.-Å. Malmqvist, B. O. Roos and L. Serrano-Andrés, The multi-state CASPT2 method, Chem. Phys. Lett., 1998, 288, 299–306.
61. J. C. Tully, Molecular dynamics with electronic transitions, J. Chem. Phys., 1990, 93, 1061–1071.
62. E. Tapavicza, A. M. Meyer and F. Furche, Unravelling the details of vitamin D photosynthesis by non-adiabatic molecular dynamics simulations, Phys. Chem. Chem. Phys., 2011, 13, 20986–20998.
63. F. Furche, R. Ahlrichs, C. Hättig, W. Klopper, M. Sierka and F. Weigend, Turbomole, Wiley Interdiscip. Rev.: Comput. Mol. Sci., 2014, 4, 91–100.
64. L. Verlet, Computer “experiments” on classical fluids. I. Thermodynamical properties of Lennard-Jones molecules, Phys. Rev., 1967, 159, 98–103.
65. B. Oruganti, P. P. Kalapos, V. Bhargav, G. London and B. Durbeej, Photoinduced changes in aromaticity facilitate electrocyclization of dithienylbenzene switches, J. Am. Chem. Soc., 2020, 142, 13941–13953.
66. B. Oruganti, J. Wang and B. Durbeej, Modulating the photocyclization reactivity of diarylethenes through changes in the excited-state aromaticity of the π-linker, J. Org. Chem., 2022, 87, 11565–11571.
67. I. Fdez. Galván, M. Vacher, A. Alavi, C. Angeli, F. Aquilante, J. Autschbach, J. J. Bao, S. I. Bokarev, N. A. Bogdanov, R. K. Carlson, L. F. Chibotaru, J. Creutzberg, N. Dattani, M. G. Delcey, S. S. Dong, A. Dreuw, L. Freitag, L. M. Frutos, L. Gagliardi, F. Gendron, A. Giussani, L. González, G. Grell, M. Guo, C. E. Hoyer, M. Johansson, S. Keller, S. Knecht, G. Kovačević, E. Källman, G. L. Manni, M. Lundberg, Y. Ma, S. Mai, J. P. Malhado, P. Å. Malmqvist, P. Marquetand, S. A. Mewes, J. Norell, M. Olivucci, M. Oppel, Q. M. Phung, K. Pierloot, F. Plasser, M. Reiher, A. M. Sand, I. Schapiro, P. Sharma, C. J. Stein, L. K. Sørensen, D. G. Truhlar, M. Ugandi, L. Ungur, A. Valentini, S. Vancoillie, V. Veryazov, O. Weser, T. A. Wesołowski, P.-O. Widmark, S. Wouters, A. Zech, J. P. Zobel and R. Lindh, OpenMolcas: from source code to insight, J. Chem. Theory Comput., 2019, 15, 5925–5964.
68. B. G. Levine, J. D. Coe and T. J. Martínez, Optimizing conical intersections without derivative coupling vectors: Application to multistate multireference second-order perturbation theory (MS-CASPT2), J. Phys. Chem. B, 2008, 112, 405–413.
69. S. Mai, P. Marquetand and L. González, Nonadiabatic dynamics: the SHARC approach, Wiley Interdiscip. Rev.: Comput. Mol. Sci., 2018, 8, e1370.
70. F. Neese, The ORCA program system, Wiley Interdiscip. Rev.: Comput. Mol. Sci., 2012, 2, 73–78.
71. M. J. Frisch, G. W. Trucks, H. B. Schlegel, G. E. Scuseria, M. A. Robb, J. R. Cheeseman, G. Scalmani, V. Barone, G. A. Petersson, H. Nakatsuji, X. Li, M. Caricato, A. V. Marenich, J. Bloino, B. G. Janesko, R. Gomperts, B. Mennucci, H. P. Hratchian, J. V. Ortiz, A. F. Izmaylov, J. L. Sonnenberg, D. Williams-Young, F. Ding, F. Lipparini, F. Egidi, J. Goings, B. Peng, A. Petrone, T. Henderson, D. Ranasinghe, V. G. Zakrzewski, J. Gao, N. Rega, G. Zheng, W. Liang, M. Hada, M. Ehara, K. Toyota, R. Fukuda, J. Hasegawa, M. Ishida, T. Nakajima, Y. Honda, O. Kitao, H. Nakai, T. Vreven, K. Throssell, J. A. Montgomery, Jr., J. E. Peralta, F. Ogliaro, M. J. Bearpark, J. J. Heyd, E. N. Brothers, K. N. Kudin, V. N. Staroverov, T. A. Keith, R. Kobayashi, J. Normand, K. Raghavachari, A. P. Rendell, J. C. Burant, S. S. Iyengar, J. Tomasi, M. Cossi, J. M. Millam, M. Klene, C. Adamo, R. Cammi, J. W. Ochterski, R. L. Martin, K. Morokuma, O. Farkas, J. B. Foresman and D. J. Fox, Gaussian 16, Revision C.01, Gaussian, Inc., Wallingford CT, 2016.

---

Footnote

† Electronic supplementary information (ESI) available: Complementary CASPT2 calculations, geometries of optimized conical intersections, reaction dynamics following internal conversion, reaction pathways for the formation of other (than Dewar) photoproducts, and Cartesian coordinates and total electronic energies of optimized geometries. See DOI: https://doi.org/10.1039/d4cp00777h

---