Open Access Article
Open Access ArticleCreative Commons Attribution 3.0 Unported Licence
Metal–ligand bond in group-11 complexes and nanoclusters†
Maryam Sabooni Asre
Hazer
 a,
Sami
Malola
b and
Hannu
Häkkinen
a,
Sami
Malola
b and
Hannu
Häkkinen
 *abc
*abc
aDepartment of Chemistry, Nanoscience Center, University of Jyväskylä, FI-40014 Jyväskylä, Finland. E-mail: hannu.j.hakkinen@jyu.fi
bDepartment of Physics, Nanoscience Center, University of Jyväskylä, FI-40014 Jyväskylä, Finland
cCarbon to Metal Coating Institute, Queen's University, Kingston, Ontario, K7L 3N6, Canada
First published on 9th July 2024
Abstract
Density functional theory is used to study geometric, energetic, and electronic properties of metal–ligand bonds in a series of group-11 metal complexes and ligand-protected metal clusters. We study complexes as the forms of M–L (L = SCH3, SC8H9, PPh3, NHCMe, NHCEt, NHCiPr, NHCBn, CCMe, CCPh) and L1–M–L2 (L1 = NHCBn, PPh3, and L2 = CCPh). Furthermore, we study clusters denoted as [M13L6Br6]− (L = PPh3, NHCMe, NHCEt, NHCiPr, NHCBn). The systems were studied at the standard GGA level using the PBE functional and including vdW corrections via BEEF-vdW. Generally, Au has the highest binding energies, followed by Cu and Ag. PBE and BEEF-vdW functionals show the order Ag–L > Au–L > Cu–L for bond lengths in both M–L complexes and metal clusters. In clusters, the smallest side group (CH3) in NHCs leads to the largest binding energy whereas no significant variations are seen concerning different side groups of NHC in M–L complexes. By analyzing the projected density of states and molecular orbitals in complexes and clusters, the M–thiolate bonds were shown to have σ and π bond characteristics whereas phosphines and carbenes were creating σ bonds to the transition metals. Interestingly, this analysis revealed divergent behavior for M–alkynyl complexes: while the CCMe group displayed both σ and π bonding features, the CCPh ligand was found to possess only σ bond properties in direct head-to-head binding configuration. Moreover, synergetic effects increase the average binding strength to the metal atom significantly in complexes of two different ligands and underline the potential of adding Cu to synthesize structurally richer cluster systems. This study helps in understanding the effects of different ligands on the stability of M–L complexes and clusters and suggests that PPh3 and NHCs-protected Cu clusters are most stable after Au clusters.
1 Introduction
Understanding the chemical nature of bonds in metal–ligand (M–L) complexes and nanoclusters aids comprehension of the probable reactions as well as learning and developing novel synthesis procedures. Such systems due to their unique functions have caught the attention of many researchers.1–17 Numerous ligand groups have been studied and implicated in protected metal nanoclusters and M–L complexes, including thiolates, phosphines, alkynyls, N-heterocyclic carbenes (NHCs), and halids.18–24 The spectrum of the known systems gets extended by considering different metals and their alloys from which group 11 coinage metals (Cu, Ag, Au) play an important role.25–34 Building upon this foundation, it becomes imperative to broaden the study beyond single M–L bonds to include the interactions of mixed ligands as L1–M–L2 configurations within the metal clusters. This approach not only enriches the spectrum of known systems but also deepens our comprehension of the multifaceted nature of metal and ligand interactions.The study of the geometric, energetic, and electronic features of metal–ligand bonds in M–L and L1–M–L2 complexes and nanoclusters is beneficial to gain a better understanding of their reactivity and stability in a variety of applications. To explain the chemical nature of such bonds, one must first understand the electronic configurations of the atoms involved. Chemical bonding of group-11 coinage metals involves s and d valence orbitals which feature a full d shell and a singly occupied s shell in the form of nd10 (n + 1)s1, where n = 3, 4, and 5 correspond to Cu, Ag, and Au, respectively. The half-filled outermost s orbital of group 11 atoms is similar to alkali metals, with the exception that the relativistic effects must be considered to describe the properties of systems properly for the elements with underlying filled d shell.35–46
The discussion surrounding the diverse properties of group-11 elements, despite their analogous valence electron configurations, can be attributed to the relativistic effects, which gain prominence as the electron count escalates from Cu to Au. Consequently, copper has a significantly smaller energy gap between its 3d and 4s orbitals compared to silver, which results in copper behaving more like a first-group transition metal and exhibiting larger electron correlation effects than silver. However, the different chemical and physical properties of gold and silver are primarily due to the large relativistic effects of gold45,46 making the 5d–6s energy gap similar in size to that of copper. One of the significant features of these effects is the direct relativistic effect, which causes the contraction of outer s- and p-orbitals. This occurs as a result of increased electron mass at high velocities, leading to a more compact distribution of electron density around the nucleus. Conversely, the indirect relativistic effect leads to the expansion of inner d- and f-orbitals. The sequence of this expansion follows the order: 5d > 4d > 3d for d-orbitals. These effects contribute to an overall relativistic contraction of atomic size, making the atom appear smaller than it would be in a non-relativistic context.47–49
Computational approaches have been used frequently to study the nature of bonds in M–L complexes. Jerabek et al.50 studied the structure and bonding properties of coinage metals bonded to cyclic (alkyl)(amino) carbene (cAACs) in complexes [M(cAAC)2] and [M(cAAC)2]+. They showed that the nature of M–L interactions incorporate M p(π) → (cAAC)2 π back-donation and M (s) ← (cAAC)2 σ donation which the former electron transfer is larger in all complexes except [Au(cAAC)2]. This study implies that the cAAC ligands in [M(cAAC)2] are superior as π acceptors than as σ donors. Granatier et al.51 found that the bond lengths of M–PPh3 for coinage metals are in the sequence Ag–P > Au–P > Cu–P. The charge transfer from lone-pair of ligand to metals occurred through π-back donation, which contributes the 3px and 3py orbitals of phosphorous and the (n − 1)d orbitals of the metals. The Au atom had the most significant relativistic effects, resulting in a larger binding energy compared to other M–L interactions. Kacprzak et al.52 discussed the nature of metal–sulfur bonds for coinage metals bonded to methylthiolate (MeS) in cyclic (MeSM)x (x = 2–12), clusters, explaining that the Cu–S bond is the strongest and most polar compared to gold and silver, whilst the Au–S bond is mostly covalent. Moreover, Shen53 showed that the use of NHC–Au–CCPh motifs in [Au16(NHC-1)5(PA)3Br2]3+ and [Au17(NHC-1)4(PA)4Br4]+ clusters highlights the pivotal role of L1–M–L2 bonding in developing a novel class of hybrid organometallic gold nanocatalysts. The increased catalytic efficiency and stability in hydroamination of these nanocatalysts are ascribed to the bidentate NHC–Au–PA motifs on the Au13 core, distinguishing them from the counterparts that are lacking these motifs. Tang and Jiang54 made a comprehensive study of various ligands (thiolates, phosphines, amines, aryl radicals, alkynyls, and N-heterocyclic carbenes) adsorbed on Au(111) surface allowing to propose stable cluster compositions. An example of extended complexity is the tri-metallic chiral cluster [Au7Ag6Cu2(R- or S-BINAP)3(SCH2Ph)6]+ protected by two different ligands, phosphines and thiolates, that was published by Shen et al.55 These special clusters arrange themselves into helices resembling three-dimensional biological structures due to unique hydrogen bonding dynamics. Understanding the structure and formation of these clusters requires a thorough understanding and systematic comparison of bonding differences of group 11 metals to a variety of different ligands.
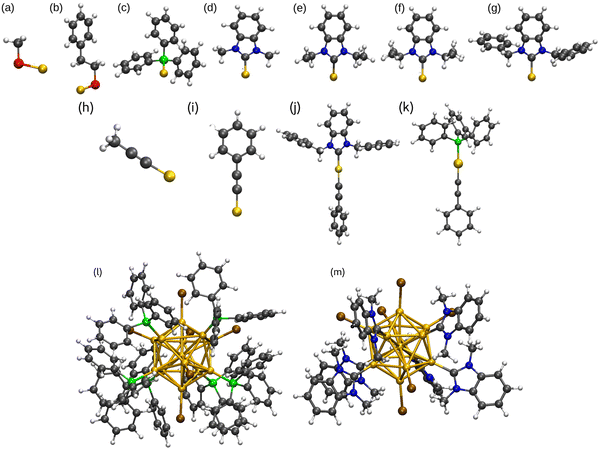
In this work, the bond properties of monodentate ligands (L) such as thiolate, phosphine, alkynyl, and NHCs with different side groups R = CH3, C2H5, C3H7, CH2C6H5 to coinage metals in M–L and L1–M–L2 complexes were studied, where L1 is NHC or PPh3 and L2 is CCPh. In addition, the properties of [M13L6Br6]− clusters featuring ligands such as PPh3 and different NHC variations in the gas phase have been compared. All optimized ligand groups bonded to Au as representative of all M–L and L1–M–L2 complexes and metal clusters are shown in Fig. 1. To study coinage metal clusters our report benefits from the experimental work performed by Shen et al.56 published in 2020 wherein they synthesized anionic icosahedral gold clusters [Au13L6Br6]− using three different NHCs, NHC-1 = 1,3-diisopropylbenzimidazolin-2-ylidene; NHC-2 = 1,3-bis(1-benzyl-1H-benzimidazol-1-ium-3-yl)propane; NHC-3 = 1,3-bis(picolyl)benzimidazolin-2-ylidene). The experimental crystal structure for [Au13(NHC-1)6Br6]− was our initial structure. We name NHC-1 as NHCiPr, and other ligands are named as NHCMe, NHCEt, NHCiPr, and NHCBn for methyl, ethyl, isopropyl, and benzyl side groups, respectively. We show that thiolate, phosphine, and NHC groups behave differently when it comes to forming bonds with metals. For instance, since the vacant p-orbitals of carbene carbon are saturated by the π-electrons in the five-membered NHC groups and σ electrons of carbene carbon are withdrawn by the neighbor N atoms, the π-accepting behavior is hardly detected in metal–NHC complexes and protected metal clusters. Many studies, however, have revealed that structural modifications in NHC can influence the bonding properties.56–62 In this work, we show the high electron-donating property of NHCs leads to the formation of stronger M–C bonds in both M–L complexes and metal nanoclusters compared to another electron donor ligand PPh3. Thiolates and alkynyls, on the other hand, withdraw electrons from coinage metals. Moreover, we address the increased stability of L1–M–L2 complexes in detail and connect the results to the observed ligand-protected metal cluster structures.
2 Computational methods
All calculations were done by using density functional theory (DFT) as implemented in the real-space code package GPAW (Grid-based projector-augmented wave method).63 Scalar-relativistic effects were included in the setups of metal atoms in GPAW. The experimental crystal structure for [Au13 (NHC-1)6Br6]− (NHC-1 = 1,3-diisopropylbenzimidazolin-2-ylidene) was used as our initial structure to which the replacement of different ligand groups and metal atoms was done. For all complexes and clusters the Perdew–Burke–Ernzerhof (PBE)64 was applied as the exchange–correlation-functional, and to study the van der Waals interactions BEEF-vdW65 was used. Geometry optimization was done in the calculations with 0.2 Å grid spacing and 0.05 eV Å−1 convergence criterion for the maximum forces acting on atoms. The binding energies for M–thiolates and M–L (L = PPh3 and NHCs) complexes were defined as ΔE = (E[H2]/2 + E[M–SR]) − (E[M] + E[HSR]) and ΔE = E[M–L] − (E[M] + E[L]), respectively, and for phosphine- and carbene-protected metal clusters ΔE = [E[M13L6Br6]− − (E([M13Br6]− + (6*L))]/6. Binding energy of L1–M–L2 complexes (L1 = PPh3 or NHC and L2 = CCPh) was defined as ΔE = E[L1–M–L2] + E[H2]/2 − (E[M] + E[L1] + E[L2]). With these definitions, the binding energies are negative numbers. Spin-dependent total energy calculations were done for all open-shell systems. The projected density of states (PDOS) of M–L complexes was calculated for metals and ligands inside a spherical cutoff region. Atom-based analysis at the metal–ligand interface was done by projecting the spherical harmonics functions centered on each of the atoms making the M–L bond. This means centering the analysis at the surface metal atoms and at the P, S, and C atoms of the ligands that bind to the metal core surface. However, Ylm-analysis was used for metal clusters to reveal the symmetry of electron states, in which the Kohn–Sham electron wavefunctions are projected to the spherical harmonics centered at the center of mass of the clusters. Bader charge method,66 was used to study the atomic charges of the coinage metals, ligand groups, and Br- atoms.3 Results and discussion
The geometric and electronic properties are reported in three main sections: 3.1 Metal complexes (M–L), 3.2 Mixed ligand–metal complexes (L1–M–L2), and 3.3 [M13L6Br6]− clusters.3.1 Metal complexes (M–L)
All metal complexes are made up of one metal atom bonded to a ligand group. Fig. 2a–d show the bond lengths (Å) and the binding energies (eV) of M–L complexes (M = Cu, Ag, Au and L = SCH3, SC8H9, PPh3, NHCMe, NHCEt, NHCiPr, NHCBn, CCMe, CCPh) calculated with PBE (Fig. 2a and b) and BEEF-vdW (Fig. 2c and d). The comparison of the bond lengths for both PBE and BEEF-vdW displays the order Ag–L > Au–L > Cu–L for M–L complexes. A similar trend for coinage metals has been seen in bonding to different ligands in various studies.50,51,67 However, BEEF-vdW yields slightly longer M–L bond lengths by 0.04–0.14 Å compared to PBE. The binding energies calculated with PBE and BEEF-vdW shown in Fig. 2b and d are proportional to the bond lengths. The binding energies of Ag–alkynyl complexes suggest that the formation of these bonds is inherently endothermic. Furthermore, these bonds exhibit metastability, which implies that while they can achieve a temporary state of stability, they are not in the lowest possible energy state. As a result, Ag–alkynyl bonds are susceptible to disruption and may readily convert to more stable configurations under certain conditions. However, Au complexes bond to electron-donating ligands (PPh3 and NHC) exhibit higher binding energies compared to their copper counterparts, with a variation of 0.09–0.28 eV. This observation can be attributed to the relativistic effects experienced by gold. As discussed earlier, these effects cause an expansion of the 5d orbitals in gold, leading to a reduced energy gap between the 5d and 6s orbitals.68–70 Consequently, electron participation in bonding with ligands is more pronounced in gold atoms, resulting in enhanced stability of these bonds.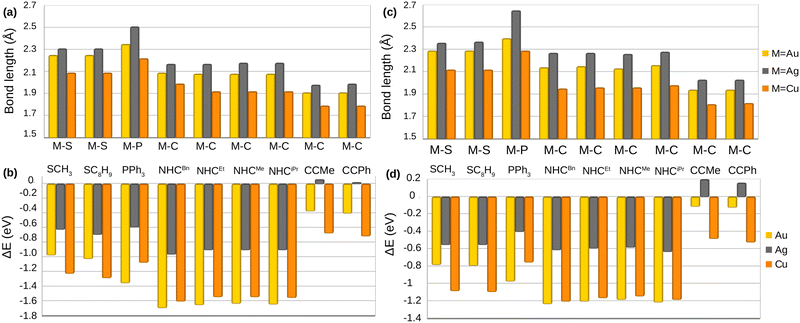 | ||
| Fig. 2 Bond length M–L (Å) and binding energy (eV) calculated by PBE (shown in (a) and (b)) and BEEF-vdW (shown in (c) and (d)) for the M–L complexes. Table S2 (ESI†) contains the numeric values. | ||
Furthermore, in a study by Muñoz et al.,71 the impact of relativistic effects on the stabilization of dative carbon–metal bonds in coinage metal complexes, represented by NHC–M–Cl species (M = Cu, Ag, Au), was investigated. By comparing scalar relativistic and non-relativistic DFT calculations, they quantified the contribution of relativistic effects to various terms associated with bond formation. They reported relativistic effects with increasing impact from Cu (7.9%) to Ag (15.3%) and most prominently for Au (39.9%). These effects contribute to the stabilization of interaction energy terms, emphasizing the strengthening of σ-PPh3 → M and σ-NHC → M bonds, as well as their electrostatic character. This finding is comparable to the influence of ligands with varying σ-donor capabilities, suggesting that relativistic effects should be considered in evaluating dative carbon–metal bonds, even for lighter group members.
According to the bond angle values for M–S–C presented in Table S1 (ESI†), the bent structure is the most stable configuration for the metal–thiolate complexes optimized by PBE and BEEF-vdW. The bond angles for M-SCH3 range from 104.0° to 105.5°, whereas those for M-SC8H9 vary between 102.2° and 105.5°. The bond angle variation in PBE and BEEF-vdW is from 0.2° to 1.1°.
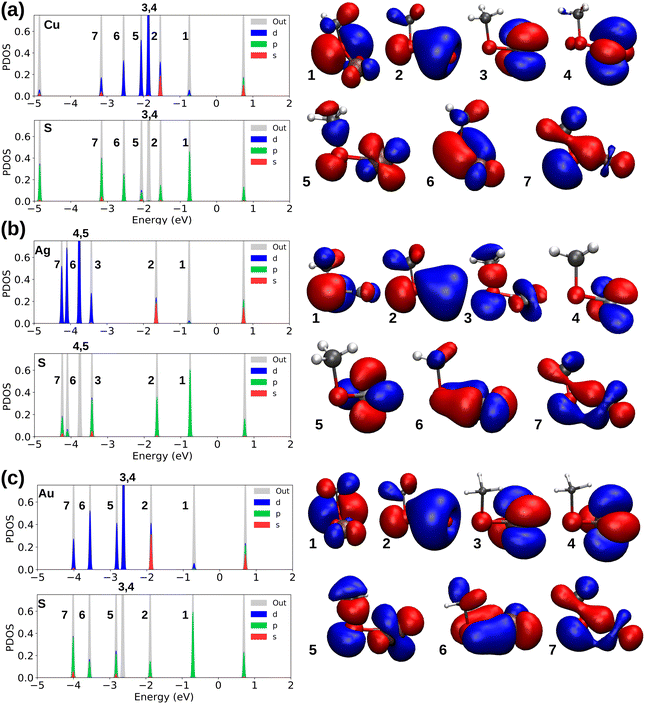
We now turn our focus to understanding the electronic properties of metal–ligand bonds to study the bond properties of coinage metals interacting with different ligands. Fig. 3a–c indicate the analysis for the binding of SCH3 radicals in M–L complexes in which the electronic density of states were analyzed via the projection of the electron states to the M and S atoms, and show the visualized frontier molecular orbitals that are important in the bonding of each M-SCH3.
Sulfur with the electronic configuration of 3s23p4 forms a closed-shell M–thiolate complex as a result of bonding to coinage metals (nd10(n + 1)s1). As shown in Fig. 3, the HOMO−1 state for coinage metals with mostly s-symmetry is involved in bonding to the ligand groups associated with p-symmetric states of S atoms. In addition, d-states of metals also couple with p-states of S-atoms forming more bonding states at lower energies like the HOMO−5 and HOMO−6 states shown in Fig. 3a and c for the Cu–SCH3 and Au–SCH3 complexes. As previously noted, Cu appears to have the shortest bond length to different ligands; nevertheless, as shown in Fig. 3, S1 (PDOS for M–PPh3), S2 (PDOS for M–NHCMe), S3 (PDOS for M–CCMe), and S4 (PDOS for M–CCPh), the frontier atomic electron states for Cu are the closest to the Fermi level, which explains the strength of the bonds in Cu complexes. Fig. 4a–d illustrate the plots for the frontier molecular orbitals involved in bonding the coinage metals to PPh3, NHCMe, CCMe, and CCPh, respectively. Fig. 4a and b show that the frontier occupied molecular orbitals for bonding in M–PPh3 and M–NHCMe have σ-type bonding features. However, as shown in Fig. 4c and d, the CCMe exhibited both σ and π bonding characteristics, whereas the CCPh group demonstrated solely σ bond characteristics in a head-to-head type of bonding configuration.
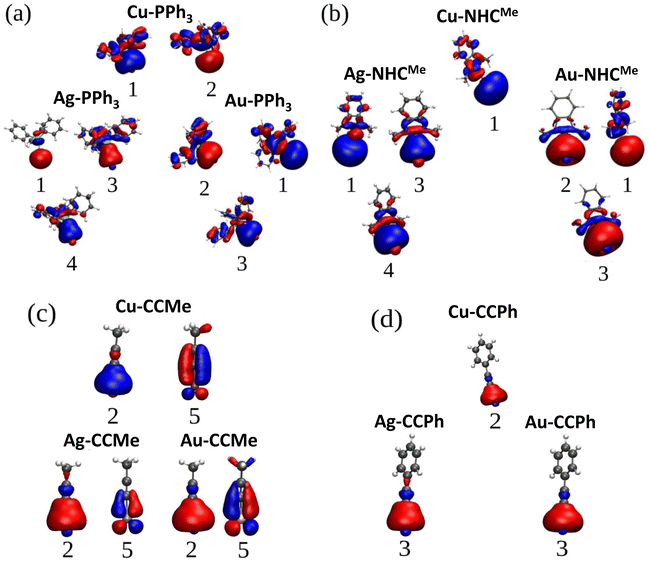 | ||
| Fig. 4 Plots for the frontier occupied molecular orbitals of (a) M–PPh3, (b) M–NHCMe, (c) M–CCMe, and M–CCPh indicating the M–L bonding (M = Cu, Ag, Au). | ||
Table S3 (ESI†) provides the analysis of the Bader charges for the M–L complexes optimized with PBE. The survey reveals that the coinage metals have different electron affinity in bonding to thiolates and alkynyls compared to PPh3 and NHC ligands. Metal atoms donate electrons to thiolates and alkynyls while withdrawing electrons from ligands in M–PPh3 and M–NHC complexes. The size of R groups in thiolates (R = CH3 and C8H9) has no significant impact on the electron donation behavior of metals. However, sulfur in SC8H9 has higher electronegativity compared to SCH3. Within alkynyls, the larger R group, Ph, in the Cu–CCPh complex leads to greater electron withdrawal from the carbon engaged in the alkyne bond compared to Me. However, the size of the R groups in Ag and Au complexes bonded to alkynyls does not significantly impact the electronic charges. The same comparison for different NHC groups shows that the bigger R groups in NHCs (R = CH3, C2H5, C3H7, CH2C6H5) have no significant impact on the electron affinity of the coinage metals.
3.2 Mixed ligand–metal complexes (L1–M–L2)
To study the mixed ligand–metal complexes we focus on NHCBn–M–CCPh and PPh3–M–CCPh complexes (M = Cu, Ag, Au). Table 1 shows a clear trend in the formation energies of mixed metal–ligand complexes. The NHCBn–Cu–CCPh complex has the largest binding energy at −3.42 eV indicating a robust binding affinity of copper, which outperforms its counterparts, with gold and silver complexes showing formation energies of −3.29 eV and −2.21 eV for NHCBn–Au–CCPh and NHCBn–Ag–CCPh, respectively. Similarly, the binding energy of PPh3–Cu–CCPh complex (−2.93 eV) demonstrates a substantial difference to M–L complexes as binding affinity is again the highest for copper when compared to its gold and silver equivalents. As a comparison, PPh3–Au–CCPh and PPh3–Ag–CCPh exhibit formation energies of −2.91 eV and −1.89 eV, respectively. This trend in the formation energies challenges the expectation of the superiority of gold in ligand binding within metal–ligand frameworks emphasizing the potential of copper utility in various applications where strong metal–ligand interactions are desired. Remarkably, the binding energies for L1–M–L2 complexes presented in Table 1 exhibit substantially higher stability than the individual M–L1 and M–L2 complexes together. This is evidenced by the sum of the separate binding energies (ΔE1 + ΔE2) being lower than the total binding energy of the combined L1–M–L2 system (ΔE), underscoring a more stable configuration in the L1–M–L2 complexes, emphasizing the cooperative effect present in the mixed–ligand motif. Tables S3 and S5 (ESI†) illustrate the Bader charge analysis for M–L and L1–M–L2 complexes, respectively. In the case of NHCBn–M–CCPh, metals exhibit a higher positive charge than metal atoms in NHCBn–M, suggesting a balance between electron donation from NHC and electron withdrawal by CCPh. This balance can lead to increased complex stability. The metals in PPh3–M–CCPh are more negatively charged compared to M–CCPh, indicating strong electron donation from PPh3, which could compensate for electron withdrawal by CCPh, thereby enhancing the stability of the complex. Table S4 (ESI†) indicates a direct proportionality between the bond lengths in L1–M–L2 complexes and their respective formation energies. Shen in his research,53 underscores the influence of L1–M–L2 configurations in the development of innovative hybrid organometallic gold nanocatalysts. The research highlights how NHC–Au–PA (PA = Phenylacetylide) motifs on the Au13 core significantly enhance the activity and stability of [Au16(NHC-1)5(PA)3Br2]3+ and [Au17(NHC-1)4(PA)4Br4]+ nanoclusters in the hydroamination of alkynes. Our analysis supports this finding on stability and further suggests that incorporating Cu motifs could potentially yield nanoclusters with enhanced activity and stability, providing new possibilities for experimental exploration in nanocatalyst design.| L1–M–L2 complex | L1–M complex | L2–M complex | |||
|---|---|---|---|---|---|
| L1–M–L2 | ΔE | ΔE/ligand | ΔE1 | ΔE2 | ΔE1 + ΔE2 |
| NHCBn–Cu–CCPh | −3.42 | −1.71 | −1.60 | −0.71 | −2.31 |
| NHCBn–Ag–CCPh | −2.21 | −1.11 | −0.96 | +0.02 | −0.94 |
| NHCBn–Au–CCPh | −3.29 | −1.65 | −1.69 | −0.40 | −2.09 |
| PPh3–Cu–CCPh | −2.93 | −1.47 | −1.07 | −0.71 | −1.78 |
| PPh3–Ag–CCPh | −1.89 | −0.95 | −0.59 | +0.02 | −0.57 |
| PPh3–Au–CCPh | −2.91 | −1.46 | −1.35 | −0.40 | −1.75 |
3.3 [M13L6Br6]− clusters
The geometric properties of [M13L6Br6]− clusters (L = PPh3, NHCMe, NHCEt, NHCiPr, NHCBn, and M = Cu, Ag, Au) and the electronic properties of M–L bonds in the coinage metal clusters protected by PPh3 and NHCMe ligands have been studied.Table 2 provides the binding energies per ligand (eV) and the average M–L bond lengths (Å) for [M13L6Br6]− (L = PPh3, NHCMe, NHCEt, NHCiPr, NHCBn) calculated by PBE and BEEF-vdW. As shown in Table 2 the van der Waals interactions have been considered for the clusters protected by PPh3 and NHCMe. Moreover, the average bond lengths for Mcenter(c) −Mperipheral(p) and M–Br in the aforementioned clusters calculated with PBE and BEEF-vdW are reported in Table S6 (ESI†). Both functionals reveal the order Ag–L > Au–L > Cu–L for the average M–L bond lengths in all clusters. Table 2 demonstrates that gold clusters exhibit the largest binding energies per ligand in comparison to Cu and Ag clusters. In the case of BEEF-vdW, however, the energies of the NHC-protected clusters are almost isoenergetic, with Cu cluster exhibiting a slight advantage over the gold clusters. Meanwhile, Cu clusters, possessing the shortest average M–L bonds, exhibit the second-highest binding energies following gold clusters. This observation in gold clusters can be ascribed to the relativistic effects experienced by gold atoms, as previously discussed for M–L complexes. Based on the binding strength and the characteristics of NHC-protected metal clusters, Cu is a viable choice for such systems, significantly superior to Ag but not as excellent as Au. By evaluating the effects of different ligands on the average bond distance values in Cu clusters, we found that this value varies between 1.96 Å and 2.00 Å. However, different ligand groups have a greater impact on the average bond distance (M–L) in Ag and Au clusters, as the average bond distance for Ag–P is 2.5 Å while this value for Ag–C in various NHCs fluctuates between 2.14 Å and 2.17 Å. Au clusters protected by PPh3 show the average bond distance of 2.35 Å for Au–P and shorter bond lengths for different NHCs bonding to Au which varies between 2.06 Å and 2.13 Å (shorter bond distance Au–C has been seen for larger NHCs), which provides the greatest difference in bond length values comparing to Ag and Cu clusters. Table S6 (ESI†) illustrates that the Cu clusters have the shortest M(c)–M(P) bond lengths, as demonstrated for the M–Br bonds in the copper clusters. It also reveals that the different ligands do not significantly alter the core metal bond to the peripheral metals in [M13L6Br6]− clusters. However, average M(c)–M(p) bond lengths in clusters protected by PPh3 are longer by 0.02–0.04 Å.
| M–L | PBE | BEEF-vdW | ||
|---|---|---|---|---|
| ΔE | M–L Bond length | ΔE | M–L Bond length | |
| [Cu13(PPh3)6Br6]− | −0.75 | 2.34 | −1.13 | 2.36 |
| [Ag13(PPh3)6Br6] | −0.75 | 2.50 | −1.04 | 2.55 |
| [Au13(PPh3)6Br6]− | −1.57 | 2.35 | −1.41 | 2.39 |
| [Cu13(NHCMe)6Br6]− | −1.67 | 2.00 | −1.62 | 2.00 |
| [Ag13(NHCMe)6Br6]− | −1.34 | 2.14 | −1.21 | 2.21 |
| [Au13(NHCMe)6Br6]− | −2.21 | 2.12 | −1.58 | 2.09 |
| [Cu13(NHCEt)6Br6]− | −1.59 | 1.96 | — | — |
| [Ag13(NHCEt)6Br6]− | −1.32 | 2.16 | — | — |
| [Au13(NHCEt)6Br6]− | −2.18 | 2.13 | — | — |
| [Cu13(NHCiPr)6Br6]− | −1.51 | 1.96 | — | — |
| [Ag13(NHCiPr)6Br6]− | −1.33 | 2.17 | — | — |
| [Au13(NHCiPr)6Br6]− | −2.18 | 2.07 | — | — |
| [Cu13(NHCBn)6Br6]− | −1.52 | 1.97 | — | — |
| [Ag13(NHCBn)6Br6] | −1.22 | 2.16 | — | — |
| [Au13(NHCBn)6Br6] | −2.04 | 2.06 | — | — |
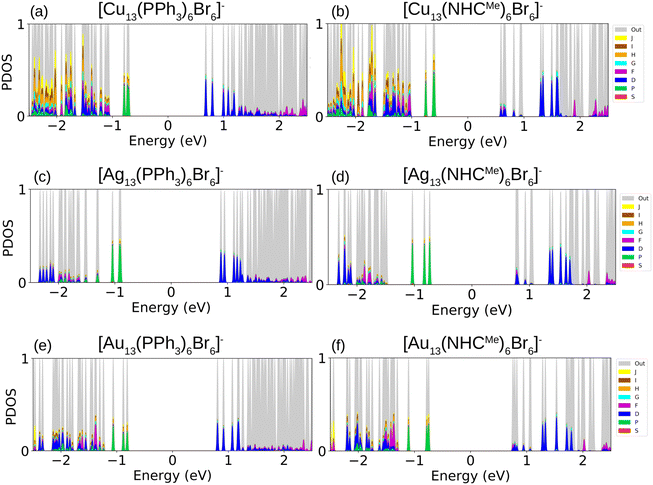
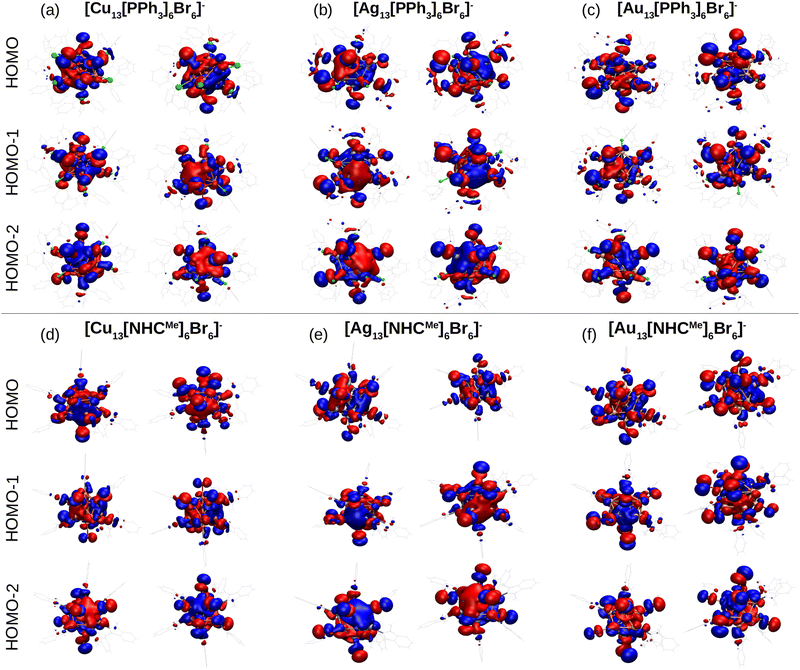
To study the electronic properties of the metal clusters protected by PPh3 and NHCMe, we first study the Ylm-analysis to reveal the symmetry of electron states, in which the Kohn–Sham electron wavefunctions are projected to spherical harmonics centered at the center of mass of the clusters. Fig. 5a–f illustrate the P-symmetry for the frontier orbitals (HOMO, HOMO−1, and HOMO−2) of all M13 clusters as expected for 8 electron superatoms. Visualized molecular orbitals shown in Fig. 6a–f confirm the result of Fig. 5. The expected variation (Cu > Au > Ag) in the position of the d-band edge for metal atom type can be seen from the atom-based projection that is shown in Fig. S5 (ESI†). Interestingly, the position of a p-symmetric band of the P and C atoms of the ligands that include binding states to the metal core surface follows the same trend. This confirms that the same underlying hybridization characteristics that were interpreted already for the simple M–L complexes are affecting the binding properties also in the more complex cluster systems. Bader charge analysis for clusters reported in Table S7 (ESI†) illustrates the charge of metal atoms involved in M–L bonds, which show similar behavior as in M–L complexes. In all clusters, metal atoms in M–L bonds are positively charged except gold atoms in [Au13 (PPh3)6Br6]− which slightly withdraw electrons. Moreover, Au atoms in gold clusters appear to be less positively charged compared to Cu and Ag atoms in other clusters. In all clusters, P and C atoms in PPh3 and NHCs ligands are positively charged (compared to C atoms in NHCs, phosphorous is more positively charged); nevertheless, non-bonded atoms to metal in these ligands, together with Br atoms, withdraw electrons.
4 Conclusion
Rational design of new materials crucially relies on prerequisite information on how the starting materials interact and what are their energetically stable reacted compounds and binding motifs in the final nanostructure product. A paradox of the design process is that the to-be-produced new materials and consequently most of the necessary prerequisite information for the design process are unknown. In reality, the main challenge is to combine the necessary ingredients from a vast sea of previous chemistry examples and a fundamental understanding of how atoms and molecules behave. To this end, we have given here a thorough systematic comparison of the binding properties of various ligands to group-11 metals Au, Ag, Cu and expanded the understanding of ligand-protected metal clusters and the underlying chemical rules to their formation.This study confirms the dominant role of Au in forming stable ligand–metal complexes and clusters but is questioning its role as an only decisive option. Our results inquire into the great potential of copper as a potential alternative choice to stabilize either special surface motifs or the whole structure of the ligand–metal complexes and clusters. Our work has summarized the relevance of understanding the charge transfer properties, characteristics of the metals, and the effect of the metal d-band on binding properties. In the context of our results, it is not a surprise why in mixed metal clusters phosphines mostly prefer binding to Au atoms55,72,73 or that Cu is often found at the outermost metal–thiolate interface layer instead of the metal core.55,74,75 The thiolate–metal bonds are known to be stronger within the protecting units than to the metal core and therefore it is favourable to maximize strongly binding metal atoms in the outermost layer if it is spatially reasonable. In larger clusters, the metal–ligand binding affinity acts against the factors like packing of the metal core and surface curvature effects, which may change the balance at the metal–ligand interface to favor flexibility for example in atom coordination.76
Silver as the weakest binder, but competitive in packing to Au, is flexible to take a role of the compromising agent in the metal core or in the metal–ligand interface and creates a basis for holding the structural integrity and molecular composition of the synthesized product. In the case of Ag, the preference should still be to bind the ligand available that maximizes the stability, namely carbenes and thiolates over phosphines as our results showed.
Most of these mentioned facts are concretized in the tri-metallic, two ligand cluster [Au7Ag6Cu2(R- or S-BINAP)3(SCH2Ph)6]+:Au in the center of the metal core binding phosphines, Cu forming metal–thiolate units on the core surface and Ag completing the capping the metal core and offering a binding site for the Cu–thiolate units.55 Based on our results it is also clear that when adding enough structural flexibility, as in some bidentate ligands, the formation of surface motifs with mixed ligands on cluster surface can become highly probable because it combines the surplus synergies from bonding and charge transfer to strengthen the binding affinity.
As a summary, our results indicate that copper could be very valuable to maximize the number of special units and enrich the properties of the metal–ligand interface in protected clusters, which can open a new avenue for applications like highly selective catalysis. We hope that examples provided here could help transfer the fundamental understanding to a rational controlled design of new cluster materials in the future.
Author contributions
M. S. A. H. performed DFT calculations, analysed the data with S. M. and wrote the first manuscript draft, which was edited by S. M. and H. H. All authors participated in conceptualization of the research which was supervised by H. H.Data availability
The data supporting this article have been included as part of the ESI.†Conflicts of interest
There are no conflicts to declare.Acknowledgements
This research is funded through the New Frontiers Research Fund (NFRF)–Transformation Program NFRFT-2020-00573 (Canada) and the Research Council of Finland. The calculations were made at the University of Jyväskylä using the Finnish National FGCI computing infrastructure.Notes and references
- V. Nesterov, D. Reiter, P. Bag, P. Frisch, R. Holzner, A. Porzelt and S. Inoue, Chem. Rev., 2018, 118, 9678–9842 CrossRef CAS PubMed.
- N. Marion and S. P. Nolan, Chem. Soc. Rev., 2008, 37, 1776–1782 RSC.
- E. Peris, Chem. Rev., 2017, 118, 9988–10031 CrossRef PubMed.
- P. A. Lummis, K. M. Osten, T. I. Levchenko, M. Sabooni Asre Hazer, S. Malola, B. Owens-Baird, A. J. Veinot, E. L. Albright, G. Schatte and S. Takano, et al. , JACS Au, 2022, 2, 875–885 CrossRef CAS PubMed.
- R. L. Whetten, H.-C. Weissker, J. J. Pelayo, S. M. Mullins, X. López-Lozano and I. L. Garzón, Acc. Chem. Res., 2019, 52, 34–43 CrossRef CAS PubMed.
- H. Shen, Z. Xu, M. S. A. Hazer, Q. Wu, J. Peng, R. Qin, S. Malola, B. K. Teo, H. Häkkinen and N. Zheng, Angew. Chem., 2021, 133, 3796–3802 CrossRef.
- M. S. A. Hazer, S. Malola and H. Häkkinen, ChemComm, 2022, 58, 3218–3221 RSC.
- H. S. N. Y. N. Lv, Acc. Chem. Res., 2018, 51, 3114–3124 CrossRef PubMed.
- Q. Yao, T. Chen, X. Yuan and J. Xie, Acc. Chem. Res., 2018, 51, 1338–1348 CrossRef CAS PubMed.
- H. Shen, Q. Wu, M. S. A. Hazer, X. Tang, Y.-Z. Han, R. Qin, C. Ma, S. Malola, B. K. Teo and H. Häkkinen, et al. , Chem, 2022, 8, 2380–2392 CAS.
- Y. Pei, P. Wang, Z. Ma and L. Xiong, Acc. Chem. Res., 2018, 52, 23–33 CrossRef PubMed.
- K. Salorinne, R. W. Man, P. A. Lummis, M. S. A. Hazer, S. Malola, J. C.-H. Yim, A. J. Veinot, W. Zhou, H. Häkkinen and M. Nambo, et al. , ChemComm, 2020, 56, 6102–6105 RSC.
- J. Yan, B. K. Teo and N. Zheng, Acc. Chem. Res., 2018, 51, 3084–3093 CrossRef CAS PubMed.
- H. Yang, Y. Wang, X. Chen, X. Zhao, L. Gu, H. Huang, J. Yan, C. Xu, G. Li and J. Wu, et al. , Nat. Commun., 2016, 7, 1–8 Search PubMed.
- Z. Lei, X.-K. Wan, S.-F. Yuan, Z.-J. Guan and Q.-M. Wang, Acc. Chem. Res., 2018, 51, 2465–2474 CrossRef CAS PubMed.
- K. Konishi, M. Iwasaki and Y. Shichibu, Acc. Chem. Res., 2018, 51, 3125–3133 CrossRef CAS PubMed.
- Q.-F. Zhang, X. Chen and L.-S. Wang, Acc. Chem. Res., 2018, 51, 2159–2168 CrossRef CAS PubMed.
- H. Al-Johani, E. Abou-Hamad, A. Jedidi, C. M. Widdifield, J. Viger-Gravel, S. S. Sangaru, D. Gajan, D. H. Anjum, S. Ould-Chikh and M. N. Hedhili, et al. , Nat. Chem., 2017, 9, 890–895 CrossRef CAS PubMed.
- J. B. Ernst, C. Schwermann, G.-I. Yokota, M. Tada, S. Muratsugu, N. L. Doltsinis and F. Glorius, J. Am. Chem. Soc., 2017, 139, 9144–9147 CrossRef CAS PubMed.
- C. M. Crudden, J. H. Horton, I. I. Ebralidze, O. V. Zenkina, A. B. McLean, B. Drevniok, Z. She, H.-B. Kraatz, N. J. Mosey and T. Seki, et al. , Nat. Chem., 2014, 6, 409–414 CrossRef CAS PubMed.
- A. V. Zhukhovitskiy, M. G. Mavros, T. Van Voorhis and J. A. Johnson, J. Am. Chem. Soc., 2013, 135, 7418–7421 CrossRef CAS PubMed.
- P. Maity, S. Takano, S. Yamazoe, T. Wakabayashi and T. Tsukuda, J. Am. Chem. Soc., 2013, 135, 9450–9457 CrossRef CAS PubMed.
- A. D. Jewell, H. L. Tierney and E. C. H. Sykes, Phys. Rev. B: Condens. Matter Mater. Phys., 2010, 82, 205401 CrossRef.
- C. Vericat, M. Vela, G. Benitez, P. Carro and R. Salvarezza, Chem. Soc. Rev., 2010, 39, 1805–1834 RSC.
- S. Y. Tee and E. Ye, Mater. Adv., 2021, 2, 1507–1529 RSC.
- R. Jazzar, M. Soleilhavoup and G. Bertrand, Chem. Rev., 2020, 120, 4141–4168 CrossRef CAS PubMed.
- M. Mora, M. C. Gimeno and R. Visbal, Chem. Soc. Rev., 2019, 48, 447–462 RSC.
- A. A. Danopoulos, T. Simler and P. Braunstein, Chem. Rev., 2019, 119, 3730–3961 CrossRef CAS PubMed.
- M. Trose, F. Nahra and C. S. Cazin, Coord. Chem. Rev., 2018, 355, 380–403 CrossRef CAS.
- M. Marinelli, C. Santini and M. Pellei, Curr. Top. Med. Chem., 2016, 16, 2995–3017 CrossRef CAS PubMed.
- O. Fenwick, E. Coutino-Gonzalez, D. Grandjean, W. Baekelant, F. Richard, S. Bonacchi, D. De Vos, P. Lievens, M. Roeffaers and J. Hofkens, et al. , Nat. Mater., 2016, 15, 1017–1022 CrossRef CAS PubMed.
- D. Manzoor, S. Krishnamurty and S. Pal, J. Phys. Chem. C, 2014, 118, 7501–7507 CrossRef CAS.
- B. M. Barngrover and C. M. Aikens, J. Phys. Chem. A, 2011, 115, 11818–11823 CrossRef CAS PubMed.
- S. orević, S. Radenković, S. Shaik and B. Brada, Molecules, 2022, 27, 490 CrossRef PubMed.
- V. Kellö and A. J. Sadlej, Chem. Phys., 1995, 103, 2991–2999 Search PubMed.
- O. Kostko, N. Morgner, M. Astruc Hoffmann and B. Von Issendorff, Eur. Phys. J. D, 2005, 34, 133–137 CrossRef CAS.
- M. De Santis, S. Rampino, L. Storchi, L. Belpassi and F. Tarantelli, Inorg. Chem., 2019, 58, 11716–11729 CrossRef CAS PubMed.
- R. H. Hertwig, W. Koch, D. Schröder, H. Schwarz, J. Hrušák and P. Schwerdtfeger, J. Phys. Chem., 1996, 100, 12253–12260 CrossRef CAS.
- A. Muñoz-Castro and H. R. Dias, J. Comput. Chem., 2022, 43, 1848–1855 CrossRef PubMed.
- C. Poggel and G. Frenking, Chem. – Eur. J., 2018, 24, 11675–11682 CrossRef CAS PubMed.
- D. Roy, A. Pal and T. Pal, RSC Adv., 2022, 12, 12116–12135 RSC.
- A. Muñoz-Castro, Phys. Chem. Chem. Phys., 2019, 21, 13022–13029 RSC.
- J. Wei, J.-F. Halet, S. Kahlal, J.-Y. Saillard and A. Muñoz-Castro, Inorg. Chem., 2020, 59, 15240–15249 CrossRef CAS PubMed.
- A. Muñoz-Castro, Inorg. Chem. Front., 2019, 6, 2349–2358 RSC.
- P. Pyykkö, Chem. Rev., 1997, 97, 597–636 CrossRef PubMed.
- D. Schröder, H. Schwarz, J. Hrušák and P. Pyykkö, Inorg. Chem., 1998, 37, 624–632 CrossRef.
- P. Pyykkö, Annu. Rev. Phys. Chem., 2012, 63, 45–64 CrossRef PubMed.
- M. Schädel, Philos. Trans. R. Soc., A, 2015, 373, 20140191 CrossRef PubMed.
- N. Pyper, Philos. Trans. R. Soc., A, 2020, 378, 20190305 CrossRef CAS PubMed.
- P. Jerabek, H. W. Roesky, G. Bertrand and G. Frenking, J. Am. Chem. Soc., 2014, 136, 17123–17135 CrossRef CAS PubMed.
- J. Granatier, M. Urban and A. J. Sadlej, Chem. Phys. Lett., 2010, 484, 154–159 CrossRef CAS.
- K. A. Kacprzak, O. Lopez-Acevedo, H. Häkkinen and H. Gronbeck, J. Phys. Chem. C, 2010, 114, 13571–13576 CrossRef CAS.
- H. Shen, Q. Wu, S. Malola, Y.-Z. Han, Z. Xu, R. Qin, X. Tang, Y.-B. Chen, B. K. Teo and H. Häkkinen, et al. , J. Am. Chem. Soc., 2022, 144, 10844–10853 CrossRef CAS PubMed.
- Q. Tang and D.-E. Jiang, Chem. Mater., 2017, 29, 6908–6915 CrossRef CAS.
- H. Shen, Z. Xu, L. Wang, Y.-Z. Han, X. Liu, S. Malola, B. K. Teo, H. Häkkinen and N. Zheng, Angew. Chem., 2021, 133, 22585–22590 CrossRef.
- H. Shen, S. Xiang, Z. Xu, C. Liu, X. Li, C. Sun, S. Lin, B. K. Teo and N. Zheng, Nano Res., 2020, 13, 1908–1911 CrossRef CAS.
- D. J. Nelson and S. P. Nolan, Chem. Soc. Rev., 2013, 42, 6723–6753 RSC.
- B. Borthakur, T. Rahman and A. K. Phukan, J. Org. Chem., 2014, 79, 10801–10810 CrossRef CAS PubMed.
- F. Ullah, G. Bajor, T. Veszprémi, P. G. Jones and J. W. Heinicke, Angew. Chem., 2007, 46, 2697–2700 CrossRef CAS PubMed.
- A. Kascatan-Nebioglu, M. J. Panzner, J. C. Garrison, C. A. Tessier and W. J. Youngs, Organometallics, 2004, 23, 1928–1931 CrossRef CAS.
- M. Alcarazo, T. Stork, A. Anoop, W. Thiel and A. Fürstner, Angew. Chem., 2010, 49, 2542–2546 CrossRef CAS PubMed.
- H. Seo, B. P. Roberts, K. A. Abboud, K. M. Merz Jr and S. Hong, Org. Lett., 2010, 12, 4860–4863 CrossRef CAS PubMed.
- J. Enkovaara, C. Rostgaard, J. J. Mortensen, J. Chen, M. Dułak, L. Ferrighi, J. Gavnholt, C. Glinsvad, V. Haikola and H. Hansen, et al. , J. Phys.: Condens.Matter, 2010, 22, 253202 CrossRef CAS PubMed.
- J. P. Perdew, K. Burke and M. Ernzerhof, Phys. Rev. Lett., 1996, 77, 3865 CrossRef CAS PubMed.
- J. Wellendorff, K. T. Lundgaard, A. Møgelhøj, V. Petzold, D. D. Landis, J. K. Nørskov, T. Bligaard and K. W. Jacobsen, Phys. Rev. B: Condens. Matter Mater. Phys., 2012, 85, 235149 CrossRef.
- G. Henkelman, A. Arnaldsson and H. Jónsson, Comput. Mater. Sci., 2006, 36, 354–360 CrossRef.
- L. F. Pasteka, T. Rajsky and M. Urban, J. Phys. Chem. A, 2013, 117, 4472–4485 CrossRef CAS PubMed.
- M. Jansen, Chem. Soc. Rev., 2008, 37, 1826–1835 RSC.
- P. Pyykkö, Angew. Chem., Int. Ed., 2004, 43, 4412–4456 CrossRef PubMed.
- P. Pyykkö, Chem. Soc. Rev., 2008, 37, 1967–1997 RSC.
- A. Muñoz-Castro, D. M. Carey and R. Arratia-Perez, Polyhedron, 2021, 197, 115020 CrossRef.
- S. Wang, X. Meng, A. Das, T. Li, Y. Song, T. Cao, X. Zhu, M. Zhu and R. Jin, Angew. Chem., 2014, 126, 2408–2412 CrossRef.
- Z. Qin, J. Wang, S. Sharma, S. Malola, K. Wu, H. Häkkinen and G. Li, J. Phys. Chem. Lett., 2021, 12, 10920–10926 CrossRef CAS PubMed.
- J. Yan, H. Su, H. Yang, C. Hu, S. Malola, S. Lin, B. K. Teo, H. Häkkinen and N. Zheng, J. Am. Chem. Soc., 2016, 138, 12751–12754 CrossRef CAS PubMed.
- H. Yang, Y. Wang, J. Yan, X. Chen, X. Zhang, H. Hakkinen and N. Zheng, J. Am. Chem. Soc., 2014, 136, 7197–7200 CrossRef CAS PubMed.
- J. Yan, S. Malola, C. Hu, J. Peng, B. Dittrich, B. K. Teo, H. Häkkinen, L. Zheng and N. Zheng, Nat. Commun., 2018, 9, 3357 CrossRef PubMed.
Footnote |
| † Electronic supplementary information (ESI) available: Additional data on bond lengths and strengths, electronic structure, and charge decomposition in Fig. S1–S5 and Tables S1–S7. See DOI: https://doi.org/10.1039/d4cp00848k |
| This journal is © the Owner Societies 2024 |