Probing microhydration-induced effects on carbonyl compounds†
Olivier
Aroule
a,
Mahmoud
Jarraya
b,
Emilie-Laure
Zins
 *a and
Majdi
Hochlaf
*a and
Majdi
Hochlaf
 *b
*b
aMONARIS UMR 8233 CNRS, Sorbonne Université, 4 place Jussieu, 75252 Paris Cedex 5, France. E-mail: emilie-laure.zins@sorbonne-universite.fr
bUniversité Gustave Eiffel, COSYS/IMSE, 5 Bd Descartes 77454, Champs sur Marne, France. E-mail: majdi.hochlaf@univ-eiffel.fr
First published on 5th June 2024
Abstract
Characterizing the microhydration of organic molecules is a crucial step in understanding many phenomena relevant to atmospheric, biological, and industrial applications. However, its precise experimental and theoretical description remains a challenge. For four organic solutes containing a C![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) O bond, and included in the recent HyDRA challenge [T. L. Fischer, M. Bödecker, A. Zehnacker-Rentien, R. A. Mata and M. A. Suhm, Phys. Chem. Chem. Phys., 2022, 24, 11442–11454.], we performed a detailed study of different monohydrate isomers and their properties; these were cyclooctanone (CON), 1,3-dimethyl-2-imidazolidinon (DMI), methyl lactate (MLA), and 2,2,2-trifluoroacetophenone (TPH) molecules. As reported in the literature, the O–H elongation shift of the water molecule appears to be a good candidate for characterizing complexation-induced effects. We also show that C
O bond, and included in the recent HyDRA challenge [T. L. Fischer, M. Bödecker, A. Zehnacker-Rentien, R. A. Mata and M. A. Suhm, Phys. Chem. Chem. Phys., 2022, 24, 11442–11454.], we performed a detailed study of different monohydrate isomers and their properties; these were cyclooctanone (CON), 1,3-dimethyl-2-imidazolidinon (DMI), methyl lactate (MLA), and 2,2,2-trifluoroacetophenone (TPH) molecules. As reported in the literature, the O–H elongation shift of the water molecule appears to be a good candidate for characterizing complexation-induced effects. We also show that C![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) O elongation shift and UV-vis spectroscopy can be successfully used for these purposes. Besides, we present a comparative analysis of the strengths of non-covalent interactions within these monohydrated complexes based on interpretative tools of quantum chemistry, including topological analysis of electron density (ρ), topological analysis of electron pairing function, and analysis of the core-valence bifurcation index (CVBI), which exhibits a close linear dependency on ρ. Accordingly, a classification of intermolecular water–solute interactions is proposed.
O elongation shift and UV-vis spectroscopy can be successfully used for these purposes. Besides, we present a comparative analysis of the strengths of non-covalent interactions within these monohydrated complexes based on interpretative tools of quantum chemistry, including topological analysis of electron density (ρ), topological analysis of electron pairing function, and analysis of the core-valence bifurcation index (CVBI), which exhibits a close linear dependency on ρ. Accordingly, a classification of intermolecular water–solute interactions is proposed.
I. Introduction
Microhydration plays a fundamental role in a wide variety of processes. We can mention, for instance, the importance of microhydration on reactivity in the context of atmospheric chemistry,1–4 biochemical processes,5 SN2 reaction mechanisms,6 proton-transfer processes,7–9 capture of CO210 and other pollutants,11 stabilization of zwitterionic species,12 (3D) folding of organic compounds,13 and stabilization of water-nucleobases in functional RNAs.14 In fact, the implicit solvent model, which is routinely implemented in quantum chemistry, is based on the perturbation of solute electronic wavefunction, without an accurate description of the non-covalent interactions occurring between the solute and solvent molecules constituting the first hydration sphere and beyond. Such a description is often considered reliable while determining the macromolecular thermodynamic quantities of a solute in a solution. Nevertheless, an explicit consideration of solvation is essential. Indeed, an explicit treatment of all cases where one or more solvent molecules are actively involved in reaction processes is necessary and relevant.8,9,15,16The interactions between solute and solvent molecules are of weak nature, such as hydrogen bonds and van der Waals interactions. Such intermolecular interactions affect local electron density and, therefore, the reactivity of molecular species. For example, a network of hydrogen bonds with water molecules surrounding a reactant leads to electronic redistribution (and possibly proton transfer8) and therefore to a modification of the electrophilicity and nucleophilicity of reactant sites. Characterizing such water complexation-induced changes remains a major challenge in both theoretical chemistry and experiments. However, a better phenomenological description of these changes in reactivity seems to be essential for giving an accurate description of basic atmospheric, biochemical, and astrochemical processes. It is therefore mandatory to set a methodological approach based on both state-of-the-art experiments and theoretical investigation. This allows to characterize simple and representative reactions between two partners A and B, determine the structures of the main microhydrated isomers of A (A(H2O)n), and study the reactivity and describe the reaction products of A(H2O)n complexes with partner B. At first glance, the identification of monohydrated complexes can be a preliminary step for the study of several water molecules solvating a chemical compound. This was the background to the recently launched HyDRA challenge,17,18 the first computational challenge to describe the perturbation of the vibrational modes of the water molecule due to the formation of 1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1 water–solute complexes. The aim of such a challenge was to predict the redshifts of the symmetrical OH elongation of water within monohydrate complexes with respect to the isolated water molecule. Beyond the numerical accuracy of this red-shift, it is interesting to question whether the right value is obtained for the right reason, i.e., with a correct prediction of the interaction energy and geometry of the monohydrated complexes. Moreover, the microhydration of small organic compounds can lead to several isomers lying sufficiently close in energy that they can coexist even while embedded in cooled rare gas matrices or in molecular jets.19,20 Furthermore, in the case of studies applied to real environments (biological, atmospheric, or astrochemical), the most stable structures are not necessarily the only relevant ones, particularly in chemical reactivity. In contrast, within the HyDRA challenge, only the microhydration of the most stable conformer was assumed and could be observed in a molecular jet; whereas the possible influence of water on the properties of the other conformers was omitted, although this could be particularly relevant for future applications involving molecules of biochemical interest, such as sugars.
1 water–solute complexes. The aim of such a challenge was to predict the redshifts of the symmetrical OH elongation of water within monohydrate complexes with respect to the isolated water molecule. Beyond the numerical accuracy of this red-shift, it is interesting to question whether the right value is obtained for the right reason, i.e., with a correct prediction of the interaction energy and geometry of the monohydrated complexes. Moreover, the microhydration of small organic compounds can lead to several isomers lying sufficiently close in energy that they can coexist even while embedded in cooled rare gas matrices or in molecular jets.19,20 Furthermore, in the case of studies applied to real environments (biological, atmospheric, or astrochemical), the most stable structures are not necessarily the only relevant ones, particularly in chemical reactivity. In contrast, within the HyDRA challenge, only the microhydration of the most stable conformer was assumed and could be observed in a molecular jet; whereas the possible influence of water on the properties of the other conformers was omitted, although this could be particularly relevant for future applications involving molecules of biochemical interest, such as sugars.
Among the C![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) O bond-containing molecules included in the HyDRA challenge, the microhydration of some carbonyls has already been extensively studied in the literature. More specifically, the monohydration of acetone21,22 and formaldehyde23,24 has been widely investigated, and will not be discussed further. We should also mention the matrix isolation (FT)IR studies on the microhydration of atmospheric α-dicarbonyls by Mucha and Mielke,25 and of small C
O bond-containing molecules included in the HyDRA challenge, the microhydration of some carbonyls has already been extensively studied in the literature. More specifically, the monohydration of acetone21,22 and formaldehyde23,24 has been widely investigated, and will not be discussed further. We should also mention the matrix isolation (FT)IR studies on the microhydration of atmospheric α-dicarbonyls by Mucha and Mielke,25 and of small C![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) O-containing molecules by Khriachtchev.26 Further, Suhm and co-workers treated in detail 10 ketones (acetone, its deuterated isotopologues, and nine symmetrically and asymmetrically aliphatic and aromatic substituted derivatives) complexed with a unique water molecule, where they focused on the OH elongation shifts of water-induced complexation as probed by IR spectroscopy.27
O-containing molecules by Khriachtchev.26 Further, Suhm and co-workers treated in detail 10 ketones (acetone, its deuterated isotopologues, and nine symmetrically and asymmetrically aliphatic and aromatic substituted derivatives) complexed with a unique water molecule, where they focused on the OH elongation shifts of water-induced complexation as probed by IR spectroscopy.27
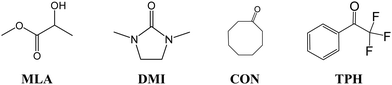
In the present first-principles investigations, we extend some of the theoretical studies initiated by the HyDRA challenge,17,18 whereby we carried out a systematic study of the most stable monohydrated complexes of four organic solutes containing a C![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) O bond and included in the HyDRA challenge. We chose carbonyls which have not yet, to the best of our knowledge, been the subject of extensive theoretical characterizations, namely the cyclooctanone (CON), 1,3-dimethyl-2-imidazolidinon (DMI), methyl lactate (MLA), and 2,2,2-trifluoroacetophenone (TPH) molecules (Scheme 1). Interestingly, CON can exist in a number of different conformers28 and here we considered the five most stable ones: CON_BC1, CON_TBC1, CON_BC2, CON_CR1, CON_TBC2 (Scheme 2). For those monohydrated complexes, we determined the preferred approach regions of the solute and the water molecule maximizing their mutual interactions, in particular between complementary sites. Afterwards, we performed full geometry optimizations followed by frequency calculations based on these “guess structures”, in order to determine the most stable water–solute clusters, their energies, and their associated vibrational frequencies. Then, we carried out QTAIM (quantum theory of atoms in molecules) and ELF (electron localization function) topological studies of the optimized complexes, in order to identify in-depth the non-covalent interactions responsible for such complex stabilization.
O bond and included in the HyDRA challenge. We chose carbonyls which have not yet, to the best of our knowledge, been the subject of extensive theoretical characterizations, namely the cyclooctanone (CON), 1,3-dimethyl-2-imidazolidinon (DMI), methyl lactate (MLA), and 2,2,2-trifluoroacetophenone (TPH) molecules (Scheme 1). Interestingly, CON can exist in a number of different conformers28 and here we considered the five most stable ones: CON_BC1, CON_TBC1, CON_BC2, CON_CR1, CON_TBC2 (Scheme 2). For those monohydrated complexes, we determined the preferred approach regions of the solute and the water molecule maximizing their mutual interactions, in particular between complementary sites. Afterwards, we performed full geometry optimizations followed by frequency calculations based on these “guess structures”, in order to determine the most stable water–solute clusters, their energies, and their associated vibrational frequencies. Then, we carried out QTAIM (quantum theory of atoms in molecules) and ELF (electron localization function) topological studies of the optimized complexes, in order to identify in-depth the non-covalent interactions responsible for such complex stabilization.
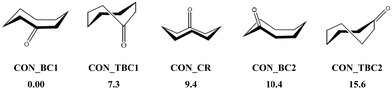 | ||
| Scheme 2 Five low-energy CON conformers as reported in ref. 28. We have also given their relative energies (in kJ mol−1) with respect to the most stable one. | ||
II. Computational methods
Optimizations and frequency calculations
All calculations were done using the GAUSSIAN 16 quantum chemistry package.30 The PBE0 hybrid functional29,31 was selected for this study, within the DFT-D3 zero-damping framework,32 as this functional was benchmarked and validated in the HyDRA challenge.17,18 Moreover, this functional has been shown to lead to an error of less than 5 kJ mol−1 for complexes involving hydrogen bonds. In any case, isomers differing by less than 5 kJ mol−1 from the most stable isomer should be considered, as they can be formed under most experimental conditions, including molecular jet and noble gas matrix isolation experiments. In addition, the CREST (conformer-rotamer ensemble sampling tool) program developed by Grimme et al.33–35 was used to complete this study and check that the most stable structures had (probably) been obtained. CREST was used with GFN2-xTB.For atoms description, the PBE0-D3 functional was used in conjunction with the aug-cc-pVTZ correlation-consistent triple-zeta basis set, as it was shown in the HyDRA challenge that this level of theory gives good results. A superfine grid was used for total geometry optimization. Each total optimization was terminated by a calculation of harmonic frequencies, and a scaling factor of 0.9604 was used to estimate the frequencies corrected for anharmonicity following an often-used procedure.36–40
Complexation energies, related to the S + H2O → (S–H2O) reaction between the solute (S) and water, were calculated from relaxed structures of S and H2O for each complex according to eqn (1):
| Ecomplexation = E(S⋯H2O) − [ES − EH2O] | (1) |
For CON, the energy of the isomer involved in the (S–H2O) was chosen for the ES. In the case of MLA, the monohydration can lead to large deformations of the molecule. For that case, in addition to complexation energies, binding energies were also calculated.
Complexation energies included zero-point vibrational energy (ZPE) corrections. Basis set superposition error (BSSE) corrections were also calculated and are shown in Table S2 (ESI†). Since all the BSSEs were much smaller than the assumed error bars emanating from our level of calculations (BSSE < 1 kJ mol−1; error ≈ 5 kJ mol−1), these values were not included in complexation energies.
To further confirm the energy orders obtained, single point computations were carried out at the CCSD(T)-F12/aug-cc-pVDZ level on the optimized structures at the PBE0/aug-cc-pVTZ level of theory. We observed that all the interaction energies were calculated to be 5 kJ mol−1 higher in the single point calculations while using the explicitly correlated coupled cluster approach, compared with the energies calculated using PBE0-D3, but there was no major difference in the energy order. Structures were also further optimized at the ωB97-XD/aug-cc-pVTZ level. The latter computations showed that the energy order was the same as the one obtained using PBE0-D3. These results are presented in Table 1.
| Complex | Complexation energy (in kJ mol−1) | Binding energy (PBE0-D3/aug-cc-pVDZ) | ν sym(O–H) | |||
|---|---|---|---|---|---|---|
| PBE0-D3/aug-cc-pVDZ | wB97-XD/aug-cc-pVDZ | CCSD(T)-F12/aug-cc-pVDZ | Calc. | Exp.18 | ||
| TPH_1 | −17.9 | −14.5 | −23.9 | 3608.8 | 3611 | |
| TPH_2 | −13.5 | −10.4 | −18.7 | 3645.3 | ||
| TPH_3 | −10.9 | −8.5 | −15.3 | 3697.3 | ||
| TPH_4 | −10.8 | −8.6 | −15.3 | 3697.2 | ||
| TPH_5 | −8.9 | −6.8 | −12.8 | 3701.7 | ||
| TPH_6 | −8.7 | −7.3 | −12.9 | 3693.1 | ||
| TPH_7 | −8.6 | −6.1 | −12.7 | 3701.6 | ||
| DMI_1 | −27.0 | −24.8 | −34.2 | 3467.7 | 3492 | |
| DMI_2 | −27.0 | −24.8 | −34.2 | 3468.2 | ||
| DMI_3 | −27.0 | −24.8 | −34.1 | 3472.4 | ||
| DMI_4 | −19.2 | −17.9 | −28.0 | 3506.8 | ||
| DMI_5 | −19.2 | −17.9 | −28.0 | 3506.6 | ||
| CON_BC1_1 | −25.8 | −23.7 | −32.4 | 3471.0 | 3503 | |
| CON_BC1_2 | −25.3 | −23.3 | −32.0 | 3493.9 | ||
| CON_BC2_1 | −25.9 | −23.9 | −31.2 | 3473.4 | ||
| CON_BC2_2 | −25.1 | −22.7 | −32.7 | 3500.0 | ||
| CON_TBC2_1 | −25.4 | −23.0 | −32.5 | 3478.3 | ||
| CON_TBC2_2 | −24.2 | −22.3 | −32.5 | 3490.4 | ||
| CON_CR_1 | −25.8 | −23.4 | −32.7 | 3475.8 | ||
| CON_CR_2 | −25.8 | −23.4 | −32.0 | 3475.4 | ||
| CON_TBC1_1 | −26.1 | −22.1 | −32.2 | 3516.8 | ||
| CON_TBC1_2 | −24.6 | −23.8 | −30.8 | 3469.1 | ||
| MLA_1 | −26.6 | −24.7 | −36.0 | −47.23 | 3491.6 | 3524 |
| MLA_2 | −23.6 | −21.1 | −32.3 | −49.91 | 3524.4 | |
| MLA_3 | −21.2 | −18.7 | −29.6 | −41.39 | 3531.4 | |
| MLA_4 | −19.5 | −17.8 | −26.9 | −27.92 | 3547.9 | |
| MLA_5 | −19.5 | −17.9 | −26.4 | −27.62 | 3582.0 | |
| MLA_6 | −19.3 | −17.5 | −27.1 | −27.68 | 3531.4 | |
| MLA_Pi | −11.9 | Not stable | −19.2 | −11.89 | 3696.8 | |
The ChemOffice suite of programs (Chem3D and ChemDraw, version 8.0) was used to draw the structures of the molecules and complexes.
Simulations of the UV-vis spectra
We calculated the absorption spectra of the monohydrated carbonyls complexes using the time dependent-density functional theory (TD-DFT) as implemented in GAUSSIAN 16. DFT calculations are known to give generally relatively correct predictions for low excitation energies, and the PBE0 functional was used for these computations.41–43 These calculations are easy to perform and give a good estimate of the orders of magnitude, although it has been shown that these methods have a tendency to consistently underestimate vertical excitation energies.44 These calculations were carried out at the optimized equilibrium geometries of the monohydrated carbonyls complexes. For these computations, the atoms were described using the 6-311++G(d,p) basis set. In addition to the singlets, we also determined the patterns of the triplets.MESP
The molecular electrostatic potential (MESP) was used to determine electrophilic and nucleophilic sites with water and carbonyls. Characterization of these sites, introduced by Murray and co-workers45,46 and Gadre and co-workers,47–49 enables the initial microhydrated structures to be constructed and optimized so as to maximize interactions between the nucleophilic and electrophilic sites. The MESP is created by all the charged particles in the molecule's space, and obeys Coulomb's law. In a molecule, it is therefore possible to determine the electrostatic potential generated by the nucleus and electrons at any point in molecular space through using eqn (2):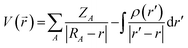 | (2) |
The electrostatic potential is then projected onto an iso-density surface with a value of 0.001 a.u., because this iso-density generally contains 95% of the system's charge and often represents the surface of the molecule.50 Here, these MESP surfaces were obtained using the AIMALL package from wfn files, wavefunction files generated by GAUSSIAN 16. MESP analysis enables electrophilic and nucleophilic sites to be localized and interactions between complementary sites to be maximized for the construction of initial structures.51
QTAIM
The QTAIM method was used to obtain information on the hydrogen bonds of the studied monohydrated carbonyls.52–54 Indeed, QTAIM makes it possible to investigate bonds by means of a topological analysis of the electron density. This analysis identifies critical points, i.e., the points at which the gradient of the electron density becomes zero. The values of the electron density, ρ, and of the Laplacian of the electron density, ∇2ρ, at these bond critical points (BCP) help describing the nature of the chemical interaction: a bond is qualified as covalent for a high electron density value and a negative sign of the Laplacian of the electron density. For a non-covalent bond, the electron density is low and the sign of the Laplacian of the electron density is positive. This method thus allows both the qualitative and quantitative classification of interactions. AIMALL (version 19.10.12) was used to visualize the results of the QTAIM and MESP analyses.55ELF
Alternatively, the ELF topological analysis was introduced to localize electron pairs.56–58 This function can be used to identify core basins from valence basins, whether they correspond to non-bonding or bonding doublets. Depending on the cutoff values used, the core and valence basins may or may not be separated. The value at which they separate is called the core-valence bifurcation index (CVBI), and it has been shown that this value is characteristic of hydrogen bond interactions, in addition to QTAIM topological analysis, and in particular of the electron density at the critical point of the hydrogen bond. For the complexes under investigation, this indicator was used to compare the hydrogen bond strengths within these complexes.III. Results and discussions
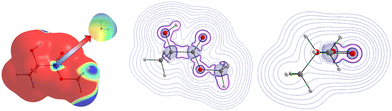
At first glance, we searched for electrophilic and nucleophilic sites on the isolated partners, so as to be able to envisage different preferred directions of the approach between a water molecule and the various solutes, that would maximize the interactions between complementary sites. These electrophilic and nucleophilic sites identified from the MESPs of the various isolated molecules are shown in Fig. 1.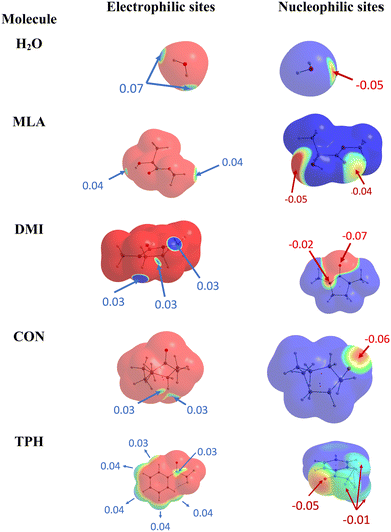 | ||
| Fig. 1 Identification of electrophilic (left) and nucleophilic (right) sites of the isolated molecules under investigation. | ||
For MLA, two electrophilic sites were identified with a value of 0.04 a.u. The first involved the hydrogen of the alcohol function, the second also involved a hydrogen atom but it was that of the methoxy group. A third electrophilic site was found perpendicular to the mid-plane of the molecule, and in the plane of the C![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) O double bond, just above and below the carbon atom. In the literature, this type of electrophilic site is known as a π-hole.59 Through analysis of the Laplacian of the electron density in two perpendicular planes, the possible directions of approach of a water molecule to this site were predicted (Fig. 2). For CON, we also identified two electrophilic sites with a value of 0.03 a.u. The first one was located on the hydrogen attached to the carbon opposite to the C
O double bond, just above and below the carbon atom. In the literature, this type of electrophilic site is known as a π-hole.59 Through analysis of the Laplacian of the electron density in two perpendicular planes, the possible directions of approach of a water molecule to this site were predicted (Fig. 2). For CON, we also identified two electrophilic sites with a value of 0.03 a.u. The first one was located on the hydrogen attached to the carbon opposite to the C![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) O bond, and the second corresponded to the hydrogen next to the aforementioned one. Similarly, we found two electrophilic sites for DMI with MESP values of 0.03 a.u. that involve the hydrogen atoms located on the carbon atoms opposite to the oxygen atom. A third electrophilic site was located in the middle of the C–C bond opposite to the oxygen atom with the same value of MESP. Besides, Fig. 1 shows that TPH possesses six electrophilic sites. The most electrophilic ones are located on the aromatic hydrogens located at the meta and para positions with respect to the O
O bond, and the second corresponded to the hydrogen next to the aforementioned one. Similarly, we found two electrophilic sites for DMI with MESP values of 0.03 a.u. that involve the hydrogen atoms located on the carbon atoms opposite to the oxygen atom. A third electrophilic site was located in the middle of the C–C bond opposite to the oxygen atom with the same value of MESP. Besides, Fig. 1 shows that TPH possesses six electrophilic sites. The most electrophilic ones are located on the aromatic hydrogens located at the meta and para positions with respect to the O![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) CCF3 group with a value of 0.04 a.u. Another one with the same value of MESP is located on the ortho position close to the CCF3 group. The other hydrogen on the other ortho position is less electrophilic. The sixth electrophilic site is located on the carbon of the C
CCF3 group with a value of 0.04 a.u. Another one with the same value of MESP is located on the ortho position close to the CCF3 group. The other hydrogen on the other ortho position is less electrophilic. The sixth electrophilic site is located on the carbon of the C![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) O bond with a value of 0.03 a.u.
O bond with a value of 0.03 a.u.
1. Equilibrium structures
On the basis of these characterizations of the isolated monomers, different “guess structures” were constructed and fully optimized. Their minimal nature was checked by all positive frequencies. In addition, CREST calculations were carried out without any a priori on the possible structures for the monohydrated complexes. CREST was only used to confirm the structures constructed by maximizing the interactions between complementary sites identified from the MESPs. The most stable complexes obtained are shown in Fig. 3. They are denoted by the carbonyl_number, where the carbonyl corresponds to TPH, MLA, DMI, or CON conformers – as specified in Schemes 1 and 2 – and the ‘number’ reflects their energy stability order with respect to the most stable form (designed as number = 1), except for the 7th one for MLA, which was labeled MLA_Pi due to the specificity of this complex (vide infra). Mostly these complexes were due to the formation of hydrogen bonds between carbonyls and water entities. Upon complexation, we found that the monomers’ equilibrium geometries were slightly affected, except MLA bearing monohydrates, where the water molecule needs to break the intra H bond between the hydroxy group and the carbonyl group and then insert into MLA via the establishment of H bonds involving the O and/or H atoms of water and the H and/or O atoms of hydroxyl and carbonyl groups of MLA. As explained in ref. 18 this is accompanied by MLA structural rearrangements after complexation compared to isolated MLA. The monomers will not be thus discussed further.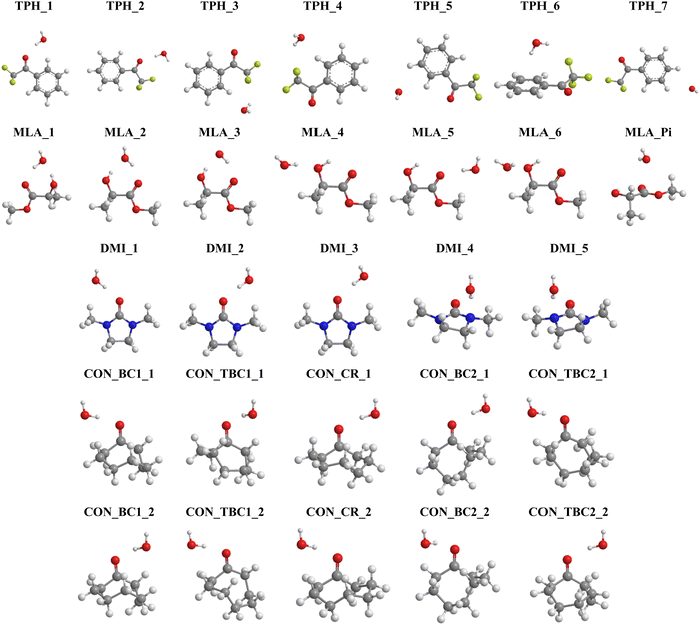 | ||
| Fig. 3 Structures of the most stable monohydrated TPH, MLA, DMI and CON complexes obtained after geometry optimization. We give also their name used throughout the manuscript. Refer to Schemes 1 and 2 for the molecular structures of these carbonyls and Table 1 for their interaction energies. Table S1 lists their Cartesian coordinates (ESI†). | ||
For TPH interacting with water, we show the 7 most stable clusters. The most stable one (TPH_1) was obtained through the establishment of an H bond between the oxygen of the carbonyl function and H of a water molecule. A further stabilization was due to a H bond between the O of water and CH aromatic in the ortho position of the aliphatic chain. The second most stable cluster (TPH_2) was also stabilized by an H bond between H of water and O of TPH, whereas it lacked the second stabilizing H bond found in TPH_1. For the other clusters, they corresponded to van der Waals interactions between TPH and water. In particular, TPH_6 was further stabilized by an OH–π interaction. The latter is of particular relevance for the stabilization of water-nucleobases in functional RNAs.14 For MLA, the three most stable clusters contained two H bonds involving one water H atom and the C![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) O and OH bonds of MLA, thus forming a cycle. This resulted in relatively large, in absolute values, interaction energies (>20 kJ mol−1) for such complexes. For the four less stable others, a unique H bond was responsible for their formation, where water interacts with the Pi hole of MLA in the 7th one. For the DMI–water complexes, the H bond between the H of water and O of C
O and OH bonds of MLA, thus forming a cycle. This resulted in relatively large, in absolute values, interaction energies (>20 kJ mol−1) for such complexes. For the four less stable others, a unique H bond was responsible for their formation, where water interacts with the Pi hole of MLA in the 7th one. For the DMI–water complexes, the H bond between the H of water and O of C![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) O led to DMI_1, DMI_2, and DMI_3, whereas the one involving the N of DMI led to the less strong DMI_4 and DMI_5 species. For CON monohydrates, the situation was rather complicated, as explained in the Introduction, because of the existence of conformers. Anyway, the CON–water clusters were stabilized by a H bond established between the H of water and O of C
O led to DMI_1, DMI_2, and DMI_3, whereas the one involving the N of DMI led to the less strong DMI_4 and DMI_5 species. For CON monohydrates, the situation was rather complicated, as explained in the Introduction, because of the existence of conformers. Anyway, the CON–water clusters were stabilized by a H bond established between the H of water and O of C![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) O. Further stabilizations of some of them were due to van der Waals interactions between water and the C–H of the carbon chain. Noteworthily, the ordering in energy of the CON conformer–water clusters did not follow the ordering of the respective conformers (Scheme 2) due to solvation-induced effects (vide infra).
O. Further stabilizations of some of them were due to van der Waals interactions between water and the C–H of the carbon chain. Noteworthily, the ordering in energy of the CON conformer–water clusters did not follow the ordering of the respective conformers (Scheme 2) due to solvation-induced effects (vide infra).
2. Spectroscopic characterizations
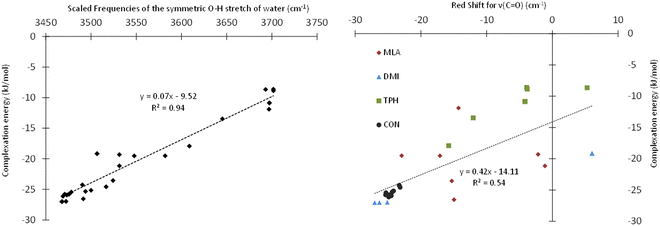
Table 1 presents the scaled frequencies for the symmetric stretching of the O–H bond of the water molecule while complexed with MLA, DMI, TPH, and CON conformers. These νsym(O–H) frequencies could be considered to be accurate to ±30 cm−1. Thus, the calculations presented in this table could be divided into two sets: (i) the first set included those that were compatible with the observed experimental frequencies, and (ii) the second set were those not compatible. It is interesting to note that the complexes calculated as being the most stable were those leading to the νsym(O–H) vibrational frequencies part of the first set of data. For each of the studied solutes, several structures of monohydrate complexes were calculated as being very close in energy, such that they could coexist under experimental conditions, and that were consistent with the experimental νsym(OH).In the HyDRA challenge, the complexation-induced red-shift associated with νsym(O–H) was used to assess the reliability of the calculations or predictions in relation to the experimental data. Implicitly, this red-shift was considered to be a representative descriptor of the structure of the calculated microhydrated complexes. For rationalization, we plotted in Fig. 4 the variation of the interaction energies of the microhydrated complexes as a function of the red-shift associated with νsym(O–H). This figure shows that the chosen red-shift is a good indicator of the stability of microhydrated complexes. Thus, the region around 3400 cm−1 seemed fairly suitable for characterizing these monohydrated complexes. However, these bands are often broad, and therefore their non-equivoque assignment could be tricky. Moreover, the presence of free water molecules, water aggregates, and/or different monohydrate isomers can further complicate the precise attribution of the bands in this spectral region. Consequently, it is worth searching for other spectral regions that could be better suited for those purposes. Obviously, we investigated the possible choice of the C![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) O band of carbonyls and its shifts during microhydration. For such organic compounds, this is fairly natural, as the 1550–2850 cm−1 region is not particularly congested and the C
O band of carbonyls and its shifts during microhydration. For such organic compounds, this is fairly natural, as the 1550–2850 cm−1 region is not particularly congested and the C![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) O bands appear as fine and intense peaks. Fig. 4 shows that this choice was indeed quite adequate: although the complexation-induced shifts in the C
O bands appear as fine and intense peaks. Fig. 4 shows that this choice was indeed quite adequate: although the complexation-induced shifts in the C![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) O elongation did not present a linear dependency upon the computed interaction energies, the shifts appeared to be fairly unambiguous and representative of the structures of the complexes formed. They could therefore be used as descriptors to confirm the tentative assignment done on the basis of the OH elongation shifts of the water molecule. Thus, such shifts would make it possible, in addition to the study of the OH elongation frequencies of carbonyl–water complexes, to confirm the assignments of the monohydrated isomeric geometries, and possibly to identify the simultaneous presence of several isomers. Experimentally, the C
O elongation did not present a linear dependency upon the computed interaction energies, the shifts appeared to be fairly unambiguous and representative of the structures of the complexes formed. They could therefore be used as descriptors to confirm the tentative assignment done on the basis of the OH elongation shifts of the water molecule. Thus, such shifts would make it possible, in addition to the study of the OH elongation frequencies of carbonyl–water complexes, to confirm the assignments of the monohydrated isomeric geometries, and possibly to identify the simultaneous presence of several isomers. Experimentally, the C![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) O stretching, in addition to the OH stretching, was used recently by Vaida and co-workers to distinguish between gas phase pyruvic acidic isomers either isolated or H bonded to water molecules, thus confirming the efficiency of such a procedure.60 Nevertheless, these authors showed that probing the C
O stretching, in addition to the OH stretching, was used recently by Vaida and co-workers to distinguish between gas phase pyruvic acidic isomers either isolated or H bonded to water molecules, thus confirming the efficiency of such a procedure.60 Nevertheless, these authors showed that probing the C![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) O band experimentally by IR spectroscopy requires an experimental setup dedicated to monohydrates and equipped with suitable laser diodes, which is not necessarily easy to implement. Alternatively, any experimental technique, not based on IR spectroscopy, which would enable determining the structure of such monohydrated isomers, in conjunction with theoretical calculations, would be highly appreciated. For those purposes, high-resolution UV-vis spectroscopy was suggested. It has been proven that this technique is also very efficient at treating the bonding between organic compounds and water molecules.58,61 We therefore calculated the pattern of the first singlet and triplet electronic excited states of TPH, MLA DMI, CON and their monohydrates in order to determine whether the HOMO–LUMO transitions of isolated molecules would be significantly shifted and therefore experimentally measurable. These computations were performed at the TD-DFT PBE0/6-311++G(d,p) level for the most stable monohydrate isomers and the results are given fully in Tables S3 and S4 of the ESI.†
O band experimentally by IR spectroscopy requires an experimental setup dedicated to monohydrates and equipped with suitable laser diodes, which is not necessarily easy to implement. Alternatively, any experimental technique, not based on IR spectroscopy, which would enable determining the structure of such monohydrated isomers, in conjunction with theoretical calculations, would be highly appreciated. For those purposes, high-resolution UV-vis spectroscopy was suggested. It has been proven that this technique is also very efficient at treating the bonding between organic compounds and water molecules.58,61 We therefore calculated the pattern of the first singlet and triplet electronic excited states of TPH, MLA DMI, CON and their monohydrates in order to determine whether the HOMO–LUMO transitions of isolated molecules would be significantly shifted and therefore experimentally measurable. These computations were performed at the TD-DFT PBE0/6-311++G(d,p) level for the most stable monohydrate isomers and the results are given fully in Tables S3 and S4 of the ESI.†
For illustration, Table 2 shows the S0 → S1 and S0 → T1 vertical transition wavelengths of the most stable complexes of TPH, MLA, DMI, and CON with a water molecule. This table gives also the complexation-induced shifts corresponding to the wavelength difference between that of the complex and the corresponding one in the isolated carbonyl, being lower in energy as those of water (which are lying at shorter wavelengths, i.e., out of the range of the investigated transitions). Indeed, Tables S3 and S4 (ESI†) reveal that the S0 → Sn and S0 → Tn (n = 1–5) correspond to the promotion of one electron from the highest occupied molecular orbitals (MOs) of the organic compound to its lowest unoccupied MOs since they are mostly located on this compound rather than on water (cf. Fig. S1, ESI†).
| Complex | λ S0→S1 | ΔλS0→S1 | λ S0→ T1 | ΔλS0→T1 |
|---|---|---|---|---|
| TPH_1 | 310.0 | −9.2 | 363.37 | −31.29 |
| TPH_2 | 310.9 | −8.3 | 400.8 | 6.14 |
| MLA_1 | 211.9 | 10.0 | 234.44 | 10.79 |
| MLA_2 | 211.7 | 9.7 | 234.28 | 10.63 |
| DMI_1 | 221.0 | −3.9 | 225.27 | −4.02 |
| DMI_2 | 221.0 | −3.9 | 225.28 | −4.01 |
| CON_BC1_1 | 279.2 | −9.9 | 322.37 | −15.53 |
| CON_BC1_2 | 280.9 | −8.1 | 324.77 | −13.13 |
| CON_TBC1_1 | 281.3 | −10.2 | 324.6 | −16.02 |
| CON_TBC1_2 | 284.9 | −6.6 | 329.73 | −10.89 |
| CON_CR_1 | 283.5 | −9.9 | 327.22 | −15.51 |
| CON_CR_2 | 283.5 | −9.9 | 327.22 | −15.51 |
| CON_BC2_1 | 284.2 | −10.0 | 329.94 | −16.02 |
| CON_BC2_2 | 286.1 | −8.1 | 332.45 | −13.51 |
| CON_TBC2_1 | 282.0 | −10.0 | 327.43 | −16.05 |
| CON_TBC2_2 | 283.0 | −9.0 | 328.69 | −14.79 |
As expected for carbonyl compounds, Table 2 and Table S3 (ESI†) shows that the S0 → S1 transitions of the carbonyls under investigation occurred for λS0 → S1 in the 290–320 nm range, except for DMI, for which this transition took place at ∼200 nm, as for esters. These transitions were red-shifted upon attaching a water molecule to these organics. Such shifts amounted to ∼10 nm for the S0 → S1 transition and even larger (∼30 nm) for the S0 → T1 transitions. Such shifts are quite large and can be used to probe the monohydration of these carbonyls, in addition to the IR spectroscopy discussed above. Interestingly, Fig. S1 (ESI†) shows that the orbitals of the water molecule were also directly involved during these transitions. Again, our findings suggest that UV-vis spectroscopy is a powerful tool to probe the subtle effects associated with the microhydration of organic compounds as done recently for the atmospheric relevant hydration of methylglyoxal.59 Besides, we suggest investigating the S0 → T1 transitions, although of weak intensities, since they present large band shifts from bare molecules while interacting with a water molecule.
3. Topological analyses of the structures and the strengths of the monohydrated carbonyls complexes
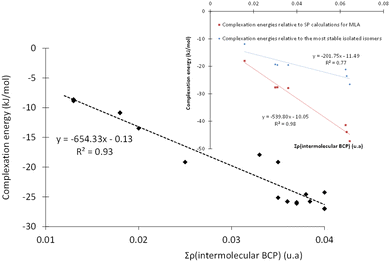
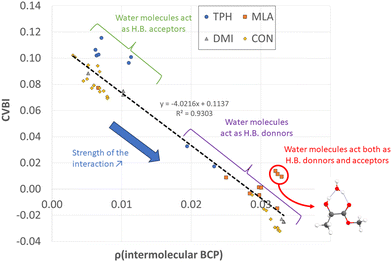
To gain a better insight into the microhydration processes, and to better understand the origin of the stabilization of the monohydrated carbonyls, we investigated the relationship between the stability of the complexes (and therefore their interaction energies) and the sum of the electron densities at the BCPs of the intermolecular bonds. For the complexes involving DMI, CON, and TPH, the interaction energy was found to be globally proportional to the total electron density at the intermolecular BCPs (Table S5, ESI†) since these organic molecules were only slightly deformed during their interaction with the water molecule. The case of MLA was trickier, as the water molecule breaks an intramolecular hydrogen bond within MLA to form the most stable respective complexes. Therefore, we recalculated the interaction energy of these MLA monohydrate complexes in relation to a single point made on the equilibrium geometry of MLA in each complex (see the inset in Fig. 5).Alternatively, more information about the strength of the hydrogen bond can be obtained after examining the core-valence bifurcation index (CVBI).62–64 This index is based on a topological value as given in eqn (3):
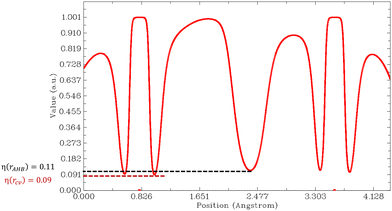
| ϑ(AHB) = η(rcv) − η(rAHB) | (3) |
Then, we must look at the sign of CVBI: if it is positive, the hydrogen bond associated with the CVB index is weak. Else, the hydrogen bond is strong. For illustration, the variation of the ELF value along the A–H–B bond path is shown in Fig. 6 for the most stable conformer of the monohydrated DMI molecule. In this case, the CVB index was −0.02, which means that the hydrogen bond was strong.
All non-covalent interactions in the monohydrated complexes herein considered were classified with the help of CVBI and the electron density at the intermolecular BCP to gain a better understanding of the strength of the hydrogen bond (cf.Fig. 7). The strongest bonds corresponded to those characterized by the highest ρ(BCP) values and negative CVBI values. Obviously, the isomers in which the water molecule acted as a hydrogen bond donor (to the C![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) O bond of the solutes) were stronger than those in which the water molecule acted as a hydrogen bond acceptor. We also noted that systems in which water plays the role of both hydrogen bond acceptor and donor with the OH and C
O bond of the solutes) were stronger than those in which the water molecule acted as a hydrogen bond acceptor. We also noted that systems in which water plays the role of both hydrogen bond acceptor and donor with the OH and C![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) O functions, in the case of MLA, were characterized by a significant relative stability.
O functions, in the case of MLA, were characterized by a significant relative stability.
IV. Conclusions
Numerous monohydrated isomers with a similar energy or even iso-energetic properties were identified for the 4 chosen solutes. We can therefore reasonably assume that different structures can coexist experimentally, including when using a molecular beam. The question of their identification on an experimental observable is therefore of prime importance. We have shown that relying solely on the OH elongation of the water molecule to identify the structure of monohydrate complexes is not sufficient, particularly because of the relatively large width of this the corresponding bands. The experimental study of C![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) O elongation appears to be complementary. The use of UV-vis spectroscopy to probe complexation-induced effects while forming these monohydrate complexes can be used also. It turns out that even for these relatively simple molecules, the analysis of their monohydrated complexes is not straightforward. In particular, different types of water–solute interactions were highlighted: the dual role of the donor and acceptor of the water molecule and the solute, the involvement of heteroatoms, the simple role of the acceptor of pseudohydrogen bonds with an aliphatic H of the solute, or π-hole type interactions. In sum, the interplay between both theoretical and experimental approaches seems essential for these studies as initiated by the HyDRA challenge.
O elongation appears to be complementary. The use of UV-vis spectroscopy to probe complexation-induced effects while forming these monohydrate complexes can be used also. It turns out that even for these relatively simple molecules, the analysis of their monohydrated complexes is not straightforward. In particular, different types of water–solute interactions were highlighted: the dual role of the donor and acceptor of the water molecule and the solute, the involvement of heteroatoms, the simple role of the acceptor of pseudohydrogen bonds with an aliphatic H of the solute, or π-hole type interactions. In sum, the interplay between both theoretical and experimental approaches seems essential for these studies as initiated by the HyDRA challenge.
Conflicts of interest
There are no conflicts to declare.References
- B. Long, J. L. Bao and D. G. Truhlar, J. Am. Chem. Soc., 2016, 138, 14409–14422 CrossRef CAS PubMed.
- D. Johnson and G. Marston, Chem. Soc. Rev., 2008, 37, 699 RSC.
- A. B. Ryzhkov and P. A. Ariya, Phys. Chem. Chem. Phys., 2004, 6, 5042 RSC.
- V. Vaida and J. E. Headrick, J. Phys. Chem. A, 2000, 104, 5401–5412 CrossRef CAS.
- H. Chen, H. Hirao, E. Derat, I. Schlichting and S. Shaik, J. Phys. Chem. B, 2008, 112, 9490–9500 CrossRef CAS PubMed.
- K. Doi, E. Togano, S. S. Xantheas, R. Nakanishi, T. Nagata, T. Ebata and Y. Inokuchi, Angew. Chem., 2013, 125, 4476–4479 CrossRef.
- M. Prakash, K. Rudharachari Maiyelvaganan, N. G. Lakshman, M. Mogren Al-Mogren and M. Hochlaf, Chem. Phys. Chem., 2023, 24, e202300267 CrossRef CAS PubMed.
- K. R. Maiyelvaganan, S. Kamalakannan, S. Shanmugan, M. Prakash, F.-X. Coudert and M. Hochlaf, J. Colloid Interface Sci., 2022, 605, 701–709 CrossRef CAS PubMed.
- R. Dahmani, S. Grubišić, S. B. Yaghlane, S. Boughdiri and M. Hochlaf, J. Phys. Chem. A, 2019, 123, 5555–5565 CrossRef CAS PubMed.
- R. Dahmani, S. Grubišić, I. Djordjević, S. Ben Yaghlane, S. Boughdiri, G. Chambaud and M. Hochlaf, J. Chem. Phys., 2021, 154, 024303 CrossRef CAS PubMed.
- S. Grubišić, R. Dahmani, I. Djordjević, M. Sentić and M. Hochlaf, Phys. Chem. Chem. Phys., 2023, 25, 954–965 RSC.
- P. Rodziewicz and N. L. Doltsinis, Chem. Phys. Chem., 2007, 8, 1959–1968 CrossRef CAS PubMed.
- M. Demireva, J. T. O’Brien and E. R. Williams, J. Am. Chem. Soc., 2012, 134, 11216–11224 CrossRef CAS PubMed.
- K. Kalra, S. Gorle, L. Cavallo, R. Oliva and M. Chawla, Nucleic Acids Res., 2020, 48, 5825–5838 CrossRef CAS PubMed.
- E.-L. Zins, J. Phys. Chem. A, 2020, 124, 1720–1734 CrossRef CAS PubMed.
- A. Jendoubi, Y. Arfaoui, J. Palaudoux, M. M. Al-Mogren and M. Hochlaf, J. Comput. Chem., 2023, jcc.27270 Search PubMed.
- T. L. Fischer, M. Bödecker, A. Zehnacker-Rentien, R. A. Mata and M. A. Suhm, Phys. Chem. Chem. Phys., 2022, 24, 11442–11454 RSC.
- T. L. Fischer, M. Bödecker, S. M. Schweer, J. Dupont, V. Lepère, A. Zehnacker-Rentien, M. A. Suhm, B. Schröder, T. Henkes, D. M. Andrada, R. M. Balabin, H. K. Singh, H. P. Bhattacharyya, M. Sarma, S. Käser, K. Töpfer, L. I. Vazquez-Salazar, E. D. Boittier, M. Meuwly, G. Mandelli, C. Lanzi, R. Conte, M. Ceotto, F. Dietrich, V. Cisternas, R. Gnanasekaran, M. Hippler, M. Jarraya, M. Hochlaf, N. Viswanathan, T. Nevolianis, G. Rath, W. A. Kopp, K. Leonhard and R. A. Mata, Phys. Chem. Chem. Phys., 2023, 25, 22089–22102 RSC.
- Y. He, C. Wu and W. Kong, J. Phys. Chem. A, 2005, 109, 748–753 CrossRef CAS PubMed.
- C. Pérez, A. Krin, A. L. Steber, J. C. López, Z. Kisiel and M. Schnell, J. Phys. Chem. Lett., 2016, 7, 154–160 CrossRef PubMed.
- X. K. Zhang, E. G. Lewars, R. E. March and J. M. Parnis, J. Phys. Chem., 1993, 97, 4320–4325 CrossRef CAS.
- K. Coutinho, N. Saavedra and S. Canuto, J. Mol. Struct. Theochem, 1999, 466, 69–75 CrossRef CAS.
- B. Nelander, Chem. Phys., 1992, 159, 281–287 CrossRef CAS.
- T. K. Ha, J. Makarewicz and A. Bauder, J. Phys. Chem., 1993, 97, 11415–11419 CrossRef CAS.
- M. Mucha and Z. Mielke, J. Phys. Chem. A, 2007, 111, 2398–2406 CrossRef CAS PubMed.
- L. Khriachtchev, J. Phys. Chem. A, 2015, 119, 2735–2746 CrossRef CAS PubMed.
- T. L. Fischer, T. Wagner, H. C. Gottschalk, A. Nejad and M. A. Suhm, J. Phys. Chem. Lett., 2021, 12, 138–144 CrossRef CAS.
- E. Burevschi, I. Peña and M. E. Sanz, Phys. Chem. Chem. Phys., 2019, 21, 4331–4338 RSC.
- C. Adamo and V. Barone, J. Chem. Phys., 1999, 110, 6158–6170 CrossRef CAS.
- M. J. Frisch, G. W. Trucks, H. B. Schlegel, G. E. Scuseria, M. A. Robb, J. R. Cheeseman, G. Scalmani, V. Barone, G. A. Petersson and H. Nakatsuji, Gaussian, Gaussian Inc., Wallingford CT, 2016.
- M. Ernzerhof and G. E. Scuseria, J. Chem. Phys., 1999, 110, 5029–5036 CrossRef CAS.
- S. Grimme, J. Antony, S. Ehrlich and H. Krieg, J. Chem. Phys Search PubMed.
- P. Pracht, F. Bohle and S. Grimme, Phys. Chem. Chem. Phys., 2020, 22, 7169–7192 RSC.
- S. Grimme, F. Bohle, A. Hansen, P. Pracht, S. Spicher and M. Stahn, J. Phys. Chem. A, 2021, 125, 4039–4054 CrossRef CAS PubMed.
- C. Plett and S. Grimme, Angew. Chem., Int. Ed., 2023, 62, e202214477 CrossRef CAS PubMed.
- J. E. Del Bene, D. H. Aue and I. Shavitt, J. Am. Chem. Soc., 1992, 114, 1631–1640 CrossRef CAS.
- J. P. Merrick, D. Moran and L. Radom, J. Phys. Chem. A, 2007, 111, 11683–11700 CrossRef CAS PubMed.
- R. S. Grev, C. L. Janssen and H. F. Schaefer III, J. Chem. Phys., 1991, 95, 5128–5132 CrossRef CAS.
- I. M. Alecu, J. Zheng, Y. Zhao and D. G. Truhlar, J. Chem. Theory Comput., 2010, 6, 2872–2887 CrossRef CAS PubMed.
- M. K. Kesharwani, B. Brauer and J. M. Martin, J. Phys. Chem. A, 2015, 119, 1701–1714 CrossRef CAS PubMed.
- R. V. Solomon, A. P. Bella, S. A. Vedha and P. Venuvanalingam, Phys. Chem. Chem. Phys., 2012, 14, 14229–14237 RSC.
- M. Prakash, G. Chambaud, M. M. Al-Mogren and M. Hochlaf, J. Mol. Model., 2014, 20, 1–14 CrossRef CAS.
- K. Boussouf, T. Khairat, M. Prakash, N. Komiha, G. Chambaud and M. Hochlaf, J. Phys. Chem. A, 2015, 119, 11928–11940 CrossRef CAS.
- Y. Shao, Y. Mei, D. Sundholm and V. R. Kaila, J. Chem. Theory Comput., 2019, 16, 587–600 CrossRef.
- J. Goldwasser, J. S. Murray and P. Politzer, New Orleans Univ Dept Chem.
- P. Politzer, J. S. Murray and T. Clark, Phys. Chem. Chem. Phys., 2010, 12, 7748–7757 RSC.
- S. R. Gadre, C. H. Suresh and N. Mohan, Molecules, 2021, 26, 3289 CrossRef CAS PubMed.
- S. R. Gadre and I. H. Shrivastava, J. Chem. Phys., 1991, 94, 4384–4390 CrossRef CAS.
- A. Kumar and S. R. Gadre, J. Chem. Theory Comput., 2016, 12, 1705–1713 CrossRef CAS PubMed.
- R. F. W. Bader, M. T. Carroll, J. R. Cheeseman and C. Chang, J. Am. Chem. Soc., 1987, 109, 7968–7979 CrossRef CAS.
- C. Kalai, M. E. Alikhani and E.-L. Zins, Theor. Chem. Acc., 2018, 137, 1–20 Search PubMed.
- R. F. Bader, Monatsh. ChemieChem. Mon., 2005, 136, 819–854 Search PubMed.
- R. F. Bader and C. F. Matta, Found. Chem., 2013, 15, 253–276 Search PubMed.
- R. F. W. Bader, J. Phys. Chem. A, 2010, 114, 7431–7444 CrossRef CAS PubMed.
- T. A. Keith, URL Httpaim Tkgristmill Com.
- B. Silvi and A. Savin, Nature, 1994, 371, 683–686 CrossRef CAS.
- A. Savin, B. Silvi and F. Colonna, Can. J. Chem., 1996, 74, 1088–1096 CrossRef CAS.
- S. Noury, X. Krokidis, F. Fuster and B. Silvi, Comput. Chem., 1999, 23, 597–604 CrossRef CAS.
- J. S. Murray, P. Lane, T. Clark, K. E. Riley and P. Politzer, J. Mol. Model., 2012, 18, 541–548 CrossRef CAS PubMed.
- S. L. Blair, A. E. Reed Harris, B. N. Frandsen, H. G. Kjaergaard, E. Pangui, M. Cazaunau, J.-F. Doussin and V. Vaida, J. Phys. Chem. A, 2020, 124, 1240–1252 CrossRef CAS PubMed.
- J. A. Kroll, A. S. Hansen, K. H. Møller, J. L. Axson, H. G. Kjaergaard and V. Vaida, ACS Earth Space Chem., 2017, 1, 345–352 CrossRef CAS.
- F. Fuster and B. Silvi, Theor. Chem. Acc. Theory Comput. Model. Theor. Chim. Acta, 2000, 104, 13–21 CrossRef CAS.
- F. Fuster and S. J. Grabowski, J. Phys. Chem. A, 2011, 115, 10078–10086 CrossRef CAS PubMed.
- B. Silvi and H. Ratajczak, Phys. Chem. Chem. Phys., 2016, 18, 27442–27449 RSC.
Footnote |
| † Electronic supplementary information (ESI) available. See DOI: https://doi.org/10.1039/d4cp01035c |
| This journal is © the Owner Societies 2024 |