Open Access Article
Open Access ArticleCreative Commons Attribution 3.0 Unported Licence
Electronic structures of three anchors of triphenylamine on a p-type nickel oxide(100) surface: density functional theory with periodic models†
Outi V.
Kontkanen
 *a,
Terttu I.
Hukka
*a,
Terttu I.
Hukka
 *a and
Tapio T.
Rantala
*a and
Tapio T.
Rantala
 b
b
aChemistry and Advanced Materials, Materials Science and Environmental Engineering, Faculty of Engineering and Natural Sciences, Tampere University, P.O. Box 541, FI-33014, Finland. E-mail: terttu.hukka@tuni.fi
bDepartment of Physics, Tampere University, P.O. Box 692, FI-33014, Finland
First published on 6th June 2024
Abstract
In this paper, we investigate the electronic structures of triphenylamine molecules with three different anchoring groups (pyridinyl, carboxyl, and phenyl-1,2-diol) before and after attachment with a p-type semiconductor, nickel oxide (100), surface. To understand the charge transfer characteristics of these structures commonly used in dyes of the dye-sensitized solar cells (DSSC), we use periodic models to study their configurations with density functional theory (DFT). We find that carboxyl and phenyl-1,2-diol anchors adsorb more strongly compared to pyridinyl anchor on NiO(100). Stronger binding is reflected as a bigger dipole moment and a more viable charge transfer from the anchors to NiO(100). Furthermore, the alignment of electronic levels favors charge transfer only for pyridinyl and phenyl-1,2-diol anchors. Despite its weaker binding on the NiO(100) surface, pyridinyl is a more promising anchoring group for transferring charge to NiO, as it does not create trap states.
Introduction
Since the pioneering paper by O’Regan and Grätzel in 1991,1 dye-sensitized solar cells (DSSCs) have attracted attention as a promising technology to obtain clean and cost-effective energy from sunlight conversion. DSSCs are a particular class of photovoltaic devices, where the processes of charge photogeneration, transport, and light harvesting in the external circuit are addressed by different components of the cell.1 In general, DSSCs are classified as n-type, when the photogenerated charge injected into the semiconductor is an electron, and p-type, when the injected charge is a hole. The charge injection from the dye to p-type oxides has been studied using spectroscopic techniques and doping strategies have been implemented to improve the semiconductor hole transport properties.2,3Most of the recent research efforts with p-type DSSCs (p-DSSCs) focus on the use of nickel oxide (NiO) as the p-type semiconductor.4–19 Unfortunately, the best efficiency reported for the NiO-based tandem p-DSSC is ≤4% with the p-DSSC efficiency of 0.35%,15 compared to ∼13% of the n-type DSSC (n-DSSC) with a Zn–porphyrin sensitizer.20 Yet, the combination of both the p- and n-type semiconductors in tandem-DSSCs offers a premise for boosting the light-to-current conversion efficiency of these devices over the theoretical Shockley–Queisser limit, (40%).21 At the present, the highest efficiency of a (TiO2–NiO-based) tandem-DSSC is ∼2%.15 Clearly, the total efficiency of a tandem-DSSC is limited by its less effective, p-type component. Therefore, new materials and architecture design directions for improving the efficiencies of the p-type DSSCs are needed.9,13,15,22
A DSSC is composed of the following three main components: dye molecules, a semiconductor surface, and an electrolyte. A molecular dye, with the optical band gap ideally within the visible range of the sunlight spectrum and a large absorption cross-section, is deposited on a wide bandgap porous semiconducting oxide. The role of the dye is to efficiently absorb the sunlight and convert the absorbed photons into electron–hole pairs. The role of the oxide is to transport the hole (or the electron) to the electrode (the countercharge being transferred to the external circuit by a liquid or solid electrolyte), to help reduce the dye molecule to the ground state, and to promote the photoinduced hole transfer.23
The anchoring group of the dye is the bridge between the dye and the semiconducting oxide surface. Therefore, the anchoring group ultimately controls the charge injection and potential voltage losses at the interface.24–26 As a result, the anchoring group needs to fulfill the following three (i)–(iii) requirements, in terms of stability and electronic structure. (i) It must provide a solid tethering of the dye to the semiconductor to avoid its desorption from the surface and the consequent degradation of the device. This is reflected by a significant adsorption (or binding) energy of the dye on the semiconductor. (ii) The anchor must guarantee the appropriate alignment of the electronic levels of the dye with those of the semiconductor. (iii) The anchor should provide an effective communication between the dye and the semiconductor, which is generally obtained by spatially localizing the highest occupied molecular orbital (HOMO) of the dye close to the valence band maximum (VBM) of the semiconductor so that there is a significant wavefunction overlap.27
Besides for the n-DSSCs,28 various organic dyes and anchors have been previously investigated for p-DSSCs, with the goal to improve the conversion efficiency.16,17,29 The most commonly used anchors have been carboxylic acid,16,28 cyanoacrylic acid,28 pyridine,16,30 catechol,31 alkoxysilanes,5 and phosphonic acid.32 Carboxylic acid has been the most studied and favored anchoring group in literature for n-DSSCs, because it has a significant binding energy with TiO2 and its strong electron withdrawing character allows polarization of the lowest unoccupied molecular orbital (LUMO) of the dye towards the oxide.27 However, the electron accepting, carboxylic acid anchoring group that suits n-DSSCs is not expected to be optimal for p-type DSSCs, because the HOMO of some dyes has a weak electronic density on this anchor.24
In the case of the carboxylic acid anchor, which can bind onto NiO(100) either in a monodentate or a bidentate form,5 it has been suspected that monodentate binding causes a negative shift of the valence band edge of NiO due to the protonation of the surface, while a pyridine ring does not have this drawback.16 The monodentate anchoring mode corresponds to the formation of a covalent, chemical bond between the oxygen (O) atom of the hydroxy (–OH) group of COOH and one surface metal, i.e., Ni, atom. In the bidentate bridging28 anchoring mode, both oxygens of a carboxyl group, i.e., in hydroxy (–OH) and carbonyl (C![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) O), are chemically bound to two different metal atoms of the surface. With perylene monoimide (PMI)-based sensitizers, the best monodentate anchor is intermediate between the strongly and weakly bound one, in terms of stability and photovoltaic performance, when having a low aggregation on the NiO surface.17 With the carboxylic anchor, the PMI dyes favor bidentate and/or bidentate chelating mode according to the Fourier transform infrared spectroscopy (FTIR) studies.17 Accordingly, carboxylic acid, which is a moderately bound anchor, and has been frequently but not thoroughly19,33 studied, provides a good reference point for studies of bidentate anchors.
O), are chemically bound to two different metal atoms of the surface. With perylene monoimide (PMI)-based sensitizers, the best monodentate anchor is intermediate between the strongly and weakly bound one, in terms of stability and photovoltaic performance, when having a low aggregation on the NiO surface.17 With the carboxylic anchor, the PMI dyes favor bidentate and/or bidentate chelating mode according to the Fourier transform infrared spectroscopy (FTIR) studies.17 Accordingly, carboxylic acid, which is a moderately bound anchor, and has been frequently but not thoroughly19,33 studied, provides a good reference point for studies of bidentate anchors.
Jin et al. achieved an efficiency of 0.14% with a triphenylamine-based (TRIA) sensitizer with two pyridine anchors.4 However, the bidentate mode has been reported to degrade the performance of various sensitizers and reduce the ability of the pyridine anchor to interact with the NiO surface.18 Good monodentate anchors for the p-DSSCs on NiO with the PMI dyes have moderately binding alcoholic OH groups.17 However, the derivations of the structure–property relationships of the p-DSSCs having anchors in a bidentate binding mode on NiO are not yet fully understood and are therefore worth investigating and comparing to previous reports.
In the perspective of optimizing the design of the anchors and molecular dyes for DSSC, computational modeling appears as an extremely useful tool.34–36 Recent works have reported density functional theory (DFT) electronic structure calculations of heterojunctions built by grafting model dyes on NiO. More specifically, Muñoz-García et al.37 carried out DFT calculations on the relative alignment of the HOMO of a coumarin-based C343 dye and the VBM of NiO on the Ni(100) for two anchoring groups: carboxylic acid and phosphonic acid. Our group investigated the adsorption of PMI-based dyes via carboxylic acid anchor both in monodentate and bidentate mode on the NiO(100) surface.38 Wykes et al.5 investigated the influence of the anchor adsorption on the electronic structure of NiO with formic and benzoic acids and alkoxysilanes on the NiO(100) surface using DFT with a surface slab unit cell of (11.81 × 8.86) Å2. Piccinin et al. applied DFT and first principles molecular dynamics (MD) simulations in water to the energy level alignment of NiO–C343–PO(OH)2.39 They avoided carboxylic acid anchor, which would desorb from the oxide surface under aqueous conditions.39 They applied a dipole in the 18 Å thick vacuum region to compensate spurious dipolar interaction among replicas in the DFT.39
Muñoz-García et al.37 were addressing the effects of the binding modes (monodentate/bidentate/tridentate). They showed that grafting of the reference coumarin C343 dye through the carboxyl acid anchoring is more stable in the bidentate form than in the monodentate form on NiO, with adsorption energies of 0.71 eV and 0.59 eV, respectively.37 Moreover, they37 found that the relative shift of the HOMO of the dye with respect to the VBM of NiO, is due to the surface dipole, which depends on the binding modes of the anchors and the topmost NiO layer. Furthermore, they stated that the anchoring groups, which form the smallest interfacial dipole are the most potential ones for p-type DSSCs. Despite the various studies, the ultimate mechanism dictating the shifts of the electronic levels of the anchors have not yet been fully addressed.
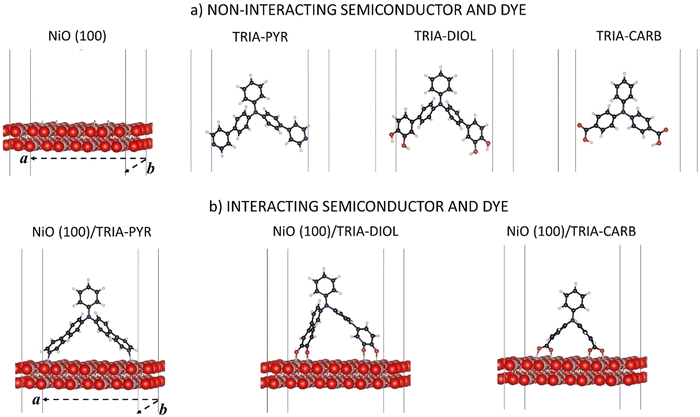
Herein, the focus is on three commonly used anchoring groups and their compatibility and interaction with the p-type NiO(100) semiconductor surface, when bound to N,N-diphenylaniline called TRIA (Fig. 1). The TRIA-anchors are components of PMI–TRIA dyes, which are known to work in p-DSSCs,10 and of other sensitizers. The anchoring groups are pyridinyl (PYR), phenyl-1,2-diol (DIOL), and carboxyl (CARB). The aim is to investigate how the interaction of anchors with the surface is reflected in chemical and electronic properties. The properties are studied with DFT calculations using periodic models. The properties of separated and interacting systems will be presented in the light of their frontier molecular orbitals, energy level alignments, dipole moments, interaction energies, and Mulliken population analyses. The hypothesis, based on literature, is that one anchoring group, PYR, stands out as a viable candidate over CARB for improving the charge transfer properties of p-DSSC architectures. The question is, which properties explain the hypothesized superiority of PYR.
Models and methods
The models are depicted in Fig. 1. Three TRIA-anchors (also called dyes in this paper) and a NiO(100) substrate, and their composite systems were investigated using DFT calculations with periodic models. Calculations on separated systems enable the disentanglement of the effects associated with the changes in a chemical structure of an anchoring group from those associated with an electron density reshuffling upon adsorption and chemical binding onto a surface. The coordinates are in ESI.†The slab model for the NiO(100) substrate is cut from the NiO bulk.38 The crystal is cubic (fcc) and has Fm3m symmetry in its antiferromagnetic phase of the (100) surface. The (100) is the most stable NiO surface.40 Atomic positions were fully relaxed with the cell parameters kept fixed at their corresponding relaxed values in bulk obtained in our earlier study (a0 = 4.213 Å).38 The slab model of NiO(100) consists of two (2) layers thick (4 × 4) supercell along the two periodic directions (Fig. 1a), for a total periodic surface of 16.71 Å × 16.71 Å. The use of a large surface is mandatory to host the chosen organic moiety and avoid spurious image effects. The thickness of the slab model was justified via additional calculations (Table S1, ESI†), which showed that the layer thickness has very little effect on the energy levels. The calculations demonstrated that our model yields converged results with reasonable computational costs for the band gap, VBM, and the conduction band minimum (CBM) of the semiconductor, when compared to the thicker models (Table S1, ESI†). The thickness of the vacuum in the z-direction is 500 Å.
In the TRIA-anchor models (Fig. 1a), two PYR or two CARB substituents are bound to a TRIA molecule at the 4,4′-, i.e., para-, positions to provide the PYR and CARB anchoring groups and two DIOLs at the 3,4- and 3′,4′-, i.e., meta- and para-, positions to provide the DIOL anchoring groups (Fig. 1). The IUPAC names of the models with hydrogens are N-phenyl-4-(pyridin-4-yl)-N-(4-(pyridin-4-yl)phenyl)aniline (TRIA–PYR), 4′,4′′′-(phenylazanediyl)bis(([1,1′-biphenyl]-3,4-diol)) (TRIA–DIOL), and 4,4′-(phenylimino)dibenzoic acid (TRIA–CARB). The energetics of the separated TRIA-anchor dyes were studied as such and without hydrogens (H-free), i.e., as radicals. We note here that a phenyl-1,2-diol anchoring group is often named ‘catechol’ in sensitizer literature after its isolated molecular form of benzene-1,2-diol.
In the final, combined systems, each TRIA-anchor model is adsorbed on the NiO(100) surface. The anchors are chemisorbed on the Ni atoms through the N or O atoms. The anchoring groups per site are –N, –COO˙, and –O˙ (Fig. 1b), omitting the OH hydrogens intentionally and focusing on the properties of anchoring groups. Besides the possibility of adsorption on the surface, hydrogens or protons could react with the electrolyte in a real device and not end up onto the surface. Therefore, our focus here is not on the role of hydrogen. The adsorption models remain neutral.
The composite systems were fully relaxed, except for lattice vectors (Fig. 1b). In the present work, only the bidentate bridging mode is considered for TRIA–CARB, as the bidentate form has been previously reported more stable on NiO(100) with carboxylic acid anchors.17,37 The same principles are applied to the binding of TRIA–DIOL. The binding sites on the NiO(100) surface were selected according to the molecular dimensions of the adsorbed species, and the adsorbates were placed symmetrically along the diagonal of the surface in the case of PYR and DIOL, which have longer spacers. In the case of CARB, which does not have the extra phenyl spacers to extend as far, the sites were chosen as close to the diagonal as possible, to keep the consistency with the other two models, still maintaining the molecular conformation.
Electronic structure calculations and nuclear geometric relaxations were performed using DFT,41 within the periodic boundary conditions (PBC), with atomic centered Gaussian basis approach, as implemented in the CRYSTAL09 code,42,43 utilizing hybrid functionals.
The B3LYP hybrid functional44,45 was chosen for both the NiO and the dye models as it is known to reproduce the experimental band gap and orbital energies of organic solids better than the standard generalized gradient approximation (GGA) functionals (see ESI†).38 The 6-31G(d,p) basis set was used for the dyes,46 and 86411/6411/4147 and 8411/411447 basis sets, which have been previously fine-tuned to yield accurate results for the Ni and O atoms, respectively, with NiO,47 and have been successfully applied to the NiO(100) surface.37 The basis sets of the surface (Ni, O) describe the number of Gaussian primitive functions for the (d)/p/s orbitals, respectively. Calculations were performed for the Γ-point only, which should give sufficient description of the small first Brillouin zone of the sizable supercell used here (Fig. 1). We note that care needs to be taken when choosing the method for describing the electronic structures as, e.g., functionals can predict band gaps of inorganic48–51 and HOMO–LUMO gaps of organic52,53 compounds with clear differences compared to other approaches and experimental results. We used the computational setup confirmed in our previous paper.38 No imaginary frequencies were found.38 Solvent effects and electrolytes, which would be worth a separate paper, were excluded, as the focal point here is on anchors. Moreover, solvent and electrolyte environments would require excessive supercomputer resources leading to even higher computational costs on top of the already heavy theoretical calculations.
Here, our main purpose is to present new insights from a LCAO-based approach for the known anchor, CARB, and to try to replicate and explain the potentially good anchors, DIOL and PYR, with the help of the CRYSTAL code. Although DFT is a standard method for similar, large systems, usually either plane waves37,39,54 or MD simulations39,54 have been used, which require less resources with periodic models than the LCAO approach. If LCAO approaches have been chosen, they have been mainly applied to isolated dye molecules to (i) confirm experimental results4,18,54 or (ii) model the HOMO/LUMO distributions.4,18,54 As such, they usually give a reasonable agreement with the experiments, but do not explain everything.54 One of our motivations was to justify our approach and show that with CRYSTAL/LCOA we can achieve reasonable results compared to experiments and yield more insight into the charge transfer mechanism within p-DSSCs.
We verified that the present computational setup, in connection with the model size adopted, provides converged values for both the VBM and CBM of NiO (Table S1, ESI†). A band gap of 3.9 eV is predicted for our two layers thick (4 × 4) NiO supercell, which is only 0.2 eV larger than the experimental optical gap (Table S1, ESI†). In all cases, the spin-polarization of Ni in the NiO slab has been incorporated to reproduce the anti-ferromagnetic (AF2) phase of NiO as described in ref. 38. Related keywords are listed and explained in the ESI.†
Results and discussion
The density of states (DOS) and partial-DOS (pDOS) are commonly used to investigate how the energy levels align, when an adsorbate adheres on the semiconductor of a DSSC. The energy levels often shift and are different in the isolated and adsorbed systems. The energy levels can be realigned by tuning the electrostatic potential using different adsorbates.Two pyridinyl anchors on nickel oxide surface
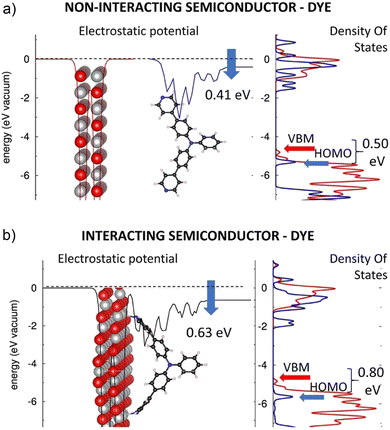
In the following, the electronic structures of the separated pyridinyl anchors, NiO(100), and their heterostructures are discussed. The planar, averaged electrostatic potentials (left) and electronic pDOSs (right) are presented in Fig. 2 for (a) the non-interacting TRIA–PYR-anchor and the NiO(100) surface, and (b) the combined interacting TRIA–PYR–NiO semiconductor system (Fig. 2).For the TRIA–PYR oriented as in Fig. 2a, the electrostatic potential downshifts by 0.41 eV along the TRIA–PYR from the PYR-anchor to TRIA. This downshift, ΔEvac, in our periodic models is due to the presence of a non-null electric dipole moment of the dye molecule in the cell, which indicates that electrons are clustered on the anchoring site. This is consistent with the Helmholtz eqn (1).55
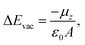 | (1) |
The electronic level alignment for the non-interacting dye and the NiO semiconductor is illustrated by the DOS of Fig. 2a. The computed VBM and CBM lie at −4.81 eV and −0.96 eV, respectively, for the isolated NiO slab (Table S4, ESI†). These energies are obtained by referring to the electronic levels with respect to the electrostatic potential in vacuum, taken as zero energy reference, in analogy to ultraviolet photoemission spectroscopy (UPS) measurements, where the corresponding value for VBM is −5.4 eV,56 which confirms a reasonable agreement between our calculations and experimental measurements. Note, that for the TRIA–PYR molecule, instead, the energetics of the electronic levels can be arbitrarily referred to the electrostatic potential on both sides of the molecule, i.e., either on the side, where the molecule is grafted onto the NiO surface, or on the side that is exposed to the vacuum.
With the aim to compare the energetics for the electronic levels of NiO, we consider the first choice conceptually more correct, as done in Fig. 2a. In this frame, DFT yields the HOMO and LUMO of the TRIA–PYR dye at −5.33 eV and −1.51 eV (Table S4, ESI†), respectively. The HOMO of the dye is ca. 0.50 eV below the VBM of the semiconducting NiO, which is a fundamental requirement for the working mechanism in the p-type DSSC devices. Referring to ‘Introduction’, the electronic configuration in Fig. 2a allows, in fact, a hole photogenerated in the dye and residing in the HOMO level to jump onto the VBM of the NiO surface, under spontaneous thermodynamic conditions.
The alignment of the electronic levels of the independent dye and semiconducting NiO components, as seen from the pDOS of Fig. 2a, does not consider the perturbation on the electronic structure arising from the dye's adsorption onto the oxide surface. To clarify the effects resulting from adsorption and to achieve a reliable description of the electronic structure of the TRIA–PYR–NiO heterointerface, DFT calculations were performed for TRIA–PYR-anchor on the NiO(100) surface, fully relaxing the atomic positions.
The planar, averaged electrostatic potential, and the projected pDOS of the heterointerface of the interacting TRIA–PYR–NiO system is presented in Fig. 2b. The electronic structure of the NiO is almost unaffected by the grafting of the molecular dye: VBM and CBM levels lie at −4.83 eV and −0.97 eV (Table S4, ESI†), respectively, and the general shape of the pDOS remains very similar (Fig. 2b) to the isolated NiO slab (Fig. 2a). Also, the electronic structure of the dye does not drastically change: the TRIA–PYR system shows a HOMO–LUMO gap of 3.78 eV on the NiO(100) surface (Table S4, ESI†), only less than 0.1 eV narrower and shifted to a lower energy, than that of the isolated TRIA–PYR dye (3.82 eV relaxed and 3.87 eV twisted).
Similarly, the pDOSs of the TRIA–PYR dye are similar in shape before and after grafting, at least in the region close to the frontier orbitals, apart from some features between 0 eV and −1 eV. Most notably, no intra gap trap states appear, which could act as recombination centers for the photogenerated electrons and holes and hence negatively affect the expected photovoltaic properties of the TRIA–PYR at the NiO heterointerface. The only significant variation between the electronic structures of the non-adsorbed and adsorbed TRIA–PYR is the change of the electrostatic potential (for the stabilized structures) by 0.22 eV from −0.41 (μz of 3.09 D per cell) eV to −0.63 eV (Fig. 2), upon grafting of the TRIA–PYR molecule on the Ni-oxide surface. The downshift of −0.63 eV corresponds to an interfacial dipole moment component of μz of 4.75 D (eqn (1), A = 2.8396 × 10−18 m2, per cell), which can be in large part explained by electrostatic effects. Disentangling the origin of this downshift of the electrostatic potential is complex. Compared to the relaxed dye, grafting stabilizes the HOMO (−0.36 eV) and LUMO (−0.40 eV) of TRIA–PYR, which assume energies of −5.69 eV and −1.91 eV, respectively (Table S4, ESI†), on the surface. Twisting of the TRIA–PYR structure due to grafting explains 0.11 eV (HOMO) and 0.06 eV (LUMO) of the lowered energies, but more importantly, HOMO remains below the VBM in the interacting system.
With the same distorted, twisted geometry for the TRIA–PYR as after the grafting on the surface, the electrostatic jump increases to 0.51 eV. On the other hand, Mulliken population analysis on the combined dye–semiconductor system shows that 0.14 electrons from NiO and 0.04 electrons from TRIA are gathered on the PYR anchor (0.18, Table S5, ESI†). All these results point to the fact that the PYR anchoring group can draw electrons from the surface to the dye (push holes to the semiconductor). In other words, a PYR anchor can favorably interact with the NiO(100) surface in the p-type dye-sensitized solar cells.
To sum up, the presence of the PYR anchoring group does not strongly perturb the electronic structure of the TRIA dye when either free or interacting with the NiO surface, i.e., there is no significant modification of the pDOS and/or appearance of intra-gap trap states. The only significant effect is related to the downshift of the frontier orbital electronic levels of the dye, which increases the VBM–HOMO offset from ca. 0.50 eV to ca. 0.80 eV (Fig. 2), hence making the hole injection from the TRIA–PYR dye to the p-type NiO semiconductor exothermic in the interacting system. It seems that the PYR is indeed a plausible and an “inert” anchoring group in TRIA, with the main effect on the electronic structure being the ca. 0.30 eV downshift of the frontier orbital energies, associated with the electrostatic effects.
Two carboxyl anchors on the nickel oxide surface
Carboxyl group of a carboxylic acid has been a very popular anchor for n-type DSSCs due to its superior performance in TiO2-based DSSC devices. Therefore, it is crucial to establish its impact also on the electronic structure of p-type heterointerfaces. Here, this will be done using TRIA with carboxyl anchor groups in two phenyls, one in each, and a NiO(100) surface. Fig. 3 reports the planar averaged electrostatic potential (left) and electronic partial DOS (right) for both (a) the non-interacting and (b) interacting systems.The TRIA–CARB dye shows a downshift (−0.13 eV) in the electrostatic potential from the CARB-anchor to TRIA, hence indicating a molecular dipole moment component μz of 0.98 D per cell. The electronic structure of TRIA–CARB, as illustrated by the pDOS (Fig. 3a), nicely parallels with that of the TRIA–PYR dye (Fig. 2a), apart from the region between 0 and −1 eV. HOMO and LUMO levels are computed at −5.62 eV and −1.65 eV for the relaxed dye and −6.64 eV and −2.61 eV for the H-free TRIA–CARB-anchor (Table S4, ESI†), respectively, compared to the vacuum on the side of the anchoring groups. The corresponding HOMO–LUMO gaps are 3.97 eV and 4.03 eV (Table S4, ESI†), respectively. Considering the electronic level alignment (Fig. 3a), the HOMO of the TRIA–CARB dye is predicted to be more stable than the VBM of the NiO with all anchor models, hence suggesting that the charge (hole) injection from the dye to the NiO might be thermodynamically spontaneous.
However, the electronic structure of the TRIA–CARB–NiO heterointerface changes strikingly, once the dye is adsorbed onto the Ni atoms of the oxide surface (Fig. 3b), in a sharp contrast to the case of the PYR anchor, where HOMO shifted only slightly downwards. In the case of TRIA–CARB, the electrostatic potential upshifts by 0.64 eV (Fig. 3b), which corresponds to an interfacial dipole moment component μz of of −4.83 D (eqn (1), A = 2.8402 × 10−18 m2). Also, a change in pDOS is visible as a strong perturbation in the electronic structure at the heterointerface. The electronic structure of the TRIA–CARB is clearly modified and shifted upwards in energy when it adsorbs onto the p-type NiO semiconductor via CARB-anchors.
After adsorption, the pDOS of the TRIA–CARB (Fig. 3b) resembles the pDOS of the NiO surface in the energy range of the valence band. The HOMO and LUMO of the TRIA–CARB dye shift upwards sizably in energy. Consequently, the HOMO shifts 0.27 eV above the VBM of NiO making the charge (hole) injection from the dye to the Ni-oxide thermodynamically undesirable. Moreover, a few intra-gap trap states appear in the band gap of NiO, which can act as recombination centers and negatively affect the working mechanism of a hypothetical p-DSSC device based on this heterointerface. Optimized spacer length might help in preventing unfavorable trap states and charge recombination in a p-DSSC.57
The ultimate questions in the case of CARB anchors come to the effects that induce the notable reorganization of the electronic structure when the anchor is grafted onto the NiO surface. (i) First, the HOMO and LUMO of the TRIA–CARB dye upshift considerably, i.e., 1.13–2.15 eV (to −4.49 eV) and 0.91–1.87 eV (to −0.74 eV) (Table S4, ESI†), respectively. This inverts the order of the HOMO and VBM, which can be explained by the electrostatic effects caused by grafting. The HOMO–LUMO gap of TRIA–CARB narrows by 0.22–0.28 eV after grafting (3.75 eV) when compared to the relaxed and H-free TRIA–CARB-anchors but 0.59 eV compared to that of the twisted molecule detached from the surface (Table S4, ESI†). Although PYR's longer spacers help to move LUMO further from the heterointerface, the HOMO–LUMO gap is only slightly smaller in energy in TRIA–CARB than in TRIA–PYR (3.78 eV) on the NiO(100) surface. (ii) Second, the pDOS of the TRIA–CARB dye reorganizes and shifts up in energy in the valence band region, when HOMO shifts up (bringing lower energies visible in Fig. 3b). (iii) Third, the Mulliken population analysis of the combined TRIA–CARB–NiO system suggests that ca. 1.4 electrons collect to the TRIA–CARB dye from the NiO surface, and the CARB anchor receives ca. 0.5 electrons of them (Table S2, ESI†). Because most electrons are gathered on the TRIA part, they create a dipole moment to the system, which is seen as an upward shift of the electrostatic potential. This explains the upward shift (the perturbation in electronic configuration) of HOMO and LUMO of the TRIA–CARB dye when in contact with the NiO surface and the possible rearrangement of the pDOS. While the energetics of the states suggests unfavorable setup, i.e., HOMO of CARB is above VBM of NiO, the upshift in electrostatic potential hints that to some extent CARB can pull electrons from the surface to the vacancy created by the excitation. However, our calculations show that the process is not very efficient due to the unfavorable energy level alignment and no spontaneous reaction results after the excitation.
In summary, the CARB anchoring group perturbs the electronic structure of the TRIA–CARB dye when grafted on the NiO(100) surface. This is visible as a significant modification of the pDOS and/or appearance of intra-gap trap states. The electronic frontier molecular orbital levels of the dye shift up by ca. 1–2 eV, which reverses the mutual order of the VBM and HOMO levels and creates an inefficient charge (hole) injection from the HOMO of the TRIA–CARB dye to the VBM of the p-type NiO semiconductor in the interacting system. In the light of these results, CARB turns out not to be a good choice for and anchor with the TRIA dye at p-type NiO heterointerfaces but preserves its demonstrated superiority in some architectures for the n-type devices.
Two phenyl-1,2-diol anchors on the nickel oxide surface
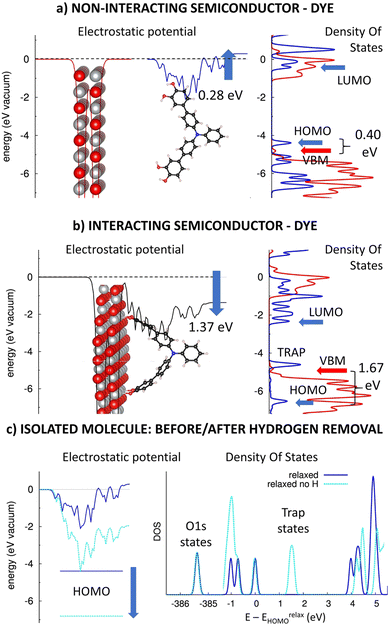
Catechol and its derivatives with a phenyl-1,2-diol group have been previously experimented as anchors in n-type TiO2-based DSSC devices with ca. 0.5–1.5% photovoltaic efficiencies.31 Here, we will computationally investigate the impact of the phenyl-1,2-diol anchors (DIOL) on the electronic structure of p-type heterointerfaces, similarly as above. Fig. 4 presents the planar averaged electrostatic potential (left) and electronic pDOS (right) for (a) the non-interacting and (b) interacting TRIA–DIOL dye grafted on the NiO(100) semiconductor. Furthermore, the effect of the hydrogen removal on the electrostatic potential (left) and DOS (right) for the isolated dye molecule is presented in Fig. 4c.As in the case of the other TRIA-anchors, the electrostatic potential is unsymmetric and now has an upshift of 0.28 eV for the isolated TRIA–DIOL dye. This shift corresponds to a molecular dipole moment component μz of −2.11 D per one TRIA–DIOL cell, created when one DIOL anchoring group perturbs the electronic structure of the other aromatic rings. This asymmetry in the molecule also explains the asymmetry in the electrostatic potential (Fig. 4a).
When comparing the energetics of the electronic levels, the HOMO and LUMO of the isolated TRIA–DIOL are −4.50 eV58 and −0.52 eV58 for the fully relaxed and −6.83 eV and −2.59 eV for the H-free structures (Table S4, ESI†), respectively, yielding correspondingly HOMO–LUMO gaps of 3.82 eV and 4.24 eV, comparable to those of the other dyes. The HOMO calculated with the relaxed TRIA–DIOL molecule is 0.31 eV above the VBM of the isolated NiO semiconductor (Fig. 4b), but below the VBM in the H-free model (Table S4, ESI†). Thus, the DFT calculations with the isolated full dye molecule suggest that the hole injection from the TRIA–DIOL to the NiO might not be thermodynamically spontaneous on the heterointerface, but when using a H-free TRIA–DIOL-anchor model would be in fact still feasible, as in the case of the CARB-anchor.
When TRIAL–DIOL-anchor is adsorbed onto the NiO(100) surface, the electronic structure of the TRIA–DIOL changes dramatically (Fig. 4) compared to the TRIA–PYR (Fig. 2). The electronic structure of the NiO slab remains almost the same, with the VBM and CBM levels, and the general features of the pDOS remain practically unaffected, as was the case with the other anchors earlier above. Thus, the most striking change is the electrostatic potential, which downshifts −1.37 eV (between the two sides of the monolayers) at the p-type heterointerface, corresponding to an interfacial dipole moment component μz of 10.33 D (eqn (1), A = 2.8416 × 10−18 m2).
Moreover, the pDOS of the TRIA–DIOL dye is perturbed and reshaped on the p-type NiO surface. Both the HOMO and LUMO levels are stabilized enormously (by ca. −2.0 eV) if compared to the molecular anchor model shifting HOMO ca. −1.7 eV below the VBM (to −6.53 eV) after grafting (Fig. 4b). However, if compared to the H-free and twisted TRIA–DIOL-anchor models, the change in the HOMO level energy is very small (Table S4, ESI†). Hydrogen free TRIA–DIOL is twisted when it is adsorbed onto the NiO surface (Fig. 4b and Fig. S7, ESI†). Removal of hydrogens pushes the energy levels below the VBM and is the main reason for the energy changes in isolated and adsorbed environments (Table S4 and Fig. S4, ESI†). The structure twisting has only a minor effect on the energy level alignment. Consequently, the hole injection from the dye to the NiO is predicted to be thermodynamically very spontaneous.
Furthermore, the Mulliken population analysis of the combined TRIA–DIOL–NiO system shows that ca. 0.2 electrons move from the NiO surface to the dye molecule, accumulating on the DIOL anchor (Table S5, ESI†). This is slightly larger than that for the TRIA–PYR–NiO system. Accordingly, the calculations suggest that DIOL is a good anchor choice to pull electrons with the TRIA dye at p-type NiO heterointerfaces.
However, an empty state is observed at ca. 0.2 eV above the VBM of NiO between the HOMO–LUMO gap, which widens by ca. 0.2 eV (Fig. 4b). Due to its energetic position, it can act as a trap state for electrons injected from the NiO to the TRIA–DIOL and increase their recombination, which impairs the functioning of the conceivable p-DSSC device based on this heterointerface. Similar trap states have been previously observed also with catechol in the n-type TiO2-based DSSC-devices.31 Further investigation revealed that the trap states are due to the removal of the hydrogens from the DIOL anchor (Fig. 4c). In other words, the removal of hydrogen creates electronegative trap states onto the anchor, which is seen as a downshift of the HOMO and DOS energies (light blue, Fig. 4c). Because the hydrogens will be removed upon adsorption on the NiO, DIOL anchors might not act ideally as the energy level alignment suggests, i.e., HOMO is located below VBM. This could partially explain the low efficiency recorded in the literature.
As a summary of all anchors, the results suggest that nitrogen would be a reasonable choice as a part of the anchoring group for TRIA, because it less likely creates trap states, which are absent in TRIA–PYR. While we do not see the empty hydrogen states in TRIA–CARB, it does not mean that they do not exist, but they are part of the pDOS in the lower energy levels, and thus, do not act as the trap states. Moreover, PYR has the lowest interfacial dipole moment compared to CARB or DIOL, which supports the conclusion by Muñoz-García39 that anchors, which are the most potential for the p-type DSSCs, have the smallest interfacial dipoles. As a result, PYR would be a safe choice for the anchoring group.
Adsorption energies
Finally, the adsorption energies of the H-free anchor groups on the NiO surface are compared to understand the behavior of anchors on p-type interfaces. The adsorption energies, Eads, of the anchors are calculated using the eqn (2) as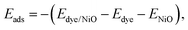 | (2) |
The results demonstrate that the adsorption energy increases in the order of PYR < CARB < DIOL as 0.57 < 2.07 < 2.19 eV for the relaxed dyes without hydrogens, corresponding to ca. 55 < 200 < 211 kJ mol−1 chemical “binding” energies. In the case of PYR this refers to “physisorption” or electrostatic interaction instead of chemical binding. The adsorption energy of CARB without hydrogens compares extremely well with the adsorption energy (−4.1 eV/2) of a bigger dye we used in our previous work, where the model and surface were both hydrogenated and the bidentate binding mode was studied.38
For the twisted dye detached from the NiO surface and kept without hydrogens, the adsorption energies of PYR and CARB resemble more of each other than above: PYR < CARB < DIOL as 0.63 < 0.71 < 2.01 eV (ca. 61, 69, 194 kJ mol−1, respectively), reflecting tension in the highly twisted, bidentate mode of the TRIA–CARB model, which weakens the adsorption strength compared to the fully relaxed adsorbate (above). The order of the adsorption energies remains the same as above, and that of the PYR is almost the same for the twisted separated model and the adsorbed model because no hydrogens need to be removed. This is also reflected in the HOMO and LUMO energies of PYR (Table S4, ESI†), which are almost the same for the fully relaxed structure, the twisted one, and on the surface. The HOMO and LUMO energies (Table S4, ESI†) of DIOL changed the least when comparing either the H-free relaxed or H-free twisted structure, and the adsorbed H-free system, and this is reflected also in adsorption energies, which are almost the same (2.19 eV and 2.01 eV, respectively).
In fact, PYR is weakly bound with vacant Ni metal orbitals at the NiO surface via the lone pair of the pyridinyl nitrogen, which is electronegative, forming a Sigma bond. The pyridinyl ring cannot only bind with the metal ion with its π-electrons, but also withdraw and accept some electron density from the metal to its delocalized π* anti-bonding orbitals.59 The trend in the adsorption energies agree also well with the calculated increasing trend of the magnitude of the dipole moment component μz and its direction for the anchors, i.e., PYR < CARB < DIOL and the Mulliken population analysis, as a small amount of electron density moves from the NiO surface to the anchoring pyridinyl ring.
Furthermore, the calculated adsorption energy of the fully relaxed, H-free CARB anchor on the NiO(100) surface equals to ca. 1/2–2/3 of a covalent C–O bond energy (ca. 360 kJ mol−1). The data also agrees with the high-resolution electron energy loss spectroscopy (HREELS) results on NiO(100) where the adsorption saturates with one carboxylate for every two nickel sites.60 The carboxyl group with its oxygens withdraws electrons strongly from neighboring molecular entities and thereby deactivates them. These characteristics are reflected in the calculated Mulliken population as electron density is strongly pulled from the NiO surface (ca. 1.4 el.) to the CARB anchor, where close to half of it resides, and the rest (ca. 0.8 el.) moves to the first phenyl groups bound to the anchoring groups. In other words, due to the strong binding and charge withdrawal effects, the electron density focuses closer to the surface. There also exists experimental evidence for a reduction of an adsorption energy as a function of an increasing carboxyl coverage on NiO surface. Namely, the differential heat of adsorption of 202 kJ mol−1 was observed for a low coverage of formic acid on a NiO(111) − (2 × 2) surface, but 99 kJ mol−1 at saturation (0.25 ML).61
The DIOL anchor adsorbs slightly more strongly than CARB onto the NiO surface. Again, the Mulliken population analysis reflects this behavior and shows that 0.2 el. leaves the surface, and one electron is distributed within the whole CARB–TRIA dye. This is also seen as a wider and more negative distribution of the electrostatic potential in the regions of the phenyl-1,2-diol and phenylamine rings (Fig. 4b).
We agree with the previous studies by Jin et al.,4 Marri et al.,18,62 and Cui et al.,16 that the PYR anchor could work better than the CARB and DIOL anchors in p-type DSSC devices, despite its weaker binding (adsorption energy) on and a low current of electrons (Mulliken) from NiO. Even though HOMO is below VBM both in PYR and DIOL, the decisive factor that favors PYR over DIOL is the absence of the trap states in PYR. This is an encouraging finding, as despite larger dye molecules are used in experiments,17 a small TRIA-anchor model can predict the experimental results indicating that pyridinyl anchor would work in a variety of selections of dyes in p-type DSSCs.
Conclusions
According to the data analysis of our DFT calculations, we find that the interactions of the anchoring groups with the NiO(100) surface vary their potential for charge transfer. While PYR shows the least interaction with the surface by Mulliken population analysis and adsorption energy, the energetic alignment after adsorption supports the thermodynamically spontaneous electron transfer. The CARB anchor draws more electrons from the NiO(100) surface than PYR. However, the energy level alignment shifts from favorable to unfavorable when CARB adsorbs onto the NiO surface. DIOL shows both the favorable energy level alignment after a strong adsorption and a possibility for the charge relocation. However, upon adsorption DIOL gains empty states, which may interfere with the charge transfer processes as potential trap states.Based on our results, we suspect PYR to be a good anchor upon adsorption. Its adsorption leads to the least dipole moment change, the electronic configuration remains almost unchanged, and the electrostatic potential suggests feasible, albeit weak surface–dye interactions. While DIOL and CARB can be plausible, functional anchoring groups, they have obstacles to bypass, such as trapping electrons, to reach the higher efficiencies than currently recorded.
In conclusion, the properties of an anchoring group, which is one of the most crucial parts, when dye–surface interactions are considered, might not be as intuitive as appears at first sight. PYR is a reasonable choice for an anchoring group: the energy level alignment prefers thermodynamically spontaneous charge transfer reactions without trap states and it is able to shuttle charges in small amounts despite its weaker binding compared to CARB or DIOL on the NiO(100) surface. Our results are consistent with the experimental literature, which supports pyridinyl for p-DSSC devices. While we can generalize pointers for other dyes, lots of research is still needed in this field, e.g., comparative studies on other binding modes, chelating, and the roles of electrolyte, protons, and solvents, which, however, would need to be addressed using computationally less-demanding approaches.
Author contributions
DSc (Tech.) Outi V. Kontkanen has carried out the calculations, data analysis, validation, visualization of the results, writing of the original draft of this investigation, and finalizing the manuscript. Prof. Tapio Rantala and Docent Terttu Hukka as the supervisors have been responsible for reviewing, writing, and editing the final version.Conflicts of interest
There are no conflicts of interest to declare.Acknowledgements
The work was supported by the Emil Aaltonen foundation. Computational resources have been provided by the Consortium des Équipements de Calcul Intensif (CÉCI) and CSC - IT Center for Science Ltd. that is administered by the Finnish Ministry of Education, which are gratefully appreciated. Claudio Quarti, Jerome Cornil, and David Beljonne at the Laboratory for Chemistry of Novel Materials, University of Mons, Place du Parc, 20, B-7000, Mons, Belgium are acknowledged for Outi Kontkanen's supervision and funding provided during her research visit. We also want to give thanks to Professor Viacheslav Golovanov for the discussion on the final conclusions of the article.References
- B. O’Regan and M. Grätzel, Nature, 1991, 353, 737–740 CrossRef.
- J. He, H. Lindström, A. Hagfeldt and S.-E. Lindquist, J. Phys. Chem. B, 1999, 103, 8940–8943 CrossRef CAS.
- Z. Huang, G. Natu, Z. Ji, P. Hasin and Y. Wu, J. Phys. Chem. C, 2011, 115, 25109–25114 CrossRef CAS.
- B. Jin, W. Wu, X. Zhang, F. Guo, Q. Zhang and J. Hua, Chem. Lett., 2013, 42, 1271–1272 CrossRef CAS.
- M. Wykes, F. Odobel, C. Adamo, I. Ciofini and F. Labat, J. Mol. Model., 2016, 22, 289 CrossRef PubMed.
- Y. Farré, L. Zhang, Y. Pellegrin, A. Planchat, E. Blart, M. Boujtita, L. Hammarström, D. Jacquemin and F. Odobel, J. Phys. Chem. C, 2016, 120, 7923–7940 CrossRef.
- L. Le Pleux, A. L. Smeigh, E. Gibson, Y. Pellegrin, E. Blart, G. Boschloo, A. Hagfeldt, L. Hammarström and F. Odobel, Energy Environ. Sci., 2011, 4, 2075–2084 RSC.
- J. Warnan, Y. Pellegrin, E. Blart, L. Zhang, A. Brown, L. Hammarström, D. Jacquemin and F. Odobel, Dyes Pigm., 2014, 105, 174–179 CrossRef CAS.
- F. Odobel, Y. Pellegrin, F. B. Anne and D. Jacquemin, in High-Efficiency Solar Cells: Physics, Materials, and Devices, ed. X. Wang and Z. M. Wang, Springer International Publishing, Cham, 2014, pp. 215–246 Search PubMed.
- F. Odobel, Y. Pellegrin, E. A. Gibson, A. Hagfeldt, A. L. Smeigh and L. Hammarström, Coord. Chem. Rev., 2012, 256, 2414–2423 CrossRef CAS.
- A. Morandeira, J. Fortage, T. Edvinsson, L. Le Pleux, E. Blart, G. Boschloo, A. Hagfeldt, L. Hammarström and F. Odobel, J. Phys. Chem. C, 2008, 112, 1721–1728 CrossRef CAS.
- T. T. T. Pham, S. K. Saha, D. Provost, Y. Farré, M. Raissi, Y. Pellegrin, E. Blart, S. Vedraine, B. Ratier, D. Aldakov, F. Odobel and J. Bouclé, J. Phys. Chem. C, 2017, 121, 129–139 CrossRef CAS.
- F. Odobel, L. Le Pleux, Y. Pellegrin and E. Blart, Acc. Chem. Res., 2010, 43, 1063–1071 CrossRef CAS PubMed.
- O. Langmar, D. Saccone, A. Amat, S. Fantacci, G. Viscardi, C. Barolo, R. D. Costa and D. M. Guldi, ChemSusChem, 2017, 10, 2385–2393 CrossRef CAS PubMed.
- Y. Farré, M. Raissi, A. Fihey, Y. Pellegrin, E. Blart, D. Jacquemin and F. Odobel, ChemSusChem, 2017, 10, 2618–2625 CrossRef PubMed.
- J. Cui, J. Lu, X. Xu, K. Cao, Z. Wang, G. Alemu, H. Yuang, Y. Shen, J. Xu, Y. Cheng and M. Wang, J. Phys. Chem. C, 2014, 118, 16433–16440 CrossRef CAS.
- Y. Farré, F. Maschietto, J. Föhlinger, M. Wykes, A. Planchat, Y. Pellegrin, E. Blart, I. Ciofini, L. Hammarström and F. Odobel, ChemSusChem, 2020, 13, 1844–1855 CrossRef PubMed.
- A. R. Marri, F. A. Black, J. Mallows, E. A. Gibson and J. Fielden, Dyes Pigm., 2019, 165, 508–517 CrossRef CAS.
- K. Prajapat, M. Dhonde, K. Sahu, P. Bhojane, V. V. S. Murty and P. M. Shirage, J. Photochem. Photobiol., C, 2023, 55, 100586 CrossRef CAS.
- S. Mathew, A. Yella, P. Gao, R. Humphry-Baker, B. F. E. Curchod, N. Ashari-Astani, I. Tavernelli, U. Rothlisberger, M. K. Nazeeruddin and M. Grätzel, Nat. Chem., 2014, 6, 242–247 CrossRef CAS PubMed.
- W. Shockley and H. J. Queisser, J. Appl. Phys., 1961, 32, 510–519 CrossRef CAS.
- I. R. Perera, T. Daeneke, S. Makuta, Z. Yu, Y. Tachibana, A. Mishra, P. Bäuerle, C. A. Ohlin, U. Bach and L. Spiccia, Angew. Chem., Int. Ed., 2015, 54, 3758–3762 CrossRef CAS PubMed.
- V. Thavasi, V. Renugopalakrishnan, R. Jose and S. Ramakrishna, Mater. Sci. Eng., R, 2009, 63, 81–99 CrossRef.
- I. Arbouch, D. Cornil, Y. Karzazi, B. Hammouti, R. Lazzaroni and J. Cornil, Phys. Chem. Chem. Phys., 2017, 19, 29389–29401 RSC.
- E. Maggio, N. Martsinovich and A. Troisi, J. Phys. Chem. C, 2012, 116, 7638–7649 CrossRef CAS.
- N. Martsinovich and A. Troisi, J. Phys. Chem. C, 2011, 115, 11781–11792 CrossRef CAS.
- N. Martsinovich and A. Troisi, Energy Environ. Sci., 2011, 4, 4473–4495 RSC.
- A. Hagfeldt, G. Boschloo, L. Sun, L. Kloo and H. Pettersson, Chem. Rev., 2010, 110, 6595–6663 CrossRef CAS PubMed.
- L. Zhang and J. M. Cole, ACS Appl. Mater. Interfaces, 2015, 7, 3427–3455 CrossRef CAS PubMed.
- Y. Ooyama, S. Inoue, T. Nagano, K. Kushimoto, J. Ohshita, I. Imae, K. Komaguchi and Y. Harima, Angew. Chem., Int. Ed., 2011, 50, 7429–7433 CrossRef CAS PubMed.
- E. L. Tae, S. H. Lee, J. K. Lee, S. S. Yoo, E. J. Kang and K. B. Yoon, J. Phys. Chem. B, 2005, 109, 22513–22522 CrossRef CAS PubMed.
- G. Guerrero, J. G. Alauzun, M. Granier, D. Laurencin and P. H. Mutin, Dalton Trans., 2013, 42, 12569–12585 RSC.
- V. Nikolaou, A. Charisiadis, G. Charalambidis, A. G. Coutsolelos and F. Odobel, J. Mater. Chem. A, 2017, 5, 21077–21113 RSC.
- F. De Angelis, Acc. Chem. Res., 2014, 47, 3349–3360 CrossRef CAS PubMed.
- L. Lasser, E. Ronca, M. Pastore, F. De Angelis, J. Cornil, R. Lazzaroni and D. Beljonne, J. Phys. Chem. C, 2015, 119, 9899–9909 CrossRef CAS.
- M. Pastore and F. De Angelis, in Multiscale Modelling of Organic and Hybrid Photovoltaics, ed. D. Beljonne and J. Cornil, Springer Berlin Heidelberg, Berlin, Heidelberg, 2014, pp. 151–236 Search PubMed.
- A. B. Muñoz-García and M. Pavone, Phys. Chem. Chem. Phys., 2015, 17, 12238–12246 RSC.
- O. V. Kontkanen, M. Niskanen, T. I. Hukka and T. T. Rantala, Phys. Chem. Chem. Phys., 2016, 18, 14382–14389 RSC.
- S. Piccinin, D. Rocca and M. Pastore, J. Phys. Chem. C, 2017, 121, 22286–22294 CrossRef CAS.
- M. Hervieu, Adv. Mater., 1995, 7, 91–92 CrossRef.
- W. Kohn, A. D. Becke and R. G. Parr, J. Phys. Chem., 1996, 100, 12974–12980 CrossRef CAS.
- R. Dovesi, R. Orlando, B. Civalleri, C. Roetti, V. R. Saunders and C. M. Zicovich-Wilson, Z. Kristallogr. - Cryst. Mater., 2005, 220, 571–573 CrossRef CAS.
- Dovesi, Saunders, Roetti and Orlando, https://www.crystal.
- A. D. Becke, J. Chem. Phys., 1993, 98, 5648–5652 CrossRef CAS.
- C. Lee, W. Yang and R. G. Parr, Phys. Rev. B: Condens. Matter Mater. Phys., 1988, 37, 785–789 CrossRef CAS PubMed.
- C. Gatti, V. R. Saunders and C. Roetti, J. Chem. Phys., 1994, 101, 10686–10696 CrossRef CAS.
- M. D. Towler, N. L. Allan, N. M. Harrison, V. R. Saunders, W. C. Mackrodt and E. Apr, Phys. Rev. B: Condens. Matter Mater. Phys., 1994, 50, 5041–5054 CrossRef CAS PubMed.
- G. E. Scuseria, Proc. Natl. Acad. Sci. U. S. A., 2021, 118, e2113648118 CrossRef CAS PubMed.
- D. Wing, J. B. Haber and L. Kronik, Proc. Natl. Acad. Sci. U. S. A., 2021, 118, e2104556118 CrossRef CAS PubMed.
- O. Lisovski, A. Chesnokov, S. Piskunov, D. Bocharov, Y. F. Zhukovskii, M. Wessel and E. Spohr, Mater. Sci. Semicond. Process., 2016, 42, 138–141 CrossRef CAS.
- K. Brlec, C. N. Savory and D. O. Scanlon, J. Mater. Chem. A, 2023, 11, 16776–16787 RSC.
- M. E. Foster and B. M. Wong, J. Chem. Theory Comput., 2012, 8, 2682–2687 CrossRef CAS PubMed.
- M. Niskanen and T. I. Hukka, Phys. Chem. Chem. Phys., 2014, 16, 13294–13305 RSC.
- A. B. Muñoz-García, I. Benesperi, G. Boschloo, J. J. Concepcion, J. H. Delcamp, E. A. Gibson, G. J. Meyer, M. Pavone, H. Pettersson, A. Hagfeldt and M. Freitag, Chem. Soc. Rev., 2021, 50, 12450–12550 RSC.
- G. Heimel, I. Salzmann, S. Duhm and N. Koch, Chem. Mater., 2011, 23, 359–377 CrossRef CAS.
- K.-C. Wang, J.-Y. Jeng, P.-S. Shen, Y.-C. Chang, E. W.-G. Diau, C.-H. Tsai, T.-Y. Chao, H.-C. Hsu, P.-Y. Lin, P. Chen, T.-F. Guo and T.-C. Wen, Sci. Rep., 2014, 4, 4756 CrossRef PubMed.
- F. Wu, S. Zhao, C. Zhong, Q. Song and L. Zhu, RSC Adv., 2015, 5, 93652–93658 RSC.
- O. V. Kontkanen, Modeling of Charge Transfer at Dye-Semiconductor Interfaces in p-Type Solar Cells, Tampere University of Technology, 2018.
- S. Pal, Pyridine, InTech, 2018 Search PubMed.
- K. W. Wulser and M. A. Langell, Catal. Lett., 1992, 15, 39–50 CrossRef CAS.
- W. Zhao, A. D. Doyle, S. E. Morgan, M. Bajdich, J. K. Nørskov and C. T. Campbell, J. Phys. Chem. C, 2017, 121, 28001–28006 CrossRef CAS.
- A. R. Marri, H. Flint, E. A. Gibson and J. Fielden, Dyes Pigm., 2022, 202, 110244 CrossRef CAS.
Footnote |
| † Electronic supplementary information (ESI) available: Computational details, calculations of the NiO(100) surface slab, antiferromagnetic AF2 phase of NiO, binding energies in literature, energy levels of the computed models, Mulliken population analysis, molecular orbitals of the three dye-anchor models, coordinates of the systems (separate .xyz files). See DOI: https://doi.org/10.1039/d4cp01313a |
| This journal is © the Owner Societies 2024 |