Computational study on the mechanism for the synthesis of active pharmaceutical ingredients nitrofurantoin and dantrolene in both solution and mechanochemical conditions†
Dayana M.
Galeas
a,
Iogann
Tolbatov
 a,
Evelina
Colacino
a,
Evelina
Colacino
 b and
Feliu
Maseras
b and
Feliu
Maseras
 *a
*a
aInstitute of Chemical Research of Catalonia (ICIQ-CERCA), The Barcelona Institute of Science and Technology, Avgda. Països Catalans 16, 43007, Tarragona, Spain
bICGM, Univ Montpellier, CNRS, ENSCM, Montpellier, France
First published on 27th August 2024
Abstract
A combination of density functional theory (DFT) calculations and microkinetic simulations is applied to the study of condensation between N-acyl-hydrazides and aldehydes in acidic media to produce the active pharmaceutical ingredients (API) nitrofurantoin and dantrolene. Previous experimental reports have shown that the use of ball milling conditions leads to a reduction in the reaction time, which is associated with a significant reduction of waste. This result is reproduced by the current calculations, which additionally provide a detailed mechanistic explanation for this behavior.
Introduction
Mechanochemistry is a sustainable approach to chemical synthesis, which complies with the 12 principles of green chemistry,1 providing a valuable alternative to traditional manufacturing methods in solution2 where the solvent accounts for 85% of the waste generated.3 In recent years, mechanochemical processes have also found applications in the synthesis of marketed active pharmaceutical ingredients (APIs).4,5 In the case of the antibacterial agent nitrofurantoin (a World Health Organisation essential medicine) and the myorelaxant dantrolene, the mechanochemical syntheses in batch (in ball-mills)6 and continuous (by twin screw extrusion)1 modes have been reported, the reaction kinetics have been examined via real-time in situ monitoring by Raman spectroscopy,7 the crystal forms have been determined,8 and the sustainability metrics have been calculated.9–11 Without any doubt, when compared to solution-based methods (Scheme 1), solvent-less mechanochemical syntheses resulted in a much better ecological foot-print, lower energy consumption and faster kinetics.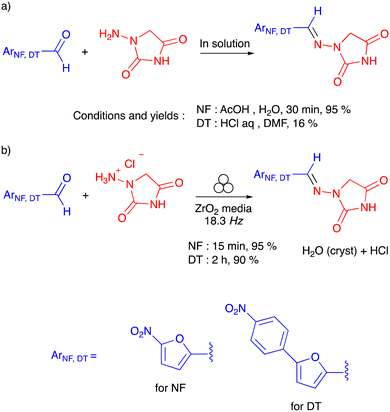 | ||
| Scheme 1 Previously reported data for (a) the preparation of nitrofurantoin (NF) and dantrolene (DT) in solution and (b) the ball-milling preparation of nitrofurantoin and dantrolene. | ||
Indeed, the conventional solvent-based synthesis of nitrofurantoin consists of a condensation reaction between an excess (up to 10 equiv.) of N-acyl hydrazide and a substituted furyl aldehyde in aqueous acetic acid, yielding the product (95%) in 30 min.12 In contrast, the stoichiometric, solvent-less reaction in the ball milling resulted in a reaction time of 15 min in a similar yield. In the case of dantrolene, the condensation reaction resulted in similar reaction kinetics for both solution-based and ball-milling processes (2 hours). However, the solvent-less synthesis in the ball mill outperformed (90% yield) the corresponding solution-based process, requiring an excess starting N-acyl hydrazide but leading to lower yields (16%)13 (Scheme 1). For both APIs, the condensation reaction in the ball mill in the absence of solvent involved N-acyl hydrazides as the solvate with hydrogen chloride.
In view of the implementation of this technology in manufacturing processes at the industrial scale, a better understanding of the underlying mechanochemical processes and the way they can be altered, the detailed mapping of the reaction mechanisms and kinetics is needed.14–16 In this regard, the mechanism underlying the condensation reaction occurring in the ball-mill is not fully explained. To date, the identification of the transition states and the reaction intermediates have not been investigated. Generally, this limited comprehension can be viewed as an illustration of a larger problem concerning the suboptimal understanding of the detailed mechanisms by which ball milling affects the reaction times. Some of us recently made a proposal based on calculations to address this problem by postulating that the main role of ball milling is to allow the efficient mixing of the solid reactants in ‘highly concentrated solid solutions’, which can follow, depending on the cases, mechanisms very similar to those in solution.17 We are aware that this view may be controversial,18 but we consider it worthy of evaluation.
The current work aims to evaluate the efficiency of this computational hypothesis to reproduce experimental reaction times for the synthesis of nitrofurantoin and dantrolene under mechanochemical conditions, with the special caveat that mechanochemical reaction is faster for nitrofurantoin. With this goal accomplished, it will be possible to have a deeper understanding of this process and continue to expand the mapping of mechanochemical processes.
Computational methods
Density functional theory (DFT) calculations were performed using the Gaussian 16 package.19 The reported energies were computed with the B3LYP-D3BJ functional20,21 including D3 dispersion corrections with Becke–Johnson damping.22 The basis set was cc-pVTZ, which includes polarization functions in its definition.23 This functional was shown to provide better agreement with the experiment than B3LYP and ωB97X-D, as shown in the electronic ESI.† The effect of the dielectric environment was introduced through implicit solvation via the PCM approach in the default IEFPCM implementation supplied in Gaussian 16.24 Frequency calculations were performed to confirm the nature of stationary points as minima or transition states. All reported energies correspond to free energies in a continuum medium. We included the reference state corrections for 1 M in the free energy profiles.The computed reactions often involve bimolecular processes, where two fragments get together to form a single adduct. This means that the calculation of the entropic contributions to the Gibbs energy is relevant. We have computed these contributions using the rigid rotor harmonic oscillator (RRHO) approach, without any specific treatment for translational and rotational degrees of freedom. This has become the generally accepted treatment in recent years in homogeneous catalysis,25 and we do not see any reason why it should not be applied to the current systems.
The dielectric constant of the medium deserves some comment. For calculations in the solution, we used the value for water (dielectric constant of 78.355) in the Gaussian16 package. For the dielectric constant in the ball-milling conditions, we used the values of 2.350 and 2.453 for nitrofurantoin and dantrolene, respectively, calculated from the refractive indices of the involved solids, as in our previous study.17 The details of the dielectric constant calculation are given in the ESI.†
Kinetic modeling26 was performed using Copasi27 to convert our computed free energy profiles into reaction times. The idea of the microkinetic model is quite simple. We formulated all kinetic differential equations considering all the processes leading to the formation or consumption of every single species in the systems. This defines a system of differential equations that is then numerically solved by introducing the initial concentrations of each species as the limit conditions. The rate constants for all the reactions were calculated from the DFT-free energy barriers by applying the Eyring–Polanyi equation. We assumed a transmission coefficient of 1, and we did not introduce any scaling in the frequencies. We are aware that better results could be obtained with more refined approaches, but we intended to fully exploit the simplified version of our approach. For the starting concentrations, we used the experimental data. For the reaction in solution, we used concentrations of 0.2 M for 1-amino-hydantoin hydrochloride and furyl aldehyde and 0.35 M for HCl.12 For the synthesis of nitrofurantoin in mechanochemical conditions, we used the value of 5.074 M for both the reactants. The starting concentration of both reactants in the ball-milling synthesis of dantrolene was 3.816 M. Details of the calculation of the starting concentrations are reported in the ESI.† The temperature for the simulations was also taken from the experiments, i.e., 298.15 K (room temperature). A collection of all the computed structures was uploaded in the ioChem-BD repository, and can be accessed viahttps://doi.org/10.19061/iochem-bd-1-343.28
Results and discussion
The computational treatment is based on the use of the DFT barriers for the estimation of rate constants. Thus, the first step is the building of the free energy profile. The formation of the N-acyl-hydrazone in nitrofurantoin and dantrolene from the same N-acyl-hydrazide hydrochloride and the corresponding furyl-aldehyde reactants is formally similar to the condensation reaction in acidic medium occurring between an amine and an aldehyde, leading to an imine.This condensation has been known for many years29 and was previously investigated through experiments30,31 and calculations.32,33 There is a general agreement on the overall mechanism proceeding through a hemiaminal intermediate. However, questions remain regarding the detailed role of acidic catalysts, which will be examined below.
We want to mention here that the comparison with experimental reaction times will be based on the published experimental data reported in Scheme 1. We understand that they are not exact in the sense that a reaction reported to take 30 min could take 30 s, but we still think they are indicative of relative reaction rates.
Synthesis of nitrofurantoin
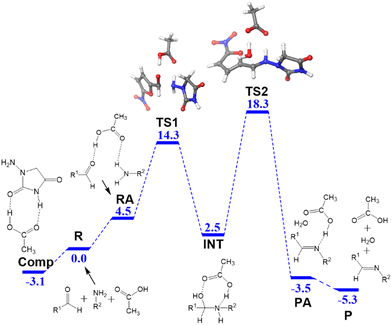
In water, the reaction is catalyzed by acetic acid, which is a weak acid. The computed free energy profile is summarized in Fig. 1. We used the reactants R as the origin of energies, where the three fragments, hydrazide, aldehyde and acetic acid, are separate. The process comprises two main steps: formation of hemiaminal and conversion into the product. The three reactants can access the adduct RA with a low energy cost (4.5 kcal mol−1). The N–C bond is formed through TS1 (14.3 kcal mol−1) and results in the hemiaminal intermediate INT (2.5 kcal mol−1). The second step of the process is the cleavage of the C–O bond through TS2 (18.3 kcal mol−1), which results in the dehydration of the intermediate and the formation of the product adduct PA (−3.5 kcal mol−1). The reaction product P corresponds to separated nitrofurantoin, acetic acid, and water (−5.3 kcal mol−1).A key feature of the free energy profile is the highest energy point, which rules the rate-determining step, which will be used in the definition of the barrier for the reaction. This is transition state TS2 (18.3 kcal mol−1) in this case. It is worth noticing the role of acetic acid in this transition state, which acts as a proton shuttle and with the participation of both of its oxygen atoms. Sometimes overlooked, the aspect of the calculation of the energy barrier is its origin, which has to be the lowest energy point before the rate-determining transition state.34 Remarkably, for the free energy profile in Fig. 1, it is not the separate reactants but a pre-reaction complex that we have labeled as Comp.
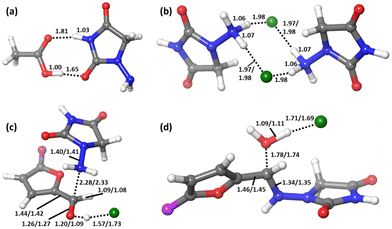
This adduct Comp will be the major species in the mixture before the reaction starts. Let us remember that in the experiment, 1-amino-hydantoin is first dissolved in water containing acetic acid, and only afterwards the aldehyde is added.12 The structure of Comp is presented in Fig. 2a. Its free energy is 3.1 kcal mol−1 below the separated species. Comp features two hydrogen bonds: a 1.81 Å bond between the carbonyl oxygen of acetic acid and an NH group of 1-amino-hydantoin, and another one (1.65 Å) between the carbonyl oxygen of 1-amino-hydantoin and the hydroxyl group of acetic acid (Fig. 2a). This Comp adduct is the point from where the barrier for the overall process must be measured. Thus, the barrier for the reaction leading to nitrofurantoin in water will be 21.4 kcal mol−1.
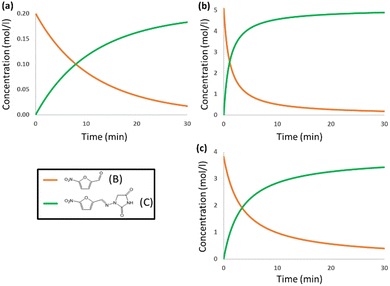
The DFT barrier reported above was used to compute the rate constants and introduce them in a microkinetic model to compute the evolution of the concentrations of the species as a function of reaction time. The results are presented in Fig. 3a. For the sake of clarity, only the evolution of concentrations of reacting aldehyde (B) and resulting nitrofurantoin (C) are presented. The agreement between calculation and experiment is excellent, with a predicted yield of 92% after 30 min, very close to the reported experimental yield of 95%. This agreement is likely to be in part fortuitous but is nevertheless remarkable.
The ball-milling process was investigated next. The free energy profile differs from the one discussed above because the acid catalysis comes from the hydrogen chloride salt formed with the N-acyl-hydrazide in the solid reactant. Even if the appropriateness of the acidity/basicity labels is questionable in the absence of solvent, it is clear that acetate has a much stronger affinity for protons than chloride. The differences are apparent from the role of the acid in the structures of the key transition states (Fig. 2c and d). The origin of energies is again the energy of the separated reactants R. 1-Amino-hydantoin and hydrogen chloride form an adduct RA1 (2.0 kcal mol−1), which binds with the aldehyde, thus producing the adduct RA2 with low energy cost (2.2 kcal mol−1). The first step is the formation of the N–C bond through TS1 (9.0 kcal mol−1), leading to the low-energy hemiaminal structure INT (1.5 kcal mol−1). The second step of the process is the cleavage of the C–O bond through TS2 (16.5 kcal mol−1), which results in the dehydration of the intermediate and the formation of the product P (−5.3 kcal mol−1).
In this free energy profile, the highest point is represented by TS2 (16.5 kcal mol−1). The origin of the barrier is again below the separate reactants. In this case, the pre-reaction complex Comp (Fig. 2b) has an energy of −4.4 kcal mol−1. This complex comprises two 1-amino-hydantoins and two hydrogen chloride fragments, forming a stable adduct in which the protons of hydrogen chloride are shifted to the neighboring hydrazides. The resulting barrier for the overall process under mechanochemical conditions is 20.9 kcal mol−1.
We put the results for the mechanochemical conditions into the microkinetic model, together with our estimated experimental concentrations in the solid mixture, and the results are presented in Fig. 3b. The results are again very accurate. The experimental yield is 95% after 15 min,6 whereas the computed value is 93% after 15 min. The reaction time for nitrofurantoin synthesis under ball milling conditions is thus rather accurately reproduced by the computational model and shown to be faster than that in solution. The reaction is faster under ball-milling conditions because of the presence of stronger proton-donors in the medium.
According to our model, the main differences between ball-milling and solution conditions are usually in the starting concentrations and the dielectric environment. However, this is an unusual example where there is a change in the mechanism associated with the different proton-donors being used; therefore, the disentangling of the different effects is not straightforward.
Synthesis of dantrolene
The free energy profile for the ball-milling-assisted synthesis of dantrolene is presented in Fig. 5. It follows the same steps as those of the above-discussed reaction yielding nitrofurantoin. The separate reactants R may form an adduct RA2 (1.6 kcal mol−1). The barrier for the formation of the N–C bond is represented by TS1 (10.5 kcal mol−1), yielding the hemiaminal intermediate INT (4.6 kcal mol−1). The breaking of the C–O bond (TS2,16.7 kcal mol−1) leads to the product adduct PA (−3.6 kcal mol−1). The transition state TS2 constitutes the highest point. Thus, considering the pre-reaction complex Comp (Fig. 2b) has an energy of −4.7 kcal mol−1, the barrier for the overall process under mechanochemical conditions is 21.4 kcal mol−1.The results of our microkinetic modeling of the process are presented in Fig. 3c and Fig. S1 (ESI†). The results are again very satisfactory. The experimental yield for the mechanochemical process is 90% after 2 h,6 whereas the computed value is 97%.
Note that the structures of nitrofurantoin and dantrolene differ only by the presence of a phenyl ring connecting furan and NO2 in dantrolene. Despite this seemingly minor difference, the reaction times in the ball-milling conditions change quite substantially: 15 min for nitrofurantoin (95%) vs. 2 h for dantrolene (90%). It is encouraging that the present computational study reproduces this difference. The different rate can be traced back to the difference in the rate-determining barriers, which are 20.9 and 21.4 kcal mol−1 for nitrofurantoin and dantrolene, respectively. We analyze in what follows the origin of these differences.
The inspection of the free energy profiles in Fig. 4 and 5 shows that the different relative energies of transition states TS2 (16.5 and 16.7 kcal mol−1, respectively) can be connected to the larger differences in the energies of the previous intermediates INT (1.5 and 4.6 kcal mol−1 for nitrofurantoin and dantrolene, respectively). The different stabilities of INT can be explained by examining the natural population analysis (NPA) of the corresponding furyl-aldehyde reactants, i.e., 5-nitro-2-furaldehyde in case of nitrofurantoin and 5-(4-nitrophenyl)-2-furaldehyde for dantrolene. The computed NPA atomic charges for the aldehyde CHO group of both systems are presented in Fig. 6.
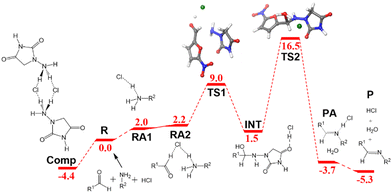 | ||
| Fig. 4 Free energy profile in kcal mol−1 for the formation of nitrofurantoin under ball milling conditions. Labels and color criteria are the same as those in Fig. 2. Color scheme: Cl (green), O (red), N (blue), C (grey), and H (white). | ||
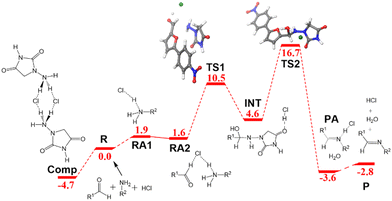 | ||
| Fig. 5 Free energy profile in kcal mol−1 for the formation of dantrolene under ball-milling conditions. Labels and color criteria are the same as those in Fig. 2. Color scheme: Cl (green), O (red), N (blue), C (grey), and H (white). | ||
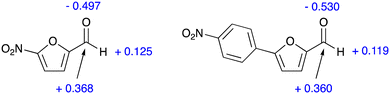 | ||
| Fig. 6 NPA charges (a.u.) for key atoms in the CHO fragment 5-nitro-2-furaldehyde (left) and 5-(4-nitrophenyl)-2-furaldehyde (right). | ||
The charge for the three atoms in the CHO group of the aldehyde leading to NF is −0.004 a.u., and the corresponding value for the aldehyde leading to DT is −0.059 a.u. This group undergoes nucleophilic attack from a lone pair in the hydrazide in the initial steps of the reaction, and this attack will be discouraged by the more negative charge in the aldehyde, leading to dantrolene. Thus, this explains why the synthesis of dantrolene is slower. The difference in the atomic charges is small, consistent with the relatively small difference in reactivity.
The theoretical calculations performed herein indicate the presence of an intermediate (INT), confirming the previously reported experimental data. The data were obtained by real-time in situ monitoring using the Raman spectra of the mechanochemical transformation (that leads to the formation of dantrolene) and indicates the formation of a low-energy intermediate.7 The DFT calculations are in agreement with this observation considering that it was possible to detect (and confirm) the formation of a stable intermediate INT (4.6 kcal mol−1), which was separated from the products by the energy barrier TS2 (16.7 kcal mol−1).
Conclusions
Our computational model based on DFT calculations and microkinetic modeling is able to accurately reproduce the reaction time for the synthesis of nitrofurantoin both in the conventional synthesis conditions in solution as well as in the ball-milling mechanochemical conditions. The reaction is a condensation between hydrazide and aldehyde fragments in acidic conditions, and the multistep mechanism, through a hemiaminal-like intermediate, is found to be qualitatively similar in different media. The barrier in the solution is slightly higher because of the weaker proton donors involved. The barrier for dantrolene is slightly higher because of the subtleties that can be explained by the analysis of the electronic structures.Author contributions
DMG and IT performed the DFT calculations and the microkinetic analysis. IT wrote the initial draft. EC and FM polished and corrected the draft. EC and FM designed the project. FM supervised the project.Data availability
The data supporting this article have been included as part of the ESI.†Conflicts of interest
There are no conflicts to declare.Acknowledgements
This article is based upon work from COST Action CA18112 Mechanochemistry for Sustainable Industry,35–38 supported by COST (European Cooperation in Science and Technology). COST (European Cooperation in Science and Technology) is a funding agency for research and innovation networks. Our Actions help connect research initiatives across Europe and enable scientists to grow their ideas by sharing them with their peers. This boosts their research, career, and innovation (www.cost.eu). E. C., is grateful to Région Occitanie (France) for the Pre-Maturation 2020 − MECH-API grant (ESR_PRE-MAT − 00262). E. C. is grateful to Campus France and French-Estonian cooperation Programme Hubert Curien France-Estonia (PHC PARROT 2021–2023). Financial support is acknowledged from CERCA Programme/Generalitat de Catalunya, MCIN/AEI (PID2020-112825RB-I00 and CEX2019-000925-S) and FEDER funds. DMG thanks support from a fellowship by LaCaixa. IT thanks support from the Generalitat de Catalunya for funding within the 2021-PROD-00042 project.Notes and references
- O. Galant, G. Cerfeda, A. S. McCalmont, S. L. James, A. Porcheddu, F. Delogu, D. E. Crawford, E. Colacino and S. Spatari, ACS Sustainable Chem. Eng., 2022, 10, 1430–1439 CrossRef
.
- F. Gomollón-Bel, ACS Central Sci., 2022, 8, 1474–1476 CrossRef PubMed
.
- D. J. C. Constable, C. Jimenez-Gonzalez and R. K. Henderson, Org. Proc. Res. Develop., 2007, 11, 133–137 CrossRef
.
- E. Colacino, A. Porcheddu, C. Charnay and F. Delogu, React. Chem. Eng., 2019, 4, 1179–1188 RSC
.
- X.-Z. Lim, Chem. Eng. News, 2020, 98, 11 CAS
.
- E. Colacino, A. Porcheddu, I. Halasz, C. Charnay, F. Delogu, R. Guerra and J. Fullenwarth, Green Chem., 2018, 20, 2973–2977 RSC
.
- I. Sović, S. Lukin, E. Meštrović, I. Halasz, A. Porcheddu, F. Delogu, P. C. Ricci, F. Caron, T. Perilli, A. Dogan and E. Colacino, ACS Omega, 2020, 5, 28663–28672 CrossRef
.
- A. Trimdale-Deksne, A. Kons, L. Orola, A. Mishnev, D. Stepanovs, L. Mazur, M. Skiba, M. K. Dudek, N. Fantozzi, D. Virieux, E. Colacino and A. Berzins, Cryst. Growth Des., 2023, 23, 930–945 CrossRef CAS
.
- E. Colacino, A. Porcheddu, I. Halasz, C. Charnay, F. Delogu, R. Guerra and J. Fullenwarth, Green Chem., 2018, 20, 2973–2977 RSC
.
- P. Sharma, C. Vetter, E. Ponnusamy and E. Colacino, ACS Sustainable Chem. Eng., 2022, 10, 5110–5116 CrossRef CAS
.
- N. Fantozzi, J.-N. Volle, A. Porcheddu, D. Virieux, F. García and E. Colacino, Chem. Soc. Rev., 2023, 52, 6680–6714 RSC
.
-
X. Li and F. Zhang, CN 101450941 A 20090610, 2009
.
- M. Mohagheghnezhad and Z. Rafiee, Polym. Bull., 2020, 77, 4739–4757 CrossRef CAS
.
- M. Carta, E. Colacino, F. Delogu and A. Porcheddu, Phys. Chem. Chem. Phys., 2020, 22, 14489–14502 RSC
.
- E. Colacino, M. Carta, G. Pia, A. Porcheddu, P. C. Ricci and F. Delogu, ACS Omega, 2018, 3, 9196–9209 CrossRef CAS PubMed
.
- K. J. Ardila-Fierro and J. G. Hernández, Angew. Chem., Int. Ed., 2024, 63, e202317638 CrossRef
.
- B. S. Pladevall, A. de Aguirre and F. Maseras, ChemSusChem, 2021, 2021(14), 2763–2768 CrossRef
.
- J. G. Hernández and C. Bolm, J. Org. Chem., 2017, 82, 4007–4019 CrossRef
.
-
M. M. J. Frisch, G. W. Trucks, H. B. Schlegel, G. E. Scuseria, M. A. Robb, J. R. Cheeseman, G. Scalmani, V. Barone, G. A. Petersson, H. Nakatsuji, X. Li, M. Caricato, A. V. Marenich, J. Bloino, B. G. Janesko, R. Gomperts, B. Mennucci, H. P. Hratchian, J. V. Ortiz, A. F. Izmaylov, J. L. Sonnenberg, D. Williams-Young, F. Ding, F. Lipparini, F. Egidi, J. Goings, B. Peng, A. Petrone, T. Henderson, D. Ranasinghe, V. G. Zakrzewski, J. Gao, N. Rega, G. Zheng, W. Liang, M. Hada, M. Ehara, K. Toyota, R. Fukuda, J. Hasegawa, M. Ishida, T. Nakajima, Y. Honda, O. Kitao, H. Nakai, T. Vreven, K. Throssell, J. A. Montgomery, Jr., J. E. Peralta, F. Ogliaro, M. J. Bearpark, J. J. Heyd, E. N. Brothers, K. N. Kudin, V. N. Staroverov, T. A. Keith, R. Kobayashi, J. Normand, K. Raghavachari, A. P. Rendell, J. C. Burant, S. S. Iyengar, J. Tomasi, M. Cossi, J. M. Millam, M. Klene, C. Adamo, R. Cammi, J. W. Ochterski, R. L. Martin, K. Morokuma, O. Farkas, J. B. Foresman and D. J. Fox, Gaussian 16, Revision C.01, (Gaussian, Inc., Wallingford CT, 2009) Search PubMed
.
- A. D. Becke, J. Chem. Phys., 1993, 98, 5648–5652 CrossRef
.
- C. Lee, W. Yang and R. G. Parr, Phys. Rev. B: Condens. Matter Mater. Phys., 1988, 37, 785–789 CrossRef
.
- S. Grimme, S. Ehrlich and L. Goerigk, J. Comput. Chem., 2011, 32, 1456–1465 CrossRef PubMed
.
- T. H. Dunning Jr, J. Chem. Phys., 1989, 90, 1007–1023 CrossRef
.
- V. Barone, M. Cossi and J. Tomasi, J. Chem. Phys., 1997, 107, 3210–3221 CrossRef
.
- M. Besora, P. Vidossich, A. Lledós, G. Ujaque and F. Maseras, J. Phys. Chem. A, 2018, 122, 1392–1399 CrossRef PubMed
.
- M. Besora and F. Maseras, WIREs Comp. Mol. Sci., 2018, 8, e1372 CrossRef
.
- S. Hoops, S. Sahle, R. Gauges, C. Lee, J. Pahle, N. Simus, M. Singhal, L. Xu, P. Mendes and U. Kummer, Bioinformatics, 2006, 22, 3067–3074 CrossRef PubMed
.
- M. Álvarez-Moreno, C. de Graaf, N. López, F. Maseras, J. M. Poblet and C. Bo, J. Chem. Inf. Model., 2015, 55, 95–103 CrossRef
.
- M. A. Sprung, Chem. Rev., 1940, 26, 297–338 CrossRef CAS
.
- J. M. Sayer and W. P. Jencks, J. Am. Chem. Soc., 1977, 99, 464–474 CrossRef CAS
.
- M. Ciaccia and S. Di Stefano, Org. Biomol. Chem., 2015, 13, 646–654 RSC
.
- A. D. Calow, J. J. Carbó, J. Cid, E. Fernández and A. Whiting, J. Org. Chem., 2014, 79, 5163–5172 CrossRef CAS PubMed
.
- R. Perez-Soto, M. Besora and F. Maseras, Org. Lett., 2020, 22, 2873–2877 CrossRef CAS PubMed
.
- S. Kozuch and S. Shaik, Acc. Chem. Res., 2011, 44, 101–110 CrossRef PubMed
.
- For more information on COST Action CA18112 ‘Mechanochemistry for Sustainable Industry’: https://www.mechsustind.eu/(accessed April 6, 2024).
- J. G. Hernández, I. Halasz, D. E. Crawford, M. Krupička, M. Baláž, V. André, L. Vella-Zarb, A. Niidu, F. García, L. Maini and E. Colacino, Eur. J. Org. Chem., 2020, 8–9 CrossRef
.
- M. Baláž, L. Vella-Zarb, J. G. Hernández, I. Halasz, D. E. Crawford, M. Krupička, V. André, A. Niidu, F. García, L. Maini and E. Colacino, Chem. Today, 2019, 37, 32–34 Search PubMed
.
- F. Gomollón-Bel, Chem. Eng. News, 2022, 100, 21–22 Search PubMed
.
Footnote |
| † Electronic supplementary information (ESI) available: Details on calculations of dielectric constants, initial concentrations for microkinetic modelling, benchmarking of functional and Cartesian coordinates. See DOI: https://doi.org/10.1039/d4cp01613k |
| This journal is © the Owner Societies 2024 |