Open Access Article
Open Access ArticleCreative Commons Attribution 3.0 Unported Licence
The strongest dative bond in main-group compounds. Theoretical study of OAeF− (Ae = Be–Ba)†‡
Lei
Qin§
a,
Ruiqin
Liu§
a,
Filip
Sagan§
b,
Zhaoyin
Zhang
a,
Lili
Zhao
 *a,
Mariusz
Mitoraj
*a,
Mariusz
Mitoraj
 *b and
Gernot
Frenking
*b and
Gernot
Frenking
 *ac
*ac
aState Key Laboratory of Materials-Oriented Chemical Engineering, School of Chemistry and Molecular Engineering, Nanjing Tech University, Nanjing 211816, China. E-mail: ias_llzhao@njtech.edu.cn
bDepartment of Theoretical Chemistry, Faculty of Chemistry, Jagiellonian University, R. Gronostajowa 2, 30-387 Cracow, Poland. E-mail: mitoraj@chemia.uj.edu.pl
cFachbereich Chemie, Philipps-Universität Marburg, Hans-Meerwein-Strasse 4, D-35043 Marburg, Germany. E-mail: frenking@chemie.uni-marburg.de
First published on 6th September 2024
Abstract
Quantum chemical calculations of the anions OAeF− (Ae = Be–Ba) have been carried out using ab initio methods at the CCSD(T)/def2-TZVPP level and density functional theory employing BP86 with various basis sets. The equilibrium structures have linear geometries for Ae = Be and Mg but they are strongly bent for Ae = Sr and Ba while the calcium species has a quasi-linear structure with a very low bending potential. The calculated bond dissociation energies suggest a record-high BDE of De = 144.08 kcal mol−1 for OBeF− at the CCSD(T)/def2-TZVPP level, which is the strongest BDE for a dative bond that has been found so far. The BDE of the heavier homologues have a continuously decreasing order for Ae with Be > Mg (113.01 kcal mol−1) > Ca (84.06 kcal mol−1) > Sr (72.06 kcal mol−1) > Ba (60.00 kcal mol−1). The calculation of the charge distribution reveals a significant charge donation OAe ← F− with a declining sequence for the heavier atoms Ae. The oxygen atom in OAeF− carries always a higher partial charge than the fluorine atom, which contradicts the standard electronegativities of the atoms. The surprising partial charges are explained with the bonding situation of the atoms in the actual electronic structure. The bonding analysis of the OAe–F− bonds using the EDA-NOCV method shows that the bonds have much more electrostatic character than the Ae–F− bonds in the diatomic anions. This finding is supported by the results of the LED partitioning approach. The dative interactions have three major and one minor component. The assignment of a quadruple bond for the heavier species with Ae = Ca, Sr, Ba is not reasonable. The driving force for the bent geometries is the accumulation of electronic charge in the lone-pair region at the Ae atoms, which enhances the electrostatic attraction with the other atoms. An adequate description of the bonding situation is given by the formula O−–Ae+ ← F−.
Introduction
Recently we reported theoretical work on the diatomic anions AeF− (Ae = Be–Ba), which possess surprisingly strong dative bonds between the closed-shell species Ae and F−.1,2 The calculated bond dissociation energies are between 87.5 kcal mol−1 for BeF− and 68.8 kcal mol−1 for MgF− and they show an unusual increasing trend MgF− < CaF− < SrF− < BaF−. The strong bonds were explained by the inductive force of F−, which heavily polarizes the (n)s2 valence electrons of the Ae atoms, inducing in turn four dative covalent interactions3–5 of the heavier species involving the (n − 1)d AOs of Ca–Ba.1,2 The fluorine anion F− being isoelectronic to Ne is a weak electron donor due to the high electronegativity of fluorine and the alkaline earth atoms are weak electron acceptors. We speculated that replacing the weak electron acceptors Ae with the stronger electron acceptors AeO could lead to even higher bond dissociation energies (BDEs). Earlier studies by one of us showed that diatomic BeO is likely the strongest neutral Lewis acid, which even binds the extremely weak Lewis base He with a BDE of De ∼ 3 kcal mol−1.6–9The objective of this work is to search for compounds that possess even stronger dative bonds than diatomic AeF−. A logical step is the replacement of the weak Lewis acceptor atom Ae by the strong Lewis acid AeO.
Here we present quantum chemical calculations using ab initio methods and density functional theory of the anions OAeF− (Ae = Be–Ba) and an analysis of the OAe–F− bonds. None of the triatomic anions has yet been observed experimentally. The calculated results show that the compounds are very stable species with record-breaking strong dative bonds and unusual properties that can be observed in the gas phase. The theoretically predicted vibrational spectra are a helpful guide for identifying the molecules in experiments.
Methods
The bond lengths, vibrational frequencies and BDEs of OAeF− (Ae = Be–Ba) and in the electronic singlet ground state were calculated at the CCSD(T)10 and BP8611,12 level in conjunction with the basis sets def2-TZVPP.13 The CCSD(T) calculations were carried out to give quantitatively accurate numerical values and the DFT calculation were performed to provide a basis for the EDA-NOCV calculations and for investigating the performance of the BP86 functional, which was found to be very good. The calculations were carried out with the program Gaussian 16.14 The NBO calculations were performed using the program NBO 7.0.15 We also calculated atomic partial charges using the Hirshfeld16 and CM517 methods with the program Gaussian 16, and calculated Voronoi18 charges and Mayer19 bond order with the program Multiwfn.20The bonding situation in the molecules was further analyzed by means of an energy decomposition analysis (EDA) which was introduced by Morokuma121 and by Ziegler and Rauk22 in conjunction with the natural orbitals for chemical valence (NOCV)23,24 method. The EDA-NOCV25,26 calculations were carried out with the ADF 2018.105 program package27,28 at the BP86-D3(BJ)29 level with Slater-type basis function of DZP quality30 using the BP86/def2-TZVPP optimized geometries. DZP is a double-ζ quality basis set augmented by a set of polarization functions. The use of larger basis sets does not lead to significantly different energy values, but can lead to unphysically large numerical contributions from atomic orbitals of higher quantum number such as (n + 1)s AOs of Ae atom, which represent numerical artifacts. In this analysis, the intrinsic interaction energy (ΔEint) between two fragments can be divided into three energy components as follows:
| ΔEint = ΔEelstat + ΔEPauli + ΔEorb | (1) |
The electrostatic ΔEelstat term represents the quasiclassical electrostatic interaction between the unperturbed charge distributions of the prepared fragments, the Pauli repulsion ΔEPauli corresponds to the energy change associated with the transformation from the superposition of the unperturbed electron densities of the isolated fragments to the wavefunction, which properly obeys the Pauli principle through explicit antisymmetrization and renormalization of the production wavefunction. The orbital term ΔEorb comprises the mixing of orbitals, charge transfer and polarization between the isolated fragments. The energy change involved in the latter step, which is the main difference between the Morokuma21 and Ziegler/Rauk22 approaches, is calculated with an extension of Slater's transition state method31 for energy differences. It is often referred as ETS method. The orbital term ΔEorb can be further decomposed into contributions from each irreducible representation of the point group of the interacting system as follows:
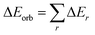 | (2) |
The combination of the EDA with NOCV enables the partition of the total orbital interactions into pairwise contributions of the orbital interactions which is very vital to get a complete picture of the bonding. The charge deformation Δρk(r), resulting from the mixing of the orbital pairs ψk(r) and ψ−k(r) of the interacting fragments presents the amount and the shape of the charge flow due to the orbital interactions (eqn (3)), and the associated energy term ΔEorb provides the size of stabilizing orbital energy originated from such interaction (eqn (4)) where FTS−k,−k and FTSk,k are the Fock matrix elements defined for the transition state electron density (the mid density between a molecule and fragments).25,26
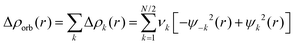 | (3) |
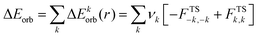 | (4) |
The EDA-NOCV approach was previously criticized because its results are allegedly path-dependent.32–34 This was rebutted in a detailed discussion of the method.35 More details about the EDA-NOCV method and its application are given in recent review articles.36–42
Upon request of one referee we carried out additional calculations for the analysis of the chemical bonds. We employed the local energy decomposition43–45 (LED) method in conjunction with ab initio calculations at the DLPNO-CCSD(T)46–50 level. DLPNO-CCSD(T) recovers >95% of triples contribution and 99.8% of correlation energy.49 The LED approach decomposes the interaction energy between the frozen fragments into the Hartree–Fock and correlation interaction energies:
| ΔEint = ΔEHFint + ΔECint + ΔEel-prep | (5) |
| ΔEHFint = ΔEelstat + ΔEexch | (6) |
| ΔECint = ΔEC-SPCT(A→B) + ΔEC-SPCT(B→A) + ΔECdisp + ΔEC-WP + ΔEC-T | (7) |
Geometries, energies and vibrational frequencies
Fig. 1 shows the calculated geometries of diatomic AeO and the triatomic anions OAeF− at the CCSD(T)/def2-TZVPP and BP86/def2-TZVPP levels of theory. The calculated bond lengths for AeO are slightly longer than the experimental values,51 especially for BP86/def2-TZVPP for the heavier species, but the differences are not a concern as we are mainly interested in the changes resulting from the binding of F−. The lighter OAeF− species with Ae = Be, Mg are predicted to have linear structures whereas the heavier anions with Ae = Sr, Ba possess a bent equilibrium geometry. The calcium species OCaF− has a linear structure at the CCSD(T)/def2-TZVPP level. It has a bending angle of 144.7° at BP86/def2-TZVPP, but this is only 0.5 kcal mol−1 higher than for the linear form. The bent equilibrium structures of OSrF− and OBaF− are 2.7 kcal mol−1 and 3.6 kcal mol−1 lower in energy than the linear forms, which are transition states (number of imaginary modes 1) at the CCSD(T)/def2-TZVPP. The energy differences at BP86/def2-TZVPP are a bit higher, i.e. 5.2 kcal mol−1 for OSrF− and 8.6 kcal mol−1 for OBaF−. The anions OAeF− are isoelectronic with the difluorides AeF2, which have been studied before. Experimental and theoretical work suggest that the lighter molecules BeF2 and MgF2 have linear geometries but the heavier homologues CaF2, SrF2, BaF2 are strongly bent but with a soft bending potential between ∼0.2 kcal mol−1 (CaF2) and ∼5 kcal mol−1 (BaF2) which is similar to the calculated values for OAeF− (Fig. 1).52,53 A theoretical study suggested that d-orbital participation of the heavier Ae atoms Ca–Ba and core-polarization make major contributions to the bending.52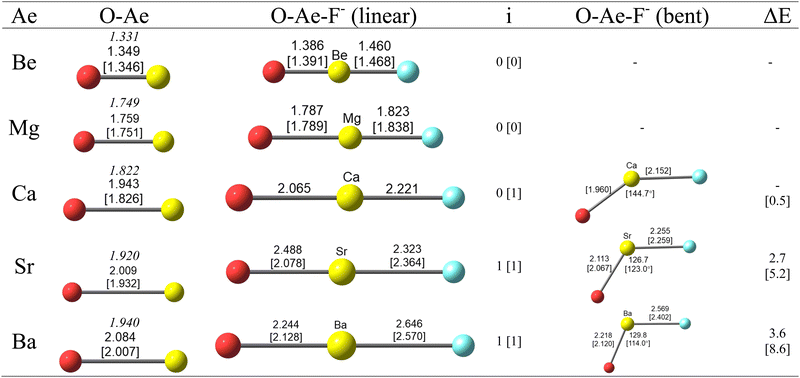 | ||
| Fig. 1 Optimized geometries of OAe and OAeF− (Ae = Be–Ba) at the CCSD(T)/def2-TZVPP [BP86/def2-TZVPP] level. Bond lengths in Å and angles in degree. The experimental value for the Ae–O bond lengths given in italics are taken from ref. 51. Number of imaginary frequencies i. The linear structures of OSrF− and OBaF− are transition states at both levels of theory, the linear structure of OCaF− is a transition state at BP86/def2-TZVPP. ΔE gives the energy differences between the linear and bent geometries in kcal mol−1. | ||
Fig. 1 shows that the Ae–O distances of the anions OAeF− are longer than in diatomic AeO. The Ae–F bonds in OAeF− are also longer than in AeF− except for the magnesium species, where the calculated Mg–F distance in OMgF− at both levels of theory is shorter than in MgF− (1.840 Å at CCSD(T)/def2-TZVPP and 1.847 Å at BP86/def2-TZVPP).54 It is interesting that the Ae–O and Ae–F bonds in the bent structures of the heavier anions are shorter than in the linear form. This does not agree with the commonly assumed trend with respect to spn hybridization.
Table 1 gives the theoretically predicted vibrational frequencies and IR intensities of the molecules OAeF− and for diatomic AeO and AeF−, which will be useful to identify the anions. The frequency shift Δ of the stretching modes between the diatomic and triatomic species shows some unexpected trends. The Ae–O stretching frequencies of OBeF− and OMgF− are predicted to possess a blue shift toward higher wave numbers compared with free BeO and MgO although the bond distances are clearly longer in the anions. In contrast, the heavier anions OAeF− (Ae = Ca, Sr, Ba) exhibit a red shift to lower wavenumbers. The red shift at CCSD(T)/def2-TZVPP is much smaller for the calcium and strontium species than at BP86/def2-TZVPP. This does not seem to be related to the structures (curved or linear) of the anions. The linear form of OCaF− at CCSD(T)/def2-TZVPP possess also a small red shift of the Ca–O stretching mode. The Ae–F stretching frequencies of all triatomic species OAeF− are red-shifted toward lower wave numbers relative to diatomic AeF−. The red shift is particularly large for OBeF−.
| Molecule | CCSD(T)/def2-TZVPP [BP86/def2-TZVPP] | |||||||
|---|---|---|---|---|---|---|---|---|
| Ae–O stretch | Ae–F stretch | O–Ae–F bent | ||||||
| υ | Δ | I.b | υ | Δ | I | υ. | I.b | |
| a Degenerate. b Intensitites are not available at CCSD(T). | ||||||||
| BeO | 1434.0 [1454.5] | — | [4.2] | — | — | — | — | — |
| BeF− | — | — | — | 1028.0 [1007.2] | — | [14.3] | — | — |
| OBe–F− | 1519.3 [1481.2] | +85.3 [+26.7] | [204.9] | 683.8 [665.0] | −344.2 [−354.7] | [4.6] | 396.0a [385.3]a | [34.0] |
| MgO | 783.7 [801.8] | — | [13.8] | — | — | — | — | — |
| MgF− | — | — | — | 577.7 [540.8] | — | [37.7] | — | — |
| OMg–F− | 847.2 [827.4] | +33.9 [+25.6] | [73.3] | 524.4 [502.8] | −53.3 [−45.5] | [10.9] | 171.4a [170.1]a | [48.6] |
| CaO | 589.3 [751.8] | — | [68.5] | — | — | — | — | — |
| CaF− | — | — | — | 485.6 [511.6] | — | [44.5] | — | — |
| OCa–F− | 584.8 [601.6] | −4.5 [−150.2] | [93.9] | 401.0 [406.2] | −84.6 [−111.1] | [91.8] | 54.3a [74.5] | [51.8] |
| SrO | 407.8 [657.3] | — | [74.5] | — | — | — | — | — |
| SrF− | — | — | — | 410.6 [428.5] | — | [48.6] | — | — |
| OSr–F− | 402.1 [526.5] | −5.7 [−130.8] | [87.9] | 306.0 [356.4] | −104.6 [−76.4] | [133.0] | 43.4 [112.3] | [26.9] |
| BaO | 618.9 [641.9] | — | [129.6] | — | — | — | — | — |
| BaF− | — | — | — | 408.3 [409.1] | — | [56.9] | — | — |
| OBa–F− | 485.6 [517.3] | −133.3 [−124.6] | [50.4] | 319.7 [317.8] | −88.6 [−93.9] | [134.5] | 88.8 [116.3] | [13.2] |
Table 2 shows the calculated BDEs of the anions for breaking the bonds. The calculated BDE for the reaction OBeF− → BeO + F− is very high at both theory levels and is De = 144.8 kcal mol−1 at CCSD(T)/def2-TZVPP and De = 142.6 kcal mol−1 at BP86/def2-TZVPP. To our knowledge, this is the highest value for the BDE of a donor–acceptor bond between two closed-shell species for main group compounds and transition metal complexes that has been reported so far. The alternative electron-sharing rupture of the OBeF− bond toward BeO− + F has an even higher BDE, because the calculated electron affinity of BeO (1.99 eV) is clearly lower than the electron affinity of fluorine (3.33 eV).55 The BDEs for the reaction of the heavier homologues OAeF− → AeO + F− (Ae = Mg–Ba) are significantly smaller than for the beryllium anion. Unlike the diatomic anions AeF−,1,2 the triatomic anions OAeF− exhibit a continuously decreasing trend Be > Mg > Ca > Sr > Ba, which concurs with the common trend of electron-sharing bonds of main-group compounds, typically becoming weaker for heavier-row atoms.
| [OAeF]− (S) → OAe (S) + F− (S) | [OAeF]− (S) → OAe− (D) + F (D) | [OAeF]− (S) → [AeF]− (S) + O (T) [O (S)]a | [OAeF]− (S) → AeF (D) + O−(D) | |||||
|---|---|---|---|---|---|---|---|---|
| CCSD(T)/def2-TZVPP | BP86/def2-TZVPP | CCSD(T)/def2-TZVPP | BP86/def2-TZVPP | CCSD(T)/def2-TZVPP | BP86/def2-TZVPP | CCSD(T)/def2-TZVPP | BP86/def2-TZVPP | |
| a Using the experimental value for the 3P → 1D excitation energy of oxygen atom 45.3 kcal mol−1: Kramida, A., Ralchenko, Yu., Reader, J., and NIST ASD Team (2022). NIST Atomic Spectra Database (ver. 5.10), [Online]. Available: https://physics.nist.gov/asd [2023, August 21]. National Institute of Standards and Technology, Gaithersburg, MD. DOI: https://doi.org/10.18434/T4W30F. | ||||||||
| [OBeF]− | 144.8 | 142.6 | 158.2 | 163.1 | 150.1 [201.3] | 164.7 [229.8] | 157.8 | 161.0 |
| [OMgF]− | 113.1 | 114.9 | 142.9 | 143.2 | 97.5 [148.7] | 113.3 [178.3] | 111.4 | 116.5 |
| [OCaF]− | 84.6 | 78.4 | 125.8 | 129.9 | 83.5 [134.7] | 108.3 [173.4] | 95.0 | 102.4 |
| [OSrF]− | 72.6 | 72.1 | 118.6 | 125.1 | 75.7 [127.0] | 101.5 [166.5] | 94.4 | 95.7 |
| [OBaF]− | 60.0 | 62.5 | 111.9 | 120.9 | 70.3 [121.5] | 108.7 [173.8] | 74.5 | 100.3 |
Table 2 gives also the BDEs for breaking the O–AeF− bonds. The bond rupture yielding the electronic ground state of the fragments O (3P) and AeF− (1Σ+) at CCSD(T)/def2-TZVPP has slightly higher De values for the bonds O–BeF− (150.1 kcal mol−1), O–SrF− (75.7 kcal mol−1) and O–BaF− (70.3 kcal mol−1), smaller De values for O–MgF− (97.5 kcal mol−1) and a comparable De value for O–CaF− (83.5 kcal mol−1) than for the respective OAe–F− bonds. Both sets of O–AeF− and OAe–F− bonds have the same regular trend of the BDEs Be ≫ Mg > Ca > Sr > Ba, which underlines the peculiar feature of the diatomic anions AeF−.1,2 But the bond dissociation reaction OAeF− (singlet) → O (3P) + AeF− (1Σ+) is spin-symmetry forbidden. The spin-symmetry allowed formation of O (1D) + AeF− (1Σ+) is thermodynamically 45.3 kcal mol−1 higher in energy. The BDE for the dissociation reaction OAeF− (singlet) → AeF (2Σ+) + O− (2P) is higher at CCSD(T)/def2-TZVPP than for the reaction yielding O (3P) and AeF− (1Σ+), whereas BP86/def2-TZVPP gives slightly lower values for Ae = Ca–Ba. Thus, the strong OAe–F− bonds are the lowest energy symmetrically allowed reaction channels for fragmentation. All triatomic anions are thermodynamically very stable species.
Bonding analysis
We analyzed the electronic structure and bonding situation in the triatomic anions OAeF− with a variety of methods. Table 3 shows the atomic partial charges calculated with four different methods. It was previously found in our study of AeF− that the charge distribution suggested by the popular NBO method is not reasonable, because the (n)p valence AOs of Ae are not treated as genuine valence orbitals, which leads to a negligible charge donation Ae ← F−.1,2 The data in Table 3 show that the same problematic results occur for OAeF−. The NBO method gives a miniscule charge donation OAe ← F− between 0.01–0.12e, whereas the other three methods suggest a much larger charge donation between 0.28–0.62e. Since a significant charge donation is supported by further analysis of the electronic structure, we think that the NBO charges are not a reliable indicator of the charge distribution in these molecules.| CCSD/def2-TZVPP [BP86/def2-TZVPP] | |||||||
|---|---|---|---|---|---|---|---|
| q | P(Ae–F−) | ||||||
| Atoms | NBOa | Hirshfelda | Voronoib | CM5a | Bond | Wiberga | Mayerb |
| a Obtained at the CCSD/def2-TZVPP (density = current) level with Gaussian program. b Obtained at the CCSD/def2-TZVPP (density = current) level with Multiwfn program. | |||||||
| O | −1.66 [−1.67] | −0.75 [−0.69] | −0.81 [−0.75] | −0.96 [−0.90] | OBe–F− | 0.18 [0.22] | 0.74 [0.87] |
| Be | 1.54 [1.55] | 0.14 [0.05] | 0.19 [0.11] | 0.48 [0.40] | |||
| OBe | −0.12 [−0.12] | −0.61 [−0.64] | −0.62 [−0.64] | −0.48 [−0.51] | O–BeF− | 0.50 [0.60] | 1.84 [2.08] |
| F | −0.88 [−0.88] | −0.39 [−0.36] | −0.39 [−0.36] | −0.52 [−0.49] | |||
| O | −1.62 [−1.58] | −0.82 [−0.74] | −0.99 [−0.90] | −0.97 [−0.89] | OMg–F− | 0.10 [0.15] | 0.53 [0.68] |
| Mg | 1.55 [1.50] | 0.34 [0.21] | 0.49 [0.38] | 0.58 [0.47] | |||
| OMg | −0.07 [−0.08] | −0.48 [−0.53] | −0.50 [−0.52] | −0.39 [−0.43] | O–MgF− | 0.53 [0.74] | 1.64 [1.93] |
| F | −0.93 [−0.92] | −0.51 [−0.47] | −0.50 [−0.48] | −0.61 [−0.57] | |||
| O | −1.62 [−1.56] | −0.88 [−0.76] | −1.05 [−0.90] | −1.05 [−0.99] | OCa–F− | 0.08 [0.13] | 0.36 [0.54] |
| Ca | 1.61 [1.49] | 0.50 [0.29] | 0.59 [0.39] | 0.76 [0.62] | |||
| OCa | −0.01 [−0.07] | −0.38 [−0.47] | −0.46 [−0.51] | −0.29 [−0.37] | O–CaF | 0.50 [0.82] | 1.41 [1.82] |
| F | −0.99 [−0.93] | −0.62 [−0.53] | −0.55 [−0.48] | −0.71 [−0.63] | |||
| O | −1.58 [−1.49] | −0.85 [−0.73] | −1.00 [−0.85] | −1.09 [−1.00] | OSr–F− | 0.07 [0.15] | 0.31 [0.52] |
| Sr | 1.53 [1.41] | 0.46 [0.26] | 0.50 [0.33] | 0.81 [0.66] | |||
| OSr | −0.05 [−0.08] | −0.39 [−0.47] | −0.50 [−0.52] | −0.28 [−0.34] | O–SrF− | 0.59 [0.91] | 1.40 [1.77] |
| F | −0.95 [−0.92] | −0.60 [−0.53] | −0.50 [−0.48] | −0.72 [−0.66] | |||
| O | −1.64 [−1.50] | −0.87 [−0.72] | −1.00 [−0.79] | −1.13 [−1.04] | OBa–F− | 0.06 [0.16] | 0.24 [0.49] |
| Ba | 1.58 [1.42] | 0.50 [0.26] | 0.50 [0.24] | 0.85 [0.70] | |||
| OBa | −0.06 [−0.08] | −0.37 [−0.46] | −0.50 [−0.55] | −0.28 [−0.34] | O–BaF− | 0.64 [0.90] | 1.42 [1.74] |
| F | −0.94 [−0.92] | −0.64 [−0.54] | −0.51 [−0.45] | −0.71 [−0.66] | |||
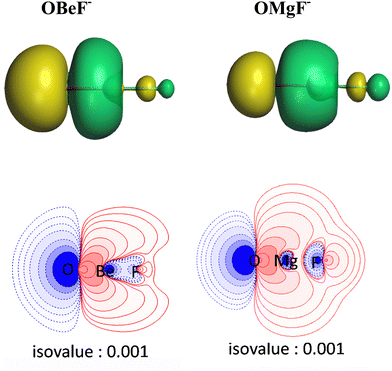
There is another interesting result concerning the charge distribution in the anions OAeF−. All four methods suggest that the oxygen atom carries a higher negative partial charge than fluorine, which does not agree with the electronegativity of the atoms. The difference between the negative charges at the terminal atoms towards oxygen is very large. The result is not an artefact of the partitioning procedures for calculating partial charges. Fig. 2 shows the molecular electrostatic potential (MEP) of the molecules, which shows clearly that the oxygen atom carries a larger negative charge than fluorine. It has been shown before that the MEP results are the physically most reliable data for giving the charge distribution in a molecule.56 The MEP result does not depend on the chosen value for the contour line. Fig. 2 is obtained with a value of 0.02 a.u. Fig. S2 of ESI,‡ shows the MEP with a much smaller value of 0.001 a.u. for the contour line. It also shows that oxygen carries a higher negative charge than fluorine.
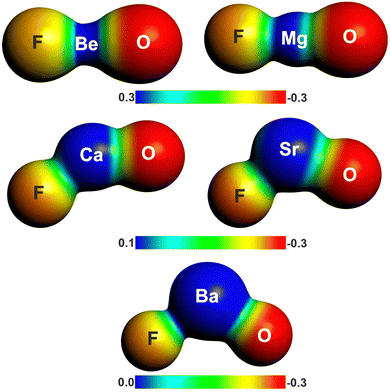 | ||
| Fig. 2 Plot of the electrostatic potentials of OAeF− at the BP86/def2-TZVPP level. Computed with value of 0.001 a.u. for the contour of the electronic density. | ||
The seemingly paradoxical result can be understood when one realizes that the common scales for atomic electronegativities are average values derived from compounds in standard electronic states. The electronegativity of an atom is the power to attract electronic charge from another atom in a chemical bond, but it is affected by the actual bonding situation. A recent example concerns the carbon atom in the compound class of carbones CL2 where the C atom has a 1D (2s22p2) reference state. There are dative bonds L → C ← L where the ligands L donate electronic charge into the vacant 2p AOs of carbon. The bonding situation makes the carbon atom in carbones to have a much higher electronegativity than in standard organic molecules.41,42,57–61 There have been early studies where different values for the electronegativity of the valence orbitals in an atom were proposed, but they are hardly ever used and it seems that this approach is forgotten.62,63 The present results suggest that the charge distribution in OAeF− is affected by the different nature of the two bonds, i.e. electron-sharing interactions between oxygen and Ae versus dative interactions between fluorine and Ae.
Table 3 gives also the bond order of the molecules using the frequently chosen Wiberg method64 as well as the Mayer bond orders.19,65 The Wiberg bond orders (WBOs) are originally derives from semiempirical CNDO/2 calculations, which neglect the orbital overlap. It has been shown that his can lead to misleading values particularly for polar bonds66–68 The data in Table 3 show that the WBO values are much smaller than the bond orders suggested by the Mayer partitioning method, which explicitly considers the interatomic overlap. The Mayer bond orders (MBOs) are significantly higher than the WBO data for the very polar OAe–F− and particularly for the O–AeF− bonds. The MBO values indicate for the latter bonds a substantial multiple bond character whereas the WBO values are always <1. But we want to point out that the bond order values of polar bonds may not be directly taken as measure for the bond multiplicity. Polar bonds have lower bond orders <1 for an electron-pair single bond due to the smaller overlap than non-polar bonds.68 A polar triple bond can have an MBO value significantly smaller than 3 and yet it may possess three bonding electron pairs. This holds in particular for very polar bonds which were found in AeF− (ref. 1 and 2) and which are present in OAeF−. More sophisticated methods are needed to provide a meaningful answer to the question of bond multiplicity.
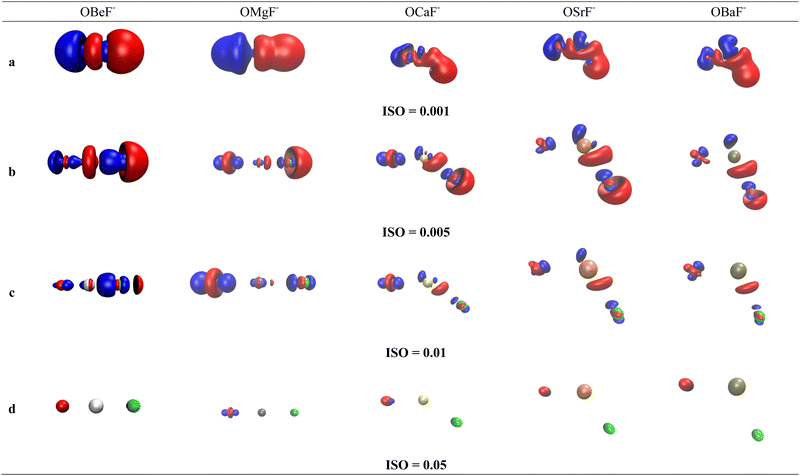
Much insight is gained by examination of the difference density maps where the charge distribution of free OAe and F− is subtracted from the charge in OAe–F−. This is shown in Fig. 3 for OBeF− using four different values for the isosurface, which gives interesting information about the charge flow. The difference density map of the rather diffuse charge with the isosurface value of 0.001e a.u.−3 in Fig. 3 shows charge depletion from F− and Be and charge enhancement in the F−–BeO bonding region and at oxygen atom. More interesting information comes from Fig. 3b and c which displays the charge flow in the areas of higher charge density, which are directly associated with the formation of the F−–BeO bond and the change in the O–Be bond. There is clearly an increase in the electronic charge between F− and BeO as well as between O and BeF−. The red and blue areas of decrease and increase of charge at Be nicely illustrate the 2s → 2pσ hybridization at Be. Note that the difference density maps do not distinguish between charge in the σ and π bonding regions, because the degenerate π bonds are rotationally symmetric. The variation in information revealed by using different values for the isosurface is a warning against the indiscriminate use of isodensity plots at a given value.
The difference density maps of OMgF− show similar features as for OBeF− but there are interesting changes in the AO shell alterations of the atoms. There is a 2s → 2pσ hybridization at oxygen which is still visible at the iso value 0.05e a.u.−3 for OMgF− but not for OBeF−. The density difference maps of the heavier homologues with bent geometries show nicely the appearance of charge concentration in the region with lone-pair character at Ae = Ca, Sr, Ba, which comes from the polarization of the rather soft valence electrons of the metal. This mechanism has already been pointed out by Kaupp et al. in their theoretical study of AeX2 (X = halogen).52 There is charge accumulation in the lone-pair region of the three heavy Ae atoms in the diffuse areas with isovalues 0.001e a.u.−3 and 0.005e a.u.−3 shown in Fig. 3b and c. It disappears for Ba in the area with an isovalue of 0.01e a.u.−3 shown in Fig. 3d, because of the more dispersed valence charge.
A very detailed information about the nature of the bonding interaction and the associated charge flow is available from EDA-NOCV calculations. The EDA provides a quantitative estimate of the attractive (covalent and electrostatic) and repulsive (Pauli repulsion) contributions to the interatomic interactions. The NOCV component partitions the covalent (orbital) interactions into pairwise contributions, relating the results to the frontier orbital model of Fukui69 and the orbital symmetry rules of Woodward and Hoffman.70 A nice feature of the EDA-NOCV approach is that the individual orbital interactions can be graphically represented by the associated deformation densities and the connected orbitals. The aim of the EDA-NOCV calculations is a detailed and quantitative analysis of the electronic interactions that lead to the unusual chemical bonds in the molecules described in this work.
Table 4 shows the numerical results for the anions OAeF− using AeO (S) and F− (S) in the electronic singlet states as interacting fragments at the BP86/def2-TZVPP optimized equilibrium geometries. The intrinsic interaction energies ΔEint have very similar values and the same trend Be > Mg > Ca > Sr > Ba as the BDE values shown in Table 2, because the only relaxation of the fragments comes from the change in the AeO bond lengths. Inspection of the various energy terms suggest that the OAe–F− binding comes mainly from the electrostatic attraction ΔEelstat which provides between 74.3% (Ae![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) Be) and 59.3% (Ae
Be) and 59.3% (Ae![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) Ba) to the total attraction. The EDA-NOCV analysis shows that the covalent character of the OAe–F− bonds given by the percentage contribution of the orbital term ΔEorb increases steadily from Be to Ba.
Ba) to the total attraction. The EDA-NOCV analysis shows that the covalent character of the OAe–F− bonds given by the percentage contribution of the orbital term ΔEorb increases steadily from Be to Ba.
| Fragments | OBe (S) + F− (S) | OMg (S) + F− (S) | OCa (S) + F− (S) | OSr (S) + F− (S) | OBa (S) + F− (S) | OBa (S) + F− (S) |
|---|---|---|---|---|---|---|
| Structure | Linear | Linear | Bent | Bent | Bent | Linear |
| a The values in parentheses give the percentage contribution to the total attractive interactions ΔEelstat + ΔEorb. b The values in parentheses give the percentage contribution to the total orbital interactions ΔEorb. | ||||||
| ΔEint | −147.5 | −113.5 | −79.5 | −73.7 | −69.8 | −62.3 |
| ΔEPauli | 57.3 | 64.4 | 53.8 | 47.8 | 48.6 | 41.9 |
| ΔEelstata | −152.2 (74.3%) | −129.9 (73.0%) | −89.7 (67.3%) | −79.5 (65.4%) | −70.2 (59.3%) | −57.4 (55.1%) |
| ΔEorba | −52.7 (25.7%) | −48.0 (27.0%) | −43.6 (32.7%) | −42.0 (34.6%) | −48.2 (40.7%) | −46.8 (44.9%) |
| ΔEorb1b | −24.4 (46.3%) | −29.1 (60.6%) | −19.3 (44.3%) | −12.7 (30.2%) | −21.0 (43.6%) | −18.3 (39.1%) |
| ΔEorb2b | −10.1 (19.2%) | −6.8 (14.2%) | −8.5 (19.5%) | −12.4 (29.5%) | −10.8 (22.4%) | −10.1 (21.6%) |
| ΔEorb3b | −10.1 (19.2%) | −6.8 (14.2%) | −6.3 (14.4%) | −9.0 (21.4%) | −10.8 (22.4%) | −10.1 (21.6%) |
| ΔEorb4b | −4.9 (9.3%) | −3.0 (6.3%) | −4.5 (10.3%) | −3.6 (8.6%) | −1.5 (3.1%) | −5.1 (10.9%) |
| ΔErestb | −3.2 (6.0%) | −2.0 (4.7%) | −5.0 (11.5%) | −4.3 (10.3%) | −4.1 (8.5%) | −3.1 (6.7%) |
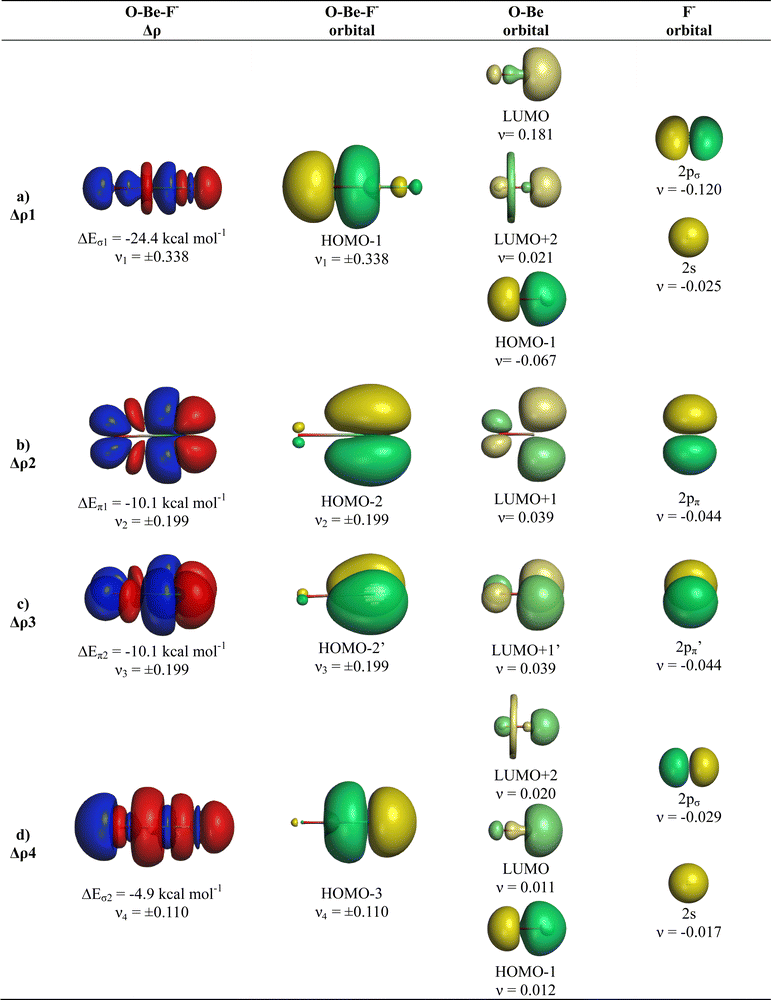
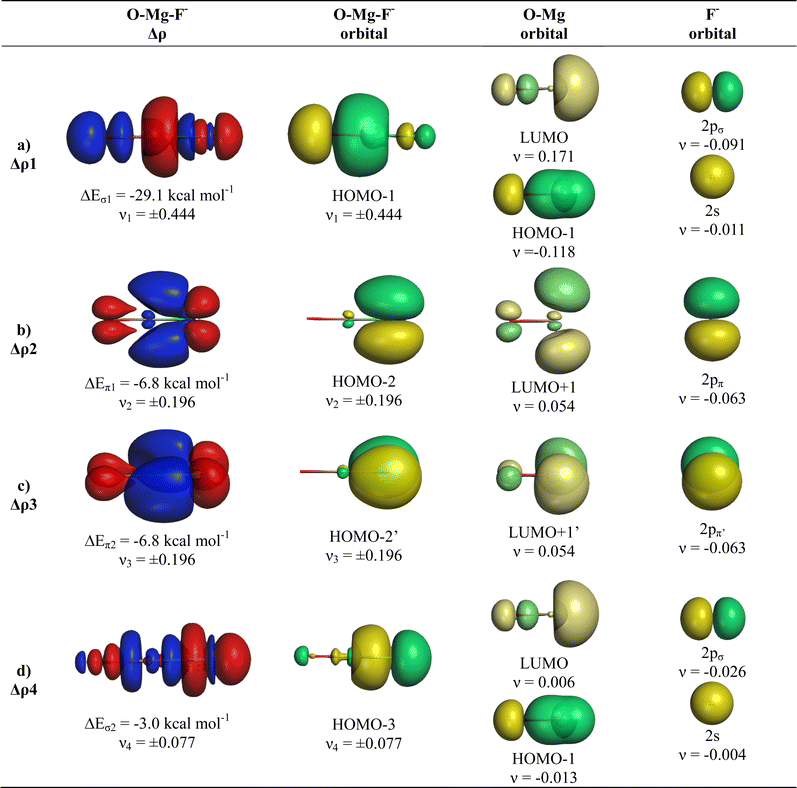
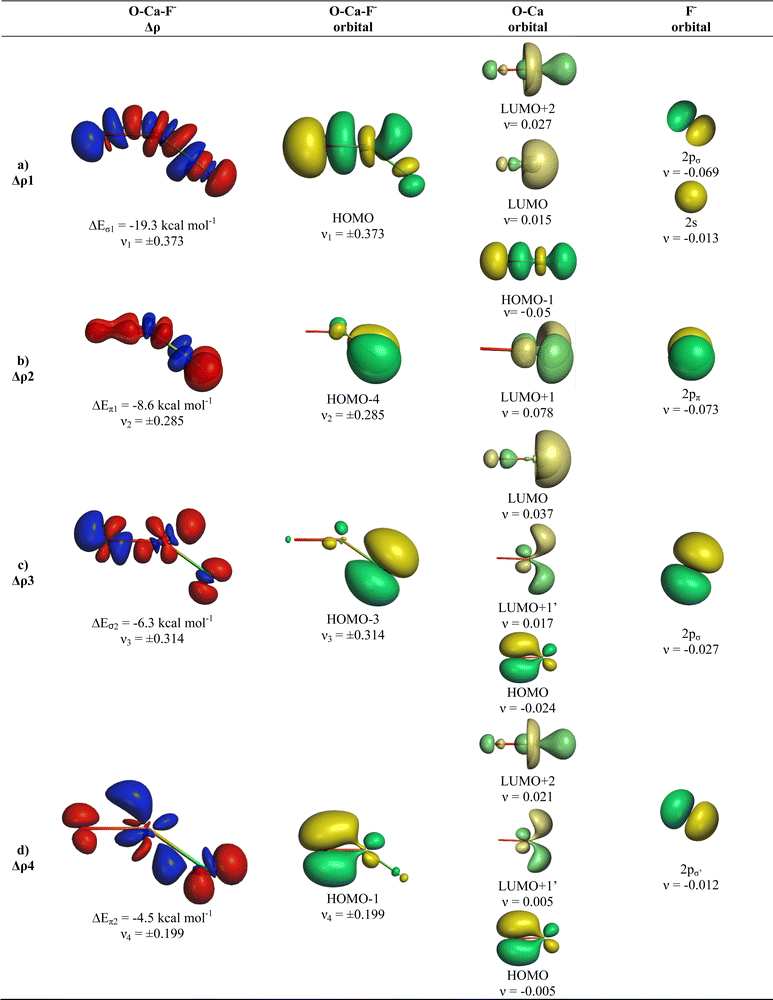
The breakdown of the total orbital term ΔEorb into pairwise contributions gives deep insight into the formation of the covalent bonds. There are four occupied AOs of F− which can serve as donor orbitals into the four vacant acceptor orbitals of AeO. For the lighter systems we found that there are indeed four pairwise contributions ΔEorb1 − ΔEorb4 which provide >90% to ΔEorb in the linear equilibrium structures of OAeF− (Ae = Be, Mg). Fig. 4 shows the deformation densities Δρ and the associated most important interacting MOs of OBeF−. The strongest orbital term ΔEorb1 comes from the σ donation OBe (LUMO) ← F− (2pσ,2s) with some further small mixing of OBe orbitals where the contribution of the fluorine 2s AO is small but important, because it allows a second albeit weak σ donation ΔEorb4 OBe (LUMO+2) ← F− (2pσ,2s). The stabilization due to the formation of the σ-bonding HOMO−1 of OBeF− comes from the bonding overlap of the 2pσ AO of F− with the small inside green area at Be atom of OBe, which is hidden by the diffuse shaped green area. It becomes visible by inspection of the HOMO−1 of OBeF− with different isodensity values, which are displayed in Fig. 5 along with the HOMO−1 of OMgF−. The figure shows on top the 3D surfaces of the orbital with an isovalue of 0.05e a.u.−3. Below are the contour line diagrams with different isovalues in the plane that contains the bond axis. The latter figure nicely shows the attractive interference of the fragment orbitals which lead to a stabilization of ΔEσ1 = 24.4 kcal mol−1 (OBeF−) and ΔEσ1 = 29.1 kcal mol−1 (OMgF−). A peculiar feature of the orbital mixing between the OAe and F− fragments is the sign reversal in the Ae–F region. There is a diffuse bonding region (red lines) away from the Be–F axis and a blue bonding region close to the axis. The latter blue region is even interrupted by the red region, which does not affect the overall positive interference (bonding interaction) of the orbitals.
The orbital interactions ΔEorb2 and ΔEorb3 are due to the degenerate π donation OBe (LUMO+1) ← F− (2pπ). Although the stabilization of ΔEorb4 in OBeF− is rather small, it contributes 9.3% to the covalent bonding and it builds up a different orbital (HOMO−3) than the σ interaction ΔEorb1 which leads to HOMO−1. The remaining orbital interactions ΔErest come from atomic polarization and O–Be interactions and they not relevant for the OBe–F− bond. The HOMO of OBeF− is a degenerate π orbital located mainly at oxygen atom which is only spuriously affected by the bonding interaction with F−. The five energetically highest lying orbitals of OBeF− along with those of the other OAeF− anions are shown in Fig. S1 of ESI.‡
It is amazing that four bonding orbitals between two main-group atoms of the first octal row elements can be formed. It was previously suggested that C2 has a quadruple bond,71–73 but this claim was disputed by several workers.74–78 As mentioned in the introduction, a quadruple bond was suggested for AeF− (Ae = Ca, Sr, Ba) because the heavier alkaline atoms use valence d-orbitals for covalent bonding. Although there are four bonding orbitals between OBe and F− we do not think that OBeF− has a genuine quadruple bond. One reason is that the OBe–F− bond comes mainly from electrostatic attraction. According to the EDA-NOCV results, only 25.7% of the bond comes from covalent (orbital) interaction. Another reason is the fact that the chemical bonds in OAeF− are delocalized over three atoms and that a localized description is not appropriate for depicting the bonding situation. We refer to the chemical bonds in OCBBCO, which has a linear structure where all atoms are bonded by triple bonds.79 The representation with a Lewis structure that has only triple bonds not only violates the octet rule, it also disregards the appearance of delocalized bonds. Bond delocalization over more than two atoms was not recognized by Gilbert Lewis and it limits the use of Lewis-type structures for describing chemical bonds.80
The deformation densities Δρ and the interacting MOs of OMgF− are very similar to those of OBeF− and they are displayed in Fig. 6. The shape of the HOMO−1 hides like the HOMO−1 of OBeF− the bonding character of the orbital. The bonding nature of the HOMO−1 becomes visible by the contour line diagrams shown in Fig. 5 where the isovalues of OMg–F− appear blue in the high-density areas. A close examination of the deformation density reveals the accumulation of electronic charge in the bonding region between Mg and F− with concomitant polarization at fluorine. The numerical results in Table 4 show that the energy contribution of the fourth bond ΔEorb4 provides only 6.3% of the total covalent bond, but the associated deformation density illustrates the accumulation of electronic charge in the OMg–F− bonding region, which is characteristic for a covalent interaction that comes from the interference of the wave functions.
The analysis of the bent equilibrium structures of OAeF− (Ae = Ca, Sr, Ba) is very interesting, because the heavier alkaline earth atoms use their (n)d functions as valence orbitals besides the (n)s orbitals in contrast to the lighter homologues which have (n)p valence orbitals. All three complexes have four pairwise orbital interactions ΔEorb1 − ΔEorb4 to the covalent OAe–F− bonding due to OAe ← F− charge donation like the linear structures of the lighter complexes, but the contribution of ΔEorb4 to the orbital interactions decreases from the calcium adduct (10.3%) to the barium complex where it is only 3.1% of ΔEorb (Table 4). Fig. 7 shows that the orbital interactions ΔEorb1, ΔEorb2 and ΔEorb4 in OCaF− come from donation of F− into vacant orbitals of CaO which involve mainly valence d AOs of Ca as acceptor orbitals. The LUMO+2 of CaO is mainly a Ca sdσ hybridized orbital whereas the degenerate LUMO+1/LUMO+1′ are sdπ hybridized orbitals. Since the molecule has a bent geometry there is only one genuine occupied π orbital (HOMO−4) whereas the other occupied valence orbitals that are formed by the interaction between CaO and F− (HOMO, HOMO−1, HOMO−3) are by definition σ orbitals. The shape of the HOMO−3 indicates that it can be considered as in-plane π interaction, although this is not a structurally correct assignment. The mixing of the HOMO of CaO in ΔEorb3 and ΔEorb4 indicates the concomitant polarization along with the bond formation due to the interference of the fragment wave functions. The five highest lying MOs of OCaF− are shown in Fig. S1 of ESI.‡
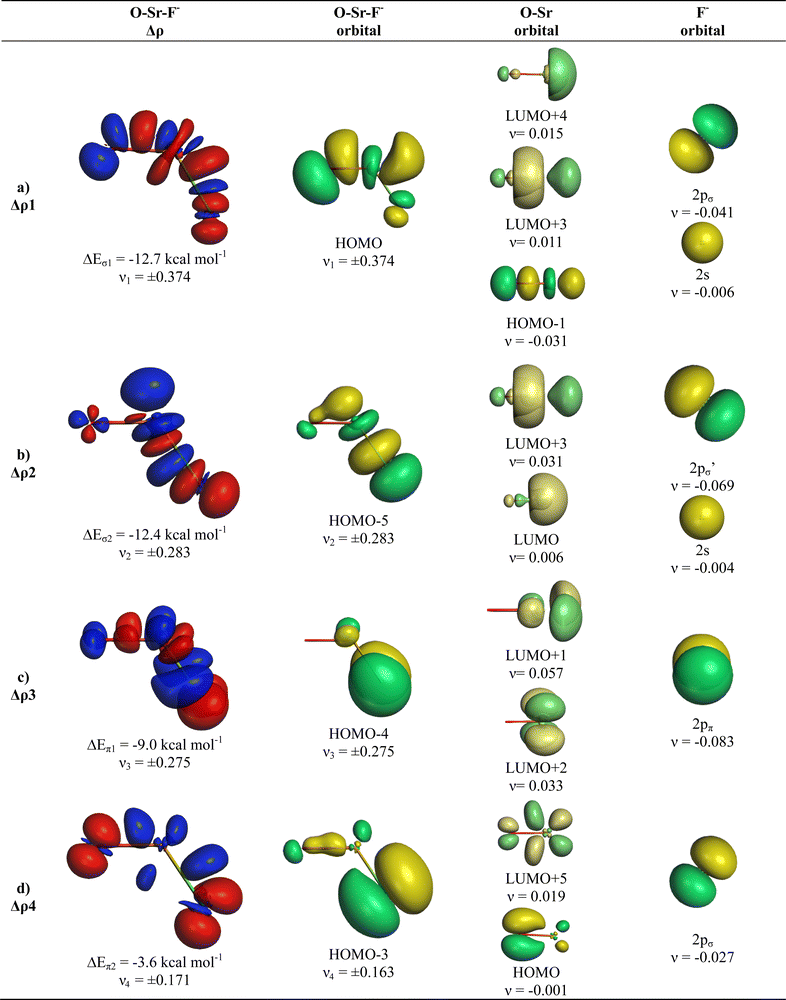
The deformation densities Δρ and the interacting MOs of OSrF− show interesting differences to those of OCaF− and are shown in Fig. 8. The π-orbital interaction ΔEorb2 and the in-plane pseudo-π interaction ΔEorb3 of OCaF− become ΔEorb3 and ΔEorb4 in OSrF−. The significantly stronger bending in OSrF− (123.0°) than in OCaF− (144.7°) enhances the second σ interaction in the former anion, which is ΔEorb4 in OCaF− and becomes the second strongest orbital term ΔEorb2 in OSrF−, which is only slightly weaker (−12.4 kcal mol−1) than ΔEorb1 (−12.7 kcal mol−1). Examination of the shape of the valence orbitals clearly shows that the d-AOs of Sr are the dominant acceptor orbitals of the metal.
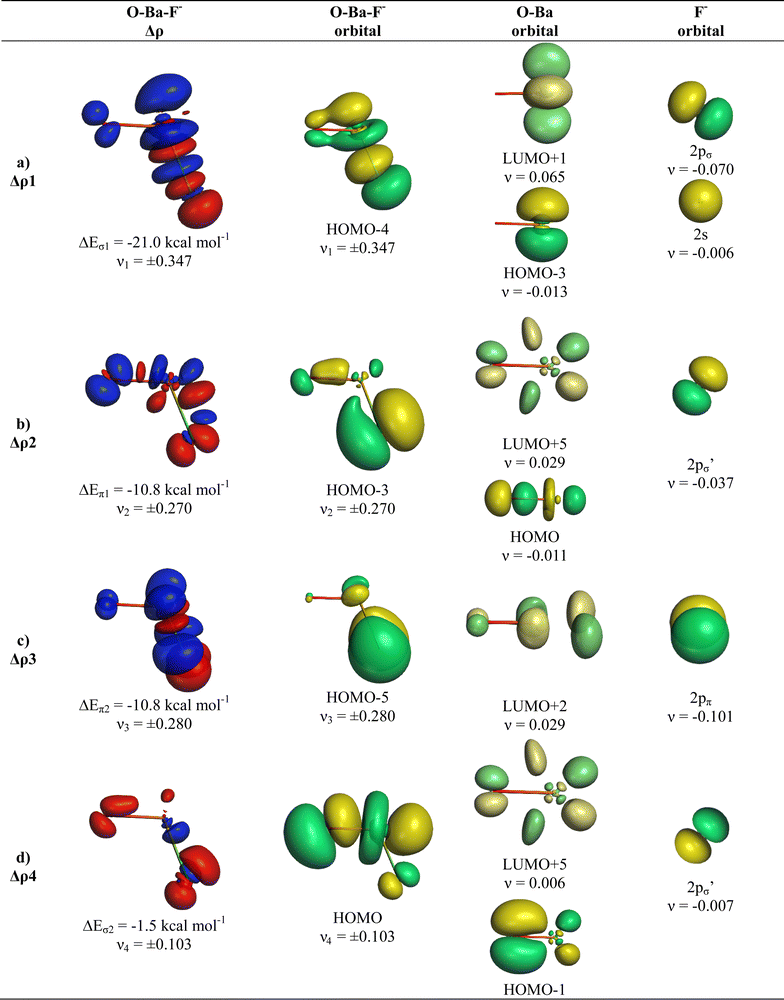
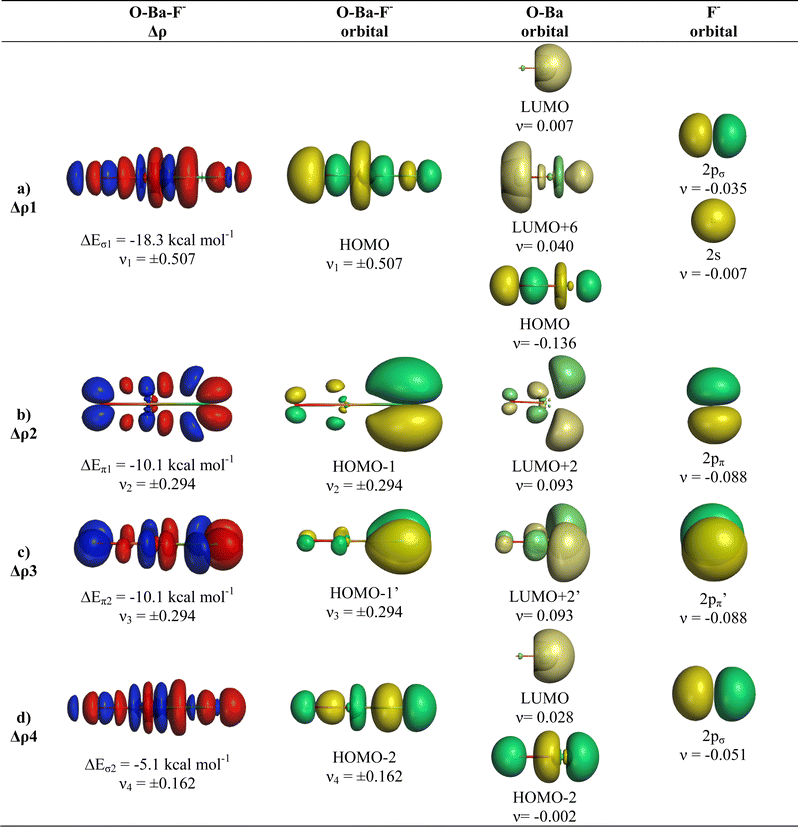
We analysed in OBaF− both using the linear structure and with the bent equilibrium geometry in order to identify the driving force for bending. Table 4 shows the numerical EDA-NOCV results for both structures. The bent equilibrium structure encounters stronger Pauli repulsion ΔEPauli than the linear form, but the total interaction energy ΔEint is clearly more attractive in the energy minimum form. This is mainly due to the larger Coulomb attraction ΔEelstat in the latter structure, which has a significantly shorter OBa–F− bond than the former. But the orbital (covalent) interactions in the bent form are also slightly stronger than in the linear form. Stronger orbital interactions in the bent structure are found for ΔEorb1 − ΔEorb3 but not for ΔEorb4, which has a negligible contribution in the equilibrium geometry. This makes the assignment of a quadruple bond between F− and BaO inappropriate. The same conclusion holds for the bent structures of the Ca and Sr homologues.
Fig. 9 and 10 show the deformation densities Δρ and the interacting MOs for ΔEorb1 − ΔEorb4 of the two structures. The orbitals of the acceptor fragment BaO suggest that the d-AOs are the most important acceptor orbitals of the metal. The strongest orbital interaction ΔEorb1 comes now from the donation of F− into the 5dπ AO and (with smaller contribution) 6pπ AOs of Ba, which underline the strong contribution of the (n − 1)d AOs for covalent bond particularly for Ba. Close examination of the deformation densities in the liner and bent structures reveals the appearance of local charge accumulation at barium in the region of lone-pair, which comes from the charge donation into vacant d-AOs of the metal. This is clearly visible in the strong orbital interactions ΔEorb1 − ΔEorb3. The results nicely agree with the finding of Kaupp et al. about the relevance of d-orbitals for the heavy alkaline earth atoms.52 The accumulation negative charge toward the lone-pair area but away from the bonding region explains why the bent structure is mainly stabilized by electrostatic (Coulomb) interaction than by stronger covalent bonding. The detailed bonding analysis suggests that the OAe–F− bonds have a higher electrostatic character than the Ae–F− bonds in the diatomic anions.1,2 The covalent contributions to the OAe–F− bonds come from dative interactions which have multiple-bond character, but the assignment of a quadruple bond like in the heavier AeF− anion with Ae = Ca, Sr, Ba is not reasonable. We suggest that the bonding situation is best described with a bond line O–AeF− for the electron-sharing bond and an arrow OAe ← F− for the dative bond where the line above Ae in the bent structures signals the accumulation of local charge in the lone-pair region, although the overall charge of Ae is positive (Fig. 11). The situation may be compared with CO, where the carbon atoms carries a positive partial charge but the chemical reactivity and the dipole moment are dominated by the local charge accumulation in the lone-pair region.
There is a common feature in the deformation densities associated with the orbital interactions ΔEorb1 and ΔEorb4 and the MOs of the AeO fragments. Fig. 4 and 6–10 show that an occupied orbital of AeO is involved in the dative interactions OAe ← F− which suggests that there is concomitant polarization in the diatomic moiety. The mode of action between OAe and F− involves a charge induced interaction of the F− ion on the OAe moiety, which in turn yields a favorable hybridization of the vacant orbitals of Ae overlapping with the occupied AOs of F− and leading to a stabilizing interference of the wave functions. This was already found in the diatomic anions AeF−, where the charge induction of F− leads to a polarization of the (n)s valence electrons of Ae and the formation of a vacant (n)sp(σ) AO. This is schematically shown in Fig. 12. A related mechanism is operative in OAeF−.
Are the OAe–F− bonds really dative bonds? The anion dissociates into the closed-shell species OAe and F−, but this does not necessarily indicate that the finally formed bond has dative character. For example, rupture of the carbon–carbon bond of many olefins like F2C![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) CF2 gives carbenes CF2 in the 1A1 singlet state but the double bond comes from the interaction between CF2 in the 3B1 triplet state.81 Likewise dissociate the NaBH3− Cluster into the closed-shell fragments Na− and BH3 but the Na–B bond is better described as electron-sharing interactions between Na and BH3− both in their doublet state.82 There is a curve crossing of the ΔEorb values along the fragmentation pathway when the two sets of fragments are used in the EDA-NOCV calculations, which indicates that the fragments that provide the best description for the chemical bond in the molecule have a different electronic state than the fully separated fragments after dissociation. It could be envisaged that the charge donation OAe ← F− at the equilibrium geometry leads to an electron-sharing interaction between OAe− anion and neutral F in the doublet states. We analysed the anions OAe–F− with the EDA-NOCV method using OAe− and neutral F as interacting fragments. The numerical results are shown in Table S1 of ESI.‡ The calculated values for the orbital interactions ΔEorb are for all species at the equilibrium geometry significantly larger than using closed-shell fragments OAe and F−. Since the final dissociation products are also OAe and F− it becomes obvious that there is no curve crossing of the ΔEorb, which clearly indicates that the OAe–F− bonds are really dative bonds. It has been shown in numerous previous studies using the EDA-NOCV method that the relative amount of ΔEorb is a useful indicator for the nature of the nature of the chemical bonds and for the best description of the interacting fragments.
CF2 gives carbenes CF2 in the 1A1 singlet state but the double bond comes from the interaction between CF2 in the 3B1 triplet state.81 Likewise dissociate the NaBH3− Cluster into the closed-shell fragments Na− and BH3 but the Na–B bond is better described as electron-sharing interactions between Na and BH3− both in their doublet state.82 There is a curve crossing of the ΔEorb values along the fragmentation pathway when the two sets of fragments are used in the EDA-NOCV calculations, which indicates that the fragments that provide the best description for the chemical bond in the molecule have a different electronic state than the fully separated fragments after dissociation. It could be envisaged that the charge donation OAe ← F− at the equilibrium geometry leads to an electron-sharing interaction between OAe− anion and neutral F in the doublet states. We analysed the anions OAe–F− with the EDA-NOCV method using OAe− and neutral F as interacting fragments. The numerical results are shown in Table S1 of ESI.‡ The calculated values for the orbital interactions ΔEorb are for all species at the equilibrium geometry significantly larger than using closed-shell fragments OAe and F−. Since the final dissociation products are also OAe and F− it becomes obvious that there is no curve crossing of the ΔEorb, which clearly indicates that the OAe–F− bonds are really dative bonds. It has been shown in numerous previous studies using the EDA-NOCV method that the relative amount of ΔEorb is a useful indicator for the nature of the nature of the chemical bonds and for the best description of the interacting fragments.
We have further investigated the nature of OAe–F− bonds with a completely different approach which is based on the electronic structures that come from the ab initio calculations at the DLPNO-CCSD(T)/def2-TZVP level using geometries optimized at CCSD(T)/TZVP. The numerical result of the local energy decomposition (LED) method43–45 are given in Table 5. The LED scheme breaks down the interaction energy between the fragments into different energy terms than the EDA-NOCV approach, but the main conclusion is the same. The electrostatic attraction ΔEHFelst is the dominant term of the attraction. The correlation interaction energy ΔECint mostly covers here the charge-transfer term, which can be interpreted as the instantaneous ion pair formation. The most important information comes from the direction of the charge transfer terms ΔECT which show that the dynamic charge transfer OAe ← F− completely dominates while the opposite stabilization is negligible. For the interpretation of the remaining terms we refer to the literature.43–45 They are not important for this study.
| [OBe]|[F−] | [OMg]|[F−] | [OCa]|[F−] | [OSr]|[F−] | [OBa]|[F−] | |
|---|---|---|---|---|---|
| ΔECint = ΔEC-SPCT(1→2) + ΔEC-SPCT(2→1) + ΔECdisp + ΔEC-WP + ΔEC-T | |||||
| ΔEint | −146.1 | −113.3 | −90.2 | −77.4 | −66.1 |
| ΔEel-prep | 176.0 | 173.0 | 130.7 | 122.9 | 96.7 |
| ΔEHFelst | −273.1 | −248.0 | −189.5 | −162.9 | −132.1 |
| ΔEHFexch | −10.5 | −9.9 | −11.1 | −13.7 | −11.3 |
| ΔECint | −38.6 | −28.5 | −20.2 | −23.7 | −19.3 |
| ΔEC-SPCT(1→2) | −0.3 | −0.2 | −0.8 | −1.6 | −1.4 |
| ΔEC-SPCT(2→1) | −38.3 | −30.3 | −22.1 | −21.3 | −16.9 |
| ΔECdisp | −1.5 | −0.9 | −1.4 | −2.0 | −1.7 |
| ΔEC-WP | −0.04 | −0.06 | −0.07 | −0.07 | −0.08 |
| ΔEC-T | 1.7 | 3.0 | 4.2 | 1.1 | 0.8 |
We want to comment on the finding of the EDA-NOCV approach and the LED method that the stabilizing interactions of the OAe–F− bonds comes mainly from electrostatic attraction, particularly in the lighter species where Ae = Be, Mg. This is sometimes referred as ionic contribution, which is misleading. Polar covalent bonds have a higher electrostatic character than nonpolar covalent bonds, because the accumulated charge in the bonding region is shifted towards the more electronegative atom where it encounters stronger nuclear attraction. It is a widespread misconception that the charge accumulation at the center of a bond is caused by the electrostatic attraction by two nuclei, which would be stronger than the attraction by only one nucleus. This is not correct, because the electrostatic attraction increases when the electronic charge moves closer to one nucleus and therefore, the contribution of the Coulomb attraction increases at polar bonds. It is the interference of the wave function which leads to a charge accumulation in the bonding region. This has been shown before in several theoretical studies83,84 and it was nicely demonstrated with a qualitative model by Rioux.85 The frequently used naming of ionic rather than electrostatic contribution comes from valence-bond (VB) calculation, which does not have a term for polar bonds. VB calculations give the electronic structure of a molecule with a mixture of two-center terms A–B which comprise the electron-sharing covalent term (λA − λB) (“Heitler–London (HL)” term) and the two ionic terms (λA|−λB+) and (λ+AλB|−) as well as the mixing of the terms.86 This is a mathematically valid approach, but the appearance of the ionic terms in the calculations must not be identified with ionic bonding. Ionic bonding is found in ionic solids and in solvents where the overlaps of the wave functions are negligible. Polar bonds in molecules are covalent bonds with higher electrostatic character but they are not ionic bonds. The widespread use of the VB model, which was strongly advocated by Pauling,87 led to the still frequent use of the term “ionic contribution” although quantum chemical calculations employ in most cases MO or DFT methods. For a more detailed discussion we refer to recent publications of the topic.68,80,88,89
The final question concerns the different trends of the BDE for Ae–F− and OAe–F−. We explained the increase of the bond strength in the diatomic anions AeF− from Ae![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) Mg to Ae
Mg to Ae![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) Ba with the availability of the (n − 1)d AOs of the heavier alkaline earth atoms as acceptor orbitals, which leads to a strengthening of the covalent interactions. It remains to explain why the diatomic oxides AeO show a decreasing order for the BDE when the Ae atoms become larger. Table 6 shows the electron affinities of Ae atoms and diatomic AeO. The experimentally known values for the atoms show that the heavier atoms have a slightly increasing trend for the heavier elements, whereas the trend of the oxides AeO has the opposite order. There is a clear decline of the electron affinity of AeO for the heavier Ae Atoms, which exhibits the same order as the BDE values of OAe–F−. Experimental values for the electron affinity of diatomic AeO are not available except for MgO.90 The measured value of 37.6 kcal mol−1 is in reasonable agreement with the calculated value of 30.0 kcal mol−1. We think that the trend of the calculated electron affinities in Table 6 is reliable. The data suggest that the Lewis acidity of AeO continuously decreases for the heavier atoms Ae whereas the acceptor ability of the atom Ae increases from Mg to Ba.
Ba with the availability of the (n − 1)d AOs of the heavier alkaline earth atoms as acceptor orbitals, which leads to a strengthening of the covalent interactions. It remains to explain why the diatomic oxides AeO show a decreasing order for the BDE when the Ae atoms become larger. Table 6 shows the electron affinities of Ae atoms and diatomic AeO. The experimentally known values for the atoms show that the heavier atoms have a slightly increasing trend for the heavier elements, whereas the trend of the oxides AeO has the opposite order. There is a clear decline of the electron affinity of AeO for the heavier Ae Atoms, which exhibits the same order as the BDE values of OAe–F−. Experimental values for the electron affinity of diatomic AeO are not available except for MgO.90 The measured value of 37.6 kcal mol−1 is in reasonable agreement with the calculated value of 30.0 kcal mol−1. We think that the trend of the calculated electron affinities in Table 6 is reliable. The data suggest that the Lewis acidity of AeO continuously decreases for the heavier atoms Ae whereas the acceptor ability of the atom Ae increases from Mg to Ba.
Summary and conclusion
The results of this work are summarized as follows:• The equilibrium structures of the anions OAeF− have linear geometries for Ae = Be and Mg but they are strongly bent for Ae = Sr and Ba. The calcium species is calculated at the CCSD(T)/def2-TZVPP level to have a linear geometry but at BP86/def2-TZVPP is has bending angle of 144.7° which is 0.5 kcal mol−1 below the linear form. The bending potential of the strontium and barium anions is rather low (<10 kcal mol−1).
• The calculated bond dissociation energies of the OAe–F− bonds suggest a record-high BDE of De = 144.8 kcal mol−1 for OBeF− at the CCSD(T)/def2-TZVPP level, which is the strongest BDE for a dative bond that has been found so far. The BDE of the heavier homologues have a continuously decreasing order for Ae with Be > Mg (113.1 kcal mol−1) > Ca (84.6 kcal mol−1) > Sr (72.6 kcal mol−1) > Ba (60.0 kcal mol−1).
• The calculations suggest that the Ae–O distances in the anions OAeF− become a bit longer than in diatomic AeO. However, the Ae–O stretching mode of OBeF− and OMgF− is predicted at both levels of theory to have a blue shift towards higher wave numbers whereas the heavier homologues OCaF−, OSrF− and OBaF− have a red shift for the Ae–O mode. The calculated Ae–O frequency shifts and the Ae–F stretching vibration are a guideline for the hitherto unknown anions OAeF−.
• The calculation of the charge distribution reveals a significant charge donation OAe ← F− with decreasing order for the heavier atoms Ae using the Hirshfeld, Voronoi and CM5 methods. In contrast, the NBO method suggests only negligible charge donation, which comes from the fact that only the (n)s but not the (n)p AOs of atoms Ae are treated as valence orbitals.
• The oxygen atom in OAeF− carries always a higher partial charge than the fluorine atom. This is suggested by all charge partitioning methods and by the molecular electrostatic map. The charge distribution contradicts the standard electronegativities of the atoms which assign fluorine to be more electronegative than oxygen. The surprising partial charges are explained with the bonding situation of the atoms in the actual electronic structure, which may lead to uncommon partial charges.
• The bonding analysis of the OAe–F− bonds using the EDA-NOCV method shows that the bonds have a much higher electrostatic character than the Ae–F− bonds in the diatomic anions. The dative interactions have three major and one minor component. The assignment of a quadruple bond for the heavier species with Ae = Ca, Sr, Ba is not reasonable. The driving force for the bent geometries is the accumulation of electronic charge in the lone-pair region at the Ae atoms, which enhances the electrostatic attraction with the other atoms. A reasonable description of the bonding situation is given by the formula O−−Ae+ ← F−.
Note added in proof
The statement about the strongest dative bond refers to atoms heavier than hydrogen and helium. Proton affinities are dative bonds which can be much stronger than calculated in this work.92Data availability
The data supporting this article have been included as part of the ESI.‡Conflicts of interest
The authors declare no conflict of interest.Acknowledgements
L. Z. and G. F. acknowledge the financial support from Nanjing Tech University (no. 39837123, 39837132 and the International Cooperation fund), the National Natural Science Foundation of China (no. 22373050), Natural Science Foundation of the Jiangsu province (no. BK20211587), and the State Key Laboratory of Materials-Oriented Chemical Engineering (no. SKL-MCE-23A06), and the Postgraduate Research & Practice Innovation Program of Jiangsu Province (KYCX23_1404). L. Q. and L. Z appreciate the Supported by Cultivation Program for The Excellent Doctoral Dissertation of Nanjing Tech University (2024-10). We appreciate the high performance center of Nanjing Tech University for supporting the computational resources. We also thank the PL-Grid Infrastructure and the Academic Computational Centre Cyfronet of the University of Science and Technology in Krakow for providing computational resources. GF is grateful to Holger Bettinger for pointing out the strength of proton affinities.References
- R. Liu, L. Qin, Z. Zhang, L. Zhao, F. Sagan, M. Mitoraj and G. Frenking, Genuine quadruple bonds between two main-group atoms. Chemical bonding in AeF− (Ae = Be–Ba) and isoelectronic EF (E = B–Tl) and the particular role of d orbitals in covalent interactions of heavier alkaline-earth atoms, Chem. Sci., 2023, 14, 4872–4887 RSC.
- L. Qin, Y.-Q. Liu, R. Liu, X. Yang, Z.-H. Cui, L. Zhao, S. Pan, S. Fau and G. Frenking, Analysis of the Unusual Chemical Bonds and Dipole Moments of AeF− (Ae = Be−Ba): A Lesson in Covalent Bonding, Chem. – Eur. J., 2024, e202304136 CrossRef CAS PubMed.
- The term “covalent” was suggested by Irving Langmuir in 1921 (Ref. 4) as expression for the two-electron bond introduced in 1921 by Gilbert Lewis (Ref. 5). There are two types of two-electron covalent bonds. One type is the electron-sharing bond A-B where both atoms contribute one electron each to the bond. The other type of covalent electron-pair bond is the dative bond A → B where both electrons are provided by one atom A. The two types of electron pair bonds were already distinguished by Lewis and the donor and acceptor fragments of a dative bond A → B are often referred to as Lewis aced and Lewis base. The symbol of an arrow → for a dative bond was introduced by Sidgwick: N. V. Sidgwick, Structure of Divalent Carbon Compounds, Chem. Rev., 1931, 9, 77–88 CrossRef CAS.
- I. Langmuir, Types of Valence, Science, 1921, 54, 59–67 CrossRef CAS PubMed.
- G. N. Lewis, The Atom and the Molecule, J. Am. Chem. Soc., 1916, 38, 762–785 CrossRef CAS.
- W. Koch, J. R. Collins and G. Frenking, Are there neutral helium compounds which are stable in their ground state? a theoretical investigation of HeBCH and HeBeO, Chem. Phys. Lett., 1986, 132, 330–333 CrossRef CAS.
- W. Koch, G. Frenking, J. Gauss, D. Cremer and J. R. Collins, Helium chemistry: theoretical predictions and experimental challenge, J. Am. Chem. Soc., 1987, 109, 5917–5934 CrossRef CAS.
- G. Frenking, W. Koch, J. Gauss and D. Cremer, Stabilities and nature of the attractive interactions in HeBeO, NeBeO, and ArBeO and a comparison with analogs NGLiF, NGBN, and NGLiH (NG = He, Ar). A theoretical investigation, J. Am. Chem. Soc., 1988, 110, 8007–8016 CrossRef CAS.
- G. Frenking, W. Koch and J. R. Collins, Fixation of nitrogen and carbon monoxide by beryllium oxide: theoretical investigation of the structures and stabilities of NNBeO, OCBeO, and COBeO, J. Chem. Soc., Chem. Commun., 1988, 1147–1148 RSC.
- G. D. Purvis, III and R. J. Bartlett, A full coupled-cluster singles and doubles model: the inclusion of disconnected triples, J. Chem. Phys., 1982, 76, 1910–1918 CrossRef.
- A. D. Becke, Density-functional exchange-energy approximation with correct asymptotic behavior, Phys. Rev. A: At., Mol., Opt. Phys., 1988, 38, 3098–3100 CrossRef CAS PubMed.
- J. P. Perdew, Density-functional approximation for the correlation energy of the inhomogeneous electron gas, Phys. Rev. B: Condens. Matter Mater. Phys., 1986, 33, 8822–8824 CrossRef PubMed.
- F. Weigend and R. Ahlrichs, Balanced basis sets of split valence, triple zeta valence and quadruple zeta valence quality for H to Rn: design and assessment of accuracy, Phys. Chem. Chem. Phys., 2005, 7, 3297–3305 RSC.
- M. J. Frisch, G. W. Trucks, H. B. Schlegel, G. E. Scuseria, M. A. Robb, J. R. Cheeseman, G. Scalmani, V. Barone, G. A. Petersson, H. Nakatsuji, X. Li, M. Caricato, A. V. Marenich, J. Bloino, B. G. Janesko, R. Gomperts, B. Mennucci, H. P. Hratchian, J. V. Ortiz, A. F. Izmaylov, J. L. Sonnenberg, D. Williams-Young, F. Ding, F. Lipparini, F. Egidi, J. Goings, B. Peng, A. Petrone, T. Henderson, D. Ranasinghe, V. G. Zakrzewski, J. Gao, N. Rega, G. Zheng, W. Liang, M. Hada, M. Ehara, K. Toyota, R. Fukuda, J. Hasegawa, M. Ishida, T. Nakajima, Y. Honda, O. Kitao, H. Nakai, T. Vreven, K. Throssell, J. A. Montgomery, Jr., J. E. Peralta, F. Ogliaro, M. J. Bearpark, J. J. Heyd, E. N. Brothers, K. N. Kudin, V. N. Staroverov, T. A. Keith, R. Kobayashi, J. Normand, K. Raghavachari, A. P. Rendell, J. C. Burant, S. S. Iyengar, J. Tomasi, M. Cossi, J. M. Millam, M. Klene, C. Adamo, R. Cammi, J. W. Ochterski, R. L. Martin, K. Morokuma, O. Farkas, J. B. Foresman and D. J. Fox, Gaussian 16 Rev. C.01, 2016 Search PubMed.
- E. D. Glendening, C. R. Landis and F. Weinhold, NBO 7.0: new vistas in localized and delocalized chemical bonding theory, J. Comput. Chem., 2019, 40, 2234–2241 CrossRef CAS PubMed.
- F. L. Hirshfeld, Bonded-atom fragments for describing molecular charge densities, Theor. Chim. Acta, 1977, 44, 129–138 CrossRef CAS.
- A. V. Marenich, S. V. Jerome, C. J. Cramer and D. G. Truhlar, Charge Model 5: An Extension of Hirshfeld Population Analysis for the Accurate Description of Molecular Interactions in Gaseous and Condensed Phases, J. Chem. Theory Comput., 2012, 8, 527–541 CrossRef CAS PubMed.
- C. Fonseca Guerra, J.-W. Handgraaf, E. J. Baerends and F. M. Bickelhaupt, Voronoi deformation density (VDD) charges: assessment of the Mulliken, Bader, Hirshfeld, Weinhold, and VDD methods for charge analysis, J. Comput. Chem., 2004, 25, 189–210 CrossRef PubMed.
- I. Mayer, Charge, bond order and valence in the AB initio SCF theory, Chem. Phys. Lett., 1983, 97, 270–274 CrossRef CAS.
- T. Lu and F. Chen, Multiwfn: a multifunctional wavefunction analyzer, J. Comput. Chem., 2012, 33, 580–592 CrossRef CAS PubMed.
- K. Morokuma, Molecular Orbital Studies of Hydrogen Bonds. III. C
![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) O⋯H–O Hydrogen Bond in H2CO⋯H2O and H2CO⋯2H2O, J. Chem. Phys., 2003, 55, 1236–1244 CrossRef.
O⋯H–O Hydrogen Bond in H2CO⋯H2O and H2CO⋯2H2O, J. Chem. Phys., 2003, 55, 1236–1244 CrossRef. - T. Ziegler and A. Rauk, On the calculation of bonding energies by the Hartree Fock Slater method, Theor. Chim. Acta, 1977, 46, 1–10 CrossRef CAS.
- M. Mitoraj and A. Michalak, Donor–Acceptor Properties of Ligands from the Natural Orbitals for Chemical Valence, Organometallics, 2007, 26, 6576–6580 CrossRef CAS.
- M. Mitoraj and A. Michalak, Applications of natural orbitals for chemical valence in a description of bonding in conjugated molecules, J. Mol. Model., 2008, 14, 681–687 CrossRef CAS PubMed.
- A. Michalak, M. Mitoraj and T. Ziegler, Bond Orbitals from Chemical Valence Theory, J. Phys. Chem. A, 2008, 112, 1933–1939 CrossRef CAS PubMed.
- M. P. Mitoraj, A. Michalak and T. Ziegler, A Combined Charge and Energy Decomposition Scheme for Bond Analysis, J. Chem. Theory Comput., 2009, 5, 962–975 CrossRef CAS PubMed.
- G. te Velde, F. M. Bickelhaupt, E. J. Baerends, C. Fonseca Guerra, S. J. A. van Gisbergen, J. G. Snijders and T. Ziegler, Chemistry with ADF, J. Comput. Chem., 2001, 22, 931–967 CrossRef CAS.
- E. J. Baerends, T. Ziegler, A. J. Atkins, J. Autschbach, O. Baseggio, D. Bashford, A. Bérces, F. M. Bickelhaupt, C. Bo, P. M. Boerrigter, C. Cappelli, L. Cavallo, C. Daul, D. P. Chong, D. V. Chulhai, L. Deng, R. M. Dickson, J. M. Dieterich, F. Egidi, D. E. Ellis, M. van Faassen, L. Fan, T. H. Fischer, A. Förster, C. Fonseca Guerra, M. Franchini, A. Ghysels, A. Giammona, S. J. A. van Gisbergen, A. Goez, A. W. Götz, J. A. Groeneveld, O. V. Gritsenko, M. Grüning, S. Gusarov, F. E. Harris, P. van den Hoek, Z. Hu, C. R. Jacob, H. Jacobsen, L. Jensen, L. Joubert, J. W. Kaminski, G. van Kessel, C. König, F. Kootstra, A. Kovalenko, M. V. Krykunov, P. Lafiosca, E. van Lenthe, D. A. McCormack, M. Medves, A. Michalak, M. Mitoraj, S. M. Morton, J. Neugebauer, V. P. Nicu, L. Noodleman, V. P. Osinga, S. Patchkovskii, M. Pavanello, C. A. Peeples, P. H. T. Philipsen, D. Post, C. C. Pye, H. Ramanantoanina, P. Ramos, W. Ravenek, M. Reimann, J. I. Rodríguez, P. Ros, R. Rüger, P. R. T. Schipper, D. Schlüns, H. van Schoot, G. Schreckenbach, J. S. Seldenthuis, M. Seth, J. G. Snijders, M. Solá, M. Stener, M. Swart, D. Swerhone, V. Tognetti, G. te Velde, P. Vernooijs, L. Versluis, L. Visscher, O. Visser, F. Wang, T. A. Wesolowski, E. M. van Wezenbeek, G. Wiesenekker, S. K. Wolff, T. K. Woo and A. L. Yakovlev, ADF, SCM, Theoretical Chemistry, Vrije Universiteit, Amsterdam, The Netherlands, 2019, https://www.scm.com Search PubMed.
- S. Grimme, J. Antony, S. Ehrlich and H. Krieg, A consistent and accurate ab initio parametrization of density functional dispersion correction (DFT-D) for the 94 elements H-Pu, J. Chem. Phys., 2010, 132, 154104 CrossRef PubMed.
- E. Van Lenthe and E. J. Baerends, Optimized Slater-type basis sets for the elements 1–118, J. Comput. Chem., 2003, 24, 1142–1156 CrossRef CAS PubMed.
- J. C. Slater, in Adv. Quantum Chem., ed. P.-O. Löwdin, Academic Press, 1972, vol. 6, pp. 1–92 Search PubMed.
- D. M. Andrada and C. Foroutan-Nejad, Energy components in energy decomposition analysis (EDA) are path functions; why does it matter?, Phys. Chem. Chem. Phys., 2020, 22, 22459–22464 RSC.
- M. Solà, M. Duran and J. Poater, The energy components of the extended transition state energy decomposition analysis are path functions: the case of water tetramer, Theor. Chem. Acc., 2021, 140, 33 Search PubMed.
- J. Poater, D. M. Andrada, M. Solà and C. Foroutan-Nejad, Path-dependency of energy decomposition analysis & the elusive nature of bonding, Phys. Chem. Chem. Phys., 2022, 24, 2344–2348 RSC.
- F. M. Bickelhaupt, C. Fonseca Guerra, M. Mitoraj, F. Sagan, A. Michalak, S. Pan and G. Frenking, Clarifying notes on the bonding analysis adopted by the energy decomposition analysis, Phys. Chem. Chem. Phys., 2022, 24, 15726–15735 RSC.
- L. Zhao, M. von Hopffgarten, D. M. Andrada and G. Frenking, Energy decomposition analysis, Wiley Interdiscip. Rev.: Comput. Mol. Sci., 2018, 8, e1345 Search PubMed.
- G. Frenking and F. Matthias Bickelhaupt, The Chemical Bond, 2014, pp. 121–157 Search PubMed.
- L. Zhao, M. Hermann, N. Holzmann and G. Frenking, Dative bonding in main group compounds, Coord. Chem. Rev., 2017, 344, 163–204 CrossRef CAS.
- L. Zhao, M. Hermann, W. H. E. Schwarz and G. Frenking, The Lewis electron-pair bonding model: modern energy decomposition analysis, Nat. Rev. Chem., 2019, 3, 48–63 CrossRef CAS.
- L. Zhao, S. Pan and G. Frenking, in Comprehensive Computational Chemistry, ed. M. Yáñez and R. J. Boyd, Elsevier, Oxford, 1st edn, 2024, pp. 322–361 Search PubMed.
- G. Frenking, R. Tonner, S. Klein, N. Takagi, T. Shimizu, A. Krapp, K. K. Pandey and P. Parameswaran, New bonding modes of carbon and heavier group 14 atoms Si–Pb, Chem. Soc. Rev., 2014, 43, 5106–5139 RSC.
- G. Frenking, M. Hermann, D. M. Andrada and N. Holzmann, Donor–acceptor bonding in novel low-coordinated compounds of boron and group-14 atoms C–Sn, Chem. Soc. Rev., 2016, 45, 1129–1144 RSC.
- A. Altun, M. Saitow, F. Neese and G. Bistoni, Local Energy Decomposition of Open-Shell Molecular Systems in the Domain-Based Local Pair Natural Orbital Coupled Cluster Framework, J. Chem. Theory Comput., 2019, 15, 1616–1632 CrossRef CAS PubMed.
- A. Altun, R. Izsák and G. Bistoni, Local energy decomposition of coupled-cluster interaction energies: interpretation, benchmarks, and comparison with symmetry-adapted perturbation theory, Int. J. Quantum Chem., 2021, 121, e26339 CrossRef CAS.
- W. B. Schneider, G. Bistoni, M. Sparta, M. Saitow, C. Riplinger, A. A. Auer and F. Neese, Decomposition of Intermolecular Interaction Energies within the Local Pair Natural Orbital Coupled Cluster Framework, J. Chem. Theory Comput., 2016, 12, 4778–4792 CrossRef CAS PubMed.
- S. Saebo and P. Pulay, Local Treatment of Electron Correlation, Annu. Rev. Phys. Chem., 1993, 44, 213–236 CrossRef CAS.
- F. Neese, F. Wennmohs and A. Hansen, Efficient and accurate local approximations to coupled-electron pair approaches: an attempt to revive the pair natural orbital method, J. Chem. Phys., 2009, 130, 114108 CrossRef PubMed.
- F. Neese, A. Hansen and D. G. Liakos, Efficient and accurate approximations to the local coupled cluster singles doubles method using a truncated pair natural orbital basis, J. Chem. Phys., 2009, 131, 064103 CrossRef PubMed.
- Y. Guo, C. Riplinger, U. Becker, D. G. Liakos, Y. Minenkov, L. Cavallo and F. Neese, Communication: an improved linear scaling perturbative triples correction for the domain based local pair-natural orbital based singles and doubles coupled cluster method [DLPNO-CCSD(T)], J. Chem. Phys., 2018, 148, 011101 CrossRef PubMed.
- C. Riplinger, B. Sandhoefer, A. Hansen and F. Neese, Natural triple excitations in local coupled cluster calculations with pair natural orbitals, J. Chem. Phys., 2013, 139, 134101 CrossRef PubMed.
- G. H. K. P. Huber, Molecular Spectra and Molecular Structure, Media, New York, 1979 Search PubMed.
- M. Kaupp, P. V. R. Schleyer, H. Stoll and H. Preuss, The question of bending of the alkaline earth dihalides MX2 (M = beryllium, magnesium, calcium, strontium, barium; X = fluorine, chlorine, bromine, iodine). An ab initio pseudopotential study, J. Am. Chem. Soc., 1991,(113), 6012–6020 CrossRef CAS.
- M. Hargittai, The molecular geometry of gas-phase metal halides, Coord. Chem. Rev., 1988, 91, 35–88 CrossRef CAS.
- The calculated Ae–F bond lengths [Å] in AeF− at CCSD(T)/def2-TZVPP [BP86/def2-TZVPP] reported in ref. 1 are 1.429 [1.428] for BeF−, 1.840 [1.847) for MgF−, 2.104 [1.992] for CaF−, 2.237 [2.134] for SrF, 2.339 [2.234] for BaF−.
- Computational Chemistry Comparison and Benchmark Data Base Release 22. Standard Reference Database 101, National Institute of Standards and Technology, 2022 Search PubMed.
- J. S. Murray and P. Politzer, Molecular electrostatic potentials and noncovalent interactions, Wiley Interdiscip. Rev.: Comput. Mol. Sci., 2017, 7, e1326 Search PubMed.
- R. Tonner, F. Öxler, B. Neumüller, W. Petz and G. Frenking, Carbodiphosphoranes: The Chemistry of Divalent Carbon(0), Angew. Chem., Int. Ed., 2006, 45, 8038–8042 CrossRef CAS PubMed.
- R. Tonner and G. Frenking, C(NHC)2: Divalent Carbon(0) Compounds with N-Heterocyclic Carbene Ligands—Theoretical Evidence for a Class of Molecules with Promising Chemical Properties, Angew. Chem., Int. Ed., 2007, 46, 8695–8698 CrossRef CAS PubMed.
- R. Tonner and G. Frenking, Divalent Carbon(0) Chemistry, Part 1: Parent Compounds, Chem. – Eur. J., 2008, 14, 3260–3272 CrossRef CAS PubMed.
- R. Tonner and G. Frenking, Divalent Carbon(0) Chemistry, Part 2: Protonation and Complexes with Main Group and Transition Metal Lewis Acids, Chem. – Eur. J., 2008, 14, 3273–3289 CrossRef CAS PubMed.
- S. Klein, R. Tonner and G. Frenking, Carbodicarbenes and Related Divalent Carbon(0) Compounds, Chem. – Eur. J., 2010, 16, 10160–10170 CrossRef CAS PubMed.
- J. Hinze, The concept of electronegativity of atoms in molecules, Theor. Comput. Chem., 1999, 6, 189–212 Search PubMed.
- D. Bergmann and J. Hinze, Electronegativity and Molecular Properties, Angew. Chem., Int. Ed. Engl., 1996, 35, 150–163 CrossRef CAS.
- K. B. Wiberg, Application of the pople-santry-segal CNDO method to the cyclopropylcarbinyl and cyclobutyl cation and to bicyclobutane, Tetrahedron, 1968, 24, 1083–1096 CrossRef CAS.
- I. Mayer, Bond order and valence: Relations to Mulliken's population analysis, Int. J. Quantum Chem., 1984, 26, 151–154 CrossRef CAS.
- A. J. Bridgeman, G. Cavigliasso, L. R. Ireland and J. Rothery, The Mayer bond order as a tool in inorganic chemistry, J. Chem. Soc., Dalton Trans., 2001, 2095–2108 RSC.
- I. Mayer, Bond order and valence indices: a personal account, J. Comput. Chem., 2007, 28, 204–221 CrossRef CAS PubMed.
- L. Zhao, S. Pan and G. Frenking, The nature of the polar covalent bond, J. Chem. Phys., 2022, 157, 034105 CrossRef CAS PubMed.
- K. Fukui, Theory of Orientation and Stereoselection, Springer Verlag, Berlin, 1975 Search PubMed.
- R. B. Woodward and R. Hoffmann, The Conservation of Orbital Symmetry, Verlag Chemie, Weinheim, 1970 Search PubMed.
- S. Shaik, D. Danovich, W. Wu, P. Su, H. S. Rzepa and P. C. Hiberty, Quadruple bonding in C2 and analogous eight-valence electron species, Nat. Chem., 2012, 4, 195–200 CrossRef CAS PubMed.
- D. Danovich, P. C. Hiberty, W. Wu, H. S. Rzepa and S. Shaik, The Nature of the Fourth Bond in the Ground State of C2: The Quadruple Bond Conundrum, Chem. – Eur. J., 2014, 20, 6220–6232 CrossRef CAS PubMed.
- S. Shaik, D. Danovich, B. Braida and P. C. Hiberty, The Quadruple Bonding in C2 Reproduces the Properties of the Molecule, Chem. – Eur. J., 2016, 22, 4116–4128 CrossRef CAS PubMed.
- W. Zou and D. Cremer, C2 in a Box: Determining Its Intrinsic Bond Strength for the X1Σ+g Ground State, Chem. – Eur. J., 2016, 22, 4087–4099 CrossRef CAS PubMed.
- M. Hermann and G. Frenking, The Chemical Bond in C2, Chem. – Eur. J., 2016, 22, 4100–4108 CrossRef CAS PubMed.
- M. Piris, X. Lopez and J. M. Ugalde, The Bond Order of C2 from a Strictly N-Representable Natural Orbital Energy Functional Perspective, Chem. – Eur. J., 2016, 22, 4109–4115 CrossRef CAS PubMed.
- D. L. Cooper, R. Ponec and M. Kohout, New insights from domain-averaged Fermi holes and bond order analysis into the bonding conundrum in C2, Mol. Phys., 2016, 114, 1270–1284 CrossRef CAS.
- D. W. O. de Sousa and M. A. C. Nascimento, Is There a Quadruple Bond in C2?, J. Chem. Theory Comput., 2016, 12, 2234–2241 CrossRef CAS PubMed.
- L. C. Ducati, N. Takagi and G. Frenking, Molecules with All Triple Bonds: OCBBCO, N2BBN2, and [OBBBBO]2−, J. Phys. Chem. A, 2009, 113, 11693–11698 CrossRef CAS PubMed.
- L. Zhao, W. H. E. Schwarz and G. Frenking, The Lewis electron-pair bonding model: the physical background, one century later, Nat. Rev. Chem., 2019, 3, 35–47 CrossRef.
- D. M. Andrada, J. L. Casals-Sainz, Á. Martín Pendás and G. Frenking, Dative and Electron-Sharing Bonding in C2F4, Chem. – Eur. J., 2018, 24, 9083–9089 CrossRef CAS PubMed.
- S. Pan and G. Frenking, Comment on “Realization of Lewis Basic Sodium Anion in the NaBH3− Cluster”, Angew. Chem., Int. Ed., 2020, 59, 8756–8759 CrossRef CAS PubMed.
- K. Ruedenberg, The Physical Nature of the Chemical Bond, Rev. Mod. Phys., 1962, 34, 326–376 CrossRef CAS.
- W. Kutzelnigg, The Physical Mechanism of the Chemical Bond, Angew. Chem., Int. Ed. Engl., 1973, 12, 546–562 CrossRef.
- F. Rioux, The Covalent Bond Examined Using the Virial Theorem, Chem. Educ., 2003, 8, 101 Search PubMed.
- S. Shaik and P. C. Hiberty, A Chemist's Guide to Valence Bond Theory, 2007, pp. 40–80 Search PubMed.
- L. Pauling, The Nature of the Chemical Bond, Cornell University Press, 1960 Search PubMed.
- S. Pan and G. Frenking, A Critical Look at Linus Pauling's Influence on the Understanding of Chemical Bonding, Molecules, 2021, 26, 4695 CrossRef CAS PubMed.
- G. Frenking, Heretical thoughts about the present understanding and description of the chemical bond*, Mol. Phys., 2022, 121, e2110168 CrossRef.
- J. H. Kim, X. Li, L.-S. Wang, H. L. de Clercq, C. A. Fancher, O. C. Thomas and K. H. Bowen, Vibrationally Resolved Photoelectron Spectroscopy of MgO- and ZnO- and the Low-Lying Electronic States of MgO, MgO-, and ZnO, J. Phys. Chem. A, 2001, 105, 5709–5718 CrossRef CAS.
- J. C. Wheeler, Electron Affinities of the Alkaline Earth Metals and the Sign Convention for Electron Affinity, J. Chem. Educ., 1997, 74, 123 CrossRef CAS.
- R. Tonner, G. Heydenrych and G. Frenking, First and Second Proton Affinities of Carbon Bases, Chem. Phys. Chem., 2008, 9, 1474 CrossRef CAS PubMed.
Footnotes |
| † This paper is dedicated to Prof. Manfred Reetz on the occasion of his 80th birthday. |
| ‡ Electronic supplementary information (ESI) available. See DOI: https://doi.org/10.1039/d4cp01909a |
| § L. Q., R. L. and F. S. contributed equally. |
| This journal is © the Owner Societies 2024 |