Vibrational circular dichroism spectra of proline in water at different pH values

Abstract

Recording VCD spectra of aqueous solution poses a particular challenge as water is a strong infrared absorber. Likewise, the computational analysis of VCD spectra by means of DFT-based spectral calculations requires the consideration of explicit solvent molecules, thus posing an even greater challenge. Several studies suggested that by modeling the solvent environment with a few water molecules in a micro-solvation approach would be sufficient to describe experimental spectra. For example, using proline at different pH values, we herein show that a change in the relative spatial orientation of a single water molecule in five-fold solvated structures strongly affects the computed VCD spectral signatures and that Boltzmann-weighted spectra do not correctly reproduce the experiment. We thus explored an approach based on molecular dynamics and subsequent DFT-calculations, in which we considered 30 water molecules (about 1.5 solvation shells). Once again, it was found that the Boltzmann-weighted spectra obtained on the basis of several hundred structures did not correctly reproduce experimental signatures, and a simple averaging scheme resulted in well-matching spectra with comparable bandwidths. The rationale behind the procedure was that sampling the configurational space of the solvent molecules is as equally important as the conformational sampling of the solute. For conformationally more flexible molecules, it is assumed that a much larger set of structures will have to be computed in order to properly sample the conformational space of both solute and solvent.

---

Introduction

Vibrational circular dichroism (VCD) is defined as the difference in the absorbance of left- and right-circularly polarized light upon excitation of vibrational transitions of chiral molecules. VCD spectra are experimentally obtained in the transmission mode; hence, it is common to use deuterated organic solvents to shift C–H vibrational modes out of the investigated fingerprint region. This prevents the overlap of solvent and solute bands and leaves a large spectral window for sample absorbance bands. Consequently, VCD spectroscopy allows for the determination of absolute configurations of chiral molecules by comparing experimental and computed spectra.

Recording VCD spectra for samples in aqueous solution, however, poses a particular challenge. Vibrational modes of water strongly overlap with the fingerprint region,¹ thus requiring very short pathlengths of about 6–8 μm and high solute concentrations. Heavy water (D₂O) allows for slightly longer pathlengths and thus lower concentrations, as the bending mode occurs below 1250 cm⁻¹ instead of in the range 1700–1500 cm⁻¹. However, using D₂O instead of H₂O also results in H/D exchange at acidic positions and consequently a shift of X–H related vibrational modes out of the spectral window of the measurement. Probing hydrogen bonding networks involving solvent molecules thus becomes challenging and must be done indirectly through the vibrational modes remaining accessible/visible.

Analysing VCD spectra recorded for aqueous solutions also requires huge computational efforts. While solute–solvent interactions with organic solvents occasionally need to be considered explicitly in the computational analysis, their modelling is somewhat straightforward as ACN-d₃ and DMSO-d₆ only act as hydrogen bond acceptors.² Even methanol, which can act as both a donor and an acceptor, can easily be modelled as its interactions are typically weak. Water, however, is a strong donor and acceptor, forming tightly bound solvation shells around solutes. As shown for small organic molecules, it can also insert into intramolecular hydrogen bonds and give rise to induced VCD phenomena.^3–7a

First, VCD studies in aqueous solution were mostly focussed on biopolymers and targeted qualitative structure–spectra relationships.^8–12 Later, combined experimental and computational studies on amino acids in aqueous solution (D₂O) and under varying pH conditions were reported. Among the investigated systems were serine,¹³ leucine,¹⁴ cysteine,¹⁵ and N-acetyl-cysteine¹⁶ for which the manual or molecular dynamics-guided placement of 4–6 D₂O molecules was found to sufficiently resemble the key spectral features.

The apparent need to consider several water molecules and to sample their configurational space around the solute stimulated the development of methods to compute VCD spectra based on molecular dynamics (MD) approaches. A numerical approach to obtain VCD spectra directly from semi-empirical QM/MM MD simulations was tested for (Ala)₂,¹⁷ Ac-Pro-NH₂^18,19 and Ac-Ala-NHCH₃²⁰ in D₂O. With the implementation of nuclear velocity perturbation theory into a plane-wave electronic structure code,^21,22 VCD spectral calculations directly from the trajectories of ab initio molecular dynamics (AIMD) simulations became possible.^23,24 As an alternative approach for computing VCD spectra directly from MD trajectories, it is also possible to post-process snapshots on a static DFT level.^25,26 This has been demonstrated for amphetamine and methamphetamine in D₂O, for which clusters with an average of 18 water molecules were extracted from the trajectory, categorized by conformers and subsequently fitted against the experimental spectra.²⁷ For this fitting procedure, the water-based molecular property tensors were set to zero, so that all vibrational modes of the solvent were suppressed. Using the quantum-cluster growth method, solvation shells could also be built up systematically.^7,28,29

In this contribution, we investigate the IR and VCD spectra of the amino acid proline (Pro) in H₂O at different pH values. Despite its unique structural properties compared to other amino acids, the experimental VCD spectra of Pro were only recorded in small regions of the fingerprint range.³⁰ Theoretical studies on Pro-H₂O clusters have been reported, but no comparison with the experiment has been established.³¹ Interestingly, also Raman optical activity (ROA) data on proline in water were not complemented with computational studies going beyond continuum solvation.^32,33 Hence, we selected it as an example to address the fundamental issues of modelling VCD spectra of solutes in aqueous solution, especially regarding the necessity for a comprehensive configurational sampling of the water hydrogen bonding network around the solute. We evaluated how the orientation of a single water molecule in a Pro-(H₂O)_n cluster affects VCD spectral signatures and we have shown how a QM/MM-MD can serve as basis for VCD spectra calculations without additional clustering or processing of the computed spectra.

Experimental and computational details

Material

Both enantiomers of proline were obtained from commercial sources (BLD Pharm) and used without further purification.

IR and VCD spectroscopy

The IR and VCD spectra were recorded on a Bruker Vertex FT-IR spectrometer equipped with a PMA 50 module for VCD measurements. Samples were held in a transmission cell assembled from CaF₂ windows with a central 6 μm deep pit, which ensures a constant path length, and a flat BaF₂ window as a counter-window. Only for measurements under acidic conditions, the flat window was replaced with CaF₂, as the latter is more resistant. Concentrations were adjusted to the IR spectra having an absorbance below 0.9 in the region of interest to avoid artefacts. The concentration of Pro in neutral water was 2 M (pH 6.4). Under acidic/basic conditions, 1.5 M solutions of proline were prepared by adding 1.5 M HCl or 4 M NaOH solution (giving final pH values of 0.9 and 14). Spectra were recorded at room temperature with 4 cm⁻¹ spectral resolution by accumulating 32 scans for IR and ∼32 000 scans (8 hours accumulation time) for VCD.

Baseline corrections of the VCD spectra were carried out by subtracting those of the racemic mixture recorded under identical conditions. This procedure gave good mirror-image quality spectra, yet they exhibited some noise and a certain degree of baseline drift. Hence, for better comparison with the computed spectra, the spectra presented in the main text are baseline corrected by subtracting the half-sum spectrum of the enantiomers, that is, the average of the VCD spectra recorded for (R)- and (S)-proline. Comparison with the racemic-corrected spectra ensured that no artificial signals were generated through this procedure (cf. Fig. S1, ESI†). The IR spectra are presented as raw spectra.

Computational details

Geometry optimizations and vibrational spectra calculations on the micro-solvated clusters ZwPro-(H₂O)₅ were carried out using Gaussian 09 Rev. E01³⁴ at the B3LYP/6-31+g(2d,p)/IEFPCM(water) level of theory. The MD simulations were carried out using the Amber 22 Molecular Dynamics Software package.³⁵ Input files were prepared, and trajectories were processed using AmberTools 23. They were run at a semi-empirical QM/MM level, treating the solute at the AM1 level surrounded by 530–550 TIP3P water molecules. In order to circumvent convergence issues with large and structurally flexible clusters, geometry optimizations of the extracted clusters ZwPro-(H₂O)₃₀, ProH⁽⁺⁾-(H₂O)₃₀ and Pro⁽⁻⁾-(H₂O)₃₀ were carried out using ORCA 5,^36,37 while the vibrational spectra were again obtained using the Gaussian software package. Due to the high number of structures, we reduced the level of theory to B3LYP/def2SVP/CPCM (water). Spectra were simulated by assigning a Lorentzian band shape of 6 cm⁻¹ half-width at half-height to the computed dipole and rotational strengths. Frequency scaling factors of 0.98 and 0.965 were employed for the Pople and Karlsruhe basis set, respectively. Conformer energy differences and Boltzmann-weights discussed in the text are based on relative zero-point corrected energies (ΔE_ZPC).

Results and discussion

Experimental IR and VCD spectra of proline at different pH values

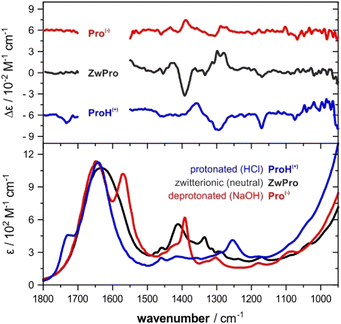
The VCD spectra of both enantiomers of proline were recorded under various pH conditions. The most characteristic region of the experimental VCD and IR spectra of the three species lies between 1500–1100 cm⁻¹, a spectral range that does not overlap with absorbance bands of water (Fig. 1). Distinct pH-dependent changes can be noted.³⁰ The zwitterionic form ZwPro shows the strongest VCD features. In comparison to the spectra of either the protonated ProH⁽⁺⁾ or deprotonated Pro⁽⁻⁾, some features are found to maintain their sign upon a change in pH, while others invert or disappear. Above 1500 cm⁻¹, there are also characteristic features observable in the IR spectrum, however, the total absorbance caused by the broad band of the water bending mode prevented any reliable VCD measurements. Below 1100 cm⁻¹, the onsets of both water libration modes and the cell-window material related cut-off limit the spectral range.

Fig. 1 IR and VCD spectra of (S)-proline in H₂O at different pH values. The concentration of Pro in water was 2 M (pH 6.4). For the other two conditions, 1.5 M solutions of proline were prepared by adding 1.5 M HCl or 4 M NaOH solution (giving final pH values of 0.9 and 14).

Conformations of proline in different protonation states

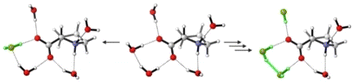
The conformational preferences of proline have been already discussed in various studies and shall only be briefly summarized here.^30–33 The zwitterionic form ZwPro, that is present under neutral conditions in water, possesses two conformers differing in the ring puckering of the five-membered ring. Both conformers show an N–H⋯O=C interaction, thereby locking the orientation of the carboxylate group. This N–H⋯O=C interaction persists in the two most stable structures of anionic Pro⁽⁻⁾. There are two additional conformers of Pro⁽⁻⁾ with the carboxylate group rotated by ∼90°, which are about 3 kcal mol⁻¹ higher in energy. Similar to the anionic species, the cationic form ProH⁽⁺⁾ also possesses four conformers, which can be obtained by protonating the carboxylate group of the zwitterionic form at either of the oxygens. The two conformers showing the N–H⋯O=C interaction are favoured by 2.5–3 kcal mol⁻¹ over those showing an N–H⋯O(H)–C interaction with the hydroxyl group. Conformer energies are summarized in Table S1 (ESI†) and selected structures of each protonation state are shown in Fig. 2.

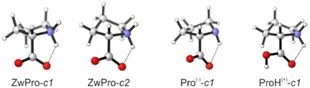Fig. 2 Structures of two zwitterionic conformers and the lowest energy anionic and protonated conformers of Pro.

ZwPro-(H₂O)₅ from a micro-solvation approach

A common approach to model the IR and VCD spectra of solutes in water (and other hydrogen bonding solvents) is to build hydrogen bonded clusters containing several solvent molecules.^7,13–16,38 We attempted such a micro-solvation approach for ZwPro and built clusters with five water molecules (Fig. 3). This number of solvent molecules was chosen to ensure that all hydrogen bonding sites of ZwPro were saturated. At first glance, it may be expected that this should result in only two solvated structures of ZwPro-(H₂O)₅. However, as each water molecule has two acceptor sites, the actual number of conformers is much higher: There are already 32 possible water configurations for each of the two conformers of ZwPro.

Fig. 3 Three different cluster structures of ZwPro-c2-(H₂O)₅ highlighting subtle changes in the water network. From the central structure to the left, one water is changed in orientation (later denoted flip 1), to the right three waters change in orientation (later denoted flip 3).

Geometry optimizations of these clusters were tedious, and due to convergence issues, we failed to optimize all 64 structures. Nonetheless, a clear picture can be drawn from the successfully converged 46 ZwPro-(H₂O)₅, of which 26 are based on ZwPro-c1 and 20 on ZwPro-c2. From an energy perspective, it is interesting to note that the structures based on ZwPro-c2 are generally lower in energy than those based on ZwPro-c1, so the explicit solvation with water flipped the conformational preferences compared to the only implicitly solvated structures. Within the set of ZwPro-(H₂O)₅ structures of each conformer, the zero-point corrected energies (ΔE_ZPC) are very similar and almost all are within a 0.2 kcal mol⁻¹ range. Flipping the orientation of a single water molecule apparently does not cost much energy, resulting in evenly distributed Boltzmann weights.

The simulated VCD and IR spectra of ZwPro-(H₂O)₅ match the experimental signatures notably better than the spectra of non-solvated ZwPro (Fig. 4A). It is possible to make band assignments, and the characteristic signature found around 1400 cm⁻¹ could be considered to be present in the simulated VCD spectrum. Yet, in terms of relative intensities, the spectral signatures are not well reproduced.

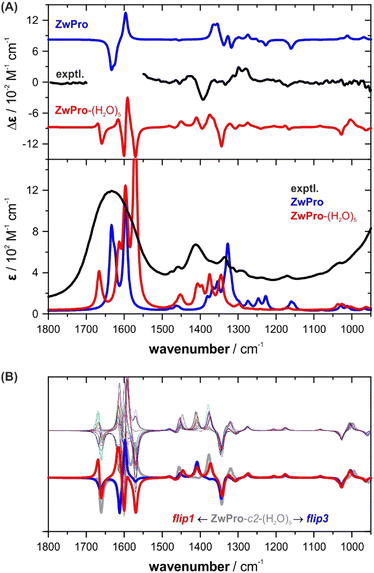Fig. 4 VCD and IR spectra of zwitterionic ZwPro. (A) Comparison of the experimental spectra of (S)-proline in water (2 M, 6 μm pathlength) with the Boltzmann-averaged computed spectra of isolated ZwPro and solvated clusters ZwPro-(H₂O)₅. (B) Overlay of all spectra of ZwPro-c2-(H₂O)₅; the offset spectra belong to the structures shown in Fig. 3.

As the conformer weights of the different solvated structures were quite similar, we investigated whether the water configuration around the solute affects the spectral signatures or if it may be sufficient to consider only one solvated structure for each conformer. Not unexpectedly, the spectral region above 1500 cm⁻¹, where the C=O stretching modes of ZwPro overlap with the water bending modes, exhibits strong differences among the clusters (Fig. 4B). However, the characteristic region of 1500–1300 cm⁻¹ also changes notably, and the two offset examples demonstrate that the changes are significant. The two bands at 1410 and 1375 cm⁻¹, which change in sign and magnitude, can both be ascribed to a combined motion of CH rocking, NH₂ twisting, and CH₂ wagging (displacement vectors are shown in Fig. S2, ESI†). The change in the orientation of a single water molecule causes a re-distribution of intensities between these two modes. Interestingly, none of the five water molecules contribute to the vibrational motion, which suggests that the influence of the water shell traces back solely to polarizing effects. The observation that the orientation of a single water molecule has such a tremendous effect on the computed spectral signatures led to a key conclusion: all or at least many water configurations need to be considered and it cannot be ruled out that higher clusters are required to better resemble the spectra.

Due to this conclusion, we did not attempt the micro-solvation approach for other cluster sizes of ZwPro-(H₂O)_n or any clusters with ProH⁽⁺⁾ and Pro⁽⁻⁾. The efforts to generate various cluster sizes, and even more so to ensure that a large number of structures also converge, did not seem feasible. Instead, we evaluated another route as described in the next section.

ZwPro-(H₂O)₃₀: the solvent-shell approach based on MD simulation

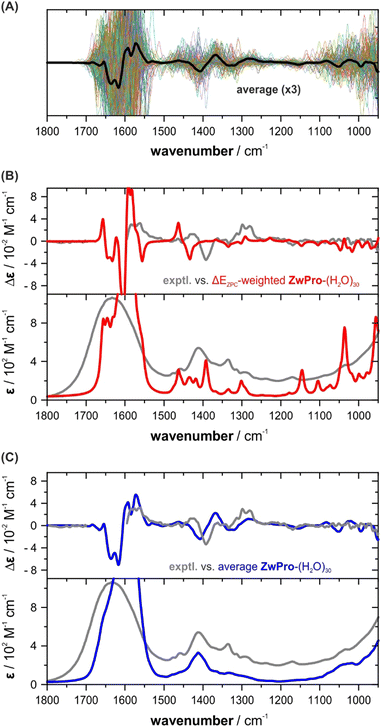
In order to more effectively sample the water configurations around the solute, we implemented an approach starting from a QM/MM MD simulation. ZwPro was considered at the AM1 semi-empirical level and immersed in around 530–550 TIP3P water molecules. MD simulations of 30 ns lengths were run from two independently generated and equilibrated starting ensembles based on ZwPro-c1 and -c2. The evaluation of the trajectories allowed several statistical analyses, for instance, regarding the number of solvent molecules in the vicinity of ZwPro or the average number of solute–solvent hydrogen bonds (cf. Fig. S3, ESI†). Defining the first and second solvation shell as water molecules within distances of 3.4 and 5.0 Å from the solute, we obtained distributions centred around 17 and 53 water molecules, respectively. Likewise, the distribution of directly hydrogen bonded water molecules around ZwPro is centred at 5. The latter number matches well with the direct hydrogen bonds assumed in our micro-solvation approach. However, as we have seen for ZwPro-(H₂O)₅ that the orientation of water molecules and their polarization effects on the solute have a tremendous effect on the spectral signatures, it is likely that at least the first solvation shell should be considered for VCD spectra simulations.

In the next step, we extracted 100 uncorrelated snapshots from each of the MD runs and removed all but the closest 30 water molecules from each of them. The decision to keep about 1.5 solvation shells was a compromise between the expected computer time required for the intended subsequent DFT-based geometry optimizations and having enough solvent molecules to stabilize the first shell during the optimization. The full structures were then optimized without any geometric constraints. All but a few structures converged, so that VCD and IR spectra calculations were subsequently carried out for 190 structures of ZwPro-(H₂O)₃₀. Expectedly, many structures showed small negative eigenvalues, but when they accounted for less than 150 cm⁻¹, we still considered them for the following analysis. Removing all structures with negative eigenvalues gave very similar spectral features, but the spectra were less smooth and appeared “noisy”.

The individual VCD spectra of the ZwPro-(H₂O)₃₀ structures continue the trend seen already in ZwPro-(H₂O)₅ structures with VCD bands varying in intensity and sign and spanning the entire investigated fingerprint range (Fig. 5a). Interestingly, when considering the zero-point corrected energies of all clusters, the Boltzmann distribution is dominated by only two structures with weights of 68 and 21%, respectively. The rather even distribution observed for ZwPro-(H₂O)₅ thus breaks down when the cluster grows. This could be related to differences in the hydrogen bonding networks of the clusters, e.g., the number and types of hydrogen bonds, as both were kept identical in the evaluated ZwPro-(H₂O)₅ structures. The conformational space of ZwPro in the 30-fold solvated structures is also not represented by two sharply defined minima c1 and c2, but rather exhibits a conformational distribution (Fig. S4, ESI†). Most importantly, however, the resulting Boltzmann weighted spectra in fact exhibit poorer matching than those of ZwPro-(H₂O)₅ (Fig. 5b). Instead of relying on the DFT-computed energies, which may be inaccurate for various reasons, we simply computed the arithmetic average spectra over all computed structures of ZwPro-(H₂O)₃₀. This approach assumes that the MD simulation would deliver a reliable conformational distribution for ZwPro itself and the large number of samples should properly account for the configurational ensemble of water molecules. The VCD and IR spectra obtained from such a simple averaging procedure are in surprisingly good agreement with the experimental data (Fig. 5c). It becomes particularly evident in the IR spectrum, that the averaging reproduced band positions, shapes and line broadening well, and it even captured the onset of the libration band at the low-energy side of the spectrum. Likewise, the predicted VCD spectral pattern resembles the experimental signatures and relative intensities are reproduced quiet well.

Fig. 5 Computed spectra of ZwPro-(H₂O)₃₀. (A). Overlay of all 190 spectra. (B) Comparison of the experimental spectra with those obtained based on Boltzmann weights derived from ΔE_ZPC. (C) Comparison of the experimental spectra with those obtained by simple averaging over all computed spectra.

ProH(+) and Pro(⁻) in the solvent-shell approach

To predict the VCD and IR spectra of protonated and anionic proline in aqueous solution, we performed MD simulations for ProH⁽⁺⁾ and Pro⁽⁻⁾ following the same procedure as for ZwPro. For each of the protonation states, 30 ns MD runs were started from four independently generated and equilibrated ensembles. Charges were balanced by introducing a chloride and a sodium ion. The larger number of simultaneous runs was chosen to account for the larger conformational flexibility of the species. From the resulting MD trajectories, 50 uncorrelated snapshots were extracted; the number of water molecules reduced to the closest 30 and the counter ions were removed. After DFT optimization, 193 converged structures of ProH⁽⁺⁾-(H₂O)₃₀ and 191 of Pro⁽⁻⁾-(H₂O)₃₀ were obtained and submitted for subsequent spectra calculations.

The main observations described for ZwPro were made again for the other two protonation states. Examining the sets of hundreds of single spectra revealed bands over the entire investigated spectral range with changing signs and magnitudes as well as frequencies (cf. Fig. S5a andb, ESI†). Again, only few structures were favoured based on zero-point corrected energies and the Boltzmann-weighted spectra of ProH⁽⁺⁾-(H₂O)₃₀ do not match well with the experimentally observed spectra (cf. Fig. S5c, ESI†). For the anionic form, the Boltzmann weighted spectra of Pro⁽⁻⁾-(H₂O)₃₀ in fact resemble the spectral pattern, but significant line broadening has to be applied to match the overall spectra shapes (cf. Fig. S5d, ESI†). Once again, the simulated spectra obtained through simple averaging over the computed hundreds of single cluster spectra exhibit high agreement with the experimental VCD and IR spectral features of both ProH⁽⁺⁾ and Pro⁽⁻⁾ (Fig. 6). They closely resemble both the spectral pattern and band shapes, as well as the broadening.

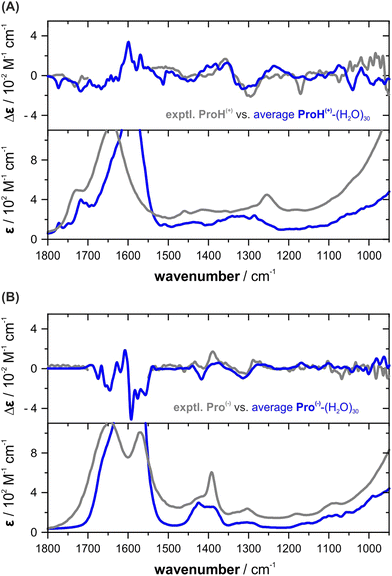Fig. 6 Comparison of the experimental VCD and IR spectra of (A) ProH⁽⁺⁾ and (B) Pro⁽⁻⁾ with the computed average spectra.

Conclusions

The VCD and IR spectra of proline recorded at different pH values in aqueous solution were found to show distinct spectral features. Attempting to compute these features, we first focussed on the example of the zwitterionic form, ZwPro, and demonstrated that the hydrogen bonding network of the surrounding water molecules has a tremendous effect on the computed and thus probably also on the experimentally observed spectral features. Examination of the computed spectra of ZwPro-(H₂O)₅ revealed that the orientation of a single water molecule in such clusters can lead to band shifts, VCD sign inversions, and a redistribution of spectral intensities. The fact that these changes occurred even for vibrational modes that did not have any contributions from any of the water molecules suggests that the surrounding water has a strongly polarizing effect on the solute. The shape of the water shell thus matters, and it was assumed that not only the conformational space of the solute but also the configurational space of the water shell needs to be properly sampled to achieve a close resemblance to the experimentally observed spectral features.

To better account for the large configurational space of water molecules around ZwPro, we applied a QM/MM-MD based procedure to compute the VCD spectrum. Based on hundreds of snapshots, we obtained optimized geometries of ZwPro-(H₂O)₃₀ clusters. The vibrational spectra of ZwPro-(H₂O)₃₀ predicted based on zero-point corrected energies and the corresponding Boltzmann weights did not correctly resemble even the most prominent spectral features. In contrast, a simple averaging over all structures yielded VCD and IR spectra that were in excellent agreement with the experimental data. This observation led to the conclusion that the energies of such large clusters are not the appropriate basis for spectral simulations as these require a broad basis of structures with a statistical distribution of solvent orientations. This conclusion was further strengthened by the fact that the spectra of the protonated form of proline, ProH⁽⁺⁾, and the anionic form, Pro⁽⁻⁾, were equally well described by averaging of several hundreds of spectra computed for clusters with 30 water molecules.

The results of this study have shown that VCD spectra may be even more sensitive to the actual shape of the solvation shell than expected. However, while the presented approach to compute the VCD spectra of proline at different pH values appears simple to apply, we must stress that the conformational space of the solute is extremely small. Hence, rather few optimized snapshots may already suffice to cover its conformational distribution, so that most snapshots sample solely the possible solvent configurations. For molecules with greater degrees of conformational freedom, the number of snapshots and most likely also the number of solvent molecules in the clusters need to be adjusted, which results in a potentially drastic increase in the required number of snapshots. Future studies will thus evaluate the transferability of the approach to more conformationally complex molecules.

Data availability statement

The data supporting this article have been included as part of the ESI.†

Conflicts of interest

There are no conflicts to declare.

Acknowledgements

This work was funded by the Deutsche Forschungsgemeinschaft (DFG, German Research Foundation) under Germany's Excellence Strategy (EXC-2033, project no. 390677874) and through the DFG's Heisenberg program (ME 4267/5–1; project no. 418661145).

References

1. J.-B. Brubach, A. Mermet, A. Filabozzi, A. Gerschel and P. Roy, J. Chem. Phys., 2005, 122, 184509.
2. C. Merten, Phys. Chem. Chem. Phys., 2023, 25, 29404–29414.
3. M. Losada and Y. Xu, Phys. Chem. Chem. Phys., 2007, 9, 3127–3135.
4. M. Losada, P. Nguyen and Y. Xu, J. Phys. Chem. A, 2008, 112, 5621–5627.
5. G. Yang and Y. Xu, J. Chem. Phys., 2009, 130, 164506.
6. M. Losada, H. Tran and Y. Xu, J. Chem. Phys., 2008, 128, 014508.
7. Y. Yang, M. Alshalalfeh and Y. Xu, Spectrochim. Acta, Part A, 2024, 307, 123634.
8. A. C. Sen and T. A. Keiderling, Biopolymers, 1984, 23, 1519–1532.
9. S. C. Yasui, T. A. Keiderling and R. Katakai, Biopolymers, 1987, 26, 1407–1412.
10. T. B. Freedman, L. A. Nafie and T. A. Keiderling, Biopolymers, 1995, 37, 265–279.
11. T. A. Keiderling, Curr. Opin. Chem. Biol., 2002, 6, 682–688.
12. W. M. Zuk, T. B. Freedman and L. A. Nafie, Biopolymers, 1989, 28, 2025–2044.
13. P. Zhu, G. Yang, M. R. Poopari, Z. Bie and Y. Xu, Chem. Phys. Chem., 2012, 13, 1272–1281.
14. M. R. Poopari, P. Zhu, Z. Dezhahang and Y. Xu, J. Chem. Phys., 2012, 137, 194308.
15. M. Kaminski, A. Kudelski and M. Pecul, J. Phys. Chem. B, 2012, 116, 4976–4990.
16. M. R. Poopari, Z. Dezhahang, G. Yang and Y. Xu, Chem. Phys. Chem., 2012, 13, 2310–2321.
17. K. Kwac, K.-K. Lee, J. B. Han, K.-I. Oh and M. Cho, J. Chem. Phys., 2008, 128, 105106.
18. K. K. Lee, S. Hahn, K. I. Oh, J. S. Choi, C. Joo, H. Lee, H. Han and M. Cho, J. Phys. Chem. B, 2006, 110, 18834–18843.
19. K.-I. Oh, J. Han, K.-K. Lee, S. Hahn, H. Han and M. Cho, J. Phys. Chem. A, 2006, 110, 13355–13365.
20. S. Yang and M. Cho, J. Chem. Phys., 2009, 131, 135102.
21. A. Scherrer, R. Vuilleumier and D. Sebastiani, J. Chem. Theory Comput., 2013, 9, 5305–5312.
22. A. Scherrer, F. Agostini, D. Sebastiani, E. K. U. Gross and R. Vuilleumier, J. Chem. Phys., 2015, 143, 074106.
23. A. Scherrer, R. Vuilleumier and D. Sebastiani, J. Chem. Phys., 2016, 145, 084101.
24. S. Jähnigen, D. Sebastiani and R. Vuilleumier, Phys. Chem. Chem. Phys., 2021, 23, 17232–17241.
25. T. Giovannini and C. Cappelli, Chem. Commun., 2023, 59, 5644–5660.
26. T. Giovannini, F. Egidi and C. Cappelli, Chem. Soc. Rev., 2020, 49, 5664–5677.
27. K. Dobšíková, P. Michal, D. Spálovská, M. Kuchař, N. Paškanová, R. Jurok, J. Kapitán and V. Setnička, Analyst, 2023, 148, 1337–1348.
28. S. A. Katsyuba and T. I. Burganov, Phys. Chem. Chem. Phys., 2023, 25, 24121–24128.
29. S. Spicher, C. Plett, P. Pracht, A. Hansen and S. Grimme, J. Chem. Theory Comput., 2022, 18, 3174–3189.
30. A. Rüther, M. Pfeifer, V. A. Lórenz-Fonfría and S. Lüdeke, J. Phys. Chem. B, 2014, 118, 3941–3949.
31. C. Cappelli, S. Monti and A. Rizzo, Int. J. Quantum Chem., 2005, 104, 744–757.
32. J. Kapitan, V. Baumruk, V. Kopecky, Jr., R. Pohl and P. Bour, J. Am. Chem. Soc., 2006, 128, 13451–13462.
33. S. Qiu, G. Li, P. Wang, J. Zhou, Z. Feng and C. Li, J. Phys. Chem. A, 2011, 115, 1340–1349.
34. M. J. Frisch, G. W. Trucks, H. B. Schlegel, G. E. Scuseria, M. A. Robb, J. R. Cheeseman, G. Scalmani, V. Barone, B. Mennucci, G. A. Petersson, H. Nakatsuji, M. Caricato, X. Li, H. P. Hratchian, A. F. Izmaylov, J. Bloino, G. Zheng, J. L. Sonnenberg, M. Hada, M. Ehara, K. Toyota, R. Fukuda, J. Hasegawa, M. Ishida, T. Nakajima, Y. Honda, O. Kitao, H. Nakai, T. Vreven, J. J. A. Montgomery, J. E. Peralta, F. Ogliaro, M. Bearpark, J. J. Heyd, E. Brothers, K. N. Kudin, V. N. Staroverov, T. Keith, R. Kobayashi, J. Normand, K. Raghavachari, A. Rendell, J. C. Burant, S. S. Iyengar, J. Tomasi, M. Cossi, N. Rega, J. M. Millam, M. Klene, J. E. Knox, J. B. Cross, V. Bakken, C. Adamo, J. Jaramillo, R. Gomperts, R. E. Stratmann, O. Yazyev, A. J. Austin, R. Cammi, C. Pomelli, J. W. Ochterski, R. L. Martin, K. Morokuma, V. G. Zakrzewski, G. A. Voth, P. Salvador, J. J. Dannenberg, S. Dapprich, A. D. Daniels, O. Farkas, J. B. Foresman, J. V. Ortiz, J. Cioslowski and D. J. Fox, Gaussian 09, Rev E.01, Wallingford CT, USA, 2013.
35. D. A. Case, H. M. Aktulga, K. Belfon, I. Y. Ben-Shalom, J. T. Berryman, S. R. Brozell, D. S. Cerutti, I. T. E. Cheatham, G. A. Cisneros, V. W. D. Cruzeiro, T. A. Darden, R. E. Duke, G. Giambasu, M. K. Gilson, H. Gohlke, A. W. Goetz, R. Harris, S. Izadi, S. A. Izmailov, K. Kasavajhala, M. C. Kaymak, E. King, A. Kovalenko, T. Kurtzman, T. S. Lee, S. LeGrand, P. Li, C. Lin, J. Liu, T. Luchko, R. Luo, M. Machado, V. Man, M. Manathunga, K. M. Merz, Y. Miao, O. Mikhailovskii, G. Monard, H. Nguyen, K. A. O’Hearn, A. Onufriev, F. Pan, S. Pantano, R. Qi, A. Rahnamoun, D. R. Roe, A. Roitberg, C. Sagui, S. Schott-Verdugo, A. Shajan, J. Shen, C. L. Simmerling, N. R. Skrynnikov, J. Smith, J. Swails, R. C. Walker, J. Wang, J. Wang, H. Wei, R. M. Wolf, X. Wu, Y. Xiong, Y. Xue, D. M. York, S. Zhao and P. A. Kollman, Amber, University of California, San Francisco, 2022.
36. F. Neese, WIREs Comput. Mol. Biosci., 2012, 2, 73–78.
37. F. Neese, F. Wennmohs, U. Becker and C. Riplinger, J. Chem. Phys., 2020, 152, 224108.
38. A. S. Perera, C. D. Carlson, J. Cheramy and Y. Xu, Chirality, 2023, 35(10), 718–731.

---

Footnote

† Electronic supplementary information (ESI) available: Additional spectra plots, conformational distributions, conformer energies and Cartesian coordinates. See DOI: https://doi.org/10.1039/d4cp01768d

---