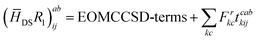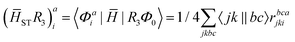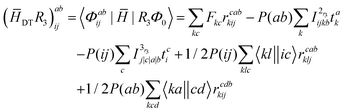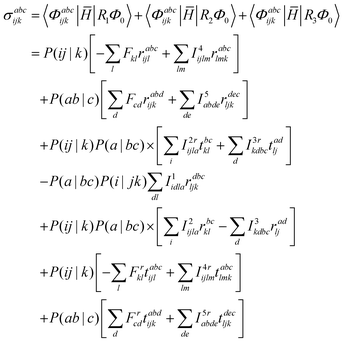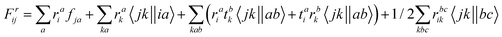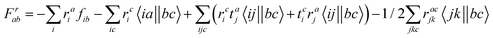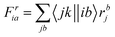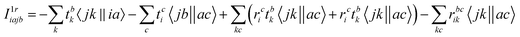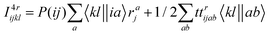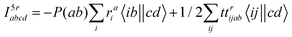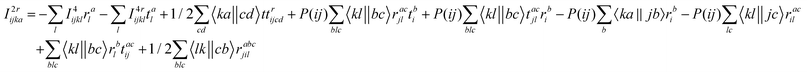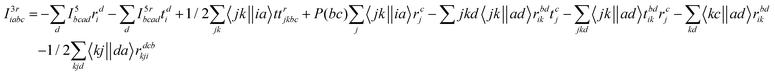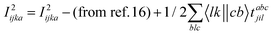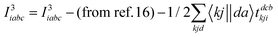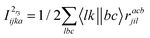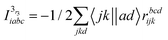Spin–flip equation-of-motion coupled cluster method with singles, doubles and (full) triples: computational implementation and some pilot applications†
Received
3rd June 2024
, Accepted 10th July 2024
First published on 17th July 2024
Abstract
We present our computational implementation of the spin–flip (SF) equation-of-motion (EOM) coupled-cluster (CC) method with singles, doubles, and (full) triples (SDT) within Q-CHEM. The inclusion of triples not only enhances the quantitative accuracy of the SF-EOM-CCSD method but also provides correct qualitative trends in the energy gaps between strongly degenerate states. To assess the accuracy, we compare our SF-EOM-CCSDT results with full configuration interaction (FCI) and complete-active-space self-consistent field second-order (CASSCF-SO) CI benchmarks to study the adiabatic energy gaps in CH2 and NH2+ diradicals, vertical excitation energies in CH radicals and the bond dissociation of the HF molecule. We have implemented SF-EOM-CCSDT using both the conventional double precision (DP) and the single precision (SP) algorithms. The use of SP does not introduce any significant errors in energies and energy gaps, and, due to low cost (relative to DP), turns out to be a promising approach to widen the applicability of EOM-CCSDT to bigger molecules.
1 Introduction
Near-degeneracy in electronic states of molecules poses a formidable challenge in their electronic structure computation due to the prominence of the static electron correlation1 in addition to the dynamical one. Balanced and effective inclusion of both these is crucial for accurate computation of energy gaps as they have a pivotal role in studying bonding patterns, spectroscopic parameters, thermochemistry, etc. Amongst the available computational methods, the EOM-CC2–18 methods are robust and methods of choice for electronic structure computation of molecules with strongly interacting electronic states in a simple and straightforward single reference (SR)6,13,19–21 formalism. Other methods such as multi-reference (MR) CC,22–30 linear response (LR) CC,20,31–33 symmetry adapted cluster (SAC) configuration interaction (CI),34,35 similarity transformed (ST)EOM-CC,13,36etc. approaches are also known to provide similar (or sometimes, equivalent) results.
In EOM-CC,5–7 the wavefunctions and energies of the desired target states are obtained by diagonalization of the (similarity transformed) CC Hamiltonian matrix expanded in a suitable configuration space (e.g., singly excited, doubly excited, etc. configurations), thereby incorporating the mixing of the strongly-interacting states in an efficient manner, ensuring balanced treatment of the static and dynamic correlation. The so-called EOM-CCSD uses single and double substitution for CC vectors as well as EOM eigen-vectors and has a scaling of O(N6). The same level of truncation for CC as well as EOM vectors also ensures core-extensivity of the EOM-CCSD wavefunction, although it lacks valence-extensivity.37 Due to core-extensivity, the excitation energies of a chromophore are unaltered by the addition or removal of the non-chromophoric fragment to the chromophore and this feature is, therefore, also referred to as “size-intensivity”.
The spin–flip (SF)38–46 formalism is well discussed in the context of EOM-CC as well as some DFT-based approaches. For excitation energies, two variants in EOM-CC, namely EE for (spin-conserving) electronic excitations5–7 and SF (for spin-flipping excitations) are well known, and they differ slightly in the way that the target states are formulated relative to the reference state. In EE-EOM-CC, the excited determinants in the configuration space are generated by the action of linear excitation operators (the right eigen-vectors) on the reference configuration in which the spins of the electrons are retained during the excitations. In contrast, in SF-EOM-CC, the excitation operators flip the spin of one and only one electron (from α to β), while the spins of the remaining electron(s) are retained. In the case of EE-EOM-CCSD, the total energies of excited states dominated by singly excited character have an accuracy of 0.2 eV44 with pronounced tendency for systematic overestimation. The SF-EOM-CCSD errors are even smaller. Moreover, the target–target energy gaps are usually much more accurate compared to the reference–target energy gaps. However, for electronic states with stronger degeneracies, such as dark states of polyenes, or some valence states of polyradicals,15,47–58 where the doubly excited character predominates, the EOM-CCSD accuracy significantly deteriorates. The increased error in these cases is due to some non-dynamical correlation effects that are missed out at the EOM-CCSD level and can be mitigated to some extent by including the effect of triples. Inclusion of full triples results in the EOM-CCSDT59 method, which has a scaling of O(N8). Due to this high cost of EOM-CCSDT, several intermediate approximations14,60–67 were proposed, which includes both iterative and non-iterative approaches. However, these approaches lack the size-intensivity, particularly for charge-transfer type excitations.68 Moreover, due to non-uniform correlation corrections for reference and target states, the energy gaps estimated by these approaches are even worse than the EOM-CCSD ones, although the total energies are improved relative to EOM-CCSD.17 Similar formulations in CC-LR,69 MRCC,70etc. have also been reported.
The balanced description of the energy gaps can thus be obtained only by employing full triples resulting in the EOM-CCSDT method with increased computational cost as a price to pay. In this article, we present our computational implementation of SF-EOM-CCSDT within the ccman2 suite71 of Q-CHEM72 for single-point energy computations. We have also implemented EE-EOM-CCSDT within Q-CHEM and also acknowledge that the method was (elsewhere) successfully implemented, long back, by Bartlett and co-workers.73 Recognizing the cost-effectivity of the SP algorithms for CCSD and EOM-CCSD variants illustrated by Krylov and co-workers,74,75 we have employed both DP as well as SP algorithms for the implementation of SF-EOM-CCSDT as well as EE-EOM-CCSDT. Section 2 presents a brief theory of EOM-CC with a focus on SF-EOM-CCSDT and the programmable expressions for the same are presented in the Appendix. In Section 3 we present some applications of SF-EOM-CCSDT and discuss the results. Finally, we present our conclusions in Section 4.
2 Theory
EOM-CC6,7,36,51,76 theory is discussed in detail in several articles. Here, we present, a brief and, rather, a less rigorous outline of the method just to get a flavor of the practical aspects. Consider the Hamiltonian eigenstates Ψ0 & Ψf. They obey the time-independent Schrödinger equation and we havewhere, E0 and Ef are the exact eigenvalues of the respective states. In the EOM formalism, the Ψf & Ψ0 are related by| | |Ψf〉 = ![[R with combining circumflex]](https://www.rsc.org/images/entities/i_char_0052_0302.gif) |Ψ0〉 |Ψ0〉 | (3) |
where ![[R with combining circumflex]](https://www.rsc.org/images/entities/i_char_0052_0302.gif) is the linear operator, which we will define later. In the case of EOM-CCSDT, Ψ0 is the CCSDT wavefunction defined by
is the linear operator, which we will define later. In the case of EOM-CCSDT, Ψ0 is the CCSDT wavefunction defined by| | |Ψ0〉 = e![[T with combining circumflex]](https://www.rsc.org/images/entities/i_char_0054_0302.gif) |Φ0〉 |Φ0〉 | (4) |
where |Φ0〉 is a single Slater determinant wavefunction – usually (but not necessarily) the Hartree–Fock wavefunction. ![[T with combining circumflex]](https://www.rsc.org/images/entities/i_char_0054_0302.gif) is the sum of the one-, two- and three-body excitation operators.
is the sum of the one-, two- and three-body excitation operators.
| | 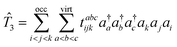 | (6) |
In eqn (6) we have set up the convention that will be continued in the article. From now onwards, the indices, i, j, k, … will be used for labelling the occupied orbitals whereas for the virtual orbitals, the indies, a, b, c … will be used.
Substituting eqn (4) in eqn (1) one can solve and simplify to get
| | Ĥ|Ψ0〉 = Ĥe![[T with combining circumflex]](https://www.rsc.org/images/entities/i_char_0054_0302.gif) |Φ0〉 = E0e |Φ0〉 = E0e![[T with combining circumflex]](https://www.rsc.org/images/entities/i_char_0054_0302.gif) |Φ0〉 |Φ0〉 | (7) |
| | e−![[T with combining circumflex]](https://www.rsc.org/images/entities/i_char_0054_0302.gif) Ĥe Ĥe![[T with combining circumflex]](https://www.rsc.org/images/entities/i_char_0054_0302.gif) |Φ0〉 = (Ĥe |Φ0〉 = (Ĥe![[T with combining circumflex]](https://www.rsc.org/images/entities/i_char_0054_0302.gif) )C|Φ0〉 = )C|Φ0〉 = ![[H with combining macron]](https://www.rsc.org/images/entities/i_char_0048_0304.gif) |Φ0〉 = E0|Φ0〉 |Φ0〉 = E0|Φ0〉 | (8) |
| | ECC = E0 = 〈Φ0|![[H with combining macron]](https://www.rsc.org/images/entities/i_char_0048_0304.gif) |Φ0〉 |Φ0〉 | (9) |
| | 0 = 〈Φ*|![[H with combining macron]](https://www.rsc.org/images/entities/i_char_0048_0304.gif) |Φ0〉 |Φ0〉 | (10) |
Substituting
Φ* in
eqn (10) by
Φai,
Φabij, and
Φabcijk, respectively, would yield the equations for the amplitudes of
![[T with combining circumflex]](https://www.rsc.org/images/entities/i_char_0054_0302.gif) 1
1,
![[T with combining circumflex]](https://www.rsc.org/images/entities/i_char_0054_0302.gif) 2
2 and
![[T with combining circumflex]](https://www.rsc.org/images/entities/i_char_0054_0302.gif) 3
3.
From eqn (2)–(4), it follows
|Ψf〉 = ![[R with combining circumflex]](https://www.rsc.org/images/entities/i_char_0052_0302.gif) e e![[T with combining circumflex]](https://www.rsc.org/images/entities/i_char_0054_0302.gif) |Φ0〉 |Φ0〉 |
| | Ĥ|Ψf〉 = Ĥ![[R with combining circumflex]](https://www.rsc.org/images/entities/i_char_0052_0302.gif) e e![[T with combining circumflex]](https://www.rsc.org/images/entities/i_char_0054_0302.gif) |Φ0〉 = Ef |Φ0〉 = Ef![[R with combining circumflex]](https://www.rsc.org/images/entities/i_char_0052_0302.gif) e e![[T with combining circumflex]](https://www.rsc.org/images/entities/i_char_0054_0302.gif) |Φ0〉 |Φ0〉 | (11) |
In the context of SF-EOM-CCSDT, the operator
R is the sum of one-, two- and three-body spin-flipping (SF) excitation operators.
| | 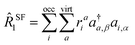 | (12) |
| | 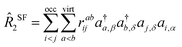 | (13) |
| | 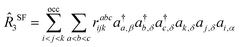 | (14) |
The operators,
![[R with combining circumflex]](https://www.rsc.org/images/entities/i_char_0052_0302.gif) 1
1,
![[R with combining circumflex]](https://www.rsc.org/images/entities/i_char_0052_0302.gif) 2
2 and
![[R with combining circumflex]](https://www.rsc.org/images/entities/i_char_0052_0302.gif) 3
3, respectively, are very similar to the
![[T with combining circumflex]](https://www.rsc.org/images/entities/i_char_0054_0302.gif) 1
1,
![[T with combining circumflex]](https://www.rsc.org/images/entities/i_char_0054_0302.gif) 2
2 and
![[T with combining circumflex]](https://www.rsc.org/images/entities/i_char_0054_0302.gif) 3
3 operators in CC, except that in
![[R with combining circumflex]](https://www.rsc.org/images/entities/i_char_0052_0302.gif)
, the excitation(s) is (are) associated with flipping of the spin of one (and only one) of the electrons from
α to
β (from
ms = 1/2 to
ms = −1/2). The spins of the remaining electrons are essentially retained (
δ →
δ, where
δ =
α or
β). Clearly,
![[R with combining circumflex]](https://www.rsc.org/images/entities/i_char_0052_0302.gif)
and
![[T with combining circumflex]](https://www.rsc.org/images/entities/i_char_0054_0302.gif)
commute and
eqn (11) simplifies to
Ĥ|Ψf〉 = Ĥ![[R with combining circumflex]](https://www.rsc.org/images/entities/i_char_0052_0302.gif) e e![[T with combining circumflex]](https://www.rsc.org/images/entities/i_char_0054_0302.gif) |Φ0〉 = Ĥe |Φ0〉 = Ĥe![[T with combining circumflex]](https://www.rsc.org/images/entities/i_char_0054_0302.gif) ![[R with combining circumflex]](https://www.rsc.org/images/entities/i_char_0052_0302.gif) |Φ0〉 = Efe |Φ0〉 = Efe![[T with combining circumflex]](https://www.rsc.org/images/entities/i_char_0054_0302.gif) ![[R with combining circumflex]](https://www.rsc.org/images/entities/i_char_0052_0302.gif) |Φ0〉 |Φ0〉 |
Action of
![[R with combining circumflex]](https://www.rsc.org/images/entities/i_char_0052_0302.gif)
on
![[H with combining macron]](https://www.rsc.org/images/entities/i_char_0048_0304.gif)
in
eqn (8) would give
Subtracting the RHS of eqn
(16) from
eqn (15), it follows
| | (![[H with combining macron]](https://www.rsc.org/images/entities/i_char_0048_0304.gif) − ECC) − ECC)![[R with combining circumflex]](https://www.rsc.org/images/entities/i_char_0052_0302.gif) |Φ0〉 = (Ef − ECC) |Φ0〉 = (Ef − ECC)![[R with combining circumflex]](https://www.rsc.org/images/entities/i_char_0052_0302.gif) |Φ0〉 |Φ0〉 | (17) |
Eqn (17) can be transformed into matrix eigenvalue equation.
| | 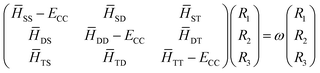 | (18) |
where, the roots,
ω =
E −
ECC, would give the SF excitation energies of the respective target states. It is important to note that the CC Hamiltonian matrix in
eqn (18) being non-hermitian, the left and right eigenvectors are not hermitian conjugates but can be chosen to be mutually biorthogonal. The solution of
eqn (18) is good enough to obtain the excitation energies and the corresponding right eigenvectors. The left eigenvectors are required only if one aims to compute gradients and/or properties. Complete diagonalization of the CC Hamiltonian matrix
eqn (18) is impractical as we are usually interested in computing only a few electronic states. Davidson's iterative diagonalization procedure
77,78 effectively eliminates the requirement for full diagonalization of the CC Hamiltonian and provides a cost-effective, pragmatic tool to compute the required roots of the matrix. The programmable expressions for the same in the SF-EOM-CCSDT context are provided in the Appendix.
3 Results and discussion
3.1 Computational details
All the EOM-CC(SD and SDT) calculations were performed using a development version of Q-CHEM.79 For the methylene diradical (CH2) and nitrenium diradical cation NH2+, respectively, the FCI/TZ2P and CISD/TZ2(f,d) optimized structures80,81 were used. The single-point computations presented in this article have also been performed using the same bases (TZ2P for CH2 and TZ2(f,d) for NH2+). For CH radicals, the experimental ground state equilibrium bond length (r(CH) = 1.1198 Å) was taken from Slipchenko et al.82 The single-point computations were done using cc-pVTZ basis. For bond-breaking of HF, the 6-31G basis was used. The bond distances and the FCI and EOM-CCSD results were taken from ref. 41. The SF-EOM-CCSDT computations using both DP and SP algorithms are presented for all the molecules. The core-orbitals are frozen in post-Hartree–Fock calculations only for the CH radical.
3.2 Adiabatic excitation energies of CH2 and NH2+ diradicals
CH2 and NH2+ diradicals are isoelectronic species with strong static electron correlation. Both these molecules have a triplet ground state of 3B1 character. The ground state UHF wavefunction (MS = +1 of 3B1; electronic configuration: 1a122a121b223a11b1) is taken as the reference configuration for the SF-EOM computations. Fig. 1 presents the isodensity surfaces of the frontier molecular orbitals (MOs) of the CH2 diradical and the schematic diagram showing the relationship between the SF-EOM reference and target states. The frontier orbitals of NH2+ are qualitatively the same.
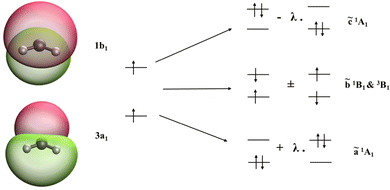 |
| | Fig. 1 Frontier MOs of CH2; the high spin reference configuration and dominant configuration of the SF target states obtained via SF-excitations. | |
Tables 1 and 2 summarise the adiabatic excitation energies for CH2, and NH2+, respectively.
Table 1 Total energies of the ground state (![[X with combining tilde]](https://www.rsc.org/images/entities/char_0058_0303.gif) 3B1) and adiabatic excitation energies (eV) of CH2
3B1) and adiabatic excitation energies (eV) of CH2
| Method |
ã1A1 |
![[b with combining tilde]](https://www.rsc.org/images/entities/char_0062_0303.gif) 1B1 1B1 |
![[c with combining tilde]](https://www.rsc.org/images/entities/char_0063_0303.gif) 1A1 1A1 |
|
From ref. 80.
From ref. 68.
|
| FCIa |
0.483 |
1.542 |
2.674 |
| SF-EOM-CCSD |
0.517 |
1.565 |
2.718 |
| SF-EOM-CCSD(fT)b |
0.500 |
1.552 |
2.688 |
| SF-EOM-CCSD(dT)b |
0.496 |
1.548 |
2.678 |
| SF-EOM-CCSDT |
0.493 |
1.545 |
2.677 |
| SF-EOM-CCSDT(SP) |
0.493 |
1.545 |
2.677 |
Table 2 Adiabatic excitation energies (eV) of NH2+ relative to the ground state (![[X with combining tilde]](https://www.rsc.org/images/entities/char_0058_0303.gif) 3B1)
3B1)
| Method |
ã1A1 |
![[b with combining tilde]](https://www.rsc.org/images/entities/char_0062_0303.gif) 1B1 1B1 |
![[c with combining tilde]](https://www.rsc.org/images/entities/char_0063_0303.gif) 1A1 1A1 |
|
From ref. 81.
From CCSDT.68
From ref. 58.
|
| CASSCF SOCIa |
1.281 |
1.935 |
3.380 |
| SF-EOM-CCSD |
1.306 |
1.918 |
3.420 |
| SF-EOM-CCSD(fT)b |
1.292 |
1.905 |
3.391 |
| SF-EOM-CCSD(dT)b |
1.289 |
1.902 |
3.382 |
| SF-EOM-CCSDT |
1.288 |
1.926 |
3.386 |
| SF-EOM-CCSDT(SP) |
1.288 |
1.926 |
3.386 |
| Expt.c |
1.306 ± 0.010 |
|
|
For the CH2 diradical, the excitation energies computed by all the methods are overestimated relative to FCI. The SF-EOM-CCSDT computed excitation energies are overestimated by 0.01 eV or less (for both DP and SP), whereas the SF-EOM-CCSD values are overestimated by 0.044 eV or less.
The trends in NH2+ are more or less the same. Relative to CASSCF-SOCI, the EOM computed excitation energies are systematically overestimated for the two 1A1 states, whereas systematically underestimated for the 1B1 state. The SF-EOM-CCSDT excitation energies differ from the CASSCF-SOCI ones by 0.01 eV or less. The 1B1 state is a typical example where approximate triples fail to provide the qualitatively correct trend. As we go from CCSD to CCSD(fT) and CCSD(dT), the perturbative corrections rather worsen the EOM-CCSD values. However, the use of the rigorous EOM-CCSDT method rectifies the trends with the excitation energy underestimated relative to CASSCF-SOCI by only 0.009 eV, for both DP and SP algorithms.
3.3 Vertical excitation energies of the CH radical
The CH radical has a 2Π ground state and is two-fold degenerate with respect to the MO configuration. The vertical excitation energies of this molecule can be computed using two variants, namely, EE and SF. The isodensity surfaces of the frontier MOs, namely, the σ* and the two π orbitals are presented in Fig. 2 along with the schematic diagram showing the relationship between EE/SF reference states and various target states.
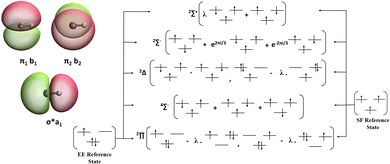 |
| | Fig. 2 Frontier MOs in CH and schematic representation of the reference–target relationships in EE-EOM versus SF-EOM variants. The target state configurations are spin-conserving excitations relative to the EE reference, whereas the spin-flipping excitations are relative to the SF reference. | |
For EE, one uses the doublet ground state reference (![[X with combining tilde]](https://www.rsc.org/images/entities/char_0058_0303.gif) 2Π, MS = +1/2) and target states are obtained using the EE-EOM-CCSDT approach. For SF, one uses the high-spin quartet reference (4Σ, MS = +3/2) and the target states are obtained as spin-flipped excitations. For both EE-EOM as well as SF-EOM, the energies were computed using both UHF and ROHF references. The total energy of the ground state (
2Π, MS = +1/2) and target states are obtained using the EE-EOM-CCSDT approach. For SF, one uses the high-spin quartet reference (4Σ, MS = +3/2) and the target states are obtained as spin-flipped excitations. For both EE-EOM as well as SF-EOM, the energies were computed using both UHF and ROHF references. The total energy of the ground state (![[X with combining tilde]](https://www.rsc.org/images/entities/char_0058_0303.gif) 2Π) (in Hartrees) and excitation energies of various states (in eV) are summarized in Table 3.
2Π) (in Hartrees) and excitation energies of various states (in eV) are summarized in Table 3.
Table 3 Total energies of the ground state (Hartree) and vertical excitation energies (eV) of several low-lying excited states of CH radical calculated using the active space SF-EOM-CCSDT methods with ROHF and UHF references. Calculations performed at the experimental ground state geometry r(CH) = 1.1198 Å, using the cc-pVTZ basis set with one frozen core orbital
| Method |
![[X with combining tilde]](https://www.rsc.org/images/entities/char_0058_0303.gif) 2Π 2Π |
![[X with combining tilde]](https://www.rsc.org/images/entities/char_0058_0303.gif) ′2Πa ′2Πa |
a4Σ− |
A2Δb |
A2Δc |
B2Σ− |
C2Σ+ |
|
The X′2Π state is the EOM target state in both EE and SF. The X2Π is the reference in EE, whereas a target state in SF.
The open-shell component of the A2Δ state.
The closed-shell component of the 2Δ state.
Estimated from adiabatic excitation energies within the harmonic approximation for the excited state PES using experimental data (ref. 83).
|
| UHF-EE-EOM-CCSD |
−38.407096 |
0.015 |
1.204 |
3.210 |
3.223 |
4.590 |
5.521 |
| UHF-EE-EOM-CC(2,3) |
−38.411018 |
0.017 |
0.743 |
3.009 |
3.004 |
3.343 |
4.113 |
| UHF-EE-EOM-CCSDT |
−38.411021 |
0.0022 |
0.725 |
2.995 |
2.991 |
3.334 |
4.103 |
| UHF-EE-EOM-CCSDT(SP) |
−38.411022 |
0.0022 |
0.725 |
2.995 |
2.992 |
3.334 |
4.103 |
| ROHF-EE-EOM-CCSD |
−38.406975 |
0.007 |
0.991 |
3.205 |
3.295 |
4.402 |
5.402 |
| ROHF-EE-EOM-CC(2,3) |
−38.410986 |
0.016 |
0.738 |
3.000 |
2.998 |
3.340 |
4.117 |
| ROHF-EE-EOM-CCSDT |
−38.410988 |
0.0002 |
0.719 |
2.986 |
2.984 |
3.329 |
4.097 |
| ROHF-EE-EOM-CCSDT(SP) |
−38.410987 |
0.0002 |
0.719 |
2.986 |
2.984 |
3.329 |
4.097 |
| UHF-SF-EOM-CCSD |
−38.407473 |
0.0 |
0.687 |
2.991 |
2.991 |
3.343 |
4.118 |
| UHF-SF-EOM-CC(2,3) |
−38.410184 |
0.0 |
0.709 |
2.965 |
2.965 |
3.332 |
4.056 |
| UHF-SF-EOM-CCSDT |
−38.410934 |
0.0 |
0.703 |
2.962 |
2.962 |
3.325 |
4.061 |
| UHF-SF-EOM-CCSDT(SP) |
−38.410934 |
0.0 |
0.703 |
2.962 |
2.962 |
3.325 |
4.061 |
| ROHF-SF-EOM-CCSD |
−38.407607 |
0.0 |
0.687 |
2.985 |
2.985 |
3.350 |
4.110 |
| ROHF-SF-EOM-CC(2,3) |
−38.410211 |
0.0 |
0.707 |
2.963 |
2.963 |
3.324 |
4.054 |
| ROHF-SF-EOM-CCSDT |
−38.410974 |
0.0 |
0.702 |
2.960 |
2.960 |
3.317 |
4.059 |
| ROHF-SF-EOM-CCSDT(SP) |
−38.410973 |
0.0 |
0.702 |
2.960 |
2.960 |
3.317 |
4.059 |
| Experiment (vertical)d |
|
|
0.745 |
2.880 |
|
3.263 |
3.943 |
Due to the structural difference between the EE and SF variants, two distinct features are observed in the results. Firstly, due to the non-uniform distribution of the unpaired electron between the π-orbitals in the reference configuration of EE, the degeneracy of these orbitals is slightly lifted which results in loss of degeneracy of the ground (2Π) level and the 2Δ (excited) level as observed in the case of all the EOM-EE methods. However, the EOM-SF methods retain the degeneracy due to the uniform distribution of electrons between the degenerate frontier MOs in the high-spin reference configuration. Secondly, the total energies and the excitation energies computed by the EE and SF variants for the same set of electronic states differ significantly, with a systematic overestimation of the EE computed values, compared to the SF values.
This discrepancy, in a sense, can be considered as a truncation error as it is expected to vanish in the FCI limit. As we move from EOM-CCSD to EOM-CCSDT via EOM-CC(2,3), the truncation error indeed decreases gradually for all the states. The trends in the truncation error in the UHF-based energies and excitation energies are summarized in Fig. 3.
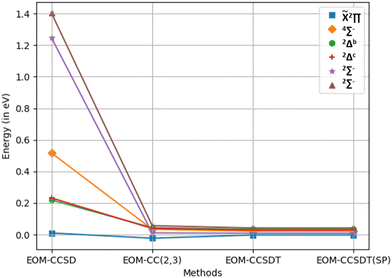 |
| | Fig. 3 Truncation error (ΔEEE − ΔESF) for various truncation levels of EOM-CC. | |
The trends for ROHF-based ones are very similar. The maximum truncation errors are 1.403 eV for EOM-CCSD, 0.057 eV for EOM-CC(2,3), 0.042 eV for EOM-CCSDT with DP and 0.042 eV for EOM-CCSDT with SP when the UHF reference is used. If the ROHF reference is employed, the maximum truncation errors are 1.292 eV for EOM-CCSD, 0.063 eV for EOM-CC(2,3), 0.038 eV for EOM-CCSDT with DP and 0.038 eV for EOM-CCSDT with SP.
As we move from EOM-CCSD to EOM-CCSDT, the computed excitation energy values come closer to the experimental values in general, with an exception for the 4Σ− state, for which the EOM-CC(2,3) values are rather closer to the experimental values than are the EOM-CCSDT values.
3.4 Bond dissociation of the HF molecule
At equilibrium and near-equilibrium geometries, the ground state of the HF molecule is fairly non-degenerate, dominated by the electronic configuration, [core],1σ21σ*21π22π2 as the LUMO 2σ is well separated in energy from the HOMO. At these geometries, the ground state properties can be accurately computed using CCSD or CCSDT. However, upon bond-stretching, the HOMO–LUMO gap keeps on reducing and the ground state gains multi-reference character in the bond dissociation limit. The strong static correlation demands the use of SF-EOM-CCSDT for correctly targeting the ground state, starting with a high-spin triplet reference.
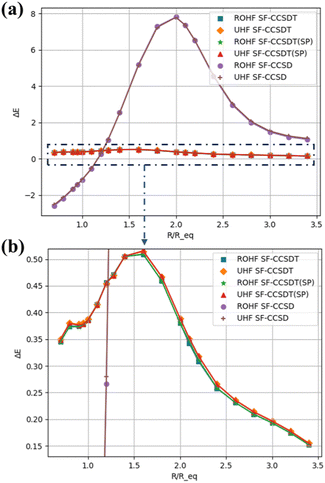
Table 4 presents the FCI/6-31G total energies of the HF ground state and the errors in the energies (δE) relative to FCI for various SF-EOM models using both the ROHF and the UHF references. Fig. 4 summarises the trends. The maximum absolute errors (MAE)s in ROHF based SF-EOM-CC methods, namely, SDT, SDT(SP) and SD are, respectively, 0.014 eV, 0.014 eV and 0.212 eV. For UHF-based models also, the MAEs are very similar. The discrepancy between UHF and ROHF is very small (of the order of a few micro-Hartrees).
Table 4 FCI/6-31G total (ground state) energies (Hartree) and relative errors (eV) for various SF-EOM-CC/6-31G methods using ROHF and UHF references
|
R
HF (in Angs) |
E
FCI
|
δEROHFSDT |
δEROHFSDT (SP) |
δEUHFSDT |
δEUHFSDT (SP) |
δEROHFSD |
δEUHFSD |
|
The FCI energies are taken from the ref. 84 and 85.
|
| 0.7 |
−100.00548 |
0.00939 |
0.00937 |
0.00952 |
0.00950 |
−0.07093 |
−0.06898 |
| 0.8 |
−100.08713 |
0.01018 |
0.01016 |
0.01035 |
0.01032 |
−0.05944 |
−0.05809 |
| 0.9 |
−100.11425 |
0.01019 |
0.01015 |
0.01028 |
0.01024 |
−0.04567 |
−0.04490 |
| 0.95 |
−100.11669 |
0.01032 |
0.01027 |
0.01034 |
0.01029 |
−0.03876 |
−0.03816 |
| 1.0 |
−100.11462 |
0.01052 |
0.01048 |
0.01054 |
0.01049 |
−0.03165 |
−0.03112 |
| 1.1 |
−100.10211 |
0.01129 |
0.01128 |
0.01129 |
0.01126 |
−0.01495 |
−0.01445 |
| 1.2 |
−100.08393 |
0.01240 |
0.01239 |
0.01237 |
0.01239 |
0.00725 |
0.00761 |
| 1.2764 |
−100.06870 |
0.01282 |
0.01282 |
0.01278 |
0.01277 |
0.02845 |
0.02855 |
| 1.4 |
−100.04428 |
0.01374 |
0.01375 |
0.01374 |
0.01376 |
0.06917 |
0.06867 |
| 1.6 |
−100.00975 |
0.01385 |
0.01387 |
0.01400 |
0.01403 |
0.14132 |
0.14005 |
| 1.8 |
−99.984078 |
0.01250 |
0.01251 |
0.01270 |
0.01272 |
0.19832 |
0.19704 |
| 2.0 |
−99.967201 |
0.01034 |
0.01035 |
0.01058 |
0.01059 |
0.21256 |
0.21210 |
| 2.1 |
−99.961487 |
0.00931 |
0.00943 |
0.00955 |
0.00958 |
0.19984 |
0.19996 |
| 2.2 |
−99.957183 |
0.00841 |
0.00849 |
0.00865 |
0.00868 |
0.17737 |
0.17802 |
| 2.4 |
−99.951656 |
0.00703 |
0.00705 |
0.00724 |
0.00723 |
0.12359 |
0.12481 |
| 2.6 |
−99.948741 |
0.00629 |
0.00630 |
0.00643 |
0.00641 |
0.08077 |
0.08214 |
| 2.8 |
−99.947238 |
0.00571 |
0.00570 |
0.00583 |
0.00581 |
0.05455 |
0.05594 |
| 3.0 |
−99.946465 |
0.00526 |
0.00525 |
0.00536 |
0.00535 |
0.04008 |
0.04153 |
| 3.2 |
−99.946065 |
0.00474 |
0.00473 |
0.00484 |
0.00482 |
0.03272 |
0.03417 |
| 3.4 |
−99.945857 |
0.00414 |
0.00413 |
0.00423 |
0.00420 |
0.02908 |
0.03051 |
 |
| | Fig. 4 Errors (δE, in millihartrees) relative to FCI in the ground-state total energies of the HF molecule using UHF and ROHF references. (a) Full range and (b) magnified range of SF-CCSDT. | |
The non-parallelity error (NPE) is another parameter to test the accuracy of the method, which is the difference between the maximum and minimum relative errors. For ROHF-based and UHF-based SF-EOM-CCSD, the NPEs are as high as 0.205 eV and 0.197 eV. For EOM-CCSDT (for DP as well as SP algorithms), the NPE reduces to 0.010 eV for both ROHF and UHF based variants.
4 Conclusions
In this article, we have presented our implementation of the SF-EOM-CCSDT method within Q-CHEM and its applications to study adiabatic energy gaps in CH2 and NH2+ diradicals, vertical excitation energies of CH radicals and bond dissociation in the HF molecule. In CH2 and NH2+ diradicals, the absolute errors in the energy gaps relative to the benchmarks are 0.01 eV or less. In bond dissociation of HF, the MAE and NPE for SF-EOM-CCSDT are, respectively, 0.014 eV and 0.010 eV. The difference between the EE and SF computed energy gaps between the same set of states is 0.001 eV or less at the EOM-CCSDT level as compared to 0.04 eV at the EOM-CCSD level as observed in the vertical excitation energies of CH. Using SP seldom introduces any significant error compared to DP. Rather, SP gives equally good results with a reduced computational cost (storage as well as RAM reduced by almost 50%), which not only leads to speed-up in the computations, but also widens the applicability of SF-EOM-CCSDT (and also EE-EOM-CCSDT) to bigger molecules for which the conventional DP algorithm may be computationally challenging.
Author contributions
Manisha contributed to software, validation and formal analysis. P. U. Manohar contributed to writing – review and editing, and supervision.
Data availability
The data supporting this article have been included as part of the ESI.†
Conflicts of interest
There are no conflicts to declare.
Appendix
The programmable expressions of SF-EOM-CCSDT within the Davidson's iterative diagonalization algorithm are presented below:| | σai = ([![[H with combining macron]](https://www.rsc.org/images/entities/i_char_0048_0304.gif) SS − ECC]R1)ai + ( SS − ECC]R1)ai + (![[H with combining macron]](https://www.rsc.org/images/entities/i_char_0048_0304.gif) SDR2)ai + ( SDR2)ai + (![[H with combining macron]](https://www.rsc.org/images/entities/i_char_0048_0304.gif) STR3)ai STR3)ai | (19) |
| | σabij = (![[H with combining macron]](https://www.rsc.org/images/entities/i_char_0048_0304.gif) DSR1)abij + ([ DSR1)abij + ([![[H with combining macron]](https://www.rsc.org/images/entities/i_char_0048_0304.gif) DD − ECC]R2)abij + ( DD − ECC]R2)abij + (![[H with combining macron]](https://www.rsc.org/images/entities/i_char_0048_0304.gif) DTR3)abij DTR3)abij | (20) |
| | σabcijk = (![[H with combining macron]](https://www.rsc.org/images/entities/i_char_0048_0304.gif) TSR1)abcijk + ( TSR1)abcijk + (![[H with combining macron]](https://www.rsc.org/images/entities/i_char_0048_0304.gif) TDR2)abcijk + ([ TDR2)abcijk + ([![[H with combining macron]](https://www.rsc.org/images/entities/i_char_0048_0304.gif) TT − ECC]R3)abcijk TT − ECC]R3)abcijk | (21) |
The programmable expressions for SF-EOM/EE-EOM-CCSD were published by Levchenko et al.16 Let these be referred to as “EOMCCSD-terms.” The additional terms in EOM-CCSDT are given below:
For computational convenience, we express the σabcijk as follows:
The intermediates used in the above expressions are mostly used from the EOM-CCSD intermediates given in ref. 16. The additional intermediates used in these expressions are summarized in
Table 5.
Table 5 Additional intermediates used in SF-EOM-CCSDT other than ref. 16
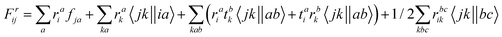
|
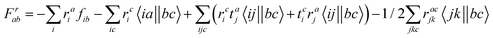
|
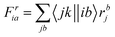
|
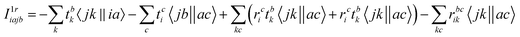
|
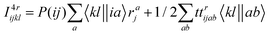
|
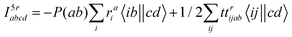
|
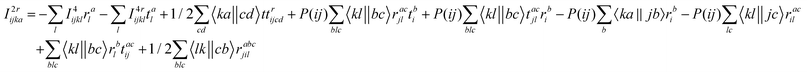
|
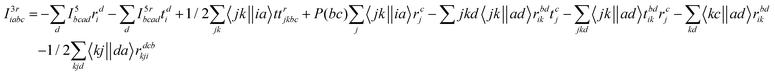
|
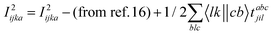
|
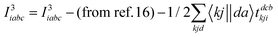
|
|
tt
r
ijab
= rabij + P(ab)P(ij)tairbj |
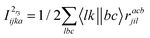
|
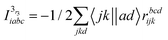
|
Acknowledgements
Manisha is thankful to BITS Pilani for the institute fellowship.
Notes and references
-
T. Helgaker, P. Jorgensen and J. Olsen, Molecular electronic-structure theory, John Wiley & Sons, 2013 Search PubMed.
- J. Čížek, J. Chem. Phys., 1966, 45, 4256–4266 CrossRef.
- D. Rowe, Rev. Mod. Phys., 1968, 40, 153 CrossRef.
-
O. Sǐnanoğlu and K. A. Brueckner, Three approaches to electron correlation in atoms, 1970 Search PubMed.
- H. Sekino and R. J. Bartlett, Int. J. Quantum Chem., 1984, 26, 255–265 CrossRef.
- H. Koch, H. J. Jensen, T. Helgaker, G. E. Scuseria and H. F. Schaefer,
et al.
, J. Chem. Phys., 1990, 92, 4924–4940 CrossRef CAS.
- J. F. Stanton and R. J. Bartlett, J. Chem. Phys., 1993, 98, 7029–7039 CrossRef CAS.
- H. G. Kümmel, Int. J. Mod. Phys. B, 2003, 17, 5311–5325 CrossRef.
- R. J. Bartlett and M. Musiał, Rev. Mod. Phys., 2007, 79, 291 CrossRef CAS.
- P. U. Manohar and S. Pal, Chem. Phys. Lett., 2007, 438, 321–325 CrossRef CAS.
-
P. U. Manohar, K. R. Shamasundar, A. Bag, N. Vaval and S. Pal, Recent Progress in Coupled Cluster Methods: Theory and Applications, 2010, pp. 375–393 Search PubMed.
- J. F. Stanton and J. Gauss, J. Chem. Phys., 1994, 101, 8938–8944 CrossRef CAS.
- M. Nooijen and R. J. Bartlett, J. Chem. Phys., 1997, 107, 6812–6830 CrossRef CAS.
- K. Kowalski and P. Piecuch, J. Chem. Phys., 2000, 113, 8490–8502 CrossRef CAS.
- L. V. Slipchenko and A. I. Krylov, J. Chem. Phys., 2002, 117, 4694–4708 CrossRef CAS.
- S. V. Levchenko and A. I. Krylov, J. Chem. Phys., 2004, 120, 175–185 CrossRef CAS PubMed.
- P. U. Manohar, L. Koziol and A. I. Krylov, J. Phys. Chem. A, 2009, 113, 2591–2599 CrossRef CAS PubMed.
- A. Ünal and U. Bozkaya, J. Chem. Theory Comput., 2022, 18, 1489–1500 CrossRef PubMed.
-
R. J. Bartlett, Geometrical Derivatives of Energy Surfaces and Molecular Properties, Springer, 1986, pp. 35–61 Search PubMed.
- H. J. Monkhorst, Int. J. Quantum Chem., 1977, 12, 421–432 CrossRef.
- A. I. Krylov, Annu. Rev. Phys. Chem., 2008, 59, 433–462 CrossRef CAS PubMed.
- D. Mukherjee, R. K. Moitra and A. Mukhopadhyay, Mol. Phys., 1977, 33, 955–969 CrossRef CAS.
- I. Lindgren, Int. J. Quantum Chem., 1978, 14, 33–58 CrossRef.
- S. Pal, M. Rittby, R. J. Bartlett, D. Sinha and D. Mukherjee, Chem. Phys. Lett., 1987, 137, 273–278 CrossRef CAS.
- S. Pal, M. Rittby, R. J. Bartlett, D. Sinha and D. Mukherjee, J. Chem. Phys., 1988, 88, 4357–4366 CrossRef CAS.
- B. Jeziorski and H. J. Monkhorst, Phys. Rev. A: At., Mol., Opt. Phys., 1981, 24, 1668 CrossRef CAS.
- I. Lindgren and D. Mukherjee, Phys. Rep., 1987, 151, 93–127 CrossRef CAS.
- J. Malrieu, P. Durand and J. Daudey, J. Phys. A: Math. Gen., 1985, 18, 809 CrossRef CAS.
- D. Mukherjee and S. Pal, Adv. Quantum Chem., 1989, 20, 291–373 CrossRef CAS.
- D. Kumar and P. U. Manohar, Chem. Phys. Lett., 2019, 730, 234–238 CrossRef CAS.
-
M. Head-Gordon, T. Lee and R. Bartlett, Modern Ideas in Coupled Cluster Theory, 1997 Search PubMed.
- H. Koch, H. J. Jensen and T. Helgaker,
et al.
, J. Chem. Phys., 1990, 93, 3345–3350 CrossRef CAS.
- H. Sekino and R. J. Bartlett, Int. J. Quantum Chem., 1984, 26, 255–265 CrossRef.
- H. Nakatsuji and K. Hirao, J. Chem. Phys., 1978, 68, 2053–2065 CrossRef CAS.
- H. Nakatsuji, Chem. Phys. Lett., 1991, 177, 331–337 CrossRef CAS.
- M. Nooijen and R. J. Bartlett, J. Chem. Phys., 1997, 106, 6441–6448 CrossRef CAS.
- M. Nooijen, K. Shamasundar and D. Mukherjee, Mol. Phys., 2005, 103, 2277–2298 CrossRef CAS.
- H. Bethe, Z. Phys., 1931, 71, 205–226 CrossRef CAS.
- T.-I. Shibuya and V. McKoy, Phys. Rev. A: At., Mol., Opt. Phys., 1970, 2, 2208–2218 CrossRef.
- A. V. Luzanov, Theor. Exp. Chem., 1982, 17, 227–234 CrossRef.
- A. I. Krylov, Chem. Phys. Lett., 2001, 338, 375–384 CrossRef CAS.
- S. Hirata, M. Nooijen and R. J. Bartlett, Chem. Phys. Lett., 2000, 326, 255–262 CrossRef CAS.
- K. Hald, P. Jørgensen, J. Olsen and M. Jaszuński, J. Chem. Phys., 2001, 115, 671–679 CrossRef CAS.
- H. Larsen, K. Hald, J. Olsen and P. Jørgensen, J. Chem. Phys., 2001, 115, 3015–3020 CrossRef CAS.
- D. Casanova, L. V. Slipchenko, A. I. Krylov and M. Head-Gordon, J. Chem. Phys., 2009, 130, 044103 CrossRef PubMed.
- D. Casanova, J. Chem. Phys., 2012, 137, 084105 CrossRef PubMed.
- L. V. Slipchenko and A. I. Krylov, J. Chem. Phys., 2003, 118, 6874–6883 CrossRef CAS.
- T. Wang and A. I. Krylov, J. Chem. Phys., 2005, 123, 104304 CrossRef.
- N. Orms and A. I. Krylov, Phys. Chem. Chem. Phys., 2018, 20, 13127–13144 RSC.
- Y. Shao, M. Head-Gordon and A. I. Krylov, J. Chem. Phys., 2003, 118, 4807–4818 CrossRef CAS.
- A. I. Krylov and C. D. Sherrill, J. Chem. Phys., 2002, 116, 3194–3203 CrossRef CAS.
- A. I. Krylov, Acc. Chem. Res., 2006, 39, 83–91 CrossRef CAS PubMed.
- P. Pokhilko, D. Izmodenov and A. I. Krylov, J. Chem. Phys., 2020, 152, 034105 CrossRef CAS PubMed.
- T. Wang and A. I. Krylov, Chem. Phys. Lett., 2006, 425, 196–200 CrossRef CAS.
- A. I. Krylov, J. Phys. Chem. A, 2005, 109, 10638–10645 CrossRef CAS PubMed.
- L. Koziol, M. Winkler, Houk, S. Venkataramani, W. Sander and A. I. Krylov, J. Phys. Chem. A, 2007, 111, 5071–5080 CrossRef CAS.
- L. V. Slipchenko and A. I. Krylov, J. Chem. Phys., 2003, 118, 9614–9622 CrossRef CAS.
- S. Gibson, J. Greene and J. Berkowitz, J. Chem. Phys., 1985, 83, 4319–4328 CrossRef CAS.
- S. A. Kucharski, M. Włoch, M. Musiał and R. J. Bartlett, J. Chem. Phys., 2001, 115, 8263–8266 CrossRef CAS.
- J. D. Watts and R. J. Bartlett, J. Chem. Phys., 1994, 101, 3073–3078 CrossRef CAS.
- J. D. Watts and R. J. Bartlett, Chem. Phys. Lett., 1995, 233, 81–87 CrossRef CAS.
- J. D. Watts and R. J. Bartlett, Chem. Phys. Lett., 1996, 258, 581–588 CrossRef CAS.
- H. Koch, O. Christiansen, P. Jørgensen and J. Olsen, Chem. Phys. Lett., 1995, 244, 75–82 CrossRef CAS.
- O. Christiansen, H. Koch and P. Jørgensen, J. Chem. Phys., 1995, 103, 7429–7441 CrossRef CAS.
- O. Christiansen, H. Koch and P. Jørgensen, J. Chem. Phys., 1996, 105, 1451–1459 CrossRef CAS.
- K. Kowalski and P. Piecuch, J. Chem. Phys., 2001, 115, 643–651 CrossRef CAS.
- M. Kállay and P. R. Surján, J. Chem. Phys., 2000, 113, 1359–1365 CrossRef.
- P. U. Manohar and A. I. Krylov, J. Chem. Phys., 2008, 129, 194105 CrossRef PubMed.
- K. Kowalski, J. Chem. Phys., 2005, 123, 014109 Search PubMed.
- L. Ravichandran, N. Vaval and S. Pal, J. Chem. Theory Comput., 2011, 7, 876–883 CrossRef CAS.
- E. Epifanovsky, D. Zuev, X. Feng, K. Khistyaev, Y. Shao and A. I. Krylov, J. Chem. Phys., 2013, 139, 134105 CrossRef PubMed.
- Y. Shao, Z. Gan, E. Epifanovsky, A. T. Gilbert, M. Wormit, J. Kussmann, A. W. Lange, A. Behn, J. Deng and X. Feng,
et al.
, Mol. Phys., 2015, 113, 184–215 CrossRef CAS.
- S. A. Kucharski, M. Włoch, M. Musiał and R. J. Bartlett, J. Chem. Phys., 2001, 115, 8263–8266 CrossRef CAS.
- P. Pokhilko, E. Epifanovsky and A. I. Krylov, J. Chem. Theory Comput., 2018, 14, 4088–4096 CrossRef CAS PubMed.
-
ANSI/IEEE Std 754-1985, 1985, pp. 1–20.
- A. I. Krylov, C. D. Sherrill and M. Head-Gordon, J. Chem. Phys., 2000, 113, 6509–6527 CrossRef CAS.
- C. Davidson, J. Comput. Phys., 1975, 17, 87–94 CrossRef.
- K. Hirao and H. Nakatsuji, J. Comput. Phys., 1982, 45, 246–254 CrossRef.
- E. Epifanovsky, A. T. Gilbert, X. Feng, J. Lee, Y. Mao, N. Mardirossian, P. Pokhilko, A. F. White, M. P. Coons and A. L. Dempwolff,
et al.
, J. Chem. Phys., 2021, 155, 084801 CrossRef CAS PubMed.
- C. D. Sherrill, M. L. Leininger, T. J. Van Huis and H. F. Schaefer III, J. Chem. Phys., 1998, 108, 1040–1049 CrossRef CAS.
- J. C. Stephens, Y. Yamaguchi, C. D. Sherrill and H. F. Schaefer, J. Phys. Chem. A, 1998, 102, 3999–4006 CrossRef CAS.
- L. V. Slipchenko and A. I. Krylov, J. Chem. Phys., 2005, 123, 084107 CrossRef PubMed.
- G. Herzberg, Mol. Spectra Mol. Struct., 1950, 1, 127 Search PubMed.
- A. I. Krylov, Chem. Phys. Lett., 2001, 338, 375–384 CrossRef CAS.
- J. S. Sears, C. D. Sherrill and A. I. Krylov, J. Chem. Phys., 2003, 118, 9084–9094 CrossRef CAS.
|
| This journal is © the Owner Societies 2024 |
Click here to see how this site uses Cookies. View our privacy policy here.  Open Access Article
Open Access Article and
Prashant Uday
Manohar
and
Prashant Uday
Manohar
 *
*
![[R with combining circumflex]](https://www.rsc.org/images/entities/i_char_0052_0302.gif) |Ψ0〉
|Ψ0〉![[R with combining circumflex]](https://www.rsc.org/images/entities/i_char_0052_0302.gif) is the linear operator, which we will define later. In the case of EOM-CCSDT, Ψ0 is the CCSDT wavefunction defined by
is the linear operator, which we will define later. In the case of EOM-CCSDT, Ψ0 is the CCSDT wavefunction defined by![[T with combining circumflex]](https://www.rsc.org/images/entities/i_char_0054_0302.gif) |Φ0〉
|Φ0〉![[T with combining circumflex]](https://www.rsc.org/images/entities/i_char_0054_0302.gif) is the sum of the one-, two- and three-body excitation operators.
is the sum of the one-, two- and three-body excitation operators.![[T with combining circumflex]](https://www.rsc.org/images/entities/i_char_0054_0302.gif) =
= ![[T with combining circumflex]](https://www.rsc.org/images/entities/i_char_0054_0302.gif) 1 +
1 + ![[T with combining circumflex]](https://www.rsc.org/images/entities/i_char_0054_0302.gif) 2 +
2 + ![[T with combining circumflex]](https://www.rsc.org/images/entities/i_char_0054_0302.gif) 3
3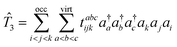
![[T with combining circumflex]](https://www.rsc.org/images/entities/i_char_0054_0302.gif) |Φ0〉 = E0e
|Φ0〉 = E0e![[T with combining circumflex]](https://www.rsc.org/images/entities/i_char_0054_0302.gif) |Φ0〉
|Φ0〉![[T with combining circumflex]](https://www.rsc.org/images/entities/i_char_0054_0302.gif) Ĥe
Ĥe![[T with combining circumflex]](https://www.rsc.org/images/entities/i_char_0054_0302.gif) |Φ0〉 = (Ĥe
|Φ0〉 = (Ĥe![[T with combining circumflex]](https://www.rsc.org/images/entities/i_char_0054_0302.gif) )C|Φ0〉 =
)C|Φ0〉 = ![[H with combining macron]](https://www.rsc.org/images/entities/i_char_0048_0304.gif) |Φ0〉 = E0|Φ0〉
|Φ0〉 = E0|Φ0〉![[H with combining macron]](https://www.rsc.org/images/entities/i_char_0048_0304.gif) |Φ0〉
|Φ0〉![[H with combining macron]](https://www.rsc.org/images/entities/i_char_0048_0304.gif) |Φ0〉
|Φ0〉![[T with combining circumflex]](https://www.rsc.org/images/entities/i_char_0054_0302.gif) 1,
1, ![[T with combining circumflex]](https://www.rsc.org/images/entities/i_char_0054_0302.gif) 2 and
2 and ![[T with combining circumflex]](https://www.rsc.org/images/entities/i_char_0054_0302.gif) 3.
3.
![[R with combining circumflex]](https://www.rsc.org/images/entities/i_char_0052_0302.gif) e
e![[T with combining circumflex]](https://www.rsc.org/images/entities/i_char_0054_0302.gif) |Φ0〉
|Φ0〉![[R with combining circumflex]](https://www.rsc.org/images/entities/i_char_0052_0302.gif) e
e![[T with combining circumflex]](https://www.rsc.org/images/entities/i_char_0054_0302.gif) |Φ0〉 = Ef
|Φ0〉 = Ef![[R with combining circumflex]](https://www.rsc.org/images/entities/i_char_0052_0302.gif) e
e![[T with combining circumflex]](https://www.rsc.org/images/entities/i_char_0054_0302.gif) |Φ0〉
|Φ0〉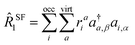
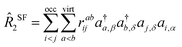
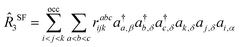
![[R with combining circumflex]](https://www.rsc.org/images/entities/i_char_0052_0302.gif) 1,
1, ![[R with combining circumflex]](https://www.rsc.org/images/entities/i_char_0052_0302.gif) 2 and
2 and ![[R with combining circumflex]](https://www.rsc.org/images/entities/i_char_0052_0302.gif) 3, respectively, are very similar to the
3, respectively, are very similar to the ![[T with combining circumflex]](https://www.rsc.org/images/entities/i_char_0054_0302.gif) 1,
1, ![[T with combining circumflex]](https://www.rsc.org/images/entities/i_char_0054_0302.gif) 2 and
2 and ![[T with combining circumflex]](https://www.rsc.org/images/entities/i_char_0054_0302.gif) 3 operators in CC, except that in
3 operators in CC, except that in ![[R with combining circumflex]](https://www.rsc.org/images/entities/i_char_0052_0302.gif) , the excitation(s) is (are) associated with flipping of the spin of one (and only one) of the electrons from α to β (from ms = 1/2 to ms = −1/2). The spins of the remaining electrons are essentially retained (δ → δ, where δ = α or β). Clearly,
, the excitation(s) is (are) associated with flipping of the spin of one (and only one) of the electrons from α to β (from ms = 1/2 to ms = −1/2). The spins of the remaining electrons are essentially retained (δ → δ, where δ = α or β). Clearly, ![[R with combining circumflex]](https://www.rsc.org/images/entities/i_char_0052_0302.gif) and
and ![[T with combining circumflex]](https://www.rsc.org/images/entities/i_char_0054_0302.gif) commute and eqn (11) simplifies to
commute and eqn (11) simplifies to![[R with combining circumflex]](https://www.rsc.org/images/entities/i_char_0052_0302.gif) e
e![[T with combining circumflex]](https://www.rsc.org/images/entities/i_char_0054_0302.gif) |Φ0〉 = Ĥe
|Φ0〉 = Ĥe![[T with combining circumflex]](https://www.rsc.org/images/entities/i_char_0054_0302.gif)
![[R with combining circumflex]](https://www.rsc.org/images/entities/i_char_0052_0302.gif) |Φ0〉 = Efe
|Φ0〉 = Efe![[T with combining circumflex]](https://www.rsc.org/images/entities/i_char_0054_0302.gif)
![[R with combining circumflex]](https://www.rsc.org/images/entities/i_char_0052_0302.gif) |Φ0〉
|Φ0〉![[H with combining macron]](https://www.rsc.org/images/entities/i_char_0048_0304.gif)
![[R with combining circumflex]](https://www.rsc.org/images/entities/i_char_0052_0302.gif) |Φ0〉 = Ef
|Φ0〉 = Ef![[R with combining circumflex]](https://www.rsc.org/images/entities/i_char_0052_0302.gif) |Φ0〉
|Φ0〉![[R with combining circumflex]](https://www.rsc.org/images/entities/i_char_0052_0302.gif) on
on ![[H with combining macron]](https://www.rsc.org/images/entities/i_char_0048_0304.gif) in eqn (8) would give
in eqn (8) would give![[R with combining circumflex]](https://www.rsc.org/images/entities/i_char_0052_0302.gif)
![[H with combining macron]](https://www.rsc.org/images/entities/i_char_0048_0304.gif) |Φ0〉 = ECC
|Φ0〉 = ECC![[R with combining circumflex]](https://www.rsc.org/images/entities/i_char_0052_0302.gif) |Φ0〉
|Φ0〉![[H with combining macron]](https://www.rsc.org/images/entities/i_char_0048_0304.gif) − ECC)
− ECC)![[R with combining circumflex]](https://www.rsc.org/images/entities/i_char_0052_0302.gif) |Φ0〉 = (Ef − ECC)
|Φ0〉 = (Ef − ECC)![[R with combining circumflex]](https://www.rsc.org/images/entities/i_char_0052_0302.gif) |Φ0〉
|Φ0〉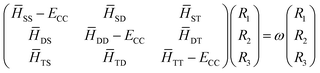

![[X with combining tilde]](https://www.rsc.org/images/entities/char_0058_0303.gif) 3B1) and adiabatic excitation energies (eV) of CH2
3B1) and adiabatic excitation energies (eV) of CH2
![[X with combining tilde]](https://www.rsc.org/images/entities/char_0058_0303.gif) 3B1)
3B1)
![[X with combining tilde]](https://www.rsc.org/images/entities/char_0058_0303.gif) 2Π, MS = +1/2) and target states are obtained using the EE-EOM-CCSDT approach. For SF, one uses the high-spin quartet reference (4Σ, MS = +3/2) and the target states are obtained as spin-flipped excitations. For both EE-EOM as well as SF-EOM, the energies were computed using both UHF and ROHF references. The total energy of the ground state (
2Π, MS = +1/2) and target states are obtained using the EE-EOM-CCSDT approach. For SF, one uses the high-spin quartet reference (4Σ, MS = +3/2) and the target states are obtained as spin-flipped excitations. For both EE-EOM as well as SF-EOM, the energies were computed using both UHF and ROHF references. The total energy of the ground state (![[X with combining tilde]](https://www.rsc.org/images/entities/char_0058_0303.gif) 2Π) (in Hartrees) and excitation energies of various states (in eV) are summarized in Table 3.
2Π) (in Hartrees) and excitation energies of various states (in eV) are summarized in Table 3.![[X with combining tilde]](https://www.rsc.org/images/entities/char_0058_0303.gif) 2Π
2Π![[X with combining tilde]](https://www.rsc.org/images/entities/char_0058_0303.gif) ′2Πa
′2Πa
![[H with combining macron]](https://www.rsc.org/images/entities/i_char_0048_0304.gif) SS − ECC]R1)ai + (
SS − ECC]R1)ai + (![[H with combining macron]](https://www.rsc.org/images/entities/i_char_0048_0304.gif) SDR2)ai + (
SDR2)ai + (![[H with combining macron]](https://www.rsc.org/images/entities/i_char_0048_0304.gif) STR3)ai
STR3)ai![[H with combining macron]](https://www.rsc.org/images/entities/i_char_0048_0304.gif) DSR1)abij + ([
DSR1)abij + ([![[H with combining macron]](https://www.rsc.org/images/entities/i_char_0048_0304.gif) DD − ECC]R2)abij + (
DD − ECC]R2)abij + (![[H with combining macron]](https://www.rsc.org/images/entities/i_char_0048_0304.gif) DTR3)abij
DTR3)abij![[H with combining macron]](https://www.rsc.org/images/entities/i_char_0048_0304.gif) TSR1)abcijk + (
TSR1)abcijk + (![[H with combining macron]](https://www.rsc.org/images/entities/i_char_0048_0304.gif) TDR2)abcijk + ([
TDR2)abcijk + ([![[H with combining macron]](https://www.rsc.org/images/entities/i_char_0048_0304.gif) TT − ECC]R3)abcijk
TT − ECC]R3)abcijk
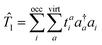
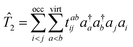
![[b with combining tilde]](https://www.rsc.org/images/entities/char_0062_0303.gif) 1B1
1B1![[c with combining tilde]](https://www.rsc.org/images/entities/char_0063_0303.gif) 1A1
1A1