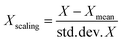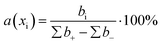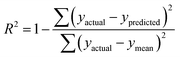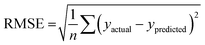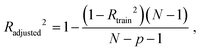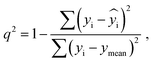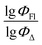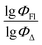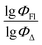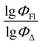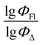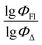Predicting fluorescence to singlet oxygen generation quantum yield ratio for BODIPY dyes using QSPR and machine learning

Abstract

Functional dyes that are capable of both bright fluorescence and efficient singlet oxygen generation are crucial for theranostic techniques, which integrate fluorescence imaging and photodynamic therapy (PDT). The development of new functional dyes for theranostics is often costly and time-consuming due to laborious synthesis and post-synthetic screening of large libraries of compounds. In this work, we describe machine learning methods suitable for simultaneous prediction of fluorescence and photosensitizing ability of heavy-atom-free boron dipyrromethene (BODIPY) compounds. We analysed the ratio between fluorescence quantum yield (Φ_Fl) and singlet oxygen quantum yield (Φ_Δ) for over 70 BODIPY structures in polar (acetonitrile) and non-polar (toluene) solvents, which mimic hydrophilic and hydrophobic cell environments, respectively. QSPR models were developed based on more than 5000 calculated molecular descriptors, including quantum chemical and topological descriptors. We applied multiple linear regression (MLR), support vector regression (SVR), and random forest regression (RFR) methods for model building and optimization. The resulting models demonstrated robust statistical parameters (R² = 0.73–0.91) for both polar and non-polar media. The relative contributions of the descriptors to the models were assessed, identifying Eig03_EA(dm), F01[C–N], and TDB06p as the most influential. These results demonstrate that QSPR machine learning methods are effective in predicting key photochemical parameters of BODIPY photosensitizers, thereby potentially streamlining the development of theranostic agents.

---

1. Introduction

Controlling the efficiency of the intersystem crossing (ISC) process in organic dyes is a fundamental problem relevant to various research fields and applications. Molecules showing efficient ISC have found multiple uses in photocatalysis,¹ photodynamic therapy (PDT),² and triplet–triplet annihilation up-conversion (TTA-UC),³ where long-lived triplet excited states are required for efficient harvesting of light energy.⁴ However, in many other applications, e.g., fluorescence detection, ISC represents a loss channel leading to a dramatic reduction in fluorescence quantum yields (Φ_Fl), reducing the brightness of fluorophores.⁵

Dyes with switchable ISC hold immense practical potential as they can serve both as probes for fluorescence-based imaging and initiate photochemical transformations. There is currently increased interest in dyes which exhibit bright fluorescence emission and, at the same time, efficiently generate singlet oxygen (¹O₂) – particularly in the area of theranostics. This is a treatment strategy where therapy and diagnostics are combined through the use of a single compound – for example, a dye fluoresces in the presence of malignant cells, and can then be light-activated to produce cytotoxic ¹O₂ and induce apoptosis.⁶ Typical organic dyes are usually only capable of one such function, as the higher the fluorescence quantum yield of a dye, the lower its photosensitizing efficiency is, and vice versa. Designing a compound having a good balance of both efficient fluorescence and reactive oxygen species (ROS) generation is challenging.

Approaches for predicting and controlling the ISC process in organic dyes are in high demand. One common approach used for switching between triplet and singlet excited states is based on reducing singlet to triplet energy gap (ΔE_S–T) which makes the reverse intersystem crossing (RISC) process feasible.⁷ This process often used for enhancement of the internal quantum efficiency of organic light-emitting diodes (OLEDs).⁸ However, the insufficient versatility of this approach is a major limitation for its use in modulation of fluorescence and triplet state yields in organic dyes. Another common approach for the enhancement of ISC efficiency relies on the introduction of heavy atoms into the structure, such as halogens or transition metals, which promote ISC via spin-orbital interactions.⁹ A representative example is shown in Fig. 1a, a halogen-substituted boron-dipyrromethenes (BODIPY) dye 1 possessing a triplet excited state yield (Φ_T) of >80%, which accounts for its uses as a photosensitizer (PS).¹⁰ Alternatively, heavy-atom-free compound 2 exhibits a high fluorescence quantum yield, while the triplet state yield is very low due to weak spin–orbit coupling.

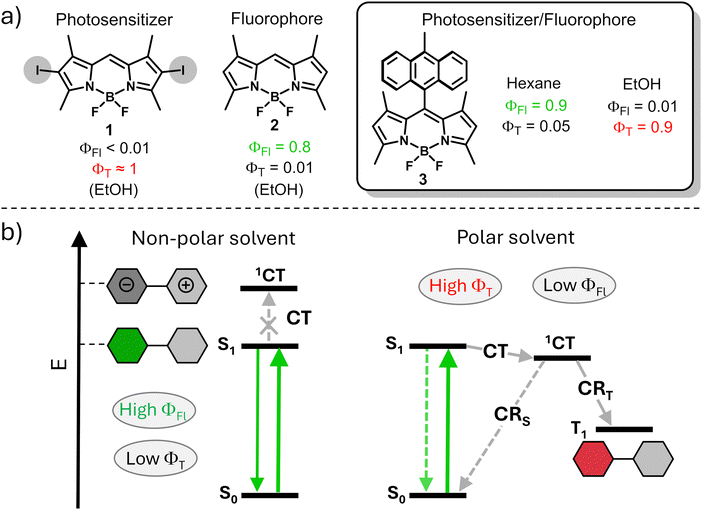Fig. 1 (a) Fluorescence and triplet state yields of BODIPY 1-3. (b) Simplified Jablonski diagram illustrating photophysical process in compound 3 in polar and non-polar solvents.^12a

In recent years, the formation of triplet excited states in electron donor–acceptor dyads via the process of spin–orbit charge transfer intersystem crossing (SOCT-ISC) has attracted particular attention. In these systems, photoinduced electron transfer between the donor and acceptor subunits leads to formation of a charge-transfer state (¹CT), which can further undergo charge recombination (CR) into the lowest triplet excited state (T₁, Fig. 1b).¹¹

SOCT-ISC has been observed in various BODIPY donor–acceptor dyads¹² and dimers,¹³ with many reported molecular systems exhibiting singlet oxygen quantum yields (Φ_Δ) comparable to or even higher than those of transition metal complexes and halogenated dyes.¹⁴ These dyes also possess additional advantages, including synthetic accessibility, high phototoxicity in cells with negligible dark toxicity (i.e. in the absence of UV-Vis light irradiation), long triplet excited state lifetimes and intense absorption in the 400–500 nm region. Unlike conventional dyes, in which fluorescence and ISC rates are predetermined by chemical structure of the molecule, SOCT-ISC dyes can exhibit either or both functions, depending on characteristics of the environment. Modulating the media polarity allows for ISC switching in these molecules. For instance, the dye can function as an efficient photosensitizer in polar media due to an efficient charge transfer process leading to high Φ_T values, as illustrated in Fig. 1b. Conversely, in non-polar media, the same dye behaves as a fluorophore because, under these conditions, the energy of the charge transfer state is higher than that of S₁, rendering SOCT-ISC inefficient. Ultimately, fluorescence and singlet oxygen quantum yields of such dyes can be programmed for specific environments, depending on the target application. Such dual performance, i.e., the combination of fluorescence and photosensitization abilities in a single molecule, offers access to a new generation of triplet–triplet annihilation upconversion (TTA-UC) systems¹⁵ and holds promise for applications in bioimaging,¹⁶ PDT¹⁷ and photocatalysis.¹⁸

There is potential for the application of quantitative structure–property relationships (QSPR) modelling in pre-synthetic screening of dyes and predicting fluorescence and singlet oxygen quantum yields. While this approach is commonly employed in medicinal chemistry, its utilization in photochemistry remains limited. QSAR/QSPR analysis¹⁹ and deep neural network modelling²⁰ has been applied in the studies of photophysics and photodynamic activity of BODIPYs.²¹ However, applying QSAR modelling for predicting ISC in BODIPYs is still challenging. Recently, we introduced the first QSPR computational study for systems undergoing SOCT-ISC, presenting a method for predicting singlet oxygen generation quantum yields for various BODIPY structures in different media: non-polar, moderately polar, and highly polar.²² Our developed QSPR models integrate quantum mechanical molecular descriptors (frontier molecular orbital energies, HOMO–LUMO gap, excited states energies), and topological descriptors related to 3D-molecular geometry, allowing for rapid and accurate prediction of quantum yields and enabling virtual screening of photosensitizers, thus expediting their development.

Here, we aimed to explore the feasibility of using QSPR for simultaneous prediction of both fluorescence and singlet oxygen generation quantum yields for heavy-atom-free BODIPYs. Such predictions would streamline the screening process for molecules with dual functionality and facilitate the identification of dyes for theranostics applications. To achieve this, we systematically investigated BODIPYs comprising electron-deficient and electron-rich aromatic subunits capable of charge transfer and SOCT-ISC processes. In this study, we: (1) identify the most significant descriptors for predicting quantum yields; (2) develop QSPR models capable of predicting the Φ_Fl/Φ_Δ ratio; and (3) assess the accuracy of the obtained QSPR models.

2. Computational methods

2.1. Geometry optimization

Conformational analysis of BODIPY molecules was performed using Spartan 20 program from Wavefunction, Inc (USA). The generation of low-energy conformers was carried out using the semi-empirical quantum chemical method AM1.²³ Next, the geometries of the compounds were optimized using the density functional theory and M062X functional with a basis set 6-31G** (Fig. 2). Similar methodology proved its efficacy in our previous studies.²⁴

Fig. 2 Modeling workflow.

2.2. Molecular descriptors

To obtain molecular descriptors, the online chemical modeling database OCHEM was used.²⁵ 10 936 descriptors were obtained within the AlvaDesc 2.0.16 (Mauri 2020) and Dragon 7 software packages.^26,27 The number of descriptors was reduced to 330 using the Generic Algorithm 4.1 developed at Jadavpur University (Calcutta, India).²⁸ Using Spartan 20 program and the M062X/6-31G** method, 22 quantum chemical descriptors were calculated, such as dipole moment, HOMO and LUMO orbital energies, electronegativity, polarizability, etc.

2.3. Machine learning (ML)

Machine learning was carried out using the Scikit-Learn 1.2.1 library of the Python programming language. Three different ML methods were used: support vector regression (SVR), multiple linear regression (MLR) and random forest regression (RFR). The scikit-learn code developed in this study can be accessed at GitHub repository using the following link: https://github.com/platonchebotaev/2024_BODIPY.

As a result of the MLR algorithm, the following equation was developed:

y = b₀ + b₁x₁ +⋯+ b_nx_n,

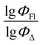where y is a dependent variable , b₀ is a constant, b₁,…, b_n are regression coefficients, x₁,…, x_n are the descriptors values. The equation obtained should contain seven descriptors for the training set (at least five compounds per molecular descriptor) to avoid overfitting.

SVR and RFR models were obtained in Scikit-Learn with gridsearch method and 5-fold cross-validation which was successfully applied in previous QSAR/QSPR studies.²⁹ The development of the SVR model was carried out by varying three parameters: C, epsilon and kernel (linear, polynomial, sigmoid or radial basis function). The search for RFR was carried out by changing the values of five parameters: the number of estimators (“trees”), the maximum depth, min_samples_split, min_samples_leaf and max_features. The remaining parameters were used by default.

Standard scaling of descriptor values was performed for the SVR and MLR models. The idea of standard scaling is that the values of each descriptor in a dataset have zero mean and unit variance according to the expression:

2.4. Relative descriptor contribution

The contribution of each descriptor was assessed. For MLR and SVR, the formula for the relative contribution of each descriptor was used:
where a(x_i) is a relative contribution of descriptor x_i, b_i – is a coefficient value of x_i, ∑b₊ is a sum of coefficients with positive values, ∑b₋ is a sum of coefficients with negative values.

In the RFR method, the importance of descriptors was estimated using the built-in function of the Scikit-Learn, since there are no coefficients in this method, and the importance is determined based on the change in entropy when dividing the sample by each feature. Relative descriptor contribution to the models is provided along with ALE (Fig. S1–S6, ESI†) and SHAP (Fig. S7–S12, ESI†) analysis in the ESI.†

2.5. Statistical parameters

The best QSPR models were selected based on statistical parameters such as R_train² (coefficient of determination of the training set), R_test² (coefficient of determination of the test set), RMSE_train (root mean square error of prediction of the training set) and RMSE_test (root mean square error of the test set), R_adjusted² (coefficient of determination of the training set with unbiased variance estimates) and q² (internally cross-validated leave-one-out (LOO) method). R_train² and RMSE_train were used for model validation and comparison. The resulting QSPR models were validated and tested for predictive ability using a test set of compounds.

R _train ² and R_test² show how well the model has trained and tested, respectively. It is calculated using the following formula:

RMSE_train and RMSE_test show how accurately the model predicts the data. It is calculated according to the following formula:
R_adjusted² considers the impact of only those independent variables that impact the variation of the dependent variable. It is calculated with the following equation:
where N is a total sample size, p is number of predictors.

Q ² is a measure of the internal stability of a model: when a compound is excluded from the training set, the performance of the model should not struggle significantly, in particular, R² (q²) does not fall below a value of 0.5. To calculate this parameter, each molecule in the training set was excluded once and 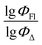of the excluded molecule was predicted by using the model developed by the remaining compounds. It is calculated according to the following formula:

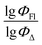where y_i and ŷ_i are the actual and predicted value of the ith molecule in the training set, respectively; y_mean is the average 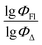of all compounds in the training set. Both summations are over all compounds in the test set. Q² metric was criticized in previous works on QSAR/QSPR.³⁰ However, we suppose that q² can be helpful for comparying different models.

3. Results and discussion

The dataset used here to build QSPR models includes compounds reported in experimental studies on heavy-atom-free BODIPYs undergoing SOCT-ISC. We examined related works published before December 2023 and combined experimental values of Φ_Fl and Φ_Δ measured in various solvents (Table S1, ESI†). This resulted in a dependent variable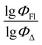 , which was analyzed further using QSPR. Several reference compounds (structures BDP1–3, Fig. 3) were included into the dataset to guarantee the reliability of models in cases when Φ_Δ values are very low. Other compounds in the dataset (4–72) include two major groups of structures: (1) dimers with various substitution patterns of the BODIPY core and nature of electron donating or electron accepting substituents; (2) donor–acceptor dyads in which the BODIPY subunit acts either as an electron acceptor (A) or as an electron donor (D). To enhance the applicability of the developed models to wider range of structures we also included the data for some NIR-absorbing BODIPYs (73–74, Fig. 3). Values of Φ_Fl and Φ_Δ measured in toluene (non-polar), and acetonitrile (highly polar) were used for analysis since these solvents have been employed to study charge transfer and singlet oxygen generation for the highest number of compounds in the dataset.

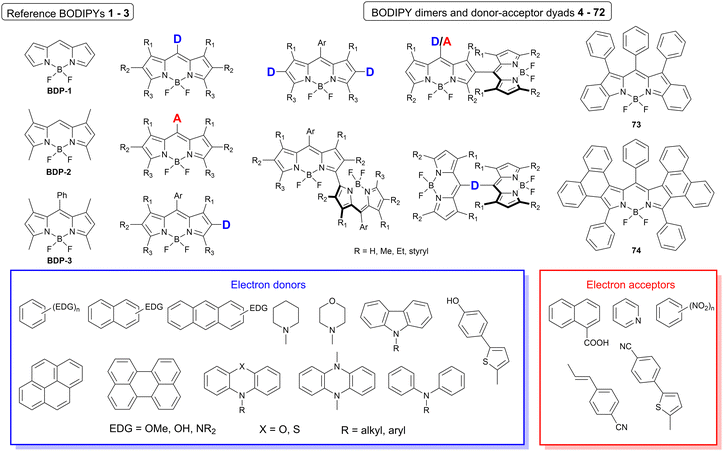Fig. 3 General structures of BODIPY dimers, donor–acceptor dyads and reference compounds investigated in this work.

Machine learning models were obtained to predict the ratio of the logarithms of the fluorescence quantum yields and singlet oxygen generation quantum yields for both solvents, toluene and acetonitrile.

3.1. Toluene model

The first group of compounds analyzed represents BODIPY undergoing SOCT-ISC in toluene. A literature analysis identified 45 BODIPYs for which singlet oxygen and fluorescence quantum yields were reported. The general structures of these compounds and their Φ_Fl and Φ_Δ values are presented in the ESI† (Table S1). The data was split into a test set (20%) and a training set (80%). Next, the models were trained and those with the best statistical parameters were selected. The statistical parameters of the resulting models are summarized in Table 1 (test set) and Table S2 (ESI†) (training set).

Table 1 Statistical parameters of the best QSPR models for BODIPYs in toluene obtained with MLR, SVR and RFR method

Parameter	MLR	SVR	RFR
R test ^2	0.777	0.811	0.912
RMSEtest	0.338	0.310	0.213

---

The QSPR model is considered effective if the following conditions are met: R_train² > 0.6, R_test² > 0.5.³⁰ The results presented in Table 1 and Table S2 (ESI†) show that all three models meet these criteria. The MLR model has the largest R_train² and the smallest RMSE_train, but among the models obtained it has the smallest R_test² and the largest RMSE_test. The SVR model is balanced, since all parameters are average in comparison with other models. The RFR model has the highest value of the most important statistical parameter R_test². The MLR, RFR and SVR models possess q² > 0.5, which indicates that the models have a good ability to explain the variation of the dependent variable based on the molecular descriptors and has a satisfactory generalizability. The SVR model is the most internally stable one (q² = 0.793). The RFR model has a q² equal to 0.556. This may indicate that the model is the least internally stable. The R_adjusted² is > 0.6 for all the models, which means that the QSPR approach is effective for the chosen molecules and descriptors.

3.1.1. MLR model 1 for BODIPYs in toluene. A linear regression equation was determined for the most successful MLR model. The coefficients of the equation are presented in Table 2. Eig03_EA(dm) is the third eigenvalue from the dipole moment weighted edge adjacency matrix. This descriptor has the largest relative contribution to the model 1 (28.0%). A dipole moment-weighted edge adjacency matrix is a matrix in which each interaction between atoms in a molecule is represented by a weight equal to the modulus of that compound dipole moment. The eigenvalues of the edge adjacency matrix are a key component for describing the electronic structure of a molecule and its properties. They are related to the energies of electronic states and can be used to describe the electronic structure and properties of a molecule. In this case, eigenvalue number 3 represents the third eigenvalue (taking into account symmetry and basis) from the set of eigenvalues. BDP-53 molecule has the highest Eig03_EA(dm) value of 0.986 (Table 3), and only 11 compounds have a value for this descriptor greater than zero. Eig03_EA(dm) value can be equal to zero for some molecules due to symmetry. In case the BODIPY molecule is highly symmetrical, the dipole moments of the individual bonds or substituents can cancel each other, resulting in a net zero dipole moment. Moreover, our analysis shows that bulky non-polar substituents have a tendency to possess zero Eig03_EA(dm), whereas BODIPYs with substituents containing heteroatoms tend to have a non-zero Eig03_EA(dm) value.

Table 2 Coefficients of the linear regression equation of the MLR model (model 1) for BODIPYs in toluene and their relative contributions. Negative values indicate a reverse correlation with

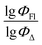
Descriptor	Coefficients	Relative contribution, %
Intercept	0.72231073	—
VE1_RG	0.20807172	11.7
G3u	−0.16770193	−10.1
MATS8i	0.10067028	5.7
TDB06p	0.43276623	22.1
Electronegativity	0.17996268	10.3
Eig03_EA(dm)	0.54257344	27.9
Mor23i	0.2239952	12.2

---

Table 3 The values of the most significant descriptors according to model 1 (MLR, toluene)

Compound	Eig03_EA (dm)	TDB06p	Mor23i
BDP-1	0	2.573	−0.633	0.108
BDP-2^test	0	2.163	−0.235	0.228
BDP-21	0	2.952	−1.21	0.111
BDP-26	0	2.892	−1.093	0.153
BDP-27	0	3.239	−1.529	0.374
BDP-28	0	3.326	−2.249	1.618
BDP-29	0	3.221	−1.91	0.121
BDP-30	0	3.104	−1.596	1.460
BDP-31^test	0	3.085	−1.635	0.049
BDP-32	0	3.484	−1.593	2.218
BDP-33	0	3.196	−1.712	0.046
BDP-37	0.6	3.283	−2.457	1.060
BDP-39^test	0.6	3.246	−3.606	0.083
BDP-40	0.86	3.301	−3.625	0.308
BDP-42^test	0.8	2.933	−2.467	0.240
BDP-43	0.6	2.864	−0.856	0.082
BDP-44	0.8	2.752	−0.412	0.705
BDP-45	0.6	3.105	−1.604	0.437
BDP-46	0.8	2.872	−0.553	0.076
BDP-47^test	0	3.098	−2.21	0.135
BDP-48	0	2.867	−1.888	0.472
BDP-49	0	3.142	−2.75	0.095
BDP-50	0	3.013	−2.614	0.393
BDP-51	0	3.100	−4.862	0.767
BDP-52	0.8	3.047	−4.187	0.389
BDP-53^test	0.986	3.227	−4.31	0.569
BDP-54	0	3.090	−2.429	1.054
BDP-55	0	3.226	−3.529	0.280
BDP-56	0.8	3.144	−5.38	0.585
BDP-57^test	0	2.683	−1.321	0.317
BDP-58	0	3.076	−1.583	2.113
BDP-59	0	2.952	−2.366	0.027
BDP-60	0	2.541	−1.852	0.635
BDP-61	0	2.643	−0.425	0.980
BDP-63	0	3.000	−0.392	2.000
BDP-64	0	2.833	−1.63	2.343
BDP-65	0	3.473	−2.428	0.286
BDP-66^test	0	3.529	−2.237	0.092
BDP-67	0	3.677	−3.593	0.538
BDP-68	0	3.657	−3.708	0.502
BDP-69	0	3.445	−3.218	2.308
BDP-70^test	0	3.306	−3.753	1.905
BDP-71	0	3.182	−1.102	0.818
BDP-72	0	3.259	−0.933	1.806
BDP-73	0	3.863	−2.782	2.463

---

TDB06p is a Dragon 7 descriptor, which is a 3D Topological distance-based descriptor – lag 6 weighted by polarizability. It belongs to a class of descriptors based on topological distance in 3D space. This descriptor takes into account the distance between atoms or fragments of a molecule in 3D space. Lag 6 means that the distance between atoms or fragments of a molecule is at least six interatomic bonds. Polarizability determines the weight that is assigned to each distance. A weight based on polarizability considers the ability of atoms or fragments of a molecule to change their electronic structure when exposed to an electric field. Thus, this descriptor factors in not only the geometric properties of the molecule, but also its chemical properties related to polarizability. This descriptor has the second most significant relative contribution to the model (22.1%). BDP-73 molecule has the highest TDB06p value of 3.863, whereas BDP-2 has the lowest value equal to 2.163. In simple terms, BODIPY molecules with bulky substituents have a tendency to possess high TDB06p values (at a topological distance lag 6), whereas small molecules like BDP-1 and BDP-2 have a low descriptor value.

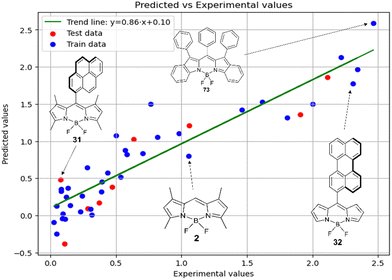
Experimental vs. predicted 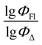values for the studied BODIPYs in toluene are presented in Fig. 4. The Mor23i is a signal value weighted by ionization potential. Signal 23 is a molecular descriptor that is associated with the electron density distribution in the molecule. It takes into account the influence of the electronic structure of a molecule on its chemical properties. Ionization potential is the minimum amount of energy required to remove an electron from a molecule. The weighting of the Mor23i descriptor by ionization potential means that the value of that descriptor has been modified to take ionization potential into account. Thus, the descriptor depends on both the electronic structure of the molecule and its chemical properties related to ionization potential. BDP-2 molecule has the highest value of this descriptor equal to −0.235, whereas BDP-56 has the lowest Mor23i value equal to −5.38.

Fig. 4 Experimental vs. predicted values of according to MLR model in toluene (model 1). The trend line refers to the training set.

3.1.2. SVR for toluene (model 2). The most precise SVR model was obtained with a linear kernel. The model possesses the following parameters: C = 300 000 and epsilon = 0.001. The linear kernel of the model allows one to evaluate the contribution of the descriptors. The model used a reduced set of molecular parameters; let us consider the three most significant descriptors. Similar to the MLR model, the most significant descriptors were Eig03_EA(dm) with an importance of 28.0% and TDB06p with an importance of 21.6% (Table 4).

Table 4 Relative contribution of descriptors to SVR model in toluene (model 2)

Descriptors	Relative contribution, %
Eig03_EA(dm)	28.0
TDB06p	21.6
VE1_RG	14.5
Electronegativity	12.7
Mor23i	10.1
G3u	7.2
MATS8i	5.9

---

VE1_RG descriptor is the sum of the last eigenvector coefficients (absolute values) from the inverse square geometric matrix. An eigenvector is a vector that does not change its direction when the matrix is transformed. The inverse square geometric matrix is a matrix that describes the geometry of a molecule. It is obtained by inverting the interatomic distances collected in a geometric matrix. The importance of this descriptor is 14.5% (Table 4). The largest value of VE1_RG is possessed by compound BDP-73 (BDP-73 also has the highest value of the dependent variable y). Compound BDP-63 has the lowest descriptor value equal to 2.512. The VE1_RG descriptor is related to the eigenvalues of the Randic matrix of a BODIPY, whereas the first eigenvalue of the Randic matrix is related to the stability and reactivity of the molecule. It can provide comprehension of the electronic distribution and the potential energy surface of the BODIPY molecule.

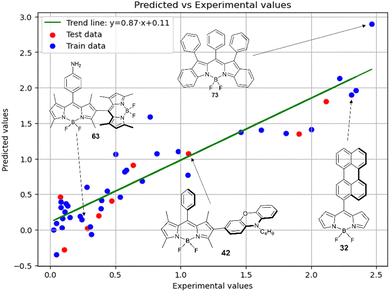
Fig. 5 shows a comparison of the experimental and SVR predicted 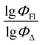values for compounds in toluene. The close correspondence of the dots to the trend is confirmed by statistical parameters.

Fig. 5 Experimental vs. predicted values of according to model 2 (SVR, toluene).

3.1.3. RFR for toluene (model 3). The RFR method uses a random selection of features for each tree node. Also, when training an RFR model, trees can be initialized randomly. This means that each time the model is trained, it takes into account different features for different nodes and the trees will grow and learn differently, which can lead to different results. Among all the trained models, the most precise one was chosen. The model had the following parameters: max_depth = 4, max_features = 1, min_samples_leaf = 1, min_samples_split = 5, n_estimators = 2.

The highest relative contribution in model 3 is observed for the ATSC4e descriptor: 34.4% (Table 5). This descriptor is used to describe the structure of a molecule and its chemical properties. It is based on the Broto–Moreau autocorrelation method, which calculates the correlation between atoms or fragments of a molecule at a certain distance: lag 4 is the distance between atoms or fragments equal to four. Thus, centered autocorrelation considers both positive and negative correlations between atoms or fragments of a molecule. ATSC4e values are Sanderson electronegativity-weighted, which means that the autocorrelation value is multiplied by the Sanderson electronegativity for each atom or fragment. Sanderson electronegativity is a measure of the ability of an atom to attract electrons in a molecule. Thus, ATSC4e takes into account both the structure of the molecule and its chemical properties related to the electronegativity of the atoms and fragments. BDP-45 molecule has the highest ATSC4e value of 0.784. In general, the presence of electron-withdrawing groups decreases the ATSC4e value, whereas electron-donating alkyl and alkoxy groups increase the ATSC4e value. BDP-66 has the lowest ATSC4e value of 0.146.

Table 5 Relative contribution of descriptors to model 3

Descriptors	Relative contribution, %
ATSC4e	34.4
Eig03_EA(dm)	30.6
TDB01e	20.9
IVDE	10.5
F10[C–N]	2.4
CATS2D_04_PL	1.2

---

In model 3, the second most significant descriptor is Eig03_EA(dm) with a relative contribution of 30.6%. This descriptor also had a high contribution in the MLR and SVR models.

Another significant descriptor is TDB01e, with a contribution of 20.9%. TDB01e (3D topological distance-based descriptor – lag 1, weighted by Sanderson electronegativity) is based on the 3D topological distance method, which calculates the distance between atoms and molecular fragments in 3D space. In this case, lag 1 means that the distance between atoms or fragments of a molecule is equal to one (only the nearest neighbors of atoms or fragments are considered). Also, the TDB01e descriptor accounts for the Sanderson electronegativity for each atom or fragment, which means that the topological distance value is multiplied by the Sanderson electronegativity for each atom. Thus, TDB01e factors in both the structure of the molecule and its chemical properties related to the electronegativity. BDP-1 has the highest TDB01e value of 1.352, whereas BDP-59 has a TDB01e value of 1.281, which is the smallest one.

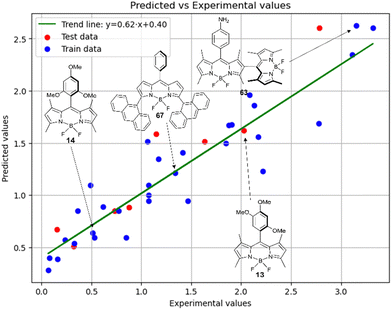
Fig. 6 demonstrates that the results obtained experimentally for BODIPYs in toluene are consistent with the predictions made using the RFR method. High statistical parameters are observed for the test set as well.

Fig. 6 Experimental vs. predicted values of according to model 3.

Therefore, different ML models in toluene use similar descriptors. For example, in model 1 (MLR, toluene) major descriptors are TDB06p and Eig03_EA(dm). Model 2 (SVR, toluene) utilizes Eig03_EA(dm) and TDB06p, whereas model 3 (RFR, toluene) uses Eig03_EA(dm) and TDB01e descriptors. All three models involve the Eig03_EA(dm) descriptor, which, in general, depicts molecular symmetry. Apparently, the Eig03_EA(dm) descriptor allows to separate highly symmetrical molecules (a feature not favorable for high 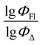) from more asymmetrical ones, which are favorable to have low SOCT-ISC and high 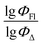. Moreover, models 1–3 all contain a TDB-type descriptor. TDB descriptors allow to distinguish molecules with polarized/electronegative substituents specific for high rate of SOCT-ISC from BODIPYs with substituents favorable for high 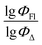. Global electronegativity descriptor is also possessed by two out of three toluene models. The dependence of singlet oxygen generation quantum yield on electronegativity is in line with previous works by us²⁴ and others.³¹

3.2. Acetonitrile model

Photophysical data for 39 BODIPY compounds in acetonitrile collected from the literature are presented in Table S1 (ESI†). This dataset was also split into test and training set. Models were trained using the training set and the best models were selected for further analysis. The statistical parameters of the models are shown in Table 6 and Table S5 (ESI†).

Table 6 Statistical parameters of the models for BODIPYs dissolved in acetonitrile

Parameter	MLR	SVR	RFR
R test ^2	0.739	0.880	0.870
RMSEtest	0.427	0.295	0.301

---

As shown in Table 6, all three models are statistically sufficient, i.e. the statistical metrics have satisfactory values (R_train² > 0.6, q² > 0.5, R_test² > 0.5), indicating that the models possess good predictive ability. The RFR model has the highest R_train² and the lowest RMSE_trian, but moderate R_test² and RMSE_test values. The MLR model is balanced in terms of training indicators, but the worst in terms of test indicators. The SVR model has the highest value of the most important statistical parameter R_test² and the lowest RMSE_test. The MLR model has a q² > 0.5, which indicates that the model is the most internally stable one for acetonitrile. The RFR and SVR model have a q² equal to 0.528 and 0.483. respectively. This may indicate that the SVR model has an average ability to predict the data, as more than 50% of the variability in the data remains unexplained. However, the study used a small number of molecules, for which q² is not as informative as R². The R_adjusted² is also > 0.6 for all the models, which means that QSPR methodology works fine for the regarded dataset.

3.2.1. Model 4 (MLR, acetonitrile). A linear regression equation was derived for the most successful MLR model. The coefficients of the equation are presented in Table 7. VE1sign_G/D is the sum of the coefficients of the last eigenvector from the distance matrix. A distance matrix is a matrix in which each element reflects the distance between pairs of atoms in a molecule. The eigenvectors of this matrix can be used to analyze the shape and size of a molecule, as well as to reveal symmetry and other structural characteristics. The sum of the last eigenvector values can provide information about the electron density distribution or the structural stability of the molecule. This descriptor has the largest relative contribution (23.9%). BDP-17 molecule has the highest VE1sign_G/D value of 0.351 (Table S6, ESI†). Although the descriptor values are well distributed from 0 to the largest value, VE1sign_G/D value is not able to predict the value of the target variable on its own. For example, the molecule BDP-63 has a low descriptor value, but its target variable y has a high value.

Table 7 Coefficients of MLR equation for BODIPYs in acetonitrile and relative contributions of the descriptors

Descriptor	Coefficient	Relative contribution, %
Intercept	1.34016439	—
CATS2D_06_PL	0.74562573	15.3
VE1sign_G/D	1.14360872	23.9
R3p+	0.17823064	3.4
F01[C–N]	0.91168208	19.4
F04[C–N]	−0.49813696	−10.3
VE2sign_G/D	−0.99441918	−21.1
B06[N–O]	0.32897972	6.7

---

VE2sign_G/D is the average coefficient of the last eigenvector from the distance matrix. The eigenvector, especially the last one in descending order of eigenvalues, often reflects the least significant structural changes in the molecule. Thus, the average coefficient of this vector can provide information about subtle but important aspects of the structure that may be related to its chemical and physical properties. The descriptor makes the second largest contribution to the model (−21.1%). A negative contribution value indicates that the descriptor is inversely correlated to the target variable y. The BDP-15 molecule has the highest value of this descriptor, equal to 0.00618. BDP-64 has the lowest VE2sign_G/D value equal to 0. VE2sign_G/D descriptor is related to the second eigenvalue of the Laplacian matrix for the BODIPY, i.e. stability and reactivity of the molecule. VE2sign_G/D descriptor provides a measure of the BODIPY topology and connectivity, weighted by the degrees of the atoms.

F01[C–N] (relative contribution equals 19.4%) shows how often bonds between carbon and nitrogen atoms occur in a molecule at topological distance equal 1. Topological distance 1 means that the carbon and nitrogen atoms directly interact with each other. Among the considered molecules, this descriptor takes discrete values: 4, 5, 7, 8 and 9. For compound BDP-63, this descriptor takes the highest value equal 9. For more than half of the molecules, the descriptor value equals 4.

Fig. 7 demonstrates that the experimental data for BODIPY compounds studied in acetonitrile correlates well with the predictions made by model 4. Thus, model 4 is suitable for predicting the ratio of the logarithms.

Fig. 7 Experimental vs. predicted values of according to model 4 (acetonitrile, MLR).

3.2.2. SVR model for acetonitrile (model 5). The most successful SVR model was obtained with a linear kernel. The model has following parameters: C = 100 000 and epsilon = 0.001. The linear kernel of the model allows one to evaluate the contribution of descriptors.

The most significant descriptor in the SVR model is F06[N–B], its relative contribution is 20.0% (Table 8). It stands for the number of times nitrogen and boron atoms are within a topological distance of six bonds from each other in a molecule. Topological distance is measured by the minimum number of bonds that must be traversed to get from one atom to another. Only four molecules have values of this descriptor that are not equal to 0. The highest values of the descriptor are for compounds BDP-61 and BDP-63: they are equal to 3. These compounds have the highest value of the target variable y.

Table 8 Relative contribution of descriptors to model 5

Descriptors	Relative contribution, %
F06[N–B]	20.0
F01[C–N]	18.3
B05[O–O]	15.3
LDI	14.2
F04[C–B]	12.6
LLS_02	10.5
E LUMO (eV)	9.1

---

The second most important descriptor is f01[C–N], its relative contribution to the model is 18.3%. This descriptor was already used in the MLR model 4 for acetonitrile.

In model 5, the third most important descriptor is B05[O–O], indicating the presence/absence of oxygen atoms at a topological distance of five bonds in the molecule. This means that if a path of five bonds can be developed between two O atoms, then this descriptor will take that arrangement into account. In cheminformatics, descriptors of this type are used to analyze the structural features of molecules and can help predict their chemical and physical properties, as well as biological activity. For example, certain distances between oxygen atoms can affect a molecule's ability to form hydrogen bonds or its reactivity in chemical reactions. Among the studied molecules, the descriptor value is not equal to 0 for only two compounds: BDP-12 and BDP-13, in which it is equal to 1.

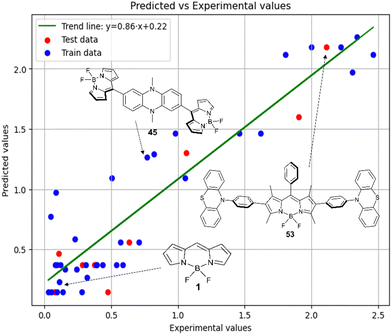
Fig. 8 illustrates sufficient agreement between the experimental results and the predictions made by the SVR method. The deviation of data points from the trend line is greater than for the SVR model in toluene (model 2), but model 5 can still be used to make predictions.

Fig. 8 Experimental versus predicted values of according to model 5 (acetonitrile, SVR).

3.2.3. RFR model for acetonitrile (model 6). Among RFR models for acetonitrile, the most significant one predicts the target variable y using the following parameters: max_depth = 6, max_features = log 2, min_samples_leaf = 1, min_samples_split = 5, n_estimators = 6.

The largest relative contribution with a value of 39.6% of the RFR model is caused by the H2u descriptor (Table 9). The molecular descriptor H2u, or unweighted H autocorrelation for lag 2, is a statistical measure that evaluates the relationship between the atomic property values of hydrogen in a molecule separated by two chemical bonds. “Lag 2” means that the relationship between hydrogen atoms that are separated by two bonds is being considered. The “unweighted” part of the description indicates that when calculating autocorrelation, no weights are used for atoms or bonds, that is, they are all considered equally important. Compounds BDP-67 and BDP-63 have the highest value of the descriptor: 4.173 and 4.118, respectively. BDP-2 has the lowest descriptor value: 2.052. Thus, H2u descriptor allows to distinguish topologically simple BODIPY molecules from topologically complex structures with multiple H–X–H groups (Table S8, ESI†).

Table 9 Relative contribution of molecular descriptors to model 6

Descriptors	Relative contribuion, %
H2u	39.6
P_VSA_log P_5	19.9
F01[C–N]	19.8
Polar area(75) (Å^2)	10.2
GATS7p	6.7
X1Av	3.9

---

The second most important descriptor is P_VSA_log P_5 (relative contribution equals 19.9%). It is related to the van der Waals surface area (VSA) descriptors associated with the logarithm of the partition coefficient (log P). log P is one of the most popular descriptors and is a measure of the hydrophobicity of a molecule: it is the logarithm of the ratio of the concentrations of a compound in two phases: octanol and water. P_VSA_log P_5 denotes the fifth interval of van der Waals surface values that correlates with log P. This can be used to evaluate how a van der Waals surface of a molecule affects its hydrophobic properties. BDP-13 and BDP-14 have the highest value (61.470) of this descriptor. BDP-2 has the lowest descriptor value which is 6.371.

The third most significant descriptor is F01[C–N] with a relative contribution of 19.8%. In models 4 and 5, F01[C–N] had a similar amount of relative contribution. It can be considered robust as its importance is confirmed in various modeling techniques.

Fig. 9 shows the experimental and predicted y values obtained using the RFR method for compounds in acetonitrile. The observed trend indicates the ability of the model to predict the target parameter.

Fig. 9 Experimental vs. predicted values of according to model 6 (acetonitrile, RFR).

Thus, in acetonitrile, the major contributor of models 4 and 5 is a F01[C–N] 2D atom pair, which is one of the major descriptors in model 6 as well. This shows that optical properties of the BODIPY can be modelled by using similar approach as for pharmacophores modeling. Model 6 is dominated by H2u descriptor (39.6% of relative contribution).

Finally, a comparison of toluene and acetonitrile models show that QSPR models for toluene possess mainly 3D topological descriptors (Eig03_EA(dm), TDB06p, etc.) reflecting molecular symmetry and taking into account the presence of heteroatoms (through local dipole moments and electronegativities) in the side substituents. For comparison, acetonitrile models utilize mostly 2D atom pairs frequency: first, F01[C–N] descriptor, but also F04[C–N], F06[N–B], etc. 2D atom pairs are usually exploited in pharmacophore modeling, however, in our case 2D representation of BODIPYs was also beneficial. In particular, the frequency of C–N atom pairs at a distance of a single bond was representative for studying BODIPY photochemistry. In simple terms, the presence of multiple nitrogen atoms in the side substituents is favorable for low SOCT-ISC and high .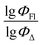

4. Conclusions

Functional dyes capable of undergoing the SOCT-ISC process and exhibiting both fluorescence emission and photosensitization ability hold great promise for various photonic technologies, yet their full potential remains largely unexplored. There are unresolved questions regarding the design of these systems, highlighting the need for additional fundamental studies to drive future technological advances. Specifically, the absence of established structure–property relationships for predicting SOCT-ISC efficiency based on molecular structure, and the lack of practical guidelines for designing structures where fluorescence and ISC can be controlled, pose significant challenges that need to be addressed.

In this study, we analysed the relationship between molecular descriptors and the ratio of fluorescence and singlet oxygen generation quantum yields (Φ_Fl/Φ_Δ) for a series of BODIPY compounds using QSPR. Three machine learning methods—support vector regression (SVR), multiple linear regression (MLR), and random forest regression (RFR)—were employed to model two groups of compounds studied in toluene and acetonitrile, respectively.

The analysis revealed the significance of various descriptors, with those related to the electronic structure, polarizability, ionization potential, and topological features playing crucial roles. Notably, descriptors related to 2D atom pairs (the shortest path between two atoms in the molecule, measured by the number of bonds), particularly the arrangement of carbon and nitrogen atoms, emerged as highly influential for compounds in acetonitrile. High statistical parameters of the models demonstrated their accuracy in predicting the Φ_Fl/Φ_Δ ratio, with the RFR model performing best for compounds in toluene and the SVR model for compounds in acetonitrile.

Our findings demonstrate the applicability of the QSPR methodology for studying the Φ_Fl/Φ_Δ ratio, providing a valuable tool for pre-synthetic screening of promising structures. These predictive models offer a simple and effective means to expedite the search for novel functional dyes, replacing the need for random synthesis of new molecular libraries. Furthermore, they can guide the synthesis of dyes with a desired Φ_Fl/Φ_Δ ratio in specific environments, such as solvents of varying polarity, potentially accelerating the search for new theranostic drugs.

Data availability

The data supporting this article have been included as part of the ESI.† The Scikit-Learn code can be accessed at GitHub repository.

Conflicts of interest

There are no conflicts of interest to declare.

Acknowledgements

A. B. is thankful to the Strategic Academic Leadership Program “Priority 2030” of the Kazan Federal University. A. S. acknowledges the TU Dublin Research Scholarship programme. M. F. acknowledges Science Foundation Ireland (SFI award 21/FFP-A/9214, DyeSICPhoto) for support of this work.

References

1. Y. Hou, L. Liu and J. Zhao, Energy Fuels, 2021, 35, 18942.
2. A. Kamkaew, S. H. Lim, H. B. Lee, L. V. Kiew, L. Y. Chung and K. Burgess, Chem. Soc. Rev., 2013, 42, 77.
3. S. E. Seo, H.-S. Choe, H. Cho, H. Kim, J.-H. Kim and O. S. Kwon, J. Mater. Chem. C, 2022, 10, 4483.
4. X. Zhang, Z. Wang, Y. Hou, Y. Yan, J. Zhao and B. Dick, J. Mater. Chem. C, 2021, 9, 11944.
5. G. Jiang, H. Liu, H. Liu, G. Ke, T.-B. Ren, B. Xiong, X.-B. Zhang and L. Yuan, Angew. Chem., Int. Ed., 2024, 63, e202315217.
6. (a) R. Prieto-Montero, A. Díaz Andres, A. Prieto-Castañeda, A. Tabero, A. Longarte, A. R. Agarrabeitia, A. Villanueva, M. J. Ortiz, R. Montero, D. Casanova and V. Martínez-Martínez, J. Mater. Chem. B, 2023, 11, 169; (b) J. Jiménez, R. Prieto-Montero, B. L. Maroto, F. Moreno, M. J. Ortiz, A. Oliden-Sánchez, I. López-Arbeloa, V. Martínez-Martínez and S. de la Moya, Chem. – Eur. J., 2020, 26, 601.
7. H. Uoyama, K. Goushi, K. Shizu, H. Nomura and C. Adachi, Nature, 2012, 492, 234.
8. R. Keruckiene, A. A. Vaitusionak, M. I. Hulnik, I. A. Berezianko, D. Gudeika, S. Macionis, M. Mahmoudi, D. Volyniuk, D. Valverde, Y. Olivier, K. L. Woon, S. V. Kostjuk, S. Reineke, J. V. Grazulevicius and G. Sini, J. Mater. Chem. C, 2024, 12, 3450.
9. (a) H. L. Wang, C. H. Du, Y. Pu, R. Adur, P. C. Hammel and F. Y. Yang, Phys. Rev. Lett., 2014, 112, 197201; (b) C. Du, H. Wang, F. Y. Yang and P. C. Hammel, Phys. Rev. B, 2014, 90, 140407.
10. T. Yogo, Y. Urano, Y. Ishitsuka, F. Maniwa and T. Nagano, J. Am. Chem. Soc., 2005, 127, 12162.
11. J. W. Verhoeven, J. Photochem. Photobiology C, 2006, 7, 40.
12. (a) M. A. Filatov, S. Karuthedath, P. M. Polestshuk, S. Callaghan, K. Flanagan, M. Telitchko, T. Wiesner, F. Laquai and M. O. Senge, Phys. Chem. Chem. Phys., 2018, 20, 8016; (b) M. A. Filatov, S. Karuthedath, P. M. Polestshuk, S. Callaghan, K. Flanagan, T. Wiesner, F. Laquai and M. O. Senge, ChemPhotoChem, 2018, 2, 606.
13. (a) N. Epelde-Elezcano, E. Palao, H. Manzano, A. Prieto-CastaCeda, A. R. Agarrabeitia, A. Tabero, A. Villanueva, S. de la Moya, C. Ljpez-Arbeloa, V. Martinez-Martinez and M. J. Ortiz, Chem. – Eur. J., 2017, 23, 4837; (b) Y. Liu, J. Zhao, A. Iagatti, L. Bussotti, P. Foggi, E. Castellucci, M. Di Donato and K.-L. Han, J. Phys. Chem. C, 2018, 122, 2502.
14. M. A. Filatov, Org. Biomol. Chem., 2020, 18, 10.
15. (a) N. Kiseleva, M. A. Filatov, M. Oldenburg, D. Busko, M. Jakoby, I. A. Howard, B. S. Richards, M. O. Senge, S. M. Borisov and A. Turshatov, Chem. Commun., 2018, 54, 1607; (b) N. Kiseleva, D. Busko, B. S. Richards, M. A. Filatov and A. Turshatov, J. Phys. Chem. Lett., 2020, 11, 6560; (c) N. Kiseleva, M. A. Filatov, J. C. Fischer, M. Kaiser, M. Jakoby, D. Busko, I. A. Howard, B. S. Richards and A. Turshatov, Phys. Chem. Chem. Phys., 2022, 24, 3568.
16. M. A. Filatov, S. Karuthedath, P. M. Polestshuk, H. Savoie, K. J. Flanagan, C. Sy, E. Sitte, M. Telitchko, F. Laquai, R. W. Boyle and M. O. Senge, J. Am. Chem. Soc., 2017, 139, 6282.
17. S. Callaghan, M. A. Filatov, H. Savoie, R. W. Boyle and M. O. Senge, Photochem. Photobiol. Sci., 2019, 18, 495.
18. (a) T. Mikulchyk, S. Karuthedath, C. S. P. De Castro, A. A. Buglak, A. Sheehan, A. Wieder, F. Laquai, I. Naydenova and M. A. Filatov, J. Mater. Chem. C, 2022, 10, 11588; (b) A. Sheehan, T. Mikulchyk, C. S. P. De Castro, S. Karuthedath, W. Althobaiti, M. Dvoracek, H. J. Sabad-e-Gul, F. Byrne, I. Laquai, M. A. Naydenova and Filatov, J. Mater. Chem. C, 2023, 11, 15084.
19. A. Schüller, G. B. Goh, H. Kim, J.-S. Lee and Y.-T. Chang, Mol. Inform., 2010, 29, 717–729.
20. A. A. Ksenofontov, M. M. Lukanov, P. S. Bocharov, M. B. Berezin and I. V. Tetko, Spectrochim. Acta, Part A, 2022, 267, 120577.
21. E. Caruso, M. Gariboldi, A. Sangion, P. Gramatica and S. Banfi, J. Photochem. Photobiol., B, 2017, 167, 269.
22. A. A. Buglak, A. Charisiadis, A. Sheehan, C. J. Kingsbury, M. O. Senge and M. A. Filatov, Chem. – Eur. J., 2021, 27, 9934.
23. M. J. S. Dewar, E. G. Zoebisch, E. F. Healy and J. J. P. Stewart, J. Am. Chem. Soc., 1985, 107, 3902.
24. A. A. Buglak, T. A. Telegina and M. S. Kritsky, Photochem. Photobiol. Sci., 2016, 15, 801.
25. I. Sushko, S. Novotarskyi, R. Körner, A. K. Pandey, M. Rupp, W. Teetz, S. Brandmaier, A. Abdelaziz, V. V. Prokopenko, V. Y. Tanchuk, R. Todeschini, A. Varnek, G. Marcou, P. Ertl, V. Potemkin, M. Grishina, J. Gasteiger, C. Schwab, I. I. Baskin, V. A. Palyulin, E. V. Radchenko, W. J. Welsh, V. Kholodovych, D. Chekmarev, A. Cherkasov, J. Aires-de-Sousa, Q.-Y. Zhang, A. Bender, F. Nigsch, L. Patiny, A. Williams, V. Tkachenko and I. V. Tetko, J. Comput. Aided Mol. Des., 2011, 25, 533.
26. A. Mauri, in alvaDesc: A Tool to Calculate and Analyze Molecular Descriptors and Fingerprints, Methods in Pharmacology and Toxicology, 2020, pp. 801–820.
27. A. Mauri, V. Consonni, M. Pavan and R. Todeschini, MATCH Commun. Math. Comput. Chem., 2006, 56, 237.
28. K. Roy, J. Indian Chem. Soc., 2019, 95, 1497.
29. (a) M. Luo, X. S. Wang, B. L. Roth, A. Golbraikh and A. Tropsha, J. Chem. Inf. Model., 2014, 54, 634; (b) A. A. Buglak, M. A. Filatov, M. A. Hussain and M. Sugimoto, J. Photochem. Photobiol. A: Chem., 2020, 403, 112833.
30. A. Golbraikh and A. Tropsha, J. Mol. Graphics Modell., 2002, 20, 269.
31. C. Schweitzer and R. Schmidt, Chem. Rev., 2003, 103, 1685.

---

Footnote

† Electronic supplementary information (ESI) available. See DOI: https://doi.org/10.1039/d4cp02471k

---