DFT and machine learning guided investigation into the design of new dual-atom catalysts based on α-2 graphyne

Abstract

The realm of atomic catalysts has witnessed notable advancements; yet, the predominant focus remains on single atomic catalysts (SACs). The exploration and successful implementation of dual atomic catalysts (DACs) pose intricate challenges, primarily concerning thermodynamic stability and optimal metallic composition. To address these issues, we present a comprehensive theoretical investigation of α-2 graphyne (GPY)-based DACs, synthesized in-house with a keen focus on formation stability. Density functional theory (DFT) simulations were leveraged to ascertain each DAC structure's stability, considering numerous transition metal permutations totalling about 823 DACs. Furthermore, we developed a machine learning (ML) model that predicts stability based solely on the physical characteristics of the constituent elements in the DACs, thus eliminating the need for extensive DFT calculations. Our findings not only offer detailed insights into atomic interactions but also highlight promising candidates for DACs, pushing beyond traditional trial-and-error synthesis approaches. This study fosters a deeper understanding of DACs and paves new pathways for exploring atomic catalysts for practical applications.

---

1 Introduction

Human society is confronted with increasingly serious challenges of resource depletion and environmental degradation as a result of the continued expansion of industrialisation and the growth of the world's population. The overuse of fossil fuels like oil, coal, and natural gas has exacerbated the already dire energy problem and increased environmental degradation.¹ Hence, a crucial area of study in the realm of catalysis and energy research is the investigation and development of clean, renewable energy sources that can replace fossil fuels.^2,3 Studies on clean energy storage and conversion technologies such as metal–air batteries,⁴ electrolytic cells,⁵ and fuel cells⁶ are particularly intriguing. These devices rely on charge transfer processes and electrocatalytic reactions that take place on the electrode material for the conversion of electrical and chemical energies, such as oxygen reduction and evolution reactions, hydrogen evolution/oxidation reactions, etc.^7–9 The primary electrode materials in these devices are electrocatalysts, and the thermodynamic and kinetic processes of electrocatalytic reactions are intimately tied to the physical characteristics and chemical states of electrocatalysts.

Nano-engineering-based solutions have been presented to create electrocatalysts with enhanced performance in response to rising expectations about catalyst efficiency and activity.^10–13 Some noble-metal surfaces, such as Pt, Pd, Rh, and Au, have been shown in prior research to be capable of catalysing CO oxidation.^14–16 However, their use in large-scale processes is constrained by their high operating temperature, poor durability, and high cost. It is well known that switching from bulk materials to supported nanoparticles improves the catalytic performance in many reactions including the CO oxidation reaction.¹⁷ The supported metal nanoparticles’ catalytic activity, though, can be significantly shape- and size-dependent.^18,19 Additionally, because only the surface atoms of the metals are active for catalysis, the overall efficiency is quite poor on a per metal atom basis. Therefore, downsizing the metal nanostructures to well-defined, atomically scattered metal active centres, that is, single-atom catalysts (SACs),^20,21 which is the ultimate goal of fine dispersion, is the most efficient technique to utilise every metal atom of supporting metal catalysts. Some examples of SACs, including single Au/Pt/Ir/Ni/Os atoms on FeO_x, Co₃O₄, CeO₂, Al₂O₃, and MgO surfaces, have been successfully fabricated using metal oxide supports since the first SAC, single Pt atoms on FeO_x, was reported in 2011.^22,23 Despite the fact that SACs have more significant uses than metal nanoclusters, there are a number of significant SAC-related difficulties that raise questions about how well they will be used.²⁴ For example, because of the low metal loading, the whole catalyst is sometimes required to have a heavy loading, which makes the mass-transfer resistance worse.²⁵ Along with this, the consistency of the SACs is still another significant factor to consider. For surface catalytic reactions that require ensemble sites, such as C–C dissociation reactions, SACs can't be a perfect choice as they do not have any ensemble sites.^26,27 In addition to the previously described issues, one significant constraint is that because SACs have only one catalytic site, reactions involving numerous reactants cannot take place because competing adsorption would significantly reduce the catalytic activity on a single-atom structure, as for example in the CO oxidation reaction.

Due to their greater versatility in catalytic tuning than SACs, dual-atom catalysts (DACs), an outgrowth of SACs, have recently received increased attention. DACs with a low number of bridge active sites can both improve the metal loading and the percentage of the active centre while maintaining the same level of metal consumption.^28,29 Moreover, DACs have a distinct competitive edge due to their metal cooperativity.³⁰ The interaction and stabilisation of two neighbouring metal atoms can increase the stability and synthesisability of DACs.³¹ The interest in DACs intensified following the groundbreaking work of He et al., who successfully fabricated and characterised graphene-supported Fe dopant pairs.³² An additional potential method to achieve DACs involves using MOFs with various metal precursors.^33,34 In both theoretical and experimental research, a growing number of homonuclear and heteronuclear DACs are being used. Nevertheless the accurate characterization, suppression of metal agglomeration, and management of metal atom anchoring provide substantial hurdles to the DACs' ongoing advances.³⁵ Furthermore, the numerous combinations of all the transition metals (TMs) present a challenge to such promising DAC techniques, necessitating an astronomically high cost to individually test the effectiveness of each catalyst. To appropriately examine and screen the most viable and probable choices, the ideal solution is to integrate theoretical calculations with machine learning algorithms, which can provide the essential direction for trials.

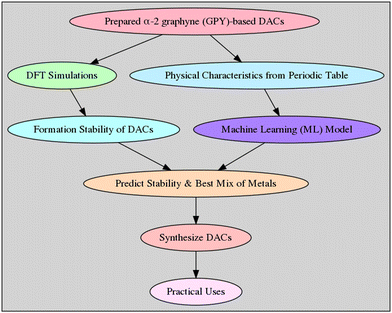
The crucial element to ensuring the stable isolation of surface metal atoms as active sites and achieving high electrocatalytic performances is the strong contacts between the anchoring metal atom and the support material.³⁶ This is the most important foundation for a good atomic catalyst. A novel kind of substrate with distinctive low-dimension structures and coordination environments has been made available by a carbon-based support. Methane has been successfully activated on a dual-atom catalyst supported by graphene, as recently demonstrated.³⁷ Many research studies have used carbon-based materials as the basis for atomic catalysts to activate various kinds of significant catalytic and electrocatalytic events.^38,39 Graphdiyne (GDY),⁴⁰ one of the several carbon-based support materials, has emerged as one of the most promising contenders. Most significantly, GDY contains both sp² and sp hybridised carbon atoms with high levels of conjugations; the special sp hybridisation enhances intermediate adsorption and coordination of metal atoms during electrocatalysis. Subramanian and coworkers⁴¹ created a special type of α-graphyne structure, namely α-2 graphyne, by inclusively introducing acetylene linkers into the graphyne precursor and it has been shown to be very interesting in terms of electronic properties. Also, due to the inclusion of acetylene linkers, there are increasing numbers of sp hybridisations, which eventually can enhance its application as a support material for catalytic applications. Motivated by the current research status, herein we have conducted parallel theoretical research on α-2 graphyne for DACs by taking into account all possible TM combinations. It is to be noted that there are a few previous studies where the s block alkaline-earth metal catalysts have also been extensively studied^42–45 and in the future we have a plan to study the details using the alkaline-earth metals as well. The overall idea of the manuscript is illustrated in Fig. 1.

Fig. 1 A flowchart illustrating the overall idea developed in the article.

2 Computational details

2.1 Details about DFT calculations

The projector augmented wave approach within the framework of density functional theory (DFT), as implemented in the Vienna ab initio simulation program (VASP), was used for all electronic structure computations.⁴⁶ The Perdew–Burke–Ernzerhof functional was used as a parameter to define the exchange–correlation energy within the framework of the generalised gradient approximation.⁴⁷ A plane wave basis set was employed with an energy threshold of 450 eV. The Grimme (DFT-D3) technique, which employs a semiempirical correction methodology, was able to take into account van der Waals interactions.⁴⁸ The influence of spin polarisation was accounted for in all calculations. The energy and force convergence criteria were set to 10⁻⁴ eV and 10⁻³ eV Å⁻¹, respectively. The Brillouin region was sampled using a 5 × 5 × 1 Monkhorst–Pack special k-point mesh for structural relaxation and a 7 × 7 × 1 mesh for density of state (DOS) computations. To prevent the introduction of any unnatural interactions caused by periodic images, a vacuum of roughly 15 Å was established between two neighbouring graphyne layers.

2.2 Details about the ML model

Our analysis includes 823 different possible setups. Without resorting to any further first-principles calculations, we construct a high-dimensional feature space by utilising the properties of the relevant systems obtained from the periodic table. As a result, we use a set of 40 features for target prediction as our primary dataset. In order to ensure that our machine learning models produce consistent results regardless of the scale or size of the underlying dataset, we convert the features before using the dataset. To pick the most relevant features, we built a Pearson correlation using permutation feature importance analysis. For feature importance analysis we used the SHapley Additive exPlanations (SHAP) technique. The SHAP values assigned to each feature indicate the alteration in the anticipated model prediction when the model is conditioned on that specific characteristic. The SHAP value provides an explanation for each feature by quantifying its contribution to the discrepancy between the average prediction made by the model and the actual prediction for a given instance. We use a wide range of supervised machine learning algorithms, such as multiple linear regression (MLR), random forest models (RF), ridge regression (RR), least absolute shrinkage and selection operator (LASSO), extra trees (ET), and gradient boosting (GB), to make predictions about the characteristics.^49–54

We used root mean squared error (RMSE) as our loss metric, which is determined using eqn (1), where y_i, 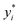and m denote the true values, predicted values and the number of samples in the dataset, respectively.

For all machine learning training and prediction, we leaned on the Scikit-learn tool.⁵⁵

3 Results and discussion

3.1 Structure of the α-2 graphyne (GPY) system

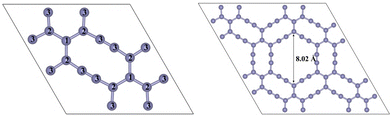
The GPY unit cell contains 20 carbon atoms and the optimised unit cell has a hexagonal lattice with a = b = 9.38 Å, which is consistent with that determined in a previous report.⁴¹ There are three different bond lengths and three different bond angles present in the unit cell, as illustrated in Table 1. These bond lengths and angles correspond to the three different hybridizations of C atoms (sp–sp, sp–sp², and sp²–sp²), which agrees well with those obtained in a previous report.⁴¹ In the 2 × 2 supercell the largest distance between the two corner positions is 8.02 Å in the hexagonal vacancy site as shown in Fig. 2. Previously it was shown that this system was stable at room temperature using first-principles molecular dynamics (FPMD) simulations and for investigating its dynamic stability phonon calculations were done, also showing a similar cohesive energy to those of α-, β- and γ-graphyne systems.⁵⁶ It also has a similar areal density to that of a graphene system.

Table 1 Structural details of the α-2 graphyne unit cell

System	Bond length (Å)	Bond angle (°)
α-2 graphyne	1.44 (C1–C2)	120 (C2–C1–C2)
	1.38 (C2–C3)	114 (C3–C2–C3)
	1.22 (C3–C3)	177 (C2–C3–C3)

---

Fig. 2 Unit cell representation of the α-2 graphyne structure (left panel) showing different types of C atoms with numbers and the supercell is shown in the right panel. The longest distance between two C atoms in the vacancy site is also shown here.

3.2 Geometric structure and stability of DACs

The DACs have been successfully formed by anchoring metal dimers to a variety of 2D materials, including graphene, graphitic carbon nitride (g-C₃N₄), nitrogen-doped carbons, and rectangular-shaped expanded phthalocyanine.^32,57–59 Recently, using first-principles calculations, researchers have explored γ-graphyne's (γ-GY's) potential as a substrate for metals in the fourth and fifth periods under single-atom and dual-atom concentration modes and eventually a few dual atomic sites have been found to be very active for the CO oxidation reaction.⁶⁰ The thermodynamic trends of formation, as the most essential aspect, should be one of the most critical criteria to determine the synthesis possibilities in experiments. We have taken into account all the 3d, 4d, and 5d transition metals from group IVB to IB, for a grand total of 823 possible combinations of metal atoms, which include both homonuclear and heteronuclear combinations, in order to create dual atom catalysts.

We have accounted for all conceivable vacancy sites in the structure by considering a α-2 graphyne unit cell with a 2 × 2 configuration. We found that only the largest hexagonal vacancy position is suitable for accommodating metal atoms, wherein placing metal atoms in other positions deformed the original structure of GPY. The initial metal is shown to have been inserted into the big hexagonal cavity and to have formed bonds with the adjacent carbon atoms in Fig. 3. The second metal also forms connections with the carbon atoms since it was positioned similarly. When examining DACs in detail, it is clear that there are two distinct ways in which metal atoms can remain in the vacant sites. Smaller-radius metal atoms (3d or early 4d) arrange themselves in a flat plane, while larger-radius metal atoms buckle a bit, with one atom remaining in the same plane as the substrate and the other below it. Sc–Sc, Zr–Zr, and Hf–Hf DACs all exhibit extremely comparable bond length variations, and under most conditions, we observe that metal atoms in the same plane within the pore of the GPY are stabilised. Distinct types of distortion are observed with the heterocoupling DACs. Because of variations in the ionic radius and electronic structure, the atomic distributions are asymmetric, which in turn distorts the GPY bonding. For 4d–5d and 5d–5d hetero-coupling DACs, we find that the metal is separated from the GPY due to the strong repulsive force, resulting in dangling metal sites on the GPY. The structure depicted in Fig. 3 turned out to be the energetically most favourable one after we investigated other sites in the GPY surface for anchoring the metal atoms. The constructed metal dimers in the DACs show a bond length ranging from 2.04 Å to 4.10 Å, resulting in a wide variety of DAC structures. Table S1 (ESI†) provides some values for bond lengths.

Fig. 3 Representation of the formation of dual atom catalysts. The different combinations of metals lead to varied interactions and formation of different DACs occurs.

We have created a variety of metrics for calculating thermodynamic stabilities in order to make direct comparisons between the formation preferences. The binding energy (E_b) was calculated to ascertain the likelihood of the uniform distribution and it was calculated using the following equation:

where , E_GPY and represent the energies of the metal intercalated system, bare GPY system and isolated metal atoms, respectively. From Fig. 4, upper left panel, it is seen that most of the considered DACs show negative binding energies, which confirms the strong binding of the metal atoms with the substrate structure, which is important for the stability of the DACs. Anchoring two TM metals from the same row appears to be the most promising method due to the similarities in atomic radii and electronic structures. After careful evaluation of binding energies, it is seen that 5d–5d combinations showed the highest binding energy followed by 4d–5d, 3d–5d and 3d–4d combinations. 3d–3d metal combinations showed lower binding energy compared to the other combinations and this corresponds well with the size of the TM atoms. To learn more about the strong binding preferences of the DACs, we made box plots for different combinations of DACs that show the energy change differences very clearly. From Fig. 5 it is seen that the 5d–5d combination shows the least variations in energy suggesting a higher synthesis probability. Also, it is seen that with the introduction of heteroatoms as for example, 3d–5d combinations, the heteronuclear DACs show a higher stability than the homonuclear counterpart and this effect is more profound for early TM atoms. Electronic structure properties of both homonuclear (MM@GPY) and heteronuclear (MM′@GPY) DACs were validated by Bader charge analysis. Table S2 (ESI†) shows that a large amount of charge is transferred from the metal dimers to the GPY surface, leading to the formation of strong-polarized and hybridised metal–C bonds. Consistent with the trend of electronegativity (Table S3, ESI†), our modelled DACs show a significant decreasing trend of charge transfer from left to right in the same period, suggesting that the increased number of unpaired electrons in metal atoms favours the charge transfer to the surrounding atoms.

Fig. 4 Mapping of binding energy (top left), aggregation energy (top right), stabilization energy (bottom left) and anchoring energy (bottom right) of all the DAC combinations.

Fig. 5 The box plots of each mix of transition metals, which mainly indicate the distribution and variation range of the binding energies.

The aggregation energy is a crucial consideration for DAC stability alongside the adsorption energy and this is calculated using the following equation:

E_agg = (E_b − E_coh), (3)

E_coh = (E_TM-bulk − E_TM-single), (4)

where E_coh is the cohesion energy of metal atoms in the bulk form. For the heteronuclear diatomic system, E_coh is calculated as the average of cohesive energies of the metal atoms. From Fig. 4, it is seen that most of the DACs show negative aggregation energies confirming the formation of DACs rather than creation of metal clusters. In order to determine thermodynamic stability, many factors, such as stabilisation energies, anchoring energies, etc., must be taken into account. The following equation can be used to determine the stabilisation energies, which represent the energetic cost of combining two SACs to produce a DAC:

As can be shown in Fig. 4, most metal atoms would rather form the DACs than two separate SACs. These findings show that the experimental synthesis, which involves a mixture of metal precursors, favours the formation of a DAC at a single, optimal anchoring site over the formation of an isolated SAC at many anchoring sites. Careful examination of the data reveals that although some DACs have a low binding energy, they are less selective for DACs than isolated SACs due to a positive stabilisation energy. These findings provide further evidence that strong thermodynamic stability is not sufficient to ensure the synthesis of DACs. A further critical aspect is the rivalry for selection between the SAC and DAC.

DACs’ stability can also be described in terms of something called “anchoring energy”, which is the amount of energy needed to anchor a second metal atom within the DAC and this is calculated as follows:

From Fig. 4, it is seen that in contrast to the stabilisation energies where most of the DACs show negative values, for a higher number of DACs the anchoring energy values are positive. The stabilisation and anchoring energies are very different, and therefore it makes sense to anchor two different metal atoms at once as a synthesis strategy. In contrast, the energy cost of adding the second metal atom to the produced SAC is significantly larger.

The interaction between the d-orbitals of the two metal atoms and the support in DACs results in a distinctive electronic environment that affects the adsorption energies of reactants and intermediates. This electronic environment is essential for catalytic activity. Using the traditional d-band centre method, we investigate the electroactivity in depth, in addition to its thermodynamic stability. The d-band centres of all possible DAC permutations are displayed in Fig. 6. Instead of regular downshifting of d band centres with more filled d-orbitals, we found a “hump” type of variation. To investigate it more clearly, we considered Sc-3d DAC combinations and we found that middle TM-based DACs demonstrate a valley-like d-band center trend, supporting a low electroactivity. More importantly, the introduction of hetero-transition metals has evidently lifted the d-band center even for the fully occupied d10 element, which indicates the evident modulations by the d-electrons from transition metals. Meanwhile, we also compare the d-band center of the DAC and SAC. Interestingly, the TM–TM DACs show a distinct d-band center with the SAC, indicating the coupling effect even between similar TM metal atoms. The d-band centre is upshifted by the addition of early TMs and shifted down by the addition of late TMs, respectively, providing an explicit direction for us to predict the electroactivity of DACs based on the change in the d-band centre in TM–TM DACs, which can achieve the optimal electronic environment for electrocatalysis by balancing the d-band centre position.

Fig. 6 Mapping of the d-band centre of all the DACs (left panel) and variation of the d-band centre with introduction of heteroatoms (right panel).

In order to enhance the thermal stability of the DACs, we conducted AIMD simulations for specific DACs (Sc–Sc, Y–Y, and Hf–Hf). In these simulations, the forces were computed based on the electronic configuration in the ground state at each iteration of the molecular dynamics (MD) process. A molecular dynamics (MD) simulation was conducted using the NVT ensemble at a temperature of 300 K. The simulation duration was 6 ps, and a time step of 1 fs was employed. The findings indicate that the overall energy fluctuations of DACs remain relatively constant, and negligible atomic displacements from the equilibrium position are detected, as depicted in Fig. 7. The findings of this study provide evidence supporting the thermal stability of the digital-to-analog converters (DACs) when exposed to room temperature conditions.

Fig. 7 Total energy fluctuations during AIMD simulations for Sc–Sc (top left), Y–Y (top right) and Hf–Hf (bottom) DAC systems.

We have found that TM–TM DACs are the most stable DACs by taking into account the present thermodynamic results. However, the most stable arrangements typically involve giving up some of the DAC's electroactivity. In order to narrow down the pool of potential DACs, we have focused mostly on making direct comparisons between their electrical architectures. We observed that heteronuclear DACs offer the best chance of achieving a high electroactivity for electron transmission. Our research suggests that this work provides useful references for determining the best element combinations to use in future DAC trials.

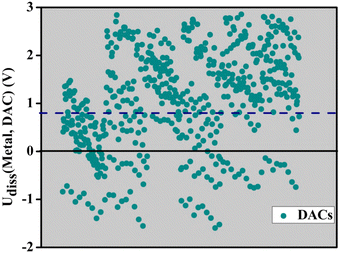
3.3 Electrochemical stability and activity

The dissolution potential (U_diss) is a crucial factor that determines the electrochemical stability of materials, especially in applications like batteries, fuel cells, and electrolysis systems. The term refers to the voltage threshold at which a substance starts to dissolve into the electrolyte, potentially causing deterioration of the electrode and compromising the material's structural integrity. Materials having a high dissolution potential are capable of enduring greater operational voltages without dissolving, which leads to a longer lifespan and consistent performance. On the other hand, a low dissolving potential indicates that the material is easily dissolved at relatively low voltages. This can lead to quick deterioration, decreased efficiency, and potential malfunction of the electrochemical system. Hence, it is crucial to comprehend and enhance the ability of electrode materials to dissolve in order to create long-lasting and effective electrochemical devices. The overall dependability and effectiveness of electrochemical systems in many applications can be improved by making sure that materials have a high dissolving potential, which enhances their stability and lifetime. In order to assess the appropriateness of our predicted DACs as electrode materials for fuel cells, we initially computed the dissolving potentials for each individual DAC. The dissolution potential has been calculated using the following equation:where U⁰_diss(metal, bulk), μ_metal,DAC, μ⁰_metal,bulk and n are the dissolution potentials of bulk metals, the chemical potential of metal atoms in DACs, the chemical potential of bulk metal and the number of electrons involved in the dissolution process, respectively. The scatter plot (Fig. 8) displays the dissolution potential, measured in volts (V), of several DACs. It reveals a consistent pattern indicating that most DACs have positive dissolution potentials, indicating their stability under the electrochemical conditions evaluated. The data points exhibit a broad dispersion, suggesting varied dissolution behaviours. A considerable number of DACs show stability above the horizontal black line at 0 V, which serves as the boundary between positive and negative potentials. The blue dashed line at 0.8 V is particularly important as it represents the potential associated with the oxygen reduction reaction (ORR). This is noteworthy since it is a commonly used operating potential for the ORR in fuel cells and metal–air batteries. The current densities are commonly evaluated at 0.8 V to assess the performance and stability of the catalysts, serving as a standard benchmark. Catalysts with dissolution potentials beyond this threshold exhibit great potential for ORR applications owing to their enhanced stability, indicating a reduced likelihood of dissolution and a greater capacity to sustain catalytic activity under ORR conditions. The stability of the systems guarantees that the active sites remain undamaged, which in turn supports consistent catalytic performance and improves the overall longevity of the catalytic systems. On the other hand, DACs that have negative potentials may be less stable and more susceptible to deterioration, which makes them less appropriate for long-term catalytic usage in ORR circumstances. In such situations, it is crucial to have consistent performance and resistance to dissolution. Based on our investigation, we have discovered numerous DACs that are appropriate for the ORR, offering useful insights for future experimental synthesis and development. Additional investigation and integration of these potential DACs could result in substantial improvements in catalytic efficiency under ORR conditions.

Fig. 8 The dissolution potential of different DACs is shown in volts (V) in the scatter plot. There is a general trend towards stability under the electrochemical conditions, since most of the DACs show positive dissolution potentials. The data points are dispersed across a range of potentials. The horizontal line at zero volts separates potentials that are positive and negative. The horizontal blue dot line at 0.8 V represents the potential at which the oxygen reduction reaction takes place.

3.4 Prediction using the machine learning model

Despite the extensive theoretical calculations conducted on the thermodynamic stability and electrical structures of GPY-based DACs, there is still a need for more analysis and study to understand the underlying causes of the observed differences. The machine learning technique possesses significant capabilities to predict probable qualities, so serving as a logical design guidance for future experimental synthesis. In order to validate the theoretical simulated outcomes, we additionally incorporate the machine learning approach.

3.4.1 Choice of the data set. The first step in developing a robust ML model is to select a large data set with sufficient variability. Distribution of the dataset for the adsorption energy is shown in Fig. 9. From Fig. 9, it is seen that in the dataset, the data distribute over a wide range and roughly obey the law of normal distribution on a whole. The data set therefore conforms to the general statistical significance.

Fig. 9 Data distribution plot of the target property (left panel) and parity plot (right panel) comparing the performance of the GB model on test data.

3.4.2 Selection of features. Appropriate input feature selection is necessary for both high-quality data analysis and an easily interpretable ML algorithm. One of the main problems with using ML to create DACs is that there aren’t enough good input features available. High simplicity, a realistic feature priority value, and physical interpretation are all necessary for a good input feature. Because of the lack of transparency in ML algorithms, it is sometimes impossible to determine the physical meaning of input features such as the d-band centre or the enthalpy of vaporisation. To represent SAC activity, for instance, the d band centre is frequently employed as an input feature with a high feature relevance value. However, it may not be able to assess the location of the d-band centre if the d levels of atomically distributed SACs on graphene and porphyrin substrates do not form a band. In addition, the properties of metal atoms and substrates are readily available without the need for costly DFT computations, making them ideal for use in the straightforward design of input features. Input features such as the ionisation energy, the number of electrons in the d orbital, the atomic number, and the coordination number of metal atoms meet the simplicity criteria but the density of states and Bader charge do not. Adsorption energy predictions can be greatly aided by using intrinsic atomic qualities collected from the periodic table, handbooks, or material databases. This, in turn, can boost the effectiveness of catalyst discovery and make ML models more comprehensible. We have chosen total 48 descriptors with a unique class of 12 features for each element of the metal and the surface of the DACs. The features chosen are: the ionic radius, electronegativity, electron affinity, covalent radius, boiling point, melting point, number of d electrons, atomic radius, atomic mass, molar volume, radius of the d orbital, and group number. Thus, the values of the descriptors were represented as a 48-dimensional vector for each element. We have chosen these features as these have a direct correlation with the predicted stability of the DACs. Electronegativity and electron affinity play a crucial role in comprehending the electrical interactions between two metal atoms, as well as their interaction with the support and adsorbates. These factors have an impact on binding energies and reactivity. The covalent radius and atomic radius offer valuable information on the spatial configuration and bonding intensity between atoms, which in turn impact the overall structural stability. Boiling and melting points serve as measures of the thermal stability and cohesive energy of atoms, which are related to their ability to resist dissolution and degradation during reactions. The quantity of d electrons is essential as it directly influences the electrical arrangement and d-band centre, hence exerting a direct influence on catalytic activity and stability. The atomic mass and molar volume are important factors in comprehending the density and efficiency of atom packing within the catalyst structure. Finally, the size of the d orbitals directly impacts the degree of orbital overlap and hybridisation with reactants, which in turn affects the adsorption and activation energies. Collectively, these characteristics offer a thorough depiction of the electrical, structural, and thermal attributes of DACs, enabling a logical forecast of their durability and effectiveness in catalytic uses. It is crucial to mention that in our examination of structural characteristics, we incorporated measurements such as the TM1–TM2 distance, TM1–support distance, and TM2–support distance. Nevertheless, the inclusion of these supplementary characteristics led to a diminished performance of the model in comparison to its performance when these factors were omitted. Although these specific structural characteristics, namely the TM1–TM2 distance, the TM1–support distance, and the TM2-support distance, have potential relevance, their addition did not improve the predictive capacity of the model. This suggests that they may not positively contribute to the accuracy of the model in this particular situation.

3.4.3 Machine learning (ML) models. Nine popular ML approaches were pre-evaluated before the final method selection was made. These methods included linear methods for linear regression, and tree ensemble methods for nonlinear regression. Although they require the assumption of linearity between the prediction objective and descriptors, linear approaches provide the most consistent foundation for prediction performance. We tried least-absolute shrinkage and selection operator (LASSO) regression and ridge regression (RD), both of which automatically reduce the number of dimensions and choose a subset of features to describe the data. We looked at random forest (RF), gradient boosting (GB), extra trees (ET), extreme gradient boosting (XGB), Decision Trees (DT), and ada boosting regression (ADB) as tree ensemble methods. Across this work, training-test splitting, cross-validation, hyperparameter tuning, and error measurement were all done in the same way. A five-fold cross-validation test was run on each model. This test stops overfitting by lowering stated bias and variance. As a way to measure how well the model worked, the mean squared error (MSE), root mean squared error (RMSE), and mean absolute error (MAE) were chosen. Each of the five folds was used as a validation set during several training rounds, and the predicted MAE for each fold was averaged across all five folds. In this way, the dataset is split 80/20 between training and testing, and each data point gets a correct test forecast error. This makes a fair guess that shows how well the trained model really does at making predictions. The best set of hyperparameters is chosen in order to lower the cross-validation error. At the end, we display each model's testing faults, but we optimise according to the validation error such that the model is never trained on the real test set. The outcomes, together with the reported error values, are displayed using a parity plot of ML predictions versus DFT values.

As discussed above we used a dataset splitting technique to build our machine learning model. We split the data into two groups of 80 : 20, keeping 80% for training and 20% for testing. This method made sure that the model was trained on the data while keeping a different set for checking. The 165 data points that made up our training set were chosen at random to avoid any intentional bias that might have skewed the model's performance. We did this random splitting and training process 100 times to make our results even more reliable and accurate. This way, we could average the results and lessen the effect of any outliers from a single split. This iterative process made the evaluation of the model's ability to guess more accurate. This gives a full picture of how well the model worked with different training datasets. Table 2 shows a comparison of the average performance metrics of various machine learning models based on these 100 experiments. As demonstrated, Gradient Boosting (GB) showed the best performance with the lowest MSE, RMSE, and MAE values. On the other hand, Lasso had the highest errors on all three metrics among the tested models.

Table 2 Average performance metrics of different models

Model	Avg MSE	Avg RMSE	Avg MAE
XGB	0.139	0.372	0.270
Random forest	0.226	0.474	0.363
Extra trees	0.227	0.475	0.358
Decision tree	0.547	0.738	0.562
Linear regression	0.545	0.737	0.604
GB	0.125	0.352	0.264
RD	0.575	0.757	0.619
ADB	0.677	0.821	0.649
Lasso	0.835	0.912	0.728

---

3.4.4 Feature importance analysis. Using the trained model as a basis, a number of techniques were used to evaluate the influence of each input feature on the model's prediction accuracy. The SHAP method is a powerful feature attribution algorithm that can evaluate the significance of each input to the model. All feature coalitions, regardless of size, are treated equally in this strategy. Feature significance analysis can also be done using the permutation method. Once the data are tabulated, permutation can be used as a model inspection tool for any fitted estimator, notably the nonlinear ones. By randomly reshuffling the feature value and specifying how much the feature affects the model output, the permutation feature importance breaks the relationship between a single feature and the model output. The linear relationships between pairs of variables, such as input features and model output, are measured using the Pearson correlation coefficient. A number between −1 and 1 is assigned by the Pearson correlation to characterise the direction and intensity of the linear relationship between two characteristics.

Fig. 10 shows the fifteen most important variables of our model. Here, we define significance as the average absolute SHAP value of all the data points, where red denotes high values and blue denotes the low ones; the colours in the graphic represent the value of the input variable. Red on the right (left) side of the plot indicates a positive (negative) connection with the target. From the SHAP analysis, it is seen that features like the group number, number of d electrons, radius of the d orbital, ionic radius, electronegativity, and electron affinity play an important role and have negative correlations with target properties. This can be explained from chemical intution as well. As discussed previously, electronegativity and electron affinity play a major role in transferring electrons to the substrate, which in turn determines the adsorption preferences. An increase in the number of d electrons at the active metal site has a dramatic effect on the charge transfer and adsorption energies of chemical intermediates. There are other ways to figure out how important a feature is besides the SHAP method. The permutation-based feature importance analysis, depicted in the top right panel of Fig. 10, shows that all of the input features have a satisfactory importance value, in good agreement with SHAP feature importance analysis. The feature–feature correlation map of the input features is displayed in the bottom panel of Fig. 10, suggesting that a few atomic attributes are linked. While building the model, we do not include the highly associated features that the Pearson correlation heatmap suggests.

Fig. 10 Feature importance analysis using the SHAP method (top left) and permutation feature importance (top right). Heatmap of the Pearson correlation matrix is shown in the bottom panel.

Our DFT models are in good agreement with those obtained using GB-based machine learning, demonstrating that thermodynamic properties may be easily predicted, but electronic properties show far more intricate contributions from various sources. The GB method, which is based on machine learning, has made it possible to construct complex multi-atomic catalysts with a wide variety of possible configurations. Machine learning-driven studies are inadequate, especially when it comes to elucidating the underlying interactions between the orbitals of the anchoring metals, and therefore trustworthy theoretical calculation-guided investigations are still necessary.

4 Conclusion

Single atom catalysts (SACs) have experienced a number of changes and have taken part in a variety of chemical reactions throughout the history of catalysis. However, notable developments in experimental strategies and methodologies for characterising these catalysts are responsible for the recent spike in study interest. By utilising the combined strength of machine learning techniques and DFT, we suggest that TM–TM DAC systems are a potential class of catalysts. It is expected that these systems will demonstrate a high degree of electroactivity together with remarkable durability over extended periods of use. We rank hetero-coupling TM–TM DACs as the best option in our methodology. This approach involves combining different transition metal elements within DAC structures. By doing so, we aim to achieve not only thermodynamic stability but also superior electroactivity, with particular emphasis on the interactions between d-orbitals, known as d–d couplings. We also include predictions based on gradient boosting (GB), which support the importance of d–d orbital interactions in influencing electroactivity. In addition, we emphasise that intrinsic physicochemical characteristics play a crucial role in determining thermodynamic stability. Taking into account the existing constraints on SACs, our work provides an important direction and a clear way ahead. We suggest creating DACs using graphyne (GPY), which has ideal electroactivity and a high likelihood of successful experimental synthesis. This work not only sets the stage for GPY-based DACs but also creates new opportunities for future research projects examining multi-atom catalyst (AC) systems. In addition to that, the aforementioned methodology can be employed for the purpose of conducting high throughput screening of DACs on alternative supports as well.

Data availability

Data will be made available upon reasonable request.

Conflicts of interest

There are no conflicts to declare.

Acknowledgements

C. C. gratefully acknowledges her sincere gratitude to Prof. Dr. Felix Studt for his generous support. C. C. acknowledges the SERB, India (PDF/2021/003445) for the funding. K. E. and Prof. V. S. acknowledge the Science and Engineering Research Board (SERB), Department of Science and Technology, New Delhi, for funding through the project entitled “First Principle Design and Development of Multifunctional van der Waals and Non-van der Waals solids” (No. CRG/2019/003876). The authors acknowledge Dr Naga Venkateswara Rao Nulakani for providing the structure of α-2 graphyne. CSIR-CLRI communication number is 2025.

References

1. L. Zhang, M. Xu, H. Chen, Y. Li and S. Chen, Globalization, green economy and environmental challenges: State of the art review for practical implications, Front. Environ. Sci., 2022, 10, 870271.
2. O. Ellabban, H. Abu-Rub and F. Blaabjerg, Renewable energy resources: Current status, future prospects and their enabling technology, Renewable Sustainable Energy Rev., 2014, 39, 748–764.
3. H. Lund, Renewable energy strategies for sustainable development, Energy, 2007, 32(6), 912–919.
4. M. A. Rahman, X. Wang and C. Wen, High energy density metal-air batteries: A review, J. Electrochem. Soc., 2013, 160(10), A1759.
5. A. P. Ferreira, R. C. Oliveira, M. M. Mateus and D. M. Santos, A review of the use of electrolytic cells for energy and environmental applications, Energies, 2023, 16(4), 1593.
6. S. M. M. Ehteshami and S. Chan, The role of hydrogen and fuel cells to store renewable energy in the future energy network-potentials and challenges, Energy Policy, 2014, 73, 103–109.
7. A. Kulkarni, S. Siahrostami, A. Patel and J. K. Nørskov, Understanding catalytic activity trends in the oxygen reduction reaction, Chem. Rev., 2018, 118(5), 2302–2312.
8. N. T. Suen, S. F. Hung, Q. Quan, N. Zhang, Y. J. Xu and H. M. Chen, Electrocatalysis for the oxygen evolution reaction: Recent development and future perspectives, Chem. Soc. Rev., 2017, 46(2), 337–365.
9. D. Strmcnik, P. P. Lopes, B. Genorio, V. R. Stamenkovic and N. M. Markovic, Design principles for hydrogen evolution reaction catalyst materials, Nano Energy, 2016, 29, 29–36.
10. J. Bao, W. Liu, Y. Zhou, T. Li, Y. Wang and S. Liang, et al., Interface nanoengineering of PdNi-S/C nanowires by sulfite-induced for enhancing electrocatalytic hydrogen evolution, ACS Appl. Mater. Interfaces, 2019, 12(2), 2243–2251.
11. E. Cuniberto, A. Alharbi, T. Wu, Z. Huang, K. Sardashti and K. D. You, et al., Nano-engineering the material structure of preferentially oriented nano-graphitic carbon for making high-performance electrochemical micro-sensors, Sci. Rep., 2020, 10(1), 9444.
12. D. Feng, L. Zhou, T. J. White, A. K. Cheetham, T. Ma and F. Wei, Nanoengineering metal-organic frameworks and derivatives for electrosynthesis of ammonia, Nano-Micro Lett., 2023, 15(1), 203.
13. J. L. Fiorio, M. L. Gothe, E. C. Kohlrausch, M. L. Zardo, A. A. Tanaka and R. B. de Lima, et al., Nanoengineering of catalysts for enhanced hydrogen production, Hydrogen, 2022, 3(2), 218–254.
14. C. Feng, X. Liu, T. Zhu and M. Tian, Catalytic oxidation of CO on noble metal-based catalysts, Environ. Sci. Pollut. Res. Int., 2021, 28, 24847–24871.
15. A. Eichler, CO oxidation on transition metal surfaces: Reaction rates from first principles, Surf. Sci., 2002, 498(3), 314–320.
16. M. Ackermann, T. Pedersen, B. Hendriksen, O. Robach, S. Bobaru and I. Popa, et al., Structure and reactivity of surface oxides on Pt (110) during catalytic CO oxidation, Phys. Rev. Lett., 2005, 95(25), 255505.
17. K. Ding, A. Gulec, A. M. Johnson, N. M. Schweitzer, G. D. Stucky and L. D. Marks, et al., Identification of active sites in CO oxidation and water-gas shift over supported Pt catalysts, Science, 2015, 350(6257), 189–192.
18. T. Schalow, B. Brandt, D. E. Starr, M. Laurin, S. K. Shaikhutdinov and S. Schauermann, et al., Size-dependent oxidation mechanism of supported Pd nanoparticles, Angew. Chem., Int. Ed., 2006, 45(22), 3693–3697.
19. K. Judai, S. Abbet, A. S. Wörz, U. Heiz and C. R. Henry, Low-temperature cluster catalysis, J. Am. Chem. Soc., 2004, 126(9), 2732–2737.
20. X. F. Yang, A. Wang, B. Qiao, J. Li, J. Liu and T. Zhang, Single-atom catalysts: A new frontier in heterogeneous catalysis, Acc. Chem. Res., 2013, 46(8), 1740–1748.
21. S. Liang, C. Hao and Y. Shi, The power of single-atom catalysis, ChemCatChem, 2015, 7(17), 2559–2567.
22. H. Wei, X. Liu, A. Wang, L. Zhang, B. Qiao and X. Yang, et al., FeOx-supported platinum single-atom and pseudo-single-atom catalysts for chemoselective hydrogenation of functionalized nitroarenes, Nat. Commun., 2014, 5(1), 5634.
23. J. Lin, A. Wang, B. Qiao, X. Liu, X. Yang and X. Wang, et al., Remarkable performance of Ir₁/FeOx single-atom catalyst in water gas shift reaction, J. Am. Chem. Soc., 2013, 135(41), 15314–15317.
24. J. Li, C. Chen, L. Xu, Y. Zhang, W. Wei and E. Zhao, et al., Challenges and perspectives of single-atom-based catalysts for electrochemical reactions, JACS Au, 2023, 3(3), 736–755.
25. K. Rigby and J. H. Kim, Deciphering the issue of single-atom catalyst stability, Curr. Opin. Chem. Eng., 2023, 40, 100921.
26. A. M. Gabelnick, A. T. Capitano, S. M. Kane, J. L. Gland and D. A. Fischer, Propylene oxidation mechanisms and intermediates using in situ soft X-ray fluorescence methods on the Pt (111) surface, J. Am. Chem. Soc., 2000, 122(1), 143–149.
27. J. Koop and O. Deutschmann, Detailed surface reaction mechanism for Pt-catalyzed abatement of automotive exhaust gases, Appl. Catal., B, 2009, 91(1–2), 47–58.
28. T. Pu, J. Ding, F. Zhang, K. Wang, N. Cao and E. J. M. Hensen, et al., Dual atom catalysts for energy and environmental applications, Angew. Chem., Int. Ed., 2023, e202305964.
29. R. Li and D. Wang, Superiority of dual-atom catalysts in electrocatalysis: One step further than single-atom catalysts, Adv. Energy Mater., 2022, 12(9), 2103564.
30. W. Xu, Y. Wang, C. Zhang, X. Ma, J. Wu and Y. Liu, et al., Insights into the electronic structure coupling effect of dual-metal atomic electrocatalytic platform for efficient clean energy conversion, Chem. Eng. J., 2023, 461, 141911.
31. Y. Ying, X. Luo, J. Qiao and H. Huang, More is different: Synergistic effect and structural engineering in double-atom catalysts, Adv. Funct. Mater., 2021, 31(3), 2007423.
32. Z. He, K. He, A. W. Robertson, A. I. Kirkland, D. Kim and J. Ihm, et al., Atomic structure and dynamics of metal dopant pairs in graphene, Nano Lett., 2014, 14(7), 3766–3772.
33. J. Sun, L. Tao, C. Ye, Y. Wang, G. Meng and H. Lei, et al., MOF-derived Ru₁Zr₁/Co dual-atomic-site catalyst with promoted performance for Fischer-Tropsch synthesis, J. Am. Chem. Soc., 2023, 145(13), 7113–7122.
34. C. C. Hou, H. F. Wang, C. Li and Q. Xu, From metal-organic frameworks to single/dual-atom and cluster metal catalysts for energy applications, Energy Environ. Sci., 2020, 13(6), 1658–1693.
35. C. Chen, M. Sun, K. Wang and Y. Li, Dual-metal single-atomic catalyst: The challenge in synthesis, characterization, and mechanistic investigation for electrocatalysis, SmartMat, 2022, 3(4), 533–564.
36. W. Wan, Y. Zhao, S. Wei, C. A. Triana, J. Li and A. Arcifa, et al., Mechanistic insight into the active centers of single/dual-atom Ni/Fe-based oxygen electrocatalysts, Nat. Commun., 2021, 12(1), 5589.
37. C. Wu, W. Yang, J. J. Wang, H. Li and I. D. Gates, Methane activation on dual-atom catalysts supported on graphene, Chem. Commun., 2021, 57(91), 12127–12130.
38. Y. Zheng, Y. Jiao, L. H. Li, T. Xing, Y. Chen and M. Jaroniec, et al., Toward design of synergistically active carbon-based catalysts for electrocatalytic hydrogen evolution, ACS Nano, 2014, 8(5), 5290–5296.
39. J. Hong, M. Chen, L. Zhang, L. Qin, J. Hu and X. Huang, et al., Asymmetrically coupled Co single-atom and Co nanoparticle in double-shelled carbon-based nanoreactor for enhanced reversible oxygen catalysis, Chem. Eng. J., 2023, 455, 140401.
40. Y. Fang, Y. Liu, L. Qi, Y. Xue and Y. Li, 2D graphdiyne: An emerging carbon material, Chem. Soc. Rev., 2022, 51(7), 2681–2709.
41. N. V. R. Nulakani and V. Subramanian, A theoretical study on the design, structure, and electronic properties of novel forms of graphynes, J. Phys. Chem. C, 2016, 120(28), 15153–15161.
42. M. Sun, H. H. Wong, T. Wu, A. W. Dougherty and B. Huang, Stepping out of transition metals: Activating the dual atomic catalyst through main group elements, Adv. Energy Mater., 2021, 11(30), 2101404.
43. D. Wu, P. Lv, J. Wu, B. He, X. Li and K. Chu, et al., Catalytic active centers beyond transition metals: Atomically dispersed alkaline-earth metals for the electroreduction of nitrate to ammonia, J. Mater. Chem. A, 2023, 11(4), 1817–1828.
44. D. Wu, J. Wu, H. Li, W. Lv, Y. Song and D. Ma, et al., Unlocking the potential of alkaline-earth metal active centers for nitrogen activation and ammonia synthesis: The role of s-d orbital synergy, J. Mater. Chem. A, 2024, 12(7), 4278–4289.
45. Y. Zang, Q. Wu, S. Wang, B. Huang, Y. Dai and Y. Ma, Coupling a main-group metal with a transition metal to create biatom catalysts for nitric oxide reduction, Phys. Rev. Appl., 2023, 19(2), 024003.
46. G. Kresse and J. Furthmüller, Efficient iterative schemes for ab initio total-energy calculations using a plane-wave basis set, Phys. Rev. B: Condens. Matter Mater. Phys., 1996, 54(16), 11169.
47. J. P. Perdew, K. Burke and M. Ernzerhof, Generalized gradient approximation made simple, Phys. Rev. Lett., 1996, 77(18), 3865.
48. S. Grimme, Semiempirical GGA-type density functional constructed with a long-range dispersion correction, J. Comput. Chem., 2006, 27(15), 1787–1799.
49. G. K. Uyank and N. Güler, A study on multiple linear regression analysis, Procedia Soc. Behav. Sci., 2013, 106, 234–240.
50. E. Schulz, M. Speekenbrink and A. Krause, A tutorial on Gaussian process regression: Modelling, exploring, and exploiting functions, J. Math. Psychol., 2018, 85, 1–16.
51. V. Svetnik, A. Liaw, C. Tong, J. C. Culberson, R. P. Sheridan and B. P. Feuston, Random forest: A classification and regression tool for compound classification and QSAR modeling, J. Chem. Inf. Comput. Sci., 2003, 43(6), 1947–1958.
52. K. Vu, J. C. Snyder, L. Li, M. Rupp, B. F. Chen and T. Khelif, et al., Understanding kernel ridge regression: Common behaviors from simple functions to density functionals, Int. J. Quantum Chem., 2015, 115(16), 1115–1128.
53. D. W. Marquardt and R. D. Snee, Ridge regression in practice, Am. Stat., 1975, 29(1), 3–20.
54. F. Emmert-Streib and M. Dehmer, High-dimensional LASSO-based computational regression models: Regularization, shrinkage, and selection, Mach. Learn Knowl. Extr., 2019, 1(1), 359–383.
55. F. Pedregosa, G. Varoquaux, A. Gramfort, V. Michel, B. Thirion and O. Grisel, et al., Scikit-learn: Machine learning in Python, J. Mach. Learn. Res., 2011, 12, 2825–2830.
56. A. R. Puigdollers, G. Alonso and P. Gamallo, First-principles study of structural, elastic and electronic properties of α -, β -and γ -graphyne, Carbon, 2016, 96, 879–887.
57. S. Tian, Q. Fu, W. Chen, Q. Feng, Z. Chen and J. Zhang, et al., Carbon nitride supported Fe2 cluster catalysts with superior performance for alkene epoxidation, Nat. Commun., 2018, 9(1), 2353.
58. L. Zhang, J. M. T. A. Fischer, Y. Jia, X. Yan, W. Xu and X. Wang, et al., Coordination of atomic Co-Pt coupling species at carbon defects as active sites for oxygen reduction reaction, J. Am. Chem. Soc., 2018, 140(34), 10757–10763.
59. O. Matsushita, V. M. Derkacheva, A. Muranaka, S. Shimizu, M. Uchiyama and E. A. Lukyanets, et al., Rectangular-shaped expanded phthalocyanines with two central metal atoms, J. Am. Chem. Soc., 2012, 134(7), 3411–3418.
60. Z. Zhang, L. Zhang, X. Wang, Y. Feng, X. Liu and W. Sun, Rational design of graphyne-based dual-atom site catalysts for CO oxidation, Nano Res., 2023, 16(1), 343–351.

---

Footnote

† Electronic supplementary information (ESI) available: Table showing bond lengths of a few DACs, charge transfer analysis, trend in electronegativity, and cohesive energy. See DOI: https://doi.org/10.1039/d4cp03171g

---