Porphyrins on acid: kinetics of the photoinduced-protonation of tetrakis(4-carboxyphenyl)-porphyrin

Abstract

Free-base porphyrins can be protonated, which significantly impacts their electronic and excited state properties. While excited state dynamics are well explored for either neutral or fully protonated porphyrins, the intermediate region has not yet been explored, although their potential implications for photocatalytic reactions are evident. This study explores how partial protonation affects the nature and properties of photoexcited states of tetrakis(4-carboxyphenyl)porphyrin (TCPP) using steady-state and nanosecond transient absorption spectroscopy. Global-fit analysis of the decay curves revealed the formation of a protonated excited triplet state from the neutral triplet state, as well as the long lifetimes of these species of up to 120 μs. The photoexcited triplet state of TCPP functions as a photobase, which was confirmed by computational analysis of the electron density of the exited states showing increased nucleophilicity at the unprotonated nitrogen atoms of the porphyrin core. These findings indicate that photoinduced protonated excited triplet states can function as electron acceptors with anodically shifted redox potentials, opening new pathways for porphyrin-based photoreactions.

---

Introduction

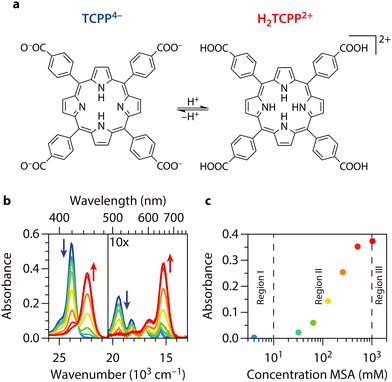
Porphyrins are studied intensively due to their important role in various biological processes and their potential applications in materials science, catalysis, energy conversion, and photodynamic therapy.^1–7 Their unique optical and electronic properties arise from their conjugated macrocyclic structure, which allows for extensive π-electron delocalization. This structure enables porphyrins to transfer energy as photosensitizers or electrons as photoredox catalysts under light irradiation, facilitating applications such as singlet oxygen generation,⁸ C–C coupling photoredox catalysis,³ and CO₂ photoreduction.^9–12 Furthermore, porphyrins have been integrated as linkers into metal–organic frameworks (MOFs), where their intrinsic reactivity can be combined with the confinement effect induced by the MOF pores.^8,13,14

Recently, we have explored free-base porphyrin-based MOFs, which are known photocatalysts for CO₂ reduction without the need for an additional co-catalyst.^15,16 As the role of the porphyrin photocatalyst in this reaction is still unclear, in our previous study we focused on the initial stage of CO₂ photoreduction, namely the co-adsorption of the reactants CO₂ and H₂O within the framework.¹⁵ Within the confinement of MOF pores, we observed that water interacts with the porphyrin incorporated as a linker into the MOF structure, causing a bending of the initially planar porphyrin molecules. Unlike metalated porphyrins, free-base porphyrins can undergo protonation at the nitrogen atoms within the macrocycle (see Fig. 1(a)). This protonation induces a significant change in the molecular geometry, disrupting the π-system, and causing the porphyrin rings to adopt non-planar conformations.¹⁷ This finding was surprising as protonation of the homogeneous porphyrin building blocks typically requires the presence of an acid, which was not added during water vapor adsorption. It appeared that simply filling the pores with water in the confinement of the MOF pores was sufficient to partially protonate the porphyrin linker. Increasing acidity in confinement has been observed in microporous materials such as zeolites or MOFs.¹⁸ Our previous study focused on MOFs with Zr-clusters, which can act as Lewis acid sites, creating Brønsted acid sites upon MOF hydration. Based on this, it was reported for UiO-66 (a Zr-based MOF with terephthalic acid linkers instead of porphyrin linkers) that hydration can lower the external pH of MOF-containing suspensions to as low as 1.6.¹⁹ As the porphyrin-based MOFs are built from the same Zr-cluster, this shift in pH might explain our findings of partial protonation of the porphyrin linkers with a pK_a of the core nitrogen atoms of around 1.^20,21 Given the widespread use of porphyrin-based porous materials in various photocatalytic reactions,²² we were surprised that this acidic environment, to the best of our knowledge, has not yet been considered for mechanistic studies on the CO₂ photoreduction. This prompted us to make the first steps in that direction by investigating how partial protonation affects the photoexcited states of porphyrins.

Fig. 1 Steady-state absorption spectroscopy of TCPP and H ₂ TCPP ²⁺ . (a) Molecular structure of carboxylate-form of tetrakis(4-carboxyphenyl)-porphyrin and its fully protonated diacid (TCPP⁴⁻ and H₂TCPP²⁺). (b) UV/vis spectra of 1.26 μM TCPP⁴⁻ in DMF at different acid concentrations from blue to red (0, 4, 32, 64, 128, 256, 512, and 1024 mM MSA). The Soret band (S₀ to S₂ transition) is located at 23.9 × 10³ cm⁻¹ (419 nm) for TCPP and at 22.4 × 10³ cm⁻¹ (446 nm) for H₂TCPP²⁺. The region with the four Q-bands of the porphyrin (lower energy section of the plot) is zoomed in 10 times for visualization purposes. H₂TCPP²⁺ only shows two Q-bands for reasons discussed in the text. (c) Absorbance at 22.4 × 10³ cm⁻¹, a direct measure to the amount of H₂TCPP²⁺, as function of MSA concentration. We indicate three regions, neutral (I), intermediately protonated (II), and fully protonated (III).

As current spectroscopic instrumentation to study excited state dynamics of MOFs still requires adjusting of measurement conditions varying from real reaction conditions, e.g. using emulsifiers for MOF suspensions,^23–25 we choose to investigate homogeneous porphyrin linker solutions as a first step. During visible light irradiation, porphyrins are excited from the ground singlet state (S₀) to higher singlet states S_n, after which they undergo fast vibrational relaxation to S₁ and high-efficiency intersystem crossing to yield a triplet state (T₁).²⁶ In contrast to neutral free-base porphyrins, protonated or ruffled porphyrins (with sterically demanding geometry, which induces bending) show enhanced S₁ → T₁ intersystem crossing and S₁ → S₀ internal conversion rates, quenching the singlet fluorescence.^27,28 Furthermore, reduced triplet lifetimes and redshifted excited triplet state absorption spectra were observed for fully protonated meso-arylporphyrin diacids in water.^29–32 However, insights in the influence of partially protonated meso-arylporphyrins on the photoexcited states are still pending.

In this work, we study the excited state dynamics of tetrakis(4-carboxyphenyl)porphyrin (TCPP) as a function of a proton source concentration using steady-state and nanosecond transient absorption spectroscopy. We find that the photoexcited triplet state of TCPP is protonated more easily compared to the ground state and thus acts as photobase. Using global fitting analysis and reference experiments, we established the full overview of the states involved and their reaction rates. The experimentally observed higher basicity of the triplet state is computationally explained by a change in electron density on the unprotonated nitrogen atoms in the porphyrin macrocycle when going from the singlet (ground) state to the triplet state. Protonated porphyrins can function as electron acceptors rather than electron donors, and their redox potentials shift anodically upon protonation.^33–35 Consequently, we believe that generating photoinduced protonated excited triplet states in the presence of only catalytic concentrations of acid represents a compelling pathway to expand the reaction scope of porphyrinic photoreactions.

Results

meso-Arylporphyrins tend to aggregate in solution, which significantly alters their optical and electronic properties. We choose dimethylformamide (DMF) as solvent to avoid aggregation and accurately assess the excited state dynamics of monomeric tetrakis(4-carboxyphenyl)porphyrin (TCPP).³⁶ Additionally, we prepared a series of concentrations to determine the range of linear correlation between concentration and absorbance in the UV/vis steady-state spectra, ensuring monomeric porphyrin solutions. For this reason and further reasons discussed below, we choose to work with a 1.26 μM solution of TCPP in DMF. The steady state UV/vis spectra of TCPP in presence of different concentrations of methane sulfonic acid (MSA) are shown in Fig. 1(b). In DMF, TCPP is present in its COO⁻ form (TCPP⁴⁻). As the carboxylate groups are more basic, they undergo protonation before the pyrrolic nitrogen atoms in the porphyrin core at MSA concentrations as low as 4 mM.²⁰ As the electronic configuration of the porphyrin changes from TCPP⁴⁻ with COO⁻ moieties to TCPP⁰ with COOH groups upon protonation, we find a slight decrease across the entire absorption spectrum. We will use ‘TCPP’ to refer to both species with unprotonated pyrrolic nitrogen atoms in the porphyrin core (TCPP⁴⁻ and TCPP⁰). Further addition of MSA, yields the fully protonated diacid (H₂TCPP²⁺) of TCPP, which shows redshifted steady-state absorption features.^27,28 When adding MSA > 4 mM, a new band arises at 22.4 × 10³ cm⁻¹ (Table 1). This feature corresponds to the Soret band (S₀ to S₂ transition, i.e. B(0,0)) of the diacid (H₂TCPP²⁺)^29,37 and appears at the expense of the Soret band of TCPP at 23.9 × 10³ cm⁻¹ (Table 1). At the same time the four weaker Q-bands (S₀ to S₁ transitions, i.e. Q_y(1,0), Q_y(0,0), Q_x(1,0), and Q_x(0,0) from high to low energy) decrease in intensity and cluster together in two broader and more intense bands at 16.6 and 15.3 × 10³ cm⁻¹, respectively Q(1,0) and Q(0,0). This can be explained by considering the origin of the Q-band transitions in TCPP: the Q-band is split into two bands due to vibrational excitations and further split because of a lower symmetry due to NH protons in the porphyrin core. Subsequently, when H₂TCPP²⁺ is formed, the symmetry is increased (see Fig. 1(a)), and the two vibrational bands remain.³⁸ For other porphyrins, monoprotonated species are also observed.^39,40 However, this is usually not the case for tetraphenyl-based porphyrins. In these compounds, the protonation of both core nitrogen atoms effectively occurs in one step, with the first protonation being the rate-determining step.^33,41 We also find no indication of a third, mono-protonated species in the spectra presented in Fig. 1(b). Instead, there is a clear isosbestic point between the spectra of TCPP and H₂TCPP²⁺ at 23.3 × 10³ cm⁻¹. Additionally, the absence of bands corresponding to H- and J-type aggregates, which would shift the Soret band at 23.9 × 10³ cm⁻¹ to around 25 × 10³ cm⁻¹ and 20 × 10³ cm⁻¹ respectively, indicates that aggregates are not formed.^37,42

Table 1 Steady-state UV/vis band assignments and positions in cm⁻¹ (nm)

TCPP	B(0,0)	Qy(1,0)	Qy(0,0)	Qx(1,0)	Qx(0,0)
	23.9 (419)	19.4 (515)	18.2 (548)	16.9 (591)	15.5 (645)
H2TCPP^2+	B(0,0)	—	—	Q(1,0)	Q(0,0)
	22.4 (447)	—	—	16.6 (602)	15.3 (655)
Δ	−1.5 (28)	—	—	−0.3 (11)	−0.2 (10)

---

Fig. 1(c) shows the absorbance at the H₂TCPP²⁺ Soret band as function of MSA concentration. Three distinct regions are indicated in this figure. The first region corresponds to neutral TCPP⁰ with only the carboxylic acid groups protonated. The second region shows the coexistence of both TCPP⁰ and H₂TCPP²⁺. The third region represents the presence of only H₂TCPP²⁺. These regions will be referenced in subsequent discussions.

To investigate the excited state dynamics in the three stages of protonation we use transient absorption (TA) spectroscopy. In short, the in-house assembled nanosecond TA setup⁴³ used in this work is composed of a tuneable nanosecond Nd:YAG-laser system as pump, a xenon flash lamp as probe, a gated intensified CCD camera coupled to a spectrograph to measure the probe spectra, and digital delay generators to change the delay time of the probe together with the gate of the camera with respect to the pump (for more details, see the Experimental section). To avoid quenching of the T₁ by singlet oxygen formation (³O₂ to ¹O₂),⁴⁴ we purged our samples with argon for 30 minutes. Additionally, we verified that the TCPP⁴⁻ concentration is low enough to prevent interaction between porphyrin molecules (e.g. aggregation). A concentration of 1.26 μM resulted in a saturation of the T₁ lifetime around 1.5 ms (Fig. S1, ESI†).⁴⁵ At higher concentrations there is an increased chance that molecules in a T₁ state collide and that T₁–T₁ annihilation occurs, shortening the T₁ lifetime.⁴⁶ To minimize the amount of excess energy we excite into the Q_y(1,0) band at 515 nm for TCPP and at Q(0,0) band at 665 nm for H₂TCPP²⁺ and not in the stronger absorbing Soret band. It is well known that within nanoseconds high-efficiency intersystem crossing from the singlet (S₁) into the triplet state (T₁) occurs. The subsequent T₁ is of high interest for photocatalytic reactions because it has a lifetime of milliseconds since the transition back to the ground state (S₀) is spin forbidden.⁴⁵Fig. 2(a) shows the Jablonski diagram for the excited state dynamics of TCPP.

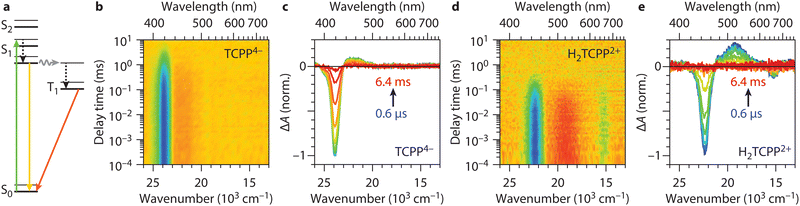Fig. 2 Excited state dynamics of TCPP ⁴⁻ and H ₂ TCPP ²⁺ . (a) Jablonski diagram for TCPP neutral environment (region I), showing the excitation into the singlet (green arrow), vibrational relaxation (black arrow), singlet relaxation (yellow arrow), intersystem crossing (grey arrow), and triplet relaxation (orange arrow) pathways. The same applies to H₂TCPP²⁺, i.e. fully protonated TCPP (region III), except that it does not have a split S₁ level (see text). (b) and (d) Transient absorption heatmaps on TCPP⁴⁻ and H₂TCPP²⁺ after excitation at respectively 515 nm and 665 nm. (c) and (e) Spectral slices of the heatmap at delay times 0.6 μs, 3.0 μs, 9.1 μs, 24 μs, 63 μs, 160 μs, 0.4 ms, 1.0 ms, 2.5 ms, and 6.4 ms from blue to red. The bleach positions correspond to the Soret bands in the steady state spectra (Fig. 1(b)). When fitting a single exponential to the bleach intensity time traces, lifetimes of 1.2 ms and 120 μs are obtained for TCPP⁴⁻ and H₂TCPP²⁺ respectively.

Fig. 2(b)–(e) shows the full TA heatmaps and differential spectra at different delay times of TCPP⁴⁻ and H₂TCPP²⁺ respectively. Note that TCPP⁰, obtained at 4 mM MSA concentration, as discussed above, shows identical heatmaps as TCPP⁴⁻ (Fig. S2, ESI†). The spectra show a negative band, i.e. less absorbance, at their respective Soret positions (see Fig. 1(b)). This ground-state bleach is due to population of the ππ* states and subsequently T₁.⁴⁷ They also show a weaker positive feature, i.e. more absorbance, originating from excited state absorbance of T₁ to higher triplet levels (T_n), also known as photoinduced absorbance. When fitting the decay of the bleach with a single exponential, we find lifetimes of 1.2 ms, 1.0 ms, and 120 μs for TCPP⁴⁻, TCPP⁰, and H₂TCPP²⁺, respectively. Furthermore, we found that the H₂TCPP²⁺ triplet lifetime, obtained when exciting the samples at 665 nm, does not show any dependence on the MSA concentration in the intermediate region (II) and the fully protonated region (III) (Fig. S3, ESI†). Upon exposure to air, the lifetimes decreased to the sub-μs range, indicating fast quenching of the T₁ by ³O₂, which can subsequently generate singlet oxygen. This suggests that the triplet states of TCPP⁴⁻, TCPP⁰, and H₂TCPP²⁺ have energies greater than 7.9 × 10³ cm⁻¹ (94 kJ).^48,49

Fig. 3 shows the excited state dynamics in the intermediate MSA concentration range (II). Fig. 3(a) presents the TA heatmap obtained for partially protonated TCPP/H₂TCPP²⁺ mixtures, with excitation into the Q_y(0,0) band of TCPP at 515 nm in an acidic environment (128 mM MSA) (Fig. S4, ESI† for other MSA concentrations). This excitation wavelength was chosen, as there is no overlap with bands of H₂TCPP²⁺, thus allowing sole excitation of TCPP. Comparing Fig. 2(b) with Fig. 3(a), an additional photoinduced absorption band (red) around 1 ms and 22.4 × 10³ cm⁻¹ is noticeable in the partially protonated sample. Note that TA data after excitation at 665 nm does not show any MSA concentration dependence and solely showed features as obtained in the fully protonated case (Fig. S3, ESI†). Fig. 3(b) shows spectral slices of the heatmap at various delay times that clearly show the photoinduced absorption at 22.4 × 10³ cm⁻¹ (446 nm) as function of MSA concentration. The spectrum at 1.0 ms, shown in Fig. 3(c), matches the difference between the steady-state UV/vis spectra of 4 mM and 1024 mM MSA in Fig. 1(c). This strong overlap confirms that the final state in the TA measurements is a photoinduced protonated ground state (H₂S₀²⁺). Since no protonated H₂S₀²⁺ was formed in the presence of oxygen, which quenches T₁, we confirmed that the pathway proceeds via T₁ (see Fig. S5, ESI†). This allowed us to draw the full picture of the excited state and (de)protonation dynamics, as outlined in Fig. 3(d): similar to the MSA-free dynamics, TCPP is initially excited from the ground state to the singlet excited states, followed by a quick intersystem crossing to T₁. However, at this point, the dynamics deviate from those shown in Fig. 2(a), as T₁ undergoes protonation to form H₂T₁²⁺, which relaxes back into a protonated ground state H₂S₀²⁺. Due to the dynamic acid-dissociation equilibrium, H₂S₀²⁺ will release the captured protons, closing the Förster cycle and yielding unprotonated S₀. A similar behaviour has been reported for tetrakis(4-sulphonatophenyl)porphyrin (TPPS) in water.⁵⁰

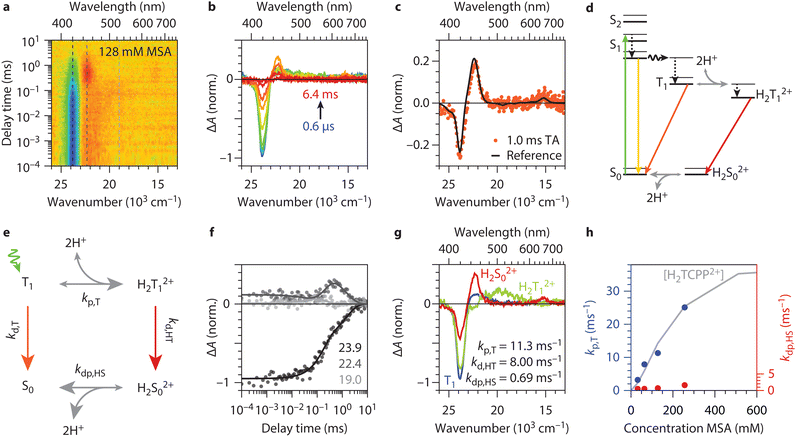Fig. 3 Excited state dynamics of TCPP in the intermediate concentration range. (a) Transient absorption (TA) heatmap for TCPP (excitation into Q_y(1,0) at 515 nm) in an acidic environment (128 mM MSA). The photoinduced absorption (red area) around 1 ms is absent in the measurements presented before. (b) Spectral slices of the heatmap at delay times 0.6 μs, 3.0 μs, 9.1 μs, 24 μs, 63 μs, 160 μs, 0.4 ms, 1.0 ms, 2.5 ms, and 6.4 ms from blue to red. The photoinduced absorption is visible in the orange spectra and located at 22.4 × 10³ cm⁻¹ (446 nm). (c) The TA spectrum at 1.0 ms, same as in panel b, overlapped with in black the difference between the steady-state UV/vis spectrum of 4 mM and 1024 mM presented in Fig. 1(c) scaled arbitrarily. The good overlap between the two proves that the final state in the TA measurements is a photoinduced protonated ground state. (d) Altered Jablonski diagram for TCPP in acidic environment but not fully protonated (region II). (e) Proposed excited-state relaxation and (de)protonation dynamics used for the global fit analysis in panel e, f (see ESI,† S2 for rate equations). (f) Time trace slices of the heatmap at energies 23.9, 22.4, and 19.0 × 10³ cm⁻¹, like indicated in the heatmap in panel a, with the global fit results (lines). (g) The three spectra of the three states in the global fit model. The three corresponding rates are 11.3, 8.0, and 0.69 ms⁻¹. They compare well with separately collected spectra (see Fig. S6, ESI†). (h) The protonation (k_p,T in red) and deprotonation (k_dp,HS in blue) rates obtained by global fitting the transient absorption data on the MSA concentrations 32, 64, 128, and 256 mM. The grey line shows the H₂TCPP²⁺ concentration obtained from steady-state UV/vis also shown in Fig. 1(c) and is scaled arbitrarily.

We applied the proposed excited state relaxation and (de)protonation dynamics to our transient absorption dataset by means of a global fitting procedure. Fig. 3(e) shows the rate model used for the global fitting. Here, the singlet dynamics and the intersystem crossing are omitted for simplicity and because they do not play a role in the photoinduced protonation as discussed above. The exact rate equations are discussed in ESI S2.† From the data shown in Fig. 2 and Fig. S2 (ESI†), the triplet decay rates of TCPP and H₂TCPP²⁺ are obtained as k_d,T = 1 ms⁻¹ and k_d,HT = 8 ms⁻¹. This leaves the triplet protonation rate k_p,T and the ground state (H₂S₀²⁺) deprotonation rate k_dp,HS as the only rates being optimized in the global fitting procedure.

The global fit yielded a successful match, as shown in the great overlap of experimental data with fitted values for time slices at three prominent spectral regions (Fig. 3(f)). This allowed us to retrieve the protonation rate of the T₁ and the deprotonation rate of H₂S₀²⁺, k_p,T = 11.3 ms⁻¹ and k_dp,HS = 0.69 ms⁻¹ for 128 mM MSA concentration. The obtained spectra of the T₁, H₂T₁²⁺, and H₂S₀²⁺ from the global fit (Fig. 3(g)) compare well to the separately recorded spectra of T₁ (Fig. 2(c) and Fig. S2b, ESI†), H₂T₁²⁺ (Fig. 2(e) and Fig. S2d, ESI† expect that the bleach is at a different position), and the difference in steady state between S₀ and H₂S₀²⁺ (black curve in Fig. 3(c)). A direct comparison of these spectra is shown in Fig. S6 (ESI†) and underlines our proposed relaxation dynamics in Fig. 3(e). Our findings align with similar slow protonation rates observed for tetraphenylporphyrin (TPP) in DMSO–water mixtures using temperature jump experiments.³³ The protonation rate is an order of magnitude higher than the deprotonation rate, leading to a considerable net build-up of H₂S₀²⁺ at higher MSA concentrations as observed in Fig. 3(b). The slow rates also correlate with long lifetimes for H₂T₁²⁺ of 120 μs, crucial for their use in chemical (redox) reactions.

We extended the global-fit analysis to data sets with varying MSA concentrations (Fig. S4, ESI†) to establish the relationship between proton source concentration and (de)protonation rates (Fig. 3(h)). The protonation rate follows the increase in H₂TCPP²⁺ concentration found in the steady-state UV/vis measurements (Fig. 3(h) grey, same as Fig. 1(c)) and we find a linear dependence of the protonation rate on the MSA concentration ranging from 3.2 ms⁻¹ (32 mM MSA) to 25.1 ms⁻¹ (256 mM MSA), shown in Fig. 3(h). This indicates first-order kinetics and a reaction-limited protonation rate of 10⁵ M⁻¹ s⁻¹, as diffusion rates are typically much higher (10¹⁰ M⁻¹ s⁻¹). As discussed earlier, this protonation rate corresponds to the addition of the first proton, which induces the structural changes and is the rate-determining step in the protonation process.³⁹ These slower rates contrast with those of other aromatic amines, suggesting that structural changes during protonation are responsible for the slower kinetics.^51,52

In contrast, we find minor dependence of the deprotonation rate of the MSA concentration (ranging from 0.48 to 1.61 ms⁻¹, see Fig. 3(h) blue). This suggests that other factors, such as the stabilization of H₂TCPP²⁺ in DMF or the abstraction of the first proton and reversing the protonation-induced porphyrin deformation, play a more significant role in determining the deprotonation rate.

To support our experimental findings, we conducted Density Functional Theory (DFT) calculations of TCPP and H₂TCPP²⁺. For all structure optimizations and electronic structure calculations, we utilized the Gaussian 09 program. Fig. S7 (ESI†) presents the obtained optimized geometries of the neutral ground state S₀ and first triplet excited state T₁. The dihedral angles of the porphyrin core increased only slightly when transitioning from S₀ to T₁ geometry, consistent with previous experimental and computational findings.^53,54 This observation contrasts with the structural changes observed upon protonation. As reported previously,^35,38 we find strong ruffling of the tetrapyrrolic unit in the protonated S₀, which is even more pronounced in the protonated T₁ geometry (Fig. S8, ESI†). The ground-state findings align with our steady state UV/vis spectra, which showed a redshift of the Soret band due to the disruption of the π-system caused by ruffling (Fig. 1(b)). We propose that the reduced triplet state lifetime observed upon excitation of protonated ground-state molecules is a result of the changed geometry (compare time traces in Fig. S2, ESI†).

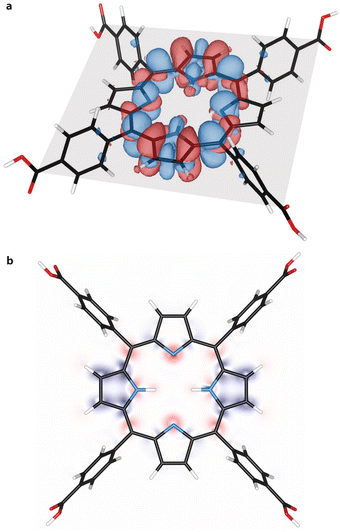
From natural population analysis, we derived the charges of the pyrrolic nitrogen atoms (see Table S1 and Fig. S9, ESI†). Here, a higher uniformity between the charges of the pyrrolic nitrogen atoms at T₁ was observed. Furthermore, electron density difference maps were derived for the ground state and the triplet state (see Fig. 4(a)). These maps revealed increased electron density, and thus nucleophilicity, at the unprotonated nitrogen atoms in the porphyrin plane. This becomes particularly evident when presenting the differential density maps between T₁ and S₀ solely in the porphyrin plane as shown in Fig. 4(b). This map shows increased electronegativity at the unprotonated nitrogen atoms (red cloud) and explains the increased basicity of the first excited triplet state, as derived from transient absorption spectroscopy experiments (Fig. 3). This finding is consistent with the presence of a free lone-pair orbital that binds the hydrogen atom upon protonation. The electron density decreased above and below the porphyrin plane and corresponds to the p-orbitals, which are not involved in the protonation. Lastly, we noted that the nucleophilicity of T₁ seems to be minimally affected by the solvent DMF (see Fig. S10, ESI†).

Fig. 4 Differential electron density of TCPP. (a) Difference in electron density (increased electron density in red, decreased density in blue) between ground state S₀ and excited triple state T₁. The porphyrin plane is indicated in grey. (b) Differential electron density in the porphyrin plane. Red indicates an increase and blue a decrease in electron density.

Conclusion

Through steady-state and transient absorption spectroscopy we established that the photoexcited triplet state of TCPP exhibits higher basicity compared to its ground state, effectively acting as a photobase. These findings are supported by DFT calculations, which reveal structural changes upon protonation and highlight the increased nucleophilicity of the first excited triplet state (T₁). Global-fit analysis revealed slow (de)protonation rates and a reaction-limited protonation step. The next step is to compare these findings with processes in the confined space of MOFs, which requires novel instrumentation that overcomes the strong light scattering of the micrometer-sized MOF crystals.

Our results provide a further step towards elucidating the reaction pathway of CO₂ photoreduction in porphyrinic porous materials. To the best of our knowledge, neither the high acidity induced by the interaction of water with the Lewis acidic Zr-cluster nor the altered excited state kinetics have been considered. The acidic environment in the pores might influence the reaction pathways by stabilizing protonated species and facilitating proton-coupled electron transfer processes, both important intermediate steps in CO₂ photoreduction. The excited state redox potentials also play a significant role. It remains to be proven if the excited state redox potentials of porphyrins shift anodically within the MOF environment as well, potentially enabling them to function as electron acceptors rather than donors. Lastly, the long lifetimes of the protonated excited state (up to 120 μs), which we found in this study, confirm their potential as reaction partners. However, the elucidation of the entire CO₂ photoreduction pathway is beyond the scope of this work. The above-mentioned factors will be the focus of future studies.

Beyond CO₂ photoreduction, the probable shift in redox behaviour opens exciting possibilities for controlling redox potentials and proton transfer reactions. If photoinduced protonation occurs within the confined environment of MOFs solely in the presence of water, it might drive otherwise unfavourable redox reactions and significantly expand the reaction scope of porphyrinic photoreactions.

Experimental section

Porphyrin solutions

1.26 μM TCPP (Porphychem, >98%) was used as is and solutions in DMF (Fisher Scientific, 99.8%) were prepared from 0.1 mg mL⁻¹ stock solutions. Methane sulfonic acid (MSA, TCI Chemicals, >99.0%) was dissolved in DMF and added to the TCPP solutions prior the experiments. 2 mL of the solutions were transferred into screw-cap cuvettes (10 × 10 mm, Helma) with septum, further wrapped with parafilm and bubbled with Argon for 30 min prior TA measurements.

Steady-state UV/vis spectroscopy

Prior and after nanosecond TA experiments steady-state UV/vis spectra were recorded on a Shimadzu UV-2700 spectrometer. Spectra were recorded with 1 nm steps between 350 and 800 nm.

Nanosecond transient absorption spectroscopy

Nanosecond transient absorptions were recorded with an in-house assembled setup.⁴³ The excitation wavelength was generated using a tuneable Nd:YAG-laser system (NT342B, Ekspla). The laser system was operated at a repetition rate of 10 Hz with a pulse length of 5 ns. The probe light was operated at 20 Hz and was generated by a high-stability short arc xenon flash lamp (FX-1160, Excelitas Technologies), using a modified PS302 controller (EG&G). Using a 50/50 beam splitter, the probe light was split equally into a signal beam and a reference beam and focused (bi-convex lens 75 mm) on the entrance slit of a spectrograph (SpectraPro-150, Princeton Instruments) with a grating of 150 g mm⁻¹, blazed at 500 nm. The probe beam (A = 1 mm²) was passed through the sample cell and orthogonally overlapped with the excitation beam on a 1 mm × 10 mm area. The excitation energy was recorded by measuring the excitation power at the back of an empty sample holder and was reduced using a variable attenuator, which contains a half-waveplate and a beamsplitter, to a pulse energy of 0.14 mJ for 515 nm and 0.07 mJ for 665 nm. To correct for fluctuations in the flash lamp spectral intensity, the reference was used to normalize the signal. The probe and reference beams were simultaneously recorded with a single gated, intensified CCD camera (PI-MAX3, Princeton Instruments), which features an adjustable gate with a minimum setting of 2.9 ns. A gate setting of 50 ns, along with software binning, was used to improve the dynamic range and signal-to-noise ratio. Two delay generators (DG535 and DG645, Stanford Research Systems) were used to trigger the excitation and to change the delay of the flash lamp together with the gate of the camera during the experiment. The setup was controlled by a LabVIEW program written in-house. The order of the delay times at which the transient spectra were measured was randomized and the absorption of the sample was monitored during the experiment. At every delay time 100 spectra were collected and subsequently averaged for a good signal-to-noise ratio.

Data processing

Data processing was performed in Mathematica. The global fitting was also performed in Mathematica via a self-written least-squares fitting procedure.

Computational characterization

The geometries of the reported structures were obtained within Density Functional Theory (DFT) using B3LYP functional^55–59 and 6-31G(d) basis set.^60,61 The influence of solvent was accounted by polarizable continuum model (PCM), using the integral equation formalism variant (IEFPCM). All calculations were done in Gaussian 09 program.⁶²

Author contributions

PTP: conceptualization, data curation, investigation, visualization, validation, formal analysis, writing – original draft; DRZ: methodology, formal analysis, investigation, writing – review & editing; SP: methodology, writing – review & editing; BB: investigation, writing – original draft, conceptualization, validation, funding acquisition, supervision.

Data availability

The data supporting this article has been included as part of the ESI.† Raw and processed data for this article, including steady-state and transient absorption spectra, as well as optimized porphyrin geometries are available at zenodo.org under the manuscript title.

Conflicts of interest

There are no conflicts to declare.

Acknowledgements

P. T. P. and B. B. acknowledges funding by the Austrian Science Fund (FWF) under the project number J4607–N and by the Dutch Research Council (NWO) under the grant number OCENW.XS22.4.067 and VI.Veni.222.253. D. R. Z. acknowledges the National Science Centre, Poland within Opus project no 2021/43/B/ST4/02969. The authors thank the Molecular Photonics group that gave us access to the nanosecond transient absorption spectrometer and in particular Michiel Hilbers for assistance with the initial measurements. The authors want to thank Eline M. Hutter and Bert M. Weckhuysen for providing access to the nanosecond transient absorption spectrometer at Utrecht University used for preliminary studies.

Notes and references

1. J. R. Darwent, P. Douglas, A. Harriman, G. Porter and M. C. Richoux, Metal phthalocyanines and porphyrins as photosensitizers for reduction of water to hydrogen, Coord. Chem. Rev., 1982, 44, 83–126.
2. X. Zhang, M. C. Wasson, M. Shayan, E. K. Berdichevsky, J. Ricardo-Noordberg, Z. Singh, E. K. Papazyan, A. J. Castro, P. Marino, Z. Ajoyan, Z. Chen, T. Islamoglu, A. J. Howarth, Y. Liu, M. B. Majewski, M. J. Katz, J. E. Mondloch and O. K. Farha, A historical perspective on porphyrin-based metal–organic frameworks and their applications, Coord. Chem. Rev., 2021, 429, 213615.
3. R. Costa e Silva, L. O. da Silva, A. de Andrade Bartolomeu, T. J. Brocksom and K. T. de Oliveira, Recent applications of porphyrins as photocatalysts in organic synthesis: Batch and continuous flow approaches, Beilstein J. Org. Chem., 2020, 16, 917–955.
4. P. Zhang, J. Hu, B. Liu, J. Yang and H. Hou, Recent advances in metalloporphyrins for environmental and energy applications, Chemosphere, 2019, 219, 617–635.
5. M. Ethirajan, Y. Chen, P. Joshi and R. K. Pandey, The role of porphyrin chemistry in tumor imaging and photodynamic therapy, Chem. Soc. Rev., 2011, 40, 340–362.
6. L. L. Li and E. W. G. Diau, Porphyrin-sensitized solar cells, Chem. Soc. Rev., 2013, 42, 291–304.
7. J. Min Park, J. H. Lee and W. D. Jang, Applications of porphyrins in emerging energy conversion technologies, Coord. Chem. Rev., 2020, 407, 213157.
8. K. Rybicka-Jasińska, W. Shan, K. Zawada, K. M. Kadish and D. Gryko, Porphyrins as photoredox catalysts: experimental and theoretical Studies, J. Am. Chem. Soc., 2016, 138, 15451–15458.
9. E. Nikoloudakis, I. López-Duarte, G. Charalambidis, K. Ladomenou, M. Ince and A. G. Coutsolelos, Porphyrins and phthalocyanines as biomimetic tools for photocatalytic H₂ production and CO₂ reduction, Chem. Soc. Rev., 2022, 51, 6965–7045.
10. L. Zou, R. Sa, H. Lv, H. Zhong and R. Wang, Recent Advances on Metalloporphyrin-Based Materials for Visible-Light-Driven CO₂ Reduction, ChemSusChem, 2020, 13, 6124–6140.
11. Y. Kuramochi, Y. Fujisawa and A. Satake, Photocatalytic CO₂ Reduction Mediated by Electron Transfer via the Excited Triplet State of Zn(II) Porphyrin, J. Am. Chem. Soc., 2020, 142, 705–709.
12. S. Amanullah, P. Gotico, M. Sircoglou, W. Leibl, M. J. Llansola-Portoles, T. Tibiletti, A. Quaranta, Z. Halime and A. Aukauloo, Second Coordination Sphere Effect Shifts CO₂ to CO Reduction by Iron Porphyrin from Fe⁰ to Fe^I, Angew. Chem., Int. Ed., 2023, 63(4), e202314439.
13. J. Chen, Y. Zhu and S. Kaskel, Porphyrin-Based Metal–Organic Frameworks for Biomedical Applications, Angew. Chem., Int. Ed., 2021, 60, 5010–5035.
14. S. Hamad, N. C. Hernandez, A. Aziz, A. R. Ruiz-Salvador, S. Calero and R. Grau-Crespo, Electronic structure of porphyrin-based metal–organic frameworks and their suitability for solar fuel production photocatalysis, J. Mater. Chem. A, 2015, 3, 23458–23465.
15. B. Baumgartner, P. T. Prins, J. N. Louwen, M. Monai and B. M. Weckhuysen, The Role of Water in Carbon Dioxide Adsorption in Porphyrinic Metal–Organic Frameworks, ChemCatChem, 2023, 15, e202300722.
16. H. Q. Xu, J. Hu, D. Wang, Z. Li, Q. Zhang, Y. Luo, S. H. Yu and H. L. Jiang, Visible-light photoreduction of CO₂ in a metal-organic framework: Boosting electron-hole separation via electron Trap states, J. Am. Chem. Soc., 2015, 137, 13440–13443.
17. B. Cheng, O. Q. Munro, H. M. Marques and W. R. Scheidt, An analysis of porphyrin molecular flexibility - Use of porphyrin diacids, J. Am. Chem. Soc., 1997, 119, 10732–10742.
18. R. A. Schoonheydt, B. M. Weckhuysen, J. Meurig Thomas, J. Carlos Hernandez-Garrido, R. Raja, R. G. Bell and P. Chem Chem Phys, Editorial Highlight: Molecules in confined spaces, Phys. Chem. Chem. Phys., 2009, 11, 2794–2798.
19. F. G. Cirujano and F. X. Llabrés I Xamena, Tuning the Catalytic Properties of UiO-66 Metal–Organic Frameworks: From Lewis to Defect-Induced Brønsted Acidity, J. Phys. Chem. Lett., 2020, 11, 4879–4890.
20. J. R. Eskelsen, Y. Wang, Y. Qui, M. Ray, M. Handlin, K. W. Hipps and U. Mazur, Protonation state of core nitrogens in the meso-tetra(4-carboxyphenyl) porphyrin impacts the chemical and physical properties of nanostructures formed in acid solutions, J. Porphyrins Phthalocyanines, 2012, 16, 1233–1243.
21. T. Gensch, C. Viappiani and S. E. Braslavsky, Structural volume changes upon photoexcitation of porphyrins: Role of the nitrogen-water interactions, J. Am. Chem. Soc., 1999, 121, 10573–10582.
22. S. Mehrzad Sajjadinezhad, L. Boivin, K. Bouarab and P. D. Harvey, Photophysical properties and photonic applications of porphyrin-based MOFs, Coord. Chem. Rev., 2024, 510, 215794.
23. Y. Benseghir, A. Solé-Daura, D. R. Cairnie, A. L. Robinson, M. Duguet, P. Mialane, P. Gairola, M. Gomez-Mingot, M. Fontecave, D. Iovan, B. Bonnett, A. J. Morris, A. Dolbecq and C. Mellot-Draznieks, Unveiling the mechanism of the photocatalytic reduction of CO₂ to formate promoted by porphyrinic Zr-based metal–organic frameworks, J. Mater. Chem. A, 2022, 10, 18103–18115.
24. B. Pattengale, S. Ostresh, C. A. Schmuttenmaer and J. Neu, Interrogating Light-initiated Dynamics in Metal–Organic Frameworks with Time-resolved Spectroscopy, Chem. Rev., 2022, 122, 132–166.
25. C. Y. Lee, O. K. Farha, B. J. Hong, A. A. Sarjeant, S. T. Nguyen and J. T. Hupp, Light-harvesting metal-organic frameworks (MOFs): Efficient strut-to-strut energy transfer in bodipy and porphyrin-based MOFs, J. Am. Chem. Soc., 2011, 133, 15858–15861.
26. J. S. Baskin, H. Z. Yu and A. H. Zewail, Ultrafast dynamics of porphyrins in the condensed phase: I. Free base tetraphenylporphyrin, J. Phys. Chem. A, 2002, 106, 9837–9844.
27. Z. B. Liu, Y. Zhu, Y. Z. Zhu, J. G. Tian and J. Y. Zheng, Study on nonlinear spectroscopy of tetraphenylporphyrin and dithiaporphyrin diacids, J. Phys. Chem. B, 2007, 111, 14136–14142.
28. S. Gentemann, C. J. Medforth, T. P. Forsyth, D. J. Nurco, K. M. Smith, J. Fajer and D. Holten, Photophysical Properties of Conformationally Distorted Metal-Free Porphyrins. Investigation into the Deactivation Mechanisms of the Lowest Excited Singlet State, J. Am. Chem. Soc., 1994, 116, 7363–7368.
29. A. Harriman and M. C. Richoux, Luminescence of porphyrins and metalloporphyrins VIII: luminescence and hydrogen photogeneration from porphyrin conjugate diacids, J. Photochem., 1984, 27, 205–214.
30. P. J. Gonçalves, L. De Boni, N. M. B. Neto, J. J. Rodrigues, S. C. Zílio and I. E. Borissevitch, Effect of protonation on the photophysical properties of meso-tetra(sulfonatophenyl) porphyrin, Chem. Phys. Lett., 2005, 407, 236–241.
31. D. S. Correa, L. De Boni, G. G. Parra, L. Misoguti, C. R. Mendonça, I. E. Borissevitch, S. C. Zílio, N. M. Barbosa Neto and P. J. Gonçalves, Excited-state absorption of meso-tetrasulfonatophenyl porphyrin: Effects of pH and micelles, Opt. Mater., 2015, 42, 516–521.
32. L. P. F. Aggarwal, M. S. Baptista and I. E. Borissevitch, Effects of NaCl upon TPPS4 triplet state characteristics and singlet oxygen formation, J. Photochem. Photobiol., A, 2007, 186, 187–193.
33. F. Hibbert and K. P. P. Hunte, Kinetic and equilibrium studies of the protonation of meso-tetraphenylporphyrin in dimethyl sulphoxide-water, J. Chem. Soc., Perkin Trans. 2, 1977, 1624–1628.
34. Y. Cui, L. Zeng, Y. Fang, J. Zhu, C. H. Devillers, D. Lucas, N. Desbois, C. P. Gros and K. M. Kadish, Tuning the Electrochemistry of Free-Base Porphyrins in Acidic Nonaqueous Media: Influence of Solvent, Supporting Electrolyte, and Ring Substituents, ChemElectroChem, 2016, 3, 228–241.
35. Y. Fang, P. Bhyrappa, Z. Ou and K. M. Kadish, Planar and Nonplanar Free-Base Tetraarylporphyrins: β-Pyrrole Substituents and Geometric Effects on Electrochemistry, Spectroelectrochemistry, and Protonation/Deprotonation Reactions in Nonaqueous Media, Chem. – Eur. J., 2014, 20, 524–532.
36. K. Kalyanasundaram and M. Neumann-Spallart, Photophysical and Redox Properties of Water-Soluble Porphyrins in Aqueous Media, J. Phys. Chem., 1982, 86, 5163.
37. G. De Luca, A. Romeo and L. M. Scolaro, Role of counteranions in acid-induced aggregation of isomeric tetrapyridylporphyrins in organic solvents, J. Phys. Chem. B, 2005, 109, 7149–7158.
38. A. Rosa, G. Ricciardi, E. J. Baerends, A. Romeo and L. M. Scolaro, Effects of Porphyrin Core Saddling, meso-Phenyl Twisting, and Counterions on the Optical Properties of meso-Tetraphenylporphyrin Diacids: The [H 4TPP](X)₂ (X = F, Cl, Br, I) Series as a Case Study, J. Phys. Chem. A, 2003, 107, 11468–11482.
39. M. Presselt, W. Dehaen, W. Maes, A. Klamt, T. Martínez, W. J. D. Beenken and M. Kruk, Quantum chemical insights into the dependence of porphyrin basicity on the meso-aryl substituents: Thermodynamics, buckling, reaction sites and molecular flexibility, Phys. Chem. Chem. Phys., 2015, 17, 14096–14106.
40. A. Stonela, E. B. Fleischerlb, P. S. Braterman, R. C. Davies, R. J. P. Williams, A. Chem Phys and J. E. Falk, The molecular and crystal structure of porphyrin diacids, J. Am. Chem. Soc., 1968, 90, 2735–2748.
41. G. De Luca, A. Romeo, L. M. Scolaro, G. Ricciardi and A. Rosa, Evidence for tetraphenylporphyrin monoacids, Inorg. Chem., 2007, 46, 5979–5988.
42. R. F. Pasternack, P. R. Huber, P. Boyd, G. Engasser, L. Francesconi, E. Gibbs, P. Fasella, G. C. Venturo and L. D. Hinds, On the Aggregation of meso-Substituted Water-Soluble Porphyrins, J. Am. Chem. Soc., 1972, 94, 4511–4517.
43. B. Limburg, M. Hilbers, A. M. Brouwer, E. Bouwman and S. Bonnet, The Effect of Liposomes on the Kinetics and Mechanism of the Photocatalytic Reduction of 5,5′-Dithiobis(2-Nitrobenzoic Acid) by Triethanolamine, J. Phys. Chem. B, 2016, 120, 12850–12862.
44. P. R. Ogilby, Singlet oxygen: There is indeed something new under the sun, Chem. Soc. Rev., 2010, 39, 3181–3209.
45. M. Gouterman and G. E. Khalil, Porphyrin free base phosphorescence, J. Mol. Spectrosc., 1974, 53, 88–100.
46. F. Edhborg, A. Olesund and B. Albinsson, Best practice in determining key photophysical parameters in triplet–triplet annihilation photon upconversion, Photochem. Photobiol. Sci., 2022, 21, 1143–1158.
47. L. Pekkarinen and H. Linschitz, Studies on Metastable States of Porphyrins. II. Spectra and Decay Kinetics of Tetraphenylporphine, Zinc Tetraphenylporphine and Bacteriochlorophyll, J. Am. Chem. Soc., 1960, 82, 2407–2411.
48. R. L. Brookfield, H. Ellul, A. Harriman and G. Porter, Luminescence of porphyrins and metalloporphyrins. Part 11. – Energy transfer in zinc-metal-free porphyrin dimers, J. Chem. Soc., Faraday Trans. 2, 1986, 82, 219–233.
49. C. Schweitzer and R. Schmidt, Physical mechanisms of generation and deactivation of singlet oxygen, Chem. Rev., 2003, 103, 1685–1757.
50. S. Tsukahara and H. Watarai, Kinetics for acid-dissociation of tetraphenylporphinetetrasulfonate in the ground state measured by laser photolysis relaxation method, Phys. Chem. Chem. Phys., 2002, 4, 1592–1597.
51. J. L. Pérez-Lustres, F. Rodriguez-Prieto, M. Mosquera, T. A. Senyushkina, N. P. Ernsting and S. A. Kovalenko, Ultrafast proton transfer to solvent: Molecularity and intermediates from solvation- and diffusion-controlled regimes, J. Am. Chem. Soc., 2007, 129, 5408–5418.
52. N. Chattopadhyay, A. Samanta, T. Kundu and M. Chowdhury, Excited state deprotonation reactions of aromatic amines: a diffusion-controlled process, J. Photochem. Photobiol., A, 1989, 48, 61–68.
53. R. Büchner, V. Vaz da Cruz, N. Grover, A. Charisiadis, M. Fondell, R. Haverkamp, M. O. Senge and A. Föhlisch, Fundamental electronic changes upon intersystem crossing in large aromatic photosensitizers: free base 5,10,15,20-tetrakis(4-carboxylatophenyl)porphyrin, Phys. Chem. Chem. Phys., 2022, 24, 7505–7511.
54. J. C. De Paula, V. A. Walters, C. Nutaitis, J. Lind and K. Hall, Transient resonance Raman spectrum of meso-tetraphenylporphine: An analysis of chemical factors that influence the dynamics of the excited triplet states of metalloporphyrins, J. Phys. Chem., 1992, 96, 10591–10594.
55. A. D. Becke, Density-functional exchange-energy approximation with correct asymptotic behavior, Phys. Rev. A: At., Mol., Opt. Phys., 1988, 38, 3098–3100.
56. P. A. M. D. Dirac, Quantum mechanics of many-electron systems, Proc. R. Soc. London, Ser. A, 1929, 123, 714–733.
57. A. D. Becke, Density-functional thermochemistry. III. The role of exact exchange, J. Chem. Phys., 1993, 98, 5648–5652.
58. J. P. Perdew, Density-functional approximation for the correlation energy of the inhomogeneous electron gas, Phys. Rev. B: Condens. Matter Mater. Phys., 1986, 33, 8822–8824.
59. J. C. Slater, A simplification of the Hartree-Fock method, Phys. Rev., 1951, 81, 385–390.
60. S. H. Vosko, L. Wilk and M. Nusair, Accurate spin-dependent electron liquid correlation energies for local spin density calculations: a critical analysis, Can. J. Phys., 1980, 58, 1200–1211.
61. W. J. Hehre, K. Ditchfield and J. A. Pople, Self-consistent molecular orbital methods. XII. Further extensions of Gaussian-type basis sets for use in molecular orbital studies of organic molecules, J. Chem. Phys., 1972, 56, 2257–2261.
62. M. J. Frisch, G. W. Trucks, H. B. Schlegel, G. E. Scuseria, M. A. Robb, J. R. Cheeseman, G. Scalmani, V. Barone, B. Mennucci, G. A. Petersson, H. Nakatsuji, M. Caricato, X. Li, H. P. Hratchian, A. F. Izmaylov, J. Bloino, G. Zheng, J. L. Sonnenberg, M. Hada, M. Ehara, K. Toyota, R. Fukuda, J. Hasegawa, M. Ishida, T. Nakajima, Y. Honda, O. Kitao, H. Nakai, T. Vreven, J. A. Montgomery, Jr., J. E. Peralta, F. Ogliaro, M. Bearpark, J. J. Heyd, E. Brothers, K. N. Kudin, V. N. Staroverov, R. Kobayashi, J. Normand, K. Raghavachari, A. Rendell, J. C. Burant, S. S. Iyengar, J. Tomasi, M. Cossi, N. Rega, J. M. Millam, M. Klene, J. E. Knox, J. B. Cross, V. Bakken, C. Adamo, J. Jaramillo, R. Gomperts, R. E. Stratmann, O. Yazyev, A. J. Austin, R. Cammi, C. Pomelli, J. W. Ochterski, R. L. Martin, K. Morokuma, V. G. Zakrzewski, G. A. Voth, P. Salvador, J. J. Dannenberg, S. Dapprich, A. D. Daniels, Ö. Farkas, J. B. Foresman, J. V. Ortiz, J. Cioslowski and D. J. Fox, 2013.

---

Footnote

† Electronic supplementary information (ESI) available: including global-analysis rate equations, further transient absorption spectroscopy data and computational analysis. Optimized geometries are added as XYZ file. See DOI: https://doi.org/10.1039/d4cp02542c

---