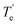On the ground and excited electronic states of LaCO and AcCO

Abstract

High-level ab initio electronic structure analysis of correlated lanthanide- and actinide-based species is laborious to perform and consequently limited in the literature. In the present work, the ground and electronically excited states of LaCO and AcCO molecules were explored utilizing the multireference configuration interaction (MRCI), Davidson corrected MRCI (MRCI+Q), and coupled cluster singles doubles and perturbative triples [CCSD(T)] quantum chemical tools conjoined with correlation consistent triple-ζ and quadruple-ζ quality all-electron Douglas–Kroll (DK) basis sets. The full potential energy curves (PECs), dissociation energies (D_es), excitation energies (T_es), bond lengths (r_es), harmonic vibrational frequencies (ω_es), and chemical bonding patterns of low-lying electronic states of LaCO and AcCO are introduced. The ground electronic state of LaCO is a ⁴Σ⁻ (1σ¹1π²) which is a product of the reaction between excited La(⁴F) versus CO(X¹Σ⁺), whereas the ground state of AcCO is a 1²Π (1σ²1π¹) deriving from ground state fragments Ac(²D) + CO(X¹Σ⁺). The spin–orbit ground states of LaCO (1⁴Σ⁻_3/2) and AcCO (1²Π_1/2) bear ∼13 and 5 kcal mol⁻¹D₀ values, respectively. At the MRCI level, the spin–orbit curves, the spin–orbit mixing, and the T_es of spin–orbit states of LaCO and AcCO were also analyzed. Lastly, the density functional theory (DFT) calculations were performed applying 16 exchange–correlation functionals that span three rungs of “Jacob's ladder” of density functional approximations (DFAs) to assess DFT errors associated on the D_e and ionization energy (IE) of LaCO.

---

I. Introduction

Electronic structure studies provide an essential avenue for analyzing and gaining insight into chemicophysical properties of highly correlated molecular species. Especially, precise theoretical representations of ground and excited states are vital for making accurate predictions of fundamental chemical reactivities, thermodynamics, and spectroscopic characteristics of highly complicated lanthanide- and actinide-based molecules. The properties of such systems are greatly challenging to calculate under electronic structure theory where the treatment of higher order electron correlation, relativistic effects, and spin–orbit effects are critical to reach higher accuracy. The multireference tools are ideal for the investigation of lanthanide- and actinide-based species where the partially occupied valence orbitals give rise to a large number of closely arranged single-reference and multireference states that are highly correlated and coupled together.

The ab initio theoretical investigation of lanthanide- and actinide-based small molecules is an area of high-interest at present owing to their importance in nuclear energy.^1,2 Especially the heavy primordial Th and U-based actinide species are the prime focus in this topic of research.^3–13 On the other hand, early lanthanide La- and actinide Ac-based species are relatively less studied. For example, we were able to find 5 experimental and theoretical studies in total on La–CO system.^14–18 To the best of our knowledge, experimental or theoretical studies are unavailable for Ac–CO. This could be due to the low abundance of Ac in the earth's crust (5.5 × 10⁻¹⁰ ppm)¹⁹ which makes it expensive, and its similarity in chemicophysical properties to the more abundant La.²⁰ Furthermore, the comparatively low interest on such species could also be due to the transition-metal-like nature of the low-lying states of La and Ac atoms. For example, the La and Ac populate their corresponding valence 4f and 5f orbitals at 12th and 16th excited states respectively, hence the molecules that they form tend to carry transition-metal-like properties rather than the characteristics of typical f-orbital populated lanthanide and actinide species.²¹

CO is the strongest ligand in the spectrochemical series which tends to form substantially strong chemical bonds with many metals in the periodic table and therefore the lack of data on the interaction between CO versus La and Ac is rather surprising. Heavy metals are known to activate C–O bond and hence the investigation of the potential of CO activation by La and Ac is beneficial for the field of catalysis.^8,22,23 Furthermore, gas-phase studies of model metal–CO species can be used to gain insight on the chemisorption process of CO on metal surfaces.²⁴ More importantly, the investigations of La + CO and Ac + CO reactions by themselves hold a spectroscopic significance. This motivated us to carry out the present quantum chemical investigation of the low-lying electronic and spin–orbit states of LaCO and AcCO molecules which is expected to serve as a guide and motivation for their future experimental and theoretical investigations.

The first study of LaCO dates back to Hong et al.'s work in 1997 which reported several energy related properties and structural patterns of linear LaCO, linear LaOC, and side-bonded La(η²-CO) isomers at the DFT/LDA+QR+GRD (local density approximation with the gradient correction and relativistic effects).¹⁴ They found that the linear LaCO is more stable compared to the linear LaOC and La(η²-CO) by ∼27 and 14 kcal mol⁻¹, respectively. This work further reported a quartet-spin ground state and a doublet-spin first excited state for the linear LaCO with 37.36 and 30.90 kcal mol⁻¹D_es, respectively. Their reported optimized La–C and C–O bond distances and the corresponding C–O stretching frequency of LaCO of the ground state are 2.392 Å, 1.177 Å, and 1778 cm⁻¹. Nine years after Hong et al.'s DFT work, the first experimental study of LaCO was reported by Xu, Jiang, and Zou.¹⁵ They studied the reaction of laser-ablated La with CO in a solid argon matrix at 7 K and reported a 1772.7 cm⁻¹ C–O stretching frequency which is in harmony with the value reported by Hong et al. Furthermore, they have performed DFT/BPW91 calculations and predicted a ⁴Σ⁻ ground state for LaCO which agrees with the findings of Hong et al. The D_e of LaCO reported in the Xu et al.'s work is (41.24 kcal mol⁻¹) which is ∼4 kcal mol⁻¹ higher than the value reported by Hong et al.¹⁴ In 2007 Jiang and Xu reported another matrix infrared spectroscopic study for LaCO and assigned a 1814 cm⁻¹ frequency for the C–O stretch which agreed reasonably well with the DFT/BPW91 frequency calculated in the same work (i.e., 1841.7 cm⁻¹).¹⁶ At the same level of theory, the obtained La–C and C–O bond distances of LaCO(⁴Σ⁻) are 2.404 and 1.186 Å respectively, which are slightly longer than the lengths reported by Hong et al.¹⁴ In the same year, Zhang et al., reported La–C and C–O distances and frequencies for the ⁴Σ⁻ (2.504 Å, 1.166 Å, 1779 cm⁻¹) and ²Π (2.495 Å, 1.160 Å, 1918 cm⁻¹) states of LaCO at the DFT/BP86.¹⁷ Furthermore, they reported an excited ²Π state for LaCO that lies 12.4 and 6.5 kcal mol⁻¹ above the ⁴Σ⁻ at the DFT/BP86 and CCSD(T) levels of theory, respectively. The most recent work on LaCO is reported in 2012 by Xu et al., who performed DFT/PBE calculations and reported La–C and C–O bond lengths of 2.299 and 1.181 Å respectively.¹⁸ Overall, the literature DFT analyses highlight that the predictions of LaCO are significantly dependent on the density functional approach being utilized.

In the present work, we have employed high-level MRCI, MRCI+Q, and CCSD(T) quantum chemical tools to investigate the interaction of La and Ac with CO. We report full PECs, equilibrium electronic configurations, energetics, and spin–orbit effects on LaCO and AcCO. The side-bonded La(η²-CO) and Ac(η²-CO) and the linear-to-bent transition energies were also investigated. Furthermore, DFT calculations were performed to calculate D_e and the IE of LaCO probing a set of exchange correlation functionals that span three rungs of Jacob's ladder of DFA; GGA (BP86,^25,26 BLYP,^27,28 PBE²⁹), MGGA (TPSS,³⁰ MN15-L³¹), and hybrid [global GGA hybrid (B3LYP,^32,33 B3P86,^25,32 B3PW91,³² PBE0^34,35), MGGA hybrid (TPSSh,³⁰ M06,³⁶ M06-2X,³⁶ MN15³⁷), and RSH (LRC-ωPBE,³⁸ CAM-B3LYP,³⁹ ωB97X⁴⁰)] to assess the associated DFT errors of these properties.

II. Computational details

The MOLPRO 2023.2^41–43 code was utilized for all wave function theory (WFT) internally contracted MRCI^44–46 (or MRCISD) and CCSD(T)⁴⁷ calculations. In all cases, default MOLPRO convergence criteria was applied. For the calculations of LaCO and AcCO, the C_2v Abelian sub point group of their true C_∞v non-Abelian symmetry was used. First, the full PECs resulting from the La(²D) + CO(X¹Σ⁺), La(⁴F) + CO(X¹Σ⁺), La(²F) + CO(X¹Σ⁺), La(⁴P) + CO(X¹Σ⁺), and La(²D) + CO(X¹Σ⁺) asymptotes were produced at the MRCI theory as a function of La⋯C distance while keeping the C–O bond length fixed to 1.168 Å, which is the CCSD(T) optimized C–O length of the ground state of LaCO. Similarly, at the MRCI method, PECs arising from the Ac(²D) + CO(X¹Σ⁺), Ac(²P^o) + CO(X¹Σ⁺), Ac(⁴F) + CO(X¹Σ⁺), and Ac(²D^o) + CO(X¹Σ⁺) asymptotes were considered to investigate the low-lying states of AcCO. Here the C–O length was kept constant to 1.159 Å, which is the C–O length of the CCSD(T) optimized AcCO(1²Π). For these calculations, cc-pVTZ-DK3⁴⁸ of La and Ac and cc-pVTZ-DK^49,50 of C and O basis set (hereafter TZ) was used with the third-order Douglas–Kroll–Hess (DKH) Hamiltonian. The complete active space self-consistent field (CASSCF)^51–54 reference wave functions (3 electrons in 9 orbitals or CAS[3,9]) were provided for MRCI calculations of both LaCO and AcCO. At the dissociation limit, the 9 orbitals are pure nd, (n + 1)s, and (n + 1)p atomic orbitals of La/Ac and at the implemented C_2v point group, they are 4a₁ [(n + 1)s, nd_z², nd_x²−y², and (n + 1)p_z], 2b₁ [nd_xz and (n + 1)p_x], 2b₂ [nd_yz and (n + 1)p_y], and 1a₂ [nd_xy] in symmetry (n = 5 for La and n = 6 for Ac). At the MRCI level, the single and double electron promotions were permitted to the virtual orbitals. Using the same active space and the basis set, full geometry optimizations were performed for 7 and 2 lowest energy electronic states of LaCO and AcCO at the MRCI level to obtain r_e, T_e, and ω_e values. Moreover, the geometries were optimized at the MRCI+Q⁵⁵ level (Davidson relaxed approach) to evaluate the approximate quadruple substitution-like effect on the aforementioned properties.

The spin–orbit coupling curves resulting from 1⁴Σ⁻, 1²Σ⁻, 1²Π, 1²Δ, and 1⁴Φ of LaCO were produced at the MRCI level as a function of La⋯C distance. The 1²Π, ⁴Σ⁻, ⁴Φ, ²Σ⁻, ²Δ, ⁴Π, ²Σ⁺, ²Π states of AcCO were used in the spin–orbit matrix to study the low energy spin–orbit curves of AcCO (see main text of the paper for more information regarding the spin–orbit analysis). For spin–orbit calculations, TZ basis set was used with the Breit–Pauli Hamiltonian as implemented in MOLPRO.

The geometries of low-lying single-reference electronic states of LaCO and AcCO and the ground state of LaCO⁺ were also optimized at the CCSD(T) level of theory that was built on top of Hartree–Fock (HF) wave functions. For each case, two sets of CCSD(T) calculations were performed with cc-pVTZ-DK3 (La) cc-pVTZ-DK (C and O) [hereafter TZ-CCSD(T)] and cc-pVQZ-DK3 (La) cc-pVQZ-DK (C and O) [hereafter QZ-CCSD(T)] basis sets using the third-order DKH Hamiltonian. The ground states of the side-bonded La(η²-CO) and Ac(η²-CO) molecules were also studied at the TZ-CCSD(T) level. Single-point CCSD(T) calculations were also performed for the La(²D), La(⁴F), and CO(X¹Σ⁺) to calculate CCSD(T) D_es. The experimental bond distance of CO(X¹Σ⁺) (1.128 Å)²¹ was used for the CCSD(T) calculation.

Single-point DFT calculations were performed for the ground states of LaCO(⁴Σ⁻), LaCO⁺(³Σ⁻), and CO(X¹Σ⁺) and excited La(⁴F) to calculate the DFT ionization energy (IE) of LaCO(⁴Σ⁻) and DFT D_e of LaCO(⁴Σ⁻) with respect to the La(⁴F) + CO(X¹Σ⁺) fragments using the Gaussian 16⁵⁶ package. For these calculations, the TZ-CCSD(T) optimized geometries of LaCO(⁴Σ⁻) and LaCO⁺(³Σ⁻) and the experimental bond distance of CO(X¹Σ⁺) (1.128 Å)²¹ were provided. The DFT calculations were performed using a set of exchange correlation functionals that span three rungs of Jacob's ladder; semi-local generalized gradient approximation (GGA: BP86,^25,26 BLYP,^27,28 PBE²⁹), meta-GGA (MGGA: TPSS,³⁰ MN15-L³¹), and hybrid [global GGA hybrid (B3LYP,^32,33 B3P86,^25,32 B3PW91,³² PBE0^34,35), MGGA hybrid (TPSSh,³⁰ M06,³⁶ M06-2X,³⁶ MN15³⁷), and range-separated hybrid (RSH: LRC-ωPBE,³⁸ CAM-B3LYP,³⁹ ωB97X⁴⁰)]. For La, the Stuttgart relativistic small-core (RSC) 1997 basis set with a 28-electron effective core potential (ECP) was used.^57,58 For C and O, the cc-pVQZ basis set was used.⁴⁹ In each case, the wave functions were optimized implementing the stable = opt keyword of Gaussian 16.⁵⁶ The default self-consistent-field convergence thresholds, grids, frozen core settings available in Gaussian 16 were provided for all DFT calculations.⁵⁶

III. Results and discussion

IIIA. LaCO

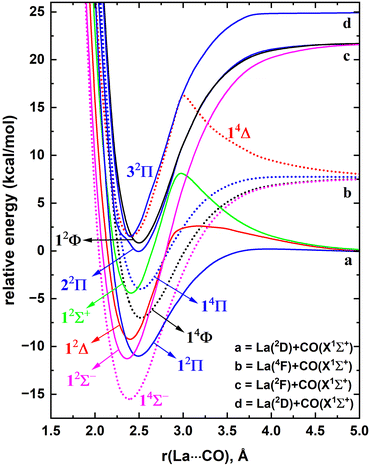
The ground electronic state of La is a ²D with a 5d¹6s² valence electron configuration. An electron promotion from 6s to 5d shells produces its first six excited states with 5d²6s¹ configuration which extend over 7.6–28.5 kcal mol⁻¹. The spin–orbit splitting of La is substantial. For example, the J = 5/2 and 3/2 splits of ²D state are separated by 3.0 kcal mol⁻¹, and the spin–orbit products of the first excited state of La(⁴F) span over 4.2 kcal mol⁻¹. Generally, the spin–orbit coupling effects of isolated atoms are substantially large compared to the spin–orbit coupling effects of the molecules that they form. However, the spin–orbit coupling effects of lanthanide-based molecular species are clearly non-negligible. Hence in the present work, spin–orbit effect disregarded low-lying electronic states of LaCO as well as their spin–orbit products were investigated.

A full potential energy profile can provide us with useful information such as relative stabilities of the states, locations of energy minima and their origins, and avoided crossings. Hence, we have produced the full PECs of LaCO as a function of La⋯C distance while keeping the CO bond distance fixed to the C–O length of the optimized geometry of the ground state of LaCO. Specifically, here La(²D) + CO(X¹Σ⁺), La(⁴F) + CO(X¹Σ⁺), La(²F) + CO(X¹Σ⁺), La(⁴P) + CO(X¹Σ⁺), and La(²D) + CO(X¹Σ⁺) reactions were considered to produce CASSCF PECs of LaCO. These reactions produce ²[Σ⁺, Π, Δ], ⁴[Σ⁻, Π, Δ, Φ], ²[Σ⁻, Π, Δ, Φ], ⁴[Σ⁻, Π], and ²[Σ⁺, Π, Δ], molecular states, respectively. Note that the first excited state of CO(a³Π) lies significantly high in energy (i.e., 139.2 kcal mol⁻¹) and hence its reactions with low-lying electronic states of La were not studied. At the MRCI+Q level, the most stable 11 electronic states of LaCO were investigated and are illustrated in Fig. 1. The PECs originating from the La(⁴P) + CO(X¹Σ⁺) are not part of the most stable 11 electronic states of LaCO and hence are not plotted in Fig. 1.

Fig. 1 Full PECs of several low-lying electronic states of LaCO as a function of La⋯C distance [r(La⋯CO), Å] at MRCI+Q level of theory. The relative energies referenced to the dissociation limit of La(²D) + CO(X¹Σ⁺), which is set to 0 kcal mol⁻¹. At each scan the C–O length is kept fixed to the 1.168 Å, which is the corresponding C–O length of the LaCO(1⁴Σ⁻). The dotted and solid PECs correspond to the quartet and doublet spins, respectively. The Σ⁻, Π, Δ, Σ⁺, and Φ states are shown in pink, blue, red, green, and black, respectively.

At the dissociation limit, the relative energies of the fragments correspond to the excitation energies of La atom (Fig. 1). Specifically, the first, second, and fourth excitation energies of La atom according to the MRCI+Q potential energy profile (Fig. 1) are 7.6, 21.6, and 24.9 kcal mol⁻¹ which are in good agreement with the corresponding experimental values for the lowest energy J states of La (i.e., 7.6, 20.0, 24.1 kcal mol⁻¹, respectively).²¹ This somewhat demonstrates the validity of the MRCI+Q level of theory for the investigation of a highly correlated system such as LaCO.

The ground state of LaCO is a ⁴Σ⁻ derived from the La(⁴F) + CO(X¹Σ⁺) fragments (Fig. 1). The ²D(5d¹6s²) to ⁴F(5d²6s¹) promotion of La minimizes the σ electron repulsion between La versus CO which ameliorates the σ electron donation from CO to La. The same is true for the previously reported ScCO (which is isovalent to LaCO), where its X⁴Σ⁻ ground state is a result of the reaction between CO and excited Sc(⁴F).^59,60 Similar to 1⁴Σ⁻, the 1⁴Φ and 1⁴Π of LaCO originating from the same fragments are substantially attractive in nature except for the 1⁴Δ which is initially strongly repulsive but turn attractive at ∼2.9 Å due to an avoided crossing. Note that an avoided crossing is a result of the interaction of two PECs with identical spins and symmetries. The initial repulsion of the 1⁴Δ PEC arises due to the electron–electron repulsion of the (5d_z²)¹ (M_L = 2 component of La) versus the two sigma dative electrons at the CO.

The first excited state of LaCO(1²Σ⁻) lies ∼4 kcal mol⁻¹ above 1⁴Σ⁻ and dissociates to the La(²F) + CO(X¹Σ⁺). The next excited state of LaCO(1²Π) lies energetically very close (less than 1 kcal mol⁻¹) to the 1²Σ⁻. The 1²Π is indeed the lowest energy electronic state that is produced by the ground state fragments [i.e., La(²D) + CO(X¹Σ⁺)]. Similar to the 1⁴Δ, the 1²Δ and 1²Σ⁺ states of La(²D) + CO(X¹Σ⁺) are first repulsive but turn attractive due to avoided crossings and become the third and fifth excited states of LaCO (Fig. 1). Overall, at the MRCI+Q level, the seven lowest energy electronic states of LaCO are stable with respect to the ground state fragments and they are congested within 12 kcal mol⁻¹ which clearly captures the complexity of the electronic spectrum of the system.

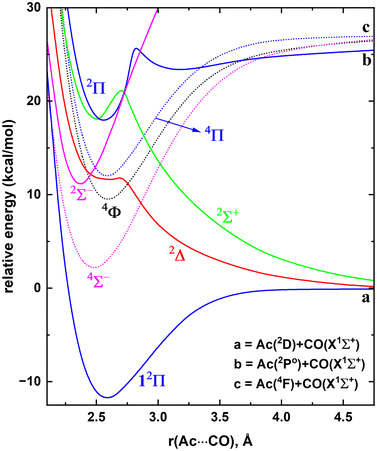
The electronic configurations of the 11 studied electronic states of LaCO and the select occupied molecular orbitals are given in Table 1 and Fig. 2, respectively. The 1σ is dominantly the polarized 6s of La (85.41%) with small contributions from 6p_z (6.22%) and 5d_z² (8.37%) of La. The polarization of the valence s orbital of a metal to the opposite direction of the CO aids the chemical bond formation.^8,24,61 The 1π_x molecular orbital demonstrates the 5d_xz(La) → π*(CO) back-donation of LaCO. The 1π_x is composed of 5d_xz of La (65.87%) + 2p_x of C (18.78%) − 2p_x of O (15.35%). Similarly, the antibonding 2π_x is made of the same atomic orbitals as in the case of 1π_x but with 5d_xz(La) – 2p_x(C) – 2p_x(O) combination. Due to the symmetry effects, the non-bonding 1δ_x²−y² of LaCO is a merely the 5d_x²−y² of La. Note that the contours of 1π_y, 2π_y, and 1δ_xy are identical to the shapes of 1π_x, 2π_x, and 1δ_x²−y² orbitals and hence are not depicted in Fig. 2.

Table 1 Dominant electronic configurations of several low-lying electronic states of LaCO [only the six occupied orbitals of the applied CAS(3,9) active space are given]

State^a	Coefficient^b	1σ	1πx	1πy	2πy	1δx^2−y^2	1δxy
a Only A1 components of Δ and B1 components of Π and Φ states at C2v symmetry are listed. b Only the configuration interaction coefficients that are larger than 0.25 of corresponding natural orbital representations are listed.
1^4Σ^−	0.98	α	α	α	0	0	0
1^2Σ^−	0.80	β	α	α	0	0	0
	−0.40	α	β	α	0	0	0
	−0.40	α	α	β	0	0	0
1^2Π	0.91	2	α	0	0	0	0
1^2Δ	−0.66	α	0	2	0	0	0
	0.66	α	2	0	0	0	0
1^4Φ	−0.69	α	0	α	0	0	α
	0.69	α	α	0	0	α	0
1^4Π	0.69	α	0	α	0	0	α
	0.69	α	α	0	0	α	0
1^2Σ^+	0.63	α	0	2	0	0	0
	0.63	α	2	0	0	0	0
2^2Π	−0.55	α	0	β	0	0	α
	0.58	α	β	0	0	α	0
	−0.33	2	α	0	0	0	0
1^2Φ	0.62	α	0	β	0	0	α
	0.62	α	β	0	0	α	0
3^2Π	0.62	0	α	2	0	0	0
	0.26	α	α	0	0	β	0
	−0.36	0	α	α	β	0	0
1^4Δ	0.96	0	α	α	0	0	α

---

Fig. 2 Select state average CASSCF molecular orbitals of LaCO. La (left most atom), C (central atom), and O (right most atom) are shown in magenta, gray, and red, respectively. A threshold of 80% was applied to produce orbital plots. The negative and positive phases of each orbital is shown in blue and red, respectively. The 90° rotation of 1π_x and 2π_x orbitals along the z-axis respectively produces 1π_y and 2π_y orbitals, whereas the 45° rotation of 1δ_x²−y² yields the 1δ_xy. IboView software was used to plot molecular orbitals.⁶²

The ground state of LaCO(1⁴Σ⁻) carries the single-reference 1σ¹1π² electron configuration (Table 1) which translates to the 5d²6s¹ valence electron configuration of the La(⁴F). The higher stability of this high spin electronic state is a typical instance of the Hund's rule. According to our QZ-HF Mullikan population analysis, LaCO(1⁴Σ⁻) has La^+0.26[CO]^−0.26 charge localization. Our findings are in harmony with the DFT/PBE Mullikan charge distribution reported by Xu et al., for LaCO in 2012 (i.e., La^+0.23[CO]^−0.23).¹⁸

The spin-pairing of the 1σ and the two 1π electrons produces the first excited state of LaCO(1²Σ⁻) which is multireference in nature. An electron promotion from 1π to 1σ creates the electron configuration of the single-reference second excited state of LaCO (i.e., 1²Π; 1σ²1π¹). Next seven states of LaCO are dominantly multireference in character (i.e., 1²Δ, 1⁴Φ, 1⁴Π, 1²Σ⁺, 2²Π, 1²Φ, 3²Π). The 1⁴Φ is the first electronic state of LaCO that populates 1δ orbitals. Specifically, an electron transfer from 1π to empty 1δ from the ground electron configuration of LaCO(1⁴Σ⁻) gives rise to the configuration of 1⁴Φ (i.e., 1σ¹1π¹1δ¹). The same electron configuration holds for the 1⁴Π state of LaCO but with positive combinations of the two dominant components (Table 1). The 2²Π and 1²Φ are the corresponding doublet spin states of the 1σ¹1π¹1δ¹ configuration (note: only two dominant configurations of 2²Π considered). Among the studied states, 3²Π is the only state to populate the 2π antibonding molecular orbital with a significant contribution. The highest energy state that was studied here (i.e., 1⁴Δ) is single-reference in character and the first state to carry an unoccupied 1σ orbital. Based on the equilibrium electron arrangements, the valence-bond-Lewis (vbL) diagrams of the studied electronic states of LaCO are introduced (Fig. 3).

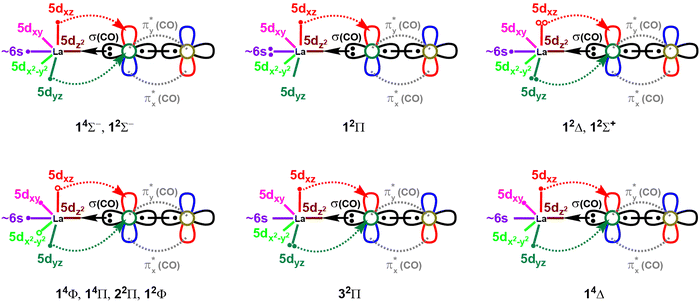Fig. 3 Proposed valence-bond-Lewis (vbL) diagrams for the studied 11 electronic states of LaCO. For clarity the π_x and π_y bonds of CO are excluded. The multireference (1π_x)² ± (1π_y)² components of the 1²Δ and 1²Σ⁺ states are shown by electron pairs with solid and open circles. Similarly, the multireference π¹δ¹ electron combinations of 1⁴Φ, 1⁴Π, 2²Π, and 1²Φ are depicted in open and solid circles. Only two and one dominant configurations of 2²Π and 3²Π states respectively are shown. See Table 1 for their exact electronic configurations.

The MRCI+Q D_e of the LaCO(1⁴Σ⁻) with respect to the La(²D) + CO(X¹Σ⁺) asymptote is 18.99 kcal mol⁻¹ which is only 0.73 kcal mol⁻¹ higher than the MRCI D_e (Table 2). The CCSD(T) D_e obtained at the same basis set [TZ-CCSD(T)] of the ground state is ∼1 kcal mol⁻¹ larger than the MRCI+Q D_e (19.93 kcal mol⁻¹). The better agreement of D_es between the MRCI+Q and CCSD(T) is a common observation in the literature.^63–65 Generally, CCSD(T) calculations are less expensive compared to the MRCI and hence here we were able to perform QZ-CCSD(T) calculations for LaCO as well (Table 2). Moving from TZ-CCSD(T) to QZ-CCSD(T), the D_e of LaCO(1⁴Σ⁻) increased by 1.51 kcal mol⁻¹. All our high-level ab initio D_es are significantly lower than the previously reported DFT D_es of LaCO. Specifically, the D_e reported by Hong et al., by LDA+QR+GRD is 37.36 kcal mol⁻¹ (ref. 14) whereas the DFT/BPW91 D_e of LaCO by Xu et al., is 41.24 kcal mol⁻¹.¹⁵

Table 2 Dissociation energy with respect to La(²D) + CO(X¹Σ⁺) fragments (D_e, kcal mol⁻¹), La–C and C–O bond lengths (r_e, Å), excitation energy (T_e, kcal mol⁻¹), and vibrational frequency (ω_e, cm⁻¹) of several low-lying electronic states of LaCO

State	Level of theory^a	D e	r e		T e	ω e
			La–C	C–O
a Davidson corrected MRCI is denoted by MRCI+Q. For all MRCI, MRCI+Q, and TZ-CCSD(T) calculations cc-pVTZ-DK3 of La and cc-pVTZ-DK of C and O basis set was applied. The cc-pVQZ-DK3 of La and cc-pVQZ-DK of C and O basis set was used for QZ-CCSD(T) calculations. b C–O stretching mode.
1^4Σ^−	QZ-CCSD(T)	21.44	2.346	1.165	0	281, 284, 322, 1860^b
	TZ-CCSD(T)	19.93	2.352	1.168	0	276, 277, 317, 1857^b
	MRCI+Q	18.99	2.362	1.160	0
	MRCI	18.26	2.379	1.149	0
	BPW91^16		2.404	1.186		1841.7^b
	BPW91^15	41.24	2.298	1.185		1790.8^b
	B3LYP^16					1901.3^b
	PBE^18		2.299	1.181
	BP86^17		2.504	1.166		1779^b
	LDA+QR+GRD^14	37.36	2.392	1.177		1778^b
	Experiment					1814.0^b,^16 1772.7^b ^15
1^2Σ^−	MRCI+Q		2.343	1.164	6.25
	MRCI		2.358	1.153	7.08
1^2Π	QZ-CCSD(T)	13.37	2.488	1.147	8.07	213, 255, 274, 1971^b
	TZ-CCSD(T)	12.80	2.492	1.151	7.14	209, 250, 267, 1963^b
	MRCI+Q		2.517	1.140	7.09
	MRCI		2.552	1.125	7.73
	CCSD(T)^17				6.5
	BP86^17		2.495	1.160	12.4	1918^b
1^2Δ	MRCI+Q		2.369	1.164	9.68
	MRCI		2.385	1.153	10.89
1^4Φ	MRCI+Q		2.530	1.148	11.51
	MRCI		2.550	1.136	11.66
1^4Π	MRCI+Q		2.520	1.151	14.05
	MRCI		2.535	1.140	14.78
1^2Σ^+	MRCI+Q		2.383	1.166	14.82
	MRCI		2.404	1.154	16.03

---

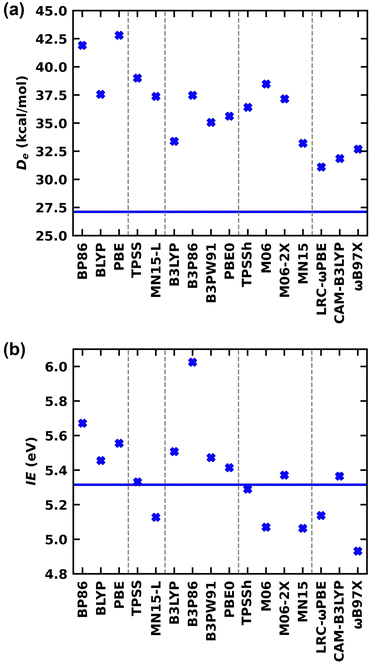
Due to the large deviations of the literature DFT D_es compared to our ab initio values, as the next step we evaluated the DFT errors on the D_e of LaCO performing DFT calculations using a series of exchange correlation functionals that span three rungs of Jacob's ladder of DFA; GGA (BP86,^25,26 BLYP,^27,28 PBE²⁹), MGGA (TPSS,³⁰ MN15-L³¹), and a set of hybrid families with different complexity [global GGA hybrid (B3LYP,^32,33 B3P86,^25,32 B3PW91,³² PBE0^34,35), MGGA hybrid (TPSSh,³⁰ M06,³⁶ M06-2X,³⁶ MN15³⁷), and RSH (LRC-ωPBE,³⁸ CAM-B3LYP,³⁹ ωB97X⁴⁰)]. The DFT D_e of LaCO(1⁴Σ⁻) were calculated with respect to La(⁴F) + CO(X¹Σ⁺) fragments and compared with the QZ-CCSD(T) D_e (i.e., 27.12 kcal mol⁻¹) obtained with respect to the same fragments. The DFT D_es are plotted in the Fig. 4a and numerical values and the % DFT errors with respect to the QZ-CCSD(T) are listed in the ESI,† Table S1. Generally, we expect better accuracy from DFT as we shift to more complicated and expensive functionals at the higher rungs of the Jacob's ladder of DFA. As expected, the largest DFT errors with respect to CCSD(T) were provided by the less expensive GGA family. Specifically, the errors of the BP86 and PBE predictions are larger than 50% (ESI,† Table S1). Among GGAs, BLYP carries the least error for D_e (∼38%). The DFT errors of the two utilized MGGAs (i.e., TPSS and MN15-L) are also high (44% and 38% respectively). The best functional among the global GGA hybrids are B3LYP with 23% errors where other functionals of the same family predicted errors of 29–39%. The performance of the MGGA hybrid MN15 is slightly better than the GGA hybrid B3LYP, which is the best performing functional of the MGGA hybrid. The DFT errors of the expensive RSHs are the lowest among all utilized DFAs. Specifically, the RSH D_e errors are less than 21%, and the comparatively better performance of RSHs was indeed our expectation. Among all, the best performing DFA for D_e of LaCO is the LRC-ωPBE with 14.7% errors compared to our CCSD(T) value (ESI,† Table S1 and Fig. 4a). Overall, all DFAs overestimated the D_e of LaCO. Based on our data, it is rather clear that the DFT D_e of LaCO is highly sensitive to the DFA utilized and hence it is reasonable to expect errors in DFA predictions on other properties of LaCO as well. To further quantify DFT errors on this system, we have calculated the DFT IE of LaCO and the findings are discussed later in the paper.

Fig. 4 (a) Dissociation energy (D_e, in kcal mol⁻¹) of LaCO(1⁴Σ⁻) obtained at various DFAs (blue cross marks) with respect to the La(⁴F) + CO(X¹Σ⁺) fragments. The horizontal blue line represents the QZ-CCSD(T) D_e of LaCO(1⁴Σ⁻) calculated with respect to the same fragments. (b) Adiabatic ionization energy (IE, in eV) of LaCO obtained at various DFAs (blue cross marks). The horizontal blue line represents the QZ-CCSD(T) IE of LaCO. In each plot, DFAs with different complexity are separated with vertical gray dashed lines (left to right: GGA, MGGA, global GGA hybrid, MGGA hybrid, and RSH).

For the ground state, r_e(La–C) increased in the order of TZ-CCSD(T) < MRCI+Q < MRCI while the trend is the opposite for the r_e(C–O) (Table 2). The same pattern was observed for the excited 1²Π as well. The QZ-CCSD(T) La–C and C–O r_e values of both 1⁴Σ⁻ and 1²Π states are shorter compared to the TZ-CCSD(T) r_es. We are familiar with the observation of shorter bonds predicted by larger basis sets.^65–67 The r_e values of LaCO have been reported by a series of DFT studies before and clearly the values are greatly dependent on the adopted DFT approach (Table 2). The 1⁴Σ⁻ carries two electrons in the 1π orbitals whereas only one electron occupies the 1π of 1²Π and hence we can expect longer La–C and a shorter C–O for the latter compared to the former. Indeed, this is correct where the La–C and C–O of 1²Π are ∼0.15 Å longer and ∼0.02 Å shorter compared to the corresponding bonds of 1⁴Σ⁻ under all utilized levels. Similarly, each 1²Π, 1⁴Φ, and 1⁴Π state hosts only one electron in their 1π orbitals which correlates to their longer La–C and shorter C–O bond distances compared to the other states of LaCO (Table 2). Overall, in all cases the MRCI predicted La–C r_e values are longer compared to the MRCI+Q r_es (by ∼0.01–0.03 Å) and the MRCI predicted C–O r_es are shorter compared to the MRCI+Q r_es (by ∼0.01 Å).

The quartet-spin ground state has been proposed for the side-bonded La(η²-CO) by Hong et al.¹⁴ In the present work, the side-bonded La(η²-CO) isomer was also investigated at the TZ-CCSD(T) level to compare its relative stability with the linear LaCO. At the TZ-CCSD(T) level, the ground state ⁴A′′ of La(η²-CO) lies 14.21 kcal mol⁻¹ above the LaCO(1⁴Σ⁻). This value is in very good agreement with the corresponding DFT value reported by Hong et al., which is 14.07 kcal mol⁻¹.¹⁴ The TZ-CCSD(T) optimized La–C, La-O, and C–O geometrical parameters of the La(η²-CO) are 2.485, 2.423, and 1.217 Å, respectively. The singly-occupied molecular orbitals of La(η²-CO) (⁴A′′) are given in ESI,† Fig. S1. According to the Mullikan population analysis performed under QZ-HF level, we observed an enhanced ionic character for the La(η²-CO) (i.e., La^+0.44C^−0.03O^−0.41) compared to the linear LaCO (i.e., La^+0.26–[CO]^−0.26). The transition state barrier corresponding to the LaCO → La(η²-CO) conversion lies 19.35 kcal mol⁻¹ above the LaCO at the TZ-CCSD(T). Note that the transition state was optimized under DFT/B3LYP using the Stuttgart RSC 1997 basis set with 28-electron ECP of La and cc-pVQZ for C and O. Then the DFT geometry was used to perform a single-point TZ-CCSD(T) calculation.

The T_e values of the first six excited states of LaCO are listed in Table 2. Notice that all these states are lower in energy than the ⁴A₂ of La(η²-CO). The exact ordering of the states predicted by both MRCI and MRCI+Q methods is 1⁴Σ⁻, 1²Σ⁻, 1²Π, 1²Δ, 1⁴Φ, 1⁴Π, and 1²Σ⁺. This is consistent with the MRCI+Q ordering of the states of Fig. 1, except for the switching of the 1²Σ⁺ and 1⁴Π. In line with the Fig. 1 the 1²Σ⁻ and 1²Π lie very close with less than 1 kcal mol⁻¹ energy difference. In 2007 Zhang et al., reported DFT/BP86 and CCSD(T) 1⁴Σ⁻ → 1²Π transition energies to be 12.4 and 6.5 kcal mol⁻¹, respectively.¹⁷ Their CCSD(T) value is in reasonable agreement with our MRCI and CCSD(T) values (Table 2). For all computed states in the present work, the MRCI T_e values are 0.1–1.3 kcal mol⁻¹ larger than the MRCI+Q values.

The two experimentally observed C–O stretching modes of LaCO are 1772.7¹⁵ and 1814.0 cm⁻¹ (ref. 16). Our ω_e values of LaCO(1⁴Σ⁻) predicted by TZ-CCSD(T) and QZ-CCSD(T) are 1857 and 1860 cm⁻¹ respectively.

Going a step further, the ground state of the LaCO⁺(³Σ⁻) was also studied at the CCSD(T) level. The optimized La–C and C–O distances of LaCO⁺(³Σ⁻) are 2.396 and 1.149 Å at the TZ-CCSD(T) and 2.390 and 1.145 Å at the QZ-CCSD(T) levels, respectively. The DFT/BPW91 La–C and C–O distances reported by Jiang and Xu¹⁶ are 2.407 and 1.169 Å respectively and are in reasonable agreement with our CCSD(T) values. The experimental C–O ω_e reported by Jiang and Xu¹⁶ for LaCO⁺(³Σ⁻) is 1903.2 cm⁻¹ and ∼90 cm⁻¹ smaller compared to our QZ-CCSD(T) ω_e value (i.e., 1994 cm⁻¹). Regarding the electronic structure of the LaCO⁺, the removal of the 1σ¹ (∼6s of La) electron from the LaCO(1⁴Σ⁻) produces the single-reference ground state of LaCO⁺(³Σ⁻). At the TZ-CCSD(T) and QZ-CCSD(T) levels, the IE of this process is 5.290 and 5.316 eV, respectively. The DFT IEs of this process was also evaluated using the same set of functionals that was used in our DFT D_e error analysis of LaCO. Our DFT IEs of LaCO are shown in the Fig. 4b and the corresponding numerical values and % errors with respect to QZ-CCSD(T) IE (i.e., 5.316 eV) are given in the ESI,† Table S2. GGAs overestimated the IE of LaCO by 0.14–0.36 eV. Among all utilized DFAs, MGGA TPSS predicted almost identical IE to the QZ-CCSD(T) IE (i.e. 5.332 vs. 5.316 eV). The IE predicted by the MN15-L of the same class is lower by ∼0.19 eV compared to the CCSD(T). All global GGA hybrids overestimated the IE of LaCO compared to the QZ-CCSD(T) with B3P86 being the one to carry the largest error (∼13.3%) among all utilized functionals (Fig. 4b and ESI,† Table S2). Both TPSSh and M06-2X of MGGA hybrids represent the IE of LaCO well with only 0.03 and 0.06 eV deviations from QZ-CCSD(T) respectively. Even though the RSH family performed D_e of LaCO comparatively well compared to the others, the RSH LRC-ωPBE and ωB97X are not among the best representations of IE of LaCO. However, the RSH CAM-B3LYP IE deviates only by 0.05 eV with respect to QZ-CCSD(T) which is the third best among all the selected DFAs in this work. Overall, among all DFAs, CAM-B3LYP is the clear choice that represents both D_e and IE of LaCO with minimal errors.

In the present work we have performed spin–orbit calculations for both La and LaCO species at the MRCI level. The MRCI spin–orbit calculations of La atom were performed under three different types of active spaces, i.e., 1. CAS(3,6) where the active orbitals are 5d and 6s of La, 2. CAS(3,9) where the active orbitals are 5d, 6s, and 6p of La, 3. CAS(3,16) where the active orbitals are 5d, 6s, 6p, and 4f of La. In all three cases, spin–orbit matrices were constructed including the ²D, ⁴F, ²F, ⁴P, ²D, ²P, and ²G states of La. The MRCI/cc-pVTZ-DK3 excitation energies calculated under these three approaches and the corresponding experimental literature values are listed in the Table 3. The MRCI excitation energies obtained under the smallest active space [i.e., MRCI/CAS(3,6)] carry the largest deviations compared to the experimental excitation energies (Table 3). The MRCI/CAS(3,9) provided excitation energies are in reasonable agreement with the experimental values. For example, the discrepancy between MRCI/CAS(3,9) versus experimental excitation energies are within 10–400 cm⁻¹ (Table 3). Interestingly, MRCI/CAS(3,9) provided a better harmony with experiment compared to the excitation energies predicted by MRCI/CAS(3,16) approach. Specifically, the discrepancy between MRCI/CAS(3,16) versus the experiment are in the range of 180–490 cm⁻¹.

Table 3 Excitation energies (cm⁻¹) for several low-energy electronic states of La at MRCI/cc-pVTZ-DK3 basis set under various active spaces

State^a	MRCI/CAS(3,6)	MRCI/CAS(3,9)	MRCI/CAS(3,16)	Experiment^b
a The ^2D3/2 and ^2D5/2 states carry 5d^16s^2 valence electron configuration, whereas others bear 5d^26s^1 configuration. b Experimental values were obtained from the ref. 21.
^2D3/2	0	0	0	0.0
^2D5/2	810	890	864	1053.2
^4F3/2	1408	2682	2389	2668.2
^4F5/2	1717	2988	2685	3010.0
^4F7/2	2117	3415	3099	3494.5
^4F9/2	2674	3971	3639	4121.6
^2F5/2	7181	7270	6830	7011.9
^2F7/2	7996	8202	7746	8052.2
^4P1/2	7024	7620	7029	7231.4
^4P3/2	7030	7798	7199	7490.5
^4P5/2	6767	8005	7410	7679.9

---

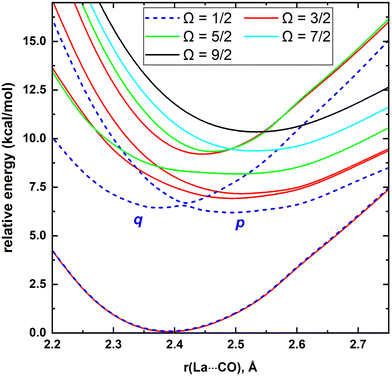
MRCI/CAS(3,9) approach was used for the spin–orbit calculations of LaCO. To evaluate its spin–orbit coupling effects, the spin–orbit states of 1⁴Σ⁻, 1²Σ⁻, 1²Π, 1²Δ, and 1⁴Φ electronic states were considered. The spin–orbit coupling produces the Ω = 3/2, 1/2 (1⁴Σ⁻), Ω = 1/2 (1²Σ⁻), Ω = 3/2, 1/2 (1²Π), Ω = 5/2, 3/2 (1²Δ), and Ω = 9/2, 7/2, 5/2, 3/2 (1⁴Φ). The spin–orbit coupling curves of these states with respect to La⋯C distance is shown in Fig. 5. The C–O length was kept fixed to the 1.168 Å at each scan. The Ω = 3/2 and 1/2 of 1⁴Σ⁻ are almost identical in energy and displayed very minimal impact from high energy spin–orbit components (Table 4). The Ω = 1/2 of 1²Σ⁻ and the Ω = 1/2 of 1²Π creates an avoided crossing around 2.42 Å which yields an Ω = 1/2 spin–orbit curve with a double minima at 2.374 Å (q) and 2.493 Å (p) (Fig. 5 and Table 4). The q and p minima dominantly correlate to the parent 1²Σ⁻ and 1²Π, respectively (Table 4). The p and q minima lie 6.13 and 6.42 kcal mol⁻¹ above the ground Ω = 3/2 state of LaCO. The Ω = 1/2 avoided crossing intersection has ∼80% (1²Σ⁻) and ∼19% (1²Π) character. The next five Ω states are highly mixed as shown in the Table 4. Since the spin–orbit matrix only has one of each Ω = 7/2 and 9/2, they solely correlate to the 1⁴Φ.

Fig. 5 Spin–orbit coupling curves resulting from 1⁴Σ⁻, 1²Σ⁻, 1²Π, 1²Δ, and 1⁴Φ of LaCO as a function of La⋯CO distance [r(La⋯CO), Å]. The relative energies are referenced with respect to the Ω = 3/2 ground state minimum of LaCO. At each scan the C–O length is kept fixed to the 1.168 Å. The Ω = 1/2, Ω = 3/2, Ω = 5/2, Ω = 7/2, and Ω = 9/2 curves are shown in blue, red, green, cyan, and black, respectively.

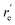Table 4 La–C bond length (, Å), excitation energy (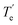, kcal mol⁻¹), and % compositions of several low-lying spin–orbit states of LaCO at the MRCI/TZ level

Ω State			Composition
a 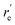values were obtained from the minima of the spin–orbit coupling curves shown in Fig. 5.
3/2	2.389	0	99.498% 1^4Σ^− + 0.502% 1^2Π
1/2	2.389	0.02	99.788% 1^4Σ^− + 0.212% 1^2Π
1/2 (p)	2.493	6.13	99.432% 1^2Π + 0.366% 1^4Σ^− + 0.202% 1^2Σ^−
1/2 (q)	2.374	6.42	99.947% 1^2Σ^− + 0.054% 1^2Π
1/2	2.419	6.62	80.458% 1^2Σ^− + 19.498% 1^2Π + 0.046% 1^4Σ^−
3/2	2.491	6.86	60.461% 1^2Π + 29.500% 1^4Φ + 9.494% 1^2Δ + 0.544% 1^4Σ^−
3/2	2.502	7.13	57.560% 1^4Φ + 37.358% 1^2Π + 4.771% 1^2Δ + 0.312% 1^4Σ^−
5/2	2.504	8.17	84.764% 1^4Φ + 15.237% 1^2Δ
3/2	2.442	9.04	71.164% 1^2Δ + 26.940% 1^4Φ + 1.890% 1^2Π
5/2	2.457	9.16	57.285% 1^2Δ + 42.698% 1^4Φ
7/2	2.522	9.34	100% 1^4Φ
9/2	2.534	10.29	100% 1^4Φ

---

To obtain a more accurate spin–orbit mixing accounted D_e for La–CO, a single point spin–orbit calculation was performed using the same spin–orbit matrix and optimized MRCI bond lengths of LaCO(1⁴Σ⁻). The resulted in D_e of the Ω = 3/2 ground state of LaCO is 16.53 kcal mol⁻¹. With the addition of the zero-point energy obtained at the TZ-CCSD(T), the estimated D₀ of the Ω = 3/2 of LaCO decreased to 12.63 kcal mol⁻¹.

IIIB. AcCO

Similar to La, the ground state of the Ac atom is a ²D with the valence nd¹(n + 1)s² electronic configuration (n = 5 and n = 6 for La and Ac, respectively). The first excited state of Ac is a ²P^o with the 7s²7p¹ valence configuration which lies 21.38 kcal mol⁻¹ (²P^o_1/2) and 35.10 kcal mol⁻¹ (²P^o_3/2) above.²¹ The next electronically excited state of Ac is a ⁴F (6d²7s¹; 26.35–34.53 kcal mol⁻¹), whereas the analogous ⁴F (5d²6s¹) state of La is its first excited state.²¹ Recall that the ground state of LaCO (1⁴Σ⁻) is a result of the reaction between La(⁴F; 5d²6s¹) versus CO(X¹Σ⁺) and with respect to these fragments it is bound by ∼23 kcal mol⁻¹. Since the ²D(5d¹6s²) → ⁴F(5d²6s¹) excitation of La (i.e., 7.63–11.78 kcal mol⁻¹) is considerably low in energy compared to the ²D(6d¹7s²) → ⁴F(6d²7s¹) transition of Ac, the ground state of AcCO is expected to be less stable (in case it is originating from ⁴F of Ac) or derived from a lower energy state of Ac.²¹ To portray a better picture of the origination of this system, the full MRCI+Q potential energy profile was produced for AcCO as a function of Ac⋯C length where C–O distance was kept constant to 1.159 Å which is the C–O length of the TZ-CCSD(T) optimized geometry of AcCO(1²Π) (Fig. 6). The ⁴Σ⁻ state originating from the Ac(⁴F) + CO(X¹Σ⁺) is bound by ∼25 kcal mol⁻¹ with respect to the corresponding fragments and lies ∼14 kcal mol⁻¹ above the ground state (1²Π) of AcCO. This is indeed in line with our expectation. The ground state of AcCO(1²Π) is originating from the Ac(²D) + CO(X¹Σ⁺) fragments and carries an ∼12 kcal mol⁻¹D_e. The ²Δ and ²Σ⁺ states deriving from the same fragments are strongly repulsive at first and become slightly attractive around ∼2.5 Å (Fig. 6). Similarly, the ²Δ and ²Σ⁺ PECs of the La(²D) + CO(X¹Σ⁺) are initially repulsive but conversely form substantially stable minima that are bound with respect to the ground state fragments (Fig. 1).

Fig. 6 Full PECs of several states of AcCO as a function of Ac⋯C distance [r(Ac⋯CO), Å] at MRCI+Q level of theory. The relative energies are with respect to the dissociation limit of Ac(²D) + CO(X¹Σ⁺), which is set to 0 kcal mol⁻¹. At each scan the C–O length is kept fixed to the 1.159 Å, which is the corresponding C–O length of the AcCO(1²Π). The dotted and solid PECs correspond to the quartet and doublet spins, respectively. The Σ⁻, Π, Δ, Σ⁺, and Φ states are shown in pink, blue, red, green, and black, respectively.

The shapes of the orbitals of AcCO are similar to the orbitals of LaCO (Fig. 2). The D_es, r_es, T_es, and ω_es of optimized 1²Π and ⁴Σ⁻ states of AcCO under MRCI, MRCI+Q, and CCSD(T) levels are given in the Table 5. The 1²Π and ⁴Σ⁻ of AcCO have analogous single-reference 1σ²1π¹ and 1σ¹1π² electron configurations as 1²Π and 1⁴Σ⁻ of LaCO, respectively. Similar to the LaCO case, the high electron density of the π* orbitals cause a shorter Ac–C and longer C–O lengths for ⁴Σ⁻ of AcCO compared to the corresponding lengths of 1²Π. At the TZ-CCSD(T) level, the AcCO(1²Π) carries 13.42 kcal mol⁻¹D_e which is larger than both MRCI+Q and MRCI D_es (Table 5). As expected, the more expensive QZ-CCSD(T) predicted slightly higher D_e than the TZ-CCSD(T) (by 0.63 kcal mol⁻¹). The zero-point energy correction decreased the QZ-CCSD(T) D₀ of AcCO(1²Π) to 10.37 kcal mol⁻¹. The TZ-CCSD(T), QZ-CCSD(T), and MRCI+Q levels predicted a bound ⁴Σ⁻ state with respect to Ac(²D) + CO(X¹Σ⁺) asymptote although it is not bound at the MRCI level. However, after inclusion of the zero-point energy, it is only bound at the QZ-CCSD(T) level by 1.61 kcal mol⁻¹. The side-bonded Ac(η²-CO) was also studied at the TZ-CCSD(T) level and its ground ²A′ state is found to lie 6.04 kcal mol⁻¹ high in energy than the 1²Π of linear AcCO. The TZ-CCSD(T) optimized Ac–C, Ac–O, and C–O lengths of Ac(η²-CO) (²A′) are 2.685, 2.531, and 1.214 Å, respectively. Select occupying molecular orbitals of Ac(η²-CO) (²A′) are given in ESI,† Fig. S2. At the TZ-CCSD(T) level the calculated vibrational frequencies of Ac(η²-CO) (²A′) are 271, 341, and 1616 cm⁻¹. Similar to the La case, the side-bonded Ac(η²-CO) showed higher ionic character (i.e., Ac^+0.51C^−0.10O^−0.41) compared to the linear AcCO (Ac^+0.29–[CO]^−0.29). A transition state of 14.45 kcal mol⁻¹ was observed for the AcCO → Ac(η²-CO) transformation at the TZ-CCSD(T) level. Similar to the La case, the energy barrier of this reaction was obtained by first optimizing the transition state at the DFT/B3LYP under the Stuttgart RSC 1997 basis set with 60-electron ECP of Ac and cc-pVQZ of C and O and then performing a single-point TZ-CCSD(T) calculation to the DFT geometry.

Table 5 Dissociation energy with respect to Ac(²D) + CO(X¹Σ⁺) fragments (D_e, kcal mol⁻¹), Ac–C and C–O bond lengths (r_e, Å), excitation energy (T_e, kcal mol⁻¹), and harmonic vibrational frequency (ω_e, cm⁻¹) of the two low-lying electronic states of AcCO

State	Level of theory^a	D e	r e		T e	ω e
			Ac–C	C–O
a Davidson corrected MRCI is denoted by MRCI+Q. For all MRCI, MRCI+Q, and TZ-CCSD(T) calculations cc-pVTZ-DK3 of Ac and cc-pVTZ-DK of C and O basis set was applied. The cc-pVQZ-DK3 of Ac and cc-pVQZ-DK of C and O basis set was used for QZ-CCSD(T) calculations.
1^2Π	QZ-CCSD(T)	14.05	2.584	1.156	0	168, 233, 258, 1915
	TZ-CCSD(T)	13.42	2.589	1.159	0	192, 251, 257, 1910
	MRCI+Q	11.32	2.591	1.151	0
	MRCI	9.81	2.601	1.141	0
^4Σ^−	QZ-CCSD(T)	5.47	2.437	1.171	8.58	274, 286, 313, 1825
	TZ-CCSD(T)	3.74	2.444	1.174	9.68	275, 281, 307, 1823
	MRCI+Q		2.451	1.166	9.40
	MRCI		2.466	1.155	11.05

---

We expect the spin–orbit coupling effects to be significant for actinide species and therefore in order to calculate more accurate energy related properties of AcCO, the spin–orbit effects must be accounted. To perform MRCI spin–orbit calculations, all the electronic states of AcCO given in the Fig. 6 were included in the spin–orbit matrix. A few low energy spin–orbit PECs of AcCO are plotted and given in ESI,† Fig. S3. The spin–orbit coupling splits 1²Π into Ω = 1/2 and Ω = 3/2 and at the equilibrium distances they are predominantly 1²Π in character (>99%). At the MRCI level 1²Π_3/2 lies 3.20 kcal mol⁻¹ above the 1²Π_1/2 making 1²Π_1/2 the ground state of AcCO. The 1²Π_1/2 and 1²Π_3/2 are 1.65 and 1.55 kcal mol⁻¹ more and less stable compared to the parent 1²Π, respectively. The next lowest energy spin–orbit minimum (i.e., ⁴Σ⁻_1/2) is 16.62 kcal mol⁻¹ high in energy than the 1²Π_1/2 and not bound with respect to the lowest energy fragments (ESI,† Fig. S3). Spin–orbit effect accounted D_e of AcCO(1²Π_1/2) is 8.94 kcal mol⁻¹. We estimated a final D₀ of 5.19 kcal mol⁻¹ for AcCO(1²Π_1/2) by applying the zero-point energy of AcCO(1²Π) at TZ-CCSD(T) level. The relatively less D₀ of AcCO could be a major reason for the absence of experimental reports on AcCO so far.

IV. Conclusions

The present work reports full PECs, D_es, r_es, T_es, and ω_es of low-lying electronic states of LaCO and AcCO complexes by means of ab initio MRCI+Q, MRCI, and CCSD(T) levels of theory. The ground state of LaCO is a single-reference 1⁴Σ⁻ (1σ¹1π²) formed via OC → La σ dative bond and La → CO π-back bonds. The LaCO(1⁴Σ⁻) is a product of the reaction between excited La(⁴F) versus CO(X¹Σ⁺). The spin–orbit effect accounted zero-point energy corrected D₀ of the 1⁴Σ⁻_3/2 ground state of LaCO is ∼13 kcal mol⁻¹. The ground ⁴A′′ of La(η²-CO) was found to be ∼14 kcal mol⁻¹ above the LaCO(1⁴Σ⁻). The first six excited electronic states of LaCO are 1²Σ⁻, 1²Π, 1²Δ, 1⁴Φ, 1⁴Π, and 1²Σ⁺ in order under both MRCI and MRCI+Q levels of theory. The ground state of the LaCO⁺ is a ³Σ⁻ formed by the ionization of the 1σ¹ electron from the LaCO(1⁴Σ⁻; 1σ¹1π²) and the corresponding IE of LaCO is 5.316 eV. We have evaluated the DFT errors associated with the D_e and IE of LaCO using 16 exchange correlation functionals that span three rungs of Jacob's ladder of DFA (GGA, MGGA, and hybrid) and compared with the QZ-CCSD(T) values. The expensive RSH provided the closest match with the QZ-CCSD(T) for D_e of LaCO (with less than 21% error). The MGGA TPSS, MGGA hybrid TPSSh and M06-2X, and RSH CAM-B3LYP predicted IEs with minimal errors with respect to CCSD(T) IE. Overall, among the chosen DFAs, the RSH CAM-B3LYP predicted D_e and IE of LaCO with relatively less errors.

Even though the ground state of LaCO is originating from the excited ⁴F state of La, the lowest energy molecular state of AcCO that ⁴F of Ac forms (⁴Σ⁻) lies 14 kcal mol⁻¹ above the 1²Π ground state of AcCO, which is clearly due to the higher energy gap between ²D [nd¹(n + 1)s²] and ⁴F [nd²(n + 1)s¹] of Ac compared to that of La. The AcCO(1²Π) is derived from the ground state fragments [i.e., Ac(²D) + CO(X¹Σ⁺)]. The spin–orbit effect accounted zero-point energy corrected D₀ of the 1²Π_1/2 ground state of AcCO is ∼5 kcal mol⁻¹. The 1²Π and ⁴Σ⁻ of AcCO have 1σ²1π¹ and 1σ¹1π² electron configurations respectively, similar to the configurations of 1²Π and 1⁴Σ⁻ of LaCO. The ground state of the side-bonded Ac(η²-CO) (²A′) lies 6 kcal mol⁻¹ above the 1²Π of AcCO. A 14 kcal mol⁻¹ transition state barrier lies in between AcCO → Ac(η²-CO) conversion which is lower by ∼5 kcal mol⁻¹ compared to the energy barrier of the LaCO → La(η²-CO) transition. The side-bonded Ac(η²-CO) bears higher ionic character compared to the linear AcCO which is consistent with the observations of the La case.

Data availability

The data supporting this article have been included as part of the ESI.†

Conflicts of interest

There are no conflicts to declare.

Acknowledgements

The support of the Los Alamos National Laboratory (LANL) Laboratory Directed Research and Development program Project No. 20240737PRD1 is acknowledged. This research used resources provided by the LANL Institutional Computing Program, which is supported by the U.S. Department of Energy National Nuclear Security Administration under Contract No. 89233218CNA000001.

References

1. G. R. Choppin, J. Radioanal. Nucl. Chem., 2007, 273, 695–703.
2. K. De Jesus, R. Rodriguez, D. L. Baek, R. V. Fox, S. Pashikanti and K. Sharma, J. Mol. Liq., 2021, 336, 116006.
3. R. M. Cox, A. Kafle, P. B. Armentrout and K. A. Peterson, J. Chem. Phys., 2019, 151, 034304.
4. P. B. Armentrout and K. A. Peterson, Inorg. Chem., 2020, 59, 3118–3131.
5. Z. Zhu, M. Marshall, K. H. Bowen and K. A. Peterson, J. Chem. Phys., 2022, 156, 054305.
6. M. Vasiliu, K. A. Peterson, M. Marshall, Z. Zhu, B. A. Tufekci, K. H. Bowen and D. A. Dixon, J. Phys. Chem. A, 2022, 126, 198–210.
7. A. Kafle, P. B. Armentrout, S. R. Battey and K. A. Peterson, Inorg. Chem., 2021, 60, 10426–10438.
8. I. R. Ariyarathna and E. Miliordos, Phys. Chem. Chem. Phys., 2019, 21, 24469–24477.
9. G. F. de Melo, M. Vasiliu, M. Marshall, Z. Zhu, B. A. Tufekci, S. M. Ciborowski, M. Blankenhorn, R. M. Harris, K. H. Bowen and D. A. Dixon, J. Phys. Chem. A, 2022, 126, 4432–4443.
10. G. F. de Melo, M. Vasiliu, G. Liu, S. Ciborowski, Z. Zhu, M. Blankenhorn, R. Harris, C. Martinez-Martinez, M. Dipalo, K. A. Peterson, K. H. Bowen and D. A. Dixon, J. Phys. Chem. A, 2022, 126, 7944–7953.
11. J. G. F. Romeu, A. R. E. Hunt, G. F. de Melo, K. A. Peterson and D. A. Dixon, J. Phys. Chem. A, 2024, 128, 5586–5604.
12. G. F. de Melo and D. A. Dixon, J. Phys. Chem. A, 2023, 127, 1588–1597.
13. G. F. de Melo, M. Vasiliu, G. Liu, S. Ciborowski, Z. Zhu, M. Blankenhorn, R. Harris, C. Martinez-Martinez, M. Dipalo, K. A. Peterson, K. H. Bowen and D. A. Dixon, J. Phys. Chem. A, 2022, 126, 9392–9407.
14. G. Hong, X. Lin, L. Li and G. Xu, J. Phys. Chem. A, 1997, 101, 9314–9317.
15. Q. Xu, L. Jiang and R. Q. Zou, Chem. – Eur. J., 2006, 12, 3226–3232.
16. L. Jiang and Q. Xu, J. Phys. Chem. A, 2007, 111, 3271–3277.
17. G. Zhang, Z. H. Li, W. N. Wang and K. N. Fan, J. Phys. Chem. A, 2007, 111, 11894–11903.
18. W. Xu, X. Jin, M. Chen, P. Pyykkö, M. Zhou and J. Li, Chem. Sci., 2012, 3, 1548–1554.
19. D. R. Lide, CRC Handbook of Chemistry and Physics, 93rd edn, CRC Press, New York, 2012.
20. R. C. Ropp, Encyclopedia of the Alkaline Earth Compounds, Elsevier, Netherlands, 2013, pp. 25–104 DOI:10.1016/B978-0-444-59550-8.00002-8.
21. A. Kramida, Y. Ralchenko and J. Reader, NIST Atomic Spectra Database (Version 5.3), National Institute of Standards and Technology, Gaithersburg, MD, 2015. https://physics.nist.gov/asd.
22. M. Zhou, L. Andrews, J. Li and B. E. Bursten, J. Am. Chem. Soc., 1999, 121, 9712–9721.
23. J. Li, B. E. Bursten, M. Zhou and L. Andrews, Inorg. Chem., 2001, 40, 5448–5460.
24. I. R. Ariyarathna, Y. Cho, C. Duan and H. J. Kulik, Phys. Chem. Chem. Phys., 2023, 25, 26632–26639.
25. J. P. Perdew, Phys. Rev. B: Condens. Matter Mater. Phys., 1986, 33, 8822–8824.
26. A. D. Becke, Phys. Rev. A: At., Mol., Opt. Phys., 1988, 38, 3098–3100.
27. B. Miehlich, A. Savin, H. Stoll and H. Preuss, Chem. Phys. Lett., 1989, 157, 200–206.
28. F. J. Devlin, J. W. Finley, P. J. Stephens and M. J. Frisch, J. Phys. Chem., 1995, 99, 16883–16902.
29. J. P. Perdew, K. Burke and M. Ernzerhof, Phys. Rev. Lett., 1996, 77, 3865–3868.
30. J. Tao, J. P. Perdew, V. N. Staroverov and G. E. Scuseria, Phys. Rev. Lett., 2003, 91, 146401.
31. H. S. Yu, X. He and D. G. Truhlar, J. Chem. Theory Comput., 2016, 12, 1280–1293.
32. A. D. Becke, J. Chem. Phys., 1993, 98, 5648–5652.
33. P. J. Stephens, F. J. Devlin, C. F. Chabalowski and M. J. Frisch, J. Phys. Chem., 1994, 98, 11623–11627.
34. C. Adamo and V. Barone, J. Chem. Phys., 1999, 110, 6158–6170.
35. M. Ernzerhof and G. E. Scuseria, J. Chem. Phys., 1999, 110, 5029–5036.
36. Y. Zhao and D. G. Truhlar, Theor. Chem. Acc., 2007, 120, 215–241.
37. H. S. Yu, X. He, S. L. Li and D. G. Truhlar, Chem. Sci., 2016, 7, 5032–5051.
38. M. A. Rohrdanz, K. M. Martins and J. M. Herbert, J. Chem. Phys., 2009, 130, 054112.
39. T. Yanai, D. P. Tew and N. C. Handy, Chem. Phys. Lett., 2004, 393, 51–57.
40. J. D. Chai and M. Head-Gordon, J. Chem. Phys., 2008, 128, 084106.
41. H. J. Werner, P. J. Knowles, G. Knizia, F. R. Manby and M. Schütz, Wiley Interdiscip. Rev.: Comput. Mol. Sci., 2011, 2, 242–253.
42. H. J. Werner, P. J. Knowles, F. R. Manby, J. A. Black, K. Doll, A. Hesselmann, D. Kats, A. Kohn, T. Korona, D. A. Kreplin, Q. Ma, T. F. Miller III, A. Mitrushchenkov, K. A. Peterson, I. Polyak, G. Rauhut and M. Sibaev, J. Chem. Phys., 2020, 152, 144107.
43. H.-J. Werner and P. J. Knowleset al., MOLPRO, version 2, a package of ab initio programs, 2023, https://www.molpro.net.
44. H.-J. Werner and P. J. Knowles, J. Chem. Phys., 1988, 89, 5803–5814.
45. P. J. Knowles and H.-J. Werner, Chem. Phys. Lett., 1988, 145, 514–522.
46. K. R. Shamasundar, G. Knizia and H. J. Werner, J. Chem. Phys., 2011, 135, 054101.
47. K. Raghavachari, G. W. Trucks, J. A. Pople and M. Head-Gordon, Chem. Phys. Lett., 1989, 157, 479–483.
48. Q. Lu and K. A. Peterson, J. Chem. Phys., 2016, 145, 054111.
49. T. H. Dunning, J. Chem. Phys., 1989, 90, 1007–1023.
50. W. A. de Jong, R. J. Harrison and D. A. Dixon, J. Chem. Phys., 2001, 114, 48–53.
51. H.-J. Werner and P. J. Knowles, J. Chem. Phys., 1985, 82, 5053–5063.
52. P. J. Knowles and H.-J. Werner, Chem. Phys. Lett., 1985, 115, 259–267.
53. D. A. Kreplin, P. J. Knowles and H. J. Werner, J. Chem. Phys., 2019, 150, 194106.
54. D. A. Kreplin, P. J. Knowles and H. J. Werner, J. Chem. Phys., 2020, 152, 074102.
55. S. R. Langhoff and E. R. Davidson, Int. J. Quantum Chem., 1974, 8, 61–72.
56. M. J. Frisch, G. W. Trucks, H. B. Schlegel, G. E. Scuseria, M. A. Robb, J. R. Cheeseman, G. Scalmani, V. Barone, G. A. Petersson, H. Nakatsuji, X. Li, M. Caricato, A. V. Marenich, J. Bloino, B. G. Janesko, R. Gomperts, B. Mennucci, H. P. Hratchian, J. V. Ortiz, A. F. Izmaylov, J. L. Sonnenberg, D. Williams, F. Ding, F. Lipparini, F. Egidi, J. Goings, B. Peng, A. Petrone, T. Henderson, D. Ranasinghe, V. G. Zakrzewski, J. Gao, N. Rega, G. Zheng, W. Liang, M. Hada, M. Ehara, K. Toyota, R. Fukuda, J. Hasegawa, M. Ishida, T. Nakajima, Y. Honda, O. Kitao, H. Nakai, T. Vreven, K. Throssell, J. A. Montgomery Jr., J. E. Peralta, F. Ogliaro, M. J. Bearpark, J. J. Heyd, E. N. Brothers, K. N. Kudin, V. N. Staroverov, T. A. Keith, R. Kobayashi, J. Normand, K. Raghavachari, A. P. Rendell, J. C. Burant, S. S. Iyengar, J. Tomasi, M. Cossi, J. M. Millam, M. Klene, C. Adamo, R. Cammi, J. W. Ochterski, R. L. Martin, K. Morokuma, O. Farkas, J. B. Foresman and D. J. Fox, Gaussian 16, Gaussian Inc., Wallingford CT, 2016.
57. X. Cao and M. Dolg, J. Chem. Phys., 2001, 115, 7348–7355.
58. X. Cao and M. Dolg, J. Mol. Struct.: THEOCHEM, 2002, 581, 139–147.
59. C. Koukounas, S. Kardahakis and A. Mavridis, J. Chem. Phys., 2005, 123, 074327.
60. M. Zhou and L. Andrews, J. Phys. Chem. A, 1999, 103, 2964–2971.
61. I. R. Ariyarathna and E. Miliordos, J. Phys. Chem. A, 2017, 121, 7051–7058.
62. G. Knizia, J. Chem. Theory Comput., 2013, 9, 4834–4843.
63. I. R. Ariyarathna, Phys. Chem. Chem. Phys., 2024, 26, 21099–21109.
64. I. R. Ariyarathna, Phys. Chem. Chem. Phys., 2024, 26, 22858–22869.
65. I. R. Ariyarathna, C. Duan and H. J. Kulik, J. Chem. Phys., 2022, 156, 184113.
66. I. R. Ariyarathna, J. Comput. Chem., 2024, 45, 2530–2538.
67. I. R. Ariyarathna and E. Miliordos, Phys. Chem. Chem. Phys., 2018, 20, 12278–12287.

---

Footnote

† Electronic supplementary information (ESI) available: Tables S1 and S2 list DFT D_e, IE, and % DFT errors of LaCO(1⁴Σ⁻); Fig. S1 and S2 illustrate the select molecular orbitals of La(η²-CO) and Ac(η²-CO); Table S3 provides the Cartesian coordinates of the transition states of the linear to side-bonded structures; Fig. S3 illustrates the spin–orbit coupling curves of AcCO. See DOI: https://doi.org/10.1039/d4cp03132f

---