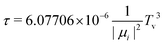Support effects on conical intersections of Jahn–Teller fluxional metal clusters on the sub-nanoscale

Abstract

The concept of fluxionality has been invoked to explain the enhanced catalytic properties of atomically precise metal clusters of subnanometer size. Cu₃ isolated in the gas phase is a classical case of a fluxional metal cluster where a conical intersection leads to a Jahn–Teller (JT) distortion resulting in a potential energy landscape with close-lying multiminima and, ultimately, fluxional behavior. In spite of the role of conical intersections in the (photo)stability and (photo)catalytic properties of surface-supported atomic metal clusters, they have been largely unexplored. In this work, by applying a high-level multi-reference ab initio method aided with dispersion corrections, we analyze support effects on the conical intersection of Cu₃ considering benzene as a model support molecule of carbon-based surfaces. We verify that the region around the conical intersection and the associated Jahn–Teller (JT) distortion is very slightly perturbed by the support when the Cu₃ cluster approaches it in a parallel orientation: Two electronic states remain degenerate for a structure with C₃ symmetry consistent with the D_3h symmetry of unsupported Cu₃ at the conical intersection. It extends over a one-dimensional seam that characterizes a physisorption minimum of the Cu₃–benzene complex. The fluxionality of the Cu₃ cluster, reflected in large fluctuations of relaxed Cu–Cu distances as a function of the active JT mode, is kept unperturbed upon complexation with benzene as well. In stark contrast, for the energetically favored perpendicular orientation of the Cu₃ plane to the benzene ring plane, the conical intersection (CI) is located 12 100 cm⁻¹ (∼1.5 eV) above the chemisorption minimum, with the fluxionality being kept at the CI's nearby and lost at the chemisorption well. The first excited state at the perpendicular orientation has a deep well (>4000 cm⁻¹), being energetically closer to the CI. The transition dipole moment between ground and excited states has a significant magnitude, suggesting that the excited state can be observed through direct photo-excitation from the ground state. Besides demonstrating that the identity of an isolated Jahn–Teller metal cluster can be preserved against support effects at a physisorption state and lifted out at a chemisorption state, our results indicate that a correlation exists between conical intersection topography and fluxionality in the metal cluster's Cu–Cu motifs.

---

1 Introduction

Present-day advances in experimental techniques allow the synthesis of atomically precise metal clusters down to the subnanometer scale (referred to as AMCs) in various environments (gas-phase, solution, within helium nanodroplets, and interacting with biologically relevant molecules), over a wide temperature range, and exposed to various gas-phase molecules at controlled pressure and temperature (see, e.g., ref. 1–3 and references cited therein). Having quantized ‘molecule-like’ structures differing largely from those of metallic nanoparticles and bulk materials, AMCs exhibit unexpected stability⁴ and ‘special’ physical and chemical properties potentially impacting fields such as sensing,⁵ catalysis,^6–11 bio-imaging,^12–14 energy conversion,¹⁵ luminescence,¹⁶ photo-catalysis,^2,17–20 and theranostics,^21–23 and bringing AMCs to the bottom scale of nanotechnology.²⁴ For instance, novel aspects have been provided by copper and silver pentamer clusters such as an unexpected resistivity to deep oxidation in spite of their tiny size;²⁵ their applicability to improve the optoelectronic and photocatalytic properties of semiconductors such as titanium dioxide;^3,17,19,26 and to unveil new insightful information into fundamental surface polarons' properties.^27–29 More generally, clusters made of a small number of copper atoms (even Cu₃) have been studied by different groups,^30–32 finding notable properties and applications in catalysis,^2,19,30–32 such as in the epoxidation of propene,³³ carbon dioxide decomposition,¹⁸ hydrogenation of olefins and carbonyl groups,^34,35 and carbon dioxide hydrogenation to methane and methanol on bimetallic Cu₃ Pd clusters.³⁶

In the quest to understand, predict and control the unique properties of AMCs at the molecular level, a great amount of effort is being dedicated to their characterization using the most advanced experimental, theoretical, and computational tools.^2,3,37 The structural fluxionality of AMCs composed of just a few atoms is a key fundamental property differentiating them from larger nanoparticles through the occurrence of dynamical fluctuations of their atomic arrangements even at relatively low temperatures.^{3,18,19,25,38–43} The appearance of fluxional dynamics in AMCs has been manifested, for instance, in the experimental evidence of a variety of nearly isoenergetic structures of cationic Cu₅⁺ clusters in infrared spectroscopic characterizations of H₂ adsorption.⁴⁴ Structural fluxionality naturally influences the AMCs’ chemical (photo)reactivity and (photo)stability, resulting in highly relevant phenomena such as reversible oxidation²⁵ and carbon dioxide (CO₂) decomposition.^3,18,19,41 In this way, it has been shown how synergic elongations and contractions of Cu–Cu motifs in Cu₅ structures allow for a bending of adsorbed CO₂ molecules, making them more prone to accept electronic charge from the cluster which, in its turn, provokes a weakening of the C–O bond and, ultimately, its breaking and desorption.¹⁸

In order to achieve a deeper insight into the concept of structural fluxionality, a very recent high-level ab initio benchmark study of Cu₃ and Cu₅ clusters has been carried out,⁴⁵ emphasizing the importance of nonadiabatic effects and Jahn–Teller (JT) distortions in causing fluxional behaviour of AMCs.³ In fact, the occurrence of Jahn–Teller effects and, more generally, conical intersections (CIs) of two or more electronic states, lead to spontaneous symmetry breaking resulting in multi-minima adiabatic potential energy surfaces, rather than a single well-defined geometry associated to a global minimum.^46–49 In its turn, the existence of a potential energy landscape with many minima bearing low energy barriers between them allows for dynamical fluctuations of the atomic structures. Conical intersections are also expected to play a crucial role in boosting photoreactivity and photostability of AMCs since the adiabatic potential energy surfaces become degenerate at their locations, enabling ultrafast decay from excited states without radiative emission.^50,51 The presence of conical intersections leading to Jahn–Teller distortions has been well probed, both experimentally and theoretically, in open-shell triatomic clusters,^45,52–59 providing ab initio evidence on bipyramidal Cu₅ clusters as well.⁴⁵

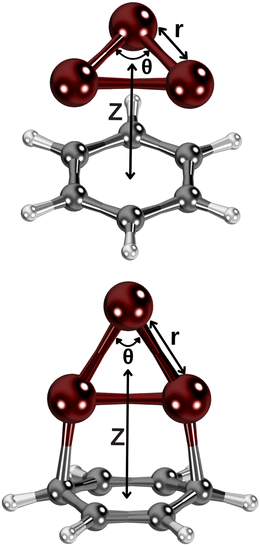
When integrated into inorganic materials that interact with environmental molecules and sunlight, conical intersections and Jahn–Teller distortions of AMCs significantly influence their activities in (photo)catalysis.³ Moreover, the spectroscopic characterization of Jahn–Teller metal clusters might use solid surface attachment so that it is necessary to know how the support affects their Jahn–Teller distortions. Experiments frequently use amorphous carbon-based surfaces as standard substrates to characterize metal clusters via transmission electron microscopy (TEM). Thus, choosing a classical Jahn–Teller fluxional cluster (Cu₃)^45,54,59 as the AMC and benzene as the smallest molecular model of a carbon-based support, we address support effects on the conical intersection of the Cu₃–benzene complex in this work. Although it is a very complex system, Cu₃–benzene is still amenable to the application of a high-level ab initio approach assessed in a previous publication of the conical intersections of Cu₃ and Cu₅ clusters isolated in the gas-phase,⁴⁵ reaching spectroscopic accuracy (within 1 cm⁻¹) in the prediction of the frequency associated with its symmetric stretching vibrational mode.^52,53 Due to their remarkable properties,⁶⁰ supports such as graphite and graphene have been selected in recent experimental-theoretical studies²⁵ and large-scale ab initio molecular dynamics simulations.⁶¹ In this way, we have applied a high-level ab initio protocol to Cu₃–benzene using internally contracted multistate multireference Rayleigh Schrödinger (second-order) perturbation theory (RS2C).⁶² Moreover, the RS2C method has helped with a methodological enhancement to improve the embedded dispersion energy contribution already proven with a single-reference coupled second-order Møller–Plesset perturbation (MP2) theory.⁶³ Specifically, we focus on exploring the following aspects: (1) two possible collision energy pathways to physisorption and chemisorption of the Cu₃ cluster onto the model support (benzene); (2) the influence of the support on the potential energy landscape of ground and excited states near the conical intersection causing the Jahn–Teller distortion in unsupported Cu₃. As two limiting cases, we have chosen collision pathways where the plane of the Cu₃ cluster is either parallel or perpendicular to the benzene ring's plane.

The article is organized as follows: in Section 2, the computational approach and the details of our calculations as well as the newly proposed dispersion-corrected RS2C approach are presented. Section 3 focuses on analyzing the conical intersection topography in the two selected collision pathways, considering both ground and excited states, and its relationship with the fluxionality of the cluster. Finally, Section 4 closes with the concluding remarks and implications of our work for future prospects.

2 Theoretical and computational methods

2.1 Theoretical methods and computational details

We have applied internally contracted multistate multireference Rayleigh Schrödinger (second-order) perturbation theory (RS2C)⁶² following the computational details of ref. 45 for Cu₃ and Cu₅ clusters. Moreover, following ref. 64, we aided the RS2C method with dispersion corrections to the interaction energies at the potential minima in ground and excited states.

2.1.1 Electronic basis sets. The polarized correlation-consistent triple-ζ basis of Dunning and collaborators⁶⁵ (cc-pVTZ) has been used for C and H atoms, while the augmented aug-cc-pVTZ-PP basis set has been employed for copper atoms,⁶⁶ including small-core (10-valence electrons) relativistic pseudopotentials.⁶⁶ It has been previously shown that the aug-cc-pVTZ-PP basis set delivers Cu–Cu distances for optimized geometries and spatial harmonic frequencies – in the normal modes approximation – of Cu₃ and Cu₅ clusters differing by less than 0.02 Å and 1.4 cm⁻¹ (on average) from the values obtained with the aug-cc-pVQZ-PP basis set.⁴⁵ Energy differences such as the relative energy at the conical intersections and the barriers between minima and transition states converged to better than 0.01 and 0.001 eV, respectively, as in ref. 45.

2.1.2 RS2C electronic structure calculations. Density fitting (DF) two-state (state-averaged) complete active space self-consistent-field (DF-CASSCF) calculations have been carried out. The DF-CASSCF approach has been used to account for the most important nondynamical correlation effects. The density-fitting internally contracted multireference Rayleigh Schrödinger (second-order) perturbation theory DF-RS2C approach⁶² has been applied to cover dynamical correlation contributions instead. The RS2C method is a modified version of the CASPT2 (complete active space with second-order perturbation theory) method developed by Celani and Werner,⁶² considering CASSCF wavefunctions as a reference in the RS2C calculations. The RS2C method allows the consideration of reference wave functions with large active spaces through the use of internally contracted configurations as a basis. For density fitting, the associated MP2FIT and JKFIT bases have been used in DF-CASSCF and DF-RS2C calculations.

DF-CASSCF and DF-RS2C calculations of the Cu₃–benzene complex have been carried out using (9,11) active space (i.e., nine valence electrons distributed in eleven active orbitals). For the separated fragments, it correlates with an active space (3,5) of the Cu₃ cluster⁴⁵ (i.e., three valence electrons distributed in five orbitals) and the standard valence π (6,6) active space of the benzene molecule (i.e., six electrons distributed in six π orbitals).⁶⁷ The eight 3s and 3p orbitals of the Cu₃ sub-unit were kept double occupied and the corresponding electrons were not correlated. These orbitals were, however, optimized at the DF-CASSCF level. The 3d electrons were not correlated at the DF-CASSCF level, but were included into dynamic correlation calculations with the DF-RS2C approach. The active space at the CASSCF and RS2C levels included thus 4s electrons of all copper atoms (i.e., 3 electrons). When addressing the distorted JT region of the potential energy surface, however, the minimal active space (3,3) was not good enough since 4p orbitals started to mix with valence 4s orbitals, leading to symmetry breaking distortions. In this way, two additional orbitals (becoming a single e-type orbital at the equilateral triangular structure of symmetry D_3h at the conical intersection of the Cu₃ cluster) were required to stabilize the symmetry behavior and avoid the symmetry breaking problem. The DF-RS2C calculation used state-averaged DF-CASSCF orbitals. A level shift of 0.2 was applied in this calculation as described by Roos and Andersson.⁶⁸ State-averaged natural orbitals were obtained from the first-order reduced density matrix calculated using the reference CASSCF wavefunctions.

2.1.3 The dispersion-corrected RS2C scheme. In this work, we have also applied a modified version of the coupled second-order Møller–Plesset perturbation (MP2) theory method by of Heßelmann and Pitonák^69,70 (so-named MP2C approach) that replaces the uncoupled second-order dispersion contribution contained in the MP2 interaction energy with the coupled dispersion energy counterpart evaluated via linear-response functions from time-dependent density functional theory (DFT). The excellent performance of the MP2C approach in correcting the overestimation of van der Waals (vdW)-dominated interaction energies at the MP2 level has been demonstrated in previous work on the Ag₂–benzene and Ag₂–coronene interactions.⁶⁴ A recent study has shown that it also works very well for correcting interaction energies on single-reference unrestricted MP2 descriptions of Cu₃–benzene and Cu₃–coronene complexes.⁶³ The MP2C approach^69,70 has been extended to estimate the overestimation of the RS2C interaction energies as follows:

(1) As described in ref. 63, dispersion energy contributions are obtained separately from symmetry-adapted perturbation theory (SAPT) calculations⁷¹ carried out using the Psi4 (see ref. 72) and the Psi4NumPy packages (see ref. 73). Specifically, the uncoupled Hartree–Fock dispersion term (E^UHF_disp) is computed at the SAPT0 level, using the unrestricted open-shell Hartree–Fock (UHF) approach for the monomers (i.e., the Cu₃ cluster and the benzene molecule). Subsequently, all relevant quantities are exported as NumPy arrays using the Psi4NumPy package,⁷³ easing accessibility within the main Python script.

(2) The script is then utilized to compute the coupled dispersion term, using the frequency-integrated linear response functions derived from unrestricted time-dependent Hartree–Fock theory (see ref. 74 and 75 for the details).

(3) The dispersion correction is next weighted with the square of the main configuration in the CASSCF wavefunctions, serving as a reference in the follow-up RS2C calculations. These corrections evaluated the equilibrium geometries in orthogonal and parallel collision energy pathways (see Section 2.2). The resulting dispersion-corrected RS2C approach will be referred to as ‘RS2CC’ or ‘weighted RS2CC’ depending on the exclusion or inclusion of the weighting factor.

(4) The same dispersion correction is applied to ground and excited electronic states so that the RS2C-based estimation of their conical intersection is kept unperturbed.

In order to verify the performance of the proposed dispersion-corrected RS2C scheme, we have carried out additional calculations with the single-reference coupled-cluster method with single, double, and perturbative triple excitations (i.e., the CCSD(T) method).

2.2 Structural models

We have considered two collision energy pathways in which the Cu₃-complex is maintained at symmetries C₃ and C_2v. In the parallel energy pathway (of symmetry C₃), the Cu₃ cluster plane is kept parallel to the benzene ring of six carbon atoms (see Fig. 1). In the orthogonal energy pathway (of symmetry C_2v), the Cu₃ cluster's plane is perpendicular to the benzene ring instead (see Fig. 1), with the apex of the triangular Cu₃ structure pointing outwards from the benzene ring. In both cases, we have considered three internal degrees of freedom: (1) the angle at the apex of the triangular Cu₃ structure, which is the active Jahn–Teller (JT) mode (referred to as θ, running from 52° to 70° in steps of 2°); (2) the intermolecular distance between the centers of mass of Cu₃ and benzene (denoted as Z), considering a Z-range from 10 to 2.0 Å; (3) the Cu–Cu bond length between the copper atoms at the apex and the base of the triangular Cu₃ structure [referred to as r, being optimized at each variable pair (θ, Z)]. In order to determine the initial structure of the Cu₃–benzene complex in the orthogonal reaction pathway, the CCSD(T) method has been applied. The structure of the benzene molecule was fixed to that optimized at the CCSD(T) level for the parallel collision pathway (see the ESI†).

Fig. 1 Cu₃–benzene complex under investigation in parallel (upper panel) and orthogonal (lower panel) configurations. Z is defined as the distance between the centers of mass of Cu₃ and the benzene molecule. Bond Cu–Cu distances are denoted as r. θ is the angle at the apex of the Cu₃ triangular structure.

In order to test the adequacy of the method, it has been verified that, in the asymptotic limit of the separated Cu₃ and benzene fragments (with Z = 40 Å), the relative energies as a function of the active Jahn–Teller mode are reproduced in the region of the conical intersection for unsupported Cu₃ clusters.⁴⁵ In particular, the values of the angles at the apex of the triangular Cu₃ structure and the relative energies at the global minimum and the transition states differed by 2 cm⁻¹ (1%) and 2° (3%) at most. In order to achieve a smooth continuous two-dimensional (2D) description of the PESs of the Cu₃–benzene complex shown in Fig. 3, the following procedure has been applied: for each θ value, from the asymptote with Z = 10 Å, Z-steps of 1 Å (long-range region), 0.5 Å (intermediate-range region) and 0.1 Å (potential energy minimum region) have been considered. At each Z-step, the value of r was optimized. All these PES calculations were carried out with the standard RS2C method. Moreover, the dispersion-corrected (referred to as RS2CC and weighted RS2CC) schemes were applied for the structures at the potential wells.

3 Results and discussion

3.1 Preservation of the identity of the Jahn–Teller fluxional Cu₃ cluster in the parallel collision energy pathway

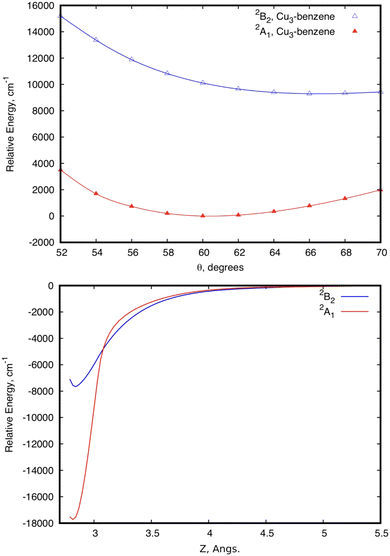
Focusing first on the case of the isolated Cu₃, the upper panel of Fig. 2 shows the typical potential energy profiles associated with an E′ ⊗ e′ Jahn–Teller distortion (see, e.g., ref. 76). The doubly degenerate vibrational (e′) mode of the isolated Cu₃ cluster is coupled to the doubly degenerate ground electronic (E′) state resulting in a distortion of the equilibrium (equilateral triangular) structure of D_3h symmetry. Specifically, Fig. 2 illustrates how, due to a conical intersection (CI) causing the Jahn–Teller distortion, the D_3h symmetry of the equilateral triangular Cu₃ structure is lowered to C_2v and the degenerate ²E′ state at the CI splits into (transition) ²A₁ and (global minimum) ²B₂ states. The Jahn–Teller stabilization energy (that is, the energy difference at the conical intersection and the global minima) is 384 cm⁻¹ in ref. 45. In the typical two-dimensional representation of the ‘Mexican hat-shaped potential’, the adiabatic potential energy surface features three symmetry-equivalent minima with a barrier between them. This barrier is the energy difference between the transition states and the minima (80 cm⁻¹ in ref. 45 and 111 cm⁻¹ from experimentally determined data in ref. 52 and 53). The zero-point energy (ZPE) level of Cu₃ (about 263 cm⁻¹ in the harmonic normal modes approximation) is above the barrier between the three symmetry equivalent minima. In this way, the copper clusters’ motion fluctuates between the minima, without being localized into a well-defined structure, a characteristic signaling fluxionality. In contrast, the energy of the Cu₃ structure at the conical intersection is above the ZPE. In this way, the nuclear wave function for the vibrational ground state becomes delocalized over the three-equivalent minima and saddle points, having a negligible probability at the position of the CI instead.⁵³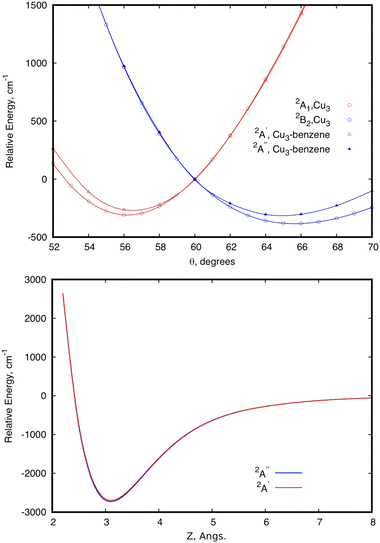

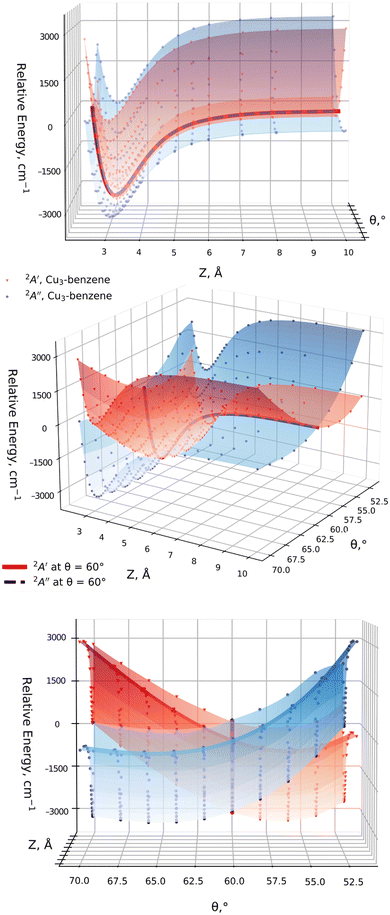
Fig. 2 Scans of the potential energy surface of a Cu₃–benzene complex in the region of the conical intersection (CI) of symmetry C₃ (²E state), correlating with the ²E′ state of the isolated Cu₃ cluster.⁴⁵ The upper panel shows scans of the relative energy as a function of the Jahn–Teller active mode at the equilibrium intermolecular Cu₃–benzene distance. The scan for unsupported Cu₃ is also shown. The zero of energy corresponds to the energy at the conical intersection in both Cu₃ and Cu₃–benzene. The lower panel shows the relative energy of the two states as a function of the distance between the centers of mass of Cu₃ and benzene (Z), with r having been optimized at each Z value, and θ having been fixed to 60°. The zero of energy defined as the energy at the asymptotic limit of separated fragments.

The analysis of the influence of the benzene support on the conical intersection in the parallel collision energy pathway of the Cu₃ cluster reveals that the Jahn–Teller distortion becomes just slightly perturbed by a model support molecule. This can be observed from the upper panel of Fig. 2. Thus, the JT stabilization energy and the energy barrier from the global minimum to the transition state decrease from 384 and 80 cm⁻¹ for the isolated Cu₃ cluster, respectively, to 310 and 32 cm⁻¹ for the Cu₃–benzene complex. Note also that the positions of the minima and the transition state for unsupported Cu₃ become almost unperturbed upon complexation with benzene. The conical intersection is located at 60° in structures of symmetry D_3h and C₃ for unsupported and benzene-supported Cu₃ clusters, respectively. The symmetry of the equilateral triangular structure of the Cu₃ cluster (D_3h) is, in fact, consistent with the C₃ symmetry of the Cu₃–benzene complex along the parallel collision pathway.

Naturally, the conservation of threefold symmetry keeps the Jahn–Teller effect. However, consideration of only symmetry does not explain why the JT distortion is so mildly perturbed upon complexation of Cu₃ with benzene. The preservation of the identity of the Cu₃ cluster is also reflected in its stabilization on the physisorption state of the Cu₃–benzene complex along the parallel collision energy pathway (see the lower panel of Fig. 2). Thus, both the equilibrium distance (3.1 Å) and the interaction well (2714 cm⁻¹) in the potential energy surface (PES) are in the range expected for physisorption species. When the coupled dispersion correction is applied with the RS2CC scheme (see the methods section), the estimated value of the potential well decreases from 2714 to 1385 cm⁻¹ (see Table 1). This outcome is even with a significant overestimation of the contribution of dispersion in van der Waals-dominated cluster support interactions at the MP2 level.^3,63,64 The accuracy of the dispersion corrections included in the RS2CC scheme has been well assessed in ref. 63 and 64 by correcting single-reference MP2 interaction energies. The estimated values of potential minima with the CCSD(T) approach are about 10% smaller than the RS2CC ones (see Table 1).

Table 1 Cu₃–benzene interaction energies for the ²A₁ and ²B₂ electronic states in the orthogonal configuration (²A′ and ²A′′ states in the parallel orientation). The tabulated values have been calculated for the two geometries corresponding to the minima at orthogonal and parallel configurations at RS2C, RS2CC, RS2CC weighted, and CCSD(T) levels (see the methods section)

	RS2C	RS2CC	RS2C weighted	CCSD(T)
E o (^2A1), cm^−1	−17 313	−13 885	−14 289	−12 665
E o (^2B2), cm^−1	−8114	−4686	−5090	−4132
E p (^2A′′), cm^−1	−2714	−1385	−1521	−1261
E p (^2A′), cm^−1	−2682	−1353	−1489	−1221

---

It can also be observed from Fig. 2 that the two relevant electronic states ²A′ and ²A′′ (²A₁ and ²B₂ states for unsupported Cu₃) remain degenerate at 60° over the one-dimensional seam characterizing the conical intersection of the Cu₃–benzene complex in the physisorption state. Moreover, as can be seen in the two-dimensional (2D) representation in Fig. 3, the Z-dependence of the PES is essentially the same for all θ values. The same holds for the θ–dependence, which is not modified by the Z intermolecular distance. Furthermore, the optimized values of r differ by less than 0.002 Å (0.05 Å) for Z ≥ Z_min (Z ≤ Z_min) from those calculated for the unsupported Cu₃ cluster. On its turn, the significantly pronounced fluctuation in the values of the relaxed r distance as a function of θ (from 2.45 Å for θ = 52° to 2.23 Å for θ = 70°) clearly indicates fluxional motion in the Cu–Cu motifs of the Cu₃ structures at the conical intersection region.

Fig. 3 Two-dimensional representation of the two electronic states ²A′ and ²A′′ of a Cu₃–benzene complex (²A₁ and ²B₂ for unsupported Cu₃) as a function of Z and θ, with the zero of energy corresponding to the separated fragments with θ = 60°.

Altogether, our results for the Cu₃–complex in a physisorption state indicate that the identity of the Jahn–Teller fluxional Cu₃ cluster is slightly perturbed by a support molecule (benzene) in a C₃ structure dominated by a van der Waals-type intermolecular interaction. In fact, for a physisorption system, it is reasonable to find a small effect due to the relatively weak nature of the intermolecular cluster-support interaction. However, previous research on (Cu₅–Cu₅)₂ has shown that preserving the identity in covalent bonding systems is possible.⁷⁷ In this way, it has been predicted that the lowest-energy structure of the (Cu₅)₂ dimer consists of two (strongly covalently bonded) bipyramidal Cu₅ geometries rotated by 90° to each other, both at 0 K in vacuum,⁷⁷ and supported on a graphene surface at a broad range of temperatures.⁶¹

3.2 Conical intersection topography: Orthogonal and parallel collision energy pathways

Let us now focus on a collision energy pathway with C_2v symmetry, where the plane of the Cu₃ cluster is orthogonal to the benzene ring plane. As can be observed in Fig. 4, the PES profiles in the ²A₁ and ²B₂ state are completely different to those shown for the parallel configuration. Specifically: (1) the lowest-energy minimum is much deeper (see Table 1) and the Z_min distance is shorter (ca. 2.6 vs. 3.1 Å); (2) its symmetry is different (²A₁vs.²B₂); (3) the minimum is located at the θ value (60°) of the conical intersection featured by unsupported Cu₃ and benzene-supported Cu₃ in the parallel orientation (see the upper panel of Fig. 2); (4) the energy at the conical intersection location at θ = 60° is 12 100 cm⁻¹ (∼1.5 eV) higher than the energy at the minimum (see the lower panel of Fig. 4); and (5) the fluctuations in the optimized r distances in the minimum are much less pronounced than those occurring in the parallel configuration (0.04 vs. 0.22 Å). The lowest-energy (²A₁) state of the Cu₃–benzene complex can be characterized as a chemisorption state (see also ref. 63). The degeneracy of the ²A₁ and ²B₂ electronic states at θ = 60° in C₃ symmetry (parallel configuration), and the associated Jahn–Teller distortion, become thus ‘lifted out’ in the C_2v-symmetry orthogonal configuration of the ²A₁ state. Notably, the ²B₂ state exhibits relatively strong binding (> 4000 cm⁻¹), making it a stable excited electronic state. The transition dipole moment and the vertical excitation energy between the ²A₁ and ²B₂ states at the bottom of the interaction well are provided in Table 2. The radiative lifetime is also presented, using the expression:⁷⁸
where |μ|² (in Debye) is the square of the transition dipole moment and T_v is the vertical excitation energy (expressed in eV). Since the magnitude of the transition dipole moment is rather large (1.20 Debye, see Table 2), direct excitation with photon energies above the vertical excitation energy [9199 cm⁻¹ (∼1.1 eV), see Table 2] can efficiently populate the ²B₂ state. Follow-up excited state dynamics in the ²B₂ state (see Fig. 2) would allow us to reach the conical intersection, thereby enhancing the potential for rapid, non-radiative decay. In fact, the estimated value of 6.25 ns for the radiative lifetime (see Table 2) indicates that the system can undergo fast decay from the excited state, favoring non-radiative emission.

Fig. 4 Scans of the potential energy surfaces of ²A₁ and ²B₂ states of the Cu–benzene complex as a function of θ in the region of the conical intersection (CI) of isolated Cu₃. Bond Cu–Cu distances are optimized at each θ value.⁷⁹ The θ-dependence of the potential energy curves at the equilibrium intermolecular Cu₃–benzene distance is depicted in the upper panel. The lower panel shows the energy of the two states as a function of the intermolecular distance Z, with r having been optimized at each Z value, and θ having been fixed to 60°. In the upper panel, the zero of energy is the energy at θ = 60°. In the lower panel, the zero of energy is the energy at the asymptotic limit of separated Cu₃ and benzene fragments.

Table 2 Transition dipole moment (μ in D), vertical excitation energy (T_v in cm⁻¹ and eV) and radiative lifetime (τ in ns) for the ²A₁ and ²B₂ electronic states for the Cu₃–benzene complex in the orthogonal configuration. The tabulated values have been calculated for the geometry corresponding to the minimum at the orthogonal configuration at the RS2C level

	μ, D	T v, cm^−1 (eV)	τ, ns
Orthogonal	1.20	9199 (1.1)	6.25

---

The coupled dispersion correction has been calculated with the RS2CC scheme (see the methods section), causing a decrease in the attractive interaction energy at the equilibrium structure from 17 313 to 13 885 cm⁻¹ for the ²A₁ state (see Table 1). Naturally, the role of the dispersion correction is less pronounced in the chemisorption than in the physisorption state. This outcome is consistent with the relatively minor role of the vdW-type cluster-support interaction at the chemisorption minimum. In contrast, the weight of the dispersion contribution is very large in the excited ²B₂ state, causing a decrease of the interaction energy from 8114 to 4686 cm⁻¹. CCSD(T) calculations consistently yield well depths that are approximately 9% and 12% smaller than those obtained using the RS2CC method for the ²A₁ and ²B₂ states, respectively. These differences align with expectations due to the small, yet non-negligible, role of multireference effects for the most stable chemisorption ²A₁ state. It should also be stressed that the associated interaction energy (13 885 cm⁻¹) differs just slightly from that reported in ref. 63 using the same dispersion correction at the MP2 level (12 998 cm⁻¹). The dispersion-corrected RS2CC method, however, allows us to deal with ground and excited electronic states, including conical intersections.

In order to illustrate the evolution of the location of the conical intersection upon decreasing the intermolecular Z distance in physisorption and chemisorption states, Fig. 5 presents a comparison of the potential energy curves of the two relevant electronic states as a function of θ for the orthogonal (left-hand panel) and parallel (right-hand panel) collision energy pathways. Starting with the parallel configuration, the conical intersection is located at θ = 60° in a structure with symmetry C₃ for the Cu₃–benzene complex (D_3h for the unsupported Cu₃ cluster). The θ-dependence of the ground and excited electronic states closely follows that of the unsupported Cu₃ cluster regardless of the Z distance. When the Z distance decreases, the potential energy curves shift overly to lower energies. In contrast, the location of the conical intersection for the Cu₃–benzene complex in the orthogonal energy pathway experiences a pronounced change to values of θ greater than 60° when the distance Z decreases. At Z = Z_min + 0.65 Å, note that the location of the conical intersection between the ²A₁ and ²B₂ states has been shifted to 63°, being 12 100 cm⁻¹ (∼1.5 eV) above the chemisorption minimum. Similarly, the ²A₁ state (transition state for unsupported Cu₃) becomes lower in energy than the ²B₂ state (global minimum for isolated Cu₃) at θ <63°. A further decrease of intermolecular distance to Z = Z_min + 0.4 Å provokes a moving of the conical intersection location to θ > 70°. Moreover, the energy difference between the ²A₁ and ²B₂ states increases to values larger than 8000 cm¹ (∼1 eV) at θ = 52°. At the chemisorption minimum with Z = Z_min, the energy separation between the ²A₁ and ²B₂ states further increases, being >8000 cm⁻¹ (∼1 eV) higher also at θ = 70°.

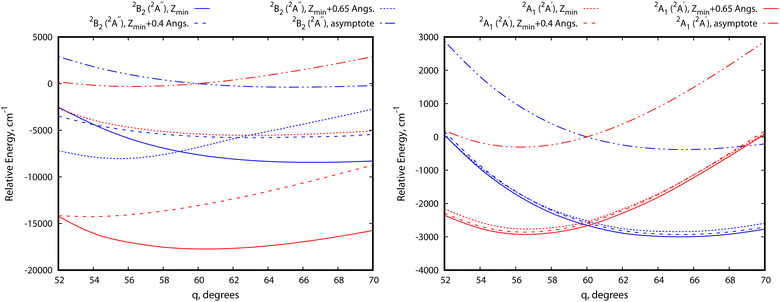Fig. 5 Figure comparing potential energy curves for the two relevant electronic states of the Cu₃–benzene complex in the region of the conical intersection (the ²B₂ and ²A₁ states for unsupported Cu₃). The bond Cu–Cu distance is optimized for each value of θ and considered values of the intermolecular Cu₃–benzene distance Z. The left-hand (right-hand) panel corresponds to the orthogonal (parallel) Cu₃–benzene configurations with symmetry C_2v (C₃) (see Fig. 1). The spin and spatial symmetry labelling of the states without (with) parenthesis correspond to the orthogonal (parallel) orientation.

It is important to emphasize that there is a clear correlation between the fluctuations of the optimized r values as a function of θ at a given distance Z and the location of the conical intersection. Interestingly, at the Z value where the conical intersection is localized, a wide range of optimized values of r (from 2.43 to 2.66 Å) is found. The ‘floppy’ character of the unsupported Cu₃ structures is thus recovered nearby the conical intersection. The range of optimized r values can thus be considered as an indicator of the fluxionality of the cluster (i.e., the Cu–Cu motifs) in a given region of the potential energy landscape. Although the Cu₃ cluster is ‘non-fluxional’ at the well of the most stable ²A₁ state, the fluxionality can be recovered upon photo-excitation to the ²B₂ state since it is energetically much closer to the conical intersection, suggesting the occurrence of a photo-induced boosting of structural fluxionality.

3.3 Natural orbitals at the conical intersection

Fig. 6 shows a comparison of the frontier natural orbitals at the conical intersection at the asymptotic region (Z = 10 Å), at the parallel configuration with Z_min = 3.1 Å, and at the orthogonal configuration with Z = Z_min + 0.65 Å (see also Fig. 5). The degenerate e-type orbital, which serves as the singly occupied molecular orbital (SOMO), is composed of contributions from the s and p orbitals of the copper atoms. The highest occupied molecular orbital (HOMO) is predominantly formed by the s orbitals of Cu atoms, while the HOMO−1, identified as the lowest-energy frontier natural orbital, is characterized by delocalized π-type orbitals of the benzene molecule. Interestingly, there is no significant overlap between the orbitals of the Cu₃ cluster and the benzene molecule. The degenerate e-type orbital, which is associated with the Jahn–Teller distortion and fluxional behavior, preserves its properties upon adsorption on the benzene support, whether the complex adopts a parallel or perpendicular orientation. However, a notable distinction arises in the perpendicular structure, where there is a much greater polarization of the SOMO with the benzene orbitals compared to the parallel configuration, in which such polarization is minimal. The wavefunction analysis reveals that the dominant configuration is characterized by a single-electron occupation of the degenerate e-type orbital, with a coefficient exceeding 0.9 (see the ESI†).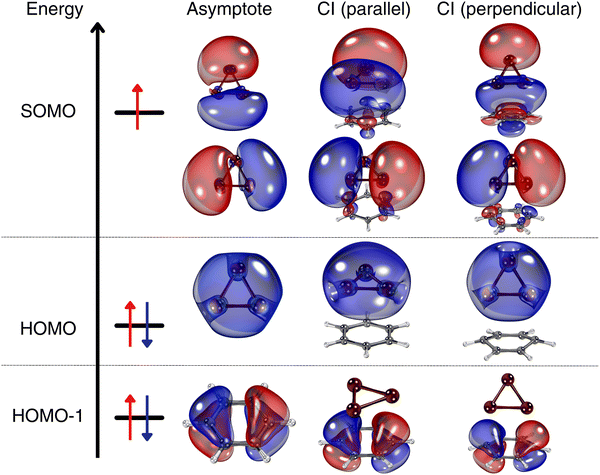

Fig. 6 Frontier natural orbitals of the Cu₃–benzene complex at the conical intersection associated to: (1) the asymptotic limit of separated Cu₃ and benzene fragments; (2) the equilibrium Cu₃–benzene structure, Z_min = 3.1 Å for the parallel orientation (see Fig. 2); (3) Z = Z_min + 0.65 Å for the orthogonal orientation (see Fig. 5). The picture shows isosurfaces of the frontier ‘singly-occupied’ (or occupied only by a single spin component) molecular orbital (referred to as the SOMO) as well as the highest-energy and second ‘doubly-occupied’ (or occupied by two spin components) molecular orbitals (referred to as the HOMO and HOMO−1, respectively).

Before concluding this section, it is important to stress that, since the energy at the conical intersection is about 12 100 cm⁻¹ (∼1.5 eV) higher than the energy at the chemisorption minimum of the Cu₃–benzene complex, single-reference electronic structure descriptions of the PES of the adiabatic ground state might suffice for the calculation of the ro-vibrational energy levels in applications such as the determination of spectra features in the infrared region. In fact, the adequacy of a single-reference CCST(T) approach at the structure of the chemisorption minimum has been ensured through coupled cluster diagnostics⁸⁰ (see also ref. 63. In contrast, the characterization of complex spectral features in the visible and near-infrared of the system might consider at least the two electronic states becoming degenerate at a C₃-symmetry structure, especially considering the large magnitude of the transition dipole moment at the most stable orthogonal configuration (see Table 2). In order to illustrate the importance of using multi-reference electronic structure descriptions for the Jahn–Teller distortion, we have carried out test calculations using the single-reference (restricted open-shell) RMP2 method for C₃-symmetric Cu₃–benzene. The JT stabilization energy is overestimated by a factor of 1.4 at the RMP2 level (422 vs. 310 cm⁻¹) but the ‘exact’ degeneracy of the ²A′ and ²A′′ states at the CI is recovered at the CASSCF level using a minimal (1,2) active space (i.e., involving just the unpaired electron and the SOMO and LUMO).

4 Conclusions

Taking benzene as a model support molecule, it is demonstrated that the conical intersection region is preserved to a large extent in a parallel orientation of the plane of the Cu₃ cluster with respect to the benzene ring plane. This configuration is associated with a physisorption minimum, with the best estimation of the deep well being 1385 cm⁻¹ (see Table 1). The symmetry at the conical intersection of the complex (C₃) is consistent with the D_3h symmetry of the conical intersection at the equilateral triangle-shaped structure of the Cu₃ cluster isolated in the gas-phase.⁴⁵ However, symmetry considerations only do not explain the slight modification of the Jahn–Teller stabilization energy and the energy barrier between the minimum and the transition state upon complexation with benzene. The multidimensional conical intersection of the Cu₃–benzene complex is shifted by 12 100 cm⁻¹ (∼1.5 eV) from the location of a chemisorption minimum, corresponding to the energetically much more stable perpendicular orientation of the Cu₃ cluster in C_2v symmetry. It is also shown that the fluctuations in the Cu–Cu distances at the chemisorption minimum are much less pronounced than for the Cu₃–benzene complex at the physisorption state so that the system is ‘non-fluxional’ at the bottom of the chemisorption well at the ground ²A₁ state. The fluxionality of the Cu–Cu motifs is recovered at the conical intersection region between the ground ²A₁ and the excited ²B₂ electronic states of the complex in the most stable perpendicular configuration. Importantly, our work also demonstrates that the excited ²B₂ state might be observable upon a direct photo-excitation from the electronic ground ²A₁ state due to the large magnitude of the transition dipole moment connecting them. Moreover, the Cu₃–complex is also rather stable in the excited ²B₂ state, being close to the conical intersection region where the fluxional Cu–Cu motifs are recovered. In fact, the clear correlation between conical intersections' topography and enhancement of fluxional motion is the most remarkable outcome of this study. From a methodological perspective, the convenience of the proposed dispersion-corrected RS2C scheme is also worth mentioning as a multi-reference approach capable of dealing with intermolecular cluster-support interactions for both ground and excited states, including conical intersections, and describing physisorption and chemisorption states for both closed- and open-shell systems.

The selection of the Cu₃–benzene complex in this work was also motivated by the role that polycyclic aromatic hydrocarbons (PAHs) could play in interstellar chemistry by forming complexes with other atoms, molecules, or clusters.⁸¹ In fact, PAHs have been suggested as carriers of a number of diffuse interstellar bands in the visible and near-infrared as well as unidentified infrared bands in the mid-infrared. The influence of PAHs on the conical intersections of astrochemically relevant molecules such as H₃⁺, the interstellar molecule most abundantly produced,⁸² is thus important. Having triangular structures, Cu₃ and H₃⁺ in the excited (quartet spin) electronic state share the common feature of having one electron in a degenerate orbital made of s-type atomic orbitals. Complex spectra features in interstellar bands in the visible and near-infrared might come from conical intersections and Jahn–Teller distortions of molecules forming complexes with PAHs having commensurable structures. However, our results also indicate that the spectra in the mid-infrared region might be well characterized considering the most stable chemisorption state only.

A future prospect is to extend our detailed study to coronene as a target PAH, also serving as a good molecular model of graphene, and starting with the C₃-symmetric Cu₃–coronene complex. The preservation of the characteristics of Jahn–Teller distortions of AMCs in spite of support effects at physisorption states is expected to be a general motive in PAHs bearing consistent symmetries. Even in PAHs lacking them, avoided crossings between the relevant electronic states associated to Jahn–Teller distortions of AMCs might happen and their exploration is worthwhile, starting with the Cu₃–naphthalene complex. At room temperature, the large energy difference between the potential wells for parallel and orthogonal configurations [>12 100 cm⁻¹ (∼1.5 eV) for Cu₃–benzene] indicates that the complexes stick to the most stable ‘non-fluxional’ chemisorption state. However, due to the large magnitude of the dipole moment, the excited ²B₂ state might be populated with photons in the visible and near-infrared. The follow-up excited state dynamics as a function of temperature would provide information about the probability of reaching the conical intersection region upon heating, located relatively close to the potential well of the ²B₂ state for Cu₃–benzene. Upon heating, the surface-supported clusters might gain enough energy in the internal rotation to, eventually, get trapped at the physisorption state in the parallel configurations and associated low-energy conical intersection. Thus, using the equipartition theorem, the temperatures needed to overcome the energy differences between orthogonal and parallel configurations in ground and excited states can be estimated to be 722 and 135 K, respectively. Detailed studies would require extensions of single-state molecular dynamics descriptions to multistate ones using, e.g., the surface hopping approach.^83–85

In conclusion, there is no doubt that conical intersections play a relevant role in the (photo)stability, (photo)reactivity, and structural fluxionality of supported metal clusters on the sub-nanoscale. In particular, the adsorption properties of reaction intermediates are greatly influenced by the ‘floppy’ character of catalysts' structures near to conical intersections, making them more prone to exhibit non-adiabatic effects in the reactivity too. Conical intersections of open-shell metal clusters isolated in the gas-phase have been well characterized.^45,52–59 However, support effects on these conical intersections have been largely unexplored. With this article, by applying a high-level multireference ab initio approach, and improving it with dispersion corrections, to the benzene-supported Cu₃ cluster, we have aimed to start filling the gap. Naturally, the description of conical intersections of supported metal (photo)catalysts represents a grand challenge for the current state-of-the-art in theoretical-computational modeling.³ However, the topic is evolving rapidly, with the development of algorithms such as the variational quantum eigensolver (VQE) enabling cost-efficient handling of multiple electronic states. Moreover, recent methodological developments have allowed conical intersections to be located more efficiently without employing derivative couplings (DC).⁸⁶ There are also significant developments in the efficient and accurate description of nonadiabatic effects in chemical processes, such as the oxidation of Cu₅ clusters. A state-of-the-art approach uses a Landau–Zener (LZ) semiclassical description,^87,88 optimizing orbitals separately for ground and excited states.^43,89,90 This strategy delivers quasi-diabatic electronic states in a natural way, avoiding large configuration-interaction expansions. In the limit of single-reference configurations derived through separate Hartree–Fock calculations for the crossing electronic states, aided with dynamical correlation contributions, this approach has been successfully applied to describe a LZ-based harpoon-type electron transfer between a metal dimer (Cs₂) and a fullerene molecule.^91–93 Work is underway to make it possible for conical intersections of AMCs to be routinely described with multistate ab initio theory followed by multistate quantum⁹⁴ or semi-classical^83–85,95 non-adiabatic descriptions of the underlying dynamics. We hope that our work might motivate further efforts in the direction of considering the role of conical intersections in the (photo)chemistry of supported atomically precise metal clusters.

Author contributions

Conceptualization: M. P. d. L.-C., investigation; K. M. K. and M. P. d. L.-C. methodology: K. M. K. and M. P. d. L.-C.; supervision: M. P. d. L.-C.; project administration: M. P. d. L.-C.; funding acquisition: M. P. d. L.-C.; software: K. M. K. and M. P. d. L.-C. formal analysis: K. M. K. and M. P. d. L.-C.; data curation: K. M. K. and M. P. d. L.-C.; visualization: K. M. K. and M. P. d. L.-C.; validation: K. M. K. and M. P. d. L.-C.; writing: M. P. d. L.-C. The two authors have edited and agree to this version of the manuscript.

Data availability

The data supporting the findings of this study are available in the ESI† of this article.

Conflicts of interest

There are no conflicts to declare.

Acknowledgements

We thank María J. López for interesting discussions. This work has been partially supported by the Spanish Agencia Estatal de Investigación (AEI) under Grant No. PID2020-117605GB-I00/AEI/10.13039/501100011033 and the EU Doctoral Network PHYMOL 101073474 (project call reference HORIZON-MSCA-2021-DN-01). This publication is also based upon the work of COST Action CA21101 “Confined molecular systems: from a new generation of materials to the stars” (COSY) supported by COST (European Cooperation in Science and Technology). The CESGA supercomputer center (Spain) and the CTI at CSIC are acknowledged for having provided the computational resources. We also acknowledge support of the publication fee by the CSIC Open Access Publication Support Initiative through its Unit of Information Resources for Research (URICI).

Notes and references

1. L. Liu and A. Corma, Chem. Rev., 2018, 118, 4981–5079.
2. J. Juraj, A. Fortunelli and S. Vajda, Phys. Chem. Chem. Phys., 2022, 24, 12083–12115.
3. M. P. de Lara-Castells, Small Struct., 2024, 2400147.
4. Q. Wu, S. Hou, D. Buceta, H. J. Ordoñez, M. Arturo López-Quintela and C. J. Lambert, Appl. Surf. Sci., 2022, 594, 153455.
5. L. Zhang and E. Wang, Nano Today, 2014, 9, 132–157.
6. A. Halder, C. Lenardi, J. Timoshenko, A. Mravak, B. Yang, L. K. Kolipaka, C. Piazzoni, S. Seifert, V. Bonačić-Koutecký, A. I. Frenkel, P. Milani and S. Vajda, ACS Catal., 2021, 11, 6210–6224.
7. H. Zhai and A. N. Alexandrova, ACS Catal., 2017, 7, 1905–1911.
8. R. T. Hannagan, G. Giannakakis, M. Flytzani-Stephanopoulos and E. C. H. Sykes, Chem. Rev., 2020, 120, 12044–12088.
9. L. Vega, H. A. Aleksandrov, R. Farris, A. Bruix, F. Viñes and K. M. Neyman, Mater. Adv., 2021, 2, 6589–6602.
10. E. Fernández and M. Boronat, J. Phys.: Condens. Matter, 2019, 31, 013002.
11. S. Sharma and A. Ansari, Results Chem., 2023, 5, 100982.
12. V. Bonačić-Koutecký and R. Antoine, Nanoscale, 2019, 11, 12436–12448.
13. M. V. Romeo, E. López-Martínez, J. Berganza-Granda, F. Goñi-de Cerio and A. L. Cortajarena, Nanoscale Adv., 2021, 3, 1331–1341.
14. L. Zhang and E. Wang, Nano Today, 2014, 9, 132–157.
15. M. A. Abbas, P. V. Kamat and J. H. Bang, ACS Energy Lett., 2018, 3, 840–854.
16. H.-T. Sun and Y. Sakka, Sci. Technol. Adv. Mater., 2014, 15, 014205.
17. M. P. de Lara-Castells, A. W. Hauser, J. M. Ramallo-López, D. Buceta, L. J. Giovanetti, M. A. López-Quintela and F. G. Requejo, J. Mater. Chem. A, 2019, 7, 7489–7500.
18. P. López-Caballero, A. W. Hauser and M. P. de Lara-Castells, J. Phys. Chem. C, 2019, 123, 23064–23074.
19. M. P. de Lara-Castells, J. Colloid Interface Sci., 2022, 612, 737–759.
20. M. P. de Lara-Castells, C. Cabrillo, D. A. Micha, A. O. Mitrushchnekov and T. Vazhappilly, Phys. Chem. Chem. Phys., 2018, 20, 19110–19119.
21. G. F. Combes, A.-M. Vuckovic, M. Peric Bakulic, R. Antoine, V. Bonacic-Koutecky and K. Trajkovic, Cancers, 2021, 13, 4206.
22. K. Zheng and J. Xie, Trends Chem., 2020, 2, 665–679.
23. Q. Zhang, M. Yang, Y. Zhu and C. Ma, Curr. Med. Chem., 2018, 25, 1379–1396.
24. Z. Luo and A. Shehzad, ChemPhysChem, 2024, e202300715.
25. D. Buceta, S. Huseyinova, M. Cuerva, H. Lozano, L. J. Giovanetti, J. M. Ramallo-López, P. López-Caballero, A. Zanchet, A. O. Mitrushchenkov, A. W. Hauser, G. Barone, C. Huck-Iriart, C. Escudero, J. C. Hernández-Garrido, J. J. Calvino, M. López-Haro, M. P. de Lara-Castells, F. G. Requejo and M. A. López-Quintela, Chem. – Eur. J., 2023, 29, e202301517.
26. A. Halder, L. A. Curtiss, A. Fortunelli and S. Vajda, J. Chem. Phys., 2018, 148, 110901.
27. P. López-Caballero, J. M. Ramallo-López, L. J. Giovanetti, D. Buceta, S. Miret-Artés, M. A. López-Quintela, F. G. Requejo and M. P. de Lara-Castells, J. Mater. Chem. A, 2020, 8, 6842–6853.
28. P. López-Caballero, S. Miret-Artés, A. O. Mitrushchenkov and M. P. de Lara-Castells, J. Chem. Phys., 2020, 153, 164702.
29. M. P. de Lara-Castells and S. Miret-Artés, Europhys. News, 2022, 53, 7–9.
30. P. Concepción, M. Boronat, S. García-García, E. Fernández and A. Corma, ACS Catal., 2017, 7, 3560–3568.
31. S. Huseyinova, J. Blanco, F. G. Requejo, J. M. Ramallo-López, M. C. Blanco, D. Buceta and M. A. López-Quintela, J. Phys. Chem. C, 2016, 120, 15902–15908.
32. J. Jašik, S. Valtera, M. Vaidulych, M. Bunian, Y. Lei, A. Halder, H. Tarábková, M. Jindra, L. Kavan, O. Frank, S. Bartling and S. Vajda, Faraday Discuss., 2023, 242, 70–93.
33. E. Fernández, M. Boronat and A. Corma, J. Phys. Chem. C, 2020, 124, 21549–21558.
34. B. Yang, C. Liu, A. Halder, E. C. Tyo, A. B. F. Martinson, S. Seifert, P. Zapol, L. A. Curtiss and S. Vajda, J. Phys. Chem. C, 2017, 121, 10406–10412.
35. P. Maity, S. Yamazoe and T. Tsukuda, ACS Catal., 2013, 3, 182–185.
36. A. Mravak, S. Vajda and V. Bonačić-Koutecký, J. Phys. Chem. C, 2022, 126, 18306–18312.
37. M. P. de Lara-Castells, C. Puzzarini, V. Bonačić-Koutecký, M. A. López-Quintela and S. Vajda, Phys. Chem. Chem. Phys., 2023, 25, 15081–15084.
38. H. Zhai and A. N. Alexandrova, ACS Catal., 2017, 7, 1905–1911.
39. Q.-Y. Fan, Y. Wang and J. Cheng, J. Phys. Chem. Lett., 2021, 12, 3891–3897.
40. Z. Zhang, B. Zandkarimi and A. N. Alexandrova, Acc. Chem. Res., 2020, 53, 447–458.
41. U. Mondal and P. Ghosh, Catal. Today, 2021, 370, 93–103.
42. P. López-Caballero, R. Garsed and M. P. de Lara-Castells, ACS Omega, 2021, 6, 16165–16175.
43. A. O. Mitrushchenkov, A. Zanchet, A. W. Hauser and M. P. de Lara-Castells, J. Phys. Chem. A, 2021, 125, 9143–9150.
44. O. V. Lushchikova, H. Tahmasbi, S. Reijmer, R. Platte, J. Meyer and J. M. Bakker, J. Phys. Chem. A, 2021, 125, 2836–2848.
45. A. O. Mitrushchenkov and M. P. de Lara-Castells, ChemPhysChem, 2023, 24, e202300317.
46. H. A. Jahn, E. Teller and F. G. Donnan, Proc. R. Soc. Lond., Ser. A, Math. Phys. Eng. Sci., 1937, 161, 220–235.
47. H. A. Jahn and W. H. Bragg, Proc. R. Soc. Lond., Ser. A, Math. Phys. Eng. Sci., 1938, 164, 117–131.
48. P. Garcia-Fernandez, I. B. Bersuker and J. E. Boggs, Phys. Rev. Lett., 2006, 96, 163005.
49. I. B. Bersuker, Phys. Chem. Chem. Phys., 2023, 25, 1556–1564.
50. C. A. Farfan and D. B. Turner, Phys. Chem. Chem. Phys., 2020, 22, 20265–20283.
51. W. Fang, E. R. Heller and J. O. Richardson, Chem. Sci., 2023, 14, 10777–10785.
52. E. A. Rohlfing and J. J. Valentini, Chem. Phys. Lett., 1986, 126, 113–118.
53. J. W. Zwanziger, R. L. Whetten and E. R. Grant, J. Phys. Chem., 1986, 90, 3298–3301.
54. R. R. Persaud, M. Chen, K. A. Peterson and D. A. Dixon, J. Phys. Chem. A, 2019, 123, 1198–1207.
55. L. H. Coudert, W. E. Ernst and O. Golonzka, J. Chem. Phys., 2002, 117, 7102–7116.
56. A. W. Hauser, C. Callegari, P. Soldán and W. E. Ernst, J. Chem. Phys., 2008, 129, 044307.
57. A. W. Hauser, J. V. Pototschnig and W. E. Ernst, Chem. Phys., 2015, 460, 2–13.
58. A. W. Hauser, G. Auböck, C. Callegari and W. E. Ernst, J. Chem. Phys., 2010, 132, 164310.
59. S. R. Langhoff, C. W. Bauschlicher, S. P. Walch and B. C. Laskowski, J. Chem. Phys., 1986, 85, 7211–7215.
60. K. Geim, Science, 2009, 324, 1530.
61. L. L. Carroll, L. V. Moskaleva and M. P. de Lara-Castells, Phys. Chem. Chem. Phys., 2023, 25, 15729–15743.
62. P. Celani and H.-J. Werner, J. Chem. Phys., 2000, 112, 5546–5557.
63. K. M. Krupka, A. Krzemińska and M. P. de Lara-Castells, RSC Adv., 2024, 14, 31348–31359.
64. M. P. de Lara-Castells, A. O. Mitrushchenkov and H. Stoll, J. Chem. Phys., 2015, 143, 102804.
65. T. H. Dunning, J. Chem. Phys., 1989, 90, 1007.
66. D. Figgen, G. Rauhut, M. Dolg and H. Stoll, Chem. Phys., 2005, 311, 227–244.
67. M. Boggio-Pasqua and G. Groenhof, Comput. Theor. Chem., 2014, 1040–1041, 6–13.
68. B. O. Roos and K. Andersson, Chem. Phys. Lett., 1995, 245, 215–223.
69. A. Heßelmann, J. Chem. Phys., 2008, 128, 144112.
70. M. Pitonák and A. Heßelmann, J. Chem. Theory Comput., 2010, 6, 168–178.
71. K. Szalewicz, Wiley Interdiscip. Rev.: Comput. Mol. Sci., 2012, 2, 254–272.
72. R. M. Parrish, L. A. Burns, D. G. A. Smith, A. C. Simmonett, A. E. DePrince, E. G. Hohenstein, U. Bozkaya, A. Y. Sokolov, R. Di Remigio, R. M. Richard, J. F. Gonthier, A. M. James, H. R. McAlexander, A. Kumar, M. Saitow, X. Wang, B. P. Pritchard, P. Verma, H. F. Schaefer, K. Patkowski, R. A. King, E. F. Valeev, F. A. Evangelista, J. M. Turney, T. D. Crawford and C. D. Sherrill, J. Chem. Theory Comput., 2017, 13, 3185–3197.
73. D. G. A. Smith, L. A. Burns, D. A. Sirianni, D. R. Nascimento, A. Kumar, A. M. James, J. B. Schriber, T. Zhang, B. Zhang, A. S. Abbott, E. J. Berquist, M. H. Lechner, L. A. Cunha, A. G. Heide, J. M. Waldrop, T. Y. Takeshita, A. Alenaizan, D. Neuhauser, R. A. King, A. C. Simmonett, J. M. Turney, H. F. Schaefer, F. A. Evangelista, A. E. DePrince, T. D. Crawford, K. Patkowski and C. D. Sherrill, J. Chem. Theory Comput., 2018, 14, 3504–3511.
74. M. Hapka, P. S. Żuchowski, M. M. Szczęśniak and G. Chałasiński, J. Chem. Phys., 2012, 137, 164104.
75. K. Madajczyk, P. S. Żuchowski, F. Brzęk, L. Rajchel, D. Kędziera, M. Modrzejewski and M. Hapka, J. Chem. Phys., 2021, 154, 134106.
76. I. B. Bersuker, Chem. Rev., 2001, 101, 1067–1114.
77. J. Garrido-Aldea and M. P. de Lara-Castells, Phys. Chem. Chem. Phys., 2022, 24, 24810–24822.
78. T. Trabelsi, J. M. Anglada, M. F. Ruiz-López and J. S. Francisco, J. Chem. Phys., 2019, 151, 111103.
79. In the optimizations, the electronic (²A₁ or ²B₂) state delivering the lowest energy was considered as the reference.
80. W. Jiang, N. J. DeYonker and A. K. Wilson, J. Chem. Theory Comput., 2012, 8, 460–468.
81. M. P. de Lara-Castells and A. W. Hauser, Phys. Life Rev., 2020, 32, 95–98.
82. M. Larsson, Int. J. Astrobiol., 2008, 7, 237–241.
83. M. F. Herman, J. Chem. Phys., 1984, 81, 754–763.
84. J. C. Tully, J. Chem. Phys., 1990, 93, 1061–1071.
85. M. Barbatti, Wiley Interdiscip. Rev.: Comput. Mol. Sci., 2011, 1, 620–633.
86. J. Sanz García, R. Maskri, A. Mitrushchenkov and L. Joubert-Doriol, J. Chem. Theory Comput., 2024, 20, 5643–5654.
87. L. D. Landau, Phys. Z. Sowjetunion, 1932, 2, 46–51.
88. C. Zener, Proc. R. Soc. Lond., Ser. A, Math. Phys. Eng. Sci., 1932, 137, 696–702.
89. M. P. de Lara-Castells and J. L. Krause, J. Chem. Phys., 2003, 118, 5098–5105.
90. M. P. de Lara-Castells, A. O. Mitrushchenkov, O. Roncero and J. L. Krause, Isr. J. Chem., 2005, 45, 59–76.
91. M. P. de Lara-Castells, A. W. Hauser and A. O. Mitrushchenkov, J. Phys. Chem. Lett., 2017, 8, 4284–4288.
92. A. Castillo-García, A. W. Hauser, M. P. de Lara-Castells and P. Villarreal, Molecules, 2021, 26, 5783.
93. A. W. Hauser and M. P. de Lara-Castells, Phys. Chem. Chem. Phys., 2017, 19, 1342–1351.
94. S. Choi and J. Vanícek, J. Chem. Phys., 2020, 153, 211101.
95. S. Mai, P. Marquetand and L. González, Wiley Interdiscip. Rev.: Comput. Mol. Sci., 2018, 8, e1370.

---

Footnote

† Electronic supplementary information (ESI) available: Cartesian coordinates of Cu₃–benzene and benzene structures, numerical values of Cu₃–benzene uncoupled dispersion (E^UHF_disp) and coupled dispersion (E^TD-UHF_disp) contributions, values of the square of the coefficient of the main configuration in the reference wavefunctions (CI²), Python code delivering a two-dimensional representation of relaxed potential energy surface scans of the Cu₃–benzene complex and data containing θ angles (in degrees), Z distances (in Å) and relative energies (in Hartree) for two crossing electronic states. See DOI: https://doi.org/10.1039/d4cp03271c

---