Open Access Article
Open Access ArticleCreative Commons Attribution 3.0 Unported Licence
Coverage-dependent stability of RuxSiy on Ru(0001): a comparative DFT and XPS study
Jonathon
Cottom
 abc,
Stefan
van Vliet
a,
Jörg
Meyer
abc,
Stefan
van Vliet
a,
Jörg
Meyer
 c,
Roland
Bliem
c,
Roland
Bliem
 ad and
Emilia
Olsson
ad and
Emilia
Olsson
 *ab
*ab
aAdvanced Research Center for Nanolithography, Science Park 106, Amsterdam 1098 XG, The Netherlands
bInstitute of Theoretical Physics, Institute of Physics, University of Amsterdam, Science Park 904, Amsterdam 1098 XH, The Netherlands. E-mail: k.i.e.olsson@uva.nl
cLeiden Institute of Chemistry, Gorlaeus Laboratories, Leiden University, 2300 RA Leiden, The Netherlands
dvan der Waals-Zeeman Institute, Institute of Physics, University of Amsterdam, Science Park 904, Amsterdam 1098 XH, The Netherlands
First published on 16th November 2024
Abstract
This work investigates the interaction of silicon with ruthenium, extending from Si-defect centers in ruthenium bulk to the adsorption of Si on the Ru(0001) surface. Using density functional theory (DFT) we calculate the interaction energies of up to 2 monolayers (MLs) of Si with this surface, uncovering the initial formation of ruthenium silicide (RuxSiy). Our results demonstrate that Si readily forms substitutional defects (SiRu) in bulk ruthenium. These defects are further stabilized on the Ru(0001) surface, resulting in a distinct propensity for forming Ru–SiRu mixed layers – which can thus be described by stoichiometry RuxSiy. Overlayers of surface-adsorbed Si adatoms and RuxSiy mixed layers are iso-energetic at 0.5 ML, with the latter becoming increasingly energetically favored at higher Si coverages. We further examine the influence of RuxSiy formation with respect to oxide formation, focusing on coverage-dependent energy differences. Our results show RuxSiy layers are energetically favored with respect to the forming oxide for silicon and oxygen coverages above 1.1 ML, respectively. In addition, the formation of RuxSiy and the subsequent oxidation of Ru and RuxSiy were also investigated experimentally using in situ XPS. This confirmed the DFT prediction, with negligible oxide formation on the RuxSiy sample, whereas the unprotected Ru surface showed extensive RuO2 formation under the same conditions. Our study not only enhances the understanding of Ru surface chemistry but also suggests a straightforward computational approach for screening the oxidation resistance of surface coatings.
Ruthenium thin films are increasingly important for a wide variety of applications that exploit the favorable chemical, physical and electronic properties this chemical element possesses. Ruthenium has been known to have high catalytic activity originally as a homogeneous catalyst1 and more recently in heterogeneous catalysis.2 As a heterogeneous catalyst, Ru surfaces provide excellent activity for the Fischer–Tropsch process (conversion of syngas into long chain aliphatic hydrocarbons), and NH3 decomposition.3–5 Ruthenium thin films have an equally long history in a variety of protective barrier layer applications.6–17 Finally, combining barrier layer properties with favorable electronic properties, Ru is used as an electrode in various MOSFET, MEMs, and memory devices, where stability against oxidation is a primary concern.18,19
Across the highlighted use cases oxidation can be both a blessing and curse. In catalytic applications the oxidation of Ru results in a number of new active phases that show a dramatic increase in catalytic activity and scope when compared to Ru. In barrier layer and device applications, the oxidation of Ru to form RuO2 can be undesirable, as this goes hand in hand with the loss of the aforementioned favorable physical, chemically and electronic properties of ruthenium.20,21 Facilitating ion accumulation in and diffusion through the barrier layer,21 resulting in the modification and breakdown of the dielectric layer beneath.22–24 Driven by the catalysis community, the oxidation of Ru has been comprehensively studied, showing a progression from a dense hcp-monolayer to the RuO2 rutile structure.2,25,26 Theoretical models, including ab initio thermodynamics and lattice gas cluster expansion, align well with experimental data for the sub-monolayer coverages of Ru oxidation.27–32 Surface phase diagrams resulting from these models predict that the oxidation proceeds via a number of ordered intermediate structures.33–37 Guided by the previous literature characterization of Ru oxidation, we define and test a computational screening framework to assess the oxidation resistance of thin surface coatings.
Transition metal silicides have long been known to show impressive oxidation resistance in the bulk and thick film context.15,38–43 This oxidation resistance has been shown in many cases to extend to thin films.40,44 Ruthenium is known to form stable silicides with varying ratios of Si and Ru. Theoretical studies predict RuSi to be the most favored bulk composition, with the silicon-rich Ru2Si3 having a similar formation energy.45 Synthetically these compositions and crystal structures have been reported, using pulsed laser deposition,46,47 arc-melting,48 and various other atomic deposition approaches.49,50 All of the characterized compositions are semiconductors with a narrow band gap of 0.2 eV to 0.6 eV, showing an increasing band gap with increasing Si content.45 Studies of the Si–Ru interface show a propensity for the layers to intermix leading to the formation of RuxSiy interlayers, reaching thicknesses of several nanometers (≈4.7 nm).43,51,52
Surface deposition of Si on Ru(0001) has been studied using RAIRS, LEED, EELS, and XPS.53,54 With increasing coverage ordered overlayers emerge, starting from a (2 × 2) and followed by a (1.5 × 1.5) structure, corresponding to coverages of 0.25 monolayers (ML) and 0.44 ML, respectively.53,54 No clear characterization was possible at the higher coverages.53,54 For Si coverage above 0.25 ML a degree of surface mixing was reported53,54 and appears to accord with interface studies.43,50–52 However, the nature of the mixed layer is challenging to quantify and, as such, merits further investigation.
Using density functional theory (DFT) we investigate Si defects in bulk Ru to identify the possible incorporation geometries. These defects are then considered at all symmetry unique positions ranging from the bulk to the near Ru(0001) surface, and finally on-surface adsorption of Si atoms. The low energy configurations and adsorption sites for Si adatoms are subsequently used to explore the energetics of Si-layer formation as a function of coverage. These results are compared to and contrasted against the RuxOy system, allowing the relative stability of the forming layers to be understood and the growth modes elucidated. In situ XPS is used to characterize the forming silicide and verify the trend predicted by comparing the coverage dependent incorporation energies for Si and O.
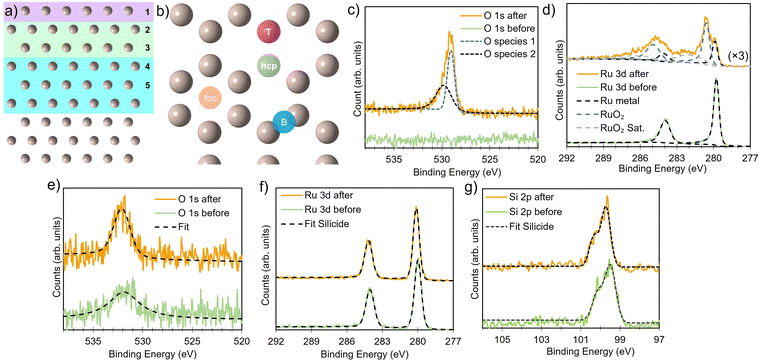
All DFT simulations were performed spin-polarized at the Γ-point using the CP2K software package,55 employing DZVP-SR-MOLOPT basis sets56 and Goedecker–Teter–Hutter (GTH) pseudopotentials.57,58 Energy cutoffs were set to 850 Ry and 60 Ry for the relative cutoff, to give precision of 0.1 meV per atom. The pristine bulk structures were modeled as a 6 × 6 × 5 expansion of the primitive hexagonal cell and a 6 × 3 × 5 orthohexagonal cell, with both lattice vectors and ion positions relaxed (for defect and surface calculations, only the ion positions were relaxed). Atomic structures were visualized using VESTA.59 The surface was constructed by adding a converged vacuum slab of 20 Å along the surface normal in the z-direction and maintained for all structures. A 9-layers Ru surface slab was sufficient to allow the bulk defect geometries and formation energies (see Fig. 1a) to be recovered at the center of the slab (vide infra). The Perdew–Burke–Ernzerhof (PBE) functional,60,61 with D3-BJ dispersion correction62–64 was used for all systems, self consistent field energy set at 1 × 10−7 eV for energy and 0.005 eV Å−1 for forces.
Average defect formation energies (Eform) were calculated per atom according to
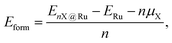 | (1) |
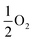 , respectively. Eqn (1) equally captures surface adsorption, where ad-atoms adsorbed on ruthenium slabs (with corresponding total energies EnX@Ru and ERu) constitute the equivalent of the bulk defects. By convention the surface coverage is referenced to hcp sites of Ru(0001) (see Fig. 1b), with one monolayer corresponding to a (1 × 1) overlayer structure with all hcp sites being occupied. Linking to structures reported in the literature, ordered overlayer structures corresponding to coverages below 1 ML are denoted by Wood's (A × B) notation commonly used in surface science.65 Finally, the configurational space was explored by an initial symmetry adapted enumeration of Si at the hcp and the sub-surface SiOcti site, based upon an expansion of the 1 × 1 hexagonal cell. The initial structures are expanded and then undergo geometry optimization, following the approach from our previous work.66–69 This approach produced a screening set of 252 structures with coverages ranging from (6 × 6)/0.03 ML to 2 ML. After geometry optimization the structures were further classified as mixed Ru–Si (RuxSiy), where Ru and Si share a given layer as defined by the z-coordinate or layered Ru–Si (Si–Ru–Si) where Ru/Si are segregated by z-coordinate.
, respectively. Eqn (1) equally captures surface adsorption, where ad-atoms adsorbed on ruthenium slabs (with corresponding total energies EnX@Ru and ERu) constitute the equivalent of the bulk defects. By convention the surface coverage is referenced to hcp sites of Ru(0001) (see Fig. 1b), with one monolayer corresponding to a (1 × 1) overlayer structure with all hcp sites being occupied. Linking to structures reported in the literature, ordered overlayer structures corresponding to coverages below 1 ML are denoted by Wood's (A × B) notation commonly used in surface science.65 Finally, the configurational space was explored by an initial symmetry adapted enumeration of Si at the hcp and the sub-surface SiOcti site, based upon an expansion of the 1 × 1 hexagonal cell. The initial structures are expanded and then undergo geometry optimization, following the approach from our previous work.66–69 This approach produced a screening set of 252 structures with coverages ranging from (6 × 6)/0.03 ML to 2 ML. After geometry optimization the structures were further classified as mixed Ru–Si (RuxSiy), where Ru and Si share a given layer as defined by the z-coordinate or layered Ru–Si (Si–Ru–Si) where Ru/Si are segregated by z-coordinate.
Ruthenium silicide thin films were prepared in ultra-high vacuum using pulsed laser deposition (PLD) of 30 nm thick Ru layers from a Ru target on Si(100) single crystals with a native oxide.46,47 After deposition in an atmosphere of 4 × 10−2 mbar of Ar, the samples were annealed in situ at 550 °C, resulting predominantly in Ru2Si3. Surface composition and oxidation state were analyzed before and after annealing and monitored in situ at elevated temperature in an oxygen environment. Near-ambient pressure XPS employing a Scienta Omicron HiPP-3 electron analyzer with a 1 mm entrance slit setting and a 0.8 mm cone opening was used. Oxygen dosing was controlled via a high-precision leak valve, and pressures were monitored using a Pfeiffer cold cathode vacuum gauge. XPS peak fitting was performed using the software KolXPD, with Shirley background and Voigt peaks for the core levels, and a Doniach–Sunjic function convoluted with a Gaussian for the metallic Ru peak (Fig. 1d).
In bulk ruthenium, Si can either be incorporated at a Ru-site (substitutional defect SiRu) or at an interstitial position (interstitial defect Sii) as shown in Fig. 2. The lowest formation energies are −1.7 eV and 3.5 eV, respectively, with the SiRu being substantially more favored. The substitutional SiRu defect is energetically favored with Si readily accommodated at the Ru lattice site with negligible distortion. The coordination is maintained with a 0.03 Å deviation with respect to the defect free Ru-site. A charge transfer from Ru to Si results in a Mulliken charge of qMul = −0.20, predominantly via donation from the first coordination shell.
 | ||
| Fig. 2 The associated formation energies for the SiRu, Sii, and VRu defects in each of the indicated layers (Fig. 1a). Purple shaded area indicates surface layer, green sub-surface, and blue bulk. Grey spheres are Ru and dark blue Si. | ||
There are two Sii sites: octahedral (Eform(SiOcti) = 3.5 eV) or tetrahedral (Eform(SiTeti) = 4.0 eV). The distortion induced by the incorporation of the large Si atom results in a significant relaxation in the surrounding Ru extending out to the next-neighbor shell driving the significant Eform resulting in a Sii bulk defect concentration of effectively zero under equilibrium conditions. For SiOcti the octahedral symmetry is distorted by a shift of the Si-atom along the [0001] crystallographic direction resulting in 3 × 2.10 Å and 3 × 2.35 Å Ru–Si separations. The steric crowding is more pronounced for SiTeti (3 × 2.16 Å and 1 × 2.09(9) Å), driving a more dramatic distortion, as expressed in the less favorable Eform. In both cases, and in contrast to SiRu charge transfer is from the Si to the neighboring Ru in the first coordination shell resulting in Mulliken charges of qMul(SiOcti) = +0.31 and qMul(SiTeti) = +0.24, accompanied by compensating negative charges on the six and four neighboring Ru, respectively.
To evaluate the energetic impact of defects transitioning from the bulk to the Ru(0001) surface, the formation energies of a ruthenium vacancy (VRu), Sii (in tetrahedral and octahedral symmetry sites) and SiRu defects were calculated within the first five layers (Fig. 2). Defects placed in the fifth layer recover the bulk defect formation energy and geometry. Interestingly and perhaps not unexpectedly the defects are more energetically favorable at the surface when compared to the bulk. The SiRu defect exhibits a smaller energetic preference for the surface, being 0.8 eV more favorable, underscoring its ease of incorporation. The VRu shows a similar trend albeit from a significantly higher formation energy that the SiRu. In contrast, the Sii defect shows substantial energy reductions of 1.87 eV and 1.98 eV for the tetrahedral and octahedral sites, respectively, from the fifth to the third layer. The energy difference of approximately 0.5 eV between these interstitial sites is maintained until the second layer, where the defects become energetically equivalent due to isostructural relaxation, resulting in the displacement of a Ru atom to form a Ruad adatom and accommodate SiRu at the surface. At the surface layer, both SiOcti and SiTeti relax to form Si adatoms (Siad) at fcc and hcp sites, respectively. Interstitial Ru defects (Rui) were examined, but were found to have a formation energy of 8.35 eV in the bulk so was not considered in the surface study. Similar to other well-studied adsorbates like O28,30,32,70 and N70–72 on Ru(0001), the hcp site is the lowest energy adsorption site, with the fcc site being 0.32 eV higher in energy.
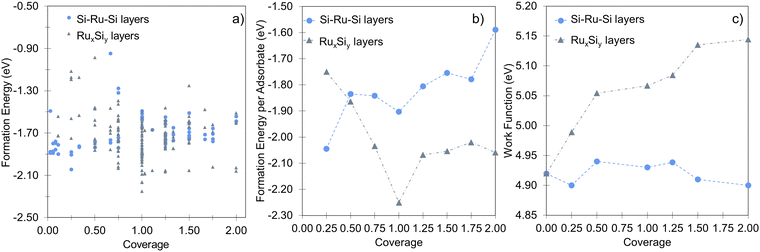
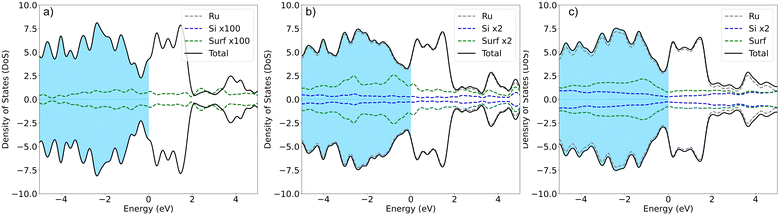
In agreement with previous experimental studies53,54 Si uptake upon prolonged exposure progresses via a number of ordered surface adsorption phases, with the (2 × 2) being most favored at low Si-coverages (Fig. 3a, blue circle at 0.25 ML). Focusing on the energetically most favorable structures shown in Fig. 3a, taken separately for the two different modes of adsorption at each coverage, results in Fig. 3b. The forming Si-layer shows a propensity for mixing and at a Si-coverage of 0.5 ML the mixed layer becomes isoenergetic with the surface adsorbed layer (Fig. 3b). As the Si concentration increases the mixed phases become dramatically more favored for coverages up to 1 ML, which represents a mixed stoichiometric-RuSi layer. Above 1 ML, the Eform shows a negligible decrease as the Si concentration increases to 2 ML. Interestingly, the work function (WF) is broadly insensitive to Si coverage (Fig. 3c) with the Si–Ru–Si layer showing only a small variation and no meaningful change in WF compared to the clean Ru(0001) (4.92 eV), to 2 ML Si coverage (4.90 eV). The shift is more pronounced for the mixed layers with a WF of 5.14 eV at 2 ML, which is already approaching that of RuSi (5.2 eV). In both cases, the WF shift is far less dramatic than reported (2.5 eV) for the oxidation of Ru(0001).28 A similar trend is seen in the DoS with extensive hybridisation between the Ru-d and the Si-p states which is apparent from the single Si-adsorption forward. The surface states are initially predominately Si-character (Fig. 4a) becoming increasingly mixed character (Fig. 4b and c).
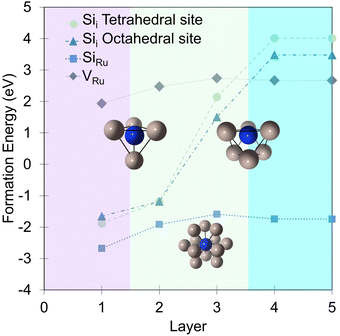
In that vein, it is instructive to compare the exposure of Ru(0001) to silicon with oxygen in more detail based on energetics that are important for the interface and overlayer formation. Oxygen structures were sampled from 0 to 2 ML, adopting the same methodology used for Si. These results accord well with the previous studies of Reuter and co-workers.27–29Fig. 5a illustrates the formation energy per Si and O atom across varying coverages, while Fig. 5b shows the relative energies for RuxSiy and RuxOy as a function of coverage. Notably, no stable mixed Ru–O configurations are found. Instead, oxide growth follows a layered structure, favoring the Oi configuration over ORu + Ruad. Below 1 ML, O-layer formation is significantly favored, decreasing in stability by +0.6 eV per atom up to 1 ML. Above 1 ML, the RuxSiy and RuxOy structure become isoenergetic and above 1.25 ML, RuxSiy is favored (Fig. 5b). The Eform for RuxSiy structures is largely independent of coverage, highlighting the limited interaction between neighboring Si as described for the single atom. For RuxOy, the opposite is true, with a significant lateral interaction (≈+0.35 eV). This interaction is comprised of both Coulombic repulsion between neighboring oxygen anions and significant lateral strain induced by local relaxation. Secondly, the negligible Si–Si interaction and the propensity to form mixed layers stabilize the forming silicide, resulting in a reduction ΔEform = −0.2 eV per atom as shown in Fig. 3a, whereas the O-layer shows an increase in ΔEform = +1.75 eV per atom over the same coverage range (Fig. 5a). The result is shown in Fig. 5b, below 1.0 ML the O-layer is favored above 1.25 ML RuxSiy is favored.
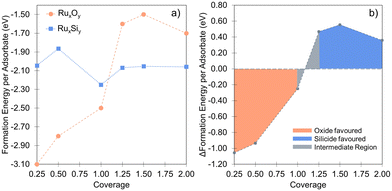 | ||
| Fig. 5 (a) Comparison between the coverage dependence of the formation energies for Si and O adlayers. For each coverage, the Si points are the lowest energy configurations from Fig. 3a. The difference of formation energies between Si and O adlayers are plotted in (b), visualizing the coverage dependent stability of the two systems with respect to each other. | ||
It is important to note that the energetic treatment presented here neglects the kinetics inherent in the process, which may play an important role. Hence, this approach should only be used as an initial screen with further theoretical or experimental investigation required to confirm the prediction. To verify whether the growth kinetics inherent in the process play an important role, the predicted stability of RuxSiy with respect to RuO2 formation is investigated experimentally by means of in situ XPS (Fig. 6a). The response of polycrystalline Ru and RuxSiy layers upon annealing in an oxidizing atmosphere is measured. Fig. 6 shows the variation in oxygen content over time at 340 °C under 1 × 10−4 mbar of O2. For polycrystalline Ru, rapid oxidation is observed, reaching a saturation level slightly above 60% (Fig. 6b). This is indicative of the formation of a RuO2 overlayer with a thickness of several nanometers. In contrast, under the same conditions, the RuSi layer exhibits remarkable stability, with only a marginal increase in oxygen content (≈5%) after an hour of annealing. Based on the unchanged peak positions and peak shapes of the Si 2p and Ru 3d core level spectra, this minimal change is interpreted as surface decoration rather than substantive oxidation. Hence, providing confirmation of the oxidation stability of RuxSiy predicted by DFT calculations extends to the macroscale. Furthermore, the lack of subsurface oxygen accords with the energetic trends predicted from our DFT calculations, and aligns with previously reported EELS and SIMS measurements where O was only found at the RuxSiy surface.50
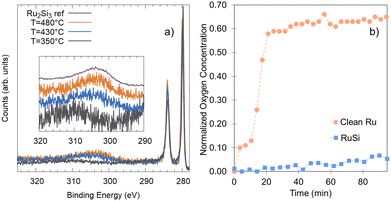 | ||
| Fig. 6 (a) Ru 3d XPS characterization of the silicide formation as a function of temperature, performed in situ during heating and referenced to Ru2Si3 previously described.46 (b) Comparison of the oxygen uptake of a clean Ru-surface (orange circles) and a RuxSiy-surface (blue squares) at 340 °C in 1 × 10−4 mbar of O2 based on the relative oxygen content measured by XPS. | ||
Employing DFT, the energetic drivers for the formation of RuxSiy films were described, and the structure-coverage relationship elucidated. Our analysis revealed the facile mixing behavior between Ru and Si, which becomes increasingly energetically favored above 0.5 ML, driving the formation of the RuxSiy observed by in situ XPS. The suitability of RuxSiy layers to act as a protective layer for Ru was investigated by comparing the relative stabilities of the oxide and silicide. Importantly, we demonstrated that for coverages above 1 ML, silicide formation becomes increasingly energetically favored with respect to the oxide. The postulated effectiveness of RuxSiy in preventing the formation of RuO2 has also been verified by in situ XPS measurements. Together, the DFT calculations and XPS measurements provide a comprehensive validation of RuxSiy's oxidation stability, bridging atomic-scale stability predictions with macroscale experimental confirmation under near-ambient conditions. Furthermore, the methodologies applied here offer a convenient framework for the initial screening of surface layer formation and associated stability prior to more detailed computational characterisation and experimental testing. The insights gained from this study could guide the design of more robust and oxidation-resistant Ru-based materials for applications where long-term stability is paramount.
Author contributions
JC: conceptualisation, formal analysis, investigation, methodology, validation, visualisation, writing – original draft preparation. SvV: formal analysis, investigation, validation, visualisation, writing – review & editing. JM: funding acquisition, project administration, resources, supervision, writing – review & editing. RB: funding acquisition, project administration, resources, supervision, writing – review & editing. EO: conceptualisation, funding acquisition, investigation, methodology, project administration, resources, supervision, writing – original draft preparation, writing – review & editing.Data availability
The datasets generated during the current study are publicly available via a Zenodo repository at https://doi.org/10.5281/zenodo.12604806.Conflicts of interest
There are no conflicts to declare.Acknowledgements
This work was conducted at the Advanced Research Center for Nanolithography, a public–private partnership between the University of Amsterdam, Vrije Universiteit Amsterdam, University of Groningen, the Dutch Research Council (NWO), and the semiconductor equipment manufacturer ASML. This work made use of the Dutch national e-infrastructure with the support of the SURF Cooperative using grant no. EINF-2434 and EINF-5451. The authors thank SURF (https://www.surf.nl) for the support in using the Lisa Compute Cluster and National Supercomputer Snellius. E. O. is grateful for a WISE Fellowship from the NWO. J. M. and E. O. acknowledge support via Holland High Tech through a public–private partnership in research and development within the Dutch top sector of High-Tech Systems and Materials (HTSM).Notes and references
- M. R. Axet and K. Philippot, Chem. Rev., 2020, 120, 1085–1145 CrossRef CAS.
- H. Over, Chem. Rev., 2012, 112, 3356–3426 CrossRef CAS PubMed.
- V. V. Ordomsky, A. Y. Khodakov, B. Legras and C. Lancelot, Catal. Sci. Technol., 2014, 4, 2896–2899 RSC.
- D. L. King, J. Catal., 1978, 51, 386–397 CrossRef CAS.
- H. Mortensen, L. Diekhöner, A. Baurichter, E. Jensen and A. C. Luntz, J. Chem. Phys., 2000, 113, 6882–6887 CrossRef CAS.
- S. Dutta, S. Kundu, A. Gupta, G. Jamieson, J. F. G. Granados, J. Bömmels, C. J. Wilson, Z. Tokei and C. Adelmann, IEEE Electron Device Lett., 2017, 38, 949–951 CAS.
- L. G. Wen, P. Roussel, O. V. Pedreira, B. Briggs, B. Groven, S. Dutta, M. I. Popovici, N. Heylen, I. Ciofi, K. Vanstreels, F. W. Østerberg, O. Hansen, D. H. Petersen, K. Opsomer, C. Detavernie, C. J. Wilson, S. V. Elshocht, K. Croes, J. Bömmels, Z. Tökei and C. Adelmann, ACS Appl. Mater. Interfaces, 2016, 8, 26119–26125 CrossRef CAS PubMed.
- R. Bernasconi and L. Magagnin, J. Electrochem. Soc., 2019, 166, D3219–D3225 CrossRef CAS.
- K. Y. Mun, T. E. Hong, T. Cheon, Y. Jang, B. Y. Lim, S. Kim and S. H. Kim, Thin Solid Films, 2014, 562, 118–125 CrossRef CAS.
- S. Bajt, Z. R. Dai, E. J. Nelson, M. A. Wall, J. B. Alameda, N. Q. Nguyen, S. L. Baker, J. C. Robinson, J. S. Taylor, A. Aquila and N. V. Edwards, J. Micro/Nanolithogr., MEMS, MOEMS, 2006, 5, 023004 CrossRef.
- S. B. Hill, I. Ermanoski, C. Tarrio, T. B. Lucatorto, T. E. Madey, S. Bajt, M. Fang and M. Chandhok, Critical parameters influencing the EUV-induced damage of Ru-capped multilayer mirrors, 2007, p. 65170G Search PubMed.
- T. E. Madey, N. S. Faradzhev, B. V. Yakshinskiy and N. V. Edwards, Appl. Surf. Sci., 2006, 253, 1691–1708 CrossRef CAS.
- L. Belau, J. Y. Park, T. Liang, H. Seo and G. A. Somorjai, J. Vac. Sci. Technol., B, 2009, 27, 1919–1925 CrossRef CAS.
- E. Louis, A. E. Yakshin, T. Tsarfati and F. Bijkerk, Prog. Surf. Sci., 2011, 86, 255–294 CrossRef CAS.
- J. Y. Park, L. Belau, H. Seo and G. A. Somorjai, J. Vac. Sci. Technol., B, 2011, 29, 041602 CrossRef.
- J.-H. Ahn, W.-J. Lee and H.-G. Kim, Mater. Lett., 1999, 38, 250–253 CAS.
- Y. B. He, A. Goriachko, C. Korte, A. Farkas, G. Mellau, P. Dudin, L. Gregoratti, A. Barinov, M. Kiskinova, A. Stierle, N. Kasper, S. Bajt and H. Over, J. Phys. Chem. C, 2007, 111, 10988–10992 CrossRef CAS.
- A. Basu, R. Hennessy, G. Adams and N. McGruer, Reliability in hot switched ruthenium on ruthenium MEMS contacts, 2013 Search PubMed.
- E. A. Smirnova, A. V. Miakonkikh, A. E. Rogozhin and K. V. Rudenko, Atomic layer deposition of Ruthenium on different interfaces for an advanced metallization system of ICs, 2020 Search PubMed.
- E. V. Jelenkovic, K. Tong, W. Cheung and S. Wong, Microelectron. Reliab., 2003, 43, 49–55 CrossRef CAS.
- A. Jadon, C. Rossi, M. Djafari-Rouhani, A. Estève and D. Pech, Phys. Open, 2021, 7, 100059 CrossRef CAS.
- A.-M. El-Sayed, M. B. Watkins, T. Grasser, V. V. Afanas’ev and A. L. Shluger, Phys. Rev. Lett., 2015, 114, 115503 CrossRef PubMed.
- A.-M. El-Sayed, Y. Wimmer, W. Goes, T. Grasser, V. V. Afanas’ev and A. L. Shluger, Phys. Rev. B: Condens. Matter Mater. Phys., 2015, 92, 014107 CrossRef.
- J. Cottom, L. Hückmann, E. Olsson and J. Meyer, J. Phys. Chem. Lett., 2024, 15, 840–848 CrossRef CAS PubMed.
- T. Tsarfati, E. Zoethout, R. van de Kruijs and F. Bijkerk, Surf. Sci., 2009, 603, 1041–1045 CrossRef CAS.
- J. C. Goritzka, B. Herd, P. P. T. Krause, J. Falta, J. I. Flege and H. Over, Phys. Chem. Chem. Phys., 2015, 17, 13895–13903 RSC.
- K. Reuter and M. Scheffler, Surf. Sci., 2001, 490, 20–28 CrossRef CAS.
- K. Reuter, M. V. Ganduglia-Pirovano, C. Stampfl and M. Scheffler, Phys. Rev. B: Condens. Matter Mater. Phys., 2002, 65, 165403 CrossRef.
- K. Reuter and M. Scheffler, Phys. Rev. Lett., 2003, 90, 046103 CrossRef PubMed.
- C. Stampfl, S. Schwegmann, H. Over, M. Scheffler and G. Ertl, Phys. Rev. Lett., 1996, 77, 3371–3374 CrossRef CAS.
- C. Stampfl and M. Scheffler, Phys. Rev. B: Condens. Matter Mater. Phys., 1996, 54, 2868–2872 CrossRef CAS.
- C. Stampfl, Phase Transitions, 2007, 80, 311–332 CrossRef CAS.
- R. Blume, H. Niehus, H. Conrad and A. Böttcher, J. Phys. Chem. B, 2004, 108, 14332–14339 CrossRef CAS.
- J. I. Flege, J. Hrbek and P. Sutter, Phys. Rev. B: Condens. Matter Mater. Phys., 2008, 78, 165407 CrossRef.
- B. Herd and H. Over, Surf. Sci., 2014, 622, 24–34 CrossRef CAS.
- A. Böttcher, H. Conrad and H. Niehus, J. Chem. Phys., 2000, 112, 4779–4787 CrossRef.
- J. I. Flege, J. Lachnitt, D. Mazur, P. Sutter and J. Falta, Phys. Chem. Chem. Phys., 2016, 18, 213–219 RSC.
- J. B. Berkowitz-Mattuck and R. R. Dils, J. Electrochem. Soc., 1965, 112, 583 CrossRef CAS.
- H. Jiang, C. Petersson and M.-A. Nicolet, Thin Solid Films, 1986, 140, 115–130 CrossRef CAS.
- S. P. Murarka, Annu. Rev. Mater. Res., 1983, 13, 117–137 CrossRef CAS.
- M. E. Schlesinger, Chem. Rev., 1990, 90, 607–628 CrossRef CAS.
- R. Mitra, Int. Mater. Rev., 2006, 51, 13–64 CrossRef CAS.
- Y. Matsui, Y. Nakamura, Y. Shimamoto and M. Hiratani, Thin Solid Films, 2003, 437, 51–56 CrossRef CAS.
- A. Bahr, S. Richter, R. Hahn, T. Wojcik, M. Podsednik, A. Limbeck, J. Ramm, O. Hunold, S. Kolozsvári and H. Riedl, J. Alloys Compd., 2023, 931, 167532 CrossRef CAS.
- C. Zhang, X. Kuang, Y. Jin, C. Lu, D. Zhou, P. Li, G. Bao and A. Hermann, ACS Appl. Mater. Interfaces, 2015, 7, 26776–26782 CrossRef CAS.
- S. van Vliet, A. Troglia, E. Olsson and R. Bliem, Appl. Surf. Sci., 2023, 608, 155139 CrossRef CAS.
- A. Troglia, S. van Vliet, G. Yetik, I. E. Wakil, J. Momand, B. J. Kooi and R. Bliem, Phys. Rev. Mater., 2022, 6, 043402 CrossRef CAS.
- Y. He, T.-L. Wang, M. Zhang, T.-W. Wang, L.-F. Wu, L. Zeng, X. Wang, M. Boubeche, S. Wang, K. Yan, S.-H. Lin and H. Luo, Small, 2021, 17, 2006153 CrossRef CAS.
- L. Perring, F. Bussy, J. Gachon and P. Feschotte, J. Alloys Compd., 1999, 284, 198–205 CrossRef CAS.
- E. V. Jelenković, S. To, M. Blackford, O. Kutsay and S. K. Jha, Mater. Sci. Semicond. Process., 2015, 40, 817–821 CrossRef.
- R. Coloma-Ribera, R. W. V. D. Kruijs, S. Kokke, E. Zoethout, A. E. Yakshin and F. Bijkerk, Appl. Phys. Lett., 2014, 105, 131601 CrossRef.
- R. C. Ribera, R. W. V. D. Kruijs, A. E. Yakshin and F. Bijkerk, J. Appl. Phys., 2015, 118, 055303 CrossRef.
- Z. H. Lu, T. K. Sham, P. R. Norton and K. H. Tan, Appl. Phys. Lett., 1991, 58, 161–163 CrossRef CAS.
- M. A. Chesters and A. B. Horn, J. Phys.: Condens. Matter, 1991, 3, S251 CrossRef CAS.
- T. D. Kühne, M. Iannuzzi, M. Del Ben, V. V. Rybkin, P. Seewald, F. Stein, T. Laino, R. Z. Khaliullin, O. Schütt, F. Schiffmann, D. Golze, J. Wilhelm, S. Chulkov, M. H. Bani-Hashemian, V. Weber, U. Borštnik, M. Taillefumier, A. S. Jakobovits, A. Lazzaro, H. Pabst, T. Müller, R. Schade, M. Guidon, S. Andermatt, N. Holmberg, G. K. Schenter, A. Hehn, A. Bussy, F. Belleflamme, G. Tabacchi, A. Glöβ, M. Lass, I. Bethune, C. J. Mundy, C. Plessl, M. Watkins, J. VandeVondele, M. Krack and J. Hutter, J. Chem. Phys., 2020, 152, 194103 CrossRef PubMed.
- J. VandeVondele and J. Hutter, J. Chem. Phys., 2007, 127, 114105 CrossRef PubMed.
- S. Goedecker, M. Teter and J. Hutter, Phys. Rev. B: Condens. Matter Mater. Phys., 1996, 54, 1703–1710 CrossRef CAS.
- C. Hartwigsen, S. Goedecker and J. Hutter, Phys. Rev. B: Condens. Matter Mater. Phys., 1998, 58, 3641–3662 CrossRef CAS.
- K. Momma and F. Izumi, J. Appl. Crystallogr., 2011, 44, 1272–1276 CrossRef CAS.
- J. P. Perdew, K. Burke and M. Ernzerhof, Phys. Rev. Lett., 1996, 77, 3865–3868 CrossRef CAS.
- J. P. Perdew, K. Burke and M. Ernzerhof, Phys. Rev. Lett., 1997, 78, 1396 CrossRef CAS.
- S. Grimme, J. Antony, T. Schwabe and C. Mück-Lichtenfeld, Org. Biomol. Chem., 2007, 5, 741–758 RSC.
- S. Grimme, S. Ehrlich and L. Goerigk, J. Comput. Chem., 2011, 32, 1456 CrossRef CAS PubMed.
- E. R. Johnson and A. D. Becke, J. Chem. Phys., 2006, 124, 174104 CrossRef.
- E. A. Wood, J. Appl. Phys., 1964, 35, 1306–1312 CrossRef CAS.
- J. Cottom, A. Bochkarev, E. Olsson, K. Patel, M. Munde, J. Spitaler, M. N. Popov, M. Bosman and A. L. Shluger, ACS Appl. Mater. Interfaces, 2019, 11, 36232–36243 CrossRef CAS PubMed.
- E. Olsson, J. Cottom, X. Aparicio-Anglès and N. H. de Leeuw, Phys. Chem. Chem. Phys., 2019, 21, 9407–9418 Search PubMed.
- E. Olsson, J. Cottom and Q. Cai, Small, 2021, 17, 2007652 CrossRef CAS PubMed.
- E. Olsson, J. Cottom, H. Alptekin, H. Au, M. Crespo-Ribadeneyra, M.-M. Titirici and Q. Cai, Small, 2022, 18, 2200177 CrossRef CAS.
- J. A. Herron, S. Tonelli and M. Mavrikakis, Surf. Sci., 2013, 614, 64–74 CrossRef CAS.
- S. Schwegmann, A. Seitsonen, H. Dietrich, H. Bludau, H. Over, K. Jacobi and G. Ertl, Chem. Phys. Lett., 1997, 264, 680–686 CrossRef CAS.
- H. Shi, K. Jacobi and G. Ertl, J. Chem. Phys., 1993, 99, 9248–9254 CrossRef CAS.
| This journal is © the Owner Societies 2024 |