Unlocking the potential: machine learning applications in electrocatalyst design for electrochemical hydrogen energy transformation

Abstract

Machine learning (ML) is rapidly emerging as a pivotal tool in the hydrogen energy industry for the creation and optimization of electrocatalysts, which enhance key electrochemical reactions like the hydrogen evolution reaction (HER), the oxygen evolution reaction (OER), the hydrogen oxidation reaction (HOR), and the oxygen reduction reaction (ORR). This comprehensive review demonstrates how cutting-edge ML techniques are being leveraged in electrocatalyst design to overcome the time-consuming limitations of traditional approaches. ML methods, using experimental data from high-throughput experiments and computational data from simulations such as density functional theory (DFT), readily identify complex correlations between electrocatalyst performance and key material descriptors. Leveraging its unparalleled speed and accuracy, ML has facilitated the discovery of novel candidates and the improvement of known products through its pattern recognition capabilities. This review aims to provide a tailored breakdown of ML applications in a format that is readily accessible to materials scientists. Hence, we comprehensively organize ML-driven research by commonly studied material types for different electrochemical reactions to illustrate how ML adeptly navigates the complex landscape of descriptors for these scenarios. We further highlight ML's critical role in the future discovery and development of electrocatalysts for hydrogen energy transformation. Potential challenges and gaps to fill within this focused domain are also discussed. As a practical guide, we hope this work will bridge the gap between communities and encourage novel paradigms in electrocatalysis research, aiming for more effective and sustainable energy solutions.

---

Rui Ding

Rui Ding is a Wendy and Schmidt AI in Science Postdoctoral Fellow at the University of Chicago under Junhong Chen and Yuxin Chen's guidance. Ding received a bachelor's degree from Nanjing University in China, and also a PhD from Nanjing University with experience as a visiting exchange student in the Hong Kong University of Science and Technology. Ding's research projects mainly focused on exploring the cross-cutting field of machine learning with renewable energy material design and theoretical simulation (First principal simulation and quantum chemistry). Ding is familiar with both nanomaterial experimental synthesis and theoretical simulation, and notably machine learning. Ding has done a series of works that applied artificial intelligence to boost the design of membrane electrode assembly in Proton Exchange Membrane Fuel Cells (PEMFCs) and other works that utilize ML to investigate the system of PEM electrolyzers and CO2 reduction reaction electrocatalysts for the purpose of renewable energy.

Junhong Chen

Junhong Chen is currently a Crown Family Professor of Molecular Engineering at Pritzker School of Molecular Engineering at the University of Chicago and lead water strategist at Argonne National Laboratory. He received his PhD in mechanical engineering from the University of Minnesota in 2002. His research interest lies in molecular engineering of nanomaterials and nanodevices, particularly hybrid nanomaterials featuring rich interfaces and nanodevices for sustainable energy and environment. His approach is to combine multidisciplinary experiments with first-principles calculations to design and discover novel nanomaterials for engineering various sensing and energy devices with superior performance.

Yuxin Chen

Yuxin Chen is an assistant professor of computer science at the University of Chicago. Previously, Chen was a postdoctoral scholar in the Department of Computing and Mathematical Sciences at the California Institute of Technology (Caltech). Prior to Caltech, he received his PhD in computer science from ETH Zurich in 2017. His research interest lies broadly in probabilistic reasoning and machine learning. He was a recipient of the Google European Doctoral Fellowship in Interactive Machine Learning, the Swiss SNSF Early Postdoc.Mobility Fellowship, and the PIMCO Postdoctoral Fellowship in Data Science.

Jianguo Liu

Jianguo Liu is a second-level professor and doctoral supervisor at the Institute of Innovative Research in Energy and Electric Power, North China Electric Power University. With a PhD from the Dalian Institute of Chemical Physics, Chinese Academy of Sciences, Liu's expertise lies in hydrogen energy and fuel cell technologies, focusing on novel electrocatalyst design, high-performance membrane electrode assemblies, and system integration for sustainable energy solutions. A recipient of the National Natural Science Second Prize and acknowledged as a national technology innovation leader, Liu has published over 120 SCI papers with significant citations. His contributions to hydrogen energy strategy and planning, along with his role in leading national research projects, establish him as a prominent figure in advancing the field of renewable energy.

Yoshio Bando

Yoshio Bando is a leading expert in nanomaterials and electron microscopy. He earned his PhD from Osaka University in 1975 and joined the National Institute for Research in Inorganic Materials (NIRIM). His international experience includes a visiting scientist position at Arizona State University (1979–1981). Bando has held key leadership roles at NIRIM and its successor, the National Institute for Materials Science (NIMS), such as Director-General of the International Center for Young Scientists and Deputy Director-General of the International Center for Materials Nanoarchitectonics (MANA). Since 2017, he has been an Executive Advisor at WPI-MANA, NIMS, and holds professorships in Australia and China, along with honorary positions at the University of Queensland and Wuhan University of Technology. His work has received numerous honors, including the Sacred Treasure from the Emperor of Japan in 2017 and multiple ISI Highly Cited Researcher awards in Materials Science.

Xuebin Wang

Xuebin Wang, from the School of Energy Science and Engineering at Nanjing University, obtained his bachelor and master's degrees at Nanjing University (2002–2009) and his PhD from Waseda University in 2013. Between 2010 and 2016, he worked at the National Institute for Materials Science (NIMS) in Japan, leading KAKENHI-funded projects. In 2015, he joined Nanjing University as a professor and principal investigator under the “Overseas High-level Talents” program. Wang's research focuses on two-dimensional functional materials, energy storage and conversion devices, composite materials, and catalysis. He has published over 50 articles in top journals like Nature Communications and Advanced Materials, with more than 5000 citations, and serves as a reviewer for prestigious journals including Nature Communications.

---

1. Introduction

Pressing environmental issues facing our planet such as climate change and the depletion of natural resources have created a global demand for clean and sustainable energy solutions. Hydrogen energy, known for its high energy density and minimal environmental impact, is gaining significant attention in the renewable energy sector as a clean and sustainable solution.¹ The efficiency of hydrogen-electricity mutual conversion technologies, such as fuel cells and electrolyzers, is crucial for determining the amount of energy that can be captured. These devices facilitate a two-way conversion process: fuel cells convert hydrogen's chemical energy into electrical power without emitting pollutants or greenhouse gases, which make them vital for generating clean electricity; conversely, electrolyzers use electrical power to split water into hydrogen and oxygen, offering a sustainable method to produce hydrogen fuel. Together, these devices play pivotal roles in building a sustainable energy system by efficiently transforming chemical energy into electrical energy and vice versa.² However, optimizing these systems to enable an energy-efficient, low-cost conversion is challenging. A wide array of parameters or descriptors are required to accurately capture simultaneous processes and complex interactions occurring across different scales, ranging from microscale surface chemical reactions and mesoscale mass transport to macroscale multiphysics coupling. Among the many challenges with optimization, designing an effective electrocatalyst is the most crucial. Electrocatalysts require large quantities of precious metals to accelerate the electrochemical reactions, particularly the hydrogen evolution reaction (HER) and oxygen evolution reaction (OER) for energy storage, and the hydrogen oxidation reaction (HOR) and oxygen reduction reaction (ORR)^3,4 for energy release. Hence, optimizing the electrocatalysts to reach a balance between economic viability and efficiency is critically important to the scalability of hydrogen-related systems.⁵ Electrocatalysts are one of the most widely studied components by researchers in hydrogen energy technologies.

Despite advances in materials science and electrochemistry, the conventional method of developing electrocatalysts is mostly dependent on time-consuming trial-and-error processes. Such processes, either experimental synthesis and evaluation or numerical simulation, heavily rely on the subjectivity and experience of researchers, and usually produce unsatisfying outcomes. Corresponding limited design spaces have resulted in costly and sluggish improvement of catalytic performances because of the inability of the traditional research paradigm to manage complex systems with a large number of variables. Thus, more effective methods are urgently needed in this labor-intensive field to more widely explore a greater variety of potential electrocatalyst candidates and optimal combinations.

The rapid evolution of artificial intelligence (AI) and machine learning (ML) has transformed various areas of human society. ML has shown its potency across various scientific domains including natural language processing (NLP),^6–8 computer vision,^9,10 and drug discovery^11,12 by revealing patterns and relationships in data that may be difficult through conventional analysis.¹³ In the field of hydrogen energy, ML is promising to reshape the development of electrocatalysts—traditionally guided by researcher intuition and subjectivity—by complementing or enhancing traditional computational and experimental approaches. Traditional theoretical simulation methods, while capable of predicting experimental outcomes often with a high degree of fidelity, are computationally intensive and often struggle with optimization tasks in high-dimensional parameter spaces requiring high-throughput calculations. For instance, using density functional theory (DFT) to screen for the optimal structure with the lowest reaction energy barrier might require thousands to millions of attempts to traverse all possible configurations—often prohibitive in computational resources. In contrast, ML-driven surrogate models, capable of processing vast, high-dimensional, multivariable datasets, can efficiently explore these vast spaces at significantly lower costs. These models accelerate brute force searches for optimal configurations and unveil innovative insights into catalyst behavior that traditional methods might overlook, such as correlation between material descriptors. Hence, they enhance both the speed and depth of insights in costly and time-consuming explorations like high-throughput experiments and DFT simulations.^14–17 This enables the rapid discovery of new optimal candidates, the improvement of existing candidates,^18,19 and the fine-tuning of catalytic performances, which are the core needs in the field. Despite the relatively recent application of ML in electrocatalyst research, with many studies predominantly utilizing “off-the-shelf” methodologies and algorithms, a practical, material-oriented perspective is essential to effectively implement ML in diverse material scenarios. Moreover, ML's ability to handle a wide range of input variables, from atomic-level descriptors to macroscale engineering factors, allows for a holistic optimization of catalytic systems. The interpretability and reliability of ML models is essential for deeper insights and thus can help to more effectively distinguish qualitatively and quantitatively the most decisive descriptors in a complex system and reveal the mechanisms of catalyst behavior.^20,21

This review offers comprehensive guidelines for materials scientists and engineers new to ML, specifically focusing on enhancing electrocatalyst designs for critical reactions such as HER, OER, HOR, and ORR. It categorizes ML-driven research by commonly studied material types such as metal alloys, 2D materials, and single-atom catalysts—providing clear material-oriented insights and facilitating connections between these materials and broader applications. This organizational approach not only elucidates the connection between material systems and their broader applications beyond hydrogen energy (Fig. 1) but also enhances understanding by detailing key novel material insights for each type of electrocatalyst. That is, for each category, we delve into the most frequently used ML algorithms and identify the critical parameters and descriptors—whether derived from experimental data or theoretical simulations—that serve as essential inputs for modeling these materials. This analysis helps chemists, materials scientists, and engineers grasp the most influential features in predicting the performance of electrocatalysts. This is especially helpful for hands-on practice by electrocatalyst researchers who are unfamiliar with ML, by facilitating their process in preparation of datasets correspondingly. Overall, this tailored breakdown makes ML applications more accessible, aiding materials scientists in understanding and applying ML techniques effectively. By summarizing descriptors and features commonly utilized in ML modeling, we also present the unique integration strategies with both theoretical and experimental approaches tailored to different material systems. This leads to a comprehensive understanding of how ML may be smoothly integrated at different fidelity levels into the design of electrocatalysts for hydrogen applications. Our in-depth discussion further examines current advancements and prospective avenues for future expansion of this rapidly changing research field, and inspects the challenges ahead, such as bridging fidelity gaps and facilitating knowledge integration. Conclusively, this review not only offers a systematic exploration of ML's transformative role in advancing electrocatalyst design for hydrogen energy transformation but also serves as a practical guide tailored specifically for electrocatalyst researchers. By demystifying ML applications through a reader-accessible material-based focus, we advocate for a paradigm shift toward more integrative, data-driven research approaches in this field and beyond.

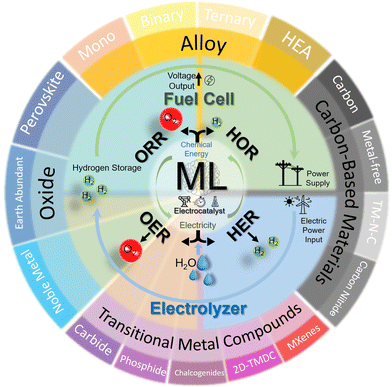Fig. 1 Schematic of the review scope for the electrocatalytic material systems covered in this work.

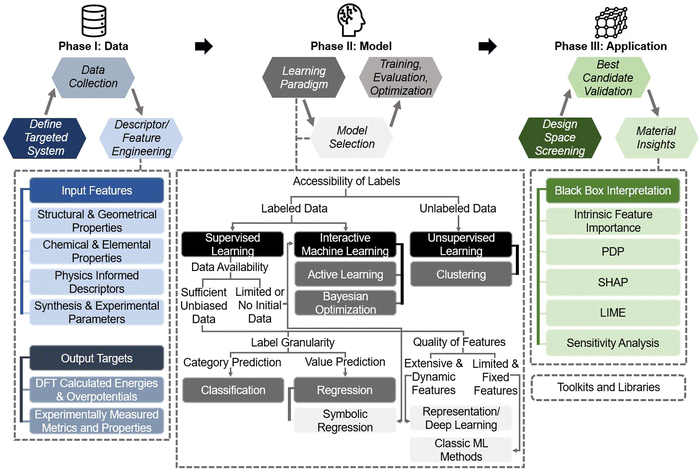
2. Practical machine learning pipeline for hydrogen electrocatalyst design

This section bridges the gap for materials scientists who are experienced in electrocatalysis but relatively new to ML. It provides a practical guide on applying ML techniques to explore design space and optimize electrocatalysts for HER, OER, HOR, and ORR. Since comprehensive ML concepts and tutorials are already well-documented,^22–25 we will adopt a more concise approach by following a typical pipeline (Fig. 2) that encapsulates the majority of ML studies in this field. The pipeline, simplified into three phases—Data, Model, and Application as shown in Fig. 2—begins with dataset construction, moves through ML surrogate model training, and culminates in identifying optimal electrocatalyst candidates and understanding impactful descriptors. We focus on the most commonly reported techniques and practically useful concepts, covering the majority of ML methods and models that appear in this specific field. These are the toolkits most likely to assist readers in solving their own electrocatalyst material system challenges and are presented with clarity, conciseness, and reader-friendliness. We aim to provide readers from the electrocatalyst community with a hands-on guide, enabling them to build datasets and use ML techniques efficiently in their material systems of interest.

Fig. 2 Pipeline for applying ML in electrocatalyst design: overview of the simplified three-phase pipeline (data, model, application) for applying ML techniques to electrocatalyst design in hydrogen energy systems. This pipeline covers the majority of the studies discussed in this review related to ML applications for HER, OER, HOR, and ORR electrocatalysts, with certain advanced methodologies or specific technologies omitted for conciseness and clarity.

2.1. Data

Successful ML models depend on quality and comprehensive data. In materials science, ML uses complex mathematical functions to identify patterns, mapping material descriptors to predict outputs. This capability is particularly valuable in the design and optimization of electrocatalysts for hydrogen energy applications. By learning from extensive datasets, ML models can quickly and accurately predict outcomes, offering a significant advantage over traditional theoretical simulations such as DFT or molecular dynamics (MD). These conventional methods involve solving complex quantum mechanical equations iteratively, such as the Kohn–Sham equations in DFT or the Newtonian equations of motion in MD, for each material configuration.²⁶ Such iterative processes require significant computational resources and time, making it impractical to efficiently explore the vast space of possible configurations.

ML models, once trained, are fast to execute and can conduct large-scale screenings of uncharted possibilities, making them invaluable as inexpensive surrogate tools in the material design space. However, data are needed in the first place for the targeted system. For instance, data derived from DFT calculations can be used to screen the best alloy compositions for optimal hydrogen species adsorption energy, where the configurations of nanoparticles related to composition play a pivotal role.²⁷ Similarly, experimental synthesis and evaluation data can significantly improve metrics like the half-wave potential in ORR for carbon-based catalysts.²⁸

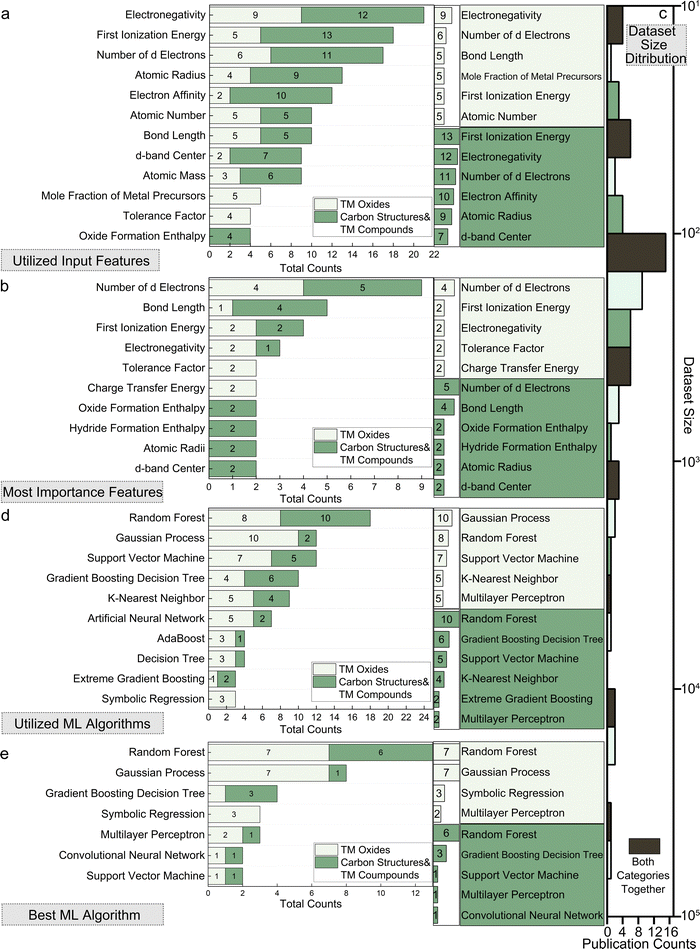
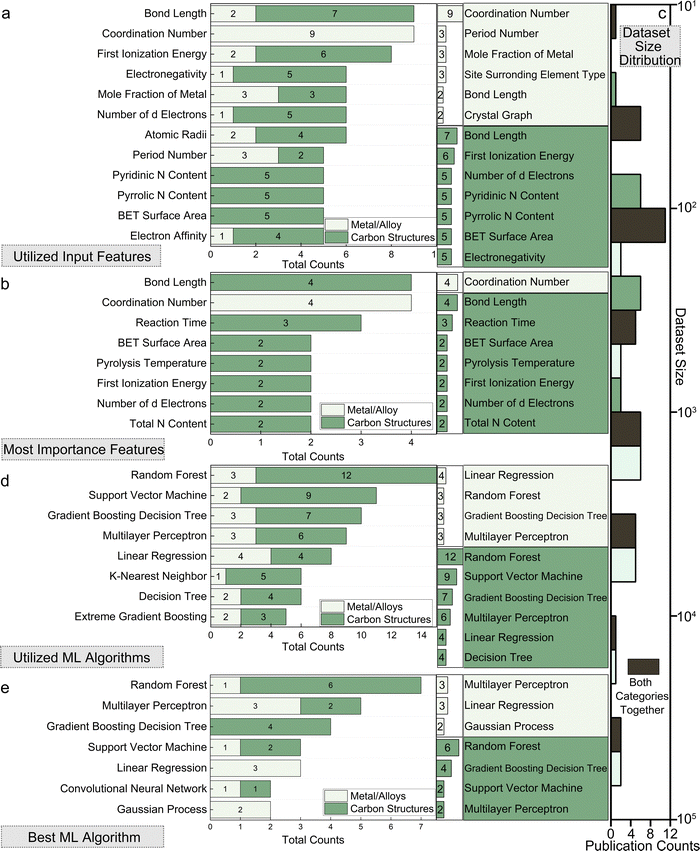
The importance of input features cannot be overstated, as they directly impact the model's performance and predictive accuracy. Poorly chosen or limited features may lack the necessary information about the material system, rendering even the best models unable to learn effectively. Conversely, an excessive number of features can lead to overfitting and increased computational complexity. Most current research still relies on customized, handcrafted features based on researchers’ subjective understanding of the targeted material systems. This domain-specific expertise has not been thoroughly summarized, highlighting a significant gap that this review aims to fill for reaching a consensus. By summarizing the general features used in current publications, we lay the groundwork for understanding the most effective descriptors for various material systems, which will be discussed in detail in the subsequent sections focused on HER, OER, HOR and ORR.

2.1.1. Input features. Considering the data collection costs—whether through computationally intensive DFT simulations or experimental methods, it is crucial to select the right features for the description of the targeted material system. Proper feature engineering ensures the model's accuracy, robustness, and cost-effectiveness. Here, we provide an overview of the types of features typically employed in electrocatalysts for HER, OER, HOR, and ORR, as reported so far.
2.1.1.1. Structural & geometrical properties. Structural and geometrical properties are foundational descriptors in the ML modeling of electrocatalysts, and are often theoretical simulation oriented. Describing the catalyst material via these features provide crucial information about the physical arrangement and spatial characteristics of atoms. Catalytic behavior is dependent on the micro-environment of the catalytic adsorption site, which implies that within the same simulated slab, different sites might exhibit different behaviors. Traditionally, a traversal is needed across sites such as surface hollow, bridge, and top sites, but now, if an ML model can learn how to map the local environment of a site with its DFT-calculated behavior, it can help us understand and screen electrocatalysts far more efficiently.

Typical structural and geometrical descriptors include bond lengths, bond angles, atomic radius, and coordination numbers. Bond length, defining the distance between bonded atoms, impacts electronic properties and reactivity. For example, transition metal (TM) atom bond lengths with adsorbates²⁹ or neighboring TM atoms³⁰ are used in predicting adsorption energies. Bond angles indicate adjacent bond angles around a central atom, for instance Fe–O–Fe³¹ angles. They influence surface-catalyst interaction strength. Atomic radii determine structural configurations, affecting how atoms pack and overall material geometry, often described through covalent, ionic, and van der Waals radius.^32,33 Coordination numbers, indicating nearest neighboring atoms around a catalytic site (or second nearest³⁴), are key in understanding local atomic environments and correlating with catalytic activity. In particular, unsaturated coordinated atoms are more active and can serve as reaction sites. Researchers would utilize these descriptors for micro-environment descriptions.

Besides these straightforward descriptors, there are other manual feature engineering techniques, such as direct one-hot encoding of atomic positions³⁵ and number of certain types of element atoms reflecting the local atomic environment,³⁶ which describe the immediate surroundings of atoms of the site. In general, comprehensive and appropriate descriptions of these structural and geometrical attributes are crucial for ML models to learn crystallographic knowledge.

2.1.1.2. Chemical & elemental properties. Building on the structural and geometrical descriptors, chemical and elemental properties further enrich the description of the catalyst's crystal structure by nuanced physical information of atoms. When combined, these descriptors provide a comprehensive view of the material, particularly from the theoretical simulation perspective like DFT simulations.

The Basic atomic properties are widely used in ML models for elemental descriptions, including electronegativity, ionization energy, atomic mass, group number, and periodic number, are crucial in determining material characteristics.^37,38 As TM elements are usually the studied target, d-orbital and valence electron characteristics hold significance, such as d-electron count, d-band center (ε_d), valence electron number, occupied and unoccupied d states near the Fermi level, and total d electrons. These features are critical in understanding catalytic behavior, influencing adsorption energies and reaction kinetics.^38–40 Electronic properties like electron affinity, charge transfer, and density of states (DOS) at the Fermi level provide insights into electronic behavior affecting catalytic performance. Local density of states (LDOS)⁴¹ and total band filling⁴² describe the electronic environment at catalytic sites, while charge distribution analyses like Bader charge analysis quantify electron density distribution, offering local electronic insights. Inputs like Bader charge at catalytic sites, charge transfers, and charge state variations are commonly used in related studies for electronic environment characterization.^43,44

Many studies use a combination of primary and derived features. For instance, a combination of primary atomic features (empirical radius, mass, electron affinity) and derived features (d-band center, formation energy of single-atom sites⁴⁰) provides a more comprehensive representation. The former features are directly available, and the later ones may require scenario-specific DFT calculations. Built on the foundation by geometrical and structural descriptors, these descriptors further provide detailed information about the material's electronic structure and local chemical environments of the catalytic sites.

2.1.1.3. Physics-informed descriptors. Beyond manual feature engineering, there are frameworks that automatically generate meaningful features from crystal structures. These descriptors represent both structural and chemical properties of materials in a physically informed manner, facilitating more efficient and accurate predictions with less requirement of user domain knowledge.

Descriptor generation methods generally transform atomic structures into fixed-size numerical fingerprints, capturing essential structural and chemical information.⁴⁵ These descriptors are designed to be physically meaningful and invariant to rotations and translations, providing a robust representation of the atomic environment. Among the representative popular methods, smooth overlap of atomic positions⁴⁶ (SOAP) captures local atomic density using Gaussian functions, many-body tensor representation⁴⁷ (MBTR) considers interactions at multiple levels, and atom-centered symmetry functions⁴⁸ (ACSF) encodes local atomic environments, all of which are particularly useful for modeling short-range atomic interactions such as adsorption energies and catalytic activities. These methods are recognized in the community as able to comprehensively represent both structural and chemical properties of the crystal structures.

Pre-built deep learning frameworks for solid systems automate feature extraction by directly accepting raw atomic structures as input. They handle both descriptor generation and supervised learning, using advanced neural network architectures to capture complex dependencies and interactions within crystal structures. Popular libraries include crystal graph convolutional neural networks⁴⁹ (CGCNN), which represents crystal structures as graphs, allowing the model to learn directly from the structure without manual feature engineering. SchNet⁵⁰ uses continuous filter convolutions to represent atoms and their interactions, providing a flexible and accurate representation of the atomic environment. SpinConv⁵¹ introduces spin convolutions to capture rotational invariance and angular dependencies in atomic interactions, achieving high performance on large-scale datasets. DimeNet++⁵² by Gasteiger et al., an advanced version of directional message passing neural network (DimeNet), excels at capturing angular dependencies in atomic interactions, crucial for modeling properties sensitive to atomic orientations. It also prioritizes computational efficiency for large datasets and complex systems. GemNet-OC,⁵³ a further advancement also by Gasteiger et al. in graph neural networks (GNNs) tailored for materials science, enhances traditional methods by incorporating directional information about atomic interactions, making it particularly effective for properties sensitive to relative atomic orientations like bond angles and torsional interactions. Recently, the community has proposed more state-of-the-art methods: MACE,⁵⁴ spherical channel network (SCN),⁵⁵ equivariant spherical channel network (eSCN),⁵⁶ neural equivariant interatomic potentials (NequIP),⁵⁷ equiformer V1⁵⁸/V2,⁵⁹ atomistic line graph neural network (ALIGNN),⁶⁰ crystal Hamiltonian graph neural network (CHGNet),⁶¹ Matformer,⁶² M3GNet.⁶³

These “off-the-shelf” deep learning libraries are recommended when feature customization needs are limited. They could automate feature extraction and eliminate the need for manual feature engineering and the use of other libraries. They are highly scalable for large datasets and complex systems. And their predefined architectures streamline the modeling process, making them efficient and user-friendly. In many communities, especially those focused on DFT and MD simulations, these frameworks are also referred to as ML potentials, as they serve as efficient surrogates for computationally expensive quantum mechanical calculations, enabling faster and more accurate simulations. In general, physics informed descriptors represent the current frontier methods that are preferred when the research fidelity is based on DFT simulations.

2.1.1.4. Synthesis & experimental parameters. Current studies involving experimental datasets for ML in hydrogen electrocatalysts, sourced through high-throughput experimentation or literature text mining, are generally more expensive. While DFT-based ML studies often handle higher-dimensional feature spaces due to complex electronic structures, experimental datasets tend to have lower dimensionality and smaller volumes. However, experimental studies offer higher fidelity with real-world performance observations compared to theoretical DFT-based approaches. These studies typically include not only chemical descriptors but also synthesis-related engineering parameters crucial for determining catalytic performance.

The experimental and synthesis-based parameters covered in this review include a wide range of features. These features comprise experimental observations like Tafel plots, mole fractions of metal precursors, and primary atomic characteristics such as empirical radius, mass, electron affinity, ionization energy, and density. Additionally, empirical synthesis parameters like annealing temperature, heating rate, hold time, and similar parameters for hydrothermal processes are crucial. Other important parameters include material characterization properties like lattice constant, crystal plane spacing, and morphology-related information.

Given the diversity in material systems and synthesis methods, establishing a universally recommended way of preparing experimental datasets is challenging. For instance, synthesis steps for alloys differ from those for 2D materials like MoS₂. Therefore, the preparation process must be tailored to the specific material system. However, a general approach involves systematically documenting and standardizing all relevant synthesis parameters and experimental conditions to ensure reproducibility and consistency across different studies. This comprehensive documentation enables the creation of high-fidelity datasets crucial for accurate prediction and optimization of electrocatalysts using ML.

2.1.2. Output targets. Output targets for HER/OER/HOR/ORR studies are more consistent compared to input feature engineering methods. Most theoretical works calculate two types of energies: (1) binding energy or (2) corresponding Gibbs free energy with the thermal correction term considered. These energies change during species adsorption (H, OH, OOH, O, or water molecules) at catalytic sites. Some studies further calculate the theoretical overpotential derived from the adsorption energies of different species throughout the entire electrochemical reaction process. This approach is grounded in the foundational work by Nørskov et al. on the theoretical origin of overpotentials on electrocatalyst surfaces for HER, OER, and ORR. As for HER, Gibbs free energy change of hydrogen adsorption (ΔG_H*) is the most commonly adopted descriptor.^64,65 For OER and ORR processes, more than one oxygen-containing intermediates’ Gibbs free energies would be concerned to balance each reaction step in order to minimize overpotential.^66–68 The detailed mechanisms will be covered in later sections separately. These DFT-calculated energies have been widely adopted in experimental studies to qualitatively align with observations of activities, bridging theoretical simulations with practical applications.

Experimental data for electrocatalysts can be derived from electrochemical tests, characterization of properties, or extraction from scientific literature. The most frequently measured parameters are the overpotentials for OER and HER, with the overpotential at 10 mA cm⁻² (η₁₀) being a widely accepted benchmark for comparing catalytic activities. For ORR, metrics like mass activity and half-wave potential (E_1/2) are preferred due to their greater reproducibility and relevance to practical performance. These electrochemical metrics are indeed well adopted for assessing and comparing the activity of electrocatalyst products within the hydrogen electrocatalyst community. Additionally, some studies would prefer current density,⁶⁹ while others focus on device-level metrics like maximum power density and area-specific resistance.⁷⁰ Beyond these primary electrochemical measurements, other material system-specific metrics include the morphology of polymerization products⁷¹ and electrochemical double-layer capacitance,⁷²etc. Given the diversity of data, it is essential to standardize experimental conditions and reporting methods to ensure the dataset's consistency and comparability, thereby enabling meaningful predictions made by ML models.

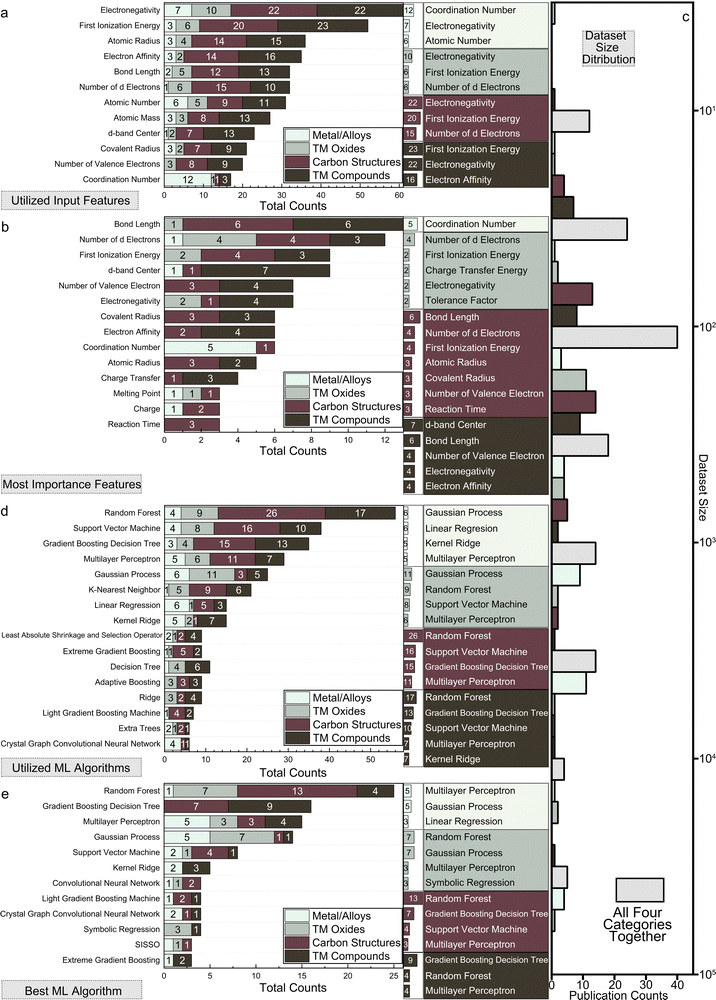
A comprehensive summary of the 151 papers covered in this review is provided in Table S1 (ESI†) through the online repository: https://github.com/ruiding-uchicago/ML-in-Hydrogen-Energy-Transformation-Electrocatalysts-Review/tree/main.

2.2. Model

After confirming the targeted material system for applying ML, the next step is to train a surrogate model to learn patterns within the data. Instead of a generic approach, we present a concrete decision-tree-based use case as shown in Fig. 2 to assist readers of the hydrogen electrocatalysts community. This guide, inspired by a similar approach by Greener et al.,⁷³ helps users make informed decisions by inspecting the properties of their dataset and their specific demands at each major node. We will also introduce relevant basic ML concepts in this section.

2.2.1. Label availability. In ML, a label is a known target value used for training as models’ output. For electrocatalysts focused on HER, OER, etc., labels are typically the measured or calculated properties that indicate the performance of the catalyst. Examples include measured overpotentials, current densities, or DFT-calculated Gibbs free energy of adsorption. Labeled data refers to datasets where these output targets are available for each data point, enabling supervised learning where the model learns to predict the output from input features. In contrast, unlabeled data lacks these target values. Understanding whether the data is labeled or unlabeled is the first crucial step in determining the appropriate ML approach.
2.2.1.1. Labeled data. Labeled data contains specific outcomes, most often performance metrics of electrocatalysts that the ML model aims to predict. Corresponding supervised learning involves randomly splitting the data into training and test sets. The training set teaches the model to map inputs to outputs.⁷⁴ And then the model's ability to generalize and accurately predict outcomes for previously unseen data is evaluated on test set. A typical volume ratio between training and test set could be 80% : 20% or 70% : 30%. In some cases, researchers also use k-fold cross-validation (CV), a method where the data is divided into k subsets, and the model is trained and validated k times, each time using a different subset as the validation set. This method ensures each data point is used for training and validation, providing more robust evaluation. The training and validation set should contain data points not seen by the test set, allowing for unbiased performance evaluation. Specifically, for electrocatalysis, supervised learning is the most adopted paradigm. It offers an approach for predicting the behavior and properties of electrocatalysts based on their composition, structure, or synthesis parameters.
2.2.1.2. Unlabeled data. Unsupervised learning on unlabeled data is relatively less studied in electrocatalysis research. Hydrogen electrocatalysis relies on performance metrics like overpotential or binding energy, needing labeled data for accurate prediction and optimization. The need for precise and quantitative evaluation of electrocatalyst performance limits the applicability of unsupervised methods, which are more suited for exploratory data analysis rather than precise predictions.

Nevertheless, researchers can still use it to categorize data based on similarities, with clustering as a popular method.⁷⁵ Clustering organizes items in a collection according to their similarities to one another in comparison to other groups. Specifically in hydrogen electrocatalysis research, unsupervised learning could be helpful in categorizing electrocatalysts based on their intrinsic properties or performance indicators. By groupings among samples, clustering could also potentially identify unexpected behaviors or anomalies, which are either potential exceptional candidates worthy of further investigation or outliers to deprecate.

2.2.2. Data availability.
2.2.2.1. Sufficient unbiased data. Sufficient unbiased data is crucial for successful ML training and validation. Diverse, representative data covering various compositions and structures is important. Insufficient data can prevent models from learning the system's true nature, leading to poor performance. One common problem arising from insufficient data is overfitting. Overfitting occurs when a model learns not only the underlying patterns but also the noise and outliers in the training data, resulting in excellent performance on the training set but poor generalization to unseen test set. This issue is particularly prevalent in complex models trained on small datasets, where the model is more likely to overfit the training data. Hence, it is generally recommended to collect more data when such phenomenon occurs. Researchers should be cautious with small datasets, as a randomly split test set may not be fully representative, leading to bias and potentially masking overfitting. This is particularly critical for experimental-based scenarios (e.g., fewer than 100 synthesized and tested samples). It is recommended to use cross-validation (e.g., k-fold cross-validation with k = 5 or 10, or Monte Carlo cross-validation) for a more comprehensive and robust evaluation.

Conversely, underfitting occurs when the model is too simple to capture the underlying structure of the data, resulting in poor performance on both the training and test sets. Underfitting is often due to overly conservative hyperparameters or an insufficiently complex model architecture. Addressing underfitting involves increasing the model's capacity and ensuring it has enough flexibility to learn from the data. Additionally, the number of features and their dimensions play a significant role, which will be discussed in Section 2.2.4 Quality of Features. In summary, the goal is a well-fitted ML model with good generalization, starting with sufficient unbiased data.

2.2.2.2. Limited or no initial data. For HER/OER/HOR/ORR electrocatalysts, some studies skip extensive database preparation step to directly find optimal candidates. Interactive machine learning (IML) is a paradigm where the system interacts with the environment to obtain useful information. IML mirrors traditional material discovery, where researchers iteratively perform trial-and-error to update their understanding. High labeling costs is often a challenge for hydrogen electrocatalyst researchers, restricting initial data points and exploration. Hence, two representative IML scenarios are commonly reported in this field: active learning (AL) and black-box function optimization.

AL represents a transformative approach in ML where the algorithm proactively queries information source to obtain labels for new data points. This method contrasts with traditional supervised learning, which uses pre-established labeled datasets passively. Supervised learning mines datasets for patterns, whereas AL allows the model to choose data points based on uncertainty sampling, representative sampling, or potential to alter the model's understanding.⁷⁶ Specifically, for electrocatalysis, AL becomes particularly valuable where data labeling is costly or time-consuming like experimental sample synthesis. By focusing on data points with the highest informational gain, AL accelerates model training and enhances data utilization, leading to a quicker improvement of model prediction.

Beyond AL applications, some works focus more directly on optimizing black-box functions (e.g., fitness functions calculated through DFT simulations), which are typical metrics discussed in 2.1.2. Bayesian optimization (BO), based on AL principles, excels in balancing the exploration of new possibilities and exploitation of known information.⁷⁷ BO is more concerned with how to obtain better target values, for example overpotentials, while AL is focused on the precision of model prediction. This method employs a surrogate model, often a Gaussian process (GP), to predict the performance of various configurations within a Bayesian framework, thereby efficiently managing the trade-off between potential exploration costs and the value of targeted outcomes. Its ability to handle uncertainty makes it valuable in resource-intensive data collection or optimizing functions with costly evaluations. Specifically, the BO + GP combination could effectively guide the optimization of electrocatalysts’ synthesis recipes and conditions for experimentally measured performance. This scenario typically faces challenges from limited labeled data, high labeling costs, and a limited query budget, but the feature dimensionality is usually low.

2.2.3. Label granularity. As the next point of concern, label granularity refers to the level of detail in the output predictions. Coarse-grained labels are used for category prediction (classification), where the goal is to distinguish between discrete categories. Fine-grained labels are used for value prediction (regression), where the goal is to predict continuous values. Understanding the granularity of labels is crucial as it determines the appropriate type of ML model and evaluation metrics to use. A well-fit ML model should be able to demonstrate excellent metric values on both the training and test sets.
2.2.3.1. Category prediction. Classification for category prediction usually could be used for distinguishing qualified or non-qualified samples, for example defining DFT binding energy within a certain preferred range. Metrics used to evaluate classification models include:
Accuracy. Measures the proportion of correctly classified samples out of the total samples and is one of the most important metrics for classification tasks, especially in deep learning.
Area under the receiver operating characteristic curve (AUC-ROC). Represents the overall performance across all thresholds, providing insights into the trade-off between true positive rate and false positive rate.
Precision. Measures the accuracy of positive predictions, indicating the proportion of true positive results in all positive predictions.
Recall. Assesses the model's ability to identify all relevant instances, showing the proportion of true positive results in all actual positive cases.
F1-score. Offers a balanced metric between precision and recall, providing a single score that balances both aspects.

Among these, accuracy remains one of the most critical metrics, providing a straightforward measure of how well the model performs overall.

2.2.3.2. Value prediction. Regression tasks are more often used in electrocatalysis because they directly predict the continuous value of metrics like overpotential, which helps researchers identify the best samples. Metrics used to evaluate regression models include:
Correlation coefficient (r). Gauges the linear relationship between predicted and actual values, indicating how well the model captures the trend.
Coefficient of determination (R²). Shows the variance explained by the model, serving as a universal benchmark due to its scale-invariant nature.
Mean absolute error (MAE). Quantifies prediction accuracy by measuring the average magnitude of the errors in a set of predictions, without considering their direction.
Mean squared error (MSE). Quantifies prediction accuracy by measuring the average of the squares of the errors, penalizing larger errors more heavily.
Root mean squared error (RMSE). Provides error metrics in the same units as the predictions, making it easier to interpret.

In the context of electrocatalyst ML modeling, where output targets can vary greatly in magnitude and scale, the R² metric is particularly useful due to its adaptability and ability to provide a standardized measure of model performance across different scales and dimensions.

Some researchers who prioritize intuitive and interpretable models apply symbolic regression. Symbolic regression aims to find mathematical expressions that best fit the data, uncovering underlying relationships in the form of human-readable formulas. This method combines basic mathematical operations such as addition, subtraction, multiplication, division, and exponentiation to derive simple yet powerful equations. Symbolic regression also aims to find relationships between material structural and electronic descriptors and output targets, with a focus on interpretability rather than just predictive accuracy.⁷⁸ Although symbolic regression may not outperform other black-box models that will be covered later in terms of metrics such as R² or MAE, it offers unique advantages. In such cases, researchers focus on finding formulas or combinations of certain descriptors to deepen their understanding of the material, rather than directly using the obtained formula as an accurate surrogate model to develop better electrocatalyst samples. This approach, often considered part of statistical learning, is especially beneficial when a straightforward, interpretable model is preferred over more complex, less transparent ones.

2.2.4. Quality of features. We've covered guidance on how to choose a learning paradigm by examining label availability, label granularity, and data availability so far. However, to obtain a properly fitted model, the choice of ML algorithm is the next critical decision. This choice is strongly dependent on the quality of input features. High-quality features, whether extensive and learnable or limited and fixed in dimensionality, play a pivotal role in determining the success of the selected algorithm and, ultimately, the model's performance. To address the varying quality of features, we introduce different ML models tailored to these conditions. Though deep learning is popular, it may not always be the best solution. Testing various algorithms can produce illuminating results and lead to the best solutions in designing electrocatalysts. Therefore, choosing wisely according to the circumstances is critical.
2.2.4.1. Extensive & learnable features. In accordance with the consensus in the computer science field, as outlined by Murphy in his seminal textbook,²² supervised learning models are broadly discussed in three principal groups: “linear models”, “deep neural networks” (DNNs) and “non-parametric models”. DNNs are often referred to as “representation learning models”, a term elucidated in the seminal work of Bengio et al.²³ Non-parametric models, on the other hand, are further refined into exemplar-based models, kernel methods, and ensemble methods which will be covered as “classic ML methods” in the next section (Fig. 2).

Deep learning is linked to representation learning, as it uses neural networks to automate feature extraction. Deep learning can be regarded as a subset of representation learning, specifically involving neural networks with multiple layers that learn representations through hierarchical feature extraction. Representation learning also includes unsupervised techniques like principal component analysis (PCA)⁷⁹ and t-distributed stochastic neighbor embedding (t-SNE).⁸⁰ However, these clustering-oriented techniques are less used for feature engineering to improve model prediction accuracy in electrocatalyst development. Thus, in our context, we use deep learning and representation learning interchangeably to refer to the same learning paradigm.

Representation learning allows a model to map input features into a new latent space, capturing the data's structure. This is achieved through layers in neural networks, which progressively learn more abstract representations. As Bengio et al. articulated,²³ deep learning techniques aim to learn representations of data with multiple levels of abstraction. Representation learning excels at handling extensive and learnable features, ideal for high-dimensional data. Essentially, deep learning performs representation learning multiple times across its layers, progressively refining the data representation to capture complex patterns and relationships. For example, autoencoders and their variants like convolutional autoencoders⁸¹ use deep learning to achieve this transformation.

In electrocatalysis, deep learning is invaluable for handling high-dimensional descriptors from Section 2.1.1. These descriptors detail chemical properties and structural characteristics of crystal structures. Neural networks excel over classical ML models in processing rich, complex data. Starting with basic feedforward neural networks (BFNNs), which are akin to multilayer perceptrons (MLPs), these models can manage straightforward descriptors effectively. PyTorch⁸² is a typical implementation library for it. As descriptor complexity increases, sophisticated architectures like convolutional neural networks (CNNs) and GNNs become necessary. CNNs excel at identifying spatial features, suitable for capturing atomic arrangements in a crystal lattice. GNNs handle graph-represented data, ideal for molecular property prediction and analyzing non-tabular relationships in crystal structures.

Frameworks like CGCNN and SchNet, introduced in Section 2.1.1.3, are prime examples of deep learning models for representation learning. They automate feature extraction from raw atomic structures. CGCNN represents crystal structures as graphs, learning features through convolutional layers for effective material property prediction. SchNet, using continuous filter convolutions, captures the interactions between atoms in a flexible and accurate manner. These advanced neural network architectures demonstrate how deep structures facilitate representation learning by efficiently handling extensive and learnable features. In general, the ability of neural networks to manage and learn from extensive and learnable features makes them the first choice for DFT surrogate modeling tasks from a theoretical front. The complexity of the data at the atomic level necessitates such techniques.

2.2.4.2. Limited & fixed features. Continuing from the previous discussion, deep learning, with its capacity for multi-level representation abstraction, can effectively address underfitting problems (2.2.2.1) by capturing complex patterns in high-dimensional data. However, this strength poses a risk of overfitting in low-dimensional datasets with fewer features. Overfitting happens because deep learning models memorize limited data instead of generalizing, especially with manually crafted, fixed features. By “limited and fixed features”, we refer to two common situations: (1) DFT-based ML studies focus on only the microenvironment of the catalytic site, describing only nearby atoms. (2) Experimental ML studies with limited synthesis parameters result in smaller datasets. Here, classical ML models are more suitable due to their simplicity and stability. They can effectively handle such low-dimensional data without overfitting.

Therefore, for limited and fixed features, classical ML models are preferable. Table S1 (ESI†) shows that over 75% of works use classical ML methods, highlighting their importance in hydrogen electrocatalysts. A typical implementation library used is Scikit-learn.⁸³ Suitable classical ML methods include K-nearest neighbors (KNN), support vector machines (SVM), and GP. KNN,⁸⁴ an instance-based learning method, excels in pattern recognition by leveraging local similarities, making it suitable for classifying electrocatalysts with low-dimensional features. Its adaptability and interpretability add value, especially in understanding electrocatalyst data patterns. SVM⁸⁵ excels in classification by finding the optimal hyperplane for data categorization, managing both linear and nonlinear decision boundaries through kernel functions. This makes SVM useful for classifying electrocatalysts based on distinctive features. GPs are notable for their probabilistic approach to regression and classification, offering predictions and uncertainty estimates, crucial for BO and AL processes.⁸⁶ This makes GPs invaluable in high-throughput explorations where prediction confidence is essential for sequential decision-making. GPs are typically the default algorithm in these processes. The flexibility and Bayesian nature of GPs support their application in complex, sequential tasks, and are often combined with BO and AL to navigate high-dimensional spaces efficiently. These traditional algorithms balance computational efficiency and meaningful insights from sparse data, ideal for smaller, finite datasets and lower-dimensional features. Their advantages in efficiency and rapid deployment are essential for tasks needing quick model development with budget constraints.

Ensemble methods, leveraging the collective intelligence of multiple models, have become key tools for improving prediction robustness and accuracy. As a typical example of ensemble methods, a Random Forest model builds on Decision Trees (DTs), which serve as the foundational base learner, providing a rule-based decision-making framework⁸⁷ (see “trees, forests, bagging, and boosting” from Murphy (2022)). This progression from simple DTs to more sophisticated ensemble methods like extra trees (ET) and random forests (RF) illustrates a transition from single models to robust aggregated models.⁸⁸ ETs and RFs employ techniques such as bagging and feature randomization to mitigate overfitting and improve diversity, making them highly adaptable and scalable for a range of applications. Among the advanced ensemble algorithms are gradient boosting decision tree (GBDT) and corresponding derivatives—LightGBM,⁸⁹ XGBoost,⁹⁰ and CatBoost.⁹¹ These algorithms refine the ensemble approach by focusing on correcting errors of previous models iteratively, which, when combined with gradient optimization, allows for unparalleled accuracy in detecting complex patterns. Their efficiency, ability to handle categorical features, and scalability have made these GBDT variations highly popular in ML.

For electrocatalysts, ensemble methods like RF and GBDT are robust in handling intricate data landscapes. They adeptly integrate diverse descriptors—chemical, engineering, structural, and operational—to predict catalytic performance with remarkable precision. Given their adaptability to both low-dimensional inputs and datasets with dozens of features, these algorithms have become a staple in electrocatalyst ML research. Their application spans from experimental datasets, including synthesis conditions, to surrogate modeling for DFT, covering atomic descriptors and crystal configurations. Ensemble methods provide high accuracy across various fidelity levels (experimental/simulation) without the computational intensity or overfitting risks of artificial neural networks (ANNs). Their widespread use highlights their potential as a first-line approach in electrocatalysis, providing a versatile tool for innovative material discovery.

2.2.5. Model optimization & uncertainty quantification. After the ML model is chosen, it should be trained on the corresponding prepared dataset and evaluated on the test set. Besides the critical steps of feature engineering and model selection, obtaining a well-fit model with accurate prediction might also require model optimization.

Hyperparameters are the external configurations that dictate a model's structure and learning process and must be determined before training begins. For deep learning, typical hyperparameters include learning rates, batch sizes, and the number of layers. In the case of KNN, the number of neighbors is crucial, while for SVM, the choice of kernel and regularization parameter are essential. For GP, kernel functions and their parameters are important. Ensemble methods like RF involve hyperparameters such as the number of trees and the maximum depth of each tree.

Regularization techniques⁹² also play a vital role in model optimization. They exist both in deep learning and boosting models. Techniques such as L₁ and L₂ regularizations help in reducing overfitting by penalizing large weights. Dropout,⁹³ specific to neural networks, prevents the co-adaptation of features by randomly disabling neurons during training. Early stopping⁹⁴ halts training when performance on a validation set drops, preventing overfitting to the training data. Batch normalization⁹⁵ improves training speed and stability by adjusting and scaling activations.

Model optimization is usually a custom trial-and-error process dependent on the database. For the hydrogen electrocatalyst community, a deep understanding of the mathematical and computational aspects of hyperparameters and algorithm architectures is less significant. The practical approach is to first use the default hyperparameter settings provided by the ML library. If excellent predictive performance is not achieved, consider whether feature engineering and model selection are appropriate and if the data is unbiased and sufficient. If the model shows good baseline performance, then refer to the library's manual to identify hyperparameters that can be further tuned. Grid search, random search, and Bayesian optimization are all viable methods for fine-tuning.

Uncertainty quantification (UQ) is also crucial for understanding and managing the uncertainty in ML models, typically categorized into aleatoric (data-based) and epistemic (model-based) uncertainties.^96,97 Techniques such as model ensembling and mean/variance estimation provide insights into prediction variability, while deep kernel learning and distance-based conformal prediction refine uncertainty estimates. Monte Carlo dropout introduces randomness during training to assess uncertainty, and evidential regression estimates uncertainty by predicting distribution parameters. As commonly adopted in BO, GP naturally incorporate UQ through their inherent probabilistic framework. Greedy acquisition, epsilon-greedy, probability of improvement (PI), expected improvement (EI), thompson sampling (TS), and upper confidence bound (UCB) are effective strategies for leveraging UQ in decision-making.⁹⁸ Additionally, information entropy serves as a data-based, model-independent measure of uncertainty. For experimental hydrogen electrocatalyst development, UQ is indispensable as it guides experimental efforts by identifying the most promising candidates with the highest certainty, ultimately accelerating the discovery of efficient and stable catalysts while minimizing costly trial-and-error approaches.

2.3. Application

After obtaining an ML model capable of making accurate predictions, the final application stage in HER/OER/HOR/ORR research typically involves using the ML surrogate to search for optimal candidates and further understanding the decision-making process to gain material insights, such as identifying the most important features of the studied material system.

2.3.1. Searching for optimal candidate. Most of the works demonstrate that after obtaining an ML model, researchers can traverse the entire design space to identify optimal candidates. For example, they can screen all possible combinations of crystal and catalytic site structures to find those with optimal binding energies, or experimental synthesis recipes that lead to superior macroscopic performance. Although using a trained ML model for such inference is much faster, enabling large-scale screening, certain techniques are needed when the dimensionality is too high to find a global minimum efficiently. One popular technique is the genetic algorithm (GA),⁹⁹ which speeds up the process of finding the optimum value by mimicking natural evolutionary processes. It operates through selection, crossover, and mutation steps to explore the search space and converge on high-quality solutions. This method is particularly effective in complex optimization problems where the search space is vast and not easily navigable by brute force search. Except for GA, other heuristic algorithms include particle swarm optimization (PSO)¹⁰⁰ and differential evolution (DE).¹⁰¹ BO could also be used in this process.

2.3.2. Model interpretation for material insights. In complex systems, comprehending the decision-making process of ML models is important to gain deeper universal material insights which are sometimes more valuable than simply finding promising candidate. The most decisive feature/descriptor that would determine the prediction is usually paid attention to.

Intrinsic feature importance, often calculated as the default method by DT-based models serves as the basic interpretation. Corresponding libraries typically use methods like Gini/entropy (DT, RF and GBDT), gain (XGBoost), split (LightGBM), or permutation (CatBoost) to rank feature contributions to the output. They are straightforward ways based on impurity reduction, prediction accuracy, or feature usage frequency. In addition to these intrinsic methods, there are several more advanced interpretation techniques to understand how input features affect output targets, providing deeper insights into the underlying mechanisms in the studied electrocatalyst system. Partial dependency plots¹⁰² (PDPs) clarify the relationship between a specific feature and the outcome by isolating its effect while holding other features constant, making it easier to visualize a feature's impact on model predictions. For a more detailed analysis, shapley additive explanations¹⁰³ (SHAP) break down predictions to quantify each feature's contribution, offering a nuanced view grounded in game theory. This method ensures equitable attribution of prediction impacts, including interactions between features. Similarly, local interpretable model-agnostic explanations¹⁰⁴ (LIME) provide local insight by approximating how changes in input affect predictions, making complex models more interpretable on a case-by-case basis. Sensitivity analysis¹⁰⁵ can further enrich understanding by illustrating how minimal changes to inputs affect the predictions. This method offers intuitive, actionable insights into the model's behavior and helps in identifying the most sensitive parameters in the electrocatalyst system.

Collectively, these interpretation techniques enable data scientists and electrocatalyst domain experts to gain a more thorough and transparent understanding of their ML models. Identification and visualization of the feature impacts could deepen the understanding of hydrogen electrocatalysts through a unique data science approach.

2.4. Toolkits and libraries

The advancements in ML for materials science and specifically electrocatalysts are significantly bolstered by the availability of open-source toolkits and comprehensive benchmark datasets. These resources not only facilitate the development and deployment of ML algorithms but also ensure accessibility and reproducibility in research. For ANN-based tasks, TensorFlow¹⁰⁶ and PyTorch⁸² remain the go-to frameworks, offering extensive libraries for designing, training, and deploying complex neural network architectures. Domain-specific frameworks such as CGCNN,⁴⁹ Schnet,⁵⁰ DimeNet++,⁵² GemNet-OC,⁵³ MatErials graph network (MEGNet),¹⁰⁷ ForceNet,¹⁰⁸ Spinconv,⁵¹ lattice convolutional neural network (LCNN),¹⁰⁹ polarizable atom interaction neural network (PaiNN),¹¹⁰ NequIP,⁵⁷ CHGNet⁶¹ and M3GNet⁶³ automate and comprehensively improve feature engineering, streamlining the deep learning pre-built steps. As introduced in Section 2.1.1.3, they are preferred for DFT-based theoretical studies because they generate physics-informed descriptors that represent both structural and chemical properties of materials, facilitating efficient and accurate predictions with minimal user domain knowledge. Recently, Google DeepMind released the graph networks for materials exploration (GNoME) model,¹¹¹ which scales graph networks to discover millions of stable inorganic materials, significantly enhancing the efficiency and scope of materials exploration. Such pretrained models could be particularly impactful for electrocatalyst research, enabling rapid identification and optimization of promising materials with minimal computational costs.

For classical ML applications that are more frequently applied, Scikit-learn is the first choice that provides a comprehensive suite of algorithms for classification, regression, and clustering that are suitable for various electrocatalyst analysis tasks. Scikit-learn also offers basic realizations of RF and GBDT. Additionally, TPOT¹¹² and PyCaret¹¹³ serve as auto ML tools, automating the machine learning pipeline and making them accessible for beginners. For advanced cases, LightGBM,⁸⁹ XGBoost,⁹⁰ and CatBoost⁹¹ have independent packages that offer highly optimized versions of GBDT, excelling in handling tabular data for predictive modeling with efficiency and scalability.

Chemical and crystallographic datasets are also crucial for data preparation. The materials project,¹¹⁴ atomic simulation environment (ASE),¹¹⁵ open quantum materials database (OQMD),¹¹⁶ the joint automated repository for various integrated simulations (JARVIS),¹¹⁷ and automatic FLOW for materials discovery (AFLOW)¹¹⁸ are pivotal in democratizing access to vast repositories of chemical and crystallographic data. These platforms provide pre-computed properties for thousands of materials, enabling data-driven discovery and design of new electrocatalysts. The open catalyst (OC) catalyst datasets, particularly OC20¹¹⁹ and OC22,¹²⁰ are extensive collections to be highlighted, with the former containing over 250 million single-point calculations and the latter featuring 62 000 DFT relaxations. These datasets cover a wide range of reactions involving various small molecules, such as CO, H₂O, and O₂, among others. This comprehensive scope is crucial for training ML models that can generalize across different catalytic systems, making them particularly valuable for advancing hydrogen electrocatalyst studies. Suitable libraries also exist for feature engineering, especially for theoretical studies. For generating sophisticated descriptors, Dscribe⁴⁵ offers a toolkit for creating a wide array of materials and molecular descriptors that are essential for ML models in materials science, typically coulomb matrix, SOAP, MBTR, and ACSF introduced in Section 2.1.1.3. Matminer¹²¹ is another valuable tool that facilitates the extraction and manipulation of materials data for ML applications. When it comes to neural network potentials for molecular dynamics (MD) simulations, libraries like Schnet⁵⁰ and DeePMD¹²² provide powerful frameworks for developing and deploying accurate and efficient models. These tools allow for the simulation of atomic-scale phenomena with unprecedented detail, opening new avenues for understanding and optimizing electrocatalytic materials. Together, these ML toolboxes and resources form a robust ecosystem that supports the entire lifecycle of materials discovery and development.

3. ML-aided design of HER electrocatalysts

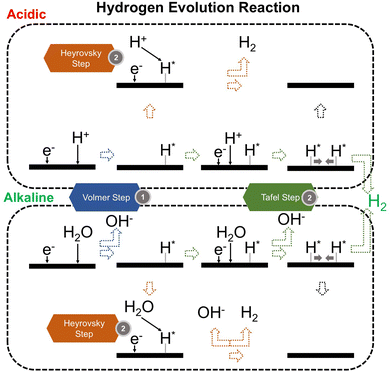
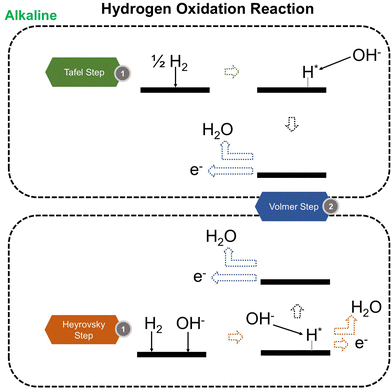
We now present the challenge for HER, followed by a comprehensive review of how ML techniques have been leveraged in various material systems to accelerate the design of efficient and cost-effective electrocatalysts for hydrogen evolution. Given the vast design space and the complex interplay of various factors influencing HER activity, ML has emerged as a powerful tool to guide the rational design and optimization of HER electrocatalysts. Later, we will also discuss the applications of ML in designing electrocatalysts for other critical reactions, such as the OER, HOR, and ORR.

HER takes place in the cathode of water electrolyzers. It is the cornerstone in producing hydrogen as a clean-energy resource driven by electrical energy input to split water. The HER mechanism unfolds through a series of electrochemical steps, each important for the overall reaction efficiency. The Volmer step, which produces an adsorbed hydrogen atom (*H) on the catalyst's active site by electrochemically reducing a proton (H⁺) with an electron (e⁻), is the first and most important stage in HER because it creates the foundation for the subsequent formation of gaseous hydrogen. After HER completes the Volmer step, it can proceed in one of two ways. During the electrochemical desorption stage of the Heyrovsky process, the *H releases the active site and combines with another proton and electron to form gaseous H₂. Alternatively, the Tafel step rereleases the active site by recombining two *H to form gaseous H₂. A brief schematic of the reaction mechanism is illustrated in Fig. 3.

Fig. 3 Schematic of HER mechanism.

The catalyst's electronic properties have a significant influence on how effectively these steps are completed in an energy-favorable manner. Particularly in acidic environments, the activity of a HER catalyst is closely correlated with the Gibbs free energy change of hydrogen adsorption (ΔG_H*). The optimal condition is an intermediate and balanced interaction between the hydrogen adsorbate and the catalyst's active site. Since these conditions can limit the initial formation of hydrogen or obstruct its release, it is preferable to have neither too strong nor too weak adsorption. A value of ΔG_H* near zero indicates theoretically high intrinsic catalytic performance, which is expected to be observed with low overpotential in corresponding electrochemistry experiments.^64,65 In alkaline conditions, however, HER becomes more complex due to the inclusion of water dissociation as another decisive step. This adds a layer of complexity to the reaction mechanism, making the understanding of activity descriptors in alkaline HER more challenging. Recent studies highlight the significance of the cooperative action of different active components in alkaline HER catalysts.^123,124 Some components facilitate the activation of water molecules with a low energy barrier, while others optimize the desorption of hydrogen atoms. This cooperative mechanism suggests both new opportunities and challenges due to the complexity in developing more effective HER electrocatalysts. After decades of exploration, platinum-based noble metal catalysts are currently the most widely used in commercial applications due to their exceptional efficiency.¹²⁵ However, due to the high cost and limited availability of these materials, research has mainly concentrated on two objectives: enhancing the intrinsic catalytic efficiency of HER and reducing the requirement for costly noble metals. Research on catalysts based on nonprecious metals has also thrived to achieve this goal, including efforts on carbon materials, transition metal (TM) compounds, and other novel systems.¹²⁶ Due to the nature of the potentially vast candidate design space, ML techniques could greatly aid these explorations.

3.1. Metal/alloy-based catalysts

3.1.1. Pt-based. As previously discussed, Pt and its alloys have been at the forefront of HER catalyst studies due to their exceptional catalytic properties. This led to the first introduction in the field of applying ML techniques to optimize Pt, binary Pt alloys, and more complex compositions such as ternary or high-entropy alloys.

Two primary data sources are usually used in subfields like electrocatalysts in materials science for ML, especially when designing electrocatalysts for HER: theoretical simulations like DFT, and experimental data. For the former, first-principles descriptors such as electronic structure and crystal geometric configurations are frequently included in input features. ML models act as surrogate models for quickly predicting outcomes such as energies and forces which might theoretically indicate catalytic activity or stability. Such a high-throughput screening would typically consume significant computational resources. The ML-DFT strategy is valued in a theoretical perspective, efficiently screening candidates from vast possibilities, especially between electrocatalyst materials that have intrinsic differences like crystal structures and element types. Even with lower fidelity, several benefits to using simulation data, such as DFT, as a source for ML should be noted, including greater speed, lower barrier of automation in high-throughput dataset preparation, and the capacity to identify underlying mechanisms. One study that has illustrated such advantages is reported by Gu et al.,¹²⁷ who focused on jagged Pt nanowires for alkaline HER. In the study, the local environments of 3413 binding sites on jagged Pt nanowires were used to obtain input features (descriptors) for ML model training (Fig. 4a). ACSF,⁴⁸ CGCNN,⁴⁹ nearest atom distance-Gaussian process, and SchNet⁵⁰ were applied and compared for this representation task. ACSF is recognized as the best, with the lowest MAE of 0.043 eV. With this experimentally well-validated ML model, the researchers could further correlate the activity of different sites on the nanowire with their intuitive descriptor: coordination number and site types (top, bridge, hollow) via unsupervised learning. The results identified an auto bifunctional catalysis mechanism (Fig. 4b and c) where distinct sites on the Pt nanowire surface synergistically contribute to the HER process: the stronger binding sites adsorb protons, and the weaker binding sites activate hydrogen. Such a discovery that would originally require an immense number of simulation calculations for statistical analysis is now enabled by the ML-DFT technique. In another study that discusses the HER mechanism, Ooka et al. investigation into hydrogen surface-binding energies on Pt, diverging from the convention of thermoneutrality, offers a significant shift in understanding the HER design rule.¹²⁸ Their database is based on experimentally acquired electrochemical data, and they employed a novel approach by integrating regression modeling with GA to effectively capture the non-linear dynamics of the HER process, allowing for a more accurate estimation of the binding energies. Their findings highlight the importance of considering overpotentials in catalyst design and suggest that optimal catalytic efficiency may require binding energies that are not thermoneutral, especially under conditions far from equilibrium. This insight opens new pathways into the design of more efficient HER electrocatalysts.

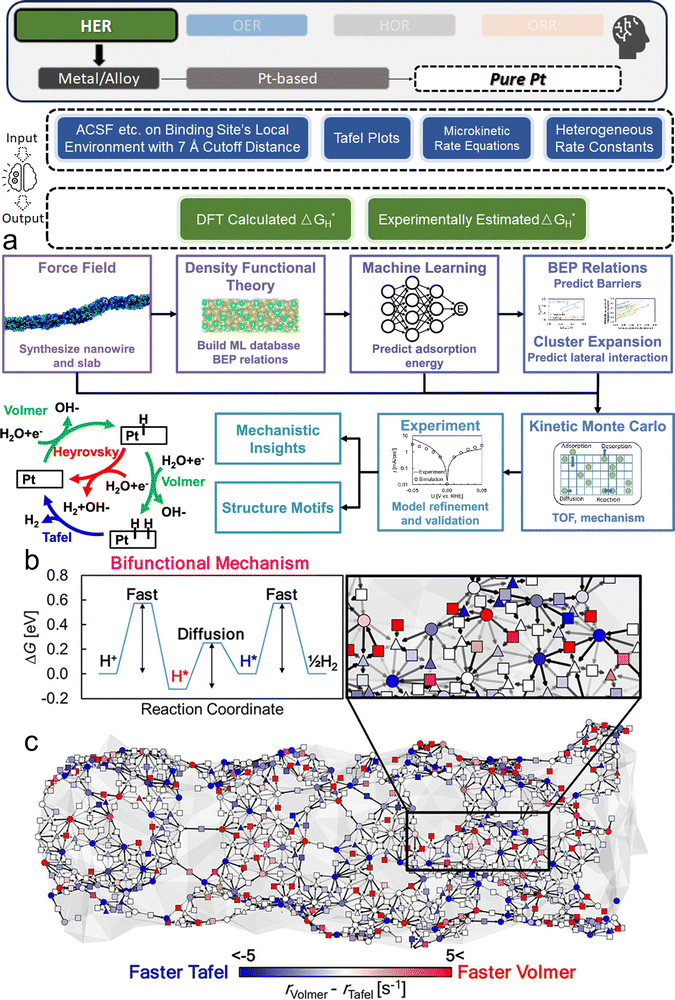Fig. 4 ML studies on pure Pt electrocatalysts for HER. (a) Integrated simulation process for jagged Pt nanowires. This involves a synergistic approach that uses force field analysis, DFT, ML techniques, and kinetic modeling, aiming at a comprehensive multiscale simulation of the alkaline HER on jagged Pt nanowires. Validation of the model is achieved through comparison with experimental data, with a focus on elucidating the underlying mechanism, which encompasses the Volmer, Heyrovsky, and Tafel reactions, as depicted in the lower left plot. (b) Illustration of the bifunctional mechanism, where protons adsorb at a Volmer-favorable site and migrate to a Tafel-favorable site for H₂(g) formation. (c) Simplified visualization of the nanowire indicating reaction preferences at different binding sites (top, bridge, and hollow sites marked by circles, squares, and triangles, respectively). Color coding (blue for Tafel, red for Volmer reactions) reflects relative reaction rates. (a–c are reproduced from ref. 127 with permission).

Except for deepening the understanding and design rule from the fundamental mechanism level, ML models are more widely recognized as powerful tools in screening the design parameters of HER electrocatalysts, such as the element types and corresponding composition in alloys. Li et al. investigated the (100) surfaces of binary alloy systems formed by strong- (Pd and Pt) and weak-binding (Ag, Au, and Cu) transition metals²⁷ (Fig. 5a). To predict the DFT-calculated H binding energies (ΔE_H*, which does not consider thermal correction: temperature and entropy), which are HER activity descriptors, a database with more than 450 entries and the manually chosen input features of 26 physical properties like electronegativity, d-orbital information, and d-band center are used. With a simple BPNN (Fig. 5b), the researchers could identify the superiority of Pd₂Au₂-d/Pd_0.75Au_0.25 among other competitors. Similarly, Jäger et al. focused on a specific model system of 55-atom bimetallic icosahedral Pt nanoclusters composed of binary combinations of the elements Ti, Fe, Co, Ni, and Cu.⁴¹ Their strategy for input feature engineering is to combine electronic descriptors with structural descriptors: SOAP-derived descriptors and the local density of states together. By using kernel ridge (KR) regressor as the ML algorithm along with an additional training set supplement in the loop, an MAE of 0.1 eV could be reached by 1767 DFT calculations. As the result, researchers revealed not only the advantage of Ni in binary, but also NiCo and NiTi in ternary Pt alloy. Li et al. also adopted the idea of iteratively generating a new training dataset by applying AL with a query strategy that measured the deviations of DFT-calculated adsorption energies¹²⁹ (Fig. 5c). By further applying previously introduced state-of-the-art GNN framework: DimeNet++⁵² and labeled site crystal graph,¹³⁰ the authors finally screened out Cu₃Pt(100) and FeCuPt₂(100) and (001) as potential candidates for replacing Pt(111). Zhang et al. uniquely focused on Pt-modified amorphous alloy (Pt@PdNiCuP) and the features used to describe the adsorption sites consist of simple geometric elements.¹³¹ Nevertheless, the ML-assisted results align well with the previous experimental study¹³² and identify a theoretical best composition of the five elements in this complex system for further exploration. For real experimental exploration that is more practical and valuable, the use of AL is a powerful and low-cost option. Kim et al. innovatively apply AL on both binary and ternary Pt-based systems, demonstrating its efficacy in rapidly identifying optimal multi-metallic alloy catalysts for HER with significantly reduced experimental costs.¹³³ By iteratively updating a GP model with experimental data, their method efficiently narrows down the vast design space. The AL process initially started with 73 preliminary random data points and conducted two loops with 40 additional data points explored in each. The exploration studied both binary and ternary (Fig. 5d and e) alloy systems. Even with such a limited data size, it still effectively led to the discovery of a high-performing Pt_0.65Ru_0.30Ni_0.05 catalyst with an overpotential of merely 54.2 mV, which remarkably surpasses the electrocatalytic efficiency of pure Pt. Beyond directly guiding experiments with ML, the literature contains a wealth of domain expertise that can be leveraged for ML modeling to offer a holistic view. Yang et al. effectively used a comprehensive database derived from an extensive literature review in their work.³⁷ They employed the sure independence screening and sparsifying operator (SISSO) method, a form of supervised regression, to refine and enhance the predictive accuracy of the Nørskov model⁶⁵ for HER kinetics on various metal surfaces.

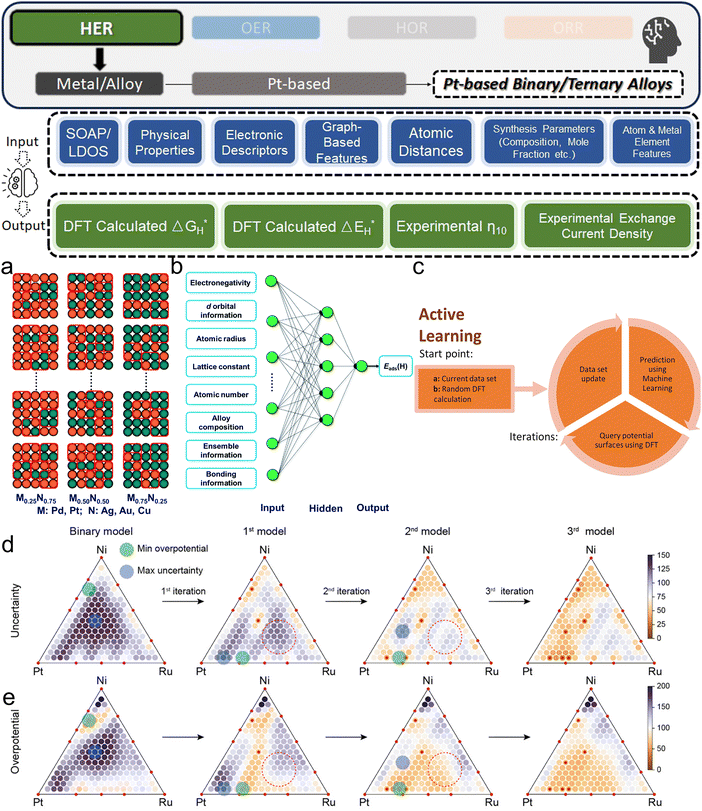Fig. 5 (a) Schematic of the random sampling method for (100) bimetallic alloys. The four-fold ensemble that offers H's particular adsorption environment is represented by red squares. (b) The BPNN model's algorithmic architecture with input features used in ref. 27 (a and b are reproduced from ref. 27 with permission). (c) Schematic representation of AL in catalyst discovery via DFT (c is reproduced from ref. 129 with permission). (d) and (e) AL results for ternary composition: with each iteration, the triangular diagrams for the (d) uncertainty and (e) overpotential of the Pt–Ru–Ni system are updated. Red dotted circles highlight shifts in predictions without additional data at specific points post-iteration (d and e are reproduced from ref. 133 with permission).

3.1.2. Non-Pt metals. In an effort to go beyond Pt-based catalysts, non-Pt metal electrocatalysts such as Ag, Cu, and their alloys provide HER applications with a plentiful and cost-effective substitute for Pt-based catalysts. Their wide range of structural and compositional characteristics, from complex binary and ternary systems to single-atom alloys, also make them ideal for applying ML techniques to discover new catalytic mechanisms and enhance performance.

Among noble metals, Pd is also commonly studied as a promising candidate to boost HER as an electrocatalyst.¹³⁴ Gao et al. investigated the amorphous alloy Pd₄₀Ni₁₀Cu₃₀P₂₀, a promising candidate for HER (Fig. 6a).¹³⁵ The electrocatalytic performance of this complex system was analyzed using the SOAP as the input feature generator and GP as the ML algorithm (Fig. 6b), which successfully mapped the catalytic activities of sites on the alloy surface with a small MSE of 0.018 (eV).² Using this ML surrogate model, the ideal atomic ratio (Pd : Cu : P : Ni = 0.51 : 0.33 : 0.09 : 0.07) for optimal HER activity was found via sampling 40 000 active sites. Hoyt et al. performed a thorough investigation on H adsorption energies on Ag alloys (211) surfaces.¹³⁶ They trained different ML algorithms on the dataset obtained from more than 5000 DFT calculations. Remarkable accuracy was shown by their innovative employment of the best-performing RF model along with a combination of standard chemical and structural descriptors as input features. On the median, the RF's absolute test error was merely 14 meV. Except for predicting with precision, the as-trained ML model also helps to reveal intricate electronic structure effects and counterintuitive behaviors in dopant atoms, further underscoring the potential of ML to uncover novel insights in electrocatalysts as a popular subfield in materials science.

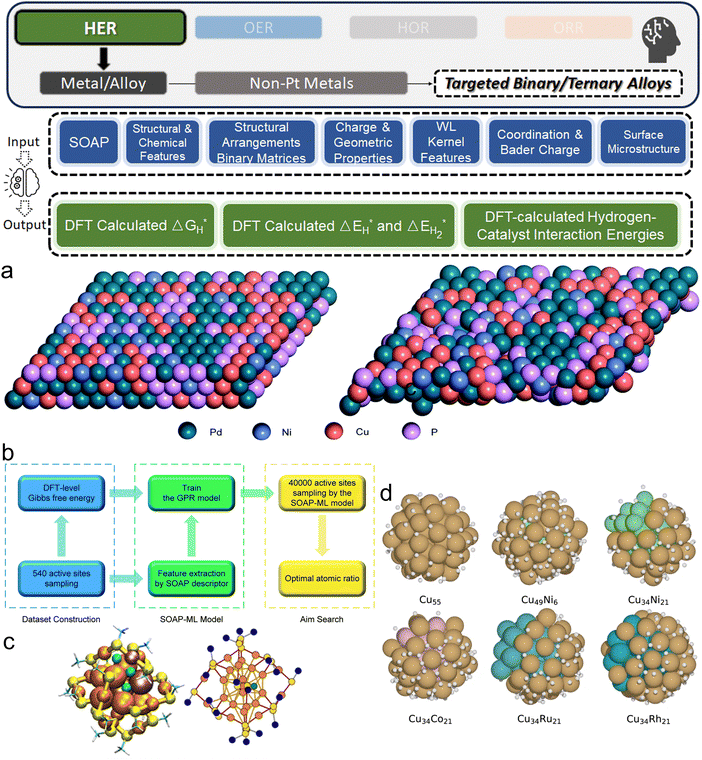Fig. 6 (a) Left: The atomic structure of the Pd₄₀Ni₁₀Cu₃₀P₂₀ amorphous alloy. Right: The DFT-optimized structure of the Pd₄₀Ni₁₀Cu₃₀P₂₀ amorphous alloy. (b) Algorithm framework of SOAP-ML model construction (a and b are reproduced from ref. 135 with permission). (c) Right: Depiction of the [M_xAu_25−x(SCH₃)₁₈ + H]^q system (M = Pd, Cu, x between 0 and 1, q between −2 and 2) and Left: Its corresponding graph representation. Various metal doping and hydrogen adsorption sites are highlighted. Color coding is as follows: orange for gold, yellow for sulfur, turquoise for carbon, white for methyl hydrogen, and violet-tinted gold atoms indicating dopant location types. Three green spheres represent potential H adsorption sites (c is reproduced from ref. 137 with permission). (d) The optimal adsorption sites for H on the surface of different 55-atom Cu binary clusters with |ΔG_H*| <  0.1 eV (reproduced from ref. 34 with permission).

Pihlajamäki et al. uniquely considered the possible organic ligands on metal clusters, investigating Cu- and Pd-doped 25-atom Au monolayer-protected clusters with thiolate ligands on the surface (Fig. 6c).¹³⁷ The innovation of this work is that instead of directly applying GNN, the authors employed graph-based representations of the local atomic environment of hydrogen, incorporating geometric, graph theoretical, and tabulated features which enabled the prediction of interaction energies between hydrogen and the nanoclusters with a high degree of accuracy. Such a strategy allows relatively simple distance-based kernel models to reach a CV RMSE of below 0.1 eV. Hence, this work not only provided insights into the HER catalysis behavior of the complex nanocluster system, but also demonstrated the power of combining graph-based methods for feature engineering. Through similar DFT-ML strategies, recent researchers have also explored binary alloy systems: Cu_55−nM_n³⁴ (Fig. 6d) (M = Co, Ni, Ru, and Rh) clusters or ternary alloy system: NiCoCu.³⁶ Except for predicting a theoretical optimum composition, ML models also allow these works to gain deeper insights into the relationship between the local microstructures of the active sites and the hydrogen adsorption behavior that determines the HER activities.

Besides exploring systems with predefined metal elements, ML models can also be extended further to screen from a vast candidate space of different combinations of metal elements. Chen et al. used the CGCNN to explore a substantial dataset of 38 484 structures, leading to the identification of 43 promising alloys from an initial pool of as many as 2973 candidates¹³⁸ (Fig. 7a). This approach, integrating ML potential for efficient structural description and simple physical properties, demonstrated a balance between computational efficiency and accuracy. The use of final configurations obtained via the SchNet⁵⁰ calculator as input features was key in accurately predicting the hydrogen adsorption values. The framework's efficacy was further validated by the close match of computational predictions with experimental results for selected candidates like AgPd alloy, showcasing the practical potential of ML in accelerating the discovery of new electrocatalysts from the various possible combinations of the elements. Similarly, Zhang et al. explored a vast candidate space of binary alloys for HER;¹³⁹ however, they chose to leverage ensemble methods and classical ML algorithms. As a result, the best performing LightGBM model, which is less computationally intensive than deep learning models, achieved a remarkable R² score of 0.921 and an RMSE of 0.224 eV. Notably, they also employed the SHAP method post-training to extract insightful interpretations; they found an interesting descriptor: mean of group number of elements in an alloy to be the most impactful on the model's ΔG_H* value prediction.

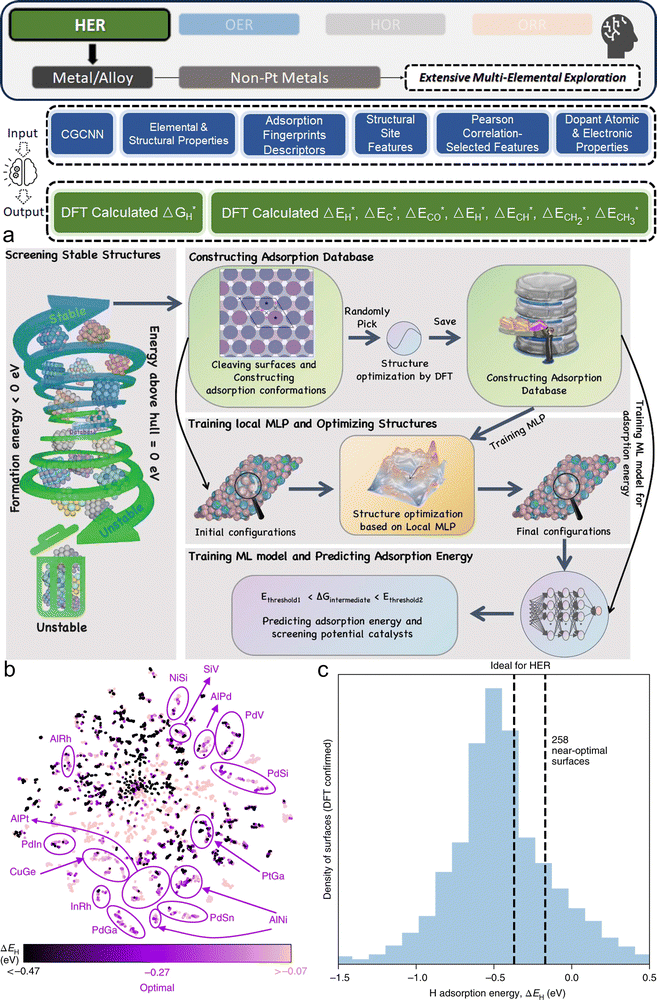Fig. 7 (a) Schematic of the ML framework for the high-throughput screening of electrocatalysts: on the left in the “constructing adsorption database” section, the depiction includes adsorption sites for binary alloys. These are represented as ontop, bridge, and hollow sites, indicated by a black star, red “+”, and blue “×”, respectively (reproduced from ref. 138 with permission). (b) t-distributed stochastic neighbor embedding visualization of all simulated adsorption sites using DFT: the visual representation shows the adsorption energy values in eV. Stronger binding sites are superimposed over weaker ones. Notably, the clusters/materials in dark purple are labeled for their potential as promising candidates. (c) Normalized distribution of low coverage ΔE_H* (electronic energy change) values from DFT Workflow: this graph presents the distribution of ΔE_H* values. Dashed lines highlight the 0.1 eV range around the optimal ΔE_H* value of −0.27 eV. Note, the authors of ref. 140 chose ΔE_H* rather than ΔG_H* for HER, hence the optimal value is not 0 eV (b and c are Reproduced from ref. 140 with permission).

As broader interest among different metal elements for forming alloys would largely increase the candidate space, and the demand for calculations of over thousands of configurations by DFT to prepare a dataset for ML could be more expensive. Hence, an efficient approach to leverage AL for a higher efficiency is needed. Tran and Ulissi reported in 2018 a pioneering work that employs a novel ML framework for integrating AL and surrogate-based optimization to streamline the discovery of electrocatalysts for CO₂ reduction and HER.¹⁴⁰ Their approach, applied to an extensive, order-of-magnitude-improved database of 1499 intermetallic crystals leading to 17 507 unique surfaces and 1.6 million adsorption sites, significantly narrows down the search space while maintaining the model's evolving accuracy. This method not only reduced the computational cost but also finally led to the identification of 131 candidate surfaces for CO₂ reduction and 258 surfaces for H₂ evolution (Fig. 7b and c, to be noted, like some of previously mentioned research. This work chooses to use ΔE_H* that has not included the entropy and zero-point energy as the HER activity metric. Most of the other ML-related works in this section for HER choose to use ΔG_H*, which has the optimal value of 0 eV as mentioned previously), highlighting its reliability for accelerating the exploration of efficient electrocatalysts in an immense candidate space. Kayode et al. have also implemented BO in their recent study.¹⁴¹ The authors applied this approach to efficiently screen for high-performance, single-atom alloys and bimetallic catalysts, which are crucial in not only HER but also for reactions such as alkane transformations and for CO₂ reduction. The BO workflow was effective even with limited initial datasets (as few as two to eight data points), and it employed simple yet insightful input features such as group and period numbers. Notably, their approach, which requires significantly fewer DFT calculations compared to traditional methods, still successfully led to the identification of promising candidates such as Hf₁Cu for alkane transformations, Y₁Au, Y₁Cu, and Y₁Ag for CO₂ reduction, and Ag–Ir binary alloy for HER. These works demonstrated the practical utility and flexibility of adaptive learning techniques like AL and BO in handling an electrocatalyst system with vast searching space.

3.2. Carbon-based materials

3.2.1. Graphene-based carbon structures. In addition to metal-based materials, carbon-based materials are quite effective as electrocatalysts for energy storage and conversion,¹⁴² including HER.¹⁴³ Because of its great conductivity, accessibility, and affordability, graphene is an excellent material for electrocatalysis in HER.¹⁴⁴ The incorporation of various dopants into graphene structures offers a pathway to tailor and enhance electrocatalytic performance, leveraging the material's intrinsic properties. Hence, the integration of ML approaches in this domain would also present an innovative avenue to systematically explore and optimize dopant combinations, further elevating the efficacy of carbon-based electrocatalysts for HER applications.

Using nitrogen (N) as the candidate dopant, Lv et al. investigated the possibility of developing bifunctional electrocatalysts via γ-graphyne (allotrope of carbon, distinct from graphene, with unique lattice structure) nanoribbons for both HER and ORR.¹⁴⁵ Among the different ML algorithms, they screened out the best performing LightGBM model and a special set of input features (Fig. 8a) such as atomic distances (d₂, d₃) and charges associated with the active site (Q₂, Q₃). With the dataset's size near 300, the MAE of overpotential was as low as 0.072 and 0.066 V for ORR and HER, respectively. They further applied SHAP for feature importance analysis to provide important new information, emphasizing in particular the strong impact of the chemical environment around the active sites (Fig. 8b). However, Kronberg et al. explored an innovative approach to further leverage SHAP in a continuous 10 × 5-fold nested CV loop, rather than as a typical one-time post-explanation after model training.¹⁴⁶ By applying this innovative method on various dataset subsets, they were able to dynamically assess the RF model's generalization performance and feature importance on a dataset with roughly 6500 DFT-calculated configurations. They also achieved strong model stability and accuracy by fine-tuning the hyperparameters inside the inner CV loops. Furthermore, the integration of SHAP into this layered CV framework allowed for a detailed, iterative examination of the feature attributions, providing important insights into the complex interplay between the structural, chemical, and electronic factors influencing the hydrogen adsorption on N-doped carbon nanotubes (Fig. 8c). Moreover, the work of Ebikade et al. takes a direct experimental approach instead of depending on theoretical simulations.¹⁴⁷ Expecting higher costs through experiments, the authors wisely applied the iterative AL strategy. Their input features constituted a nine-dimensional parameter space that takes into account structural characteristics like N species and pore volume in addition to synthesis conditions like hold time and final temperature. Despite resource limitations, this approach resulted in effective exploration and optimization in a complicated multidimensional space. The authors were able to determine the ideal final conditions with better HER performance than earlier reports,^148,149 all in less than 20 experimental runs. Moreover, graphitic N content was identified as the most decisive material feature for electrochemical performance.

Fig. 8 (a) Heat map of the Pearson correlation coefficient among the selected features for ML modeling of γ-graphyne nanoribbons, (b) measurement of the feature importance using the SHAP method (a and b are reproduced from ref. 145 with permission). (c) Left: Global SHAP importance rankings for the top 10 features in adsorption energy prediction: Bar heights represent CV averages, with error bars showing ±1 standard deviation across outer CV folds. Each bar is annotated with correlation coefficients between the SHAP values and the feature values. Right: Local SHAP value distributions for the 10 most impactful features: this is shown across all test set observations. Vertical data point dispersion indicates dense clusters of similar ϕ_j values, with color-coding reflective of corresponding feature values (c is reproduced from ref. 146 with permission).

TM metal atoms doped into a graphene matrix could serve effectively as electrochemical reaction catalytic centers while tuning local electronic structures of the carbon materials.¹⁵⁰ Among the popular experimentally reported doped TM-(N)C structures, Liu et al. have made significant strides in integrating ML with theoretical methods as well as experimental validation to explore cobalt single-atom catalysts (Co SACs).¹⁵¹ Using supervised learning, particularly a BPNN with three hidden layers, they analyzed MD-extended X-ray absorption fine structure (EXAFS) spectra to accurately determine the local chemical environments of Co SACs. This ML approach, trained on a dataset of 1000 configurations generated from EXAFS simulations, enabled the elucidation of the atomic structure of edge-rich Co single atoms, revealing proportions that were 65.49% of Co-4N-plane (Co-4N-P), 13.64% in Co-2N-armchair (Co-4N-A), and 20.86% in Co-2N-zigzag (Co-4N-Z). Except for the outstanding electrochemical performance for HER, the leveraged ML method in this work has successfully deepened understanding of the HER mechanism on this electrocatalyst system. Besides Co–(N)C, there is a wide range of TMs that are potential candidates. Fung et al. investigated the vast possibilities of 3d–5d TM atoms doped in N-doped two-dimensional (2D) graphene (Fig. 9a) and nanographenes of several sizes.¹⁵² Using descriptors such as d-band centers, formation energies, and atomic properties, they applied regression models such as KR regression and neural networks and achieved notable accuracy, with the RMSE as low as 0.15 eV. Despite that V, Rh, and Ir have been identified as the top candidates that could significantly enhance HER activity, SISSO was applied to directly provide a straightforward formula. Similarly, Baghban et al. reported approximately the same screening candidate space in the same system,⁴⁰ and they have drawn consistent results identifying Ir, Rh, Fe, V, Sc, and Co as the most promising TM dopants. Moreover, the contribution of this work is that sensitivity analysis as a post-method has been applied to bring deeper insights into feature importance (Fig. 9b). Several valence electrons and the covalent radius have shown a high relevancy of 0.74, indicating their dominant impact on the adsorption energy. Recently, Zhou et al. further delved into the complex interplay between TM and their surrounding atoms in single-atom catalysts, investigating configurations where N atoms in typical TM–N₄ structures are directly substituted with C atoms with different degrees.³⁸ They employed a novel topology-based, multi-scale convolution kernel ML algorithm and used input features like atomic group number and electron count. The strategy employs multi-scale convolution kernels of varying sizes, enabling the simultaneous extraction of both global and local information from the material's feature matrix (Fig. 9c). Notably, Zhou et al. also leveraged ML models to predict not only the typically studied ΔG_H* but also, comprehensively, the energies of H₂ dissociation and water molecule adsorption. The models have achieved impressive prediction accuracies (R² scores ranging from 0.931 to 0.965), which allowed the authors to identify promising electrocatalyst materials for HER and hydrogen sensing, such as Pt and Sc atoms in specific coordination environments.

Fig. 9 (a) Three examples of optimized structures of H adsorption on the transition-metal single atom embedded on N-doped graphene (reproduced from ref. 152 with permission). (b) The relevance factor of different input variables by sensitivity analysis (reproduced from ref. 40 with permission). (c) Schematic of the topology-based, multi-scale convolution kernel ML model (reproduced from ref. 38 with permission).

Researchers have also explored other more complex variations, like dual-TM-atom doped graphene¹⁵³ (TM₁TM₂@N₆) and TM-graphdyine (GDY).¹⁵⁴ As expected, ML surrogate modeling of DFT has also been proven effective in these systems by successfully screening out the best candidate configurations, AuCo/NiNi@N₆ and GDY-Eu/Sm, while saving immense computational costs.

3.2.2. Special carbon structures. Besides the commonly studied graphene, other 2D carbon structures can serve as flexible substrates for capturing and anchoring heteroatoms, leading to vast exploration space and possibilities. Graphitic carbon nitride (g-C₃N₄) is distinguished by its well-defined 2D structure, featuring a distinctive arrangement of cavities formed by tri-s-triazine units linked through planar amine bonding. These structural voids, or cavities, are not merely physical spaces, but play a critical role in the material's chemical reactivity and physical properties by facilitating the capture and distribution of heteroatoms and molecules. The homogeneous, high-density distribution of nitrogen atoms within the matrix further contributes to the unique electronic and physical properties of g-C₃N₄, making it an excellent substrate like graphene.¹⁵⁵ Jyothirmai et al. extensively studied TM single atoms on four different types of anchoring sites on g-C₃N₄¹⁵⁶ (Fig. 10a). High-throughput DFT calculation identified that B@N₁, Mn@N₁, and Co@N₁ have promising HER performance (Fig. 10b). The authors further trained ML models combined with feature engineering to remove redundant features and successfully obtained a best-performing support vector regressor (SVR) with an R² of 0.95 and a low MAE of 0.08 eV. With it, not only the top three candidates for g-C₃N₄ were further validated, the feature importance ranking analysis also provided valuable insights into the structure–activity relationship. Umer et al., however, broadened the scope beyond g-C₃N₄, incorporating more substrates like π-conjugated polymer, pyridinic graphene, and hexagonal boron nitride with single- and double-vacancy defects¹⁵⁷ (Fig. 10c). Their most notable innovation is addressing the practical issue of catalyst stability by innovatively implementing a classification-regression approach. They initially used an ET classification model to identify stable candidates via thermodynamic stability energy (E_stab) and dissolution potential (U_diss). Then, the authors employed a CatBoost regressor to predict HER activities. With good accuracy, an RMSE of 0.18 eV and an R² score of 0.88, the model has finally led to the discovery of 20 efficient candidates, such as Pd@B₄ and Ru@N₂C₂, that are both stable and active. Similarly, Wang et al. reported multiple N–C systems as a substrate for TM dopants, with the addition of phthalocyanine (Pc), covalent organic frameworks (COFs), and metal–organic frameworks (MOFs).¹⁵⁸ In this work, ML is primarily used to determine the most important factors that could affect HER activity (Fig. 10d). The authors used recursive feature removal to prevent dimensionality catastrophes caused by an excessive number of input features. Correspondingly, the top performing GBDT regressor achieved an acceptable R² and MAE of 0.87 and 0.25 eV, respectively, with the help of the key 14 features. This enabled the authors to further demonstrate the pattern that the most important parameters influencing the HER process are the geometric structure surrounding the TM active center and the electronic structure of the d orbitals for the TM atom. Based on the same purpose, Tahini et al. investigated fullerene C₆₀ (Fig. 10e) using ML models to unravel the origin of activity, and found that the most decisive feature related to the electronic property of the active C atom rather than the captured TM atom.⁴²

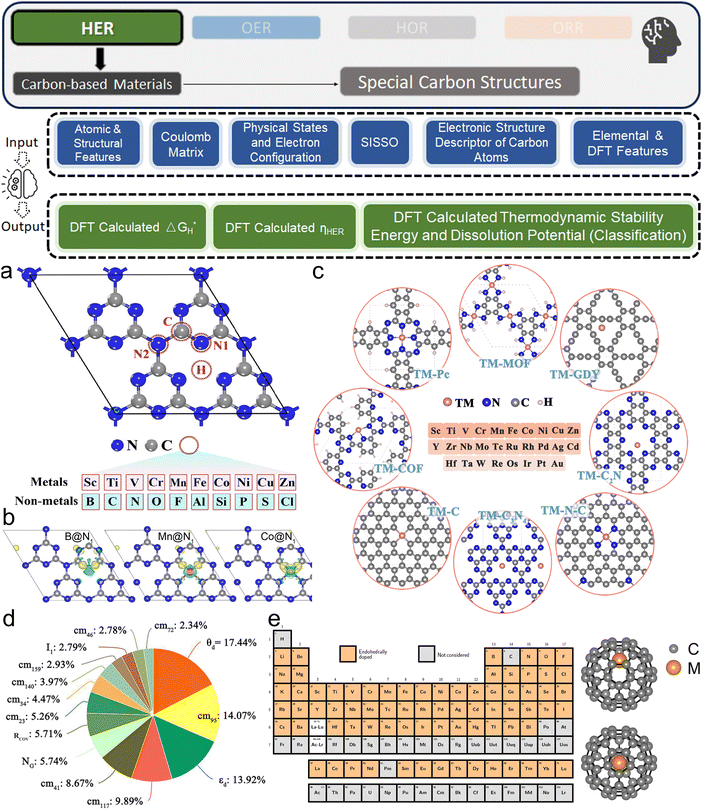Fig. 10 (a) The top view of the g-C₃N₄ catalyst's optimized shape. The C and N atoms are represented by the blue and gray colored balls, respectively. Different dopant locations are indicated by the dashed circles with letters: Two-fold coordinated nitrogen bonded to two C atoms (N1), triazine ring-connecting nitrogen (N2), and carbon bridging three N atoms. (b) The structure and charge density differences of: B@N1-site, Mn@N1-site, and Co@N1-site, in the order of left to right. Electron depletion and accumulation are indicated by the blue and yellow isosurfaces (0.002 e Å⁻³), respectively (a and b are reproduced from ref. 156 with permission). (c) 2D materials structures with TM embedded at various defect sites (reproduced from ref. 157 with permission). Color code: metal, magenta; B, light pink; N, blue; C, gray; O, red; H, cyan. (d) The feature importance of the GBDT model (reproduced from ref. 158 with permission). (e) Left: The periodic table with the elements that have been thought to have endohedral sites in C₆₀ shaded in orange. Right: Schematics showing dopants may be positioned inside the cage in the middle or off-center (reproduced from ref. 42 with permission).

3.3. TM compounds

3.3.1. Chalcogenides. In the pursuit of efficient, durable, and cost-effective electrocatalysts for HER, in addition to the previously discussed metal and carbon materials, nonmetal TM compounds have emerged as promising alternatives to noble metal catalysts.¹⁵⁹ These catalysts, which typically include TM chalcogenides,^160,161 phosphides,¹⁶² carbides,¹⁶³ and MXenes,¹⁶⁴ have demonstrated remarkable HER performance that is comparable to Pt-containing catalysts, owing to their ability to fine-tune electronic structures and improve interaction with substrates. Therefore, the abundant possibilities in doping control strategies have also led to numerous recent works employing ML methods to accelerate research in this system. Among them, transition metal chalcogenides (TMCs) are the most extensively studied systems by experts in this field.

Beginning with the basic pure 2D MoS₂ clusters, Jäger et al. extensively investigated the system,¹⁶⁵ focusing on the training set size and structural descriptors (SOAP, MBTR, ACSF etc.) that could better predict the potential energy surface (Fig. 11a), reflected in the ΔE_H*. They employed a comprehensive dataset of approximately 10 000 DFT-based single-point calculations, featuring MoS₂ and AuCu nanoclusters, to train their models. The study highlighted the effectiveness of the SOAP descriptor in accurately predicting hydrogen adsorption energy, with a notable MAE of 0.13 eV for MoS₂ clusters. Wei et al., however, drive their exploration based on experiments in order to optimize the synthesis conditions of MoS₂ within a BO framework.¹⁶⁶ They employed hydrothermal synthesis techniques with parameters such as temperature, reaction time, and precursor concentrations as input features for their ML model. The ML approach, particularly using GP belief models and the upper confidence bound policy, effectively identified optimal synthesis conditions, resulting in the optimum sample with notable HER performance. The ML approach or the HER performance is evidenced by its low overpotential at 10 mA cm⁻² (η₁₀ = 240 mV) and Tafel slope (64 mV dec⁻¹). Patra et al. employed GA alongside MD and high-resolution transmission electron microscopy (HRTEM) to investigate the defect dynamics in 2D MoS₂.¹⁶⁷ Their approach determined that extended line defects are more stable sulfur vacancy configurations than isolated vacancies. This finding further elucidated the critical role of defects in the 2H-to-1T phase transition and demonstrated the effectiveness of ML in advancing the understanding of complex material phenomena.

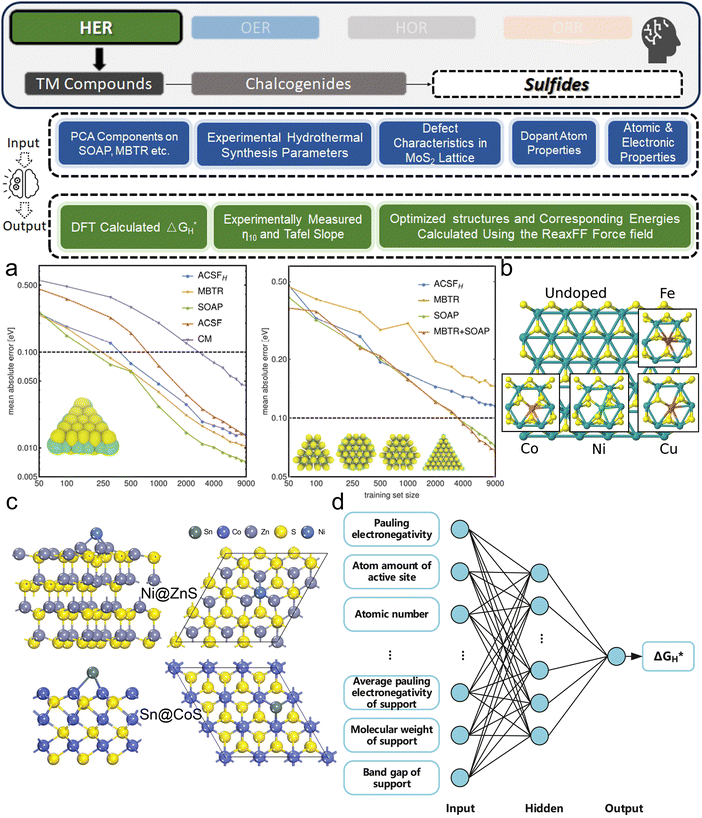Fig. 11 (a) Learning curves for different MoS₂ datasets show the MAE for different training set sizes (reproduced from ref. 165 with permission). (b) Basal plane of 2H-MoS₂ and its local structural deformations (insets) when Fe, Co, Ni and Cu are doped at substitutional Mo sites (reproduced from ref. 168 with permission). (c) Structure models of two example chalcogenides-supported TM single-atom catalysts: Ni@ZnS and Sn@CoS, and (d) BPNN input and output schematic (c and d are reproduced from ref. 169 with permission).

Incorporating heteroatoms as dopants into TMCs serving as substrates can lead to modifications in local electronic structures and other material characteristics, meriting detailed exploration. Hakala et al. delved into typical cases where common TMs such as single Fe, Co, Ni, Cu atoms are doped into MoS₂¹⁶⁸ (Fig. 11b). They applied RF for both classification and regression tasks, targeting regularly chosen ΔG_H* as the output feature for accessing HER potentials. The ML model revealed that the type of edge (Mo or S) and the specific dopant (Fe, Co, Ni, Cu) are the most decisive factors that would determine the hydrogen adsorption characteristics. Tu et al. further extended the diversity by including more TM dopants and more sulfides beyond MoS₂: CdS, CoS, FeS, and ZnS.¹⁶⁹ But unlike the last work's assumption, in which the TM atoms have directly replaced Mo atoms, the TM atoms in this work are loaded on the surface (Fig. 11c). A three-layer BPNN (Fig. 11d) could reach a promising R² over 0.95 and MSE less than 0.016 (eV)² for predicting ΔG_H* after training. With it, the authors successfully identified Sn@CoS and Ni@ZnS as the most promising catalysts among candidates with a theoretical ΔG_H* of only 0.04 eV and −0.05 eV, respectively.

In addition to the sulfides, the chalcogen elements in TMCs can include Se or Te. Similar to the previously mentioned MoS₂ structure, transition metal dichalcogenides (TMDCs) can be experimentally synthesized into monolayers of 2D materials. This would yield a rich specific surface area and abundant active sites. Further considering combinations of various 2D TMDCs for heterojunction structures, the potential exploration space for ML applications could be extensively expanded. Lee et al. proposed to use symbolic regression to find optimal descriptors for predicting ΔG_H* on 2D TMDCs.¹⁷⁰ Their novel genetic descriptor search method efficiently identified descriptors without intensive calculations, using a dataset of only 70 TMDCs. Like other typical ML algorithms, this approach successfully leveraged 27 primary TMD features, including atomic radii and valence electrons, to generate descriptors that align with chemical knowledge. The model has facilitated the discovery of optimal materials for catalytic performance by successfully identifying MnS₂/FeS₂/TaS₂ with chalcogen vacancy as best candidates. Ran et al. also studied various 2D TMDCs (Fig. 12a) and combined both black-box ML modeling with symbolic strategy using linear square regression.¹⁷¹ By narrowing down from 27 features to five key features, including local electronegativity and valence electron number, they developed ML models using RF and BPNN (possibly with skip-layer connections). These models achieved a high fitting degree (up to 0.94) but were poor in explainability. Linear square regression (Fig. 12b) revealed a quantitative expression as ΔG_H* = 0.093 − (0.195*LEf + 0.205*LEs) – 0.15 Vtmx (LEf/LEs: nearest/next nearest neighbor local electronegativity; Vtmx: average valence electron number of TM-X). This formula could reach an impressive R² of 0.74 (Fig. 12c), further indicating that ΔG_H* decreases with the valence electron number and electronegativity of local structure. Doping a second TM into existing TMDCs significantly expands the pool of potential catalysts for ML exploration. Lee et al. studied TM-doped MX₂ systems (Fig. 12d), employing an ML approach that used 28 atomic features to predict ΔG_H*.¹⁷² The tree-based regression models revealed that the most influential are (i) the number of valence electrons, (ii) the distance of the valence electrons, and (iii) the electronegativity of the TM dopant. Chen et al. additionally explored macroscopic patterns in a similar system,¹⁷³ revealing that certain doping concentrations in TMDCs significantly influence the ΔG_H*, indicating enhanced HER performance at specific alloying ratios (Fig. 12e). They attributed this trend to the alloying effect, which alters the electronic structure and p-band center of the adsorption sites, thereby modulating the catalytic activity for HER. Lastly, novel heterojunctions could be obtained by stacking different 2D materials like TMDCs. Additionally, the formation of interfaces can potentially optimize electrical conductivity, electronic structures, and the density of active sites.^174,175 Ge et al. considered in their study the heterostructures formed by different 2D MX₂ single layers,¹⁷⁶ taking the rotation angle, bond length, layer distance, and the ratio of bandgaps of two materials into consideration. Using the simple least absolute shrinkage and selection operator (LASSO) regression method, they efficiently identified key physical descriptors affecting the adsorption performance of these heterostructures. This approach led to the discovery of MoTe₂/WTe₂, with a 300° rotation angle as the optimal structure, achieving remarkably low overpotentials of 0.03 V for HER and 0.17 V for OER. Pham et al. ambitiously broadened the investigated space beyond the heterostructure formed by MX₂ layers, but also MX₂ with M′X′ (e.g., ZnO, GaN) layers.¹⁷⁷ To describe such complex systems for ML models, they meticulously screened 46 input features derived from atomic properties and positional information, and the ML surrogate model successfully identified MoS₂/ZnO as the best candidate. This is proven by both its exceptional theoretical performance via a ΔG_H* of −0.02 eV and dynamical stability without imaginary frequency in phonon dispersion calculations.

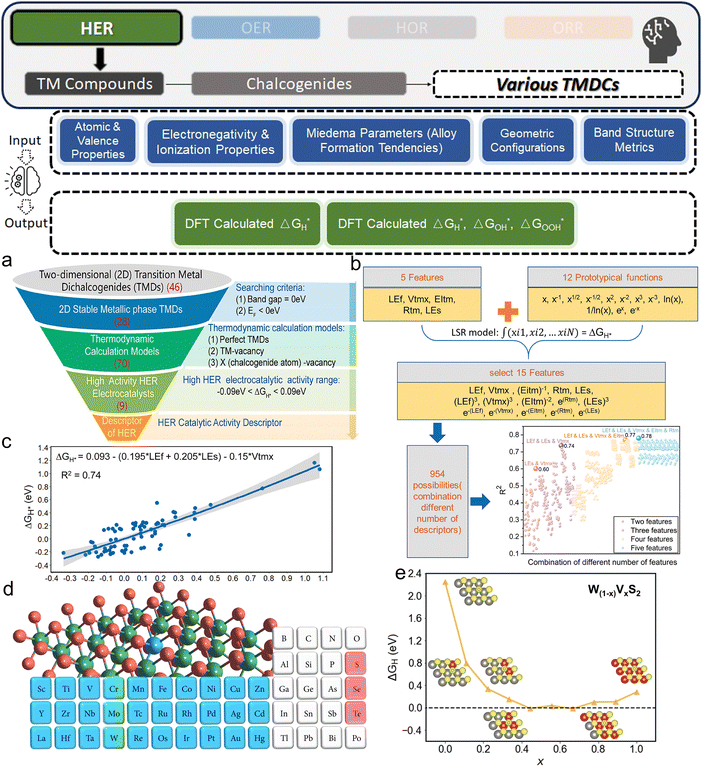Fig. 12 (a) Workflow of multilevel, high-throughput calculations for seeking metallic, lowest-energy, −0.09 eV ≤ ΔG_H* ≤ 0.09 eV 2D-TMD materials. (b) Illustration of the linear regression fitting process. (c) distribution of the ΔG_H* versus the descriptor obtained by least-squares regression (a–c are reproduced from ref. 171 with permission). (d) Geometric structure and colored periodic table representation of TM@MX₂: in this illustration, the TMs are depicted in blue, M elements (Cr, Mo, and W) in green, and X elements (S, Se, and Te) in red (reproduced from ref. 172 with permission). (e) Lowest ΔG_H* values for hydrogen adsorption on a W_(1−x)V_xS₂ system across various compositions (x): the graph displays how ΔG_H* values change with different V concentrations in W_(1−x)V_xS₂. Insets provide visual examples of adsorption configurations that result in the lowest ΔG_H*. In these configurations, V, W, S, and hydrogen atoms are represented in red, grey, yellow, and pink, respectively (reproduced from ref. 173 with permission).

3.3.2. Phosphides, carbides, and borides. In addition to chalcogenides, other TM compounds like phosphides, carbides, and borides have been proven effective in HER electrocatalysts.¹⁷⁸ Wexler et al. investigated the Ni₂P system,¹⁷⁹ focusing on enhancing the HER activity at the Ni₃-hollow site through nonmetal surface doping, particularly with chalcogens (Fig. 13a). They trained regularized RF to predict ΔG_H* and further identified the Ni–Ni bond length as a critical structural descriptor. Following this, their ML analysis, using a dataset of 55 DFT-derived structures, demonstrated that such dopants predominantly exert a “chemical pressure” effect on Ni₃P₂ (0001), a structural influence surpassing electronic interactions and emphasizing the paramount importance of geometric considerations in the enhancement of electrocatalytic performance. Zhang et al. focused on comparatively more complicated amorphous Ni₂P surfaces by uniquely separating the relaxation and the adsorption processes apart.¹⁸⁰ They first used GA to obtain a stable configuration of the complex amorphous system, then deployed a novel two-step ML approach (Fig. 13b) to predict hydrogen adsorption energies E_H (like ref. 165 and equals to E_frozen + E_relax). Initially, they applied GBDT and a high-dimensional neural network model to predict the frozen adsorption energy E_frozen, relying solely on the local structural environment. Subsequently, they introduced an atomic expansion method to estimate the relaxation energy E_relax induced by hydrogen adsorption, effectively incorporating structural flexibilities into the model. This innovative “two steps” approach allowed for a more accurate prediction of total adsorption energies as well as the consequent recognition of five local active site patterns that are superior for HER. Hu et al. put their interest in another stoichiometric composition of Ni₅P₄,¹⁸¹ which is experimentally validated to be superior for HER.¹⁸² Similarly, in the system they found that the bond number and relative position with neighbors are crucial for catalytic activity, and a detailed investigation revealed how these factors affect the efficiency of top P and bridge Ni–Ni sites. Cao et al. investigated CoP systems with potential TM dopants, employing a multi-level screening methodology that combined DFT calculations and symbolic regression.¹⁸³ Their study revealed the critical role of the work function difference (ΔΦ) and d-band center in regulating ΔG_H* in the system. Subsequently, they experimentally validated ML predictions by synthesizing Al, Mo, and V-doped CoP samples. The Al-CoP showed a low η₁₀ of 75 mV, which could be attributed to a larger surface area that introduces a higher density of active sites. The doping has also endowed the active sites with a higher average turnover frequency. Yan et al. extensively explored the realm of various TM phosphides up to ternary systems.¹⁸⁴ Their approach incorporated a rich dataset comprising data from existing literature and self-contributed calculations, encompassing diverse TM phosphides systems. Notably, their feature importance analysis shed light on the critical influence of factors such as the p orbital electron number and atomic volume, uncovering valuable insights into the design of efficient TM phosphide catalysts, which is partially consistent with previous studies focused on Ni/Co phosphides. Lu et al. studied TM single atoms anchored on phosphorus carbide (PC₃) monolayers as catalysts¹⁸⁵ (Fig. 13c). In addition to identifying Fe, Nb, and Mo@PC₃ as the top candidates based on their catalytic activity, the authors used ML for data mining. The results revealed that the first ionization energy, bond length of TM–H, and d band center were the most influential descriptors for H atom adsorption activity on TM@PC₃. In a parallel exploration of TM-doped materials, Chen et al. delved into a similar system of TM-doped diamondlike boride C₃B monolayers for both HER and OER¹⁸⁶ (Fig. 13d). Their investigation unveiled Fe, Ag, Re, and Ir as promising candidates for HER, while Ni- and Pt-doped C₃B demonstrated the potential to function as bifunctional catalysts. Employing a similar ML data mining approach, they also identified the first ionization energy and the number of d electrons as impactful, consistent with the previously mentioned study on PC₃.

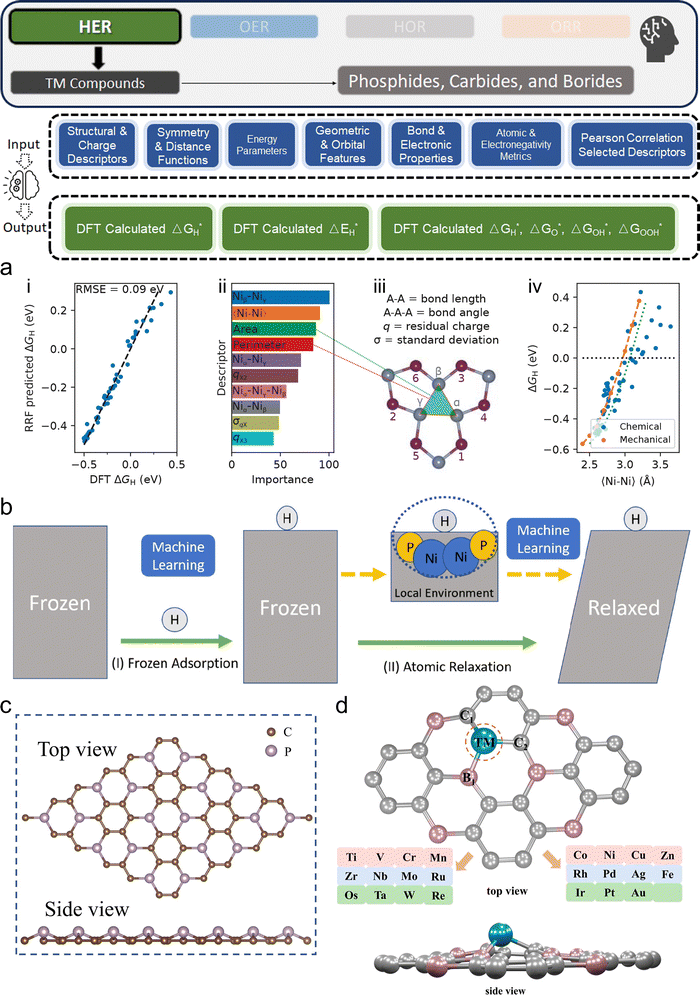Fig. 13 (a) (i) ΔG_H* predictions by the regularized RF versus DFT: the black-dashed line indicates perfect correlation. (ii) Top 10 descriptors’ relative importance from the model. (iii) Descriptor definitions: The three Ni atoms closest to the first doping site are labeled α, β, and γ, based on proximity. (iv) Impact on ΔG_H* by Ni–Ni bond length: the role of chemical (via nonmetal doping) and mechanical pressure (by immobilizing surface Ni atoms), identifying the optimal Ni–Ni bond length for HER as 2.97 to 3.07 Å, with adjustments for bond contraction upon H adsorption, highlighted by a green dotted line (reproduced from ref. 179 with permission). (b) Workflow of the proposed stepwise strategy for predicting adsorption energy E_H on amorphous catalyst surfaces using ML: this includes two key stages – (I) calculating frozen adsorption energy, where the initial adsorption energy is estimated without considering atomic rearrangements, and (II) determining structural relaxation energy, which accounts for the energy changes resulting from structural adjustments upon adsorption (reproduced from ref. 180 with permission). (c) Schematic structure of 3 × 3 PC₃ monolayer (reproduced from ref. 185 with permission). (d) Top and side views of the TM/C3B monolayer structure (reproduced from ref. 186 with permission).

3.3.3. MXenes. MXene-related systems (M_xX_yT_z, M = TM; X = typically C and/or N; some studies also include B; T: terminal group, typically chalcogenide elements.) are promising for HER due to their high electronic conductivity, large active surface area, and structural stability, which facilitate enhanced catalytic activity and efficiency.¹⁸⁷ While MXenes’ sensitivity to oxidation is a consideration, it is less critical in the low-potential environments typical of HER processes. Their compositional versatility allows for extensive tuning of properties through element substitution and surface functionalization, making ML a powerful tool for accelerating discovery. Liang et al. studied a typical widely studied system of Ti-based MXenes with a Ti₃C₂T₂ basic structure (Fig. 14a).⁴⁴ Using a set of 32 elemental properties as input features, they successfully predicted not only ΔG_H* but also the per-atom cohesive energies. Notably, their approach revealed 21 novel MXene catalysts with HER activity surpassing that of Pt, and seven of them were dynamically and thermally stable. Similarly, Wang et al. also explored the Ti₂CO₂ system with doped single TM atoms.¹⁸⁸ They identified several promising candidates, notably Ti₂CO₂–W, which exhibits exceptional catalytic activity, conductivity, and stability due to p–d orbital hybridization effects. Moreover, the authors used symbolic regression to obtain a predictive descriptor based on the Fermi level and M–O bond lengths. As a result, this descriptor not only facilitates the discovery of efficient HER catalysts within the Ti₂CO₂ system source domain, but also could show considerable potential in terms of accuracy to similar Zr₂CO₂ and Ta₂CO₂ systems. In their subsequent research,⁴³ the team shifted from using symbolic regression for single descriptor identification to applying a comprehensive input feature study for single TM atom-doped Mo-based Mo_n+1C_nT_x systems (Fig. 14b). In addition to identifying Ru, Zn, and Os as the best elements, this nuanced approach led to the identification of five key descriptors, including Fermi level and d-band center, thus significantly enhancing the prediction accuracy for ΔG_H* in Mo₂CO₂ systems. Furthermore, they successfully extended these ML-derived descriptors to the W₂CO₂ system, highlighting the robustness and transferability of their ML methodology in electrocatalyst discovery. Sun et al. considered a single-TM atom doped particularly in MBenes with n = 1, 2 of the layer ratio.¹⁸⁹ Their results led to the identification of Co₂B₂ and Mn/Co₂B₂ as the best catalyst candidates, with near-zero ΔG_H* values. Besides, their ML data mining highlighted the Bader charge transfer and the d-band center as the most decisive descriptors, in good agreement with the previous two works.

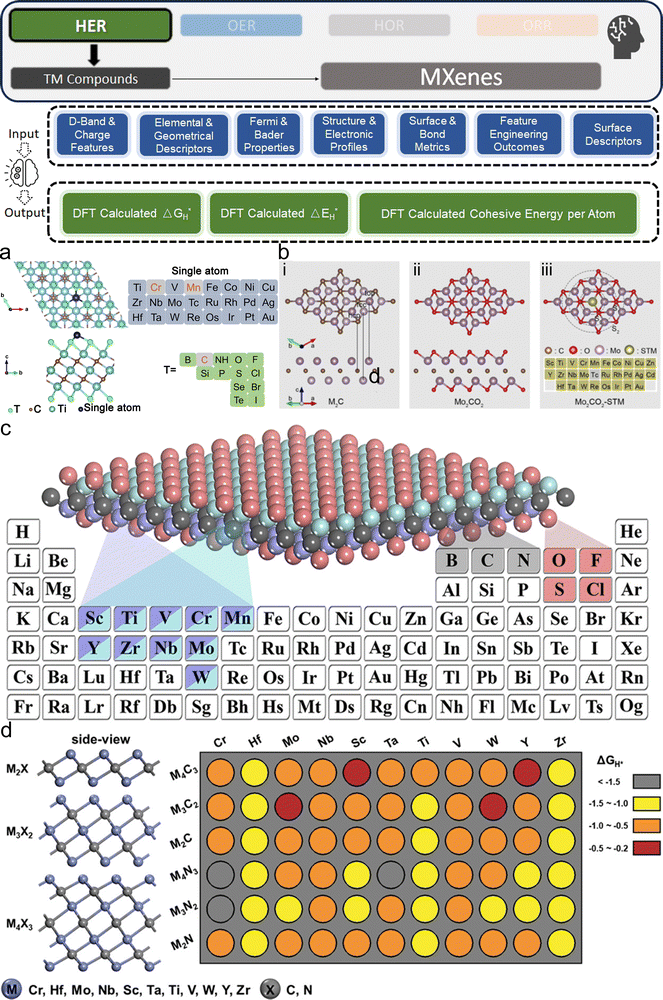Fig. 14 (a) Optimized atomic structure of single-atom-loaded MXenes with surface termination elements and single-atom elements, excluding Cr and Mn for the single atom position and C for the surface termination position (reproduced from ref. 44 with permission). (b) Top and side views of a 3 × 3 × 1 supercell of Mo-based MXene structures. (i) M₂C structure: Top, fcc, and hcp sites indicating potential O adsorption areas; (ii) Mo₂CO₂ with functional group O; (iii) single-atom-doped model of Mo₂CO₂-STM (single transition metal), where STM includes 3d, 4d, and 5d metals. S₀, S₁, and S₂ denote three types of O equivalent positions for H adsorption. The Tc atom is excluded due to its radioactivity (reproduced from ref. 43 with permission). (c) The selected elements for MM′XT₂ MXenes (M/M′ = Sc, Ti, V, Cr, Mn, Y, Zr, Nb, Mo, or W; X = B, C, or N; T = O, F, Cl, or S), leading to optimized structures of pristine and functionalized MXenes (reproduced from ref. 190 with permission). (d) Left: Side views of bare MXenes, with early transition metals (purple) and C/N (gray) depicted. Right: Color block map showing ΔG_H* for bare MXenes, where gray, yellow, orange, and wine-red circles indicate ΔG_H* intervals of <−1.5, −1.5 to −1.0, −1.0 to −0.5, and −0.5–0.2 eV, respectively (reproduced from ref. 191 with permission).

Aside from single-atom TM doping, the TM element in MXenes could be further tuned in different ratios and types. Wang et al. studied 2D MXene-ordered binary alloy M₂M′X₂O₂ and M₂M′₂X₃O₂, allowing the second TM to exist in large amounts.¹⁹² Their interdisciplinary ML approach identified 110 promising MXene catalyst candidates with superior HER activity compared to Pt, out of a pool of as many as 2520 candidates. Abraham et al., however, further expanded the search space for 2D MXene-based catalysts by including F, S, and Cl terminations alongside O (Fig. 14c).¹⁹⁰ They trained a GBDT regressor with feature selection and hyperparameter optimization on 1125 systems to further predict the activity of all possible 4500 MM′XT₂-type MXenes. But in the post-ML analysis for insights in structural and electronic descriptors, they revealed that the number of valence electrons and the electron affinity of the terminating groups are decisive. Similarly, Zheng et al. considered M₂X, M₃X₂, and M₄X₃ structures with different M and X, also with and without the S as T (Fig. 14d). Notably, they also took hydrogen coverage into consideration.¹⁹¹ As a result, Os₂B and Sc–N based S-MXenes exhibited promising catalytic activity, with ΔG_H* values approaching zero over a wide range of hydrogen coverages. Additionally, their ML data mining revealed that the atomic mass and electronegativity of the T atom play crucial roles in determining catalytic performance. Although we can see that it is in good agreement with ref. 190 where T is considered as a variable, it is different from ref. 192 for M₂M′X₂O₂ and M₂M′₂X₃O₂ systems. As the authors of ref. 192 have only considered O as the terminal element, geometrical and electronic features related to the alloying effect are found to be the most important. Such comparisons between different ML works on similar systems should remind readers of the multifaceted nature of materials discovery and catalyst optimization, where the importance of specific descriptors and factors can vary depending on the alloying effects, terminations, composition of the electrocatalysts, and, most importantly, the search space that was defined.

3.3.4. Emerging materials. In the quest for efficient electrocatalysts for HER, the exploration has already extended beyond the well-trodden paths of previously mentioned chalcogenides, phosphides, and MXenes to encompass a diverse array of emerging materials, showcasing the potential of innovative compositions and structures in enhancing electrocatalytic performance. Zheng et al. investigated pnictides like novel 2D MA₂Z₄ type materials, where A is C, Si, Ge, or Sn, and Z stands for N, P, or As.¹⁹³ They uniquely applied recursive feature elimination and genetic programming to refine and reduce the feature set for their ML model, optimizing prediction accuracy and computational efficiency by identifying an optimal feature dimension. As a result, the model with optimized features could predict ΔG_H* with a low RMSE of 0.14 eV. Based on this, NbSi₂N₄ and VSi₂N₄ were further studied as the most promising HER catalysts. Chen et al. explored the application of ML to stable β phase 2D-arsenenes doped with heteroatoms.¹⁹⁴ To address the challenge of a skewed distribution in their dataset, where the number of materials with ideal catalytic performance was significantly smaller than those with less desirable properties, they implemented the novel synthetic minority oversampling technique (SMOTE). This data augmentation method effectively balanced the dataset, enhancing the generalization performance of their ensemble learning model and preventing the overfitting typically associated with stochastic oversampling. By generating 120-dimensional input feature vectors using Matminer,¹²¹ their approach significantly improved, achieving a prediction accuracy of 81% for identifying promising catalysts. This is a substantial increase from the 69% accuracy observed without SMOTE preprocessing. This strategic use of SMOTE enabled the successful identification of 13 Fe-doped arsenenes as potential HER catalysts. Liu et al. investigated novel single-atom TM doped on 2D GaPS₄ materials.¹⁹⁵ The GBDT regressor surrogate model achieved a high R² score of 0.935, which led to the identification of Pt@VS₁-GaPS₄ as an optimal catalyst with desirable stability (U_diss > 1 V versus SHE) and activity (|ΔG_H*| < 0.2 eV). Their data mining also found a strong correlation of electron affinity and first ionization energy with adsorption behavior in the system, while strain engineering notably further enhanced the catalytic efficacy of Pt@VS₁-GaPS₄. Yang et al. used the comprehensive database 2DMatPedia¹⁹⁶ based on high-throughput first-principles calculations, which includes as many as 1037 exfoliable 2D materials.¹⁹⁷ They prescreened materials based on criteria such as exfoliation energy and electrical conductivity, and, most importantly, differential ΔG_H* as a key thermodynamic descriptor for screening. This resulted in the identification of nine promising 2D catalysts, including NbS₂ and IrTe₂, with active basal planes showing potential HER performance comparable to that of Pt-based catalysts. Wu et al. further applied ML on the 2DMatPedia database,¹⁹⁸ leveraging a CGCNN to efficiently predict adsorption energies. Their approach, using properties of atoms and bonds as input features, achieved a remarkable prediction accuracy of 95.2%, enabling the rapid identification of 38 stable and high-performance catalysts from an immense pool with more than 6531 candidates.

3.4. Statistical analysis and summary

The ML approaches across metal/alloy, carbon-based, and TM compound electrocatalysts for HER, as introduced in this section, reveal a vibrant and dynamic field that is rapidly evolving to meet the challenges of sustainable energy. A common theme is the integration of ML with high-throughput computational methods, typically via DFT and, in some cases, MD or experimental data, to accelerate electrocatalyst discovery and optimization. Iterative model refinement, leveraging techniques like feature importance analysis, is a shared strategy across material classes. Adaptive learning and surrogate-based optimization are particularly notable for their efficiency in research methodologies. Across all material classes, ΔG_H* is commonly adopted as an indicator metric for HER activity, though some studies prefer hydrogen binding energy ΔE_H*, which is ΔG_H* without thermal correction. Interpretation methods like feature importance ranking and SHAP are utilized to identify critical descriptors, enhancing the interpretability of ML models. This approach not only aids in pinpointing factors governing catalytic performance but also highlights the nuanced differences in what makes each material class effective.

The nuanced differences in algorithm application, feature selection, and paradigm adoption reflect the unique characteristics and complexities of each material class. Hence, we have visualized the statistical data of input features, applied ML algorithms, etc., for meta insights as shown in Fig. 15 (based on Table S1, ESI†). The bar plot summaries provide a direct trend of popular choices of input features chosen and identified as decisive, and ML algorithms used and identified as the best-performing.

Fig. 15 Statistics for the HER section, including (a) utilized input features; (b) most important features recognized by ML model interpretation. (c) distribution of the dataset sizes used. (d) Utilized ML algorithms; (e) best ML algorithms.

Features. Through Fig. 15a, atomic intrinsic physical properties are the most popular, with electronegativity and first ionization energy frequencies significantly exceeding others. Fig. 15b provides more valuable results regarding the most important features identified by ML model interpretation results in the publications. The d-band center and the number of valence electrons are the top two features, followed by covalent radius and bond length. This might indicate that the electronic structure of valence electrons, particularly the d-band electrons of active metal atoms (whether within alloy crystal lattices or doped into carbon or TM compounds such as MXene), largely determines adsorption behavior and thus catalytic activity. This is particularly suitable for TM compounds and carbon structures, as these materials often exhibit complex electronic structures where the site d-band characteristics play a crucial role in determining their catalytic properties and adsorption behavior. For studies focused on metal and alloy electrocatalysts, coordination number is emphasized as a unique descriptor, representing the local microenvironment rather than the properties of the site itself. Whether the catalytic atom is unsaturated or saturated in coordination greatly impacts its electronic structure and adsorption behavior. Metal and alloy systems typically exhibit densely packed structures, such as the face-centered cubic structure of Pt, leading to shorter bond lengths. The valence electron properties of active site atoms are significantly influenced by their neighboring atoms. Consequently, catalytic studies on metals and alloys place great importance on crystal facets, with researchers considering whether active sites are coordinatively saturated or unsaturated, as this can significantly affect site activity. Therefore, crystallographic structural information is crucial for metal and alloy electrocatalyst studies. We hence suggest researchers interested in this system adopt physical-informed advanced frameworks like SOAP, ACSF, CGCNN, or instead have comprehensive consideration of structural relations description during manual feature engineering.

Dataset and ML algorithms. In Fig. 15c, the distributions of datasets prepared in HER-related ML research works are provided. A clear trend is that for metal/alloy, the average dataset size is significantly larger than that of carbon structures, with TM compounds having the smallest average dataset size with a median value lower than 100. These differences might be due to the complexity of TM compounds’ structures, but they are considered the most promising material system. Hence, based on Fig. 15d, the top three most utilized ML algorithms are RF, GBDT, and SVM, generally suitable for limited size datasets. In comparison, MLP, the basic ANN without special layers is becoming a popular choice for carbon structures and metal/alloy studies. As summarized in Fig. 15e, it was further revealed that representative/deep learning methods are the most frequently reported best-performing methods, surpassing commonly chosen GBDT and RF. The advantages might derive from their better non-linear ability to learn and numerically surrogate modeling the complex structural and electronic interactions. CGCNN is notable, as its graph representation strategy has proven effective in all three categories. However, researchers should still note that neural network frameworks are suitable for large and complex datasets, typically several thousand structures, as shown by the metal/alloy peak in Fig. 15c. Classical ML algorithms such as GP, RF, GBDT, and SVM might still be robust, with better interpretability when the dataset preparation budget is limited or target candidate space is of lower magnitude like for carbon structures or TM compounds.

4. ML-aided design of OER electrocatalysts

Building upon the prior discussion of the HER in electrolysis processes, it is crucial to delve into the equally significant, yet more challenging counterpart: the OER. While HER is necessary for hydrogen production, it is the OER that often dictates the efficiency and feasibility of the overall water-splitting process, particularly in practical water electrolyzers. The OER is marked by its anodic oxidation of water to produce oxygen, a step characterized by considerably more challenging kinetics due to a complex four-electron transfer mechanism. This complexity not only sets OER as the rate-determining step (RDS) in electrolysis but also elevates its importance as the main bottleneck to achieving overall system efficiency and sustainability. Despite the effectiveness of state-of-the-art Ir and Ru oxide catalysts in facilitating OER,^199,200 their high cost and scarcity pose significant hurdles. This reality has intensified efforts to explore alternative catalysts that can offer both economic viability and high performance, marking it a critical area of research in the advancement of energy conversion technologies.

The fundamental mechanistic understanding of OER has evolved, recognizing two primary pathways: the adsorbate evolution mechanism (AEM) and the lattice oxygen mechanism (LOM). AEM, the traditional pathway, emphasizes the sequential adsorption and desorption of intermediates on the catalyst surface, with the activity significantly influenced by the binding energies of these intermediates. Under alkaline conditions, the four steps involved four OH⁻ ions and the intermediate converted from *OH to *O then finally *OOH:⁵ (1) * + OH⁻ → *OH + e⁻; (2) *OH + OH⁻ → *O + H₂O + e⁻; (3) *O + OH⁻ → *OOH + e⁻; (4) *OOH + OH⁻ → * + O₂ + H₂O + e⁻. As for AEM in acidic conditions, the four steps and the corresponding oxygen-containing intermediates are the same with OH⁻ replaced by H⁺: (1) * + H₂O → *OH + H⁺ + e⁻; (2) *OH → *O + H⁺ + e⁻; (3) *O + H₂O → *OOH + H⁺ + e⁻; (4) *OOH → * + O₂ + H⁺ + e⁻. This mechanism aligns with the Sabatier principle, where optimal catalyst activity is achieved when intermediates are neither bound too strongly nor too weakly to the catalyst surface. However, the inherent scaling relationships among the adsorption energies of the intermediates pose limitations to the activity enhancement achievable through AEM. In contrast, LOM offers a paradigm shift by implicating the lattice oxygen atoms of a certain type of catalyst material (typically perovskite) in the OER process,²⁰¹ bypassing the limitations imposed by scaling relationships in AEM. This mechanism suggests that oxygen evolution can proceed through the participation of lattice oxygen, leading to the formation and subsequent refill of oxygen vacancies. This insight into the active involvement of lattice oxygen has been supported by experimental evidence such as oxygen isotope labeling and advanced spectroscopic techniques,²⁰² underscoring the dynamic nature of catalyst surfaces during OER. A brief schematic of OER mechanism is provided in Fig. 16.

Fig. 16 Schematic of the OER mechanism.

Both mechanisms are underpinned by the thermodynamics and kinetics of intermediate species formation and evolution, with the Gibbs free energy change of adsorption playing a central role in determining catalytic activity. The activity of OER catalysts is often depicted in volcano plots, illustrating the trade-off between intermediate adsorption energies that are too strong or too weak. This relationship has been instrumental in guiding the theoretical screening and rational design of new OER catalysts, leveraging descriptors such as the difference in the Gibbs free energy change of adsorption between critical intermediates. Specifically, difference in the Gibbs free energy change of adsorption between O and OH, namely, ΔG_O*–ΔG_OH* was found by Norskov et al.²⁰³ to be a concise but effective descriptor of the theoretical overpotential of OER in common AEM pathways. Meanwhile, ΔG_O* is proposed by Kolpak et al.²⁰⁴ to be the descriptor when LOM is taken as the mechanism. Nevertheless, due to the complexity of catalyst surfaces, computation and examination on all the four steps to find the real RDS is more comprehensive and reliable. The exploration of OER mechanisms has also highlighted the significance of the electrocatalyst's electronic structure, particularly the d-band center theory for metal-based electrocatalysts, in influencing the adsorbate binding strength and, consequently, catalytic activity.²⁰⁵

Like HER, as previously mentioned, the operational environment—whether alkaline or acidic—plays a pivotal role in dictating the choice of materials and the mechanisms at play. Commonly used catalysts in both environments include oxides of noble TMs like Ir, Ru. However, the differences between alkaline and acidic conditions have profound implications on the catalyst's performance and durability. In alkaline media, catalysts often exhibit lower overpotentials and enhanced stability due to the less corrosive nature of the environment, which is conducive to the use of a broader range of materials, including non-noble metals and their oxides. This versatility facilitates the development of cost-effective and efficient catalysts. Alkaline conditions also allow for the exploitation of mechanisms like LOM with greater efficacy, which is attributed to the favorable interaction between OH⁻ ions and the catalyst surface. Conversely, acidic environments necessitate the use of more corrosion-resistant materials, typically noble metals, to withstand the harsh conditions, thereby limiting the material choices. Hence, for both situations in addressing the limitations of noble metal-based catalysts, research has pivoted toward developing non-noble metal catalysts, including TM oxides, hydroxides, and perovskites,²⁰⁶ as well as carbon-based²⁰⁷ and hybrid compound.²⁰⁸ These efforts are driven by the dual goals of achieving high catalytic activity and stability while reducing costs. The rational design of these catalysts often involves strategies such as doping, alloying, and surface modification to optimize electronic structures, enhance active site availability, and promote favorable adsorption energetics. In light of these considerations, the intricate challenges of OER present a prime opportunity for the application of ML to unravel and optimize the multifaceted design of catalysts.

4.1. TM oxides

4.1.1. Noble metal-based oxides. As previously discussed, researchers have identified RuO₂ and IrO₂-based electrocatalyst systems as the most promising transition metal candidates over the years because of their enhanced electrical characteristics.^199,200 Early in 2016, senior researchers Ulissi and Nørskov (who laid the foundation for the OER mechanism) et al., used ML to automate the discovery and construction of surface-phase diagrams for electrocatalysis on IrO₂ and MoS₂ surfaces.²⁰⁹ By applying GP regression with adsorbate coverages as the input features, they efficiently predicted free-energy landscapes, reducing the computational effort from approximately 90 to just 20 DFT relaxations for accurate Pourbaix diagram construction. Timmermann et al. also used GP, but different from directly predicting OER activity descriptors, their target was to train a Gaussian approximation potential (GAP) to facilitate the global geometry optimization of rutile IrO₂ surfaces through simulated annealing.²¹⁰ This approach, powered by a dataset comprising 136 DFT-calculated structures, led to the discovery of thermodynamically stable surface complexions on (101) and (111) facets. This methodology revealed the significant potential of these surface complexions in reducing environments, a conclusion that was supported by comprehensive experimental investigations. Considering many unstudied IrO₂ and IrO₃ polymorphs, Ulissi et al. advanced the ML application using CGCNN to predict various ΔG values.²¹¹ They not only included different types of intermediates (O, OH, OOH), but also took surface H coverage into account. Their approach not only identified active sites with significantly lower overpotentials between 0.22 to 0.28 V, but also offered concrete design strategies, such as exposing more active low-index surfaces, creating smaller nanoparticles, and increasing the oxidation states of surface Ir atoms. Finally, as previously introduced, AL is an effective strategy when an exploration budget is limited. Flores et al. used an AL framework with GP regression.²¹² By incorporating uncertainty quantification through the GP lower-confidence-bound acquisition function, the study achieved a substantial reduction in required DFT calculations, needing fewer than 30 calculations to acquire the most stable polymorphs. Through this approach, they not only reaffirmed the stability of the known structures but also discovered a previously unknown, highly stable α-IrO₃ phase as a novel candidate.

ML-assisted investigation on RuO₂ has also been reported. Timmermann et al., building upon their innovative application of GAP for the surface structure determination of rutile IrO₂, extended their methodology to include RuO₂,²¹³ showcasing the versatility and efficiency of their approach for discovering novel surface structures. In this advancement, they employed a data-efficient iterative training protocol for GAPs, leveraging sparse GP regression alongside simulated annealing, to explore and optimize the surface geometries of both IrO₂ and RuO₂. This refined ML process, enriched by a dataset that eventually encompassed an additional 143 structures beyond the initial bootstrapping set, not only reaffirmed the discovery of thermodynamically stable surface complexions on IrO₂ but also unveiled similar energetically favorable complexions on RuO₂. Similarly, GAP was also used in the DFT calculation part by Singh et al. in their experimental exploration on Na-substituted disordered rock salt as OER electrocatalysts.²¹⁴ Feng et al. introduced CrystalGNN with a dynamic embedding layer to self-update the atomic features adaptively along with the iteration of the neural network (Fig. 17a).²¹⁵ Impressively, by accurately predicting the formation energies of more than 10 500 IrO₂ configurations, they discovered eight previously unreported metastable phases. They also innovatively used transfer learning to enable the discovery of RuO₂ and MnO₂, showcasing significant improvements in prediction efficiency and accuracy for these electrocatalysts, thereby highlighting the potential of transferring the capability of as-trained ML models across different electrocatalyst systems. TM dopants into IrO₂ and RuO₂ are another well-studied strategy to enhance their activity and durability.²¹⁶ Researchers have already reported successful doping by TM elements including, Mn,²¹⁷ Ni,²¹⁸ Co,²¹⁹ Mo,²²⁰ Cu,²²¹ and Pb,²²²etc. Xu et al. focused on doped RuO₂ and IrO₂ electrocatalysts,²²³ leveraging the SISSO method for data-driven descriptor engineering to predict OER adsorption enthalpies with remarkable accuracy. Their novel approach, involving an extensive dataset of 684 DFT calculations and innovative input features, enabled the identification of promising dopants like Co and Fe that are in agreement with experimental validations.

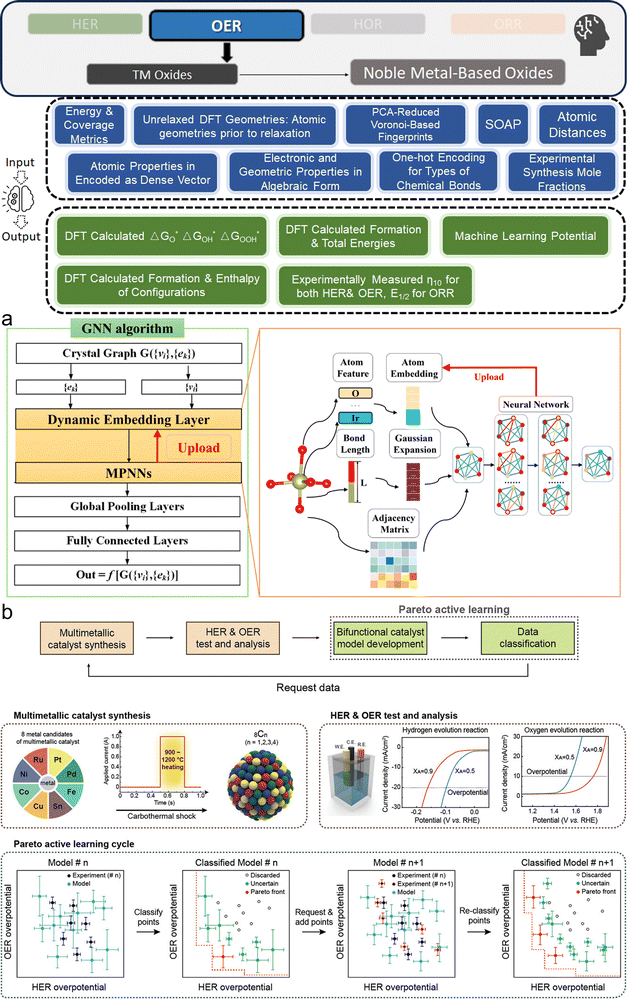Fig. 17 (a) Framework of CrystalGNN and workflow of the dynamic embedding layer (reproduced from ref. 215 with permission). (b) The exploration process for efficient bifunctional multimetallic alloy catalysts integrates computational and experimental strategies. It begins with a comprehensive search for potential catalysts, followed by the experimental validation of selected candidates. Throughout this process, a Pareto AL cycle is employed to refine predictions and focus on promising alloys. Data points from predictions are categorized into three types: discarded points, which are overshadowed by superior options; uncertain points, requiring further analysis to determine their value; and Pareto front points, which represent optimal candidates undominated by others, highlighting the most efficient catalysts for further development (reproduced from ref. 224 with permission).

Researchers have also directly applied ML in experimental exploration despite higher expenses. Jiang et al. approached the design of bifunctional oxygen electrocatalysts for ORR and OER from a unique perspective of chemical bonds for composite electrocatalyst material systems.²²⁵ They used a dataset from 151 published studies to develop ML models that predict the E_1/2, η₁₀, and their difference as metrics of potential catalysts based on their chemical bonds. By employing SHAP values, they identified a promising combination of C–N, C–C, Fe–N, Ru–O, and C–P bonds, demonstrating a novel and efficient strategy for electrocatalyst discovery that led to a promising RuO₂@Fe–N–P–C catalyst. In their most recent study, Kim et al. further refine the application of AL to electrocatalyst experimental discovery by targeting bifunctional catalysts for both HER and OER,²²⁴ extending their elemental palette to eight: Pt, Pd, Ru, Ni, Fe, Cu, Co, and Sn (Fig. 17b). They also applied the previous data¹³³ for training the initial model. Their expanded approach efficiently pinpointed an optimal catalyst composition, Pt_0.15Pd_0.30Ru₀.₃₀Cu_0.25, achieving a notable cell voltage of 1.56 V at 10 mA cm⁻² for water splitting. This advancement is facilitated by a refined Pareto AL framework using GP regressors for multi-objective optimization. By integrating more than 110 experimental data points from possible 77 946 points over five iterations, the method exhibited a remarkable efficiency in navigating the complex design space for bifunctional catalysts.

4.1.2. Earth-abundant metal oxides. Earth-abundant TM elements have also been commonly studied due to their lower cost and great potential, especially in alkaline electrolytes. Sun et al. reported training an RF regressor based on 300 DFT-calculated spinel oxides to predict band centers of oxygen 2p, octahedral cations (M_O) d, and tetragonal cations (M_T) d in AB₂O₄ spinel systems²²⁶ (Fig. 18a), achieving an MAE of just 0.05 eV. This ML-driven approach further led to the identification of [Mn]_T[Al_0.5Mn_1.5]_OO₄ as a highly active OER catalyst, which was experimentally validated to exhibit an impressive overpotential of only 240 mV at a current density of 25 μA cm⁻², positioning it at the pinnacle of OER performance among spinel oxides. Likewise, Sugawara et al. studied Fe-based oxides in alkaline media,³¹ but they uniquely used DFT-based input features such as Fe–O bond length, metal–metal interatomic distance, and metal–O–metal bond angle, while targeting experimentally obtained specific activity (mA cm⁻²) and overpotentials as the output features. Their ML-data mining further revealed the Fe–O bond length as the most critical structural descriptor for OER efficiency in the system.

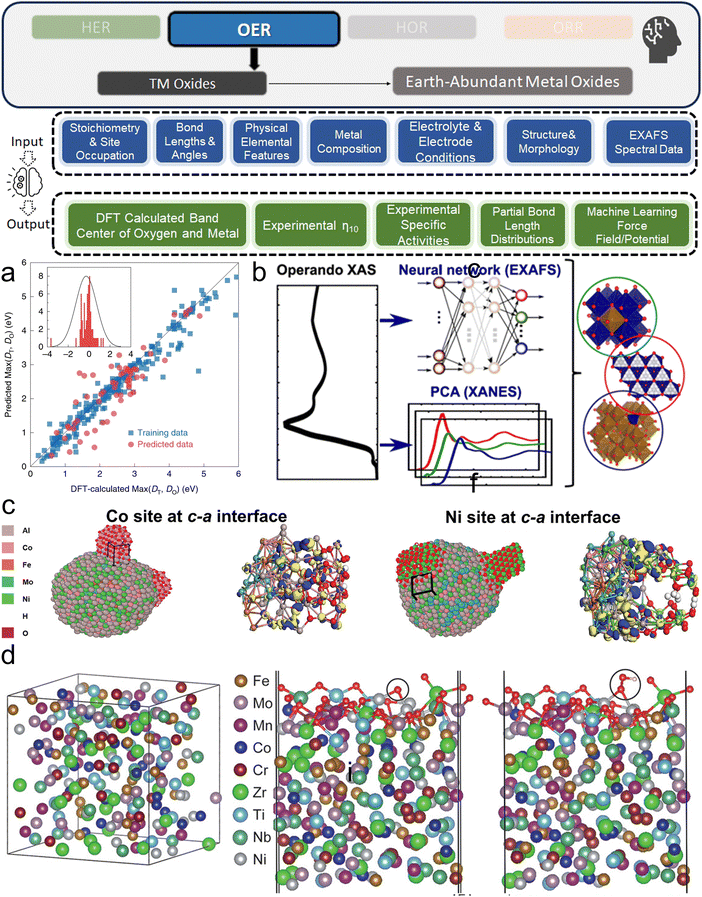Fig. 18 (a) The ML model's prediction on covalency competition in spinel oxides; inset compares the model predictions to DFT for Max(D_T, D_O), with counts on the y-axis (reproduced by ref. 226 with permission). (b) Schematic of ML trained on EXAFS and XANES data (reproduced by ref. 227 with permission). (c) Models of the crystalline–amorphous interface (close packed atoms) paired with differential charge density outcomes (atom-bonds), where yellow indicates charge accumulation and blue signifies charge depletion. The structure is obtained by high-dimensional neural network potential-boosted MD and DFT provided by the DeePMD-kit package (reproduced from ref. 228 with permission). (d) DFT calculations boosted by ML force field on 9e-HEA: Left shows the model without oxidation. Center and right depict models with pre-oxidation for *O and *OOH intermediates, respectively. Black circles highlight Ni as catalytically active sites, with red and white spheres for O and H atoms. (reproduced from ref. 229 with permission).

Following the same idea, there are also a series of experiment data-based ML research works regarding η₁₀ as the output fitting target to explore similar systems from binary to quinary: FeNiO_xH_y,²³⁰ (Ni–Fe–Co)O_x,³² (Ni–Fe–Co–Ce)O_x,²³¹ pseudo-quaternary metal oxide combinations from six earth-abundant TM (Co, Ni, Fe, Mn, etc.) elements,²³² Ni_aCo_bFe_cX_{1−a−b−c}.²³³ These studies leverage various ML techniques, including ANNs, SVR, and deep symbolic regression, to analyze and predict overpotential in these earth-abundant TM oxide systems. The studies collectively examined thousands of data points by experiments, spanning compositions of binary to quinary systems. The research demonstrated that experimental dataset-based ML models could also uncover complex mechanism relationships in electrocatalysis. Like in the work that Jiang et al. investigated (Ni–Fe–Co)O_x ternary systems,³² the ML model revealed a complex relationship, indicating that the variance in the first ionization energies and outermost d-orbital electron numbers of catalyst compositions correlates linearly with the reduction in overpotential. As expected, by achieving significant accuracy in forecasting electrocatalyst performance, these works could show the successful prediction of optimal catalyst compositions. For example, in the following work by Jiang et al., they successfully synthesized a novel Ni_0.77Fe_0.13La_0.1 (OH)_x sample with an ultra-low η₁₀ of only 226 mV under ML's guidance.²³³ Wei et al., however, noticed that η₁₀ is not the only effective descriptor.⁷² They used a domain knowledge database to predict electrochemical double-layer capacitance (C_dl) for earth-abundant TM-layered double hydroxides (LDHs) in OER. By incorporating features such as chemical compositions, structural morphology, and testing conditions into their models, they identified Ce as a pivotal element in modifying the double-layer capacitance of LDHs. The importance of enhancing OER activity is further validated by the authors’ experiments. Timoshenko et al. proposed to use EXAFS and X-ray absorption near-edge structure (XANES) spectra data to predict the partial bond length distributions²²⁷ (Fig. 18b) for deeper comprehension of the structural and chemical transformations in Co_xFe_3−xO₄ nanocatalysts during OER. By leveraging a combination of unsupervised and supervised ML methods, including PCA and ANN, they were able to elucidate the evolution of tetrahedrally and octahedrally coordinated species. They unveiled that the active OER mechanism likely involves the reversible formation and oxidation of Co³⁺–O₆ octahedral clusters, which vary with the Co-to-Fe ratio and the electrochemical conditions. In conclusion, the works described in this section have firmly demonstrated the power of ML in guiding the discovery of efficient non-noble metal OER electrocatalysts and deepening our comprehension of their mechanisms, with comparatively less abundant but higher fidelity experimental datasets.

Recently, researchers have extended interest in multi-element alloys containing five or more metals, namely high-entropy alloys (HEAs) for OER, but such systems could hardly be investigated efficiently without the help of ML. Before experimental synthesis, Cui et al. applied ML-boosted MD and DFT via high-dimensional neural network potential to provide guidance in the FeCoNiMoAl HEA system²²⁸ (Fig. 18c). The results revealed optimized atomic configurations and electronic structures, thereby significantly reducing the electron transfer resistance, and enhancing the catalytic active sites for OER. Through this computational approach, the team successfully synthesized HEA fibers, demonstrating superior OER performance with an overpotential of 470 mV at 2 A cm⁻² and remarkable stability. Moreover, Tajuddin et al. applied a similar strategy but more boldly investigated 9e (element)-HEAs including Ti, Cr, Mn, Fe, Co, Ni, Zr, Nb, and Mo,²²⁹ where ML force fields were also generated from DFT-MD simulations to estimate the Gibbs free energy for both OER and HER in challenging acid electrolytes (Fig. 18d). They used an innovative top-down approach for designing HEAs, focusing on the self-selection and self-reconstruction of elements under operational conditions, which enabled the automatic identification of both catalytically active and passivation sites on the alloy surface. Their findings revealed that certain elements like Mn and Fe are as effective as platinum for HER, and the combination of elements in the nonary alloy achieved high catalytic activity and remarkable stability during OER.

4.1.3. Advanced oxide systems. In the quest for efficient OER, advanced oxide systems, particularly perovskite and pyrochlore structures, are emerging as frontrunners due to their unique electronic structures, high covalency in metal–oxygen bonding, and potential to reduce reliance on scarce noble metals.^234,235 For the typical ABO₃ perovskite systems, early in 2015, Hong et al. managed to gather publication data²³⁶ and explored the intrinsic OER activity through a comprehensive statistical analysis of 14 physical and chemical descriptors, highlighting the critical role of electron occupancy and metal–oxygen covalency. Although they use the term “statistical learning” rather than currently commonly used “machine learning”, they still managed to employ advanced regression techniques, including penalized methods and factor analysis, to predict OER activities with notable accuracy, achieving prediction errors within 0.5 standard deviations. From a theoretical perspective, Wang et al. proposed a surface center-environment strategy for feature engineering, integrating 114 descriptors derived from the elemental and structural characteristics of perovskites into RF regressors²³⁷ (Fig. 19a). This approach enabled the accurate prediction of DFT-calculated Gibbs adsorption free energies and overpotentials for both existing and 610 newly hypothesized structures, revealing perovskites with notably low overpotentials such as YRuO₃, YIrO₃, and YFeO₃. Weng et al., considering the higher cost of experimental synthesis, applied symbolic regression based on merely 18 samples and successfully identified a decisive descriptor μ/t, where μ and t are the octahedral and tolerance factors, respectively.⁷⁸ This innovative approach further accelerated the discovery of new high-activity catalysts such as Cs_0.4La_0.6Mn_0.25Co_0.75O₃ and Cs_0.3La_0.7NiO₃. These new catalysts, synthesized under the guidance of data science, have shown a remarkable activity boost compared to previous works in the literature. Similarly, Li et al. also used symbolic regression to analyze more than 105 experimental perovskite-type OER electrocatalysts,²³⁸ identifying the simple yet impactful descriptor N_d/(0.55 − r_B), which correlates B-site cation properties with OER activity and leads to the proposal of Ni⁴⁺, Co⁴⁺, and Fe⁴⁺ as optimal candidates.

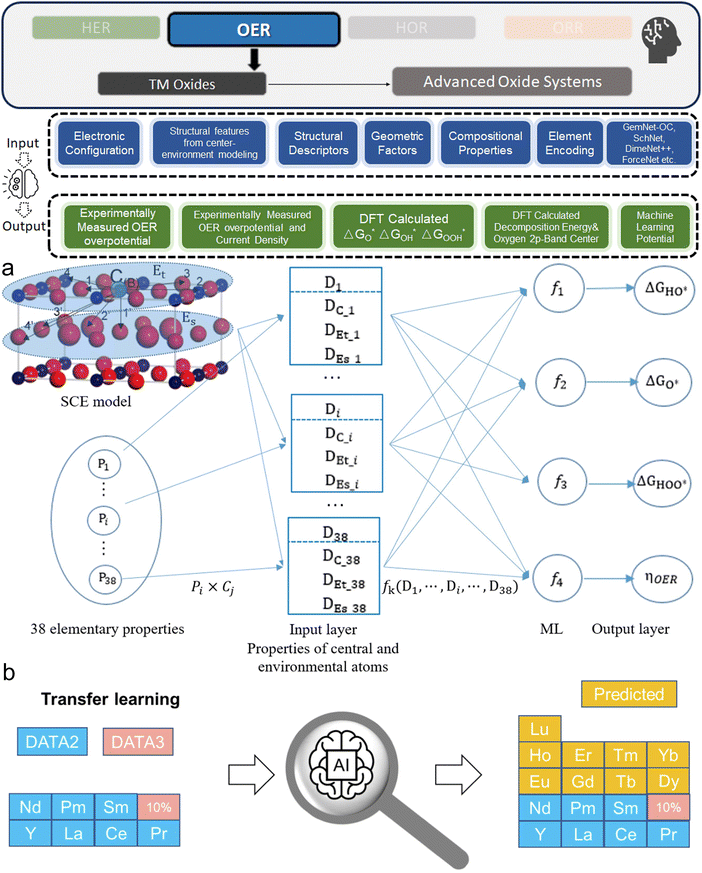Fig. 19 (a) The surface center-environment model for ML input feature construction includes the central surface atom (B), top surface environment (excluding B), and subsurface atoms. ML targets ΔG_O*, ΔG_OH*, ΔG_OOH*, and η_OER, with D representing the elementary properties of the center and the surrounding atoms (reproduced from ref. 237 with permission). (b) Transfer learning pipeline to predict the property of unknown pyrochlore oxides (reproduced from ref. 239 with permission).

In addition to typical ABO₃ type perovskites, other advanced oxide systems have been studied using ML. Li et al. investigated AA′B₂O₆-type double perovskites,²⁴⁰ employing an adaptive learning strategy with GP regressors. Their approach led to the discovery of several novel perovskites with promising OER activity, such as KRbCo₂O₆ and BaPbTi₂O₆, highlighting the model's effectiveness in guiding the design of next generation electrocatalysts that have a calculated overpotential of ∼0.5 V and tolerance factors greater than 0.90. Song et al. also investigated double perovskite catalysts, using a multi-task symbolic regression method to distill universal activity descriptors from diverse datasets gathered via publications.²⁴¹ They successfully applied the ML-derived 2D descriptor to predict and experimentally validate two new nickel-based perovskites, Cs_0.4La_0.6NiO₃ and K_0.5Ce_0.5NiO₃. Wang et al. focused on pyrochlore compounds, which are promising for acidic conditions.²³⁹ The team innovatively implemented a nuanced transfer learning strategy to navigate the vast compositional space (Fig. 19b). By leveraging a two-stage model, where the first stage trained on the formation energies of inorganic compounds to craft a nuanced representation of individual elements and the second stage applied this knowledge to predict the critical properties of pyrochlore oxides, the team efficiently pinpointed 61 promising candidates from an initial set of 6912. Tran et al. comprehensively built the “Open Catalyst 2022” dataset,¹²⁰ which comprehensively includes 62 331 DFT relaxations and approximately 10 million single-point calculations across various oxide materials. They utilized advanced neural network frameworks, including GemNet-OC,⁵³ SchNet,⁵⁰ DimeNet++,⁵² ForceNet,¹⁰⁸ SpinConv,⁵¹ GNN, and PaiNN,²⁴² with GemNet-OC demonstrating the best performance. Their work highlights the effectiveness of fine-tuning pre-trained models on this large, specialized dataset, improving prediction accuracy for complex oxide surfaces and providing key insights into the stability and energy dynamics of these electrocatalysts.

4.2. Carbon-based structures

4.2.1. Basic carbon structures. Similar to HER, carbon-based electrocatalyst materials have proven promising for OER due to their low cost, high electrical conductivity, environmental friendliness, and ability to enhance catalytic performance through structural and compositional modifications such as heteroatom doping and nanostructuring,²⁴³ which could benefit from ML techniques. Kapse et al. systematically studied the graphene nanoribbon systems with N, S, P as dopants.²⁴⁴ Besides the identification of optimal active sites (Fig. 20a) and configurations with only 0.29 V overpotential, their work revealed the significant role of π-electron-based descriptors in determining catalytic activity via an ML model. TM-doped, nitrogen-carbon, single-atom catalysts on graphene are a more popular and frequently studied system for hydrogen-related electrochemistry (Fig. 20b), as we introduced for HER in Section 3.2.1. Hence, there are also several similar works using ML to investigate the electrocatalyst system's potential in OER^245–248 (2020; 2021; 2021; 2023). However, it should be noted that all these studies are based on DFT calculations, possibly because current experimentally validated systems are mostly TM oxides while other systems still remain in the theoretical stage.

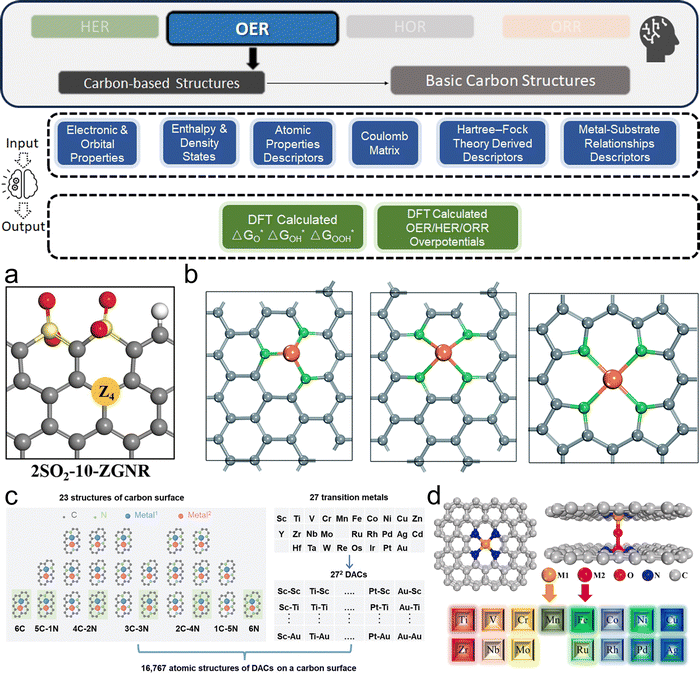Fig. 20 (a) Model structure of the optimal site on a zigzag nanoribbon (reproduced from ref. 244 with permission). (b) Schematic of graphene-supported SACs for ML models: Single vacancy (three carbon atoms), double vacancy (four nitrogen/carbon atoms), and four pyridine nitrogen configurations. TM atoms in orange, neighboring N/C in green, and other C atoms in gray (reproduced from ref. 245 with permission). (c) Atomic structures of TM dual-metal catalysts on carbon surfaces include 23 defect types across seven N-doping levels (e.g., 4C-2N for two nitrogen substitutions) and 729 compositional combinations, totaling 16 767 unique DAC structures (reproduced from ref. 249 with permission). (d) Top and side views of MN₄–O–MN₄ show upper (orange) and lower (magenta) transition metals (M₁ and M₂). Red, blue, and gray depict oxygen, nitrogen, and carbon atoms, respectively (reproduced from ref. 250 with permission).

These studies collectively highlight the potential of ML to reduce the computational cost associated with DFT calculations. Commonly, the input features for ML models in these studies include atomic and electronic properties of the TMs, such as atomic mass, atomic radius, d-electron number, and electronegativity. Moreover, as we concluded in Section 3.4 for HER, the structural properties of the catalyst, including the coordination environment and bond connectivity, are also preferred and considered in carbon materials. Material insights gleaned from these studies generally underline the importance of electronic structure and atom-environment interactions in determining catalytic activity. For instance, the electron number of the d orbital, the oxide and hydride formation enthalpies, and the electronegativity values of the central TM atom and its surrounding atoms emerge as critical descriptors. These features directly relate to the catalyst's ability to facilitate electron transfer and bond formation/breaking during the OER process. Finally, across the works, elements such as Fe, Co, Ni, and non-precious metals embedded in nitrogen-doped graphene are often identified as promising candidates for efficient OER catalysts.

In addition to the regular TM–N–C system that we have discussed, some researchers also considered related variants. Wu et al. explored the potential of double-atom catalysts in carbon matrices, which has increased the complexity (Fig. 20c).²⁴⁹ They innovatively applied a topological information-based feature-engineering method to handle model input that integrates atomic properties and the structural topology of active sites and their substrate environment. They also found an effective intrinsic descriptor for clarity. Besides the d-band properties of two TM atoms, the descriptor also includes the number and electronegativity of nearby C and N atoms, reflecting their unique impacts. Shan et al., however, think of another possibility in which the TM–N₄ active sites are bridge-bonded by an O atom (Fig. 20d).²⁵⁰ Their calculation results pinpointed CoN₄–O–RhN₄ and RhN₄–O–AgN₄ as standout monofunctional catalysts for ORR and OER, respectively, and CoN₄–O–AgN₄ as an exceptionally efficient bifunctional catalyst. The electronic structure analysis reveals that the d-band centers of the active sites in the bifunctional catalysts result in moderate TM atom adsorption on intermediates due to the synergistic effects from bridge-bonded O ligands. This finding aligns with the previously discussed research on single-layer TM–N–C systems.

4.2.2. Carbon nitrides. As one of the special carbon structures previously mentioned in Section 3.2.2, graphitic carbon nitride (g-C₃N₄), with its unique 2D structure, high nitrogen content, and semiconductor properties, provides a versatile and chemically stable framework for hosting transition metal atoms. Therefore, it could serve as a promising alternative to graphene as an efficient electrocatalyst platform. Niu et al. studied the standard g-C₃N₄ as a substrate for hosting TM single atoms (Fig. 21a).³⁹ Despite the identification of Rh as the best candidate for both OER and ORR, ML was used for data mining, which had revealed the most impactful descriptors on adsorption behavior as first ionization energy and charge transfer of the center TM atom. Ying et al. similarly investigated C₂N-supported SACs and expanded their work to include N₁C₁ and N₁S₁ coordination.²⁵¹ Their analysis identified the oxide formation enthalpy and outer electron number as key predictors for catalytic performance, leading to the discovery of Rh, Au, and Pd@C₂N as outstanding bifunctional catalysts for OER and ORR activities. Wan et al. further broadened the searching space to include various C_xN_y structures from C₃N to C₃N₅ (Fig. 21b).²⁵² Through detailed analysis, they discovered RhPc, Co–N–C, and Rh–C₄N₃ as superior electrocatalysts, partially in alignment with ref. 39. The feature importance analysis highlighted the electron number of the d orbital as a crucial descriptor for catalytic performance. Finally, Zhang et al. studied the dual TM atom-doping situation in g-C₃N₄ (Fig. 21c),³⁰ revealing that specific combinations of heteronuclear structures like Ag–Pd and Au–Co to be OER active. As for ML data mining, it was found that not only the TM atoms’ d-band centers are as impactful as expected, but also the geometric structures’, such as the distance between the two metal atoms and the average bond lengths between the surrounding N atoms and TM atoms.

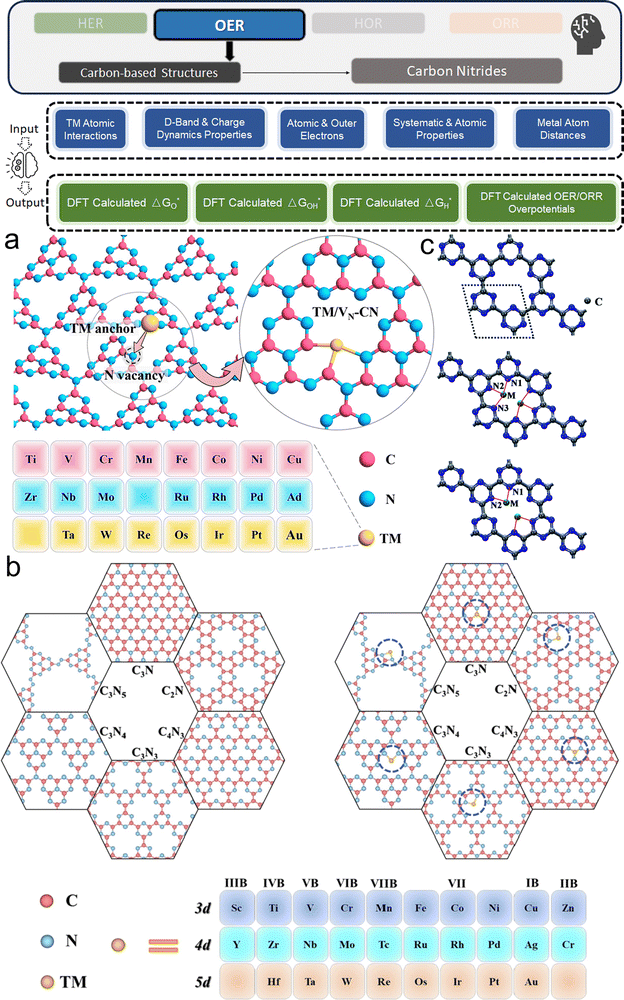Fig. 21 (a) Illustration of the configuration of TM/VN-CN and the considered TM atoms as SAC candidates (reproduced from ref. 39 with permission). (b) Atomic structures of prevalent carbon nitrides, their C_xN_y-based SACs with single TM atoms indicated by blue circles, and screened transition metals on C_xN_ys (reproduced from ref. 252 with permission). (c) Optimized g-CN structure, selection of metal atoms (Sc to Au), and binding configurations of M2 dimers on g-CN, showing both M atoms bonded with either three or two N atoms. Additionally, calculated formation energies (E_f) and U_diss for M2/g-CN are presented (reproduced from ref. 30 with permission).

4.3. Emerging material systems

Like carbon-based materials, other emerging materials have been studied for their potential in boosting OER as electrocatalysts from theoretical perspectives, such as 2D TM compounds like MXenes. These studies generally consider both OER and ORR reactions due to same intermediate species and apply the standard ML workflow to train DFT surrogate models. Anand et al. investigated O-terminated M₂M′X₂O₂-type doped MXenes (Fig. 22a) by Fe/Co/Ni,²⁵³ using an ML classifier to classify the MXenes into efficient and non-efficient catalysts for HER/ORR/OER. Their study revealed Ni–Sc₂YN₂O₂ and Ni–Cr₂ScC₂O₂ as efficient bifunctional catalysts with lower overpotentials. The data mining process also revealed the d-band center, which would impact the charge transfer pathway, as the most critical descriptor, in alignment with the previously mentioned studies. Similarly, Ma et al. focused on dual-transition metal Janus-MXenes-based SACs, particularly Pt-doped variants.²⁵⁴ By leveraging a feature set that encompassed atomic, electronic, and environmental characteristics, they demonstrated that the adsorption energy of *OH, the binding energy of Pt on the substrate, and the d-band center of the Pt atom are critical descriptors impacting OER/ORR overpotential. This approach enabled the identification of SACs with significantly reduced overpotentials, notably Pt–VO–MnTiCO₂ and Pt–VO–PdTiCO₂. Chen et al. focused on more complex M–N₄–Gr(aphene)/MXene heterojunction nanosheets systems (Fig. 22b), employing ML to analyze the catalytic activities of 78 such candidates.²⁵⁵ Their approach successfully identified key electrocatalysts like Ni–N₄–Gr/Nb₂C and Ru–N₄–Gr/Nb₂C. The importance analysis again revealed the d and p electron number of the TM active site as the most influential descriptor in determining the catalytic efficiency.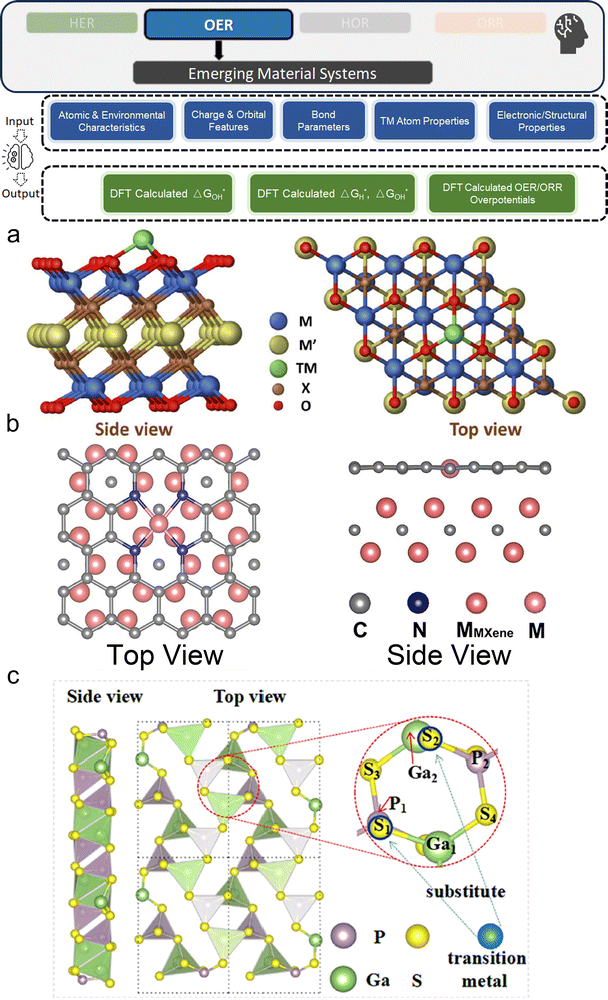

Fig. 22 (a) Schematic illustration of the side and top views of the investigated O-terminated M2M′X₂O₂-type doped MXenes. TM acts as the active site for the adsorption of intermediates (reproduced with ref. 253 with permission). (b) Top view and front view of the M–N₄–Gr(aphene)/MXene heterojunction structure (reproduced from ref. 255 with permission). (c) The optimized structures of the 2D MnPS₃ monolayer and the TM/MnPS₃ catalysts (reproduced from ref. 256 with permission).

Researchers have also investigated other unique TM compound systems. Liu et al. studied 2D GaPS₄ as a substrate for hosting TM single atoms on sulfur vacancies,²⁵⁷ namely TM@V_S-GaPS₄. Using a GBDT regressor, they identified key descriptors such as the number of d electrons, bond length, and electronegativity as crucial in their ML data mining, and Pt@V_S1-GaPS₄ was identified as the most outstanding candidate in this system. Similarly, Li et al. investigated single TM atoms anchored on MnPS₃ (Fig. 22c),²⁵⁶ identifying Rh/MnPS₃ and Ni/MnPS₃ as the best candidates. Unsurprisingly, the ML analysis revealed the number of d electrons in the TM atoms influenced the adsorption strength of OH* species, thus becoming the crucial feature. In addition, the authors of ref. 186 studied OER besides HER on a monolayer C₃B substrate. It should be reminded that their results revealed Ni and Pt as the best doping candidates, and ML data mining revealed that the number of d electrons surpasses other most important features: electronegativity, atomic radius, and first ionization energy of the TM as the most significant factor.

Although these studies investigated different substrates for hosting TM atoms, ranging from MXenes with different structures/doping strategies to GaPS₄, MnPS₃ and C₃B, we can see that the results are similar. TM d-band-related features such as the number of d electrons should be considered the most decisive feature in determining oxygen intermediate adsorption behaviors. Moreover, Ni and Pt are consistently discovered to be optimal candidates in these 2D systems. We might also consider it as the embodiment of robustness, transferability, repeatability, and reliability of ML. In contrast to the previously mentioned studies that are highly homogeneous in terms of methodology and research system, Craig et al. uniquely investigated molecular OER catalysts,³³ targeting TM catalysts coordinated with specific ligands such as porphyrins using an AL approach. This method was adeptly applied to identify catalysts capable of operating through an extra oxidation mechanism, a novel area in OER catalyst research. The balance they sought between low overpotentials, and achievable proton transfer barriers was critically dependent on the use of GP regressors for predicting binding energies. A significant aspect of their methodology was the employment of reduced autocorrelation functions to generate input features, paired with a bespoke acquisition function developed for their AL framework.

4.4. Membrane electrode assembly (MEA) perspective

So far, we have introduced the significant progress in the application of ML to boost the design of electrocatalysts for HER and OER in electrolyzers. Most research efforts predominantly rely on theoretical simulations such as DFT, and those works that are experimentally based were often limited to half-cell tests using experimental datasets. However, for practical applications, the focus must shift to a more macroscopic perspective, considering the complexities of the membrane electrode assembly (MEA) that encompasses not just chemical but also engineering parameters. This approach necessitates a comprehensive understanding of the MEA's multifaceted nature, where chemical intricacies intertwine with a myriad of engineering parameters, including catalyst loading,²⁵⁸ ionomer mass fraction,²⁵⁹ membrane characteristics,²⁶⁰ and the dynamics of the gas–liquid–solid interface.²⁶¹ These factors, compounded by the complexity of balancing electrochemical reactions, proton and charge transfer, reactant diffusion, and varying operating conditions, are pivotal for achieving the desired efficiency and sustainability in real-world applications. This holistic view, considering the MEA's operational environment and its microscale to macroscale processes, is essential for optimizing precious metal utilization and enhancing the overall performance and durability of the whole device.

Ding et al. comprehensively studied the various aspects of MEA optimization in proton exchange membrane (PEM) water electrolyzers, including OER electrocatalyst design rules for MEA that best balance cost and durability.⁶⁹ They compiled an extensive database from 122 research papers, resulting in 578 entries which included detailed operating conditions, electrocatalyst compositions, and performance metrics. Their models showed great regression prediction performance for both MEA's activity and long-term stability, especially in the large current density area which is most important for the electrolyzer efficiency. The best-performing model for predicting current density at 1.9 V achieved an impressive R² of 0.943 (Fig. 23a), demonstrating the model's accuracy. Furthermore, the researchers realized that basic feature importance ranking was not enough to capture the nuanced interplay of factors influencing MEA performance. Hence, they innovatively noticed the importance of qualitative black-box interpretation for engineering and industry targets like MEA, so they used advanced 2D SHAP and PDP interaction plots to visualize the complex relationships between variables. They also innovatively proposed to use Friedman's H statistics method²⁶² to analyze the non-linear interaction degree between input features to help with inspecting the most impactful feature interaction pairs (Fig. 23b). Their analysis finally revealed that certain combinations of MEA design features, such as Ir weight percentage in anode electrocatalysts, would be suggested to be around 80% to balance durability and activity (Fig. 23c). Similarly, Günay et al. presented another comprehensive study,²⁶³ incorporating a wide array of components like porous transport layers and various electrode electrocatalysts in their analysis. They meticulously compiled a database from 30 recent publications, culminating in 789 data points which included intricate details like electrode compositions and operational parameters. The researchers adeptly applied a combination of ML techniques, including PCA and classification and regression tree modeling, to unravel the complex interrelations in PEM electrolyzer performance. Their nuanced approach enabled them to identify key performance indicators such as the mole fractions of Ni and Co on electrode surfaces, leading to the precise prediction of electrolyzer polarization with an impressive RMSE of 0.18 A cm⁻² (Fig. 23d). Moreover, the study shed light on high-performance electrocatalysts for PEM electrolyzers, affirming the superiority of proton conductor electrolyzers over their anion exchange counterparts and highlighting the potential risks associated with certain materials like unsupported/V-doped TiO₂.

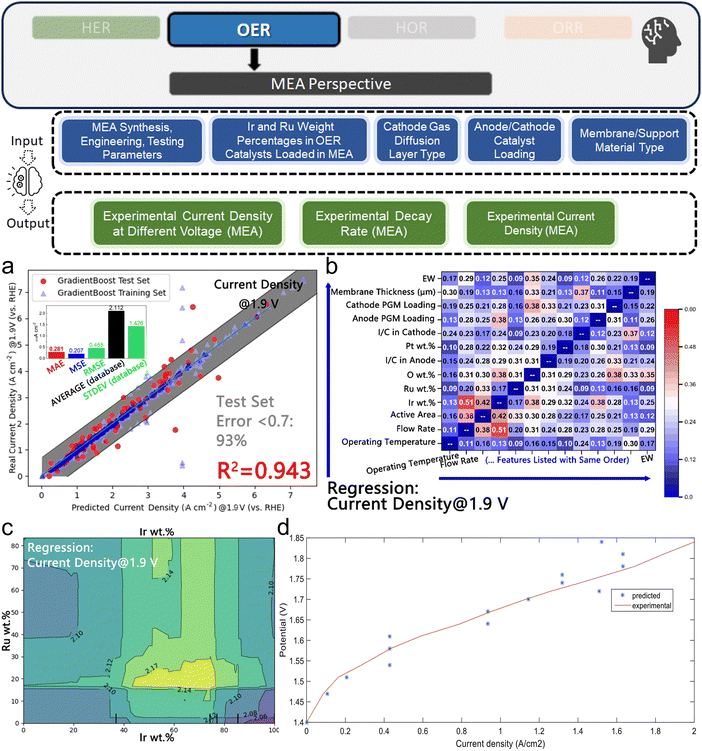Fig. 23 (a) Best ML algorithms' performance in predicting current density at 1.9 V, with 21 features shown by red points plotting predicted values against actual values; proximity to the Y = X reference line (blue) indicates accuracy. The gray area shows the common prediction range. Bar charts display the average and standard deviation of current densities, with MAE, MSE, and RMSE gauging prediction errors; lower values signify better model performance. (b) Second-order Friedman H-statistic matrices after weighted averaging of the ML models trained with the selected core features for the regression of current density. (c) 2D PDP interaction plots of Ir wt% and Ru wt% in different tasks for modeling current densities at different voltages. (a–c are reproduced from ref. 69 with permission). (d) Regression tree model prediction of the electrolyzer polarization curve's unseen observations (reproduced from ref. 263 with permission).

Although electrocatalysts fundamentally operate at the microscale, their real-world industrial application necessitates a transition to a more holistic approach in future research. Using actual MEA data, the research community should now focus on understanding and optimizing the interplay between the intricate microscale phenomena of electrocatalysts and the macroscale operational dynamics of electrolyzer systems. This shift is crucial for tailoring electrocatalyst designs that not only excel in theoretical and laboratory settings, but also thrive in practical commercial electrolyzers, thereby bridging the gap between experimental research and industrial application for sustainable and efficient hydrogen production.

4.5. Statistical analysis and summary

In this section, we present an analysis of the progress made in applying ML to the study of OER electrocatalysts, focusing on various material systems. We categorize related studies into TM oxides, carbon-based structures, and emerging systems like 2D TM compounds. Similar to Section 3.4, a high-level analysis of features and ML algorithms of these 48 publications in Fig. 24 would be helpful for researchers preparing their ML studies on systems of interest.

Fig. 24 Statistics for the OER section, including (a) utilized input features; (b) most important features recognized by ML model interpretation. (c) Distribution of the dataset sizes used. (d) Utilized ML algorithms; (e) best ML algorithms.

Features. Fig. 24a shows a general consistency in the most adopted input features between OER and previously discussed HER studies. However, while HER studies prefer the number of valence electrons, OER studies specifically use the number of d electrons. Another difference is that structural descriptors like bond length and tolerance factor have also gained high rankings. Fig. 24b further indicates that the most important feature identified is the number of d electrons, which has obvious advantages in comparison. Bond length takes second place, surpassing other atomic physical properties. Tolerance factor, charge transfer energy, and oxide/hydride formation energies have also gained attention. Therefore, it can be concluded that HER emphasizes electronic interactions and atomic-scale configurations, whereas OER emphasizes surface chemistry and structural properties. This difference reflects the unique challenges inherent to each electrocatalytic process, as OER involves a more complex four-electron reaction. The conversion between intermediate species (*O, *OH, *OOH) and the unique LOM mechanism, involving surrounding lattice O atoms, significantly highlights the importance of structural effects.

When further breaking down the results based on material categories, notable differences can be discerned. TM oxides typically have catalytic sites on specific crystal facets exposed in a homogeneous phase with short-range periodicity, whereas carbon-based and other TM compound systems often involve atomically dispersed TM heteroatoms incorporated into the substrate material. While both categories identify the number of d electrons as the most decisive feature, TM oxides focus more on electronic properties and chemical stability, while carbon-based and other TM compound systems rely heavily on their structural configuration due to their diverse bonding environments.

Dataset and algorithms. As indicated by Fig. 24c, dataset sizes reported in the publications generally range from several dozen to several hundred. Correspondingly, as summarized in Table S1 (ESI†), among the 48 studies in this section, 39 include classical ML methods, with 33 of these exclusively using classical ML methods. This trend is also shown in Fig. 24d, with the top five frequently leveraged ML methods being RF, GP, SVM, GBDT, and KNN. The popularity of neural networks is generally lower in comparison. Fig. 24e emphasizes that RF and GP are the top two algorithms, cited as the best-performing far more often than others. In general, deep learning or physically informed descriptor frameworks like CGCNN are less popular and currently have no advantage in OER-related research. This may be because OER material systems are more complex, and descriptor feature engineering relies more on the subjective experience of researchers. Another reason is that calculating theoretical OER activity requires computing the adsorption energies of more intermediates, increasing the cost of dataset preparation and hindering deep learning from unleashing its capabilities.

Finally, when breaking down the data into material categories, minor preference differences can be observed. Though both categories favor ensemble algorithms like RF and GBDT, TM oxides uniquely favor GP. GP is the most used for TM oxide systems and is reported as the best-performing algorithm as frequently as RF. This preference might be due to the popularity of AL and BO in TM oxide studies. Among the corresponding five studies, GP is adopted for its inherent flexibility and ability to provide uncertainty estimates. Additionally, symbolic regression, despite its weaker fitting ability, is uniquely favored in TM oxide studies. This trend might indicate that for TM oxides, researchers prefer interpretability over ML model capability. Due to the more complex OER mechanism on TM oxide surfaces and limited budget in query, researchers prefer using ML strategies to identify key decisive design factors rather than directly predicting OER activities, for example, straightforward combination of formulas like the octahedral factor divided by the tolerance factor in perovskites.

5. ML-aided design of HOR electrocatalysts

Building on the foundational knowledge of HER and OER in water electrolyzers, it is vital to recognize the significance of their reverse processes in fuel cell technologies. Both anion exchange membrane fuel cells (AEMFCs) and proton exchange membrane fuel cells (PEMFCs) are pivotal in this context, where both HOR and ORR play crucial roles. These fuel cells, which had been the subject of intensive research before electrolyzers, boast several advantages. Notably, they offer a high energy conversion efficiency and cleaner energy alternatives compared to traditional combustion-based technologies. Intriguingly, the components of fuel cells mirror those in electrolyzers, particularly in the reliance on electrocatalysts. Here, the dependence on Pt-based noble metals is pronounced, as previously discussed, underscoring a significant challenge in fuel cell technology. In PEMFCs, the ORR is often a rate-limiting step due to its complex four-electron process. HOR, in contrast, proceeds very swiftly in acidic environments. As previously mentioned for HER, the reverse reaction goes first through either the Tafel (H₂ + 2* ↔ 2*H) or Heyrovsky step (H₂ + * ↔ *H + H⁺ + e⁻), then the Volmer step (*H ↔ H⁺ + * + e⁻) to finish the process. Currently, research on the HOR in acidic conditions, particularly using Pt/C catalysts, has reached a stage of common knowledge, with the consensus that only a small amount of Pt/C is required to effectively drive the reaction.²⁶⁴ This has rendered the reaction economically viable and, as a result, further investigations in this area are not currently being pursued extensively. However, the narrative changes drastically in alkaline conditions. The kinetics of HOR in alkaline media are markedly slower, presenting a unique set of challenges.²⁶⁵ In short, this disparity in the reaction kinetics between acidic and alkaline conditions stems from several factors.²⁶⁶ In alkaline media, the interaction between hydrogen and catalyst surfaces is altered, often leading to weaker adsorption and subsequent recombination processes. This results in a significant increase in the energy barrier for the reaction, thus slowing down the HOR. Moreover, the involvement of hydroxide ions in the reaction mechanism adds complexity, as it influences both the adsorption and desorption steps of hydrogen on the catalyst surface. Thus, the performance of AEMFCs is critically dependent on developing effective HOR catalysts that can overcome these kinetic limitations. A schematic of the HOR mechanism in alkaline is shown in Fig. 25.

Fig. 25 Schematic of the HOR mechanism.

To address this, recent research has been directed toward exploring non-precious metal catalysts and innovative electrocatalyst designs that can enhance HOR activity in alkaline conditions. This includes the use of TM alloys, carbides, nitrides, and engineered nanostructures that aim to optimize the hydrogen binding energy and facilitate effective adsorption–desorption processes.²⁶⁷ Despite fewer numbers, some research still seeks to use ML in boosting HOR electrocatalysts design, especially in HEA systems. Men et al., in their experimental study of the PdNiRuIrRh HEA system,²⁶⁸ employed ML potential-based Monte Carlo simulations (Fig. 26a) for an in-depth analysis of the alloy's catalytic properties. They used a novel approach to construct the deep potential for the HEA, involving a dual neural network setup and a sophisticated training process via the deep potential generator, which iteratively refined the dataset based on DFT calculations. This method enabled the accurate prediction of high-dimensional potential energy surfaces, leading to the identification of key surface atomic distributions and coordination environments, such as the critical Pd–Pd–Ni and Pd–Pd–Pd bonding environments and Ni/Ru oxophilic sites. The study's findings revealed a significant enhancement in the HEA's HOR activity, with a mass activity of 3.25 mA μg⁻¹, far surpassing that of conventional Pt/C catalysts. Moreover, the authors further used ML's potential to simulate the particle surface dissolution process, which provided insights into the enhanced stability mechanisms of the HEA nanoparticles (Fig. 26b). Hitt et al., however, had applied ML to drive their entire experimental exploration based on the parallel fluorescent screening of a broad array of alloy electrocatalysts.²⁶⁹ Using a unique combination of experimental data comprised of catalyst compositions, onset potentials, and extensive material characterization, they applied ML to not only predict new active catalysts, but also to uncover key insights such as the critical role of average work function and metal-oxygen bond enthalpy to determine the catalytic activity (Fig. 26c). Their approach notably identifies Pt₆Sn₄ as a highly effective alloy, surpassing traditional Pt/C in alkaline polymer membrane fuel cells with a higher power density of 132 mW cm⁻² mgPt⁻¹. In conclusion, less studied HOR in alkaline conditions remains challenging and could benefit from ML in boosting the catalyst design in complex alloy systems and revealing the mechanisms.

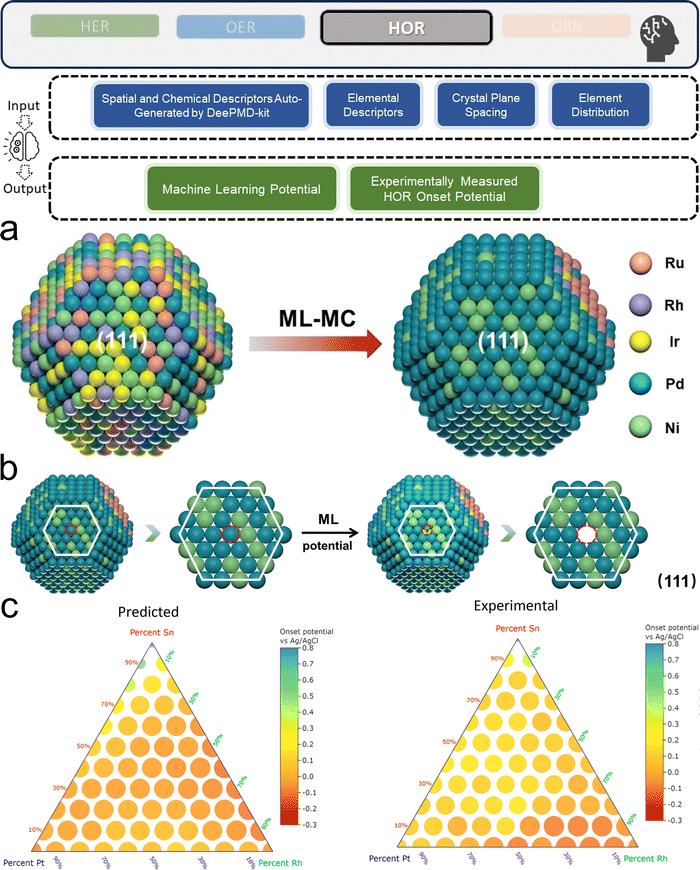Fig. 26 (a) Optimization of the HEA nanoparticle model via ML–MC simulations. (b) The schematic of the process dissolving surface metal atoms in HEA nanoparticle to evaluate the stability. The energies of various nanoparticle systems are obtained based on the trained ML potential. (a and b are reproduced by ref. 268 with permission). (c) Left: Neural network-predicted onset potential for the alkaline HOR of an SnPtRh array. Right: Experimental onset potential for an SnPtRh array with slight discrepancies, notably along the Pt–Rh binary line (reproduced by ref. 269 with permission).

6. ML-aided design of ORR electrocatalysts

Building on the comprehensive insights previously discussed for HER, OER, and HOR, we turn our attention to the ORR, a process that is equally critical and challenging. Like OER, the reverse process ORR is a multi-step reaction involving four electrons. Though sharing similar oxygen-containing intermediate species like *O, *OH, *OOH, its mechanism is more intricate, comprising both direct and indirect pathways.^67,68 The direct pathway is a four-electron process: O₂ + 4H⁺ + 4e⁻ → 2H₂O in acidic or O₂ + 2H₂O + 4e⁻ → 4OH⁻ in alkaline electrolytes. However, in contrast, possibilities exist to go through another indirect pathway that involves a two-electron process. This process initially forms hydrogen peroxide (H₂O₂) or peroxide anions (HO₂⁻) as an intermediate, which can either be released as a product or further reduced to water: O₂ + 2H⁺ + 2e⁻ → H₂O₂; H₂O₂ + 2H⁺ + 2e⁻ → 2H₂O in acidic or O₂ + H₂O + 2e⁻ → HO₂⁻ + OH⁻; HO₂⁻ + H₂O + 2e⁻ → 3OH⁻ in alkaline electrolytes. This bifurcation makes the ORR not only energetically demanding but also complex in terms of catalysis and reaction kinetics. Hence, in the quest for optimal ORR catalysts, selectivity is a critical parameter that must be carefully considered. The inadvertent production of H₂O₂ or HO₂⁻ during the ORR can have detrimental effects, as these species not only are corrosive, but they also compromise the long-term performance and overall efficiency of fuel cells on a macroscopic scale. Hence, the development of ORR catalysts that favor the direct four-electron pathway, thus minimizing the formation of these harmful intermediates, is a key objective in enhancing the viability and sustainability of fuel cell technologies. A schematic of the ORR mechanism is shown in Fig. 27.

Fig. 27 Schematic of the ORR mechanism.

For ORR electrocatalysts, currently there is a heavy reliance on Pt-based noble metals in commercial applications.²⁷⁰ The superior catalytic performance of Pt and its alloys has set a high benchmark both in ORR efficiency and predominantly four-electron direct reaction selectivity. However, due to the high cost and scarcity of Pt, researchers have been exploring alternative strategies such as doping Pt with other elements to enhance its catalytic activity or stability, and more recently, the use of high-entropy alloys (HEAs).²⁷¹ HEAs have gained significant attention in the field of ORR due to their unique properties arising from their complex compositions. Despite these benefits, there remains a strong interest in non-precious metal-based electrocatalysts, especially carbon-based catalysts such as TM–N–C.²⁷² These catalysts, particularly those featuring single-atom sites, have shown promising ORR activity. The use of transition metals such as Fe and Co combined with nitrogen-doped carbon structures has led to the development of catalysts that offer a cost-effective alternative to Pt-based electrocatalysts.²⁷³ Given the complexity of ORR mechanisms and the diverse range of catalysts being explored, this field also presents an ideal scenario for the application of ML techniques.

6.1. Metal/alloy-based catalysts

Pt-based electrocatalysts stand at the forefront of ORR applications, primarily due to their exceptional catalytic activity and durability.²⁷⁰ One of the pivotal advantages of Pt in ORR catalysis is its ability to facilitate the electron transfer process, a critical factor in fuel cell efficiency. Another proficiency stems from the unique electronic structure of Pt, particularly its d-band center, which plays a crucial role in binding oxygen-containing intermediates. The d-band model, as elucidated by Nørskov et al. (2004),²⁷⁴ demonstrates how the electronic properties of Pt, including the d-band center and Pt–Pt distances, significantly influence the adsorption energy of intermediates and, consequently, the ORR activity. This understanding has guided the evolution of Pt-based electrocatalysts, leading to the development of advanced nanoarchitectures that maximize active site exposure and enhance mass transport, thereby boosting the ORR performance. By optimizing these electronic interactions through strategies such as alloying with other elements and designing open nanostructures,²⁷⁵ researchers aim to help Pt-based catalysts achieve a delicate balance of optimal oxygen-binding energies for efficient ORR pathways and low noble metal cost. Moreover, stability is not to be ignored under the demanding conditions of fuel cells. To simultaneously achieve excellence across multiple metrics, the doping design of Pt-based metal alloys requires the careful modulation of numerous parameters, presenting a prime opportunity for the application of ML techniques.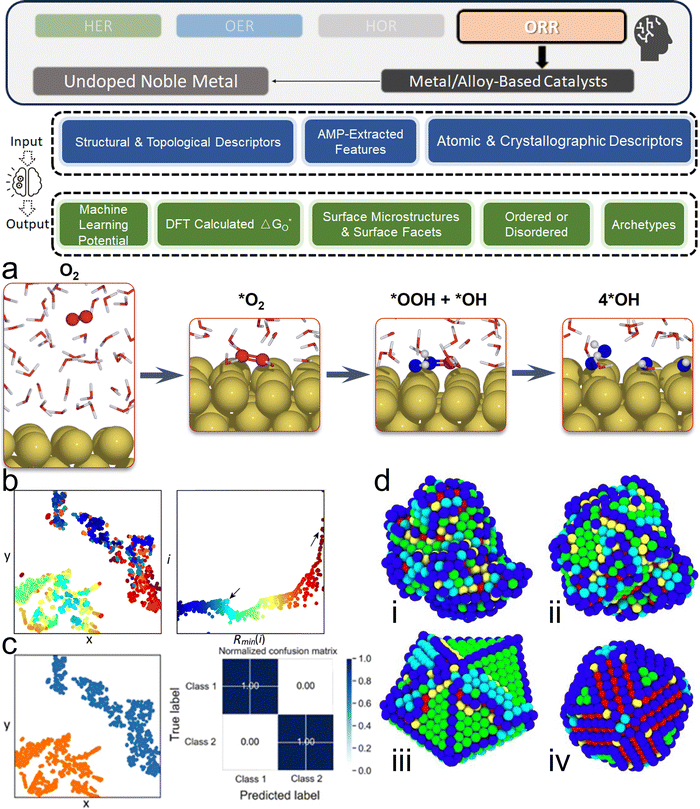

6.1.1. Undoped noble metal. Starting from pure Pt nanoparticles, Robacado et al. employed a sophisticated approach using the geometrical features and electronic properties of various Pt surfaces and isolated nanoparticles to predict oxygen-binding energy.²⁷⁶ This study revealed that for Pt surfaces, the average nearest-neighbor Pt–Pt distance and the generalized coordination number are key descriptors. And for Pt nanoparticles, a combination of five descriptors, including nearest neighbor (NN) bond orders and d-band centers, is significant. The most critical finding was a simple linear combination of five descriptors via structural and electronic properties depending on NN and second NN atoms. This combination formula could reach an R² of 0.976 as a proof of well describing the chemisorption of O atoms. Instead of predicting adsorption energies, Nigussa proposed to use Amp²⁷⁷ and ænet²⁷⁸ packages to train ML potentials for understanding the reaction paths and electronic structures on platinum surfaces,²⁷⁹ specifically focusing on the (100), (110), and (111) facets. This approach revealed the (110) surface's superior catalytic role in facilitating the dissociation processes for hydrogen and oxygen, with detailed insights into the electronic interactions and charge transfers that are critical for the fuel cell efficiency. Similarly, Yang et al. also trained an ML potential for energies and forces as surrogate model for MD calculations in the Au (100)–water interface system,²⁸⁰ employing Behler–Parrinello symmetry functions as input. This approach led to a detailed understanding of the ORR on Au (100), particularly uncovering an associative reaction mechanism (Fig. 28a) without the formation of *O intermediates and identifying a low energy barrier of 0.3 eV, a finding that aligns closely with experimental observations and highlights the significant influence of water molecules in the reaction process. Parker et al. proposed to comprehensively use both unsupervised and supervised ML techniques in investigating Pt nanoparticle structures.²⁸¹ They innovatively employed a combination of iterative label spreading (ILS) and archetypal analysis strategies. The unsupervised learning phase (Fig. 28b), particularly clustering, was pivotal in distinguishing between ordered and disordered Pt nanoparticles, laying the groundwork for more targeted analysis. In the subsequent classification phase (Fig. 28c), these two distinct nanoparticle types were identified, which then guided the regression analysis to predict the normalized concentrations of surface microstructures and surface facets. This layered approach highlighted the influence of nanoparticle disorder (Fig. 28d) on ORR efficiency and the role of size and surface facets in determining HER and HOR performance, offering a nuanced understanding that is essential for the advanced design of Pt-based catalysts for energy applications. In their following study, they further advanced the understanding of disordered Pt nanoparticles to identify key structural prototypes and archetypes from a dataset of 1300 particles.²⁸² Unlike their previous work which focused on classifying and regressing the structural features of Pt nanoparticles, this study distinctly categorized nanoparticles into pure and representative types, unveiling seven archetypes and two prototypes which collectively embody the full spectrum of structural diversity and complexity. Hence, they offered a refined theoretical basis for discussing the structure/property relationships in non-ideal Pt nanocatalysts.

Fig. 28 (a) Snapshots for O₂ in bulk water, the initial state, the transitional state, and the final state. The substrate is Au (100) surface (reproduced from ref. 280 with permission). (b) Left: t-SNE plot of 1300 platinum nanoparticles showing x–y distribution based on similarity in 121 dimensions. Right: Order-labeled minimum distance plot from ILS clustering with two peaks indicating distinct clusters, color-graded from blue to red based on label iteration. (c) Left: t-SNE distribution of 1300 Pt nanoparticles, colored by ILS-assigned clusters. Right: Confusion matrix confirming perfect separability of classes, primarily influenced by processing conditions and order parameters. (d) Examples of Pt nanoparticles in the set, of comparable size, with atoms encoded by the coordination number. Atoms are color-coded by coordination number: dark blue for 7, light blue for 8, green for 9, yellow for 10, and red for 11. (i) Class 1 Pt nanoparticle featuring abundant surface microstructures, (ii) Class 1 with numerous surface facets, (iii) Class 2 with a high density of surface microstructures, and (iv) Class 2 rich in surface facets. (b-d are reproduced by ref. 281 with permission).

6.1.2. Binary and ternary alloys. To tune the electronic structure and reduce the amount of Pt usage, doping other TM elements into Pt to form alloys has long been a strategy adopted by researchers. For a typical PtNi binary alloy cluster system, Zhen et al. developed a physically niche genetic-ML approach to efficiently explore the vast structural space of Pt_(85−x)–Ni_x nanoclusters (Fig. 29a),²⁸³ pinpointing the Pt₄₃–Ni₄₂ composition as the most stable configuration (Fig. 29b). They identified the segregation-extent bond order parameter and the shell-resolved undercoordination ratio as key features impacting the structural stability, offering insights into the detailed surface-sites occupations and the solid solution nature of these nanoclusters. Their work not only aligns closely with experimental observations but also provides a reliable theoretical reference for the future design and optimization of Pt–Ni systems. Similarly, Chen et al. investigated the 55-atom Au@Pt nanocluster, employing an ML neural network potential trained on DFT data to analyze gold segregation effects.²⁸⁴ They used ab initio molecular dynamics (AIMD) and GA to explore the cluster's configurational space, which revealed that gold atoms tend to segregate to the surface and thus form a distorted amorphous structure. This gold segregation significantly enhances the ORR activity. In addition to Au, Rück et al. further considered other transition metals including Ag, Pd, Cu, Ni, focusing on the size effect which required the effective medium theory (EMT) as a simulation tool.²⁸⁵ The ML model that predicts strain on Pt core–shell nanocatalysts with site-specific precision revealed that the optimal mass activities for ORR are significantly influenced by nanoparticle size, strain effects, and core material. Key findings include the identification of optimal nanoparticle sizes for each core material (Fig. 29c) (e.g., 1.94 nm for Cu and Ni, and 2.83–2.88 nm for Ag and Au) and the conclusion that compressive strain on Pt@Cu and Pt@Ni enhances mass activities, while Pt@Au and Pt@Ag showed best activities under weak compressive strain. Finally, Zhang et al. broadened the search of the interest area to include wide range of TM elements for PtM-, Pt₃M-, and PtM₃-type alloys.²⁸⁶ Their comprehensive workflow integrated high-throughput DFT calculations with an AL approach. In three rounds of AL, they pinpointed Pt₃Co (211) as the most promising candidate. Moreover, SISSO was applied to reveal that the electronegativity difference between Pt and heteroatoms, the number of valence electrons in the heteroatoms, and the ratio of heteroatoms around Pt structure are most impactful in the binary Pt alloy systems.

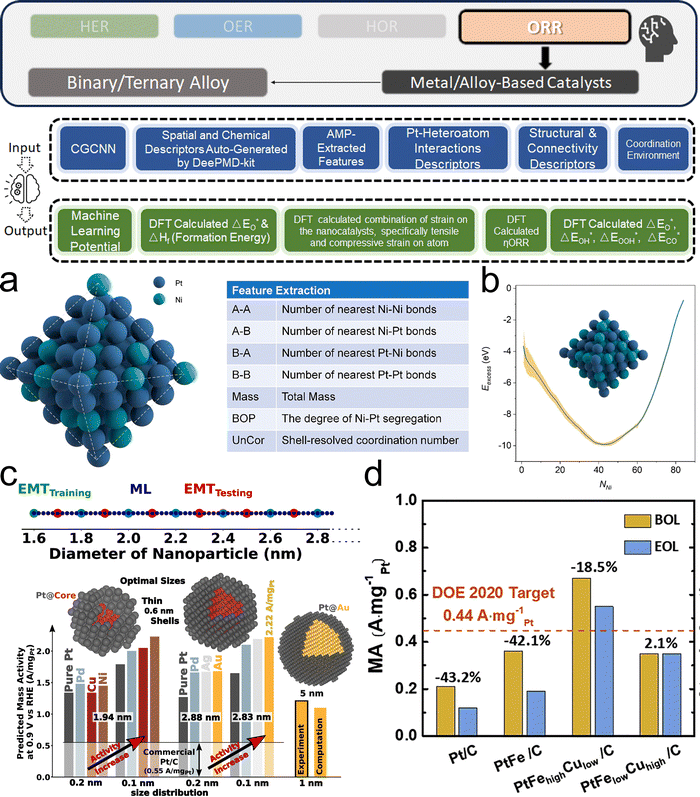Fig. 29 (a) Structure of a randomly ordered Pt–Ni 85 atom octahedron. (b) Global search results of physically niche genetic-ML in the homotopic space of a Pt_(85–x)–Ni_x nanocluster. (a and b are reproduced from ref. 283 with permission). (c) Upper: Training (green), testing (red) nanoparticles sizes used, and ML predictions of strain, with size scale truncated at 2.86 nm. Bottom: Forecasted optimal mass activities for nanoparticles with Pt shells and fcc core metals vary by size and distribution (reproduced from ref. 285 with permission). (d) Mass activity at 0.9 V (versus RHE) before and after 30 000 accelerated stress test cycles (reproduced from ref. 287 with permission).

Besides binary alloys, researchers have also investigated possibilities in ternary alloys. Chun et al. studied PtFeCu ternary alloys and trained neural network potentials to predict forces and energies in the crystal, enabling high-throughput screening of 396 862 structures to pinpoint the most active and stable configurations.²⁸⁷ The DFT-ML emulator guided the identification of candidate compositions for experimental exploration: Pt_0.82Fe_0.18 (PtFe), Pt_0.82Fe_0.12Cu_0.06 (PtFe_highCu_low), and Pt_0.8Fe_0.08Cu_0.12 (PtFe_lowCu_high). Moreover, the authors revealed the atomic distribution of Cu as a critical factor for enhancing activity and stability. In a half-cell test, the best Pt_0.82Fe_0.12Cu_0.06 synthesized not only showed a three-fold higher mass activity than that of Pt/C (Fig. 29d), but also performed well in accelerated stability tests. Kang et al. also applied a similar strategy, incorporating neural network potential with Monte Carlo and MD simulations as an efficient emulator for the ternary PtNiCu system.²⁸⁸ They adeptly employed Gaussian descriptors for radial and angular symmetry functions (G2 and G4) as input features to predict the total energy of nanoparticles, leading to the discovery of an optimal 2.6 nm icosahedron ternary nanocatalyst, comprising 60% Pt and 40% Ni/Cu, as the best theoretical candidate with enhanced activity and stability for ORR in acidic environments. Lee et al. further broadened the choice of the doping element to include a wider range of TMs in a Pt₁₅M_mN_n (m + n = 5) system, representing typical Pt₃M systems.²⁸⁹ They employed CGCNN to efficiently predict the stability (ΔH_f) and activity (ΔE_O) of more than two million surface structures, using crystal structures as input to identify 29 ternary Pt alloys with enhanced ORR activity and stability under acidic conditions. This approach revealed that certain combinations, notably those including elements like Ir and Rh as secondary doping elements, could significantly stabilize the Pt-skin surface. Park et al. used a modified CGCNN, a slab-graph convolutional neural network,³⁵ which significantly enhanced the prediction of adsorption energies by incorporating slab-graph constructions tailored for catalytic system applications. Their interest is in the ternary core–shell structure like X₃Y@Z, which demands exploration of the vast ternary alloy space. As a result, the authors successfully identified Cu₃Au as core and Pt as shell as a superior catalyst, demonstrating a roughly two-fold increase in kinetic current density and a significant reduction in Pt usage through experimental validation.

6.1.3. High-entropy alloys. High-entropy alloy (HEA) systems could benefit from the synergistic effect among multiple metal elements for optimized electronic and other properties, delivering superior performances. However, compared to the previously mentioned binary and ternary alloys, the challenges for exploration in the candidate spaces increase exponentially. Hence, ML is needed to boost the process. The research groups of Rossmeisl, Schumann, and Ludwig have collaborated from 2018 to 2022 on such an effort. Focusing on HEA as ORR electrocatalysts, they have developed a series of impactful and comprehensive research works that can serve as excellent research examples. Their first pioneering work²⁹⁰ focused on the surface HEA consisting of Ir, Pd, Pt, Rh, and Ru. By using the compositions of the nearest-neighbor atoms as input features (Fig. 30a), a simple least squares algorithm is trained as a DFT surrogate model to predict ΔE_OH and ΔE_O for screening HEA compositions. They discovered the optimized HEA composition Ir_10.2Pd_32.0Pt_9.30Rh_19.6Ru_28.9, which significantly surpasses the catalytic activity of pure Pt. Building on this, the following work expanded the methodology by integrating computational predictions with high-throughput experimentation to refine the search for optimal Ag–Ir–Pd–Pt–Ru complex solid solutions compositions.²⁹¹ Leveraging a dataset of 3317 DFT-calculated binding energies, the authors employed linear regression and sequential least squares programming to predict electrocatalytic activity. The ML surrogate model guided the synthesis and characterization of thin-film material libraries, revealing Ag₅Ir₅Pt₂₀Pd₃₅Ru₃₅ and Ag₅Ir₅Pd₁₇Pt₆₈Ru₅ as compositions with the highest ORR activity. By further analyzing the distribution of ΔE_OH and ΔE_O, the authors also proposed a model that estimated the total current density at 0.82 V (Fig. 30b), aligning theoretical predictions with experimental outcomes. Subsequent scanning droplet cell measurements in 0.1 M HClO₄ electrolyte validated these compositions, confirming their superior ORR activity through systematic high-throughput experimentation.

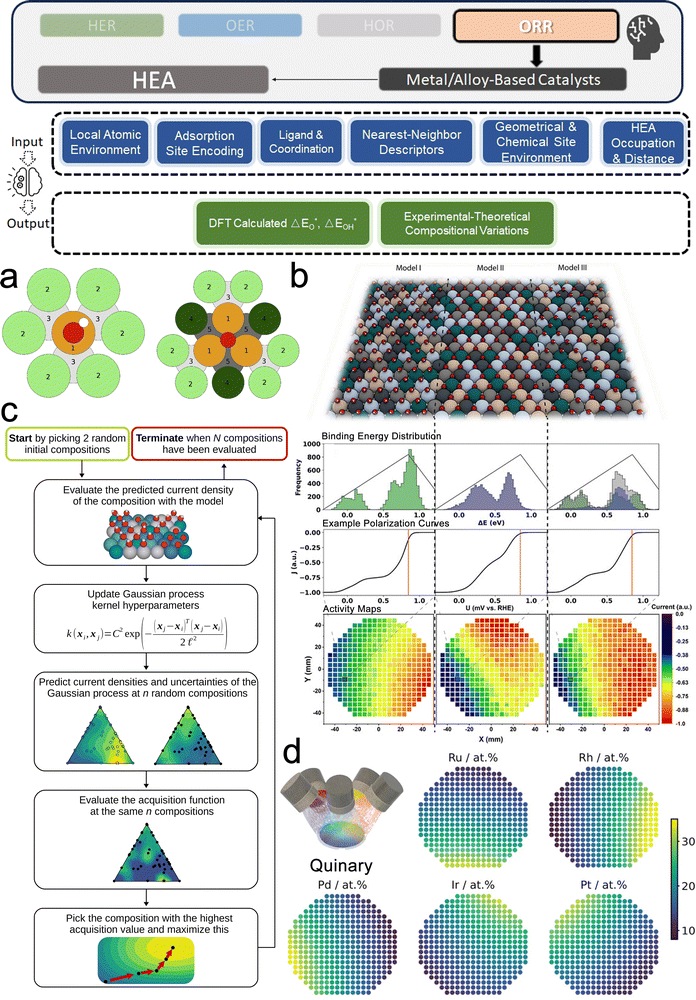Fig. 30 (a) Surface configurations parameterized by nearest neighbors. Left: *OH on-top binding highlighted by zones—binding site (orange), single-coordinated surface (light green), and subsurface (light gray) neighbors. Right: *O fcc hollow binding with zones—binding site (orange, 35 parameters), single-coordinated (light green/light gray), and double-coordinated (dark green/dark gray) neighbors (reproduced from ref. 290 with permission). (b) From top to bottom, on the top is a schematic of the complex solid solutions surface populations: Red for oxygen, white for hydrogen, with varied colors for complex solid solutions. The second layer shows histograms depicting *OH (green), *O (blue), and combined (grey) binding energy distributions across a 10 000-atom surface, showing optimum energies on volcano curves. The third layer shows example polarization curves for Ag₄Ir₁₆Pd₃₀Pt₁₄Ru₃₆ measured against potential, with red lines at 0.82 V versus RHE. The bottom are activity maps from models I, II, and III, showing current at 0.82 V versus RHE for selected compositions highlighted by a black box (reproduced from ref. 291 with permission). (c) Workflow of the BO algorithm: Terminated at N = 150 samples to assess the deviation in samples needed for optimal composition discovery. Acquisition function evaluated with n = 1000 random compositions (reproduced from ref. 292 with permission). (d) Visualization of compositional coverage for ternary and quaternary libraries across 342 measurement areas on a 100-mm diameter substrate, spaced at 4.5 mm intervals. Bottom: Demonstration of co-deposition from five sources and compositional gradients in a co-sputtered quinary materials library, with the same measurement grid (reproduced from ref. 293 with permission).

Further advancing the field, their third paper introduced BO to efficiently navigate the compositional space of Ag–Ir–Pd–Pt–Ru and Ir–Pd–Pt–Rh–Ru systems²⁹² (Fig. 30c). Using a kinetic model informed by DFT calculations, the study input features involved molar fraction vectors for alloy compositions. The authors targeted the optimization of current density corresponding to different compositions that were computed based on models proposed in the previous work.²⁹¹ This approach allowed for the prediction and experimental validation of optimal catalytic activities with a significantly reduced experimental dataset in only about 50 attempts, exemplified by discovering optimal binary alloys such as Ag₁₄Pd₈₆, Ir₃₅Pt₆₅, and Pd₆₅Ru₃₅ with high ORR activity. Recently, the authors advanced their methodology from previous works by incorporating a unique combinatorial strategy, building upon their established foundation of integrating computational predictions with high-throughput experimentation. This latest effort systematically covered the vast composition space of Ru–Rh–Pd–Ir–Pt.²⁹³ By deploying a data-guided experimentation approach, which involved permutations of deposition source arrangements, they efficiently expanded the experimentally explored composition space beyond their earlier achievements with BO and DFT surrogate models. This methodology enabled the identification of an optimal electrocatalytic composition, Ru₂₅Rh₁₅Pd₃₁Ir₁₅Pt₁₄, demonstrating the enhanced power of combining advanced simulation with large experimental datasets (Fig. 30d). The study also revealed the critical importance of Ru and Pd content for enhancing electrocatalytic activity in HEA systems for ORR. Across these studies, the team adeptly navigated from scale-specific, DFT-based microscale predictions to macroscale experimental validations, highlighting a transition from conventional DFT surrogate models to employing advanced optimization and high-throughput experimental approaches. This progression demonstrates a strategic application of ML to bridge theoretical models with empirical evidence, effectively exploring the complex composition space of HEAs for identifying superior electrocatalysts.

There are also several other notable works. Lu et al. investigated the Ir–Pd–Pt–Rh–Ru system,²⁹⁴ like ref. 290, but chose neural networks for regression modeling, uniquely applying them to decouple the ligand and coordination effects in HEA catalysts. By leveraging a neural network trained on DFT-calculated adsorption energies, they achieved a MAE of 0.09 eV. Moreover, their approach allowed them to dive deeper into mechanisms. They identified that coordination number and element identity are critical factors in determining the adsorption energy. This derived the pattern that more undercoordinated sites bind to *OH more strongly, ending up with higher ORR activities. Similarly, Saidi reported a work on Pt-free multinary PdAuAgTi alloy.²⁹⁵ By focusing on the ΔE_OH as the ORR activity descriptor, the study identified an optimal composition range of 8–12 at% Ti, which showed enhanced ORR performance close to that of Pt. Further, the research unveiled that substituting Au and Ag with more cost-effective elements like Cu and Zn not only maintained but potentially improved the catalytic activity, thereby opening avenues for more economically viable catalyst options. Yuan et al. further investigated the HEA without noble metals in the system of CoFeNi–X (X = Mo, Mn, or Cr).²⁹⁶ Through a standard DFT-ML strategy, they found that Mo and Cr could enhance the formation of bridge and on-top binding sites, which are crucial for ORR processes. Remarkably, they demonstrated that the typical scaling relationship between ΔE_OH and ΔE_O remains consistent across equimolar HEAs, yet stoichiometric adjustments can disrupt this balance. Of particular note, we found that in this section's research works the output fitting targets are all ΔE_OH and ΔE_O, rather than the commonly used ΔG previously adopted by works in the HER and OER studies. We speculate that the focus on adsorption energies in these studies is due to the complexity of the thermodynamics on HEA surfaces, where site variations cause different thermodynamic behaviors. This simplifies catalytic activity exploration by prioritizing a key step in electrocatalysis and avoiding the detailed thermodynamic corrections that could usually be managed with constants in other research works.

6.2. Carbon-based materials

Carbon-based materials, particularly those doped with heteroatoms like N or TM, have been extensively studied as promising substitution candidates for Pt as ORR catalysts due to their high activity, stability, and cost-effectiveness.²⁹⁷ Like previously introduced research on carbon-based materials, these materials benefit from the unique electronic properties imparted by heteroatom doping and the catalytic activity provided by transition metal sites to enable efficient ORR pathways.^298,299 However, unlike the situation for HER and OER in the ML studies discussed in Sections 3.2 and 4.2, which are mainly based on theoretical simulations, ORR carbon catalysts have long been studied experimentally. In addition, considering the homogeneity in research methods, in this section we divide the ML research on carbon-based ORR catalysts into two categories: those based on theoretical simulations and those based on experimental data. This distinction allows for a comprehensive understanding of the ORR mechanisms and the optimization of catalyst designs through both theoretical and practical approaches.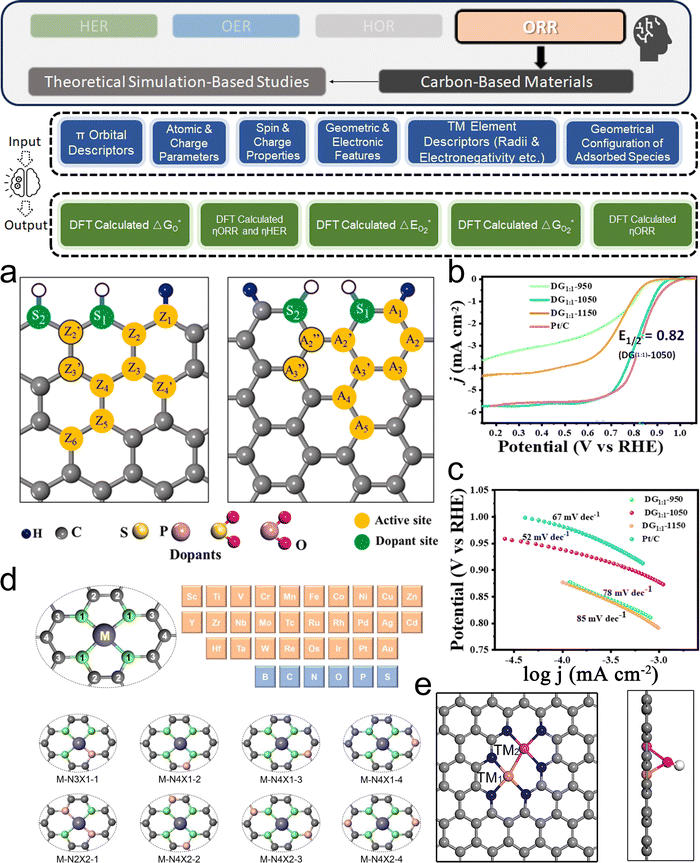

6.2.1. Theoretical simulation-based studies. Starting from metal-free carbon, besides the previously discussed ref. 145 which the authors also discussed ORR overpotential, graphene nanoribbons (Fig. 31a) have raised the interest of Kapse et al.³⁰⁰ Their results showed that the π orbital descriptors—the density of states at the Fermi level and relative π orbital occupancy—as pivotal for predicting ORR activities. They also found that the ML model could be extensively applied to similar carbon systems in different sizes, supporting validation of the insights in larger graphene configurations. Lv et al. investigated another type of N-doped γ-graphdiyne³⁰¹ nanoribbon, focusing on the edge effects to enhance the ORR and HER activity. They identified the distance between the adsorption site and the closest atom, along with the atomic charge of the adsorption site, as key determinants of electrocatalytic performance. This analytical method revealed that sp²-N doping near the edges significantly boosts the bifunctional activity. Bhardwaj et al. further used this type of DFT-ML strategy to provide guidance for their experimental synthesis.³⁰² In the DFT calculations integrated with ML, they focused on defect-engineered, nitrogen-doped graphene, identifying 5–8–5 defect sites and nitrogen dopants as key to enhancing catalytic activity. As for the synthesized sample under DFT-ML guidance, it demonstrated a notable ORR performance with a E_1/2 of 0.82 V (Fig. 31b and c), matching the benchmark set by commercial Pt/C catalysts. Lodaya et al. innovatively investigated graphite-conjugated catalysts that combined both advantages of heterogeneous and homogeneous catalysts, specifically focusing on their effectiveness without metal utilization.³⁰³ They identified carbon atoms ortho or para to nitrogen and at the edge of aromatic systems as key active sites for ORR, revealing the significant role of spin density and charge difference in predicting catalytic activity.

Fig. 31 (a) Left: Zigzag graphene nanoribbons with sulfur dopants at various sites (S), and active sites (Z), with absent hydrogen marked by blue circles. Z2′ and Z3′ sites specific to dual-atom doping. Right: Armchair graphene nanoribbons featuring substitutional (S) and active sites (A), with A2′′ and A3′′ exclusive to single-atom doping (reproduced from ref. 300 with permission). (b) Linear sweep voltammetry polarization curves of samples annealed at 950, 1050, and 1150 °C and Pt/C catalyst at 1600 rpm in 0.1 M KOH saturated with O₂. (c) Corresponding Tafel plots. (b and c are reproduced from ref. 302 with permission,) (d) Top: Structure of M–N₄C₁₀ with 28 central metals and six environmental atoms illustrated. Bottom: Eight configurations of SACs defining the sample space, with blue-violet for M, green for N, gray for C, and pink for doped atoms (reproduced from ref. 304 with permission). (e) Geometric structure of left: bare and right: OH-modified TM₁TM₂–N₆ structures. Gray, red, blue, and white balls represent C, O, N, and H atoms, respectively, while pink and brown balls represent TM atoms (reproduced from ref. 305 with permission).

As a consensus in the field,^298,299 further doping of TM atoms would increase the electrocatalytic activity, validated by both experiments and theoretical simulations. Therefore, the TM–N–C configurations have attracted attention and resulted in several similar studies aimed at expediting the discovery and optimization of such SACs^304,306,307 (2023; 2023; 2020). These investigations have systematically explored the influence of transition metals and environmental atoms on SACs’ performance by applying DFT calculations alongside ML to predict catalytic activities with high precision. For instance,³⁰⁴ one study considered other non-metal environmental atoms besides N: P, S, O, etc. (Fig. 31d). The authors identified 30 high-performance catalysts from a vast sample space of 1344 structures by combining geometric and electronic features, achieving an impressive predictive accuracy (RMSE of 0.12 V). In another work,³⁰⁶ the incorporation of unique descriptors such as the valence electron correction and the degree of construction differences has significantly improved model predictions, highlighting the importance of local structural configurations surrounding the active centers. As for deeper insights into the structure-performance relationships, key findings across these studies underscore the pivotal role of the central metal's electronic structure, particularly the number of d-electrons, radius, and electronegativity, in determining SACs’ ORR activity. Among the various TM–N–C configurations studied, Fe–N–C and Co–N–C emerged as the most promising candidates, owing to their optimal balance of catalytic activity and stability, as revealed through importance analysis. Such results are highly consistent with domain consensus validated by experiments.

Wang et al. further explored more possible types of N–C substrates (15 types) for hosting TM single atoms,³⁰⁸ leveraging ML to decouple the effects of adsorbate geometry and substrate-specific properties on the adsorption energy of O₂, which is crucial for optimizing electrocatalytic activity. Their innovative approach identified a novel, data-driven descriptor related to the geometrical configuration of the adsorbed O₂, which emerged as the most significant factor influencing adsorption energy, thereby providing a quantitative basis for the design of TM–N–C SACs with tailored catalytic properties for ORR. Finally, two different groups have coincidentally noticed dual-TM–N–C sites with geometric structures (Fig. 31e) like TM₁TM₂–N₆. Deng et al. and Zhu et al. both targeted the design and efficiency optimization of this system. Deng et al. discovered that Co₂–N–C and other eight configurations exhibit superior ORR activity,³⁰⁹ surpassing Pt benchmarks, with Co–Ni–N–C showing a notable limiting potential of 0.88 V. Zhu et al., however, identified Cu–Fe and Ni–Cu as candidates.³⁰⁵ Nevertheless, both studies highlighted the pivotal role of geometric parameters as critical factors, a finding revealed through ML, which underscored the simple geometric distances between TM atoms and coordinated N atoms as key to enhancing ORR performance. The impact of electronic descriptors such as electron affinity and electronegativity are also consistent between the two studies.

6.2.2. Experimental-based studies. While most of the research works introduced thus far are based on theoretical simulations like DFT, especially for non-precious metal systems such as TM compounds and carbon-based materials, a notable shift can be observed in the domain of ORR catalyst design towards leveraging ML methodologies grounded on experimental data. Though with limited database size, these studies typically use experimental parameters such as doping elements, synthesis conditions, and physicochemical properties as input features to predict ORR performance metrics like E_1/2.

First for metal-free systems, Dan et al. focused on N-doped graphene,³¹⁰ with their main emphasis on investigating the electron transfer numbers. This value is crucial for determining the two-electron or four-electron ORR pathway, as previously introduced. By applying ML to correlate synthesis parameters and material characteristics with ORR performance, they discovered that synthesis time and N doping levels are critical for optimizing the electrocatalytic efficiency of N-doped graphene materials. Jiang et al. investigated polymer hollow spheres (Fig. 32a) using ML to guide the choice for reactants like dopamine, trioctylamin, ammonia, and so forth.⁷¹ Their method revealed that reaction time and the amount of TOA and water were critical for the morphology of the spheres. The quantitative ML approach could successfully predict product morphologies to be solid or hollow, which could benefit the fine control of nano-synthesis. Xia et al. further proposed to build their ML models based on 123 different metal-free carbon materials collected from 50 works,³¹¹ focusing on N content and surface area as critical descriptors for predicting the onset potential of ORR. Their application of materials informatics led to the identification of nitrogen-doped graphene nanomesh as an optimal substrate for anchoring iron phthalocyanine, culminating in the fabrication of the sample under ML guidance. This catalyst showcased an unprecedented electrocatalytic activity for ORR in alkaline environments, with the most positive ORR peak at 0.87 V and an onset potential of 0.99 V in alkaline condition, surpassing even commercial product 20 wt% Pt/C.

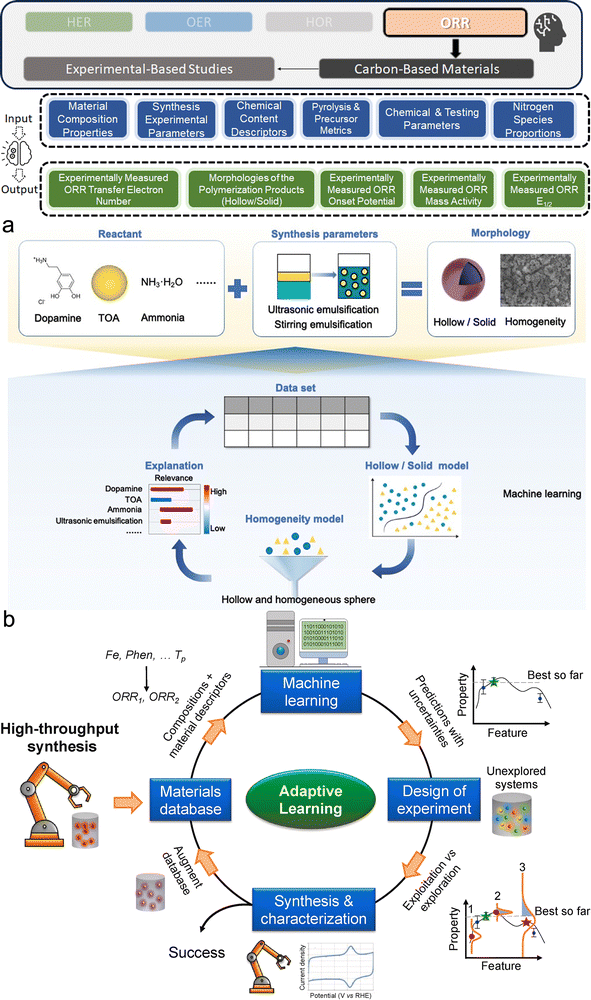Fig. 32 (a) Schematic diagram for guiding emulsion interfacial polymerization to prepare hollow spheres by ML (reproduced from ref. 71 with permission). (b) Adaptive learning in material design uses existing data and ML to correlate material properties with performance outcomes. By integrating uncertainty quantification and optimization, it guides the selection of new materials for testing to achieve specific targets and reduce model uncertainty. The highlighted approach prioritizes testing materials with greater predictive uncertainty, enhancing algorithmic performance and refining computational models with each iteration (reproduced from ref. 28 with permission).

Like OER, the acidic medium is more challenging for carbon-based materials. A group of researchers led by Zelenay et al. investigated the zeolitic imidazolate framework-8 (ZIF-8) derived Fe–N–C, as such systems have been regarded as some of the most promising candidates in acid medium. Their initial study³¹² focused on input features such as Fe precursor identity, content, and pyrolysis temperature. Through this approach, they discovered that GBDT and SVR models were most effective, leading to a 36% increase in measured mass activity. The importance analysis revealed the pyrolysis temperature as the most critical parameter influencing catalyst performance. Building upon this foundation, their subsequent work introduced an adaptive learning framework (Fig. 32b),²⁸ enhancing the methodology by incorporating statistical inference and uncertainty quantification to navigate a six-dimensional search space efficiently. This advanced approach resulted in the identification of four catalysts outperforming the original dataset, with the best catalyst showing a 33% improvement in ORR activity, specifically, an impressive mass activity of 16.3 mA mg⁻¹. Ding et al. also explored the ZIF-8 system, with a unique angle, uncovering the often-overlooked significance of pyrolysis time alongside pyridinic nitrogen species as decisive factors through the ML analysis of comprehensive experimental datasets.³¹³ Their approach, underpinned by data mining from 103 studies and a dataset encompassing 225 entries, revealed that pyrolysis time, typically not varied in previous studies, plays a crucial role in catalytic performance. By integrating ML predictions with experimental validations, they demonstrated a volcano-like relationship under different pyrolysis temperatures between pyrolysis time and E_1/2, pinpointing an optimal pyrolysis time that led to a superior E_1/2 of 0.82 V in acidic conditions for the best-performing catalyst. Moreover, combining characterization results and SHAP analysis, the authors revealed that the deeper mechanism of such a trend is the conversion of N species throughout the pyrolysis process, which has further proven the potential of ML in electrocatalyst research.

6.3. Other materials and MEA perspectives

In addition to commonly studied Pt-based alloy systems and carbon-based materials, there are several new emerging electrocatalyst systems for ORR that have been studied using ML. Using a typical DFT-ML surrogate modeling strategy, Liu et al. investigated TM and N doped AlP monolayers²⁹ for bifunctional oxygen electrocatalysis, pinpointing Co@VAl–2NP–AlP and Ni@VAl–2NP–AlP as systems with outstanding catalytic activity for OER/ORR with specific overpotentials of 0.38/0.25 V and 0.23/0.39 V, respectively. As for post-data mining, the authors identified the number of TM-d electrons, the radius of the TM atom, and the charge transfer of TM atoms as critical descriptors influencing adsorption behavior. This is quite consistent with the conclusions from previously introduced research that studied TM SACs on different substrates. In comparison, Zhai et al. leveraged domain knowledge from published experimental data to construct ML models.³¹⁴ They aimed to inform their experimental strategies for ABO₃-type perovskite oxides in alkaline electrolyte oxygen reduction electrodes. By introducing the ionic Lewis acid strength as a novel descriptor, their ML approach enabled the screening of 6871 perovskite compositions, ultimately identifying four with superior activity. The guided experiments validated the ML predictions, particularly highlighting Sr_0.9Cs_0.1Co_0.9Nb_0.1O₃, which exhibited an exceptionally low area-specific resistance of 0.0101 Ω cm² at 700 °C, underscoring the critical role of the A-site and B-site ionic Lewis acid strengths in enhancing surface exchange kinetics and ORR activity.

Similar to the case of OER in Section 4.3, looking at ORR electrocatalysts from an MEA perspective is critical for real-world fuel cell applications. Due to the difference in reaction conditions, candidates that are theoretically or experimentally half-cell validated might not be able to have the same performance in the MEA component. From the chemical engineering perspective, the macro electrochemical performance does not solely depend on the intrinsic activity of electrocatalysts. The component, preparation methods, support type of the ORR electrocatalysts, as well as engineering parameters like catalyst loading, solvent type, recipe, and thickness of ion-conducting membrane, are coupled together.¹⁶ As a result, experimental and theoretical research on electrocatalysts alone often cannot achieve satisfactory results in fuel cell single cells. Noticing this point, Ding et al. have leveraged ML to streamline the optimization of Pt-based MEA for PEMFCs.³¹⁵ Their comprehensive approach used a dataset constructed from 295 articles spanning 17 years, resulting in 918 entries with 66 initial features, and focused on identifying key parameters that influence MEA performance. Their feature importance analysis on the domain knowledge revealed the pattern that, compared to parameters related to nano- and micro-scale synthesis and electrocatalysts components, the engineering parameters of MEA are more decisive toward power density as macro performance (Fig. 33a). For the next step of ML workflow, they distilled 27 critical features (Fig. 33b) from the initial 66 to obtain good regressors that could predict MEA power densities with less than 15% error (Fig. 33c). Moreover, the visualized DT and apriori associate rule mining found that for Pt-based catalysts in MEA, the recommended carbon substrate mass fraction should be kept lower than 57.75 wt%. This is not a good strategy in more idealized half-cell tests in pursuing higher ORR activity, but it is a practical approach to ensuring good macro electrochemical performance in MEAs. The authors also investigated non-precious metal (namely carbon-based TM–N–C)-based MEAs.⁷⁰ First, they found consistent patterns showing that MEA engineering parameters are more decisive in feature importance ranking (Fig. 33d). They also obtained several applicable catalyst design rules recommended for carbon-based ORR electrocatalysts, specifically in MEA. For example, due to increased TM–N_x active site density, micropores are generally preferred for increasing the intrinsic ORR activity for TM–N–C-type carbon-based materials. However, through visualized DT, the authors identified mesopore and macropore in child nodes, indicating a balanced tradeoff between increasing intrinsic activity and ensuring enhanced mass transfer. Huo et al. further used the dataset collected by Ding et al.'s previous work⁷⁰ for the carbon-based MEA system, and introduced more advanced ML algorithms like CNN to increase the prediction accuracy for single-cell polarization curves.³¹⁶ Their enhanced model can serve as good experimental surrogate models in guiding the optimization of TM–N–C carbon-based ORR electrocatalysts with much less cost on trial-and-error attempts.

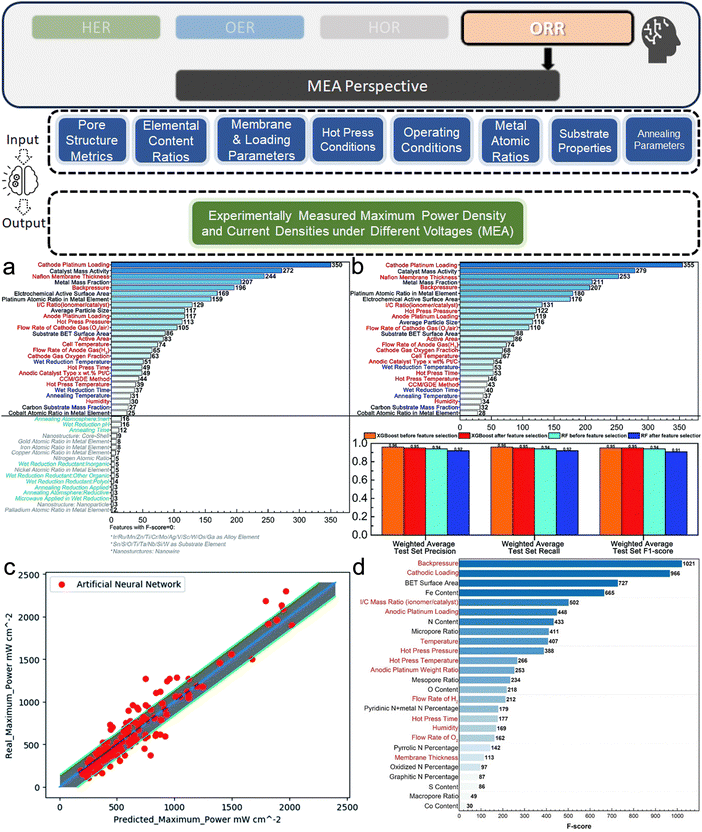Fig. 33 (a) Feature importance heuristic by XGBoost algorithm pre-feature selection, categorizing features into the microscopic properties of Pt-based nanocatalysts (black), preparation process parameters (blue), and single-cell device operating conditions plus MEA preparation (red). (b) Top: Feature importance after the selection. Bottom: Test set classification performance comparison before and after feature selection, illustrating the algorithm's efficiency in identifying and using key features for predictive accuracy. (c) Predictions output by the best performing ANN regressor on the test set (a–c are reproduced from ref. 315 with permission). (d) Feature importance heuristic from the XGBoost algorithm, with red features linked to PEMFC operating conditions and black features linked to non-precious metal electrocatalysts’ intrinsic properties (reproduced from ref. 70 with permission).

6.4. Statistical analysis and summary

We have covered the “last piece of the puzzle” for electrocatalysts toward hydrogen energy—the ORR. Similar to Sections 3.4 and 4.5, an intuitive statistical analysis in Fig. 34 and a summary would help readers better understand the related 41 publications.

Fig. 34 Statistics for the ORR section, including (a) utilized input features; (b) most important features recognized by ML model interpretation. (c) distribution of the dataset sizes used. (d) utilized ML algorithms; (e) best ML algorithms.

Features. For ORR, the main material systems studied can be categorized into metal/alloy and carbon-based structures. As shown in Fig. 34a, these two systems exhibit unique preferences. Studies on metal/alloy systems have shown a significant interest in including coordination numbers as an input feature. As discussed in the HER summary section, the coordination environment in close-packed structures of metals and alloys is crucial for catalytic behavior. This has led to extensive research in ORR studies to identify the best facet and to nano-engineer selective exposure of more active facets like Pt(111). Fig. 34b supports this conclusion, showing that coordination number is the most decisive input feature identified by ML models across multiple publications.

For carbon-based materials, typically TM and N-doped graphene, a different trend in descriptors is observed. Beyond bond length, which describes topological structure and intrinsic physical atomic properties like ionization energy and the number of d-electrons, studies have adopted unique features such as pyridinic nitrogen content, pyrrolic nitrogen content, and Brunauer–Emmett–Teller (BET) surface area. These features are not frequently used for carbon materials in the HER and OER sections. The reason for this difference is that, unlike HER/OER studies which are typically theoretically based on DFT simulations, ORR studies of carbon-based electrocatalysts emphasize ML based on datasets derived from direct experimental synthesis and evaluation. This emphasis results in the use of techniques like AL and BO, which are suitable for limited data cases, and brings insights from a meso-macro perspective. The segmentation of nitrogen species and pore structures is dominant in the performance of carbon-based materials for ORR. Typical Pt-based metal/alloy electrocatalysts do not require a high surface area for the substrate carbon. For example, commercial Pt/C uses Vulcan XC-72 carbon black rather than BP2000. However, due to the intrinsic difference in active sites, to enrich the density of ORR active M–N–C sites, carbon-based electrocatalysts focus on nano-engineering to increase surface area and the abundance of pyridinic (metallic)-type nitrogen species. These species are important both for their intrinsic ORR activities and their ability to host TM dopant atoms to form more effective M–N–C sites.^317–319 The demand for achieving good ORR activity is further revealed in Fig. 34b by the emergence of synthesis parameters: reaction (hydrothermal and pyrolysis) time and pyrolysis temperature. This trend is consistent with the focus on facet engineering in metal/alloy systems,³²⁰ while for carbon-based materials, the focus is on identifying better atomically dispersed defect doping structures or optimizing synthesis conditions to improve experimentally observed performance.

Dataset and ML algorithms. In Fig. 34c, we observe that researchers generally prepare larger datasets for metal/alloy systems compared to those focused on carbon materials. This may be due to the larger candidate space derived from different design strategies. As illustrated in Fig. 34d and e, RF is both the most commonly chosen and best-performing ML algorithm. GBDT, another popular ensemble algorithm, is also preferred. When examining the differences between the two material systems, linear regression is frequently used for metal/alloy systems. While it is the least complex method, it is also the most interpretable. Nevertheless, a complex algorithm with powerful fitting ability like MLP unexpectedly obtained a similar ranking position. This reflects the current status of research on metal/alloy ORR electrocatalysts, where researchers need to explore the vast unknown design space while providing intuitive descriptors through linear combinations of input features to deeply understand the mechanism. In contrast, studies on carbon materials prioritize RF and GBDT, not only because their datasets are generally smaller but also because these studies aim to identify the most important features through SHAP feature sorting without proceeding to the next step of linear formula induction.

7. Conclusion and outlook

7.1. Overall statistics

In this comprehensive review, we systematically explored the application of ML in designing electrocatalysts for crucial hydrogen energy conversion reactions: HER, OER, HOR, and ORR. Our analysis spans various electrocatalyst systems, underscoring ML's pivotal role in identifying optimal solutions within vast candidate spaces and deciphering complex multiparametric challenges. We have summarized the preferred input features, ML methods, and the most decisive features identified by ML models for each material system. In Sections 3.4, 4.5, and 6.4, we present an overall statistical analysis as summarized in Fig. 35, combining data from all four types of electrochemical reactions. The four main material categories are metals/alloys, TM oxides, carbon structures (including doped graphene and carbon nitride), and TM compounds (such as sulfides, phosphides, borides, MoS₂, and 2D materials like MXene). Generally, studies on metal/alloy systems show unique differences from the other three categories. From a feature perspective (Fig. 35a and b), coordination number is highly valued in metals/alloys, while d-band properties and bond length are dominant in the other three categories. From a dataset size perspective (Fig. 35c), the typical size ranges from smallest to largest as follows: TM compounds < carbon structures < TM oxides < metals/alloys, with the latter being more than an order of magnitude larger than the others. This difference in dataset size has influenced the choice of ML algorithms (Fig. 35d and e). Research on metals/alloys tends to prefer either deep learning or simpler methods like linear regression or GP. In contrast, ensemble algorithms such as RF and GBDT are more popular and best performing in the other three categories, surpassing ANN's ranking. Our statistical analysis reveals the intrinsic differences between material categories when used as hydrogen electrocatalysts. This provides a valuable domain-level reference for researchers in their feature engineering, dataset preparation, and ML algorithm selection based on the material system of interest.

Fig. 35 Statistics for all HER/OER/HOR/ORR publications, including (a) utilized input features; (b) most important features recognized by ML model interpretation. (c) Distribution of the dataset sizes used. (d) Utilized ML algorithms; (e) best ML algorithms.

From paradigm perspective, ML, particularly through supervised learning for surrogate model training, has advanced both computational simulations and experimental explorations, enabling the rapid discovery and optimization of novel electrocatalysts. Moreover, data mining and interpretative analysis of “black-box” models have offered deep insights into the physical and chemical attributes of these electrocatalysts, aiding in the identification of key descriptors and design parameters. The integration of ML marks a significant paradigm shift toward data-centric approaches in electrocatalyst design, significantly enhancing the pace of electrocatalyst discovery and the understanding of electrocatalytic processes. This shift has not only led to the prediction of catalytic performance and the discovery of novel electrocatalysts with unparalleled speed, but also highlighted the potential of ML in addressing the economic and sustainability challenges in hydrogen energy production. As we move forward, ML's ability to bridge the gap between computational predictions and experimental validations is poised to revolutionize electrocatalyst development for hydrogen energy conversion, promising more sustainable and energy-efficient solutions.

7.2. Future outlooks

However, as we reflect on our current achievements, it becomes evident that several challenges remain, and the landscape of electrocatalysis research is rapidly evolving with new opportunities on the horizon. This pivotal moment in research invites us not only to celebrate our progress but also to project our gaze towards future directions where the potential of ML in catalyzing further innovations remains vast and largely untapped. Building upon the foundation laid by our current achievements in applying ML to electrocatalysis, we now turn our attention to the unresolved challenges and emerging opportunities that define the future trajectory of this field. Based on the insights gathered from the review, the following outlook articulate key challenges and potential future directions in ML-aided electrocatalysis design. From the reliance on DFT simulations to the nascent stages of experimental automation, the journey towards fully realizing ML's potential in electrocatalysis is fraught with complex, multiparametric issues that span across multiple scales of reaction mechanisms and electrocatalyst systems:

7.2.1. Integration of multiscale and multi-fidelity simulations with ML. A significant body of research focuses on employing theoretical simulation like DFT calculation paired with ML as surrogate models for computational experimental design. While this approach aligns with chemical intuition by incorporating geometric and electronic structure descriptions of catalytic sites as inputs, it remains confined to a relatively small research scale. The calculation results are not of high fidelity compared with real experimental explorations. Electrocatalysis, being inherently a multiscale coupled reaction, demands broader exploration beyond surface reactions to include dynamic interactions across different scales of the catalytic process.

To overcome this, leveraging ML's capability as surrogate models for cross-scale and multi-fidelity simulations, for example from DFT to MD, might be a possible choice. Though it requires more dataset preparation cost, this approach enables comprehensive modeling of electrocatalytic processes, from atomic interactions to macro-scale fluid dynamics, significantly enhancing the accuracy and predictive power of simulations. This is already a hot topic in life sciences and can be applied to electrocatalysis.³²¹ By integrating these scales, theoretical simulation-based ML can rapidly identify optimal configurations and conditions with higher fidelity to be validated by experiments.

7.2.2. Autonomous discovery of electrocatalysts. Experimental data, noted for its high fidelity but costly nature, plays a crucial role in advancing electrocatalyst research. As discussed, common approaches involve extracting insights from domain knowledge, notably previous publications, or initiating manual high-throughput synthesis, both of which are typically expensive. However, in recent years, automation in these processes have emerged.

To enable automated experimental investigation, robotic automated laboratories have been established, such as the autonomous mobile robot reported by Cooper et al.,³²² which optimizes photocatalytic electrocatalysts using a Bayesian decision-making method. Brabec et al. reported a high-throughput autonomous decision and experimental platform for the rapid synthesis of ABO₃-type perovskites for ML data analysis.³²³ Since then, similar reports of robotic autonomous electrocatalyst synthesis and evaluation platforms have gradually increased over the past two years^324,325 (2022; 2023).

On the other hand, the advent of generative AI, for instance, large language models (LLMs) like ChatGPT have made the NLP work of scientific publications, which typically requires expertise in materials science and chemistry, much faster. For example, Yaghi et al. recently reported the use of ChatGPT to rapidly extract information from MOF-related publications,³²⁶ directly obtaining a large amount of tabular data from synthesis-related paragraphs to aid ML modeling and guide experiments. Recently, Dagdelen et al. leveraged LLMs like GPT-3 and Llama-2 to perform joint named entity recognition and relation extraction tasks in materials science.³²⁷ By fine-tuning these models on annotated text passages, the study demonstrates how LLMs can extract complex, structured information about materials, such as dopants, host materials, and metal–organic frameworks, from scientific texts. The approach simplifies the creation of large, structured databases of specialized scientific knowledge, facilitating the advancement of materials discovery and design.

There is also more complex system that combine all the above-mentioned ML models based on different knowledge sources together. Ceder et al. proposed A-lab for the discovery of oxides in lithium-ion batteries.³²⁸ Their innovation lies in the push for high-throughput automated robotic experiments using a multi-decision framework. In their work, which employs multiple ML expert systems for different processes, researchers have enabled decision-making based on DFT simulations and extensive scientific text mining to participate simultaneously in the active learning cycle of robotic synthesis. This equates to allowing the autonomous discovery process of electrocatalysts to benefit from multiple data sources and expert system decisions from domain knowledge (published literature), theoretical simulations (DFT), and local experimental data (e.g., both manual and automated laboratories). The power of generative AI also extends to the development of more advanced and efficient generative models for theoretical molecular and material design. For instance, Daigavane et al. recently introduced Symphony,³²⁹ an E (3)-equivariant autoregressive model that uses higher-degree spherical harmonic projections to generate accurate 3D molecular geometries, outperforming existing models in capturing complex molecular symmetries. Similarly, Zeni et al. presented MatterGen,³³⁰ a diffusion-based generative model that not only produces stable, diverse inorganic materials across the periodic table but can also be fine-tuned to meet specific property constraints, such as symmetry or magnetic density. These advancements in generative AI highlight its potential to significantly surpass traditional surrogate ML models, enabling faster and more autonomous discovery of electrocatalysts by integrating diverse data sources and experts.

As discussed in this review, researchers in hydrogen electrocatalysts have experimented with manually crafted high-throughput electrolysis cells,²⁶⁹ co-sputtering deposition,²⁹³ and automated platforms²⁸ for weighing, dispensing, and shaking. However, these approaches are not yet mainstream due to the lengthy synthesis routes and high costs associated with electrocatalyst evaluation. While high-throughput synthesis instruments are not widely adopted in electrocatalysis due to their high costs, more accessible alternatives can be explored. For instance, inkjet printers, popular in the sensor field and easily programmable, can be adapted for high-throughput catalyst preparation.^331,332 Studies have demonstrated that integrating ML with these systems can facilitate the design of flexible electronics, and similar methodologies can be applied to hydrogen electrocatalysts. By using cost-effective, readily available devices like inkjet printers, researchers can potentially achieve rapid, data-driven discovery and optimization in electrocatalyst development.

7.2.3. Bridging fidelity gaps and facilitating knowledge transfer. A recurring challenge in electrocatalysis research is the isolated focus on specific material systems and scales. As we have emphasized repeatedly in this review, current ML research on electrocatalysts has not adequately accomplished the task of seamless bridging, whether between theoretical DFT simulations and experiments or among multiple material systems. Moving forward, we should adopt more flexible approaches, blending data from multiple fidelity levels within the same system and transferring knowledge across different systems. Here we propose possible directions:

The first viable approach is to employ DFT data for early rapid screening and subsequently use targeted experimental data to identify potential candidates, allowing researchers to achieve focused optimization of electrocatalysts. This phased method, using data of varying fidelity, mirrors the engineering design process's funnel approach: starting broadly and then narrowing down to specific details. Researchers can learn from the ideas in multi-fidelity ML, and regard DFT as cheap low-fidelity data and experimental observation as expensive high-fidelity data. Taking into account the cost factor (using a certain indicator to quantify the computational cost and experimental cost) for query budget, the mature multi-fidelity active learning workflow is used to complete efficient optimization development.³³³

Another approach is through techniques like transfer learning. We can disseminate insights and knowledge across these datasets and corresponding systems, thereby reducing the costs associated with training data. For example, within the same system, data of different fidelity levels, typically from DFT simulations and actual experimental data, can be leveraged to capitalize on their respective strengths within the same electrocatalyst discovery process. Drawing inspiration from the fields of NLP and computer vision, a potential strategy could involve using high-throughput DFT data to train initial ML models, followed by fine-tuning these models with a selected set of costly experimental data. This approach not only ensures efficient resource utilization, but also guarantees that models accurately reflect real-world experimental conditions. Furthermore, for similar electrocatalyst systems, we should also explore the possibility of transferring knowledge between them. For instance, recent work by Ding et al., based on automated text mining, has shown that models based on alkaline and acidic HER/OER publication data can achieve favorable results by fine-tuning them on a small set of neutral HER/OER publication data.³³⁴

7.2.4. Enhancing interpretability and reliability of ML models. For real-world applications and product development, the explainability and reliability of ML models are critical aspects that cannot be ignored. Black-box models, while powerful, often lack transparency, making it difficult to understand and trust their predictions. This opacity can lead to issues in reliability, where models might perform well on test data but fail in real-world scenarios due to unaccounted factors or overfitting. Based on our statistical results, we see efforts using methods like SISSO or other linear regression techniques to identify formula-like or straightforward descriptors for explanation, particularly in metal/alloy systems. However, the majority of research tends to rely on techniques such as SHAP to identify the most important features without further detailed explanations.

To address these challenges, there is a need to shift from solely relying on black-box ML models to adopting more transparent, white-box or grey-box models. These models not only provide greater interpretability but also enhance the reliability and acceptance of ML predictions in practical applications, reducing risks associated with model deployment and facilitating deeper insights into electrocatalytic processes. Such models are integrated with fundamental physical and chemical principles, or other types of domain knowledge, alongside data science. Moreover, enhancing interpretability is not only a matter of reducing risks but also vital in creating chances for mining deeper insights into the mechanisms underlying processes. Here we present some practical strategies for white box models: Incorporating domain knowledge involves embedding physical and chemical laws directly into the ML models, which constrains predictions to be physically plausible by using known reaction mechanisms or material properties as part of the model input. Model simplification can also enhance interpretability by utilizing simpler models such as linear regression, decision trees, or SISSO, especially when these models effectively capture the essential relationships within the data. Additionally, hybrid models that combine ML models with mechanistic models can leverage the strengths of both approaches; for example, using ML to predict parameters in a mechanistic model can provide interpretable and reliable results.

7.2.5. The need to improve uncertainty quantification. A key observation from this review is the insufficient use of UQ in studies applying surrogate ML models to electrocatalyst development. While some active learning and Bayesian optimization studies have begun to incorporate UQ, most research neglects this critical aspect, leading to overconfident predictions and potentially overlooking promising areas of exploration. The lack of UQ can result in wasted resources on experiments driven by overly optimistic models and missed opportunities to investigate uncertain but potentially fruitful regions. To advance the field, it is crucial that the electrocatalyst community integrates UQ more systematically into their workflows. Techniques such as model ensembling, deep kernel learning, and Monte Carlo dropout, alongside inherently uncertain methods like Gaussian Processes, should be standard practice. By embedding UQ into ML workflows, researchers can better guide experimental efforts, optimize resources, and enhance the reliability of model predictions. This shift will not only improve the robustness of individual studies but also accelerate the discovery of innovative and effective catalysts with greater confidence in their real-world applicability.

7.2.6. Addressing economic and sustainability challenges and promoting collaborative efforts. Economic and sustainability challenges are critical considerations in the advancement of hydrogen energy production using ML approaches. While ML has the potential to optimize material usage and reduce waste, it also comes with its own set of economic and sustainability challenges. The computational cost of running large-scale ML models can be significant, requiring substantial energy and resources. Moreover, high-throughput synthesis, although efficient in generating large datasets, can lead to material waste if not managed properly. To mitigate these issues, researchers need to focus on developing more energy-efficient ML algorithms and adopting sustainable practices in experimental setups. For instance, leveraging cloud computing resources with a focus on energy efficiency, or using more localized, energy-saving hardware can help reduce the carbon footprint of ML computations. Additionally, implementing recycling and reusing strategies for materials in high-throughput experiments can minimize waste. Recent advancements in federated learning, which allows model training across decentralized devices, can also reduce the need for extensive data transfer and centralized computing, further lowering the environmental impact.

A significant oversight in current studies is the lack of consideration for MEA requirements for electrocatalysts at the engineering level. The gap between the idealized conditions often represented in DFT simulations and the complex, real-world operational environments of electrolyzers and fuel cells is substantial. Future research must prioritize high-throughput experimental approaches that focus on device-level synthesis and testing. Such high-throughput experiments are instrumental in facilitating the practical deployment of ML-optimized electrocatalysts, making the leap from theoretical models to tangible, operational systems.

To address these challenges effectively, collaboration between academia and industry (including national labs) is essential. Industry partners provide real-world needs and support, along with practical problems that need solutions, which can guide academic research toward more applicable solutions. Specific collaborative initiatives could include joint research projects, shared datasets, and industry-sponsored research programs. Successful collaborations in related fields, such as the development of ML models for drug discovery, provide a blueprint for similar efforts in electrocatalysis. For instance, AlphaFold is a successful collaborative outcome by Google DeepMind and European Molecular Biology Laboratory. Recommendations for future collaborative efforts should focus on the transition from high-throughput materials screening to real-time applications, ensuring that ML-optimized electrocatalysts are not only developed efficiently but also deployed effectively in practical settings. The benefits of these collaborations are manifold. Accelerated innovation, resource sharing, and the practical deployment of research outcomes are just a few. By working together, academia and industry can leverage their respective strengths to overcome the economic and sustainability challenges in hydrogen energy production. This collaborative approach will enable the rapid advancement of ML applications in electrocatalysis, driving the development of more efficient and sustainable hydrogen energy conversion technologies.

Data availability

A summary Table S1 (ESI†) is enclosed separately as an Excel file and is also available in the GitHub online repository. https://github.com/ruiding-uchicago/ML-in-Hydrogen-Energy-Transformation-Electrocatalysts-Review/tree/main.

Conflicts of interest

There are no conflicts to declare.

Acknowledgements

This project is supported by Schmidt Sciences, LLC. Specifically, R. Ding acknowledges the financial support from the Eric and Wendy Schmidt AI in Science Postdoctoral Fellowship, a Schmidt Futures program at the University of Chicago. X. B. Wang acknowledges the partial support by National Natural Science Foundation of China (U23B2075, 52272039, 51972168), Jiangsu Provincial Natural Science Foundation (BK20231406), Jiangsu Provincial Key Research and Development Program (BE2023085).

References

1. M. Yue, H. Lambert, E. Pahon, R. Roche, S. Jemei and D. Hissel, Renewable Sustainable Energy Rev., 2021, 146, 111180.
2. Y. Wang, Y. H. Pang, H. Xu, A. Martinez and K. S. Chen, Energy Environ. Sci., 2022, 15, 2288–2328.
3. K. Kodama, T. Nagai, A. Kuwaki, R. Jinnouchi and Y. Morimoto, Nat. Nanotechnol., 2021, 16, 140–147.
4. S. Sultan, J. N. Tiwari, A. N. Singh, S. Zhumagali, M. Ha, C. W. Myung, P. Thangavel and K. S. Kim, Adv. Energy Mater., 2019, 9, 1900624.
5. Y. Jiao, Y. Zheng, M. T. Jaroniec and S. Z. Qiao, Chem. Soc. Rev., 2015, 44, 2060–2086.
6. C. L. Bockting, E. A. M. van Dis, J. Bollen, R. van Rooij and W. Zuidema, Nature, 2023, 614, 224–226.
7. Z. Y. Niu, G. Q. Zhong and H. Yu, Neurocomputing, 2021, 452, 48–62.
8. T. Young, D. Hazarika, S. Poria and E. Cambria, IEEE Comput. Intell. Mag., 2018, 13, 55–75.
9. A. Voulodimos, N. Doulamis, A. Doulamis and E. Protopapadakis, Comput. Intell. Neurosci., 2018, 2018, 7068349.
10. L. Alzubaidi, J. Zhang, A. J. Humaidi, A. Al-Dujaili, Y. Duan, O. Al-Shamma, J. Santamaria, M. A. Fadhel, M. Al-Amidie and L. Farhan, J. Big Data, 2021, 8, 53.
11. P. Bryant, G. Pozzati and A. Elofsson, Nat. Commun., 2022, 13, 1265.
12. J. Vamathevan, D. Clark, P. Czodrowski, I. Dunham, E. Ferran, G. Lee, B. Li, A. Madabhushi, P. Shah, M. Spitzer and S. R. Zhao, Nat. Rev. Drug Discovery, 2019, 18, 463–477.
13. E. O. Pyzer-Knapp, J. W. Pitera, P. W. J. Staar, S. Takeda, T. Laino, D. P. Sanders, J. Sexton, J. R. Smith and A. Curioni, npj Comput. Mater., 2022, 8, 84.
14. Z. Li, S. W. Wang and H. L. Xin, Nat. Catal., 2018, 1, 641–642.
15. R. Ding, Y. Chen, Z. Rui, K. Hua, Y. Wu, X. Li, X. Duan, J. Li, X. Wang and J. Liu, J. Power Sources, 2023, 556, 232389.
16. R. Ding, S. Zhang, Y. Chen, Z. Rui, K. Hua, Y. Wu, X. Li, X. Duan, X. Wang, J. Li and J. Liu, Energy AI, 2022, 9, 100170.
17. R. Batra, L. Song and R. Ramprasad, Nat. Rev. Mater., 2021, 6, 655–678.
18. B. Ryu, L. Wang, H. Pu, M. K. Y. Chan and J. Chen, Chem. Soc. Rev., 2022, 51, 1899–1925.
19. Z. P. Yao, Y. W. Lum, A. Johnston, L. M. Mejia-Mendoza, X. Zhou, Y. G. Wen, A. Aspuru-Guzik, E. H. Sargent and Z. W. Seh, Nat. Rev. Mater., 2023, 8, 202–215.
20. P. P. Angelov, E. A. Soares, R. C. Jiang, N. I. Arnold and P. M. Atkinson, Wiley Interdiscip. Rev. Data Min. Knowl. Discov., 2021, 11, e1424.
21. I. Ahmed, G. Jeon and F. Piccialli, IEEE Trans. Industr. Inform., 2022, 18, 5031–5042.
22. K. P. Murphy, Probabilistic machine learning: an introduction, MIT Press, 2022.
23. Y. Bengio, A. Courville and P. Vincent, IEEE Trans. Pattern Anal. Mach. Intell., 2013, 35, 1798–1828.
24. C. M. Bishop and N. M. Nasrabadi, Pattern recognition and machine learning, Springer, 2006.
25. T. Hastie, R. Tibshirani, J. H. Friedman and J. H. Friedman, The elements of statistical learning: data mining, inference, and prediction, Springer, 2009.
26. J. A. Santana, J. J. Mateo and Y. Ishikawa, J. Phys. Chem. C, 2010, 114, 4995–5002.
27. H. Li, S. Xu, M. Wang, Z. Chen, F. Ji, K. Cheng, Z. Gao, Z. Ding and W. Yang, J. Mater. Chem. A, 2020, 8, 17987–17997.
28. W. J. M. Kort-Kamp, M. Ferrandon, X. Wang, J. H. Park, R. K. Malla, T. Ahmed, E. F. Holby, D. J. Myers and P. Zelenay, J. Power Sources, 2023, 559, 232583.
29. X. Liu, Y. Zhang, W. Wang, Y. Chen, W. Xiao, T. Liu, Z. Zhong, Z. Luo, Z. Ding and Z. Zhang, ACS Appl. Mater. Interfaces, 2022, 14, 1249–1259.
30. L. H. Zhang, X. Y. Guo, S. L. Zhang and S. P. Huang, J. Mater. Chem. A, 2022, 10, 11600–11612.
31. Y. Sugawara, S. Ueno, K. Kamata and T. Yamaguchi, ChemElectroChem, 2022, 9, e202101679.
32. X. Jiang, Y. Wang, B. R. Jia, X. H. Qu and M. L. Qin, ACS Omega, 2022, 7, 14160–14164.
33. M. J. Craig and M. Garcia-Melchor, Molecules, 2021, 26, 6362.
34. X. Mao, L. Wang, Y. Xu, P. Wang, Y. Li and J. Zhao, npj Comput. Mater., 2021, 7, 46.
35. Y. Park, C.-K. Hwang, K. Bang, D. Hong, H. Nam, S. Kwon, B. C. Yeo, D. Go, J. An, B.-K. Ju, S. H. Kim, J. Y. Byun, S. Y. Lee, J. M. Kim, D. Kim, S. S. Han and H. M. Lee, Appl. Catal., B, 2023, 339, 123128.
36. N. K. Pandit, D. Roy, S. C. Mandal and B. Pathak, J. Phys. Chem. Lett., 2022, 13, 7583–7593.
37. T. T. Yang, R. B. Patil, J. R. McKone and W. A. Saidi, Catal. Sci. Technol., 2021, 11, 6832–6838.
38. L. Zhou, P. Tian, B. Zhang and F.-Z. Xuan, Nano Res., 2024, 17, 3352–3358.
39. H. Niu, X. Wan, X. Wang, C. Shao, J. Robertson, Z. Zhang and Y. Guo, ACS Sustainable Chem. Eng., 2021, 9, 3590–3599.
40. A. Baghban, S. Habibzadeh and F. Zokaee Ashtiani, Sci. Rep., 2021, 11, 21911.
41. M. O. J. Jager, Y. S. Ranawat, F. F. Canova, E. V. Morooka and A. S. Foster, ACS Comb. Sci., 2020, 22, 768–781.
42. H. A. Tahini, X. Tan and S. C. Smith, Adv. Theory Simul., 2019, 2, 1800202.
43. C. Wang, M. Yang, S. Cao, X. Wang, H. Fu, Y. Bai, T. Lookman, P. Qian and Y. Su, Phys. Rev. Mater., 2023, 7, 085801.
44. H. Liang, P. F. Liu, M. Xu, H. Li and E. Asselin, Int. J. Quantum Chem., 2022, 123, e27055.
45. L. Himanen, M. O. J. Jäger, E. V. Morooka, F. F. Canova, Y. S. Ranawat, D. Z. Gao, P. Rinke and A. S. Foster, Comput. Phys. Commun., 2020, 247, 106949.
46. A. P. Bartók, R. Kondor and G. Csányi, Phys. Rev. B: Condens. Matter Mater. Phys., 2013, 87, 184115.
47. H. Huo and M. Rupp, Mach. Learn.: Sci. Technol., 2022, 3, 045017.
48. J. Behler, J. Chem. Phys., 2011, 134, 074106.
49. T. Xie and J. C. Grossman, Phys. Rev. Lett., 2018, 120, 145301.
50. K. T. Schutt, H. E. Sauceda, P. J. Kindermans, A. Tkatchenko and K. R. Muller, J. Chem. Phys., 2018, 148, 241722.
51. M. Shuaibi, A. Kolluru, A. Das, A. Grover, A. Sriram, Z. Ulissi and C. L. Zitnick, arXiv, 2021, preprint, arXiv:2106.09575,  DOI:10.48550/arXiv.2106.09575.
52. J. Gasteiger, S. Giri, J. T. Margraf and S. Günnemann, arXiv, 2020, preprint, arXiv:2011.14115,  DOI:10.48550/arXiv.2011.14115.
53. J. Gasteiger, M. Shuaibi, A. Sriram, S. Günnemann, Z. Ulissi, C. L. Zitnick and A. Das, arXiv, 2022, preprint, arXiv:2204.02782,  DOI:10.48550/arXiv.2204.02782.
54. I. Batatia, D. P. Kovacs, G. Simm, C. Ortner and G. Csányi, Adv. Neural Inf. Process. Syst., 2022, 35, 11423–11436.
55. L. Zitnick, A. Das, A. Kolluru, J. Lan, M. Shuaibi, A. Sriram, Z. Ulissi and B. Wood, Adv. Neural Inf. Process. Syst., 2022, 35, 8054–8067.
56. S. Passaro and C. L. Zitnick, International Conference on Machine Learning, Proceedings of Machine Learning Research, 2023, pp. 27420–27438.
57. S. Batzner, A. Musaelian, L. Sun, M. Geiger, J. P. Mailoa, M. Kornbluth, N. Molinari, T. E. Smidt and B. Kozinsky, Nat. Commun., 2022, 13, 2453.
58. Y.-L. Liao and T. Smidt, arXiv, 2022, preprint, arXiv:2206.11990,  DOI:10.48550/arXiv.2206.11990.
59. Y.-L. Liao, B. Wood, A. Das and T. Smidt, arXiv, 2023, preprint, arXiv:2306.12059,  DOI:10.48550/arXiv.2306.12059.
60. K. Choudhary and B. DeCost, npj Comput. Mater., 2021, 7, 185.
61. B. Deng, P. Zhong, K. Jun, J. Riebesell, K. Han, C. J. Bartel and G. Ceder, Nat. Mach. Intell., 2023, 5, 1031–1041.
62. K. Yan, Y. Liu, Y. Lin and S. Ji, Adv. Neural Inf. Process. Syst., 2022, 35, 15066–15080.
63. C. Chen and S. P. Ong, Nat. Comput. Sci., 2022, 2, 718–728.
64. R. Michalsky, Y.-J. Zhang and A. A. Peterson, ACS Catal., 2014, 4, 1274–1278.
65. J. K. Nørskov, T. Bligaard, A. Logadottir, J. R. Kitchin, J. G. Chen, S. Pandelov and U. Stimming, J. Electrochem. Soc., 2005, 152, J23.
66. I. C. Man, H. Y. Su, F. Calle-Vallejo, H. A. Hansen, J. I. Martínez, N. G. Inoglu, J. Kitchin, T. F. Jaramillo, J. K. Nørskov and J. Rossmeisl, ChemCatChem, 2011, 3, 1159–1165.
67. S. J. Guo, S. Zhang and S. H. Sun, Angew. Chem., Int. Ed., 2013, 52, 8526–8544.
68. J. Stacy, Y. N. Regmi, B. Leonard and M. H. Fan, Renewable Sustainable Energy Rev., 2017, 69, 401–414.
69. R. Ding, Y. Chen, Z. Rui, K. Hua, Y. Wu, X. Li, X. Duan, X. Wang, J. Li and J. Liu, ACS Sustainable Chem. Eng., 2022, 10, 4561–4578.
70. R. Ding, R. Wang, Y. Q. Ding, W. J. Yin, Y. D. Liu, J. Li and J. G. Liu, Angew. Chem., Int. Ed., 2020, 59, 19175–19183.
71. X. Jiang, Y. Zhao, J. Liu, B. Jia, X. Qu and M. Qin, ACS Appl. Nano Mater., 2022, 5, 17095–17104.
72. C. Wei, D. Shi, F. Zhou, Z. Yang, Z. Zhang, Z. Xue and T. Mu, Phys. Chem. Chem. Phys., 2023, 25, 7917–7926.
73. J. G. Greener, S. M. Kandathil, L. Moffat and D. T. Jones, Nat. Rev. Mol. Cell Biol., 2022, 23, 40–55.
74. Y. LeCun, Y. Bengio and G. Hinton, Nature, 2015, 521, 436–444.
75. K. P. Sinaga and M. S. Yang, IEEE Access, 2020, 8, 80716–80727.
76. S. J. Huang, R. Jin and Z. H. Zhou, IEEE Trans. Pattern Anal. Mach. Intell., 2014, 36, 1936–1949.
77. B. Shahriari, K. Swersky, Z. Y. Wang, R. P. Adams and N. de Freitas, Proc. IEEE, 2016, 104, 148–175.
78. B. Weng, Z. Song, R. Zhu, Q. Yan, Q. Sun, C. G. Grice, Y. Yan and W. J. Yin, Nat. Commun., 2020, 11, 3513.
79. S. Wold, K. Esbensen and P. Geladi, Chemom. Intell. Lab. Syst., 1987, 2, 37–52.
80. L. van der Maaten and G. Hinton, J. Mach. Learn. Res., 2008, 9, 2579–2605.
81. M. Chen, X. Shi, Y. Zhang, D. Wu and M. Guizani, IEEE Trans. Big Data, 2021, 7, 750–758.
82. A. Paszke, S. Gross, F. Massa, A. Lerer, J. Bradbury, G. Chanan, T. Killeen, Z. M. Lin, N. Gimelshein, L. Antiga, A. Desmaison, A. Köpf, E. Yang, Z. DeVito, M. Raison, A. Tejani, S. Chilamkurthy, B. Steiner, L. Fang, J. J. Bai and S. Chintala, Presented in part at the 33rd Conference on Neural Information Processing Systems (NeurIPS), Vancouver, Canada, Dec 08-14, 2019.
83. F. Pedregosa, G. Varoquaux, A. Gramfort, V. Michel, B. Thirion, O. Grisel, M. Blondel, P. Prettenhofer, R. Weiss, V. Dubourg, J. Vanderplas, A. Passos, D. Cournapeau, M. Brucher, M. Perrot and E. Duchesnay, J. Mach. Learn. Res., 2011, 12, 2825–2830.
84. P. Cunningham and S. J. Delany, ACM Comput. Surv., 2021, 54, 1–25.
85. C. J. C. Burges, Data Min. Knowl. Discovery, 1998, 2, 121–167.
86. M. Seeger, Int. J. Neural Syst., 2004, 14, 69–106.
87. S. B. Kotsiantis, Artif. Intell. Rev., 2013, 39, 261–283.
88. L. Breiman, Mach. Learn., 2001, 45, 5–32.
89. G. L. Ke, Q. Meng, T. Finley, T. F. Wang, W. Chen, W. D. Ma, Q. W. Ye and T. Y. Liu, in Advances in Neural Information Processing Systems 30, ed. I. Guyon, U. V. Luxburg, S. Bengio, H. Wallach, R. Fergus, S. Vishwanathan and R. Garnett, Neural Information Processing Systems (Nips), La Jolla, 2017, vol. 30.
90. T. Q. Chen and C. Guestrin, Kdd′16: Proceedings of the 22nd Acm Sigkdd International Conference on Knowledge Discovery and Data Mining, 2016, pp. 785–794 DOI:10.1145/2939672.2939785.
91. J. T. Hancock and T. M. Khoshgoftaar, J. Big Data, 2020, 7, 45.
92. Y. J. Tian and Y. Q. Zhang, Inf. Fusion, 2022, 80, 146–166.
93. N. Srivastava, G. Hinton, A. Krizhevsky, I. Sutskever and R. Salakhutdinov, J. Mach. Learn. Res., 2014, 15, 1929–1958.
94. L. Prechelt, in Neural Networks: Tricks of the Trade, ed. G. B. Orr and K. R. Muller, 1998, vol. 1524, pp. 55–69.
95. S. Ioffe and C. Szegedy, Presented in part at the 32nd International Conference on Machine Learning, Lille, France, Jul 07-09, 2015.
96. M. Abdar, F. Pourpanah, S. Hussain, D. Rezazadegan, L. Liu, M. Ghavamzadeh, P. Fieguth, X. Cao, A. Khosravi and U. R. Acharya, Inf. Fusion, 2021, 76, 243–297.
97. E. Hüllermeier and W. Waegeman, Mach. Learn., 2021, 110, 457–506.
98. P. I. Frazier, arXiv, 2018, preprint, arXiv:1807.02811,  DOI:10.48550/arXiv.1807.02811.
99. D. Whitley, Stat. Comput., 1994, 4, 65–85.
100. J. Kennedy and R. Eberhart, Proceedings of ICNN'95 – International Conference on Neural Networks, Perth, WA, Australia, 1995, vol. 4, pp. 1942–1948.
101. J. Liu and J. Lampinen, Soft Comput., 2005, 9, 448–462.
102. B. M. Greenwell, R Journal, 2017, 9, 421–436.
103. H. Aziz and B. de Keijzer, Presented in part at the 31st International Symposium on Theoretical Aspects of Computer Science (STACS), Lyon, France, Mar 05-08, 2014.
104. M. R. Zafar and N. Khan, Mach. Learn. Knowl. Extr., 2021, 3, 525–541.
105. H. Christopher Frey and S. R. Patil, Risk Anal., 2002, 22, 553–578.
106. M. Abadi, P. Barham, J. M. Chen, Z. F. Chen, A. Davis, J. Dean, M. Devin, S. Ghemawat, G. Irving, M. Isard, M. Kudlur, J. Levenberg, R. Monga, S. Moore, D. G. Murray, B. Steiner, P. Tucker, V. Vasudevan, P. Warden, M. Wicke, Y. Yu, X. Q. Zheng and U. Assoc, Presented in part at the 12th USENIX Symposium on Operating Systems Design and Implementation (OSDI), Savannah, GA, Nov 02-04, 2016.
107. C. Chen, W. Ye, Y. Zuo, C. Zheng and S. P. Ong, Chem. Mater., 2019, 31, 3564–3572.
108. W. Hu, M. Shuaibi, A. Das, S. Goyal, A. Sriram, J. Leskovec, D. Parikh and C. L. Zitnick, arXiv, 2021, preprint, arXiv:2103.01436,  DOI:10.48550/arXiv.2103.01436.
109. J. Lym, G. H. Gu, Y. Jung and D. G. Vlachos, J. Phys. Chem. C, 2019, 123, 18951–18959.
110. K. Schütt, O. Unke and M. Gastegger, International Conference on Machine Learning, Proceedings of Machine Learning Research, 2021, pp. 9377–9388.
111. A. Merchant, S. Batzner, S. S. Schoenholz, M. Aykol, G. Cheon and E. D. Cubuk, Nature, 2023, 624, 80–85.
112. R. S. Olson and J. H. Moore, Workshop on automatic machine learning, Proceedings of Machine Learning Research, 2016, pp. 66–74.
113. M. Ali, PyCaret: An open source, low-code machine learning library in Python, 2020, https://www.pycaret.org.
114. A. Jain, S. P. Ong, G. Hautier, W. Chen, W. D. Richards, S. Dacek, S. Cholia, D. Gunter, D. Skinner, G. Ceder and K. A. Persson, APL Mater., 2013, 1, 011002.
115. A. Hjorth Larsen, J. Jorgen Mortensen, J. Blomqvist, I. E. Castelli, R. Christensen, M. Dulak, J. Friis, M. N. Groves, B. Hammer, C. Hargus, E. D. Hermes, P. C. Jennings, P. Bjerre Jensen, J. Kermode, J. R. Kitchin, E. Leonhard Kolsbjerg, J. Kubal, K. Kaasbjerg, S. Lysgaard, J. Bergmann Maronsson, T. Maxson, T. Olsen, L. Pastewka, A. Peterson, C. Rostgaard, J. Schiotz, O. Schutt, M. Strange, K. S. Thygesen, T. Vegge, L. Vilhelmsen, M. Walter, Z. Zeng and K. W. Jacobsen, J. Phys.: Condens. Matter, 2017, 29, 273002.
116. J. E. Saal, S. Kirklin, M. Aykol, B. Meredig and C. Wolverton, JOM, 2013, 65, 1501–1509.
117. K. Choudhary, K. F. Garrity, A. C. E. Reid, B. DeCost, A. J. Biacchi, A. R. Hight Walker, Z. Trautt, J. Hattrick-Simpers, A. G. Kusne, A. Centrone, A. Davydov, J. Jiang, R. Pachter, G. Cheon, E. Reed, A. Agrawal, X. Qian, V. Sharma, H. Zhuang, S. V. Kalinin, B. G. Sumpter, G. Pilania, P. Acar, S. Mandal, K. Haule, D. Vanderbilt, K. Rabe and F. Tavazza, npj Comput. Mater., 2020, 6, 173.
118. S. Curtarolo, W. Setyawan, G. L. W. Hart, M. Jahnatek, R. V. Chepulskii, R. H. Taylor, S. Wang, J. Xue, K. Yang, O. Levy, M. J. Mehl, H. T. Stokes, D. O. Demchenko and D. Morgan, Comput. Mater. Sci., 2012, 58, 218–226.
119. L. Chanussot, A. Das, S. Goyal, T. Lavril, M. Shuaibi, M. Riviere, K. Tran, J. Heras-Domingo, C. Ho, W. Hu, A. Palizhati, A. Sriram, B. Wood, J. Yoon, D. Parikh, C. L. Zitnick and Z. Ulissi, ACS Catal., 2021, 11, 6059–6072.
120. R. Tran, J. Lan, M. Shuaibi, B. M. Wood, S. Goyal, A. Das, J. Heras-Domingo, A. Kolluru, A. Rizvi, N. Shoghi, A. Sriram, F. Therrien, J. Abed, O. Voznyy, E. H. Sargent, Z. Ulissi and C. L. Zitnick, ACS Catal., 2023, 13, 3066–3084.
121. L. Ward, A. Dunn, A. Faghaninia, N. E. R. Zimmermann, S. Bajaj, Q. Wang, J. Montoya, J. Chen, K. Bystrom, M. Dylla, K. Chard, M. Asta, K. A. Persson, G. J. Snyder, I. Foster and A. Jain, Comput. Mater. Sci., 2018, 152, 60–69.
122. H. Wang, L. Zhang, J. Han and E. Weinan., Comput. Phys. Commun., 2018, 228, 178–184.
123. J. Chen, Q. Jin, Y. Li, Y. Li, H. Cui and C. Wang, ACS Appl. Mater. Interfaces, 2019, 11, 38771–38778.
124. C. Hu, L. Zhang and J. Gong, Energy Environ. Sci., 2019, 12, 2620–2645.
125. C. Li and J. B. Baek, ACS Omega, 2020, 5, 31–40.
126. J. Zhu, L. Hu, P. Zhao, L. Y. S. Lee and K. Y. Wong, Chem. Rev., 2020, 120, 851–918.
127. G. H. Gu, J. Lim, C. Wan, T. Cheng, H. Pu, S. Kim, J. Noh, C. Choi, J. Kim and W. A. Goddard III, J. Am. Chem. Soc., 2021, 143, 5355–5363.
128. H. Ooka, M. E. Wintzer and R. Nakamura, ACS Catal., 2021, 11, 6298–6303.
129. X. Li, R. Chiong, Z. Hu and A. J. Page, J. Phys. Chem. Lett., 2021, 12, 7305–7311.
130. G. H. Gu, J. Noh, S. Kim, S. Back, Z. Ulissi and Y. Jung, J. Phys. Chem. Lett., 2020, 11, 3185–3191.
131. X. Zhang, K. Li, B. Wen, J. Ma and D. Diao, Chin. Chem. Lett., 2023, 34, 107833.
132. Y. Yan, C. Wang, Z. Huang, J. Fu, Z. Lin, X. Zhang, J. Ma and J. Shen, J. Mater. Chem. A, 2021, 9, 5415–5424.
133. M. Kim, M. Y. Ha, W. B. Jung, J. Yoon, E. Shin, I. D. Kim, W. B. Lee, Y. Kim and H. T. Jung, Adv. Mater., 2022, 34, e2108900.
134. S. Sarkar and S. C. Peter, Inorg. Chem. Front., 2018, 5, 2060–2080.
135. S. Gao, H. Zhen, B. Wen, J. Ma and X. Zhang, Nanoscale, 2022, 14, 2660–2667.
136. R. A. Hoyt, M. M. Montemore, I. Fampiou, W. Chen, G. Tritsaris and E. Kaxiras, J. Chem. Inf. Model., 2019, 59, 1357–1365.
137. A. Pihlajamäki, S. Malola, T. Kärkkäinen and H. Häkkinen, J. Phys. Chem. C, 2023, 127, 14211–14221.
138. L. T. Chen, Y. Tian, X. Hu, S. Yao, Z. Y. Lu, S. Y. Chen, X. Zhang and Z. Zhou, Adv. Funct. Mater., 2022, 32, 2208418.
139. J. Zhang, Y. Wang, X. Zhou, C. Zhong, K. Zhang, J. Liu, K. Hu and X. Lin, Nanoscale, 2023, 15, 11072–11082.
140. K. Tran and Z. W. Ulissi, Nat. Catal., 2018, 1, 696–703.
141. G. O. Kayode, A. F. Hill and M. M. Montemore, J. Mater. Chem. A, 2023, 11, 19128–19137.
142. J. Zhang, Z. Xia and L. Dai, Sci. Adv., 2015, 1, e1500564.
143. W. Zhou, J. Jia, J. Lu, L. Yang, D. Hou, G. Li and S. Chen, Nano Energy, 2016, 28, 29–43.
144. H. Huang, M. Yan, C. Yang, H. He, Q. Jiang, L. Yang, Z. Lu, Z. Sun, X. Xu, Y. Bando and Y. Yamauchi, Adv. Mater., 2019, 31, e1903415.
145. Y. Lv, B. Kang, Y. Yuan, G. Chen and J. Y. Lee, Chem. Eng. J., 2022, 430, 133126.
146. R. Kronberg, H. Lappalainen and K. Laasonen, J. Phys. Chem. C, 2021, 125, 15918–15933.
147. E. O. Ebikade, Y. Wang, N. Samulewicz, B. Hasa and D. Vlachos, React. Chem. Eng., 2020, 5, 2134–2147.
148. H. Jiang, J. Gu, X. Zheng, M. Liu, X. Qiu, L. Wang, W. Li, Z. Chen, X. Ji and J. Li, Energy Environ. Sci., 2019, 12, 322–333.
149. Y. Zheng, Y. Jiao, L. H. Li, T. Xing, Y. Chen, M. Jaroniec and S. Z. Qiao, ACS Nano, 2014, 8, 5290–5296.
150. Q. Hu, G. Li, Z. Han, Z. Wang, X. Huang, H. Yang, Q. Zhang, J. Liu and C. He, J. Mater. Chem. A, 2019, 7, 14380–14390.
151. X. Liu, L. Zheng, C. Han, H. Zong, G. Yang, S. Lin, A. Kumar, A. R. Jadhav, N. Q. Tran and Y. Hwang, Adv. Funct. Mater., 2021, 31, 2100547.
152. V. Fung, G. Hu, Z. Wu and D.-E. Jiang, J. Phys. Chem. C, 2020, 124, 19571–19578.
153. K. Boonpalit, Y. Wongnongwa, C. Prommin, S. Nutanong and S. Namuangruk, ACS Appl. Mater. Interfaces, 2023, 15, 12936–12945.
154. M. Sun, A. W. Dougherty, B. Huang, Y. Li and C. H. Yan, Adv. Energy Mater., 2020, 10, 1903949.
155. X. Zhang, X. Zhang and P. Yang, J. Electroanal. Chem., 2021, 895, 115510.
156. M. V. Jyothirmai, D. Roshini, B. M. Abraham and J. K. Singh, ACS Appl. Energy Mater., 2023, 6, 5598–5606.
157. M. Umer, S. Umer, M. Zafari, M. Ha, R. Anand, A. Hajibabaei, A. Abbas, G. Lee and K. S. Kim, J. Mater. Chem. A, 2022, 10, 6679–6689.
158. Y. Wang, X. Huang, H. Fu and J. Shang, J. Mater. Chem. A, 2022, 10, 24362–24372.
159. J. Hu, C. Zhang, X. Meng, H. Lin, C. Hu, X. Long and S. Yang, J. Mater. Chem. A, 2017, 5, 5995–6012.
160. Y. Zhang, Q. Zhou, J. Zhu, Q. Yan, S. X. Dou and W. Sun, Adv. Funct. Mater., 2017, 27, 1702317.
161. Y. Liu, Y. Guo, Y. Liu, Z. Wei, K. Wang and Z. Shi, Energy Fuels, 2023, 37, 2608–2630.
162. P. Xiao, W. Chen and X. Wang, Adv. Energy Mater., 2015, 5, 1500985.
163. P. Chen, J. Ye, H. Wang, L. Ouyang and M. Zhu, J. Alloys Compd., 2021, 883, 160833.
164. A. Liu, X. Liang, X. Ren, W. Guan, M. Gao, Y. Yang, Q. Yang, L. Gao, Y. Li and T. Ma, Adv. Funct. Mater., 2020, 30, 2003437.
165. M. O. J. Jäger, E. V. Morooka, F. Federici Canova, L. Himanen and A. S. Foster, npj Comput. Mater., 2018, 4, 37.
166. S. Wei, S. Baek, H. Yue, M. Liu, S. J. Yun, S. Park, Y. H. Lee, J. Zhao, H. Li, K. Reyes and F. Yao, J. Electrochem. Soc., 2021, 168, 126523.
167. T. K. Patra, F. Zhang, D. S. Schulman, H. Chan, M. J. Cherukara, M. Terrones, S. Das, B. Narayanan and S. Sankaranarayanan, ACS Nano, 2018, 12, 8006–8016.
168. M. Hakala, R. Kronberg and K. Laasonen, Sci. Rep., 2017, 7, 15243.
169. L. Tu, Y. Yang and J. Liu, Int. J. Hydrogen Energy, 2022, 47, 31321–31329.
170. J. Lee, S. Shin, J. Lee, Y. K. Han, W. Lee and Y. Son, Sci. Rep., 2023, 13, 12729.
171. N. Ran, B. Sun, W. Qiu, E. Song, T. Chen and J. Liu, J. Phys. Chem. Lett., 2021, 12, 2102–2111.
172. J. Lee, J. Lee, S. Shin, Y. Son and Y.-K. Han, Int. J. Energy Res., 2023, 2023, 6612054.
173. Y. Chen, Y. Zhao, P. Ou and J. Song, J. Mater. Chem. A, 2023, 11, 9964–9975.
174. H. Hu and J. H. Choi, RSC Adv., 2020, 10, 38484–38489.
175. T. Su, Q. Shao, Z. Qin, Z. Guo and Z. Wu, ACS Catal., 2018, 8, 2253–2276.
176. L. Ge, H. Yuan, Y. X. Min, L. Li, S. Q. Chen, L. Xu and W. A. Goddard, J. Phys. Chem. Lett., 2020, 11, 869–876.
177. T. H. Pham, E. Kim, K. Min and Y. H. Shin, ACS Appl. Mater. Interfaces, 2023, 15, 27995–28007.
178. K. N. Dinh, Q. Liang, C.-F. Du, J. Zhao, A. I. Y. Tok, H. Mao and Q. Yan, Nano Today, 2019, 25, 99–121.
179. R. B. Wexler, J. M. P. Martirez and A. M. Rappe, J. Am. Chem. Soc., 2018, 140, 4678–4683.
180. J. Zhang, P. Hu and H. Wang, J. Phys. Chem. C, 2020, 124, 10483–10494.
181. J. Hu, X. Cao, X. Zhao, W. Chen, G. P. Lu, Y. Dan and Z. Chen, Front. Chem., 2019, 7, 444.
182. Y. Pan, Y. Liu, J. Zhao, K. Yang, J. Liang, D. Liu, W. Hu, D. Liu, Y. Liu and C. Liu, J. Mater. Chem. A, 2015, 3, 1656–1665.
183. X. Cao, S. Xing, D. Ma, Y. Tan, Y. Zhu, J. Hu, Y. Wang, X. Chen and Z. Chen, J. Energy Chem., 2023, 82, 307–316.
184. M. Yan, S. Dong, Y. Li, Z. Liu, H. Zhao, Z. Ma, F. Geng, Z. Li and C. Wu, Mol. Catal., 2023, 548, 113402.
185. S. Lu, J. Cao, Y. Zhang, F. Lou and Z. Yu, Appl. Surf. Sci., 2022, 606, 154945.
186. C. Chen, B. Xiao, Z. Qin, J. Zhao, W. Li, Q. Li and X. Yu, ACS Appl. Mater. Interfaces, 2023, 15, 40538–40548.
187. S. Bai, M. Yang, J. Jiang, X. He, J. Zou, Z. Xiong, G. Liao and S. Liu, npj 2D Mater. Appl., 2021, 5, 78.
188. C. X. Wang, X. X. Wang, T. Y. Zhang, P. Qian, T. Lookman and Y. J. Su, J. Mater. Chem. A, 2022, 10, 18195–18205.
189. X. Sun, J. Zheng, Y. Gao, C. Qiu, Y. Yan, Z. Yao, S. Deng and J. Wang, Appl. Surf. Sci., 2020, 526, 146522.
190. B. M. Abraham, P. Sinha, P. Halder and J. K. Singh, J. Mater. Chem. A, 2023, 11, 8091–8100.
191. J. Zheng, X. Sun, C. Qiu, Y. Yan, Z. Yao, S. Deng, X. Zhong, G. Zhuang, Z. Wei and J. Wang, J. Phys. Chem. C, 2020, 124, 13695–13705.
192. X. Wang, C. Wang, S. Ci, Y. Ma, T. Liu, L. Gao, P. Qian, C. Ji and Y. Su, J. Mater. Chem. A, 2020, 8, 23488–23497.
193. J. Zheng, X. Sun, J. Hu, S. Wang, Z. Yao, S. Deng, X. Pan, Z. Pan and J. Wang, ACS Appl. Mater. Interfaces, 2021, 13, 50878–50891.
194. A. Chen, J. Cai, Z. Wang, Y. Han, S. Ye and J. Li, J. Energy Chem., 2023, 78, 268–276.
195. T. Liu, X. Zhao, X. Liu, W. Xiao, Z. Luo, W. Wang, Y. Zhang and J.-C. Liu, J. Energy Chem., 2023, 81, 93–100.
196. J. Zhou, L. Shen, M. D. Costa, K. A. Persson, S. P. Ong, P. Huck, Y. Lu, X. Ma, Y. Chen, H. Tang and Y. P. Feng, Sci. Data, 2019, 6, 86.
197. T. Yang, J. Zhou, T. T. Song, L. Shen, Y. P. Feng and M. Yang, ACS Energy Lett., 2020, 5, 2313–2321.
198. S. Wu, Z. Wang, H. Zhang, J. Cai and J. Li, Energy Environ. Mater., 2022, 6, e12259.
199. Z. C. Chen, L. Guo, L. Pan, T. Q. Yan, Z. X. He, Y. Li, C. X. Shi, Z. F. Huang, X. W. Zhang and J. J. Zou, Adv. Energy Mater., 2022, 12, 2103670.
200. T. Reier, H. N. Nong, D. Teschner, R. Schlögl and P. Strasser, Adv. Energy Mater., 2017, 7, 1601275.
201. X. Rong, J. Parolin and A. M. Kolpak, ACS Catal., 2016, 6, 1153–1158.
202. A. Grimaud, O. Diaz-Morales, B. Han, W. T. Hong, Y. L. Lee, L. Giordano, K. A. Stoerzinger, M. T. M. Koper and Y. Shao-Horn, Nat. Chem., 2017, 9, 457–465.
203. I. C. Man, H. Y. Su, F. Calle-Vallejo, H. A. Hansen, J. I. Martinez, N. G. Inoglu, J. Kitchin, T. F. Jaramillo, J. K. Norskov and J. Rossmeisl, ChemCatChem, 2011, 3, 1159–1165.
204. J. S. Yoo, X. Rong, Y. Liu and A. M. Kolpak, ACS Catal., 2018, 8, 4628–4636.
205. X. Wang, H. Zhong, S. Xi, W. S. V. Lee and J. Xue, Adv. Mater., 2022, 34, e2107956.
206. J. S. Kim, B. Kim, H. Kim and K. Kang, Adv. Energy Mater., 2018, 8, 1702774.
207. G. Wu, A. Santandreu, W. Kellogg, S. Gupta, O. Ogoke, H. G. Zhang, H. L. Wang and L. M. Dai, Nano Energy, 2016, 29, 83–110.
208. J. Mohammed-Ibrahim, J. Power Sources, 2020, 448, 227375.
209. Z. W. Ulissi, A. R. Singh, C. Tsai and J. K. Norskov, J. Phys. Chem. Lett., 2016, 7, 3931–3935.
210. J. Timmermann, F. Kraushofer, N. Resch, P. Li, Y. Wang, Z. Mao, M. Riva, Y. Lee, C. Staacke, M. Schmid, C. Scheurer, G. S. Parkinson, U. Diebold and K. Reuter, Phys. Rev. Lett., 2020, 125, 206101.
211. S. Back, K. Tran and Z. W. Ulissi, ACS Catal., 2019, 9, 7651–7659.
212. R. A. Flores, C. Paolucci, K. T. Winther, A. Jain, J. A. G. Torres, M. Aykol, J. Montoya, J. K. Nørskov, M. Bajdich and T. Bligaard, Chem. Mater., 2020, 32, 5854–5863.
213. J. Timmermann, Y. Lee, C. G. Staacke, J. T. Margraf, C. Scheurer and K. Reuter, J. Chem. Phys., 2021, 155, 244107.
214. A. N. Singh, A. Hajibabaei, M. Ha, A. Meena, H. S. Kim, C. Bathula and K. W. Nam, Nanomaterials, 2022, 13, 10.
215. J. Feng, Z. Dong, Y. Ji and Y. Li, JACS Au, 2023, 3, 1131–1140.
216. L. An, C. Wei, M. Lu, H. W. Liu, Y. B. Chen, G. G. Scherer, A. C. Fisher, P. X. Xi, Z. C. J. Xu and C. H. Yan, Adv. Mater., 2021, 33, 2006328.
217. Z. P. Shi, Y. Wang, J. Li, X. Wang, Y. B. Wang, Y. Li, W. L. Xu, Z. Jiang, C. P. Liu, W. Xing and J. J. Ge, Joule, 2021, 5, 2164–2176.
218. W. Jin, H. B. Wu, W. Q. Cai, B. H. Jia, M. Batmunkh, Z. X. Wu and T. Y. Ma, Chem. Eng. J., 2021, 426, 130762.
219. G. H. Moon, Y. Wang, S. Kim, E. Budiyanto and H. Tuysuz, ChemSusChem, 2022, 15, e202102114.
220. J. He, W. Q. Li, P. Xu and J. M. Sun, Appl. Catal., B, 2021, 298, 120528.
221. Y. Y. Feng, S. Si, G. Deng, Z. X. Xu, Z. Pu, H. S. Hu and C. B. Wang, J. Alloys Compd., 2022, 892, 162113.
222. R. Huang, Y. Z. Wen, H. S. Peng and B. Zhang, Chin. J. Catal., 2022, 43, 130–138.
223. W. Xu, M. Andersen and K. Reuter, ACS Catal., 2020, 11, 734–742.
224. M. Kim, Y. Kim, M. Y. Ha, E. Shin, S. J. Kwak, M. Park, I. D. Kim, W. B. Jung, W. B. Lee and Y. Kim, Adv. Mater., 2023, 35, 2211497.
225. X. Jiang, J. Liu, Y. Zhao, S. Liu, B. Jia, X. Qu and M. Qin, J. Phys. Chem. C, 2022, 126, 19091–19100.
226. Y. M. Sun, H. B. Liao, J. R. Wang, B. Chen, S. N. Sun, S. J. H. Ong, S. B. Xi, C. Z. Diao, Y. H. Du, J. O. Wang, M. B. H. Breese, S. Z. Li, H. Zhang and Z. C. J. Xu, Nat. Catal., 2020, 3, 554–563.
227. J. Timoshenko, F. T. Haase, S. Saddeler, M. Ruscher, H. S. Jeon, A. Herzog, U. Hejral, A. Bergmann, S. Schulz and B. Roldan Cuenya, J. Am. Chem. Soc., 2023, 145, 4065–4080.
228. Y. F. Cui, S. D. Jiang, Q. Fu, R. Wang, P. Xu, Y. Sui, X. J. Wang, Z. L. Ning, J. F. Sun, X. Sun, A. Nikiforov and B. Song, Adv. Funct. Mater., 2023, 33, 2306889.
229. A. A. H. Tajuddin, M. Wakisaka, T. Ohto, Y. Yu, H. Fukushima, H. Tanimoto, X. Li, Y. Misu, S. Jeong, J. I. Fujita, H. Tada, T. Fujita, M. Takeguchi, K. Takano, K. Matsuoka, Y. Sato and Y. Ito, Adv. Mater., 2023, 35, e2207466.
230. J. Park, S. Kang and J. Lee, J. Mater. Chem. A, 2022, 10, 15975–15980.
231. R. Palkovits and S. Palkovits, ACS Catal., 2019, 9, 8383–8387.
232. B. Rohr, H. S. Stein, D. Guevarra, Y. Wang, J. A. Haber, M. Aykol, S. K. Suram and J. M. Gregoire, Chem. Sci., 2020, 11, 2696–2706.
233. X. Jiang, Y. Wang, B. Jia, X. Qu and M. Qin, ACS Appl. Mater. Interfaces, 2022, 14, 41141–41148.
234. H. J. Song, H. Yoon, B. Ju and D. W. Kim, Adv. Energy Mater., 2020, 11, 2002428.
235. J. Hwang, R. R. Rao, L. Giordano, Y. Katayama, Y. Yu and Y. Shao-Horn, Science, 2017, 358, 751–756.
236. W. T. Hong, R. E. Welsch and Y. Shao-Horn, J. Phys. Chem. C, 2015, 120, 78–86.
237. X. Wang, B. Xiao, Y. Li, Y. Tang, F. Liu, J. Chen and Y. Liu, Appl. Surf. Sci., 2020, 531, 147323.
238. W. Li, F. Yang and J. Zhang, J. Phys.: Conf. Ser., 2022, 2393, 012019.
239. S. Wang, H. Lin, Y. Wakabayashi, L. Q. Zhou, C. A. Roberts, D. Banerjee, H. Jia and C. Ling, J. Energy Chem., 2023, 80, 744–757.
240. Z. Li, L. E. K. Achenie and H. Xin, ACS Catal., 2020, 10, 4377–4384.
241. Z. Song, X. Wang, F. Liu, Q. Zhou, W. J. Yin, H. Wu, W. Deng and J. Wang, Mater. Horiz., 2023, 10, 1651–1660.
242. K. T. Schütt, O. T. Unke and M. Gastegger, arXiv, 2021, preprint, arXiv:2102.03150,  DOI:10.48550/arXiv.2102.03150.
243. C. Lei, S. Lyu, J. Si, B. Yang, Z. Li, L. Lei, Z. Wen, G. Wu and Y. Hou, ChemCatChem, 2019, 11, 5855–5874.
244. S. Kapse, S. Janwari, U. V. Waghmare and R. Thapa, Appl. Catal., B, 2021, 286, 119866.
245. S. Lin, H. Xu, Y. Wang, X. C. Zeng and Z. Chen, J. Mater. Chem. A, 2020, 8, 5663–5670.
246. L. Wu, T. Guo and T. Li, iScience, 2021, 24, 102398.
247. M. Ha, D. Y. Kim, M. Umer, V. Gladkikh, C. W. Myung and K. S. Kim, Energy Environ. Sci., 2021, 14, 3455–3468.
248. M. Secor, A. V. Soudackov and S. Hammes-Schiffer, J. Phys. Chem. C, 2023, 127, 15246–15256.
249. L. Wu, T. Guo and T. Li, Adv. Funct. Mater., 2022, 32, 2203439.
250. P. Shan, X. Bai, Q. Jiang, Y. Chen, S. Lu, P. Song, Z. Jia, T. Xiao, Y. Han, Y. Wang, T. Liu, H. Cui, R. Feng, Q. Kang, Z. Liang and H. Yuan, Renewable Energy, 2023, 203, 445–454.
251. Y. Ying, K. Fan, X. Luo, J. Qiao and H. Huang, J. Mater. Chem. A, 2021, 9, 16860–16867.
252. X. H. Wan, W. Yu, H. Niu, X. T. Wang, Z. F. Zhang and Y. Z. Guo, Chem. Eng. J., 2022, 440, 135946.
253. R. Anand, B. Ram, M. Umer, M. Zafari, S. Umer, G. Lee and K. S. Kim, J. Mater. Chem. A, 2022, 10, 22500–22511.
254. N. Ma, Y. Zhang, Y. Wang, C. Huang, J. Zhao, B. Liang and J. Fan, Appl. Surf. Sci., 2023, 628, 157225.
255. Y. Chen, H. Cui, Q. Jiang, X. Bai, P. Shan, Z. Jia, S. Lu, P. Song, R. Feng, Q. Kang, Z. Liang and H. Yuan, ACS Appl. Nano Mater., 2023, 6, 7694–7703.
256. X. Li, S. Lin, T. Yan, Z. Wang, Q. Cai and J. Zhao, Nanoscale, 2023, 15, 11616–11624.
257. X. F. Liu, T. Y. Liu, W. J. Xiao, W. T. Wang, Y. F. Zhang, G. Wang, Z. J. Luo and J. C. Liu, Inorg. Chem. Front., 2022, 9, 4272–4280.
258. M. Bernt, A. Siebel and H. A. Gasteiger, J. Electrochem. Soc., 2018, 165, F305–F314.
259. M. Bernt and H. A. Gasteiger, J. Electrochem. Soc., 2016, 163, F3179–F3189.
260. S. Siracusano, V. Baglio, N. Van Dijk, L. Merlo and A. S. Aricò, Appl. Energy, 2017, 192, 477–489.
261. J. Garcia-Navarro, M. Schulze and K. A. Friedrich, ACS Sustainable Chem. Eng., 2018, 7, 1600–1610.
262. J. H. Friedman and B. E. Popescu, Annals Appl. Stat., 2008, 2, 916–954.
263. M. E. Gunay, N. A. Tapan and G. Akkoc, Int. J. Hydrogen Energy, 2022, 47, 2134–2151.
264. J. Durst, C. Simon, F. Hasché and H. A. Gasteiger, J. Electrochem. Soc., 2014, 162, F190–F203.
265. E. S. Davydova, S. Mukerjee, F. Jaouen and D. R. Dekel, ACS Catal., 2018, 8, 6665–6690.
266. T. Tang, L. Ding, Z. C. Yao, H. R. Pan, J. S. Hu and L. J. Wan, Adv. Funct. Mater., 2021, 32, 2107479.
267. Y. Qiu, X. Xie, W. Li and Y. Shao, Chin. J. Catal., 2021, 42, 2094–2104.
268. Y. Men, D. Wu, Y. Hu, L. Li, P. Li, S. Jia, J. Wang, G. Cheng, S. Chen and W. Luo, Angew. Chem., Int. Ed., 2023, 62, e202217976.
269. J. L. Hitt, D. Yoon, J. R. Shallenberger, D. A. Muller and T. E. Mallouk, ACS Sustainable Chem. Eng., 2022, 10, 16299–16312.
270. Z. Ma, Z. P. Cano, A. Yu, Z. Chen, G. Jiang, X. Fu, L. Yang, T. Wu, Z. Bai and J. Lu, Angew. Chem., Int. Ed., 2020, 59, 18334–18348.
271. H. Li, J. Lai, Z. Li and L. Wang, Adv. Funct. Mater., 2021, 31, 2106715.
272. C. X. Zhao, B. Q. Li, J. N. Liu and Q. Zhang, Angew. Chem., Int. Ed., 2021, 60, 4448–4463.
273. A. A. Gewirth, J. A. Varnell and A. M. DiAscro, Chem. Rev., 2018, 118, 2313–2339.
274. J. K. Norskov, J. Rossmeisl, A. Logadottir, L. Lindqvist, J. R. Kitchin, T. Bligaard and H. Jonsson, J. Phys. Chem. B, 2004, 108, 17886–17892.
275. C. Li, H. Tan, J. Lin, X. Luo, S. Wang, J. You, Y.-M. Kang, Y. Bando, Y. Yamauchi and J. Kim, Nano Today, 2018, 21, 91–105.
276. D. S. Rivera Rocabado, Y. Nanba and M. Koyama, ACS Omega, 2021, 6, 17424–17432.
277. A. Khorshidi and A. A. Peterson, Comput. Phys. Commun., 2016, 207, 310–324.
278. N. Artrith and A. Urban, Comput. Mater. Sci., 2016, 114, 135–150.
279. K. N. Nigussa, Mater. Chem. Phys., 2020, 253, 123407.
280. X. Yang, A. Bhowmik, T. Vegge and H. A. Hansen, Chem. Sci., 2023, 14, 3913–3922.
281. A. J. Parker, G. Opletal and A. S. Barnard, J. Appl. Phys., 2020, 128, 014301.
282. A. J. Parker, B. Motevalli, G. Opletal and A. S. Barnard, Nanotechnology, 2021, 32, 095404.
283. H. Zhen, L. Liu, Z. Lin, S. Gao, X. Li and X. Zhang, J. Phys. Chem. Lett., 2021, 12, 1573–1580.
284. D. Chen, Z. Lai, J. Zhang, J. Chen, P. Hu and H. Wang, Chin. J. Chem., 2021, 39, 3029–3036.
285. M. Ruck, B. Garlyyev, F. Mayr, A. S. Bandarenka and A. Gagliardi, J. Phys. Chem. Lett., 2020, 11, 1773–1780.
286. X. Zhang, Z. Wang, A. M. Lawan, J. Wang, C. Y. Hsieh, C. Duan, C. H. Pang, P. K. Chu, X. F. Yu and H. Zhao, InfoMat, 2023, 5, e12406.
287. H. Chun, E. Lee, K. Nam, J.-H. Jang, W. Kyoung, S. H. Noh and B. Han, Chem. Catal., 2021, 1, 855–869.
288. J. Kang, S. H. Noh, J. Hwang, H. Chun, H. Kim and B. Han, Phys. Chem. Chem. Phys., 2018, 20, 24539–24544.
289. J. Lee and R. Jinnouchi, J. Phys. Chem. C, 2021, 125, 16963–16974.
290. T. A. A. Batchelor, J. K. Pedersen, S. H. Winther, I. E. Castelli, K. W. Jacobsen and J. Rossmeisl, Joule, 2019, 3, 834–845.
291. T. A. A. Batchelor, T. Loffler, B. Xiao, O. A. Krysiak, V. Strotkotter, J. K. Pedersen, C. M. Clausen, A. Savan, Y. Li, W. Schuhmann, J. Rossmeisl and A. Ludwig, Angew. Chem., Int. Ed., 2021, 60, 6932–6937.
292. J. K. Pedersen, C. M. Clausen, O. A. Krysiak, B. Xiao, T. A. A. Batchelor, T. Loffler, V. A. Mints, L. Banko, M. Arenz, A. Savan, W. Schuhmann, A. Ludwig and J. Rossmeisl, Angew. Chem., Int. Ed., 2021, 60, 24144–24152.
293. L. Banko, O. A. Krysiak, J. K. Pedersen, B. Xiao, A. Savan, T. Löffler, S. Baha, J. Rossmeisl, W. Schuhmann and A. Ludwig, Adv. Energy Mater., 2022, 12, 2103312.
294. Z. Lu, Z. W. Chen and C. V. Singh, Matter, 2020, 3, 1318–1333.
295. W. A. Saidi, J. Phys. Chem. Lett., 2022, 13, 1042–1048.
296. G. Yuan, M. Wu and L. Ruiz Pestana, J. Phys. Chem. C, 2023, 127, 15809–15818.
297. X. Huang, T. Shen, T. Zhang, H. Qiu, X. Gu, Z. Ali and Y. Hou, Adv. Energy Mater., 2019, 10, 1900375.
298. Y. Deng, J. Luo, B. Chi, H. Tang, J. Li, X. Qiao, Y. Shen, Y. Yang, C. Jia, P. Rao, S. Liao and X. Tian, Adv. Energy Mater., 2021, 11, 2101222.
299. J. Masa, W. Xia, M. Muhler and W. Schuhmann, Angew. Chem., Int. Ed., 2015, 54, 10102–10120.
300. S. Kapse, N. Barman and R. Thapa, Carbon, 2023, 201, 703–711.
301. Y. Lv, B. Kang, G. Chen, Y. Yuan, J. Ren and J. Y. Lee, Appl. Surf. Sci., 2023, 613, 156084.
302. S. Bhardwaj, S. Kapse, S. Dan, R. Thapa and R. S. Dey, J. Mater. Chem. A, 2023, 11, 17045–17055.
303. K. Lodaya, N. D. Ricke, K. Chen and T. Van Voorhis, J. Phys. Chem. C, 2023, 127, 2303–2313.
304. H. Sun, Y. Li, L. Gao, M. Chang, X. Jin, B. Li, Q. Xu, W. Liu, M. Zhou and X. Sun, J. Energy Chem., 2023, 81, 349–357.
305. X. Zhu, J. Yan, M. Gu, T. Liu, Y. Dai, Y. Gu and Y. Li, J. Phys. Chem. Lett., 2019, 10, 7760–7766.
306. Z. Chen, H. Qi, H. Wang, C. Yue, Y. Liu, Z. Yang, M. Pu and M. Lei, Phys. Chem. Chem. Phys., 2023, 25, 18983–18989.
307. L. Wu, T. Guo and T. Li, J. Mater. Chem. A, 2020, 8, 19290–19299.
308. Z. Wang, W. Zhong, J. Jiang and S. Wang, J. Phys. Chem. Lett., 2023, 14, 4760–4765.
309. C. Deng, Y. Su, F. Li, W. Shen, Z. Chen and Q. Tang, J. Mater. Chem. A, 2020, 8, 24563–24571.
310. M. Dan, A. Vulcu, S. A. Porav, C. Leostean, G. Borodi, O. Cadar and C. Berghian-Grosan, Molecules, 2021, 26, 3858.
311. W. Xia, Z. Hou, J. Tang, J. Li, W. Chaikittisilp, Y. Kim, K. Muraoka, H. Zhang, J. He, B. Han and Y. Yamauchi, Nano Energy, 2022, 94, 106868.
312. M. R. Karim, M. Ferrandon, S. Medina, E. Sture, N. Kariuki, D. J. Myers, E. F. Holby, P. Zelenay and T. Ahmed, ACS Appl. Energy Mater., 2020, 3, 9083–9088.
313. R. Ding, Y. Chen, P. Chen, R. Wang, J. Wang, Y. Ding, W. Yin, Y. Liu, J. Li and J. Liu, ACS Catal., 2021, 11, 9798–9808.
314. S. Zhai, H. P. Xie, P. Cui, D. Q. Guan, J. Wang, S. Y. Zhao, B. Chen, Y. F. Song, Z. P. Shao and M. Ni, Nat. Energy, 2022, 7, 866–875.
315. R. Ding, Y. Ding, H. Zhang, R. Wang, Z. Xu, Y. Liu, W. Yin, J. Wang, J. Li and J. Liu, J. Mater. Chem. A, 2021, 9, 6841–6850.
316. W. Huo, W. Li, Z. Zhang, C. Sun, F. Zhou and G. Gong, Energy Convers. Manage., 2021, 243, 114367.
317. Z. Luo, S. Lim, Z. Tian, J. Shang, L. Lai, B. MacDonald, C. Fu, Z. Shen, T. Yu and J. Lin, J. Mater. Chem., 2011, 21, 8038–8044.
318. X. R. Wang, J. Y. Liu, Z. W. Liu, W. C. Wang, J. Luo, X. P. Han, X. W. Du, S. Z. Qiao and J. Yang, Adv. Mater., 2018, 30, 1800005.
319. X. Cui, S. Yang, X. Yan, J. Leng, S. Shuang, P. M. Ajayan and Z. Zhang, Adv. Funct. Mater., 2016, 26, 5708–5717.
320. M. Liu, Z. Zhao, X. Duan and Y. Huang, Adv. Mater., 2019, 31, 1802234.
321. G. C. Y. Peng, M. Alber, A. Buganza Tepole, W. R. Cannon, S. De, S. Dura-Bernal, K. Garikipati, G. Karniadakis, W. W. Lytton and P. Perdikaris, Arch. Comput. Methods Eng., 2021, 28, 1017–1037.
322. B. Burger, P. M. Maffettone, V. V. Gusev, C. M. Aitchison, Y. Bai, X. Wang, X. Li, B. M. Alston, B. Li, R. Clowes, N. Rankin, B. Harris, R. S. Sprick and A. I. Cooper, Nature, 2020, 583, 237–241.
323. Y. C. Zhao, J. Y. Zhang, Z. W. Xu, S. J. Sun, S. Langner, N. T. P. Hartono, T. Heumueller, Y. Hou, J. Elia, N. Li, G. J. Matt, X. Y. Du, W. Meng, A. Osvet, K. C. Zhang, T. Stubhan, Y. X. Feng, J. Hauch, E. H. Sargent, T. Buonassisi and C. J. Brabec, Nat. Commun., 2021, 12, 2191.
324. Q. Zhu, F. Zhang, Y. Huang, H. Xiao, L. Zhao, X. Zhang, T. Song, X. Tang, X. Li, G. He, B. Chong, J. Zhou, Y. Zhang, B. Zhang, J. Cao, M. Luo, S. Wang, G. Ye, W. Zhang, X. Chen, S. Cong, D. Zhou, H. Li, J. Li, G. Zou, W. Shang, J. Jiang and Y. Luo, Natl. Sci. Rev., 2022, 9, nwac190.
325. Q. Zhu, Y. Huang, D. Zhou, L. Zhao, L. Guo, R. Yang, Z. Sun, M. Luo, F. Zhang, H. Xiao, X. Tang, X. Zhang, T. Song, X. Li, B. Chong, J. Zhou, Y. Zhang, B. Zhang, J. Cao, G. Zhang, S. Wang, G. Ye, W. Zhang, H. Zhao, S. Cong, H. Li, L.-L. Ling, Z. Zhang, W. Shang, J. Jiang and Y. Luo, Nat. Synth., 2023, 3, 319–328.
326. Z. Zheng, O. Zhang, C. Borgs, J. T. Chayes and O. M. Yaghi, J. Am. Chem. Soc., 2023, 145, 18048–18062.
327. J. Dagdelen, A. Dunn, S. Lee, N. Walker, A. S. Rosen, G. Ceder, K. A. Persson and A. Jain, Nat. Commun., 2024, 15, 1418.
328. N. J. Szymanski, B. Rendy, Y. Fei, R. E. Kumar, T. He, D. Milsted, M. J. McDermott, M. Gallant, E. D. Cubuk, A. Merchant, H. Kim, A. Jain, C. J. Bartel, K. Persson, Y. Zeng and G. Ceder, Nature, 2023, 624, 86–91.
329. A. Daigavane, S. Kim, M. Geiger and T. Smidt, arXiv, 2023, preprint, arXiv:2311.16199,  DOI:10.48550/arXiv.2311.16199.
330. C. Zeni, R. Pinsler, D. Zügner, A. Fowler, M. Horton, X. Fu, S. Shysheya, J. Crabbé, L. Sun and J. Smith, arXiv, 2023, preprint, arXiv:2312.03687,  DOI:10.48550/arXiv.2312.03687.
331. C. Yao, L. Wang, Q. Wang, Z. Liu, G. Liu and M. Zhang, ACS Appl. Mater. Interfaces, 2024, 16, 13326–13334.
332. M. A. Shirsavar, M. Taghavimehr, L. J. Ouedraogo, M. Javaheripi, N. N. Hashemi, F. Koushanfar and R. Montazami, Biosens. Bioelectron., 2022, 212, 114418.
333. S. Li, J. M. Phillips, X. Yu, R. Kirby and S. Zhe, Adv. Neural Inf. Process. Syst., 2022, 35, 995–1007.
334. R. Ding, X. Wang, A. Tan, J. Li and J. Liu, ACS Catal., 2023, 13, 13267–13281.

---

Footnote

† Electronic supplementary information (ESI) available. See DOI: https://doi.org/10.1039/d4cs00844h

---