First principles investigation of manganese catalyst structure and coordination in the p-xylene oxidation process

Abstract

The oxidation of p-xylene to terephtalic acid has global importance, with the product used as a precursor for polyethylene terephthalate (PET). The oxidation of p-xylene proceeds via a redox cascade that involves cobalt, manganese, and bromide, with a synergy allowing for high selectivity and reactivity; however, the equilibrium coordination environment of the catalyst species remains uncertain due to the hostile industrial operating conditions. To build knowledge of the catalyst speciation and develop understanding of the reaction process, a density functional theory approach is applied herein to determine the static and dynamic properties of the divalent (reduced) and trivalent (oxidized) manganese catalysts in the redox cascade. The Gibbs free energy has been calculated for manganese as a function of ligands in the inner coordination sphere, with the octahedrally-coordinated Mn(OAc)₂(HOAc)₂ and Mn(OAc)₃(H₂O)₁ identified as the most thermodynamically stable coordination environments for Mn(II) and Mn(III), respectively. Dynamic properties of these catalysts in the presence of an explicit solvent environment have been determined using first principles molecular dynamics simulations. The simulations indicate 0–2 coordinating water ligands are present in the inner coordination sphere under standard industrial temperatures and pressures. The dynamical simulations have been extended to include HBr, which couples with Mn in the redox cascade, and the bromide species does not enter in the inner-coordination sphere of the oxidized Mn(III) catalyst, providing evidence that the electron transfer between bromide and Mn(III) proceeds via an outer sphere mechanism. Our results suggest that oxidation of Mn(II) has the potential for facilitating L-type ligand exchange in the inner-sphere coordination environment. The results are a platform for developing a more complete knowledge of the reaction mechanism at the atomistic scale.

---

1 Introduction

The homogeneous oxidation of p-xylene to terephthalic acid (pTA) is a widely-used and large-scale industrial process, with over 38 active plants globally and 77 million tons of pTA produced annually.¹ Terephthalic acid is used as a precursor in the production of the polymer polyethylene terephthalate (PET).² The main applications of PET are in polyester fibres, food and drink packaging, and polyester film; as of 2015, PET met 7% of the global plastic demand and 62% of produced bottles, highlighting the significance of the commercial application globally.^2,3

Modern commercial production of terephthalic acid is done through the oxidation of p-xylene, using a Co/Mn/Br catalyst, where Co and Mn are introduced as their acetates, in a solution of acetic acid and water. The oxidation is carried out using high temperatures (190–205 °C) and pressures (15–30 bar). The synergy between the oxidation states of the cobalt, manganese, and bromide are vital to achieving both high selectivity and high yield for the oxidation.⁴ The oxidation process occurs by a series of redox reactions that involve Co(II/III), Mn(II/III), and Br⁻/Br˙, as illustrated in Fig. 1.^4,5 Initially, hydrogen is abstracted from p-xylene to form a p-xylyl radical and bromide species; the p-xylyl radical then reacts with oxygen to form a peroxy radical, which initiates the oxidation of Co(II) to Co(III). The Co(III) species subsequently facilitates the oxidation of Mn(II), with the newly formed Mn(III) species oxidizing the bromide back to a bromine radical, that can abstract more hydrogen from p-xylene.^4–6

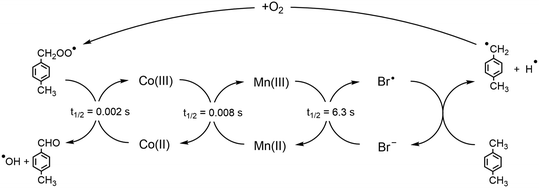Fig. 1 Redox cascade for the Co/Mn/Br oxidation of p-xylene. Half-lives are shown for each redox process, as taken from Pérez et al.⁴

The current model for the redox cascade does not explicitly consider the impact of solvent on the coordination environment of the manganese and cobalt catalysts. The coordination environment of these catalysts are unclear due to the hostile operating temperature and pressure, which makes them challenging to characterize experimentally.^7–9 Studies have indicated the presence of monomeric complexes,^10,11 dimers,^10,12 binuclear¹² and trinuclear complexes⁶ for the manganese and cobalt catalysts, with acetate ligands bridging the metal centers.¹² Recent electron spin echo envelope modulation (ESEEM) results have suggested that, under industrial operating conditions, an average of one water molecule is present in the inner coordination sphere of Mn(II).¹³ This contrasts with approximated stability constants that indicate an average of four water molecules in the Mn(II) inner coordination sphere.¹² Therefore, further studies are needed to help clarify the coordination environment.

Knowledge of the catalyst coordination environment is important to understand and optimise the catalytic processes, as strong correlation often exists between the nature of the catalyst and its activity.¹² For example, bromide coordination to manganese occurs under low water concentrations, aiding the redox cascade, whereas the inner coordination sphere sites surrounding the metal cation are occupied by water ligands under high water concentrations, preventing the coordination of bromide and reducing the activity of the catalyst.^13,14 The coordination environment around the metal center affects the associated redox potential, which may impact the efficiency of the redox cascade.¹⁴ Indeed, whether there is a thermodynamic driving force for rearrangement of the inner coordination sphere during the redox cascade upon a change in manganese oxidation state is not well understood; a change in the coordination environment upon oxidation could impact the relative kinetics of the organic oxidation chemistry, and aid in understanding the observed catalytic activity.

Computational modelling of the p-xylene oxidation process can provide crucial insight to the catalyst coordination and reactivity, though studies are limited despite the significant commercial value. Homogeneous catalytic systems have benefited particularly from computational insight provided by density functional theory (DFT). For instance, Yuan et al. used free energies obtained using DFT to provide insight on the mechanism of 1,3 diyne alcohol hydroarylation using a homogeneous Mn(I) catalyst. Substituting ligands in the inner coordination sphere of the Mn(I) catalyst, they were able to construct free energy pathways for the formation of the active manganese catalyst and the hydroarylation process.¹⁵ Beyond static DFT calculations, molecular dynamics simulations have allowed for additional insight in homogeneous catalysis. Qian et al. used first principles molecular dynamics (FPMD) to model both the methanol assisted cleavage of hydrogen coordinated to the Mn(I) pincer complex, as well as the subsequent hydrogenation of acetophenone. They showed that the FPMD simulations supported the mechanism predicted using free energies obtained using static DFT calculations.¹⁶ First principles DFT calculations therefore provide opportunity to investigate the relative stability of the many possible coordination environments of the manganese catalyst at commercial operating conditions, and linking these properties to reactivity, without need to address the challenges in experimental characterisation.

In the work presented, static and dynamic simulations with Kohn–Sham DFT are used to gain insight into the coordination environment around the Mn(II) and Mn(III) catalysts during the p-xylene redox cascade. To build knowledge of the cation coordination under operating conditions, the different permutations of coordinating ligands are investigated to derive Gibbs free energy of these structures, and thus determine their stability. The work is complemented by dynamic DFT simulations at elevated temperatures and pressures to investigate the behavior of the Mn(II) and Mn(III) catalysts in aqueous acetic acid.

2 Methodology

2.1 Molecular DFT calculations

Density functional theory (DFT) calculations were performed using the FHI-aims software package.^17,18 The zeroth order regular approximation (ZORA) was used throughout to account for relativistic effects. The 2010 version of the “tight” basis set was used, with a strict convergence criteria on the self-consistent field cycle of 1 × 10⁻⁸ eV for the change in energy, 1 × 10⁻⁶ eV for the change in the eigenvalue summation, and 1 × 10⁻⁶ e/a³₀ for the change in charge/spin density.¹⁹ Initial testing of exchange correlation density functionals (ESI,† section S1) showed that geometry optimisations were structurally accurate using the PBE density functional and many body dispersion (MBD) scheme to account for non-local correlation effects,^20–22 with higher-level PBE0 required for energetic analysis.²³ For Mn(II) and Mn(III), the energetically preferable high-spin configurations were considered (5 and 4 unpaired electrons, respectively) unless stated otherwise. For all the metal complexes considered, structural optimisation was performed on all possible geometric isomers (ESI,† section S3), with the lowest energy (most stable) isomer used to evaluate the Gibbs free energy.

To account for the long-range dielectric response of the solvent, single-point energy evaluations with PBE0 were performed on the PBE-MBD optimised structures with inclusion of an implicit solvent environment via the size-modified Poisson Boltzmann (MPB) scheme.²⁴ The counter-ion concentration in the MPB scheme was set to zero, which, with the Andreussi and Marzari dielectric function, reduces the formalism to the self-consistent continuum solvation (SCCS) scheme.²⁵ For the implicit water solvent, a dielectric constant (ε) of 78.358 was applied with optimised electrostatic parameters (ρ_min = 0.00025 e and ρ_max = 0.003 e) obtained by performing DFT calculations over a two dimensional {ρ_min, ρ_max} grid on hydrated water, and the results benchmarked against the free solvation energy of water in water (ESI,† section S2).^26,27 The non-electrostatic parameters were taken from Andreussi et al. ((α + γ) = 50 dyn cm⁻¹, β = −0.35 GPa).^23,25 For the implicit acetic acid solvent, ε of 6.2528 was applied with optimised electrostatic (ρ_min = 0.00025 e, ρ_max = 0.002 e) and non-electrostatic parameters ((α + γ) = 43.1 dyn cm⁻¹, β = −0.5 GPa) taken from Hille et al.^26–28

To consider the dilute acetic acid environment encountered under industrial operating conditions, a linear interpolation between the solvated free energy in 100% acetic acid and 100% water was used. The approximation assumes that the solvent is uniformly distributed beyond the inner coordination sphere; preferential solvation is a possibility under the industrial solvent composition, which is between 0.15 and 0.37 for the molar ratios of water in acetic acid, but not explicitly considered.¹² For the linear interpolation, a molar ratio of 0.346 water in acetic acid was used to evaluate the solvation energy (E_solv) under industrial operating conditions.⁶E_solv is expressed as:

E_solv = 0.654 × E_{solv,acetic acid} + 0.346 × E_solv,water (1)

where E_{solv,acetic acid} and E_solv,water are the energies of the manganese complexes in implicit acetic acid and water, respectively.

The enthalpic (H) and entropic (S) contributions to the free energy under industrial operating conditions were evaluated within the ideal gas limit, with the PBE exchange correlation functional. Vibrational contributions were calculated by the finite difference approach implemented in the atomic simulation environment (ASE).²⁹ To ensure the structures were not transition states on the potential energy surface, vibrational modes with imaginary frequencies greater than 30i cm⁻¹ were reviewed and reoptimised where necessary, with imaginary frequencies below 30i cm⁻¹ considered as noise from the finite difference evaluation of the force constants. The free energy was evaluated under the open-literature industrial operating temperature and pressure of (T = 473 K, p = 2.25 MPa).³⁰ The solvated enthalpy (H_solv) is first calculated as:

H_solv = E_solv + E_ZPE + pV (2)

where H_solv is defined as the sum of the solvated electronic energy (E_solv), the zero point energy (E_ZPE) as evaluated for the unsolvated structure, and the pressure energy (pV). The free energy G_solv can then be calculated using H and entropy (S) as:

G_solv = H_solv − TS (3)

where S includes translational, rotational, and vibrational degrees of freedom as evaluated for the unsolvated structure at the given T and p.

2.2 Periodic first principles molecular dynamics

Periodic first principle molecular dynamics (FPMD) simulations were performed using the same DFT infrastructure as the molecular simulations, using the PBE-MBD density functional. For computational efficiency, the 2010 “light” basis set was applied (as per section S1 of ESI,† change in Mn–O bond lengths between ‘light’ and ‘tight’ basis is approximately 0.01 Å). A Hartree potential force correction was applied to obtain the Hellmann–Feynman forces, which reduces the required accuracy of self-consistency without compromising force accuracy; thus convergence of the self-consistent field cycle was set to the FHI-Aims defaults for the change in charge/spin density (4.3 × 10⁻⁵ e/a³₀).^17,31

To maintain the desired pressure and temperature during the MD simulations, combined Nose–Hoover and Parrinello–Rahman dynamics were used as implemented in ASE, with a calibrated timestep of 1 fs.^29,32,33 Coupling constants of 200 fs and 300 fs were used for the thermostat and barostat, respectively, as determined via extensive system testing (ESI,† section S5).

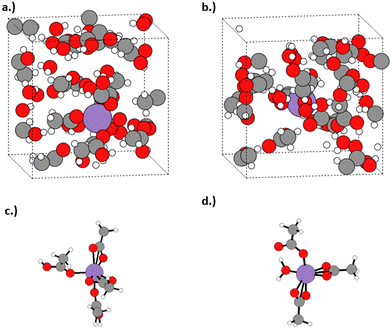
Initially, a total of 27 solvent molecules were included in the unit cell, to ensure sufficient species were present to model both first and second coordination shells for the solvated Mn complex. The reciprocal space sampling was performed using a Γ-centred 1 × 1 × 1 k-grid, as determined via system testing (ESI,† section S5). Cell angles on the unit cell were constrained to 90° throughout. Benchmarking of pure water and acetic acid with an NPT ensemble returned accurate densities (ESI,† section S6), and allow us to confidently apply this method to determine the unit cell size (and thus density) for our dilute acetic acid system, which was unavailable in literature at industrial operating conditions. The NPT ensemble molecular dynamics calculations were performed for 33.3 mol% water in acetic acid at operating conditions of 473 K and 2.25 MPa. The solvent composition differs marginally to the 34.6 mol% ratio used in the molecular DFT calculations, as it is the closest achievable value for a unit cell of 27 solvent molecules; the error in the change in free energy associated with this change in solvent conditions is calculated in our molecular simulations to be negligible (<0.01 eV). Equilibration was achieved after 27 ps, with an equilibrated density of 0.885 g cm⁻³ (ESI,† section S6). The calculated density has been applied in all subsequent molecular dynamics simulations on Mn(II) and Mn(III) in 33.3 mol% aqueous acetic acid, which were performed using the NVT ensemble to maintain the solvent density of the industrial process. The starting structures were constructed from the most thermodynamically stable octahedral Mn complexes, as identified in the initial molecular DFT calculations, with the complex placed with additional solvent molecules in a physically appropriate manner peripherally (Fig. 2). The NVT ensemble simulations of the solvated Mn(II) and Mn(III) species were performed for 80 ps.

Fig. 2 Supercells of the initial periodic models for the (a.) Mn(II) and (b.) Mn(III) complexes solvated in 33.3 mol% aqueous acetic acid, with one manganese cation and 27 solvent molecules. The optimized octahedrally-coordinated (c.) Mn(II) and (d.) Mn(III) complexes, around which the solvent were placed, are shown for clarity. H, C, O, and Mn atomic species are represented in white, grey, red, and purple, respectively.

When considering the interaction between Mn(III) and HBr, additional MD simulations were performed with H⁺ and hydrogen bromide moieties inserted into the simulation model of Mn(III) in 33.3 mol% aqueous acetic acid at 10 ps. The H⁺ was placed on an acetate ligand in the inner-sphere of Mn(III), and bromide placed in the outer-sphere. These simulations were run for 50 ps duration.

3 Results and discussion

3.1 Thermodynamics of metal acetate dissociation

To elucidate the catalyst speciation for manganese under industrial conditions, we investigate the change in Gibbs free energy (ΔG) for molecular systems as a function of the ligand environment in the inner solvation sphere. The commercial catalyst consists of an equimolar mixture of manganese acetate, cobalt acetate, and hydrogen bromide in aqueous acetic acid, meaning the ligands present in the solvent are acetate, acetic acid, water, and bromide; however, bromide is excluded from our initial investigations as electrochemical studies indicate that inner-sphere bromide coordination only becomes relevant at water concentrations below that applicable for the industrial process.¹² In solutions that contain both water and acetic acid, the generalized form of Mn(II) and Mn(III) is assumed as [Mn(OAc)_v(HOAc)_q(H₂O)_t]_n^(2−v)+ and [Mn(OAc)_v(HOAc)_q(H₂O)_t]_n^(3−v)+, respectively; where v, q, and t are the number of coordinating acetate, acetic acid, and water ligands. Furthermore, n represents the nuclearity of the catalyst, and the total charge of the complex is (2 − v)+ and (3 − v)+ for Mn(II) and Mn(III), respectively. The manganese complexes are considered to be mononuclear in our investigations (i.e., n = 1), though we note that polynuclear species have been postulated in literature.⁶

In solution, the manganese acetates can ionize and then dissociate to form a cationic salt and an acetate anion. The process may be considered as monodentate acetate substituting for a solvent acetic acid or water species, or alternatively as the acetate ligand deprotonating a solvent acetic acid species. The competing mechanisms for acetate dissociation are shown in eqn (4) and (5), where v = 2 for Mn(II), v = 3 for Mn(III), and all complexes are assumed to have octahedral coordination (v + q + t = 6).

Mn(OAc)_v(HOAc)_q(H₂O)_t + HOAc ⇌ [Mn(OAc)_(v−1)(HOAc)_(q+1)(H₂O)_t]⁺ + AcO⁻. (4)

Mn(OAc)_v(HOAc)_q(H₂O)_t + H₂O ⇌ [Mn(OAc)_(v−1)(HOAc)_q(H₂O)_(t+1)]⁺ + AcO⁻. (5)

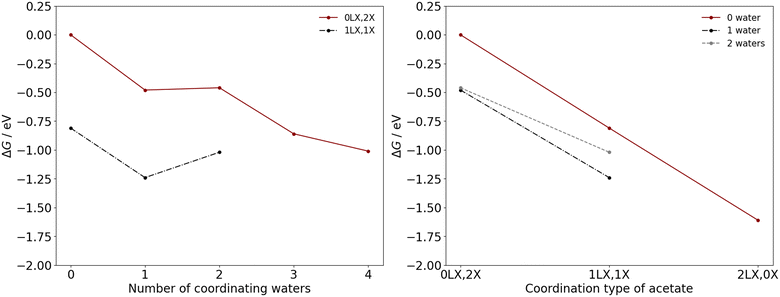
The thermodynamic feasibility of these transitions for the manganese acetates are determined by the ΔG at the industrial conditions outlined, with the acetate ligands considered here to be in their monodentate form. As illustrated in Fig. 3, the removal of an acetate ligand from either divalent or trivalent manganese are endergonic, with a positive ΔG in the range of 0.27–1.28 eV. Therefore, there is a thermodynamic driving force for acetate to remain associated to the manganese, which is consistent with ion-migration studies of the third-row transition metals in acetic acid.¹² For the competing mechanisms in eqn (4) and (5), the difference in ΔG between the mechanisms is generally less than 0.25 eV with the exception of Mn(OAc)₃(HOAc)₃ and Mn(OAc)₂(H₂O)₄, where substituting acetate with water has a ΔG that is 0.59 eV and 0.31 eV lower, respectively; additionally upon an increase in coordinating waters, the ΔG tends to increase for Mn(II) and decrease for Mn(III). These trends can likely be attributed to a subtle interplay between hydrogen bonding and steric interactions in the reactants and products.

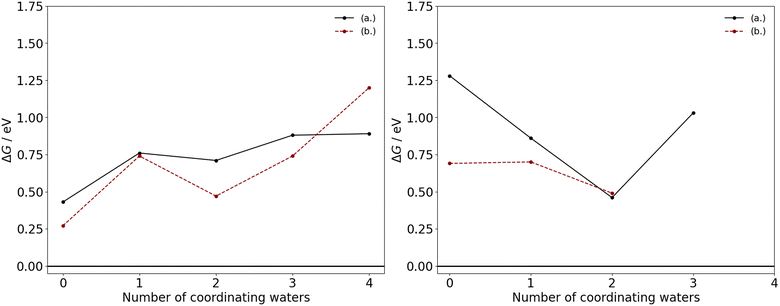Fig. 3 ΔG as a function of the number of coordinating water ligands in the neutral molecular complexes of Mn(II) (left) and Mn(III) (right), with acetate ligands in their monodentate coordination mode. In each graph, the competing mechanisms of eqn (4) and (5) are considered as replacement of the acetate species by (a.) acetic acid or (b.) water.

3.2 Thermodynamics of ligand coordination

Given that dissociation of acetate from divalent and trivalent manganese is thermodynamically unfavourable, the predominant form of the catalyst is assumed, e.g., for Mn(II), as Mn(OAc)₂(HOAc)_q(H₂O)_t. Under the industrial operating conditions with a dilute acetic acid environment, ligand rearrangement (rather than dissociation) may be considered via substitution of acetic acid ligands by water (or vice versa); or reconfiguration of the acetate species from a monodentate to a bidentate ligand, coupled with loss of an L-type ligand from the complex. These processes are illustrated in eqn (6) and (7), where v = 2 for Mn(II), v = 3 for Mn(III), and complexes are assumed to have octahedral coordination (v + q + t = 6).

Mn(OAc)_v(HOAc)_q(H₂O)_t + H₂O ⇌ Mn(OAc)_v(HOAc)_(q−1)(H₂O)_(t+1) + HOAc (6)

Mn(OAc)_v(HOAc)_q(H₂O)_t ⇌ Mn(OAc)_v(HOAc)_(q−1)(H₂O)_t + HOAc (7)

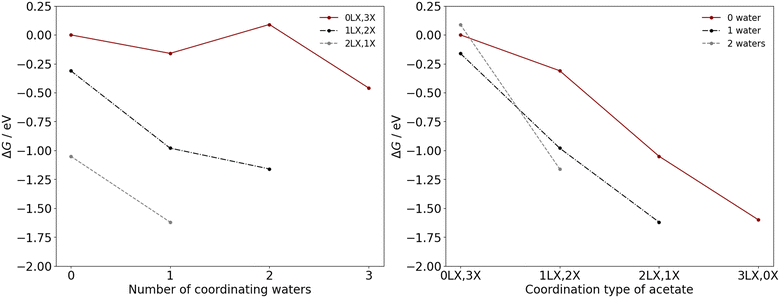
To determine the coordination environment of the manganese catalysts under industrial operating conditions, ΔG were calculated for the processes illustrated in eqn (6) and (7). Calculations were performed for both Mn(II) and Mn(III) as a function of the number of coordinated water ligands and the acetate coordination type (Fig. 4 and 5), considering bidentate acetate (LX type ligand) and monodentate acetate (X type ligand). Herein, the notation aLX, bX is used to denote a complex with a bidentate acetate ligands and b monodentate acetate ligands, with the remaining ligands consisting of water and acetic acid molecules.

Fig. 4 ΔG as calculated for octahedrally coordinated Mn(II) complexes for (left.) substitution of acetic acid for water and (right.) chelation of a coordinating monodentate acetate ligand. ΔG are calculated with the PBE0 density functional and include an implicit solvent model assuming a solvent environment of 34.6 mol% water in acetic acid, and industrial operating conditions of 473 K and 2.25 MPa. ΔG are calculated relative to the value of octahedrally coordinated Mn(OAc)₂(HOAc)₄, giving ΔG = 0 for this species.

Fig. 5 ΔG as calculated for octahedrally coordinated Mn(III) complexes for (left.) substitution of acetic acid for water and (right.) chelation of a coordinating monodentate acetate ligand. ΔG are calculated with the PBE0 density functional and include an implicit solvent model assuming a solvent environment of 34.6 mol% water in acetic acid, and industrial operating conditions of 473 K and 2.25 MPa. ΔG are calculated relative to the value for the neutral monodentate complex, namely Mn(OAc)₃(HOAc)₃, giving ΔG = 0 for this species.

The ΔG for chelation of monodentate acetate when considering a fixed quantity of water ligands is exergonic for Mn(II) and Mn(III) at industrial operating conditions. Chelation is favourable also at standard conditions (298 K, 0.1 MPa), and chelation is thermodynamically unfavourable only at very low temperatures (ESI,† section S4). The results occur because removing an acetic acid from the inner coordination sphere increases the disorder of the system, i.e., is entropically favourable, which is promoted by higher temperatures.

The favoured number of coordinating water ligands to Mn(II) is noted as dependent on the acetate coordination type. For the Mn(II) complexes with two (0LX,2X), one (1LX,1X), and zero (2LX,0X) monodentate acetate ligands, the favoured number of coordinating water molecules are one, one, and zero water, respectively, with these complexes having the lowest ΔG (Fig. 4). The monodentate acetate ligands tend to stabilize more water ligands due to hydrogen bonding interactions between the water and the acetate.

For Mn(III), a similar effect is observed with greater quantites of monodentate acetates leading to stabilisation of more water ligands, i.e., there is a discernible relationship. The Mn(III) complexes with three (0LX,3X), two (1LX,2X), one (2LX,1X), and zero (3LX,0X) monodentate acetate ligands favour the coordination of three, two, one, and zero water molecules, respectively. The preference for chelation of acetate ligands under standard and industrial operating conditions leads to the conclusion that 0–1 water ligands will typically be coordinated to the Mn species.

The most thermodynamically stable coordination environment for Mn(II) is the Mn(OAc)₂(HOAc)₂ complex, with two bidentate acetate ligands; the Mn(OAc)₂(HOAc)₂(H₂O)₁ complex, with one bidentate acetate ligand, is +0.37 eV higher in free energy. The most thermodynamically stable Mn(III) coordination environment is the Mn(OAc)₃(H₂O)₁ complex, with two chelating and one monodentate acetate ligand. The Mn(OAc)₃ complex, with three chelating acetate ligands, and Mn(OAc)₃(H₂O)₂, with one chelating and two monodentate acetate ligands, are +0.02 eV and +0.46 eV higher in free energy, respectively. The similar favourability for two bidentate (LX) acetate ligands indicates limited coordination change may occur during the transitions between Mn(II) and Mn(III) during the redox cascade, with only exchange of L-type ligands. However, the free energy landscape for Mn(III) is more shallow than for Mn(II), with more Mn(III) complexes with chelating acetate ligands within +0.5 eV of the most stable catalyst speciation. The shape of the landscape indicates a potentially greater dynamic variability of Mn(III) catalyst structures under the industrial operating conditions, which is considered further herein.

3.3 Dynamics of Mn(II) and Mn(III) in aqueous acetic acid

The detailed investigation of relative stabilities for Mn(II) and Mn(III) catalyst species suggest they are most stable under industrial operating conditions as Mn(OAc)₂(HOAc)₂ and Mn(OAc)₃(H₂O)₁, respectively. To understand the effect of an explicit solvent environment on the catalyst structure, as well as to probe the dynamical behaviour of the catalyst under operating conditions, first principles MD simulations were performed for the most stable Mn(II) and Mn(III) acetates, considering industrially relevant conditions of 33.3 mol% aqueous acetic acid, temperature of 473 K, and pressure of 2.25 MPa.

To determine the catalyst structures present in the simulation, a Python script was used with a cutoff of 1.5× the covalent radii of each atomic species to assess coordination of ligands (full details of the protocol are provided in the ESI,† section S8). Table 1 shows the statistical analysis of the coordination numbers present in the first principles MD simulations; it is observed the coordination number of Mn(II) and Mn(III) in aqueous acetic acid varies between 5 and 6 coordinate. Coordination numbers of 4 and 7 were observed in small quantities; however, these were identified to be transient in nature, typically existing for less than a few hundred femtoseconds (ESI,† section S9). The transient 7-coordinate species exist due to additional outer-sphere ligands coordinating to either Mn(II) or Mn(III). The 4-coordinate species exist due to the lability of the bidentate acetate ligands in aqueous acetic acid; one of the coordinating bidentate acetate oxygen atoms can rapidly uncoordinate from manganese, forming monodentate acetate, then re-coordinate reforming the bidentate acetate.

Table 1 Statistical analysis of the quantities and duration of the inner-sphere complexes observed in the first principles molecular dynamics simulations of Mn(II) and Mn(III) in 33.3 mol% aqueous acetic acid, as a function of the coordination number of Mn(II) and Mn(III), respectively. A small fraction of the Mn(III) structures (1.3%) are not shown in the quantities as the coordination environments include hydroxyl ligands, where a water ligand has been deprotonated by a ligand in the outer-sphere

Coordination number	Mn(II)		Mn(III)
	Quantity/%	Duration/fs	Quantity/%	Duration/fs
4	14.0	50–300	0.7	20–600
5	49.7	Non-transient	40.5	Non-transient
6	36.0	Non-transient	55.6	Non-transient
7	0.3	30–200	1.9	10–70

---

Over the entirety of the 80 ps MD simulation, between 0 and 1 water molecules coordinate to Mn(II), with 31.7% of complexes having one coordinating water; the corresponding residence times of water and acetic acid in the inner-sphere were 153.7 fs and 246.4 fs, respectively. The average inner-sphere water coordination obtained here at the industrially relevant conditions is lower than the one molecule average obtained by recent ESEEM measurements, which we attribute to the entropic favourability of the outer-sphere water given the latter experiments were conducted at 5 K.¹³ The average number of coordinating water molecules in both the MD simulations and the ESEEM measurements are significantly lower than the previously proposed average of four coordinating water molecules, based off stepwise formation constants.^12,13 Coordination environments with greater than one coordinating water molecule are also surprisingly absent from our MD simulations, and this is proposed to occur because water can form stronger hydrogen bonds than acetic acid, meaning it is energetically favourable for the water to be in the outer-sphere rather than in the reduced coordination environment around the Mn(II) species.

To compare the structures observed in the first principles MD simulations with the most stable species predicted by the molecular DFT calculations in section 3.2, an analysis of the structural data for the observed six-coordinate Mn(II) species was performed, with the results shown in Fig. 6; a full analysis of all observed structures can be found in the ESI† (section S9). The most frequently observed six coordinate Mn(II) complex is Mn(OAc)₂(HOAc)₂ (45.8%), followed by Mn(OAc)₂(HOAc)₂(H₂O)₁ (31.6%). These results are in agreement with the static simulations and thermodynamic stability presented in Fig. 4, with Mn(OAc)₂(HOAc)₂ identified as the most thermodynamically stable complex and Mn(OAc)₂(HOAc)₂(H₂O)₁ +0.37 eV greater in free energy than Mn(OAc)₂(HOAc)₂.

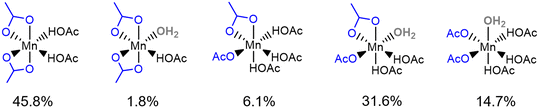Fig. 6 Statistical analysis of the six-coordinate structures observed in the 80 ps first principles MD simulation of Mn(II) species in 33.3 mol% aqueous acetic acid.

In the first principles MD simulation of Mn(III) in 33.3 mol% aqueous acetic acid, statistical analysis of the structures revealed between 0 and 2 water molecules coordinate to Mn(III), with 76.8% of complexes having 0 coordinating water, 21.8% have 1 coordinating water, and 1.4% have 2 coordinating waters, which results in a marginally lower average water coordination than for Mn(II); the corresponding residence times of water and acetic acid in the inner-sphere of Mn(III) were 47.0 fs and 64.9 fs, respectively. The result suggests that the coordination environment for Mn(II) and Mn(III) species under the industrial operating conditions will include zero or one water molecules only, and that the number of coordinating waters is unlikely to change significantly when Co(III) oxidizes Mn(II) to Mn(III).

Fig. 7 presents analysis of the six-coordinate species observed in the first principles MD simulation of Mn(III) in 33.3 mol% aqueous acetic acid. The most frequently observed of the six coordinate Mn(III) species is Mn(OAc)₃(HOAc)₁ (63.9%), followed by Mn(OAc)₃ (21.8%) and Mn(OAc)₃(HOAc)₁(H₂O)₁ (11.8%); the observations differ from the relative stability calculated in Fig. 5, where ΔG relative to Mn(OAc)₃(HOAc)₃ is −1.05 eV, −1.60 eV, and −0.98 eV for the same respective structures. The free energies indicate that Mn(OAc)₃ is more stable than Mn(OAc)₃(HOAc)₁; the lability of the acetate ligands, coupled with a propensity for explicit hydrogen bonds via the monodentate acetate, is proposed to result in greater proportions of monodentate acetate during the MD simulations. It is noted also that Mn(OAc)₃(H₂O)₁ was predicted to have the lowest free energy in Fig. 5, with a ΔG of −1.62 eV, but this structure is not observed in the MD simulations; instead, the dehydrated Mn(OAc)₃(HOAc)₁ complex is observed. The result could be attributed to the entropic favourability of solvated water molecules, which promotes the formation of dehydrated complexes by preference of water to positions in the outer solvent sphere.

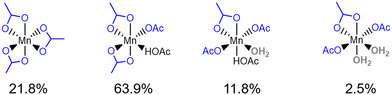Fig. 7 Statistical analysis of the six-coordinate structures observed in the 80 ps production MD simulation of Mn(III) species in 33.3 mol% aqueous acetic acid.

Considering the most commonly observed coordination environments in our MD simulations and their specific relevance to the redox cascade, the Mn(II) catalyst is proposed to have a coordination environment of Mn(OAc)₂(HOAc)₂ (45.8%) or Mn(OAc)₂(HOAc)₂(H₂O)₁ (31.6%) when in the resting state. Upon oxidation by Co(III) in the redox cascade, an acetate ligand is proposed to form on the Mn(III) from an associated acetic acid species, given the strongest propensity for the acetate ligands in our static simulations, and the inner-sphere ligands are most likely to rearrange to form Mn(OAc)₃(HOAc)₁; substitution of the coordinating water for acetic acid would be expected for oxidation of Mn(OAc)₂(HOAc)₂(H₂O)₁, whilst no rearrangement would be expected for oxidation of Mn(OAc)₂(HOAc)₂ to the most commonly observed product. Mn(OAc)₃(HOAc)₁ would then be proposed to oxidise a bromide species, forming the active bromine species as either a bromine radical or a dibromide radical anion, which is involved in the abstraction of hydrogen from p-xylene to continue the redox cascade.

3.4 Dynamics of Mn(III) and hydrogen bromide in aqueous acetic acid

The commercial pTA process is performed with hydrogen bromide (HBr) as the bromide source.³⁰ In the redox cascade (Fig. 1), an electron transfer occurs from the bromide to Mn(III), resulting in reformation of Mn(II) and a complementary bromine radical or dibromide radical anion.⁵ To better understand the coordination environment of Mn(III) in the industrial operating conditions, and to learn how the bromide interacts with the Mn(III) complex, MD simulations were performed for Mn(III) with HBr included in the simulation cell, whilst also maintaining a solvent of 33.3 mol% aqueous acetic acid. The inclusion of hydrogen bromide changes the pH of the system, and the Mn : Br ratio, and complementary MD simulations were therefore performed to better distinguish these effects, with only H⁺ included in the simulations rather than HBr, and these results are included in our discussion herein.

The coordination number of Mn(III) varies between 5–6, similar to the observations in section 3.3 for the Mn(III) species without a HBr or H⁺ moiety present; a full analysis of all observed structures is shown in the ESI† (section S9). In regards to water coordination, 0–2 water molecules coordinate to Mn(III), with 7.9% having 0 coordinating water, 20.9% with 1 coordinating water and 71.2% with 2 coordinating waters; this corresponds to residence times of water and acetic acid in the inner-sphere of 128.5 fs and 50.0 fs, respectively. The increase in the quantity of structures with two coordinating water is significant, from 1.4% in the absence of HBr (section 3.3) to 71.2% with HBr; in contrast, in the presence of H⁺ only, no water molecules coordinate to Mn(III); and residence times cannot be presented. The results suggest that the introduction of the bromide species is specifically responsible for the changes in water coordination.

For the simulations with HBr included in the solvent environment, the Br⁻ species does not enter the inner coordination sphere of the Mn complex during the entire MD simulation. The result agrees with experimental data where bromide coordination is not observed under industrial operating conditions, arising only under low water concentrations due to a reduction of the dielectric constant for the solvent.^12,13 The result therefore suggests that the electron transfer between Mn(III) and the bromide species is an outer sphere electron transfer, rather than requiring inner sphere coordination of the bromide for the electron transfer to occur.

4 Conclusions

The activity of the cobalt, manganese, and bromide catalyst that is used at industrial scales for the p-xylene oxidation process has a strong correlation with the solvent environment, but the coordination of the active metal species under operating conditions remains unclear despite the significant commercial value. In this work, a Kohn–Sham DFT approach has been used to investigate the coordination environment of the Mn(II) and Mn(III) catalysts that are involved in the p-xylene redox cascade. The thermodynamic stability of varying inner-sphere coordination environments have been determined at industrial operating conditions (T = 473 K, p = 2.25 MPa) and in industrial solvent composition (34.6 mol% water in acetic acid) by calculation of the Gibbs free energy. The free energy change (ΔG) for dissociation of acetate ligands from the neutrally charged Mn(II) and Mn(III) acetates are endergonic, in the range of 0.27–1.28 eV, suggesting the Mn(II) and Mn(III) complexes exist in the neutrally charged form. The most stable coordination environments for the neutral complexes are calculated to be Mn(OAc)₂(HOAc)₂ and Mn(OAc)₃(H₂O)₁ for Mn(II) and Mn(III), respectively.

Molecular dynamics simulations of the Mn(II) and Mn(III) catalysts in aqueous acetic acid were performed to better understand the dynamical nature of the coordination environment under industrial operating conditions. The most stable six-coordinate coordination environments are observed to be Mn(OAc)₂(HOAc)₂ and Mn(OAc)₃(HOAc)₁ for Mn(II) and Mn(III), respectively. The structures observed have an average of 0–1 water molecules in the inner coordination sphere, which agrees with recently published experimental ESEEM results and supports conclusions that a lower number of water molecules (0–1) coordinate to Mn(II) than the four molecules suggested prior from stepwise formation constants.^12,13 Further dynamical simulations were performed with HBr introduced, as bromide is an essential component of the industrial redox cascade. Bromide is not observed in the inner-coordination sphere of Mn(III), which agrees with experimental findings and suggests that electron transfer between bromide and Mn(III) is an outer sphere process.^12,13 The bromide species also changes the coordination environment of the Mn(III), promoting coordination of additional water molecules.

Often the perception of a catalyst is a static structure but these results highlight the dynamic nature of the manganese catalyst species under operating conditions, and how the most common coordination environments may be subtly impacted by environment changes. Further molecular dynamics simulations would be beneficial to investigate how changes in the water concentration affect the coordination environment and the catalyst deactivation processes. We envisage that emergent machine learning approaches will make the challenge of completing such simulations more tractable, via derivation of machine-learning potentials that allow for larger and longer simulations, and thus this area will be the subject of concerted effort in our ongoing studies.

Data availability

Data supporting the DFT simulations of this study are openly available from the CONVERIS repository at DOI: 10.17035/d.2024.0308195128.

Conflicts of interest

There are no conflicts of interest to declare.

Acknowledgements

Via our membership of the UK's HEC Materials Chemistry Consortium, which is funded by EPSRC (EP/R029431), this work used the UK Materials and Molecular Modelling Hub for computational resources, MMM Hub, which is partially funded by EPSRC (EP/T022213). We acknowledge the support of the Supercomputing Wales project, which is part-funded by the European Regional Development Fund (ERDF) via Welsh Government. HT acknowledges funding of a PhD scholarship by Koch Technology Solutions Ltd. AJL acknowledges funding by the UKRI future leaders fellowship program (MR/T018372/1, MR/Y034279/1).

Notes and references

1. PTA Technology, https://www.kochtechsolutions.com/technologies/polyester-value-chain/pta/, 2022, [Online; accessed 01-April-2022].
2. M. Li, F. Niu, D. H. Busch and B. Subramaniam, Ind. Eng. Chem. Res., 2014, 53, 9017–9026.
3. R. Zhang, X. Ma, X. Shen, Y. Zhai, T. Zhang, C. Ji and J. Hong, J. Environ. Manage., 2020, 260, 110062.
4. E. Pérez, J. Fraga-Dubreuil, E. García-Verdugo, P. A. Hamley, M. L. Thomas, C. Yan, W. B. Thomas, D. Housley, W. Partenheimer and M. Poliakoff, Green Chem., 2011, 13, 2397–2407.
5. P. D. Metelski and J. H. Espenson, J. Phys. Chem. A, 2001, 105, 5881–5884.
6. S. Chavan, S. Halligudi, D. Srinivas and P. Ratnasamy, J. Mol. Catal. A: Chem., 2000, 161, 49–64.
7. X.-D. Jiao and J. H. Espenson, Inorg. Chem., 2000, 39, 1549–1554.
8. X.-D. Jiao, P. D. Metelski and J. H. Espenson, Inorg. Chem., 2001, 40, 3228–3233.
9. Q. Wang, Y. Cheng, L. Wang and X. Li, Ind. Eng. Chem. Res., 2007, 46, 8980–8992.
10. E. Scott and A. Chester, J. Phys. Chem., 1972, 76, 1520–1524.
11. C. F. Hendriks, H. C. van Beek and P. M. Heertjes, Ind. Eng. Chem. Prod. Res. Dev., 1979, 18, 43–46.
12. W. Partenheimer, J. Mol. Catal. A: Chem., 2001, 174, 29–33.
13. R. L. Taylor, D. Housley, M. Barter, A. Porch, K. Whiston, A. Folli and D. M. Murphy, Catal. Sci. Technol., 2022, 12, 5274–5280.
14. Q. Wang, X. Li, L. Wang, Y. Cheng and G. Xie, Ind. Eng. Chem. Res., 2005, 44, 4518–4522.
15. X.-A. Yuan, C. Huang, X. Wang, P. Liu, S. Bi and D. Li, Organometallics, 2021, 40, 3124–3135.
16. F. Qian, X. Chen and X. Yang, Chem. Phys. Lett., 2019, 714, 37–44.
17. V. Blum, R. Gehrke, F. Hanke, P. Havu, V. Havu, X. Ren, K. Reuter and M. Scheffler, Comput. Phys. Commun., 2009, 180, 2175–2196.
18. X. Ren, P. Rinke, V. Blum, J. Wieferink, A. Tkatchenko, A. Sanfilippo, K. Reuter and M. Scheffler, New J. Phys., 2012, 14, 053020.
19. W. P. Huhn and V. Blum, Phys. Rev. Mater., 2017, 1, 033803.
20. J. P. Perdew, K. Burke and M. Ernzerhof, Phys. Rev. Lett., 1996, 77, 3865.
21. A. Tkatchenko, R. A. DiStasio Jr, R. Car and M. Scheffler, Phys. Rev. Lett., 2012, 108, 236402.
22. A. Tkatchenko, A. Ambrosetti and R. A. DiStasio Jr, J. Chem. Phys., 2013, 138, 074106.
23. C. Adamo and V. Barone, J. Chem. Phys., 1999, 110, 6158–6170.
24. S. Ringe, H. Oberhofer, C. Hille, S. Matera and K. Reuter, J. Chem. Theory Comput., 2016, 12, 4052–4066.
25. O. Andreussi, I. Dabo and N. Marzari, J. Chem. Phys., 2012, 136, 064102.
26. C. J. Cramer and D. G. Truhlar, Free Energy Calc. Ration. Drug Des., 2001, 63–95.
27. C. J. Cramer and D. G. Truhlar, Trends and Perspectives in Modern Computational Science, 2006, vol. 6, pp. 112–140.
28. C. Hille, S. Ringe, M. Deimel, C. Kunkel, W. E. Acree, K. Reuter and H. Oberhofer, J. Chem. Phys., 2019, 150, 041710.
29. A. H. Larsen, J. J. Mortensen, J. Blomqvist, I. E. Castelli, R. Christensen, M. Dułak, J. Friis, M. N. Groves, B. Hammer, C. Hargus, E. D. Hermes, P. C. Jennings, P. B. Jensen, J. Kermode, J. R. Kitchin, E. L. Kolsbjerg, J. Kubal, K. Kaasbjerg, S. Lysgaard, J. B. Maronsson, T. Maxson, T. Olsen, L. Pastewka, A. Peterson, C. Rostgaard, J. Schiøtz, O. Schütt, M. Strange, K. S. Thygesen, T. Vegge, L. Vilhelmsen, M. Walter, Z. Zeng and K. W. Jacobsen, J. Phys.: Condens. Matter, 2017, 29, 273002.
30. R. A. Tomás, J. C. Bordado and J. F. Gomes, Chem. Rev., 2013, 113, 7421–7469.
31. P. Bendt and A. Zunger, Phys. Rev. Lett., 1983, 50, 1684.
32. S. Melchionna, G. Ciccotti and B. Lee Holian, Mol. Phys., 1993, 78, 533–544.
33. S. Melchionna, Phys. Rev. E, 2000, 61, 6165.

---

Footnote

† Electronic supplementary information (ESI) available: Testing of computational simulation settings for static simulations and parameterisation of solvent model, analysis of geometric isomers in static simulations, assessment of the effect of temperature and energy on the free energy landscape, testing of computational simulation settings for dynamic simulations, equilibration of isothermal–isobaric dynamic simulations, analysis of structures in dynamic simulations. See DOI: https://doi.org/10.1039/d4cy00284a

---