Open Access Article
Open Access ArticleCreative Commons Attribution 3.0 Unported Licence
Accelerated design of nickel-cobalt based catalysts for CO2 hydrogenation with human-in-the-loop active machine learning†
Yasemen
Kuddusi
 *ab,
Maarten R.
Dobbelaere
*ab,
Maarten R.
Dobbelaere
 c,
Kevin M.
Van Geem
c,
Kevin M.
Van Geem
 c and
Andreas
Züttel
c and
Andreas
Züttel
 ab
ab
aLaboratory of Materials for Renewable Energy (LMER), Institute of Chemical Sciences and Engineering (ISIC), Basic Science Faculty (SB), École Polytechnique Fédérale de Lausanne (EPFL) Valais/Wallis, Energypolis, Rue de l'Industrie 17, 1951 Sion, Switzerland. E-mail: yasemen.kuddusi@epfl.ch
bEmpa Materials Science & Technology, 8600 Dübendorf, Switzerland
cLaboratory for Chemical Technology, Department of Materials, Textiles and Chemical Engineering, Ghent University, Technologiepark 125, 9052 Gent, Belgium
First published on 10th September 2024
Abstract
Thermo-catalytic conversion of CO2 into more valuable compounds, such as methane, is an attractive strategy for energy storage in chemical bonds and creating a carbon-based circular economy. However, designing heterogeneous catalysts remains a challenging, time- and resource-consuming task. Herein, we present an interpretable, human-in-the-loop active machine learning framework to efficiently plan catalytic experiments, execute them in an automated set-up, and estimate the effect of experimental variables on the catalytic activity. A dataset with 48 catalytic activity tests was compiled from a design space of Ni–Co/Al2O3 catalysts with over 50 million potential combinations in only eight iterations. This small dataset was found sufficient to predict CO2 conversion, methane selectivity, and methane space–time yield with remarkable accuracy (R2 > 0.9) for untested catalysts and reaction conditions. New experiments and catalysts were selected with this methodology, leading to experimental conditions that improved the methane space–time yield by nearly 50% in comparison to the previously obtained maximum in the dataset. Interpretation of the model predictions unveiled the effect of each catalyst descriptor and reaction condition on the outcome. Particularly, the strong predicted inverse trend between the calcination temperature and the catalytic activity was validated experimentally, and characterization implied an underlying structure–performance relationship. Finally, it is demonstrated that the deployed active learning model is excellently suited to predict and fit kinetic trends with a minimal amount of data. This data-driven framework is a first step to faster, model-based, and interpretable design of catalysts and holds promise for broader applications across catalytic processes.
1. Introduction
CO2 plays a key role in the many carbon cycles that nature exhibits and exploits to store energy.1 It remains one of the main societal challenges to mimic the natural energy storage capacities by technology and secure the future energy supply while minimizing CO2 emissions.1 So-called chemical energy carriers provide a promising way of storing renewable energy. In such processes, CO2 is used as feedstock and catalytically reduced to synthetic hydrocarbons in which the energy is stored in the chemical bonds.2,3 In particular, the Sabatier or methanation reaction (eqn (1)), which converts CO2 into CH4, is of paramount importance. This reaction has a high technological readiness level due to the existing natural gas grid infrastructure and realizations that transitioned methanation endeavors from lab to pilot and industrial scale.4–8 Nevertheless, catalyst design and reaction modeling improvements are still heavily needed to make it a mature energy storage method.9CO2 + 4H2 ![[left over right harpoons]](https://www.rsc.org/images/entities/char_21cb.gif) CH4 + 2H2O ΔH298 K = −165.0 kJ mol−1 CH4 + 2H2O ΔH298 K = −165.0 kJ mol−1 | (1) |
CO2 + H2 ![[left over right harpoons]](https://www.rsc.org/images/entities/char_21cb.gif) CO + H2O ΔH298 K = +41.0 kJ mol−1 CO + H2O ΔH298 K = +41.0 kJ mol−1 | (2) |
Ni/Al2O3 catalysts, while susceptible to deactivation, have shown some enhancements with the introduction of additional metals. Especially Co, also a non-noble metal, has sparked interest as a Ni promoter because of its beneficial effect on Ni dispersion, stability, reducibility, coke deposition, and activity.9,15–17 As altered catalyst synthesis recipes and reaction conditions may change the kinetics and mechanistic pathway of CO2 methanation, it can be assumed that the rate expressions will differ as a result of these alterations.12 Ideally, the design of catalysts and the exploration of reaction conditions should be viewed as a unified, multi-dimensional challenge to guarantee the best possible reactor design and operation across various scales.
Optimization of heterogeneous catalysts is a high-dimensional problem that encompasses a vast space of different material compositions, preparation methods, and reaction conditions. The extent of the search space results in the number of experiments typically being constrained by the project time and materials cost, even when automated high-throughput setups are available.18,19 Therefore, the scope of many studies is limited to a single catalysts modeled following a “postdictive” approach.20 That is, all necessary experiments must be performed to fit power-law rate expressions. This approach has the benefit that it is interpretable, can be used in reactor design, and is easy to solve numerically, but it requires a large number of experiments.21 Therefore, a shift towards “predictive” modeling, where catalytic activity can be estimated before performing any costly experiments, is heavily desired.
In recent years, machine learning tools have increasingly been used to extract information from kinetic catalytic data and provide predictive insights into catalyst action.22–26 Yılmaz et al.27 published a purely data-driven study in which they applied random forests to analyze the methanation reaction using data from 100 publications. While this kind of predictive approach can provide new insights, it is also limited to simple output predictions and impedes reverse design of catalysts because of the lack of standardization in published catalytic data. Indeed, catalytic data can be categorized into various types, of which synthesis and kinetic catalytic data play a central role.28 Subtle differences in synthetic procedures (e.g., calcination temperature, reduction time) reported in different laboratories can drastically influence the reproducibility of reported reaction outcomes. Therefore, it is essential to compare heterogeneous catalysts under identical conditions to create reliable predictive models.29,30 In addition, direct comparison between various catalyst reports is hampered by missing reaction metrics, such as space–time yields or turnover frequencies.31–33
The scarcity of standardized catalytic data and the large dimensionality of catalytic research problems have especially boosted the application of active machine learning algorithms, which integrate machine learning and the design of experiments (DoE).34 Bayesian optimization and active learning are common strategies within active machine learning for optimizing experimental planning.35 The general workflow of these strategies consists of iteratively computing a surrogate model of the objective function. Then, an acquisition function is created to select the next point with the predicted posterior distribution. This acquisition function can be used to balance exploration and exploitation of the search space. The difference between active learning and Bayesian optimization lies in the research objective. While Bayesian optimization aims to find an extremum of the black-box objective function, it is in active learning the goal to optimize the performance of the surrogate model and create a generalized model over the entire design space. A recent work by Ramirez et al.36 demonstrates the use of Bayesian optimization and a high-throughput screening platform to optimize heterogeneous catalysts in eight iterations for the reduction of CO2 to methanol. In that work, up to 24 catalysts were synthesized per iteration in a nearly fully automated way. However, in the absence of high-throughput synthesis and reaction platforms, parallel querying is typically not possible. Sequential querying, on the other hand, is constrained by experimental specifications. For example, a reactor can ramp up the temperature but requires more time to cool down. Moreover, catalyst synthesis is a time-consuming step that is often investigated with categorical variables, rather than by iterative synthesis of suggested catalysts.37 Therefore, limited to a single reactor, Ureel et al.38 restricted their active learning study for the catalytic pyrolysis of plastic waste to two pre-selected catalysts. We addressed these constraints in our work by introducing batch acquisition in a single reactor with multiple suggested reaction conditions per queried catalyst.
Active machine learning approaches make use of black-box regression algorithms (e.g., Gaussian processes) so that the relationship between input and output cannot be interpreted.39 On the other end of the model spectrum are glass-box models, such as microkinetic models or symbolic regression models, that have interpretability as an inherent feature.40 A compromise lies in the development of grey-box models to make black boxes interpretable.29 Recent examples have illustrated the use of grey-box models to speed up information extraction from kinetic catalytic data. Suvarna et al.41 used black-box ensemble methods followed by a posteriori feature-importance analysis for the CO2 hydrogenation reaction to methanol. Such analysis aims to add understanding to the effect of input variables on the output and was also demonstrated, among others, for dry reforming of methane42,43 and CO2-assisted propane dehydrogenation.44 Using hydrodeoxygenation as a model reaction, Mendes et al.45 created an automated gray-box tool to recognize patterns in kinetic catalytic data. While it is inevitable that data science and machine learning will become a standard tool for reaction engineers, new and reliable methodologies need to be developed to integrate these new tools into an experimental campaign.
The aim of this work is to provide a robust, interpretable, and efficient methodology that integrates data science and experimental reaction engineering, using the screening of catalysts and reaction conditions for the CO2 methanation reaction as a case study. Our approach includes a novel human-in-the-loop active learning workflow to plan, execute, and analyze catalytic experiments so that an informative dataset can rapidly be generated in a single reactor system without the need for a high-throughput platform. To achieve this, we establish an automated reaction platform that incorporates online chromatographic analysis and an active learning tool. We explore various machine learning models to predict the catalytic activity for new sets of experimental variables and find good agreement between predictions and experiments. Additionally, it is demonstrated that the underlying relationships between the experimental variables and the catalytic activity are learned by the machine learning model and can again be linked with physical insights. This study provides a data-driven workflow to accelerate experimental catalytic research and that is deployable to other catalytic systems and reactions.
2. Materials and methods
2.1. Experimental design space
The evaluation of the catalytic CO2 methanation is limited to an experimental design space consisting of 7 parameters, which are given in Fig. 2. These design parameters are grouped into 3 input categories: the reaction conditions, catalyst properties, and catalyst treatment conditions. The possible reaction conditions include temperatures between 523 and 773 K, pressures between 1 and 10 bar, and gas-hourly space velocities between 3300 and 26![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 400 ml h−1 gcat−1. The catalyst properties define the composition of the catalyst, which is limited to Al2O3-supported catalysts. Two metals, Ni and Co, are selected as primary base and promoter because of their large commercial availability at low cost. The maximal Ni and Co loading are 25 and 10 wt%, respectively. An experimental step size of 1 wt% is considered for the metal loadings. The catalyst treatment is limited to catalysts prepared via the incipient wetness impregnation method. The calcination and reduction temperature are defined in steps of 50 K between 623 K and 923 K. Multiplying the number of selectable experimental variables leads to a total of 54
400 ml h−1 gcat−1. The catalyst properties define the composition of the catalyst, which is limited to Al2O3-supported catalysts. Two metals, Ni and Co, are selected as primary base and promoter because of their large commercial availability at low cost. The maximal Ni and Co loading are 25 and 10 wt%, respectively. An experimental step size of 1 wt% is considered for the metal loadings. The catalyst treatment is limited to catalysts prepared via the incipient wetness impregnation method. The calcination and reduction temperature are defined in steps of 50 K between 623 K and 923 K. Multiplying the number of selectable experimental variables leads to a total of 54![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 654
654![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 600 accessible configurations for the experimental design space.
600 accessible configurations for the experimental design space.
2.2. Catalyst preparation
Ni/Al2O3, Co/Al2O3, and Ni–Co/Al2O3 catalysts with different Ni and Co weight percentages were synthesized by the incipient wetness impregnation method. The notation of the catalysts will be xNi–yCo/Al2O3-T where x and y are the weight percentages of nickel and cobalt loading respectively and T is the calcination temperature. The desired loading was achieved by impregnation of aqueous solutions of Ni(NO3)2·6H2O (Sigma-Aldrich) and Co(NO3)2·6H2O (Sigma-Aldrich) onto γ-alumina pellets (Alfa Aesar) with a pore volume of 1.20 cm3 g−1. The nominal metal loading in the catalyst was varied for Ni from 0 to 25 wt% and for Co from 0 to 10 wt%. The impregnated catalyst was dried for 12 h at 383 K prior to calcination in static air for 4 h using a heating rate of 5 K min−1 at various temperatures between 623 to 923 K. The calcined catalysts were reduced under H2 flow for 2 h at various temperatures from 623 to 923 K.2.3. Catalyst characterization
Nitrogen sorption at 77 K was carried out using the Belsorp Max II instrument. The total surface area was determined via the Brunauer–Emmett–Teller (BET) method. X-ray diffraction (XRD) patterns were obtained with a Bruker D8 Advance instrument using Cu Kα radiation (λ = 0.154 nm) at 40 kV and 40 mA. The data were acquired in the 2θ range of 10–80°, with an angular step size of 0.025° and a counting time of 1.5 s per step. The dried catalyst (∼20 mg) was put inside an alumina crucible to conduct thermogravimetric analysis (TGA) using a Netzsch TG209 F1 instrument under a dry air flow of 10 mL min−1 with 20 mL min−1 N2 as the protective gas from 30 to 700 °C at a ramp rate of 5 °C min−1. High-angle annular dark-field scanning transmission electron microscopy (HAADF-STEM) imaging and energy-dispersive X-ray spectroscopy (EDX) were performed using a Thermo Fisher Scientific Tecnai Osiris transmission electron microscope in scanning mode at an acceleration potential of 200 kV. Morphological analysis was conducted with a FEI Teneo 250 scanning electron microscope at 1.0–5.0 kV and a working distance of 2.5–5.0 mm. X-ray photoelectron spectroscopy (XPS) measurements were carried out on an Axis Supra instrument (Kratos Analytical) using the monochromated Kα X-ray line of an aluminum anode, with the pass energy set to 40 eV. The binding energy scale was referenced at 284.8 eV using the CC/CH component of the C1s orbital. Peak fitting was performed using CasaXPS, employing the Shirley method for background subtraction.2.4. Catalyst evaluation
The catalytic performance of the catalysts was evaluated in a fixed-bed tubular reactor (8 mm O.D.) that was heated in a tube furnace. The reactor temperature and catalyst bed temperature were measured by thermocouples and all gas flowrates were monitored by mass flow controllers. The experimental system was monitored and controlled by LabVIEW. The diagram of experimental set-up is given Fig. S3.1.†Prior to the reaction, 200 mg catalyst was placed in the reactor within quartz wool. The catalyst was then reduced in 5% H2 in N2 flow at the desired reduction temperature for 2 hours. The molar ratio of CO2 to H2 was 1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 4 in the feed in which N2 was used an internal standard. The tubing in which the outlet gasses were flowed through was heated to 393 K and passed through a condenser to remove water. For automating the entire experimental process without user supervision, the Laboratory Virtual Instrument Engineering Workbench (LabVIEW) platform was used.
4 in the feed in which N2 was used an internal standard. The tubing in which the outlet gasses were flowed through was heated to 393 K and passed through a condenser to remove water. For automating the entire experimental process without user supervision, the Laboratory Virtual Instrument Engineering Workbench (LabVIEW) platform was used.
2.5. On-line product analysis
The composition of the outlet gas products was analyzed on-line using a gas chromatograph (SRI Instruments Multi Gas Analyzer 1) equipped with a silica gel and molecular sieve 13x column as well as a thermal conductivity detector (TCD) and a flame ionization detector (FID). He was used as the carrier gas. The microreactor unit which enables the product analysis is directly integrated into the computational workflow based on LabVIEW and Python. The product analysis is directly integrated into the computational workflow. The raw TCD and FID data are exported in ASCII format. Subsequently, the data is processed in Python using SciPy for peak detection and NumPy for peak integration. Peak areas were automatically quantified using calibration curves so that catalytic activity was reported in terms of CO2 conversion (XCO2), selectivity towards CH4 (SCH4) and CO (SCO), yield of CH4 (YCH4), and space–time yield of CH4 (STYCH4). The expressions given in eqn (3)–(7) were used.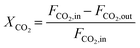 | (3) |
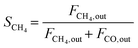 | (4) |
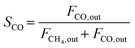 | (5) |
| YCH4 = SCH4·XCO2 | (6) |
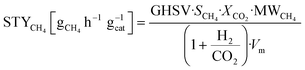 | (7) |
![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 400 cm3 mol−1 and the units of the gas-hourly space velocity (GHSV) and molar weight of methane (MWCH4) are in cm3 h−1 gcat−1, and gCH4 mol−1, respectively.
400 cm3 mol−1 and the units of the gas-hourly space velocity (GHSV) and molar weight of methane (MWCH4) are in cm3 h−1 gcat−1, and gCH4 mol−1, respectively.
2.6. Active machine learning
Active learning is performed to explore and model a process with a minimal amount of experiments. The open-source algorithm Gaussian n-dimensional Active Learning Framework (GandALF) is used. This algorithm creates, when trained on labeled experimental data, a surrogate model for the objective using Gaussian processes. Then, the next experiment that meets informativeness, representativeness, and diversity criteria is identified using the expected model output change (EMOC) acquisition function. The working principle of the active learning framework is described in detail elsewhere.38In the original implementation of the active learning framework, only one experiment is selected and performed at a time. This way of sequentially acquiring and performing experiments is not optimal for the objective of this study given the time-consuming aspect of synthesizing a selected catalyst. Therefore, we modified the code to overcome sequential single data selection so that it allows to select up to three different catalysts and three reaction conditions per catalyst, per iteration, in order to save up practical experimental time in the lab. The batch acquisition of next experiments allows up to nine activity tests to be performed per iteration. We refer to section S3 of the ESI† for the details about the active learning strategy.
2.7. Regression models
The dataset compiled using human-in-the-loop active learning was used to create a predictive model. Three kinds of supervised machine learning models for regression were investigated for this task: random forests (RF), extreme gradient boosting (XGB) regressors, and Gaussian processes (GP). All models were created in Python 3 using the open-source packages scikit-learn,46 xgboost,47 and GPy.48 Nested cross-validation was employed to tune the models and avoid overfitting. In the outer folds, the dataset is split into a training set and a test set (multiple outer folds). The training set is reduced in the inner folds into an inner training set and a validation set (multiple inner folds per outer fold). The best set of hyperparameters is chosen by the average performance over all inner folds. The model is evaluated for the outer fold by training the best model on the training set and testing it on the test set. This procedure is repeated for all outer folds. The prediction accuracy was calculated by the mean absolute error (MAE), the root mean squared error (RMSE), and the coefficient of determination (R2). Shapley additive explanation (SHAP) values49 were calculated for feature importance analysis and to provide local interpretability.3. Results and discussion
3.1. Human-in-the-loop active learning CO2 hydrogenation study
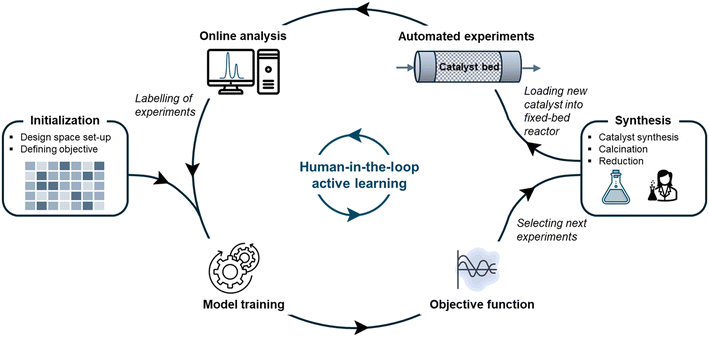
Modeling a chemical process with satisfactory accuracy requires the development of a representative dataset from which information can be extracted. In active learning, similar to traditional design of experiments, the aim is to extract maximum information from minimum experiments. In particular, the objective is to learn trends arising from the intrinsic effect of variables within the design space and achieve high XCO2 and SCH4. To achieve fast information acquisition, an automated workflow is established that includes planning, executing, and analyzing catalytic experiments.The workflow of this study is illustrated in Fig. 1 and comprises six steps: (1) initializing the active learning algorithm, (2) training the algorithm, (3) selecting new experiments, (4) synthesizing catalysts, (5) performing catalytic activity tests, and (6) analyzing the activity tests. This workflow is a human-in-the-loop machine learning process in the sense that the researcher produces the catalysts and supervises the accuracy of experiments and analyses.
At first, the researcher sets up the experimental design space to be explored (see section 2.1) and defines the objective to be modeled. Since it is of interest to know the conversion, selectivity, and space–time yield, the methane yield (YCH4) was selected as the objective based on which experiments are suggested. YCH4, namely, contains information about XCO2 and SCH4 without the strong GHSV-dependence that defines STYCH4. After the initialization, the researcher performed five experiments and the iterative process by training the Gaussian processes for the first time. From then on, new sets of experiments were iteratively suggested with the EMOC algorithm from the objective function. The manual steps are a sequence of synthesizing, drying, calcining, and reducing the catalyst, before reaction initialization in the fixed-bed reactor. The reaction conditions are controlled via LabVIEW and the raw analytical reaction output data that analyzes the product concentration at the reactor outlet is automatically processed into a format that allows retraining the machine learning model. The threshold was set at eight experimental rounds, resulting in a total of 26 synthesized catalysts and 48 performed catalytic tests.
The distribution of the experimental variables over the training database that is created by human-in-the-loop active learning is shown in Fig. 2. It can be observed that data is spread evenly over the complete design space. However, the reaction conditions are more uniformly distributed than the catalyst properties and treatment. This is due to the fact that 48 distinctive reaction conditions were performed while only 26 catalysts were synthesized.
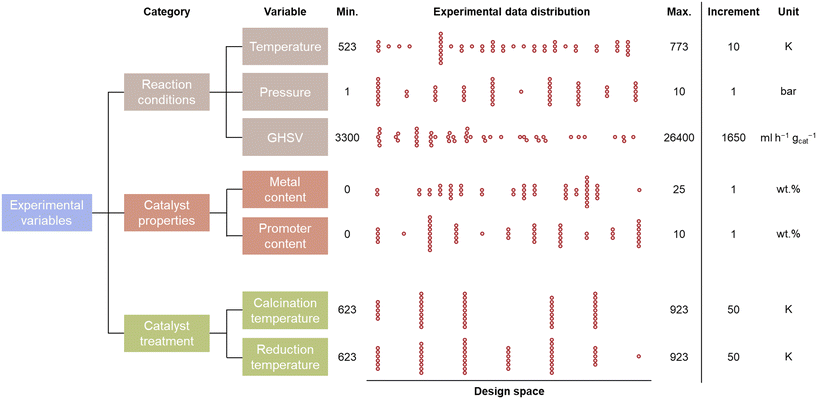 | ||
| Fig. 2 The distribution of the experimental variables in the acquisition of a catalytic activity training database, with the boundaries and step size of the experimental design space. | ||
The output distribution is given by Fig. 3 with respect to XCO2, SCH4, and STYCH4. In terms of XCO2 and SCH4, the data is well-distributed despite a missing quadrant of high conversion-low selectivity catalysts. This missing quadrant is attributable to thermodynamic limitations. Namely, the CO2 methanation reaction is able to reach full conversion at these reaction conditions but the reverse water-gas-shift reaction is limited to lower conversions.50 When it comes to STYCH4, bias towards STYCH4 below 1 gCH4 h−1 gcat−1 is observed.
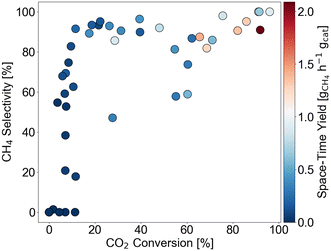 | ||
| Fig. 3 Output distribution of data points in the training set with respect to CO2 conversion, CH4 selectivity, and space–time yield. | ||
3.2. Prediction of catalyst activity
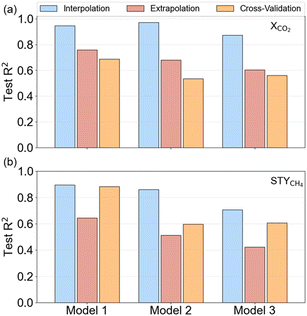
Three supervised machine learning regression algorithms were employed to predict the XCO2 and STYCH4 for sets of experimental variables. Gaussian processes, which are the driving force behind the active learning workflow, are an obvious first choice. Next to Gaussian processes (GP, model 1), extreme gradient boosting (XGB, model 2), random forests (RF, model 3) and are evaluated. A stratified 8-fold cross-validation scheme with 4 repeats was used to cross-validate the model. Herein, we applied nested cross-validation in which the performance was evaluated on the outer folds. Hyperparameter optimization was performed solely on the training database and the best model was selected based on the average performance on the inner folds. Fig. 4a and b show the cross-validation accuracy of the three models on XCO2 and STYCH4 prediction, respectively, tested on an interpolation and extrapolation test set. The coefficient of determination (R2) was chosen as the performance metric. A higher R2 indicates a better predictive performance.
The model performance is measured on various test sets. An extrapolative test set was constructed out of ten samples, randomly drawn from the pool of potential experiments, with a low similarity to the training samples. The similarity is calculated using the Mahalanobis distance,51 following the same procedure (see ESI†) as in previous works.52,53 A test sample is in the interpolative range if its Mahalanobis distance to the center of the training set is smaller than the average distance over the whole training set. To construct an interpolation set, the 48 experiments from the training set and the external data points were combined to a large set of 58 data points. Ten samples that met the Mahalanobis distance criterion were then drawn from these 58 data points, whereby the 48 remaining samples were used as a new training set.
Fig. 4 illustrates the accuracies obtained with the different algorithms for XCO2 and STYCH4 prediction. It can be seen that GP and XGB achieve higher R2 values than the RF. Moreover, the scores for XCO2 predictions are higher than for STYCH4. This finding can be linked to the output data distribution, which is more imbalanced for STYCH4 (see Fig. 3) and, hence, pose a more difficult prediction task. Overall, predictions are poorer on the extrapolation task, so that caution is required when relying upon model predictions. GPs achieve the highest R2 on the interpolative tests, respectively 0.95 and 0.90 for XCO2 and STYCH4. The repeated cross-validation results were found to be in the same order of magnitude as the interpolation and extrapolation sets, implying no overfitting. From these results, it is suggested that a decent initial guess of the catalytic activity can be made with a dataset as small as 48 samples. However, it is essential to use the model in the interpolative zone to obtain predictions with higher accuracy.
![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 000 data points from the design space using the GP regression model in the active learning framework. Then, the data point is selected for which the posterior mean is maximized with XCO2 and STYCH4 as objectives. We did not consider SCH4 as an objective as multiple points had already been found in the training set reaching a maximal SCH4 of 100%. This approach reflects Bayesian optimization in which an explorative acquisition function is used for several rounds, followed by an extremum search with a fully exploitative acquisition function. Another strategy for optimal catalyst design would be to immediately make use of an optimization-oriented algorithm with an acquisition function that balances exploration and exploitation.
000 data points from the design space using the GP regression model in the active learning framework. Then, the data point is selected for which the posterior mean is maximized with XCO2 and STYCH4 as objectives. We did not consider SCH4 as an objective as multiple points had already been found in the training set reaching a maximal SCH4 of 100%. This approach reflects Bayesian optimization in which an explorative acquisition function is used for several rounds, followed by an extremum search with a fully exploitative acquisition function. Another strategy for optimal catalyst design would be to immediately make use of an optimization-oriented algorithm with an acquisition function that balances exploration and exploitation.
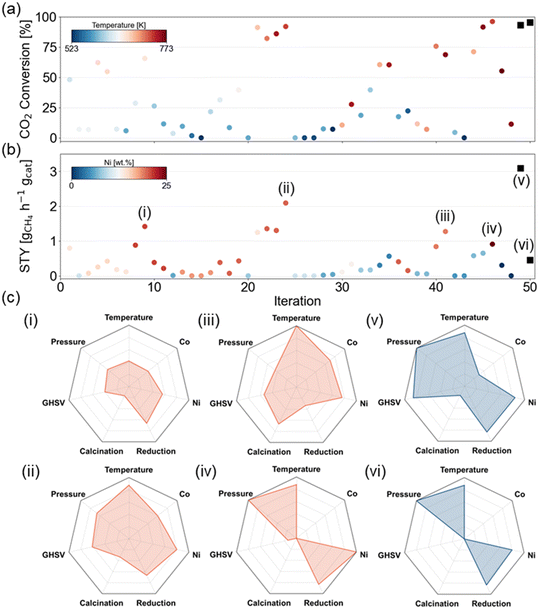
Fig. 5 shows the XCO2 and STYCH4 for each experiment that was picked by the active learning framework. Since this tool was not used as an optimization algorithm but rather as a screening tool in the training phase, an increasing trend in the objectives over the experiments is not expected. In terms of XCO2, the currently measured maximum is 96.1% which is found in the 46th experiment. The room for improvement is limited to only a few percent, and this is reflected in the optimal experiment choice of the active learning framework. The set of experimental variables that should optimize XCO2 is highly resembling to the earlier found maximum and with 95.6% the objective is not improved. The highest STYCH4, on the other hand, amounts to 2.09 gCH4 h−1 gcat−1 and was found in the 24th experiment in the training set. In this design space, the theoretically maximal STYCH4 is 3.8 gCH4 h−1 gcat−1 (at the highest GHSV, full conversion and selectivity) and the current optimum is only 55% of this aforementioned theoretically maximal STYCH4. According to the model interpretations, the ideal set of experimental variables to maximize STYCH4 consists of an elevated reaction temperature, pressure, and reduction temperature, a high GHSV and metal load, and a low to medium calcination temperature. The selected experiment from the active learning framework is a 21Ni–3Co/Al2O3 catalyst calcined at 673 K and reduced at 873 K, which is tested at 733 K and 10 bar with a GHSV of 23![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 100 ml h−1 gcat−1, which demonstrates that these trends are learned by the model itself. Indeed, in the experimental activity test, a STYCH4 of 3.10 gCH4 h−1 gcat−1 was observed. This observation indicates that the model-predicted set of experimental variables increased the STYCH4 with nearly 50%.
100 ml h−1 gcat−1, which demonstrates that these trends are learned by the model itself. Indeed, in the experimental activity test, a STYCH4 of 3.10 gCH4 h−1 gcat−1 was observed. This observation indicates that the model-predicted set of experimental variables increased the STYCH4 with nearly 50%.
3.3. Effect of experimental variables on reaction rate
Fig. 6 shows the relative impact of each experimental variable on the prediction of XCO2, SCH4, and STYCH4. The repeated stratified 8-fold cross-validation approach from section 3.2.1 was utilized to make sure that the feature importance analysis holds over multiple train-test splits. The relative importance of a feature is thus the average importance over 32 trials. It is observed that temperature emerges as the most important experimental variable for XCO2, where the reaction rate increases with temperature. However, thermodynamically, it is known that the lower temperatures are preferential for the methanation reaction. This is reflected in Fig. 6b, where the contribution of temperature is only 15.4% to the methane selectivity. Compared to thermal effects, the contribution of pressure is rather limited. The main metal load, in this case, Ni content, is another large driver of the catalytic activity. In SCH4 prediction, Ni content has the largest contribution with a higher load having a positive effect on the selectivity.
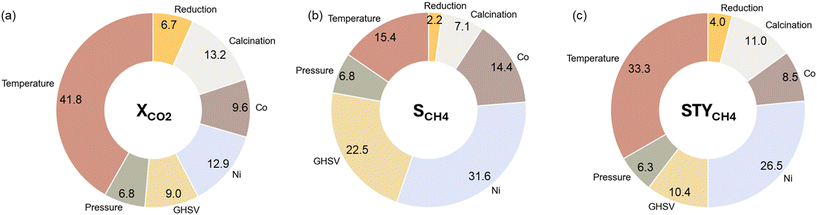 | ||
| Fig. 6 Relative importance based on Shapley Additive Explanations (SHAP) values of the considered experimental variables for (a) XCO2, (b) SCH4, and (c) STYCH4. | ||
The calcination temperature has a nonnegligible influence on the predicted XCO2, SCH4, and STYCH4. In all three cases, increasing the calcination temperature within our range of 623 to 873 K has a negative effect on the output. This shows that a higher calcination temperature indicates a lower catalytic activity. However, it can be observed in the summary plots that an optimum temperature must be present for Ni–Co catalytic systems. The impact of the reduction temperature is limited, but higher reduction temperatures appear to have a beneficial impact on the catalytic activity, possibly due to the complete reduction of the active metallic species.
We characterized the catalysts that were calcinated at various temperatures to investigate the effect of the calcination on the structure and the performance. The purpose of the calcination step in catalyst synthesis is to activate the catalyst so that the metal oxides are formed, which later can be followed by reduction to achieve the metal phase if needed. The method of the chosen calcination (calcination temperature, heating rate, gas flow, etc.) procedure often affects the final particle size.57
XRD patterns of the 15Ni–5Co/Al2O3 samples calcined at different temperatures are given in Fig. 8a. Commonly, the diffractions of γ-Al2O3 (PDF 00-029-0063) are present in all of the samples. Some of the X-ray diffraction patterns of some oxides and aluminates of nickel and cobalt are difficult to distinguish from each other fully as they are very close to each other.58,59 The possible phases that were considered in this study were NiO (PDF 01-073-1519), NiAl2O4 (PDF 01-081-0715), Co3O4 (PDF 04-003-0984), CoAl2O4 (PDF 04-016-4504), NiCo2O4 (PDF 04-013-0797).
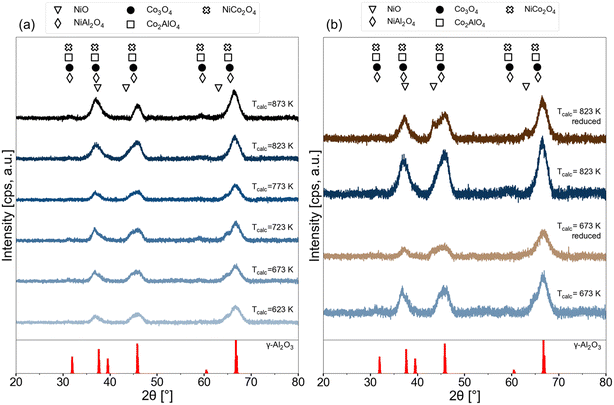 | ||
| Fig. 8 XRD patterns of 15Ni–5Co/Al2O3 samples (a) at various calcination temperatures (b) freshly calcined at 673 K and 823 K and reduced versions of these freshly calcined catalysts at 823 K. | ||
In the XRD patterns in Fig. 8a, broadening of the peak at around 36° is observed with increasing the calcination temperature, which indicates that the crystallite size is decreasing. With higher calcination temperatures, the intensity of the peaks that can be ascribed to the existence of the aluminates decreases. This weaker intensity can suggest that high calcination temperatures (above 823 K) treatments maintain lower crystallinity (higher degree of disorder, more of an amorphous structure) and/or higher dispersion of the spinel aluminate phases. After prolonged calcination at high temperatures (>500 K), the nickel species are reported to be stabilized against sintering by forming a nickel aluminate phase at the surface of the particles, as shown in eqn (8).60,61
| NiO or CoO + Al2O3 → NiAl2O4 or CoAl2O4 | (8) |
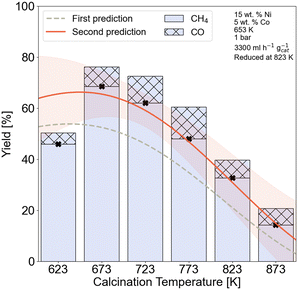
Thermogravimetric analysis (TGA) and X-ray photoelectron spectroscopy (XPS) measurements were done to further investigate the effect of calcination temperature on the nickel species. The TGA results for the 15Ni–5Co/Al2O3 up to 973 K with a heating rate of 5 K min−1 are given in Fig. S3.2 and Table S3.2† illustrating no significant thermal events occurrence after 693 K. The XPS spectra for Ni 2p are given in Fig. S3.3† and the peak fitting ESCA parameters62 are given on Table S3.3.† It is seen from the Ni 2p spectra that the main surface Ni species belong to those of NiAl2O4 at calcination temperatures between 623 and 873 K. Nickel aluminates also seemed to be the main bulk phase as XRD confirmed. A full summary of the relative surface concentrations of NiAl2O4 and NiO, derived from the deconvoluted Ni 2p spectra is given in Table S3.4.† The relative surface concentration of NiAl2O4 increases from 89.48% at 623 K to 97.54% to 873 K, while the relative NiO surface concentration drops from 10.52% to 2.46%. However, the highest surface concentration of NiO belonged to the sample calcined at 673 K with 11.77%. This temperature-dependent variations in surface concentrations indicate that higher calcination temperatures strengthen the interaction between the γ-Al2O3 support and nickel species, hence lead to NiAl2O4 formation. On the other hand, lower calcination temperatures increase the relative NiO content. NiAl2O4 species are reported to be inactive and more difficult to be reduced in comparison with NiO.63,64 The relative increase in NiAl2O4 species can be correlated to the drop in CH4 yield with increasing calcination temperature of 15Ni–5Co/Al2O3 catalysts, as was observed in Fig. 7.
The highest BET surface area owning sample in our study was 15Ni–5Co/Al2O3, which was calcined at 673 K as given in Table S3.2.† As Table S3.5† shows, for the 15Ni–5Co/Al2O3 samples that were calcined higher than 673 K, we observed a slight decrease in the BET surface area with an increase in the calcination temperature.
The HAADF-STEM images of the 15Ni–5Co/Al2O3 catalysts that are calcined at 673 K and 823 K and both reduced at 823 K are shown in Fig. 9. The average nickel nanoparticle sizes of the reduced catalysts are 12.6 nm ± 1.2 nm for 15Ni–5Co/Al2O3-673 and 8.4 nm ± 1.8 nm for 15Ni–5Co/Al2O3-823. It was observed that the nickel particle size decreases with the increasing calcination temperature, which was in line with the XRD. Even though metal particle size decreases with calcination temperature increase, the metal nanoparticles seem rather to be located in clusters. This can be explained by the higher dispersion of the metal aluminate phases at higher calcination temperatures, as suggested by XRD. As Fig. 9 illustrates, the smaller metal nanoparticles are dispersed throughout bigger clusters which may influence the accessibility of the reactants to the active metal sites. Fig. 7 and section S5† already demonstrated the predicted detrimental effect of increasing calcination temperature on to XCO2, SCH4, and STYCH4, which aligned with experimental catalytic activity tests. Evidently, lower to medium calcination temperatures presumably lead to higher BET surface areas. Furthermore, there are indications that these temperatures facilitate the reduction of metal species due to the weaker interaction with the support and that the metal species are better dispersed throughout sample but with bigger particle sizes.
In this section, we derived the understanding behind the combination of the reaction conditions and catalyst features that give superior yield that our active machine learning algorithm arrived to. The optimum point was able to be explained by surface and bulk characterizations. As simultaneous multi-dimensional changes are not easy-to-comprehend by humans, our methodology helps experimental researchers to speed up their work by providing a better start for optimizing their parameters with fewer experiments and characterizations amongst an immense chemical design space. Our strategy can save experimental time and cost which paves the way to discoveries in more complex reaction systems.
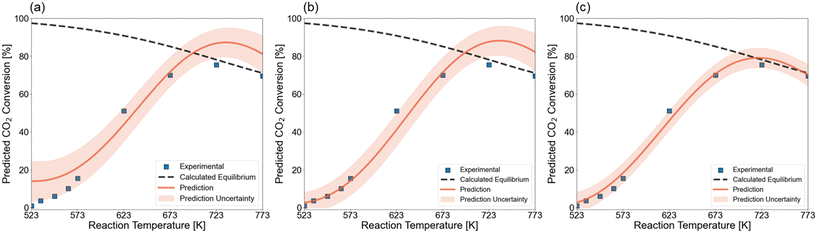
In first instance, we predicted the light-off curve without any information about the tested catalytic systems. This prediction is shown in Fig. 10a and resulted in a light-off curve that follows the experimental data but lacks accuracy in the higher and lower temperature area. As such, an infeasible maximum XCO2 is predicted that would be above the thermodynamic equilibrium. It has already been shown that accuracy is lower at the boundaries of the design space due to reduced data availability. To improve the prediction accuracy, one data point in the zone with the highest uncertainty was added to the training set. This point, which corresponds to a temperature of 523 K, adds confidence to the lower end of the temperature range. Fig. 10b depicts the light-off curve that is predicted with the GP after adding this one data point. It is observed that the trend in the low-conversion zone is now perfectly learned. Still, above 623 K the prediction does not change. In Fig. 10c, we illustrate the posterior prediction over the kinetic catalytic data. That is, the model is trained on the experimental data points and is able to model the trend without overfitting on the individual data points. Traditionally, researchers create power-law models or more detailed microkinetic models via numerous experiments to first calculate kinetic descriptors and then a posteriori simulate the effect of reaction conditions on the catalytic activity. Here, the model is capable of fitting experimental data accurately given a representative dataset and a minimal number of additional experiments.
4. Conclusion
In this study, we present a novel approach employing a human-in-the-loop workflow enhanced by active machine learning to evaluate the performance of Ni- and Co-based catalysts supported on Al2O3 for the thermo-catalytic conversion of CO2 into CH4. We assembled an experimental dataset comprising 48 catalytic activity tests conducted within a vast design space exceeding 50 million potential experiments. These tests were conducted utilizing an automated reactor system, ensuring systematic and controlled conditions throughout the experimentation process. The design space consisted out of variables that can be modified during the experimentation and/or during the catalyst synthesis, including the temperature, pressure, Ni and Co load, space velocity, calcination temperature, and reduction temperature. The compiled dataset was then used to train regression algorithms for predicting the CO2 conversion, methane selectivity, and methane space–time yield of new experiments. Three different regression algorithms were compared for the catalyst activity predictions: Gaussian processes, random forests, and extreme gradient boosting. It was found that Gaussian processes excelled in the interpolative range, while the extreme gradient boosting technique led to a more generalized model with the most accurate predictive performance for extrapolative tests. Feature importance analysis revealed that, next to temperature and Ni load, the calcination temperature also plays a crucial role for the activity of Ni–Co/Al2O3 catalysts in the methanation reaction. This finding was experimentally validated and it was seen that there is an optimal calcination temperature for Ni–Co/Al2O3 catalysts, lying between 673 and 723 K. Further increase of the calcination temperature is detrimental to the activity. Structurally, this was linked to the presence of oxide, aluminate and/or metallic species that were stable in the given calcination temperature. Our findings illustrate the efficacy of utilizing a modest database comprising only 48 catalytic tests to forecast a new set of experimental variables, resulting in a remarkable enhancement of methane space–time yield by nearly 50% compared to the highest value observed in the training set. Moreover, Gaussian processes exhibited exceptional accuracy in modeling the relationship between experimental variables and outcomes, enabling predictive kinetics provided the interpolation criterion is satisfied. Despite these advancements, interpreting black-box models remains a challenge. Nevertheless, the methodology outlined in this study, initially applied to the methanation reaction, can readily be adapted and transferred to address diverse chemical reactions with distinct design spaces.Data availability
The data supporting this article have been included as part of the ESI.† The entire source code is provided as open-source software under MIT license in the following repository: https://www.github.com/mrodobbe/gandalf-doe. All conclusions from the paper can be reproduced using the provided scripts. A demo notebook is available in the folder notebooks/demo.ipynb.Conflicts of interest
There are no conflicts of interest to declare.Acknowledgements
Y. K. and A. Z. acknowledge the financial support from EPFL and EMPA. The Centre Interdisciplinaire de Microscopie Electronique (CIME) is thanked for the access to the electron microscopes. M. D. acknowledges financial support from the Fund for Scientific Research Flanders (FWO-Vlaanderen) through doctoral fellowship grant 1S45522N. K. M. V. G. acknowledges funding from the European Research Council under the European Union's Horizon 2020 research and innovation programme/ERC grant agreement n° 818607.References
- R. Schlögl, Chemical Batteries with CO2, Angew. Chem., Int. Ed., 2022, 61(7), e202007397, DOI:10.1002/anie.202007397.
- A. Züttel, P. Mauron, S. Kato, E. Callini, M. Holzer and J. Huang, Storage of Renewable Energy by Reduction of CO2 with Hydrogen, Chimia, 2015, 69(5), 264, DOI:10.2533/chimia.2015.264.
- R. Mutschler, E. Moioli, W. Luo, N. Gallandat and A. Züttel, CO2 hydrogenation reaction over pristine Fe, Co, Ni, Cu and Al2O3 supported Ru: Comparison and determination of the activation energies, J. Catal., 2018, 366, 139–149, DOI:10.1016/j.jcat.2018.08.002.
- C. Vogt, et al., Understanding carbon dioxide activation and carbon–carbon coupling over nickel, Nat. Commun., 2019, 10(1), 5330, DOI:10.1038/s41467-019-12858-3.
- N. Gallandat, R. Mutschler, V. Vernay, H. Yang and A. Züttel, Experimental performance investigation of a 2 kW methanation reactor, Sustainable Energy Fuels, 2018, 2(5), 1101–1110, 10.1039/C8SE00073E.
- S. Rönsch, et al., Review on methanation – From fundamentals to current projects, Fuel, 2016, 166, 276–296, DOI:10.1016/j.fuel.2015.10.111.
- C. Bassano, P. Deiana, L. Lietti and C. G. Visconti, P2G movable modular plant operation on synthetic methane production from CO2 and hydrogen from renewables sources, Fuel, 2019, 253, 1071–1079, DOI:10.1016/j.fuel.2019.05.074.
- T. Chwoła, et al., Pilot plant initial results for the methanation process using CO2 from amine scrubbing at the Łaziska power plant in Poland, Fuel, 2020, 263, 116804, DOI:10.1016/j.fuel.2019.116804.
- B. Alrafei, I. Polaert, A. Ledoux and F. Azzolina-Jury, Remarkably stable and efficient Ni and Ni-Co catalysts for CO2 methanation, Catal. Today, 2020, 346, 23–33, DOI:10.1016/j.cattod.2019.03.026.
- W. Wang, S. Wang, X. Ma and J. Gong, Recent advances in catalytic hydrogenation of carbon dioxide, Chem. Soc. Rev., 2011, 40(7), 3703–3727, 10.1039/C1CS15008A.
- M. Cai, J. Wen, W. Chu, X. Cheng and Z. Li, Methanation of carbon dioxide on Ni/ZrO2-Al2O3 catalysts: Effects of ZrO2 promoter and preparation method of novel ZrO2-Al2O3 carrier, J. Nat. Gas Chem., 2011, 20(3), 318–324, DOI:10.1016/S1003-9953(10)60187-9.
- J. Yang Lim, J. McGregor, A. J. Sederman and J. S. Dennis, Kinetic studies of CO2 methanation over a Ni/γ-Al2O3 catalyst using a batch reactor, Chem. Eng. Sci., 2016, 141, 28–45, DOI:10.1016/j.ces.2015.10.026.
- W. Wei and G. Jinlong, Methanation of carbon dioxide: an overview, Front. Chem. Sci. Eng., 2011, 5(1), 2–10, DOI:10.1007/s11705-010-0528-3.
- R. Jalali, M. Rezaei, B. Nematollahi and M. Baghalha, Preparation of Ni/MeAl2O4-MgAl2O4 (Me=Fe, Co, Ni, Cu, Zn, Mg) nanocatalysts for the syngas production via combined dry reforming and partial oxidation of methane, Renewable Energy, 2020, 149, 1053–1067, DOI:10.1016/j.renene.2019.10.111.
- P. Shafiee, S. M. Alavi and M. Rezaei, Investigation of the effect of cobalt on the Ni–Al2O3 catalyst prepared by the mechanochemical method for CO2 methanation, Res. Chem. Intermed., 2022, 48(5), 1923–1938, DOI:10.1007/s11164-022-04700-1.
- V. R. Choudhary, A. M. Rajput, B. Prabhakar and A. S. Mamman, Partial oxidation of methane to CO and H2 over nickel and/or cobalt containing ZrO2, ThO2, UO2, TiO2 and SiO2 catalysts, Fuel, 1998, 77(15), 1803–1807, DOI:10.1016/S0016-2361(98)00072-6.
- T. Zhang and Q. Liu, Mesostructured cellular foam silica supported bimetallic LaNi1-xCoxO3 catalyst for CO2 methanation, Int. J. Hydrogen Energy, 2020, 45(7), 4417–4426, DOI:10.1016/j.ijhydene.2019.12.006.
- C. M. Friend and B. Xu, Heterogeneous Catalysis: A Central Science for a Sustainable Future, Acc. Chem. Res., 2017, 50(3), 517–521, DOI:10.1021/acs.accounts.6b00510.
- R. Wijngaarden, A. Kronberg, K. R. Westerterp and A. N. R. Bos, Industrial Catalysis: Optimizing Catalysts and Processes, Wiley, 2008, [Online], available: DOI:10.1021/ja985759d.
- W. H. Green, Moving from postdictive to predictive kinetics in reaction engineering, AIChE J., 2020, 66(11), e17059, DOI:10.1002/aic.17059.
- J. A. Onrubia-Calvo, et al., Kinetics, Model Discrimination, and Parameters Estimation of CO2 Methanation on Highly Active Ni/CeO2 Catalyst, Ind. Eng. Chem. Res., 2022, 61(29), 10419–10435, DOI:10.1021/acs.iecr.2c00164.
- J. R. Kitchin, Machine learning in catalysis, Nat. Catal., 2018, 1(4), 230–232, DOI:10.1038/s41929-018-0056-y.
- W. Yang, T. T. Fidelis and W.-H. Sun, Machine Learning in Catalysis, From Proposal to Practicing, ACS Omega, 2020, 5(1), 83–88, DOI:10.1021/acsomega.9b03673.
- T. Toyao, Z. Maeno, S. Takakusagi, T. Kamachi, I. Takigawa and K. Shimizu, Machine Learning for Catalysis Informatics: Recent Applications and Prospects, ACS Catal., 2020, 10(3), 2260–2297, DOI:10.1021/acscatal.9b04186.
- M. R. Dobbelaere, P. P. Plehiers, R. Van de Vijver, C. V. Stevens and K. M. Van Geem, Machine Learning in Chemical Engineering: Strengths, Weaknesses, Opportunities, and Threats, Engineering, 2021, 7(9), 1201–1211, DOI:10.1016/j.eng.2021.03.019.
- M. Quaglio, L. Roberts, M. S. Bin Jaapar, E. S. Fraga, V. Dua and F. Galvanin, An artificial neural network approach to recognise kinetic models from experimental data, Comput. Chem. Eng., 2020, 135, 106759, DOI:10.1016/j.compchemeng.2020.106759.
- B. Yılmaz, B. Oral and R. Yıldırım, Machine learning analysis of catalytic CO2 methanation, Int. J. Hydrogen Energy, 2023, 48(64), 24904–24914, DOI:10.1016/j.ijhydene.2022.12.197.
- P. S. F. Mendes, S. Siradze, L. Pirro and J. W. Thybaut, Open Data in Catalysis: From Today's Big Picture to the Future of Small Data, ChemCatChem, 2021, 13(3), 836–850, DOI:10.1002/cctc.202001132.
- J. A. Esterhuizen, B. R. Goldsmith and S. Linic, Interpretable machine learning for knowledge generation in heterogeneous catalysis, Nat. Catal., 2022, 5(3), 175–184, DOI:10.1038/s41929-022-00744-z.
- A. Lazaridou, et al., Recognizing the best catalyst for a reaction, Nat. Rev. Chem., 2023, 7(4), 287–295, DOI:10.1038/s41570-023-00470-5.
- D. W. Flaherty and A. Bhan, Improving the rigor and reproducibility of catalyst testing and evaluation in the laboratory, J. Catal., 2024, 431, 115408, DOI:10.1016/j.jcat.2024.115408.
- G. B. Marin, V. V. Galvita and G. S. Yablonsky, Kinetics of chemical processes: From molecular to industrial scale, J. Catal., 2021, 404, 745–759, DOI:10.1016/j.jcat.2021.09.014.
- X. Companyó and J. Burés, Distribution of Catalytic Species as an Indicator To Overcome Reproducibility Problems, J. Am. Chem. Soc., 2017, 139(25), 8432–8435, DOI:10.1021/jacs.7b05045.
- Y. Ureel, et al., Active Machine Learning for Chemical Engineers: A Bright Future Lies Ahead!, Engineering, 2023, 27, 23–30, DOI:10.1016/j.eng.2023.02.019.
- G. Tom, et al., Self-Driving Laboratories for Chemistry and Materials Science, Chem. Rev., 2024, 124(16), 9633–9732, DOI:10.1021/acs.chemrev.4c00055.
- A. Ramirez, et al., Accelerated exploration of heterogeneous CO2 hydrogenation catalysts by Bayesian-optimized high-throughput and automated experimentation, Chem Catal, 2024, 4(2), 100888, DOI:10.1016/j.checat.2023.100888.
- C. J. Taylor, et al., A Brief Introduction to Chemical Reaction Optimization, Chem. Rev., 2023, 123(6), 3089–3126, DOI:10.1021/acs.chemrev.2c00798.
- Y. Ureel, et al., Active learning-based exploration of the catalytic pyrolysis of plastic waste, Fuel, 2022, 328, 125340, DOI:10.1016/j.fuel.2022.125340.
- R. Guidotti, A. Monreale, S. Ruggieri, F. Turini, F. Giannotti and D. Pedreschi, A Survey of Methods for Explaining Black Box Models, ACM Comput. Surv., 2019, 51(5), 1–42, DOI:10.1145/3236009.
- J. W. Thybaut, J. Sun, L. Olivier, A. C. Van Veen, C. Mirodatos and G. B. Marin, Catalyst design based on microkinetic models: Oxidative coupling of methane, Catal. Today, 2011, 159(1), 29–36, DOI:10.1016/j.cattod.2010.09.002.
- M. Suvarna, T. P. Araújo and J. Pérez-Ramírez, A generalized machine learning framework to predict the space-time yield of methanol from thermocatalytic CO2 hydrogenation, Appl. Catal., B, 2022, 315, 121530, DOI:10.1016/j.apcatb.2022.121530.
- J. Roh, et al., Interpretable machine learning framework for catalyst performance prediction and validation with dry reforming of methane, Appl. Catal., B, 2024, 343, 123454, DOI:10.1016/j.apcatb.2023.123454.
- K. Vellayappan, et al., Impacts of catalyst and process parameters on Ni-catalyzed methane dry reforming via interpretable machine learning, Appl. Catal., B, 2023, 330, 122593, DOI:10.1016/j.apcatb.2023.122593.
- H. Liu, K. Liu, H. Zhu, W. Guo and Y. Li, Explainable machine-learning predictions for catalysts in CO2-assisted propane oxidative dehydrogenation, RSC Adv., 2024, 14(11), 7276–7282, 10.1039/D4RA00406J.
- P. S. F. Mendes, S. Siradze, L. Pirro and J. W. Thybaut, Extracting kinetic information in catalysis: an automated tool for the exploration of small data, React. Chem. Eng., 2022, 7(1), 142–155, 10.1039/D1RE00215E.
- F. Pedregosa, et al., Scikit-learn: Machine Learning in Python, J. Mach. Learn. Res., 2011, 12, 2825–2830 Search PubMed.
- T. Chen and T. He, Xgboost: extreme gradient boosting.
- GPy, GPy: A Gaussian process framework in python, 2012, [Online], available: https://github.com/SheffieldML/GPy.
- S. M. Lundberg and S.-I. Lee, A Unified Approach to Interpreting Model Predictions, in Advances in Neural Information Processing Systems, ed. I. Guyon, U. V. Luxburg, S. Bengio, H. Wallach, R. Fergus, S. Vishwanathan and R. Garnett, Curran Associates, Inc., 2017, [Online], available: https://proceedings.neurips.cc/paper_files/paper/2017/file/8a20a8621978632d76c43dfd28b67767-Paper.pdf Search PubMed.
- M. González-Castaño, B. Dorneanu and H. Arellano-García, The reverse water gas shift reaction: a process systems engineering perspective, React. Chem. Eng., 2021, 6(6), 954–976, 10.1039/D0RE00478B.
- R. De Maesschalck, D. Jouan-Rimbaud and D. L. Massart, The Mahalanobis distance, Chemom. Intell. Lab. Syst., 2000, 50(1), 1–18, DOI:10.1016/S0169-7439(99)00047-7.
- M. R. Dobbelaere, Y. Ureel, F. H. Vermeire, L. Tomme, C. V. Stevens and K. M. Van Geem, Machine Learning for Physicochemical Property Prediction of Complex Hydrocarbon Mixtures, Ind. Eng. Chem. Res., 2022, 61(24), 8581–8594, DOI:10.1021/acs.iecr.2c00442.
- S. P. Pyl, K. M. Van Geem, M.-F. Reyniers and G. B. Marin, Molecular reconstruction of complex hydrocarbon mixtures: An application of principal component analysis, AIChE J., 2010, 56(12), 3174–3188, DOI:10.1002/aic.12224.
- S. M. Lundberg, et al., From local explanations to global understanding with explainable AI for trees, Nat. Mach. Intell., 2020, 2(1), 56–67, DOI:10.1038/s42256-019-0138-9.
- L. S. Shapley, A value for n-person games, 1953 Search PubMed.
- K. Stangeland, D. Kalai, H. Li and Z. Yu, CO2 Methanation: The Effect of Catalysts and Reaction Conditions, Energy Procedia, 2017, 105, 2022–2027, DOI:10.1016/j.egypro.2017.03.577.
- P. Munnik, P. E. de Jongh and K. P. de Jong, Recent Developments in the Synthesis of Supported Catalysts, Chem. Rev., 2015, 115(14), 6687–6718, DOI:10.1021/cr500486u.
- S. Bona, P. Guillén, J. G. Alcalde, L. García and R. Bilbao, Toluene steam reforming using coprecipitated Ni/Al catalysts modified with lanthanum or cobalt, Chem. Eng. J., 2008, 137(3), 587–597, DOI:10.1016/j.cej.2007.05.022.
- T. K. Hari and Z. Yaakob, Production of diesel fuel by the hydrotreatment of jatropha oil derived fatty acid methyl esters over γ-Al2O3 and SiO2 supported NiCo bimetallic catalysts, React. Kinet., Mech. Catal., 2015, 116(1), 131–145, DOI:10.1007/s11144-015-0874-8.
- B. Vos, E. Poels and A. Bliek, Impact of Calcination Conditions on the Structure of Alumina-Supported Nickel Particles, J. Catal., 2001, 198(1), 77–88, DOI:10.1006/jcat.2000.3082.
- S. Y. Foo, C. K. Cheng, T.-H. Nguyen and A. A. Adesina, Syngas production from CH4 dry reforming over Co–Ni/Al2O3 catalyst: Coupled reaction-deactivation kinetic analysis and the effect of O2 co-feeding on H2:CO ratio, Int. J. Hydrogen Energy, 2012, 37(22), 17019–17026, DOI:10.1016/j.ijhydene.2012.08.136.
- C. P. Li, A. Proctor and D. M. Hercules, Curve Fitting Analysis of ESCA Ni 2p Spectra of Nickel-Oxygen Compounds and Ni/Al2O3 Catalysts, Appl. Spectrosc., 1984, 38(6), 880–886 CrossRef CAS.
- T. Huang, Q. Peng, W. Shi, J. Xu and Y. Fan, An anionic surfactant-assisted equilibrium adsorption method to prepare highly dispersed Fe-promoted Ni/Al2O3 catalysts for highly selective mercaptan removal, Appl. Catal., B, 2018, 230, 154–164, DOI:10.1016/j.apcatb.2018.02.053.
- C. Jiménez-González, et al., Structural characterisation of Ni/alumina reforming catalysts activated at high temperatures, Appl. Catal., A, 2013, 466, 9–20, DOI:10.1016/j.apcata.2013.06.017.
Footnote |
| † Electronic supplementary information (ESI) available. See DOI: https://doi.org/10.1039/d4cy00873a |
| This journal is © The Royal Society of Chemistry 2024 |